Quenching of OH (A 2Σ+, v′=0) by several collision partners between 200 and 344 K. Cross-section measurements and model comparisons
Dwayne E. Heard* and David A. Henderson
School of Chemistry, University of Leeds, Leeds, UK LS2 9JT. E-mail: dwayneh@chem.leeds.ac.uk
First published on UnassignedUnassigned22nd December 1999
Abstract
The cross-sections for the collisional quenching of OH(A 2Σ+, v′=0) by CO, CH4, H2 and Kr were determined between 200 and 344 K in a flash-photolysis system. In all cases cross-sections increased with decreasing temperature, consistent with attractive forces dominating the collision process. For CO, the cross-section increased from 30.0±2.3 Å2 at 344±1 K to 50.3±3.8 Å2 at 200±1 K. The corresponding values for the other collision partners are: 25.3±1.9 to 37.4±2.8 Å2 (CH4); 8.0±0.6 to 11.8±0.9 Å2 (H2) and 7.3±0.5 to 11.6±0.8 Å2 (Kr). Cross-sections were also determined at 344 K for N2, O2, CO2 and H2O collision partners, for which values had previously been measured in the range 204–294 K. For all collision partners, an empirical formula was used to describe the data over the range 200–2300 K in order to enable quenching corrections to be made during the detection of OH by laser-induced fluorescence in a variety of media. The temperature-dependent cross-sections were analysed using a Parmenter–Seaver well-depth correlation, and are compared with the predictions of a model based on the ‘harpooned ’ mechanism, together with a realistic interaction potential.
Introduction
Laser excitation of OH to the A 2Σ, v′=0 state at 308 nm, followed by detection of the ensuing fluorescence, is commonly used as a diagnostic tool for monitoring OH in a variety of media.1–6 The fluorescence lifetime of the excited state is ≈700 ns, and except at very low pressures, collisional relaxation back to the ground state competes strongly with fluorescence. For many applications, particularly in flames, plasmas and aerodynamic systems, the temperature, density and gas composition may vary enormously on short spatial scales, and a correction for the effects of quenching is required to relate spatially-resolved signal levels to relative OH concentrations.7 In addition, the determination of absolute OH concentration from observed signals requires knowledge of the fluorescence quantum yield.4 If a known source of OH is used to calibrate the signal, any change in the quenching environment between calibration and application must still be understood. The fluorescence quantum yield can be calculated if the cross-sections for quenching by all collision gases present are known at the temperature of the measurement. It is not feasible to determine quenching cross-sections at all temperatures of interest, and reliance must be placed on empirical relationships, which are often based on inadequate datasets.As well as being of fundamental interest,8,9 the development of a model to describe the mechanism of quenching of OH (A 2Σ+, v′=0) is desirable as a tool for the prediction of cross-sections. Quenching data for many collision partners are sparse or non-existent, particularly for atoms or other unstable species which may reach appreciable concentrations in flames, and which are likely to have large cross-sections.10 There have been several conceptual models considered in an attempt to correlate the observed quenching cross-sections with specific molecular parameters, in order that the mechanism of quenching might be understood and cross-sections predicted. The Parmenter–Seaver well-depth correlation demonstrates the role played by attractive forces,11,12 and the multipole attractive forces model11,13,14 is able to reproduce the observed temperature dependence, but does not contain a mechanism for quenching and cannot predict the species dependence of the cross-section. Ab initio potential energy surfaces do exist for the interaction of OH(X 2Πi) or OH(A 2Σ+) with several collision partners for selected configurations and separation distances.15,16 However, no dynamical calculations have been performed to predict cross-sections for quenching to allow a comparison with experiment. The mechanism of quenching may involve reaction, for example, in the case of H2:
| OH(A 2Σ+)+H2→H+H2O | (1) |
In a recent experiment by Anderson et al.,17 a significant yield of H atoms was observed following the break up of the OH(A 2Σ+)–H2 van der Waals cluster, proceeding via a non-adiabatic transition at a conical intersection that has been identified on the potential energy surface.16
The ‘harpooned’ mechanism, developed by Paul and co-workers,18,19 postulates that quenching occurs via an ion-pair intermediate:
| OH(A 2Σ+)+M→OH−(X1Σ+)+M+→OH(X2Πi)+M | (2) |
involving crossings with a surface associated with OH− and the positive ion of the collision partner. Once the collision partners are brought to a radius where electron transfer is energetically favourable, transfer occurs irreversibly. Although the ‘harpooned’ process provides a quenching mechanism, and is able to predict the relative efficiencies for various collision gases, it is calculated to have very little temperature dependence, in contrast to observations at lower temperatures. Paul has combined the harpooned mechanism with a realistic interaction potential for the formation of the collision complex,19 and the predicted cross-sections for quenching of OH(A 2Σ+) by O2 and CO2 partners agreed well with those measured at low temperature in this laboratory.20 A Lennard–Jones potential modified to include dipole moment effects was developed to describe quenching by water vapour, and the predicted cross-sections reproduced the experimental data over the range 211–2300 K.21 In both cases, account was taken of the rotational level dependence of the quenching cross-section.22 The harpooned model has also predicted quenching cross-sections for species such as O and HF, for which no experimental data are available.19
In this paper we report quenching cross-sections for eight collision partners over a range of low-temperatures, which are combined with previous data at higher temperatures to generate empirical formulae that are applicable over a wide temperature range. The experimentally determined cross-sections are analysed using a Parmenter–Seaver well-depth correlation. Using the dataset at 294 K, the correlation is able to predict the cross-sections at 200 K with reasonable accuracy, although with some exceptions. The data are also compared with the predictions of the ‘ harpooned’ model, which appears to work well for a wide range of collision partners and temperatures.
Experimental
OH was generated by excimer laser flash-photolysis of HNO3 at 248 nm, for which the quantum yield for OH production is 0.95±0.09.23,24 Nitric acid (Aldrich, 90%) was dehydrated by mixing with sulfuric acid (sp.gr. 1.84, Fisher Scientific) in a Pyrex bubbler held at constant temperature in a water bath. The vapour pressure of H2SO4 is negligible compared with that of HNO3. Helium at atmospheric pressure was passed through the solution via a sintered glass frit for at least 30 min prior to experiments. The flows of ca. 5% HNO3 in He (0–15 sccm), quenching gas (0–300 sccm) and He buffer gas (0–1500 sccm) were controlled by calibrated flow-controllers (Tylan FC-280) and mixed in a Pyrex manifold 50 cm (≈0.1 s flow time) from a fluorescence cell constructed from a six-sided-stainless-steel cross (Caburn MDC). The total pressure was maintained at 50 Torr (He) and monitored with a 0–100 Torr capacitance manometer (Tylan CDL-21). Operating at 10 Hz, the excimer photolysis laser (Lambda Physik MINex) generated 20 mJ, 10 ns pulses at 248 nm, and a 10 mm diameter beam was aligned in a collinear and counter propagating fashion to the probe laser beam through the cell. The OH concentration in the cell was estimated to be 2×1010 molecule cm−3 following photolysis of 5×1013 molecule cm−3 of HNO3.The probe laser and the detection of laser-induced fluorescence (LIF) from OH v′=0 have been described previously.20 Briefly, OH was excited from v″=0 to the A 2Σ+ (v′=0, N′=2, J′=2.5) state via the Q1(2) line at 307.995 nm, using a probe laser energy of <10 µJ pulse−1 in a 4 mm diameter beam. The resulting fluorescence decay was digitised at 10 ns resolution and averaged over 1000 laser shots. The delay between the lasers was maintained at 20 µs for these experiments, in order to eliminate completely any excimer laser-induced scatter or fluorescence, and the shot-to-shot fluctuations in the power of both lasers were monitored using photodiodes.
The fluorescence cell was surrounded by an insulated Perspex box, through which flowed propan-2-ol coolant (or a mixture with propan-1-ol) that was chilled by a temperature controlled refrigerated bath/recirculator (Neslab ULT-95). Temperatures between 204 and 300 K were achieved at the detection region using the chiller, as measured using a retractable thermocouple. The accuracy of the thermocouple was determined to be ±1 K using ice and steam baths. Fixed temperatures of 200 and 344 K were achieved using a propan-1-ol–dry ice mixture and heated water, respectively. At the lowest temperatures, HNO3 begins to condense in the cell, and an alternative discharge flow method was employed as a source of OH, using either the reaction H+NO2→OH+NO, as described previously,20 or a microwave discharge of water vapour.
Gases used: He (BOC, 99.999%), CO2 (BOC, 99.995%), O2 (BOC, 99.9995%), N2 (BOC, 99.9995%), H2 (BOC, 99.995%), CO (Messer, 99.997%), CH4 (BOC, 99.995%), Kr (MG, 99.998%).
Results
A single exponential decay was fitted to the fluorescence signals, from which the decay constant was obtained. The cross-section for quenching of OH(A 2Σ+) by He at 300 K is <0.002 Å2,25 and any quenching by the 50 Torr of He buffer gas is negligible. The rate constants for rotational energy transfer (RET) of individual levels within A 2Σ+, v′=0 by He26 are such that equilibration should be complete within 10 ns of the probe laser pulse. The early part of the decay was not included in the fitting process to avoid any uncertainties introduced by probe laser scattered light or incomplete RET. Translational and rotational relaxation of OH generated by HNO3 photolysis will be complete following the 20 µs delay prior to the probe laser pulse. Vibrational energy transfer is rather inefficient for collisions of OH(X2Πi), but any OH present in v″>0 after 20 µs will not affect the determination of quenching cross-sections. The decay constants were determined at a variety of concentrations, [i], of the collision partner from which the rate constant for quenching, kQ(T), was determined using the expression:| τ−1=τ0−1+kQ(T)[i] | (3) |
where τ−1 is the decay constant, and τo−1 is the decay constant at [i]=0, being the sum of the Einstein coefficient for spontaneous emission and the quenching rate of OH(A 2Σ+) by HNO3 and He. The pressure of HNO3 was kept constant for a given temperature and collision partner, and values of kQ(T) were obtained from the linear-least-squares gradient of τ−1 plotted against [i]. Table 1 lists the measured quenching rate constants, kQ(T), and the thermally averaged cross sections, σQ(T), for the collision gases CO, CH4, H2 and Kr in the temperature range 200–344 K. Each value of kQ(T) was determined from measurements of τ−1 at 18 pressures of collision gas, and σQ(T) was obtained by dividing kQ(T) by the average thermal collision velocity, given by 〈v〉=(8RT/πμ)1/2, where μ is the reduced mass of the collision. The statistical error (1σ) in the determination of the decay constants was very small, and the reported error in kQ(T) of 7.6% (6.6% for Kr) is due mainly to errors in the determination of the collision gas pressure. The cross-sections increase with decreasing temperature for all the collision partners studied. The quenching efficiency was found to be CO>CH4>H2≈Kr, with an increase of up to ≈70% between 344 and 200 K. Kenner et al.27 report σQ=41.3±2 Å2 (CO), 29.5±0.5 Å2 (CH4) and 9.2±0.5 Å2 (H2) at 300 K, and Wysong et al.28 report σQ=8.27±0.6 Å2 (Kr) at 300 K, in good agreement with the present results. Copeland et al.22 measured the functional form of the rotational dependence of kQ for CO and CH4 at 294 K, from which thermally averaged cross-sections were derived of 44±3 and 31.5±1.5 Å2, respectively, slightly higher than the present results. The only previous low temperature data for these collision partners are reported for H2 by Copeland and Crosley29 at 238 K (12.7±0.5 Å2), 278 K (10.9±0.4 Å2) and 304 K (9.2±0.4 Å2), which lie within or just outside quoted error limits.
| kQ/10−10 cm3 molecule−1 s−1 | σQ/Å2 | |||||||
|---|---|---|---|---|---|---|---|---|
| T±1 K | CO | CH4 | H2 | Kr | CO | CH4 | H2 | Kr |
| 344 | 2.49±0.19 | 2.38±0.18 | 1.60±0.12 | 0.53±0.04 | 30.0±2.3 | 25.3±1.9 | 8.0±0.6 | 7.3±0.5 |
| 297 | 0.57±0.04 | 8.5±0.6 | ||||||
| 294 | 2.99±0.23 | 2.51±0.19 | 1.62±0.12 | 39.0±3.0 | 28.8±2.2 | 8.7±0.7 | ||
| 283 | 3.05±0.23 | 2.63±0.20 | 1.73±0.13 | 40.5±3.1 | 30.9±2.4 | 9.5±0.7 | ||
| 273 | 3.10±0.24 | 2.61±0.20 | 1.72±0.13 | 42.0±3.2 | 31.2±2.4 | 9.6±0.7 | ||
| 263 | 3.10±0.24 | 2.77±0.21 | 1.79±0.14 | 42.7±3.2 | 33.7±2.6 | 10.2±0.8 | ||
| 253 | 3.28±0.25 | 2.69±0.20 | 1.80±0.14 | 46.1±3.5 | 33.4±2.5 | 10.4±0.8 | ||
| 243 | 3.01±0.23 | 2.82±0.21 | 1.84±0.14 | 43.2±3.3 | 35.7±2.7 | 10.9±0.8 | ||
| 233 | 2.92±0.22 | 2.77±0.21 | 1.80±0.14 | 42.8±3.3 | 35.9±2.7 | 10.9±0.8 | ||
| 223 | 3.08±0.23 | 1.77±0.13 | 46.0±3.5 | 10.9±0.8 | ||||
| 200 | 3.18±0.24 | 2.68±0.20 | 1.81±0.14 | 0.63±0.04 | 50.3±3.8 | 37.4±2.8 | 11.8±0.9 | 11.6±0.8 |
The quenching cross-sections at 344 K were also determined for the atmospherically important collision partners, N2, O2, CO2 and H2O. Values in the temperature range 204–294 K had already been determined in this laboratory using a discharge flow method at a total pressure of 1.5 Torr in He.20,21 The values obtained at 344 K are σQ=3.4±0.3 Å2 (N2), 18.0±1.0 Å2 (O2), 45.3±3.0 Å2 (CO2) and 55.0±5.8 Å2 (H2O), and continue the trend of decreasing cross-section with increasing temperature. As a consistency check, σQ for N2 was determined at 294 K using both flash-photolysis (50 Torr He) and discharge flow (1.5 Torr He) as the source of OH, with the values agreeing within 6%.
Discussion and model calculations
Cross-sections for the quenching of OH(A 2Σ+, ν′=0) by CO, CH4 and H2 have been determined at ca. 1200 K in laser-heated cells,11,30 and at ca. 2000 K for CO and Kr in a shock tube.31 The present work extends the database to lower temperatures, and when combined with data at higher temperatures, enables empirical relationships to be derived which are accurate over a very wide temperature range. An expression of the form: | (4) |
where σQ(T) and A have units of Å2, and T is in K, was fitted to the combined dataset for each collision partner, and Table 2 lists the coefficients obtained. Values are also given for N2, O2, CO2 and H2O, making use of the additional data point at 344 K. Fig. 1 shows experimental data and the empirical fit for CH4, a gas commonly encountered in combustion systems. Eqn. (4) and Table 2 will enable the calculation of cross-sections in order to correct OH LIF signals for the effects of quenching.
| Collision partner | A/Å2 | B | C |
|---|---|---|---|
| CO | 16.3 | 4.55 | 1.19 |
| H2 | 5.47 | 4.15 | 1.77 |
| CH4 | 12.58 | 5.07 | 1.31 |
| Kr | 1.13 | 20.07 | 1.15 |
| H2O | 25.59 | 13.73 | 1.9 |
| N2 | 0.59 | 36.78 | 1.84 |
| O2 | 9.49 | 3.83 | 1.37 |
| CO2 | 11.83 | 10.99 | 1.02 |
![Temperature-dependent cross-sections for quenching of OH (A 2Σ+, v′=0) by CH4, together with an empirical fit [eqn. (4)] using the coefficients given in Table 2.](/image/article/2000/CP/a908221b/a908221b-f1.gif) | ||
| Fig. 1 Temperature-dependent cross-sections for quenching of OH (A 2Σ+, v′=0) by CH4, together with an empirical fit [eqn. (4)] using the coefficients given in Table 2. | ||
Quenching cross-sections do not correlate well with parameters such as polarisability and molecular radius, which are indicative of dispersion forces dominating the interaction of OH(A 2Σ+) and the collision partner. The well-depth model proposes that attractive forces dominate the quenching process, and that there is a correlation between σQ and the depth of the potential well between OH(A 2Σ+) and the collision partner. Lin et al.12 proposed the following relationship, known as the Parmenter–Seaver correlation:
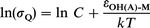 | (5) |
where C is a constant, and εOH(A)-M is the (generally unknown) Lennard-Jones potential well-depth between OH(A) and M, which is approximated by the geometric average of the well-depths of each species: εOH(A)-M=(εOH(A)-OH(A)·εM-M).1/2 If β is defined by β=(εOH(A)-OH(A)/kT2)1/2, eqn. (5) becomes:
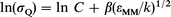 | (6) |
In previous studies, such a correlation has been used to interpret the cross-sections for electronic quenching by different collision partners,11,32–33 and also for collision-induced near-resonant electronic energy transfer in excited states, for example, of SiCl.34Fig. 2(a) shows ln(σQ), measured at 294 K, plotted against (εMM/k)1/2 for all the collision partners studied in this work, with values of εMM taken from Lin et al.12 A reasonable correlation is observed, and a linear-least-squares fit to the data yielded ln C=0.98 and β=0.17, from which (εOH(A)-OH(A)/k)1/2=50.3. The value of β was then calculated for 200 K, and together with ln C used to calculate ln σQ at 200 K for each collision partner. Fig. 2(b) compares the calculated values of ln σQ together with those measured in this work at 200 K. The model is predicting correctly the inverse temperature dependence, and good absolute agreement is found with the exception of N2 and Kr. Using cross-sections obtained at 1200 K by other groups, a correlation is also observed, but the model consistently under-predicts observations by a factor of ≈2.5, with the exception of Kr and N2, for which the model over-predicts the cross-section by a factor of ≈4 and ≈7, respectively. The model appears to be more applicable at low temperatures, where collision energies are low and attractive forces play a more dominant role. The OH–H2,16 OH–N235 and OH–Kr36 van der Waals complexes have been detected by LIF in a jet expansion, and binding energies for OH A 2Σ+ and these partners determined spectroscopically, yielding 631 (v′=0), 1372 (v′=0) and 1131 cm−1 (v′=1), respectively. In addition, ab initio studies16 report the calculated well-depths for the minimum energy configuration to be 2900 cm−1 for H2 (T-shaped O–H···H2 configuration) and 3770 cm−1 for N2 (linear O–H···N≡N configuration), although no value for Kr has been reported. It is interesting to compare the spectroscopic binding energies and ab initio well-depths with the values of εOH(A)-M obtained from the Parmenter–Seaver correlation, which are 216, 330 and 452 cm−1 for H2, N2 and Kr, respectively. For H2, the values of these parameters are significantly lower than for N2 or Kr. It is difficult to make a direct comparison of the ab initio and Parmenter–Seaver well-depths, as the former correspond to minimum energy configurations (the potential is highly anisotropic16), whereas the latter are derived from Lennard–Jones potentials which have no angular dependence.12 In addition, it is difficult to assess the accuracy of the combining rule εOH(A)-M=(εOH(A)-OH(A) ·εM-M)1/2, which must be considered approximate. However, these results demonstrate that attractive forces will influence the formation of the collision complex, although other factors will control the probability of quenching. The Parmenter–Seaver correlation is founded on the principle that a common mechanism should apply to all collision partners, but as mentioned in the Introduction, for some collision partners quenching of OH(A 2Σ+) may occur via a reactive mechanism. For H2, N2, O2, CO and CH4 collision partners there exist thermodynamically allowed channels for reactive removal, whereas for Kr, CO2 and H2O none is possible. However, the data given in Fig. 2 do not indicate any obvious link between the degree of correlation and the ability to quench OH(A 2Σ+) via a reactive channel, which is discussed below in more detail for H2.
 | ||
| Fig. 2 (a) Parmenter–Seaver well-depth correlation at 294 K, together with a linear least-squares fit of eqn. (6), which yielded β=0.17 and hence (εOH(A)-OH(A)/k)1/2=50.3. (b) The corresponding correlation at 200 K, with the dotted line indicating the calculated value of ln(σQ) from eqn. (6), and using the value of β determined at 294 K. | ||
The multipole forces model13 treats the long range part of the interaction potential as the sum of dipole–dipole, dipole–quadrupole, dipole-induced–dipole and dispersion forces, together with a repulsive centrifugal barrier. For each collision energy there exists an impact parameter, bo, for which the barrier to formation of the collision complex is equal to the collision energy, and quenching proceeds for all impact parameters less than bo. The cross-section for complex formation is thus given by σ(E)=πb02. A thermal average over σ(E) gives the cross-section at a particular temperature. In order to determine the cross-section for quenching, the probability, PM, that quenching will occur during the lifetime of the complex must be known for each collision partner. A weakness of this model is that PM is not known, and so the model is not able to predict the magnitude and species dependence of quenching cross-sections. When modified to incorporate the rotational level dependence for OH quenching, this collision complex model is able to reproduce the observed temperature dependence in a reasonable fashion, particularly at low temperatures.20
The harpooned model provides a mechanism for the quenching process, and offers a means to calculate PM for different collision partners, and is described in detail by Paul.19 When combined with a suitable potential for the bringing together of OH(A 2Σ+) and a collision partner, this model successfully reproduced the temperature variation of quenching cross-sections for a large number of species, including O2,20 CO220 and H2O,21 that were measured in this laboratory at low temperature. Paul et al.37 have provided an easily evaluated functional form to calculate the cross-section for a given collision partner and temperature, which is given by:
 | (7) |
where Tr=300 K, γ(a, x) is the incomplete gamma function, and the coefficients c0, c1, c2 and α were obtained by fitting to the result of the full harpooned calculation.37PA is a freely adjustable parameter that was set to match the calculation to the experimental data at a particular temperature. Fig. 3 shows a comparison of the prediction of eqn. (7) together with experimental data for CO, CH4, H2 and Kr, obtained at low temperatures in this work, and data at higher temperatures taken from the literature. The temperature dependence is in good agreement for all collision partners, and provides further support for the usefulness of this model for the prediction of quenching rate constants.
 | ||
| Fig. 3 Temperature-dependent cross-sections for quenching of OH(A 2Σ+, v′=0), together with the predictions of the harpooned model, eqn. (7), for (a) CO, (b) CH4, (c) H2 and (d) Kr. | ||
Although useful for predicting the temperature dependence of σQ, and giving some information on the species dependence, the conceptual models offer little information on the detailed dynamics of the quenching process. Insights into this have been obtained from the study of weakly bound complexes of OH(A 2Σ+, v′=0). For example, Anderson et al.17 demonstrated that for H2, a significant fraction of the deactivating collisions might proceed by the reactive pathway generating H atoms [eqn. (1)], as well as by a non-reactive quenching mechanism to yield OH(X2Πi), although the yield of each channel was not determined. Ab initio calculations of the potential energy surface for H2 with OH(X2Πi) and OH(A 2Σ+) indicate the presence of a conical intersection between the ground and electronically excited adiabatic surfaces at specific orientations.16 The excited state potential has a large well-depth of ≈2900 cm−1 in the T-shaped O–H···H2 minimum configuration, although it is the T-shaped H–O···H2 configuration that is calculated to have a conical intersection with the ground-state OH(X 2Πi)+H2 potential. The translational energy distribution of the H atom products was found to be bimodal, and was postulated to originate from two different dynamical pathways through the conical intersection that converts OH(A 2Σ+)+H2 into H+H2O.17 One pathway may involve direct passage through the conical intersection via a non-adiabatic transition, whereas in the other pathway the collision partners miss the conical intersection on the first approach, and are trapped in the OH(A 2Σ+)–H2 potential well, permitting energy redistribution prior to eventual passage through the conical intersection. Ab initio calculations have also identified a conical intersection between the ground and excited potentials of OH interacting with N2via a collinear H–···ON≡N configuration,16 suggesting a pathway by which OH A 2Σ+ can be quenched by N2, although no reactive channels (→H+N2O or NH+NO) were identified in the ab initio calculations, despite being energetically accessible.
Under thermal conditions, when collisions sample all orientations of partners, rather than from the restricted geometry of the complex, it would be interesting (but likely very difficult) to probe the H atoms products of quenching. For all collision partners, it would also be interesting to attempt to detect the vibrationally excited levels of the OH(X2Πi) state that are formed following quenching, through LIF detection via the A 2Σ+–X 2Πi or B2Σ+–X2Πi transitions. Such an experiment would probe whether the final vibrational state distribution is determined by an energy gap (or other scaling) law or Franck–Condon dependence,8,9 and would further elucidate the quenching mechanism. Finally, with the advent of high quality ab initio surfaces for the interaction of collision partners with OH, both in its ground and excited states, it would be instructive to perform dynamical calculations, in order to predict the total cross-sections for quenching, and also the internal energy distributions within the inelastically or reactively scattered products. Comparison of the former with experiment would provide a meaningful test of the accuracy of the ab initio surfaces.
Conclusion
For CO, CH4, H2 and Kr, cross-sections for quenching of OH(A 2Σ+, v′=0) were measured in the range 200–344 K, and found to increase with decreasing temperature, continuing the trend observed at higher temperatures. The results are in good agreement with previous determinations, and extend the range to lower temperatures. Empirical relationships were derived using measurements in the range 200–2300 K, and will prove useful in the modeling of the effects of quenching of LIF signals in a variety of environments. A good correlation was observed between the quenching cross-section and the Lennard-Jones well-depth between OH(A 2Σ+) and the collision partner. Using the correlation at 294 K, quenching cross-sections were calculated as a function of the well-depth for other temperatures, and compared with experiment. At 200 K, the predictions were in good agreement with experiment, demonstrating the important role played by attractive forces. The harpooned model, developed by Paul and co-workers,18,19 provides a mechanism for quenching, and when combined with a realistic potential for the approach of OH and the collision partner, was able to reproduce the temperature dependence of the quenching cross-sections for CO, CH4, H2 and Kr.Acknowledgements
D.E.H. is grateful to the Royal Society for the award of a University Research Fellowship, and D.A.H. is grateful to the EPSRC for the award of a Research Studentship. The authors thank the reviewers for useful comments.References
- K. Kohse-Höinghaus, Prog. Energy Combust. Sci., 1994, 20, 203 CrossRef.
- K. Kohse-Hoinghaus, J. B. Jeffries, R. A. Copeland, G. P. Smith and D. R. Crosley, Twenty-Second Symposium (International) on Combustion, The Combustion Institute, Pittsburgh, PA, 1988, p. 1857. Search PubMed.
- D. R. Crosley, in Current Problems and Progress in Atmospheric Chemistry, ed. J. R. Barker, World Scientific Publishing, Singapore, 1995, p. 1000. Search PubMed.
- D. E. Heard, J. B. Jeffries, G. P. Smith and D. R. Crosley, Combust. Flame, 1992, 88, 137 CrossRef CAS.
- D. J. Creasey, P. Halford-Maw, D. E. Heard, M. J. Pilling and B. J. Whitaker, J. Chem. Soc., Faraday Trans., 1997, 93, 2907 RSC.
- D. J. Creasey, D. E. Heard, M. J. Pilling, B. J. Whitaker, M. Berzins and R. Fairlie, Appl. Phys., 1997, B65, 375 Search PubMed.
- M. Tamura, P. A. Berg, J. E. Harrington, J. Luque, J. B. Jeffries, G. P. Smith and D. R. Crosley, Combust. Flame, 1998, 114, 502 CrossRef CAS.
- K. G. McKendrick, J. Chem. Soc., Faraday Trans., 1998, 94, 1921 RSC.
- P. J. Dagdigian, Annu. Rev. Phys. Chem., 1997, 48, 95 CrossRef CAS.
- J. Bittner, K. Kohse-Hoinghaus, U. Meier and T. Just, Chem. Phys. Lett., 1988, 143, 571 CrossRef CAS.
- P. W. Fairchild, G. P. Smith and D. R. Crosley, J. Chem. Phys., 1983, 79, 1795 CrossRef CAS.
- H.-M. Lin, M. Seaver, K. Y. Tang, A. E. W. Knight and C. S. Parmenter, J. Chem. Phys., 1979, 70, 5442 CrossRef CAS.
- D. L. Holtermann, E. K. C. Lee and R. Nanes, J. Chem. Phys., 1982, 77, 5327 CrossRef CAS.
- N. L. Garland and D. R. Crosley, Twenty-First Symposium (International) on Combustion, The Combustion Institute, Pittsburgh, PA, 1986, p. 1693. Search PubMed.
- S. M. Miller, D. C. Clary, A. Kliesch and H. J. Werner, Mol. Phys., 1994, 83, 405 CAS.
- M. I. Lester, R. A. Loomis, B. L. Schwartz and S. P. Walch, J. Phys. Chem. A, 1997, 101, 9195 CrossRef CAS.
- D. T. Anderson, M. W. Todd and M. I. Lester, J. Chem. Phys., 1999, 110, 11117 CrossRef CAS.
- P. H. Paul, J. A. Gray, J. L. Durant and J. W. Thoman, Appl. Phys. B, 1993, 57, 249.
- P. H. Paul, J. Quant. Spectrosc. Radiat. Transfer, 1994, 51, 511 CrossRef CAS.
- A. E. Bailey, D. E. Heard, P. H. Paul and M. J. Pilling, J. Chem. Soc., Faraday Trans., 1997, 92, 2915 RSC.
- A. E. Bailey, D. E. Heard, D. A. Henderson and P. H. Paul, Chem. Phys. Lett., 1999, 302, 132 CrossRef CAS.
- R. A. Copeland, M. J. Dyer and D. R. Crosley, J. Chem. Phys., 1985, 82, 4022 CrossRef CAS.
- A. A. Turnipseed, G. L. Vaghjiani, J. E. Thompson and A. R. Ravishankara, J. Chem. Phys., 1992, 96, 5887 CrossRef CAS.
- A. Schiffman, D. D. Nelson and D. J. Nesbitt, J. Chem. Phys., 1993, 98, 6935 CrossRef CAS.
- G. L. Vaghjiani and A. R. Ravishankara, J. Chem. Phys., 1987, 87, 7050 CrossRef CAS.
- A. Jörg, U. Meier and K. K-Höinghaus, J. Chem. Phys., 1990, 93, 6453 CrossRef.
- R. D. Kenner, F. P. Capetanakis and F. Stuhl, J. Phys. Chem., 1990, 94, 2441 CrossRef CAS.
- I. J. Wysong, J. B. Jeffries and D. R. Crosley, J. Chem. Phys., 1990, 92, 5218 CrossRef CAS.
- R. A. Copeland and D. R. Crosley, J. Chem. Phys., 1986, 84, 3099 CrossRef CAS.
- G. P. Smith and D. R. Crosley, J. Chem. Phys., 1986, 85, 3896 CrossRef CAS.
- P. H. Paul, J. L. Durant, Jr., J. A. Gray and M. R. Furlanetto, J. Chem. Phys., 1995, 102, 8378 CrossRef CAS.
- D. R. Crosley, J. Phys. Chem., 1989, 93, 6273 CrossRef CAS.
- R. D. Kenner, S. Pfannenberg, P. Heinrich and F. Stuhl, J. Chem. Phys., 1991, 95, 6585 CAS.
- S. Singleton and K. G. McKendrick, J. Phys. Chem., 1993, 97, 1389 CrossRef CAS.
- R. L. Schwartz, L. C. Giancarlo, R. A. Loomis, R. T. Bonn and M. I. Lester, J. Chem. Phys., 1996, 105, 10224 CrossRef CAS.
- G. W. Lemire and R. C. Sausa, J. Phys. Chem., 1992, 96, 4821 CrossRef CAS.
- P. H. Paul, C. D. Carter, J. A. Gray, J. L. Durant and M. R. Furlanetto, Report No. SAND 94-8244, Sandia National Laboratories, 1994. Search PubMed.
| This journal is © the Owner Societies 2000 |
