The role of the electrostatic potential, electric field and electric field gradient on the acidity of AFI and CHA zeotypes
German Sastrea, Dewi W. Lewisb and Avelino Cormaa
aInstituto de Tecnologia Quimica U.P.V.-C.S.I.C., Universidad Politecnica de Valencia, Avenida Los Naranjos s/n, 46022, Valencia, Spain
bCentre for Theoretical & Computational Chemistry, Department of Chemistry, University College London, 20 Gordon St., London, UK WCIH OAJ
First published on UnassignedUnassigned22nd December 1999
Abstract
We consider the role of short- and long-range interactions in determining the acidity of microporous solids. Within the context of an interatomic forcefield approach and a correct treatment of long-range electrostatics we demonstrate the role of the electrostatic potential, electric field and electric field gradient in determining the vibrational frequency of a Brønsted acid centre. We demonstrate the applicability of these concepts for AlPO4-5, AlPO4-34, SSZ-24 and SSZ-13, in whose unit cells a single Brønsted acid site was introduced in the four different oxygens. Furthermore, we show, by using the energy required to elongate the OH bond—essentially the first stage of proton transfer—as a measure of acidity, how the vibrational frequency is related to the acid strength.
1. Introduction
The unique structure of crystalline microporous solids, such as zeolites, gives rise to a number of characteristic physical properties which have been exploited in such fields as catalysis, separation science and in ion exchange applications. Of particular note is the ability of such materials to be prepared as solid acids, which coupled with the molecular dimensions of the porous structure, has led to applications as highly (size and shape) selective catalysts. Over the past 30 years, much research has been focused on understanding the influence of the microporous structure, not only on the intrinsic physical properties of the acid sites present, but also on the sorbed species. In particular, the role of the electric field has often been noted as important in assessing the physical properties of the materials.1A number of experimental observations in catalysis have been explained, at least in part, in terms of the electric fields created by a zeolitic lattice: the influence of the electric fields in the formation of NO+ cations from adsorbed NO,2 the stabilisation of positively charged species such as templates,3,4 adsorbates,5,6 and transition states,7,8 changes in selectivity in cracking of alkanes due to the effect of electric field gradients,9,10 changes in the energy of the molecular orbitals of adsorbed molecules due to electric fields which change their reactivity with respect to the gas phase behaviour;11–14 changes in protonation energies of organic compounds with zeolites of different Si/Al ratio as a result of electrostatic effects;15 changes in OH stretching frequencies;16,17 and the influence of electric fields on the adsorption energy of sorbates.18 Here, we will consider further the role of the electric field in determining the acidity of microporous solids. Since we will be discussing both zeolites and the analogous microporous aluminophosphates, we shall refer to these materials as zeotypes for the remainder of our discussions.
From an intuitive standpoint, it is clear that the charge distribution of a molecule sorbed within the pores or channels of a microporous solid will be modified so as to minimise the interaction energy with the electric field of the zeotype lattice. To be more precise, it is the total potential energy which tends to reach a minimum, and here consideration needs to be made of both ionic and covalent interactions. The distinction between covalent and ionic interactions is somewhat arbitrary as it requires a determination of atomic charge, a subject of considerable discussion in quantum chemistry for the past forty years.19 This arbitrary distinction between ionic and covalent arises from the fact that it is not trivial to split the delocalised electronic cloud into the individual atoms.20 Nevertheless, the differentiation between ionic and covalent interactions provides an intuitive and approximate understanding of their contribution to chemical bonding, which in turn can be successfully used to explain many aspects of chemical structure and reactivity.21,22
Whilst quantum mechanical methods can therefore, provide a detailed description of the electron distribution and hence the concomitant physical properties, these methods are often computationally unfeasible. We do however, note a growing number of high quality studies. For example, a number of first principles calculations have been reported recently using periodic boundary conditions to study Brønsted acidity and proton siting in zeotypes, particularly for the chabasite structure.23–28 However, determination of the electric field and its influence on acidity has yet to be reported. Although first principles methodologies are clearly a way forward given that computing power will continue to improve, many calculations remain unfeasible. As an alternative, many studies have been performed using interatomic potential methods. Interactions between atoms are described using appropriate interaction functions and although the electronic contributions are implicitly included in such potentials, they are not considered explicitly. However, there are a number of shortcoming of using atomistic simulations, particularly the need to use fixed atomic charges and difficulties in developing formalisms which allow formation and breaking of bonds, which are, in principle, obstacles to study reactivity. Nevertheless, many other aspects, particularly structure, can be successfully treated. Indeed, it is not only static properties that have been determined with this methodology29,30 but also other properties such as Brønsted acidity,31–33 vibrational spectra34 and the dynamics of sorbed species.35–41 One of the major concerns in such applications is the quality of the forcefields employed and their ability to reproduce experimental properties; much as are concerns over basis set quality and level of approximation used in quantum chemical treatments. Consequently, a great deal of effort has been put into the parameterisation of potentials for microporous materials over the last fifteen years, resulting in, amongst other, forcefields for all silica zeolites,42–45 aluminosilicates,46–50 aluminophospates,51 and SAPOs.52 Indeed, with the development of the latter forcefield we possess a self-consistent set of parameters which allow the simulation of acidic microporous solids from the purely siliceous, via aluminosilicates and SAPOs to the pure aluminophosphate structures.46,47 Such atomistic simulations can be considered suitable for the study of electric fields in zeotypes since this field is of infinite range and zeolite crystals can be treated as infinite periodic systems at modest computational expense.53 Furthermore, forcefield calculations remain the only computationally feasible way of studying a number of properties such as structure characterisation, vibrational spectra and Brønsted acidity, particularly if comparisons are to be made between different sites and structures.
Brønsted acidity can be characterised by the proton affinity of the acid site, the energy required to bring the proton from infinity to the reference compound at its equilibrium geometry. Although the proton affinity provides a well defined proton transfer process, it is somewhat unrealistic for microporous materials where the crystallinc lattice also acts as a solid solvent of the base molecule,54 thus modifying its intrinsic basicity. In spite of this, the intrinsic acidity allows direct comparison between the acidity of the different centres in the same and different structures. Here, we will determine relative acid strength as the energy required to elongate the OH bond a given distance away from its equilibrium position. It is clear that this represents only a fraction of the proton affinity, but using an equal degree of elongation in all the cases will allow a comparison between the different acid centres. This scheme resembles that of relating acidity to OH stretching frequencies, where the frequencies arise from differential displacements of the proton along the OH bond. Whilst the relative position of the vibrational frequency of the acid site is often cited as being indicative of acidity, it is clearly an approximation. However, it does provide a convenient and intuitive indicator of acidity.
Our approach also allows us to calculate the electric field created by the periodic structure as well as the different contributions to the energy required to elongate the O–H bond and from there, the role of the electric field on Brønsted acidity. Initially our study will only focus on two structural types, AFI and CHA,55 with only one Brønsted acid site per unit cell. Further studies will extend this approach to more structural zeotypes and other chemical substitutions.
2. Theoretical background
Acid strength depends in essence on the electrostatic stability of the species, the electron distribution and their geometry relaxation. Although polarisation effects are included for lattice oxygen in our studies, through the use of a shell model, we do not include polarisation of the acid site—although one forcefield does include a degree of polarisation on the oxygen of the acid site. Thus each acid site has the same charge distribution regardless of site and zeotype structure. We do however note, that calculations performed using the semi-empirical EEM (electronegativity equalisation method)56,57 and some of its extensions58,59 show little variation in the OH charge distributions among the different zeotypes. Furthermore, first principles calculations report similar OH charge distributions for the isostructural SAPO-34 and aluminosilicate chabasite in spite of the different chemical composition.23–25 These electronic structure calculations suggest therefore, that the distribution of charge within the acid sites is determined by local rather than long-range phenomena. Note how in both SAPO-34 and chabasite the atomic nature of the acid sites are the same to 2nd neighbour, i.e. –O3Si(OH)AlO3–.Considering further the approximation of a fixed charge model, it is clear that the quality of the forcefield used is critical in ensuring the reliability of the simulations. We will therefore consider two different forcefields in this study. First, we consider an empirical forcefield52 already employed and discussed in previous studies.17,31–33,60 We also employ a forcefield parameterised from DFT results.61 Both sets of potentials have been specifically parameterised for the study of microporous materials and have been found to accurately reproduce experimental cell parameters, bond distances and angles, and elastic properties at an accurate level.29,30,62 However, we do note that neither forcefield have been derived with any particular attention to the variability noted in zeolite acidity. The O–H potentials in the empirical forcefield were determined originally for NaOH, and a number of acidic clusters were considered in the derivation of the DFT-derived forcefield. Thus, our comparison will also focus on the generality of each forcefield in reproducing trends in acidity across the zeotypes considered.
The vibrational frequency of the acid site, ν(OH) has often been considered as a simple measure of acidity in zeotypes, and from a simple approach (see Appendix 1) the frequency can be related to the total energy by:
 | (1) |
where ‘μ’ is the reduced mass, ‘U’ is the potential energy, ‘r’ is the OH distance, and the subindex ‘0 ’ refers to the equilibrium position. Although this equation strictly applies only to the case of an isolated OH group (i.e. an O–H group in vacuo), it can be considered a reasonable approximation for a solid structure containing an OH group.
In this study we will consider as a measure of acidity the energy to displace the proton from its equilibrium position to a finite elongated position. We have chosen this approach instead of calculating the proton affinities for two reasons. Firstly, since we are performing periodic calculations, removing the proton to infinity would result in infinite electrostatic contribution when considering the charged unit cell formed. Secondly, it is more realistic to consider the proton being displaced only a short distance from its equilibrium position, since in reality the proton is transferred to a nearby base. However, our approach does have the disadvantage of the arbitrary choice of the elongation of the O–H distance. Nevertheless, as we are not introducing here a new definition of acidity, we can consider this approach sufficiently valid for our comparative purposes. Furthermore, since we are focussing here on the vibrational property of the acid group, we are not considering the structure after proton transfer. We have chosen a distance of 0.66 Å as the final elongation of the proton with respect to its equilibrium position.
Accordingly, this measure of acidity can be shown to be related to the OH vibrational frequency by substituting eqn. (1) into eqn. (A1.1) in Appendix 1;
 | (2) |
and thus increasing acidity (decreasing ΔU) corresponds to decreasing OH frequency.
We will also attempt to determine the relative contributions of the ionic and the covalent terms to the total energy. The influence of the electric field gradient (EFG) on the reactivity of zeolites has been claimed in some studies,9,10 suggesting a dominant role for long range electrostatic contribution in determining acidity. If, therefore, the ionic part makes a sub stantial contribution to the total energy, the following expression [derived in Appendix 1, eqn. (A1.7)] would be applicable:
 | (3) |
Finally, in this study we will try to establish a theoretical justification for a relationship, found in previous studies,16,17 between the electric field at the proton site and the OH stretching frequency; the derivation of such a correlation is presented in Appendix 3 and discussed below.
3. Methodology
The AlPO4-5,63,64 AlPO4-34,65,66 SSZ-2467 and SSZ-1368 structures, with a single Brønsted site introduced in the unit cell have been chosen for our simulations. These structures have the advantage of containing one topologically distinct T (Si, Al) site resulting in the need to consider only four different acid site geometries (Fig. 1). Also, the structures of AlPO-5 and AlPO-34 are isomorphic with SSZ-24 and SSZ-13 having the International Zeolite Association AFI and CHA structure codes respectively.55 Finally, our choice of structures allows comparison with our previous results31–33 and with experimental data.63–68 The Brønsted site is introduced by replacing a Si with Al in the siliceous (SSZ) structures and by replacing a P with Si in the AlPO4 structures respectively, with the proton being attached onto each adjacent bridging oxygen in turn. Once the acid centre is introduced the atomic coordinates of all atoms and the unit cell parameters were fully optimised to constant pressure using an RFO69 optimisation scheme. The calculations of the normal vibrational modes of the cells have been performed to assure that a true minimum was found and to calculate the OH vibrational frequencies. The electrostatic properties, namely the electrostatic potential, the electric field, and the electric field gradient have also been calculated for all the structures; all calculations were performed using the GULP code.53 | ||
| Fig. 1 Fragments of the structures AlPO-5 and SSZ-24 (left) and AlPO-34 and SSZ-13 (right) showing the position of the four different oxygen where the proton can be attached. There is only one topologically distinct T site (Si,Al,P) labelled as T1. The labelling in AlPO-34 and SSZ-13 corresponds to that found in the chabasite structure.65 which in the literature is different to that used for the SAPO material.66 The correspondence between the two sets is given in ref. 71. | ||
In order to estimate how the total energy and its various components change upon OH elongation, we have manually constructed geometries of the unit cell with the OH bond elongated in steps of 0.01 Å from the equilibrium distance, r0 , to a final distance of r0+0.66 Å. At each step the contents of the unit cell were again fully optimised within the RFO scheme, but with the O–H distance being kept fixed. The con formations between r0 and r0+0.66 Å have been used to calculate the energy contributions and the electrostatic potential, and the first and second derivatives at the equilibrium distance, r0, of both energy and electrostatic potential have been calculated. The derivatives were calculated numerically from the curves using the central point approximation.
Two forcefields have been used in this study for the sake of comparison. We will focus mainly on an empirical forcefield originally derived for aluminosilicates with formal charges on the atoms (except the bridging OH) and short range potentials described by a Buckingham potential. In addition a shell model70 is used to simulate the polarisation of the oxygen atoms, although no such term is included for the oxygen of the acid site. A harmonic three body term is included between O–T–O atoms, whilst the acid site is modelled by a charge-subtracted Morse potential between the O and H atoms.42,46,47 Originally derived for aluminosilicates, the forcefield was recently extended to include terms for silico–alumino–phosphates by Gale and Henson.52 We shall refer to this combined forcefield as empFF. We will also discuss calculation using the ab initio derived forcefield for aluminosilicates by Sierka and Sauer.61 This forcefield again has formally charged atoms, including here, on the proton and the oxygen to which it is bonded. Short range interactions are described by Buckingham and harmonic three body terms, whilst a shell model is again included to model polarisation. This forcefield will be referred to as dftFF during our discussions.
4. Results and discussion
4.1. Contributions to proton elongation energy from short range and long range interactions
The total potential energy as the OH bond elongates has been calculated with the empFF42,46,47,52 (Fig. 2). As the unit cells have a different number of atoms, we present the total energy per TO4 unit, for the sake of comparison. Here, we are considering the acidity of different sites to be related to the energy required to elongate the OH bond a fixed distance from its equilibrium position, r0, to r0+0.66 Å. The final bond elongation energy is obtained from the difference between the initial and final energies, and the corresponding energies, Utotal , are given in Table 1. There are several contributions to the total energy expression:| Utotal=Uelec+UBuck+Ucore-shell+Uthree-body+UMorse | (4) |
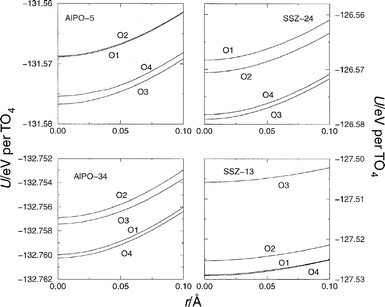 | ||
| Fig. 2 Energy to elongate the OH bond from its equilibrium position, r0, to a final distance of r0+0.1 Å, where a step of 0.01 Å has been considered between configurations. Although the curve is calculated to a final elongation of 0.66 Å, only the initial elongation to 0.1 Å is shown here, in order to highlight the details near the equilibrium distance. The structures considered were AlPO-5, AlPO-34, SSZ-24, and SSZ-13 in which a single Brønsted site per unit cell was introduced. The empFF forcefield42,46,47,52 has been used. Oxygen labels are as shown in Fig. 1. | ||
| Energy contribution/eV | |||
|---|---|---|---|
| Structure | Utotal | UBuck | Uelec |
| a Only the two most important contributions (Buckingham and electrostatic) and the total energy are shown. All calculations use the empFF forcefield.12,40,47,52 Oxygen labels as in Fig. 1. | |||
| AlPO-34 | |||
| O1 | 2.630 | 2.684 | −1.157 |
| O2 | 2.678 | 2.535 | −0.781 |
| O3 | 2.607 | 2.946 | −1.454 |
| O4 | 2.610 | 2.745 | −1.254 |
| AlPO-5 | |||
| O1 | 2.533 | 2.950 | −1.703 |
| O2 | 2.524 | 2.151 | −0.290 |
| O3 | 2.572 | 4.064 | −3.659 |
| O4 | 2.683 | 3.510 | −2.415 |
| SSZ-13 | |||
| O1 | 2.637 | 0.650 | 1.047 |
| O2 | 2.616 | 2.592 | −0.930 |
| O3 | 2.412 | 2.104 | −0.680 |
| O4 | 2.582 | 0.931 | 0.662 |
| SSZ-24 | |||
| O1 | 2.500 | 2.334 | −0.686 |
| O2 | 2.477 | 2.433 | −1.079 |
| O3 | 2.597 | 1.271 | 0.130 |
| O4 | 2.599 | 0.747 | 0.707 |
We have calculated the various contributions to the total energy and the values obtained for the two most important terms, the short-range Buckingham term, UBuck, and the long-range electrostatic term, Uelec, are both given in Table 1. It can be seen that both contributions are significant and hence neither can be neglected in any discussion of acidity. We note that although not constant, the contribution from the Morse potential—the O–H stretching potential—is very small (ca. 0.45 eV) which varies little; a standard deviation of 0.02 eV. Therefore, our study of bond elongation energy (Table 1) indicates that acidity, within this forcefield scheme, is a result of a combination of both long-range and short-range contributions. The electrostatic and short-range terms contribute favourably (negative) and unfavourably respectively (Table 1). That is, the electrostatic contribution facilitates the elongation of the O–H bond. However, we should note that, in this forcefield, the electrostatic attraction between the O and H atoms is excluded, being implicity included in the Morse potential.
There is considerable variation in the electrostatic contribution to the elongation energy even within the same structure; for example in AlPO-5, we find values ranging from −0.290 eV (when the proton site is O2) to −3.659 eV (in O3), a difference of 3.369 eV; much larger than the variation in total energy. Such variation is due to the heterogencity of the electrostatic potential in the different parts of the structure. Moreover, we also find that there is a significant variation in the electrostatic term for sites which can be considered to be similar. For example, consider protons attached to O1 and O4 in AlPO-5; although both are orientated into the main channel (see Fig. 1), the electrostatic contribution to the bond elongation energy varies by 0.712 eV. Therefore, the electrostatic contribution to the acidity of the centres which are, in principle, rather similar, vary considerably as a direct consequence of the long-range nature of these interactions. From these results we conclude, as in previous studies17 that no simple intuitive structural feature, such as ring or cavity size, can be related to the electrostatic contribution to a site's energy and hence, we believe, to be related to its relative acidity. We conclude, therefore, that a full periodic determination of the electrostatics is necessary to determine and rationalise trends in acidity and to allow variations in acidity between different sites to be considered.
Of course a similar variation is found in the magnitude of the short-range Buckingham potential contribution to the bond elongation energy, since the variation in total energy is small. For example, the Buckingham contribution varies by 1.913 eV in AlPO-5 (Table 1). Whilst these terms are indeed short-range, there is of course a significant difference in the spatial distribution of atoms around the different acid sites beyond the first and second neighbour shells. Such differences are therefore manifested in the variations found in the Buckingham contribution. Therefore, again, it is difficult to identify any simple structural feature which can be related to the short-range contribution and hence its contribution to the acidity of a particular site. This picture would be further complicated if the other, less important, energy terms were taken into account.
Comparing isostructural zeotypes—AlPO-5 with SSZ-24, and AlPO-34 with SSZ-13—we note no direct correspondence between sites with respect to the relative magnitude of the electrostatic contribution. For example, the more negative electrostatic contribution to the elongation energy is found when the site is located at O3 in AlPO-34 and on O2 in SSZ-13, whilst the largest electrostatic contribution is found at O2 in AlPO-34 and at O1 in SSZ-13. This results makes it clear that subtle changes in structure, rather than topology, are critical and that it is essential to determine lattice relaxation prior to consideration of any physical properties.
From the above results, it is clear that it is not possible at first glance to attribute changes in acidity to long-range electrostatics alone, since there is considerable interaction with short-range forces. Nor does it appear appropriate to invoke any simple structure–acidity relationship, given the complex nature of the potential energy surface.
4.2. Relation between bond elongation energy and OH frequency
We now consider the approximation presented in eqn. (2); that the frequency of the O–H vibration is directly related to the energy required to elongate the bond and hence facilitate proton transfer. Fig. 3 shows the correlation between the square of ν(OH) and the total bond elongation energy. Although there is a fair amount of scatter, there is a reasonable correlation, which can be seen as justification for relating ν(OH) to acidity. Whilst it has often been stated that such a relationship can only be considered crude (due to the neglect of the acid–base interactions) such an approximation appears to be a justifiable first approximation of relative acidity.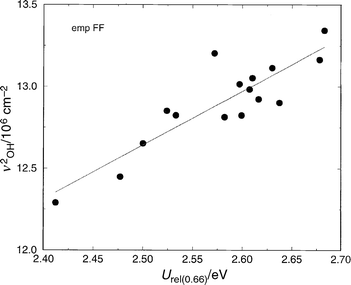 | ||
| Fig. 3 Total energy to elongate the OH bond from its equilibrium position, r0, to a final distance of r0+0.66 Å, vs. the square of the OH frequency. The structures AlPO-5, AlPO-34, SSZ-24, and SSZ-13 in which a single Brønsted site per unit cell has been introduced have been considered. The empFF forcefield42,46,47,52 has been used. The linearity of the plot is established by eqn. (2). | ||
4.3. Contributions to OH frequency from short- and long-range second derivatives of the energy
From eqn. (1) we note a correlation between the 2nd derivative of the energy at the equilibrium O–H separation and ν(OH). Using values of ∂2U/∂r2 determined from Fig. 2, we present in Fig. 4 a plot of the square root of the derivative against OH frequency. Again, a reasonable correlation is found, supporting the use of vibrational frequencies as an indicator of acidity; as suggested by eqn. (1). Although there is scatter in the data, there are potentially a number of reasons why this may be so as a result of our procedures. Firstly, the calculated OH normal mode is coupled to other vibrations in the structure; secondly, inaccuracies may arise from the quadratic approximation used to calculate the frequencies,53 and thirdly errors may arise from the calculation of the energy and its second derivative.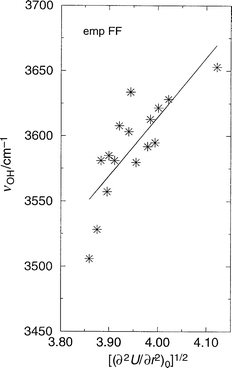 | ||
| Fig. 4 OH stretching frequency (cm−1) vs. the square root of the second derivative of the total energy with respect to OH bond elongation at the origin (minimum energy position) (energy in eV, distance in Å) in the structures AlPO-5, AlPO-34, SSZ-24, and SSZ-13 in which a single Brønsted site per unit cell has been introduced. The linearity of this plot is justified by the relationship given in eqn. (1). The empFF forcefield42,46,47,52 has been used. | ||
We now examine the electrostatic contribution to the second derivative of the total energy in order to establish whether consideration of the electrostatic potential alone is suitable to evaluate relative acidity. The variation of the electrostatic potential with OH bond length is presented in Fig. 5. From these plots, we calculate numerically the second derivative of the energy giving the electric field gradient which is subsequently shown in Fig. 6. A reasonable linear relationship is now observed between the root of the electric field gradient16 and ν(OH), again suggesting the critical role of long range electrostatics in determining the relative position of ν(OH). However, such a correlation does not necessarily suggest that the OH stretching frequencies are determined mainly by the electrostatic part of the potential energy, but rather that the ionic contribution can be considered to be a constant proportion of the total energy; such a relationship is indicated by eqn. (A1.7) (Appendix 1).
 | ||
| Fig. 5 Variation of the electrostatic potential (in V) as the OH bond (in Å) elongates in the structures AlPO-5, AlPO-34, SSZ-24, and SSZ-1 in which a single Brønsted site per unit cell has been introduced. Although the curve is calculated to a final elongation of 0.66 Å, only the initial elongation to 0.1 Å is shown here, in order to better highlight the details near the equilibrium distance. The empFF forcefield42,46,47,52 has been used. | ||
 | ||
| Fig. 6 Correlation between square root of the electric field gradient (EFG) at the H atomic site in the minimum energy configuration (electrostatic potential in V and distance in Å), and OH stretching frequency (cm−1). A rationalisation of the linearity of the plot is given by eqn. (A1.7). (Appendix 1). The structures considered were AlPO-5, AlPO-34, SSZ-24, and SSZ-13 in which a single Brønsted site per unit cell was introduced. The empFF forcefield42,46,47,52 has been used. | ||
We should also note that the shifts observed in ν(OH) between different sites and different structures are in fact relatively large. Although only of the order of 100 cm−1, it should be noted that the contribution (see Appendix 2) from the Morse potential is significant; the vibrational frequency of an isolated O–H bond being 4434.48 cm−1 (see eqn. (A2.6) in Appendix 2). Therefore, the total contribution from the remaining energy terms, which we have already determined to be those dominant in determining proton transfer, is of the order of 630–790 cm−1. Therefore shifts of 100 cm−1 represent a considerable change. However, the magnitude of the contribution from the Morse term should not be misinterpreted as being significant in determining the variation in position of the vibrational frequency amongst different zeotypes, or indeed variation among different centres of the same zeotype, since the Morse function (see eqn. (A2.1) in Appendix 2) is constant for all structures. Thus, in our calculation, all the variations in vibrational frequencies are a consequence of variation in the Buckingham and electrostatic interactions, which are, in turn, a direct consequence of the structure. Whilst the conclusion drawn here regarding the relative importance of bonded (the Morse potential) and non-bonded (essentially all other interactions) terms in determining both the absolute value and relative shifts in ν(OH), is a consequence of the forcefield used, we consider it to be a reasonable model of the bonding and interactions in such materials. Given the success of this potential model in describing both the structure and vibrational properties of such materials and given the seemingly small changes in electron distribution between sites found in ab initio calculations23,25 we conclude that variations in acidity are not a consequence of variation in local electronic distribution.
4.4. Justification of the linear relationship between electric field and OH stretching frequency
In previous studies17 we identified what appeared to be a linear relationship between the electric field at the proton site (at equilibrium geometry) and the calculated OH stretching frequency. We should also note that good agreement is found between the frequencies calculated using this forcefield method and those observed experimentally.17 Although our observation was used to suggest the importance of long-range interactions in determining acidity differences in zeotypes, a theoretical justification was not provided. In Appendix 3 we derive a relationship between the electric field and the square of the vibrational frequency, based only on the assumption of a constant weighting of the electrostatic contribution to the frequency (as discussed above):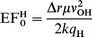 | (5) |
The resulting quadratic expression is shown in Fig. 7. This quadratic expression can be readily approximated as linear over a certain limited range of vibrational frequencies (ca. <200 cm−1). Such an approximate linear relationship has been illustrated elsewhere for the structures considered here.17
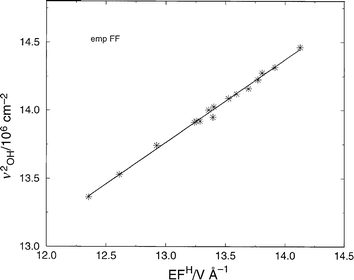 | ||
| Fig. 7 Correlation between electric field (EF) at the H atomic site in the minimum energy configuration (electrostatic potential in V and distance in Å), and the square of the OH stretching frequency (in cm−2). The justification for the linearity of the plot is found in eqn. (A3.6) (Appendix 3). The structures considered were AlPO-5, AlPO-34, SSZ-24, and SSZ-13 in which a single Brønsted site per unit cell was introduced. The empFF forcefield42,46,47,52 has been used. | ||
Regarding the corresponding theoretical justification for eqn. (5), as shown in Appendix 3, we recall that it does not indicate that the ionic contribution is the only one of importance in determining relative acidity in these microporous materials.
4.5. Forcefield dependence
As when using more sophisticated methodologies, such as ab initio calculations, the conclusions drawn can often be dependent on the model used. Hence a different forcefield has been selected to determine if the conclusions presented above are a consequence of the empff forcefield used. We now present results obtained using the forcefield derived by Sierka and Sauer61 from DFT ab initio calculations on zeolite clusters. We stress again that this forcefield, dftFF, not only differs in the source of the data used to derive the potential parameters, but also in the expression used to formulate the total energy function. Again, formal charges are used but here the acid site (O–H) is also treated as being formally charged, whilst a polarisation function is also included on the acid site oxygen. The short range interactions are also treated here by Buckingham and quadratic three body terms. However, the interactions between the oxygen and proton of the acid site are also treated by a Buckingham (and Coulombic) potential, in contrast to the Morse potential employed in empFF. We restrict our comparison to the SSZ-24 and SSZ-13 materials as the parameterisation was restricted to aluminosilicates. We do not repeat here all the discussion of the previous sections but present only the main results. Firstly, we again find the linear relationship between bond elongation energy and the square of the OH stretching frequency (Fig. 8). Secondly, a correlation is found between the second derivative of the total energy and ν(OH) (Fig. 9). Finally, the correlation between the square root of the electric field gradient and OH stretching frequency is also again found (Fig. 10). Thus, we find that all the correlations found with the empirical forcefield, above, are also found here. Given the significant differences between the derivation and formulation of these forcefields we conclude that the trends observed are unlikely to be primarily artefacts of our methodology or model. | ||
| Fig. 8 Total energy to elongate the OH bond from its equilibrium position, r0, to a final distance of r0+0.66 Å, vs. square OH frequency. The structures considered are SSZ-24, and SSZ-13 with a single Brønsted site per unit cell as before. The forcefield dftFF from reference61 has been used. | ||
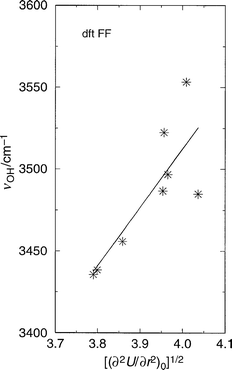 | ||
| Fig. 9 OH stretching frequency (cm−1) vs. the square root of the second derivative of the total energy with respect to OH bond elongation at the origin (minimum energy position) (energy in eV, distance in Å) in the structures SSZ-24, and SSZ-13 with a single Brønsted site per unit cell as before. The forcefield dftFF from reference61 has been used. | ||
 | ||
| Fig. 10 Correlation between square root of the electric field gradient (EFG) at the H atomic site in the minimum energy configuration (electrostatic potential in V and distance in Å), and OH stretching frequency (in cm−1). The reason for the linearity of the plot is found in eqn. (A1.7) (Appendix 1). The structures considered were SSZ-24, and SSZ-13 with a single Brønsted site per unit cell. The forcefield dftFF from reference61 has been used. | ||
We do however, note that the relationships here are less convincing than those found for the empirical forcefield. This, we believe, is a consequence of the derivation of the forcefield and not of any fundamental flaw in our models of acidity. The potential describing the acid centre in the empFF was derived in an ionic field representing NaOH and therefore includes a description of the long-range electrostatics. However, the DFT derived forcefield was determined from cluster calculations with no long-range potential included. Thus, it should not be a surprise to find a stronger correlation between the acid and electrostatic properties determined using the empirical forcefield compared to the DFT forcefield.
5. Conclusions
In this paper we have attempted to set out a theoretical basis for our discussions of acidity in microporous solids. Whilst working within a forcefield approximation we have identified a number of relationships between the structure, energy and vibrational properties of Brønsted acid sites in zeolites and aluminosilicates. Although such forcefield methods are, at first sight, not only approximate but also perhaps considered to be unsuitable for the consideration of what is essentially a reactive process, we believe these relationships have a firm theoretical basis corresponding to intuitive ideas on chemical bonding. Furthermore, we believe that the results have important consequences for more accurate ab initio calculations which aim to treat acid functionality.When acidity is considered as being related to the elongation of the O–H bond, prior to transfer to a base, we find that the relative acid strength are related to the vibrational properties of the acid site. The importance of both the Buckingham and the electrostatic components as the main contributions to the energy required to elongate the O–H bond has also been shown, illustrating how the resulting acidity is a combination of short- and long-range interactions. However, since each acid site has been described by the same effective potential, this result suggests that it is critical to include long-range—greater than 2nd order neighbours—when attempting to either calculate properties which are dependent on the acidity of the site or in attempting to establish further structure–acidity relationships. Such a conclusion has ramifications for ab initio calculations of reactions on acid sites if explanations for differences between the activity of different structures (or even different sites within the same material) are to be realised. Thus, if cluster models are to be used then we would consider it important that some treatment of the electric field, beyond the extent of the clusters is necessary.
Electric field gradients (EFG) have been shown to be correlated to the vibrational frequency of the acid site and consequently to the acidity—since the vibrational frequency can be considered as being related to the bond elongation energy. Whilst the EFG is not the only contribution to the second derivative of the energy it can be useful in explaining the acidity of microporous materials. We have now established a relationship between the electric field (EF) at the H atomic site and OH stretching frequency, which had previously been identified.16,17 Although in our previous studies17 we suggested a linear correlation, the expression obtained is quadratic. However, over the limited range of frequencies observed, a linear correlation is a reasonable approximation.
Finally, the dependence of our conclusions on the use of a particular forcefield has been tested through the use of an alternative forcefield. Even given the differences in derivation and functional form, the same conclusion can be drawn, suggesting that once explicit considerations of long-range interactions are made, accurate descriptions of relative acidity can be obtained. However, we consider the empirical forcefield, which was fitted with respect to (periodic) crystalline properties will be superior, if all other concerns are equal, to any forcefield derived from cluster calculations (regardless of quality). This is due to the importance, not only of the long-range electrostatics but also of the need to describe accurately the electrostatic field.
Considering the intermolecular energy between atom pairs, U=U(r) (where r is the atomic separation between any two atoms) as a Taylor expansion around the energy minimum, r0: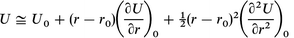 | (A1.1) |
The solution of the classical equation of motion gives:
 | (A1.2) |
where:
 | (A1.3) |
with ‘m’ the reduced mass of the atom pair,
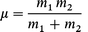 | (A1.4) |
and ‘ν’ being the vibrational frequency of the atom pair.
Now we consider the special case of a system which is purely ionic. The energy can be expressed as
 | (A1.5) |
where ‘Uelec ’ is the electrostatic energy, ‘qi’ the atomic charge on atom i, and ‘V’ the electrostatic potential. A factor of 1/2 avoids double counting as the i index runs through all the atoms of the system.
The elongation of the O–H bond will mainly affect the electrostatic potential at the H site and therefore in the summation over all the atomic sites, all terms not involving the H atom can be neglected and thus when taking the 2nd derivative of the energy we can make the following approximation:
 | (A1.6) |
Now, on substitution into eqn. (A1.3) the OH frequency becomes:
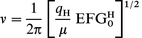 | (A1.7) |
This equation can be useful not only for the case of a purely ionic solid but also to study the influence of the electrostatic part on the OH frequency in a partially covalent solid. Similarly, we can also consider the equation to hold for a system in which the proportion of the total energy contributed by the electrostatic term to be constant so that:
| U=kUelec | (A1.8) |
If eqn. (A1.8) is true and we substitute into eqn. (A1.3), then a linear relationship between the square root of the EFG and the OH vibrational frequency is obtained as in eqn. (A1.7).
The vibrational frequency of the OH bond due only to the Morse term is calculated here.The energy, and its first and second derivatives are:
| UMorse=D[1−e−γ]2−D | (A2.1) |
where:
| UMorse′=2Dβ1−e−γe−γ | (A2.2) |
| UMorse″=2Dβ22(e−γ)2−e−γ | (A2.3) |
| UMorse″(r=r0)=2Dβ2 | (A2.4) |
Now, substituting into eqn. (A1.3) to calculate the frequency we have:
 | (A2.5) |
where ‘μ’ is the reduced mass of the system and ‘c ’ is the speed of light.
Using the following constants and conversion factors: c=2.998×1010 cm s1; m(O)=16.00 u; m(H)=1.01 u; 1 eV=1.602×10−19 J; 1 u=1.661×10−27 kg, we obtain a value of:
 | (A2.6) |
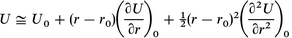 | (A3.1) |
Again, considering that the first derivative term vanishes at the equilibrium geometry and substitute the expression for the second derivative at the origin from eqn. (A1.3), we obtain:
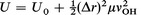 | (A3.2) |
where r is the separation as we elongate the OH bond and U is the corresponding total energy of the system as we perform this elongation.
We now make the assumption that, within our forcefield approach, the electrostatic energy represents a constant contribution to the total energy along the energy curve U(r). Such an assumption is justified by the fact that atomic charges do not change with bond distances and this is discussed further in the text. Hence, we have:
 | (A3.3) |
Now if we substitute the value of ‘U ’ from eqn. (A3.3) into eqn. (A3.2):
 | (A3.4) |
We can assume that the changes in the electrostatic potential when displacing the proton from its equilibrium position are very minor at the other atomic positions. Hence all the terms except those involving the H atom vanish, giving:
 | (A3.5) |
Considering the definition of electric field as the variation of electrostatic potential with respect to the coordinates we arrive to our final expression:
 | (A3.6) |
In this equation the electric field (EF) is calculated as the gradient of electrostatic potential along the OH bond elongation coordinate. If we therefore consider equally elongated O–H bonds in a number of systems, a plot of the EF at the position of the hydrogen atom against square νOH should give a straight line.
Acknowledgements
G.S. thanks The Royal Society of Chemistry for providing an RSC Journals Grant, and the Spanish CICYT project MAT-97-1016-C02-01 for financial support. We thank Dr Furio Corà and Dr J. D. Gale for many useful discussions.References
- E. Dempsey, in Molecular Sieves, Society of Chemical Industry, London, 1968, p. 293. Search PubMed.
- J. A. Rabo and P. H. Kasai, Prog. Solid State Chem., 1975, 9, 1 CrossRef CAS.
- M. Briend, R. Vemscheid, M. J. Peltre, P. P. Man and D. Barthomeuf, J. Phys. Chem., 1995, 99, 8270 CrossRef CAS.
- D. W. Lewis, C. R. A. Catlow, G. Sankar and S. W. Carr, J. Phys. Chem., 1995, 99, 2377 CrossRef CAS.
- M. Allavena, K. Seiti, E. Kassab, G. Ferenczy and J. G. Angyan, Chem. Phys. Lett., 1990, 168, 461 CrossRef CAS.
- E. Kassab, K. Seiti and M. Allavena, J. Phys. Chem., 1991, 95, 9425 CrossRef CAS.
- J. D. Gale, R. Shab, M. C. Payne, I. Stich and K. Terakura, Catal. Today, 1999, 50, 525 CrossRef CAS.
- I. Stich, J. D. Gale, K. Terakura and M. C. Payne, J. Am. Chem. Soc., 1999, 121, 3292 CrossRef CAS.
- C. Mirodatos and D. Barthomeuf, J. Catal., 1985, 93, 246 CrossRef CAS.
- C. Mirodatos, A. Biloul and D. Barthomeuf, J. Chem. Soc., Chem. Commun., 1987, 149 RSC.
- A. Corma, G. Sastre and P. Viruela, Stud. Surf. Sci. Catal., 1994, 84, 2171 Search PubMed.
- A. Corma, G. Sastre and P. Viruela, J. Mol. Catal., 1995, 100, 75 Search PubMed.
- G. Sastre, P. Viruela and A. Corma, Chem. Phys. Lett., 1997, 264, 565 CrossRef CAS.
- A. Corma, H. Garcia, G. Sastre and P. Viruela, J. Phys. Chem. B, 1997, 101, 4575 CrossRef CAS.
- P. Dziekonski, W. A. Sokalski, E. Kassab and M. Allavena, Chem. Phys. Lett., 1998, 288, 538 CrossRef CAS.
- N. Y. Topsoe, K. Pederson and E. G. Derouane, J. Catal., 1981, 70, 41 CrossRef CAS.
- D. W. Lewis and G. Sastre, Chem. Commun., 1999, 349 RSC; G. Sastre and D. W. Lewis, J. Chem. Soc., Faraday Trans., 1998, 94, 3049 RSC.
- L. Uytterhoeven, D. Dompas and W. J. Mortier, J. Chem. Soc., Faraday Trans., 1992, 88, 2753 RSC.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1841 CAS.
- D. E. Williams and J. M. Yan, Adv. At. Mol. Phys., 1988, 23, 87 Search PubMed.
- G. N. Lewis, Valence and the Structure of Atoms and Molecules, Chemical Catalog. Co., New York, 1923. Search PubMed.
- N. V. Sidgwick, The Electronic Theory of Valency, Clarendon Press, Oxford, 1927. Search PubMed.
- R. Shah, J. D. Gale and M. C. Payne, J. Chem. Soc., Chem. Commun., 1997, 131 RSC.
- R. Shah, J. D. Gale and M. C. Payne, Phase Trans. B, 1997, 61, 67 Search PubMed.
- R. Shah, J. D. Gale and M. C. Payne, J. Phys. Chem., 1996, 100, 11688 CrossRef CAS.
- E. Nusterer, P. E. Blochl and K. Schwarz, Chem. Phys. Lett., 1996, 253, 448 CrossRef CAS.
- Y. Jeanvoine, J. G. Angyan, G. Kresse and J. Hafner, J. Phys. Chem. B, 1998, 102, 7307 CrossRef CAS.
- Y. Jeanvoine, J. G. Angyan, G. Kresse and J. Hafner, J. Phys. Chem. B, 1998, 102, 5573 CrossRef CAS.
- Computer Simulation in Solids, ed. C. R. A. Catlow and W. C. Mackrodt, Lecture Notes in Physics, Springer, Berlin, 1992, vol. 166. Search PubMed.
- Modelling of Structure of Reactivity in Zeolites, ed. C. R. A. Catlow, Academic Press, London, 1992. Search PubMed.
- G. Sastre, D. W. Lewis and C. R. A. Catlow, J. Phys. Chem., 1996, 100, 6722 CrossRef CAS.
- G. Sastre, D. W. Lewis and C. R. A. Catlow, J. Mol. Catal. A, 1997, 119, 349 CrossRef CAS.
- G. Sastre, D. W. Lewis and and C. R. A. Catlow, J. Phys. Chem. B, 1997, 101, 5249 CrossRef CAS.
- R. A. van Santen, A. J. M. de Man, W. P. J. H. Jacobs, E. H. Teunissen and G. J. Kramer, Catal. Lett., 1991, 9, 273 Search PubMed.
- P. Demontis and G. B. Suffritti, Chem. Rev., 1997, 97, 2845 CrossRef CAS.
- E. J. Maginn, A. T. Bell and D. N. Theodorou, J. Phys. Chem., 1996, 100, 7155 CrossRef CAS.
- C. R. A. Catlow, C. M. Freeman, B. Vessal, S. M. Tomlinson and M. Leslie, J. Chem. Soc., Faraday Trans., 1991, 87, 1947 RSC.
- G. Schrimpf, M. Schlenkrich, J. Brickmann and P. Bopp, J. Phys. Chem., 1992, 96, 7404 CrossRef CAS.
- S. M. Auerbach, N. H. Henson, A. K. Cheetham and H. I. Metiu, J. Phys. Chem., 1995, 99, 10600 CrossRef CAS.
- G. Sastre, N. Raj, C. R. A. Catlow, R. Roque-Malherbe and A. Corma, J. Phys. Chem. B, 1998, 102, 3198 CrossRef CAS.
- A. Corma, C. R. A. Catlow and G. Sastre, J. Phys. Chem. B, 1998, 102, 7085 CrossRef CAS.
- R. A. Jackson and C. R. A. Catlow, Mol. Simul., 1988, 1, 207 Search PubMed.
- B. W. H. van Beest, G. J. Kramer and R. A. van Santen, Phys. Rev. Lett., 1990, 16, 1955 CrossRef CAS.
- E. de Vos Burchart, V. A. Verheij, H. van Bekkum and B. van de Graaf, Zeolites, 1992, 12, 183 CrossRef CAS.
- J.-R. Hill and J. Sauer, J. Phys. Chem., 1994, 98, 1238 CrossRef CAS.
- P. Saul, C. R. A. Catlow and J. Kendrick, Philos. Mag. B, 1985, 51, 107 Search PubMed.
- K.-P. Schröder, J. Sauer, M. Leslie, C. R. A. Catlow and J. M. Thomas, Chem. Phys. Lett., 1992, 188, 320 CrossRef.
- J.-R. Hill and J. Sauer, J. Phys. Chem., 1995, 99, 9536 CrossRef CAS.
- K.-P. Schröder and J. Sauer, J. Phys. Chem., 1996, 100, 11043 CrossRef.
- M. Sierka, U. Eichler, J. Datka and J. Sauer, J. Phys. Chem. B, 1998, 102, 6397 CrossRef CAS.
- E. de Vos Burchart, H. van Bekkum, B. van de Graaf and E. T. C. Vogt, J. Chem. Soc., Faraday Trans., 1992, 88, 2761 RSC.
- J. D. Gale and N. H. Henson, J. Chem. Soc., Faraday Trans., 1994, 90, 3175 RSC.
- J. D. Gale, J. Chem. Soc., Faraday Trans., 1997, 93, 629 RSC.
- D. Barthomeuf, Mater. Chem. Phys., 1987, 17, 49 CrossRef CAS.
- W. M. Meier, D. H. Olson and Ch. Baerlocher, Atlas of Zeolite Structure Types, Elsevier, Amsterdam, 4th edn., 1996. Search PubMed.
- W. J. Mortier, S. K. Ghosh and S. Shankar, J. Am. Chem. Soc., 1986, 108, 4315 CrossRef CAS.
- G. O. Janssens, H. Toufar, B. G. Baekelandt, W. J. Mortier and R. A. Schoonheydt, Stud. Surf. Sci., Catal., 1997, 105, 725 Search PubMed.
- S. L. Njo, J. Fan and B. van de Graaf, J. Mol. Catal. A, 1998, 134, 79 CrossRef CAS.
- J. N. Louwen and E. T. C. Vogt, J. Mol. Catal. A, 1998, 134, 63 CrossRef CAS.
- A. R. Ruiz-Salvador, G. Sastre, D. W. Lewis and C. R. A. Catlow, J. Mater. Chem., 1996, 6, 1837 RSC.
- M. Sierka and J. Sauer, Faraday Discuss., 1997, 106, 41 RSC.
- C. R. A. Catlow and A. N. Cormack, Int. Rev. Phys. Chem., 1987, 6, 227 CAS.
- J. M. Bennett, J. P. Cohen, E. M. Flanigen, J. J. Pluth and J. V. Smith, Intrazeolite Chemistry, ed. G. D. Stucky and F. G. Dwyer, ACS Symp. Ser. 218, American Chemical Society, Washington DC, 1983, p. 109. Search PubMed.
- A. J. Mora, A. N. Fitch, M. Cole, R. Goyal, R. H. Jones, H. Jobic and S. W. Car, J. Mater. Chem., 1996, 6, 1831 RSC.
- M. Calligaris, G. Nardin, L. Randaccio and P. C. Chiaramonli, Acta Crystallogr. B, 1982, 38, 602 CrossRef.
- M. Ito, Y. Shimoyama, Y. Saito, Y. Tsurita and M. Otake, Acta Crystallogr. C, 1985, 41, 1698 CrossRef.
- R. Bialek, W. M. Meier, M. E. Davis and M. J. Annen, Zeolites, 1991, 11, 438 CAS.
- L. J. Smith, A. Davidson and A. K. Cheetham, Catal. Lett., 1997, 49, 143 Search PubMed.
- J. Simons, P. Jorgensen, H. Taylor and J. Ozment, J. Phys. Chem., 1983, 87, 2745 CrossRef CAS.
- B. G. Dick and A. W. Overhauser, Phys. Rev., 1958, 112, 90 CrossRef.
- O1, O2, O3 and O4 in the setting of ref. 65 correspond to O1, O4, O2 and O3 in the setting of ref. 66..
| This journal is © the Owner Societies 2000 |

