Molecular structures and non-linear optical properties of donor–acceptor quinoid-type molecules
Weihua Zhu and Yuansheng Jiang*
Department of Chemistry, Nanjing University, Nanjing, 210093, China
First published on UnassignedUnassigned22nd December 1999
Abstract
AM1 calculations are performed to study the molecular structures and the linear and non-linear polarizabilities of the donor–acceptor quinoid-type molecules under the influence of an external electric field defined by point charges (Sparkles). We investigate and compare the relationships between the molecular structures and the molecular polarizabilities of the substituted quinoid-type molecules. The results show that the relative sizes of the molecular polarizability values for the three molecules depend on the selection of the donor–acceptor pair. We also systematically examine the influence of molecular architecture on the hyperpolarizabilities. It is found that the substituted quinoid-type molecules have considerably larger hyperpolarizabilities than the substituted aromatic heteroring molecules and the corresponding polyenes with chain extension, and yet the hyperpolarizabilities of the substituted polyenes are larger than that of the substituted aromatic heteroring molecules with chain extension. In addition, the increasing extents of the hyperpolarizabilities for the substituted quinoid-type molecules are far larger than that for the substituted aromatic heteroring molecules and the corresponding polyenes. These properties make the quinoid-type molecules interesting candidates for applications in the non-linear optics, particularly in the area of poled polymer films.
1. Introduction
Organic conjugated materials possessing large non-linear optical (NLO) properties are of interest in materials science and technology because of their potential optoelectronic applications.1–3 The synthesis and characterization of candidate materials for application in non-linear optics is a tedious way to investigate the field of these fascinating compounds. An alternative and complementary way is to use quantum chemical methods that may help to orientate the synthesis towards the most interesting systems. Indeed, theoretical calculations provide numerical estimates of the NLO properties, help the understanding of the phenomena, and finally lead to the establishment of structure–property relationships.3,4 It has been shown that a large NLO response can result from combining donor and acceptor groups separated by a conjugated linker. Several studies have demonstrated that for a given bridge, there is an optimal combination of donor and acceptor groups that will maximize the molecular polarizability.1,3–6 Much work has tested the effects of donor and acceptor group strength or the nature of the conjugated linker on molecular NLO response.1,3–4 Recently, Marder et al.7,8 have studied how substituent and/or solvation-induced geometric distortion of the conjugated polyenic bridge from the equilibrium arrangement can play an important role in determining molecular NLO response. Since then, we have investigated the relationships between the molecular structures and the linear and non-linear polarizabilities of the donor–acceptor cumulenes.9 So far, for donor–acceptor quinoid-type molecules, such as donor–acceptor 2,5-dimethylenethiocyclopentenes, donor–acceptor 2,5-dimethyleneoxocyclopentenes etc., similar studies are hardly reported.Push–pull quinoid-type molecules, another class of organic π-conjugated systems with intrinsically large NLO responses, have not been extensively investigated for NLO applications. A family of quinonoid molecules possesses several positive fea tures at the molecular level, like potentially large hyperpolarizability, negligible absorption in the visible region, ease of synthesis, and chemical and thermal stability. These properties make the quinoid molecules interesting candidates for applications in non-linear optics. Lalama et al.10 found that 2-(4-dicyanomethylenecyclohexa-2,5-dienylidene)imidazolidine has an unexpectedly large β and calculations on the model system 7,7′-diamino-8,8′-dicyanoquinodimethane (DADQ) supported this observation. Ravi and Radhakrishnan11 have presented a theoretical analysis of the large hyperpolarizabilities of push–pull quinonoid molecules as a function of the quinonoid–benzenoid character (QBC). Recently, Sheng and Jiang12 have investigated the structure–property relationships of push–pull quinones. So far, these studies have been devoted to the hyperpolarizability of push–pull quinones. Thus, further studies of donor–acceptor quinoid molecules are necessary.
Similar to the study of structure–property relationships of donor–acceptor cumulenes,9 we select the bridge atomic charge sum (BACS) (the summation of the charge of each atom on molecular bridge)13 as a structural parameter to study the relationships between the molecular structures and the linear and non-linear polarizabilities of the donor–acceptor quinoid-type molecules. The BACS has an advantage in not setting any demands on molecular bridge structure, that is, it may be useful for studying the structure–property relationships of these molecules containing specifically a structural bridge, such as substituted cumulenes, polyynes, pyrroles etc. except for substituted polyenes. However, bond length alternation (BLA) may be applicable only to systems with alternating single and double bonds.
In this work, we perform AM1 calculations on the donor–acceptor quinoid-type molecules (I, II and III, Scheme 1) under the influence of an external electric field defined by point charges (Sparkles).8b The molecule is polarized by applying an external electric field produced by Sparkles, and then allowing the molecule to assume a new equilibrium geometry and electronic configuration. The polarization in the molecule created by this external electric field is employed to simulate the polarization created by donors and acceptors or by solvent stabilization of charge separation. This approach allows us to follow the evolution of the molecular properties from the neutral form to the fully charge-separated form and therefore to gain a more complete picture. Although the polar nature of the molecule is established by the inclusion of the donors and acceptors or by the solvent medium, it may not easy to follow the evolution of the whole picture of the molecular properties using this method. Then, we investigate and compare the structure–property relationships of the donor–acceptor quinoid-type molecules. In addition, we also examine the influence of molecular architecture on the hyperpolarizabilities.
 | ||
| Scheme 1 | ||
The methodology is outlined in Section 2. In Section 3, we compare and discuss the results of geometry optimizations for the donor–acceptor quinoid-type molecules (I, II and III). The electric field dependence of the static polarizabilities α, β and γ is presented and discussed in Section 4. Then we examine the influence of molecular architecture on the hyperpolarizabilities. The conclusions are formulated in Section 6.
2. The computational methodology
The calculations were performed by using the MOPAC system14,15 with MNDO Hamiltonian14 and the AM1 parametrization.14,16 Geometries were fully optimized and the SCF convergence is set to 10−12, A finite field approach employing an energy expansion17–19 was used to calculate the NLO properties for zero frequency. The energy E under the influence of a static electric field F can be expanded as a Taylor series:| E(F)=E(0)−μiFi−αijFiFj/2− |
 | (1) |
The calculated tensors were transformed to mean scalar values by applying
 | (2) |
 | (3) |
 | (4) |
where μi is the ith component of the dipole moment, ‖μ‖ is the norm of the dipole moment and βi in eqn. (3) is defined as
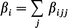 | (5) |
Here, the three quinoid-type molecules I, II and III were examined under the influence of an external electric field designed to vary the ground-state polarization and geometry. This electric field was defined by point charges (Sparkles) moved in steps from 40 to 2.6 Å from each end of the molecule as shown in Fig. 1. At each fixed Sparkle distance (r), the geometry was optimized, and α, β and γ were calculated by a finite field subroutine19 in the presence of these point charges. It is important to note that although two explicit fields are applied to the molecule, the external point charge field and the electric field within the finite field calculation, these fields have distinctly different effects on the molecule. The first field is permitted to influence both its geometric and electronic structure. When once the molecular geometry has been established, the geometry and the Sparkles charges are held fixed while the second field is applied in the finite field calculation to calculate molecular polarizabilities.
 | ||
| Fig. 1 The molecule (where X=S, O, NH) represented in the neutral resonance structure. The point charges lie perpendicular to the plane of the molecule at a distance (r) from the nitrogen and fluorine atoms. BACS=q(C1)+q(C2)+q(C3)+q(C4)+q(C5)+q(C6) +q(X)+q(H(1)+q(H3)+q(H4)+q(H6). | ||
3. Geometric structures
The optimized geometric structures of the molecules I, II, III are reported in Table 1. With decrement of the Sparkles distances r (increment of external electric field strength), the C1–C2, C3–C4 and C5–C6 bond lengths of the molecular chains (I) increase from 1.3520 to 1.4263 Å, 1.3515 to 1.4118 Å and 1.3488 to 1.3876 Å, respectively, and the C2–C3, C4–C5 bond lengths decrease from 1.4523 to 1.3852 Å, 1.4601 to 1.4071 Å, respectively. A similar picture emerges for the geometric evolution of the molecules II, III. The C1–C2, C3–C4 and C5–C6 bond lengths of the molecular chains (II) increase from 1.3525 to 1.4294 Å, 1.3598 to 1.4262 Å, and 1.3485 to 1.3894 Å, respectively, and the C2–C3, C4–C5 bond lengths decrease from 1.4596 to 1.3881 Å, 1.4662 to 1.4112 Å, respectively. And for the molecules III, the C1–C2, C3–C4 and C5–C6 bond lengths of the molecular chains increase from 1.3536 to 1.4331 Å, 1.3552 to 1.4173 Å, and 1.3500 to 1.4045 Å, respectively, and the C2–C3, C4–C5 bond lengths decrease from 1.4836 to 1.4111 Å, 1.4842 to 1.4326 Å, respectively. We find that at first (r=40 Å), the C1–C2, C3–C4 and C5–C6 bond lengths of the molecules I, II and III are all close to a normal double bond length value of 1.35 Å, and the C2–C3, C4–C5 bond lengths approach a normal single bond length value of 1.45 Å. It appears that three molecules have a neutral polyene-like (bond-alternated) structure. At last (r=3 Å), the C1–C2, C3–C4, C5–C6, C2–C3 and C4–C5 bond lengths of three molecules are between 1.35 and 1.45 Å. This shows that the bond lengths tend to non-alternate, thus, it seems that three molecules have an aromatic-like structure.| I | II | III | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ra | a | b | c | d | e | a | b | c | d | e | a | b | c | d | e |
| a r is the Sparkle distance, in Å. | |||||||||||||||
| 3.0 | 1.4263 | 1.3852 | 1.4118 | 1.4071 | 1.3876 | 1.4294 | 1.3881 | 1.4262 | 1.4112 | 1.3894 | 1.4331 | 1.4111 | 1.4173 | 1.4326 | 1.4045 |
| 4.0 | 1.3969 | 1.4065 | 1.3857 | 1.4314 | 1.3676 | 1.3966 | 1.4113 | 1.3964 | 1.4375 | 1.3690 | 1.4002 | 1.4340 | 1.3915 | 1.4578 | 1.3834 |
| 5.0 | 1.3780 | 1.4228 | 1.3699 | 1.4457 | 1.3577 | 1.3768 | 1.4302 | 1.3783 | 1.4531 | 1.3586 | 1.3821 | 1.4470 | 1.3761 | 1.4672 | 1.3648 |
| 6.0 | 1.3683 | 1.4321 | 1.3625 | 1.4521 | 1.3534 | 1.3673 | 1.4409 | 1.3701 | 1.4598 | 1.3539 | 1.3720 | 1.4581 | 1.3675 | 1.4741 | 1.3590 |
| 7.0 | 1.3631 | 1.4373 | 1.3588 | 1.4551 | 1.3513 | 1.3623 | 1.4469 | 1.3661 | 1.4628 | 1.3517 | 1.3655 | 1.4662 | 1.3626 | 1.4782 | 1.3562 |
| 8.0 | 1.3600 | 1.4404 | 1.3569 | 1.4565 | 1.3503 | 1.3596 | 1.4504 | 1.3640 | 1.4642 | 1.3505 | 1.3616 | 1.4715 | 1.3599 | 1.4804 | 1.3548 |
| 9.0 | 1.3581 | 1.4423 | 1.3557 | 1.4573 | 1.3498 | 1.3579 | 1.4526 | 1.3628 | 1.4649 | 1.3499 | 1.3594 | 1.4748 | 1.3583 | 1.4817 | 1.3541 |
| 10.0 | 1.3569 | 1.4435 | 1.3550 | 1.4578 | 1.3495 | 1.3567 | 1.4540 | 1.3620 | 1.4653 | 1.3495 | 1.3580 | 1.4770 | 1.3574 | 1.4824 | 1.3537 |
| 15.0 | 1.3544 | 1.4460 | 1.3537 | 1.4585 | 1.3491 | 1.3538 | 1.4580 | 1.3603 | 1.4660 | 1.3487 | 1.3543 | 1.4826 | 1.3555 | 1.4840 | 1.3531 |
| 20.0 | 1.3537 | 1.4467 | 1.3534 | 1.4586 | 1.3490 | 1.3530 | 1.4589 | 1.3599 | 1.4661 | 1.3486 | 1.3538 | 1.4833 | 1.3553 | 1.4841 | 1.3500 |
| 30.0 | 1.3521 | 1.4521 | 1.3515 | 1.4601 | 1.3489 | 1.3526 | 1.4595 | 1.3598 | 1.4661 | 1.3486 | 1.3537 | 1.4836 | 1.3552 | 1.4842 | 1.3500 |
| 40.0 | 1.3520 | 1.4523 | 1.3515 | 1.4601 | 1.3488 | 1.3525 | 1.4596 | 1.3598 | 1.4662 | 1.3485 | 1.3536 | 1.4836 | 1.3552 | 1.4842 | 1.3500 |
From the situation of no applied electric field to r=40 Å,it is observed that the double bond lengths of the molecule chains (I) are hardly altered. When r=3 Å, the C2–C3 and C4–C5 bond lengths are very close to the double bond lengths in the 2-dimethylamino-5-fluorothiophene ((CH3)2N–(C4SH2)–F), and the C3–C4 bond lengths approach the single bond lengths in (CH3)2N–(C4SH2)–F (see Fig. 2). These differences of the bond lengths between the molecule (I) and (CH3)2N–(C4SH2)–F may be due to the donor–acceptor pair effects. The same is true of molecules II and III. Thus, one may envision two major resonance forms, as shown in Scheme 2.
 | ||
| Fig. 2 AM1 optimized bond lengths (in Å). | ||
 | ||
| Scheme 2 | ||
Resonance form A is referred to as quinoid-like, and resonance form B is aromatic-like. In substituted molecules I, II, and III with weak donors and acceptors, the quinoid-like (neutral) resonance forms dominates the ground state; when donor and acceptor substituents become stronger, the contribution of the aromatic-like (charge-separated) resonance form to the ground state increases.
4. Molecular polarizabilities
The evolution of the linear polarizabilities α, the first-order hyperpolarizabilities β and the second-order hyperpolar izabilities γvs. BACS for molecules I, II and III is shown in Fig. 3. The evolution patterns of curves for molecules I, II and III are qualitatively similar. In addition, it is also seen in Fig. 3 that there is asymmetry in the curves between the quinoid and aromatic limits, which is not observed for pull–push polyenes.9,13 This is obviously due to the different bridge polarizability of the quinoid compared to aromatic bridge. This naturally is not observed with the polyenic structure since the ground-state and charge-separated bridges are symmetric. | ||
| Fig. 3 Plot of α, β, γ of the donor–acceptor 2,5-dimethylenethiocyclopentenes (I) (squares), 2,5-dimethyleneoxopentenes (II) (triangles) and 2,5-dimethylenepyrrolines (III) (circles) vs. BACS. | ||
With increment of BACS, the evolution pattern of the linear polarizabilities for all three molecules is very similar (Fig. 3, top); it initially increases at smaller BACS, peaks in a positive sense, and then decreases. No matter what the BACS value is, the α curve of molecule I is always at the top of the other two α curves. When BACS<ca. −0.2, the α curve of molecule II mingles with that of molecule III, and when BACS>ca. −0.2, the former ascends over the latter, and then descends and crosses the latter. The variation of the first-order hyperpolarizabilities with BACS for all three molecules is more complex than that of α (Fig. 3, middle): it first increases, peaks in a positive sense, passes through zero, peaks negatively, and finally increases again. The evolution pattern of the β curve is consistent with previous studies7c,8a,8b,20 and experimental results.7a,21 This trend in the first-order hyperpolarizability is the same for all three molecules. The differences of the β values between the three molecules are very small. The β curve of molecule I first lies under the other two β curve as BACS increases, crosses them, and then ascends over them, yet the β curve of molecule II mingles with that of molecule III. From Fig. 3, it is observed that the relative sizes of the β values for the three molecules depend on the selection of the r value.
The evolution of the second-order hyperpolarizabilities vs. BACS for the three molecules is more complicated than that of α and β: it first increases, peaks positively, decreases, peaks in a negative sense, then increases and exhibits a small positive maximum and again decreases. The evolution pattern of the γ curve is in agreement with previous studies7c,8a,8b,20 and experimental observation.22 The trend of the second-order hyperpolarizability is the same for all three molecules. The differences between the three γ curves are very small. The γ, curve of molecule I first lies under the other two γ curves as BACS increases, crosses them, and then ascends over them, yet the γ curve of molecule II mingles with that of molecule III. It is seen from Fig. 3 that the relative sizes of the γ values for the three molecules depend on the selection of the r value.
In contrast to the behavior of the polyenes.9,13 the charge transfer in the systems of each of the three molecules is between the π-orbitals on the carbon atoms and heteroatoms. This leads to a reduction in the polarization and hence to a reduction in the NLO responses. An important localization of the π-charge on the sulfur, oxygen and nitrogen atoms of the three molecules leads to a π-charge deficit on the conjugated chains. The heteroatoms thus play the role of π-electron acceptors and anchor part of the π-electron cloud, which limits the capacity of π-charge delocalization. This may be responsible for the reduction of molecular polarizabilities. In addition, we also find that for the conpounds I, II and III, the order of the NLO responses increases from compound II, III to compound I. One of the parameters affecting the coupling between the donor and acceptor substituents is the energy barrier imposed by the conjugating bridge. This factor becomes relevant and important especially if the conjugated pathway is made up of aromatic rings. The lower the aromatic delocalization energy barrier, the higher the NLO responses should be. The order of the delocalization energy for the aromatic heterorings (thiophene, furan and pyrrole) is as follows: Ethiophene>Epyrrole>Efuran. Therefore, one could expect that the order of NLO responses increases from compound II, III to compound I. This seems to be consistent with the results reported here. Certainly, NLO response is determined not only by the nature of the heterocyclic ring but also by the substituents.
5. Influence of molecular architecture on the hyperpolarizabilities
In the discussions above, we studied molecular polarizabilities of the three molecules (I, II and III) and found that the conjugated molecules with quinoidicity possess large molecular polarizabilities. In this section, we systematically examine the hyperpolarizabilities of the conjugated molecules sketched in Fig. 4. Our main concern here is to illustrate the influence of molecular architecture and thereby to provide useful information for the design of structures optimized for the second-order non-linear optical applications. We pay special attention to the quinoid and aromatic structures, i.e., to the evolution of the β values with quinoidicity, and also investigate molecular polarizabilities of their oligomers. Since polyenes are considered as the prototypical π–conjugated systems, we also perform similar calculations for the corresponding substituted polyenes. | ||
| Fig. 4 Molecular structure of the NO2–NH2 substituted quinoid-type molecules, polythiophenes, polyfurans and polypyrroles. | ||
The results are reported in Table 2. As expected, from the comparison of the hyperpolarizabilities of the aromatic heterorings (O2N–NH2 substituted thiophene, furan and pyrrole) with these obtained for their quinoid-type counterpart, one observes a large enhancement of the hyperpolarizability values: β evolves from 5.208×10−30 to 12.232×10−30 esu for the thiophene-based molecules, from 5.659×10−30 to 11.553×10−30 esu for the furan-based molecules and from 5.868×10−30 to 10.839×10−30 esu for the pyrrole-based molecules. With increment of N (where N is the number of conjugated double bonds between the donor and acceptor groups), the quinoid-type molecules have larger hyperpolarizabilities than their aromatic heterorings counterpart. Among the above comparisons, although the quinoid-type molecule is longer than the aromatic-type molecule, if their hyperpolarizabilities are plotted vs. N (see Fig. 5), one may find that the quinoid-type molecules have the high efficiency of the second-order non-linear response. Thus, the switch from a purely aromatic structure to a quinoid structure appears as a right move to boost the hyperpolarizabilities. Compared with these aromatic heteroring and quinoid-type molecules, the hyperpolarizability of trans O2N–NH2 substituted hexatriene has a larger value. This again demonstrates the high efficiency of the polyene second-order non-linear response.
| β | β | β | β | ||||
|---|---|---|---|---|---|---|---|
| Nb | IVa | Va | IVb | Vb | IVc | Vc | O2N–(CH![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) CH)n–NH2c CH)n–NH2c |
| a Units for β are 10−30 esu.b N is the number of conjugated double bonds between the donor and acceptor groups.c n is the number of structural units in the conjugated chains. | |||||||
| 1 | 2.070 | ||||||
| 2 | 5.208 | 5.659 | 5.868 | 11.496 | |||
| 3 | 12.232 | 11.553 | 10.839 | 31.159 | |||
| 4 | 23.440 | 22.386 | 20.336 | 57.527 | |||
| 5 | 48.147 | 40.934 | 37.534 | 85.738 | |||
| 6 | 40.623 | 44.254 | 37.799 | 112.548 | |||
| 7 | 139.841 | 98.837 | 91.651 | 136.520 | |||
| 8 | 65.862 | 61.181 | 51.524 | 157.233 | |||
| 9 | 341.788 | 194.781 | 189.132 | 174.866 | |||
| 10 | 82.379 | 76.990 | 65.596 | 189.667 | |||
| 11 | 733.224 | 328.615 | 327.578 | 202.077 | |||
| 12 | 93.866 | 85.891 | 71.908 | 212.415 | |||
| 13 | 1410.642 | 494.376 | 220.979 | ||||
| 14 | 103.712 | 95.667 | 79.035 | 228.209 | |||
| 15 | 2531.922 | 688.535 | 234.131 | ||||
| 16 | 108.801 | 99.463 | 81.714 | 238.959 | |||
| 17 | 4265.216 | 894.841 | 243.234 | ||||
| 18 | 113.725 | 105.666 | 84.543 | 246.614 | |||
| 19 | 7018.922 | 1118.296 | 249.470 | ||||
| 20 | 114.649 | 106.722 | 88.238 | 252.027 | |||
| 21 | 11300.079 | 1334.135 | 253.957 | ||||
 | ||
| Fig. 5 Effect of increasing chain length (N) on the hyperpolaizabilities (β) of the substituted quinoid-type molecules IVa (solid squares), IVb (solid triangles), IVc (solid circles), polythiphenes Va (open circles), polyfurans Vb (open triangles), polypyrroles Vc (open diamonds) and polyenes (open squares). | ||
It is seen from Table 2 that the substituted quinoid-type oligomers (IVa, IVb and IVc) have considerably larger hyperpolarizabilities than the substituted aromatic heteroring oligomers (Va, Vb and Vc) and the corresponding polyenes with chain extension, and yet the hyperpolarizabilities of the substituted polyenes are larger than that of the substituted aromatic heteroring oligomers. For the substituted quinoid-type oligomers series, the order of the hyperpolarizabilities is as follows: βVIa>βVIb>βVIc, moreover, the increasing extents of the hyperpolarizabilities for VIa are far larger than that for the other two molecules (VIb, VIc) with chain extension. The same conclusions are reached from the results obtained for the Va, Vb and Vc series, except the increasing extents of the hyperpolarizabilities for the Va, Vb and Vc series are not so large as that for the IVa, IVb and IVc series with chain extension. In addition, one may also find that the increasing extents of the hyperpolarizabilities for the substituted polyenes are not so large as that for the IVa, IVb and IVc series with chain extension too. With chain extension, the geometric ground state structures of oligomers IVa changes and goes from a purely quinoidic character to a more aromatic character. This would shift to the right position of the molecule in the β-BACS curves of Fig. 3, i.e. closer to the optimal structure, and hence be responsible for the huge calculation chain-length dependence; yet the geometric structures of the donor–acceptor polyenes changes with chain size and goes from a purely bond alternated character to a more non-alternated character, that is, BLA first increases, gradually gets slowly and finally reaches saturation. This results in the saturation of the hyperpolarizabilities for the donor–acceptor polyenes with increasing N.
The variation of the hyperpolarizabilities for the substituted quinoid-type molecules, aromatic heteroring molecules and corresponding polyenes with the increment of the number of conjugated double bonds between the donor and acceptor groups (N) is shown in Fig. 5. These curves show two kinds of completely different trends. For small N, the increment of the hyperpolarizabilities for the substituted aromatic heteroring oligomers (Va, Vb and Vc) and the corresponding polyene is quite rapid, eventually saturating (becoming linear in N) for N>20. However, with the increment of N, the hyperpolarizabilities of the substituted quinoid-type molecules (IVa, IVb and IVc) first increases very slowly, gradually gets fast and finally seems not to show any signs of saturation. There seems little doubt, therefore, on the basis of these results that the substituted quinoid-type molecules (IVa, IVb and IVc) have very large hyperpolarizabilities.
6. Conclusions
AM1 calculations are performed to study the molecular structures and the linear and non-linear polarizabilities of the donor–acceptor quinoid-type molecules (I, II and III) under the influence of an external electric field defined by point charges (Sparkles). We investigate and compare the relationships between the molecular structures and the molecular polarizabilities of the substituted quinoid-type molecules. The results show that the relative sizes of the molecular polarizability values for the three molecules depend on the selection of the donor–acceptor pair. We also systematically examine the influence of molecular architecture on the hyperpolarizabilities. It is found that the substituted quinoid-type molecules (IVa, IVb and IVc) have considerably larger hyperpolarizabilities than the substituted aromatic heteroring molecules (Va, Vb and Vc) and the corresponding polyenes with chain extension, and yet the hyperpolarizabilities of the substituted polyenes are larger than those of the substituted aromatic heteroring molecules with chain extension. In addition, the increasing extents of the hyperpolarizabilities for the substituted quinnoid-like molecules are far larger than those for the substituted aromatic heteroring mlecules and the corresponding polyenes. These properties make the quinoid-type molecules interesting candidates for applications in non-linear optics, particularly in the area of poled polymer films.References
- Nonlinear Optical Properties of Organic Molecules and Crystals, ed. D. S. Chemla and J. Zyss, Academic Press, New York, 1987; vols. 1 and 2. Search PubMed.
- P. N. Prasad and D. J. Williams, Introduction to Nonlinear Optical Effects in Molecules and Polymers, Wiley, New York, 1990. Search PubMed.
- (a) D. R. Kanis, M. A. Ratner, T. J. Marks, Chem. Rev., 1994, 94, 195; (b) Search PubMed; Chem. Rev., 1994, 94 (1) (issue dedicated to non-linear optics) Search PubMed.
- S. R. Marder, D. N. Beratan and L.-T. Cheng, Science, 1991, 252, 103 CrossRef CAS; S. R. Marder, C. B. Gorman, B. G. Tiemann and L.-T. Cheng, J. Am. Chem. Soc., 1993, 115, 3006 CrossRef CAS.
- Y. Sheng, Y. Jiang and X.-C. Wang, J. Chem. Soc., Faraday Trans., 1998, 94, 47 RSC.
- L.-T. Cheng, W. Tam, S. H. Stevenson and G. R. Meredith, J. Phys. Chem., 1993, 95, 10631; L.-T. Cheng, W. Tam, S. R. Marder, A. E. Stiegman, G. Rikken and C. W. Spangler, J. Phys. Chem., 1993, 95, 10643.
- S. R. Marder, L.-T. Cheng, B. G. Tiemann, A. C. Friedli, M. Blanchard-Desce, J. W. Perry and J. Skindhøj, Science, 1994, 263, 511 CrossRef CAS; S. R. Marder, J. W. Perry, G. Bourhill, C. B. Gorman and B. G. Tiemann, Science, 1994, 261, 183; S. R. Marder, C. B. Gorman, J. W. Perry, G. Bourhill and J.-L. Brédas, Science, 1994, 265, 632 CAS.
- F. Meyers, S. R. Marder, B. M. Pierce and J.-L. Brédas, J. Am. Chem. Soc., 1994, 116, 10703 CrossRef CAS; C. B. Gorman and S. R. Marder, Proc. Natl. Acad. Sci. USA, 1993, 90, 11297 CAS; S. M. Risser, D. N. Beratan and S. R. Marder, J. Am. Chem. Soc., 1993, 115, 7719 CrossRef CAS.
- W. Zhu and Y. Jiang, Phys. Chem. Chem. Phys., 1999, 1, 4169 RSC.
- S. J. Lalama, K. D. Singer, A. F. Garito and K. N. Desai, Appl. Phys. Lett., 1981, 39, 940 CrossRef CAS.
- M. Ravi and T. P. Radhakrishnan, J. Phys. Chem., 1995, 99, 17624 CrossRef CAS.
- Y. Sheng and Y. Jiang, J. Chem. Soc., Faraday Trans., 1998, 94, 1823 RSC; Y. Sheng and Y. Jiang, J. Chem. Soc., Faraday Trans., 1998, 94, 1829 RSC.
- W. Zhu and Y. Jiang, THEOCHEM, in the press. Search PubMed.
- J. J. P. Stewart, J. Comput.-Aided Mol. Des., 1990, 4, 1 Search PubMed.
- M. B. Coolige, J. J. P. Stewart and J. Frank, Seiler Research Laboratory, United States Air Force Academy, Colorado Spring, CO 80840..
- M. J. S. Dewar, E. G. Zoebisch, E. F. Healy and J. J. P. Stewart, J. Am. Chem. Soc., 1985, 107, 3902 CrossRef.
- A. D. Mclean and M. Yoshimine, J. Chem. Phys., 1988, 89, 385 CrossRef CAS.
- J. Applequist, J. Chem. Phys., 1984, 85, 279 CrossRef CAS.
- H. A. Kurtz, J. J. P. Stewart and K. M. Dieter, J. Comput. Chem., 1990, 11, 82 CrossRef.
- I. D. L. Albert, T. J. Marks and M. A. Ratner, J. Phys. Chem., 1996, 100, 9714 CrossRef CAS.
- G. Bourhill, J.-L. Brédas, L.-T. Cheng, S. R. Marder, F. Meyers, J. W. Perry and B. G. Tiemann, J. Am. Chem. Soc., 1994, 116, 2619 CrossRef CAS.
- S. R. Marder, J. W. Perry, G. Bourhill, C. B. Gorman, B. G. Tiemann and K. Mansour, Science, 1993, 261, 186 CrossRef CAS.
| This journal is © the Owner Societies 2000 |
