Supercritical fluid extraction of solids. Statistical thermodynamic approach

Abstract

To study the effect of non-sphericity of solvent and solute molecules on the main characteristics of supercritical fluid extraction we consider the fourth-order virial expansion in which the individual virial coefficients (and cross terms) were determined from the formula proposed recently for the Kihara generalized pair potential. The Kihara four-step square-well potential was assumed; its form makes it possible to write analytic expressions for the considered virial coefficients and, consequently, for the main thermodynamic functions—the residual chemical potential of solute and total pressure. The method is applied to determine the dependence of the mole fraction of solute on temperature or pressure in the binary systems carbon dioxide–naphthalene and ethylene–naphthalene and the effect of the cosolvent on the solute concentration in the system ethylene–naphthalene–acetone at 308 K. Fair agreement with the simulation and experimental data was found.

---

1. Introduction

Supercritical fluid extraction is a gentle separation method employed in laboratories and industry to obtain higher-molecular products. Typically, different low-volatility materials are extracted from solids by supercritical carbon dioxide, the simplest hydrocarbons (e.g. ethene), water, etc.¹ All the solvents used are of non-sperical shape, often with permanent dipoles, quadrupoles, etc.

Within statistical thermodynamics, the equilibrium behaviour of binary or ternary fluid systems at conditions corresponding to the supercritical fluid extraction (SFE) of solids is described by the perturbation theory of fluids, by the virial expansion (to a sufficiently high order) and by simulations.² In the vast majority of the statistical thermodynamic methods, the simple fluid interaction pair potential, most often that of Lennard-Jones, has been considered.²

Recently, we studied³ the ternary system carbon dioxide–benzoic acid–methanol applying a variant of the perturbation theory⁴ in which the Kihara generalized pair potential was assumed. This variant made it possible to determine the effect of non-sphericity (as well as electrostatic forces) of considered molecules on the characteristic thermodynamic properties of SFE. It was concluded that the shape effect played the most important role and the introduction of the (non-zero) rod-like core considered e.g. as the core of CO₂ in the Kihara pair potential was inevitable to obtain the correct values of the residual chemical potential of the solute (in the limit of an infinitely diluted mixture). The effect of the shape factor increased with increasing density. Due to the limits and approximations inherent to the perturbation theory (the second-order perturbation expansion essentially neglects terms of O(T³), the approximative expression used for the average correlation function and the fact of the numerical differentiation to obtain the pressure and the residual chemical potential) definitive conclusions could not be drawn.

Virial expansions of pressure, Helmholtz energy and residual chemical potential offer a considerably simpler and straightforward approach, provided all the virial coefficients (including the cross terms) up to the fourth order are known with sufficient accuracy. To meet this precondition, Goldman et al.² determined for the Lennard-Jones pair potential all the necessary coefficients by numerical integration and compared the resulting residual chemical potential with their simulation data. The extension to non-spherical molecules has not been given and the possibility of pre-averaging of the Mayer function and the determination of the virial coefficients for the modified (but still simple-fluid) pair potential, as proposed by the authors, has not been examined.

Recently a method has been proposed from our laboratory,⁵ enabling the determination of the virial coefficients of non-spherical convex molecules; the ‘‘shape’’ and distance contributions are factorized and the virial coefficient expressed as a product of the corresponding hard convex body virial coefficient and derivatives of the Mayer functions (for the simple fluid pair potential). In the case of the second-order coefficient, the well known expression⁶ is obtained. The accuracy of the method for the third virial coefficient depends on the quality of the approximation for the hard convex body third virial coefficients (see refs. 5 and 7). At present, our ignorance of the formula for three contributions to the hard convex body fourth virial coefficient prevents the determination of the Kihara fourth virial coefficient from the above-mentioned general formula; we approximated the (total) fourth virial coefficient by that of the hard convex bodies with the thicknesses given by the σ-parameters of the Kihara pair potential. This approximation is supported by the relatively small effect of the fourth-order term on the compression factor even at high densities and the fact that at higher temperatures its values are small and positive.⁸

2. Theory

Thermodynamics of the supercritical fluid extraction of solute from a solid material relates^2,3 the solute mole fraction, x₂, to the vapour pressure of pure compound in the solid state, P₂⁰, molar volume, V₂⁰ , total pressure of the fluid phase, P, density, ρ and the residual chemical potential (i.e. the difference of the actual function and that of the perfect gas at the same conditions) of the solute, Δμ₂:

In eqn. (1) both the pressure and residual chemical potential depend on the properties of binary (or ternary if cosolvent is considered) mixtures. The expression was derived under assumption of the zero solvent solubility in a solid and its negligible volume changes with pressure; for details see discussion in ref. 9.

In the perturbation theory of Kihara molecule fluids the residual Helmholtz energy is expressed³ in terms of the reference hard body term, first- and second-order perturbation terms and a small correction term. By differentiating the reduced residual Helmholtz energy (ΔF) with respect to density and multiplying by density, the compression factor results. The residual chemical potential of solute (in an infinite diluted mixture) is obtained by differentiating ΔF with respect to the number of solute molecules, N₂; the final expressions are quite complex.³ Thus, the contribution to the residual chemical potential of solute from the reference term is

Similarly, the first-order perturbation term possesses the form

Terms (μ₂)_pint/kT and (μ₂)_p2/kT (which both include correlation functions) are determined numerically. In the above-mentioned expressions, R_i, S_i, V_i are geometric characteristics (the mean curvature integral divided by 4π, surface area and volume) of molecule i and r, s, q, ν are similar characteristics of the representative hard convex body (hcb) mixture, i.e. a system of the parallel hard convex bodies to the cores of the individual molecules (in the Kihara potential) with thicknesses related to σ-parameters.

The perturbation theory works well at densities typical for the liquid phase, it is less good at conditions near the critical point.

Virial expansion for the residual Helmholtz energy, pressure and the residual chemical potential leads, even in the case of mixtures, to easily tractable expressions and the whole problem reduces to the accurate determination of all the necessary coefficients. Whereas for pure simple fluids whose molecular interactions are orientationally independent, the second-, third- and fourth-order virial coefficients are readily available,^2,8,10 in the case of mixtures of nonspherical molecules the evaluation of all the cross terms is more difficult. Until recently these quantities were available for the Kihara molecules only from numerical calculations.

Recently it was shown from our laboratory⁵ that the virial coefficients of the Kihara non-spherical molecules can be expressed as integrals from the product of the corresponding hcb cluster integrals (hcb virial coefficients) and derivatives of the Mayer functions, f_M, with respect to the (length) coordinates

Thus e.g. for the Kihara square-well potential

where

δ=e^(ε/kT)−1 (7)

and C_i stands for a combination of the hcb cross virial coefficients for a triplet of hcb's. (Both B^hcb and C^hcb can be determined from the exact or approximative (in the latter case) expressions in terms of V_i, S_i and R_i of the individual parallel hard convex bodies to the given cores); γ denotes the square-well parameter.

In principle, similar expressions can be written for the fourth and higher virial coefficients; however, we are not aware of any approximation for three contributions to the fourth virial coefficient of hard convex bodies. Thus, we substitute for D^Kih the approximative expression¹¹ for the hard convex body fourth virial coefficient, D^hcb.

Knowledge of all the necessary virial coefficients—i.e. up to the fourth order—makes it possible to determine the total pressure, the residual Helmholtz energy and the residual chemical potential of the solute:

3. Pair potential

In the majority of the statistical thermodynamic studies, the Lennard-Jones 12–6 pair potential,

has been considered. Its generalized form is the Kihara pair potential⁶ which possesses a similar functional form where, however, instead of the centre–centre distance, r, the shortest surface–surface distance, s, (depending on the orientation coordinates ω₁, ω₂) is used,

To simplify the determination of the third virial coefficient we introduce the Kihara four-step square-well potential, which mimics the Mayer function for the 12–6 (in the special case LJ) pair potential, and equals zero for distances greater than 2σ. The first step takes into account softness of the repulsive branch (on the interval s*⩽1), the division point between second and third step and values of ε₂/k and ε₃/k were obtained by optimization of the Mayer functions for the present and LJ potentials. Then,

where a=0.937, b=1.507, c=2.000, ε₁=0.833ε, ε₂=−0.7ε, and ε₃=−0.2ε. This pair potential (which is a modification of the potential introduced by Chen and Kreglewski¹²) yields, in the case of the point-wise core, the second virial coefficient in agreement with values for LJ 12–6 interactions in a broad range of temperatures; the potential makes it possible to write both the second and third (and, in principle, also higher) virial coefficients of the non-spherical convex molecules in an analytic form. A comparison of the dependence of this potential and LJ 12–6 form on the reduced distance is shown in Fig. 1.

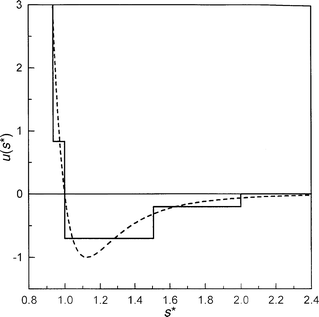Fig. 1 The dependence of the Kihara four-step square-well and the corresponding LJ pair potentials on the reduced distance. (——— Kihara potential, – – – – LJ function).

The carbon dioxide molecule is considerably non-spherical; we ascribe to it a rod-like core. Because of the fact that the (relatively high) quadrupole moment is not taken into account, the length of the rod exceeds the double of the O–C bond length. Also an ethene molecule is of rod-like shape with the core length slightly larger than that of the C[double bond, length half m-dash]C bond, obviously due to the contribution of hydrogen atoms.

The naphthalene molecule is of oblate shape; as its core we take the slab enveloping two benzene rings; parameter a denotes the C–C distance. All three parameters of the Kihara pair potentials were obtained by fitting the low-temperature orthobaric data, cf. ref. 13. Values of the LJ parameters were taken from ref. 2. Parameters of the Kihara four-step square-well and LJ potentials for the considered compounds are given in Table 1.

Table 1 Parameters of the Kihara four-step square-well and LJ pair potentials

Compound	(ε/k)/K	σ/nm	(l/a)/nm
Kihara SW potential
Carbon dioxide	347.49	0.2734	0.2734
Ethylene	283.17	0.3366	0.1870
Naphthalene	975.79	0.3975	0.0996
LJ potential
Carbon dioxide	246.1	0.3753
Ethylene	202.5	0.4499
Naphthalene	629.5	0.5627
Acetone	443.0	0.4670

---

Lorentz–Berthelot combining rules were assumed to hold for the potential parameters of unlike pairs.

4. Applications to the model systems

In order to find out how well the prediction from the considered virial expansion (together with the used pair potential and the approximate expression for the four-order coefficient) compares with that from the virial expansion for the LJ molecules (where all the virial coefficients were determined numerically) we studied the dependence and the residual chemical potential of solute on the ratio (σ₁₂/σ₁₁)³ in the binary system of LJ molecules at the reduced temperature T*=(kT/ε₁₁)=1.5, reduced density ρ*=ρσ₁₁³=0.4 and (ε₁₂/ε₁₁)=1. Results are listed in Table 2. It is obvious that values of the excess chemical potential calculated within the above-mentioned approach agree well both with the exact four-order virial expansion and the simulation data.²

Table 2 The residual chemical potential of solute, Δμ₂/kT, in the model binary system at T*=1.5 and ρ*=0.4

(σ12/σ11)^3	4-step SW	LJ	Simulation
0.5	−0.761	−0.773	−0.787
1.0	−1.028	−1.267	−1.327
2.0	−1.988	−2.333	−2.433
2.7	−3.025	−3.133	−3.280
3.5	−4.587	−4.147	−4.333

---

In Table 3 we compare values of the residual chemical potential in the model binary system with (σ₁₂/σ₁₁)³=1 and ε₁₂/ε₁₁=1.5 at the reduced temperature T*=1.5 calculated from the virial expansion and from the perturbation theory at several values of the reduced density ρ*. It is obvious that both methods yield very similar results; at ρ*=0.4 both calculated residual chemical potentials compare well with the simulation value² (Δμ₂/kT)=−3.24.

Table 3 Comparison of the residual chemical potential of solute calculated from the perturbation theory (per) and the virial expansion (vir) at T*=1.5

ρ*	(Δμ2/kT)vir	(Δμ2/kT)per
0.1	−1.00	−0.93
0.2	−1.87	−1.88
0.3	−2.58	−2.55
0.4	−3.11	−3.20
0.5	−3.45	−3.76

---

Next, we studied two binary systems—carbon dioxide–naphthalene and ethene–naphthalene and one ternary system—ethene–naphthalene–acetone. Carbon dioxide is the most often used supercritical extractive agent. We determined the dependence of the logarithm of the naphthalene mole fraction, log x₂, on pressure at constant temperature T=328 K or its dependence on temperature at constant pressures P=80 and 100 bar in the system carbon dioxide–naphthalene (see Figs. 2 and 3); the dashed line depicts results for the point-wise cores). It is apparent that the present theory yields data in reasonable agreement with experiments and predicts correctly the trends of the dependences on pressure or temperature. It can be concluded that if the shape of molecules is properly taken into account, fair predictions are obtained.

Fig. 2 Mole fraction of naphthalene vs. pressure in the binary system CO₂—naphthalene at T=328 K. (——— Kihara, – – – – LJ, ● experimental data¹⁴).

Fig. 3 Mole fraction of naphthalene vs. temperature in the binary system CO₂–naphthalene at P=80 bar (– – – –) and 100 bar (———); (● experimental data¹⁵).

Model systems mostly suited for the present study of the effect of nonsphericity on the SFE characteristics are systems containing ethene, such as e.g. ethene–naphthalene. Contrary to carbon dioxide, the ethene molecule is practically nonpolar and can be correctly modelled as the Kihara molecule with the rod-like core. Naphthalene is an example of the oblate Kihara molecule—its core is a planar object, the geometric characteristics of which are readily available. In Fig. 4 we compare the dependence of the logarithm of the mole fraction of naphthalene on pressure at temperature 285.15 K calculated for the Lennard-Jones and Kihara pair potentials with experimental data of Tsekhanskaya et al.¹⁴ The comparison of the dependences for the point-wise and non-zero convex shaped molecular cores in Figs. 2 and 4 reveals the importance of the correct description of the intermolecular interactions both of solute and solvent molecules.

Fig. 4 Mole fraction of naphthalene vs. pressure in the binary system ethene–naphthalene at T=285.15 K. (———) Kihara, (– – – –) LJ, ● experimental data¹⁴).

Fig. 5 depicts the dependence of the solute concentration on pressure at temperatures 285.15 and 308.15 K. It is obvious that accuracy of the description increases with temperature (this is, however, true also for the experimental data).

Fig. 5 Mole fraction of naphthalene vs. pressure in the binary system ethene–naphthalene at T=285.15 K (———) and 308.15 K (– – – –); ● and ○ experimental data¹⁴).

Finally, we have studied the ternary system of solvent–solute–cosolvent; ethene–naphthalene–acetone at 308 K was taken as a convenient model system. The geometric characteristics of the acetone planar triangular core are available too. However, in this study we consider for simplicity molecules of acetone to possess a point-wise core. (Compounds with small molecules but non-negligible permanent dipoles, quadrupoles etc. usually serve as cosolvents. Because we limited our considerations to non-polar molecules we ascribed here the point-wise core to molecules of acetone and took the parameters from the literature.² The electrostatic contributions to the pair interactions were taken into account in the previous study³ of the SFE systems by the perturbation approach.) From Fig. 6 it is apparent that theory, in agreement with experiment, predicts considerable increase of the concentration of solute in the fluid phase after addition of a small amount of cosolvent.

Fig. 6 Mole fraction of naphthalene vs. pressure for several concentrations of acetone (x₃) in the ternary system ethene–naphthalene–acetone at T=308 K.

5. Conclusion

From the list of solvents used in the supercritical fluid extraction it is evident that the shape of their molecules and their electrostatic properties are decisive for compounds to act as extractive agents and cosolvents in supercritical fluid extraction. Recently we have found the shape effect to be of great importance. To study the SFE equilibrium behaviour of binary or ternary systems, the perturbation theory (of the Kihara molecule fluids) and virial expansion technique are both exact and convenient methods, however, the virial expansion approach is simpler and straightforward.

Application of the virial expansion technique depends on the possibility of determining the virial coefficients B_ij, C_ijk, D_ijkl of the general Kihara molecules without excessive effort. This condition is met by the method proposed recently from our laboratory, where the evaluation of the Kihara virial coefficient depends on knowledge of the cluster integral for the corresponding hard convex bodies. This fact gives a strong support to the—up to recently ‘academic ’—effort to improve our knowledge and increase accuracy for the determination of the higher hcb virial coefficient.

With a fair knowledge of all the virial coefficients, the procedure is straighforward and exact and a large variety of systems and properties can be readily studied.

Acknowledgements

This work was supported by grant No. 203/97/0241 of the Grant Agency of the Czech Republic.

References

1. M. McHugh and V. Krukonis, Supercritical Fluid Extraction, 1994, Butterworth..
2. S. Goldman, C. S. Gray, W. Li, B. Tomberli and C. G. Joslin, J. Phys. Chem., 1996, 100, 7246.
3. T. Boublík, Mol. Phys., 1997, 90, 585.
4. T. Boublík, J. Chem. Phys., 1987, 87, 1751.
5. M. Šindelka and T. Boublík, Mol. Phys., 1999, 97, 1035.
6. T. Kihara, Adv. Chem. Phys., 1963, 5, 147.
7. M. Šindelka and T. Boublík, Mol. Phys., 1999, 96, 243.
8. J. A. Barker and J. Monogham, J. Chem. Phys., 1962, 36, 2558; J. A. Barker and J. Monogham, J. Chem. Phys., 1962, 36, 2564.
9. U. K. Deiters and I. Swaid, Ber. Bunsen-Ges. Phys. Chem., 1984, 88, 791.
10. J. O. Hirschfelder, C. F. Curtiss and R. B. Bird, Molecular Theory of Gases and Liquids, Wiley, New York, 1954..
11. T. Boublík, Mol. Phys., 1981, 42, 209.
12. S. S. Chen and A. Kreglewski, Ber. Bunsen-Ges. Phys. Chem., 1977, 81, 1048.
13. J. Pavlíček and T. Boublík, J. Phys. Chem., 1992, 98, 2298.
14. Y. V. Tsekhanskaya, M. V. Iomtev and E. V. Mushkina, Zh. Fiz. Khim., 1964, 38, 2106.
15. Z. Suoqi, W. Renan and Y. Guanghua, J. Supercrit. Fluids, 1995, 8, 15.

---

Footnote

† Presented at the 1st Workshop on Global Phase Diagrams (Bunsen-Kolloquium 77), Walberberg, Germany, 21st–24th March, 1999.

---