Analysis of the NQR parameters in 2-nitro-5-methylimidazole derivatives by quantum chemical calculations
Received 3rd August 1999, Accepted 10th November 1999
First published on UnassignedUnassigned22nd December 1999
Abstract
The present study involves nitrogen NMR-NQR measurements and semiempirical as well as ab initio
calculations at the different levels in three 2-nitro-5-methylimidazole derivatives. The NMR-NQR data were compared with the results of the quantum chemical calculations with the geometry optimization by seven semiempirical and a few ab initio methods. Since the use of a finite basis set is always a source of uncertainties in the electric field gradient (EFG) tensor components, the calculations were performed in different basis sets, and—regarding the effect of the functional—also at different levels of the theory. The results closest to experimental ones were obtained at the BLYP level of theory.
Introduction
Imidazole and its numerous derivatives have long been the
subject of interest of interdisciplinary researchers such as biophysicists or biochemists. The presence of such imidazole
derivatives as histidine, histamine or polycarpine in the
natural environment, together with the fact that imidazole is a
component of proteins and pure nucleic bases, makes this
compound fundamental for synthesis of many compounds
which occur in biologically active systems. Particularly interesting medical applications are the antimycotics metronidazole,
tynidazole, clotrimazole, oxykonazole, sulconazole,
bifonazole, imazazlyl.1–3
Metronidazole in appropriate doses
is also one of the most frequently used radiosensibilisers, in
vivo and in vitro.4 In recent years much attention has been
devoted to the nitro derivatives of imidazole because of their
anticancerous effect. So far only metronidazole from this class
of compounds has been introduced to medical therapy,
however, the studies on the cytostatic effect of the others are
still under way. As toxicity of a given compound seems to be
related to its electronic structure, it was interesting to investigate electron density distribution in the compounds of interest. In our previous paper5 we have found that the
introduction of a substituent at 1H position of the imidazole
ring leads to a redistribution of p-electron density and its
delocalisation from the nitrogen atom –N![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) onto the nitrogen –NH–.
Moreover, we concluded that even very subtle substitution effects could significantly change the electron density distribution
in imidazoles.
onto the nitrogen –NH–.
Moreover, we concluded that even very subtle substitution effects could significantly change the electron density distribution
in imidazoles.
This work reports results of quantum chemical studies for
the selected three derivatives of 2-nitro-5-methylimidazole
(Fig. 1). The specific substituents and chemical names are
given in Table 1. It is well known that 2-nitroimidazole compounds
may appear in two different tautomeric forms (Fig. 2).
We have performed the appropriate calculations and found
that the form with the nitro group in the 2 position is more
stable, however, the difference between the energies of the two
forms is rather small and equal to 0.1 Eh. As a result of the
substitution of a nitrogen group at position 2 and a methyl
group at position 5, the quadrupole coupling constants on the
nitrogen atoms in the imidazole ring increase and in the nitro
group decrease.
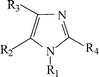 |
| | Fig. 1 Structural formula of the studied compounds. | |
Table 1
The chemical names and substituents of the compounds studied
| No | Compound | R1 | R2 | R3 | R4 |
|---|
| |
|---|
| 1 | Imidazole | H | H | H | H |
| 2 | 2-Nitro-5-methylimidazole | H | NO2 | H | CH3 |
| 3 | 1-(2-Hydroxyethyl)- | CH2CH2OH | NO2 | H | CH3 |
| 2-Nitro-5-methylimidazole |
| (metronidazole) |
| 4 | 1-(2-Carboxymethyl)ethyl-2- | CH2CH2OCOCH3 | NO2 | H | CH![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) CHPhCH3O CHPhCH3O |
| nitro-5-[2-(p-methoxy |
| phenyl)ethenyl]imidazole |
 |
| | Fig. 2 The tautomeric forms of imidazole. | |
The aim of this paper is a comparison of the experimental
and calculated NQR parameters. The effect of the parametrisation (in the case of semiempirical methods) as well as the
basis set and the functional (in the case of ab initio methods)
was analysed and the best basis set as well as the method best
reproducing NQR parameters was proposed.
Calculation
details
It is well known that the calculation methods of quantum
chemistry can be divided into two basic groups that is the
semiempirical ones and ab initio calculations. In many works
semiempirical methods have been successfully applied, bringing valuable results for analysis of electron density. It is
known that in the case of nitrogen these methods do not
always lead to values close to experimental ones, however, the
results we obtained for sulfonamides or 4N-substituted cytosine derivatives were close to the experimental values. Therefore, we applied semiempirical methods for analysis of
electron density distribution in imidazole derivatives. It
seemed even more justified because in the case of triasines the
results were in agreement with the experimental values.
Although semiempirical methods differ only in the percent of
neglected diatomic differential overlap and parametrisation,
we can show that the results obtained by them could lead to
completely different conclusions.The semiempirical calculations were carried out with the
program package AMPAC6 and by seven different methods:
INDO, MINDO/3, MNDO, AM1, PM3, CNDO and
ZINDO/1. The 35Cl-NQR frequencies were calculated from
the density matrix using a program written by the authors by
the method proposed in ref. 7.
The ab initio molecular calculations were carried out with
the program package GAUSSIAN948 in PCSS (Poznań). In
non-empirical methods—the ab initio
calculations—the main
role is the functional chosen and the size of the basis set. We
have optimized geometry at the HF and BLYP levels of theory. Two different basis sets, i.e. middle 6-31g(d,p) and
extended 6-311g(2df,2pd) were used for the calculations and
both were the TZ2P triple-ζ double polarized sets. The optimization
of molecular geometries using the criterion of the minimum
gradient of the energy relative to the nuclear coordinates
was possible with all SCF wavefunctions.
The calculations of the EFG tensor components were
carried on the HF, MP2 and BLYP levels of the theory. The
35Cl-NQR frequencies were calculated from the principal
components of electric field gradient localised on chlorine
atom using a program written by the author. The quadrupole
constant due to a single 2p electron (e2Qq0h−1) was taken to
be 9.4 MHz.9,10
Results
and discussion
The results of NMR-NQR double resonance studies are collected in Table 2 and Table 3. Table 2 gives the frequencies
while Table 3 contains the quadrupole coupling constants and
asymmetry parameters. It should be pointed out, Table 2, that
the introduction of NO2 and CH3 groups into the imidazole
ring results in an increase in e2Qqh−1 constants on both nitrogens of the ring and a decrease in e2Qqh−1 on the nitrogen
from the NO2 group (nitro group).
Table 2
The NQR frequencies for the imidazole derivatives at 193 and 296 K
| Nitrogen nucleus |
|---|
| |
|---|
–N![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) | –NR1 | –NO2 |
|---|
| | | |
|---|
| No | T/K | ν+/MHz | ν−/MHz | ν0/MHz | ν+/MHz | ν−/MHz | ν0/MHz | ν+/MHz | ν−/MHz | ν0/MHz |
|---|
| |
|---|
| Data from ref. 14. Data from ref. 15. |
|---|
| 1 | 291a | 2.511 | — | 0.192 | 1.367 | 0.721 | 0.647 | — | — | — |
| 77b | 2.556 | 2.345 | 0.21 | 1.417 | 0.719 | 0.698 | — | — | — |
| 2 | 296 | 2.635 | 2.230 | 0.405 | 1.499 | 0.855 | 0.644 | 1.028 | 0.810 | 0.218 |
| 193 | 2.639 | 2.235 | 0.404 | 1.499 | 0.820 | 0.679 | 1.045 | 0.821 | 0.224 |
| 3 | 296 | 2.598 | 2.350 | 0.248 | 2.046 | 1.655 | 0.391 | 0.792 | 0.613 | 0.179 |
| 193 | 2.605 | 2.348 | 0.257 | 2.057 | 1.661 | 0.396 | 0.803 | 0.622 | 0.181 |
| 4 | 296 | 2.852 | 2.781 | 0.071 | 2.077 | 1.772 | 0.305 | 0.746 | 0.636 | 0.11 |
| 193 | 2.871 | 2.797 | 0.074 | 2.076 | 1.771 | 0.305 | 0.753 | 0.644 | 0.109 |
Table 3
The quadrupole coupling constants and asymmetry parameters (η) for imidazole derivatives
| Nitrogen nucleus |
|---|
| |
|---|
–N![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) | –NR1 | –NO2 |
|---|
| | | |
|---|
| No | T/K | (e2Qqzz/h)/ MHz | η | (e2Qqzz/h)/ MHz | η | (e2Qqzz/h)/ MHz | η |
|---|
| |
|---|
| Data from ref. 14. Data from ref. 15. |
|---|
| 1 | 291a | 3.222 | 0.119 | 1.391 | 0.93 | — | — |
| 77b | 3.253 | 0.135 | 1.418 | 0.997 | — | — |
| 2 | 296 | 3.243 | 0.250 | 1.569 | 0.821 | 1.225 | 0.356 |
| 193 | 3.249 | 0.249 | 1.546 | 0.878 | 1.244 | 0.360 |
| 3 | 296 | 3.299 | 0.150 | 2.467 | 0.317 | 0.936 | 0.381 |
| 193 | 3.302 | 0.156 | 2.479 | 0.320 | 0.950 | 0.381 |
| 4 | 296 | 3.755 | 0.038 | 2.566 | 0.238 | 0.921 | 0.239 |
| 193 | 3.779 | 0.039 | 2.565 | 0.238 | 0.931 | 0.230 |
The main aim of this paper is a comparison between the
experimental and calculated NQR parameters.
Since the time taken to perform calculations increases with
a growing number of degrees of freedom of a molecule, we
decided to perform an initial optimization of the method for
pure imidazole. This compound seemed ideal as its crystal
structure was well recognised. Crystallographic studies of
imidazole were carried out in the years 1977–1982 by Craven
et al.11–13 It is well known that imidazole crystallises in the
space group P21/c with four molecules in an elementary cell.
For an imidazole molecule we performed calculations with
7 semiempirical methods of quantum chemistry. We checked
the influence of the geometry on the results. Table
4 presents
the values of effective charge calculated assuming the experimental geometry at 103 and 293 K and the results obtained
for the optimized geometry. As follows from these data the
negative charge on the nitrogen –N![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) is always higher than on the
nitrogen NH–. This result is in qualitative agreement with the
NQR data. On the other hand, the analysis of NQR parameters
such as frequency, asymmetry parameters and quadrupole
coupling constants calculated by the method proposed
by Kaplansky and Whitehead7 leads to a completely different
conclusion. Irrespective of whether we use the optimized or experimental geometry, the results are in contradiction to experiment. The calculated resonance frequencies and coupling
constants are higher on the –NH– nitrogen than on the
–N
is always higher than on the
nitrogen NH–. This result is in qualitative agreement with the
NQR data. On the other hand, the analysis of NQR parameters
such as frequency, asymmetry parameters and quadrupole
coupling constants calculated by the method proposed
by Kaplansky and Whitehead7 leads to a completely different
conclusion. Irrespective of whether we use the optimized or experimental geometry, the results are in contradiction to experiment. The calculated resonance frequencies and coupling
constants are higher on the –NH– nitrogen than on the
–N![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) nitrogen which is in obvious contradiction to the experiments.
It should be emphasised that the assignment of the experimental
frequencies to particular positions does not arouse doubts.
Tables 5–7 present a comparison of the measured and
calculated NQR frequency. Table 5 gives the results for the
optimized geometry, and Tables 6 and 7
have been obtained
assuming the crystal structure at 103 and 293 K, respectively.
Only the CNDO calculations and only with the experimental
geometry assumed lead to the conclusions in agreement
with experiment.
nitrogen which is in obvious contradiction to the experiments.
It should be emphasised that the assignment of the experimental
frequencies to particular positions does not arouse doubts.
Tables 5–7 present a comparison of the measured and
calculated NQR frequency. Table 5 gives the results for the
optimized geometry, and Tables 6 and 7
have been obtained
assuming the crystal structure at 103 and 293 K, respectively.
Only the CNDO calculations and only with the experimental
geometry assumed lead to the conclusions in agreement
with experiment.
Table 4
Effective
charges on imidazole nitrogen nucleus calculated by semiempirical methods—experimental geometry
| Nucleus | CNDO | INDO | MINDO/3 | MNDO | AM1 | PM3 | ZINDO/1 | T/Ka |
|---|
| |
|---|
| T indicates crystallographic structure. |
|---|
| –NH– | −0.070 | −0.048 | 0.052 | −0.215 | −0.189 | 0.319 | −0.098 | 103 |
–N![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) | −0.199 | −0.248 | −0.172 | −0.227 | −0.149 | −0.099 | −0.199 | 103 |
| –NH– | −0.088 | −0.067 | 0.021 | −0.230 | −0.204 | 0.322 | −0.177 | 293 |
–N![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) | −0.179 | −0.228 | −0.149 | −0.210 | −0.132 | −0.072 | −0.234 | 293 |
| –NH– | −0.096 | −0.078 | 0.046 | −0.246 | −0.208 | 0.311 | −0.123 | opt. |
–N![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) | −0.192 | −0.236 | −0.171 | −0.229 | −0.141 | −0.118 | −0.251 | opt. |
Table 5
The results of the calculations of NQR parameters for the optimized geometry (imidazole)
| Method |
|---|
| |
|---|
| Quantity | INDO | CNDO | MINDO/3 | MNDO | AM1 | PM3 | ZINDO/1 |
|---|
| |
|---|
| –NH– |
| ν+/MHz | 4.000 | 4.010 | 4.020 | 3.940 | 3.580 | 3.970 | 3.600 |
| ν−/MHz | 2.880 | 2.830 | 3.250 | 3.810 | 3.480 | 3.920 | 2.880 |
| ν0/MHz | 1.120 | 1.170 | 0.770 | 0.130 | 0.100 | 0.050 | 0.720 |
| (e2Qq/h)/MHz | 4.587 | 4.560 | 4.847 | 5.167 | 4.707 | 5.260 | 4.320 |
| η | 0.490 | 0.510 | 0.320 | 0.050 | 0.040 | 0.020 | 0.340 |
–N![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) |
| ν+/MHz | 2.290 | 2.170 | 2.170 | 2.230 | 2.070 | 2.820 | 2.340 |
| ν−/MHz | 1.600 | 1.740 | 2.020 | 1.660 | 1.550 | 1.720 | 1.570 |
| ν0/MHz | 0.690 | 0.430 | 0.150 | 0.570 | 0.530 | 1.090 | 0.780 |
| (e2Qq/h)/MHz | 2.593 | 2.607 | 2.793 | 2.593 | 2.413 | 3.027 | 2.607 |
| η | 0.530 | 0.330 | 0.110 | 0.440 | 0.440 | 0.720 | 0.600 |
Table 6
The results of the calculations of NQR parameters for the experimental geometry at 103 K (imidazole)
| Method |
|---|
| |
|---|
| Quantity | INDO | CNDO | MINDO/3 | MNDO | AM1 | PM3 | ZINDO/1 |
|---|
| |
|---|
| –NH– |
| ν+/MHz | 3.760 | 2.440 | 4.060 | 3.720 | 3.450 | 3.710 | 3.380 |
| ν−/MHz | 2.650 | 1.890 | 3.150 | 3.610 | 3.310 | 3.680 | 2.620 |
| ν0/MHz | 1.110 | 0.550 | 0.910 | 0.120 | 0.140 | 0.030 | 0.760 |
| (e2Qq/h)/MHz | 4.273 | 2.887 | 4.807 | 4.887 | 4.507 | 4.927 | 4.000 |
| η | 0.520 | 0.380 | 0.380 | 0.050 | 0.070 | 0.010 | 0.380 |
–N![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) |
| ν+/MHz | 2.540 | 3.750 | 2.070 | 2.220 | 2.150 | 2.680 | 2.480 |
| ν−/MHz | 1.790 | 2.610 | 1.920 | 1.640 | 1.550 | 1.480 | 1.700 |
| ν0/MHz | 0.740 | 1.140 | 0.150 | 0.580 | 0.600 | 1.200 | 0.780 |
| (e2Qq/h)/MHz | 2.887 | 4.242 | 2.660 | 2.573 | 2.467 | 2.773 | 2.787 |
| η | 0.510 | 0.540 | 0.110 | 0.450 | 0.490 | 0.860 | 0.560 |
Table 7
The results of the calculations of NQR parameters for the experimental geometry at 293 K (imidazole)
| Method |
|---|
| |
|---|
| Quantity | INDO | CNDO | MINDO/3 | MNDO | AM1 | PM3 | ZINDO/1 |
|---|
| |
|---|
| –NH– |
| ν+/MHz | 3.920 | 2.80 | 4.400 | 3.850 | 3.540 | 3.870 | 3.550 |
| ν−/MHz | 2.760 | 2.240 | 3.230 | 3.670 | 3.400 | 3.820 | 2.730 |
| ν0/MHz | 1.150 | 0.140 | 0.960 | 0.180 | 0.140 | 0.060 | 0.820 |
| (e2Qq/h)/MHz | 4.453 | 3.076 | 5.087 | 5.013 | 4.627 | 5.127 | 4.187 |
| η | 0.520 | 0.090 | 0.390 | 0.070 | 0.060 | 0.020 | 0.390 |
–N![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) |
| ν+/MHz | 2.490 | 3.920 | 2.070 | 2.210 | 2.140 | 2.670 | 2.430 |
| ν−/MHz | 2.070 | 2.740 | 1.660 | 1.460 | 1.370 | 1.430 | 1.970 |
| ν0/MHz | 0.420 | 1.180 | 0.410 | 0.750 | 0.780 | 1.240 | 0.460 |
| (e2Qq/h)/MHz | 3.040 | 4.442 | 2.487 | 2.447 | 2.340 | 2.733 | 2.933 |
| η | 0.270 | 0.530 | 0.330 | 0.620 | 0.660 | 0.910 | 0.310 |
The next problem was whether the strong hydrogen bonds
(2.86 Å bond length) can play an important role. To check this
we carried out ZINDO/1 calculations. This method was
chosen as it is rather fast and it is a combination of CNDO
and INDO methods. The results obtained for a monomer,
dimer and an elementary cell containing 4 molecules of imidazole were compared, Table 8. Although a decrease in NQR
frequency was obtained as expected as a result of hydrogen
bond formation, the results still are not in agreement with the
experimental ones. On the other hand, we obtained similar
results (also in disagreement with the experimental ones) for
other five-membered heterocyclic compounds like triasine.
Moreover, the assumption of perpendicular orbitals did not
lead to results consistent with experiment. The source of
failure of the semiempirical quantum chemistry methods in
these applications is in the way they force a redistribution of
electron density among the nitrogen atom orbitals and the kind
of parametrisation they are based on. In these circumstances it was not a surprise that the results obtained for 2-nitro-5-methylimidazole did not agree with the experimental ones.
Moreover, the data on the crystal structure of this compound are not available so we were not able to verify if the results
obtained by CNDO assuming the experimental geometry
agree with experiment. In conclusion, the semiempirical
methods have proved totally useless for investigation of electron
density distribution in 2-nitroimidazole derivatives.
Table 8
The
influence
of the hydrogen bonds on the NQR parameters (imidazole)
| ZINDO/1 |
|---|
| |
|---|
| Quantity | Monomer | Dimer | Elementary cell | NQR |
|---|
| |
|---|
| –NH– |
| ν+/MHz | 3.600 | 3.460 | 1.520 | 1.367 |
| ν−/MHz | 2.880 | 2.780 | 1.060 | 0.721 |
| ν0/MHz | 0.720 | 0.680 | 0.470 | 0.647 |
| (e2Qq/h)/MHz | 4.320 | 4.160 | 1.720 | 1.391 |
| η | 0.340 | 0.320 | 0.540 | 0.930 |
–N![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) |
| ν+/MHz | 2.340 | 1.310 | 0.980 | 2.511 |
| ν−/MHz | 1.570 | 0.710 | 0.730 | 2.319 |
| ν0/MHz | 0.780 | 0.600 | 0.250 | 0.192 |
| (e2Qq/h)/MHz | 2.607 | 1.347 | 1.140 | 3.222 |
| η | 0.600 | 0.890 | 0.460 | 0.119 |
Having checked this we resorted to the non-empirical quantum
chemistry methods known as the ab initio methods. Using
these methods we performed analogous calculations, that
is we studied the influence of geometry on the results. Since
the use of a finite basis set is always a source of uncertainties in the EFG components, the calculations were performed in different basis sets, and—regarding the effect of the functional—also
at different levels of the theory. The effect of different
basis sets and functionals was analysed. As our earlier
studies for cytosine had proved better results can be obtained
using a BLYP or MP2 functional we did not carry out
calculations with a HF functional. The results for imidazole are
given in Table 9. As follows from these results, the
best agreement is obtained using the BLYP functional in the 6-311g(2df,
2pd) basis set at fully optimized geometry, although the differences are rather small. Moreover, as indicated by the slope of the regression curves the results are in agreement with experiment. The results obtained by BLYP in the 6-311(2df, 2dp) basis set were the best. 14N-NQR frequencies,
closest to the experimental ones, can be obtained by using BLYP or MP2 with full optimization methods (correlation
coefficients are 0.916 and 0.905 and curve fit standard deviation
0.123 and 0.144, respectively). A comparison of the results
obtained for imidazole in the experimental geometry at
103 and 293 K proves that the geometry has an essential
effect on the quality of the results (Table 10)
| | | (a)forgeometryat103K:ν(calc.)=1.023ν(NQR)+0.148;r=0.939,s=0.395 |
(1)
|
| | | (b)forgeometryat293K:ν(calc.)=0.984ν(NQR)+0.251;r=0.929,s=0.413
|
(2)
|
| | | (c)foroptimisedgeometry:ν(calc.)=1.039ν(NQR)+0.114;r=0.911,s=0.500
|
(3)
|
where
r is a correlation coefficient and s stands for the curve
fit standard error. The frequencies closest to the experimental
ones were obtained at the BLYP level of theory with the
application of the extended basis set.
Table 9
The results of the ab initio calculations of NQR parameters—optimized geometry (imidazole)
| Method |
|---|
| |
|---|
| BLYP | MP2 | BLYP |
|---|
| |
|---|
| Basis set |
|---|
| |
|---|
| Quantity | 6-31g (d,p) | 6-311g (2df,2pd) | NQR |
|---|
| |
|---|
–N![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) |
| ν+ MHz | 2.24 | 2.15 | 2.61 | 2.511 |
| ν− MHz | 2.19 | 2.14 | 2.47 | 2.319 |
| ν0 MHz | 0.05 | 0.10 | 0.13 | 0.192 |
| (e2Qq/h) MHz | 2.952 | 2.862 | 3.381 | 3.222 |
| η | 0.03 | 0.07 | 0.08 | 0.119 |
| –NH– |
| ν+ MHz | 1.85 | 1.58 | 1.77 | 1.367 |
| ν− MHz | 1.59 | 1.39 | 1.59 | 0.721 |
| ν0 MHz | 0.26 | 0.19 | 0.18 | 0.647 |
| (e2Qq/h) MHz | 2.297 | 1.984 | 2.245 | 1.391 |
| η | 0.22 | 0.19 | 0.16 | 0.930 |
Table 10
The results of the ab initio calculations of NQR parameters—experimental geometry (imidazole)
| BLYP/6-311g(2df,2pd) |
|---|
| |
|---|
| Temperature (T/K) |
|---|
| |
|---|
| Quantity | 103 | 293 | NQR |
|---|
| |
|---|
–N![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) |
| ν+ MHz | 2.605 | 2.699 | 2.511 |
| ν− MHz | 2.456 | 2.382 | 2.319 |
| ν0 MHz | 0.149 | 0.317 | 0.192 |
| (e2Qq/h) MHz | 3.375 | 3.388 | 3.222 |
| η | 0.088 | 0.190 | 0.12 |
| –NH– |
| ν+ MHz | 1.808 | 1.869 | 1.367 |
| ν− MHz | 1.440 | 1.504 | 0.721 |
| ν0 MHz | 0.369 | 0.365 | 0.647 |
| (e2Qq/h) MHz | 2.165 | 2.249 | 1.391 |
| η | 0.340 | 0.320 | 0.930 |
The fact that the results for imidazole were correct prompted us to perform analogous calculations for two 2-nitroimidazole
derivatives: 2-nitro-5-methylimidazole and
metronidazole. The results for 2-nitro-5-methylimidazole are collected
in Table 11 and for metronidazole in Table 12. The influence
of the basis set and the functional on the results for 2-nitro-5-methylimidazole
and metronidazole illustrated by the data in
Tables 11 and 12. Unfortunately, a high number of degrees of freedom
and the lack of crystalline data prevented us from performing
the calculations for one-third of the compounds.
Table 11
The results
of
the ab initio calculations of NQR parameters—optimized geometry (2-nitro-5-methylimidazole)
| Method |
|---|
| |
|---|
| BLYP | MP2 | BLYP |
|---|
| |
|---|
| Basis set |
|---|
| |
|---|
| Quantity | 6-31g (d,p) | 6-311g (2df,2pd) | NQR |
|---|
| |
|---|
–N![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) |
| ν+ MHz | 2.29 | 2.23 | 2.55 | 2.635 |
| ν− MHz | 2.18 | 2.19 | 2.51 | 2.230 |
| ν0 MHz | 0.12 | 0.04 | 0.04 | 0.450 |
| (e2Qq/h) MHz | 2.979 | 2.948 | 3.300 | 3.243 |
| η | 0.08 | 0.02 | 0.02 | 0.250 |
| –NH– |
| ν+ MHz | 1.78 | 1.56 | 1.75 | 1.499 |
| ν− MHz | 1.637 | 1.38 | 1.60 | 0.855 |
| ν0 MHz | 0.14 | 0.19 | 0.15 | 0.644 |
| (e2Qq/h) MHz | 2.277 | 1.958 | 2.239 | 1.569 |
| η | 0.13 | 0.19 | 0.13 | 0.82 |
| –NO2 |
| ν+ MHz | 0.42 | 0.59 | 0.39 | 1.03 |
| ν− MHz | 0.34 | 0.49 | 0.21 | 0.81 |
| ν0 MHz | 0.08 | 0.10 | 0.18 | 0.22 |
| (e2Qq/h) MHz | 0.51 | 0.72 | 4.00 | 1.23 |
| η | 0.31 | 0.27 | 0.91 | 0.36 |
Table 12
The results of the ab initio calculations of NQR parameters—optimized geometry (metronidazole)
| Method |
|---|
| |
|---|
| Quantity | BLYP/6-31g (d,p) | NQR |
|---|
| |
|---|
–N![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) |
| ν+ MHz | 2.22 | 2.60 |
| ν− MHz | 2.14 | 2.35 |
| ν0 MHz | 0.08 | 0.25 |
| e2Qq/h MHz | 2.909 | 3.299 |
| η | 0.05 | 0.15 |
| –NH– |
| ν+ MHz | 1.88 | 2.05 |
| ν− MHz | 1.629 | 1.655 |
| ν0 MHz | 0.21 | 0.39 |
| (e2Qq/h) MHz | 2.316 | 2.467 |
| η | 0.19 | 0.32 |
| –NO2 |
| ν+ MHz | 0.41 | 0.79 |
| ν− MHz | 0.32 | 0.61 |
| ν0 MHz | 0.09 | 0.18 |
| (e2Qq/h) MHz | 0.49 | 0.94 |
| η | 0.36 | 0.38 |
In general, the correlation between the experimental and
calculated frequencies (ν), quadrupole coupling constants (e2Qqzzh−1)
and asymmetry parameters (η) is good. The following correlation dependencies were obtained between the experimental
and calculated by BLYP NQR parameters:
| | 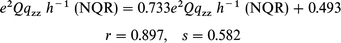 | (1) |
| | 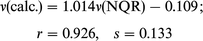 | (2) |
and
| | 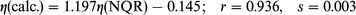 | (3) |
where r is a correlation coefficient and s stands for the curve
fit standard error.
The regression lines are shown in Figs. 3–5. A comparison of
the results of our calculations shows that the electron density
distribution is correctly reproduced on –NH– and the nitro
group while on –N![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) results are in disagreement with the
experimental ones (Fig. 5) although the differences are rather small. The
asymmetry parameters are reproduced within the error for
the –N
results are in disagreement with the
experimental ones (Fig. 5) although the differences are rather small. The
asymmetry parameters are reproduced within the error for
the –N![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) atom, i.e. in the case when the asymmetry parameters are
very high.
atom, i.e. in the case when the asymmetry parameters are
very high.
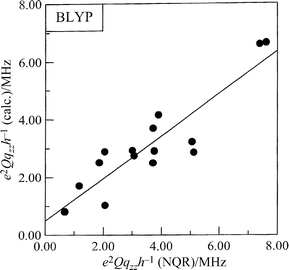 |
| | Fig. 3 Comparison of the calculated and the experimental NQR quadrupole coupling constants for imidazole derivatives. | |
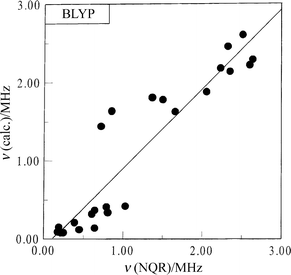 |
| | Fig. 4 Comparison of the calculated and the experimental frequencies for imidazole derivatives. | |
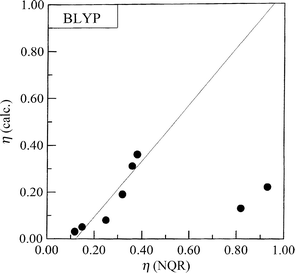 |
| | Fig. 5 Comparison of the calculated and the experimental asymmetry parameters for imidazole derivatives. | |
Conclusions
1. When using the semiempirical methods, it is possible to
obtain results which do not completely match the experimental ones. The parametrisation of semiempirical methods and
redistribution of the electron density between nitrogen orbitals
in five-membered heterocyclic nitrogen nucleus does not lead to the adequate quantitative or qualitative results.2.
The adequacy of the calculations of effective charges on
nitrogen nucleus cannot be the main criterion for a correlation
between the calculations and experiment. However, the
charges may be adequate in each case, the NQR frequencies
may not. The 14N-NQR frequencies, closest to the experimental ones, can be obtained by using BLYP or MP2 methods starting
with the experimental geometry.
3.
The correlation between the experimental and calculated
frequencies (ν), quadrupole coupling constants (e2Qqzzh−1) and
asymmetry parameters (η) is good. However, the asymmetry parameters
are reproduced with the error for the –N![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) atom, i.e.
in the case when the asymmetry parameters are very high.
atom, i.e.
in the case when the asymmetry parameters are very high.
4.
The size of the basis set and the functional used for the
calculations may radically influence the results. Much better
results are obtained when the calculations are carried out in a
larger basis set and for the experimental geometry.
References
- P. A. Kass, P. Palmberg and B. Becker, Invest. Opthalmol. Vis. Sci., 1977, 16, 66 Search PubMed.
- W. K. Anderson, D. Bhattachorjee and D. M. Houston, J. Med. Chem., 1989, 32, 119 CrossRef CAS.
- P. Benefield and S. P. Clissols, Drugs, 1989, 35, 143 Search PubMed.
- J. D. Chapman, A. P. Reuvers and J. Borsa, Br. J. Radiol., 1973, 46, 623 Search PubMed.
- J. N. Latosińska, J. Seliger and B. Nogaj, Magn. Reson. Chem., , , in the press Search PubMed.
- M. J. S. Dewar, E. G. Zoebisch, E. F. Healy and J. J. P. Stewart, J. Am. Chem. Soc., 1985, 107, 3902 CrossRef.
- M. Kaplansky and M. A. Whitehead, Trans.
Faraday Soc., 1969, 65, 641 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, P. M. W. Gill,
B. G. Johnson, M. A. Robb, J. R. Cheeseman, T. Keith, G. A. Petersson, J. A. Montgomery, K. Raghavachari,
M. A. Al-Laham, V. G. Zakrzewski, J. V. Ortiz, J. B. Foresman,
J. Ciaslowski, B. B. Stefanov, A. Nanayakkara, M. Challacombe,
C. Y. Peng, P. Y. Ayala, W Chen, M. W. Wong, J. L. Andres,
E. S. Reptogle, R. Gomperts, R. L. Martin, D. J. Fox, J. S. Binkley,
D. J. Defrees, J. Baker, J. P. Stewart, M. Head-Gordon,
C. Gonzalez, and J. A. Pople, GAUSSIAN 94 Revision B.1.,
Gaussian, Inc., Pittsburg, PA, 1992..
- E. A. C. Lucken, Nuclear Quadrupole
Coupling Constants, Academic Press, London and New York,
1969. Search PubMed.
- E. Schemp and P. J. Bray, J. Chem. Phys., 1967, 46, 1186 CrossRef.
- R. K. McMullan, J. Epstein, J. R. Ruble and B. M. Craven, Acta Crystallogr., Sect. B, 1979, 35, 688 CrossRef.
- J. Epstein, J. R. Ruble and B. M. Craven, Acta Crystallogr., Sect. B, , 38, 140 Search PubMed.
- B. M. Craven, R. K. McMullan, J. D. Bell and H. C. Freeman, Acta Crystallogr., Sect. B, 1977, 33, 2585 CrossRef.
- M. L. S. Garcia, J. A. Smith, P.
M. G. Bavin and C. R. Gnellin, J. Chem. Soc.,
Perkin. Trans. 2, 1983, 00, 1391 RSC.
- J. Koo and Y. N. Hsieh, Chem. Phys. Lett., 1971, 9, 238 CrossRef CAS.
|
| This journal is © the Owner Societies 2000 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) onto the nitrogen –NH–.
Moreover, we concluded that even very subtle substitution effects could significantly change the electron density distribution
in imidazoles.
onto the nitrogen –NH–.
Moreover, we concluded that even very subtle substitution effects could significantly change the electron density distribution
in imidazoles.
![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) CHPhCH3O
CHPhCH3O
![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif)
![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif)
![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) is always higher than on the
nitrogen NH–. This result is in qualitative agreement with the
NQR data. On the other hand, the analysis of NQR parameters
such as frequency, asymmetry parameters and quadrupole
coupling constants calculated by the method proposed
by Kaplansky and Whitehead7 leads to a completely different
conclusion. Irrespective of whether we use the optimized or experimental geometry, the results are in contradiction to experiment. The calculated resonance frequencies and coupling
constants are higher on the –NH– nitrogen than on the
–N
is always higher than on the
nitrogen NH–. This result is in qualitative agreement with the
NQR data. On the other hand, the analysis of NQR parameters
such as frequency, asymmetry parameters and quadrupole
coupling constants calculated by the method proposed
by Kaplansky and Whitehead7 leads to a completely different
conclusion. Irrespective of whether we use the optimized or experimental geometry, the results are in contradiction to experiment. The calculated resonance frequencies and coupling
constants are higher on the –NH– nitrogen than on the
–N![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) nitrogen which is in obvious contradiction to the experiments.
It should be emphasised that the assignment of the experimental
frequencies to particular positions does not arouse doubts.
Tables 5–7 present a comparison of the measured and
calculated NQR frequency. Table 5 gives the results for the
optimized geometry, and Tables 6 and 7
have been obtained
assuming the crystal structure at 103 and 293 K, respectively.
Only the CNDO calculations and only with the experimental
geometry assumed lead to the conclusions in agreement
with experiment.
nitrogen which is in obvious contradiction to the experiments.
It should be emphasised that the assignment of the experimental
frequencies to particular positions does not arouse doubts.
Tables 5–7 present a comparison of the measured and
calculated NQR frequency. Table 5 gives the results for the
optimized geometry, and Tables 6 and 7
have been obtained
assuming the crystal structure at 103 and 293 K, respectively.
Only the CNDO calculations and only with the experimental
geometry assumed lead to the conclusions in agreement
with experiment.![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif)
![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif)
![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif)
![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif)
![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif)
![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif)
![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif)
![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif)
![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif)
![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif)
![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif)
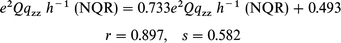
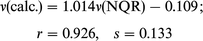
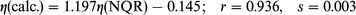
![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) results are in disagreement with the
experimental ones (Fig. 5) although the differences are rather small. The
asymmetry parameters are reproduced within the error for
the –N
results are in disagreement with the
experimental ones (Fig. 5) although the differences are rather small. The
asymmetry parameters are reproduced within the error for
the –N![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) atom, i.e. in the case when the asymmetry parameters are
very high.
atom, i.e. in the case when the asymmetry parameters are
very high.


![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) atom, i.e.
in the case when the asymmetry parameters are very high.
atom, i.e.
in the case when the asymmetry parameters are very high.