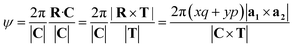Open Access Article
Open Access ArticleChiraltube, rolling 2D materials into chiral nanotubes†
José M.
de Albornoz-Caratozzolo
 and
Felipe
Cervantes-Sodi
and
Felipe
Cervantes-Sodi
 *
*
Universidad Iberoamericana, Physics and Mathematics Department, Prol. Paseo de la Reforma 880, Lomas de Santa Fe, Ciudad de México, Mexico. E-mail: felipe.cervantes@ibero.mx; Tel: +52 55 59504275
First published on 11th October 2023
Abstract
Carbon nanotubes (NTs) are graphene sheets rolled into a 1D material, with a specific chirality that defines its structure and properties. Graphene has triggered the development of thousands of 2D materials, which in principle could also be rolled into 1D NTs. However, most of these NTs have not been proposed due to difficulties in the generation of atomic coordinates for chiral NTs from 2D materials with a non-hexagonal lattice or multi-layered materials. In this paper we present Chiraltube, an open-source Python code that allows the quick generation of a complete NT with any chirality from the unit cell of its original 2D material. We explain the inner workings of the code as well as the theoretical background on which it is built, generalizing concepts from the construction of chiral and achiral carbon NTs to work on any other 2D material. We show various examples of the resulting chiral NT structures built from phosphorene, MoS2 and Ti3C2, and present some analysis on the interatomic distortion in the outermost layers of these NTs, as well as the results of ab initio electronic structure calculations on a set of phosphorene NTs generated by the program, showing the immediate practicality and usefulness of the program. We also explore some limitations and details of the tool as well as further work to be done.
1 Introduction
During the last 30 years an immense effort has been devoted to the study of first nanotubes (NTs) and then two dimensional (2D) materials. Their archetypes are carbon based nanostructures: carbon nanotubes (CNTs)1–3 and graphene,4,5 respectively. CNTs are commonly described as “rolled” sheets of graphene and are defined by their chiral angle (θ) and chiral vector (C)6 (Fig. 1).Each CNT has its chirality6–8 defined by the angle at which a graphene sheet is wrapped to form a specific nanotube (NT). It is a geometrical classification of CNTs and a topological feature that governs all CNTs' properties, like electronic and optical ones.6,9,10 A minimal difference between two CNTs' chiralities may differentiate one as metallic and the other as a semiconductor.
Chirality is related to CNTs' symmetry; chiral and achiral NTs are non-symmorphic and symmorphic respectively. Zigzag and armchair CNTs are both achiral, with their structure being identical to their mirror.10 In contrast, chiral CNTs mirror's images are not superposed with the original ones.10 Chiral tubes are called this way from the chemical nomenclature, axially chiral, presenting a spiral symmetry.
CNTs have been studied in depth, with a huge amount of theoretical6,7,10–14 and experimental work15–22 devoted to CNTs wrapped in armchair, zigzag or any other chirality, which in turn have completely different electronic, optoelectronic, mechanical and catalytic properties. This diversity hinders the experimental endeavour of obtaining a specific chirality CNT for its applications, but it has also opened an endless path for potential applications.
Generating a supercell of chiral CNTs, with the atomic coordinates of each atom, is easy, and in fact, there are many tools and freely available resources to generate sets of coordinates of virtually any chiral/achiral CNT,8,23–25 which can then be the input of further studies, like density functional theory (DFT) calculations to obtain the geometrically relaxed structure, electronic properties, etc. While these tools could be adapted for other materials, they are made for the specific hexagonal shape in graphene's unit cell.
As with carbon and graphene, NTs of other elements or compounds have also been studied, especially their achiral zigzag and armchair structures, in part because their coordinates are easier to obtain. Some examples are silicene NTs (SiNTs),26,27 phosphorene NTs (PNTs),28–30 boron nitride NTs (BNNTs),31 GaAs NTs (GaAsNTs)32,33 transition metal dichalcogenide (TMD) NTs (TMDNTs) (MoS2,34 WS2,35 and MoSSe36), MXene NTs (MXene-NTs),37 and others.38–40
However, for most of these materials, their chiral counterparts present higher complexity in the construction of their supercell and the generation of their atomic coordinates. These supercells are usually bigger in size, constituted by hundreds of atoms, making their simulations and theoretical studies more difficult.
Although there are a few examples of theoretical studies in the literature dealing with chiral NTs (i.e. a molecular dynamics (MD) study of PNTs self-assembled from phosphorene ribbons,41 a study on spin orbit effects on chiral MoS2 NTs42 or electronic structure calculations of NTs made out of two dimensional (2D) materials with a unit cell similar to that of graphene or a simple monolayer as BNNTs43,44 and TMD-NTs45), chiral NTs are still an almost virgin field to be explored. Examining the characteristics of chiral nanotubes will reveal changes in their properties attributable to their unique chirality, as it occurs with CNTs. Such distinctions hold promise for potential applications across various scientific domains, where nanotubes and 2D materials have already made significant contributions.
With the rise of 2D materials,46 there is an uncountable number of NT possibilities to be addressed.47 The broadening of the spectrum to include not only the achiral, but also the chiral NTs, would be possible with a tool that could generate the atomic coordinates of the NTs with the only input being the unit cell of the 2D material in question (cell parameters and atomic positions can be found elsewhere47–49).
In this paper we present Chiraltube,50 a concise code written in Python that allows for the generation of not only CNTs, but also NTs from any 2D material, with any unit cell and in any chirality desired.
In the body of this paper, first, we generalize the notion of chirality and related concepts (i.e., chiral vector, wrapping angle, nanoribbons (NRs), translational vectors, symmetry vector, rotation angle, and NT reciprocal lattice unit vectors), that have been used for CNTs since the 90s,10 to any type of 2D material rolled into a chiral NT. This is integrated into an open-source code capable of dealing with materials with an asymmetrical unit cell and a width of either single layer or multiple layers, such as phosphorene, TMDs and MXenes. Second, we present an explanation of the general methodology of the code in Python, which generates a NR from a unit cell of a 2D material, and later wraps it into a NT of the chosen chirality. Later, in the results and discussion, some families of NTs are presented, analysing geometrical aspects related to the generated coordinates. As a proof of concept, the atomic coordinates of chiral phosphorene nanotubes were used as input in ab initio calculations, specifically geometry optimization ones, proving the capability of the coordinate generator code. Finally, the discussion includes some scenarios of applicability using examples in the literature, followed by the conclusions.
2 Methodology
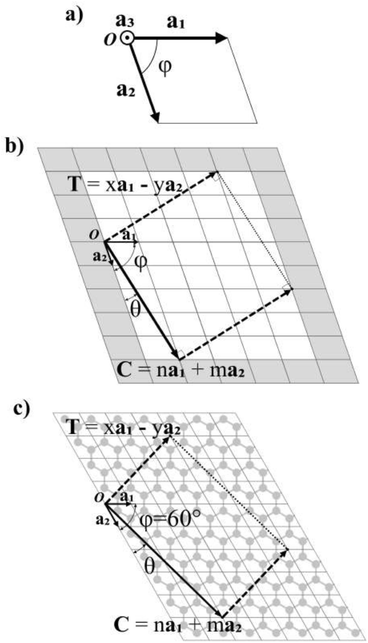
In Fig. 1a, the vectors of an arbitrary unit cell are defined as a1, a2, and a3, and it's important to note the third vector a3, pointing out of the page, as it will be important for the folding of multilayered materials such as MoS2. The angle formed between a1 and a2 is defined as φ and goes from 0° to 90°. This angle has a value φ = 60° for graphene (shown in Fig. 1c).The chiral vector C is defined as C = na1 + ma2, where n and m are the chiral indices, as for CNTs.3,6,7,11,21 In fact, several of the cells, ribbons and nanotube parameters presented here are a generalization of those for CNTs in Table 3.3 of ref. 10.Fig. 1b shows the crystalline lattice of a general 2D material with arbitrary φ, only the outline of the unit cells is shown, and the unit cell could contain any number of atoms in any configuration. The chiral vector C defines the angle θ, which will be measured from the a2 axis in the counter-clockwise direction (Fig. 1b), and goes from 0 to φ. The chiral vector defines the rolling direction of the 2D material to form a NT. Thus, the nanoribbon (NR) which will be rolled into a NT is formed between the chiral vector and the vectors perpendicular to it, called the translational vector T (Fig. 1b and c). The translational vector is defined as T = xa1 − ya2, where x and y are positive integers, called from now on the translational indices. The minus sign is there in order to keep y positive. T also defines the NT axis.
2.1 Ab initio calculations
The electronic structure calculations were performed with the DFT plane wave code, Quantum Espresso.51 Ultrasoft pseudopotential type Rappe Rabe Kaxiras Joannopoulos52 were used with cutoff energies of 544 eV, and the Perdew–Burke–Ernzerhof (PBE)53 functional was chosen for exchange correlation approximation. The convergence energy for self-consistent calculation was set to 0.001 eV. The Brillouin zone of the supercells was sampled by using Monkhorst-Pack54 grids of P × 1 × 1, with P such that the density of k-points in the periodic direction (along the nanotube axis) was not larger than 0.1 Å−1. The supercells were built with the periodic direction of the nanotube along the z axis and allowing a free space of at least 6.5 Å between adjacent nanotubes in the xy plane. Geometry optimization of the phosphorene nanotubes was performed with the Broyden–Fletcher–Goldfarb–Shanno algorithm. The thresholds in the Hellmann–Feynman forces and the stress along z were set to 0.02 eV Å−1 and 0.05 GPa respectively.3 Description of the program
The program's main functionality is to return a set of atom coordinates for a rolled NT made out of a 2D material. These coordinates are generated and calculated geometrically from the unit cell of the 2D material, the only input to the program, which can be either in special-xyz format or as an input file for Quantum Espresso51 (an example for MoS2 is included in Section 2 of the ESI†).Firstly, the unit cell of the 2D material is read from the input file, the unit vectors are defined and the angle φ is calculated. The atomic positions within the unit cell are stored. The user then inputs the (n,m) chiral indices of the desired NT, which is used by the program to build the chiral vector.
The program looks for a T that satisfies (1) being perpendicular to C and (2) having integer components x and y (in such a way that the translational vector, when folded, lands exactly on the origin vertex of another unit cell). For a general lattice with angle φ, the following relation was found between x and y, satisfying both requirements for a given chiral angle θ:
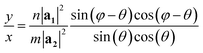 | (1) |
The program then finds integer solutions for x and y. Since eqn (1) has an infinite number of solutions, the program orders them according to the magnitude of the corresponding T vector and uses the (x, y) pair that minimizes |T|. For zigzag and armchair nanotubes where n or m might be zero, the following relations should be used:
• When n = 0:
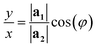 | (2) |
• When m = 0:
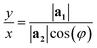 | (3) |
However, for cells where |a1| = |a2| and φ = 60° (E.g.: CNTs and MoS2 NTs), eqn (1) does have exact integer solutions, and in fact the relation simplifies greatly to the well known equation:3
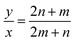 | (4) |
In orthorhombic unit cells like phosphorene or biphenylene,40,55φ = 90° and thus eqn (1) also simplifies neatly to produce the following relation:
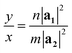 | (5) |
For generality, the program always uses eqn (1)–(3), which yield the same results.
After calculating the translational vector, the program creates an array of atoms following the distribution of the unit cells in the lattice. This array is of dimensions (n + x + 2)|a1| in the a1 direction, and (m + y + 2)|a2| in the a2 direction, corresponding to the shaded area in Fig. 1b. It would be sufficient for this array to only have dimensions (n + x)|a1| and (m + y)|a2| (unshaded area in Fig. 1b), as the ribbon fits exactly inside this area, but one more cell is added in each direction for redundancy in case the unit cell has atoms very close to or on the boundary of the cell.
The array is rotated (φ − θ)° counter-clockwise so that C lays horizontally and then the 2D nanoribbon is cut out of this array, with dimensions specified by |C| and |T| (Fig. 1b). The chiral vector's magnitude |C| also defines the peripheral length of the NT, so that the radius rc is given by:
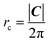 | (6) |
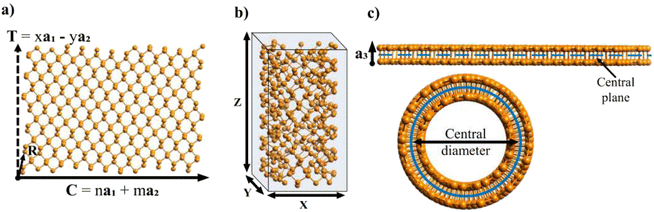
After generating the NR and calculating the radius, the program rolls the NR into a NT. There is also an option within the program to just build the NR, which is useful for studies focusing on the properties of nanoribbons. This is a fairly simple process for 2D materials with only one layer, like CNTs or BNNTs, but for multi-layered materials like PNTs or MoS2 NTs, we have to take into account the distribution of atoms along the a3 direction. For multi-layered materials, atoms are shifted so that they are distributed symmetrically about a central plane (blue dashed line in Fig. 2c). This plane is defined by 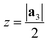 . This central plane will become the central circumference in the NT (blue solid circle in Fig. 2c). This means that anything in the central plane will have the ‘proper’ radius given by eqn (6). The radius corresponding to each atom ri is given by its z coordinate (zi):
. This central plane will become the central circumference in the NT (blue solid circle in Fig. 2c). This means that anything in the central plane will have the ‘proper’ radius given by eqn (6). The radius corresponding to each atom ri is given by its z coordinate (zi):
| ri = rc + (zi − zc) | (7) |
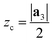 ), so that any atom that lies above the central plane will have a larger radius when the NT is generated, and any atom below the central plane will have a lower radius, as shown in Fig. 2c. Eqn (7) works so that the distance between layers in the rolled NT is the same as the distance between layers for the 2D material. This also has the effect of ‘spreading out’ the atoms on the outer layers and compressing the inner layers. The value of zc can be chosen by the user so that certain layers of the 2D materials or certain regions of it have the proper radius, while the rest of it is expanded/compressed.
), so that any atom that lies above the central plane will have a larger radius when the NT is generated, and any atom below the central plane will have a lower radius, as shown in Fig. 2c. Eqn (7) works so that the distance between layers in the rolled NT is the same as the distance between layers for the 2D material. This also has the effect of ‘spreading out’ the atoms on the outer layers and compressing the inner layers. The value of zc can be chosen by the user so that certain layers of the 2D materials or certain regions of it have the proper radius, while the rest of it is expanded/compressed.
Because the a3 component is usually unimportant in the study of 2D materials and usually left as a big number so that other layers don't interact with each other, the unit cell given as input for the program does not have to be centred around the z = |a3|/2 plane. The program will automatically centre the atoms in the cell around that plane.
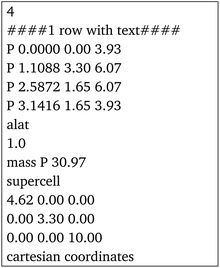
After rolling the nanotube, the program outputs the coordinates of each atom in the special-xyz format (see example in Section 2 of the ESI†). It also outputs the total number of atoms and the parameters of the nanotube: its central diameter, outer and inner diameters, its height Z (the magnitude of its translational vector) and X and Y parameters, which indicate the size of the box surrounding the nanotube central diameter, shown in Fig. 2. Note that Z may not be equal to the z coordinate of the highest atom, but rather it is the height of the NT unit cell.
Since the program generates the translational vector's indices (x, y) → T, it is also able to compute easily other relevant parameters and quantities such as the number of lattice unit cells (the number of hexagons for CNTs) N, the surface area of the nanotube ANT, and the symmetry vector R. Since the ribbon is delimited by the chiral vector C and the translational vector T, which are perpendicular, its area and thus the area of the NT will be given by:
| ANT = |C × T| = |C‖T| | (8) |
Note that this area represents the surface area corresponding to the central plane of the ribbon/central diameter of the NT, and the actual surface area of the complete NT may be bigger because of the expansion of outer layers.
The number of unit cells N in the ribbon, and therefore in the NT, is given by the ratio of the total area of the ribbon ANT divided by the area of the unit cell. This ratio is given by:
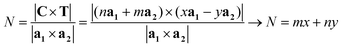 | (9) |
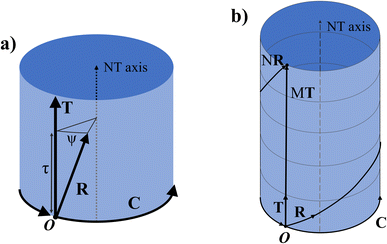
Any of the N unit cells forming the nanotube can be denoted by a vector from the origin to its origin vertex. One such vector which has the smallest component in the C direction is called the symmetry vector R, shown in Fig. 2a, and is expressed in terms of the lattice unit vectors:10
| R = pa1 + qa2 | (10) |
By the requirements imposed on R (minimizing R·C and pointing directly to a unit cell within the ribbon), p and q are uniquely determined10 by
| xq + yp = 1, (1 < mp − nq ≤ N) | (11) |
The program uses eqn (11) to find p and q and thus have the components of the symmetry vector R. The position of any other unit cell within the NT can be expressed in terms of a multiple of the symmetry vector iR, where i is an integer from 1 to N. When iR goes out of the ribbon supercell, the vector is shifted to lie within the supercell using a translation by an integer number of C or T vectors, using periodic boundary conditions. As such, the vector NR returns to the origin and (N + k)R = kR.
Viewed from another perspective, if the NT is extended beyond its unit cell through the T direction, then the multiples iR will point to the ith lattice unit cell, possibly on another NT supercell. Thus, the vector R consists of a combination of a rotation ψ around the NT axis and a translation τ in the axial direction (the T direction), as shown in Fig. 3a. Therefore, applying N times R results in a full rotation around the NT combined with a translation of an integer number M of unit cells along the axial direction, pointing to a point in the NT identical to the origin, as shown in Fig. 3b.
The symmetry vector can therefore be completely defined by its indices (p, q), like C and T, or by the parameters (τ, ψ).
The translation τ across the T direction is given by the projection of R on T, and it can be shown that:
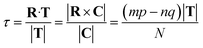 | (12) |
It can easily be seen from eqn (12) and the restrictions on p and q from eqn (11) that τ will always be a fraction of |T|, as expected.
The angle of rotation ψ around the NT axis is proportional to the projection of R on the chiral vector C, which means that eqn (11) also minimizes ψ. This angle is given by:
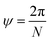 | (13) |
4 Results
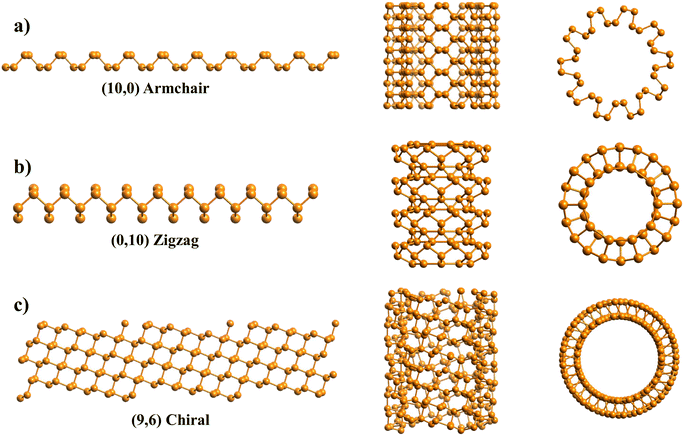
First, we use black phosphorene nanotubes as an example to illustrate the main attributes of the code. The input file containing the unit cell of phosphorene is in the special-xyz format following its description in ref. 56:where the lattice parameters come from DFT calculations in ref. 41. These are the only input lines that the program needs in order to build any chiral or achiral NT desired from this particular material. All the parameters are given in Å.
Fig. 4a includes an armchair phosphorene NR of indices (n, m) = (10, 0), and its cell has 40 atoms and |T| = 3.3 Å; however, for visualization purposes, the NT shown in Fig. 4a is 5 times the repetition of the unit cell along the NT axis. This PNT has in total 200 atoms, a height of Z = 16.5 Å and a central radius of rc = 7.35 Å. The generation of the coordinates of 5 unit cells is also a feature of the program. Fig. 4b presents a zigzag PNT with indices (0,10), and its PNT unit cell has 40 atoms as well, with a height of |T| = 4.62 Å, and it is repeated 3 more times along its axis to give a total of 160 atoms, a height of Z = 18.48 Å and a central radius of rc = 5.25 Å. Since these are armchair/zigzag and the phosphorene unit cell is orthorhombic, eqn (1) has exact integer solutions and so the error eT = 0.
In Fig. 4c, a (n, m) = (9, 6) chiral PNT is presented, corresponding to a chiral angle of θ = 64.54°. This specific chirality was used because it has an approximate solution of x = 1, y = 3 for the translational indices, with an error of eT = 0.02. Therefore, the NT unit cell is sufficiently small, with only 135 atoms and a height of Z = 10.92 Å. Note that this is not in agreement with eqn (9), which predicts that the NT supercell has N = mx + ny = 6 + 27 = 33 unit cells. Since the unit cell has 4 atoms, this would mean there are 33·4 = 132 atoms. However, this doesn't take into account the error found in eqn (1) when calculating the values for x and y. A function within the program was used to look for this NT; the function searches for chiral NTs, the dimensions of which are small enough so that they can be easily studied. Like for the previous ones, in Fig. 4c, the NT is repeated 1 time along its axis to yield a total of 270 atoms, with Z = 21.85 Å and a central radius of rc = 7.33 Å. This chirality was also chosen because it has a similar radius to the other two PNTs.
With an in-built function of the program, one can look for NTs of a selected radius or diameter, instead of looking for a specific (n, m) pair. The program goes through all combinations of n and m (up to a user-customised limit) and calculates their radii with eqn (6). It then prints out those combinations that give a radius similar to the wanted radius, up to an error er.
In Table 1 we present the translational vector and the NT parameters of a few chiral PNTs to illustrate the capabilities of the program.
| C(n, m) | NT parameters | NT size (eT = 0.025) | T(x, y) (eT = 0.025) | NT size (eT = 0.01) | T(x, y) (eT = 0.01) | ||||
|---|---|---|---|---|---|---|---|---|---|
| n | m | d c (Å) | θ (deg.) | N | Z (Å) | x, y | N | Z (Å) | x, y |
| 6 | 7 | 11.49 | 50.19 | 51 | 21.55 | 3,5 | 427 | 180.42 | 25,42 |
| 9 | 7 | 15.14 | 60.95 | 237 | 18.91 | 2,5 | 2968 | 237.83 | 25,63 |
| 10 | 4 | 15.29 | 74.05 | 218 | 17.13 | 1,5 | 2120 | 168.17 | 10,49 |
| 10 | 13 | 20.07 | 47.12 | 226 | 13.54 | 2,3 | 7300 | 441.32 | 65,98 |
| 14 | 9 | 22.66 | 65.34 | 205 | 10.92 | 1,3 | 4137 | 221.49 | 20,61 |
As explained before, since eqn (1) in general does not have exact integer solutions, the program looks for approximate solutions up to an error eT. To be more specific, eT represents the maximum accepted difference between a non-integer x (or y) value that satisfies eqn (1) and the closest integer to it. It therefore has units relative to the size of the unit cell vectors, e.g., if eT = 0.2, then the translational vector would be off by a maximum value of |a1|· eT ≈ 0.9 Å. eT is a user-customisable parameter, which defines the allowed error, and thus increasing the error will yield more solutions (and smaller solutions), but those solutions will in general be farther from being exact. The two columns in Table 1 include two different values of eT. It is clear that decreasing the accepted error from eT = 0.025 to eT = 0.01 makes several (n, m) pairs not suitable for study due to the gigantic proportions of the corresponding NT unit cells. This is better illustrated in Fig. 5, where four chiral PNTs were generated with different errors eT. One can see clearly that increasing the error decreases the size of the NT. The program has eT = 0.025 as default, yielding moderately sized NTs with high precision. However, as explained, this setting is user-customisable and it is recommended to tune it for every material and purpose. For example, we recommend decreasing the accepted error when working with CNTs, because these have suitable exact solutions for (x, y) and having a large eT returns approximate answers, especially for large n + m and for near-armchair CNTs where (n, m) = (n, n ± 1). Setting the error to eT = 0.01 yields results that reproduce exactly those of Maruyama8 in the translational indices, chiral angle, diameter, and number of hexagons of hundreds of chiral and achiral CNTs. In fact, the agreement with Maruyama's results was an important benchmark to achieve in order to validate the code.
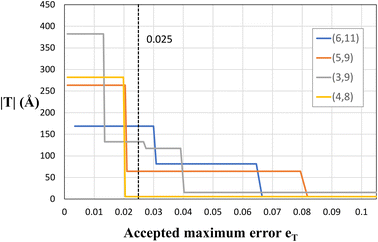 | ||
| Fig. 5 Plot of the size of nanotubes (its height, |T|) vs. the error eT for several chiral PNTs. The dashed line represents the default value of the program eT = 0.025. | ||
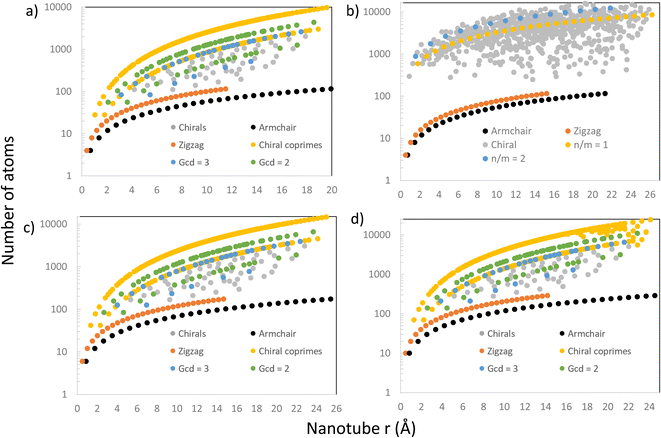
Further comparison with Maruyama's results8 was done by looking at the relation between the nanotube size (the number of atoms or the number of unit cells in its supercell) and radius. The results are presented in Fig. 6, where there are 4 graphs showing the number of atoms (on a logarithmic scale) in every nanotube (chiral and achiral) with n, m < 30, ordered by their radius for different materials, including CNTs, PNTs, MoS2 NTs and Ti3C2 NTs. In Fig. 6a, we were able to reproduce exactly the patterns from the literature8 for CNTs. The results for the number of atoms were produced through completely general methods, using eqn (1) and the steps explained above to create the NT, and then counting how many atoms were in the final structure. Setting eT = 0.01, these results matched perfectly with theoretical results from eqn (4) and (9), and produced the patterns shown in Fig. 6a.
Following the same entirely general procedure, results for MoS2 NTs and Ti3C2 NTs were obtained and are presented in Fig. 6c and d, respectively. They share the same patterns as for CNTs, as expected, since all have hexagonal unit cells. This specific lattice structure distinguishes precisely between those NTs having (n, m) pairs where n and m are coprime, and those where the greatest common divisor (gcd) of n and m is another number. The distinction is clear in Fig. 6a, c and d, where these NTs have been highlighted in yellow, those with a gcd = 2 in green, and those with a g.c.d = 3 in blue. For hexagonal unit cells, whether n − m is divisible by 3 is also an important distinguishing factor in the electronic properties of NTs, and those NTs that do not have this divisibility criteria (and are coprime) form the upper curve in Fig. 6a, c and d.
However, for PNTs (Fig. 6b) the same pattern does not emerge because they do not share the same type of unit cell. For PNTs, the main feature is n/m, as can be seen directly from eqn (5). This creates a different pattern for the PNTs, exemplified by the yellow and blue curves in Fig. 6b, which represent those NTs with n/m = 1 and n/m = 2, respectively.
In all four cases, armchair and zigzag NTs are all confined to a relatively small number of atoms compared to chiral NTs. This is due to all zigzag and armchair NTs of a certain material having the same height (same translational vector) regardless of their radius. Therefore, their increase in size comes only from their radius in a linear tendency, and they stay small compared to their chiral counterparts.
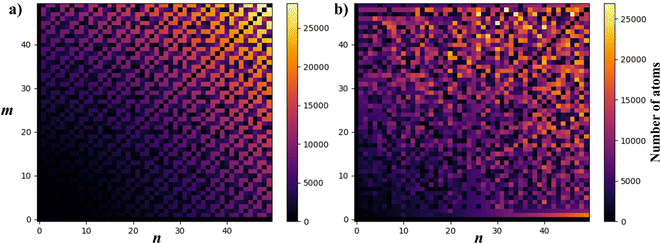
To visualise how the number of atoms in a NT supercell depends on the (n, m) pair, in Fig. 7 we present two plots of the number of atoms corresponding to all (n, m) pairs with n, m < 50. CNTs (Fig. 7a) show a periodic and size increasing behaviour as n and m increase. The pattern, besides its beauty, allows the line for n = m (armchair) to be distinguished, which stays with a small number of atoms. The plot is perfectly mirrored around the armchair line because of the symmetry in CNTs (and other materials with hexagonal unit cells as MoS2), where (n, m) = (m, n). Note that those NTs around this line (near-armchair) have a large number of atoms. On the other hand, in Fig. 7b, PNTs do not present a periodic behaviour. However, lines corresponding to n/m = 1 and n/m = 2 can be distinguished, along with the general increase in NT size as n and m increase.
All of these results were calculated using the code and setting the error to eT = 0.01 (eT = 0.001 for Fig. 7a). This yielded some NTs with thousands of atoms in their supercell, as can be seen in Fig. 6, but gave much more exact results for the desired purpose. Using the default error (0.025) would give much smaller NTs, which are more easily studied using other computational tools, but would give less accuracy for these results.
The lack of precision in the values of x and y results in a slightly altered geometry on the NTs. Since the purpose of the program is to geometrically generate NT coordinates for several 2D materials, so that these coordinates can be used in further computational studies and simulations, we advise to first relax/optimise the structures obtained by the program, so that these slight inaccuracies will be ultimately negligible. The error also impacts other parameters, which depend on x and y, such as N, R and its components (p, q) or (τ, ψ), whose calculated values may not be completely accurate.
Another source of geometric alteration we have talked about is the different radii of different layers of the same material, where atoms above the central plane will be spread out and the ones below the central plane will be compressed. This compression/expansion changes the interatomic distances of atoms in each layer, introducing positive/negative stress within the structure. To exemplify the construction of multilayered NTs (MLNTs) (which is different than the commonly used acronym MWNTs for multiwall CNTs) and features in them, we will use MoS2 with 3 atomic layers, and the MXene Ti3C2, with 5 atomic layers, and the results will be compared against CNTs and PNTs, with 1 and 2 atomic layers respectively. All the input files used are in Section 1 of the ESI.†
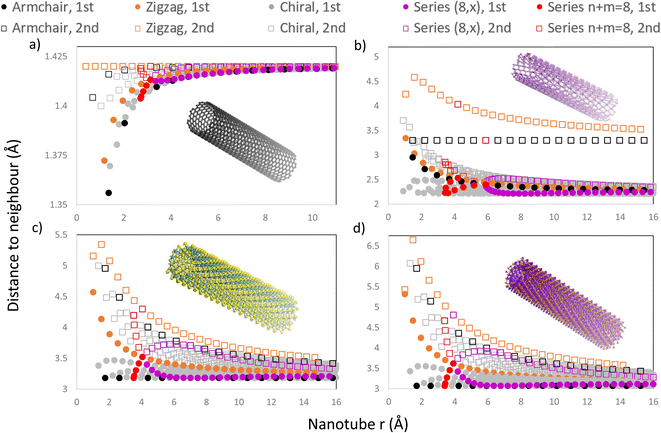
In Fig. 8, we present four graphs with the distance to the first and second neighbours of the outermost layer for all NTs with n, m < 30 for different materials, including CNTs, PNTs, MoS2 NTs and Ti3C2 NTs, materials with 1, 2, 3 and 5 atomic layers respectively. Using the program allowed us to include all chiral NTs in this range, as well as the usual zigzag and armchair NTs, making certain patterns more obvious to find. One can see from Fig. 8 that most NTs present some change in the distance to the 1st and 2nd neighbours due to the curvature and that this behaviour depends heavily on the radius of the NT.
NTs generated from materials with more than one atomic layer present an increased distance to the 1st and 2nd neighbours as expected due to the outermost layer being expanded. For these NTs with more than one layer, the increase in the distance depends on the direction towards the 1st and 2nd neighbours relative to the NT axis. If the distance to a neighbour is directly in the direction of the NT axis, then the curvature will not change this distance as the curvature is present only in the chiral vector's direction. This behaviour can be seen in the 1st neighbours of armchair MoS2 NTs and armchair Ti3C2 NTs, which remain constant as the radius increases, as shown in Fig. 8c and d, respectively. This also occurs for the 2nd neighbours of armchair PNTs and of zigzag CNTs. SWCNTs, as shown in Fig. 8a, show a different behaviour as expected due to being a single layer, where the distance falls very slightly as the radius decreases, and beyond r ≈ 10 Å every NT has a typical interatomic distance for graphene (1.42 Å).
On all graphs from Fig. 8 patterns emerge for different series of NTs. Those NTs with chiral indices (n, m) sum to the same number, and form trends in a curve with a high slope (e.g. (8,0), (4,4), (3,5), (2,6) and (1,7)), because they have a similar radius, as shown in Fig. 8, where the n + m = 8 families have been highlighted in red. Out of the 4 materials presented, phosphorene is the only one to have a rectangular unit cell with |a1| ≠ |a2|, which effectively means that the NT characterized by the chiral indices (n, m) is completely different from the (m, n) NT. This splits the vertical trend into two curves, each corresponding to armchair-like NTs (n > m) or to zigzag-like NTs (m > n), and they meet at the point where n = m (in this case, where n = m = 4), as shown in Fig. 8b.
Another pattern can be found for all four materials for NTs sharing the same n or m. This is exemplified in Fig. 8 where the series (8, m) has been highlighted in purple, forming an almost horizontal curve, which is mirrored around the curve defined by the 1st neighbours of zigzag NTs (highlighted in orange). We note that all the 1st neighbours of chiral and armchair NTs are situated below the orange curve of zigzag NT 1st neighbours. On the other hand, all 2nd neighbours are located above this orange curve, Fig. 8. A zoomed-in version of these plots is included in Fig. 1 of the ESI,† in which the regions of series n + m = 8 and (8, x) are amplified.
It should be noted that these results were obtained prior to any relaxation of the structures and were calculated purely from the geometric structure given as output by Chiraltube. The relaxation of the generated structures is briefly explored in the following section for four phosphorene nanotubes. However, a systematic relaxation and calculation of the electronic structure of full nanotube families is proposed as future work.
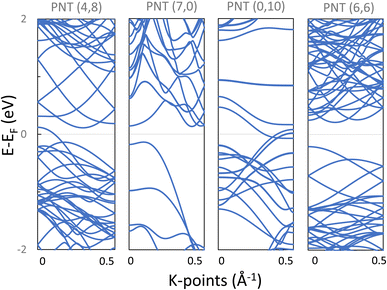
4.1 Electronic properties of phosphorene nanotubes
As a proof of concept, electronic structure calculations with Quantum Espresso were performed on four phosphorene nanotubes: two with chiral indices (4,8) and (6,6), and also one armchair NT (7,0) and a zigzag NT (0,10). Black phosphorene was selected for the calculations because its unit cell is not hexagonal and it consists of 2 atomic layers, representing important variations in contrast with conventional cells as that of CNTs and thus representing the utility of the proposed program. These PNTs were selected with a relatively similar radius 5 < r < 6 Å, and with a relatively small number of atoms (between 28 and 72 atoms) in order to reduce computational costs (again, using built-in functions of the program).The atomic coordinates generated by the program provide the input to the ab initio calculations. Firstly, the atomic coordinates and the length of the z dimension of the supercell were allowed to fully relax. Table 2 includes the characteristics of these PNTs before geometry relaxation, and the effect of the relaxation on their diameter and height. PNTs (7,0) and (6,6) present a negligible adjustment of the nanotube height, while NTs (4,8) and (0,10) have an increment of 9% and 7.3%, respectively. All NTs had their (central) diameters increased in the range of 5–12%. The chiral (4,8) PNT had the lowest increase in the diameter of 5.82%, while the zigzag (0,10) had the highest increase, with 12.62%. Interestingly, within this small sample of the 4 PNTs, the zigzag (0,10) and the chiral (4,8) present a higher strain when folded as NTs, and although their original supercell presents high initial stresses along Z, relaxation was successfully achieved in all cases. The four PNTs present a very similar total energy (ET) per atom, with variations in the thousandth of eV; all nanotube supercells are equally stable.
| C(n, m) | Parameters | Initial size | E T/atom | Δ% | E g | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Classification | n | m | d c (Å) | θ (deg) | N | Z (Å) | (eV) | d c | Z | (eV) |
| Chiral | 4 | 8 | 10.26 | 34.99 | 48 | 5.68 | −19.0823 | 5.82 | 9.02 | Metallic |
| Armchair | 7 | 0 | 10.29 | 90 | 28 | 3.30 | −19.0969 | 7.68 | 0.16 | 0.27 |
| Zigzag | 0 | 10 | 10.50 | 0 | 40 | 4.62 | −19.0895 | 12.62 | 7.33 | Metallic |
| Chiral | 6 | 6 | 10.84 | 54.46 | 72 | 8.06 | −19.0915 | 9.59 | −0.09 | 0.42 |
Secondly, after obtaining the relaxed structures, the band structures were calculated and are presented in Fig. 9. Notice that armchair (7,0) and chiral (6,6) PNTs are semiconducting with indirect bandgaps (Eg) of 0.27 eV and 0.42 eV respectively, while the chiral (4,8) and the zigzag (0,10) PNTs presented a metallic character.
5 Discussion
The large number of different NT (especially chiral NT) configurations that could be explored having at hand their atomic coordinates could unveil either interesting specific properties of an individual NT with a particular (n, m), or trends in a physical property of a family of NTs. For example, it has been experimentally found that the broken inversion symmetry of chiral WS2 NTs endows them with a bulk photovoltaic effect.57 An approach to this phenomenon from the theoretical point of view could shed light onto which specific chirality would enhance this effect. Calculating the electronic structure of the relaxed coordinates obtained from our program could unveil similar properties in other TMD NTs. On the other hand, experimental evidence has shown that BNNTs present a chiral distribution that not only includes armchair or zigzag NTs.58 This evidence could be corroborated with DFT calculations of the cohesion energy of these nanotubes, hopefully matching the experimental evidence.Some interesting features could be first studied theoretically, for example, finding the smallest (in radius) NT possible of a certain material through DFT calculations and corroborating them with experiments. Going back to the CNT archetype, SWCNTs, their minimum diameter proposed to be structurally stable and characterised by transmission electron microscopy is the (2,2) armchair SWCNT with a diameter ∼3 Å13. Thus, relying on a set of atomic coordinates for any 2D material, their NT with the minimum diameter could be predicted.
There are even more options considering functionalised 2D materials leading to functionalised NTs. Theoretical calculations have been done for hydrogenated graphene (graphane)59 and hydrogenated BN.44 Their respective functionalised NT coordinates are easily obtained by the program presented here, allowing the calculation of any functionalised NT, not only with H, but also with any desired functionalisation.
As graphene, phosphorene is also an interesting and well studied 2D material, existing in one of two allotropes, blue and black phosphorene. The last one presents an Eg = 1.0 eV at Γ60 and its tunability through doping has been reported.61 PNTs in their zigzag and armchair configurations have been reported,29,30 but the properties of their chiral NTs remain unknown, presenting an area of opportunity now made readily available through the use of this tool as shown in the short example of Table 2.
Other stars among 2D materials are TMDs. From the early studies of Tenne et al., the issue of chiral NTs, analogous to chiral CNTs, has been stated.62 The chirality of experimental TMD NTs is ambiguous in some experimental studies;35,63–65 however high resolution transmission electron microscopy and electron diffraction studies have proved the presence of chiral NTs.57,66,67 Some remarkable properties have been proven in chiral TMDNTs. For example asymmetric superconducting transport has been proved in chiral WS2 NTs.68 Regarding TMD NTs, some theoretical studies have focused on a tiny sample of them45 and also on self-scrolling MoS2,69 which are similar to NTs. It has been suggested that single-walled TMDs have electronic properties that depend on their chirality: zigzag TMD NTs present a direct band gap, resembling their 1H 2D forms, and armchair TMD NTs are similar to the 2H 2D structures;34 however the electronic structure of their chiral configurations is an open problem. Counting with accurate atomic positions of any chiral TMD NT will open the field to high-throughput calculations, allowing experimental data to be proved and expanding the theoretical results that are currently only available for a limited number of NTs.
Perhaps the most promising avenue is the prediction of Van Hove singularities, and the interband energy transition for any nanotube, as has been done with SWCNTs.16,70 Knowing the electronic configuration of a 2D material, and their reciprocal lattice geometry, could bring forward a set of Kataura-like plots for many other 2D materials rolled into 1D NTs. Multilayered materials may face Eg shrinkage due to the stress accumulated in the inner and outer layers.
6 Conclusions
Most current theoretical research on nanotubes focuses on the structure of well-known materials and is usually limited to the study of achiral NTs, especially for more complex materials.The program here presented, Chiraltube, is a tool that allows the expansion of current research of 2D materials into 1D chiral NTs of the same materials. It does this by generalising the concepts learned from the construction of CNTs and applying them to an arbitrary 2D unit cell, thus working with any conceivable 2D material. Knowing the unit cell of a certain 2D material, one can now immediately generate any number of NTs from that material with any chirality desired. The capability of the code was confirmed by comparing the resulting parameters and structures to those in the literature, mostly with CNTs but also with a few achiral examples of PNTs and MoS2 NTs. Additionally, ab initio calculations were performed on generated PNT structures, proving their stability after a successful relaxation simulation and extracting important characteristics from these NTs such as their electronic bandgap.
A user-customised error parameter allows for the generation of shorter nanotube supercells for easier study in further ab initio calculations, at the expense of slight geometric alterations which might affect the overall stability of the structure.
One can easily obtain important parameters of generated NTs like their height, radius, translational vector, symmetry vector or the number of unit cells in the NT supercell. This provides immediate understanding into the trends and main characteristics of NTs of a certain material, exemplified in this work by the analysis of the number of atoms and the interatomic distances of the 1st and 2nd neighbours on the outermost layers of PNTs, MoS2 NTs, Ti3C2 NTs and CNTs.
The main advantages are anticipated to result from the employment of Chiraltube to produce nanotube coordinates that will be a source of information for future research and calculations.
Future work includes calculations of the reciprocal space from the generated structures, in order to give a rough prediction of the electronic properties of the nanotube families purely from a geometric standpoint. Additionally, with the use of Chiraltube, there is an opportunity for a larger project that gives a quick relaxation to the generated NTs and determines their stability to form a massive database of stable nanotube structures of different materials and make it freely available online.
Author contributions
The conceptualisation, funding acquisition, ab initio calculations and visualization were done by FCS. The investigation, methodology and writing were shared tasks. The algorithms, coding, and data curation were done by JMAC.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank J. A. Reyes-Retana for fruitful discussions and encouragement. FCS acknowledges funding from FICSAC and FISMAT, at Universidad Iberoamericana, and also from CONACYT Synergy project 1564464. JMAC acknowledges Universidad Iberoamericana for his Scholarship to Talent. Computational resources were provided by FISMAT.References
- S. Iijima, Nature, 1991, 354, 56–58 CrossRef CAS.
- A. Oberlin, M. Endo and T. Koyama, J. Cryst. Growth, 1976, 32, 335–349 CrossRef CAS.
- A. Jorio, G. DresselhausandM. S. Dresselhaus, Carbon Nanotubes: Advanced Topics in the Synthesis, Structure, Properties and Applications, Springer, Germany, 2008, vol. 111 Search PubMed.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D.-e. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, science, 2004, 306, 666–669 CrossRef CAS.
- A. Geim and K. Novoselov, Nat. Mater., 2007, 183–191 CrossRef CAS.
- R. Saito, M. Fujita, G. Dresselhaus and M. Dresselhaus, Appl. Phys. Lett., 1992, 60, 2204–2206 CrossRef CAS.
- R. Saito, M. Fujita, G. Dresselhaus and M. S. Dresselhaus, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 1804 CrossRef CAS.
- S. Maruyama, Kataura-Plot for Resonant Raman, https://www.photon.t.u-tokyo.ac.jp/%7Emaruyama/kataura/kataura.html Search PubMed.
- V. I. Artyukhov, E. S. Penev and B. I. Yakobson, Nat. Commun., 2014, 5, 1–6 Search PubMed.
- G. Dresselhaus, M. S. Dresselhaus and R. Saito, Physical Properties of Carbon Nanotubes, Imperial College Press, London, 1998 Search PubMed.
- G. G. Samsonidze, A. R. Saito, D. A. Jorio, E. Pimenta, F. Souza, F. A. Grüneis, D. G. Dresselhaus and M. Dresselhaus, J. Nanosci. Nanotechnol., 2003, 3, 431–458 CrossRef CAS.
- D. Hedman, H. Reza Barzegar, A. Rosén, T. Wågberg and J. Andreas Larsson, Sci. Rep., 2015, 5, 1–10 CrossRef PubMed.
- X. Zhao, Y. Liu, S. Inoue, T. Suzuki, R. Jones and Y. Ando, Phys. Rev. Lett., 2004, 92, 125502 CrossRef CAS.
- N. Hamada, S.-I. Sawada and A. Oshiyama, Phys. Rev. Lett., 1992, 68, 1579 CrossRef CAS PubMed.
- T. W. Odom, J.-L. Huang, P. Kim and C. M. Lieber, Nature, 1998, 391, 62–64 CrossRef CAS.
- H. Telg, J. Maultzsch, S. Reich, F. Hennrich and C. Thomsen, Phys. Rev. Lett., 2004, 93, 177401 CrossRef CAS PubMed.
- S. J. Tans, A. R. Verschueren and C. Dekker, Nature, 1998, 393, 49–52 CrossRef CAS.
- A. L. Antaris, J. T. Robinson, O. K. Yaghi, G. Hong, S. Diao, R. Luong and H. Dai, ACS Nano, 2013, 7, 3644–3652 CrossRef CAS PubMed.
- S. Pisana, A. Jungen, C. Zhang, A. M. Blackburn, R. Sharma, F. Cervantes-Sodi, C. Stampfer, C. Ducati, A. C. Ferrari and C. Hierold, J. Phys. Chem. C, 2007, 111, 17249–17253 CrossRef CAS.
- M. Irita, T. Yamamoto and Y. Homma, Nanomaterials, 2021, 11, 2309 CrossRef CAS PubMed.
- J. W. Wilder, L. C. Venema, A. G. Rinzler, R. E. Smalley and C. Dekker, Nature, 1998, 391, 59–62 CrossRef.
- W. Su, X. Li, L. Li, D. Yang, F. Wang, X. Wei, W. Zhou, H. Kataura, S. Xie and H. Liu, Nat. Commun., 2023, 14, 1672 CrossRef CAS PubMed.
- J. T. Frey and D. J. Doren, TubeGen 3.4, 2011, http://turin.nss.udel.edu/research/tubegenonline.html Search PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 1–17 Search PubMed.
- X. Yang and J. Ni, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 195426 CrossRef.
- J. Bai, X. C. Zeng, H. Tanaka and J. Zeng, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 2664–2668 CrossRef CAS PubMed.
- Z. Zhang, M.-Q. Cheng, Q. Chen, H.-Y. Wu, W. Hu, P. Peng, G.-F. Huang and W.-Q. Huang, Nanoscale Res. Lett., 2019, 14, 1–11 CrossRef PubMed.
- J. Hao, Z. Wang and Q. Jin, Sci. Rep., 2019, 9, 1–8 CrossRef.
- H. Guo, N. Lu, J. Dai, X. Wu and X. C. Zeng, J. Phys. Chem. C, 2014, 118, 14051–14059 CrossRef CAS.
- X. Blase, A. Rubio, S. G. Louie and M. L. Cohen, EPL, 1994, 28, 335 CrossRef CAS.
- C. Ghosh, S. Pal, B. Goswami and P. Sarkar, J. Phys. Chem. C, 2007, 111, 12284–12288 CrossRef CAS.
- R. Fathi and T. Movlarooy, J. Electron. Mater., 2018, 47, 7358–7364 CrossRef CAS.
- G. Seifert, H. Terrones, M. Terrones, G. Jungnickel and T. Frauenheim, Phys. Rev. Lett., 2000, 85, 146 CrossRef CAS.
- Y. Zhang, T. Ideue, M. Onga, F. Qin, R. Suzuki, A. Zak, R. Tenne, J. Smet and Y. Iwasa, Nature, 2019, 570, 349–353 CrossRef CAS PubMed.
- H.-H. Wu, Q. Meng, H. Huang, C. Liu and X.-L. Wang, Phys. Chem. Chem. Phys., 2018, 20, 3608–3613 RSC.
- X. Zhang, Z. Ma, X. Zhao, Q. Tang and Z. Zhou, J. Mater. Chem. A, 2015, 3, 4960–4966 RSC.
- V. Nagarajan and R. Chandiramouli, Chem. Phys., 2017, 495, 35–41 CrossRef CAS.
- G. B. Pinhal, N. L. Marana, G. S. Fabris and J. R. Sambrano, Theor. Chem. Acc., 2019, 138, 1–11 Search PubMed.
- M. A. Hudspeth, B. W. Whitman, V. Barone and J. E. Peralta, ACS Nano, 2010, 4, 4565–4570 CrossRef CAS PubMed.
- D. Pan, T.-C. Wang, C. Wang, W. Guo and Y. Yao, RSC Adv., 2017, 7, 24647–24651 RSC.
- M. Milivojevic, S. Dmitrovic, M. Damnjanovic and T. Vukovic, J. Phys. Chem. C, 2020, 124, 11141–11149 CrossRef CAS.
- A. Rubio, J. L. Corkill and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 5081 CrossRef CAS.
- J. Kroes, A. Fasolino and M. Katsnelson, Phys. Chem. Chem. Phys., 2016, 18, 19359–19367 RSC.
- M. Damnjanović, T. Vuković and I. Milošević, Isr. J. Chem., 2017, 57, 450–460 CrossRef.
- G. R. Bhimanapati, Z. Lin, V. Meunier, Y. Jung, J. Cha, S. Das, D. Xiao, Y. Son, M. S. Strano and V. R. Cooper, et al. , ACS Nano, 2015, 9, 11509–11539 CrossRef CAS.
- N. Mounet, M. Gibertini, P. Schwaller, D. Campi, A. Merkys, A. Marrazzo, T. Sohier, I. E. Castelli, A. Cepellotti, G. Pizzi and N. Marzari, Nat. Nanotechnol., 2018, 13, 246–252 CrossRef CAS PubMed.
- P. Miró, M. Audiffred and T. Heine, Chem. Soc. Rev., 2014, 43, 6537–6554 RSC.
- J. Reyes-Retana and F. Cervantes-Sodi, Sci. Rep., 2016, 6, 1–10 CrossRef PubMed.
- J. M. de Albornoz-Caratozzolo and F. Cervantes-Sodi, Chiraltube, 2023 Search PubMed , https://github.com/Chema-dac/chiraltube.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef.
- A. M. Rappe, K. M. Rabe, E. Kaxiras and J. Joannopoulos, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 1227 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188 CrossRef.
- Q. Fan, L. Yan, M. W. Tripp, O. Krejčí, S. Dimosthenous, S. R. Kachel, M. Chen, A. S. Foster, U. Koert, P. Liljeroth and J. M. Gottfried, Science, 2021, 372, 852–856 CrossRef CAS.
- P. Hirel, Format: XYZ, https://atomsk.univ-lille.fr/doc/en/format_xyz.html Search PubMed.
- Y. Zhang, T. Ideue, M. Onga, F. Qin, R. Suzuki, A. Zak, R. Tenne, J. Smet and Y. Iwasa, Nature, 2019, 570, 349–353 CrossRef CAS.
- A. Celik-Aktas, J. Zuo, J. Stubbins, C. Tang and Y. Bando, Appl. Phys. Lett., 2005, 86, 133110 CrossRef.
- J. O. Sofo, A. S. Chaudhari and G. D. Barber, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 153401 CrossRef.
- H. Liu, A. T. Neal, Z. Zhu, Z. Luo, X. Xu, D. Tománek and P. D. Ye, ACS Nano, 2014, 8, 4033–4041 CrossRef CAS PubMed.
- J. Kim, S. S. Baik, S. H. Ryu, Y. Sohn, S. Park, B.-G. Park, J. Denlinger, Y. Yi, H. J. Choi and K. S. Kim, Science, 2015, 349, 723–726 CrossRef CAS PubMed.
- R. Tenne, Colloids Surf., A, 2002, 208, 83–92 CrossRef CAS.
- R. L. Whitby, W. K. Hsu, C. B. Boothroyd, P. K. Fearon, H. W. Kroto and D. R. Walton, ChemPhysChem, 2001, 2, 620–623 CrossRef CAS PubMed.
- R. L. Whitby, W. K. Hsu, P. K. Fearon, N. C. Billingham, I. Maurin, H. W. Kroto, D. R. Walton, C. B. Boothroyd, S. Firth, R. J. Clark and D. Collison, Chem. Mater., 2002, 14, 2209–2217 CrossRef CAS.
- W. K. Hsu, B. H. Chang, Y. Q. Zhu, W. Q. Han, H. Terrones, M. Terrones, N. Grobert, A. K. Cheetham, H. W. Kroto and D. R. Walton, J. Am. Chem. Soc., 2000, 122, 10155–10158 CrossRef CAS.
- M. B. Sadan, L. Houben, A. N. Enyashin, G. Seifert and R. Tenne, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 15643–15648 CrossRef CAS PubMed.
- Y. Chen, H. Deniz and L.-C. Qin, Nanoscale, 2017, 9, 7124–7134 RSC.
- F. Qin, W. Shi, T. Ideue, M. Yoshida, A. Zak, R. Tenne, T. Kikitsu, D. Inoue, D. Hashizume and Y. Iwasa, Nat. Commun., 2017, 8, 1–6 CrossRef.
- Q. Qian, R. Zu, Q. Ji, G. S. Jung, K. Zhang, Y. Zhang, M. J. Buehler, J. Kong, V. Gopalan and S. Huang, ACS Nano, 2020, 14, 13333–13342 CrossRef CAS PubMed.
- H. Kataura, Y. Kumazawa, Y. Maniwa, I. Umezu, S. Suzuki, Y. Ohtsuka and Y. Achiba, Synth. Met., 1999, 103, 2555–2558 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: A document with examples of input and output files and a zoomed-in figure into a small region of manuscript Fig. 8. A zip file with the code in Python and the special-xyz input files of the 4 materials used in the manuscript. The code is available at https://github.com/Chema-dac/chiraltube. See DOI: https://doi.org/10.1039/d3na00301a |
| This journal is © The Royal Society of Chemistry 2024 |