Buckling of geometrically confined shells†
Abstract
We study the periodic buckling patterns that emerge when elastic shells are subjected to geometric confinement. Residual swelling provides access to range of shapes (saddles, rolled sheets, cylinders, and spherical sections) which vary in their extrinsic and intrinsic curvatures. Our experimental and numerical data show that when these moderately thick structures are radially confined, a single geometric parameter – the ratio of the total shell radius to the amount of unconstrained material – predicts the number of lobes formed. We present a model that interprets this scaling as the competition between radial and circumferential bending. Next, we show that reducing the transverse confinement of saddles causes the lobe number to decrease with a similar scaling analysis. Hence, one geometric parameter captures the wave number through a wide range of radial and transverse confinement, connecting the shell shape to the shape of the boundary that confines it. We expect these results to be relevant for an expanse of shell shapes, and thus applicable to the design of shape-shifting materials and the swelling and growth of soft structures.
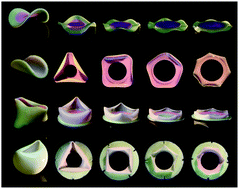
- This article is part of the themed collection: Soft Matter Emerging Investigators


 Please wait while we load your content...
Please wait while we load your content...
