Boundary layer description of directional polymer crystallisation

Abstract

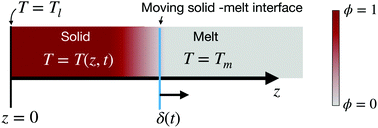
Nearly fifty years ago Lovinger and Gryte suggested that the directional crystallization of a polymer was analogous to the quiescent isothermal crystallization experiment but at a supercooling where the crystal growth velocity was equal to the velocity of the moving front. Our experiments showed that this equivalence holds in a detailed manner at low directional velocities. To understand the underlying physics of these situations, we modeled the motion of a crystallization front in a liquid where the left side boundary is suddenly lowered below the melting point (Stefan's problem) but with the modification that the crystallization kinetics follow a version of the Avrami model. Our numerical results surprisingly showed that the results of the polymer analog track with the Stefan results which were derived for a simple liquid that crystallizes completely at its melting point; in particular, the position of the crystal growth-front evolved with time exactly as in the Stefan problem. The numerical solution also showed that the temperature in the immediate vicinity of the growth-front decreased with increasing front velocity, which is in line with Lovinger and Gryte's ansatz. To provide a clear theoretical understanding of these numerical results we derive a boundary layer solution to the governing coupled differential equations of the polymer problem. The analytical results are in agreement with our observations from experiments and numerical computations but show that this equivalence between the small molecule and polymer analog only holds in the limit where the crystallization enthalpy is much larger than the rate at which heat is conducted away in the polymer. In particular, in the context of the temperature profile, the enthalpy generated by the crystallisation process which is spread out over a narrow spatial region can be approximated as a point source whose location and temperature correspond to the Lovinger–Gryte ansatz.