New models for the time dependent toxicity of individual and combined toxicants
Abstract
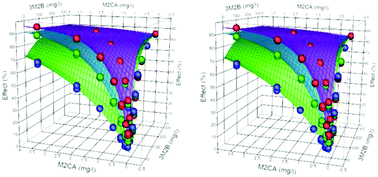
Time-dependent toxicity data of specific toxicants observed against A. fischeri were analysed using a single time-dependent Weibull cumulative distribution function (CDF). For binary mixtures the individual Weibull parameters provided the marginals for a bivariate copula model, characterised by a single extra parameter, the interaction exponent, θ. The copula model unites both the dose addition (DA, Loewe additivity) and dose independence (DI, Bliss independence) hypotheses of combinations into a single explicit equation and returns both hypotheses as special cases. The model predicts the linear isoboles from sham (like against like) experiments and the linear, concave, convex and mixed concave–convex isoboles from true binary mixtures. Systems are defined as being independent when θ = 1, additive when min(n1, n2) ≤ θ ≤ max(n1, n2), antagonistic when θ < min(n1, n2) and synergistic when θ > max(n1, n2), where ni are the individual dose (concentration) exponents. More complex mixtures were analysed by developing n-dimensional copulas: two ternary systems were analysed using a ternary copula that returned the three bivariate marginals and the three individual marginals of the mixture. The general model can also be used for time-independent studies by simply removing the time dependency. Research into combined effects has often assumed that if both the parameters for all the individual components in a mixture and the model for combinations were known then the additive effect of the whole could be predicted. This hypothesis has been shown to be false because without knowing how the components in a mixture interact the predictions from the standard DI or DA models provide only an initial, best guess, analysis.
- This article is part of the themed collection: Toxicology Research Recent HOT articles


 Please wait while we load your content...
Please wait while we load your content...