A new paradigm on the chemical potentials of components in multi-component nano-phases within multi-phase systems†
Abstract
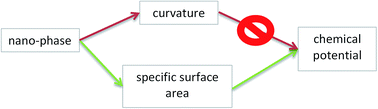
The chemical potentials of components in nano-phases determine the equilibrium of nano-materials. In this paper the difference between the equilibrium of a nano-phase and the equilibrium of an analogous macro-phase under the same constraints is called a “nano-effect”. Historically the first paper to describe the nano-effect was published by Kelvin (1871), claiming that it is due to the increased curvature of the nano-phase. This approach forms the basis of the Kelvin paradigm, still widely used in chemistry, biology and materials science (but not in physics). The Kelvin paradigm is the basis of the Kelvin equation, the Gibbs–Thomson equation and the Ostwald–Freundlich equation for the vapor pressure, melting point and solubility of nano-phases, respectively. The Kelvin paradigm is also successful in the interpretation of more complex phenomena, such as capillary condensation. However, the Kelvin paradigm predicts no nano-effect for not curved nano-phases, such as crystals and thin films, contradicting experimental facts. Moreover, it wrongly predicts that a cubic (or any other crystal-shaped) nano-droplet is more stable than a spherical nano-droplet of the same volume (this contradiction is shown here for the first time). In addition to its positive features, these and other shortcomings of the Kelvin paradigm call for a paradigm shift. A new paradigm is presented in this paper, claiming that the nano-effect is due to the increased specific surface area of the nano-phase. Chemical potentials of components in multi-component phases are derived in this paper within this new paradigm. These equations are extended for nano-phases in multi-phase situations, such as liquids confined within nano-capillaries, or nano-sized sessile drops attached to flat solid substrates. The new paradigm leads to similar results compared to the Kelvin paradigm for the case of capillary condensation into capillaries (this is because the specific surface area of a cylindrical wall is the same as the curvature of the spherical phase: 2/r). However, the new paradigm is able to provide meaningful solutions also for problems, not tractable by the Kelvin equation, such as the case of crystals and thin films having no curvature.


 Please wait while we load your content...
Please wait while we load your content...