Failing softly: a fracture theory of highly-deformable materials

Abstract

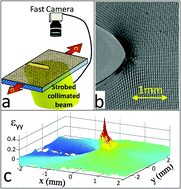
Highly-deformable materials, from synthetic hydrogels to biological tissues, are becoming increasingly important from both fundamental and practical perspectives. Their mechanical behaviors, in particular the dynamics of crack propagation during failure, are not yet fully understood. Here we propose a theoretical framework for the dynamic fracture of highly-deformable materials, in which the effects of a dynamic crack are treated with respect to the nonlinearly deformed (pre-stressed/strained), non-cracked, state of the material. Within this framework, we derive analytical and semi-analytical solutions for the near-tip deformation fields and energy release rates of dynamic cracks propagating in incompressible neo-Hookean solids under biaxial and uniaxial loading. We show that moderately large pre-stressing has a marked effect on the stress fields surrounding a crack's tip. We verify these predictions by performing extensive experiments on the fracture of soft brittle elastomers over a range of loading levels and propagation velocities, showing that the newly developed framework offers significantly better approximations to the measurements than standard approaches at moderately large levels of external loadings and high propagation velocities. This framework should be relevant to the failure analysis of soft and tough, yet brittle, materials.