Diffusion, sedimentation equilibrium, and harmonic trapping of run-and-tumble nanoswimmers

Abstract

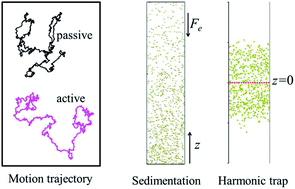
The diffusion of self-propelling nanoswimmers is explored by dissipative particle dynamics in which a nanoswimmer swims by forming an instantaneous force dipole with one of its nearest neighboring solvent beads. Our simulations mimic run-and-tumble behavior by letting the swimmer run for a time τ, then it randomly changes its direction for the next run period. Our simulations show that the swimming speed (ν_a) of a nanoswimmer is proportional to the propulsion force and the mobility of a pusher is the same as that of a puller. The effective diffusivity is determined by three methods: mean squared displacement, velocity autocorrelation function, and sedimentation equilibrium. The active colloid undergoes directed propulsion at short time scales but changes to random motion at long time scales. The velocity autocorrelation function decreases with time and becomes zero beyond the run time. Under gravity, the concentration profile of active colloids follows Boltzmann distribution with a sedimentation length consistent with that acquired from the drift–diffusion equation. In our simulation, all three methods yield the same result, the effective diffusivity of an active colloid is the sum of the diffusivity of a passive colloid and ν_a²τ/6. When the active colloids are confined by a harmonic well, they are trapped within a confinement length defined by the balance between the swimmer active force and restoring force of the well. When the confinement length is large compared to the run length, the stationary density profile follows the Boltzmann distribution. However, when the run length exceeds the confinement length, the density distribution is no longer described by Boltzmann distribution, instead we found a bimodal distribution.