The chemical roots of the matching polynomial†
Abstract
The interpretation of topological resonance energy (TRE), the mathematical measure of energetic chemical aromaticity at the Hückel level of theory, is revisited by providing a concise analysis of the matching polynomial of a chemical graph. Whereas the matching (or acyclic) polynomial is not a properly characteristic polynomial in general, it is the arithmetic mean of the characteristic polynomials of the corresponding Hückel and Möbius chemical graphs. For unicyclic graphs, the roots of the matching polynomial (serving to calculate the TRE values) can be graphically approximated from generalized Frost–Musulin–Zimmermann diagrams, the results becoming exact for annulenic monocycles. The matching polynomial is also shown to be a weighted sum of characteristic polynomials of subgraphs: the whole graph itself and the exocyclic graphs obtained by suppression of individual circuits. The performance of these ring twisting and ring masking processes is compared to that of the previously proposed ring opening process. Further prospects for the interpretation and approximation of TRE are discussed.
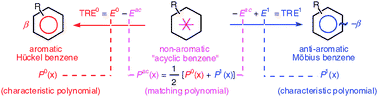

 Please wait while we load your content...
Please wait while we load your content...