DOI:
10.1039/C6RA28628C
(Paper)
RSC Adv., 2017,
7, 13003-13009
The reactive wetting kinetics of interfacial tension: a reaction-limited model†
Received
23rd December 2016
, Accepted 17th February 2017
First published on 24th February 2017
Abstract
A new dynamics model describing the time-dependent change of solid–liquid interfacial tension is first established to explain the driving force and physical essence of the spreading process of reaction-limited wetting. The model has been successfully verified through the wetting experiments of Al–Si/SiC systems (Si content = 0, 7, 12 wt%, respectively) at different temperatures, in which the logarithmic plots of driving force versus time present a linear relationship in the reaction-limited spreading stage. Furthermore, the mechanisms of reactive spreading are discussed in detail.
1. Introduction
During the past few decades, the mechanisms of reactive wetting and spreading with solidification in various systems have been under extensive investigations.1–18 Most of the reported studies focus on the effect of interfacial reactions on the spreading kinetics, and there are some dynamics models of spreading, e.g., the molecular dynamics model of Blake and Haynes,19 the semi-empirical formula of de Gennes,20 the diffusion-limited model of Mortensen et al.,9 and the characteristic equation of the reaction-limited spreading model by Dezellus et al.21 From Young's equation,22 one can see that solid–liquid interfacial tension (γsl) is indeed an essential factor affecting the spreading process.| |
γsv = γsl + γlv![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θe θe
| (1) |
Where γsv is solid-vapor surface tension, γlv is liquid–vapor surface tension, θe is the equilibrium contact angle. In our opinion, the commonalities of all the reactive wetting systems are the variation of interfacial character, which is related to γsl directly. However, most dynamics models mentioned above are built on the basis of a macroscopic perspective, which show a similar relationship between dynamic contact angle (θ) or spreading radius (R) versus time (t). A detailed explanation of wetting mechanism based on the γsl is rarely given i.e. there is few dynamics models about the decrease rate of γsl which is important to study the reactive wetting dynamics.
Some phenomena in reactive wetting system can be essentially explained by γsl theory. For example, the interfacial reaction can be realized in Cu-10 at% Si/C system through the dissolution of carbon atoms in liquid alloy with θ unchanging.21 There is no chemical reaction in the system, so the γsl keeps constant. This phenomenon means that the change of θ should be attributed to the γsl. The same inference can also be drawn from the other common reactive wetting systems.23,24 Once the γsl becomes stable, the θ will not change. In conclusion, γsl is the most fundamental starting point for understanding the complex field of wetting, which definitely deserves a further investigation.
The primary purpose of our work reported in this paper is to build a new dynamics model from the view point of γsl to explain the driving force and wetting mechanism. The wetting experiments of Al/SiC, Al-7 wt% Si/SiC and Al-12 wt% Si/SiC systems at different temperatures have been investigated through a improved sessile drop method to examine the rationality of the model. The measurements on reactive surface can also take place if more moderate conditions are investigated like water on a reactive de-wetting on freshly cleaned silicon wafer surface.25
2. Experimental procedure
For all contact angle (CA) measurements, 98.5 wt% pure silicon carbide (SiC) solid plates, with a density of 3.1 g cm−3 and dimensions of 20 mm in diameter and 5 mm in thickness, are used as substrate. The Al specimens with a purity of 99.999 wt% are in the form of small cubes with dimensions of 3 × 3 × 3 mm3. The Al–Si alloys are prepared by arc-melting of high-purity Al (99.999 wt%) and Si (99.999 wt%) plates in argon (99.999 wt% purity) atmosphere, where Ti (99.8 wt% purity) metals are put inside to getter oxygen impurities. The raw materials are melted and solidified in a water-cooled copper crucible four times under constant electromagnetic stirring. And then the obtained Al–Si alloys are cut into cubes with dimensions of 3 × 3 × 3 mm3. The surfaces of SiC substrates are mechanically polished by different micrometer-size diamond pastes and the average roughness is 20 nm. Before the wetting experiments, both the substrates and specimens are ultrasonically cleaned in alcohol.
The wetting experiments are investigated through a dispensed sessile drop method under high vacuum (10−4 Pa), which is proposed by Shen et al.26–28 One significant characteristic of this method is that the droplets and substrates are separated before the wetting experiments to avoid pre-reaction upon heating. Besides, the initial oxide layers covering the molten Al droplet can be mechanically stripped to obtain a more exact measurement result of the θ and the spreading dynamics. The contact between different parts of the wetting system begins when the predetermined testing temperature is reached. In a typical wetting experiment procedure, the molten Al is slowly extruded through a narrow orifice at the bottom of an alumina tube (99.6 wt%) and then rested horizontally onto the SiC surface. During the wetting procedure, the θ is directly measured from drop profiles using an axisymmetric drop shape analysis (ADSA) program.29 The detailed description of the performed experiments can be found in the ESI.† The wetting experiments are carried out at 973–1273 K (Tables 1 and 2).
Table 1 The relevant datas of Al/SiC system at different temperaturesa
| Temperature/K |
θini(Al)/° |
θfin(Al)/° |
θini/θfin |
k |
c |
Fitting range |
| ini= initial, fin=final. |
| 973 |
125 |
95 |
1.31 |
— |
1 |
— |
| 1073 |
117 |
91 |
1.28 |
— |
1 |
— |
| 1123 |
118 |
71 |
1.66 |
8.29 × 10−5 |
1 |
188–7200 s |
| 1173 |
109 |
57 |
1.90 |
3.73 × 10−4 |
1 |
157–3307 s |
| 1273 |
105 |
57 |
1.86 |
4.12 × 10−3 |
1 |
36–255 s |
Table 2 The relevant datas of Al-7 Si/SiC system at different temperatures
| Temperature/K |
θini(Al-7 wt% Si)/° |
θfin(Al-7 wt% Si)/° |
θini/θfin |
k |
c |
Fitting |
| 973 |
121 |
90 |
1.34 |
— |
0.93 |
— |
| 1023 |
116 |
67 |
1.75 |
— |
0.93 |
— |
| 1073 |
109 |
73 |
1.50 |
5.5252 × 10−4 |
0.93 |
0–1131 s |
| 1123 |
105 |
74 |
1.42 |
1.39 × 10−3 |
0.93 |
0–566 s |
| 1173 |
101 |
72 |
1.40 |
5.53 × 10−3 |
0.93 |
0–124 s |
| 1273 |
103 |
51 |
2.03 |
— |
0.93 |
— |
3. Modelling and deducing
Here, we try to explain problems in reactive wetting by using changes for γsl. First of all, Fig. 1(a) is a schematic diagram of the Young's equation, in which the diameter of the drop is relatively less than the size of the substrate and the θ1 is the initial contact angle. While Fig. 1(b) is a schematic diagram of the equilibrium state in a finite interface designed for this study, the θ2 (θ2 → θmax) of which is defined as the theoretical maximum contact angle when gravitational pull is neglected and loss is prevented at the initial state. According to tensions balance on the horizontal and vertical direction, eqn (2) and (3) can be obtained:| |
γsl = −γlv![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2, 90° ≤ θ2 ≤ 180° θ2, 90° ≤ θ2 ≤ 180°
| (2) |
| |
γsv = γlv![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2, 90° < θ2 ≤ 180° θ2, 90° < θ2 ≤ 180°
| (3) |
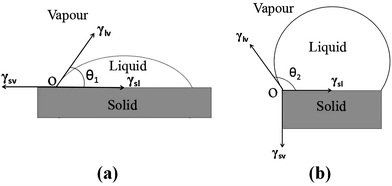 |
| | Fig. 1 The wetting schematic diagrams of (a) infinite and (b) finite solid–liquid interface. | |
Chemical reactions existing at the interface of reactive wetting systems would change the physicochemical properties of solid–liquid interface. Now we assume that the interfacial chemical reaction is a combination reaction:
It has been found that the value of γsl would reduce during the whole wetting process, which leads to the spreading of the liquid at the interface.30 Basing on this, one can assume that the driving force of wetting process is related to Δγsl(t) through the following relation:
| | |
Δγsl(t) = γsl(t) − (γsl)e
| (5) |
where
γsl(
t) and (
γsl)
e are the dynamic and equilibrium solid–liquid interfacial tensions, respectively. The decrease rate of interfacial tension, d
γsl/d
t, is an important parameter to describe the wetting mechanism. Usually, the value of d
γsl/d
t is in proportion to Δ
γsl(
t) and the interfacial reaction rate
v. We can roughly describe the rate of interfacial tension change as follow:
| |
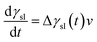 | (6) |
Combining eqn (5) and (6), the following expression of dγsl/dt is derived:
| |
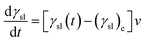 | (7) |
where
v is related to temperature and concentration of active atoms. Assume that the reactive wetting system is controlled by interfacial chemical reaction, the value of
v could be described as follow:
where
CA,
CB is the concentration of active atoms for reactant A and B, respectively.
n1,
n2 is the reaction order for reactant A and B, respectively. For wetting systems in this work, the interfacial reaction is the first-order reaction, and then:
where
C is the consumed concentration of active atoms in the liquid phase, and
k is reaction rate constant following the Arrhenius equation:
| |
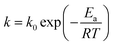 | (10) |
where
k0 is the pre-exponential factor,
Ea is the activation energy,
R is the molar gas constant, and
T is the thermodynamic temperature.
Integrating eqn (7), the following equation can be produced:
| |
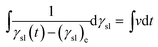 | (11) |
It can be simplified as:
| | |
ln[γsl(t) − (γsl)e] = vt + b
| (12) |
where
b is integration constant. When
t = 0, and then:
| | |
b = ln[(γsl)i − (γsl)e] = ln(Δγsl)max
| (13) |
Eqn (12) leads to the following expression:
| |
γsl(t) = (γsl)e + (Δγsl)max![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−kCt) exp(−kCt)
| (14) |
| |
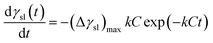 | (15) |
The features of the dynamics model derived from an interfacial tension perspective could be summarized as followed:
(i) It relates γsl directly to the spreading time by an exponential relationship.
(ii) The greater the driving force is, the faster the interfacial tension decreases.
(iii) Both the interfacial reaction velocity and the decrease rate of interfacial tension present a positive correlation with the temperature and the concentration of interfacial reactive atoms, in accordance with the basic rules of solid–liquid interfacial reactions.
4. Experiment verification
4.1 The relationship between the contact angle and time
In order to verify the rationality of the dynamics model proposed above, we investigated the wetting procedures of Al–Si/SiC systems (Si content = 0, 7, 12 wt%, respectively) from the point of view of γsl.
For Al/SiC, Al-7 wt% Si/SiC and Al-12 wt% Si/SiC systems, Cong et al.28 have already published their findings of the relations between θ and t at temperatures ranging from 973 to 1273 K. A transition from non-wetting (i.e., θe ≥ 90°) to wetting (i.e., θe < 90°) observed at a temperature in the Al/SiC system suggests that the interfacial reaction between Al and SiC may be not obvious at T ≤ 1073 K, while it is significant at T ≥ 1123 K. The contact angle in the Al-7 wt% Si/SiC system experienced a hysteresis stage after rapid spreading at 1073–1173 K, which is not observed in the Al-12 wt% Si/SiC system. This phenomenon may be related to the concentration of Si atom. The reasons for the changes in contact angle are complicated which can not be only described as a total exponential decay process (e.g., Gompertz's law31). Detailed descriptions can be seen from their report. In all cases mentioned above, an increase of temperature would produce an acceleration of spreading velocity as illustrated by the decrease of spreading time.
4.2 The relationship between the interfacial tension and time
Based on the concept of infinite and finite solid–liquid interface, as shown in Fig. 1. The reactive wetting equations for finite wetting systems have been defined by our previous work and an efficient computational method for the reactive solid–liquid interfacial tension is listed as follow:32| |
γsv = γsl + γlv[cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1 − f(θ1)], 0° ≤ θ1 ≤ 180° θ1 − f(θ1)], 0° ≤ θ1 ≤ 180°
| (16) |
| |
γsv = γlv![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2, 90° ≤ θ2 ≤ 180° θ2, 90° ≤ θ2 ≤ 180°
| (17) |
| |
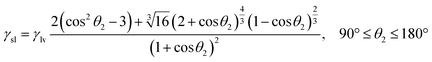 | (18) |
with| |
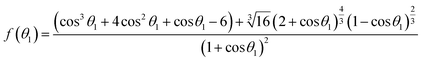 | (19) |
Detailed derivation steps of above equations can be seen in the ESI.† Compared with the equilibrium Young's equation, eqn (16) is relatively more universal for reactive wetting on infinite solid–liquid interface with an angle correct factor f(θ), which is built on the basis of the work performed by unbalanced forces at non-equilibrium. For given solid and liquid matters, the numerical values of γsv and γlv have uniqueness. Eqn (17) and (18) could be applied to describe the initial state of reactive wetting on finite solid–liquid interface only. As the initial interfacial tension (γsl)i of the two systems is identical, the mathematical relation between initial θ1 and θ2 could be derived:
| |
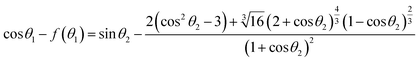 | (20) |
According to the analysis above, once the initial contacting angle θ1 of infinite solid–liquid interface is measured, the θ2 will be figured out by eqn (20), and then the corresponding γsv and (γsl)i will be determined through eqn (17) and (18), respectively. Thus the θ(t) curves can be converted into γsl(t) curves through eqn (16).
Fig. 2(a)–(c) demonstrate the variations of γsl with time for Al/SiC, Al-7 wt% Si/SiC and Al-12 wt% Si/SiC systems at different temperatures, respectively. We can see that the trends of the γsl(t) curves are consistent with the corresponding θ(t) curves for three wetting systems. As the spreading is fast at higher temperature, the drop can reach a final equilibrium state in a relatively shorter time, such as Al/SiC system at 1273 K, while some curves at lower temperature still have not reached their equilibrium states by the end of the testing time, suggesting that the interfacial reactions between the molten droplets and the SiC substrates at lower temperature should not be very significant. As shown in Fig. 2(d), three kinetic stages can be defined on the γsl(t) curve of Al/SiC system at 1173 K between t0 ≈ 0 and t3. In the first stage (t0 < t < t1), the γsl decreases rapidly with time, which might be explained by the reaction between Al and SiO2 on the oxidized SiC surface. The second stage (t1 < t < t2) is called as reaction-limited spreading, in which the γsl decreases slowly with time. This suggests an interfacial reaction happening between Al and SiC. In the third stage (t2 < t < t3), the γsl nearly keeps a constant value of 300 mN m−1. This phenomenon reveals that the reaction between Al and SiC reaches an equilibrium state at t2, i.e., the Al/SiC system stays at a diffusion-limited spreading stage from t2 to t3.33 For Al-7 wt% Si/SiC system, there is a hysteresis stage after initial rapid spreading at 1073–1173 K, because the driving force we proposed is close to 0 and the retarding force resulted from the rough interface of the reaction product Al4C3 is large enough to inhibit the movement of the triple line. However, increasing temperature can favor deoxidization by a self-cleaning reaction in a high vacuum and also accelerates the reaction between Al and SiC. As a consequence, the spreading can continue to happen in Al-7 wt% Si/SiC system at 1273 K. Such stranded behavior is not observed in the Al-12 wt% Si/SiC system because the reaction is fully inhibited (i.e., the interface roughness of Al-12 wt% Si/SiC system is quite smaller than that of Al-7 wt% Si/SiC system) and the driving force is large enough to overcome the impedance. The equilibrium Si content required to prevent the formation of Al4C3 as a function of temperature has been investigated in many works34–38 through theoretical calculations and experimental methods.
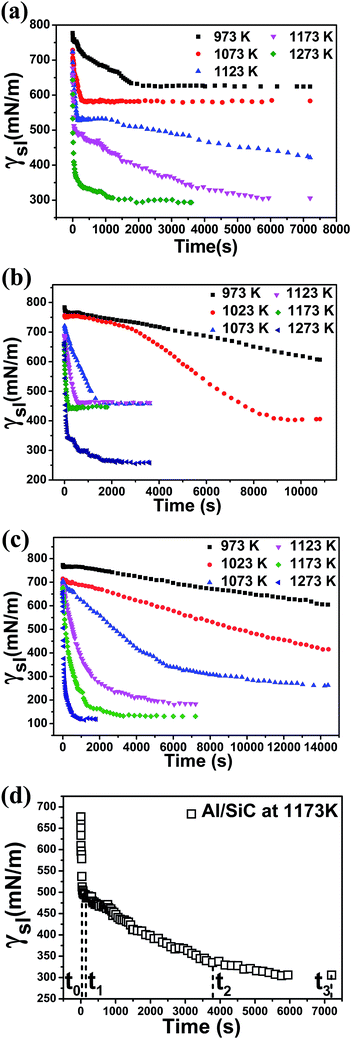 |
| | Fig. 2 Variations in the dynamic interfacial tension with time for (a) Al/SiC system, (b) Al-7 wt% Si/SiC system, (c) Al-12 wt% Si/SiC system at different temperatures and (d) Al/SiC system at 1173 K. | |
4.3 The verification of the dynamics model of reactive wetting
Fig. 3(a–c) show the logarithmic plots of γsl(t)–(γsl)e as a function of time for Al/SiC system at different temperatures. In the reaction-limited spreading stage, as fitted by the red line, the linear correlation coefficients R is very close to unity (R2 > 0.99) in all cases. It is noted that in order to draw the straight line, the value chosen for (γsl)e must be a little smaller than the experimental value in the reaction-limited spreading stage to avoid the mutation of the curve. Based on the eqn (9) and the Arrhenius law, where kC (C = 1 for pure Al) is the slope of the fitting curves (see eqn (12)), the activation energy Ea in this linear spreading stage is calculated to be 308 kJ mol−1, as shown in Fig. 3(d). This result is close to the activation energy of 330 kJ mol−1 for Al/SiC system evaluated by Choh and Oki,39 who measured the wetting rates in the range of 1173–1373 K using a dip coverage method. The slope of the fitted straight line (k) in Fig. 3(a–c) are −8.29 × 10−5, −3.73 × 10−4 and −4.12 × 10−3, respectively, which indicated that an increase in temperature would produce a strong acceleration of the interfacial reaction rate. Similar results can be drawn for Al-7 wt% Si/SiC system in the reaction-limited spreading stage, as shown in Fig. 4, with the linear correlation coefficients R close to unity (R2 > 0.99) too. The slope of the fitted straight line (kC) are −5.5252 × 10−4, −1.39 × 10−3 and −5.53 × 10−3, respectively.
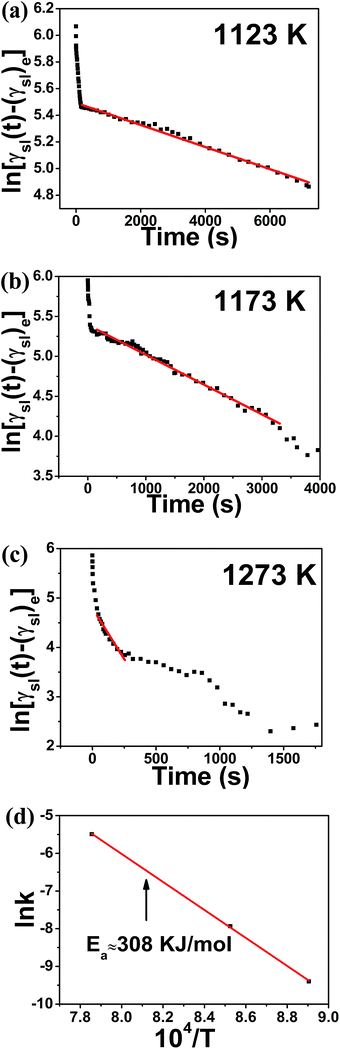 |
| | Fig. 3 ln[γsl(t) − (γsl)e] versus time for Al/SiC system at temperatures (a) 1123 K, (b) 1173 K, and (c) 1273 K, respectively; (d) Arrhenius plot of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k against 104/T for calculation of the activation energy of the spreading (Ea) in the second stage. k against 104/T for calculation of the activation energy of the spreading (Ea) in the second stage. | |
 |
| | Fig. 4 ln[γsl(t) − (γsl)e] versus time for Al-7 wt% Si/SiC system at different temperatures. | |
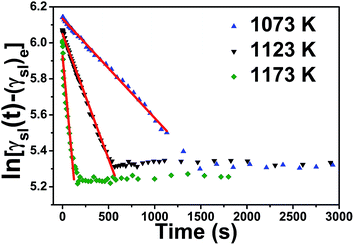
Furthermore, the phenomenon of Al-12 wt% Si/SiC system is unique, as indicated in Fig. 5, the slope of the fitted line in Al-12 wt% Si/SiC system (−1.73 × 10−3) at 1173 K is smaller than that of Al-7 wt% Si/SiC system (−5.53 × 10−3). In general, two reactions present in the Al/SiC wetting system under certain thermodynamics conditions:
| | |
4Al(l) + Al2O3(s) → 3Al2O(g)↑
| (21) |
| | |
4Al + 3SiO2 → 2Al2O3 + 3Si
| (22) |
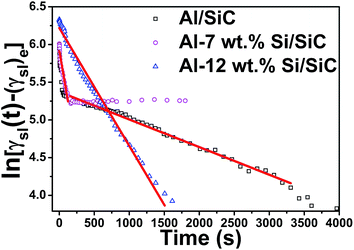 |
| | Fig. 5 ln[γsl(t) − (γsl)e] versus time for Al–Si/SiC systems with different contents of Si at 1173 K. | |
At the reaction-limited stage, the addition of Si indeed accelerates the reaction of Al/SiC system. However, as σlv(Si) < σlv(Al), we suspect that Si tends to accumulate more easily on the surface of Al droplet after a much more addition of Si (e.g., 12 wt%), which will weaken the above reaction to some extent. As a result, the reaction rate of Al-12 wt% Si/SiC system will be slower than that of Al-7 wt% Si/SiC system.
5. Conclusions
In this work, we have proposed a new reactive wetting dynamics model to better explain the driving force and wetting mechanism on the basis of solid–liquid interfacial tension γsl. This model indicates that the decrease of interfacial tension follows an exponential relation with spreading time:
γsl(t) = (γsl)e + (Δγsl)max![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−kCt) exp(−kCt) |
The γsl(t) curves at different temperatures converted from the θ(t) curves of Al/SiC, Al-7 wt% Si/SiC and Al-12 wt% Si/SiC systems have the synchronous decreasing tendencies with θ(t) curves as temperature increasing. In addition, the linear fitting results (R2 > 0.99) of the kinetics curves reveal that the driving force of reaction-limited wetting is indeed the variation of solid–liquid interfacial tension Δγsl(t), confirming the rationality of the dynamics model we build. Moreover, the value of activation energy calculated in the reaction-limited spreading stage of Al/SiC system is 308 kJ mol−1, which is close to 330 kJ mol−1 in other reference.
As far as we know, the dynamics model, which appears to be well verified by experimental data, is first proposed to explain the spreading mechanism in terms of interfacial tension for reaction-limited wetting.
Acknowledgements
This work is supported by the program of the National Natural Science Foundation of China (50471007, 51102045). The authors are thankful to the Key Laboratory of Automobile Materials in Jilin University for their kind help in high temperature experiment.
References
- R. Bhola and S. Chandra, J. Mater. Sci., 1999, 34, 4883–4894 CrossRef CAS.
- V. H. López and A. R. Kennedy, J. Colloid Interface Sci., 2006, 298, 356–362 CrossRef PubMed.
- N. Eustathopoulos, Acta Mater., 1998, 46, 2319–2327 CAS.
- E. Saiz, C. W. Hwang, K. Suganuma and A. P. Tomsia, Acta Mater., 2003, 51, 3185–3197 CrossRef CAS.
- H. Kamusewitz, W. Possart and D. Paul, Colloids Surf., A, 1999, 156, 271–279 CrossRef CAS.
- D. E. Peebles, H. C. Peebles and J. A. Ohlhausen, Colloids Surf., A, 1998, 144, 89–114 CrossRef CAS.
- P. Shen, H. Fujii, T. Matsumoto and K. Nogi, Metall. Mater. Trans. A, 2004, 35, 583–588 CrossRef.
- Y. Liang, S. J. Meschter and T. J. Singler, Acta Mater., 2004, 52, 2873–2888 CrossRef.
- A. Mortensen, B. Drevet and N. Eustathopoulos, Scr. Mater., 1997, 36, 645–651 CrossRef CAS.
- A. Contreras, C. A. León, R. A. L. Drew and E. Bedolla, Scr. Mater., 2003, 48, 1625–1630 CrossRef CAS.
- K. Landry and N. Eustathopoulos, Acta Mater., 1996, 44, 3923–3932 CrossRef CAS.
- N. Eustathopoulos, J. P. Garandet and B. Drevet, Philos. Trans. R. Soc., A, 1998, 356, 871–884 CrossRef CAS.
- B. Drevet, K. Landry, P. Vikner and N. Eustathopoulos, Scr. Mater., 1996, 35, 1265–1270 CrossRef CAS.
- K. Landry, S. Kalogeropoulou, N. Eustathopoulos, Y. Naidich and V. Krasovsky, Scr. Mater., 1996, 34, 841–846 CrossRef.
- L. Espié, B. Drevet and N. Eustathopoulos, Metall. Mater. Trans. A, 1994, 25, 599–605 CrossRef.
- N. Eustathopoulos, Curr. Opin. Solid State Mater. Sci., 2005, 9, 152–160 CrossRef CAS.
- F. G. Yost, R. R. Rye and J. A. Mann, Acta Mater., 1997, 45, 5337–5345 CrossRef CAS.
- F. G. Yost and E. J. O'Toole, Acta Mater., 1998, 46, 5143–5151 CrossRef CAS.
- T. D. Blake and J. M. Haynes, J. Colloid Interface Sci., 1969, 30, 421–423 CrossRef CAS.
- P. G. D. Gennes, Rev. Mod. Phys., 1985, 57, 827–863 CrossRef.
- O. Dezellus, F. Hodaj and N. Eustathopoulos, Acta Mater., 2002, 50, 4741–4753 CrossRef CAS.
- T. Young, Philos. Trans. R. Soc. London, 1805, 95, 65–87 CrossRef.
- G. Kumar and K. N. Prabhu, Adv. Colloid Interface Sci., 2007, 133, 61–89 CrossRef CAS PubMed.
- N. Eustathopoulos and R. Voytovych, J. Mater. Sci., 2015, 51, 1–13 CrossRef.
- M. Schmitt, K. Gross, J. Grub and F. Heib, J. Colloid Interface Sci., 2015, 447, 229–239 CrossRef CAS PubMed.
- L. Y. Zhang, P. Shen, Y. Qi and Q. C. Jiang, Appl. Surf. Sci., 2013, 276, 424–432 CrossRef CAS.
- P. Shen, Q. Lin and Q. Jiang, J. Mater. Res., 2009, 24, 2420–2427 CrossRef CAS.
- X. S. Cong, P. Shen, Y. Wang and Q. Jiang, Appl. Surf. Sci., 2014, 317, 140–146 CrossRef CAS.
- M. Hoorfar and A. W. Neumann, Adv. Colloid Interface Sci., 2006, 121, 25–49 CrossRef CAS PubMed.
- D. Zhang, D. Y. Zhu, T. Zhang and Q. F. Wang, Trans. Nonferrous Met. Soc. China, 2015, 25, 2473–2480 CrossRef CAS.
- Y. S. Chiu and J. E. Zajic, Biotechnol. Bioeng., 1976, 18, 1167–1170 CrossRef CAS PubMed.
- D. Y. Zhu, X. M. Liao and P. Q. Dai, Chin. Sci. Bull., 2012, 57, 4517–4524 CrossRef CAS.
- G. W. Liu, M. L. Muolo, F. Valenza and A. Passerone, Ceram. Int., 2010, 36, 1177–1188 CrossRef CAS.
- J. Narciso, C. García-Cordovilla and E. Louis, Mater. Sci. Eng., B, 1992, 15, 148–155 CrossRef.
- D. J. Lloyd, H. Lagace, A. Mcleod and P. L. Morris, Mater. Sci. Eng., A, 1989, 107, 73–80 CrossRef.
- T. Iseki, T. Kameda and T. Maruyama, J. Mater. Sci., 1984, 19, 1692–1698 CrossRef CAS.
- H. Nakae, K. Yamamoto and K. Sato, Mater. Trans., 1991, 32, 531–538 CrossRef CAS.
- J. C. Lee, S. B. Park, H. K. Seok, C. S. Oh and H. I. Lee, Acta Mater., 1998, 46, 1771–1780 CrossRef CAS.
- T. Choh and T. Oki, Mater. Sci. Technol., 1987, 3, 378–385 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra28628c |
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *
*
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θe
θe
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2, 90° ≤ θ2 ≤ 180°
θ2, 90° ≤ θ2 ≤ 180°
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2, 90° < θ2 ≤ 180°
θ2, 90° < θ2 ≤ 180°
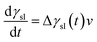
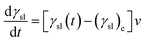
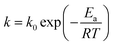
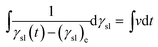
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−kCt)
exp(−kCt)
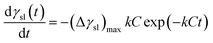
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1 − f(θ1)], 0° ≤ θ1 ≤ 180°
θ1 − f(θ1)], 0° ≤ θ1 ≤ 180°
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2, 90° ≤ θ2 ≤ 180°
θ2, 90° ≤ θ2 ≤ 180°
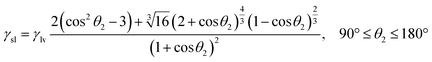
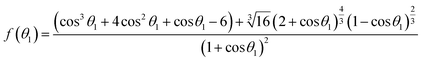
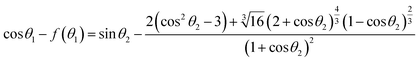

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−kCt)
exp(−kCt)



