DOI:
10.1039/C3CP43439G
(Perspective)
Phys. Chem. Chem. Phys., 2013,
15, 3348-3371
Understanding photosynthetic light-harvesting: a bottom up theoretical approach
Received
28th September 2012
, Accepted 11th January 2013
First published on 14th January 2013
Abstract
We discuss a bottom up approach for modeling photosynthetic light-harvesting. Methods are reviewed for a full structure-based parameterization of the Hamiltonian of pigment–protein complexes (PPCs). These parameters comprise (i) the local transition energies of the pigments in their binding sites in the protein, the site energies; (ii) the couplings between optical transitions of the pigments, the excitonic couplings; and (iii) the spectral density characterizing the dynamic modulation of pigment transition energies and excitonic couplings by protein vibrations. Starting with quantum mechanics perturbation theory, we provide a microscopic foundation for the standard PPC Hamiltonian and relate the expressions obtained for its matrix elements to quantities that can be calculated with classical molecular mechanics/electrostatics approaches including the whole PPC in atomic detail and using charge and transition densities obtained with quantum chemical calculations on the isolated building blocks of the PPC. In the second part of this perspective, the Hamiltonian is utilized to describe the quantum dynamics of excitons. Situations are discussed that differ in the relative strength of excitonic and exciton-vibrational coupling. The predictive power of the approaches is demonstrated in application to different PPCs, and challenges for future work are outlined.

Thomas Renger
| Thomas Renger studied physics at the Humboldt University of Berlin, where he obtained his PhD degree under the supervision of Volkhard May in 1998. Afterwards he became a Feodor Lynen fellow to work with Rudy Marcus at Caltech (Pasadena) and in 2001 an Emmy Noether fellow at the Free University of Berlin. Since 2009 he has been a professor of theoretical physics at the Johannes Kepler University of Linz. His research interests include the theory of charge and excitation energy transfer and optical spectra of macromolecules, including a structure-based calculation of the parameters involved. |

Frank Müh
| Frank Müh studied chemistry at the Technical University of Berlin, where he received his PhD in Physical Chemistry in 1999. The quest for a theoretical underpinning of spectroscopic data led him to join the group of Thomas Renger in Berlin and Linz, where he is primarily working on structure–function relationships of photosynthetic systems. His further research interests range from solvent effects via the thermodynamics of self-assembly and crystallization to fundamental problems of condensed matter physics. |
1 Introduction
The investigation of primary reactions of photosynthesis1 is an exciting research topic for many reasons. First of all, these reactions provide the basis of our life on earth, which relies on the conversion and storage of solar energy. Second, we know the molecular structures (e.g.ref. 2–4 and references therein) and the photophysical properties5 of the key proteins, involved in these reactions, in great detail. Third, the complexity of these systems on the one hand requires theory for a structure-based interpretation of experimental results.6,7 On the other hand, it is a challenge for theory itself6,8 to find the right approximations that still allow us to describe the reactions and to draw conclusions about structure–function relationships.
In this perspective, we will focus on the light-harvesting process in photosynthetic pigment–protein complexes (PPCs) and discuss bottom up theoretical approaches that shall be used to understand building principles realized by Nature in different systems for efficient light-harvesting. Two important interactions that need to be described are the pigment–pigment and the pigment–protein coupling. In most PPCs, the distances between atoms of different pigments are large enough, so that pigments do not exchange electrons. Nevertheless, the excited state wavefunctions of PPCs are often delocalized due to the Coulomb coupling between optical transitions of the pigments, the excitonic coupling. This coupling allows for a non-radiative transfer of excitation energy between different pigments. By dynamically modulating the transition energies of the pigments and their excitonic couplings, the protein introduces a dissipative element that allows for a directional energy transfer to the low-energy exciton states, which may still be delocalized over a certain number of pigments. The spatial location of these states is also controlled by the protein environment, for example, by tuning the average optical transition energies of the individual pigments, the site energies.
The description of the dynamics of interacting electrons and nuclei after optical excitation towards quasi-equilibrium is a complicated many-body problem. In the spirit of the Born–Oppenheimer approximation,9 the mass differences between electrons and nuclei can be used to introduce potential energy surfaces (PES) that govern the motion of nuclei in different electronic states of the PPC. If appropriate PES have been defined and nuclear relaxation in these PES is fast, excitation energy transfer can be described by using the weak inter-PES coupling as a perturbation and assuming a thermally relaxed initial state of nuclei. For weak excitonic couplings, the nuclei relax in PES of localized excited states of the PPC and the transfer between such different PES is described by Förster theory.9–11 If, on the other hand, the excitonic coupling is strong, any nuclear reorganization, occurring upon optical excitation or excitation energy transfer, may be neglected, nuclei stay relaxed and provide a dissipative environment for the excitons during relaxation between different delocalized states, as described by Redfield theory (e.g.ref. 12 and references therein). If the excitonic coupling between pigments and the modulation of the pigments' transition energies by the protein are of similar strength, more advanced theories are needed. In Modified Redfield theory,13–15 the nuclear reorganization after optical excitation of a delocalized exciton state is taken into account by introducing excitonic PES. If relaxation in these PES is fast compared to exciton transfer, a rate constant can be defined. In photosynthetic complexes, often pigments can be divided into domains with strong intradomain excitonic couplings and weak excitonic couplings between pigments in different domains. In this case, excitonic PES can be defined for the pigments in one domain and second order perturbation theory is used for the interdomain couplings, resulting in the Generalized Förster theory rate constant.16–20 If, in a domain of strongly coupled pigments, the coupling between different excitonic PES and the corresponding exciton-vibrational reorganization energy are of equal magnitude, there is no small parameter, and the exciton-vibrational quantum dynamics should be described using non-perturbative approaches,21–28 which are, however, numerically costly.
Besides the development of a dynamic theory necessary for a description of the quantum-dissipative motion of excitons, the PPC Hamiltonian has to be parameterized by structure-based simulations. Three classes of parameters need to be determined: (i) the excitonic couplings between pigments, (ii) the site energies of the pigments and (iii) the spectral density of the exciton-vibrational coupling, describing the modulation of (i) and (ii) by the protein dynamics.
Five principle approaches to the calculation of these parameters can be distinguished: (a) quantum chemical subsystem approaches (QM/QM),3,29 (b) quantum mechanics/molecular mechanics (QM/MM) approaches,30–38 (c) polarizable continuum models (PCM),39–42 (d) quantum chemical/classical background charge approaches (QC/Back),43,44 and (e) quantum chemical/electrostatic two-step approaches (QC/E2).45–48 These methods differ in the way they account for the electronic and nuclear polarization as well as the charge density of the environment of a pigment. The most detailed description of the protein environment is obtained with QM/QM and QM/MM approaches. In QM/QM, the PPC is divided into subsystems (e.g., pigments and protein parts) that all are described with quantum chemistry (QC, which in this context is a synonym for QM). Approximations occur in the treatment of subsystem couplings and an eventually limited number of subsystems that can be considered.3,29 In QM/MM, the environment is described by classical (i.e., non-quantum) molecular mechanics. Here, one has to distinguish two basic strategies. In the actual QM/MM framework, the pigment is treated with QC, while the dynamics of the environment is obtained from a classical molecular dynamics (MD) simulation.49,50 Application of this procedure to a PPC with many pigments is cumbersome, however, as a separate simulation has to be performed for each pigment being exclusively the QC part. Therefore, applications to light-harvesting complexes employed an alternative strategy, where the whole PPC is treated with classical MD, and single-point QC calculations are performed on snapshots along the MD trajectory.30–38 A major drawback of the latter strategy is the mismatch between the pigment geometries generated by MD and the optimal QC geometry.36,51 In any QM/MM approach, the nuclear polarization is described explicitly by propagating the classical equations of motion for the atoms and the electronic polarization is taken into account either implicitly or explicitly by using a polarizable force field.38,52 The charge density of the protein is included in the QC calculation in the form of classical background charges. The latter type of QC is also performed in the QC/Back approaches, but on a single geometry that is meant to represent the average equilibrium structure of the PPC in the electronic ground state.43,44 In PCM, the electronic and nuclear polarization of the environment is approximated by that of a dielectric continuum, where the reaction field produced by the pigment–environment interaction is included in the electronic Schrödinger equation.39–42 A critical point in the semi-classical approaches (b)–(d) is the neglect of the Pauli repulsion between electrons of the pigment and the protein due to the classical treatment of the latter. The electrons tend to be solvated by the classical dielectric or attracted by positive classical point charges and, therefore, a distortion of the electronic wavefunction may result, referred to as the electron-leakage problem.3,53,54 In the alternative QC/E2 approaches,45–48 first QC calculations are performed on the pigment in vacuo and the electrostatic potentials of the charge and transition densities are fitted by atomic partial charges. These charges are used in a second step in classical electrostatics calculations including the polarizability of the environment. In this way, leakage artifacts are avoided, however, at the price of neglecting all changes of the charge and transition densities due to the pigment–protein interaction. We note that in all approaches, one encounters the problem of the limited accuracy of QC resulting from the necessarily approximate treatment of the many-electron system.
In the light of the complexity of the problem, an evaluation of the dynamic theories and parameter calculation schemes by testing with experimental data is needed. Concerning the site energies and excitonic couplings, a critical check is already obtained from a simulation of linear optical spectra like absorbance, and circular and linear dichroism.43–48 Concerning the spectral density of exciton-vibrational coupling, line-narrowing spectra55–58 provide valuable information to compare with ref. 33, 37, 51 and 59. Exciton dynamics is investigated by nonlinear time-resolved spectroscopy. Much of our current knowledge about time scales of exciton transfer and relaxation was obtained from pump–probe spectroscopy.6,7 In recent years, 2D Fourier transform electronic spectroscopy, pioneered in the Fleming group,60,61 has been applied to various PPCs and has revealed the most detailed visualization of exciton-vibrational motion in PPCs.62–65 In particular, long-lived quantum beats detected with this technique in PPCs at low temperature,61 and even at room temperature66 and for weakly coupled pigments,67 have raised the attention of researchers from different fields68 and of the general public.69
This perspective is organized in the following way. We start with defining the standard PPC Hamiltonian that contains the minimal ingredients for the study of the quantum dynamics of excitons and point out the underlying assumptions and approximations. In the next section, we provide a microscopic foundation for this Hamiltonian and discuss its parameterization by structure-based microscopic theory with a focus on QC/E2 approaches, since the latter so far have led to the best agreement with experimental data. Afterwards, the PPC Hamiltonian is used to study the interplay of excitonic and vibrational motion for different relative strengths of excitonic and exciton-vibrational coupling. Finally, we discuss applications of the theory and calculation schemes to simulate light-harvesting in the Fenna–Matthews–Olson (FMO) protein from green sulfur bacteria, the major light-harvesting complex of photosystem II of higher plants (LHCII), cyanobacterial photosystem I and photosystem II.
2 Hamiltonian of the pigment–protein complex
The standard Hamiltonian of a PPC used to study energy transfer contains three parts| | | H = Hex + Hex-vib + Hvib. | (1) |
The exciton Hamiltonian Hex, expanded with respect to localized excited states |m〉 and |n〉 of the PPC, reads| | 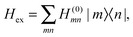 | (2) |
where the exciton matrix H(0)mn contains the local excitation energies Em of the pigments in the diagonal and the interpigment excitonic couplings Vmn in the off-diagonal parts| | | H(0)mn = δmnEm + (1 − δmn)Vmn, | (3) |
and the superscript (0) indicates that these quantities are taken at the equilibrium position of nuclei in the electronic ground state of the PPC. In terms of molecular wavefunctions of the pigments, the localized excited state |m〉 is given as the product of the excited state wavefunction φ(e)m of pigment m and ground state wavefunctions φ(g)k of pigments k ≠ m, that is 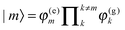 . The excitation energy Em corresponds to the energy at which pigment m in its local binding site in the protein would absorb light, if its optical transition was not coupled by Vmn to the optical transitions of the other pigments n. Below, we will use microscopic theory to derive expressions for Em and Vmn.
. The excitation energy Em corresponds to the energy at which pigment m in its local binding site in the protein would absorb light, if its optical transition was not coupled by Vmn to the optical transitions of the other pigments n. Below, we will use microscopic theory to derive expressions for Em and Vmn.
The exciton-vibrational coupling Hamiltonian Hex-vib describes the modulation of site energies and excitonic couplings by the vibrational dynamics of the complex. It is assumed that the exciton parameters depend linearly on the displacements of nuclei from their equilibrium position, that is
| | 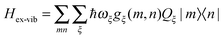 | (4) |
where
gξ(
m,
n) and
Qξ are dimensionless coupling constants and vibrational coordinates, respectively, and ℏ
ωξ is the energy of vibrational quanta in mode
ξ. A normal mode analysis (NMA) will be used below to provide a microscopic foundation for this Hamiltonian. We note that
Qξ is related to creation and annihilation operators
C†ξ and
Cξ, respectively, of vibrational quanta by
9Qξ =
Cξ +
C†ξ. Rate constants for exciton transfer as well as lineshape functions of optical transitions are related in the second part of this perspective to the spectral density of exciton vibrational coupling
| | 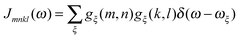 | (5) |
containing the coupling constants
gξ(
m,
n), introduced in
eqn (4), describing the fluctuations of site energies (
m =
n) and excitonic couplings (
m ≠
n).
In the spirit of a NMA, the nuclear dynamics is described by a Hamiltonian
| | 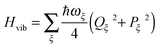 | (6) |
of uncoupled harmonic oscillators with the dimensionless momentum
9Pξ =
i(
C†ξ −
Cξ).
2.1 Underlying assumptions and applicability
Concerning the electronic Hamiltonian Hex it is assumed that electron exchange between different pigments is negligible. In other words, the electrons stay at their pigments and change their local quantum state by optical excitation and excitation energy transfer. In most PPCs, the interpigment distances are large enough to prevent considerable wavefunction overlap. The presence of the latter would be a prerequisite for electron exchange. Notable exceptions are the special pairs in the photosynthetic reaction centers70 and a few long-wavelength absorbing chlorophylls in photosystem I.71 In the latter case, there exits, however, methods to treat electron exchange in an effective way by including short-range contributions to site energy shifts and excitonic couplings in the electronic Hamiltonian in eqn (2). One way to obtain these short-range contributions is by relating monomer and dimer QC calculations using an effective Hamiltonian of the type in eqn (2).72,73 In this way, it became clear that 80% of the excitonic coupling in the special pairs of purple bacteria and photosystem I is of the short-range type and that the site energies are also considerably red-shifted by electron exchange.73
Concerning the assumed linear coordinate dependence of the exciton-vibrational coupling and the harmonic oscillator form of the vibrational Hamiltonian in eqn (4) and (6), a recent NMA and a comparison of the resulting spectral density with experimental data showed that this Hamiltonian can be justified qualitatively by microscopic calculations.51 There are, however, some quantitative deviations that most likely result from anharmonicities experienced by the soft degrees of freedom that govern the conformational flexibility of the macromolecule. However, it is known that even a strongly anharmonic system, in the spirit of a second-order cumulant expansion, can be described by an effective spectral density of harmonic oscillators.74
In summary, we may conclude that the present Hamiltonian provides a description of a wide class of systems and that the two missing aspects, namely, electron exchange and anharmonic vibrational motion, may be included in an effective way by adjusting the system parameters.
3 Microscopic foundation of the PPC Hamiltonian and parameterization
In terms of elementary quantum mechanics/chemistry, the electrons of the pigments move in the Coulomb field of the other electrons and the nuclei of the PPC. Since the pigments in most PPCs are non-covalently bound to the protein and the interpigment distances are large enough, electron exchange between pigments and between pigments and the protein can be neglected to a good approximation. Hence, a Hartree ansatz can be chosen for the electronic states of the PPC, where the individual building blocks are the pigments and the protein chains and residues, in which electrons delocalize. In principle, the wavefunctions of the electronic ground and excited states of these building blocks, when they are isolated from each other, can be obtained from quantum chemical calculations. We want to see in the following, how the optical properties of the pigments change when the Coulomb coupling between these building blocks is switched on. For this purpose, we consider one pigment m with wavefunction |A(m)a〉 (a = 0, 1, 2, 3,…), where the index a counts the electronic states of the pigment, which is surrounded by the N − 1 remaining building blocks of the PPC. The latter comprise the other cofactors and different parts of the protein of the PPC described by wavefunctions |B(η)b〉, where η = 1 … N − 1 counts the building blocks and b = 0, 1, 2, 3,… the respective electronic states. The wavefunctions |A(m)a〉 and |B(η)b〉 are eigenfunctions of the molecular Hamiltonians H(m)A and H(η)B of the isolated building blocks, respectively. Hence, we have H(m)A|A(m)a〉 = E(m)a|A(m)a〉 and H(η)B|Bb〉 = F(η)b|B(η)b with the respective electronic energies E(m)a of pigment m and F(η)b of building block η. The total Hamiltonian of the PPC reads 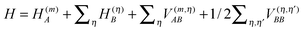 , where V(m,η)AB is the Coulomb coupling between pigment m and building block η and
, where V(m,η)AB is the Coulomb coupling between pigment m and building block η and 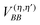 that between building blocks η and η′. In the absence of electron exchange between building blocks, the Hartree product for the eigenfunction
that between building blocks η and η′. In the absence of electron exchange between building blocks, the Hartree product for the eigenfunction 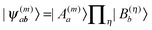 of the Hamiltonian of isolated building blocks, with
of the Hamiltonian of isolated building blocks, with 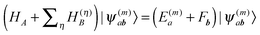 , can be used to investigate the shift ΔE(m)a of the electronic energies E(m)a of pigment m by the Coulomb coupling
, can be used to investigate the shift ΔE(m)a of the electronic energies E(m)a of pigment m by the Coulomb coupling 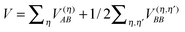 between building blocks. The multi index b = b1, b2,…,bη,… was introduced to abbreviate the notation for the electronic states of the environment. Within perturbation theory up to second order in the Coulomb coupling V, the shift ΔE(m)a is given as
between building blocks. The multi index b = b1, b2,…,bη,… was introduced to abbreviate the notation for the electronic states of the environment. Within perturbation theory up to second order in the Coulomb coupling V, the shift ΔE(m)a is given as| | 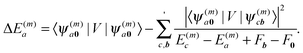 | (7) |
The index 0 = 0, 0,…,0 denotes the state, where all environmental building blocks are in their electronic ground state, and the prime at the sum indicates that c and b should not be simultaneously a and 0, respectively, that is, the sum includes only off-diagonal matrix elements of the Coulomb coupling. For the convergence of the perturbation theory, it is required that the denominator in the sum be sufficiently large. If the environment is in the electronic ground state, i.e., for b = 0, we have c ≠ a and, therefore, a large electronic transition energy of the pigment in the denominator. For c = a we have b ≠ 0 and a large electronic transition energy of the environmental building blocks appears in the denominator. Finally, we investigate the case b ≠ 0 and c ≠ a. We are mainly interested in the shifts of the ground (a = 0, S0) and first excited (a = 1, S1) states of pigment m, since these are the states that are predominantly involved in energy transfer (due to fast internal conversion between higher excited and the first excited states of the pigments). For a = 0, the denominator in eqn (7) is again large, since it contains now the sum of electronic excitation energies of m and of the building blocks. The only critical case is obtained for a = 1. If c = 0, the negative electronic transition energy E(m)0 − E(m)1 of pigment m may be compensated by the electronic transition energy Fb − F0 of the building blocks. For such a compensation, a single excitation on another building block is required with transition energy F(η)b − F(η)0. If η corresponds to a protein part, the denominator in eqn (7) is still large, since the protein starts to absorb light at much higher energies than the pigments. However, if the building block η is another pigment n, the denominator may even vanish for resonant S0 → S1 transitions of the two pigments. Therefore, we have to exclude those particular states, where one pigment building block is in its first excited state and the remaining are in their ground state. The respective Coulomb coupling 〈ψ(m)10|V|ψ(n)0b〉 is, instead, explicitly included in the exciton Hamiltonian in eqn (3) as excitonic coupling Vmn and, in this way, can be treated non-perturbatively. Evaluating the Coulomb coupling V in this matrix element gives| | | Vmn = 〈A(m)0B(n)1|V(mn)AB|A(m)1B(n)0〉 | (8) |
It describes the Coulomb coupling between the transition densities of the S0 → S1 transitions of pigments m and n, as described in more detail below.
3.1 Site energies
The remaining parts of eqn (7) are used in the following to derive a microscopic expression for the site energy Em in eqn (3). The site energy of the optical transition between the ground and the first excited state of pigment m then follows as| | | Em = E0 + ΔE(m)1 − ΔE(m)0, | (9) |
where E0 is the S0 → S1 transition energy of the isolated pigment and ΔE(m)1 and ΔE(m)0 are the shifts of the S1 and S0 state energies, respectively, of this pigment that result from the Coulomb coupling between the building blocks in the PPC, excluding the excitonic couplings with the S0 → S1 (0 → 1) transitions of the other pigments as discussed above.
By evaluating the Coulomb matrix elements in eqn (7), we obtain for the shift of the electronic energy of state a = 0, 1 of pigment m
| | 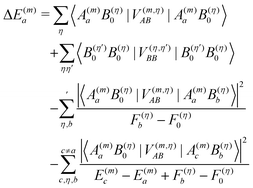 | (10) |
where the first term on the r.h.s. denotes the Coulomb coupling between the charge densities of pigment
m in electronic state
a and building block
η in the electronic ground state, the second line is the Coulomb coupling between the charge densities of building blocks
η and
η′ in their electronic ground states, the third line contains the Coulomb coupling between the charge density of pigment
m in electronic state
a and the transition density of the 0 →
b transition of building block
η and the last line is the Coulomb coupling between the latter transition density and the transition density of the
a →
c transition of pigment
m. Note that the first-order terms involving couplings between environmental building blocks
η and
η′ cancel out in the calculation of differences Δ
E(m)a − Δ
E(m)b.
A rigorous examination of matrix elements of the type occurring in eqn (8) and (10) was presented in ref. 75, where these matrix elements were related to Coulomb interactions involving charge and transition densities, starting from a many-electron wavefunction. As shown there also, a matrix element of the type
| | 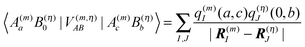 | (11) |
can be described by the Coulomb interaction between atomic partial charges
q(m)I(
a,
c) and
q(η)J(0,
b) that are placed at the positions
R(m)I and
R(η)J of the
Ith atom of pigment
m and
Jth atom of building block
η. These charges are determined from a fit of the electrostatic potential of the respective transition or charge densities calculated with QC on the isolated building blocks. In the following, we use these partial charges to obtain insight into the physical origin of the third term on the r.h.s. of
eqn (10), which we denote with
Wa. If a dipole approximation is adopted for building block
Bη and
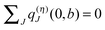
is used, the matrix elements in
Wa become
| | 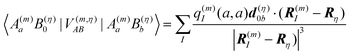 | (12) |
where
Rη points to the center of building block
η with transition dipole moment
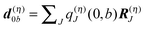
, and
Wa can be written as
| | 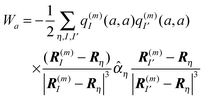 | (13) |
where the polarizability tensor
76![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) η
η of building block
η with elements
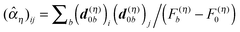
and
i,
j =
x,
y,
z was introduced.
The physical meaning of Wa now becomes clear. The electric field 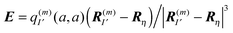 of the partial charge
of the partial charge 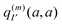 induces a dipole moment pη =
induces a dipole moment pη = ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) ηE at molecule (building block) η, and the field of this dipole moment interacts with the partial charge q(m)I(a,a) of the pigment. Hence, Wa is the solvation energy of the permanent charge density of electronic state a of pigment m.
ηE at molecule (building block) η, and the field of this dipole moment interacts with the partial charge q(m)I(a,a) of the pigment. Hence, Wa is the solvation energy of the permanent charge density of electronic state a of pigment m.
In a similar way, the last term on the r.h.s. of eqn (10) can be related to solvation energies of transition densities for all electronic transitions that start from state a.77 Physically, these terms represent the London dispersive interactions of pigment m in electronic state a with its environment for b ≠ 0 and an inductive effect of the environment on the pigment for b = 0.
3.1.1. The CDC method.
In the charge density coupling (CDC) method,46–48 only the first order shifts in eqn (10) are explicitly considered for the calculation of the site energy in eqn (9). The higher order terms arising from polarization are included implicitly by scaling the Coulomb coupling by an inverse effective dielectric constant εeff−1. The site energy Em of pigment m then is obtained as| | 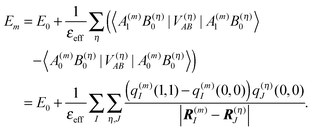 | (14) |
As noted above, the partial charges q(m)I(0,0) and q(m)I(1,1) of the ground and the excited state of the pigment, respectively, are based on in vacuo QC calculations on the pigments and a fit of the electrostatic potential.75
The ground state partial charges q(η)J(0,0) of the background, formed by the remaining atoms of the PPC, comprise those of the other pigments and those of the protein. The latter are taken from standard molecular mechanics (MM) force fields (e.g. CHARMM78,79). Since the protein contains residues with variable charge density, the titratable groups, the protonation pattern has to be determined before the site energy shifts can be calculated. This problem is discussed in the following.
3.1.2. The protonation probabilities of titratable residues of the protein.
Every protein has titratable groups, i.e. groups that can release a proton. Besides the N- and C-terminus of each polypeptide chain (if not chemically modified), a number of amino acid side chains are considered titratable including those of the acidic amino acid residues Asp and Glu, the basic residues Arg, Lys, and His as well as Tyr and Cys. Deprotonation of any of these sites in the protein (and subsequent release of the proton into the outer medium) changes the net charge state of the respective site and hence affects the charge distribution in the protein. Since the protonation states of different titratable groups depend on each other by virtue of their electrostatic interaction, the elucidation of the protonation pattern of a PPC on the basis of a crystal structure poses a formidable problem. This problem can be tackled by methods that involve a numerical solution of the linearized Poisson–Boltzmann equation (LPBE) and Monte-Carlo techniques. In the following sections, we shall briefly summarize how these methods work (for further details, see ref. 80–82 and references therein). The methods have been extended to include the calculation of redox potentials of protein-bound groups and their dependence on protonation states.82–84 Our PB/QC method is a further extension of this approach to the calculation of excited state energy shifts. Thus, parts of the following sections are also the basis for the description of site energy calculations in Section 3.1.4.
Since each titratable site has two possible protonation states, a PPC with N titratable groups has 2N possible protonation patterns. (In the case of His, even three possible protonation states are taken into account. For the sake of simplicity, we shall not consider this case explicitly in the following.) A protonation pattern can be characterized by a vector
| | | xσ = (x(σ)1, x(σ)2, …, x(σ)N) | (15) |
where
x(σ)μ = 1, if site
μ is protonated, and
x(σ)μ = 0, if it is deprotonated. Here,
σ = 1,…,2
N counts the protonation patterns and
μ = 1,…,
N the titratable sites. In thermal equilibrium, the protonation probability 〈
xμ〉 of group
μ is obtained from the Boltzmann average
| | 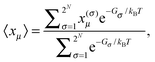 | (16) |
where
Gσ is the Gibbs free energy of protonation pattern
σ. Due to the huge number of possible protonation patterns, direct evaluation of the statistical average is normally impossible. The solution to this problem is the application of a Monte-Carlo technique described in detail earlier.
82 Note that
Gσ contains entropic contributions arising from the distribution of
protons in the solution and the polarization of the dielectric. Hence, a free energy is used instead of an energy.
3.1.2.1. Calculation of the Gibbs free energy of a protonation pattern.
For the evaluation of the average in eqn (16), the dependence of Gσ on the protonation vector xσ is needed. This dependence is obtained by introducing a reference protonation state x(0)σ and defining Gσ with respect to this state, that is, setting G0 = 0. The choice of the reference state is arbitrary. We take the state of the protein, in which all titratable groups are uncharged, as the reference state. Hence, x(0)μ = 0 for Arg, His, N-terminus, Lys and x(0)μ = 1 for Asp, Glu, C-terminus, Cys, Tyr. The free energy of an arbitrary protonation pattern σ can then be written as| | 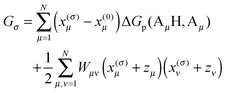 | (17) |
where ΔGp(AμH,Aμ) is the free energy difference between the protonated (AμH) and the deprotonated (Aμ) state of the protein-bound group μ at a given pH of the surrounding solution and with all the remaining titratable sites in their reference state. The second term is a correction for the interaction between titratable residues, where we introduced the dimensionless formal charge zμ of the deprotonated group, i.e., zμ = 0 for Arg, His, N-terminus, Lys and zμ = −1 for Asp, Glu, C-terminus, Cys, Tyr. These formal charges are such that the second line only has a non-zero contribution, if both sites μ and ν are in their non-reference (i.e., charged) state. It is clear that in this case the ΔGp(AμH,Aμ) and ΔGp(AνH,Aν) alone cannot describe the whole change in free energy, since the latter only consider single non-reference states and, therefore, miss the interaction between two such states. The detailed form of Wμν will be inferred below. We will first discuss the calculation of ΔGp(AμH,Aμ).
3.1.2.2. Thermodynamic cycle.
The ΔGp(AμH,Aμ) contains an electrostatic contribution and a contribution that is due to the breaking of the chemical bond between the proton and the amino acid Aμ. The calculation of the latter part can be circumvented by considering the thermodynamic cycle in Fig. 1. In this figure are depicted the four relevant states of the titratable group: protonated (AμH) and deprotonated (Aμ) and in each case either bound to the protein (left, index p) or isolated in an aqueous solvent (right, index s). Accordingly, ΔGp(AμH,Aμ) and ΔGs(AμH,Aμ) are the Gibbs free energies of deprotonation for the protein-bound and isolated group, respectively, at a given pH, while ΔGsp(Aμ) and ΔGsp(AμH) are the Gibbs free energies of transfer from the aqueous environment to the protein site for the deprotonated and protonated form of the group, respectively. The thermodynamic cycle connecting these states (Fig. 1) indicates that| | | ΔGp(AμH,Aμ) = ΔGs(AμH,Aμ) + ΔGsp(Aμ) − ΔGsp(AμH). | (18) |
Here, ΔGs(AμH,Aμ) at a given pH value of the solution can be determined from the experimental pKa value of a model compound that represents the titratable group in an aqueous environment (for a comprehensive list of pKa values and references, see ref. 82)| | ΔGs(AμH,Aμ) = kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10(pKa − pH). 10(pKa − pH). | (19) |
To complete the thermodynamic cycle, we have to calculate ΔGsp(Aμ) and ΔGsp(AμH). This is done on the basis of an electrostatic model of the protein.
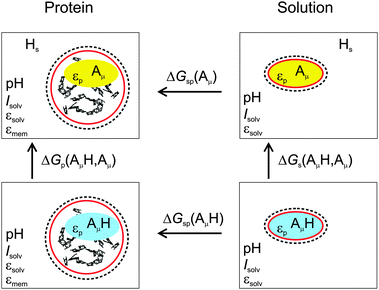 |
| | Fig. 1 Thermodynamic cycle for the calculation of the deprotonation free energy ΔGp(AμH,Aμ) of a protein-bound group AμH at site μ. The red and dashed circumferences symbolize the molecular surface and the ion exclusion layer, respectively, and Hs the solvated proton. | |
| | 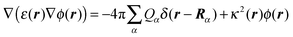 | (20) |
where Rα is the position of the αth atom of group μ. In eqn (20), ε(r) and κ(r) are the position dependent dielectric constant and inverse Debye length, respectively. The latter is related to the ionic strength I(r) of the solvent by κ2(r) = 8πFI(r)/ε(r)kBT, where F is Faraday's constant. The r dependence of ε(r) and I(r) arises from the distinction of protein, membrane and solvent volume. Hence, I(r) is zero except, if r points to the solvent region (outside the ion exclusion layer), where I(r) = Isolv. The dielectric environment is divided into a membrane part with ε(r) = εmem, a solvent part with ε(r) = εsolv and a protein part with ε(r) = εp. The definition of the protein part is based on the molecular surface (Connolly surface)85,86 of the PPC.
Whereas the solvent properties Isolv and εsolv can be determined experimentally, the membrane and in particular the protein dielectric constants are not so well defined, because of inhomogeneities and rigidities of the latter parts. Accordingly, there has been a long-lasting debate about the appropriate value of εp to be used in the computation of protonation patterns.81,82,87,88 In early work, a value of εp = 4 was suggested89,90 and is still widely used. The problem of heterogeneity in the protein interior is actually not as severe as one might think at first sight. Simonson and Perahia91 tackled this problem by microscopic simulations. They found that the fast component of the polarization can be well approximated by a homogeneous continuum model with an optical dielectric constant εopt = n2 = 2 (a result that is exploited in the Poisson-TrEsp method, see Section 3.2.2). The static dielectric constant, containing both the fast and the slow component, was found to be less homogeneous and a fit to a continuum model less satisfactory, but still reasonable with an optimal value of εp = 4, which is supported also by other microscopic simulations.92–94 In the case of membrane proteins, it is possible to approximate the dielectric properties of the membrane (or a detergent belt) by defining a slab outside the PPC, to which εmem is assigned95 as implemented in the software TAPBS96 based on APBS.97 We use εmem = 2 akin to a liquid hydrocarbon phase. An illustrative example is shown in Fig. 2. We note that there are other membrane models98–100 that remain to be tested in the present context of photosynthetic light-harvesting complexes. Another application of the slab approximation is the modeling of a water soluble PPC in the interstitial region between two membranes (e.g. the FMO protein between the cytoplasmic membrane/reaction center complex and the chlorosome/baseplate48).
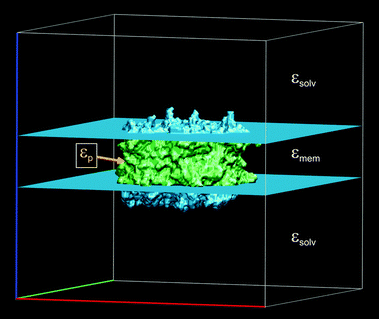 |
| | Fig. 2 Assignment of static dielectric constants to different regions of space in the calculation of protonation patterns of trimeric LHCII.101 The figure created with VMD.102 | |
The LPBE can be solved numerically on a grid as detailed elsewhere.81,82,87,103,104 The interaction energy W is then given by
| | 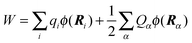 | (21) |
where
qi =
qi(0,0) and
Ri are the partial charge and position, respectively, of atom
i of the environment in the electronic ground state. The sum over
i in
eqn (21) runs over all environmental atoms including those of the other groups
ν ≠
μ with partial charges corresponding to the reference protonation state as well as those atoms of group
μ that carry the same partial charge in both protonation states. The two terms in
eqn (21) represent the interaction of the charges
Qα with the background charges
qi and with their own reaction field contained in
ϕ(
r). In order to determine
W for the four states depicted in
Fig. 1, the LPBE has to be solved four times for each group
μ with two different charge sets
Q(h)α and
Q(d)α corresponding to the protonated (index h) and deprotonated form (index d) of
μ and with two different dielectric environments corresponding to
protein (p) and
solvent (s). (In the case of His, even three different protonation states are considered, and the LPBE has to be solved six times.) Thus, in general, we obtain for each group four different electrostatic potentials
ϕ(h/d)p,μ/s,μ(
r) that, when put into
eqn (21), yield four different energy terms
W(h/d)p/s finally resulting in
| | | ΔGsp(Aμ) − ΔGsp(AμH) = W(d)p − W(d)s − W(h)p + W(h)s | (22) |
By using
eqn (19), (21) and (22), we obtain from
eqn (18) the deprotonation free energy of group
μ for the reference protonation state of the
protein as
| | ΔGp(AμH,Aμ) = kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10(pKa − pH) + ΔΔG(μ)back + ΔΔG(μ)pol 10(pKa − pH) + ΔΔG(μ)back + ΔΔG(μ)pol | (23) |
with the background charge term
| | 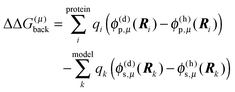 | (24) |
and the polarization term (often referred to as “Born-term”)
| | 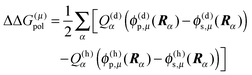 | (25) |
Note that the first sum in
eqn (24) runs over all background charges of the PPC and the second sum over all background charges of the model compound. Note also that the sum over
α in
eqn (25) contains no self-interaction of any charge
Qα, since the corresponding terms drop out in the calculation of the differences.
Finally, we identify the correction term Wμν in eqn (17) from the following considerations. As seen above, the change in free energy contains a background and a polarization term. The coupling between charge densities contributes to the background term. If we consider two titratable groups μ and ν, which are both in their non-reference (charged) state, the sum over i has to be corrected for those atoms that belong to the titratable group ν. This correction is done by the term
| | | Wμν(x(σ)μ + zμ)(x(σ)ν + zν) | (26) |
in
eqn (17) with
| | 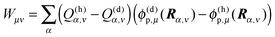 | (27) |
If, for example, we consider a state where
ν is a protonated Arg, the respective
qi in
eqn (24) correspond to
Q(d)α,ν which are replaced by the non-reference state charges
Q(h)α,ν due to
eqn (26) and (27), since
x(σ)ν +
zν = 1 in this case. If, on the other hand,
ν is a deprotonated Asp, the
qi in
eqn (24) would correspond to
Q(h)α,ν, which are replaced by
Q(d)α,ν, since
x(σ)ν +
zν = −1.
3.1.2.4. Temperature dependence of the protonation pattern.
PPCs are routinely investigated at cryogenic temperatures. In order to obtain an optically transparent sample for spectroscopic studies, the buffered aqueous solution has to be supplemented with a glass-forming agent to a significant amount (e.g., 70% glycerol). For an adequate structure-based simulation of optical spectra under these conditions, we have to take into account the influence of temperature and the dielectric properties of the glass on the protonation pattern. In earlier work,45 we assumed the protonation states to be equilibrated at all temperatures. Later, we learned that this assumption was a severe oversimplification. Unfortunately, information about proton activities and pKa values under cryo-conditions is scarce. The only work that we are aware of is that of Schulze et al.105 who studied proton activities in 70% aqueous glycerol as a function of temperature. They found that above 210 K, the pKa values followed the expected behavior (i.e., obeying van't Hoff's equation with a constant enthalpy for deprotonation). Therefore, we concluded that in this temperature range, the standard procedure outlined above can be applied with εp = 4, εsolv = 80 and εmem = 2 as reasonable approximations and using the appropriate temperature in the Monte-Carlo titration.101 The only critical parameter is the pH, which has to be rescaled according to the temperature coefficient of the used buffer. Thereby, it is assumed that the glass-forming agent has a negligible influence on the temperature coefficient based on the work of Douzou.106 Schulze et al.105 found the pKa values to approach constants between 210 and 180 K, which they ascribed to an increase in the viscosity of the glycerol–water mixture close to the glass transition at 180 K. At this temperature, the acid–base-equilibria were found to be frozen in, and no further change of pKa values or proton activities was found upon further cooling. Hence, proton transfer is kinetically hindered at temperatures below 210 K, and the protonation pattern does not represent that of a true thermal equilibrium. This interpretation is further substantiated by the finding of Schulze et al.105 that the cooling rate has an influence on the finally established pKa value. Based on these results, we use in our simulations, as a first approximation, the equilibrium protonation pattern established at 210 K, also at lower temperatures. We note that the problem of non-equilibrium protonation states in cryo-samples requires further research.
3.1.3. Protonation state dependent site energies with the CDC method.
In order to take into account the dependence of the site energy Em in eqn (14) on the protonation state σ of the PPC, we introduce a site energy value Em(0) which refers to the site energy obtained for the reference protonation state and take into account the deviations from this value. We have| | 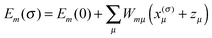 | (28) |
where Em(0) is given by eqn (14) and for the atom J = α of titratable group η = μ includes the partial charge of the reference protonation state. The second term on the r.h.s. of eqn (28) with| | 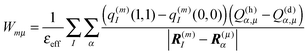 | (29) |
corrects the Coulomb interaction contained in Em(0) between pigment m and those titratable groups μ that are in a non-reference state. There are different possibilities to proceed with the calculation of energy transfer and optical spectra as will be discussed further below. Before that we will describe another method for the calculation of site energies.
3.1.4. The PB/QC method.
In the Poisson–Boltzmann/quantum chemical (PB/QC) method45,46,101,107 besides the first-order contributions in eqn (10) representing the charge density interaction, also the part of the second-order site energy shift, that has been identified as solvation energy Wa (eqn (13)) and higher order terms, representing the screening and local field corrections of the charge density interaction, are explicitly taken into account. This is done in an approximate way by assigning dielectric constants to certain regions of space and solving the LPBE. Any dispersive interactions, which are of the type given in the fourth term on the r.h.s. of eqn (10) (b ≠ 0), are neglected.
3.1.4.1. Thermodynamic cycle.
In Fig. 3 are depicted four relevant states involving pigment m: the state |m〉 of the PPC, in which pigment m is in its first electronic excited singlet state S1 and all other pigments n ≠ m are in their electronic ground state S0, the state |0〉, in which all pigments are in their electronic ground state S0, as well as the electronic ground state |S0〉 and first excited state |S1〉 of the isolated pigment in an aqueous environment. The site energy is defined as a vertical transition energy, i.e., with the nuclei fixed to the equilibrium positions of the electronic ground state. In the framework of an electrostatic solvation model, this means that the excited state is equilibrated only with respect to the fast polarization component of the environment representing the instantaneous response of the solvent or protein electrons to the change of the pigments' electronic state. However, the slow polarization component of the environment needs more time to relax, so that the excited state is initially out of equilibrium. Thus, the site energy Em of pigment m has two contributions:| | 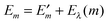 | (30) |
where 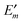 is the energy difference between excited and ground states, when both are fully equilibrated, and Eλ(m) is the reorganization energy. In the following, the calculation of
is the energy difference between excited and ground states, when both are fully equilibrated, and Eλ(m) is the reorganization energy. In the following, the calculation of 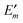 is described. The treatment of Eλ(m) will be discussed in Section 3.1.4.4. The thermodynamic cycle in Fig. 3 indicates that
is described. The treatment of Eλ(m) will be discussed in Section 3.1.4.4. The thermodynamic cycle in Fig. 3 indicates that| | 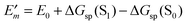 | (31) |
Here, ΔGsp(S1) and ΔGsp(S0) are the Gibbs free energies of transfer from the aqueous environment to the protein site for the pigment in the first excited and the ground state, respectively, which are computed on the basis of the LPBE (see Section 3.1.4.2). E0 is a reference value that corresponds to the transition energy of the pigment in the solvent environment. At present, E0 is an adjustable parameter that is determined from a comparison of simulated and measured optical spectra of the PPC. Note that E0 is different for chemically distinct pigments (e.g., chlorophyllsa and b in LHCII). However, the site energies of chemically identical pigments are calculated with respect to the same reference value E0, so that the actually computed quantities are the site energy differences between pigments of the same type. In the application of eqn (31), conformational variations between pigments in different sites are neglected. The inclusion of these variations requires a quantum chemical treatment that is discussed in Section 3.1.5.
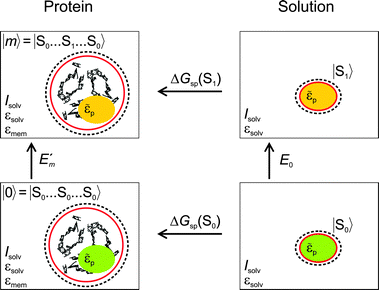 |
| | Fig. 3 Thermodynamic cycle for the calculation of the site energy 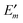 of a protein-bound pigment with the PB/QC method. of a protein-bound pigment with the PB/QC method. | |
Direct experimental information about E0 is not available, because the pigments are not water-soluble. A possible solution to this problem is the extension of the thermodynamic cycle in Fig. 3 to include the transfer of the pigment from a non-aqueous solvent to water. Then, one has to critically check the limits of a continuum description of the solvent.
3.1.4.2. Calculation of site energies based on the LPBE.
The electrostatic model of the PPC is the same as described in Section 3.1.2.3. In addition, we need for each pigment the two sets of atomic partial charges q(m)I(0,0) and q(m)I(1,1) introduced in Section 3.1.1, describing the permanent charge distribution of the chromophore in the ground and the excited state, respectively. We note that these charges are the same for chemically identical pigments as long as conformational variations are neglected. Nonetheless, the index m is justified, as the position, to which the charge is assigned, is different for different sites. The determination of these charges is discussed in Section 3.1.5. As in the case of the CDC method, the protonation state dependent site energy 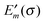 can be written as
can be written as| | 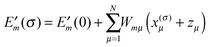 | (32) |
where 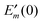 is the site energy obtained for the reference protonation state, which in addition to the charge density coupling term (background term ΔΔG(m)back) includes a polarization term ΔΔG(m)pol
is the site energy obtained for the reference protonation state, which in addition to the charge density coupling term (background term ΔΔG(m)back) includes a polarization term ΔΔG(m)pol| | 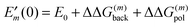 | (33) |
with| | 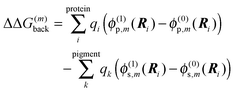 | (34) |
and| | 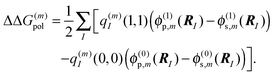 | (35) |
Here ϕ(0/1)p,m/s,m are the four solutions of the LPBE (eqn (20) with Qα replaced by q(m)I) corresponding to the four states depicted in Fig. 3 with (0) and (1) referring to the charge sets q(m)I(0,0) and q(m)I(1,1), respectively.
The background charges qi comprise all partial charges in the PPC that do not belong to pigment m (including those of all pigments n ≠ m in their electronic ground state) as well as those charges of pigment m that are the same in the ground and the excited state (e.g., the phytyl chains of chlorophylls). The latter subset is termed qk in the second sum in eqn (34) (representing the pigment in an aqueous environment). In complete analogy to eqn (27) and (29), the Coulomb correction term Wmμ for non-reference protonation states in eqn (32) reads
| | 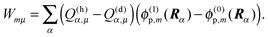 | (36) |
3.1.4.3. Choice of dielectric constants.
In contrast to the protonation states discussed in Section 3.1.2.4, the solvent dielectric constant εsolv relevant to the calculation of site energies is the one found for the temperature, at which the experiments are performed that are to be simulated. Thus, we use εsolv = 80 for ambient temperatures. At cryogenic temperatures, one has to take into account that the protonation patterns are frozen below 210 K and that the static dielectric constant of a glass-forming medium changes drastically due to the glass transition. Unfortunately, information about dielectric constants of the glasses used in optical experiments with light-harvesting complexes under cryo-conditions is as scarce as information about proton activities. Yu108 investigated glycerol–water mixtures. The data suggest that εsolv = 5 is a reasonable approximation at temperatures below 200 K, but the dielectric constant in the range of 4 to 77 K relevant for most spectroscopic data is actually unknown. In applications of the PB/QC method, the effective dielectric constant of the protein![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) p is varied to optimize simulated optical spectra and, therefore, is essentially an adjustable parameter. This parameter not only accounts for dielectric screening and local field effects in the protein interior at different temperatures, but also compensates for a possible inadequateness of the quantum chemical charge sets of the pigments. Thus,
p is varied to optimize simulated optical spectra and, therefore, is essentially an adjustable parameter. This parameter not only accounts for dielectric screening and local field effects in the protein interior at different temperatures, but also compensates for a possible inadequateness of the quantum chemical charge sets of the pigments. Thus, ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) p does not solely represent the static polarizability of the protein. As a consequence, its value used in site energy calculations may differ from εp used for protonation patterns and may be even smaller than εopt.
3.1.4.4. Non-equilibrium corrections.
Finally, we turn to the non-equilibrium correction Eλ(m) of the site energy shift in eqn (30). As discussed above the optical excitation occurs between the equilibrium ground state and an excited state of the PPC where only the electronic polarization is in equilibrium, but the nuclear polarization is not. Hence, we may write the transition energy as
p does not solely represent the static polarizability of the protein. As a consequence, its value used in site energy calculations may differ from εp used for protonation patterns and may be even smaller than εopt.
3.1.4.4. Non-equilibrium corrections.
Finally, we turn to the non-equilibrium correction Eλ(m) of the site energy shift in eqn (30). As discussed above the optical excitation occurs between the equilibrium ground state and an excited state of the PPC where only the electronic polarization is in equilibrium, but the nuclear polarization is not. Hence, we may write the transition energy as| | Em = ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) m − G0 m − G0 | (37) |
where ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) m is the non-equilibrium free energy of the excited state and G0 is the equilibrium free energy of the ground state. According to Marcus,109 a non-equilibrium free energy of an excited state may be obtained from the equilibrium free energy Gm of the excited state and equilibrium free energies G(1−0,opt)m and G(1−0)m of two fictitious systems, which carry the charge density difference between excited and ground states of state |m〉 of the PPC and are embedded in a dielectric with optical dielectric constant εopt or static dielectric constant ε, respectively,
m is the non-equilibrium free energy of the excited state and G0 is the equilibrium free energy of the ground state. According to Marcus,109 a non-equilibrium free energy of an excited state may be obtained from the equilibrium free energy Gm of the excited state and equilibrium free energies G(1−0,opt)m and G(1−0)m of two fictitious systems, which carry the charge density difference between excited and ground states of state |m〉 of the PPC and are embedded in a dielectric with optical dielectric constant εopt or static dielectric constant ε, respectively,| | ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) m = Gm + G(1−0,opt)m − G(1−0)m m = Gm + G(1−0,opt)m − G(1−0)m | (38) |
With eqn (30) and 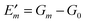 considered in the thermodynamic cycle above, we obtain for the reorganization energy
considered in the thermodynamic cycle above, we obtain for the reorganization energy| | | Eλ(m) = G(1−0,opt)m − G(1−0)m. | (39) |
Since the terms on the r.h.s. only contain charge differences, which are zero for all atoms of the PPC except for those on pigment m, which take part in the excitation, i.e., Δq(m)I = q(m)I (1,1) − q(m)I (0,0), there are no background charges and only polarization terms contribute to G(1−0,opt)m and G(1−0)m. Then, Eλ(m) is obtained as
| | 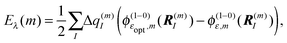 | (40) |
where the potentials
ϕ(1−0)f,m are obtained from the solution of the Poisson equation
| | 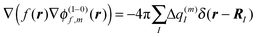 | (41) |
for
f(
r) =
εopt(
r) and
f(
r) =
ε(
r).
It turned out that the site-dependence of Eλ(m) is weak and can be neglected in applications of the PB/QC method.45,101 This result does not mean that Eλ(m) is really site-independent, but rather that the electrostatic continuum model of the PPC is not able to reveal such a dependence. The recently introduced calculation of exciton-vibrational coupling on the basis of a NMA offers a new approach to the reorganization energy discussed further below (eqn (55) and (59)). Results obtained so far for the FMO protein suggest that, indeed, the contribution of Eλ(m) to site energy differences is small.51
3.1.5. Atomic partial charges of the pigments and quantum chemical correction.
In the CDC and PB/QC methods, relative site energy shifts are calculated by electrostatics rather than site energies Em directly by quantum chemistry (QC). Nonetheless, the electrostatic methods use atomic partial charges q(m)I(1,1) and q(m)I(0,0) of the pigments obtained from QC, based on methods described in detail earlier.75 If conformational variations between pigments in different sites of the PPC are neglected, these calculations are based on pigment structures optimized in a vacuum. Here, one encounters the problem that different QC methods (e.g., different exchange–correlation functionals in time-dependent density functional theory) may produce different sets of atomic partial charges and, hence, different site energy shifts, and it is not clear a priori, which method to use. Decisions can be made based on a comparison of simulated and experimental optical spectra of the PPC, but in this way of evaluating the charge sets, the result depends on details of modeling the optical lineshape, so that different approaches may suggest different charge sets to be optimal (see, e.g., LHCII110). Ideally, the QC method should reproduce several properties of the pigment molecule with high accuracy, so that the electronic wavefunctions and atomic partial charges are trustworthy without such an a posteriori evaluation, but this ideal is far from being reached for molecules as large as photosynthetic pigments. Nonetheless, present research activities aim at an implementation of recent developments in QC3,4,111 to closer approach this ideal.
If conformational variations between chemically identical pigments in different sites become relevant, one encounters two additional problems: (i) the QC calculations require a careful structure re-optimization of each individual pigment, while keeping the characteristics of the conformational change by introducing constraints.45,46,112 Sub-optimal structures can cause large errors. (ii) The site energy shift has an additional contribution from the changed electronic wavefunction of the pigment, the quantum-chemical correction. The problem of the limited accuracy of the QC method then shows up in a new guise, as there is now not only a QC influence on the atomic partial charges, but also a direct QC contribution to the transition energy shift.45 As with the unconstraint pigments, there is research activity to investigate this contribution by exploiting recent innovations in QC methodology.3,4,111
3.1.6. Protonation state dependent site energies and calculation of energy transfer and optical spectra.
There are different possibilities to proceed after the protonation state dependent site energies Em(σ) have been determined either with CDC (eqn (28)) or with PB/QC (eqn (30) and (32)): (a) we can take the site energies Em(σ) and excitonic couplings Vmn (determined as described in the next section) and put them into the exciton Hamiltonian Hex in eqn (2), resulting in Hex(σ). Based on the latter we can calculate optical spectra, energy transfer rates etc. for each protonation pattern separately and determine the proper thermal average over these spectra or rates by taking into account the Gibbs free energies Gσ (eqn (17)). This procedure is cumbersome and has not yet been applied, but work in this direction is in progress. (b) As an approximation, we can thermally average the site energies over protonation patterns and use the averaged site energies as input to Hex. This procedure has been applied in our earlier work on the FMO protein,45 but is actually an oversimplification. (c) We can single out the most probable protonation pattern or a small fraction of patterns. In particular at cryogenic temperatures, where the optical spectra with the highest resolution are measured, most of the protonation probabilities are close to either zero or one. Specifically, we set x(σ)μ = 1 in eqn (28) and (32), if 〈xμ〉 ≥ 0.8, and x(σ)μ = 0, if 〈xμ〉 ≤ 0.2. For groups with 0.2 ≤ 〈xμ〉 ≤ 0.8, the two cases x(σ)μ = 0 and x(σ)μ = 1 are checked separately for their influence on site energies. For an application of this procedure, see ref. 48, 101 and 107. If these influences are significant, spectra, etc. can be calculated for a smaller number of protonation patterns and averaged by taking into account the free energy Gσ of these patterns.
3.2 Excitonic couplings
As noted before, the excitonic coupling, in general, contains a short-range contribution due to electron exchange and a Coulombic part, where the electrons stay at their molecules73 (for recent reviews see ref. 11 and 113). The Coulombic part, which dominates the large majority of excitonic couplings between photosynthetic pigments, Vmn is obtained from the matrix element in eqn (8) reading| | 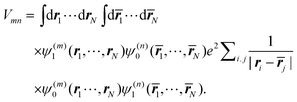 | (42) |
The integration is over the spatial coordinates of the N electrons r1,…,rNm of molecule Am and ![[r with combining macron]](https://www.rsc.org/images/entities/b_i_char_0072_0304.gif) 1,…,
1,…,![[r with combining macron]](https://www.rsc.org/images/entities/b_i_char_0072_0304.gif) Nn of molecule Bn. The integration over the respective spin variables is also included, but not explicitly denoted, and real wavefunctions are assumed for simplicity. The intermolecular Coulomb coupling between pigments V(mn)AB in eqn (8) contains the intermolecular coupling between electrons, between electrons and nuclei and between nuclei. Of these three contributions, only the first is shown in eqn (42), since it is the only one that gives a non-zero contribution, because of the orthogonality of electronic wavefunctions, i.e., 〈A(m)1|A(m)0〉 = 〈B(n)0|B(n)1〉 = 0.
Nn of molecule Bn. The integration over the respective spin variables is also included, but not explicitly denoted, and real wavefunctions are assumed for simplicity. The intermolecular Coulomb coupling between pigments V(mn)AB in eqn (8) contains the intermolecular coupling between electrons, between electrons and nuclei and between nuclei. Of these three contributions, only the first is shown in eqn (42), since it is the only one that gives a non-zero contribution, because of the orthogonality of electronic wavefunctions, i.e., 〈A(m)1|A(m)0〉 = 〈B(n)0|B(n)1〉 = 0.
By using Pauli's principle for the exchange of electrons and changing names of integration variables, the above matrix element can be written as75
| | 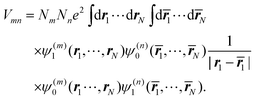 | (43) |
It is seen thereby that the integrations over coordinates
r2…
rNm and
![[r with combining macron]](https://www.rsc.org/images/entities/b_i_char_0072_0304.gif) 2
2…
![[r with combining macron]](https://www.rsc.org/images/entities/b_i_char_0072_0304.gif) Nn
Nn can be performed by introducing one-particle densities
ρ(m)10(
r1) and
ρ(n)10(
![[r with combining macron]](https://www.rsc.org/images/entities/b_i_char_0072_0304.gif) 1
1) with
| | 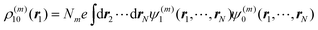 | (44) |
of molecule
Am and similarly
ρ(n)01 (
![[r with combining macron]](https://www.rsc.org/images/entities/b_i_char_0072_0304.gif) 1
1) of molecule
Bn.
The matrix element in eqn (43) then follows from the Coulomb coupling of the transition densities of the two pigments:
| | 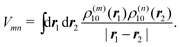 | (45) |
The above 6-dimensional integral may be evaluated numerically, as in the transition density cube (TDC) method.114 A numerically much less involved method of the same accuracy is given by the transition charge from the electrostatic potential (TrEsp) method,75 which will be discussed in the next subsection.
For large intermolecular distances, a multipole expansion may be used to evaluate the integral in eqn (45). By using the orthogonality of molecular wavefunctions, which gives rise to the relation 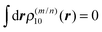 , it is seen that the first non-vanishing contribution to Vmn is due to the coupling between transition dipole moments, the point-dipole approximation:
, it is seen that the first non-vanishing contribution to Vmn is due to the coupling between transition dipole moments, the point-dipole approximation:
| | 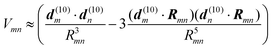 | (46) |
where the transition dipole moment
d(10)m is the first moment of the transition density
ρ(m)10(
r),
| | 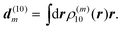 | (47) |
Examples for the validity of the point-dipole approximation are discussed below.
Finally, we note that the shape of the transition density of chlorine type pigments has a dipolar form that can be qualitatively well approximated by two point charges of opposite sign that are placed at a distance of about 9 Å.75,77 Therefore, often a considerable improvement in the point-dipole approximation is obtained by just replacing the point-dipole by an extended dipole.
3.2.1. TrEsp method.
In the TrEsp method,75 the Coulomb coupling Vmn between transition densities in eqn (45) is evaluated by using atomic partial charges that are determined such that they fit the ESP of the transition densities ρ(m)10(r1) and ρ(n)10(r2). The numerical fit is performed on a three dimensional grid surrounding the pigments.
A scaling factor f for the Coulomb coupling is included in order to implicitly take into account screening and local field effects by the dielectric environment,
| | 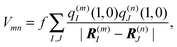 | (48) |
where the atomic transition charges of the 0 → 1 transitions of the pigments are placed at the atom positions
R(m)I of pigment
m and
R(n)J of
n. As the results obtained with different quantum chemical methods show, there are uncertainties about the absolute magnitude of the transition charges, whereas the relative magnitudes, characterizing the shape of the transition density, differ much less. These uncertainties can be removed by comparing the resulting first moment of the transition charges, the transition dipole moment, with the experimental vacuum transition dipole moment of the pigment. The transition charges are rescaled by a constant factor in order to reach agreement. The experimental values for different pigment types were obtained by Knox and Spring
115 from their analysis of the pigments' oscillator strengths in different
solvents.
3.2.2. Poisson-TrEsp method.
In the Poisson-TrEsp method, the influence of the dielectric environment on the excitonic coupling is modelled explicitly, removing thereby the unknown scaling factor of the TrEsp approach discussed above. As quantum mechanical derivations suggest,116,117 these effects can be considered in the following way: the transition charges of the pigments are placed in molecule-shaped cavities that are surrounded by a homogeneous dielectric with dielectric constant ε = n2, which equals the square of the refractive index and represents the optical polarizability of the protein and solvent environments. A Poisson equation is solved for the potential ϕm(r) of the transition charges of pigment m46,118| | 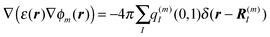 | (49) |
where the dielectric constant ε(r) = 1, if r points inside a pigment cavity, and ε(r) = n2 otherwise. The excitonic coupling of pigment m with pigment n is then obtained as| | 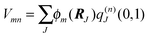 | (50) |
The transition charges q(m)I(0,1) of the pigments are obtained and corrected as described above for the TrEsp method. The value of the optical dielectric constant of PPCs is approximately 2, as determined119 from the change in oscillator strength of protein-bound and solvent-extracted pigments of photosystem I,120 and from microscopic simulations.91 Comparison of Poisson-TrEsp couplings obtained with ε = 2 and ε = 1 (corresponding to TrEsp with f = 1) showed that the screening and local field corrections of the Coulomb coupling can be well approximated by a constant factor f, which varies between 0.6107 and 0.8118 for the different complexes investigated.47,107,110,118 Detailed analysis shows that f depends on the mutual orientation of the pigments rather than on their distance. In exceptional cases,117 the surrounding dielectric can increase the excitonic coupling between two pigments compared to vacuum.116,117 Comparison of the Poisson-TrEsp and TrEsp couplings to excitonic couplings obtained with the point-dipole and extended-dipole approximations shows that the point-dipole approximation is reasonable for the FMO protein (we note, however, that the effective dipole strength has to be determined with Poisson-TrEsp). In the case of the LHCII complex, the point-dipole approximation is reasonable as well, except for one pigment pair.101 In the case of the CP43 core antennae of photosystem II, the coupling of one pigment pair connecting the stromal and the lumenal layer of pigments shows large deviations in point-dipole approximation, whereas an extended dipole approximation was found to be valid.107 Finally, neither the point- nor the extended-dipole approximation is valid for a large number of closely spaced pigments in photosystem I.47
3.3 Spectral density
So far, we have determined site energies and excitonic couplings for the equilibrium positions of nuclei in the electronic ground state of the PPC. In the following, we want to study how these quantities change, if the nuclei are displaced, and determine the linear exciton-vibrational coupling constants gξ(m,n) introduced in eqn (4). For this purpose, we consider the coordinate dependence of the exciton matrix elements Hmn, whose equilibrium position values H(0)mn were introduced in eqn (3). The Hmn are expanded into a Taylor series with respect to small displacements of the positions RJ of atoms J = 1…Natom of the PPC from their equilibrium values R(0)J. Including terms up to first order in the displacements gives| | 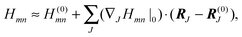 | (51) |
where H(0)mn and (∇JHmn|0) are the values of Hmn and of its gradient taken with respect to the three Cartesian coordinates of atom J, respectively, at the equilibrium position of nuclei in the electronic ground state of the PPC.
The mass-weighted normal coordinates qξ(t) are related to the displacements (RJ(t) − R(0)J) by12
| | 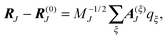 | (52) |
where
MJ is the mass of atom
J and
A(ξ)J contains the contributions of this atom to the eigenvector of normal mode
ξ. From
eqn (51) and (52) we obtain, using also
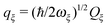
,
| | 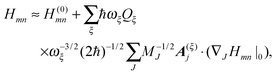 | (53) |
which equals
Hex +
Hex-vib introduced in
eqn (2) and (4), if the dimensionless coupling constant
gξ(
m,
n) is introduced as
| | 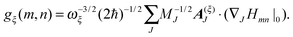 | (54) |
In order to evaluate the r.h.s. of
eqn (54), we need to know how the matrix elements
Hmn({
RJ}) depend on the nuclear coordinates
RJ. These dependencies are revealed by the TrEsp and CDC methods introduced above. Using
eqn (14) and (48), the coupling constants
gξ(
m,
n) finally are obtained as
51| | 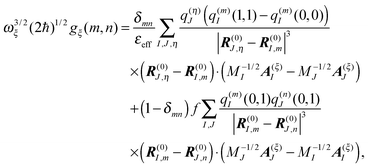 | (55) |
where the equilibrium vectors
R(0)J are taken from the crystal structure after modeling of hydrogen atoms and energy minimization. The
A(ξ)J are obtained from the eigenvectors of the NMA, providing also the vibrational frequencies
ωξ. Since a NMA provides a microscopic model for the atomic polarization, the
εeff should be chosen smaller than the one used for static site energy calculations with the CDC method (
eqn (14)). In the application to the FMO
protein, we used
εeff = 1/
f = 1.25, where
f = 0.8 was obtained from a comparison of Poisson-TrEsp and TrEsp excitonic couplings
118 and takes into account the effect of the electronic polarizability. The resulting spectral density
Jmnkl(
ω) is dominated by site energy fluctuations (
Jmmmm(
ω)) and correlations between site energy fluctuations (
Jmmnn(
ω),
m ≠
n), whereas those parts containing fluctuations of excitonic couplings are at least one order of magnitude smaller.
51 The dominating diagonal parts of the spectral density
Jmmmm(
ω) are close in shape and in magnitude to the experimental
J(
ω) (
Fig. 4). There are, however, some systematic deviations. At low frequencies, the NMA spectral density is above and at higher frequencies it is below the experimental values. One reason could be the neglect of anharmonicities, another reason the neglect of intramolecular modes of the pigments. Anharmonicities were included in a recent combination of molecular dynamics with CDC by Jing
et al.,
36 which, however, did not reach long enough timescales to resolve the important low-frequency region of the spectral density and the correlations in site energy fluctuations. Intramolecular modes of the pigments can be included by performing a QC-based NMA for the pigments in their ground and excited states.
36,121
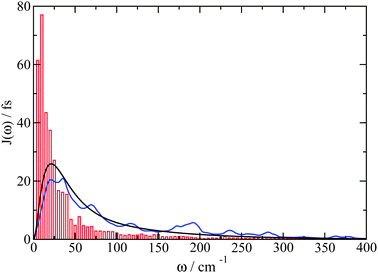 |
| | Fig. 4 Average diagonal part of the spectral density 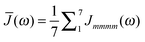 obtained by NMA on the monomeric subunit of the FMO protein (histogram, red bars)51 compared to spectral densities extracted from experimental data. The black solid line was obtained59 from an analysis of fluorescence line narrowing spectra of the B777 complex55 and the blue solid line from the FLN spectra of the FMO protein.56 The area under the curves corresponds to the Huang-Rhys factor S, which for the two experimental spectral densities was obtained from a fit of the temperature dependence of the absorbance spectrum of the FMO protein resulting in S = 0.42. The NMA value for the average S is 0.39. obtained by NMA on the monomeric subunit of the FMO protein (histogram, red bars)51 compared to spectral densities extracted from experimental data. The black solid line was obtained59 from an analysis of fluorescence line narrowing spectra of the B777 complex55 and the blue solid line from the FLN spectra of the FMO protein.56 The area under the curves corresponds to the Huang-Rhys factor S, which for the two experimental spectral densities was obtained from a fit of the temperature dependence of the absorbance spectrum of the FMO protein resulting in S = 0.42. The NMA value for the average S is 0.39. | |
3.4 Critical approximations and comparison with other methods
In most of our applications of the methods described above to chlorophyll-binding PPCs, we neglected conformational variations between pigments in different sites. This appears to be a suitable approximation so far.45,46,48,101,110 Nonetheless, additional contributions to site energy shifts can be expected, as it is well known that out-of-plane distortions of tetrapyrroles have an influence on their optical spectra.122,123 This concerns the out-of-plane orientation of conjugated substituents such as acetyl or vinyl groups as well as of the four pyrrole moieties and eventually the isocyclic ring E, leading to a distortion of the π-system (for a discussion of chlorophyll structures, see ref. 124). To take into account these conformational variations in a QC/E2 approach, one has to add a quantum chemical correction to the electrostatically calculated site energy shift as discussed in Section 3.1.5 besides considering deformation effects on the charge distributions and transition densities. Such a procedure has two strict requirements: (i) the crystal structure of the PPC has to be of sufficiently high resolution to get reliable information about structural variations, and (ii) a QC method has to be available that allows for a sufficiently accurate determination of molecular properties as a function of nuclear coordinates. Concerning requirement (i), we think that the crystal structure has to have a resolution of 2.0 Å or better. At lower resolutions, it is particularly difficult to pinpoint the orientation of conjugated substituents (for a recent example, see ref. 125). Concerning requirement (ii), there is ongoing research activity to improve electronic structure methods.3,4,111 As an alternative to a rigorous ab initio calculation, one may apply a semi-empirical approach. First steps in this direction were taken by Zucchelli et al.,126,127 who estimated ring deformation effects on the chlorophyll site energies in LHCII. Their method is based on a normal mode decomposition method developed by Shelnutt and coworkers,123,128 who found that the distortions of protein-bound porphyrins are dominated by displacements along the macrocycle normal modes with the lowest frequencies. By projecting the pigment conformations, found in the crystal structures, on the eigenvectors of the low frequency normal modes, the structural information for an evaluation of site energy changes due to macrocycle deformations becomes available. However, for a comparison with experimental data, besides the influence of the substituents discussed above, one has to take into account also the electrostatic pigment–protein interaction. Combining the normal mode decomposition method reported by Zucchelli et al. with the CDC or PB/QC methods might be a promising direction for future work.
A subtlety, when combining classical force field calculations of molecular geometries with QC calculations of electronic transition energies lies in the geometry mismatch. The latter is due to the fact that the classical force field constants are not fully compatible with the QC.36,51 This artifact most likely is responsible for the drastic deviations observed between spectral densities of the exciton-vibrational coupling calculated by using a QM/MM approach (see the Introduction) and the experimental data (e.g.Fig. 5d of ref. 37 and Fig. 6 of ref. 33), in particular at high frequencies. Fortunately, for chlorine type photosynthetic pigments the Franck–Condon factors of intramolecular vibronic transitions are very small and the spectral density in the energy range relevant for exciton relaxation is dominated by intermolecular vibrational degrees of freedom. As discussed above, the latter has been studied with NMA,51 revealing good qualitative agreement, but also some systematic deviations. The latter might be removed by including anharmonic molecular motion and intramolecular vibrational degrees of freedom, e.g., by MD simulations and QC-based NMA, respectively.
Another object of future research concerns the inclusion of so-far missing terms of the perturbation theory. These terms, e.g., include dispersive and inductive intermolecular couplings that may involve the heterogeneous polarizability of the PPC.
Within polarizable continuum models (PCMs),39–42 it is possible to include the homogeneous polarizability of the environment directly in QC calculations of electronic properties. However, the neglect of Pauli repulsion between the electron density of the QC part and the environment in this type of treatment may cause an overpolarization of the former, also known as an electron leakage problem.3,53,54 The inclusion of the charge density of the environment by classical point charges in QC calculations30,33,37 causes the same problem. To avoid these artifacts, a two step procedure can be applied, as discussed above, however, at the expense of neglecting all polarization effects on the wavefunctions of the pigments. A quantification of these effects is an important future goal.
A first treatment of the heterogeneous polarizability of the protein, in the framework of a polarizable force field model, was presented recently by Curutchet et al.38 in calculations of excitonic couplings. They reported an enhancement of resulting energy transfer rates by as much as a factor of 4, as compared to calculations assuming a homogeneous dielectric environment38 with average dielectric constant.
Another promising route to include the mutual polarization of building blocks of the PPC is the density-fragment interaction (DFI) approach proposed by Fujimoto and Yang.29 This method has recently been applied to calculate excitonic couplings (referred to as the transition density fragment interaction (TDFI) method) either excluding129,130 or including131 interpigment electron exchange. What is still missing is the effect of the polarization of the protein environment. A combination of TDFI with Poisson-TrEsp might be one possible way to go. Related in spirit to DFI is the subsystem DFT approach.3
In the methods discussed in the previous subsections there is still one adjustable parameter, namely the transition energy E0.† So far, this quantity can only be evaluated indirectly via the calculation of optical spectra. As long as a single pigment type is considered, varying E0 would just displace the resulting optical spectrum along the energy (wavelength) axis and would have no influence on its shape. In the case of different pigment types absorbing in close spectral regions, the determination of the related E0 values becomes more ambiguous. In any case, improved QC calculations would be desirable for an independent evaluation of these parameters. We will not discuss the pitfalls and challenges of QC calculations, but refer, instead, to some comprehensive reviews on this topic.3,4,111
4 Quantum dynamics of excitons
In this section, we use the exciton Hamiltonian given in Section 2, which was motivated and parameterized by microscopic theory in the previous section, to study excitation energy transfer. Different possible scenarios are discussed, which result from different relative strengths of pigment–pigment and pigment–protein couplings.
4.1 Weak excitonic coupling
In the case of weak excitonic coupling, it is reasonable to assume that the exciton-vibrational coupling is dominated by the fluctuation of site energies and that the fluctuation of excitonic couplings is negligible. Then, the exciton-vibrational coupling constants gξ(m,n) in Hex-vib (eqn (4)) are dominated by the diagonal parts m = n. After optical excitation, the strong fluctuation of site energies on the one hand localizes the excited states, and on the other hand leads to a fast relaxation of nuclei in response to the change in charge density between the ground and the excited state of the pigment. In order to describe the change in equilibrium positions of nuclei, occurring after excitation energy transfer, we introduce potential energy surfaces (PES) of localized excited states of the PPC by rewriting the PPC Hamiltonian (eqn (1)) as| | 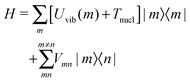 | (56) |
where Tnucl denotes the kinetic energy of nuclei, and the PES of the excited state of the PPC localized at pigment m reads| | 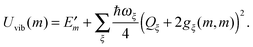 | (57) |
It contains the energy difference 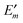 between the minimum of the PES of the excited state and that of the PES of the ground state. Due to the exciton-vibrational coupling, these PES are shifted with respect to each other by −2gξ(m,m) along the coordinate axis.
between the minimum of the PES of the excited state and that of the PES of the ground state. Due to the exciton-vibrational coupling, these PES are shifted with respect to each other by −2gξ(m,m) along the coordinate axis. 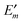 is given as
is given as| | 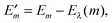 | (58) |
with the reorganization energy Eλ(m) of the mth excited state reading| | 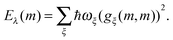 | (59) |
Eλ(m) is the energy that is released after optical excitation by relaxation of the nuclei into a new equilibrium position. It corresponds to the non-equilibrium correction obtained from continuum electrostatics calculations in eqn (40). If Eλ(m) is much larger than the excitonic coupling, the system can lower its energy more by keeping the excited states localized than by delocalization of excited states, discussed below. From another point of view, the vibrational environment introduces a large dephasing of electronic coherences that does not allow for delocalization to occur. The Liouville–von Neumann equation for the statistical operator Ŵmn in the representation of localized states reads| | 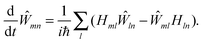 | (60) |
For a perturbative treatment of the coupling Vmn, we use the interaction representation| | 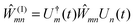 | (61) |
where the time evolution operator Uk(t) of the vibrational degrees of freedom in the PES of the kth electronic state is given as| | 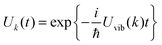 | (62) |
The equation of motion for Ŵ(I)mn then reads| | 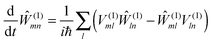 | (63) |
with| | 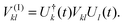 | (64) |
The population Pm of the excited state of pigment m is obtained by performing a trace over all vibrational degrees of freedom of Ŵmm
| | | Pm(t) = trvib{Ŵmm} = trvib{Ŵ(I)mm}. | (65) |
A second-order perturbation theory in the excitonic coupling
V(I)mn then results in the generalized rate equation
| | 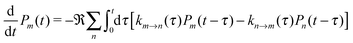 | (66) |
where
![[Fraktur R]](https://www.rsc.org/images/entities/char_e18f.gif)
denotes the real part. The generalized (time-dependent) rate constant
km→n(
t) reads
| | 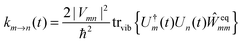 | (67) |
containing the equilibrium statistical operator of the vibrational degrees of freedom of the PPC in the
mth electronic state
| | 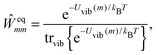 | (68) |
which describes the vibrationally relaxed initial state. Since harmonic
PES have been assumed, the trace over the vibrational degrees of freedom in
eqn (67) can be carried out analytically (
e.g. by using a second order cumulant expansion, which is exact for harmonic oscillators), giving
| |  | (69) |
with
| | 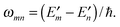 | (70) |
The time-dependent function
Gmn(
t) is related to the spectral densities
Jmmmm(
ω),
Jnnnn(
ω), and
Jmmnn(
ω), characterizing the fluctuations of site energies of pigments
m,
n, and the correlations between both, respectively, by
| | 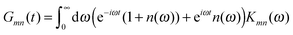 | (71) |
where
| | 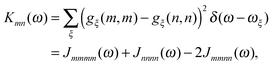 | (72) |
and
n(
ω) is the Bose–Einstein distribution function of vibrational quanta
| | 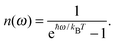 | (73) |
It is seen, thereby, that for perfectly correlated site energy fluctuations,
i.e., for
gξ(
m,
m) =
gξ(
n,
n), there would be no energy transfer possible.
4.1.1. Förster theory.
The Förster rate constant follows from the above expressions, if two simplifying assumptions are made: (i) the generalized rate constant km→n(t) decays rapidly on the time scale of the changes of the populations Pm(t) and Pn(t). In this case, the Pk(t − τ) (k = m,n) in the integral in eqn (66) may be approximated by their value at time t and taken out of the integral, and the upper integration limit may be formally extended to ∞, giving a master equation with the rate constant 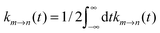 . Using
. Using 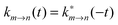 , this rate constant reads
, this rate constant reads| | 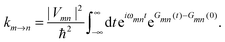 | (74) |
A second approximation of Förster theory is to assume that there is no correlation in site energy fluctuations. In this case, Jmmnn(ω) = 0 for (m ≠ n) in eqn (72), and we may write the rate constant as| | 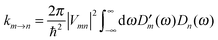 | (75) |
with the line shape function for donor emission| | 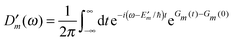 | (76) |
and acceptor absorbance| | 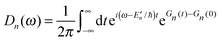 | (77) |
with| | 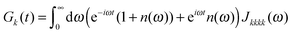 | (78) |
We note that for correlated site energy fluctuations, such a factorization of the integrand in eqn (75) into donor and acceptor properties is not possible.132
4.2 Strong excitonic coupling − Redfield theory
In the case of strong excitonic coupling, delocalized states 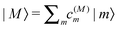 are excited, which are obtained by diagonalizing the exciton Hamiltonian Hex in eqn (2) giving
are excited, which are obtained by diagonalizing the exciton Hamiltonian Hex in eqn (2) giving| | 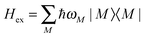 | (79) |
with eigenenergies 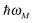 and eigenvectors containing the coefficients c(M)m. The exciton-vibrational coupling in the representation of delocalized states
and eigenvectors containing the coefficients c(M)m. The exciton-vibrational coupling in the representation of delocalized states| | 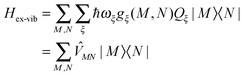 | (80) |
with| | 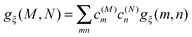 | (81) |
is treated in the following as a small perturbation to derive a rate constant kM→N for exciton relaxation between two delocalized states |M〉 and |N〉. The following interaction representation of the statistical operator is used| | 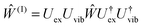 | (82) |
with the time evolution operators 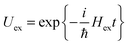 and
and 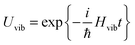 of the excitonic and vibrational degrees of freedom, respectively, using the Hvib in eqn (6).
of the excitonic and vibrational degrees of freedom, respectively, using the Hvib in eqn (6).
The Liouville–von Neumann equation for this statistical operator expanded with respect to the delocalized states  then reads
then reads
| | 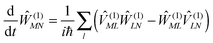 | (83) |
with
| | 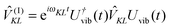 | (84) |
where
ωKL =
ωK −
ωL, and the exciton-vibrational coupling
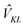
(
eqn (80)). A quantum master equation can be derived along the same lines as for the weak coupling case studied above, but using this time a second order perturbation theory for the exciton vibrational coupling
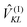
. The resulting Redfield-type rate constant reads
| | 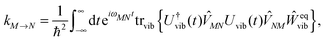 | (85) |
where
| | 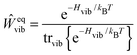 | (86) |
describes thermally equilibrated vibrational degrees of freedom of the electronic ground state of the complex. The shift in equilibrium position of nuclei that may occur upon changing the electronic state of the PPC is neglected. Later, we will include this shift in modified Redfield theory. For the harmonic oscillator Hamiltonian (
eqn (6)), the trace over the vibrational degrees of freedom in
eqn (85) can be performed and the rate constant
| | 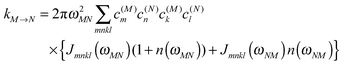 | (87) |
can be related to the spectral density
Jmnkl(
ω), which enters the rate constant at the transition frequency
ω = ±
ωMN between the two exciton levels. This spectral density contains different contributions resulting from the fluctuations of site energies (
Jmmmm(
ω)), fluctuations of excitonic couplings (
Jmnmn(
ω)) and correlations among and between them.
4.3 Intermediate excitonic coupling
In the case of equal strengths of excitonic coupling and exciton-vibrational coupling, in general, a non-perturbative approach is needed. Recent normal mode calculations of the microscopic coupling constants gξ(m,n) of Hex-vib (eqn (4) and (55)) and a subsequent transformation of these coupling constants to the basis of delocalized states (eqn (81)) show that the diagonal elements gξ(M,M) are larger than the off-diagonal elements gξ(M,N) (M ≠ N) (Fig. 5). Modified Redfield theory13–15 and time-local Non-Markovian Density Matrix theory59 make use of this inequality by providing an exact description of the diagonal parts and using perturbation theory only for the off-diagonal parts.
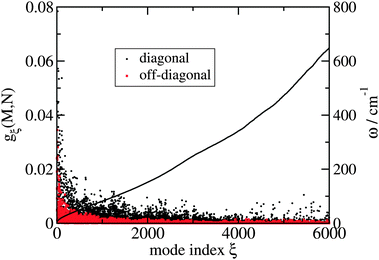 |
| | Fig. 5 Off-diagonal exciton-vibrational coupling constants gξ(M, N) (M ≠ N) are compared with diagonal coupling constants gξ(M,M) of exciton states for the first 6000 normal modes of the FMO protein.51 The black solid line shows the corresponding vibrational frequencies ω = ωξ. | |
4.3.1. Modified Redfield theory.
If the diagonal parts gξ(M,M) of the exciton-vibrational coupling dominate, it is appropriate to assume that there is fast nuclear relaxation in PES of exciton states, which are constructed by rewriting the Hamiltonian in the exciton representation (eqn (6), (79) and (80)) in the following way:| | 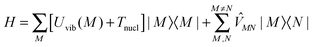 | (88) |
where the PES of exciton state |M〉 reads| | 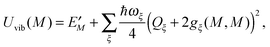 | (89) |
with the PES minimum at position −2gξ(M,M). The energy| | 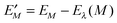 | (90) |
contains the reorganization energy of exciton state |M〉| | 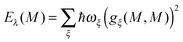 | (91) |
The ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) MN in eqn (88) comprise the off-diagonal elements of the exciton-vibrational coupling (eqn (81)).
MN in eqn (88) comprise the off-diagonal elements of the exciton-vibrational coupling (eqn (81)).
Along the same lines as used above in the derivation of the rate constants for weak and strong excitonic couplings, a second order perturbation theory in ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) MN yields the following expression for the rate constant kM→N
MN yields the following expression for the rate constant kM→N
| | 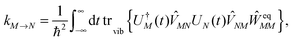 | (92) |
where
| | 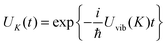 | (93) |
describes the time evolution of vibrational degrees of freedom in the PES of exciton state |
K〉, and
| | 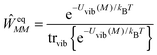 | (94) |
is the equilibrium statistical operator of nuclei in exciton state |
M〉.
Comparison of eqn (92) with the Redfield rate constant (eqn (85)) shows that now the mutual shifts of PES, neglected before, are taken into account. A comparison with the Förster-type rate constant (eqn (67)) shows that the coupling between the PES now depends linearly on the vibrational coordinates Qξ, whereas it is coordinate-independent in eqn (67). Nevertheless, for harmonic PES as considered here, the trace over vibrational degrees of freedom can be performed giving15
| | 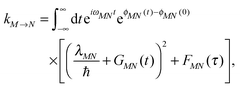 | (95) |
with the reorganization energy
| | 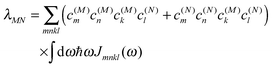 | (96) |
and the time-dependent functions
| | 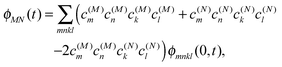 | (97) |
| | | GMN(t) = (c(M)mc(M)nc(M)kc(N)l − c(N)mc(N)nc(M)kc(N)l) ϕmnkl(1,t) | (98) |
| | | FMN(t) = c(M)mc(N)nc(M)kc(N)lϕmnkl(2,t) | (99) |
with
| | 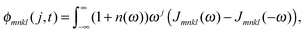 | (100) |
containing the spectral density
Jmnkl(
ω) and the Bose–Einstein distribution function
n(
ω) (
eqn (73)). Note that
Jmnkl(
ω) = 0 for
ω < 0 and
n(
ω) = −(1 +
n(−
ω)) holds.
In Fig. 6, the relaxation of excitons in the monomeric subunit of the FMO protein, calculated by assuming a δ-pulse excitation at t = 0, is shown. The site energies were obtained with the CDC method.48 The excitonic couplings were calculated by using a point-dipole approximation,48 verified before by Poisson-TrEsp,118 which also revealed the effective transition dipole strength to be used. The original spectral density Jmnkl(ω) was obtained directly from a combination of CDC and TrEsp with NMA.51 The corrected spectral density reads Jcmnkl(ω) = f(ω)Jmnkl(ω) and contains a frequency-dependent factor f(ω) = Jexp(ω)/![[J with combining macron]](https://www.rsc.org/images/entities/i_char_004a_0304.gif) (ω) with the average diagonal part of the NMA spectral density
(ω) with the average diagonal part of the NMA spectral density 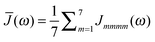 and the experimental spectral density Jexp(ω) of the FMO protein (Fig. 4). f(ω) is introduced to correct for the limitations of the harmonic approximation. The larger amplitude of the high-frequency part of the corrected spectral density allows the protein to dissipate the excess energy of excitons faster (Fig. 6 and eqn (87)). The relaxation times obtained for the corrected spectral density are in agreement with pump–probe experiments.133 For both spectral densities, the relaxation obtained with modified Redfield theory is somewhat faster than the Redfield relaxation. This effect is due to the inclusion of multi-vibrational quanta transitions in modified Redfield theory.14,134 In this way, the protein can bridge the energy gaps between different exciton states by multiple vibrational quanta and not only by single quanta as in Redfield theory. Finally, we note that although the correlation in site energy fluctuations in the spectral density has a large amplitude, its influence on exciton relaxation was found to be negligible.51 The inhomogeneous charge distribution of the protein was found to be responsible for this effect.
and the experimental spectral density Jexp(ω) of the FMO protein (Fig. 4). f(ω) is introduced to correct for the limitations of the harmonic approximation. The larger amplitude of the high-frequency part of the corrected spectral density allows the protein to dissipate the excess energy of excitons faster (Fig. 6 and eqn (87)). The relaxation times obtained for the corrected spectral density are in agreement with pump–probe experiments.133 For both spectral densities, the relaxation obtained with modified Redfield theory is somewhat faster than the Redfield relaxation. This effect is due to the inclusion of multi-vibrational quanta transitions in modified Redfield theory.14,134 In this way, the protein can bridge the energy gaps between different exciton states by multiple vibrational quanta and not only by single quanta as in Redfield theory. Finally, we note that although the correlation in site energy fluctuations in the spectral density has a large amplitude, its influence on exciton relaxation was found to be negligible.51 The inhomogeneous charge distribution of the protein was found to be responsible for this effect.
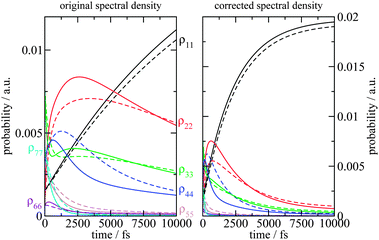 |
| | Fig. 6 Relaxation of excitons in the monomeric subunit of the FMO protein at T = 77 K after excitation by a δ-pulse at t = 0, calculated with modified Redfield theory (solid lines) and Redfield theory (dashed lines) using either the spectral density Jmnkl(ω) obtained directly from the NMA or a corrected spectral density Jcmnkl(ω) obtained as described in the text. | |
4.3.2. Non-perturbative approaches and explicit treatment of dynamic localization.
A shortcoming of the perturbation theory in the off-diagonal parts of the exciton-vibrational coupling, used in the above modified Redfield theory, is the neglect of dynamic localization effects of the exciton wavefunction. For example, if two pigments are located at a large enough distance such that their excitonic coupling is much smaller than the local reorganization energy of the exciton-vibrational coupling, but they happen to have the same site energy, their wavefunction will be delocalized for all times, since the exciton coefficients resulting from the diagonalization of Hex are time-independent. However, in reality, the slightest fluctuation of the site energies would localize the wavefunction. Since the only approximation used above in Modified Redfield theory concerns the off-diagonal part of the exciton-vibrational coupling, we have to conclude that a description of dynamic localization requires a higher-order perturbation theory or an exact theory of the latter. Recently, such non-perturbative approaches became available through the development of the hierarchical equation of motion (HEOM) approach,21–24 the density matrix renormalization/polynomial transformation approach,25,26 and path integral techniques.27,28 Although numerically very expensive, these approaches will undoubtedly provide a deeper understanding of the exciton-vibrational motion in PPCs. The explicit treatment of dynamic localization effects will allow description of excitation energy transfer in networks with intermediate and weak couplings more realistically than with Generalized Förster theory. A second important application is the inclusion of high-frequency pigment vibrations in the description of exciton dynamics. Since the related Frank–Condon factors of these high-frequency modes are very small, the effective excitonic coupling involving these excited vibronic transition are also small and the mixing with vibronic transitions of neighboring pigments can easily be affected by dynamic localization effects due to the coupling with protein vibrations. Finally, a third interesting application is in the description of optical properties of pigments at very close distance, where electron exchange becomes possible. In this case the mixing of exciton states with charge transfer states70,73 leads to very strong exciton-vibrational coupling that can lead to dynamic localization effects.135
5 Applications
Although the structure of this protein has been known since 1975136 it took until the end of the 1990s to obtain a realistic set of site energies and excitonic couplings. The key new assumption of Aartsma and coworkers137 was a much smaller effective dipole strength of the pigments for the calculation of the excitonic couplings. In 2005, the first 2D spectra of the FMO protein were reported60 and interpreted by using the Hamiltonian of Aartsma and coworkers, with a modification of one excitonic coupling. This modification was later shown to be incorrect.118 A calculation of excitonic couplings without adjustable parameters became possible with the Poisson-TrEsp method118 and by the determination of the vacuum dipole strength of bacteriochlorophylla (and related pigments) by Knox and Spring.115 The verification of Aartsma's effective dipole strength, the validity of the point-dipole approximation used for the calculation of excitonic couplings and of the inferred site energies by using also an improved lineshape theory in 2006 lead to the prediction of the relative orientation of the FMO protein with respect to the reaction center complex.118 This prediction was confirmed experimentally using chemical labeling and mass spectrometry by Blankenship and coworkers in 2009.138 In 2007, a structure-based simulation using PB/QC45 supported the fitted site energies. It was found that the electric fields of two α-helix backbones contribute significantly to the creation of an energy sink at a particular pigment in the FMO protein. In 2007, 2D spectra showed long-lived quantum beats61 and triggered a fundamental discussion about the role of coherences and their possible protection by the protein, e.g., by correlated site energy fluctuations for the efficiency of light-harvesting. QM/MM approaches did not find any correlation in site energy fluctuations, but it was argued36 that longer MD propagation times might be needed to resolve them. Indeed, a recent NMA/CDC/TrEsp analysis found strong correlations in site energy fluctuations at low frequencies. However, these correlations were shown to have practically no influence on the decay of coherences between different exciton states and on exciton relaxation.51 The inhomogeneous charge distribution of the FMO protein was found to be responsible for this effect. In this way, it became clear that the same mechanism, which creates an excitation energy funnel in this system, leads to a fast dissipation of the excitons's excess energy. In 2009, an eighth pigment was (re)discovered that is bound at the periphery of each monomeric subunit of the FMO protein.139 Its location led Blankenship and coworkers to suggest that this pigment is the linker to the baseplate connecting the FMO protein with the outer antenna system. Indeed, CDC calculations showed that this pigment is the most blue-shifted pigment in FMO and, thereby, completes the excitation energy funnel created by the pigment–protein coupling in this system.48 Located at the periphery of the FMO protein, the eighth pigment is found to interact with charged amino acids, where the large blue shift results from three deprotonated Asp and one deprotonated Glu. These residues are situated in the region of negative difference potential of this pigment, thereby causing the blueshift. Since in vivo the surface of the FMO protein is interacting with another protein rather than with water, the influence of the lower dielectric polarization of the former on the site energy of the eighth pigment has been investigated as well. It was found that just one titratable group in the environment of the eighth pigment changes its protonation state and that this pigment remains the most blue shifted pigment of all.48
5.2 The light-harvesting complex LHCII of higher plants
LHCII is the major light-harvesting complex in the thylakoid membrane of higher plants and can be considered the most abundant membrane protein on earth. In the native system, it forms supercomplexes with minor homologous antenna proteins and the photosystem II core complex.140,141 The latter is the site of photosynthetic water oxidation.1,2 The task of the antenna system surrounding the core complex is not only to deliver excitation energy, but also to regulate the energy flow. However, the precise role of LHCII in this regulation is still elusive. Elucidation of the 3D-structure of isolated LHCII was a major breakthrough in the field142 and showed that LHCII is a trimeric complex, where each monomeric subunit binds eight chlorophyll (Chl) a and six Chl b pigments as well as four carotenoids of three different types and a structurally important lipid molecule. Based on this structural information, Novoderezhkin et al.143 developed an exciton Hamiltonian for the Chl pigments in LHCII, using excitonic couplings calculated with the point-dipole approximation and fitted site energies, which is an important benchmark and allows for a simulation of stationary and time-resolved optical spectra (see also ref. 7 and 144). Application of the Poisson-TrEsp method for the excitonic couplings and the PB/QC method for the site energies largely confirmed this Hamiltonian, except for assigning lower site energies to one Chl a and one Chl b, higher site energies to two Chl b and a weaker excitonic coupling to one Chl b pair, and thus permitted us to link the exciton Hamiltonian to the molecular structure on an electrostatic basis.101 To achieve good agreement between simulated and measured linear optical spectra, it was necessary to include high-frequency vibrational pigment modes explicitly into the Hamiltonian.110,145 The Chl system of LHCII is divided into domains by virtue of a cut-off coupling Vc to simulate the dynamic localization of exciton states in an implicit way. Thus, for excitonic couplings of pigments m and n belonging to different domains, it holds that Vmn < Vc, and exciton delocalization is allowed for only within domains. Within this model, it became possible to understand the slow energy transfer times measured in the Chl a spectral region.145 A consequence of this treatment is that also the excitonic couplings involving vibronic states are smaller than the cut-off coupling, and these states remain localized on the respective pigments. We note that in the work of Novoderezhkin et al.,7,143,144 the high-frequency modes are treated in a different way, as they are included in the spectral density. A goal of current research is to better understand the implications of these different treatments of modes for optical lineshapes and excitation energy transfer.
Concerning energy flow in LHCII, the main result of the structure-based simulations is that the energy sink (i.e., the terminal emitter domain) is located at Chl a610 at the periphery of the LHCII trimer and at the stromal side of the thylakoid membrane, probably involving also Chls a611 and a612 at physiological temperatures. This assignment is in agreement with earlier proposals146,147 based on the Novoderezhkin–Hamiltonian and mutagenesis studies.148,149 The terminal emitter domain is likely one of the sites in the photosystem II antenna system, where excitation energy flow is regulated. However, the simulations also revealed problems that remain to be solved. Three of these problems are: (i) possible temperature-dependent structural changes of LHCII that affect exciton states in a yet unknown way,148 (ii) detergent-induced structural changes that cause pigment orientations to be altered in solubilized LHCII trimers compared to the crystal structure,110 and (iii) a mismatch between simulated and measured circular dichroism spectra in the Chl b region at around 650 nm.101,110,144
5.3 Cyanobacterial photosystem I and photosystem II
The trimeric cyanobacterial photosystem I core complex contains 96 Chl a pigments per monomer.150 This large size represents a particular challenge for theory. Attempts have been made to use the 96 site energies as parameters to be determined from a fit of optical spectra.151,152 However, an unambiguous determination of 96 site energies that is based on a fit of a few linear optical spectra is rather unlikely. On the other hand, these fits describe the spectra quantitatively, whereas early structure-based calculations30,44 could only describe the absorbance spectrum, but failed, e.g., for the linear dichroism. A first structure-based explanation of linear absorbance and linear and circular dichroism spectra was obtained by using Poisson-TrEsp for the excitonic couplings and the CDC method, in combination with an evaluation of the protonation pattern of titratable residues of the protein, for the site energies.47 A detailed evaluation of the pigment–protein coupling revealed the importance of long-range electrostatic interactions. Most of the site energies are determined by multiple interactions with a large number (>20) of amino acid residues. Out of 78 titratable residues of the protein, 23 were calculated to be in a non-standard protonation state at pH 6.5 and 300 K (where the standard is defined as the protonation state observed at pH 7.0 in an aqueous environment). Nevertheless, the site energies obtained for the standard protonation state are within 100 cm−1 of those obtained for the non-standard pattern, except for Chl 51, where the site energy is blue-shifted by 500 cm−1 in the non-standard protonation pattern. Interestingly, the calculations reveal a higher concentration of low-energy exciton states on the side of the A-branch of the reaction center. This finding could provide an explanation for the more frequent use of this branch in electron transfer reactions. Another finding concerns the presence of an excitation energy barrier formed by pigments that are located between the reaction center pigments and the low-energy pigments of the antennae. The latter are found at an average distance of about 25 Å from the special pair of the reaction center. Since electron exchange was not considered in this work, the identity of a few long-wavelength absorbing Chls was not obtained. A calculation scheme has been developed,73 which seems to be a promising tool, in combination with spectroscopic data,71 to provide these identities in future work.
Concerning photosystem II (PSII), based on calculations of optical spectra, various functional states of PSII reaction centers were identified and the overall decay of excited states by excitation energy transfer and trapping by the reaction center was found to be transfer-to-the-trap limited. These results have been explained in detail in earlier reviews.153–156 The site energies used in these calculations have been obtained from a fit of optical spectra of the CP43, CP47 and D1D2cytb559 subunits of PSII as well as from optical difference spectra of PSII core complexes. An important future goal is the direct evaluation of the site energies by structure-based calculations. Preliminary results,107 largely supporting the earlier fits,20 have been obtained for the CP43 subunit based on the 2.9 Å resolution structure.157 Work is in progress to exploit the most recent structural refinement at 1.9 Å resolution.158
6 Summary and outlook
In the present perspective, we have put together ingredients necessary to bridge the gap between the structural data of photosynthetic PPCs and their photophysical function. It is a great advantage that the optical properties of these systems and their building blocks are so well known, and a challenge for theory. A major simplification arises from the fact that different pigments do not exchange electrons but only excitons. Therefore, a rather simple-looking PPC Hamiltonian can be used to describe the dissipative exciton motion in these systems. Nevertheless, the motion of excitation energy resulting from such a Hamiltonian can have many different characteristics, arising from the relative strength of pigment–pigment (excitonic) and pigment–protein (exciton-vibrational) coupling. Microscopic theories provide the means to parametrize the PPC Hamiltonian, which can then be used to calculate the quantum dissipative motion of excitons. The predictive power of these methods and calculation schemes of parameters is steadily increasing and allows us already to draw conclusions about building principles of photosynthetic antennae that might be useful also for the creation of artificial light-harvesting devices. For example, in the FMO protein the inhomogeneous charge distribution of the protein is responsible for creating an excitation energy funnel that guides the excitons towards the reaction center and for a fast dissipation of the excitons' excess energy. It is an important future goal of structure-based theory to reach a similar understanding of photophysical properties also for larger PPCs including their interplay in the photosynthetic membrane and their ability to switch from the light-harvesting to a photoprotection mode.
Acknowledgements
Financial support by the Austrian Science Fund (FWF): P 24774-N27 is gratefully acknowledged.
References
-
Primary Processes of Photosynthesis, ed. G. Renger, RSC Publishing, Cambridge, UK, 2008 Search PubMed.
- F. Müh, C. Glöckner, J. Hellmich and A. Zouni, Biochim. Biophys. Acta, 2012, 1817, 44–65 CrossRef.
- J. Neugebauer, ChemPhysChem, 2009, 10, 3148–3173 CrossRef CAS.
- C. König and J. Neugebauer, ChemPhysChem, 2012, 13, 386–425 CrossRef.
-
Biophysical Techniques in Photosynthesis, ed. T. J. Aartsma and J. Matysik, Springer, Dordrecht, The Netherlands, 2008 Search PubMed.
- R. van Grondelle and V. I. Novoderezhkin, Phys. Chem. Chem. Phys., 2006, 8, 793–807 RSC.
- V. I. Novoderezhkin and R. van Grondelle, Phys. Chem. Chem. Phys., 2010, 12, 7352–7365 RSC.
- T. Renger, Photosynth. Res., 2009, 102, 471–485 CrossRef CAS.
-
V. May and O. Kühn, Charge and Energy Transfer Dynamics in Molecular Systems: A Theoretical Introduction, Wiley–VCH, Berlin, 2011 Search PubMed.
- T. Förster, Ann. Phys., 1948, 2, 55–75 CrossRef.
- D. L. Andrews, C. Curutchet and G. D. Scholes, Laser Photonics Rev., 2011, 5, 114–123 CrossRef CAS.
- T. Renger, V. May and O. Kühn, Phys. Rep., 2001, 343, 138–254 CrossRef.
- W. M. Zhang, T. Meier, V. Chernyak and S. Mukamel, J. Chem. Phys., 1998, 108, 7763–7774 CrossRef CAS.
- M. Yang and G. R. Fleming, Chem. Phys., 2002, 275, 355–372 CrossRef CAS.
- T. Renger and R. A. Marcus, J. Chem. Phys., 2003, 107, 8404–8419 CrossRef CAS.
- Z. Fetisova, A. Freiberg, K. Mauring, V. Novoderezhkin, A. Taisova and K. Timpmann, Biophys. J., 1996, 71, 995–1010 CrossRef CAS.
- K. Mukai, S. Abe and H. Sumi, J. Phys. Chem. B, 1999, 103, 6096–6102 CrossRef CAS.
- G. D. Scholes and G. R. Fleming, J. Phys. Chem. B, 2000, 104, 1854–1868 CrossRef CAS.
- S. Jang, M. D. Newton and R. J. Silbey, Phys. Rev. Lett., 2004, 92, 218301 CrossRef.
- G. Raszewski and T. Renger, J. Am. Chem. Soc., 2008, 130, 4431–4446 CrossRef CAS.
- A. Ishizaki and Y. Tanimura, J. Phys. Soc. Jpn., 2005, 74, 3131–3134 CrossRef CAS.
- A. Ishizaki and G. R. Fleming, J. Chem. Phys., 2009, 130, 234111 CrossRef.
- R. Chen, L. Zheng, Q. Shi and Y. Yan, J. Chem. Phys., 2009, 131, 094502 CrossRef.
- C. Kreisbeck and T. Kramer, J. Phys. Chem. Lett., 2012, 3, 2828–2833 CrossRef CAS.
- A. W. Chin, A. Rivas, S. F. Huelga and M. B. Plenio, J. Math. Phys., 2010, 51, 092109 CrossRef.
- J. Prior, A. Chin, S. F. Huelga and M. B. Plenio, Phys. Rev. Lett., 2010, 105, 050404 CrossRef.
- P. Huo and D. F. Coker, J. Chem. Phys., 2010, 133, 184108 CrossRef CAS.
- P. Nalbach, D. Braun and M. Thorwart, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 041926 CrossRef CAS.
- K. J. Fujimoto and W. Yang, J. Chem. Phys., 2008, 129, 054102 CrossRef.
- A. Damjanovic, I. Kosztin, U. Kleinekathöfer and K. Schulten, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 031919 CrossRef.
- L. Janosi, I. Kosztin and A. Damjanovic, J. Chem. Phys., 2006, 125, 014903 CrossRef.
- C. Olbrich and U. Kleinekathöfer, J. Phys. Chem. B, 2010, 114, 12427–12437 CrossRef CAS.
- C. Olbrich, J. Strümpfer, K. Schulten and U. Kleinekathöfer, J. Phys. Chem. Lett., 2011, 2, 1771–1776 CrossRef CAS.
- C. Olbrich, J. Strümpfer, K. Schulten and U. Kleinekathöfer, J. Phys. Chem. B, 2011, 115, 758–764 CrossRef CAS.
- H. W. Kim, A. Kelly, J. W. Park and Y. M. Rhee, J. Am. Chem. Soc., 2012, 134, 11640–11651 CrossRef CAS.
- Y. Jing, R. Zheng, H.-X. Li and Q. Shi, J. Phys. Chem. B, 2011, 116, 1164–1171 CrossRef.
- S. Shim, P. Rebentrost, S. Valleau and A. A. Aspuru-Guzik, Biophys. J., 2012, 102, 649–660 CrossRef CAS.
- C. Curutchet, J. Kongsted, A. Munoz-Losa, H. Hossein-Nejad, G. D. Scholes and B. Mennucci, J. Am. Chem. Soc., 2011, 133, 3078–3084 CrossRef CAS.
- J. Tomasi, R. Cammi, B. Mennucci, C. Cappelli and S. Corni, Phys. Chem. Chem. Phys., 2002, 4, 5697–5712 RSC.
- C. Curutchet, G. D. Scholes, B. Mennucci and R. Cammi, J. Phys. Chem. B, 2007, 111, 13253–13265 CrossRef CAS.
- G. D. Scholes, C. Curutchet, B. Mennucci, R. Cammi and J. Tomasi, J. Phys. Chem. B, 2007, 111, 6978–6982 CrossRef CAS.
- B. Mennucci and C. Curutchet, Phys. Chem. Chem. Phys., 2011, 13, 11538–11550 RSC.
- A. Damjanovic, H. M. Vaswani, P. Fromme and G. R. Fleming, J. Phys. Chem. B, 2002, 106, 10251–10262 CrossRef CAS.
- S. Yin, M. G. Dahlbom, P. J. Canfield, N. S. Hush, R. Kobayashi and J. R. Reimers, J. Phys. Chem. B, 2007, 111, 9923–9930 CrossRef CAS.
- F. Müh, M. E. Madjet, J. Adolphs, A. Abdurahman, B. Rabenstein, H. Ishikita, E. W. Knapp and T. Renger, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 16862–16867 CrossRef.
- J. Adolphs, F. Müh, M. E. Madjet and T. Renger, Photosynth. Res., 2008, 95, 197–209 CrossRef CAS.
- J. Adolphs, F. Müh, M. E. Madjet, M. Schmidt am Busch and T. Renger, J. Am. Chem. Soc., 2010, 132, 3331–3343 CrossRef CAS.
- M. Schmidt am Busch, F. Müh, M. E. Madjet and T. Renger, J. Phys. Chem. Lett., 2011, 2, 93–98 CrossRef CAS.
- H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229 CrossRef CAS.
- M. Hoffmann, M. Wanko, P. Strodel, P. H. König, T. Frauenheim, K. Schulten, W. Thiel, E. Tajkhorshid and M. Elstner, J. Am. Chem. Soc., 2006, 128, 10808–10818 CrossRef CAS.
- T. Renger, A. Klinger, F. Steinecker, M. Schmidt am Busch, J. Numata and F. Müh, J. Phys. Chem. B, 2012, 116, 14565–14580 CrossRef CAS.
- A. Warshel, M. Kato and A. V. Pisliakov, J. Chem. Theory Comput., 2007, 3, 2034–2045 CrossRef CAS.
- M. Schmidt am Busch and E. W. Knapp, J. Am. Chem. Soc., 2005, 127, 15730–15737 CrossRef CAS.
- H. M. Senn and W. Thiel, Top. Curr. Chem., 2007, 268, 173–290 CrossRef CAS.
- T. M. H. Creemers, C. A. De Caro, R. W. Visschers, R. van Grondelle and S. Völker, J. Phys. Chem. B, 1999, 103, 9770–9776 CrossRef CAS.
- M. Wendling, T. Pullerits, M. Przyjalgowski, S. Vulto, T. Aartsma, R. van Grondelle and H. van Amerongen, J. Phys. Chem. B, 2000, 104, 5825–5831 CrossRef CAS.
- R. Jankowiak, M. Reppert, V. Zazubovich, J. Pieper and T. Reinot, Chem. Rev., 2011, 111, 4546–4598 CrossRef CAS.
- M. Rätsep and A. Freiberg, J. Lumin., 2007, 127, 251–259 CrossRef.
- T. Renger and R. A. Marcus, J. Chem. Phys., 2002, 116, 9997–10019 CrossRef CAS.
- T. Brixner, J. Stenger, H. M. Vaswani, M. Cho, R. E. Blankenship and G. R. Fleming, Nature, 2005, 434, 625–628 CrossRef CAS.
- G. S. Engel, T. R. Calhoun, E. L. Read, T.-K. Ahn, T. Mancal, Y.-C. Cheng, R. E. Blankenship and G. R. Fleming, Nature, 2007, 446, 782–786 CrossRef CAS.
- A. Ishizaki, T. R. Calhoun, G. S. Schlau-Cohen and G. R. Fleming, Phys. Chem. Chem. Phys., 2010, 12, 7319–7337 RSC.
- G. S. Schlau-Cohen, A. Ishizaki and G. R. Fleming, Chem. Phys., 2011, 132, 3331–3343 Search PubMed.
- A. Ishizaki and G. R. Fleming, Annu. Rev. Condens. Matter Phys., 2012, 3, 333–361 CrossRef CAS.
- G. S. Olaya-Castro and G. D. Scholes, Int. Rev. Phys. Chem., 2011, 30, 49–77 CrossRef.
- G. Panitchayangkoon, D. Hayes, D. Franstedt, J. R. Caram, E. Harel, J. Wen, R. E. Blankenship and G. S. Engel, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 12766–12770 CrossRef CAS.
- E. Collini, C. Y. Wong, K. E. Wilk, P. M. Curmi, P. Brumer and G. D. Scholes, Nature, 2010, 463, 644–647 CrossRef CAS.
-
G. R. Fleming, G. D. Scholes and Y. C. Cheng, 22nd Solvay Conference on Chemistry: Quantum effects in Chemistry and Biology, Procedia Chemistry, Elsevier, Amsterdam, The Netherlands, 2011, vol. 3 Search PubMed.
- P. Ball, Nature, 2011, 474, 272–274 CrossRef CAS.
- A. Warshel and W. W. Parson, J. Am. Chem. Soc., 1987, 109, 6143–6152 CrossRef CAS.
- E. Schlodder, V. Shubin, E. El-Mohsnawy, M. Roegner and N. V. Karapetyan, Biochim. Biophys. Acta, 2007, 1767, 732–741 CrossRef CAS.
- G. D. Scholes, I. R. Gould, R. Cogdell and G. R. Fleming, J. Phys. Chem. B, 1999, 103, 2543–2553 CrossRef CAS.
- M. E. Madjet, F. Müh and T. Renger, J. Phys. Chem. B, 2009, 113, 12603–12614 CrossRef.
- Y. Georgievskii, C.-P. Hsu and R. A. Marcus, J. Chem. Phys., 1999, 110, 5307–5317 CrossRef CAS.
- M. E. Madjet, A. Abdurahman and T. Renger, J. Phys. Chem. B, 2006, 110, 17268–17281 CrossRef CAS.
-
P. Atkins and R. Friedmann, Molecular Quantum Mechanics, Oxford University Press, Oxford, UK, 2005 Search PubMed.
- T. Renger, B. Grundkötter, M. E. Madjet and F. Müh, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 13235–13240 CrossRef.
- B. R. Brooks, C. L. Brooks, A. D. MacKerell and M. Karplus, J. Comput. Chem., 2009, 30, 1545–1614 CrossRef CAS.
- A. D. MacKerell Jr., D. Bashford, M. Bellott and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef.
- D. Bashford and M. Karplus, Biochemistry, 1990, 29, 10219–10225 CrossRef CAS.
- D. Bashford, Front. Biosci., 2004, 9, 1082–1099 CrossRef CAS.
- G. M. Ullmann and E. W. Knapp, Eur. Biophys. J., 1999, 28, 533–550 CrossRef CAS.
- G. M. Ullmann, E. Kloppmann, T. Essigke, E. M. Krammer, A. Klingen, T. Becker and E. Bombarda, Photosynth. Res., 2008, 97, 33–53 CrossRef CAS.
- M. R. Gunner, J. J. Mao, Y. F. Song and J. Kim, Biochim. Biophys. Acta, 2006, 1757, 942–968 CrossRef CAS.
- F. M. Richards, Annu. Rev. Biophys. Bioeng., 1977, 6, 151–176 CrossRef CAS.
- M. L. Connolly, J. Appl. Crystallogr., 1983, 16, 548–558 CrossRef CAS.
- T. Simonson, Rep. Prog. Phys., 2003, 66, 737–787 CrossRef CAS.
- Y. Sham, Z. Chu and A. Warshel, J. Phys. Chem. B, 1997, 101, 4458–4472 CrossRef CAS.
- W. H. Orttung, Biochemistry, 1970, 9, 2394–2402 CrossRef CAS.
- C. Tanford and R. Roxby, Biochemistry, 1972, 11, 2192–2198 CrossRef CAS.
- T. Simonson and D. Perahia, J. Am. Chem. Soc., 1995, 117, 7987–8000 CrossRef CAS.
- J. Antosiewicz, J. M. Briggs, A. H. Elcock, M. K. Gilson and J. A. McGammon, J. Comput. Chem., 1996, 17, 1633–1644 CrossRef CAS.
- T. Simonson and C. L. Brooks, J. Am. Chem. Soc., 1996, 118, 8452–8458 CrossRef CAS.
- T. Simonson, G. Archontis and M. Karplus, J. Phys. Chem. B, 1999, 103, 6142–6156 CrossRef CAS.
- G. Kieseritzky and E. W. Knapp, J. Biol. Chem., 2011, 286, 2976–2986 CrossRef CAS.
- G. Kieseritzky and E. W. Knapp, Proteins, 2008, 71, 1335–1348 CrossRef CAS.
- N. A. Baker, D. Sept, S. Joseph, M. J. Holst and J. A. McGammon, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 10037–10041 CrossRef CAS.
- M. B. Ulmschneider, J. Ulmschneider, M. Sansom and A. Di Nola, Biophys. J., 2007, 92, 2338–2349 CrossRef CAS.
- A. R. Klingen, H. Palsdottier, C. Hunte and G. M. Ullmann, Biochim. Biophys. Acta, 2007, 1767, 204–221 CrossRef CAS.
- A. Onufriev, A. Smondyrev and D. Bashford, J. Mol. Biol., 2003, 332, 1183–1193 CrossRef CAS.
- F. Müh, M. E. Madjet and T. Renger, J. Phys. Chem. B, 2010, 114, 13517–13535 CrossRef.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS.
- M. Holst, N. Baker and F. Wang, J. Comput. Chem., 2000, 21, 1319–1342 CrossRef CAS.
- N. Baker, M. Holst and F. Wang, J. Comput. Chem., 2000, 21, 1343–1352 CrossRef CAS.
- H. Schulze, O. Ristau and C. Jung, Biochim. Biophys. Acta, 1994, 1183, 491–498 CrossRef CAS.
-
P. Douzou, Cryobiochemistry, Academic Press, London, 1977 Search PubMed.
- F. Müh, M. E. Madjet and T. Renger, Photosynth. Res., 2012, 111, 87–101 CrossRef.
- I. Yu, Meas. Sci. Technol., 1993, 4, 344–348 CrossRef.
- R. A. Marcus, J. Chem. Phys., 1963, 38, 1858–1862 CrossRef CAS.
- F. Müh and T. Renger, Biochim. Biophys. Acta, 2012, 1817, 1446–1460 CrossRef.
- M. Wormit and A. Dreuw, Phys. Chem. Chem. Phys., 2007, 9, 2917–2931 RSC.
- A. Dreuw, P. H. P. Harbach, J. M. Mewes and M. Wormit, Theor. Chem. Acc., 2010, 125, 419–426 CrossRef CAS.
- C. Hsu, Acc. Chem. Res., 2009, 42, 509–518 CrossRef CAS.
- B. P. Krueger, G. D. Scholes and G. R. Fleming, J. Phys. Chem. B, 1998, 102, 5378–5386 CrossRef CAS.
- R. S. Knox and B. Q. Spring, Photochem. Photobiol., 2003, 77, 497–501 CrossRef CAS.
- C. Hsu, M. Head-Gordon, T. Head-Gordon and G. R. Fleming, J. Chem. Phys., 2001, 114, 3065–3072 CrossRef CAS.
- T. Renger and F. Müh, Photosynth. Res., 2012, 111, 47–52 CrossRef CAS.
- J. Adolphs and T. Renger, Biophys. J., 2006, 91, 2778–2797 CrossRef CAS.
- T. Renger, M. E. Madjet, F. Müh, I. Trostmann, F.-J. Schmitt, C. Theiss, H. Paulsen, H.-J. Eichler, A. Knorr and G. Renger, J. Phys. Chem. B, 2009, 113, 9948–9957 CrossRef CAS.
- F. Müh and A. Zouni, Biochim. Biophys. Acta, 2005, 1708, 219–228 CrossRef.
- J. Megow, A. Kulesza, Z. W. Qu, T. Ronneberg, V. Bonacic-Koutecky and V. May, Chem. Phys., 2010, 377, 10–14 CrossRef CAS.
- J. Fajer, J. Porphyrins Phthalocyanines, 2000, 4, 382–385 CrossRef CAS.
- J. A. Shelnutt, X. Z. Song, J. G. Ma, S.-L. Jia, W. Jentzen and C. J. Medforth, Chem. Soc. Rev., 1998, 27, 31–41 RSC.
-
H. Scheer, in Chlorophylls and Bacteriochlorophylls, ed. B. Grimm, R. J. Porra, W. Rüdiger and H. Scheer, Springer, Dordrecht, The Netherlands, 2006, pp. 1–26 Search PubMed.
- X. Pan, M. Li, T. Wan, L. Wang, C. Jia, Z. Hou, X. Zhao, J. Zhang and W. Chang, Nat. Struct. Mol. Biol., 2011, 18, 309–315 CAS.
- G. Zucchelli, D. Brogioli, A. P. Casazza, F. M. Garlaschi and R. C. Jennings, Biophys. J., 2007, 93, 2240–2254 CrossRef CAS.
- G. Zucchelli, S. Santabarbara and R. C. Jennings, Biochemistry, 2012, 51, 2717–2736 CrossRef CAS.
- W. Jentzen, X.-Z. Song and J. A. Shelnutt, J. Phys. Chem. B, 1997, 101, 1684–1699 CrossRef CAS.
- K. J. Fujimoto and S. Hayashi, J. Am. Chem. Soc., 2009, 131, 14152 CrossRef CAS.
- K. J. Fujimoto, J. Chem. Phys., 2010, 133, 124101 CrossRef.
- K. J. Fujimoto, J. Chem. Phys., 2012, 137, 034101 CrossRef.
- D. Beljonne, C. Curutchet, G. D. Scholes and R. J. Silbey, J. Phys. Chem. B, 2009, 113, 6583–6599 CrossRef CAS.
- A. Freiberg, S. Lin, K. Timpmann and R. E. Blankenship, J. Phys. Chem. B, 1997, 37, 7211–7220 CrossRef.
- T. Renger, I. Trostmann, C. Theiss, M. E. Madjet, M. Richter, H. Paulsen, H. J. Eichler, A. Knorr and G. Renger, J. Phys. Chem. B, 2007, 111, 10487–10501 CrossRef CAS.
- T. Renger, Phys. Rev. Lett., 2004, 93, 188101 CrossRef.
- R. E. Fenna and B. W. Matthews, Nature, 1975, 258, 573–577 CrossRef CAS.
- R. J. W. Louwe, J. Vrieze, A. J. Hoff and T. J. Aartsma, J. Phys. Chem. B, 1997, 101, 11280–11287 CrossRef CAS.
- J. Wen, H. Zhang, M. L. Gross and R. E. Blankenship, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 6134–6139 CrossRef CAS.
- D. E. Tronrud, J. Wen, L. Gay and R. E. Blankenship, Photosynth. Res., 2009, 100, 79–87 CrossRef CAS.
- R. Kouril, J. P. Dekker and E. J. Boekema, Biochim. Biophys. Acta, 2012, 1817, 2–12 CrossRef CAS.
- R. Croce and H. van Amerongen, J. Photochem. Photobiol., B, 2011, 104, 142–153 CrossRef CAS.
- T. Barros and W. Kühlbrandt, Biochim. Biophys. Acta, 2009, 1787, 753–772 CrossRef CAS.
- V. I. Novoderezhkin, M. A. Palacios, H. van Amerongen and R. van Grondelle, J. Phys. Chem. B, 2005, 109, 10493–10504 CrossRef CAS.
- V. I. Novoderezhkin, A. Marin and R. van Grondelle, Phys. Chem. Chem. Phys., 2011, 13, 17093–17103 RSC.
- T. Renger, M. E. Madjet, A. Knorr and F. Müh, J. Plant Physiol., 2011, 168, 1497–1509 CrossRef CAS.
- A. A. Pascal, Z. Liu, K. Broess, B. van Oort, H. van Amerongen, C. Wang, P. Horton, B. Robert, W. Chang and A. Ruban, Nature, 2005, 436, 134–137 CrossRef CAS.
- G. S. Schlau-Cohen, T. R. Calhoun, N. S. Ginsberg, E. L. Read, M. Ballottari, R. Bassi, R. van Grondelle and G. R. Fleming, J. Phys. Chem. B, 2009, 113, 15352–15363 CrossRef CAS.
- H. Rogl, R. Schödel, H. Lokstein, W. Kühlbrandt and A. Schubert, Biochemistry, 2002, 41, 2281–2287 CrossRef CAS.
- R. Remelli, C. Varotto, D. Sandona, R. Croce and R. Bassi, J. Biol. Chem., 1999, 274, 33510–33521 CrossRef CAS.
- P. Jordan, P. Fromme, H. T. Witt, O. Klukas, W. Saenger and N. Krauß, Nature, 2001, 411, 909–917 CrossRef CAS.
- M. Byrdin, P. Jordan, N. Krauss, P. Fromme, D. Stehlik and E. Schlodder, Biophys. J., 2002, 83, 433–457 CrossRef CAS.
- B. Brüggemann, K. Sznee, V. Novoderezhkin, R. van Grondelle and V. May, J. Phys. Chem. B, 2004, 108, 13536–13546 CrossRef.
- T. Renger and E. Schlodder, ChemPhysChem, 2010, 11, 1141–1153 CrossRef CAS.
- T. Renger and E. Schlodder, J. Photochem. Photobiol., B, 2011, 104, 126–141 CrossRef CAS.
- F. Müh, T. Renger and A. Zouni, Plant Physiol. Biochem., 2008, 46, 238–264 CrossRef.
- G. Renger and T. Renger, Photosynth. Res., 2008, 98, 53–80 CrossRef CAS.
- A. Guskov, A. Gabdulkhakov, M. Broser, C. Glöckner, J. Hellmich, J. Kern, J. Frank, F. Müh, W. Saenger and A. Zouni, ChemPhysChem, 2010, 11, 1160–1171 CrossRef CAS.
- Y. Umena, K. Kawakami, J. Shen and N. Kamiya, Nature, 2011, 473, 55–60 CrossRef CAS.
Footnote |
| † In fact, also the vacuum dipole strength of the optical transition of the pigments is not calculated directly, but taken from experiment and used to rescale the transition charges, as described before. |
|
| This journal is © the Owner Societies 2013 |
 Open Access Article
Open Access Article

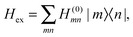
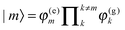 . The excitation energy Em corresponds to the energy at which pigment m in its local binding site in the protein would absorb light, if its optical transition was not coupled by Vmn to the optical transitions of the other pigments n. Below, we will use microscopic theory to derive expressions for Em and Vmn.
. The excitation energy Em corresponds to the energy at which pigment m in its local binding site in the protein would absorb light, if its optical transition was not coupled by Vmn to the optical transitions of the other pigments n. Below, we will use microscopic theory to derive expressions for Em and Vmn.
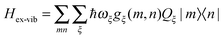
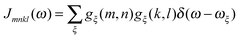
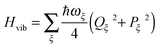
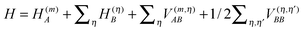 , where V(m,η)AB is the Coulomb coupling between pigment m and building block η and
, where V(m,η)AB is the Coulomb coupling between pigment m and building block η and 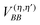 that between building blocks η and η′. In the absence of electron exchange between building blocks, the Hartree product for the eigenfunction
that between building blocks η and η′. In the absence of electron exchange between building blocks, the Hartree product for the eigenfunction 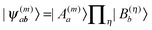 of the Hamiltonian of isolated building blocks, with
of the Hamiltonian of isolated building blocks, with 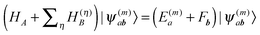 , can be used to investigate the shift ΔE(m)a of the electronic energies E(m)a of pigment m by the Coulomb coupling
, can be used to investigate the shift ΔE(m)a of the electronic energies E(m)a of pigment m by the Coulomb coupling 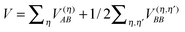 between building blocks. The multi index b = b1, b2,…,bη,… was introduced to abbreviate the notation for the electronic states of the environment. Within perturbation theory up to second order in the Coulomb coupling V, the shift ΔE(m)a is given as
between building blocks. The multi index b = b1, b2,…,bη,… was introduced to abbreviate the notation for the electronic states of the environment. Within perturbation theory up to second order in the Coulomb coupling V, the shift ΔE(m)a is given as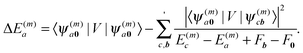
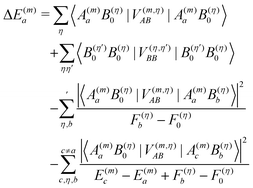
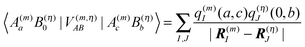
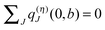 is used, the matrix elements in Wa become
is used, the matrix elements in Wa become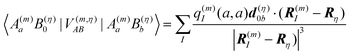
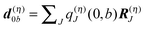 , and Wa can be written as
, and Wa can be written as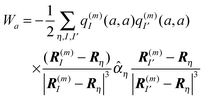
![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) η of building block η with elements
η of building block η with elements 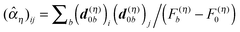 and i, j = x, y, z was introduced.
and i, j = x, y, z was introduced.
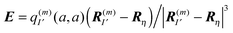 of the partial charge
of the partial charge 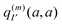 induces a dipole moment pη =
induces a dipole moment pη = ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) ηE at molecule (building block) η, and the field of this dipole moment interacts with the partial charge q(m)I(a,a) of the pigment. Hence, Wa is the solvation energy of the permanent charge density of electronic state a of pigment m.
ηE at molecule (building block) η, and the field of this dipole moment interacts with the partial charge q(m)I(a,a) of the pigment. Hence, Wa is the solvation energy of the permanent charge density of electronic state a of pigment m.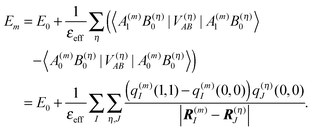
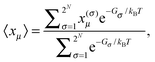
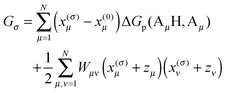
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10(pKa − pH).
10(pKa − pH).
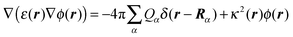

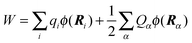
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10(pKa − pH) + ΔΔG(μ)back + ΔΔG(μ)pol
10(pKa − pH) + ΔΔG(μ)back + ΔΔG(μ)pol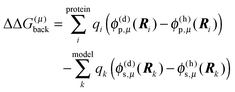
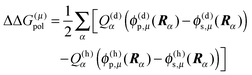
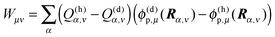
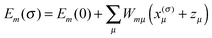
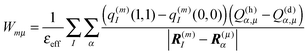
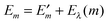
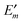 is the energy difference between excited and ground states, when both are fully equilibrated, and Eλ(m) is the reorganization energy. In the following, the calculation of
is the energy difference between excited and ground states, when both are fully equilibrated, and Eλ(m) is the reorganization energy. In the following, the calculation of 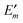 is described. The treatment of Eλ(m) will be discussed in Section 3.1.4.4. The thermodynamic cycle in Fig. 3 indicates that
is described. The treatment of Eλ(m) will be discussed in Section 3.1.4.4. The thermodynamic cycle in Fig. 3 indicates that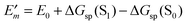

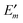 of a protein-bound pigment with the PB/QC method.
of a protein-bound pigment with the PB/QC method.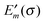 can be written as
can be written as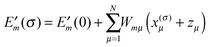
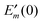 is the site energy obtained for the reference protonation state, which in addition to the charge density coupling term (background term ΔΔG(m)back) includes a polarization term ΔΔG(m)pol
is the site energy obtained for the reference protonation state, which in addition to the charge density coupling term (background term ΔΔG(m)back) includes a polarization term ΔΔG(m)pol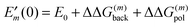
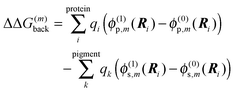
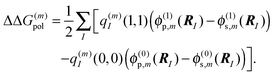
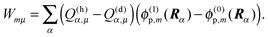
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) p is varied to optimize simulated optical spectra and, therefore, is essentially an adjustable parameter. This parameter not only accounts for dielectric screening and local field effects in the protein interior at different temperatures, but also compensates for a possible inadequateness of the quantum chemical charge sets of the pigments. Thus,
p is varied to optimize simulated optical spectra and, therefore, is essentially an adjustable parameter. This parameter not only accounts for dielectric screening and local field effects in the protein interior at different temperatures, but also compensates for a possible inadequateness of the quantum chemical charge sets of the pigments. Thus, ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) p does not solely represent the static polarizability of the protein. As a consequence, its value used in site energy calculations may differ from εp used for protonation patterns and may be even smaller than εopt.
p does not solely represent the static polarizability of the protein. As a consequence, its value used in site energy calculations may differ from εp used for protonation patterns and may be even smaller than εopt.
![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) m − G0
m − G0![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) m is the non-equilibrium free energy of the excited state and G0 is the equilibrium free energy of the ground state. According to Marcus,109 a non-equilibrium free energy of an excited state may be obtained from the equilibrium free energy Gm of the excited state and equilibrium free energies G(1−0,opt)m and G(1−0)m of two fictitious systems, which carry the charge density difference between excited and ground states of state |m〉 of the PPC and are embedded in a dielectric with optical dielectric constant εopt or static dielectric constant ε, respectively,
m is the non-equilibrium free energy of the excited state and G0 is the equilibrium free energy of the ground state. According to Marcus,109 a non-equilibrium free energy of an excited state may be obtained from the equilibrium free energy Gm of the excited state and equilibrium free energies G(1−0,opt)m and G(1−0)m of two fictitious systems, which carry the charge density difference between excited and ground states of state |m〉 of the PPC and are embedded in a dielectric with optical dielectric constant εopt or static dielectric constant ε, respectively,![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) m = Gm + G(1−0,opt)m − G(1−0)m
m = Gm + G(1−0,opt)m − G(1−0)m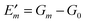 considered in the thermodynamic cycle above, we obtain for the reorganization energy
considered in the thermodynamic cycle above, we obtain for the reorganization energy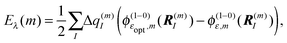
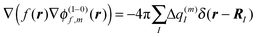
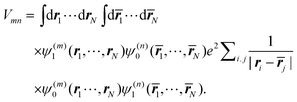
![[r with combining macron]](https://www.rsc.org/images/entities/b_i_char_0072_0304.gif) 1,…,
1,…,![[r with combining macron]](https://www.rsc.org/images/entities/b_i_char_0072_0304.gif) Nn of molecule Bn. The integration over the respective spin variables is also included, but not explicitly denoted, and real wavefunctions are assumed for simplicity. The intermolecular Coulomb coupling between pigments V(mn)AB in eqn (8) contains the intermolecular coupling between electrons, between electrons and nuclei and between nuclei. Of these three contributions, only the first is shown in eqn (42), since it is the only one that gives a non-zero contribution, because of the orthogonality of electronic wavefunctions, i.e., 〈A(m)1|A(m)0〉 = 〈B(n)0|B(n)1〉 = 0.
Nn of molecule Bn. The integration over the respective spin variables is also included, but not explicitly denoted, and real wavefunctions are assumed for simplicity. The intermolecular Coulomb coupling between pigments V(mn)AB in eqn (8) contains the intermolecular coupling between electrons, between electrons and nuclei and between nuclei. Of these three contributions, only the first is shown in eqn (42), since it is the only one that gives a non-zero contribution, because of the orthogonality of electronic wavefunctions, i.e., 〈A(m)1|A(m)0〉 = 〈B(n)0|B(n)1〉 = 0.
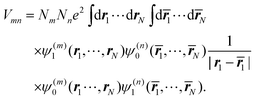
![[r with combining macron]](https://www.rsc.org/images/entities/b_i_char_0072_0304.gif) 2…
2…![[r with combining macron]](https://www.rsc.org/images/entities/b_i_char_0072_0304.gif) Nn can be performed by introducing one-particle densities ρ(m)10(r1) and ρ(n)10(
Nn can be performed by introducing one-particle densities ρ(m)10(r1) and ρ(n)10(![[r with combining macron]](https://www.rsc.org/images/entities/b_i_char_0072_0304.gif) 1) with
1) with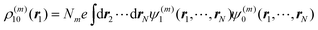
![[r with combining macron]](https://www.rsc.org/images/entities/b_i_char_0072_0304.gif) 1) of molecule Bn.
1) of molecule Bn.
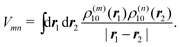
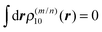 , it is seen that the first non-vanishing contribution to Vmn is due to the coupling between transition dipole moments, the point-dipole approximation:
, it is seen that the first non-vanishing contribution to Vmn is due to the coupling between transition dipole moments, the point-dipole approximation: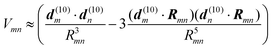
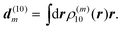
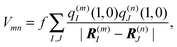
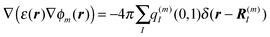
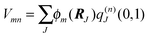
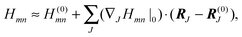
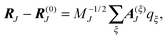
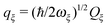 ,
,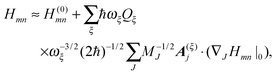
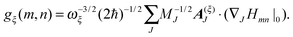
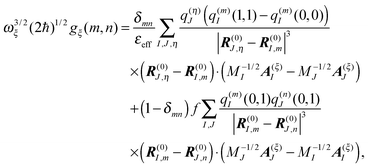

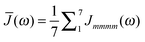 obtained by NMA on the monomeric subunit of the FMO protein (histogram, red bars)51 compared to spectral densities extracted from experimental data. The black solid line was obtained59 from an analysis of fluorescence line narrowing spectra of the B777 complex55 and the blue solid line from the FLN spectra of the FMO protein.56 The area under the curves corresponds to the Huang-Rhys factor S, which for the two experimental spectral densities was obtained from a fit of the temperature dependence of the absorbance spectrum of the FMO protein resulting in S = 0.42. The NMA value for the average S is 0.39.
obtained by NMA on the monomeric subunit of the FMO protein (histogram, red bars)51 compared to spectral densities extracted from experimental data. The black solid line was obtained59 from an analysis of fluorescence line narrowing spectra of the B777 complex55 and the blue solid line from the FLN spectra of the FMO protein.56 The area under the curves corresponds to the Huang-Rhys factor S, which for the two experimental spectral densities was obtained from a fit of the temperature dependence of the absorbance spectrum of the FMO protein resulting in S = 0.42. The NMA value for the average S is 0.39.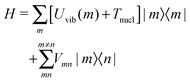
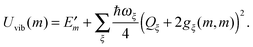
 between the minimum of the PES of the excited state and that of the PES of the ground state. Due to the exciton-vibrational coupling, these PES are shifted with respect to each other by −2gξ(m,m) along the coordinate axis.
between the minimum of the PES of the excited state and that of the PES of the ground state. Due to the exciton-vibrational coupling, these PES are shifted with respect to each other by −2gξ(m,m) along the coordinate axis.  is given as
is given as
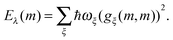
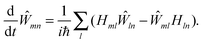
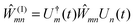
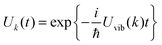
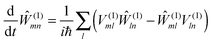
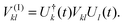
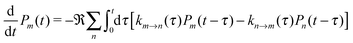
![[Fraktur R]](https://www.rsc.org/images/entities/char_e18f.gif) denotes the real part. The generalized (time-dependent) rate constant km→n(t) reads
denotes the real part. The generalized (time-dependent) rate constant km→n(t) reads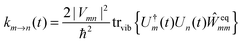
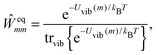

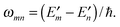
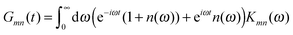
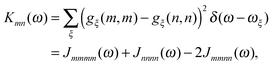
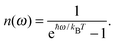
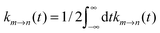 . Using
. Using 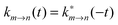 , this rate constant reads
, this rate constant reads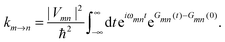
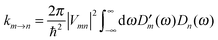
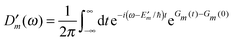
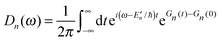
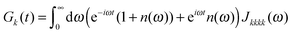
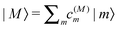 are excited, which are obtained by diagonalizing the exciton Hamiltonian Hex in eqn (2) giving
are excited, which are obtained by diagonalizing the exciton Hamiltonian Hex in eqn (2) giving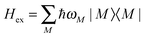
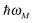 and eigenvectors containing the coefficients c(M)m. The exciton-vibrational coupling in the representation of delocalized states
and eigenvectors containing the coefficients c(M)m. The exciton-vibrational coupling in the representation of delocalized states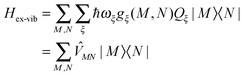
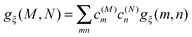
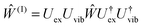
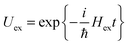 and
and 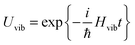 of the excitonic and vibrational degrees of freedom, respectively, using the Hvib in eqn (6).
of the excitonic and vibrational degrees of freedom, respectively, using the Hvib in eqn (6).
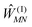 then reads
then reads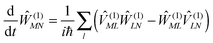
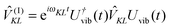
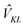 (eqn (80)). A quantum master equation can be derived along the same lines as for the weak coupling case studied above, but using this time a second order perturbation theory for the exciton vibrational coupling
(eqn (80)). A quantum master equation can be derived along the same lines as for the weak coupling case studied above, but using this time a second order perturbation theory for the exciton vibrational coupling 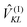 . The resulting Redfield-type rate constant reads
. The resulting Redfield-type rate constant reads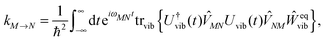
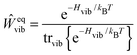

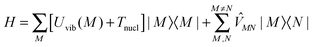
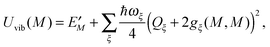
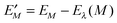
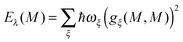
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) MN in eqn (88) comprise the off-diagonal elements of the exciton-vibrational coupling (eqn (81)).
MN in eqn (88) comprise the off-diagonal elements of the exciton-vibrational coupling (eqn (81)).
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) MN yields the following expression for the rate constant kM→N
MN yields the following expression for the rate constant kM→N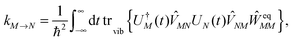
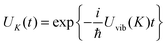
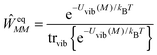
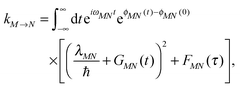
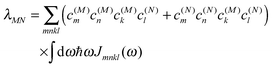
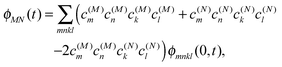
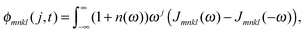
![[J with combining macron]](https://www.rsc.org/images/entities/i_char_004a_0304.gif) (ω) with the average diagonal part of the NMA spectral density
(ω) with the average diagonal part of the NMA spectral density 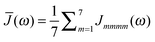 and the experimental spectral density Jexp(ω) of the FMO protein (Fig. 4). f(ω) is introduced to correct for the limitations of the harmonic approximation. The larger amplitude of the high-frequency part of the corrected spectral density allows the protein to dissipate the excess energy of excitons faster (Fig. 6 and eqn (87)). The relaxation times obtained for the corrected spectral density are in agreement with pump–probe experiments.133 For both spectral densities, the relaxation obtained with modified Redfield theory is somewhat faster than the Redfield relaxation. This effect is due to the inclusion of multi-vibrational quanta transitions in modified Redfield theory.14,134 In this way, the protein can bridge the energy gaps between different exciton states by multiple vibrational quanta and not only by single quanta as in Redfield theory. Finally, we note that although the correlation in site energy fluctuations in the spectral density has a large amplitude, its influence on exciton relaxation was found to be negligible.51 The inhomogeneous charge distribution of the protein was found to be responsible for this effect.
and the experimental spectral density Jexp(ω) of the FMO protein (Fig. 4). f(ω) is introduced to correct for the limitations of the harmonic approximation. The larger amplitude of the high-frequency part of the corrected spectral density allows the protein to dissipate the excess energy of excitons faster (Fig. 6 and eqn (87)). The relaxation times obtained for the corrected spectral density are in agreement with pump–probe experiments.133 For both spectral densities, the relaxation obtained with modified Redfield theory is somewhat faster than the Redfield relaxation. This effect is due to the inclusion of multi-vibrational quanta transitions in modified Redfield theory.14,134 In this way, the protein can bridge the energy gaps between different exciton states by multiple vibrational quanta and not only by single quanta as in Redfield theory. Finally, we note that although the correlation in site energy fluctuations in the spectral density has a large amplitude, its influence on exciton relaxation was found to be negligible.51 The inhomogeneous charge distribution of the protein was found to be responsible for this effect.
