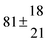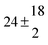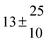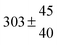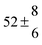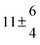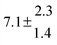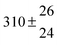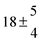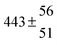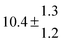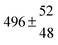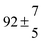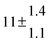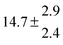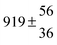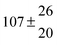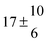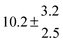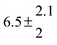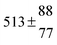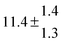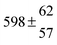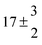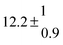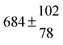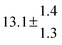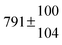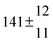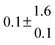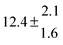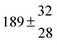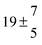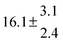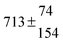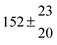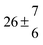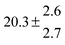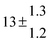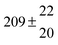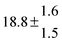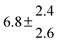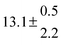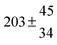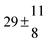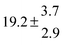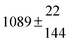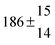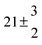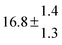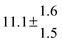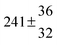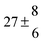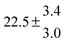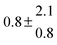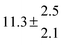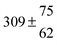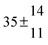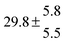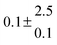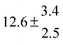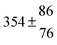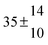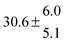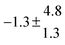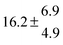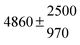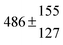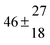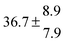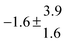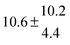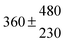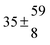Reversible addition of the OH radical to p-cymene in the gas phase: multiple adduct formation. Part 2
Received
13th May 2014
, Accepted 30th June 2014
First published on 3rd July 2014
Abstract
A flash photolysis-resonance fluorescence (FP-RF) system was used to study the p-cymene (PC) + OH reaction at temperatures between 299 and 349 K in helium. Triexponential functions were fitted to groups of observed OH decay curves according to a model considering a reversible addition to form two adducts as thermolabile reservoirs of OH. Compared to Part 1 of this paper, consideration of a second adduct strongly improved the fits to our measurements, and the rate constants for the major pathways were optimized between 299 and 349 K. The Arrhenius expression for the rate constant of the sum of OH addition and H-atom abstraction pathways was found to be kOH = 1.9 × 10−12 exp[(610 ± 210) K/T] cm3 s−1. Rate constants of unimolecular decomposition reactions of the adducts were similar to other aromatic compounds with the following Arrhenius expressions: 1 × 1012 exp[(−7600 ± 800) K/T] s−1 for adduct 1 and 4 × 1011 exp[(−8000 ± 300) K/T] s−1 for adduct 2. Adduct yields increased and decreased with temperature for adduct 1 and 2, respectively, but were similar (∼0.4) around room temperature. Equilibrium constants yielded values for reaction enthalpies and entropies of adduct formations. While for one adduct reasonable agreement was obtained with theoretical predictions, there were significant deviations for the other adduct. This indicates the presence of more than two adduct isomers that were not accounted for in the reaction model. Quantum chemical calculations (DFT M06-2X/6-31G(d,p)) and RRKM kinetics were employed with the aim of clarifying the mechanism of the OH addition to PC. These calculations show that formation of adducts with OH in ortho positions to the isopropyl and methyl substituents is predominant (55% and 24%) to those with OH in ipso positions (21% and 3%). A large fraction (>90%) of the ipso-C3H7 adduct is predicted to react by dealkylation forming p-cresol (in the absence of oxygen) and isopropyl radicals. These theoretical results agree well with the interpretation of the experimental results showing that the two ortho adducts (which appeared as OH reservoirs in the experiment) have been observed.
1. Introduction
Non methane volatile organic compounds (NMVOCs) are emitted into the atmosphere by anthropogenic and biogenic sources. It has been estimated that globally biogenic emissions significantly exceed anthropogenic emissions.1,2 NMVOCs play a major role in the photochemical formation of ozone and secondary organic aerosols, and both processes are initiated by OH radicals, NO3 radicals and O3 oxidation.3,4
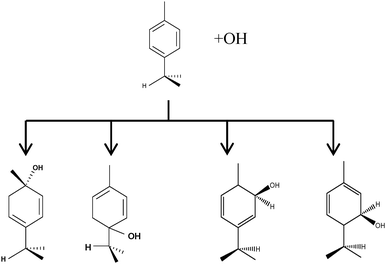
The biogenic aromatic compound p-cymene (1-methyl-4-isopropylbenzene or 4-isopropyltoluene) has four distinguishable positions where the OH radicals may add to the aromatic ring, as illustrated in Scheme 1: two equivalent ones ortho to the isopropyl group (PCortho–C3H7), two equivalent ones ortho to the methyl group (PCortho–CH3), and two non-equivalent ipso positions at the site of the methyl and the isopropyl group (PCipso–CH3 and PCipso–C3H7). Addition to an already occupied position (ipso-addition) is in general considered to be less important, but triexponential decays of OH have been observed by VUV flash photolysis/resonance fluorescence (FP-RF) in the presence of 1,3,5-trimethylbenzene, indicating that two different thermolabile adducts can regenerate OH.5 The observation of hexamethyl-2,4-cyclohexadienone by GC-MS as the only product from the reaction of OH with hexamethylbenzene in the presence of NO2 implies that an addition of OH is a major first step of this reaction.6 Biexponential FP-RF-decays of OH in the presence of hexamethylbenzene as a prototype molecule, where ipso positions alone are available for addition, demonstrated a reversible reaction,7 and the molecular ion of the adduct has been observed by single-photon VUV photoionization as an intermediate in a flow reactor very recently.8Ipso-type adducts may react by dealkylation and corresponding products from the reaction of toluene, o-, m-, and p-xylene with OH radicals have been observed by chemical ionization mass spectrometry in a flowtube study (5.4% phenol from toluene and similar yields of the cresols expected from dealkylation of the xylenes).9 However, these results are not in agreement with an earlier smog chamber result of a phenol yield <0.1% from OH + toluene10 and are not confirmed in a more recent smog chamber study with GC-FID analysis11 that stated an upper limit of <1% formation of each cresol from OH + m-xylene and <2% for each cresol isomer from OH + p-cymene.
 |
| | Scheme 1
p-Cymene + OH addition reactions, leading to the four adducts. From left to right: PCipso–CH3, PCipso–C3H7, PCortho–CH3 and PCortho–C3H7. | |
A total OH rate constant of (15.1 ± 4.1) × 10−12 cm3 s−1 was derived in a previous study on p-cymene12 in a smog chamber at room temperature and 1 atm pressure of air. In another work,11 the rate constant of H-atom abstraction was determined measuring the 4-methylacetophenone yield (the major product formed subsequent to the H-atom abstraction from the isopropyl substituent) and assuming a H-atom abstraction rate constant from the methyl substituent similar to the one determined for toluene. This led to an estimated 20 ± 4% contribution of abstraction to the overall OH rate constant. In our previous work,13 the p-cymene + OH reaction was studied over a wide temperature range assuming a single adduct formation (biexponential model). This simplification was found to be satisfactory for temperatures below 320 K and higher than about 350 K, but between these temperatures our applied model could not describe the data. A preliminary study of the OH decay curves in the intermediate temperature range revealed that triexponential functions led to better fits to groups of observed curves than biexponential ones, indicating that more than one adduct was being formed. A similar behaviour has been observed for 1,3,5-trimethylbenzene, for which a kinetic model was proposed and the system of differential equations was solved.5 In the present work we apply that new model of formation of two adducts (triexponential model) to the kinetic data previously13 obtained on p-cymene by the flash photolysis-resonance fluorescence (FP-RF) technique over the temperature range between 297 and 350 K in helium buffer gas and perform theoretical calculations in order to identify the adducts, their energies and transition states.
2. Experimental
The experimental setup used in this work has been described elsewhere.5,13–15 Briefly, OH radicals were generated by flash photolysis of water vapour using a Perkin Elmer FX 1165 short arc xenon flash lamp as photolytic light source at an energy of 540 mJ per flash. A quartz resonance lamp was mounted at right angles to the VUV photolysis beam and to the photomultiplier. A gas mixture of H2O–He was allowed to flow through the resonance lamp. The electrodeless microwave discharge dissociated H2O to produce electronically excited OH (A2Π). The radiation leaving the lamp was focused into the observation zone exciting the photolytically produced OH radicals in the reaction cell.
The fluorescence from the reaction cell passed through a 308 nm interference filter and was focused onto the photocathode of a photomultiplier tube (Thorn-EMI, 9789QB). The signal was processed and accumulated using the photon-counting technique with a discriminator and a multichannel scaler board (EG&G Ortec, model ACE MCS) at a dwell time of 0.98 ms, corresponding to a total of 4 s observation time after the flash. The concentration of water vapour in the reaction cell was kept constant at 1.5 × 1015 cm−3, leading to an estimated initial OH radical concentration of 2 × 1010 cm−3.16,17 The p-cymene concentration was varied between 5 × 1012 cm−3 and 43 × 1012 cm−3, which is high enough to assure pseudo first order conditions for OH. In contrast to our previous work,13 only experiments performed with the xenon flash lamp were used as the set made with the N2 spark discharge lamp seemed to be affected by impurities increasing the reactivity towards OH. The experimental conditions are summarized in Table 1. Differences between this table and Table 1 of the preceding part arise because some curves were removed from the biexponential fits. These curves were assumed to be deficient when the intensity ratio and lifetime of the first decay did not increase with increasing p-cymene concentration. The results presented in this work were obtained from all measurements as fits to individual decays were found to be difficult to perform at some combinations of temperature and p-cymene concentrations.
Table 1 Experimental conditions. Total pressure 203 ± 2 mbar of helium
| Set # |
T and ΔT/K |
N
|
[p-Cymene] (min., max.)/1012 cm−3 |
|
Number of measurements.
|
| 1 |
299.0 |
0.2 |
28 |
5.1 |
38.8 |
| 2 |
314.6 |
0.5 |
43 |
4.9 |
39.2 |
| 3 |
316.8 |
0.5 |
15 |
7.0 |
42.1 |
| 4 |
324.1 |
0.3 |
22 |
7.6 |
43.4 |
| 5 |
325.9 |
0.2 |
36 |
7.0 |
42.2 |
| 6 |
326.0 |
1.8 |
9 |
6.7 |
16.4 |
| 7 |
327.3 |
0.0 |
12 |
7.5 |
19.8 |
| 8 |
328.5 |
0.0 |
57 |
7.1 |
42.9 |
| 9 |
329.9 |
0.2 |
22 |
7.3 |
42.4 |
| 10 |
332.0 |
0.2 |
58 |
6.9 |
42.6 |
| 11 |
334.2 |
0.3 |
21 |
4.8 |
39.6 |
| 12 |
334.3 |
0.2 |
20 |
7.2 |
32.3 |
| 13 |
335.3 |
0.2 |
20 |
6.7 |
42.1 |
| 14 |
335.7 |
0.2 |
26 |
6.6 |
39.8 |
| 15 |
336.2 |
0.0 |
66 |
7.1 |
42.7 |
| 16 |
339.9 |
1.0 |
38 |
5.8 |
41.6 |
| 17 |
343.5 |
0.2 |
18 |
6.9 |
41.7 |
| 18 |
345.2 |
0.1 |
23 |
7.3 |
42.3 |
| 19 |
348.0 |
0.4 |
19 |
7.4 |
41.7 |
| 20 |
348.9 |
0.1 |
45 |
4.8 |
39.3 |
The gases used in this work had the following stated minimum purities: He (Rießner) – 99.996%; N2 (Linde) – 99.999%. Liquid p-cymene (Aldrich) had a stated minimum purity of 99%. Deionized water was doubly distilled by a quartz still.
3. Theoretical approach
The reaction of OH with p-cymene (PC) is complex due to the presence of two alkyl chains, isopropyl and methyl, which differentiates each site of the molecule with respect to OH attack. The aim of the theoretical calculations is to shed some light into this complex mechanism and help to interpret the experimental results by presenting a comprehensive theoretical investigation of the OH attack on p-cymene. No theoretical investigation of this type has been reported so far on this system.
3.1 Computational details
All calculations were performed using the GAUSSIAN 09 package.18 The geometries and energies were optimized using density functional theory (DFT) with the hybrid meta exchange–correlation functional M06-2X,19 coupled to the split valence basis set 6-31G(d,p). This highly nonlocal M06-2X functional developed by Zhao and Truhlar19 is well suited for structures and energetics, specifically for the determination of energy barriers. The unrestricted Hartree–Fock (UHF) formulation has been used since it is a convenient way to describe open-shell and bond-breaking processes. Its use is justified in our study because we did not observe any significant spin contamination for all the stationary points explored, the quantum average value 〈S2〉 of the square of the total spin operator remaining close to 0.75, i.e., the characteristic value for a doublet state. Full geometry optimization has been performed throughout. We have checked carefully that all the saddle points found are correctly connected to two minima and are characterized by the existence of only one negative eigenvalue of the Hessian matrix corresponding to an imaginary frequency in the normal-mode analysis.
Since one of our goals is the determination of branching ratios of all the reactive channels, Transition State Theory (TST) is a convenient tool to determine rate constants. In terms of activation free energy ΔG#, TST formula reads:
| | 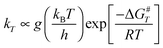 | (1) |
where
kB and
h are respectively the Boltzmann and Planck constants and
g is the number of equivalent carbon atom sites. Our aim in these calculations is not to obtain absolute values for the rate constants, but rather to look at the relative reactivity of each carbon atom site with respect to OH.
4. Experimental results and discussion
4.1 Kinetic analysis and data evaluation
As outlined above the reversible addition of OH radicals to the aromatic ring in p-cymene can occur at four different positions, leading to the formation of adducts with potentially different properties. The decay curves of OH can deliver first hints about the quantity of distinguishable adducts formed. The initial fast decay corresponds to the consumption of OH radicals by H-atom abstraction and OH addition, while the subsequent slower OH decays are caused by regeneration of OH by a unimolecular decomposition of unstable adducts. A biexponential OH decay indicates the formation of only one adduct or the formation of several adducts with similar kinetic properties, whereas a triexponential OH decay indicates the formation of at least two distinguishable adducts.
Decays curves of OH in the presence of p-cymene were found to be mostly biexponential at temperatures below around 320 K and at temperatures above about 350 K (Fig. 1).13 In the intermediate range deviations from biexponential behaviour were observed, and the following mechanism for the formation of two adduct species that results in triexponential decay curves was applied to fit the decay curves:5
| | | OH + p-cymene ↔ adduct1; k11a, k−11a | (R1) |
| | | OH + p-cymene ↔ adduct2; k12a, k−12a | (R2) |
| | | OH + p-cymene → products; k1b | (R3) |
The rate equations that describe the change in the concentrations of OH radicals and of the adducts are shown below.
| | 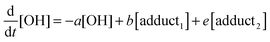 | (2) |
| | 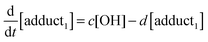 | (3) |
| | 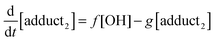 | (4) |
The combined first-order rate constants are given by:
| | | a = k2 + (k11a + k12a + k1b)[p-cymene] | (5) |
Bohn and Zetzsch5 proposed the mechanism shown above ((R1)–(R6)) for the reaction of the trimethylbenzenes with OH radicals and obtained the analytical solution of the corresponding system of differential equations. This solution allows us to determine the parameters a, bc, d, ef, and g for a set of measurements at a given temperature and total pressure. Details on the analytical solution and its limitations in terms of separable parameters are given elsewhere.5 Although up to four different adducts can be formed in the OH reaction studied here, we confined our reaction model to two adduct species for two reasons. Firstly, because analytical solutions are not available for a greater number of adducts. Secondly, because the precision of the OH decay curves is too poor to permit a proper distinction of three or even four exponentials (Fig. 1).
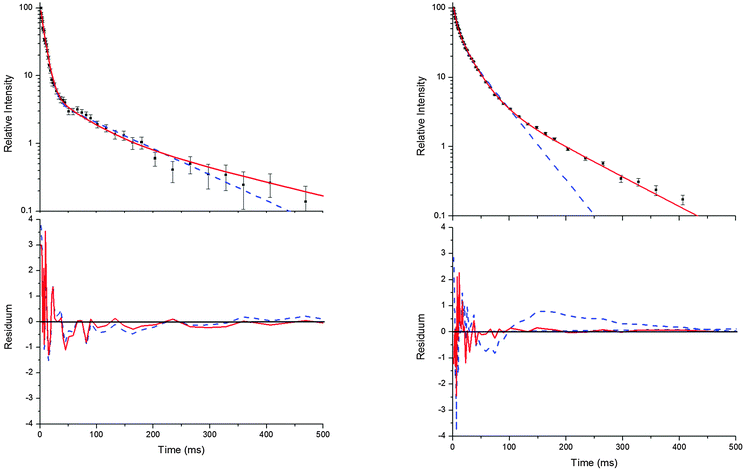 |
| | Fig. 1 Typical decay curves of OH (background subtracted), biexponential (blue dashed line) and triexponential (red solid line) model curves and fit residuals for measurements at 299 K (left side) and 330 K (right side) at a p-cymene concentration of 9 × 1012 cm−3 from simultaneous fits to a number (28 and 20 for the left and right side, respectively) of such curves at various concentrations. Obviously, the biexponential model curve satisfactorily describes the data at 299 K but not at 330 K while the triexponential model curves are applicable at both temperatures in agreement with the reaction model considering two adduct species ((R1)–(R6)). | |
Independent of the model applied, the approach has further limitations. If the decay time of the first exponential decay approaches the time resolution of our experiment (0.98 ms) fit results become distorted. Another limit is reached when the intensity ratio of the first and the second or third decay becomes too small. Then a small and quickly vanishing contribution of the first exponential remains, turning the decays into apparently bi- or monoexponentials. In this work, these limits were reached at temperatures larger than about 350 K and therefore higher temperatures were not considered.
Technical details on the fitting procedure and on the estimation of parameter uncertainties can be found elsewhere.5,13 Error estimates for the exponential term in the Arrhenius and van't Hoff expressions were obtained by fitting the maximum and minimum parameter values, respectively. Due to the small temperature range, errors in the pre-exponential factors were large and therefore will not be presented here. Table 2 summarizes the combined rate constants for each isothermal set of measurements.
| Set # |
k
2/s−1 |
k
11a + k12a + k1b/10−12 cm3 s−1 |
k
11a
k
−11a/10−12 cm3 s−2 |
k
−11a + k31/s−1 |
k
12a
k
−12a/10−12 cm3 s−2 |
k
−12a + k32/s−1 |
| 1 |
−9.9 ± 4.5 |
14.9 ± 0.9 |
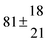
|
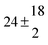
|
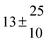
|
6 ± 0.2 |
| 2 |
2.3 ± 2.1 |
13.1 ± 0.8 |
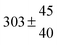
|
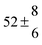
|
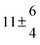
|
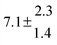
|
| 3 |
12.9 ± 1.9 |
12.7 ± 0.5 |
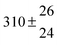
|
61 ± 5 |
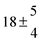
|
10.3 ± 1.5 |
| 4 |
5.7 ± 2.1 |
12 ± 0.7 |
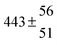
|
85 ± 7 |
15 ± 3 |
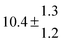
|
| 5 |
8.3 ± 1.8 |
11.9 ± 0.5 |
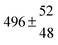
|
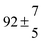
|
15 ± 3 |
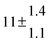
|
| 6 |
5.4 ± 4.4 |
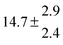
|
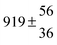
|
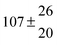
|
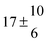
|
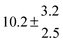
|
| 7 |
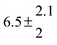
|
11.5 ± 0.7 |
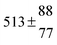
|
99 ± 10 |
15 ± 3 |
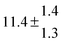
|
| 8 |
7 ± 1.4 |
11.8 ± 0.5 |
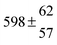
|
109 ± 7 |
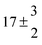
|
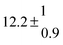
|
| 9 |
6.2 ± 0.1 |
11.7 ± 0.7 |
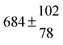
|
123 ± 10 |
18 ± 3 |
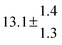
|
| 10 |
6.3 ± 1.2 |
11.7 ± 0.7 |
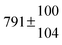
|
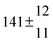
|
18 ± 2 |
13.9 ± 1.1 |
| 11 |
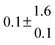
|
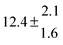
|
1255 ± 25 |
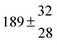
|
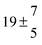
|
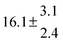
|
| 12 |
12.1 ± 1.8 |
10 ± 1 |
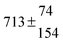
|
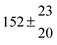
|
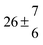
|
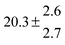
|
| 13 |
2.1 ± 1.3 |
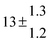
|
1387 ± 28 |
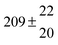
|
28 ± 4 |
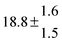
|
| 14 |
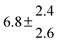
|
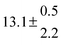
|
1541 ± 31 |
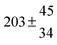
|
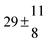
|
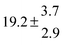
|
| 15 |
4.1 ± 1.1 |
11.7 ± 0.7 |
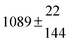
|
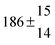
|
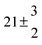
|
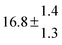
|
| 16 |
4.9 ± 1.7 |
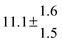
|
1450 ± 29 |
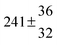
|
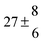
|
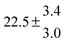
|
| 17 |
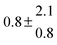
|
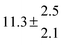
|
1854 ± 37 |
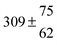
|
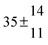
|
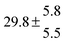
|
| 18 |
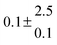
|
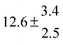
|
2520 ± 50 |
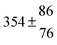
|
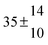
|
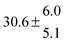
|
| 19 |
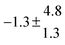
|
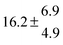
|
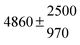
|
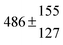
|
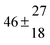
|
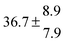
|
| 20 |
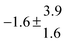
|
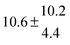
|
1847 ± 40 |
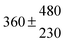
|
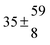
|
34.3 ± 19.4 |
4.2 Background losses of OH radicals (k2)
OH radicals may also react with minor impurities that can enter the cell from the dosing system (previous or present sample), the carrier gas or from wall desorption and leaks. Diffusion of OH radicals from the observation zone due to concentration gradient between the irradiated volume and the cell walls as well as transport due to the constant gas flow may contribute to the OH radical losses described by the rate constant k2. This rate constant comprised several processes, and therefore its complete understanding is complicated and related to the experimental conditions applied. In this work, the average loss rate constant was found to be 4 s−1 in good agreement with the experimental lifetime of OH radicals in our system without any reactant of about 3 s−1. In contrast to the previous paper, applying the triexponential model to our measurements, some k2 values were negative. This irregularity was found to have no effect on the determination of other combined rate constants, corroborated by the good agreement with other constants determined at similar temperatures.
4.3 OH + p-cymene (kOH = k11a + k12a + k1b)
Analogous to the biexponential model, the fitting procedure allows us to determine the total rate constant for the reaction between OH radicals and p-cymene, but not each rate constant individually. In the case of the triexponential model, the total rate constant consists of three rate constants: OH addition for the formation of adducts 1 (k11a) and 2 (k12a), and H-atom abstraction (k1b). The total rate constant was found to be (14.9 ± 0.9) × 10−12 cm3 s−1 at 299 K. This value is in good agreement with the value published by Corchnoy and Atkinson (15.1 ± 4.1) × 10−12 cm3 s−1.12 At temperatures up to around 320 K, biexponential13 and triexponential models show good agreement, but deviating results at higher temperatures where the fit quality for the biexponential model was also poor (Fig. 2). This behaviour was also observed for 1,3,5-trimethylbenzene,5 an aromatic compound which can react with OH radicals to form two different adducts alone.
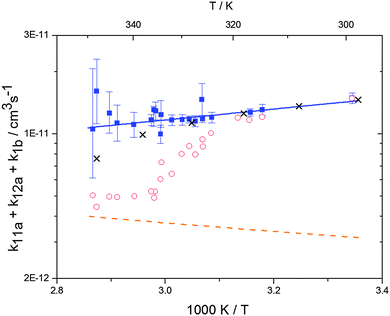 |
| | Fig. 2 Arrhenius plot of the total rate constant (k11a + k12a + k1b) for the reaction OH + p-cymene. The blue solid line shows the Arrhenius curve for the total rate constants from the triexponential model (blue squares). Red open circles show the results of the biexponential model.13 The orange dashed line shows the estimated H-atom abstraction for p-cymene.13 Exes show simulated results from a combined theoretical/experimental approach (Section 6). | |
The Arrhenius expression for the total rate constant was determined as kOH = 1.9 × 10−12 exp(610 ± 210) K/T cm3 s−1, comparable with the previously obtained for temperatures below 320 K.13
4.4 Forward and backward reactions (k11ak−11a; k12ak−12a)
The analytical solution of the differential equation system for the triexponential model does not allow us to separate the rate constants for the forward (k11a and k12a) and backward reactions (k−11a and k−12a), but allows us to determine their products (k11ak−11a and k12ak−12a).5 A semi-logarithmic plot of these products versus the inverse temperature (Fig. 3) was used to determine the sum of the activation energies for OH addition and unimolecular decay for each of the adducts.
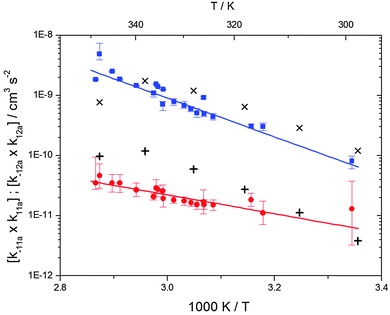 |
| | Fig. 3 Arrhenius plot for the product of the forward and backward reaction rate constants for the formation of adduct 1 (blue squares) and adduct 2 (red circles). Solid blue and red lines represent the Arrhenius curves for adduct 1 and 2, respectively. Exes and crosses show simulated results from a combined theoretical/experimental approach (Section 6) for adduct 1 and 2, respectively. | |
The product of the rate constants for the forward and backward reaction for both adducts increases with increasing temperature. Simple Arrhenius expressions of the form k = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−B/T) were fitted to the data at temperatures between 299 and 349 K resulting in k11ak−11a = 4 exp[(−7400 ± 550) K/T] cm3 s−2 for adduct 1 and k12ak−12a = 1.2 × 10−6 exp[(−3620 ± 1200) K/T] cm3 s−2 for adduct 2. The sums of activation energies of forward and backward reactions were calculated from the B parameters to be (62 ± 5) kJ mol−1 and (30 ± 10) kJ mol−1 for adduct 1 and 2 respectively.
exp(−B/T) were fitted to the data at temperatures between 299 and 349 K resulting in k11ak−11a = 4 exp[(−7400 ± 550) K/T] cm3 s−2 for adduct 1 and k12ak−12a = 1.2 × 10−6 exp[(−3620 ± 1200) K/T] cm3 s−2 for adduct 2. The sums of activation energies of forward and backward reactions were calculated from the B parameters to be (62 ± 5) kJ mol−1 and (30 ± 10) kJ mol−1 for adduct 1 and 2 respectively.
4.5 Unimolecular decay and background loss of the adducts (k−11a + k31; k−12a + k32) and adduct formation yields
Another combined rate constant that can be directly determined is the sum of the rate constants of unimolecular decay of the adducts back to the reactants and other products and of background losses by reactions with impurities. Possible perturbations by radical–radical reactions and diffusion processes have been already investigated.5 While the unimolecular decay of the adducts strongly depends on the temperature, background reactions are assumed to be constant in the studied temperature range. Adduct loss rate constants for each adduct were fitted between 299 and 350 K to a function of the form k = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−B/T) + C. However, in a first step optimized parameters C (Fig. 4) were determined using expressions for the adduct yields and OH budget considerations.
exp(−B/T) + C. However, in a first step optimized parameters C (Fig. 4) were determined using expressions for the adduct yields and OH budget considerations.
Adduct formation yields were determined using eqn (12)–(15). The rate constants k1b of H atom abstraction were taken from our previous work:13k1b = 2 × 10−17 (T/K)2 exp(170 K/T) cm3 s−1. At low temperatures, the denominators (d − k31) and (g − k32) are getting very small, making the obtained yields strongly dependent on k31 and k32. Optimized values (7.5 ± 3.2) and (4.1 ± 0.3) s−1 were determined for k31 and k32, respectively, that correspond to an average total yield of unity.
| | 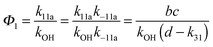 | (12) |
| | 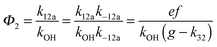 | (13) |
| | 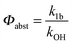 | (14) |
The various yields are shown in Fig. 5. The yields of adduct 1 and adduct 2 are similar at room temperature but then increase and decrease with temperature, respectively. Expectedly, the total adduct yield decreases with temperature because of an increasing yield of H-atom abstraction. Background loss rate constants were found to be in good agreement with those found in the literature for benzene,20,21 toluene,20,21p-xylene,22 1,3,5-TMB5 and hexamethylbenzene,16 ranging from 2 to 8 s−1 Using the optimized values of k31 and k32, Arrhenius expressions for the rate constants of unimolecular decompositions of the adducts were obtained: k−11a = 1 × 1012 exp[(−7600 ± 800) K/T] s−1 and k−12a = 3 × 1011 exp[(−8000 ± 300) K/T] s−1.
Activation energies for both adducts are very similar with values of 60 ± 7 and 67 ± 2 kJ mol−1 for adduct 1 and 2, respectively. These are rather similar to adducts formed from the OH radical addition to a non-occupied position as in the case of benzene (72 kJ mol−1).20Fig. 4 shows the adduct loss rate constants for both p-cymene adducts in comparison with hexamethylbenzene7 and both mesitylene5 adducts. The dissociation rate constants found for the p-cymene adducts are very similar to the ones corresponding to the mesitylene adducts where only two isomers, ipso and ortho, can be formed. Furthermore, adducts 2 of p-cymene and mesitylene have low dissociation rate constants that are comparable to those obtained for hexamethylbenzene16 where only ipso adducts are possible. The similarity of the activation energies of the adducts with the one of benzene, as well as the similarity of the dissociation rate constants of adduct 2 with the ones published for hexamethylbenzene make it very difficult to identify which adduct or group of adducts is responsible for the triexponential OH decays observed.
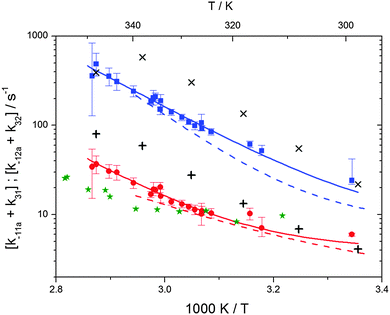 |
| | Fig. 4 Arrhenius plot for the sum of unimolecular and background loss rate constants for adduct 1 (blue squares) and adduct 2 (red circles), the hexamethylbenzene adduct (green asterisks).7 The blue and red dashed lines show the rate constants of the ortho and ipso adduct of 1,3,5-trimethylbenzene.5 Solid lines represent the modified Arrhenius curves for the adduct 1 and 2, respectively. Exes and crosses show simulated results from a combined theoretical/experimental approach (Section 6) for adduct 1 and 2, respectively. | |
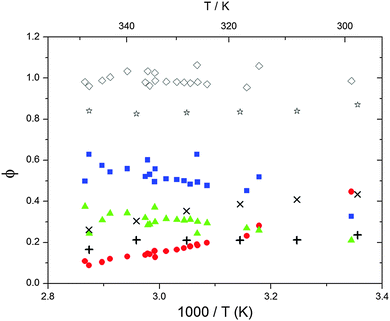 |
| | Fig. 5 Formation yields for adduct 1 (blue squares), adduct 2 (red circles) and H-atom abstraction (green triangles) after optimization of k31 and k32. Rhombi show the sum of the calculated yields. Exes, crosses and asterisks show simulated results of a combined theoretical/experimental approach (Section 6) for adduct 1 and 2, and their sum, respectively. | |
4.6 Equilibrium constants (Keq1, Keq2) and thermochemical data
A measure of the stability of the adducts is given by their equilibrium constants, Keq1, Keq2 (Fig. 6). These constants were estimated using eqn (16) and (17) with background losses (k31 and k32) determined in the previous section.| | 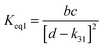 | (16) |
| | 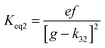 | (17) |
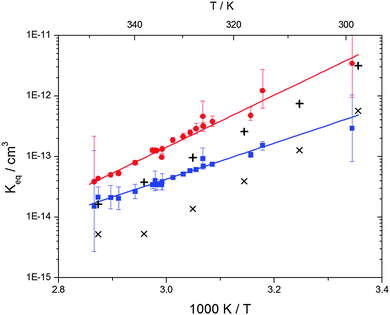 |
| | Fig. 6 Equilibrium constants for adduct 1 (blue squares) and adduct 2 (red circles). Solid lines represent the regression curves between 299 and 345 K (eqn (18) and (19)). Exes and crosses show the simulated results from a combined theoretical/experimental approach (Section 6) for adduct 1 and 2, respectively. | |
Equilibrium constants for both adducts are shown in Fig. 6 and can be expressed between 299 and 345 K by following equations:
| | | Keq1 = 6.2 × 10−26 (T/K) exp[(7150 ± 170) K/T] cm3 | (18) |
| | Keq2 = 2.3 × 10−29 (T/K) exp[(10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 ± 1200) K/T] cm3 200 ± 1200) K/T] cm3 | (19) |
Standard reaction enthalpies and entropies were determined for each adduct using a van't Hoff expression (20). The values obtained were: ΔH1 = (−59 ± 1) kJ mol−1, ΔS1 = (−64 ± 6) J mol−1 K−1 for the first and ΔH2 = (−85 ± 10) kJ mol−1, ΔS2 = (−130 ± 27) J mol−1 K−1 for the second adduct.
| | 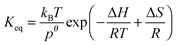 | (20) |
The reaction enthalpy of adduct 2 is in reasonable agreement with results for other OH aromatics adducts from the literature.23 However, the reaction enthalpy of adduct 1 is significantly smaller which is also in contradiction with theoretical predictions for different adduct isomers from other aromatics.24–28 Moreover, the reaction entropy of adduct 1 is clearly too small for an association reaction and should in any case be very similar for both adducts. These inconsistencies point towards a perturbation possibly caused by the presence of more than two adduct species.
In our previous work,13 the reduced χ2 was applied to reject the simpler model for the formation of one single adduct. The mechanism proposed in the present work strongly improves the fit quality. However, despite the huge improvements reached by the triexponential model, there are still some high χ2 values at temperatures between 330 and 340 K. These values might indicate the influence of further adduct species producing a departure from triexponential decays. To evaluate these deviations, OH decay curves with much higher precision would be needed as well as numerical tools to fit these curves but this is beyond our current capabilities.
5. Theoretical results
5.1 OH addition to p-cymene
As shown in Scheme 1, OH radical addition to the aromatic ring of p-cymene may form four isomers of p-cymene–OH adducts, two ipso isomers (PCipso–CH3 and PCipso–C3H7) and two ortho isomers (PCortho–CH3 or PCortho–C3H7). The correlation diagram between the relevant stationary states is illustrated in Fig. 7, and the corresponding zero-point corrected energies are gathered in Table 3. The pathways are initiated by the formation of the pre-reactive complex (PRC in Fig. 7) typical of electrophilic addition to aromatics29 which corresponds to a long range interaction between p-cymene and the OH radical and is common to each addition channel. In this structure, the radical OH is situated above the aromatic ring. This PRC lies 26 kJ mol−1 below the energy of the separated reactants. On the way from the PRC to TSadd, the C–O distance diminishes from 2.5 Å to ∼2.0 Å. It can be seen that the reactions are all exothermic by −85 kJ mol−1 in a narrow range of 5 kJ mol−1. The ΔE#0 barriers, called TSadd in a generic way, are also very close together in a range between −2.4 and +2.5 kJ mol−1. Such small values could suggest that the yields of ipso and ortho adducts are similar. In fact, the entropy change from the reactants to the TS is no more negligible and its value can be different from one pathway to the other. It is therefore essential to take into account the change of entropy in each pathway by calculating the Gibbs free energy barriers ΔG#T = ΔH#T − TΔS#T at temperature T. On the basis of the calculated ΔG#298 values, bimolecular OH-addition rate constants were calculated from eqn (1). The branching ratios ρadd are easily determined from the ratio of each rate constant channel over the total rate constant. All these data are collected in Table 3.
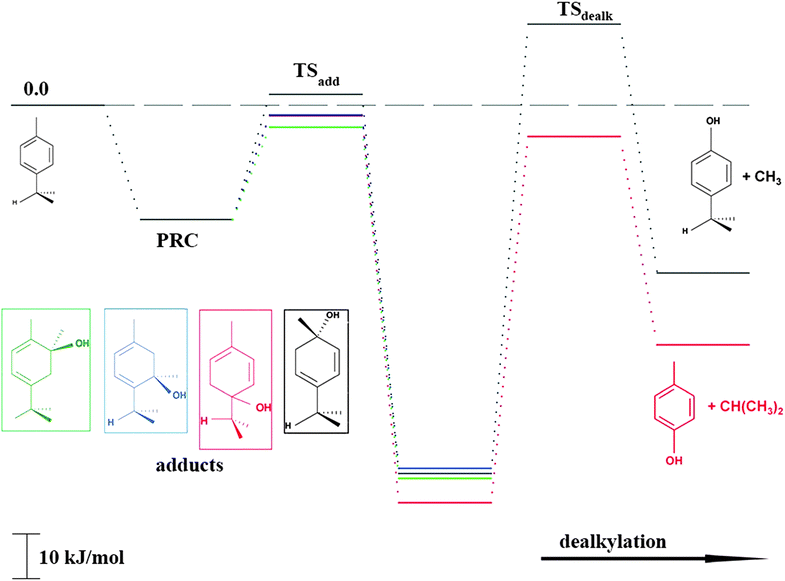 |
| | Fig. 7 Energy diagram for the addition reaction p-cymene + OH and successive dealkylation of the ipso adducts. | |
Table 3 M06-2X/6-31G(d,p) zero-point corrected energy barriers (ZPE), ΔE#0, activation enthalpies ΔH#298, activation entropies ΔS#298, free energy barriers, ΔG#298, and reaction energies, relative to the reactants p-cymene + OH,a and branching ratios, ρadd (i.e. the percentage of each addition site). The ZPE barrier for dealkylation ΔE#0 (TSdealk) and energy for cresol formation, ΔE0 (cresol formation). The energy of the pre-reactive complex, ΔE0 (PRC), is −25.9 kJ mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a,b
a,b
| |
ΔE#0 |
ΔH#298 |
ΔS#298 |
ΔG#298 |
ΔE0 adduct |
ρ
add (%) |
ΔE#0 TSdealk |
ΔE0 cresol formation |
|
Energies are given in kJ mol−1.
Entropies in J mol−1 K−1.
|
| PCipso–CH3 |
2.5 |
−1.9 |
−149.8 |
42.7 |
−83.6 |
3 |
18.4 |
−38.1 |
| PCipso–C3H7 |
−2.4 |
−6.6 |
−151.3 |
38.5 |
−90.3 |
18 |
−7.1 |
−52.3 |
| PCortho–CH3 |
−0.8 |
−5.1 |
−149.5 |
39.5 |
−84.7 |
24 |
|
|
| PCortho–C3H7 |
−2.2 |
−6.2 |
−146.3 |
37.4 |
−82.4 |
55 |
|
|
As a result of our calculations, it can be predicted that, among the four different addition possibilities: (i) the formation of the ipso-CH3 adduct can be neglected from the reaction mechanism (3% of the total addition); (ii) the formation of ortho adducts is predominant (79%); (iii) the ipso-C3H7 adduct is formed (by 18% of total addition) but can further dissociate, via dealkylation, to give new products. This is the subject of the following section.
5.2 Formation of cresol by dealkylation of ipso adducts
PCipso–C3H7 and PCipso–CH3 may dealkylate to form the phenol type compounds p-cresol + isopropyl radical (C3H7) and 4-isopropyl phenol + methyl radical (CH3). The calculated transition state and reaction energies for both of these decompositions are sketched in the right part of Fig. 7. The overall reaction energies OH + p-cymene, leading to the formation of 4-isopropyl phenol + CH3 or p-cresol + C3H7, are exothermic by −38 kJ mol−1 and −52 kJ mol−1.
The corresponding free energies of activation, ΔG#298 for 298 K, suggest that only the isopropyl departure from the ipso-C3H7 adduct can occur at room temperature, since the energy barrier is lower by −7 kJ mol−1 than the energy of the reactants p-cymene + OH. In order to test this assumption, we have performed some preliminary kinetic calculations on this dealkylation channel by using a statistical approach based on a Rice–Ramsperger–Kassel–Marcus-like (RRKM)30 methodology. Based on the potential energy profile obtained from DFT calculations, data presented in Table 3 was used for the kinetic analysis. For each of these stationary points, harmonic vibrational wavenumbers and the rotational constants calculated by the GAUSSIAN09 quantum chemistry program18 were used. Table 4 summarizes these results at two temperatures and two pressures.
Table 4 Kinetic calculations on the dealkylation channel from the ipso-C3H7 adducta
|
T/K |
P/mbar |
k
loss/10−13 cm3 s−1 |
k
prod/10−18 cm3 s−1 |
k
adduct/10−13 cm3 s−1 |
β
|
|
k
loss: disappearance of the reactants for this addition channel; kprod: immediate formation of products p-cresol + C3H7; kadduct: stabilization of the ipso adduct; β: rate of regeneration of the reactants OH and p-cymene from the adduct divided by the formation of products p-cresol + C3H7 from the adduct.
|
| 298 |
760 |
0.166 |
6.18 |
0.166 |
0.05 |
| 400 |
760 |
0.194 |
116 |
0.193 |
0.1 |
| 298 |
380 |
0.166 |
12.3 |
0.166 |
0.05 |
While there is no significant direct formation of cresol from OH + cymene, cresol is the main product of the unimolecular decomposition of the stabilized PCipso–C3H7 as indicated by the factor β. This finding is not in contradiction with product studies that showed no significant (<2%) cresol formation11 because in the presence of O2 cresol formation competes with the PCipso–C3H7 + O2 reaction that is expected to be much faster under atmospheric conditions. However, in the absence of O2, confirmation of cresol formation would be a strong indicator for the presence of the ipso adduct.
5.3 Results for reaction entropies, enthalpies and equilibrium constants
Reaction entropies ΔS298, reaction enthalpies ΔH298 and equilibrium constants Keq have been calculated for the addition reactions at 298 K and are collected in Table 5, together with the corresponding experimental results obtained in this work. Calculated enthalpies are in good agreement with literature data for different OH adduct isomers from other aromatics.23–28 As the ipso-CH3 contribution is minor, and the ipso-C3H7 is expected to mainly dealkylate to cresol, the two adducts that are theoretically expected to determine OH regeneration are the remaining ortho-CH3 and ortho-C3H7 adducts. Experimental entropy and enthalpy changes for adduct 1 are much smaller than those obtained from DFT calculations. This disagreement might arise from a wrongful application of the triexponential model to a system with three or four adducts, as mentioned in Section 4.6. Even though the obtained experimental enthalpy and entropy for adduct 2 are more comparable with the theoretical values, the experimental uncertainty does not allow to clearly identify this adduct. Nevertheless, the lower yields and greater equilibrium constants are closer to the predictions for the ortho-CH3 adduct. In order to make the theoretical and experimental results more comparable, numerical simulations were performed and will be presented in the following section.
Table 5 Calculated M06-2X/6-31G(d,p) reaction entropiesa ΔS298, reaction enthalpies, ΔH298, reaction free energies, ΔG298 at 298 K (relative to the reactants p-cymene + OHb) and calculated equilibrium constants, Keq(T) = kBT/p° exp[−ΔGT/RT] for the four theoretically possible adducts and experimental results for comparison
| |
ΔS298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
ΔH298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
ΔG298![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
K
eq
(298 K)/10−13 |
|
Entropies in J mol−1 K−1.
Energies in kJ mol−1.
K
eq in cm3.
This work (experimental).
|
| PCipso–CH3 |
−161.1 |
−89.2 |
−41.2 |
7.0 |
| PCipso–C3H7 |
−155.2 |
−95.3 |
−49.0 |
160 |
| PCortho–CH3 |
−154.0 |
−89.6 |
−43.7 |
19 |
| PCortho–C3H7 |
−163.2 |
−87.9 |
−39.3 |
3.2 |
|
|
| Adduct 1d |
−64 ± 6 |
−59 ± 1 |
−40 ± 1 |
4.9 |
| Adduct 2d |
−130 ± 27 |
−85 ± 10 |
−46 ± 2 |
50 |
6. Comparison of experimental and theoretical results using simulated OH decays
The theoretical results presented in the previous section predict the formation of all four possible adduct isomers. However, the relative yields and kinetic properties regarding back-decomposition and dealkylation are different for the different isomers. The question arises what results would be obtained from corresponding OH decay curves using the same data analysis that was applied for the experimental data of this work. To answer this question, OH decay curves were simulated by numerical calculations at a similar range of temperatures and reactant concentrations for direct comparison. For this purpose, a complete set of rate constants as a function of temperature is necessary.
We used the TST predicted adduct yields and the measured total rate constants of adduct formation (kadd) to make simulations and measurements more comparable. Values of kadd were obtained by subtracting the rate constants of abstraction k1b from the kOH obtained in this work:
using the Arrhenius expressions of
kOH and
k1b given in Sections 4.3 and 4.5. The total rate constant
kOH is considered to be a robust quantity that can be extracted from the experimental data without knowing the actual number of isomers formed. Using
eqn (1) and the Δ
H#298 and Δ
S#298 data (
Table 3), adduct yields
ρT were calculated for six temperatures in a range 298–348 K and scaled with the corresponding
kadd.
| | | kadd(i) = kadd × ρ(i) | (22) |
Here i stands for the different isomers and the resulting individual rate constants kadd(i) are listed in Table 6. It should be noted that the temperature dependencies of enthalpies and entropies are negligible (<1%) in the narrow range considered here. In a second step, the first-order rate constants of adduct dissociation back to OH + p-cymene, kcym(i) were determined from the equilibrium constants Keq obtained from the theoretically calculated ΔH298 and ΔS298 of the adduct formation reactions (Table 5).
| | | kcym(i) = kadd(i)/Keq(i) | (23) |
For the PCipso–C3H7 isomer also the rate constants of cresol formation were calculated from the estimated ratios β of rate constants of back-dissociation and cresol formation for this isomer (Table 4).
| | | kcresol(PCipso–C3H7) = kcym(PCipso–C3H7)/β | (24) |
In Table 7 the obtained first-order rate constants kcresol(PCipso–C3H7) and the kcym(i) for all isomers are listed. The rate constants in Tables 6 and 7 reveal that theoretically only a slight variation of adduct yields with temperature is expected. Moreover, the yield of PCipso–CH3 remains below 5% at all temperatures and the predicted main fate of PCipso–C3H7 is decomposition to cresol + C3H7.
Table 6
k
OH, k1b and individual rate constants of adduct formation kadd(i) of four adduct isomers at different temperatures. The kadd(i) were calculated from theoretically predicted isomer yields and the experimental total rate constant of adduct formation kadd = kOH − k1b
|
T/K |
k
OH/10−11 cm3 s−1 |
k
1b/10−12 cm3 s−1 |
k
add (PCipso–CH3)/10−12 cm3 s−1 |
k
add (PCipso–C3H7)/10−12 cm3 s−1 |
k
add (PCortho–CH3)/10−12 cm3 s−1 |
k
add (PCortho–C3H7)/10−12 cm3 s−1 |
| 298.0 |
1.47 |
3.14 |
0.380 (3%) |
2.06 (18%) |
2.78 (24%) |
6.35 (55%) |
| 308.0 |
1.38 |
3.29 |
0.362 |
1.84 |
2.54 |
5.73 |
| 318.0 |
1.29 |
3.45 |
0.344 |
1.65 |
2.32 |
5.16 |
| 328.0 |
1.22 |
3.61 |
0.326 |
1.48 |
2.12 |
4.66 |
| 338.0 |
1.15 |
3.78 |
0.307 |
1.33 |
1.93 |
4.20 |
| 348.0 |
1.10 |
3.95 |
0.289 (4%) |
1.19 (17%) |
1.76 (25%) |
3.78 (54%) |
Table 7 First-order rate constants of cresol + C3H7 formation from the PCipso–C3H7 isomer and individual rate constants of OH + p-cymene formation kcym(i) from all four OH adduct isomers at different temperatures. The kcym(i) were calculated from theoretically predicted equilibrium constants and the kadd(i) of Table 5. The ratios kcym/kcresol correspond to the theoretically predicted β (see Section 5.2)
|
T/K |
k
cresol (PCipso–C3H7)/s−1 |
k
cym (PCipso–CH3)/s−1 |
k
cym (PCipso–C3H7)/s−1 |
k
cym (PCortho–CH3)/s−1 |
k
cym (PCortho–C3H7)/s−1 |
| 298.0 |
2.56 |
0.545 |
0.128 |
1.48 |
19.8 |
| 308.0 |
7.06 |
1.62 |
0.387 |
4.24 |
54.6 |
| 318.0 |
18.1 |
4.46 |
1.08 |
11.3 |
141 |
| 328.0 |
43.8 |
11.5 |
2.83 |
28.0 |
339 |
| 338.0 |
99.5 |
27.6 |
6.93 |
65.6 |
769 |
| 348.0 |
214 |
62.7 |
16.0 |
145 |
1650 |
Based on the rate constants in Tables 6 and 7, OH decay curves were simulated numerically using FACSIMILE (MCPA Software Ltd., Oxfordshire, UK) assuming a realistic OH starting concentration of 1 × 1010 cm−3. Additional background loss rate constants of 3 s−1 for all adduct isomers and 10 s−1 for OH were also implemented to improve the comparability with experimental conditions. Decay curves were produced for five p-cymene concentrations in the range 0.8–4 × 1013 cm−3 as in the real experiments for the six temperatures under consideration. The obtained concentration profiles were then converted to count rates including background and finally to count numbers binned exactly as in the real experiments. Poisson random noise was added dependent on the count numbers and 150 single OH decay curves were accumulated to simulate the typical repetition of single shot experiments.
For each temperature simultaneous fits to the five decay curves at different p-cymene concentrations were then performed with the software tools developed for the experimental data. Fit results varied slightly when the procedure described in the last paragraph was repeated caused by the applied random noise. Experiment simulations and fits were therefore repeated 100 times to obtain mean values and standard deviations of fit parameters and fit qualities. The results are listed in Table 8 and shown as black symbols for direct comparison in Fig. 2–6.
Table 8 Mean fit results and fit qualities with standard deviations from the analysis of numerically calculated OH decay curves and simulated experiments with random noise. Parameters correspond to those in Table 2 but standard deviations were obtained from 100 simulated experiments for each set of OH decay curves
|
T/K |
k
2/s−1 |
k
11a + k12a + k1b/10−11 cm3 s−1 (=kOH) |
k
11a
k
−11a/10−10 cm3 s−2 |
k
12a
k
−12a/10−11 cm3 s−2 |
k
−11a + k31/s−1 |
k
−12a + k32/s−1 |
χ
2/DOF |
| 298.0 |
9.3 ± 1.1 |
1.464 ± 0.013 |
1.20 ± 0.02 |
0.38 ± 0.10 |
21.9 ± 0.6 |
4.1 ± 0.6 |
1.17 ± 0.10 |
| 308.0 |
8.9 ± 0.8 |
1.365 ± 0.014 |
2.91 ± 0.06 |
1.13 ± 0.07 |
55.1 ± 0.9 |
6.9 ± 0.3 |
1.12 ± 0.09 |
| 318.0 |
9.4 ± 0.7 |
1.258 ± 0.022 |
6.44 ± 0.28 |
2.73 ± 0.11 |
135.6 ± 3.3 |
13.3 ± 0.3 |
1.09 ± 0.09 |
| 328.0 |
10.1 ± 0.6 |
1.134 ± 0.034 |
12.0 ± 1.2 |
5.92 ± 0.21 |
303 ± 15 |
27.8 ± 0.6 |
1.07 ± 0.09 |
| 338.0 |
10.4 ± 0.8 |
0.996 ± 0.091 |
17.5 ± 7.1 |
11.8 ± 0.8 |
580 ± 110 |
59.0 ± 1.6 |
1.05 ± 0.08 |
| 348.0 |
11.2 ± 1.0 |
0.76 ± 0.11 |
7.7 ± 8.5 |
9.7 ± 8.5 |
390 ± 310 |
80 ± 38 |
1.04 ± 0.10 |
Previous applications of the method showed that simulations based on the pure two-adduct model ((R1)–(R6)) exactly returned the rate constants used for the numerical calculations. Moreover, in these cases the mean fit quality parameter χ2/DOF was unity.5 This is the expected ideal result when experimental uncertainties are known as for the simulations. A significant deviation from unity therefore indicates a departure of the mechanism from the two-adduct model. In the case discussed here there is merely a slight deviation which is hardly significant. Thus within the simulated uncertainties OH decay curves are effectively triexponential in agreement with the two-adduct model. The explanation of course is that two of the four adduct isomers that are formed play a minor role because either their yield is low (PCipso–CH3) or they mainly decompose to products other than OH (PCipso–C3H7).
While the OH background loss rate constant k2 is reproduced in all cases, with increasing temperature the fitted kOH tend to deviate from those applied in the simulations (Table 6). Note that this deviation is not accompanied by a decrease of fit quality, so there are compensating effects, and fit quality therefore is a necessary but not sufficient condition that a reaction model is correct. Moreover, in the presence of a fast decomposing adduct the range of useful temperatures for such an analysis is clearly limited as explained in Section 4.1. In the simulated measurements this limit is already reached around 340 K as is evident from the levelling off of adduct 1 rate constants at greater temperatures.
Expectedly, the parameters k11ak−11a and k12ak−12a roughly correspond to the products kadd(PCortho–C3H7) × kcym(PCortho–C3H7) and kadd(PCortho–CH3) × kcym(PCortho–CH3), respectively. And the parameters k−11a + k31 and k−12a + k32 more or less resemble kcym(PCortho–C3H7) + 3 s−1 and kcym(PCortho–CH3) + 3 s−1, respectively, but the agreement is not perfect showing that the influence of the two ipso-isomers is not completely negligible even at the lowest temperature. Nevertheless, the further analysis reveals that the two adduct approach is also sufficient to extract reasonable values of adduct yields (Fig. 5) and equilibrium constants (Fig. 6) of the two adducts.
Moreover, the decomposition of the PCipso–C3H7 to cresol can be recognized by the fact that only about 90% of kOH can be accounted for by k11a + k12a + k1b. However, no such missing yield was recognized in the experiments that show no evidence for any unaccounted loss of OH.
Regarding the thermodynamic data, reaction enthalpies of −90 kJ mol−1 (adduct 1) and −89 kJ mol−1 (adduct 2) were obtained considering a temperature range <340 K that compare very well with the data applied to calculate the rate constants: −88 kJ mol−1 (PCortho–C3H7) and −90 kJ mol−1 (PCortho–CH3). Reaction entropies are also in good agreement: −166 J mol−1 K−1 (adduct 1) and −146 J mol−1 K−1 (adduct 2) compared to −163 J mol−1 K−1 (PCortho–C3H7) and −154 J mol−1 K−1 (PCortho–CH3) listed in Table 5. For all fit parameters in Fig. 2–6 a qualitative agreement is obtained but differences are clearly outside experimental uncertainties. Because the accuracies of the experimental and the theoretical approach are hard to quantify we conclude that the experimental results are not inconsistent with the theoretical prediction that the two experimentally distinguished adducts are PCortho–C3H7 (adduct 1) and PCortho–CH3 (adduct 2).
7. Conclusions
The reaction p-cymene + OH was reinvestigated using a reaction model assuming formation of two adduct species. This model results in triexponential OH decay curves in the presence of p-cymene that can be evaluated to extract the rate constants of the underlying reaction model. Despite the fact that the reaction between p-cymene and OH radicals can form four different adducts (two ipso-type and two ortho-type adducts) observed OH decays fit to that model within experimental error. Good agreement with literature data was found for the rate constant of OH reaction at room temperature. In a temperature range been 299 and 349 K Arrhenius expressions for rate constants of the reaction model were obtained, as well as the yields of the supposed two adducts. Thermodynamic data were derived from temperature dependent equilibrium constants. For one adduct reasonable results were obtained but for the second adduct the reaction enthalpy and reaction entropy are not within expectations and probably influenced by the presence of further adduct species. DFT calculations were made that indeed predict the formation of all four possible adducts with different yields. A full set of thermodynamic data for all relevant reactions was obtained. The formation of the two ortho-adducts was found to be predominant while the ipso-adducts are either almost negligible (ipso-CH3) or react mostly by dealkylation rather than back-dissociation to OH and p-cymene (ipso-C3H7). This led to the conclusion that mainly the two ortho adducts were in equilibrium with OH and therefore detected in the experiments, resulting in triexponential OH decays. Finally, numerical simulations of OH decay curves were made using a combination of the theoretical results and measured OH rate constants. These decay curves were evaluated to quantify any departure from triexponential behavior and to reproduce the consequences of using the simplified reaction model. Results from these simulations show a qualitative agreement with experiments but differences are outside experimental uncertainties. The results from these simulations show a reasonable agreement with experimental results confirming the theoretical prediction that two distinguished adducts are PCortho–C3H7 (adduct 1) and PCortho–CH3 (adduct 2).
Acknowledgements
This work was supported by the Deutsche Forschungsgemeinschaft under grant ZE 792/6-1 and BO 1580/3-1, and by CNRS/INSU within the French-German CNRS-INSU/DFG bilateral program ATMOCHEM. We thank Rafal Strekowski (University of Provence) for the first, exploratory experiments with p-cymene and OH and the group of Roger Atkinson (University of California, Riverside) for the determination of the abstraction and dealkylation channels.
References
- S. D. Piccot, J. J. Watson and J. W. Jones, J. Geophys. Res.: Atmos., 1992, 97, 9897–9912 CrossRef CAS.
- A. Guenther, C. N. Hewitt, D. Erickson, R. Fall, C. Geron, T. Graedel, P. Harley, L. Klinger, M. Lerdau, W. A. McKay, T. Pierce, B. Scholes, R. Steinbrecher, R. Tallamraju, J. Taylor and P. Zimmerman, J. Geophys. Res., 1995, 100, 8873–8892 CrossRef CAS.
- R. Atkinson and J. Arey, Atmos. Environ., 2003, 37, 197–219 CrossRef.
-
J. G. Calvert, R. Atkinson, K.-H. Becker, R. M. Kamens, J. H. Seinfeld, T. J. Wallington and G. Yarwood, The Mechanisms of Atmospheric Oxidation of Aromatic Hydrocarbons, Oxford University Press, 2002 Search PubMed.
- B. Bohn and C. Zetzsch, Phys. Chem. Chem. Phys., 2012, 14, 13933–13948 RSC.
- T. Berndt and O. Böge, Int. J. Chem. Kinet., 2001, 33, 124–129 CrossRef CAS.
- J. von Buttlar, R. Koch, M. Siese and C. Zetzsch, Geophys. Res. Abstr., 2008, 10, EGU2008-A-10576 Search PubMed.
- J.-C. Loison, M.-T. Rayez, J.-C. Rayez, A. Gratien, P. Morajkar, C. Fittschen and E. Villenave, J. Phys. Chem. A, 2012, 116, 12189–12197 CrossRef CAS PubMed.
- J. Noda, R. Volkamer and M. J. Molina, J. Phys. Chem. A, 2009, 113, 9658–9666 CrossRef CAS PubMed.
- D. F. Smith, C. D. McIver and T. E. Kleindienst, J. Atmos. Chem., 1998, 30, 209–228 CrossRef CAS.
- S. M. Aschmann, J. Arey and R. Atkinson, Atmos. Environ., 2010, 44, 3970–3975 CrossRef CAS PubMed.
- S. B. Corchnoy and R. Atkinson, Environ. Sci. Technol., 1990, 24, 1497–1502 CrossRef CAS.
- P. Alarcon, R. Strekowski and C. Zetzsch, Phys. Chem. Chem. Phys., 2013, 15, 20105–20114 RSC.
- A. Wahner and C. Zetzsch, J. Phys. Chem., 1983, 87, 4945–4951 CrossRef CAS.
- R. Koch, R. Knispel, M. Elend, M. Siese and C. Zetzsch, Atmos. Chem. Phys., 2007, 7, 2057–2071 CrossRef CAS.
- S. Zhang, R. Strekowski, L. Bosland, A. Monod and C. Zetzsch, Phys. Chem. Chem. Phys., 2011, 13, 11671–11677 RSC.
- S. Zhang, R. S. Strekowski, L. Bosland, A. Monod and C. Zetzsch, Int. J. Chem. Kinet., 2011, 43, 547–556 CrossRef CAS.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.1, Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
- Y. Zhao and D. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- R. Knispel, R. Koch, M. Siese and C. Zetzsch, Ber. Bunsenges. Phys. Chem., 1990, 94, 1375–1379 CrossRef CAS.
-
R. Koch, Kinetische Untersuchung der Folgereaktionen der OH-Addukte von aromaten mit NO, NO2 und O2 mit simultaner Auswertung von Kurvenscharen, PhD dissertation, University of Hannover, 1992 Search PubMed.
-
R. Knispel, Reaktionen von OH-Radikalen mit Aromaten und Folgereaktionen entstandener OH-Addukte von Aromaten, PhD dissertation, University of Hannover, 1993 Search PubMed.
- R. A. Perry, R. Atkinson and J. N. Pitts, J. Phys. Chem., 1977, 81, 296–304 CrossRef CAS.
- V. H. Uc, I. García-Cruz, A. Hernández-Laguna and A. Vivier-Bunge, J. Phys. Chem. A, 2000, 104, 7847–7855 CrossRef CAS.
- I. Suh, D. Zhang, R. Zhang, L. T. Molina and M. J. Molina, Chem. Phys. Lett., 2002, 364, 454–462 CrossRef CAS.
- D. Johnson, S. Raoult, R. Lesclaux and L. N. Krasnoperov, J. Photochem. Photobiol., A, 2005, 176, 98–106 CrossRef CAS PubMed.
- J. Fan and R. Zhang, J. Phys. Chem. A, 2006, 110, 7728–7737 CrossRef CAS PubMed.
-
J. M. Andino and A. Vivier-Bunge, in Adv. Quantum. Chem., ed. E. G. Michael and S. J. Matthew, Academic Press, 2008, vol. 55, pp. 297–310 Search PubMed.
- I. V. Tokmakov and M. C. Lin, J. Phys. Chem. A, 2002, 106, 11309–11326 CrossRef CAS.
- M. R. Berman and M. C. Lin, J. Phys. Chem., 1983, 87, 3933–3942 CrossRef CAS.
|
| This journal is © the Owner Societies 2014 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article
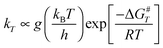
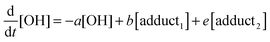
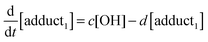
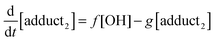


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−B/T) were fitted to the data at temperatures between 299 and 349 K resulting in k11ak−11a = 4 exp[(−7400 ± 550) K/T] cm3 s−2 for adduct 1 and k12ak−12a = 1.2 × 10−6 exp[(−3620 ± 1200) K/T] cm3 s−2 for adduct 2. The sums of activation energies of forward and backward reactions were calculated from the B parameters to be (62 ± 5) kJ mol−1 and (30 ± 10) kJ mol−1 for adduct 1 and 2 respectively.
exp(−B/T) were fitted to the data at temperatures between 299 and 349 K resulting in k11ak−11a = 4 exp[(−7400 ± 550) K/T] cm3 s−2 for adduct 1 and k12ak−12a = 1.2 × 10−6 exp[(−3620 ± 1200) K/T] cm3 s−2 for adduct 2. The sums of activation energies of forward and backward reactions were calculated from the B parameters to be (62 ± 5) kJ mol−1 and (30 ± 10) kJ mol−1 for adduct 1 and 2 respectively.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−B/T) + C. However, in a first step optimized parameters C (Fig. 4) were determined using expressions for the adduct yields and OH budget considerations.
exp(−B/T) + C. However, in a first step optimized parameters C (Fig. 4) were determined using expressions for the adduct yields and OH budget considerations.
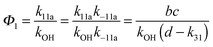
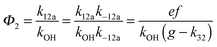
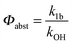

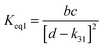
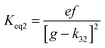

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 ± 1200) K/T] cm3
200 ± 1200) K/T] cm3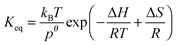

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a,b
a,b
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a
a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b
b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b
b