Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Intra-host π–π interactions in crown ether complexes revealed by cryogenic ion mobility-mass spectrometry†
Ryosuke
Ito
,
Keijiro
Ohshimo
 * and
Fuminori
Misaizu
* and
Fuminori
Misaizu
 *
*
Department of Chemistry, Graduate School of Science, Tohoku University, Sendai 980-8578, Japan. E-mail: ohshimo@tohoku.ac.jp; misaizu@tohoku.ac.jp
First published on 8th April 2024
Abstract
Cryogenic ion mobility-mass spectrometry was performed to investigate the relative abundance of conformers of dinaphtho-24-crown-8 (DN24C8) complexes with alkali metal cations M+ (M = Li, Na, K, Rb, and Cs). The “closed” conformers of M+(DN24C8) with short distances between two naphthalene rings in the crown ethers were predominantly observed for all complexes at 86 K. The two noncovalent interactions, host–guest and intra-host interactions, were analyzed separately by density functional theory calculations to reveal the origin of the stability of the closed conformers. As a result, it was revealed that the intra-host π–π interactions have a more critical role in determining the stability of the conformers than the host–guest interactions. The closed conformers of M+(DN24C8) also have wider regions of the π–π interactions than those of the M+(dibenzo-24-crown-8) complexes.
1. Introduction
Noncovalent interactions (NCIs) influence the conformation of a variety of molecules and the formation of supramolecular systems.1–4 For example, π–π interactions play an important role in stabilizing the higher-order structure of DNA double strands in addition to hydrogen bonding between nucleobases. Biomolecules are designed to exhibit a variety of functionalities through a skillful combination of weak interactions. The in-depth understanding of NCIs such as π–π interactions could therefore provide guidelines for designing molecules with biomolecular-like functionalities. The key to the functional expression of soft molecules composed of weak NCIs is their flexibility. The structures of the soft molecules fluctuate among several conformers using thermal energy. This flexibility in structures makes detailed analysis of their conformation difficult. Therefore, supramolecular structures are mainly studied by X-ray crystallography in the solid phase without structural fluctuations.5In recent years, gas-phase laser photodissociation spectroscopy has been actively performed to study the structures of cold supramolecular ions.6 In particular, the vibrational temperature of an isolated ion is lowered to ∼10 K by employing a cryogenic ion trap. This cryogenic technique allows us to observe vibrationally resolved sharp absorption spectra of supramolecules. However, complicated spectra are often obtained also at low temperatures due to the coexistence of multiple conformers of the flexible supramolecular ions. Therefore, it is still difficult to determine the structures and the abundance ratio of the conformers even from the cryogenic spectra in which the bands of the conformers are overlapped.
Host–guest complex is one of the simple models for a flexible supramolecule. Ion mobility-mass spectrometry (IM–MS) has been used to study conformers of host–guest complexes in the gas phase at room temperature.7–9 IM–MS is a powerful technique to separate conformers in the gas phase.7,10,11 Size- and conformer-selected absorption spectra of supramolecular ions can be obtained by the coupling of IM–MS with photodissociation spectroscopy.12–14 In the conventional drift-tube IM–MS, we measured the time distribution of the ions to pass through the drift tube (several milliseconds) and determined collision cross sections (CCSs) of the ions with a buffer gas. Conformations of the complex ions can be determined from the comparison between experimental and theoretical CCSs of the ions. Cryogenic IM–MS has also been performed using a drift tube cooled by liquid nitrogen.15–32
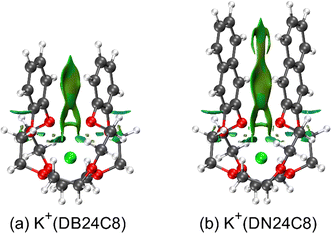
Crown ether complexes with metal ions are one of the most common host–guest compounds. The encapsulation structures of crown ether complexes in crystal forms were studied by X-ray diffraction.33–36 Nuclear magnetic resonance studies of structures of the conformations of the dibenzo-30-crown-10 (DB30C10) complexes with alkali metal ions, M (M = Na and K), M+(DB30C10), in solution also showed the same configuration of DB30C10 as that reported for the crystal.37,38 The conformation of the crown ether complexes in the gas phase was studied by ultraviolet photodissociation (UVPD)26,39–46 and IM–MS.8–10,26–30 Previously, we studied the conformations of M+(DB24C8) (M = Na, K, Rb, and Cs) using cryogenic IM–MS. The coexistence of two conformers, open and closed conformers, were confirmed in the study, which have long and short distances between the two benzene rings in a molecule, respectively.30 These conformers were also assigned by a UVPD spectrum of M+(DB24C8) at ∼10 K.46 For the closed conformer of K+(DB24C8), the relative orientation of the two benzene rings in the complex was found to be quite close to that of the benzene dimer. Therefore, this closed conformer was concluded to be highly stabilized by the strong π–π interaction between the benzene rings due to its special benzene dimer-like conformation.30
In the present study, we investigated the effect of enhancement of π–π interaction by expanding the aromatic rings in the complexes on the conformation and the stability of the complexes. The conformation of the complexes of alkali metal cations (Li+, Na+, K+, Rb+, and Cs+) with dinaphtho-24-crown-8 (DN24C8) shown in Fig. 1 was determined by combining the results of cryogenic IM–MS experiments at 86 K in the gas phase and quantum chemical calculations. The relative abundance ratio of the closed conformer of the M+(DN24C8) complexes was larger than that of the M+(DB24C8) complexes. The extraordinary stability of the closed conformers of the DN24C8 complexes was discussed based on a quantitative evaluation of the strength of intra-host π–π interactions between the two aromatic rings in the complexes.
2. Experimental and theoretical methods
2.1. Experimental methods
Details of the experimental setup were given elsewhere.30,31 M+(DN24C8) complex ions were generated by electrospray ionization. 0.1 mM alkali metal chlorides (LiCl, NaCl, KCl, RbCl, or CsCl) and DN24C8 were dissolved in methanol. The solution was delivered to a metal capillary at 2.0 μL min−1. High voltage (+2.6 kV) was applied between the metal capillary and a heated desolvation capillary (∼350 K). The entrance of an ion funnel was positioned close to the exit of the heated capillary. After focusing the ions by the funnel, ions were introduced into a quadrupole ion trap (QIT). Ions were accumulated for 40 ms in the QIT. To trap ions efficiently, helium gas was introduced to the QIT with 16 sccm. After accumulation, ions were injected into the cryogenic ion drift tube by a pulsed electric field at a given time (t = t0). The temperature and pressure of helium buffer gas in the drift tube were 86 K and 0.600 torr, respectively. A static electric field (E = 6.1 V cm−1) was applied in the drift tube for ion drifting. The E/N value was 9.0 Td under the above conditions (N is the number density of the buffer gas, 1 Td = 10−17 V cm2). Thus, the low-field condition (ca. E/N < 10 Td) was achieved in our experiments. After passing through the drift tube, the ions were transported to the acceleration region of the time-of-flight mass spectrometer (TOF-MS). The ions were accelerated to ∼4 keV by pulsed electric fields at a given time later from the pulse for the injection into the drift tube: t = t0 + Δt. The ions were detected by a microchannel plate of the TOF-MS. The delay time between the two pulses, Δt, was defined as “arrival time”. The drift velocity of the ions in the drift tube, vd, was calculated numerically from the measured arrival time. It is known that vd is proportional to E, and the proportional constant (K) is called ion mobility.47,48 The mobility K depends on the number density of the buffer gas N. To compare the mobility under different experimental conditions, the reduced mobility K0 is defined as K0 = K·(N/N0), where N0 is Loschmidt's number. From the Mason–Schamp equation, the reduced mobility K0 in the drift tube was given as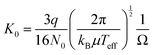 | (1) |
2.2. Computational methods
Density functional theory (DFT) calculations were performed to determine the structures of the M+(DN24C8) complex ions. The initial conformational search was performed by the CONFLEX 8 program with the MMFF94s force field.49,50 In total 20 conformers with relatively low steric energy on the CONFLEX were further optimized at the M05-2X/6-311++G(d,p) level with the Stuttgart RLC ECP for Rb and Cs atoms51–53 by the Gaussian 16 program.54 The vibrational analysis, zero-point energy correction, and natural population analysis were also performed at the same level. The theoretical CCSs of candidate structures of M+(DN24C8) obtained by DFT calculations were calculated by the trajectory method in the MOBCAL program.55 In the trajectory method, the Lennard–Jones parameters between constituent atoms of a complex ion and a He atom (εX–He and σX–He) are needed. In the present study, we used the previously reported εX–He and σX–He for X = C, H, and O.56 The values for X = Li, Na, K, Rb, and Cs were determined from calculations of X–He diatomic systems at the CCSD(T)/6-311+G(d,p) level with the Stuttgart RLC ECP for Rb and Cs atoms (εLi–He = 0.80165 meV, σLi–He = 1.7610 Å, εNa–He = 0.7511 meV, σNa–He = 2.1925 Å, εK–He = 0.5151 meV, σK–He = 2.6368 Å, εRb–He = 0.3224 meV, σRb–He = 2.9985 Å, εCs–He = 0.2982 meV, σCs–He = 3.1956 Å).30 Standard deviations of theoretical CCSs were less than ±0.7%.π–π interactions between the two aromatic rings in the M+(DB24C8) and M+(DN24C8) complexes were visualized by the NCI method57 in the Multiwfn program.58 The NCI method can identify the region where noncovalent interactions are working based on the values of the reduced density gradient (RDG) and the product of the sign of the second largest eigenvalue of electron density Hessian matrix and electron density (sign(λ2)·ρ). The extent of the π–π interactions can be distinguished from the fact that the RDG value is small (<0.5 in atomic units) and the sign(λ2)·ρ value is about zero. The strength of the π–π interactions was estimated by the domain analysis implemented in the Multiwfn program.
3. Results and discussion
3.1. Structure assignments of M+(DN24C8) from IM–MS measurements
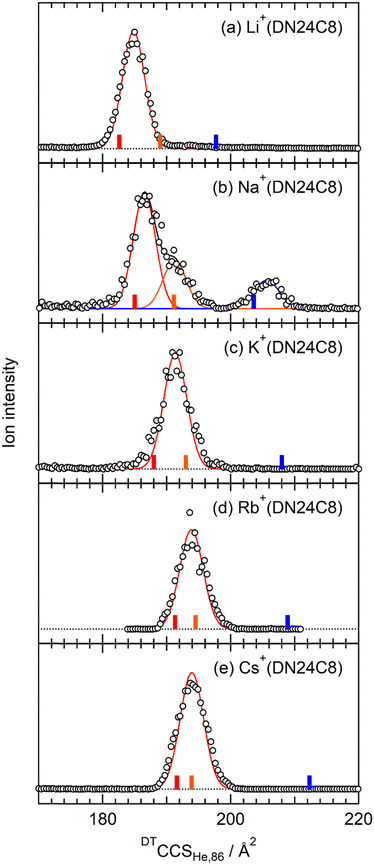
Fig. 2 shows CCS distributions of M+(DN24C8) (M = Li, Na, K, Rb, and Cs) complexes measured with He buffer gas at 86 K in the drift tube. For Na+(DN24C8), three Gaussian functions were necessary for the fittings (Fig. 2b). Therefore, at least three conformers with different CCSs coexist for this complex. For M+(DN24C8) (M = Li, K, Rb, and Cs), CCS distributions were fitted well with one Gaussian function (Fig. 2a and c–e). Structures of the most stable conformers are shown in Fig. 3. Experimental CCSs (DTCCSHe,86), relative intensities determined from the CCS distributions, theoretical CCSs, and relative Gibbs free energies (ΔG86) of the stable conformers are summarized in Table 1. In the most stable conformers of M+(DN24C8), the distance between the centers of the two naphthalene rings in the complexes (rc) was short. These conformers have the “closed” form of the DN24C8. For Na+(DN24C8), conformers with the second and third lowest relative Gibbs free energies have longer rc. Based on the conformation of DN24C8, we hereafter call the second and third stable conformers “closed′” and “open”, respectively.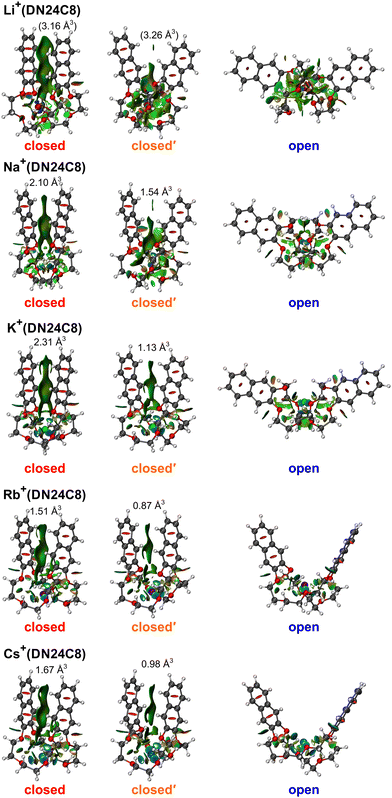 | ||
| Fig. 3 The most stable closed, closed′, and open conformers of M+(DN24C8) (M = Li, Na, K, Rb, and Cs) calculated at the M05-2X/6-311++G(d,p) level with the Stuttgart RLC ECP for Rb and Cs atoms. | ||
| Complexes | Experiments | Theory | |||
|---|---|---|---|---|---|
| DTCCSHe,86/Å2 | Relative intensity | CCS/Å2 | Conformers | ΔG86/kJ mol−1 | |
| Li+(DN24C8) | 184.3 ± 0.4 | 1 | 182.6 | closed | 0 |
| 189.0 | closed′ | 13.9 | |||
| 197.7 | open | 12.3 | |||
| Na+(DN24C8) | 186.4 ± 0.3 | 1 | 185.0 | closed | 0 |
| 191.7 ± 0.3 | 0.42 ± 0.08 | 191.1 | closed′ | 2.5 | |
| 205.4 ± 0.6 | 0.28 ± 0.14 | 203.6 | open | 4.0 | |
| K+(DN24C8) | 191.2 ± 0.3 | 1 | 188.0 | closed | 0 |
| 193.0 | closed′ | 13.8 | |||
| 208.0 | open | 12.8 | |||
| Rb+(DN24C8) | 194.0 ± 0.6 | 1 | 191.3 | closed | 0 |
| 194.5 | closed′ | 9.9 | |||
| 208.9 | open | 8.0 | |||
| Cs+(DN24C8) | 193.7 ± 0.3 | 1 | 191.6 | closed | 0 |
| 193.9 | closed′ | 9.2 | |||
| 212.3 | open | 6.2 | |||
The theoretical CCS of the closed conformer of Na+(DN24C8) (185.0 Å2) was close to the experimental CCS of the strong band (186.4 ± 0.3 Å2). The experimental CCS of the shoulder on the strong band (191.7 ± 0.3 Å2) was in good agreement with the theoretical CCS of the closed′ conformer (191.1 Å2). The larger CCS band had a relatively weak peak at 205.4 Å2. The theoretical CCS of the open conformer (203.6 Å2) was close to this peak. The closed′ and open conformers were less stable in Gibbs free energy than the closed conformer by 2.5 and 4.0 kJ mol−1, respectively. It is worth noting that the Gibbs free energies are sensitive to the DFT functional. For example, the relative free energy with respect to the most stable conformer at 86 K, ΔG86, is 4.0 kJ mol−1 for the open conformer of Na+(DN24C8) in the DFT calculations at the M05-2X/6-311++G(d,p) level as shown in Table 1, whereas it amounted to 15.3 kJ mol−1 at ωB97X-D/6-311++G(d,p). However, these energy differences were consistent with the order of relative ion intensity in the IM–MS regardless of the DFT functional.
For the M+(DN24C8) (M = Li, K, Rb, and Cs) complexes, only one band was observed in each CCS distribution (Fig. 2a and c–e). In the calculations, the most stable conformers of these complexes were the closed ones similar to the most stable structure of the Na+(DN24C8) complex. However, there are small differences in the relative orientations of the two naphthalene rings in the closed conformers of the complexes: the rings are slightly tilted outward in Li+(DN24C8) and Na+(DN24C8), nearly parallel in K+(DN24C8), and tilted inward in Rb+(DN24C8) and Cs+(DN24C8). The theoretical CCSs of the closed conformers were in good agreement with the experimental CCSs (∼190 Å2). The theoretical CCSs of the open conformers (∼210 Å2) were found to be much larger than the experimental CCS peaks. In addition, the open conformers were less stable in Gibbs free energy than the closed conformers by more than 6.2 kJ mol−1 at 86 K. This energy difference corresponded to the thermal abundance ratio of the open conformer being less than 0.02%. Since the closed′ conformers were as unstable as the open conformers in Gibbs free energy at 86 K, probably due to steric hindrance, the thermal abundance ratio of the closed′ conformers was lower than that of the open conformers. Thus, only the closed conformers were observed for M+(DN24C8) (M = Li, K, Rb, and Cs) unlike Na+(DN24C8).
3.2. Relative conformer stability analyzed by host–guest interactions
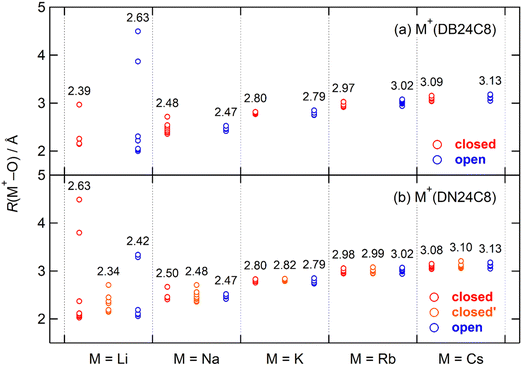
In our previous study on the DB24C8 complexes, the open conformers were strongly observed in M+(DB24C8) (M = Na, K, Rb, and Cs) in addition to the closed conformers.30 In contrast, the closed conformers were predominant for all five guest ions of the DN24C8 complexes in the present study. The M+(DB24C8) and M+(DN24C8) complexes are stabilized by strong host–guest interactions and relatively weak intra-host interactions. To show the differences in conformer stability between the M+(DB24C8) and the M+(DN24C8) complexes, host–guest and intra-host interactions were analyzed separately. In this section, we first analyze the host–guest interactions, which are governed by the positional relationships between the eight oxygen atoms and the guest M+ ions in the complexes. The lengths of the M+–O bonds, R(M+–O), in the most stable closed, closed′, and open conformers are plotted in Fig. 4. The R(M+–O) lengths showed surprisingly close trends in the DB24C8 and DN24C8 complexes in the figure. The lengths were hardly dependent on both the conformation (closed, closed′, or open) and the host molecule (DB24C8 or DN24C8) except for the Li+ complexes. For example, the average R(M+–O) for the closed conformer of Na+(DB24C8) was 2.48 Å. This value is very close to that of the open conformer of Na+(DB24C8) (2.47 Å) and the closed (2.50 Å), closed′ (2.48 Å), and open (2.47 Å) conformers of Na+(DN24C8). In contrast, the average R(M+–O) depended sensitively on the guest ions. The average R(M+–O) of the complexes have an order of Na+ (∼2.5 Å) < K+ (∼2.8 Å) < Rb+ (∼3.0 Å) < Cs+ (∼3.1 Å), which corresponds to the order of the ionic radii of the guest ions.59 In summary, the host–guest interactions are exerted to almost the same extent for the complexes with the same guest ions. Therefore, the differences in conformer stability between the DB24C8 and the DN24C8 complexes could not be explained from the host–guest interactions. In the next section, we analyze the intra-host interactions, especially the π–π interactions between the two aromatic rings.For Li+(DB24C8) and Li+(DN24C8), the R(M+–O) lengths took a wide range of values because the Li+ is too small to form an 8-coordination structure with the crown ethers. In the closed conformer of Li+(DN24C8), three oxygen atoms were located within 2.1 Å of the guest ion. However, in the open conformer there was only one oxygen atom within 2.1 Å of the guest ion, and there was no oxygen atom within 2.1 Å of the guest ion in the closed′ conformer. Only the closed conformer was observed for Li+(DN24C8), in part because these oxygen positions highly stabilize the closed conformer. Although the R(M+–O) (M = Na, K, Rb, and Cs) lengths were similarly distributed for each complex in Fig. 4, two oxygen atoms (overlapped) and one oxygen atom were located more than 0.15 Å far from the guest ion in the closed and closed′ conformers of Na+(DN24C8), respectively. These oxygen positions should destabilize the most stable closed and closed′ conformers, and consequently, the relative energies of the three (closed, closed′, and open) conformers become closer in this complex than in other complexes. At present, the reason why the closed′ and the open conformers of the Na+(DN24C8) were observed can thus be explained from the consideration of the R(M+–O) distributions.
3.3. Quantitative evaluation of intra-host π–π interactions
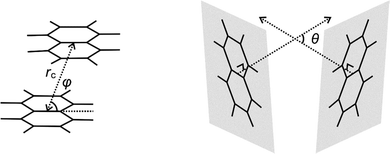
The intra-host π–π interactions between the two aromatic rings of the most stable closed conformers of M+(DN24C8) are evaluated in this section by extracting the relative orientations and distances between the two naphthalene rings in the complexes from the calculated structures. Three positional relationship parameters (rc, θ, φ) were defined similarly to the previous analysis of the DB24C8 complexes30 as shown in Fig. 5. The rc is the distance between the naphthalene ring centers, θ is the angle formed by normal vectors of the two naphthalene planes, and φ is the angle between the naphthalene plane and the central line. Table 2 summarizes the values of these parameters in the M+(DN24C8) complexes. For comparison, the parameters of parallel-displaced conformer of a naphthalene dimer (C10H8)2 obtained by ab initio calculation60 are also shown in Table 2. As a result, the relative positions of the naphthalene rings in K+(DN24C8) were found to be quite close to that of the naphthalene dimer. Therefore, this closed conformer was concluded to show extraordinary stability because of the strong π–π interaction between the naphthalene rings due to its special naphthalene dimer-like conformation. These results were nearly identical to those of the closed conformer of K+(DB24C8) becoming particularly stable due to the special orientation of benzene rings in the complex.30| Complexes | r c/Å | θ/deg. | φ/deg. |
|---|---|---|---|
| Li+(DN24C8) | 3.82 | 11.4 | 57.7, 67.6 |
| Na+(DN24C8) | 4.01 | 1.8 | 55.3 |
| K+(DN24C8) | 3.86 | 0.1 | 61.2 |
| Rb+(DN24C8) | 4.30 | 16.2 | 44.2, 60.2 |
| Cs+(DN24C8) | 4.25 | 16.3 | 45.3, 61.7 |
| Naphthalene dimer | 3.87 | 0 | 64.9 |
To visualize the π–π interaction between the two aromatic rings in the complexes, the NCI analysis was conducted. The RDG isosurfaces of the closed conformers of K+(DB24C8) and K+(DN24C8) are shown in Fig. 6. These surfaces were generated by evaluating the electron density calculated by DFT calculations and RDGs on cuboid grids with a 0.1 au step size. The green distribution indicates weak attractive interactions such as π–π interaction. In the closed conformers, π–π interactions work between the two aromatic rings as shown in Fig. 6. K+(DN24C8) had wider regions of π–π interactions than K+(DB24C8). Domain analysis was performed to confirm the difference in the size of the π–π interaction regions. The volume of the π–π interaction region between the two aromatic rings determined by the domain analysis in the Multiwfn program was 2.31 Å3 for K+(DN24C8), which was larger than that of K+(DB24C8) (1.44 Å3). Furthermore, the volume of the π–π interaction region for K+(DN24C8) was equivalent to 89% of that for the parallel-displaced naphthalene dimer (2.59 Å3). This large interaction volume means that the π–π interaction between the two naphthalene rings of K+(DN24C8) is comparable to the π–π interaction energy of a naphthalene dimer. These results suggest that the DN24C8 complexes are more stabilized than the DB24C8 complexes due to the large π–π interaction between the two aromatic rings in the complexes, supporting the experimental results that the closed conformers were predominantly observed in IM–MS.
4. Conclusions
We performed cryogenic ion mobility-mass spectrometry of the dinaphtho-24-crown-8 (DN24C8) complexes with alkali metal ions M+ (M = Li, Na, K, Rb, and Cs) to investigate the effect of π–π interaction in the complex on the relative abundance of the conformers. The “closed” conformer with short distance between two naphthalene rings in the complex was predominant in the distributions of collision cross sections of M+(DN24C8). For Na+(DN24C8), the “closed′” and the “open” conformers with longer naphthalene–naphthalene distance were also observed. The order of conformer stability is explained from the host–guest interactions and intra-host interactions. The attraction between oxygen atoms of the crown ether and the guest M+ ion was strongly dependent on the guest M+ ion and less dependent on the host molecule or the conformation. For the closed conformer of Na+(DN24C8), two oxygen atoms were located far from the Na+ ion, which destabilized the closed conformer and made the closed′ and the open conformers relatively stable. The intra-host attractive π–π interaction region between the two aromatic rings of the closed conformer was wider in M+(DN24C8) than in M+(DB24C8). The stability of the crown ether complex was revealed to be controlled by a balance of noncovalent interactions.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by JSPS KAKENHI (Grant No. JP16K05641 and JP21H05418), The Institute for Quantum Chemical Exploration, The Salt Science Research Foundation (Grant No. 1916, 2022, 2116), and JST, the establishment of university fellowships towards the creation of science technology innovation, Grant Number JPMJFS2102. The computation was performed using Research Center for Computational Science, Okazaki, Japan (Projects: 21-IMS-C054, 22-IMS-C054, 23-IMS-C048) and supercomputing resources at Cyberscience Center, Tohoku University.References
- J. L. Atwood, G. A. Koutsantonis and C. L. Raston, Nature, 1994, 368, 229 CrossRef CAS.
- C. K. McLaughlin, G. D. Hamblin and H. F. Sleiman, Chem. Soc. Rev., 2011, 40, 5647 RSC.
- N. C. Seeman, Annu. Rev. Biochem., 2010, 79, 65 CrossRef CAS PubMed.
- S. Zuluaga, P. Canepa, K. Tan, Y. J. Chabal and T. Thonhauser, J. Phys.: Condens. Matter, 2014, 26, 133002 CrossRef PubMed.
- T. Akutagawa, K. Shitagami, S. Nishihara, S. Takeda, T. Hasegawa, T. Nakamura, Y. Hosokoshi, K. Inoue, S. Ikeuchi, Y. Miyazaki and K. Saito, J. Am. Chem. Soc., 2005, 127, 4397 CrossRef CAS PubMed.
- T. Ebata and M. Fujii, Physical chemistry of cold gas-phase functional molecules and clusters, Springer, Singapore, 2019 Search PubMed.
- S. C. Henderson, S. J. Valentine, A. E. Counterman and D. E. Clemmer, Anal. Chem., 1999, 71, 291 CrossRef CAS PubMed.
- T. Wyttenbach, G. V. Helden, J. J. Batka, D. Carlat and M. T. Bowers, J. Am. Soc. Mass Spectrom., 1997, 8, 275 CrossRef CAS.
- T. Wyttenbach, G. von Helden and M. T. Bowers, Int. J. Mass Spectrom. Ion Processes, 1997, 165–166, 377 CrossRef.
- S. Lee, T. Wyttenbach, G. von Helden and M. T. Bowers, J. Am. Chem. Soc., 1995, 117, 10159 CrossRef CAS.
- J. N. Bull, M. S. Scholz, E. Carrascosa, G. da Silva and E. J. Bieske, Phys. Rev. Lett., 2018, 120, 223002 CrossRef CAS PubMed.
- J. Seo, S. Warnke, K. Pagel, M. T. Bowers and G. von Helden, Nat. Chem., 2017, 9, 1263 CrossRef CAS PubMed.
- S. Warnke, A. Ben Faleh and T. R. Rizzo, ACS Meas. Sci. Au, 2021, 1, 157 CrossRef CAS PubMed.
- W. Zagorec-Marks, L. G. Dodson, P. Weis, E. K. Schneider, M. M. Kappes and J. M. Weber, J. Am. Chem. Soc., 2021, 143, 17778 CrossRef CAS PubMed.
- H. Milloy and M. Elford, Int. J. Mass Spectrom. Ion Phys., 1975, 18, 21 CrossRef CAS.
- R. Johnsen, A. Chen and M. A. Biondi, J. Chem. Phys., 2008, 72, 3085 CrossRef.
- T. Koizumi, N. Kobayashi and Y. Kaneko, J. Phys. Soc. Jpn., 1980, 48, 1678 CrossRef CAS.
- F. Misaizu, N. Hori, H. Tanaka, K. Komatsu, A. Furuya and K. Ohno, Eur. Phys. J. D, 2009, 52, 59 CrossRef CAS.
- T. Wyttenbach, P. R. Kemper and M. T. Bowers, Int. J. Mass Spectrom., 2001, 212, 13 CrossRef CAS.
- J. C. May and D. H. Russell, J. Am. Soc. Mass Spectrom., 2011, 22, 1134 CrossRef CAS PubMed.
- K. A. Servage, J. A. Silveira, K. L. Fort and D. H. Russell, Acc. Chem. Res., 2016, 49, 1421 CrossRef CAS PubMed.
- J. Ujma, K. Giles, M. Morris and P. E. Barran, Anal. Chem., 2016, 88, 9469 CrossRef CAS PubMed.
- G. von Helden, T. Wyttenbach and M. T. Bowers, Int. J. Mass Spectrom. Ion Processes, 1995, 146–147, 349 CrossRef.
- J. Gidden and M. Bowers, Eur. Phys. J. D, 2002, 20, 409 CrossRef CAS.
- P. Weis, T. Bierweiler, E. Vollmer and M. M. Kappes, J. Chem. Phys., 2002, 117, 9293 CrossRef CAS.
- S. Tainaka, T. Ujihira, M. Kubo, M. Kida, D. Shimoyama, S. Muramatsu, M. Abe, T. Haino, T. Ebata, F. Misaizu, K. Ohshimo and Y. Inokuchi, J. Phys. Chem. A, 2020, 124, 9980 CrossRef CAS PubMed.
- K. Ohshimo, X. He, R. Ito and F. Misaizu, J. Phys. Chem. A, 2021, 125, 3718 CrossRef CAS PubMed.
- R. Ito, K. Ohshimo and F. Misaizu, Chem. Phys. Lett., 2022, 794, 139510 CrossRef CAS.
- R. Ito, X. He, K. Ohshimo and F. Misaizu, J. Phys. Chem. A, 2022, 126, 4359 CrossRef CAS PubMed.
- K. Ohshimo, X. He, R. Ito, K. Tsunoda, S. Tainaka and F. Misaizu, EPJ Tech. Instrum., 2023, 10, 11 CrossRef.
- K. Ohshimo, R. Sato and F. Misaizu, J. Phys. Chem. A, 2020, 124, 7999 CrossRef CAS PubMed.
- K. Ohshimo, R. Sato, Y. Takasaki, K. Tsunoda, R. Ito, M. Kanno and F. Misaizu, J. Phys. Chem. Lett., 2023, 14, 8281 CrossRef CAS PubMed.
- D. Bright and M. R. Truter, J. Chem. Soc. B, 1970, 1550 Search PubMed.
- M. A. Bush and M. R. Truter, J. Chem. Soc., Perkin Trans. 2, 1972, 345 RSC.
- M. A. Bush and M. R. Truter, J. Chem. Soc. D, 1970, 1439 RSC.
- M. A. Bush and M. R. Truter, J. Chem. Soc. B, 1971, 1440 RSC.
- D. Live and S. I. Chan, J. Am. Chem. Soc., 1976, 98, 3769 CrossRef CAS.
- M. Shamsipur and A. I. Popov, J. Am. Chem. Soc., 1979, 101, 4051 CrossRef CAS.
- C. M. Choi, H. J. Kim, J. H. Lee, W. J. Shin, T. O. Yoon, N. J. Kim and J. Heo, J. Phys. Chem. A, 2009, 113, 8343 CrossRef CAS PubMed.
- C. M. Choi, J. H. Lee, Y. H. Choi, H. J. Kim, N. J. Kim and J. Heo, J. Phys. Chem. A, 2010, 114, 11167 CrossRef CAS PubMed.
- Y. Inokuchi, O. V. Boyarkin, R. Kusaka, T. Haino, T. Ebata and T. R. Rizzo, J. Am. Chem. Soc., 2011, 133, 12256 CrossRef CAS PubMed.
- R. Kusaka, S. Kokubu, Y. Inokuchi, T. Haino and T. Ebata, Phys. Chem. Chem. Phys., 2011, 13, 6827 RSC.
- Y. Inokuchi, T. Ebata and T. R. Rizzo, J. Phys. Chem. A, 2018, 122, 3754 CrossRef CAS PubMed.
- M. Kida, M. Kubo, T. Ujihira, T. Ebata, M. Abe and Y. Inokuchi, ChemPhysChem, 2018, 19, 1331 CrossRef CAS PubMed.
- Y. Kitamura, S. Muramatsu, M. Kida, T. Ebata and Y. Inokuchi, J. Phys. Chem. A, 2019, 123, 9185 CrossRef CAS PubMed.
- M. Kida, T. Ujihira, M. Kubo, S. Muramatsu, T. Ebata and Y. Inokuchi, J. Phys. Chem. A, 2023, 127, 3210 CrossRef CAS PubMed.
- H. E. Revercomb and E. A. Mason, Anal. Chem., 1975, 47, 970 CrossRef CAS.
- V. Gabelica, A. A. Shvartsburg, C. Afonso, P. Barran, J. L. Benesch, C. Bleiholder, M. T. Bowers, A. Bilbao, M. F. Bush, J. L. Campbell, I. D. Campuzano, T. Causon, B. H. Clowers, C. S. Creaser, E. De Pauw, J. Far, F. Fernandez-Lima, J. C. Fjeldsted, K. Giles, M. Groessl, C. J. Hogan Jr, S. Hann, H. I. Kim, R. T. Kurulugama, J. C. May, J. A. McLean, K. Pagel, K. Richardson, M. E. Ridgeway, F. Rosu, F. Sobott, K. Thalassinos, S. J. Valentine and T. Wyttenbach, Mass Spectrom. Rev., 2019, 38, 291 CrossRef CAS PubMed.
- H. Goto and E. Osawa, J. Am. Chem. Soc., 1989, 111, 8950 CrossRef CAS.
- H. Gotō and E. Ōsawa, J. Chem. Soc., Perkin Trans. 2, 1993, 187 RSC.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814 CrossRef CAS PubMed.
- L. von Szentpály, P. Fuentealba, H. Preuss and H. Stoll, Chem. Phys. Lett., 1982, 93, 555 CrossRef.
- P. Fuentealba, H. Stoll, L. von Szentpaly, P. Schwerdtfeger and H. Preuss, J. Phys. B, 1983, 16, L323 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- M. F. Mesleh, J. M. Hunter, A. A. Shvartsburg, G. C. Schatz and M. F. Jarrold, J. Phys. Chem., 1996, 100, 16082 CrossRef CAS.
- I. Campuzano, M. F. Bush, C. V. Robinson, C. Beaumont, K. Richardson, H. Kim and H. I. Kim, Anal. Chem., 2012, 84, 1026 CrossRef CAS PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580 CrossRef CAS PubMed.
- R. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751 CrossRef.
- N. K. Lee, S. Park and S. K. Kim, J. Chem. Phys., 2002, 116, 7910 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Reduced density gradient isosurfaces and geometrical coordinates of conformers of M+(dinaphtho-24-crown-8) (M = Li, Na, K, Rb, and Cs) in Table 1. See DOI: https://doi.org/10.1039/d4cp00835a |
| This journal is © the Owner Societies 2024 |