Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Assignment of the methanol OH-stretch overtone spectrum using the pattern recognition method†
Alexis
Libert
 ab,
Anthony
Roucou
ac,
Brian
Hays
ad,
Robin
Glorieux
ab,
Anthony
Roucou
ac,
Brian
Hays
ad,
Robin
Glorieux
 a,
Séverine
Robert
a,
Séverine
Robert
 b,
Baptiste
Fabre
b,
Baptiste
Fabre
 e,
Samir
Kassi
f,
Xavier
Urbain
e,
Samir
Kassi
f,
Xavier
Urbain
 a and
Clément
Lauzin
a and
Clément
Lauzin
 *a
*a
aInstitute of Condensed Matter and Nanosciences, Université catholique de Louvain, B-1348 Louvain-la-Neuve, Belgium. E-mail: clement.lauzin@uclouvain.be
bRoyal Belgian Institute for Space Aeronomy, B-1180 Uccle, Belgium
cLaboratoire de Physico-Chimie de l'Atmosphère, Université du Littoral Côte d'Opale, UR4493, 189A Avenue Maurice Schumann, 59140 Dunkerque, France
dUniversité de Lille, CNRS, UMR 8523 – PhLAM – Physique des Lasers, Atomes et Molécules, F-59000 Lille, France
eUniversité de Bordeaux, CNRS, CEA, CELIA, UMR5107, F33405 Talence, France
fUniversité Grenoble Alpes, CNRS, LIPhy, Grenoble, France
First published on 30th May 2024
Abstract
We present the measurement and analysis of the 2OH stretching band of methanol between 7165 cm−1 and 7230 cm−1 cooled down to 26 ± 12 K in a buffer gas cooling experiment. Measurements were performed with a cavity ring-down spectrometer having a detection limit αmin = 2 × 10−10 cm−1. A total of 350 rovibrational transitions were assigned and 62 rovibrational transitions were tentatively assigned. This assignment was performed using the pattern recognition method developed by Rakvoský et al. [Phys. Chem. Chem. Phys., 2021, 23, 20193–20200]. In this work, we extended their method by using information on the relative intensities of the transitions to add one criterion to the validation of the assignments, allowing us to firmly assign 188 additional rovibrational transitions and to tentatively assign 14 more compared to the ir work.
1 Introduction
Methanol is an interesting molecule for various fields of physics, i.e. astro-,1 high-energy,2,3 and molecular physics.4,5 Due its relatively large dipole moment, this molecule can be observed in the microwave and millimeter ranges in a series of interstellar environments.6 Its spectral signature in the infrared range can also be used for remote sensing purposes.7 In particular it is one of the few molecules presenting several transitions which can be detected at cosmological distances on the order of a few gigalight-years. In addition, the observed transitions present a favorable sensitivity to any variation of the proton-to-electron mass ratio . This feature makes methanol a molecule of choice to probe any variation of this ratio over cosmological time scales.3,8
. This feature makes methanol a molecule of choice to probe any variation of this ratio over cosmological time scales.3,8
In terms of molecular and chemical physics, it is one of the smallest molecules presenting an internal rotation. It, therefore, has represented a reference system to study such phenomenon since the first part of the twentieth century.9–12 Notably, Xu et al. compiled all the experimental data up to 2008 to retrieve the most precise spectroscopic parameters of the ground vibrational state.13 Because of the increase in states density, the study of vibrational excited states of this molecule has always represented a challenge. In the early 90's, the OH stretching fundamental band of methanol was recorded with sub-Doppler resolution using a molecular-beam optothermal spectrometer to achieve a low effective rotational temperature of 6 K.14 A total of 350 transitions were assigned in that work and fitted using ground state combination differences calculated by a program15 based on the internal axis method described by Herbst et al.5 A standard deviation of 0.0013 cm−1 was obtained, being four times the experimental error (0.0003 cm−1). Boyarkin et al.16 and Rueda et al.17 have then performed a series of spectroscopic studies combining the selective approach of double resonance and the cooling of a supersonic expansion. This infrared laser assisted photofragment spectroscopy (IRLAPS) method appeared to be very efficient and allowed for building a global modeling of the vibrations of methanol. This work was done at relatively low resolution (0.05 cm−1) and only allowed for the assignment of a limited number of rovibrational transitions per vibrational band. They basically circumvented the complexity of the spectral signature through their experimental methodology. David S. Perry, a regular co-author of that series of works, also used a pulsed supersonic expansion combined with a continuous cavity ring-down spectroscopy to study the ν1 + ν3, i.e. OH + CH stretch combination band.18 On the order of 300 transitions were assigned from this work but the state-of-the-art effective Hamiltonians19,20 were unable to reproduce the line positions within the experimental accuracy, with an RMS value of ≃0.1 cm−1 compared with 1.4 × 10−3 cm−1 of experimental accuracy. In the overtone range, the 2ν1 band, i.e. 2OH stretching mode, at the center of this work has already been studied at high resolution by the group of Ondrej Votava.21,22 Experimentally, their spectrum was recorded using a pulsed slit expansion and double-pass laser diode absorption spectroscopy. The analysis of this spectral signature represents a challenge in itself with on the order of one thousand transitions over 60 cm−1. This band represents a formidable playground to test original approaches for spectroscopic assignment without the use of any modeling of the excited vibrational state. The group of Ondrej Votava followed this track and used first a two-temperature analysis (TTA), leading to the assignment of 15 transitions21 and then developed a generalization of the ground state combination differences technique, i.e. the pattern recognition method.22
In this work we have developed a state-of-the-art instrument to study the rovibrational spectral signature of complex molecules in the overtone range. The experiment, composed of a buffer gas cooling cell and a continuous wave cavity ring-down spectrometer, is briefly described in Section 2. In Section 3, a description of the pattern recognition method and its application to the 2OH stretching band spectrum of methanol are detailed, along with our innovative approach to assess whether or not the assignment is valid, which relies on the comparison of experimental and theoretically-evaluated relative intensities.
2 Experiment
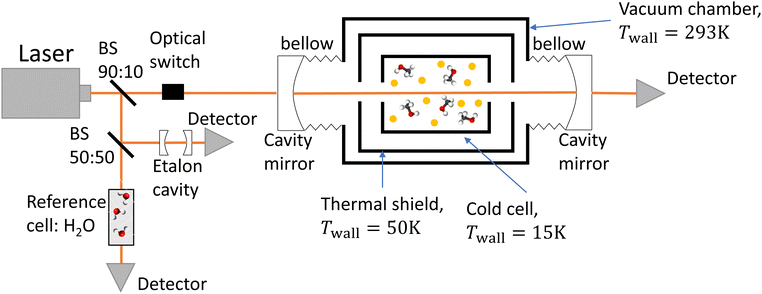
The experimental setup consists of a buffer gas cooling setup (BGC) and a continuous wave cavity ring-down spectrometer (cw-CRDS). The goal of the BGC is to cool down molecules to cryogenic temperatures while keeping them in the gaseous phase, allowing for the simplification of the measured spectrum due to a depopulation of the higher rotational states and a narrowing of the Doppler-broadened transitions.23–25 Molecules are then probed using a cw-CRDS measurement scheme. This technique allows for a high spectral resolution and a high sensitivity while being insensitive to fluctuations in intensity of the laser probing the gaseous sample.26,27 The setup is fully described in A. Libert's PhD manuscript (ref. 28).A schematic of the setup is shown in Fig. 1. Briefly, three distributed feedback (DFB) lasers covering the spectral range from 7160 cm−1 to 7235 cm−1 (models EP1398-DM-B, EP1392-DM-B and EP1388-DM-B from Eblana Photonics) are successively injected into an acousto-optic modulator (AOM) (model MGAS80-A1 from AA opto-electronics), their wavelength being swept by changing their temperature. The AOM allows for rapidly switching off the coupling between the DFB laser and the 1-meter long linear optical cavity in order to observe the light decay at the output of the cavity with an InGaAs photodiode. The two cavity mirrors (model 140989 from Layertec) exhibit a reflectivity higher than 99.995% at 7184 cm−1, leading to characteristic decay times longer than 120 μs. The cavity's finesse is estimated to 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, leading to 2.5 kHz wide cavity modes. We used a booster optical amplifier (BOA1410S from Thorlabs) to circumvent the poor coupling between the laser and cavity modes by increasing the number of photons by about a factor 10. About 90% of the laser light is injected inside the cavity. The remaining ten percent does not pass through the AOM. Instead, light is equally shared between a reference cell and an etalon cavity in order to precisely evaluate the emission wavelength of the DFB during the scan in temperature. The etalon cavity is composed of two 90
000, leading to 2.5 kHz wide cavity modes. We used a booster optical amplifier (BOA1410S from Thorlabs) to circumvent the poor coupling between the laser and cavity modes by increasing the number of photons by about a factor 10. About 90% of the laser light is injected inside the cavity. The remaining ten percent does not pass through the AOM. Instead, light is equally shared between a reference cell and an etalon cavity in order to precisely evaluate the emission wavelength of the DFB during the scan in temperature. The etalon cavity is composed of two 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 beamsplitters positioned on a 7.5 cm long tubular spacer, which is constructed from ultra-low expansion glass. This etalon is placed in a vacuum environment to achieve two objectives: thermal isolation and suppression of fluctuations in the refractive index of air caused by changes in pressure. These two factors can significantly affect the etalon's free spectral range (FSR). The interference pattern at the output of the etalon cavity consists in consecutive transmission peaks, each of them being separated by one FSR. The relative wavenumber grid is retrieved from the interference fringe pattern of the etalon. The reference cell consists of a vessel under vacuum with two viewports. Light has a single path inside the cell, efficiently interacting with water desorbing from the vessel walls. Absolute calibration was performed by fitting the relative wavenumber grid to 53 water transitions known with a precision better than 10−3 cm−1.29,30 The root mean square value of the residuals of the linear fit was equal to 9 × 10−4 cm−1. This value is used as the frequency tolerance criterion when looking for patterns in the molecular spectrum, as detailed in Section 3.1. The wavenumber axis is then shifted down by the excitation frequency of the AOM.
10 beamsplitters positioned on a 7.5 cm long tubular spacer, which is constructed from ultra-low expansion glass. This etalon is placed in a vacuum environment to achieve two objectives: thermal isolation and suppression of fluctuations in the refractive index of air caused by changes in pressure. These two factors can significantly affect the etalon's free spectral range (FSR). The interference pattern at the output of the etalon cavity consists in consecutive transmission peaks, each of them being separated by one FSR. The relative wavenumber grid is retrieved from the interference fringe pattern of the etalon. The reference cell consists of a vessel under vacuum with two viewports. Light has a single path inside the cell, efficiently interacting with water desorbing from the vessel walls. Absolute calibration was performed by fitting the relative wavenumber grid to 53 water transitions known with a precision better than 10−3 cm−1.29,30 The root mean square value of the residuals of the linear fit was equal to 9 × 10−4 cm−1. This value is used as the frequency tolerance criterion when looking for patterns in the molecular spectrum, as detailed in Section 3.1. The wavenumber axis is then shifted down by the excitation frequency of the AOM.
In the process known as beam injection,31 a small flow of methanol was introduced ballistically inside the cold cell by passing it through a hole in its lid, using helium as a carrier gas. The rotational temperature was evaluated using a two-temperature analysis,21,28,32 utilising the twelve transitions that were unambiguously assigned by Svoboda et al.21 as a reference. The rotational temperature was estimated to be 26 ± 12 K. The translational temperature of methanol was evaluated to 28 ± 4 K by assuming that the only contribution to the line broadening of these twelve methanol transitions is the Doppler effect.
A Labview program, originally developed for the FANTASIO setup33,34 manages the wavenumber scan of the DFB lasers and the simultaneous measurements of the light at the output of the etalon cavity and at the output of the reference cell, and the decay times of light leaking from the CRDS cavity. For the latter, once the intensity on the detector placed at the output of the cavity exceeds a threshold value, the AOM is turned off and the software records the light decay, it then performs the exponential decay fit to finally retrieve the absorption coefficient from the characteristic decay time. For a given spectral element, several decays are recorded and averaged. The cavity length is swept back-and-forth by moving the end mirror with a piezoelectric actuator to ensure that coupling between the laser and the cavity occurs periodically. After a proper calibration, the absorption coefficient with respect to the wavenumber is known. The absorption coefficient actually consists of the molecular fingerprint superimposed on a slowly varying baseline, i.e. the empty-cavity response. The contribution of the latter is evaluated using a weighted penalized least squares method, also known as the Whittaker algorithm.35–37 It is then subtracted, as suggested by Didriche et al.,33 using the following relationship:
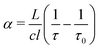 | (1) |
3 Results and discussion
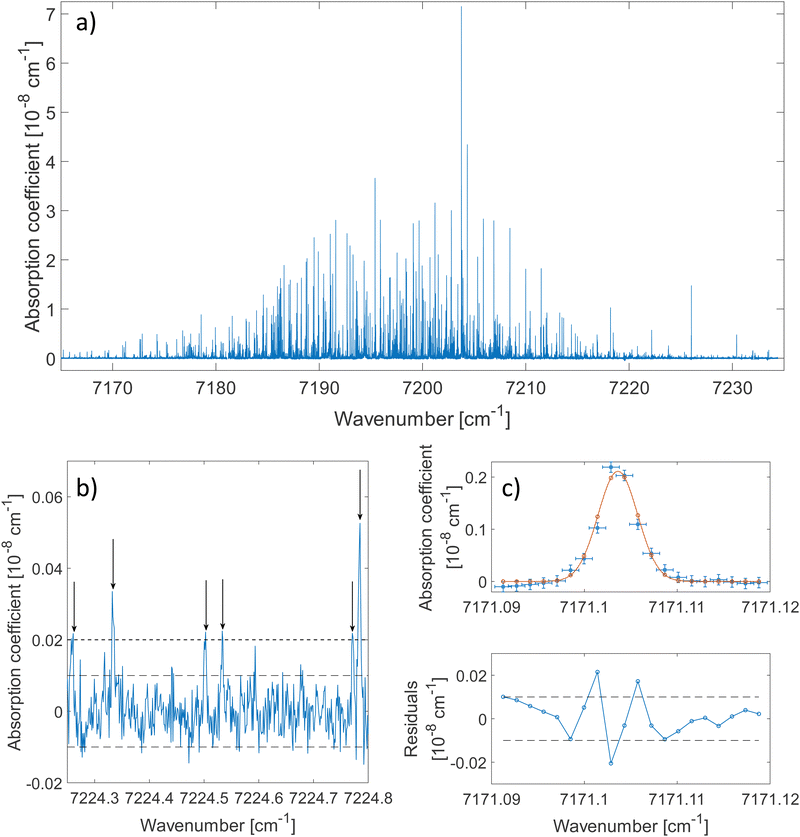
The 2ν1 band of methanol that was measured between 7160 cm−1 and 7235 cm−1 is shown in Fig. 2(a). About 80 ringdowns per spectral element were averaged to record this spectrum. A zoomed-in view on a 0.5 cm−1 wide spectral range is depicted in Fig. 2(b). The latter illustrates the complexity of the dense methanol molecular fingerprint and the high dynamic range of the measurement, with peaks covering 3 orders of magnitude in terms of intensity. More than 2500 transitions are spread over the spectral region of the measurement with up to 70 resolved transitions per cm−1. Under these conditions and because of the failure of traditional molecular Hamiltonians to treat floppy molecular systems in the overtone range,18,38 alternatives to traditional assignment methods are required. The method developed by Rakvoský et al.22 consists in seeking for patterns in the peaks positions. This method is detailed in Section 3.1, along with its application to methanol.The fit of an isolated transition is given in Fig. 2(c). The discrepancies plotted in the residuals panel are assigned to the presence of warmer methanol molecules within the cell. A more detailed analysis of the lineshape of molecular transitions in our buffer gas cooled environment can be found in ref. 28.
3.1. Pattern recognition method
In molecular spectroscopy, the ground state combination differences (GSCD) method is a commonly employed technique for the assignment of molecular spectra. This method relies on the fact that two transitions terminating in a same upper state are separated by the energy difference between the two lower states involved in these transitions. Rakovský et al.22 extended the GSCD method by looking for all the allowed transitions that lead to a same upper state. These lower energy states form a group, called combination difference multiplet (CDM). Each upper rotational state possesses a unique CDM, determined by applying the selection rules for allowed transitions. Assignment of the rovibrational transitions then consists in the recognition of the CDM patterns in the molecular spectrum, as illustrated in Fig. 3. All the transitions belonging to a given CDM are spaced in the molecular spectral signature by the differences in energy of their lower energy states.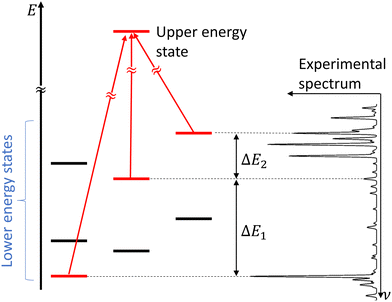 | ||
| Fig. 3 Concept of combination difference multiplet and its application to the assignment of molecular spectra. Figure adapted from Rakvoský et al.22 | ||
Methanol is an asymmetric top molecule containing six atoms with ground rotational constants A = 4.254 cm−1, B = 0.824 cm−1 and C = 0.793 cm−1.13 The near prolate character of this molecule can be illustrated by Ray's asymmetry parameter, κ = (2B − A − C)/(A − C) = −0.982, very close to κ = −1, the limiting case of a prolate symmetric top rotor. Methanol is the smallest covalently bonded molecule exhibiting an internal rotation. The three equivalent minima of the molecule39 and the relatively low barrier to internal rotation give rise to two tunnelling components noted A and E, where E is doubly degenerate. The spin statistical weights of these components are 4 and 2 respectively.40 The CDMs were generated, for A and E components, using the selection rules given below,5,22 where the ± indicates the sign in the following linear combination of basis vectors |JKM〉 ± |J − KM〉 for K ≠ 0:
• For A component (K ≥ 0):
| ± ↔ ∓, ΔJ = 0, |ΔK| = 0,1 | (2) |
| ± ↔ ±, |ΔJ| = 1, |ΔK| = 0,1. | (3) |
• For E component:
| ΔJ = 0, |ΔK| = 1 | (4) |
| |ΔJ| = 1, |ΔK| = 0,1. | (5) |
In these equations, J is the angular momentum number and K is the projection of J along the principal symmetry axis. As one can see from these selection rules, the 2ν1 mixed band character (parallel and perpendicular) of methanol allows for having up to nine transitions reaching the same upper level. This provides a significant decrease of fortuitous match in the pattern detection, as explained by Rakvoský et al.22
The lower state energy levels used for the generation of the CDMs were extracted from the work done by Xu et al.13 Their spectral analysis included 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 far-infrared transitions and 5600 rotational transitions in the subTHz range for 119 parameters, allowing for producing a fit with an uncertainty of 150 kHz for the vt = 0 torsional state. Although the output file of the fit was accessible from Appendix A of the publication, it was necessary to re-evaluate the energy levels to get a list of the rotational energy levels in the torsional states up to J = 10 with sufficient decimals.
000 far-infrared transitions and 5600 rotational transitions in the subTHz range for 119 parameters, allowing for producing a fit with an uncertainty of 150 kHz for the vt = 0 torsional state. Although the output file of the fit was accessible from Appendix A of the publication, it was necessary to re-evaluate the energy levels to get a list of the rotational energy levels in the torsional states up to J = 10 with sufficient decimals.
The CDMs were generated using the selection rules and looked for in the peak list from Section 2 in order to assign the transitions. Due to the density of peaks and to the experimental accuracy, this method leads to a relatively important set of fortuitous detections, as discussed in ref. 22. To circumvent this issue, they suggested to display the upper energies associated with the CDMs in a reduced energy plot with respect to J′, (where ′ denotes the upper state) for a given tunneling component (A or E) and for a given K′ value, the reduced energy being defined as:
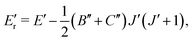 | (6) |
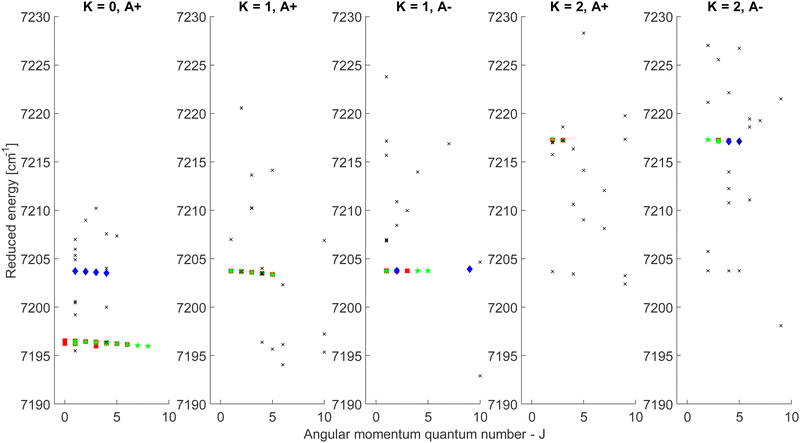 | ||
| Fig. 4 Reduced energy plot of the A component of methanol. Black crosses are rejected CDMs, blue diamonds are tentative assignments and green stars are validated assignments. The red squares correspond to the CDMs previously detected by Rakvoský et al.22 | ||
Because of the increased sensitivity of CRDS, the molecular fingerprint we measured contains about 2.5 times more peaks than the molecular spectrum recorded by Rakvoský et al.22 Under such conditions, the reduced energy plots look like clouds of scattered data and the chance of false identification of progressions in J′ in the reduced energy plots increases. Another criterion is therefore required to separate “the wheat from the chaff”. We suggest using information on the intensities of the transitions as a second feature for distinguishing between fortuitous and confirmed assignments. While the experimental intensities, i.e. the area under the peaks, can be easily evaluated using the results from the fitting of the spectrum, a model is needed to compute the theoretical ones. Evaluation of the theoretical intensities is detailed in Section 3.2.
3.2. Evaluation of the relative intensities
Information on the relative intensities of the transitions belonging to a given CDM can be used as a way to distinguish between the correct assignments and fortuitous ones. On one side, the integrated absorption coefficient can be evaluated experimentally by evaluating the area under the peaks, i.e. the transitions, in the experimental spectrum measured with the CRDS setup. On the other side, a theoretical integrated absorption coefficient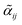 can be estimated using the following expression:41,42
can be estimated using the following expression:41,42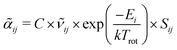 | (7) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ij is the wavenumber of the transition, Ei is the energy of the lower energy state involved in the transition and expressed in cm−1, k is the Boltzmann constant in wavenumber per Kelvin, Trot is the rotational temperature and Sij the line strength. The constant value C is common to all transitions within a CDM and since we are interested in relative intensities, there is no need to evaluate it. In eqn (7), a factor
ij is the wavenumber of the transition, Ei is the energy of the lower energy state involved in the transition and expressed in cm−1, k is the Boltzmann constant in wavenumber per Kelvin, Trot is the rotational temperature and Sij the line strength. The constant value C is common to all transitions within a CDM and since we are interested in relative intensities, there is no need to evaluate it. In eqn (7), a factor 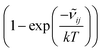 relative to the population of the upper state was neglected since kT ≪
relative to the population of the upper state was neglected since kT ≪ ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ij. An analytical expression of Sij is required to evaluate the theoretical integrated absorption coefficient. For a rigid symmetric top molecule, which is nearly the case of methanol, and if we are only interested in relative intensities, the line strength Sij depends only on the J and K values of the lower energy state:41,42
ij. An analytical expression of Sij is required to evaluate the theoretical integrated absorption coefficient. For a rigid symmetric top molecule, which is nearly the case of methanol, and if we are only interested in relative intensities, the line strength Sij depends only on the J and K values of the lower energy state:41,42
• ΔK = 0, ΔJ = + 1 (R branch)
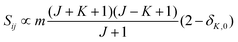 | (8) |
• ΔK = 0, ΔJ = 0 (Q branch)
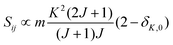 | (9) |
• ΔK = 0, ΔJ = −1 (P branch)
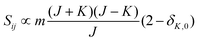 | (10) |
• ΔK = ±1, ΔJ = +1 (R branch)
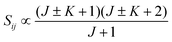 | (11) |
• ΔK = ±1, ΔJ = 0 (Q branch)
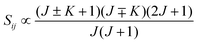 | (12) |
• ΔK = ±1, ΔJ = −1 (P branch)
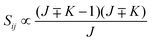 | (13) |
4 Conclusions
The spectral signature of methanol in the 2OH stretching region was recorded using a new apparatus combining a cw-CRDS and a buffer gas cooling cell. Even at low temperatures (Trot = 26 K), the assignment of such complicated spectrum appeared to be quite challenging.21,22 To tackle this difficulty, the technique suggested by Rakvoský22 was used, consisting in the detection of patterns in the position of the molecular transitions. Due to the large number of pattern detections, intensity information was included in the construction of the reference patterns. Reference intensities were evaluated using the analytical formula available for symmetric tops based on the nearly prolate character of this molecule. Using this extended approach, 162 transitions assigned by Rakvoský et al. were firmly confirmed and 48 others were tentatively confirmed. A further 188 transitions were firmly assigned and 14 more transitions were tentatively assigned. However, the challenge of digging into the complexity of methanol remains, with more than 2000 transitions observed but not yet assigned. We plan in the future to modify our set-up to improve significantly the accuracy in the determination of the line positions using a stabilized frequency comb to determine the wavenumber axis of the observed spectra. This will lead to a decrease of the erroneous detection of CDMs and thus an improvement of the efficiency of the assignment procedure. We also plan to simplify even further the molecular fingerprint by going lower in temperature with the fabrication of a new buffer gas cooling setup, going below 10 K. In these conditions, the pattern recognition method with the inclusion of the intensity information, which promises to be a relevant method for the assignment of complex spectral signatures often associated with the overtone range, could be fully automatized. This approach should prove to be particularly appropriate in the case of bands presenting a mixed character: parallel and perpendicular.Author contributions
Alexis Libert: supervision, construction of the buffer gas cooling experiment, extension and implementation of the pattern recognition method, formal analysis, writing – original draft. Anthony Roucou: part of the collaboration on the buffer gas cooling cell and CW-CRDS preliminary testing, formal analysis, extension of the pattern recognition method, writing – original draft. Brian Hays: recording of the final spectrum at the basis of the analysis. Robin Glorieux: work on the frequency calibration hardware and software development. Séverine Robert: part of the collaboration on the development of the buffer gas cooling cell and CW-CRDS. Baptiste Fabre: part of the collaboration on the development of the buffer gas cooling cell and CW-CRDS. Samir Kassi: improvement of the sensitivity of the CW-CRDS. Xavier Urbain: supervision of the experimental development. Clément Lauzin: supervision, extension of the pattern recognition method, funding acquisition, formal analysis, writing – original draft.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful for the discussions with Benoit Darquié and Benoit Hackens concerning the design of the BCG setup and for the involvement of Marc Daman, Hervé Laurent and Guilhem Vanlancker in its fabrication. We thank Isabelle Kleiner and Jean Vander Auwera for their help concerning the characterization of the lower energy states and for the discussion about the evaluation of the relative intensities of the transitions respectively. This work was supported by the Fonds de la Recherche Scientifique-FNRS (CDR J.0129.20, J.0113.23, IISN Grant no. 4.4504 and MIS), the FED-tWIN program (RT-MOLEXO project), the ARC (iBEAM project 18/23-090), Wallonie Bruxelles International (WBI) and the UCLouvain.References
- C. Ceccarelli, Faraday Discuss., 2023, 245, 11–51 RSC.
- P. Jansen, L.-H. Xu, I. Kleiner, W. Ubachs and H. L. Bethlem, Phys. Rev. Lett., 2011, 106, 100801 CrossRef PubMed.
- S. Muller, W. Ubachs, K. Menten, C. Henkel and N. Kanekar, Astron. Astrophys., 2021, 652, A5 CrossRef CAS.
- J. S. Koehler and D. M. Dennison, Phys. Rev., 1940, 57, 1006 CrossRef CAS.
- E. Herbst, J. Messer, F. C. De Lucia and P. Helminger, J. Mol. Spectrosc., 1984, 108, 42–57 CrossRef CAS.
- C. Walsh, R. A. Loomis, K. I. Öberg, M. Kama, M. L. R. van t Hoff, T. J. Millar, Y. Aikawa, E. Herbst, S. L. Widicus Weaver and H. Nomura, Astrophys. J. Lett., 2016, 823, L10 CrossRef.
- L. Paganini, M. N. Camarca, M. J. Mumma, S. Faggi, M. Lippi and G. L. Villanueva, Astron. J., 2019, 158, 98 CrossRef CAS.
- J. Bagdonaite, P. Jansen, C. Henkel, H. L. Bethlem, K. M. Menten and W. Ubachs, Science, 2013, 339, 46–48 CrossRef CAS PubMed.
- A. Borden and E. Barker, J. Chem. Phys., 1938, 6, 553–563 CrossRef CAS.
- E. V. Ivash and D. M. Dennison, J. Chem. Phys., 1953, 21, 1804–1816 CrossRef CAS.
- B. Fehrensen, D. Luckhaus, M. Quack, M. Willeke and T. R. Rizzo, J. Chem. Phys., 2003, 119, 5534–5544 CrossRef CAS.
- D. Lauvergnat, L. Coudert, S. Klee and M. Smirnov, J. Mol. Spectrosc., 2009, 256, 204–215 CrossRef CAS.
- L.-H. Xu, J. Fisher, R. Lees, H. Shi, J. Hougen, J. Pearson, B. Drouin, G. Blake and R. Braakman, J. Mol. Spectrosc., 2008, 251, 305–313 CrossRef CAS.
- I. Kleiner, G. T. Fraser, J. T. Hougen and A. Pine, J. Mol. Spectrosc., 1991, 147, 155–172 CrossRef CAS.
- I. Kleiner, M. Godefroid, M. Herman and A. McKellar, J. Mol. Spectrosc., 1990, 142, 238–253 CrossRef CAS.
- O. Boyarkin, T. Rizzo and D. S. Perry, J. Chem. Phys., 1999, 110, 11359–11367 CrossRef CAS.
- D. Rueda, O. V. Boyarkin, T. R. Rizzo, A. Chirokolava and D. S. Perry, J. Chem. Phys., 2005, 122, 044314 CrossRef PubMed.
- S. Xu, J. J. Kay and D. S. Perry, J. Mol. Spectrosc., 2004, 225, 162–173 CrossRef CAS.
- I. Kleiner, J. Mol. Spectrosc., 2010, 260, 1–18 CrossRef CAS.
- J. T. Hougen, I. Kleiner and M. Godefroid, J. Mol. Spectrosc., 1994, 163, 559–586 CrossRef CAS.
- V. Svoboda, V. Horká-Zelenková, J. Rakovsky, P. Pracna and O. Votava, Phys. Chem. Chem. Phys., 2015, 17, 15710–15717 RSC.
- J. Rakovský, V. Svoboda, V. Horká-Zelenková and O. Votava, Phys. Chem. Chem. Phys., 2021, 23, 20193–20200 RSC.
- P. B. Changala, B. Spaun, D. Patterson, J. M. Doyle and J. Ye, Appl. Phys. B: Lasers Opt., 2016, 122, 292 CrossRef.
- D. Patterson and J. M. Doyle, Mol. Phys., 2012, 110, 1757–1766 CrossRef CAS.
- B. Spaun, P. B. Changala, D. Patterson, B. J. Bjork, O. H. Heckl, J. M. Doyle and J. Ye, Nature, 2016, 517–520 CrossRef CAS PubMed.
- D. Romanini, A. Kachanov, N. Sadeghi and F. Stoeckel, Chem. Phys. Lett., 1997, 264, 316–322 CrossRef CAS.
- J. T. Hodges, H. P. Layer, W. W. Miller and G. E. Scace, Rev. Sci. Instrum., 2004, 75, 849–863 CrossRef CAS.
- A. Libert, PhD thesis, Université catholique de Louvain, 2022.
- I. E. Gordon, L. S. Rothman, R. J. Hargreaves, R. Hashemi, E. V. Karlovets, F. M. Skinner, E. K. Conway, C. Hill, R. V. Kochanov, Y. Tan, P. Wcislo, A. A. Finenko, K. Nelson, P. F. Bernath, M. Birk, V. Boudon, A. Campargue, K. V. Chance, A. Coustenis, B. J. Drouin, J.-M. Flaud, R. R. Gamache, J. T. Hodges, D. Jacquemart, E. J. Mlawer, A. V. Nikitin, V. I. Perevalov, M. Rotger, J. Tennyson, G. C. Toon, H. Tran, V. G. Tyuterev, E. M. Adkins, A. Baker, A. Barbe, E. Canè, A. G. Cs’asz’ar, A. Dudaryonok, O. Egorov, A. J. Fleisher, H. Fleurbaey, A. Foltynowicz, T. Furtenbacher, J. J. Harrison, J.-M. Hartmann, V.-M. Horneman, X. Huang, T. Karman, J. Karns, S. Kassi, I. Kleiner, V. Kofman, F. Kwabia-Tchana, N. N. Lavrentieva, T. J. Lee, D. A. Long, A. A. Lukashevskaya, O. M. Lyulin, V. Y. Makhnev, W. Matt, S. T. Massie, M. Melosso, S. N. Mikhailenko, D. Mondelain, H. S. P. Muller, O. V. Naumenko, A. Perrin, O. L. Polyansky, E. Raddaoui, P. L. Raston, Z. D. Reed, M. Rey, C. Richard, R. T'obi'as, I. Sadiek, D. W. Schwenke, E. Starikova, K. Sung, F. Tamassia, S. A. Tashkun, J. Vander Auwera, I. A. Vasilenko, A. A. Vigasin, G. L. Villanueva, B. Vispoel, G. Wagner, A. Yachmenev and S. N. Yurchenko, J. Quant. Spectrosc. Radiat. Transfer, 2022, 277, 107949 CrossRef CAS.
- R. Tóbiás, T. Furtenbacher, I. Simkó, A. G. Császár, M. L. Diouf, F. M. Cozijn, J. M. Staa, E. J. Salumbides and W. Ubachs, Nat. Commun., 2020, 11, 1708 CrossRef PubMed.
- W. C. Campbell and J. M. Doyle, Cold molecules: theory, experiment, applications, 2009, pp. 473–508 Search PubMed.
- L. Santamaria, V. Di Sarno, I. Ricciardi, M. De Rosa, S. Mosca, G. Santambrogio, P. Maddaloni and P. De Natale, Astrophys. J., 2015, 801, 50 CrossRef.
- K. Didriche, T. Földes, C. Lauzin, D. Golebiowski, J. Liévin and M. Herman, Mol. Phys., 2012, 110, 2781–2796 CrossRef CAS.
- M. Herman, T. Földes, K. Didriche, C. Lauzin and T. Vanfleteren, Int. Rev. Phys. Chem., 2016, 35, 243–295 Search PubMed.
- J. C. Cobas, M. A. Bernstein, M. Martn-Pastor and P. G. Tahoces, J. Magn. Reson., 2006, 183, 145–151 CrossRef CAS PubMed.
- Z. Li, D.-J. Zhan, J.-J. Wang, J. Huang, Q.-S. Xu, Z.-M. Zhang, Y.-B. Zheng, Y.-Z. Liang and H. Wang, Analyst, 2013, 138, 4483–4492 RSC.
- Z.-M. Zhang, S. Chen, Y.-Z. Liang, Z.-X. Liu, Q.-M. Zhang, L.-X. Ding, F. Ye and H. Zhou, J. Raman Spectrosc., 2010, 41, 659–669 CrossRef CAS.
- V. Svoboda, J. Rakovský and O. Votava, J. Quant. Spectrosc. Radiat. Transfer, 2022, 292, 108319 CrossRef CAS.
- P. R. Bunker and P. Jensen, Molecular symmetry and spectroscopy, NRC Research Press, 2006, vol. 46853 Search PubMed.
- M. Hepp, I. Pak, K. Yamada, E. HERBsT and G. Winnewisser, J. Mol. Spectrosc., 1994, 166, 66–78 CrossRef CAS.
- H. C. Allen and P. C. Cross, Molecular Vib-rotors: The theory and interpretation of high resolution infrared spectra, John Wiley and Sons, 1963 Search PubMed.
- J. Vander Auwera, Quantitative high resolution Fourier transform infrared spectroscopy, 2004, Agrégation de lEnseignement Supérieur (Habilitation), Sciences, Université libre de Bruxelles.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00757c |
| This journal is © the Owner Societies 2024 |