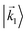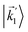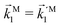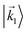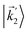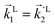A geometric approach to decoding molecular structure and dynamics from photoionization of isotropic samples†
Received
10th December 2021
, Accepted 21st April 2022
First published on 27th May 2022
Abstract
We propose a geometric approach to the description and analysis of photoelectron angular distributions resulting from isotropic samples in the case of few-photon ionization by electric fields of arbitrary polarization. This approach formulates the standard photoionization observables – the bl,m expansion coefficients of the photoelectron angular distribution, in terms of geometrical properties of the vector field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) ≡ 〈
) ≡ 〈![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) |
|![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) |0〉 describing the electronic transition from a bound state |0〉 into a scattering state |
|0〉 describing the electronic transition from a bound state |0〉 into a scattering state |![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉 – the photoionization transition dipole. Besides revealing selection rules for the enantio-sensitivity of bl,m coefficients in multiphoton ionization, our approach yields very compact expressions for both chiral and achiral molecules revealing how the molecular rotational invariants couple to the rotational invariants of the setup defined by the electric field polarization and the arrangement of photoelectron detectors. We apply this approach to one-photon ionization and find that the forward–backward asymmetry parameter b1,0, emerging exclusively in chiral molecules and encoded in the field
〉 – the photoionization transition dipole. Besides revealing selection rules for the enantio-sensitivity of bl,m coefficients in multiphoton ionization, our approach yields very compact expressions for both chiral and achiral molecules revealing how the molecular rotational invariants couple to the rotational invariants of the setup defined by the electric field polarization and the arrangement of photoelectron detectors. We apply this approach to one-photon ionization and find that the forward–backward asymmetry parameter b1,0, emerging exclusively in chiral molecules and encoded in the field ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) ≡ i
) ≡ i![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) *(
*(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) ×
) × ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ), is sensitive only to the components of
), is sensitive only to the components of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) perpendicular to
) perpendicular to ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) , while the regular asymmetry parameter b2,0 emerging in chiral and achiral molecules is sensitive only to the component of
, while the regular asymmetry parameter b2,0 emerging in chiral and achiral molecules is sensitive only to the component of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) parallel to
) parallel to ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) . Next, we analyze resonantly enhanced two-photon ionization and show that b0,0 and b1,0 can be written in terms of an effectively stretched
. Next, we analyze resonantly enhanced two-photon ionization and show that b0,0 and b1,0 can be written in terms of an effectively stretched ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ), and how b1,0 and b3,0 can be used to probe
), and how b1,0 and b3,0 can be used to probe ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ).
).
1 Introduction
Photoelectrons provide an important window into the structure of matter and have long been used as a probe of molecular structure in static and time-resolved experiments.1,2 Photoelectron angular distributions3 (PADs) encode structural information which goes well beyond the energy spectrum of the molecule, even if the molecule is randomly oriented in space. Chiral molecules present a paramount example of such structural sensitivity: opposite enantiomers of a chiral molecule randomly oriented in space yield markedly different PADs when illuminated with circularly polarized light – a phenomenon known as photoelectron circular dichroism (PECD).4–8 PECD, with its unusually high enantio-sensitivity, clearly stands out as a tool for exploring structure and dynamics of chiral molecules. It has been studied across a wide range of molecular species9 and extended to the multiphoton and tunneling ionization regimes.10–14 Crucially, the extension of PECD into the realm of multiphoton ionization10,11 provides both access to time-resolved ultrafast enantio-sensitive electronic dynamics14–17 and the means to control the enantio-sensitive signal observed in the photoelectron angular distributions.18,19
The fact that molecular handedness can be inferred from the PAD of a randomly oriented sample raises the following question: how can we recover the molecular-frame information (not just handedness) encoded in the PAD of randomly oriented molecular samples? This encoding of molecular-frame information proceeds in several steps: the nuclear configuration is encoded in the electronic wave functions of the ground |0〉 and scattering states |![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉, these states are subsequently encapsulated into photoionization transition dipoles
〉, these states are subsequently encapsulated into photoionization transition dipoles ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) ≡ 〈
) ≡ 〈![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) |
|![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) |0〉, and these dipoles are in turn used to calculate the laboratory-frame PAD. The last step requires averaging over molecular orientations and drastically reduces the amount of information contained in the vector field
|0〉, and these dipoles are in turn used to calculate the laboratory-frame PAD. The last step requires averaging over molecular orientations and drastically reduces the amount of information contained in the vector field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) to a handful of coefficients bl,m describing the laboratory-frame PAD in terms of spherical harmonics Yml(
) to a handful of coefficients bl,m describing the laboratory-frame PAD in terms of spherical harmonics Yml(![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) ) (see e.g. ref. 4). So we might as well ask: what do these few bl,mcoefficients tell us about the molecular-frame vector field
) (see e.g. ref. 4). So we might as well ask: what do these few bl,mcoefficients tell us about the molecular-frame vector field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) )? Answering this question is the main objective of this paper.
)? Answering this question is the main objective of this paper.
The standard approach to the computation of molecular bl,m coefficients4,20–24 provides the connection between molecular and laboratory frame PADs25–27 and is the basis for the accurate description of PADs in complex polyatomic molecules.28 However, it does not provide a simple answer to our question. This motivated the development of the alternative approach to the analysis of PADs presented here.
Our approach provides insightful connections between the bl,m coefficients and the photoionization dipole vector field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ). A previous version of this approach limited to b0,0 and b1,0 has already proven to be very useful for photoionization of chiral molecules (see ref. 17 and 29). We expect the general version provided here to be useful beyond chiral molecules and throughout the field of molecular photoionization for comparison of different non-linear signals generated due to fields with complex geometries.
). A previous version of this approach limited to b0,0 and b1,0 has already proven to be very useful for photoionization of chiral molecules (see ref. 17 and 29). We expect the general version provided here to be useful beyond chiral molecules and throughout the field of molecular photoionization for comparison of different non-linear signals generated due to fields with complex geometries.
In particular, we applied this alternative approach to the cases of one- and two-photon resonantly-enhanced ionization of randomly oriented molecules and found that the bl,m coefficients encode concrete geometrical information about ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) and about the associated field
) and about the associated field ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) ≡ i
) ≡ i![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) *(
*(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) ×
) × ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ), which plays a central role in the photoionization of chiral molecules.29,30 The geometrical character of our findings suggests potential connections to geometrical and topological properties31,32 in other research fields such as structured light,33–36 magnetism,37 and electron dynamics in crystals.38
), which plays a central role in the photoionization of chiral molecules.29,30 The geometrical character of our findings suggests potential connections to geometrical and topological properties31,32 in other research fields such as structured light,33–36 magnetism,37 and electron dynamics in crystals.38
Another fundamental aspect we address here is that due to the isotropic distribution of molecular orientations, the observables can only depend on rotational invariants (RIs), i.e. on quantities independent of the molecular orientation, such as the angle between two transition dipoles, or the angle between the photon spin and the z axis defined by the photoelectron detection setup. This is in fact a common feature enabling meaningful comparisons across different enantio-sensitive methods working in diverse detection regimes with isotropic samples, from microwave excitation to optical wave-mixing to photoionization and standard absorption circular dichroism and optical activity.17 The RIs are divided into those describing the molecule – molecular RIs, and those describing the light and detection setup – setup RIs. The observables, here the bl,m coefficients, must therefore be functions of those two groups of RIs. Our approach provides these functions, which we show to be linear both in the molecular and in the setup RIs, and thus reveals how the molecular RIs are coupled to the setup RIs. The understanding of this coupling is very relevant for schemes looking for effective ways of maximizing the enantio-sensitive response,19 a highly non-trivial task for multi-color fields of arbitrary polarization.
The paper is organized as follows. Section 2 describes the idea of our approach in simple terms, summarizing the key technical steps of Section 3. The latter is complemented by further mathematical details in the ESI.† Section 4 contains the analysis of local properties of bl,m coefficients and the underlying vector fields relevant to one-photon ionization. Sections 2–4 are relevant for both chiral and achiral molecules subject to electric fields of arbitrary polarization. Section 5 explores PECD in two-photon resonantly-enhanced ionization of chiral molecules and provides the first steps towards the ambitious goal of reconstructing ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) ≡ i
) ≡ i![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) *(
*(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) ×
) × ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) )29,30 from the bl,m coefficients. Section 6 concludes the work. Further applications of the approach presented here can be found in ref. 29 and 39.
)29,30 from the bl,m coefficients. Section 6 concludes the work. Further applications of the approach presented here can be found in ref. 29 and 39.
2 Idea of the method
The interpretation of molecular structure and dynamics probed via photoionization of randomly oriented samples usually relies on a mathematical formulation employing a partial wave expansion of the scattering wave function, which is normally performed at the outset of any PAD derivation4,20,24,40,41 before the orientation averaging step. This traditional approach yields bl,m coefficients in a form in which it is not clear how the geometric properties of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) are encoded in bl,m. For example, in chiral molecules, this approach obscures the connection between b1,0 (describing PECD) and the geometry of
) are encoded in bl,m. For example, in chiral molecules, this approach obscures the connection between b1,0 (describing PECD) and the geometry of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) beyond the fact that b1,0 results from complex interference of many (about 15, see ref. 41–45) partial waves.
) beyond the fact that b1,0 results from complex interference of many (about 15, see ref. 41–45) partial waves.
The key idea of the approach we present here is that it is possible to obtain analytical expressions for the b
l,m
coefficients without invoking any type of expansion for the scattering wave function. These expressions reveal the link between b
l,m
and ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) and show how the geometry of the vector field
) and show how the geometry of the vector field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) maps into the bl,mcoefficients.
) maps into the bl,mcoefficients.
In particular, we found a way to perform the orientation averaging step without expanding the scattering wave function. To achieve this it is important to identify the natural frame of reference of each vector involved in the photoionization process. As usual, the natural frame of reference of transition dipoles is the molecular frame, while that of the electric fields and laboratory axes is the laboratory frame. For the photoelectron momentum, identifying the natural reference frame is less straightforward. Indeed, while the photoelectron momentum ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) is detected in the laboratory frame and keeping it in this frame throughout PAD derivations is the usual practice,4 its natural frame of reference is the molecular frame. This is because
is detected in the laboratory frame and keeping it in this frame throughout PAD derivations is the usual practice,4 its natural frame of reference is the molecular frame. This is because ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) labels the electronic scattering wave function, which, like the bound electronic wave functions, is fixed in the molecular frame. Fig. 1 illustrates that scattering states having the same
labels the electronic scattering wave function, which, like the bound electronic wave functions, is fixed in the molecular frame. Fig. 1 illustrates that scattering states having the same ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) in the laboratory frame (
in the laboratory frame (![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 1 and
1 and 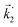 ) but corresponding to different molecular orientations are not related to each other in any simple way, while scattering states having the same
) but corresponding to different molecular orientations are not related to each other in any simple way, while scattering states having the same ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) in the molecular frame (
in the molecular frame (![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 1 and
1 and 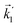 ) are related to each other via a simple rotation of their wave functions.
) are related to each other via a simple rotation of their wave functions.
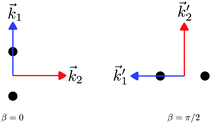 |
| | Fig. 1 Two orientations of a diatomic molecule. The black circles indicate the nuclei. The scattering state depends on the relative angle between the molecular axis and the propagation direction ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) of the outgoing (asymptotically plane) wave. Therefore, while the states of the outgoing (asymptotically plane) wave. Therefore, while the states  and and  satisfying satisfying 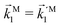 are related to each other by a simple rotation, the states are related to each other by a simple rotation, the states 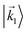 and and 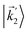 satisfying satisfying 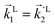 are not related to each other in any simple way. are not related to each other in any simple way. | |
The desire of keeping each vector in its natural reference frame and of relying on the techniques for orientation averaging of tensors46 will dictate the sequence of steps described in the next section. This sequence yields expressions for the bl,m coefficients as products of molecular RIs and setup RIs, or in general, as sums of such products.
We shall see that the molecular RIs will be represented in terms of ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) -dependent molecular vector fields. Such fields are unique to every molecule and encode its structure. Thus, the key differences of our approach from the standard approach are (i) avoiding partial wave expansion of scattering states, (ii) keeping the photoelectron momentum
-dependent molecular vector fields. Such fields are unique to every molecule and encode its structure. Thus, the key differences of our approach from the standard approach are (i) avoiding partial wave expansion of scattering states, (ii) keeping the photoelectron momentum ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) in the molecular frame, and (iii) exchanging the order of integrals over the molecular orientations and over the orientations of
in the molecular frame, and (iii) exchanging the order of integrals over the molecular orientations and over the orientations of ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) . This approach reveals physics that are otherwise obscured by the partial wave expansion. Naturally, the standard expressions can also be recovered from our representation. Note that we are not suggesting that our approach allows the numerical calculation of the bl,m coefficients without doing a partial wave expansion. The partial wave expansion may still be needed for the computation of
. This approach reveals physics that are otherwise obscured by the partial wave expansion. Naturally, the standard expressions can also be recovered from our representation. Note that we are not suggesting that our approach allows the numerical calculation of the bl,m coefficients without doing a partial wave expansion. The partial wave expansion may still be needed for the computation of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ), but what we are interested in is the connection between bl,m and
), but what we are interested in is the connection between bl,m and ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ), not the calculation of
), not the calculation of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) itself.
) itself.
3 General methodology
The photoionization of an isotropic molecular sample results in a photoelectron spectrum WL(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) L) given by
L) given by| | 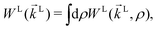 | (1) |
where WL(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) L, ρ) is the photoelectron spectrum for a given molecular orientation ρ ≡ αβγ, αβγ are the Euler angles,
L, ρ) is the photoelectron spectrum for a given molecular orientation ρ ≡ αβγ, αβγ are the Euler angles, 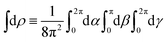 is the integral over all molecular orientations, and the superscript L indicates vectors and functions in the laboratory frame. Since we can always expand WL(
is the integral over all molecular orientations, and the superscript L indicates vectors and functions in the laboratory frame. Since we can always expand WL(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) L) into real spherical harmonics‡Ỹml(
L) into real spherical harmonics‡Ỹml(![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) L),
L),| | 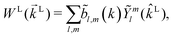 | (2) |
then any information about the molecule and the ionizing field encoded in the photoelectron spectrum WL(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) L) is now neatly summarized in the expansion coefficients
L) is now neatly summarized in the expansion coefficients ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m(k),
l,m(k),| | 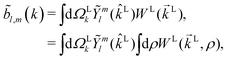 | (3) |
where 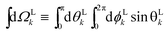 ,
, ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) L = (1, θLk, ϕLk) in spherical coordinates, and
L = (1, θLk, ϕLk) in spherical coordinates, and ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) L = k
L = k![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) L. Measured as well as calculated values for these coefficients for particular systems can be found for example in ref. 7, 25, 26 and 47–51.
L. Measured as well as calculated values for these coefficients for particular systems can be found for example in ref. 7, 25, 26 and 47–51.
Following the definition of a rotated function (see e.g. ref. 52), the photoelectron spectrum in the molecular frame is given by the relation WM(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M, ρ) = WL(
M, ρ) = WL(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) L, ρ), or equivalently WM(S−1(ρ)
L, ρ), or equivalently WM(S−1(ρ)![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) L, ρ) = WL(
L, ρ) = WL(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) L, ρ), where
L, ρ), where ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) L = S(ρ)
L = S(ρ)![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M and S(ρ) is the rotation matrix that takes vectors from the molecular to the laboratory frame and the superscript M indicates vectors and functions in the molecular frame. This means that
M and S(ρ) is the rotation matrix that takes vectors from the molecular to the laboratory frame and the superscript M indicates vectors and functions in the molecular frame. This means that
| | 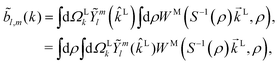 | (4) |
where in the second line we exchanged the integration order because we want to make the change of variables
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M
M =
S−1(
ρ)
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) L
L, which only exists inside the integral over orientations and yields
| | 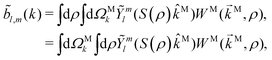 | (5) |
where in the second line we exchanged the integration order again because now
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M
M is an integration variable independent of
ρ. At this point two questions arise: Why would we want to have the photoelectron momentum in the molecular frame instead of having it in the laboratory frame, where the photoelectron is actually measured? And why would we prefer to do the integral over orientations in
eqn (5) instead of the apparently simpler integral over orientations in
eqn (3)? The answer to both questions has to do with the form that the photoelectron spectrum
WM(
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M
M,
ρ) takes in the case of ionization in the perturbative regime.
As an example, let's consider the simple scenario depicted in Fig. 2: two-photon absorption with a single color field in a three-level system where the two lower levels are bound and non-degenerate and the higher level is an infinitely degenerate scattering state. For a Gaussian pulse with central frequency ωL and spectral width γ the field can be written as
| | 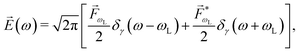 | (6) |
where
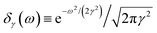
and the resulting second-order contribution to the probability amplitude of the scattering state |
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M
M〉 reads as
| | 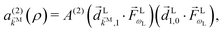 | (7) |
where
![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) i,j
i,j ≡ 〈
i|
![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif)
|
j〉 is the transition dipole matrix element and
A(2) is a function of the difference of the level spacings
ωk1 −
ω10, the total detuning 2
Δ =
ωk0 − 2
ωL, and the spectral width
γ,
ωij ≡
ωi −
ωj,
ωi is the energy of the state |
i〉, and the superscript
(2) indicates the order of the process. The photoelectron spectrum in the molecular frame then reads as
| | 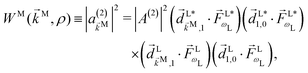 | (8) |
where the
ρ dependence is implicit in the transition dipoles according to
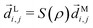
[see
eqn (7)]. Replacing in
eqn (5) we obtain
| | 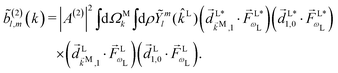 | (9) |
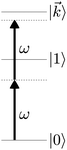 |
| | Fig. 2 Excitation scheme for resonantly enhanced photoionization. | |
Note that when written in component form, the product of four transition dipole vectors (tensors of rank 1) in this expression forms irreducible spherical tensors of rank μ up to 4 (twice the number of photons N exchanged with the field) which transform according to the Wigner matrix ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (μ)(ρ). Similarly, the real spherical harmonic Ỹml(
(μ)(ρ). Similarly, the real spherical harmonic Ỹml(![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) L) is a superposition of two spherical tensors of rank l that transform according to
L) is a superposition of two spherical tensors of rank l that transform according to ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (l)(ρ).52 Then, from eqn (9) and the orthogonality relation of the Wigner matrices52 it is evident that the
(l)(ρ).52 Then, from eqn (9) and the orthogonality relation of the Wigner matrices52 it is evident that the ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (2)l,m coefficients with l > lmax = 4 (in general lmax = 2N) vanish, as is well known. Expressions analogous to eqn (9) can be obtained for the case of fields with multiple frequencies. In the case of terms
(2)l,m coefficients with l > lmax = 4 (in general lmax = 2N) vanish, as is well known. Expressions analogous to eqn (9) can be obtained for the case of fields with multiple frequencies. In the case of terms 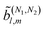 resulting from the interference of pathways involving N1 and N2 photons we get lmax = N1 + N2.
resulting from the interference of pathways involving N1 and N2 photons we get lmax = N1 + N2.
If instead of relying on the Wigner matrices to perform the orientation averaging we take into account that the spherical harmonics in eqn (9) are just polynomials of kLx/k, kLy/k, and kLz/k, then ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m becomes a sum of terms of the form
l,m becomes a sum of terms of the form
| | 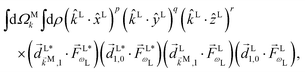 | (10) |
where
p +
q +
r ≤
l and
p +
q +
r has the same parity as
l. The vectors in this expression are of two types. The set
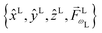
is fixed in the laboratory frame, while the set
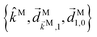
(which appears in the expression above rotated into the laboratory frame
![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) L
L =
S(
ρ)
![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) M
M) is fixed in the molecular frame. We take
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M
M fixed in the molecular frame because
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M
M is the quantum label that characterizes the scattering state |
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M
M〉, which (like the bound states) is fixed in the molecular frame (see
e.g.Fig. 1).
Eqn (10) has the form we wanted to achieve, it is a product of scalar products between vectors fixed in the molecular frame and vectors fixed in the laboratory frame. In this form the integration over orientations can be performed at once applying the technique in ref.
46, which yields a result of the form
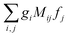
, where the
gi are rotational invariants (RIs) formed with the set of vectors fixed in the molecular frame, the
fj are RIs formed by the set of vectors fixed in the laboratory frame, and the
Mij are constants coupling both sets of RIs. Examples of such invariants will be given in the next section.
The structure of the RIs (see ref. 46) and the fact that eqn (10) involves only polar vectors allows us to conclude that if the number of dot products in eqn (10) is odd (even) then the RIs are pseudoscalars (scalars). This means that enantio-sensitivity can only be observed in coefficients ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (N)l,m such that l is odd, in agreement with previous works (see e.g. ref. 10 and 53). More interestingly, for coefficients
(N)l,m such that l is odd, in agreement with previous works (see e.g. ref. 10 and 53). More interestingly, for coefficients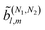 resulting from interference between pathways with N1and N2photons, the condition for enantio-sensitivity is that l + N1 + N2is odd. That is, if N1 + N2is odd, coefficients
resulting from interference between pathways with N1and N2photons, the condition for enantio-sensitivity is that l + N1 + N2is odd. That is, if N1 + N2is odd, coefficients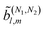 with even l can be enantio-sensitive, in agreement with the recent works in ref. 18 and 54. This is a general condition independent of the polarization of the field and of the photon energies and will be explored in more detail in ref. 39.
with even l can be enantio-sensitive, in agreement with the recent works in ref. 18 and 54. This is a general condition independent of the polarization of the field and of the photon energies and will be explored in more detail in ref. 39.
Now we will discuss two elementary applications of our methodology. First, we will derive the expression for the b(1)l,m coefficients in one-photon ionization and discuss the molecular information they reveal. Afterwards we will derive and discuss the expressions for the b(2)0,0, b(2)1,0, and b(2)3,0 coefficients relevant for PECD in two-photon ionization. Note that the expressions for b(1)0,0 and b(1)1,0 coefficients in one-photon ionization and the b(2)1,0 coefficient in two-photon ionization have already been derived using a less general procedure in ref. 17.
4 The photoionization dipole field and the bl,m coefficients in one-photon ionization
For the field in eqn (6), the first-order amplitude of the scattering state |![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M〉 reads as
M〉 reads as| | 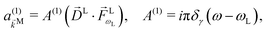 | (11) |
where we use the shorthand notations 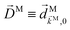 ,
, 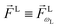 , and as usual
, and as usual ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) L = S(ρ)
L = S(ρ)![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M. From here on, we must keep in mind that
M. From here on, we must keep in mind that ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M =
M = ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) is a complex vector field that depends on
M) is a complex vector field that depends on ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M. That is, for a fixed initial state |0〉,
M. That is, for a fixed initial state |0〉, ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) is a mapping from the space of real three-dimensional vectors
M) is a mapping from the space of real three-dimensional vectors ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M ∈
M ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3 to the space of complex three-dimensional vectors
3 to the space of complex three-dimensional vectors ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M ∈
M ∈ ![[Doublestruck C]](https://www.rsc.org/images/entities/char_e166.gif) 3. From eqn (11) it is clear that this complex vector field fully determines the response of the molecule to the ionizing field and therefore the coefficients
3. From eqn (11) it is clear that this complex vector field fully determines the response of the molecule to the ionizing field and therefore the coefficients ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (1)l,m must correspond to properties of this vector field. The question is: which property of the photoionization vector field
(1)l,m must correspond to properties of this vector field. The question is: which property of the photoionization vector field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) is reflected in a given
M) is reflected in a given ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (1)l,mcoefficient?
(1)l,mcoefficient?
Since for first order amplitudes all frequencies act separately and the most general polarization of a single frequency is elliptical, we will assume an electric field that is elliptically polarized in the xy plane with its major axis along either the ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L or the ŷL axis. From symmetry it follows that the only non-zero
L or the ŷL axis. From symmetry it follows that the only non-zero ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (1)l,m coefficients are b(1)0,0, b(1)1,0, b(1)2,0,
(1)l,m coefficients are b(1)0,0, b(1)1,0, b(1)2,0, ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (1)2,2, and
(1)2,2, and ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (1)2,−2 (we omit the tilde for m = 0). With the help of eqn (5) and (10), and performing the orientation integrals according to ref. 46 we obtain§ (see ESI†)
(1)2,−2 (we omit the tilde for m = 0). With the help of eqn (5) and (10), and performing the orientation integrals according to ref. 46 we obtain§ (see ESI†)
| | 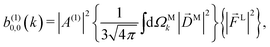 | (12) |
| | 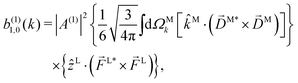 | (13) |
| | 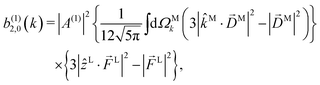 | (14) |
| | 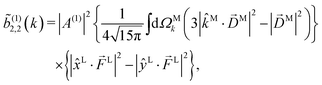 | (15) |
and
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (1)2,−2
(1)2,−2 = 0, a peculiarity of the one-photon case. That is, each
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (1)l,m
(1)l,m coefficient is the product of: a coupling term |
A(1)|
2 depending on the energy level spacing of the molecule and the spectrum of the electric field, a molecular term expressed in the molecular frame and averaged over all
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M
M directions, and a setup (field and laboratory axes) term expressed in the laboratory frame. Unlike the usual expressions for
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (1)l,m
(1)l,m (see
e.g. ref.
4),
eqn (12)–(15) provide a rather simple expression for the molecular terms which, as we will now discuss, are simply related to concrete properties of the photoionization vector field
![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M
M(
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif)
).
As expected, eqn (12) shows that b(1)0,0, which is simply the total cross section, records only the ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M-averaged value of the magnitude of the field
M-averaged value of the magnitude of the field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M). More interestingly, eqn (13) shows that b(1)1,0 is sensitive to the
M). More interestingly, eqn (13) shows that b(1)1,0 is sensitive to the ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M-averaged value of the triple product
M-averaged value of the triple product ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M·(
M·(![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M* ×
M* × ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M), which, unlike b(1)0,0, depends on the angles between
M), which, unlike b(1)0,0, depends on the angles between ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M,
M, ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M, and
M, and ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M*. The meaning of this quantity can be made evident if we use an appropriate basis for our vector field
M*. The meaning of this quantity can be made evident if we use an appropriate basis for our vector field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M. Starting from the unit vectors in spherical coordinates
M. Starting from the unit vectors in spherical coordinates ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) ,
, ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) k, and
k, and 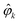 we define spherical vectors
we define spherical vectors
| | 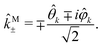 | (16) |
If we now write ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M in terms of these contravariant helicity-basis vectors,55
M in terms of these contravariant helicity-basis vectors,55
| | 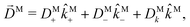 | (17) |
then
| | 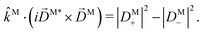 | (18) |
The right hand side of eqn (18) is analogous to the s3 Stokes parameter for light waves in the circular polarization basis, which describes the difference in intensity between left and right circular polarization.56 Here we identify the right hand side of eqn (18) with the circular dichroism (CD) of the photoionization vector field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M in the direction
M in the direction ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M. Indeed, the right hand side of eqn (18) is proportional to the difference between the probability of inducing the transition |0〉 → |
M. Indeed, the right hand side of eqn (18) is proportional to the difference between the probability of inducing the transition |0〉 → |![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M〉 using left and right circularly polarized light such that left (+) and right (−) rotations are defined with respect to
M〉 using left and right circularly polarized light such that left (+) and right (−) rotations are defined with respect to ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M (see Fig. 3). Therefore, the molecular term in b(1)1,0 is simply the
M (see Fig. 3). Therefore, the molecular term in b(1)1,0 is simply the ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M-averaged value of the
M-averaged value of the ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M-specific CD in the molecular frame. Note that the
M-specific CD in the molecular frame. Note that the ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M-specific CD can be non-zero even for achiral molecules, but its average over
M-specific CD can be non-zero even for achiral molecules, but its average over ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M is only non-zero for chiral molecules. Further discussion of b(1)1,0 can be found in ref. 30. Remarkably, eqn (18) shows that b(1)1,0 depends only on the tangential components of
M is only non-zero for chiral molecules. Further discussion of b(1)1,0 can be found in ref. 30. Remarkably, eqn (18) shows that b(1)1,0 depends only on the tangential components of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M, namely DM+ and DM− (or equivalently DMθ and DMφ). Since the electric field term of b(1)1,0 has the same form as the molecular part we can apply a similar procedure and rewrite b(1)1,0 as
M, namely DM+ and DM− (or equivalently DMθ and DMφ). Since the electric field term of b(1)1,0 has the same form as the molecular part we can apply a similar procedure and rewrite b(1)1,0 as
| | 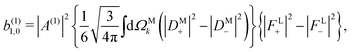 | (19) |
where
| | 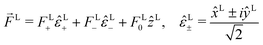 | (20) |
and |
FL+|
2 − |
FL−|
2 is the Stokes parameter
s3 in the circular polarization basis.
56
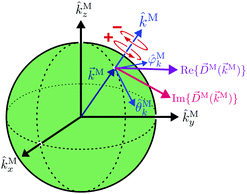 |
| | Fig. 3 Sketch of the (complex) photoionization dipole ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M( M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) ≡ 〈 M) ≡ 〈![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M| M|![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) |0〉 for a particular value of the photoelectron momentum |0〉 for a particular value of the photoelectron momentum ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M. Red circular arrows indicate the direction of left (+) and right (−) circular polarization with respect to M. Red circular arrows indicate the direction of left (+) and right (−) circular polarization with respect to ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M. M. | |
If we now take the ratio between b(1)1,0 [eqn (19)] and b(1)0,0 [eqn (12)] we get rid of the coupling term |A(1)|2, and therefore obtain an expression which factorizes into a purely molecular and a purely electric field part,
| | 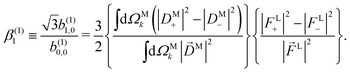 | (21) |
As discussed in ref. 57 [see eqn (8)–(10) there], for any number of photons N, we have that 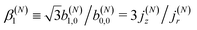 , where j(N)z is the net photoelectron current (i.e. vector sum of photoelectron currents in all directions) and j(N)r is the total photoelectron current (i.e. sum of magnitudes of photoelectron currents in all directions). Eqn (21) shows that the molecular factor is a measure of the degree of “circular polarization” of the photoionization vector field
, where j(N)z is the net photoelectron current (i.e. vector sum of photoelectron currents in all directions) and j(N)r is the total photoelectron current (i.e. sum of magnitudes of photoelectron currents in all directions). Eqn (21) shows that the molecular factor is a measure of the degree of “circular polarization” of the photoionization vector field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) and takes values between −1 and +1, which correspond to the limits
M) and takes values between −1 and +1, which correspond to the limits ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M = DM+
M = DM+![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M+ (left circularly polarized
M+ (left circularly polarized ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M) and
M) and ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M = DM−
M = DM−![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M− (right circularly polarized
M− (right circularly polarized ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M), respectively. Since the electric field factor is also a measure of the circular polarization of the electric field, then β(1)1 = 3j(1)z/j(1)r is given by the product of the
M), respectively. Since the electric field factor is also a measure of the circular polarization of the electric field, then β(1)1 = 3j(1)z/j(1)r is given by the product of the ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M-averaged “circular polarization” of the photoionization vector field
M-averaged “circular polarization” of the photoionization vector field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) and the circular polarization of the ionizing electric field. Clearly, for a known electric field, β(1)1 is a measure of the
M) and the circular polarization of the ionizing electric field. Clearly, for a known electric field, β(1)1 is a measure of the ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M-averaged “circular polarization” of
M-averaged “circular polarization” of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M). Finally, eqn (21) shows that |β(1)1| ≤ 1.5, with the maximal value taking place for circularly polarized light and a “circularly polarized”
M). Finally, eqn (21) shows that |β(1)1| ≤ 1.5, with the maximal value taking place for circularly polarized light and a “circularly polarized” ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M vector field, or equivalently, a purely longitudinal
M vector field, or equivalently, a purely longitudinal ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M ≡ i
M ≡ i![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M* ×
M* × ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M vector field.
M vector field.
Moving on to the next coefficient, eqn (14) shows that, complementarily to b(1)0,0 and b(1)1,0, which depend on the magnitude and on the tangential components of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M, respectively, the coefficient b(1)2,0 depends on the projection of
M, respectively, the coefficient b(1)2,0 depends on the projection of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M along
M along ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M, i.e. on its radial component DMk [see eqn (17)]. We can also consider the ratio between b(1)2,0 and b(1)0,0 to get rid of the coupling term, and obtain the asymmetry parameter,¶
M, i.e. on its radial component DMk [see eqn (17)]. We can also consider the ratio between b(1)2,0 and b(1)0,0 to get rid of the coupling term, and obtain the asymmetry parameter,¶
| | 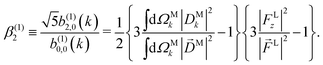 | (22) |
which satisfies the well known fact
40 that the values of
β(1)2 for linear polarization along
z and circular polarization in the
xy plane are related to each other by a factor of −2,
i.e. β(1,circ)2 = −
β(1,lin)2/2. More interestingly, we see that
β(1)2 is a linear function of the molecular property
| | 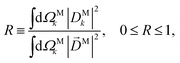 | (23) |
which measures to what extent the vector field
![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M
M(
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M
M) is a radial field and takes values between 0 and 1, corresponding to the limits
![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M
M =
DM+![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M+
M+ +
DM−![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M−
M− (tangential field) and
![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M
M =
DMk![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif)
(radial field), respectively.
Fig. 4 shows
β(1)2 as a function of
R for linear (
![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) L
L = F
zẑL) and circular polarization (
![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) L
L =
F±![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) ±
±) along with the angular distributions obtained in the limits
R = 0 (tangential
![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M
M) and
R = 1 (radial
![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M
M). We can see that for both linearly and circularly polarized fields, a predominantly tangential field
![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M
M will yield most photoelectrons with directions perpendicular to the electric field, while a predominantly radial field
![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M
M will yield most photoelectrons with directions parallel to the electric field.
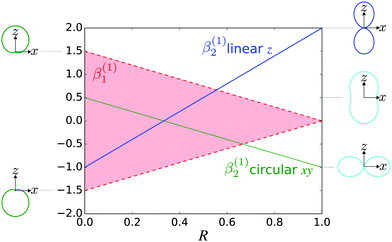 |
| | Fig. 4 The relation between β(1)2 and the molecular property R, which measures how radial the photoionization dipole field 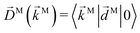 is in average for a given k [see eqn (22) and (23)], for the case of linear polarization along ẑ (blue line) and circular polarization in the xy plane (green line). The red shaded area shows the range of values that β(1)1 can take for a given value of β(1)2 (and correspondingly of R) for the circularly polarized case [see eqn (24)]. β(1)1 is zero for linear polarization. The insets on the left show the angular distributions for the extreme values β(1)1 = ±1.5 and β(1)2 = 0.5 obtained for circular polarization. The insets on the right show the angular distributions for β(1)1 = 0 (for simplicity) and β(1)2 = −1 (bottom), β(1)2 = 0.5 (center), and β(1)2 = 2 (top), which are the values reached for linear and circular polarizations in the limits R = 0 (tangential is in average for a given k [see eqn (22) and (23)], for the case of linear polarization along ẑ (blue line) and circular polarization in the xy plane (green line). The red shaded area shows the range of values that β(1)1 can take for a given value of β(1)2 (and correspondingly of R) for the circularly polarized case [see eqn (24)]. β(1)1 is zero for linear polarization. The insets on the left show the angular distributions for the extreme values β(1)1 = ±1.5 and β(1)2 = 0.5 obtained for circular polarization. The insets on the right show the angular distributions for β(1)1 = 0 (for simplicity) and β(1)2 = −1 (bottom), β(1)2 = 0.5 (center), and β(1)2 = 2 (top), which are the values reached for linear and circular polarizations in the limits R = 0 (tangential ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M) and R = 1 (radial M) and R = 1 (radial ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M). M). | |
Fig. 4 also shows the range of values that β(1)1 can take as a function of R for light circularly polarized in the xy plane. Using the expressions for b(1)0,0, b(1)1,0, and b(1)2,0 in eqn (12), (14), and (19), and taking into account that |D+|2 + |D−|2 ≥ |D+|2 − |D−|2, one can show that for circularly polarized light β(1)1 and β(1)2 satisfy the inequality (see ESI†)
| | 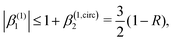 | (24) |
where we used
β(1,circ)2 ≡ (1 − 3
R)/2 as follows from
eqn (22) and (23) for circularly polarized light. This inequality follows naturally from the fact that, for circularly polarized light, values of
R close to one indicate that the field
![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif)
(
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif)
) is (in average) mostly radial and therefore the tangential components along with
β(1)1 are very small. On the contrary, values of
R close to zero indicate that the field
![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif)
(
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif)
) has (in average) a very small radial component, which means that the field is mostly tangential and can
potentially display a large dichroism |
D+|
2 − |
D−|
2. The maximum value of |
β(1)1| = 1.5 and requires
β(1,circ)2 = 0.5 and
R = 0,
i.e. ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M
M(
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M
M) purely tangential
and perfectly “circularly polarized”. As explained in ref.
57 [
eqn (9) and (10)], the net photoelectron current (
i.e. the vector sum of all photoelectron currents) is given by
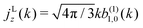
and the total photoelectron current (
i.e. the sum of the magnitudes of all photoelectron currents) is given by
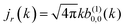
. Therefore, the maximum value of the ratio of net photoelectron current to total current is |
jz|/
jr = 1/2. Note that
eqn (24) can also be derived exclusively from the condition that the angular distribution
WL(
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) L
L) [
eqn (2)] is positive for every
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) L
L.
In practice, the values of β(1)1 and β(1)2 typically measured or calculated are far from these extreme values. For example, Fig. 3 of ref. 47 shows that for the HOMO orbital of camphor, photoelectrons in the range of 0–60 eV|| display 0 < β(1,lin)2 < 1. From this we can deduce that 1/3 < R < 2/3 (see Fig. 4 here). That is, the field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) has a balanced mixture of radial and tangential components. Furthermore, Fig. 3 of ref. 47 also shows that |β(1)1| ≤ 0.2, which is well below the maximum value |β(1)1| = 1 allowed for R = 1/3 (see Fig. 4 here). This indicates that while
M) has a balanced mixture of radial and tangential components. Furthermore, Fig. 3 of ref. 47 also shows that |β(1)1| ≤ 0.2, which is well below the maximum value |β(1)1| = 1 allowed for R = 1/3 (see Fig. 4 here). This indicates that while ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) has a significant tangential component, it is still far from being perfectly “circularly polarized”. Nevertheless, this remnant of “circular polarization” in
M) has a significant tangential component, it is still far from being perfectly “circularly polarized”. Nevertheless, this remnant of “circular polarization” in ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) is enough to yield very significant enantio-sensitive signals. From the behavior of β(1,lin)2 as a function of energy (see Fig. 3 in ref. 47) we can also deduce that R has an overall tendency to increase with photoelectron energy. That is,
M) is enough to yield very significant enantio-sensitive signals. From the behavior of β(1,lin)2 as a function of energy (see Fig. 3 in ref. 47) we can also deduce that R has an overall tendency to increase with photoelectron energy. That is, ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) tends to become more and more radial for increasing photoelectron energies. This is in agreement with the fact that for a plane wave continuum
M) tends to become more and more radial for increasing photoelectron energies. This is in agreement with the fact that for a plane wave continuum ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) is parallel to
M) is parallel to ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M and also with the usual decrease of |β(1)1| with increasing photoelectron energy.
M and also with the usual decrease of |β(1)1| with increasing photoelectron energy.
An important difference between β(1)1 and β(1)2 is that while β(1)1 encodes the average magnitude and sign of the “circular” component of the field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M, the coefficient β(1)2 encodes only the average magnitude of the radial component of the field
M, the coefficient β(1)2 encodes only the average magnitude of the radial component of the field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M, but not its sign, i.e. it doesn't keep track of whether that radial component points inwards or outwards. This is a plausible explanation of why β(1)1 is more sensitive than β(1)2 to molecular structure details. This is complementary to the explanation in terms of sines (β(1)1) and cosines (β(2)2) of phase-shifts differences provided by the partial-wave approach.41
M, but not its sign, i.e. it doesn't keep track of whether that radial component points inwards or outwards. This is a plausible explanation of why β(1)1 is more sensitive than β(1)2 to molecular structure details. This is complementary to the explanation in terms of sines (β(1)1) and cosines (β(2)2) of phase-shifts differences provided by the partial-wave approach.41
Eqn (15) shows that, up to constants, ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (1)2,2 differs from b(1)2,0 only in the electric field factor, which in the case of
(1)2,2 differs from b(1)2,0 only in the electric field factor, which in the case of ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (1)2,2 yields the s1 Stokes parameter in the linear polarization basis.56 That is,
(1)2,2 yields the s1 Stokes parameter in the linear polarization basis.56 That is, ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (1)2,2 and b(1)2,0 reveal the same information about the photoionization vector field
(1)2,2 and b(1)2,0 reveal the same information about the photoionization vector field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) and differ only on the electric field information they encode. This is a general property of
M) and differ only on the electric field information they encode. This is a general property of ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficients with the same value of l and corresponding to the same quantum pathway. It reflects the fact that such coefficients differ only on their laboratory frame vectors [see e.g.eqn (9) and (10)] but not on their molecular vectors (photoelectron momentum and transition dipoles), and therefore they involve the same molecular rotational invariants.
l,m coefficients with the same value of l and corresponding to the same quantum pathway. It reflects the fact that such coefficients differ only on their laboratory frame vectors [see e.g.eqn (9) and (10)] but not on their molecular vectors (photoelectron momentum and transition dipoles), and therefore they involve the same molecular rotational invariants.
While so far we have discussed β(1)1 and β(1)2 in terms of the ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M-averaged magnitudes of the components of
M-averaged magnitudes of the components of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M [eqn (17), (21), and (22)], it is also interesting to note that for a circularly polarized field
M [eqn (17), (21), and (22)], it is also interesting to note that for a circularly polarized field ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) L = Fσ
L = Fσ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) Lσ with σ = ±1 [see eqn (20)], eqn (12)–(14) can be inverted to reconstruct the
Lσ with σ = ±1 [see eqn (20)], eqn (12)–(14) can be inverted to reconstruct the ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M-averaged magnitudes of the components of
M-averaged magnitudes of the components of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M using the measured values of β(1)1 and β(1,circ)2. Such procedure yields
M using the measured values of β(1)1 and β(1,circ)2. Such procedure yields
| | 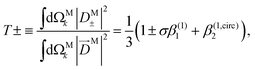 | (25) |
| | 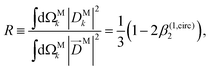 | (26) |
where 0 ≤
T± ≤ 1, 0 ≤
R ≤ 1, and
T+ +
T− +
R = 1. As an example,
Fig. 5 shows the values of
T+,
T−, and
R as a function of the photoeletron energy for ionization from the HOMO orbital of alanine and reconstructed from the corresponding values of
β(1)1 and
β(1)2 reported in ref.
58 for the conformer 3. In agreement with the previous discussion of the results in ref.
47, we see that
R tends to increase while
T+ and
T− tend to decrease as the photoelectron energy increases. Unlike the usual figures for
β(1)1 and
β(1)2, which are a statement about the PAD,
Fig. 5 is a statement about the geometrical properties of the underlying photoionization vector field
![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M
M(
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif)
).
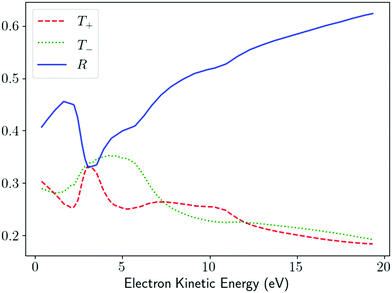 |
| | Fig. 5
T
+, T−, and R [eqn (25) and (26)] as a function of the photoelectron energy for photoionization of alanine from the HOMO orbital. The curves were reconstructed from the values of β(1)1 and β(1)2 reported in Fig. 9 and 10 of ref. 58 for conformer 3 and σ = 1. | |
5 PECD in resonantly enhanced two-photon ionization
We begin by rewriting eqn (9) as| | 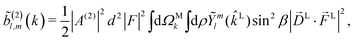 | (27) |
where we used the shorthand notation 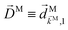 for the photoionization dipole from the intermediate state,
for the photoionization dipole from the intermediate state, 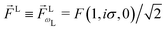 , σ = ±1, and we chose the molecular axis so that
, σ = ±1, and we chose the molecular axis so that ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) M ≡
M ≡ ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) M1,0 = dẑM and therefore
M1,0 = dẑM and therefore ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) L = d(sin
L = d(sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β
β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α, sin
α, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β
β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α, cos
α, cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β) where αβγ are the Euler angles in the ZYZ convention, and in particular β is the angle between the molecular and laboratory ẑ axes. This yields
β) where αβγ are the Euler angles in the ZYZ convention, and in particular β is the angle between the molecular and laboratory ẑ axes. This yields 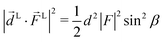 . Written like this, the second order coefficients
. Written like this, the second order coefficients ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (2)l,m(k) take the form of the first order coefficients
(2)l,m(k) take the form of the first order coefficients ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (1)l,m for an anisotropic (in this case anti-aligned) sample with an orientation distribution given by w(β) ∝ sin2
(1)l,m for an anisotropic (in this case anti-aligned) sample with an orientation distribution given by w(β) ∝ sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β and an initial state |1〉 instead of |0〉 (see also ref. 11, 30 and 58). Such anisotropy gives a certain preference to the z components of the molecular vectors. Performing the orientation averaging according to ref. 46, the expressions for the total absorption b(2)0,0, and for the enantio-sensitive terms b(2)1,0 and b(2)3,0 yield (see ESI† and ref. 17)
β and an initial state |1〉 instead of |0〉 (see also ref. 11, 30 and 58). Such anisotropy gives a certain preference to the z components of the molecular vectors. Performing the orientation averaging according to ref. 46, the expressions for the total absorption b(2)0,0, and for the enantio-sensitive terms b(2)1,0 and b(2)3,0 yield (see ESI† and ref. 17)| | 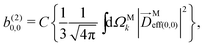 | (28) |
| | 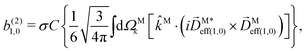 | (29) |
| | 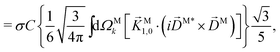 | (30) |
| | 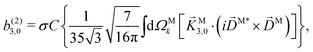 | (31) |
where C ≡ d2|F|4|A(2)|2 is a common factor to all b(2)l,m coefficients that simply encodes the bound-bound transition and the second order character of the process, and the expressions for ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) Meff(0,0),
Meff(0,0), ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) Meff(1,0),
Meff(1,0), ![[K with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004b_20d1.gif) M1,0, and
M1,0, and ![[K with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004b_20d1.gif) M3,0 are given below. We wrote eqn (28)–(31) so that we can draw a parallel to the corresponding eqn (12) and (13) in the one-photon case. Eqn (28) and (29) show that we can recover the forms obtained in the one-photon case if we introduce effectively stretched photoionization dipoles given by
M3,0 are given below. We wrote eqn (28)–(31) so that we can draw a parallel to the corresponding eqn (12) and (13) in the one-photon case. Eqn (28) and (29) show that we can recover the forms obtained in the one-photon case if we introduce effectively stretched photoionization dipoles given by| | 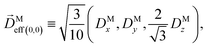 | (32) |
and| | 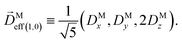 | (33) |
In view of the discussion in Section 4, eqn (28) shows that b(2)0,0 records the ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M-averaged magnitude of an effective photoionization dipole
M-averaged magnitude of an effective photoionization dipole ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) Meff(0,0)(
Meff(0,0)(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M). Similarly, eqn (29) shows that b(2)1,0 records the “circular polarization” [see eqn (18)] or equivalently the
M). Similarly, eqn (29) shows that b(2)1,0 records the “circular polarization” [see eqn (18)] or equivalently the ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M-averaged value of the
M-averaged value of the ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M-specific CD of an effective photoionization dipole
M-specific CD of an effective photoionization dipole ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) Meff(1,0)(
Meff(1,0)(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M). Their ratio,
M). Their ratio, 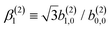 , can be interpreted as the average “circular polarization” of
, can be interpreted as the average “circular polarization” of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) Meff(1,0) normalized with respect to the average magnitude of
Meff(1,0) normalized with respect to the average magnitude of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) Meff(0,0).
Meff(0,0).
In the case of b(2)3,0, quadratic terms in kz (see ESI†) hinder a straightforward interpretation of the integrand in terms of an effectively stretched ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M. However, like b(1)1,0 and b(2)1,0 [eqn (13) and (30)], eqn (31) shows that b(2)3,0 depends on the photoionization dipole
M. However, like b(1)1,0 and b(2)1,0 [eqn (13) and (30)], eqn (31) shows that b(2)3,0 depends on the photoionization dipole ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) only through the
M) only through the ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M-dependent field29,30
M-dependent field29,30
and we can therefore attempt an interpretation of
b(2)3,0 in terms of
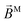
directly.
We have already found rigorous physical interpretations for the projections ÂM·![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M for ÂM =
M for ÂM = ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) M, ŷM, ẑM,
M, ŷM, ẑM, ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M (see ref. 30 and Section 4). In these cases we found that ÂM·
M (see ref. 30 and Section 4). In these cases we found that ÂM·![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M yields the
M yields the ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M-specific CD associated to the transition |0〉 → |
M-specific CD associated to the transition |0〉 → |![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M〉 for light circularly polarized with respect to the axis ÂM (see Fig. 3). In fact, this interpretation is valid for an arbitrary ÂM. To see this, note that for a given ÂM one can always build ÂM-dependent unit vectors êM± associated to positive and negative rotations around ÂM, write
M〉 for light circularly polarized with respect to the axis ÂM (see Fig. 3). In fact, this interpretation is valid for an arbitrary ÂM. To see this, note that for a given ÂM one can always build ÂM-dependent unit vectors êM± associated to positive and negative rotations around ÂM, write 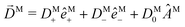 and obtain
and obtain 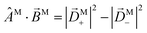 . This scalar product is evidently maximized for ÂM =
. This scalar product is evidently maximized for ÂM = ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) M, and therefore the direction of
M, and therefore the direction of ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M indicates the axis with respect to which the
M indicates the axis with respect to which the ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M-specific CD is maximal. The magnitude of
M-specific CD is maximal. The magnitude of ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M is then the magnitude of such maximal
M is then the magnitude of such maximal ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M-specific CD. Light circularly polarized with respect to axes perpendicular to
M-specific CD. Light circularly polarized with respect to axes perpendicular to ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M yield zero
M yield zero ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M-specific CD.
M-specific CD.
While eqn (13) shows that b(1)1,0 involves the projection of ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M on the radial vector
M on the radial vector ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M, eqn (30) and (31) show that b(2)1,0 and b(2)3,0 involve the projection of
M, eqn (30) and (31) show that b(2)1,0 and b(2)3,0 involve the projection of ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M on the vector fields
M on the vector fields ![[K with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004b_20d1.gif) M1,0 and
M1,0 and ![[K with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004b_20d1.gif) M3,0, respectively, defined as (see ESI†)
M3,0, respectively, defined as (see ESI†)
| | 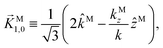 | (35) |
| | 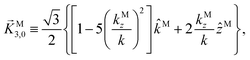 | (36) |
and shown in
Fig. 6 as a function of
θMk on a plane parallel to
kMz. The integrations over all
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M
M directions in
eqn (29) and (31) tell us that
b(2)1,0 and
b(2)3,0 record the extent to which the vector field
![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M
M resembles the vector fields
![[K with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004b_20d1.gif) M1,0
M1,0 and
![[K with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004b_20d1.gif) M3,0
M3,0, respectively, and therefore record structural information about
![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M
M. Such information can be made more explicit by expanding
![[K with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004b_20d1.gif) M1,0
M1,0,
![[K with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004b_20d1.gif) M3,0
M3,0, and
![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M
M in terms of vector spherical harmonics
59
, and
,
| | 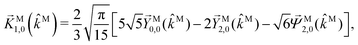 | (37) |
| | 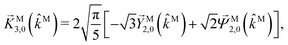 | (38) |
| | 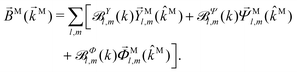 | (39) |
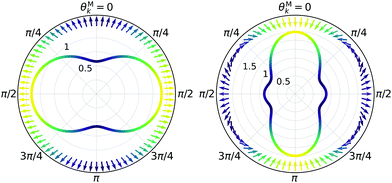 |
| | Fig. 6 Direction (arrows) and magnitude (color and solid lines) of the vector fields ![[K with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004b_20d1.gif) M1,0( M1,0(![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M) and M) and ![[K with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004b_20d1.gif) M3,0( M3,0(![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M) in eqn (35) and (36). M) in eqn (35) and (36). | |
Replacing eqn (34), (37)–(39) in eqn (30) and (31) and using the orthonormality relations for the vector spherical harmonics,59 we obtain
| | 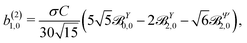 | (40) |
| | 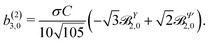 | (41) |
That is, while in the one-photon case
b(1)1,0 encodes
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) Y0,0
Y0,0 (because
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M
M ∝
![[Y with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0059_20d1.gif) M0,0
M0,0), in the two-photon case
b(2)1,0 and
b(2)3,0 encode
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) Y0,0
Y0,0,
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) Y2,0
Y2,0, and
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) Ψ2,0
Ψ2,0. This motivates looking for a third linearly independent equation to solve for
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) Y0,0
Y0,0,
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) Y2,0
Y2,0, and
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) Ψ2,0
Ψ2,0. This is delivered by the equation for
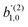
for the complementary process where the first photon is linearly polarized along
ẑL and the second photon is circularly polarized in the
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) LŷL
LŷL plane (see ESI
†),
| | 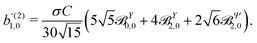 | (42) |
Eqn (42) together with (40) and (41) yield
| | 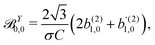 | (43) |
| | 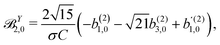 | (44) |
| | 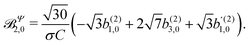 | (45) |
These coefficients quantify the contributions of the fields ![[Y with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0059_20d1.gif) M0,0(
M0,0(![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M) ∝
M) ∝ ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M,
M, ![[Y with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0059_20d1.gif) M2,0(
M2,0(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) ∝ (3
M) ∝ (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θMk − 1)
θMk − 1)![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M, and
M, and ![[capital Psi, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e6.gif) M2,0(
M2,0(![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M) ∝ −cos
M) ∝ −cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θMk
θMk![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θMk
θMk![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) Mk to the total field
Mk to the total field ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M(
M(![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M) [eqn (34)]. Eqn (43)–(45) thus clearly show how structural information of the molecular field
M) [eqn (34)]. Eqn (43)–(45) thus clearly show how structural information of the molecular field ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M(
M(![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M) can be reconstructed from photoelectron angular distributions resulting from an initially isotropic sample of chiral molecules.
M) can be reconstructed from photoelectron angular distributions resulting from an initially isotropic sample of chiral molecules.
In Table VII of ref. 11, the resonantly enhanced two-photon ionization of camphor with circularly polarized light yields**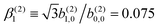 and
and 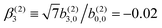 . While this is not enough to reconstruct
. While this is not enough to reconstruct ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) Y0,0,
Y0,0, ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) Y2,0, and
Y2,0, and ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) Ψ2,0 using eqn (43)–(45), it is enough to state that
Ψ2,0 using eqn (43)–(45), it is enough to state that 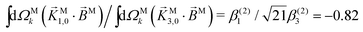 . That is, the overlap between
. That is, the overlap between ![[K with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004b_20d1.gif) M1,0 and
M1,0 and ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M is only slightly smaller than that between
M is only slightly smaller than that between ![[K with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004b_20d1.gif) M3,0 and
M3,0 and ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M.
M.
6 Conclusions
We have presented an alternative approach to obtain expressions for the b(N)l,m coefficients of photoelectron angular distributions resulting from perturbative N-photon ionization of isotropic samples. These expressions are explicitly written in terms of products between the molecular rotational invariants and the setup rotational invariants, and do not invoke a partial wave expansion for the scattering wave function. The molecular rotational invariants are expressed in terms of vector products involving only molecular vectors: transition dipoles and the photoelectron momentum labeling a particular scattering state in the molecular frame. The setup rotational invariants are expressed in terms of vector products involving only setup vectors: field polarization vectors and detection axes. Our expressions reveal how the molecular rotational invariants are coupled to the setup rotational invariants. Knowledge of this coupling can assist the interpretation and design of future experiments and simulations. The standard expressions can be recovered by subsequent expansion of the scattering wave function if needed.
With the help of this methodology we found that, independently of the polarization of the field, enantio-sensitive  coefficients resulting from interference between pathways involving N1 and N2 photons have odd l + N1 + N2.
coefficients resulting from interference between pathways involving N1 and N2 photons have odd l + N1 + N2.
The application of our methodology to the case of one-photon ionization |0〉 → |![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉 reveals a clear meaning for the molecular information encoded in each of the b(1)l,m coefficients, which is otherwise obscured in the usual (and equivalent) formulation in terms of partial waves: b(1)0,0 encodes the average magnitude of the photoionization dipole
〉 reveals a clear meaning for the molecular information encoded in each of the b(1)l,m coefficients, which is otherwise obscured in the usual (and equivalent) formulation in terms of partial waves: b(1)0,0 encodes the average magnitude of the photoionization dipole ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) ≡ 〈
) ≡ 〈![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) |
|![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) |0〉; b(1)1,0 encodes the average radial component of the field
|0〉; b(1)1,0 encodes the average radial component of the field ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) ≡ i
≡ i![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) * ×
* × ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) ,29,30 which in turn encodes the average ‘circular dichroism’ of
,29,30 which in turn encodes the average ‘circular dichroism’ of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) and depends only on its transverse components; and b(1)2,0 encodes the average radial component of
) and depends only on its transverse components; and b(1)2,0 encodes the average radial component of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ). The averages are taken with respect to the direction of the photoelectron momentum
). The averages are taken with respect to the direction of the photoelectron momentum ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) in the molecular frame. b(1)1,0 is sensitive to a single coefficient of the vector spherical harmonic expansion of
in the molecular frame. b(1)1,0 is sensitive to a single coefficient of the vector spherical harmonic expansion of ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ).
).
We also derived expressions for the coefficients b(2)0,0, b(2)1,0, and b(2)3,0 relevant for two-photon resonantly enhanced ionization |0〉 → |1〉 → |![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉 of isotropic chiral samples with circularly polarized light. The coefficients b(2)0,0 and b(2)1,0 have analogous interpretations to those found in the one-photon case provided one takes into account an effective anisotropic stretching of the photoionization dipoles. b(2)1,0 and b(2)3,0 yield structural information about the propensity field
〉 of isotropic chiral samples with circularly polarized light. The coefficients b(2)0,0 and b(2)1,0 have analogous interpretations to those found in the one-photon case provided one takes into account an effective anisotropic stretching of the photoionization dipoles. b(2)1,0 and b(2)3,0 yield structural information about the propensity field ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) ≡ i
≡ i![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) * ×
* × ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) ,29,30 which encodes the
,29,30 which encodes the ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) -specific circular dichroism. In particular they depend only on three coefficients of the vector spherical harmonic expansion of
-specific circular dichroism. In particular they depend only on three coefficients of the vector spherical harmonic expansion of ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ). These coefficients can be solved for in terms of b(2)1,0, b(2)3,0, and
). These coefficients can be solved for in terms of b(2)1,0, b(2)3,0, and  , where the latter corresponds to the process where the first photon is linearly polarized.
, where the latter corresponds to the process where the first photon is linearly polarized.
Further application of the methodology introduced here can be found in ref. 39, where it is used to analyze the enantio-sensitive asymmetry recently found in the photoelectron angular distributions resulting from interaction of chiral samples with a field containing ω and 2ω frequencies linearly polarized orthogonal to each other.18,54
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
A. F. O. and O. S. gratefully acknowledge the MEDEA Project, which has received funding from the European Union's Horizon 2020 Research and Innovation Programme under the Marie Skłodowska-Curie Grant Agreement No. 641789. A. F. O. and O. S. gratefully acknowledge support from the DFG SPP 1840 “Quantum Dynamics in Tailored Intense Fields” and DFG Grant No. SM 292/5-2. A. F. O. gratefully acknowledges grants supporting his research at ICFO: Agencia Estatal de Investigación (the R&D project CEX2019-000910-S, funded by MCIN/AEI/10.13039/501100011033, Plan Nacional FIDEUA PID2019-106901GB-I00, FPI), Fundació Privada Cellex, Fundació Mir-Puig, Generalitat de Catalunya (AGAUR Grant No. 2017 SGR 1341, CERCA program), and EU Horizon 2020 Marie Skłodowska-Curie grant agreement no. 101029393.
Notes and references
- A. Stolow, A. E. Bragg and D. M. Neumark, Chem. Rev., 2004, 104, 1719–1758 CrossRef CAS PubMed.
-
A. Stolow and J. G. Underwood, Advances in Chemical Physics, John Wiley & Sons, Ltd, 2008, pp. 497–584 Search PubMed.
- K. L. Reid, Mol. Phys., 2012, 110, 131–147 CrossRef CAS.
- B. Ritchie, Phys. Rev. A, 1976, 13, 1411 CrossRef.
- I. Powis, J. Chem. Phys., 2000, 112, 301–310 CrossRef CAS.
- N. Böwering, T. Lischke, B. Schmidtke, N. Müller, T. Khalil and U. Heinzmann, Phys. Rev. Lett., 2001, 86, 1187–1190 CrossRef PubMed.
- V. Ulrich, S. Barth, S. Joshi, U. Hergenhahn, E. Mikajlo, C. J. Harding and I. Powis, J. Phys. Chem. A, 2008, 112, 3544–3549 CrossRef CAS PubMed.
- M. H.-M. Janssen and I. Powis, Phys. Chem. Chem. Phys., 2013, 16, 856–871 RSC.
- L. Nahon, G. A. Garcia and I. Powis, J. Electron Spectrosc. Relat. Phenom., 2015, 204(Part B), 322–334 CrossRef CAS.
- C. Lux, M. Wollenhaupt, T. Bolze, Q. Liang, J. Köhler, C. Sarpe and T. Baumert, Angew. Chem., Int. Ed., 2012, 51, 5001–5005 CrossRef CAS PubMed.
- C. S. Lehmann, R. B. Ram, I. Powis and M. H.-M. Jansenn, J. Chem. Phys., 2013, 139, 234307 CrossRef PubMed.
- I. Dreissigacker and M. Lein, Phys. Rev. A, 2014, 89, 053406 CrossRef.
- S. Beaulieu, A. Ferré, R. Géneaux, R. Canonge, D. Descamps, B. Fabre, N. Fedorov, F. Légaré, S. Petit, T. Ruchon, V. Blanchet, Y. Mairesse and B. Pons, New J. Phys., 2016, 18, 102002 CrossRef.
- S. Beaulieu, A. Comby, A. Clergerie, J. Caillat, D. Descamps, N. Dudovich, B. Fabre, R. Géneaux, F. Légaré, S. Petit, B. Pons, G. Porat, T. Ruchon, R. Taïeb, V. Blanchet and Y. Mairesse, Science, 2017, 358, 1288–1294 CrossRef CAS PubMed.
- A. Comby, S. Beaulieu, M. Boggio-Pasqua, D. Descamps, F. Légaré, L. Nahon, S. Petit, B. Pons, B. Fabre, Y. Mairesse and V. Blanchet, J. Phys. Chem. Lett., 2016, 7, 4514–4519 CrossRef CAS PubMed.
- S. Beaulieu, A. Comby, D. Descamps, B. Fabre, G. A. Garcia, R. Géneaux, A. G. Harvey, F. Légaré, Z. Mašín, L. Nahon, A. F. Ordonez, S. Petit, B. Pons, Y. Mairesse, O. Smirnova and V. Blanchet, Nat. Phys., 2018, 14, 484–489 Search PubMed.
- A. F. Ordonez and O. Smirnova, Phys. Rev. A, 2018, 98, 063428 CrossRef CAS.
- P. V. Demekhin, A. N. Artemyev, A. Kastner and T. Baumert, Phys. Rev. Lett., 2018, 121, 253201 CrossRef CAS PubMed.
- R. E. Goetz, C. P. Koch and L. Greenman, Phys. Rev. Lett., 2019, 122, 013204 CrossRef CAS PubMed.
- J. C. Tully, R. S. Berry and B. J. Dalton, Phys. Rev., 1968, 176, 95–105 CrossRef CAS.
- D. Dill, J. Chem. Phys., 1976, 65, 1130–1133 CrossRef CAS.
- R. R. Lucchese, G. Raseev and V. McKoy, Phys. Rev. A, 1982, 25, 2572–2587 CrossRef CAS.
- S. N. Dixit and V. McKoy, J. Chem. Phys., 1985, 82, 3546–3553 CrossRef CAS.
- N. Chandra, J. Phys. B: At. Mol. Phys., 1987, 20, 3405 CrossRef CAS.
- D. J. Leahy, K. L. Reid and R. N. Zare, J. Chem. Phys., 1991, 95, 1757–1767 CrossRef CAS.
- K. L. Reid, D. J. Leahy and R. N. Zare, J. Chem. Phys., 1991, 95, 1746–1756 CrossRef CAS.
- J. G. Underwood and K. L. Reid, J. Chem. Phys., 2000, 113, 1067–1074 CrossRef CAS.
- P. Decleva, M. Stener and D. Toffoli, Molecules, 2022, 27, 2026 CrossRef CAS PubMed.
-
A. F. Ordonez, D. Ayuso, P. Decleva and O. Smirnova, 2021, arXiv:2106.14264 [physics].
- A. F. Ordonez and O. Smirnova, Phys. Rev. A, 2019, 99, 043417 CrossRef CAS.
- M. V. Berry, Proc. R. Soc. A, 1984, 392, 45–57 Search PubMed.
- R. Resta, J. Phys.: Condens. Matter, 2000, 12, R107–R143 CrossRef CAS.
- S. Tsesses, E. Ostrovsky, K. Cohen, B. Gjonaj, N. H. Lindner and G. Bartal, Science, 2018, 361, 993–996 CrossRef CAS PubMed.
- L. Du, A. Yang, A. V. Zayats and X. Yuan, Nat. Phys., 2019, 15, 650–654 Search PubMed.
- E. Pisanty, G. J. Machado, V. Vicuña-Hernández, A. Picón, A. Celi, J. P. Torres and M. Lewenstein, Nat. Photonics, 2019, 13, 569–574 CrossRef CAS.
- R. Gutiérrez-Cuevas and E. Pisanty, J. Opt., 2021, 23, 024004 CrossRef.
- Y. Tokura and N. Kanazawa, Chem. Rev., 2021, 121, 2857–2897 CrossRef CAS PubMed.
- G. Sundaram and Q. Niu, Phys. Rev. B, 1999, 59, 14915–14925 CrossRef CAS.
- A. F. Ordonez and O. Smirnova, Phys. Chem. Chem. Phys., 2022, 24, 7264 RSC.
- K. L. Reid, Annu. Rev. Phys. Chem., 2003, 54, 397–424 CrossRef CAS PubMed.
-
I. Powis, Advances in Chemical Physics, John Wiley & Sons, Inc., 2008, vol. 138, pp. 267–329 Search PubMed.
- M. Stener, G. Fronzoni, D. D. Tomasso and P. Decleva, J. Chem. Phys., 2004, 120, 3284–3296 CrossRef CAS PubMed.
- A. Giardini, D. Catone, S. Stranges, M. Satta, M. Tacconi, S. Piccirillo, S. Turchini, N. Zema, G. Contini, T. Prosperi, P. Decleva, D. D. Tommaso, G. Fronzoni, M. Stener, A. Filippi and M. Speranza, ChemPhysChem, 2005, 6, 1164–1168 CrossRef CAS PubMed.
- C. J. Harding and I. Powis, J. Chem. Phys., 2006, 125, 234306 CrossRef PubMed.
- D. D. Tommaso, M. Stener, G. Fronzoni and P. Decleva, ChemPhysChem, 2006, 7, 924–934 CrossRef PubMed.
- D. L. Andrews and T. Thirunamachandran, J. Chem. Phys., 1977, 67, 5026–5033 CrossRef CAS.
- M. Stener, D. Di Tommaso, G. Fronzoni, P. Decleva and I. Powis, J. Chem. Phys., 2006, 124, 024326 CrossRef CAS PubMed.
- Z. Lu, J. E. Oakman, Q. Hu and R. E. Continetti, Mol. Phys., 2008, 106, 595–606 CrossRef CAS.
- M. Staniforth, S. Daly, K. L. Reid and I. Powis, J. Chem. Phys., 2013, 139, 064304 CrossRef PubMed.
- M. M. Rafiee Fanood, M. H.-M. Janssen and I. Powis, J. Chem. Phys., 2016, 145, 124320 CrossRef PubMed.
- C. Lux, M. Wollenhaupt, C. Sarpe and T. Baumert, ChemPhysChem, 2015, 16, 115–137 CrossRef CAS PubMed.
-
D. M. Brink and G. R. Satchler, Angular Momentum, Clarendon Press, Oxford, 2nd edn, 1968 Search PubMed.
- M. M. Rafiee Fanood, I. Powis and M. H.-M. Janssen, J. Phys. Chem. A, 2014, 118, 11541–11546 CrossRef CAS PubMed.
- P. V. Demekhin, Phys. Rev. A, 2019, 99, 063406 CrossRef CAS.
-
D. A. Varschalovich, A. N. Moskalev and V. K. Khersonskii, Quantum Theory of Angular Momentum, World Scientific, 1988 Search PubMed.
-
J. D. Jackson, Classical Electrodynamics, John Wiley & Sons, 3rd edn, 1999 Search PubMed.
- A. F. Ordonez and O. Smirnova, Phys. Rev. A, 2019, 99, 043416 CrossRef CAS.
- R. E. Goetz, T. A. Isaev, B. Nikoobakht, R. Berger and C. P. Koch, J. Chem. Phys., 2017, 146, 024306 CrossRef CAS PubMed.
- R. G. Barrera, G. A. Estevez and J. Giraldo, Eur. J. Phys., 1985, 6, 287 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d1cp05645j |
| ‡ We will use tildes to distinguish the real spherical harmonics Ỹl,m from the usual complex spherical harmonics Yl,m (see ESI†). For m = 0 we will omit the tilde. |
§ Note that the expressions (12)–(15) apply for arbitrary polarization of the electric field (in particular for linear polarization along ẑL). The assumption that the field is contained in the xy plane with its major axis along ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L or ŷL simply serves the purpose of reducing the number of non-zero L or ŷL simply serves the purpose of reducing the number of non-zero ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (1)l,m coefficients. (1)l,m coefficients. |
¶ The factor of 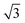 in eqn (21) and in eqn (21) and 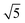 in eqn (22) are included to recover the ratio obtained when the expansion is done in terms of Legendre polynomials (instead spherical harmonics), as is usual for the cylindrically symmetric cases when the light is either linearly polarized along z or circularly polarized in the xy plane. in eqn (22) are included to recover the ratio obtained when the expansion is done in terms of Legendre polynomials (instead spherical harmonics), as is usual for the cylindrically symmetric cases when the light is either linearly polarized along z or circularly polarized in the xy plane. |
| || The notation used in the figures of ref. 47 is defined in eqn (1) there. |
| ** The notation used in Table VII of ref. 11 is defined in eqn (8) there. |
|
| This journal is © the Owner Societies 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ab and
Olga
Smirnova
ab and
Olga
Smirnova
 ac
ac
![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) ≡ 〈
) ≡ 〈![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) |
|![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) |0〉 describing the electronic transition from a bound state |0〉 into a scattering state |
|0〉 describing the electronic transition from a bound state |0〉 into a scattering state |![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉 – the photoionization transition dipole. Besides revealing selection rules for the enantio-sensitivity of bl,m coefficients in multiphoton ionization, our approach yields very compact expressions for both chiral and achiral molecules revealing how the molecular rotational invariants couple to the rotational invariants of the setup defined by the electric field polarization and the arrangement of photoelectron detectors. We apply this approach to one-photon ionization and find that the forward–backward asymmetry parameter b1,0, emerging exclusively in chiral molecules and encoded in the field
〉 – the photoionization transition dipole. Besides revealing selection rules for the enantio-sensitivity of bl,m coefficients in multiphoton ionization, our approach yields very compact expressions for both chiral and achiral molecules revealing how the molecular rotational invariants couple to the rotational invariants of the setup defined by the electric field polarization and the arrangement of photoelectron detectors. We apply this approach to one-photon ionization and find that the forward–backward asymmetry parameter b1,0, emerging exclusively in chiral molecules and encoded in the field ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) ≡ i
) ≡ i![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) *(
*(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) ×
) × ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ), is sensitive only to the components of
), is sensitive only to the components of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) perpendicular to
) perpendicular to ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) , while the regular asymmetry parameter b2,0 emerging in chiral and achiral molecules is sensitive only to the component of
, while the regular asymmetry parameter b2,0 emerging in chiral and achiral molecules is sensitive only to the component of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) parallel to
) parallel to ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) . Next, we analyze resonantly enhanced two-photon ionization and show that b0,0 and b1,0 can be written in terms of an effectively stretched
. Next, we analyze resonantly enhanced two-photon ionization and show that b0,0 and b1,0 can be written in terms of an effectively stretched ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ), and how b1,0 and b3,0 can be used to probe
), and how b1,0 and b3,0 can be used to probe ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ).
).![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉, these states are subsequently encapsulated into photoionization transition dipoles
〉, these states are subsequently encapsulated into photoionization transition dipoles ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) ≡ 〈
) ≡ 〈![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) |
|![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) |0〉, and these dipoles are in turn used to calculate the laboratory-frame PAD. The last step requires averaging over molecular orientations and drastically reduces the amount of information contained in the vector field
|0〉, and these dipoles are in turn used to calculate the laboratory-frame PAD. The last step requires averaging over molecular orientations and drastically reduces the amount of information contained in the vector field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) to a handful of coefficients bl,m describing the laboratory-frame PAD in terms of spherical harmonics Yml(
) to a handful of coefficients bl,m describing the laboratory-frame PAD in terms of spherical harmonics Yml(![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) ) (see e.g. ref. 4). So we might as well ask: what do these few bl,mcoefficients tell us about the molecular-frame vector field
) (see e.g. ref. 4). So we might as well ask: what do these few bl,mcoefficients tell us about the molecular-frame vector field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) )? Answering this question is the main objective of this paper.
)? Answering this question is the main objective of this paper.![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ). A previous version of this approach limited to b0,0 and b1,0 has already proven to be very useful for photoionization of chiral molecules (see ref. 17 and 29). We expect the general version provided here to be useful beyond chiral molecules and throughout the field of molecular photoionization for comparison of different non-linear signals generated due to fields with complex geometries.
). A previous version of this approach limited to b0,0 and b1,0 has already proven to be very useful for photoionization of chiral molecules (see ref. 17 and 29). We expect the general version provided here to be useful beyond chiral molecules and throughout the field of molecular photoionization for comparison of different non-linear signals generated due to fields with complex geometries.![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) and about the associated field
) and about the associated field ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) ≡ i
) ≡ i![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) *(
*(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) ×
) × ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ), which plays a central role in the photoionization of chiral molecules.29,30 The geometrical character of our findings suggests potential connections to geometrical and topological properties31,32 in other research fields such as structured light,33–36 magnetism,37 and electron dynamics in crystals.38
), which plays a central role in the photoionization of chiral molecules.29,30 The geometrical character of our findings suggests potential connections to geometrical and topological properties31,32 in other research fields such as structured light,33–36 magnetism,37 and electron dynamics in crystals.38![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) ≡ i
) ≡ i![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) *(
*(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) ×
) × ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) )29,30 from the bl,m coefficients. Section 6 concludes the work. Further applications of the approach presented here can be found in ref. 29 and 39.
)29,30 from the bl,m coefficients. Section 6 concludes the work. Further applications of the approach presented here can be found in ref. 29 and 39.![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) are encoded in bl,m. For example, in chiral molecules, this approach obscures the connection between b1,0 (describing PECD) and the geometry of
) are encoded in bl,m. For example, in chiral molecules, this approach obscures the connection between b1,0 (describing PECD) and the geometry of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) beyond the fact that b1,0 results from complex interference of many (about 15, see ref. 41–45) partial waves.
) beyond the fact that b1,0 results from complex interference of many (about 15, see ref. 41–45) partial waves.
![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) and show how the geometry of the vector field
) and show how the geometry of the vector field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) maps into the bl,mcoefficients.
) maps into the bl,mcoefficients.![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) is detected in the laboratory frame and keeping it in this frame throughout PAD derivations is the usual practice,4 its natural frame of reference is the molecular frame. This is because
is detected in the laboratory frame and keeping it in this frame throughout PAD derivations is the usual practice,4 its natural frame of reference is the molecular frame. This is because ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) labels the electronic scattering wave function, which, like the bound electronic wave functions, is fixed in the molecular frame. Fig. 1 illustrates that scattering states having the same
labels the electronic scattering wave function, which, like the bound electronic wave functions, is fixed in the molecular frame. Fig. 1 illustrates that scattering states having the same ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) in the laboratory frame (
in the laboratory frame (![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 1 and
1 and 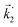 ) but corresponding to different molecular orientations are not related to each other in any simple way, while scattering states having the same
) but corresponding to different molecular orientations are not related to each other in any simple way, while scattering states having the same ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) in the molecular frame (
in the molecular frame (![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 1 and
1 and 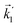 ) are related to each other via a simple rotation of their wave functions.
) are related to each other via a simple rotation of their wave functions.![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) -dependent molecular vector fields. Such fields are unique to every molecule and encode its structure. Thus, the key differences of our approach from the standard approach are (i) avoiding partial wave expansion of scattering states, (ii) keeping the photoelectron momentum
-dependent molecular vector fields. Such fields are unique to every molecule and encode its structure. Thus, the key differences of our approach from the standard approach are (i) avoiding partial wave expansion of scattering states, (ii) keeping the photoelectron momentum ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) in the molecular frame, and (iii) exchanging the order of integrals over the molecular orientations and over the orientations of
in the molecular frame, and (iii) exchanging the order of integrals over the molecular orientations and over the orientations of ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) . This approach reveals physics that are otherwise obscured by the partial wave expansion. Naturally, the standard expressions can also be recovered from our representation. Note that we are not suggesting that our approach allows the numerical calculation of the bl,m coefficients without doing a partial wave expansion. The partial wave expansion may still be needed for the computation of
. This approach reveals physics that are otherwise obscured by the partial wave expansion. Naturally, the standard expressions can also be recovered from our representation. Note that we are not suggesting that our approach allows the numerical calculation of the bl,m coefficients without doing a partial wave expansion. The partial wave expansion may still be needed for the computation of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ), but what we are interested in is the connection between bl,m and
), but what we are interested in is the connection between bl,m and ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ), not the calculation of
), not the calculation of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) itself.
) itself.![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) L) given by
L) given by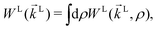
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) L, ρ) is the photoelectron spectrum for a given molecular orientation ρ ≡ αβγ, αβγ are the Euler angles,
L, ρ) is the photoelectron spectrum for a given molecular orientation ρ ≡ αβγ, αβγ are the Euler angles, 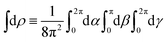 is the integral over all molecular orientations, and the superscript L indicates vectors and functions in the laboratory frame. Since we can always expand WL(
is the integral over all molecular orientations, and the superscript L indicates vectors and functions in the laboratory frame. Since we can always expand WL(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) L) into real spherical harmonics‡Ỹml(
L) into real spherical harmonics‡Ỹml(![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) L),
L),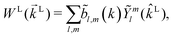
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) L) is now neatly summarized in the expansion coefficients
L) is now neatly summarized in the expansion coefficients ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m(k),
l,m(k),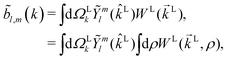
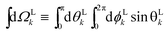 ,
, ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) L = (1, θLk, ϕLk) in spherical coordinates, and
L = (1, θLk, ϕLk) in spherical coordinates, and ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) L = k
L = k![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) L. Measured as well as calculated values for these coefficients for particular systems can be found for example in ref. 7, 25, 26 and 47–51.
L. Measured as well as calculated values for these coefficients for particular systems can be found for example in ref. 7, 25, 26 and 47–51.
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M, ρ) = WL(
M, ρ) = WL(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) L, ρ), or equivalently WM(S−1(ρ)
L, ρ), or equivalently WM(S−1(ρ)![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) L, ρ) = WL(
L, ρ) = WL(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) L, ρ), where
L, ρ), where ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) L = S(ρ)
L = S(ρ)![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M and S(ρ) is the rotation matrix that takes vectors from the molecular to the laboratory frame and the superscript M indicates vectors and functions in the molecular frame. This means that
M and S(ρ) is the rotation matrix that takes vectors from the molecular to the laboratory frame and the superscript M indicates vectors and functions in the molecular frame. This means that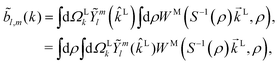
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M = S−1(ρ)
M = S−1(ρ)![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) L, which only exists inside the integral over orientations and yields
L, which only exists inside the integral over orientations and yields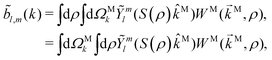
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M is an integration variable independent of ρ. At this point two questions arise: Why would we want to have the photoelectron momentum in the molecular frame instead of having it in the laboratory frame, where the photoelectron is actually measured? And why would we prefer to do the integral over orientations in eqn (5) instead of the apparently simpler integral over orientations in eqn (3)? The answer to both questions has to do with the form that the photoelectron spectrum WM(
M is an integration variable independent of ρ. At this point two questions arise: Why would we want to have the photoelectron momentum in the molecular frame instead of having it in the laboratory frame, where the photoelectron is actually measured? And why would we prefer to do the integral over orientations in eqn (5) instead of the apparently simpler integral over orientations in eqn (3)? The answer to both questions has to do with the form that the photoelectron spectrum WM(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M, ρ) takes in the case of ionization in the perturbative regime.
M, ρ) takes in the case of ionization in the perturbative regime.
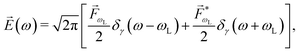
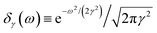 and the resulting second-order contribution to the probability amplitude of the scattering state |
and the resulting second-order contribution to the probability amplitude of the scattering state |![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M〉 reads as
M〉 reads as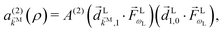
![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) i,j ≡ 〈i|
i,j ≡ 〈i|![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) |j〉 is the transition dipole matrix element and A(2) is a function of the difference of the level spacings ωk1 − ω10, the total detuning 2Δ = ωk0 − 2ωL, and the spectral width γ, ωij ≡ ωi − ωj, ωi is the energy of the state |i〉, and the superscript (2) indicates the order of the process. The photoelectron spectrum in the molecular frame then reads as
|j〉 is the transition dipole matrix element and A(2) is a function of the difference of the level spacings ωk1 − ω10, the total detuning 2Δ = ωk0 − 2ωL, and the spectral width γ, ωij ≡ ωi − ωj, ωi is the energy of the state |i〉, and the superscript (2) indicates the order of the process. The photoelectron spectrum in the molecular frame then reads as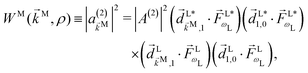
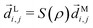 [see eqn (7)]. Replacing in eqn (5) we obtain
[see eqn (7)]. Replacing in eqn (5) we obtain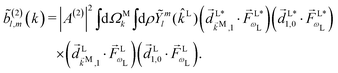
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (μ)(ρ). Similarly, the real spherical harmonic Ỹml(
(μ)(ρ). Similarly, the real spherical harmonic Ỹml(![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) L) is a superposition of two spherical tensors of rank l that transform according to
L) is a superposition of two spherical tensors of rank l that transform according to ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (l)(ρ).52 Then, from eqn (9) and the orthogonality relation of the Wigner matrices52 it is evident that the
(l)(ρ).52 Then, from eqn (9) and the orthogonality relation of the Wigner matrices52 it is evident that the ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (2)l,m coefficients with l > lmax = 4 (in general lmax = 2N) vanish, as is well known. Expressions analogous to eqn (9) can be obtained for the case of fields with multiple frequencies. In the case of terms
(2)l,m coefficients with l > lmax = 4 (in general lmax = 2N) vanish, as is well known. Expressions analogous to eqn (9) can be obtained for the case of fields with multiple frequencies. In the case of terms 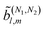 resulting from the interference of pathways involving N1 and N2 photons we get lmax = N1 + N2.
resulting from the interference of pathways involving N1 and N2 photons we get lmax = N1 + N2.![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m becomes a sum of terms of the form
l,m becomes a sum of terms of the form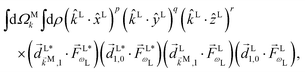
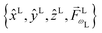 is fixed in the laboratory frame, while the set
is fixed in the laboratory frame, while the set 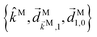 (which appears in the expression above rotated into the laboratory frame
(which appears in the expression above rotated into the laboratory frame ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) L = S(ρ)
L = S(ρ)![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) M) is fixed in the molecular frame. We take
M) is fixed in the molecular frame. We take ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M fixed in the molecular frame because
M fixed in the molecular frame because ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M is the quantum label that characterizes the scattering state |
M is the quantum label that characterizes the scattering state |![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M〉, which (like the bound states) is fixed in the molecular frame (see e.g.Fig. 1). Eqn (10) has the form we wanted to achieve, it is a product of scalar products between vectors fixed in the molecular frame and vectors fixed in the laboratory frame. In this form the integration over orientations can be performed at once applying the technique in ref. 46, which yields a result of the form
M〉, which (like the bound states) is fixed in the molecular frame (see e.g.Fig. 1). Eqn (10) has the form we wanted to achieve, it is a product of scalar products between vectors fixed in the molecular frame and vectors fixed in the laboratory frame. In this form the integration over orientations can be performed at once applying the technique in ref. 46, which yields a result of the form 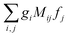 , where the gi are rotational invariants (RIs) formed with the set of vectors fixed in the molecular frame, the fj are RIs formed by the set of vectors fixed in the laboratory frame, and the Mij are constants coupling both sets of RIs. Examples of such invariants will be given in the next section.
, where the gi are rotational invariants (RIs) formed with the set of vectors fixed in the molecular frame, the fj are RIs formed by the set of vectors fixed in the laboratory frame, and the Mij are constants coupling both sets of RIs. Examples of such invariants will be given in the next section.
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (N)l,m such that l is odd, in agreement with previous works (see e.g. ref. 10 and 53). More interestingly, for coefficients
(N)l,m such that l is odd, in agreement with previous works (see e.g. ref. 10 and 53). More interestingly, for coefficients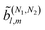 resulting from interference between pathways with N1and N2photons, the condition for enantio-sensitivity is that l + N1 + N2is odd. That is, if N1 + N2is odd, coefficients
resulting from interference between pathways with N1and N2photons, the condition for enantio-sensitivity is that l + N1 + N2is odd. That is, if N1 + N2is odd, coefficients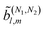 with even l can be enantio-sensitive, in agreement with the recent works in ref. 18 and 54. This is a general condition independent of the polarization of the field and of the photon energies and will be explored in more detail in ref. 39.
with even l can be enantio-sensitive, in agreement with the recent works in ref. 18 and 54. This is a general condition independent of the polarization of the field and of the photon energies and will be explored in more detail in ref. 39.![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M〉 reads as
M〉 reads as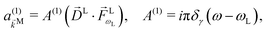
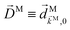 ,
, 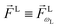 , and as usual
, and as usual ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) L = S(ρ)
L = S(ρ)![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M. From here on, we must keep in mind that
M. From here on, we must keep in mind that ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M =
M = ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) is a complex vector field that depends on
M) is a complex vector field that depends on ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M. That is, for a fixed initial state |0〉,
M. That is, for a fixed initial state |0〉, ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) is a mapping from the space of real three-dimensional vectors
M) is a mapping from the space of real three-dimensional vectors ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M ∈
M ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3 to the space of complex three-dimensional vectors
3 to the space of complex three-dimensional vectors ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M ∈
M ∈ ![[Doublestruck C]](https://www.rsc.org/images/entities/char_e166.gif) 3. From eqn (11) it is clear that this complex vector field fully determines the response of the molecule to the ionizing field and therefore the coefficients
3. From eqn (11) it is clear that this complex vector field fully determines the response of the molecule to the ionizing field and therefore the coefficients ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (1)l,m must correspond to properties of this vector field. The question is: which property of the photoionization vector field
(1)l,m must correspond to properties of this vector field. The question is: which property of the photoionization vector field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) is reflected in a given
M) is reflected in a given ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (1)l,mcoefficient?
(1)l,mcoefficient?
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L or the ŷL axis. From symmetry it follows that the only non-zero
L or the ŷL axis. From symmetry it follows that the only non-zero ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (1)l,m coefficients are b(1)0,0, b(1)1,0, b(1)2,0,
(1)l,m coefficients are b(1)0,0, b(1)1,0, b(1)2,0, ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (1)2,2, and
(1)2,2, and ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (1)2,−2 (we omit the tilde for m = 0). With the help of eqn (5) and (10), and performing the orientation integrals according to ref. 46 we obtain§ (see ESI†)
(1)2,−2 (we omit the tilde for m = 0). With the help of eqn (5) and (10), and performing the orientation integrals according to ref. 46 we obtain§ (see ESI†)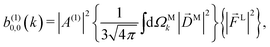
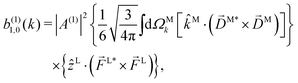
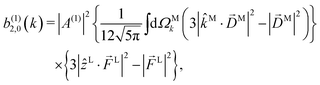
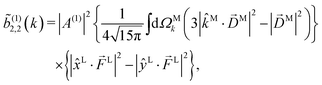
![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (1)2,−2 = 0, a peculiarity of the one-photon case. That is, each
(1)2,−2 = 0, a peculiarity of the one-photon case. That is, each ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (1)l,m coefficient is the product of: a coupling term |A(1)|2 depending on the energy level spacing of the molecule and the spectrum of the electric field, a molecular term expressed in the molecular frame and averaged over all
(1)l,m coefficient is the product of: a coupling term |A(1)|2 depending on the energy level spacing of the molecule and the spectrum of the electric field, a molecular term expressed in the molecular frame and averaged over all ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M directions, and a setup (field and laboratory axes) term expressed in the laboratory frame. Unlike the usual expressions for
M directions, and a setup (field and laboratory axes) term expressed in the laboratory frame. Unlike the usual expressions for ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (1)l,m (see e.g. ref. 4), eqn (12)–(15) provide a rather simple expression for the molecular terms which, as we will now discuss, are simply related to concrete properties of the photoionization vector field
(1)l,m (see e.g. ref. 4), eqn (12)–(15) provide a rather simple expression for the molecular terms which, as we will now discuss, are simply related to concrete properties of the photoionization vector field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ).
).
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M-averaged value of the magnitude of the field
M-averaged value of the magnitude of the field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M). More interestingly, eqn (13) shows that b(1)1,0 is sensitive to the
M). More interestingly, eqn (13) shows that b(1)1,0 is sensitive to the ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M-averaged value of the triple product
M-averaged value of the triple product ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M·(
M·(![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M* ×
M* × ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M), which, unlike b(1)0,0, depends on the angles between
M), which, unlike b(1)0,0, depends on the angles between ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M,
M, ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M, and
M, and ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M*. The meaning of this quantity can be made evident if we use an appropriate basis for our vector field
M*. The meaning of this quantity can be made evident if we use an appropriate basis for our vector field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M. Starting from the unit vectors in spherical coordinates
M. Starting from the unit vectors in spherical coordinates ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) ,
, ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) k, and
k, and  we define spherical vectors
we define spherical vectors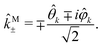
![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M in terms of these contravariant helicity-basis vectors,55
M in terms of these contravariant helicity-basis vectors,55
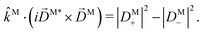
![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M in the direction
M in the direction ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M. Indeed, the right hand side of eqn (18) is proportional to the difference between the probability of inducing the transition |0〉 → |
M. Indeed, the right hand side of eqn (18) is proportional to the difference between the probability of inducing the transition |0〉 → |![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M〉 using left and right circularly polarized light such that left (+) and right (−) rotations are defined with respect to
M〉 using left and right circularly polarized light such that left (+) and right (−) rotations are defined with respect to ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M (see Fig. 3). Therefore, the molecular term in b(1)1,0 is simply the
M (see Fig. 3). Therefore, the molecular term in b(1)1,0 is simply the ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M-averaged value of the
M-averaged value of the ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M-specific CD in the molecular frame. Note that the
M-specific CD in the molecular frame. Note that the ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M-specific CD can be non-zero even for achiral molecules, but its average over
M-specific CD can be non-zero even for achiral molecules, but its average over ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M is only non-zero for chiral molecules. Further discussion of b(1)1,0 can be found in ref. 30. Remarkably, eqn (18) shows that b(1)1,0 depends only on the tangential components of
M is only non-zero for chiral molecules. Further discussion of b(1)1,0 can be found in ref. 30. Remarkably, eqn (18) shows that b(1)1,0 depends only on the tangential components of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M, namely DM+ and DM− (or equivalently DMθ and DMφ). Since the electric field term of b(1)1,0 has the same form as the molecular part we can apply a similar procedure and rewrite b(1)1,0 as
M, namely DM+ and DM− (or equivalently DMθ and DMφ). Since the electric field term of b(1)1,0 has the same form as the molecular part we can apply a similar procedure and rewrite b(1)1,0 as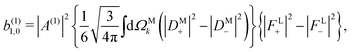
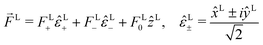
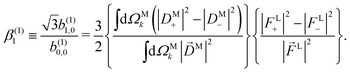
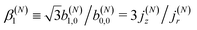 , where j(N)z is the net photoelectron current (i.e. vector sum of photoelectron currents in all directions) and j(N)r is the total photoelectron current (i.e. sum of magnitudes of photoelectron currents in all directions). Eqn (21) shows that the molecular factor is a measure of the degree of “circular polarization” of the photoionization vector field
, where j(N)z is the net photoelectron current (i.e. vector sum of photoelectron currents in all directions) and j(N)r is the total photoelectron current (i.e. sum of magnitudes of photoelectron currents in all directions). Eqn (21) shows that the molecular factor is a measure of the degree of “circular polarization” of the photoionization vector field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) and takes values between −1 and +1, which correspond to the limits
M) and takes values between −1 and +1, which correspond to the limits ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M = DM+
M = DM+![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M+ (left circularly polarized
M+ (left circularly polarized ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M) and
M) and ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M = DM−
M = DM−![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M− (right circularly polarized
M− (right circularly polarized ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M), respectively. Since the electric field factor is also a measure of the circular polarization of the electric field, then β(1)1 = 3j(1)z/j(1)r is given by the product of the
M), respectively. Since the electric field factor is also a measure of the circular polarization of the electric field, then β(1)1 = 3j(1)z/j(1)r is given by the product of the ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M-averaged “circular polarization” of the photoionization vector field
M-averaged “circular polarization” of the photoionization vector field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) and the circular polarization of the ionizing electric field. Clearly, for a known electric field, β(1)1 is a measure of the
M) and the circular polarization of the ionizing electric field. Clearly, for a known electric field, β(1)1 is a measure of the ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M-averaged “circular polarization” of
M-averaged “circular polarization” of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M). Finally, eqn (21) shows that |β(1)1| ≤ 1.5, with the maximal value taking place for circularly polarized light and a “circularly polarized”
M). Finally, eqn (21) shows that |β(1)1| ≤ 1.5, with the maximal value taking place for circularly polarized light and a “circularly polarized” ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M vector field, or equivalently, a purely longitudinal
M vector field, or equivalently, a purely longitudinal ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M ≡ i
M ≡ i![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M* ×
M* × ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M vector field.
M vector field.![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M, respectively, the coefficient b(1)2,0 depends on the projection of
M, respectively, the coefficient b(1)2,0 depends on the projection of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M along
M along ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M, i.e. on its radial component DMk [see eqn (17)]. We can also consider the ratio between b(1)2,0 and b(1)0,0 to get rid of the coupling term, and obtain the asymmetry parameter,¶
M, i.e. on its radial component DMk [see eqn (17)]. We can also consider the ratio between b(1)2,0 and b(1)0,0 to get rid of the coupling term, and obtain the asymmetry parameter,¶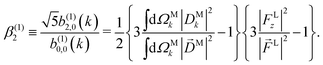
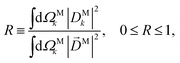
![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) is a radial field and takes values between 0 and 1, corresponding to the limits
M) is a radial field and takes values between 0 and 1, corresponding to the limits ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M = DM+
M = DM+![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M+ + DM−
M+ + DM−![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M− (tangential field) and
M− (tangential field) and ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M = DMk
M = DMk![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) (radial field), respectively. Fig. 4 shows β(1)2 as a function of R for linear (
(radial field), respectively. Fig. 4 shows β(1)2 as a function of R for linear (![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) L = FzẑL) and circular polarization (
L = FzẑL) and circular polarization (![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) L = F±
L = F±![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) ±) along with the angular distributions obtained in the limits R = 0 (tangential
±) along with the angular distributions obtained in the limits R = 0 (tangential ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M) and R = 1 (radial
M) and R = 1 (radial ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M). We can see that for both linearly and circularly polarized fields, a predominantly tangential field
M). We can see that for both linearly and circularly polarized fields, a predominantly tangential field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M will yield most photoelectrons with directions perpendicular to the electric field, while a predominantly radial field
M will yield most photoelectrons with directions perpendicular to the electric field, while a predominantly radial field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M will yield most photoelectrons with directions parallel to the electric field.
M will yield most photoelectrons with directions parallel to the electric field.

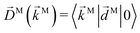 is in average for a given k [see eqn (22) and (23)], for the case of linear polarization along ẑ (blue line) and circular polarization in the xy plane (green line). The red shaded area shows the range of values that β(1)1 can take for a given value of β(1)2 (and correspondingly of R) for the circularly polarized case [see eqn (24)]. β(1)1 is zero for linear polarization. The insets on the left show the angular distributions for the extreme values β(1)1 = ±1.5 and β(1)2 = 0.5 obtained for circular polarization. The insets on the right show the angular distributions for β(1)1 = 0 (for simplicity) and β(1)2 = −1 (bottom), β(1)2 = 0.5 (center), and β(1)2 = 2 (top), which are the values reached for linear and circular polarizations in the limits R = 0 (tangential
is in average for a given k [see eqn (22) and (23)], for the case of linear polarization along ẑ (blue line) and circular polarization in the xy plane (green line). The red shaded area shows the range of values that β(1)1 can take for a given value of β(1)2 (and correspondingly of R) for the circularly polarized case [see eqn (24)]. β(1)1 is zero for linear polarization. The insets on the left show the angular distributions for the extreme values β(1)1 = ±1.5 and β(1)2 = 0.5 obtained for circular polarization. The insets on the right show the angular distributions for β(1)1 = 0 (for simplicity) and β(1)2 = −1 (bottom), β(1)2 = 0.5 (center), and β(1)2 = 2 (top), which are the values reached for linear and circular polarizations in the limits R = 0 (tangential ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M) and R = 1 (radial
M) and R = 1 (radial ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M).
M).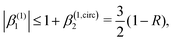
![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) is (in average) mostly radial and therefore the tangential components along with β(1)1 are very small. On the contrary, values of R close to zero indicate that the field
) is (in average) mostly radial and therefore the tangential components along with β(1)1 are very small. On the contrary, values of R close to zero indicate that the field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) has (in average) a very small radial component, which means that the field is mostly tangential and can potentially display a large dichroism |D+|2 − |D−|2. The maximum value of |β(1)1| = 1.5 and requires β(1,circ)2 = 0.5 and R = 0, i.e.
) has (in average) a very small radial component, which means that the field is mostly tangential and can potentially display a large dichroism |D+|2 − |D−|2. The maximum value of |β(1)1| = 1.5 and requires β(1,circ)2 = 0.5 and R = 0, i.e. ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) purely tangential and perfectly “circularly polarized”. As explained in ref. 57 [eqn (9) and (10)], the net photoelectron current (i.e. the vector sum of all photoelectron currents) is given by
M) purely tangential and perfectly “circularly polarized”. As explained in ref. 57 [eqn (9) and (10)], the net photoelectron current (i.e. the vector sum of all photoelectron currents) is given by 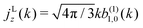 and the total photoelectron current (i.e. the sum of the magnitudes of all photoelectron currents) is given by
and the total photoelectron current (i.e. the sum of the magnitudes of all photoelectron currents) is given by 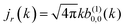 . Therefore, the maximum value of the ratio of net photoelectron current to total current is |jz|/jr = 1/2. Note that eqn (24) can also be derived exclusively from the condition that the angular distribution WL(
. Therefore, the maximum value of the ratio of net photoelectron current to total current is |jz|/jr = 1/2. Note that eqn (24) can also be derived exclusively from the condition that the angular distribution WL(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) L) [eqn (2)] is positive for every
L) [eqn (2)] is positive for every ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) L.
L.
![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) has a balanced mixture of radial and tangential components. Furthermore, Fig. 3 of ref. 47 also shows that |β(1)1| ≤ 0.2, which is well below the maximum value |β(1)1| = 1 allowed for R = 1/3 (see Fig. 4 here). This indicates that while
M) has a balanced mixture of radial and tangential components. Furthermore, Fig. 3 of ref. 47 also shows that |β(1)1| ≤ 0.2, which is well below the maximum value |β(1)1| = 1 allowed for R = 1/3 (see Fig. 4 here). This indicates that while ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) has a significant tangential component, it is still far from being perfectly “circularly polarized”. Nevertheless, this remnant of “circular polarization” in
M) has a significant tangential component, it is still far from being perfectly “circularly polarized”. Nevertheless, this remnant of “circular polarization” in ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) is enough to yield very significant enantio-sensitive signals. From the behavior of β(1,lin)2 as a function of energy (see Fig. 3 in ref. 47) we can also deduce that R has an overall tendency to increase with photoelectron energy. That is,
M) is enough to yield very significant enantio-sensitive signals. From the behavior of β(1,lin)2 as a function of energy (see Fig. 3 in ref. 47) we can also deduce that R has an overall tendency to increase with photoelectron energy. That is, ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) tends to become more and more radial for increasing photoelectron energies. This is in agreement with the fact that for a plane wave continuum
M) tends to become more and more radial for increasing photoelectron energies. This is in agreement with the fact that for a plane wave continuum ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) is parallel to
M) is parallel to ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M and also with the usual decrease of |β(1)1| with increasing photoelectron energy.
M and also with the usual decrease of |β(1)1| with increasing photoelectron energy.![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M, the coefficient β(1)2 encodes only the average magnitude of the radial component of the field
M, the coefficient β(1)2 encodes only the average magnitude of the radial component of the field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M, but not its sign, i.e. it doesn't keep track of whether that radial component points inwards or outwards. This is a plausible explanation of why β(1)1 is more sensitive than β(1)2 to molecular structure details. This is complementary to the explanation in terms of sines (β(1)1) and cosines (β(2)2) of phase-shifts differences provided by the partial-wave approach.41
M, but not its sign, i.e. it doesn't keep track of whether that radial component points inwards or outwards. This is a plausible explanation of why β(1)1 is more sensitive than β(1)2 to molecular structure details. This is complementary to the explanation in terms of sines (β(1)1) and cosines (β(2)2) of phase-shifts differences provided by the partial-wave approach.41![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (1)2,2 differs from b(1)2,0 only in the electric field factor, which in the case of
(1)2,2 differs from b(1)2,0 only in the electric field factor, which in the case of ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (1)2,2 yields the s1 Stokes parameter in the linear polarization basis.56 That is,
(1)2,2 yields the s1 Stokes parameter in the linear polarization basis.56 That is, ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (1)2,2 and b(1)2,0 reveal the same information about the photoionization vector field
(1)2,2 and b(1)2,0 reveal the same information about the photoionization vector field ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) and differ only on the electric field information they encode. This is a general property of
M) and differ only on the electric field information they encode. This is a general property of ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) l,m coefficients with the same value of l and corresponding to the same quantum pathway. It reflects the fact that such coefficients differ only on their laboratory frame vectors [see e.g.eqn (9) and (10)] but not on their molecular vectors (photoelectron momentum and transition dipoles), and therefore they involve the same molecular rotational invariants.
l,m coefficients with the same value of l and corresponding to the same quantum pathway. It reflects the fact that such coefficients differ only on their laboratory frame vectors [see e.g.eqn (9) and (10)] but not on their molecular vectors (photoelectron momentum and transition dipoles), and therefore they involve the same molecular rotational invariants.![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M-averaged magnitudes of the components of
M-averaged magnitudes of the components of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M [eqn (17), (21), and (22)], it is also interesting to note that for a circularly polarized field
M [eqn (17), (21), and (22)], it is also interesting to note that for a circularly polarized field ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) L = Fσ
L = Fσ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) Lσ with σ = ±1 [see eqn (20)], eqn (12)–(14) can be inverted to reconstruct the
Lσ with σ = ±1 [see eqn (20)], eqn (12)–(14) can be inverted to reconstruct the ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M-averaged magnitudes of the components of
M-averaged magnitudes of the components of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M using the measured values of β(1)1 and β(1,circ)2. Such procedure yields
M using the measured values of β(1)1 and β(1,circ)2. Such procedure yields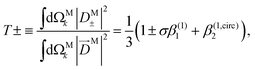
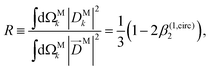
![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ).
).

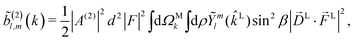
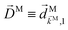 for the photoionization dipole from the intermediate state,
for the photoionization dipole from the intermediate state, 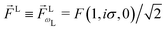 , σ = ±1, and we chose the molecular axis so that
, σ = ±1, and we chose the molecular axis so that ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) M ≡
M ≡ ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) M1,0 = dẑM and therefore
M1,0 = dẑM and therefore ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) L = d(sin
L = d(sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β
β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α, sin
α, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β
β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α, cos
α, cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β) where αβγ are the Euler angles in the ZYZ convention, and in particular β is the angle between the molecular and laboratory ẑ axes. This yields
β) where αβγ are the Euler angles in the ZYZ convention, and in particular β is the angle between the molecular and laboratory ẑ axes. This yields 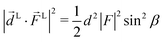 . Written like this, the second order coefficients
. Written like this, the second order coefficients ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (2)l,m(k) take the form of the first order coefficients
(2)l,m(k) take the form of the first order coefficients ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (1)l,m for an anisotropic (in this case anti-aligned) sample with an orientation distribution given by w(β) ∝ sin2
(1)l,m for an anisotropic (in this case anti-aligned) sample with an orientation distribution given by w(β) ∝ sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β and an initial state |1〉 instead of |0〉 (see also ref. 11, 30 and 58). Such anisotropy gives a certain preference to the z components of the molecular vectors. Performing the orientation averaging according to ref. 46, the expressions for the total absorption b(2)0,0, and for the enantio-sensitive terms b(2)1,0 and b(2)3,0 yield (see ESI† and ref. 17)
β and an initial state |1〉 instead of |0〉 (see also ref. 11, 30 and 58). Such anisotropy gives a certain preference to the z components of the molecular vectors. Performing the orientation averaging according to ref. 46, the expressions for the total absorption b(2)0,0, and for the enantio-sensitive terms b(2)1,0 and b(2)3,0 yield (see ESI† and ref. 17)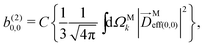
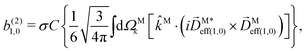
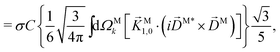
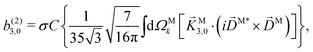
![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) Meff(0,0),
Meff(0,0), ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) Meff(1,0),
Meff(1,0), ![[K with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004b_20d1.gif) M1,0, and
M1,0, and ![[K with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004b_20d1.gif) M3,0 are given below. We wrote eqn (28)–(31) so that we can draw a parallel to the corresponding eqn (12) and (13) in the one-photon case. Eqn (28) and (29) show that we can recover the forms obtained in the one-photon case if we introduce effectively stretched photoionization dipoles given by
M3,0 are given below. We wrote eqn (28)–(31) so that we can draw a parallel to the corresponding eqn (12) and (13) in the one-photon case. Eqn (28) and (29) show that we can recover the forms obtained in the one-photon case if we introduce effectively stretched photoionization dipoles given by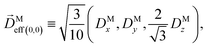
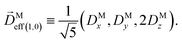
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M-averaged magnitude of an effective photoionization dipole
M-averaged magnitude of an effective photoionization dipole ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) Meff(0,0)(
Meff(0,0)(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M). Similarly, eqn (29) shows that b(2)1,0 records the “circular polarization” [see eqn (18)] or equivalently the
M). Similarly, eqn (29) shows that b(2)1,0 records the “circular polarization” [see eqn (18)] or equivalently the ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M-averaged value of the
M-averaged value of the ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M-specific CD of an effective photoionization dipole
M-specific CD of an effective photoionization dipole ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) Meff(1,0)(
Meff(1,0)(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M). Their ratio,
M). Their ratio, 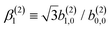 , can be interpreted as the average “circular polarization” of
, can be interpreted as the average “circular polarization” of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) Meff(1,0) normalized with respect to the average magnitude of
Meff(1,0) normalized with respect to the average magnitude of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) Meff(0,0).
Meff(0,0).![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M. However, like b(1)1,0 and b(2)1,0 [eqn (13) and (30)], eqn (31) shows that b(2)3,0 depends on the photoionization dipole
M. However, like b(1)1,0 and b(2)1,0 [eqn (13) and (30)], eqn (31) shows that b(2)3,0 depends on the photoionization dipole ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M(
M(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) only through the
M) only through the ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M-dependent field29,30
M-dependent field29,30![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M ≡ i
M ≡ i![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M* ×
M* × ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) M,
M, directly.
directly.
![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M for ÂM =
M for ÂM = ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) M, ŷM, ẑM,
M, ŷM, ẑM, ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M (see ref. 30 and Section 4). In these cases we found that ÂM·
M (see ref. 30 and Section 4). In these cases we found that ÂM·![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M yields the
M yields the ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M-specific CD associated to the transition |0〉 → |
M-specific CD associated to the transition |0〉 → |![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M〉 for light circularly polarized with respect to the axis ÂM (see Fig. 3). In fact, this interpretation is valid for an arbitrary ÂM. To see this, note that for a given ÂM one can always build ÂM-dependent unit vectors êM± associated to positive and negative rotations around ÂM, write
M〉 for light circularly polarized with respect to the axis ÂM (see Fig. 3). In fact, this interpretation is valid for an arbitrary ÂM. To see this, note that for a given ÂM one can always build ÂM-dependent unit vectors êM± associated to positive and negative rotations around ÂM, write 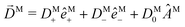 and obtain
and obtain 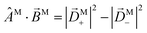 . This scalar product is evidently maximized for ÂM =
. This scalar product is evidently maximized for ÂM = ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) M, and therefore the direction of
M, and therefore the direction of ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M indicates the axis with respect to which the
M indicates the axis with respect to which the ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M-specific CD is maximal. The magnitude of
M-specific CD is maximal. The magnitude of ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M is then the magnitude of such maximal
M is then the magnitude of such maximal ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M-specific CD. Light circularly polarized with respect to axes perpendicular to
M-specific CD. Light circularly polarized with respect to axes perpendicular to ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M yield zero
M yield zero ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M-specific CD.
M-specific CD.![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M on the radial vector
M on the radial vector ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M, eqn (30) and (31) show that b(2)1,0 and b(2)3,0 involve the projection of
M, eqn (30) and (31) show that b(2)1,0 and b(2)3,0 involve the projection of ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M on the vector fields
M on the vector fields ![[K with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004b_20d1.gif) M1,0 and
M1,0 and ![[K with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004b_20d1.gif) M3,0, respectively, defined as (see ESI†)
M3,0, respectively, defined as (see ESI†)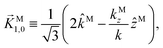
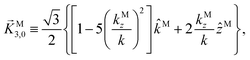
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M directions in eqn (29) and (31) tell us that b(2)1,0 and b(2)3,0 record the extent to which the vector field
M directions in eqn (29) and (31) tell us that b(2)1,0 and b(2)3,0 record the extent to which the vector field ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M resembles the vector fields
M resembles the vector fields ![[K with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004b_20d1.gif) M1,0 and
M1,0 and ![[K with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004b_20d1.gif) M3,0, respectively, and therefore record structural information about
M3,0, respectively, and therefore record structural information about ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M. Such information can be made more explicit by expanding
M. Such information can be made more explicit by expanding ![[K with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004b_20d1.gif) M1,0,
M1,0, ![[K with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004b_20d1.gif) M3,0, and
M3,0, and ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M in terms of vector spherical harmonics59
M in terms of vector spherical harmonics59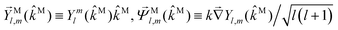 , and
, and 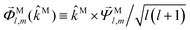 ,
,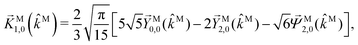
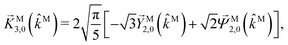
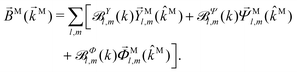

![[K with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004b_20d1.gif) M1,0(
M1,0(![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M) and
M) and ![[K with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004b_20d1.gif) M3,0(
M3,0(![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M) in eqn (35) and (36).
M) in eqn (35) and (36).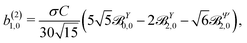
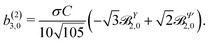
![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) Y0,0 (because
Y0,0 (because ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M ∝
M ∝ ![[Y with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0059_20d1.gif) M0,0), in the two-photon case b(2)1,0 and b(2)3,0 encode
M0,0), in the two-photon case b(2)1,0 and b(2)3,0 encode ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) Y0,0,
Y0,0, ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) Y2,0, and
Y2,0, and ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) Ψ2,0. This motivates looking for a third linearly independent equation to solve for
Ψ2,0. This motivates looking for a third linearly independent equation to solve for ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) Y0,0,
Y0,0, ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) Y2,0, and
Y2,0, and ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) Ψ2,0. This is delivered by the equation for
Ψ2,0. This is delivered by the equation for 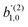 for the complementary process where the first photon is linearly polarized along ẑL and the second photon is circularly polarized in the
for the complementary process where the first photon is linearly polarized along ẑL and the second photon is circularly polarized in the ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) LŷL plane (see ESI†),
LŷL plane (see ESI†),
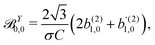
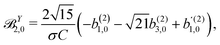
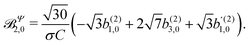
![[Y with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0059_20d1.gif) M0,0(
M0,0(![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M) ∝
M) ∝ ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M,
M, ![[Y with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0059_20d1.gif) M2,0(
M2,0(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) M) ∝ (3
M) ∝ (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θMk − 1)
θMk − 1)![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M, and
M, and ![[capital Psi, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e6.gif) M2,0(
M2,0(![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M) ∝ −cos
M) ∝ −cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θMk
θMk![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θMk
θMk![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) Mk to the total field
Mk to the total field ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M(
M(![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M) [eqn (34)]. Eqn (43)–(45) thus clearly show how structural information of the molecular field
M) [eqn (34)]. Eqn (43)–(45) thus clearly show how structural information of the molecular field ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M(
M(![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) M) can be reconstructed from photoelectron angular distributions resulting from an initially isotropic sample of chiral molecules.
M) can be reconstructed from photoelectron angular distributions resulting from an initially isotropic sample of chiral molecules.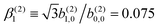 and
and 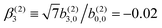 . While this is not enough to reconstruct
. While this is not enough to reconstruct ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) Y0,0,
Y0,0, ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) Y2,0, and
Y2,0, and ![[scr B, script letter B]](https://www.rsc.org/images/entities/char_e13f.gif) Ψ2,0 using eqn (43)–(45), it is enough to state that
Ψ2,0 using eqn (43)–(45), it is enough to state that 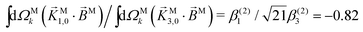 . That is, the overlap between
. That is, the overlap between ![[K with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004b_20d1.gif) M1,0 and
M1,0 and ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M is only slightly smaller than that between
M is only slightly smaller than that between ![[K with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004b_20d1.gif) M3,0 and
M3,0 and ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) M.
M. coefficients resulting from interference between pathways involving N1 and N2 photons have odd l + N1 + N2.
coefficients resulting from interference between pathways involving N1 and N2 photons have odd l + N1 + N2.![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉 reveals a clear meaning for the molecular information encoded in each of the b(1)l,m coefficients, which is otherwise obscured in the usual (and equivalent) formulation in terms of partial waves: b(1)0,0 encodes the average magnitude of the photoionization dipole
〉 reveals a clear meaning for the molecular information encoded in each of the b(1)l,m coefficients, which is otherwise obscured in the usual (and equivalent) formulation in terms of partial waves: b(1)0,0 encodes the average magnitude of the photoionization dipole ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) ≡ 〈
) ≡ 〈![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) |
|![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) |0〉; b(1)1,0 encodes the average radial component of the field
|0〉; b(1)1,0 encodes the average radial component of the field ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) ≡ i
≡ i![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) * ×
* × ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) ,29,30 which in turn encodes the average ‘circular dichroism’ of
,29,30 which in turn encodes the average ‘circular dichroism’ of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) and depends only on its transverse components; and b(1)2,0 encodes the average radial component of
) and depends only on its transverse components; and b(1)2,0 encodes the average radial component of ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ). The averages are taken with respect to the direction of the photoelectron momentum
). The averages are taken with respect to the direction of the photoelectron momentum ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) in the molecular frame. b(1)1,0 is sensitive to a single coefficient of the vector spherical harmonic expansion of
in the molecular frame. b(1)1,0 is sensitive to a single coefficient of the vector spherical harmonic expansion of ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ).
).![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉 of isotropic chiral samples with circularly polarized light. The coefficients b(2)0,0 and b(2)1,0 have analogous interpretations to those found in the one-photon case provided one takes into account an effective anisotropic stretching of the photoionization dipoles. b(2)1,0 and b(2)3,0 yield structural information about the propensity field
〉 of isotropic chiral samples with circularly polarized light. The coefficients b(2)0,0 and b(2)1,0 have analogous interpretations to those found in the one-photon case provided one takes into account an effective anisotropic stretching of the photoionization dipoles. b(2)1,0 and b(2)3,0 yield structural information about the propensity field ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) ≡ i
≡ i![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) * ×
* × ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) ,29,30 which encodes the
,29,30 which encodes the ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) -specific circular dichroism. In particular they depend only on three coefficients of the vector spherical harmonic expansion of
-specific circular dichroism. In particular they depend only on three coefficients of the vector spherical harmonic expansion of ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ). These coefficients can be solved for in terms of b(2)1,0, b(2)3,0, and
). These coefficients can be solved for in terms of b(2)1,0, b(2)3,0, and  , where the latter corresponds to the process where the first photon is linearly polarized.
, where the latter corresponds to the process where the first photon is linearly polarized.![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) L or ŷL simply serves the purpose of reducing the number of non-zero
L or ŷL simply serves the purpose of reducing the number of non-zero ![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) (1)l,m coefficients.
(1)l,m coefficients.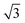 in eqn (21) and
in eqn (21) and 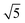 in eqn (22) are included to recover the ratio obtained when the expansion is done in terms of Legendre polynomials (instead spherical harmonics), as is usual for the cylindrically symmetric cases when the light is either linearly polarized along z or circularly polarized in the xy plane.
in eqn (22) are included to recover the ratio obtained when the expansion is done in terms of Legendre polynomials (instead spherical harmonics), as is usual for the cylindrically symmetric cases when the light is either linearly polarized along z or circularly polarized in the xy plane.