Normal and off-normal incidence dissociative dynamics of O2(v,J) on ultrathin Cu films grown on Ru(0001)
J. G.
Fallaque
 ab,
M.
Ramos
ab,
M.
Ramos
 c,
H. F.
Busnengo
c,
H. F.
Busnengo
 c,
F.
Martín
c,
F.
Martín
 abd and
C.
Díaz
abd and
C.
Díaz
 *e
*e
aDepartamento de Química, Módulo 13, Universidad Autónoma de Madrid, 28049 Madrid, Spain
bInstituto Madrileño de Estudios Avanzados en Nanociencia (IMDEA-nanociencia), Cantoblanco, 28049 Madrid, Spain
cInstituto de Física Rosario, CONICET and Universidad Nacional de Rosario, Bv. 27 de Febrero 210 bis, 2000 Rosario, Argentina
dCondensed Matter Physics Center (IFIMAC), Universidad Autónoma de Madrid, 28049 Madrid, Spain
eDepartamento de Química Física, Facultad de CC. Químicas, Universidad Complutense de Madrid, 28040 Madrid, Spain. E-mail: crdiaz08@ucm.es
First published on 10th September 2020
Abstract
The dissociative adsorption of molecular oxygen on metal surfaces has long been controversial, mostly due to the spin-triplet nature of its ground state, to possible non-adiabatic effects, such as an abrupt charge transfer from the metal to the molecule, or even to the role played by the surface electronic state. Here, we have studied the dissociative adsorption of O2 on CuML/Ru(0001) at normal and off-normal incidence, from thermal to super-thermal energies, using quasi-classical dynamics, in the framework of the generalized Langevin oscillator model, and density functional theory based on a multidimensional potential energy surface. Our simulations reveal a rather intriguing behavior of dissociative adsorption probabilities, which exhibit normal energy scaling at incidence energies below the reaction barriers and total energy scaling above, irrespective of the reaction channel, either direct dissociation, trapping dissociation, or molecular adsorption. We directly compare our results with existing scanning tunneling spectroscopy and microscopy measurements. From this comparison, we infer that the observed experimental behavior at thermal energies may be due to ligand and strain effects, as already found for super-thermal incidence energies.
1 Introduction
The interaction of molecular oxygen with transition metals is a fundamental chemical reaction that has been studied since the 40's of the past century.1 This phenomenon is of huge technological importance in many industrial applications, such as heterogeneous and electro-catalysis, corrosion, oxidation or fuel cell development, which explains the continuous attention it receives from the surface science community (see ref. 2–8 and references therein). Furthermore, from a purely fundamental point of view, the mechanism behind the dissociative chemisorption of O2 on metals has long puzzled scientists, and still does. It has been shown for a number of relevant O2/metal systems that their electronic structure cannot be reasonably well described within the standard density functional theory (DFT) periodic boundary condition (PBC) method. For example, adiabatic dynamics simulations based on standard DFT-PBC completely fail to reproduce experimental results for O2/Al(111), which show that the sticking probability increases with incidence energy,9,10 compatible with a high reaction barrier, whereas the simulations show no reaction barrier at all.11,12 Alternatively, the presence of the reaction barrier has been explained, on one hand, in terms of non-adiabatic spin dynamics that freezes the triplet state of the molecule as it approaches the surface.13–15 This mechanism would be favored by the relatively small mass of the Al atoms, which involves a small spin–orbit coupling, and by the low density of Al states at the Fermi level, which prevents efficient triplet–singlet spin quenching through tunneling of electrons between the metal and the molecule. On other hand, the presence of the reaction barrier has been rationalized in terms of non-adiabatic charge transfer from the surface to the molecule,16–19 a mechanism favored by the small work function of Al and the high electron affinity of O2. None of these mechanisms can be properly described by standard DFT semi-local exchange–correlation functionals. A similar failure could be expected for other transition metals that show Al-like characteristics. However, the interaction of O2 on Ag(111) is fairly well described by adiabatic dynamics simulations. As shown in ref. 20 and 21 both scattering and dissociative adsorption phenomena are well described within this approximation. The adiabatic dynamics calculations have also yielded results for O2 dissociative adsorption on Ag(110)22 consistent with the absence of direct dissociation in experiments performed at low incidence energies,23,24 but do not properly describe molecular adsorption.25 In the latter case, it has been suggested that the discrepancy between theory and experiment could be due to the limited accuracy of the Perdew, Burke, and Ernzerhof (PBE)26,27 functional used in DFT calculations. It is also worth mentioning that a theoretical study devoted to the interaction of O2 with Pd(100),28 in which simulations based on time-dependent perturbation theory and DFT electronic structure calculations show that, despite the high density of states at the Pd Fermi level, non-adiabatic electron–hole excitation processes are almost negligible, and that the system is well described within the adiabatic dynamics formalism.All these studies mentioned above share the use of the PBE functional. This functional has been also used to study the interaction of O2 with Cu surfaces. But, in this case, adiabatic dynamics studies show spontaneous dissociation,29–31 in contrast with the activated behavior found experimentally.32–34 However, as we have recently shown for O2/Cu(111),35,36 theoretical and experimental results can be reconciled if the revised Perdew–Burke–Ernzerhof (RPBE) functional37 is used in the DFT electronic calculations. The dependence of the dynamics calculations on the DFT functional used to compute the PES is not a surprise in molecule/surface systems (see for example ref. 38 and references therein), however such a notable change, from non-activated to activated, is more unusual. In our previous work, carried out at normal incidence using pure classical dynamics, we also showed that, due to the nature of the chemisorption wells, the inclusion of the surface degrees of freedom (DOFs) was essential to reproduce qualitatively King and Wells sticking experimental measurements;31 contrary to results obtained for other O2/metal systems, where the effect of the surface DOFs was found to be relatively small21 or even negligible.39
In our previous studies,35,36 we also simulated the sticking (molecular + dissociative adsorption) probabilities for one and two layers of Cu grown on Ru(0001). For these two systems, our simulations also reproduced qualitatively the experimental measurements at super-thermal energies.31 However, results at normal incidence, without any extra knowledge, were not enough to perform a meaningful comparison with tunneling spectroscopy and microscopy (STS-STM) measurements performed by Otero et al.40 These authors showed a very strong dependence of O2 reactivity as a function of the number of Cu layers, decreasing sharply with the increasing number of Cu layers, and related this behavior to the population of the surface electronic state.40,41
Here, we have performed a complete set of quasi-classical dynamics simulations based on the RPBE-PES published in ref. 36. Our simulations show a complex behavior of sticking probabilities as a function of the incidence angle, following normal energy scaling at low energies, and a negligible effect of the rotational internal molecular DOFs. A proper average of the simulated sticking probabilities at thermal energies has allowed us to perform a direct comparison with STS-STM experimental measurements.
2 Theoretical tools
To perform our study, we used a similar theory level to that described in ref. 35 and 36. Therefore, only a brief summary is provided here. We relied on the Born–Oppenheimer approximation. The potential energy surface (PES) was built by interpolation – using the CRP method42 – of a data set of DFT energies, which have been computed within the periodic boundary conditions approach using the plane-wave based VASP code,43–46 with the semi-local RPBE exchange–correlation functional.37 The choice of the RPBE functional has allowed us to reconcile theoretical results35,36 with the activated character of sticking probability found experimentally.29–31 A more detailed description of the parameters used to compute the PES can be found in ref. 36.Based on our previous studies35,36 showing the key role that surface temperature plays in O2/CuML/Ru(0001), we have taken into account the surface temperature by means of the generalized Langevin Oscillator (GLO) model47,48 (see ref. 36 for further details). However, unlike those previous calculations, here we have performed quasi-classical dynamics, i.e., we have included the zero point energy (ZPE) of the molecule in the calculations. At this point, we can anticipate that the unwanted phenomenon of vibrational energy leakage associated with the quasi-classical calculations plays a minor role here, because of the relatively low ZPE of O2 in the gas phase, 95.1 meV (obtained solving the 1D Hamiltonian by expanding the wave function on the basis of B-spline functions49), and the relatively high vibrational softening (the adiabatic transfer of energy from the vibrational to the translational DOF) that makes the ZPE decrease down to 56.2 meV for a molecule close to the surface. In performing the quasi-classical simulations, to obtain meaningful probabilities for the different final reactive channels, we have run up to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trajectories for each set of initial incidence conditions (Ei, θi, φi, v, and J) – see Table 1, where Ei is the total incidence energy, θi and φi are the polar and azimuthal angles, respectively (see Fig. 1), and v and J are the vibrational and rotational states, respectively. At the end of each trajectory, we analyze the atomic or molecular coordinates and velocities to assign the final channel. Thus, the dissociative adsorption channel is defined by a O–O distance r ≥ 2.4 Å (around twice the equilibrium value of O2 in the gas phase) with dr/dt > 0. If the molecule bounces (change the sign of its velocity normal to the surface) five or more times before dissociation, we assign this trajectory to the trapping dissociation channel, otherwise we assign it to the direct dissociation channel. If at the end of the integration time (1 ns) the molecule remains trapped in a molecular chemisorption well, the trajectory is assigned to the molecular adsorption channel.
000 trajectories for each set of initial incidence conditions (Ei, θi, φi, v, and J) – see Table 1, where Ei is the total incidence energy, θi and φi are the polar and azimuthal angles, respectively (see Fig. 1), and v and J are the vibrational and rotational states, respectively. At the end of each trajectory, we analyze the atomic or molecular coordinates and velocities to assign the final channel. Thus, the dissociative adsorption channel is defined by a O–O distance r ≥ 2.4 Å (around twice the equilibrium value of O2 in the gas phase) with dr/dt > 0. If the molecule bounces (change the sign of its velocity normal to the surface) five or more times before dissociation, we assign this trajectory to the trapping dissociation channel, otherwise we assign it to the direct dissociation channel. If at the end of the integration time (1 ns) the molecule remains trapped in a molecular chemisorption well, the trajectory is assigned to the molecular adsorption channel.
| Study | Rotational | Vibrational | Off-normal incidence |
|---|---|---|---|
| φ i (deg.) | 0 | 0 | 0 |
| θ i (deg.) | 0 | 0 | 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85 |
| v | 0 | 1, 2, 3, 4, 5, 6 | 0 |
| J | 1, 3, 9, 31 | 0 | 0 |
| E i (eV) | 0.01, 0.03, 0.06, 0.09, 0.12, 0.18, 0.21, 0.24, 0.27, 0.3, 0.4, 0.5, 0.6 | 0.0001, 0.005, 0.01, 0.03, 0.06, 0.09, 0.12, 0.18, 0.21, 0.24, 0.27, 0.3, 0.4, 0.5, 0.6 | 0.06, 0.1, 0.18, 0.3 |
| Number of sets | 52 | 90 | 58 |
3 Results and discussion
3.1 O2(v,J)/Cu1ML/Ru(0001) at normal incidence
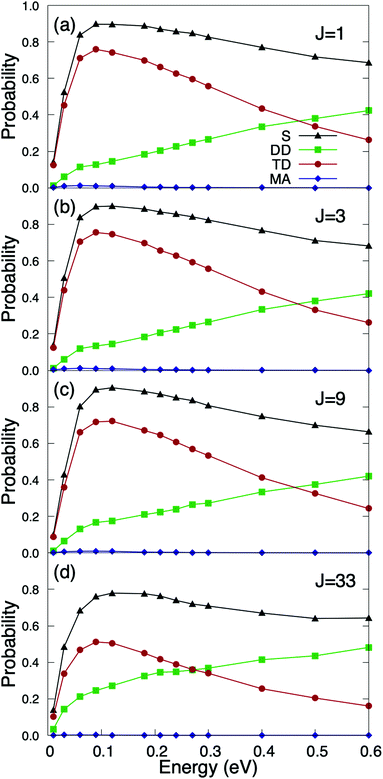
We have first studied the role of the internal rovibrational DOFs of the molecule. To perform such analysis, we define the rotational energy in eV as Erot = [BeJ(J + 1) − De(J(J + 1))2]hc with Be = 1.4456 cm−1 and De = 4.81 × 10−6 cm−1,50 and we have taken into account the nuclear statistics for O2 molecules according to which only odd rotational states are populated. In Fig. 2, we have displayed the quasi-classical probabilities computed for the different reaction channels, namely, direct dissociation, trapping dissociation, and molecular adsorption (almost negligible), as a function of the incidence energy, for a surface temperature equal to 350 K, several initial rotational states and normal incidence. From Fig. 2, we can observe that none of the reaction channels depend on the initial rotational state of the molecule, at least for the J states expected to be appreciably populated in an O2 molecular beam at room temperature. In fact, we have found that the maximum reaction probability barely drops from 0.9 for J = 1 to 0.8 for J = 33 (see Fig. 2(a) and (d)), in spite of the fact that the rotational energy for J = 33 is 200.48 meV, i.e., almost an order of magnitude higher than the 25.86 meV associated with a molecular beam temperature of 300 K. These results suggest that rotational and translational motions are barely coupled, i.e., there is very little energy transfer from rotation to translation. A similar finding has been reported for other diatomic molecules of comparable mass, as e.g., N2/Ru(0001),51 where dissociative chemisorption was found to be independent of the initial J state up to J = 8. This behavior is in contrast with that observed in H2/metal surface systems,52–55 where reaction probabilities strongly depend on the initial rotational state of the molecule.It is also important to note that if we compare Fig. 2(a) with Fig. 6(a) of ref. 36, where reaction probabilities were obtained from pure classical trajectory calculations, we can conclude that classical (C) and quasi-classical (QC) simulations only differ by a small shift of the QC probabilities towards lower energies, roughly 40 meV. This shift is compatible with the vibrational softening experienced by the molecule when approaching the surface. This small shift does not have any significant effect when compared with typical King and Wells results measured at super-thermal energies.31 However, as we show below, the effect of vibrational softening, even as small as the present one, cannot be ignored at thermal energies.
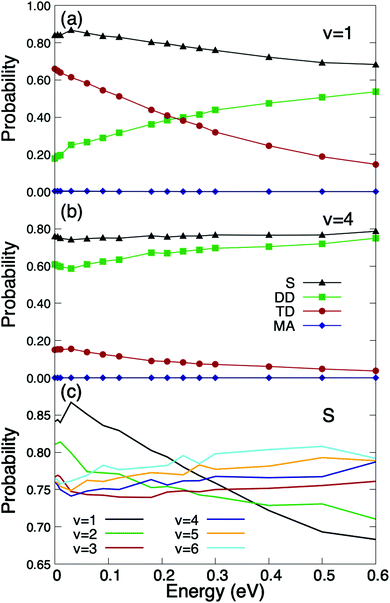
We have also performed calculations for vibrationally excited molecules, whose presence in the experimental molecular beams, specially at thermal energies, is expected to be small, but not at super-thermal energies. The results are shown in Fig. 3. As can be seen the O2/Cu/Ru(0001) system becomes non-activated when O2 is vibrationally excited. As shown in Fig. 3(a) the total sticking probability for O2(J = 1, v = 1) is close to 0.9 at very low incidence energies. It can also be seen that trapping dissociation decreases monotonously with the incidence energy, while direct dissociation does the opposite. These results point to a very strong vibration-translation coupling, and therefore, to a very efficient transfer of energy from the vibrational to the translational motion. A similar strong coupling has been observed previously for O2/Ag(110),22 where a vibrational efficacy (i.e. the efficiency of vibrational energy to promote reaction56) was found to be larger than one. In spite of this, the O2/Ag(110) system still remains activated for v = 1. Coming back to the O2/Cu/Ru(0001) system, one can see (Fig. 3(c)) that by further increasing the vibrational energy, the sticking probability decreases at low incidence energy, and the sticking curves exhibit a subtle non-monotonous behavior. This is the consequence of the non-monotonous behavior of direct dissociation, which governs the total dissociation at high vibrational energies (see Fig. 3(b)). Similar findings have been reported for H2/metal surface systems in ref. 57, where it was shown to be the consequence of the balance between the ability of the vibrationally excited molecule to reach the appropriate orientation for dissociation and the number of accessible reaction paths. Nevertheless, as shown in Fig. 3(c), the sticking probability varies very little in the range v = 1 − v = 6. At this point, it is worth pointing out that, although molecular beam experiments for vibrationally excited O2 molecules are not available in the literature, they could be carried out using pulsed narrow bandwidth laser Raman excitation, as suggested in ref. 58, or using induced adiabatic Raman passage (SARP), as proposed in ref. 59.
Finally, we will mention that the reaction probabilities barely depend on the surface temperature in the 250–550 K range.
3.2 O2(v = 0, J = 1)/Cu1ML/Ru(0001) at off-normal incidence
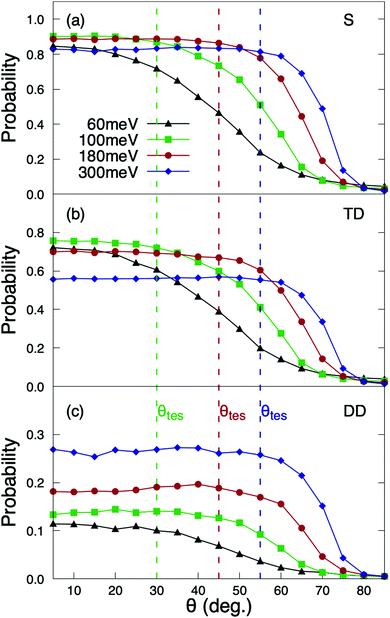
The reaction probabilities as a function of the incidence angle θi exhibit a very peculiar behavior (see Fig. 4). Contrary to previous results for systems in which dynamic trapping also plays a prominent role, such as H2/Pd(111)60 and H2/Pd(110),61 where it was found that direct dissociation follows normal energy scaling and trapping dissociation follows total energy scaling, here we see that all reaction channels (direct dissociation, trapping dissociation, and even molecular adsorption) show the same behavior. From Fig. 4, we can see that for incidence energies of ≥100 meV, reaction probabilities do not depend on the initial polar angle up to a certain value of θtes. Thus, we define θtes as the maximum polar incidence angle for which the reaction probability do not depend on θi. The value of θtes increases with incidence energy. A simple analysis of these curves reveals that the value of the normal component of the incidence energy, E⊥ = cos2(θtes)Ei, is similar for the three curves with Ei ≥ 100 meV displayed in Fig. 4, namely 75 meV. This value of E⊥ is close to that at which the total sticking probability at normal incidence shows a maximum (see Fig. 2(a)). Hence, we observe total energy scaling for incidence energies above the entrance reaction barriers, which have been found to be in the range of 26–77 eV (see Fig. 5 of ref. 36).For θi higher than θtes the reaction probabilities follow normal energy scaling. This can be clearly seen in Fig. 5, where we have plotted the sticking probabilities as a function of the normal energy, Ei![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2(θi). We can observe normal energy scaling up to E⊥ = 75 meV. This result has important implications when comparing with experimental results, as discussed in Section 3.3.
cos2(θi). We can observe normal energy scaling up to E⊥ = 75 meV. This result has important implications when comparing with experimental results, as discussed in Section 3.3.
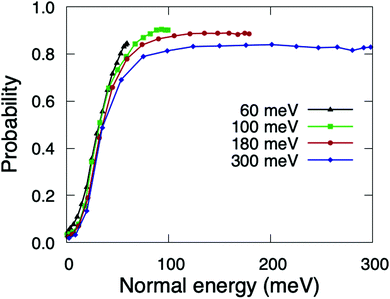 | ||
| Fig. 5 Quasi-classical total sticking probabilities for O2(v = 0, J = 0) on Cu1ML/Ru(0001) as a function of the normal energy. | ||
Finally, we should point out that the results shown in this section have been obtained for molecular incidence along the azimuthal angle φi = 0° (see Fig. 1). However, we have checked that, qualitatively, similar results are obtained for an incidence along other φi angles. We have also verified that these results do not depend on the surface temperature within the range of 250–550 K.
3.3 Comparison with previous experimental results
Taking into account that the total sticking probability does not depend on the initial rotational state of the molecule, and that at low incidence energies (thermal and quasi-thermal energies) this probability follows normal energy scaling, we can properly compare our theoretical sticking probabilities with those obtained experimentally by Otero et al.40 by computing the thermally averaged sticking probability using the following expression:62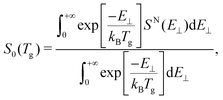 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2(θi), SN is the total sticking probability at normal incidence, kB is the Boltzmann constant, and Tg the temperature of the molecular beam, 300 K – see the ESI of ref. 63 for details.
cos2(θi), SN is the total sticking probability at normal incidence, kB is the Boltzmann constant, and Tg the temperature of the molecular beam, 300 K – see the ESI of ref. 63 for details.
In ref. 40, results for O2/CunML/Ru(0001) for up to n = 4 monolayers are available. However computing sticking probabilities beyond n = 1 is not an easy task. A single monolayer of Cu grows pseudomorphically on Ru(0001), but adding a second monolayer leads to a unit cell periodicity (16 × 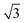 ).64 The periodicity is lost for more than two monolayers. Therefore, building a DFT-based PES for O2/CunML/Ru(0001) with n > 1 is virtually unapproachable from the computational point of view. However, as shown in ref. 36, we can reasonably estimate the sticking probability for O2/Cu2ML/Ru(0001) by shifting the sticking probabilities obtained for O2/Cu1ML/Ru(0001) by an amount equal to the difference between the minimum reaction barrier for n = 1 and the average minimum reaction barrier for n = 2. As discussed in ref. 36, in the (16 ×
).64 The periodicity is lost for more than two monolayers. Therefore, building a DFT-based PES for O2/CunML/Ru(0001) with n > 1 is virtually unapproachable from the computational point of view. However, as shown in ref. 36, we can reasonably estimate the sticking probability for O2/Cu2ML/Ru(0001) by shifting the sticking probabilities obtained for O2/Cu1ML/Ru(0001) by an amount equal to the difference between the minimum reaction barrier for n = 1 and the average minimum reaction barrier for n = 2. As discussed in ref. 36, in the (16 × 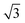 ) unit cell we can distinguish three zones (see Fig. 9 of ref. 36), fcc, dislocation, and hcp, characterized by three different minimum reaction barriers, 30, 56, and 57 meV, respectively. Thus, the shift δE is computed as:
) unit cell we can distinguish three zones (see Fig. 9 of ref. 36), fcc, dislocation, and hcp, characterized by three different minimum reaction barriers, 30, 56, and 57 meV, respectively. Thus, the shift δE is computed as:
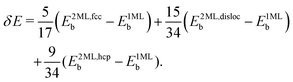 | (2) |
The accuracy of this estimation method relies, beyond the barrier heights, on the differences between the PESs of O2/Cu1ML/Ru(0001) and O2/Cu2ML/Ru(0001). In ref. 36, we showed that the shapes of 2D cuts corresponding to the fcc region of O2/Cu2ML/Ru(0001) were very similar to those obtained for O2/Cu1ML/Ru(0001), and the shapes of the 2D cuts corresponding to the hcp and dislocation regions of O2/Cu2ML/Ru(0001) were also qualitatively similar to those obtained for the fcc region, the barrier heights being the only appreciable difference. Therefore, once the molecules overcome the minimum reaction barriers in O2/Cu2ML/Ru(0001), they are expected to follow a similar reaction path as in O2/Cu1ML/Ru(0001). Hence, the dynamics results are expected to be similar except for a shift reflecting the different reaction barrier heights. The validity of this estimation method is supported by the good qualitative agreement between classical theoretical results and Kings and Wells experimental measurements (see Fig. 11 of ref. 36). The quasi-classical total sticking probabilities for O2/Cu2ML/Ru(0001) estimated using this procedure are shown in Fig. 6. It is worth noticing that, if the shapes of the PES for the surface terminations (fcc, hcp, and dislocation) had been very different, we would have to follow a more general (and computationally much more expensive) procedure, consisting of (i) the calculation of the PES for the three systems, (ii) the computation of the corresponding sticking probabilities, and (iii) performing a weighted average of the former probabilities.
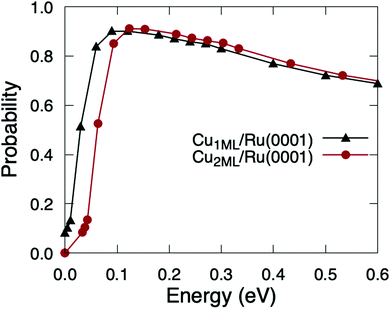 | ||
| Fig. 6 Quasi-classical total sticking probabilities of O2(v = 0, J = 0) on Cu1ML/Ru(0001) (black triangles) and Cu2ML/Ru(0001) (red circles) as a function of the normal incidence energy. | ||
Finally, we have applied eqn (1) to the sticking probabilities shown in Fig. 6 to obtain the thermally averaged sticking probabilities (S0), which can be directly compared with the experimental data of ref. 40. We show this comparison in Fig. 7. One can see that our theoretical simulations reproduce fairly well the variation of S0 as a function of the number of Cu monolayers. In the case of two monolayers the agreement is even quantitative, although we should keep in mind that this probability is just an estimation. It is worth noticing that experimental uncertainties are higher for the one-monolayer system. For the sake of completeness, we have also included S0 values obtained from classical sticking calculations. These probabilities also show the right trend, but are lower than the experimental values and those obtained from the quasi-classical calculations.
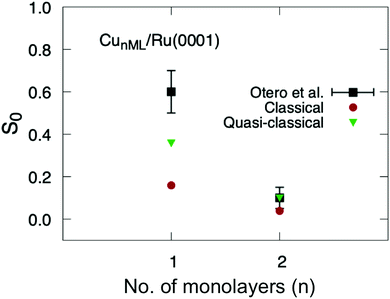 | ||
| Fig. 7 Thermally averaged sticking probabilities of O2/CuML/Ru(0001) as a function of the number of monolayers ML. Red: circles classical results; green triangles: quasi-classical calculations; black squares: experimental data from ref. 40. | ||
This qualitative agreement between theory and experiment, at thermal energy, allows us to conclude that the surface state population is not the only possible explanation for the sharp decrease of the O2 sticking probabilities when moving from Cu1ML/Ru(0001) to Cu2ML/Ru(0001), as previously suggested,40,41 because our PES does not describe such a state properly due to the limited number of Ru(0001) layers included in our DFT calculations of the PES. Instead, the sharp decrease resulting from our calculations is mainly due to strain effects, as already pointed out in our previous work at super-thermal energies.36 Indeed, in Cu1ML/Ru(0001), the Cu overlayer adopts the lattice parameter of Ru(0001) (2.71 Å), and this strain, together with the modification of the electronic structure induced by the binding of the Cu atoms to the Ru atoms (ligand effect), causes a substantial reduction of the reaction barrier compared to that of Cu(111) – a pure Cu surface with the same symmetry as Cu1ML/Ru(0001) – from 97 meV to 26 meV. In Cu2ML/Ru(0001), ligand effects become negligible, and the strain is slightly relaxed, since the average lattice parameter decreases to ≈2.63 Å, while the average minimum reaction barrier increases up to almost 49 meV, leading to the steep drop of the total sticking probability. As the number of Cu layers increases, the average lattice parameter is expected to go on decreasing, and the average minimum reaction barrier to increase even more, thus causing a further decrease in the sticking probability, until the system becomes a Cu(111)-like system.
4 Conclusions and final remarks
We have studied the dissociative chemisorption of O2(v,J) on CuML/Ru(0001) using quasi-classical dynamics within the generalized Langevin Oscillator method, to include the surface temperature, and a multidimensional potential energy surface obtained from interpolation of a set of DFT energies. Our results at normal incidence reveal that rotational molecular degrees of freedom have a negligible effect on the different reaction channels. The sticking probabilities for vibrationally excited molecules with v > 3, on the other hand, show the non-monotonous behavior typical of non-activated systems. Off-normal incidence simulations show an unexpected behavior of the reaction probabilities. Contrary to previous findings for other molecule/surface systems, all reaction channels show total energy scaling for perpendicular energy above the reaction barriers and normal energy scaling for energies below. Our computed thermally averaged sticking probability, as a function of the number of monolayers, agrees qualitatively well with previous experimental measurements carried out at thermal energies. In view of this good agreement, we conclude that the lattice strain effect is a plausible explanation for the steep drop of the total sticking probability observed for O2/CunML/Ru(0001) as a function of the number of Cu monolayers. However, we cannot completely discard that the population of the surface electronic state also contributes to this effect due to the poor description of the surface electronic state in our calculated potential energy surface.The current analysis completes our previous study carried out for super-thermal energies.36 The whole picture shows that our theoretical model, based on quasi-classical dynamics and DFT-based PESs modeled considering a low number of metal layers, is able to qualitatively describe the interaction between O2 and CunML/Ru(0001) (n = 1, 2) from thermal40 to super-thermal31 energies.
Finally we can conjecture about the origin of the remaining disagreement between theory and experiment, beyond possible experimental inaccuracies. Plausible sources of inaccuracies of our theoretical simulations could be due to the following:
• A poor description of surface phonons: to include the effect of the surface temperature, we have used the GLO model, which accounts for the molecule-surface energy exchange, thermal fluctuations and energy dissipation to the bulk, but does not account for the individual motions of the surface atoms. However, as shown for H2 dissociation on Cu(111),65 by means of ab initio molecular dynamics (AIMD), the surface atom motion may have a measurable influence on both the barrier heights and locations, which would have an influence on the sticking probabilities and, therefore, on the thermallyaveraged sticking probability. Here, we should point out that running AIMD for an O2/metal surface system is not an easy task, due to the possibility of introducing unphysical spin-flipping from triplet to singlet multiplicity states of the molecule before it reaches the reaction barriers. This phenomenon may confer extra energy to the molecule to overcome the reaction barriers and dissociate regardless of the incidence energy, which may lead the system to behave as non-activated.
• We cannot rule out possible non-adiabatic mechanisms, such as electron–hole excitation or charge transfer from the surface to the molecule. Based on previous results for O2/metal surfaces,20,28 electron–hole excitations are expected to play a minor role. Charge transfer, on the other hand, cannot be totally ruled out, although, in view of the qualitative agreement with the experimental data, it seems to play a less important role than in the case of O2/Al(111).16–19
• A third source of inaccuracy could be the semi-local exchange–correlation functional used in the calculations. Although the RPBE functional employed here yields much better results than the PBE functional, previously used to study this system, more accurate results could be obtained using the specific reaction parameter (SRP) strategy,66 which has been already tested for a number of H2/metal surface (see, for example ref. 67–69 and references therein) and CHD3/metal surface systems.70 However, to properly implement this strategy, more experimental data would be needed than currently available.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to Prof. A. E. Martínez, who participated in the construction of the PESs of O2/CunML/Ru(0001) used in this work, for useful discussions. This work has been supported by the MICINN projects PID2019-105458RB-I00 and PID2019-106732GB-I00, ‘Severo Ochoa’ Programme for Center of Excellence in R&D (SEV-2016-0686), ‘María de Maeztu’ Programme for Units of Excellence in R&D (CEX2018-000805-M), and ANPCyT project PICT-2016 2750. We acknowledge the allocation of computer time by the Red Española de Supercomputación and the Centro de Computación Científica at the Universidad Autónoma de Madrid (CCC-UAM). J. G. Fallaque acknowledges the PFI program of the MICINN co-financed by the European Social Fund.References
- N. Cabrera and N. F. Mott, Rep. Prog. Phys., 1949, 12, 163–184 CrossRef CAS.
- T. Zambelli, J. Barth, J. Winterlin and G. Ertl, Nature, 1997, 390, 495–497 CrossRef CAS.
- S. J. Roosendaal, A. M. Vredenberg and F. H. P. M. Habraken, Phys. Rev. Lett., 2000, 84, 3366–3369 CrossRef CAS.
- L. Vattuone, A. Gerbi, D. Cappelletti, F. Pirani, R. Gunnella, L. Savio and M. Rocca, Angew. Chem., Int. Ed., 2009, 48, 4845–4848 CrossRef CAS.
- Z. Guo, B. Liu, Q. Zhang, W. Deng, Y. Wang and Y. Yang, Chem. Soc. Rev., 2014, 43, 3480–3524 RSC.
- B. V. Andryushechkin, V. M. Shevlyuga, T. V. Pavlova, G. M. Zhidomirov and K. N. Eltsov, Phys. Rev. Lett., 2016, 117, 056101 CrossRef CAS.
- M. Shao, Q. Chang, J.-P. Dodelet and R. Chenitz, Chem. Rev., 2016, 116, 3594–3657 CrossRef CAS.
- M. Kurahashi, Prog. Surf. Sci., 2016, 91, 29 CrossRef CAS.
- J. Z. Komrowski, J. Z. Sexton, A. C. Kummel, M. Binetti, O. Weisse and E. Hasselbrink, Phys. Rev. Lett., 2001, 87, 246103 CrossRef.
- M. Binetti and E. Hasselbrink, Phys. Rev. Lett., 2001, 87, 246103 CrossRef.
- K. Honkala and K. Laasonen, Phys. Rev. Lett., 2000, 84, 705 CrossRef CAS.
- B. Yourdshahyan, B. Razaznejad and B. I. Lundqvist, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 075416 CrossRef.
- J. Behler, B. Delley, S. Lorenz, K. Reuter and M. Scheffler, Phys. Rev. Lett., 2004, 94, 036104 CrossRef.
- J. Behler, K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 115421 CrossRef.
- C. Carbogno, J. Behler, A. Gross and K. Reuter, Phys. Rev. Lett., 2008, 101, 096104 CrossRef.
- G. Katz, R. Kosloff, Y. Zeiri and K. Reuter, J. Chem. Phys., 2004, 120, 3931 CrossRef CAS.
- F. Libisch, C. Huang, P. Liao, M. Pavone and E. A. Carter, Phys. Rev. Lett., 2012, 109, 198303 CrossRef.
- J. Cheng, F. Libisch and E. A. Carter, J. Phys. Chem. Lett., 2015, 6, 1661 CrossRef CAS.
- R. Yin, Y. Zhang, F. Libisch, E. A. Carter, H. Guo and B. Jiang, J. Phys. Chem. Lett., 2018, 9, 3271 CrossRef CAS.
- I. Goikoetxea, J. Beltrán, J. Meyer, J. I. Juaristy, M. Alducin and K. Reuter, New J. Phys., 2012, 14, 013050 CrossRef.
- I. Goikoetxea, J. Meyer, J. I. Juaristi, M. Alducin and K. Reuter, Phys. Rev. Lett., 2014, 112, 156101 CrossRef CAS.
- I. Loncaric, M. Alducin and J. I. Juaristi, Phys. Chem. Chem. Phys., 2015, 17, 9436 RSC.
- C. Vattuone, M. Boragno, M. Pupo, P. Restelli, M. Rocca and U. Valbusa, Phys. Rev. Lett., 1994, 72, 510 CrossRef.
- A. Raukema, D. A. Butler and A. W. Kleyn, J. Phys.: Condens. Matter, 1996, 8, 2247 CrossRef CAS.
- I. Loncaric, M. Alducin and J. I. Juaristi, Phys. Chem. Chem. Phys., 2016, 18, 27366 RSC.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- J. P. Erdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 Search PubMed.
- J. Meyer and K. Reuter, New J. Phys., 2011, 13, 085010 CrossRef.
- M. Yata and H. Rouch, Appl. Phys. Lett., 1999, 75, 1021 CrossRef CAS.
- A. Hodgson, A. Lewin and A. Nesbitt, Surf. Sci., 1993, 293, 211 CrossRef CAS.
- M. Minniti, D. Farías, P. Perna and R. Miranda, J. Chem. Phys., 2012, 137, 074706 CrossRef CAS.
- A. Liem, J. Clarke and G. Kresse, Surf. Sci., 2000, 459, 104 CrossRef.
- Y. Xu and M. Mavrikakis, Surf. Sci., 2001, 494, 131 CrossRef CAS.
- L. Martin-Gondre, C. Crespos and P. Larregaray, Surf. Sci., 2019, 688, 45 CrossRef CAS.
- M. Ramos, C. Díaz, A. E. Martínez, H. F. Busnengo and F. Martín, Phys. Chem. Chem. Phys., 2017, 19, 10217 RSC.
- M. Ramos, C. Díaz, A. E. Martínez, F. Martín and H. F. Busnengo, J. Phys. Chem. C, 2018, 122, 15529 CrossRef CAS.
- B. Hammer, I. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 54, 11169 Search PubMed.
- G. J. Kroes and C. Díaz, Chem. Soc. Rev., 2016, 45, 3658 RSC.
- L. Vattuone, L. Savio, M. Okada, K. Moritani and M. Rocca, Surf. Sci., 2008, 602, 2689 CrossRef CAS.
- R. Otero, F. Calleja, V. GarcÌa-Suárez, J. Hinarejos, J. de la Figuera, J. Ferrer, A. V. de Parga and R. Miranda, Surf. Sci., 2004, 550, 65–72 CrossRef CAS.
- F. Calleja, V. M. García-Suárez, J. J. Hinarejos, J. Ferrer, A. L. Vázquez de Parga and R. Miranda, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 125412 CrossRef.
- H. F. Busnengo, A. Salin and W. Dong, J. Chem. Phys., 2000, 112, 7641–7651 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- S. A. Adelman and J. D. Doll, J. Chem. Phys., 1976, 64, 2375–2388 CrossRef CAS.
- J. C. Tully, G. H. Gilmer and M. Shugard, J. Chem. Phys., 1979, 71, 1630–1642 CrossRef CAS.
- H. Bachau, E. Cormier, P. Decleva, J. E. Hansen and F. Martín, Rep. Prog. Phys., 2001, 64, 1815–1943 CrossRef CAS.
- K. K. Irikura, J. Phys. Chem. Ref. Data, 2007, 36, 389–397 CrossRef CAS.
- C. Díaz, J. K. Vincent, G. P. Krishnamohan, R. A. Olsen, G. J. Kroes, K. Honkala and J. K. Nørskov, J. Chem. Phys., 2006, 125, 114706 CrossRef.
- M. Beutl, K. D. Rendulic and G. R. Castro, J. Chem. Soc., Faraday Trans., 1995, 91, 3639–3643 RSC.
- H. F. Busnengo, E. Pijper, G. J. Kroes and A. Salin, J. Chem. Phys., 2003, 119, 12553–12562 CrossRef CAS.
- P. Rivière, H. F. Busnengo and F. Martín, J. Chem. Phys., 2005, 123, 074705 CrossRef.
- C. Díaz, R. A. Olsen, D. J. Auerbach and G. J. Kroes, Phys. Chem. Chem. Phys., 2010, 12, 6499 RSC.
- C. Díaz and A. Olsen, J. Phys. Chem., 2009, 130, 094706 CrossRef.
- G. Laurent, C. Díaz, H. F. Busnengo and F. Martín, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 161404(R) CrossRef.
- P. Maroni, D. Papageorgopoulos, A. Ruf, R. D. Beck and R. T. Rizzo, Rev. Sci. Instrum., 2006, 77, 054103 CrossRef.
- W. E. Perreault, N. Mukherjee and R. Z. Zare, J. Chem. Phys., 2016, 145, 154203 CrossRef.
- C. Díaz, H. F. Busnengo, F. Martín and A. Salin, J. Chem. Phys., 2003, 118, 2886–2892 CrossRef.
- C. Díaz, F. Martín, H. F. Busnengo and A. Salin, J. Chem. Phys., 2004, 120, 321–328 CrossRef.
- G. Comsa and R. David, Surf. Sci. Rep., 1985, 5, 145 CrossRef CAS.
- M. Ramos, M. Minniti, C. Díaz, D. Farías, R. Miranda, F. Martín, A. E. Martínez and H. F. Busnengo, Phys. Chem. Chem. Phys., 2013, 15, 14936–14940 RSC.
- H. Zajonz, A. P. Baddorf, D. Gibbs and D. M. Zehner, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 10436 CrossRef CAS.
- M. Bonfanti, C. Díaz, M. F. Somers and G. J. Kroes, Phys. Chem. Chem. Phys., 2011, 13, 4552 RSC.
- C. Díaz, E. Pijper, R. A. Olsen, H. F. Busnengo, D. J. Auerbach and G. J. Kroes, Science, 2009, 326, 832 CrossRef.
- T. Tchakoua, E. W. F. Smeets, M. F. Somers and G. J. Kroes, J. Phys. Chem. C, 2019, 123, 20420 CrossRef CAS.
- E. W. F. Smeets, J. Voss and G. J. Kroes, J. Phys. Chem. A, 2019, 123, 5395 CrossRef CAS.
- E. N. Ghassemi, M. F. Somers and G. J. Kroes, J. Phys. Chem. C, 2019, 123, 10406 CrossRef CAS.
- H. J. Chadwick, A. Gutiérrez-González, R. D. Beck and G. J. Kroes, J. Chem. Phys., 2019, 150, 124702 CrossRef.
| This journal is © the Owner Societies 2021 |