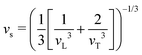Alloy scattering of phonons
Ramya
Gurunathan
 ,
Riley
Hanus
,
Riley
Hanus
 and
G. Jeffrey
Snyder
and
G. Jeffrey
Snyder
 *
*
Materials Science and Engineering, Northwestern University, Evanston, IL 60208, USA. E-mail: jeff.snyder@northwestern.edu
First published on 22nd April 2020
Abstract
Solid-solution alloy scattering of phonons is a demonstrated mechanism to reduce the lattice thermal conductivity. The analytical model of Klemens works well both as a predictive tool for engineering materials, particularly in the field of thermoelectrics, and as a benchmark for the rapidly advancing theory of thermal transport in complex and defective materials. This comment/review outlines the simple algorithm used to predict the thermal conductivity reduction due to alloy scattering, as to avoid common misinterpretations, which have led to a large overestimation of mass fluctuation scattering. The Klemens model for vacancy scattering predicts a nearly 10× larger scattering parameter than is typically assumed, yet this large effect has often gone undetected due to a cancellation of errors. The Klemens description is generalizable for use in ab initio calculations on complex materials with imperfections. The closeness of the analytic approximation to both experiment and theory reveals the simple phenomena that emerges from the complexity and unexplored opportunities to reduce thermal conductivity.
Solid-solution alloy scattering in engineering materials
The use of solid-solution alloys and doped materials is ubiquitous in materials science, as the electronic, optical, thermal, and structural properties of a material can be tailored through the introduction of point defects such as impurities, vacancies, interstitial atoms or anti-site defects. In many applications, such as thermoelectrics, thermal barrier coatings, and microelectronics, the influence of these point defects, or solute atoms, on thermal conductivity must be understood and controlled to engineer their properties.1–3Typically, experimental trends of thermal conductivity versus point defect concentration are modeled using the expression originally derived by Klemens.4–7 These closed-form expressions that simply use the mass and size of the defect are attractive because of their simplicity and utility for determining the source of phonon scattering and thermal conductivity suppression in a solid solution. By calculating the impact of an impurity from just its mass or size, one can uncover material design strategies to optimize the thermal conductivity for a given technological application.8–11 The alloy scattering model has been used to identify the dominant phonon scattering mechanisms for several alloy systems important to the field of thermoelectrics including PbTe–PbSe,2 Bi2Te3–Bi2Se3,7 and Mg3Sb2–Mg3Bi2.12 While first-principles methods are essential to understanding the details of phonon interactions,13–16 the Klemens alloy scattering model describes the emergent phenomena across material systems well, even given the ostensibly limiting approximations, and therefore continues to be widely used.15,17–19
Klemens model of point-defect scattering
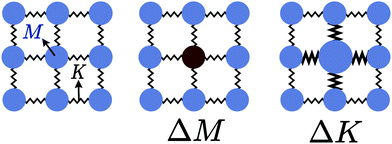
The thermal conductivity reduction caused by point defects can be understood as a result of the perturbation of the kinetic energy (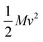 for each atom) or potential energy (
for each atom) or potential energy (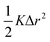 for each bond) of the lattice (Fig. 1). A mass difference on a defect site (ΔM) perturbs the kinetic energy term, while the potential energy term is perturbed by a force constant difference (ΔK). This often arises from a structural distortion (mechanical strain) caused by the defect that can be described by a site radius difference (ΔR) (see Fig. 1). In several cases, mass difference is the dominant effect, with the strain effect ignored, since large volume differences are often energetically unfavorable for solid solution. Additionally, the magnitude of the strain scattering effect around a point defect is not as easily estimated, as it should strictly be determined by structural distortions and changes in bond strength around the defect site.20 For simplicity, we start by introducing the equations for only mass difference scattering, with analogous expressions for the force constant difference added later.
for each bond) of the lattice (Fig. 1). A mass difference on a defect site (ΔM) perturbs the kinetic energy term, while the potential energy term is perturbed by a force constant difference (ΔK). This often arises from a structural distortion (mechanical strain) caused by the defect that can be described by a site radius difference (ΔR) (see Fig. 1). In several cases, mass difference is the dominant effect, with the strain effect ignored, since large volume differences are often energetically unfavorable for solid solution. Additionally, the magnitude of the strain scattering effect around a point defect is not as easily estimated, as it should strictly be determined by structural distortions and changes in bond strength around the defect site.20 For simplicity, we start by introducing the equations for only mass difference scattering, with analogous expressions for the force constant difference added later.
The Klemens analytic model predicts the ratio of the defective solid's lattice thermal conductivity to that of the pure solid without defects (κL/κ0). This ratio is a function of the disorder parameter u which depends on properties of the pure material: its lattice thermal conductivity (κ0), elastic properties through its average speed of sound (vs)†, the average volume per atom (V), as well as a scattering parameter to capture the influence of point defects (Γ = ΓM + ΓK),
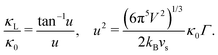 | (1) |
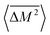 , relative to the average mass squared,
, relative to the average mass squared, 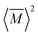 (eqn (3))9,21–23
(eqn (3))9,21–23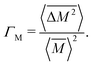 | (2) |
The average mass and mass variance are most easily computed by considering each element (or crystallographic site) separately.9,21,22 Consider a generic compound with formula unit: A1c1A2c2A3c3…Ancn (e.g. Mg2Sn), where An refers to the nth component (e.g. Mg, or Sn) and cn refers to the stoichiometry of that component (e.g. 2 or 1). Each site Ancn(e.g. Sn) can be occupied by a set of atomic species i, including the host atom (e.g. Sn) and any substitutional defects (e.g. Si) with species site fraction (fi,n) (e.g. 1 − x and x in Sn1−xSix). Then, the average mass of the compound 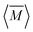 is given by the stoichiometry weighted average of each site average mass
is given by the stoichiometry weighted average of each site average mass 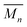
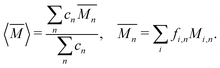 | (3) |
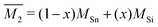 , while the atomic mass averaged over the full solid is
, while the atomic mass averaged over the full solid is 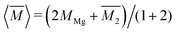 .
.
Similarly, the average mass variance of the compound 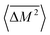 is given by the stoichiometry weighted average of the all site mass variances
is given by the stoichiometry weighted average of the all site mass variances 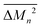
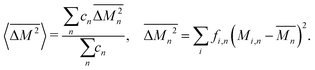 | (4) |
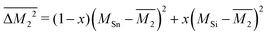 . Then, because the atomic mass variance averaged over this full solid has no contribution from the Mg site due to lack of defects on this site, we simply have
. Then, because the atomic mass variance averaged over this full solid has no contribution from the Mg site due to lack of defects on this site, we simply have 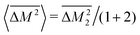 .
.
The Klemens model using mass difference alone (Γ = ΓM) quantitatively describes the κL trends with alloy composition for several material systems.3,10,13,24 The solid solution between Mg2Sn and Mg2Si is a case in which the Klemens mass difference model works well, and is recreated here to demonstrate use of these equations in a multiatomic system. For a given composition, the value of κ0, V, and vs are taken to be the linear interpolation between the values for the end-member species (Fig. 2). Here, the inputs for Mg2Sn and Mg2Si are, respectively, V = 25.7 and 21.5 Å3 for the average volumes per atom, vs = 3160 and 6715 m s−1 for the average sound velocities, and a scattering parameter of
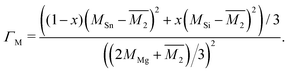 | (5) |
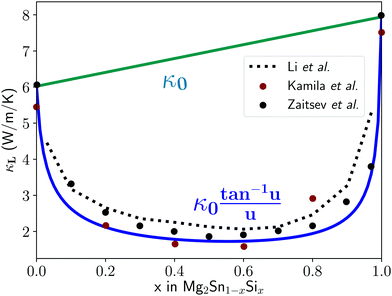 | ||
| Fig. 2 Lattice thermal conductivity for the full composition range of the solid solution between Mg2Sn and Mg2Si. Red and black data points are experimental thermal conductivity measurements,25,26 while the blue U-curve is the prediction from the mass difference Klemens model and the dotted black line comes from first principles T matrix scattering theory.13 Finally, the κ0 curve interpolates linearly between the two end-members. The fit helps identify mass-difference scattering as the dominant effect in this system, as it explains the trend without needing to invoke other scattering or softening mechanisms. | ||
Using these inputs, the full κLversus composition trend shown in Fig. 2 is calculated without fitting parameters, and shows good correspondence with experimental measurements. As a result, one can conclude that the contribution of the mass difference term in point defect scattering is the dominant effect for this materials system and explains the experimental results without having to invoke other scattering or lattice softening mechanisms. This result is consistent with the fact that the cell volume of Mg2Sn(1−x)Six is fairly constant with changes in composition x, leading to negligible mechanical strain contributions.
For vacancy scattering, the perturbation to lattice energy emerges from both the missing mass and the missing bonds to its neighbors. Klemens suggests that the scattering parameter Γ for this case can be modeled as a mass difference scattering with 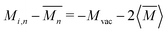 , where Mvac is the mass of the vacant atom. This leads to a ∼10 × stronger scattering parameter than a typical point defect.27 Indeed, vacancy scattering has been demonstrated to induce a large reduction in thermal conductivity in several thermoelectric compounds,28–35 although the enhanced scattering effect of vacancies is often overlooked. Recent data analysis suggests that the same mass difference model describes interstitial defect scattering as well.8,36,37
, where Mvac is the mass of the vacant atom. This leads to a ∼10 × stronger scattering parameter than a typical point defect.27 Indeed, vacancy scattering has been demonstrated to induce a large reduction in thermal conductivity in several thermoelectric compounds,28–35 although the enhanced scattering effect of vacancies is often overlooked. Recent data analysis suggests that the same mass difference model describes interstitial defect scattering as well.8,36,37
The mass difference model captured in eqn (3) and (4) follows the recommendation originally proposed by Berman et al., and is suggested here for its conceptual clarity. Several discussions, including those of Klemens,4,7,21,38,39 describe this model as being equivalent to a monatomic lattice approximation, which involves a summation of the atoms in the unit cell into one large, vibrating mass. This alternate description of a compound has led to ambiguity in the meaning of the volume V. A misinterpretation has resulted in some studies over-approximating the mass scattering effect by a factor equal to the number of atoms in the unit cell. Typically, however, a cancellation of errors due to an underestimation of the effect of vacancies allows the broader conclusions of the studies about the importance of point defect scattering in a materials system to remain valid.8,29–31,35
As mentioned previously, the strain due to a defect that is larger or smaller than the host atom perturbs the lattice energy through its potential energy term. Therefore, the force constant variance (ΔK2) is typically expressed through the average variance in atomic radius (ΔR2) scaled by a fitting parameter (ε). As before, the atomic radius variance on the nth site is defined from the atomic radius of the ith species which may occupy that site, Ri,n, and the average atomic radius of the site, 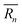 . Although there exist theoretical models40 or heuristical correlations20 for ε, it is considered here as an adjustable parameter that typically varies between 1–500 in order to fit the experimental data.
. Although there exist theoretical models40 or heuristical correlations20 for ε, it is considered here as an adjustable parameter that typically varies between 1–500 in order to fit the experimental data.
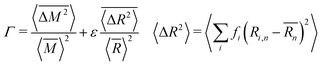 | (6) |
Complex systems and the Tamura Model
The mass difference perturbation model used by Klemens works surprisingly well for even complex systems with large unit cells. This suggests that the validity of the essential physics transcends the stated assumptions, allowing the model to be applied towards complex, engineering materials. For example, the Debye model or linear phonon dispersion is often assumed, which coarsens over the complexities of real band structures. It can be shown that there is some cancellation of band structure properties, particularly stemming from the density of states dependence of several quantities in the model, which allows for this reduced sensitivity to band structure.37The simple mass and volume perturbations can be generalized for materials with complex phonon dispersions or even non-crystalline materials. Tamura defines a similar mass difference perturbation parameter for each phonon eigenstate (ek(s)) that can be implemented in numerical Boltzmann transport equation solvers for thermal conductivity.13,15,18,19,23,41–45 In many thermal conductivity solvers, the Tamura model is the standard treatment for isotope-phonon scattering in pure compounds.43,44 The mass difference parameter in the Tamura model (ΓTM) is given as a sum over all the s atom sites in a simulation, where i again labels the species that may occupy site s including the host and impurity atoms
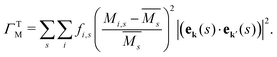 | (7) |
The description of scattering here is general enough that it could be used to describe the perturbation induced to any vibrational mode. Therefore, in addition to plane wave phonons, which are only strictly defined in periodic crystals, the vibrational modes of amorphous solids, codified in the Allen and Feldman formalism as diffusons, locons, and propagons, are describable within the same alloy scattering theory.46–48
A place for analytical theory
The analytical alloy scattering model is a simple tool for predicting the thermal conductivity of disordered materials. The success of alloy scattering models, even in complex, non-ideal systems demonstrates their widespread applicability. When applied correctly, it can identify potent scattering effects and illuminate the route for optimally tailoring the thermal properties via defect engineering.8,32,36,49 Even the large thermal conductivity reduction induced by vacancies and interstitial atoms appears to be well described within the simple model by including the effect of removing or forming the nearest neighbor bonds. The study of thermal conductivity has benefited from these simple, physics-based models for over 70 years, as they are easily implemented, elucidate underlying mechanisms, and can even help point to exotic physics when they fail to describe a system. In the past, qualitative and quantitative comparison to analytical models in specific materials systems has led to the identification of breakdowns in the Born approximation,50 novel scattering cross-sections associated with impurity clusters or low-dimensional materials,16 and proposed phonon-trapping effects.51 Their lasting relevance supports the argument for continued work on analytical, physical expressions in emerging fields of materials science even as new techniques in simulation and materials informatics become widespread.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Thanks to Ankita Katre and Max Dylla for helpful discussions. We thank NSF DMREF award #1729487 and award #70NANB19H005 from U.S. Department of Commerce, National Institute of Standards and Technology as part of the Center for Hierarchical Materials Design (CHiMaD) for support.Notes and references
- C. L. Wan, W. Pan, Q. Xu, Y. X. Qin, J. D. Wang, Z. X. Qu and M. H. Fang, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 144109 CrossRef.
- H. Wang, A. D. Lalonde, Y. Pei and G. J. Snyder, Adv. Funct. Mater., 2012, 23, 1586–1596 CrossRef.
- E. S. Toberer, A. Zevalkink and G. J. Snyder, J. Mater. Chem., 2011, 21, 15843–15852 RSC.
- P. G. Klemens, Proc. Phys. Soc., London, Sect. A, 1955, 68, 1113–1128 CrossRef.
- J. Callaway and H. C. von Baeyer, Phys. Rev., 1960, 120, 1149–1154 CrossRef CAS.
- P. Klemens, Phys. Rev., 1960, 119, 507–509 CrossRef CAS.
- H. J. Goldsmid, J. Appl. Phys., 1961, 32, 2198–2202 CrossRef CAS.
- G. P. Meisner, D. T. Morelli, S. Hu, J. Yang and C. Uher, Phys. Rev. Lett., 1998, 80, 3551–3554 CrossRef CAS.
- J. Yang, G. P. Meisner and L. Chen, Appl. Phys. Lett., 2004, 85, 1140–1142 CrossRef CAS.
- M. Wood, U. Aydemir, S. Ohno and G. J. Snyder, J. Mater. Chem. A, 2018, 6, 9437–9444 RSC.
- E. S. Toberer, A. F. May, B. C. Melot, E. Flage-Larsen and G. J. Snyder, Dalton Trans., 2010, 39, 1046–1054 RSC.
- K. Imasato, S. D. Kang and G. J. Snyder, Energy Environ. Sci., 2019, 12, 965–971 RSC.
- W. Li, L. Lindsay, D. A. Broido, D. A. Stewart and N. Mingo, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 174307 CrossRef.
- A. Katre, J. Carrete, B. Dongre, G. K. Madsen and N. Mingo, Phys. Rev. Lett., 2017, 119, 75902 CrossRef PubMed.
- C. A. Polanco and L. Lindsay, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 98, 014306 CrossRef CAS.
- N. Mingo, K. Esfarjani, D. A. Broido and D. A. Stewart, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 45408 CrossRef.
- M. Schrade and T. G. Finstad, Phys. Status Solidi B, 2018, 255, 1800208 CrossRef.
- T. Shiga, T. Hori and J. Shiomi, Jpn. J. Appl. Phys., 2014, 53, 021802 CrossRef.
- T. Feng, B. Qiu and X. Ruan, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 235206 CrossRef.
- B. R. Ortiz, H. Peng, A. Lopez, P. A. Parilla, S. Lany and E. S. Toberer, Phys. Chem. Chem. Phys., 2015, 17, 19410–19423 RSC.
- R. Berman, E. Foster and J. Ziman, Proc. R. Soc. London, Ser. A, 1956, 237, 344–354 CAS.
- G. A. Slack, Phys. Rev., 1962, 126, 427–441 CrossRef.
- S.-i. Tamura, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 849–854 CrossRef CAS.
- A. Kundu, N. Mingo, D. A. Broido and D. A. Stewart, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 125426 CrossRef.
- H. Kamila, P. Sahu, A. Sankhla, M. Yasseri, H.-n. Pham, T. Dasgupta, E. Mueller and J. D. Boor, J. Mater. Chem. A, 2019, 7, 1045–1054 RSC.
- V. Zaitsev, E. Tkalenko and E. Nikitin, Sov. Phys. Solid State, 1969, 11, 3000–3002 Search PubMed.
- C. A. Ratsifaritana and P. G. Klemens, Int. J. Thermophys., 1987, 8, 737–750 CrossRef CAS.
- Y. Wang, F. Yang and P. Xiao, Appl. Phys. Lett., 2013, 102, 141902 CrossRef.
- Y. Wang, F. Li, L. Xu, Y. Sui, X. Wang, W. Su and X. Liu, Inorg. Chem., 2011, 50, 4412–4416 CrossRef CAS PubMed.
- Y. Pei and D. T. Morelli, Appl. Phys. Lett., 2009, 94, 122112 CrossRef.
- G. Tan, W. G. Zeier, F. Shi, P. Wang, G. Je, V. P. Dravid and M. G. Kanatzidis, Chem. Mater., 2015, 27, 7801–7811 CrossRef CAS.
- G. Tan, S. Hao, R. C. Hanus, X. Zhang, S. Anand, T. P. Bailey, A. J. Rettie, X. Su, C. Uher, V. P. Dravid, G. J. Snyder, C. Wolverton and M. G. Kanatzidis, ACS Energy Lett., 2018, 3, 705–712 CrossRef CAS.
- J. Shen, X. Zhang, S. Lin, J. Li, Z. Chen, W. Li and Y. Pei, J. Mater. Chem. A, 2016, 4, 15464–15470 RSC.
- F. Böcher, S. P. Culver, J. Peilstöcker, K. S. Weldert and W. G. Zeier, Dalton Trans., 2017, 46, 3906–3914 RSC.
- Z. Qu, T. D. Sparks, W. Pan and D. R. Clarke, Acta Mater., 2011, 59, 3841–3850 CrossRef CAS.
- Y. Pei, L. Zheng, W. Li, S. Lin, Z. Chen, Y. Wang, X. Xu, H. Yu, Y. Chen and B. Ge, Adv. Electron. Mater., 2016, 2, 1600019 CrossRef.
- R. Gurunathan, R. Hanus, M. Dylla, A. Katre and G. J. Snyder, Phys. Rev. Appl., 2019, 13, 034011 CrossRef.
- P. G. Klemens, Proc. Phys. Soc., 1957, 70, 833–836 CrossRef.
- H. J. Goldsmid, Introduction to Thermoelectricity, Springer, US, 2nd edn, 2010, pp. 67–74 Search PubMed.
- B. Abeles, Phys. Rev., 1963, 131, 1906–1911 CrossRef.
- S. Tamura, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27, 858–866 CrossRef CAS.
- J. M. Larkin and A. J. H. Mcgaughey, J. Appl. Phys., 2017, 114, 023507 CrossRef.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- J. Carrete, B. Vermeersch, A. Katre, A. van Roekeghem, T. Wang, G. K. Madsen and N. Mingo, Comput. Phys. Commun., 2019, 220, 351–362 CrossRef.
- W. Li, J. Carrete, N. A. Katcho and N. Mingo, Comput. Phys. Commun., 2014, 185, 1747–1758 CrossRef CAS.
- P. B. Allen, J. L. Feldman, J. Fabian and F. Wooten, Philos. Mag. B, 1999, 79, 1715–1732 CrossRef CAS.
- F. Deangelis, M. G. Muraleedharan, J. Moon, H. R. Seyf, A. J. Minnich, A. J. H. Mcgaughey and A. Henry, Nanoscale Microscale Thermophys. Eng., 2018, 23, 81–116 CrossRef.
- M. Simoncelli, N. Marzari and F. Mauri, Nat. Phys., 2019, 15, 809–813 Search PubMed.
- Q. Zheng, C. A. Polanco, M. H. Du, L. R. Lindsay, M. Chi, J. Yan and B. C. Sales, Phys. Rev. Lett., 2018, 121, 105901 CrossRef CAS PubMed.
- N. H. Protik, J. Carrete, N. A. Katcho, N. Mingo and D. A. Broido, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 045207 CrossRef.
- M. B. Bebek, C. M. Stanley, T. M. Gibbons and S. K. Estreicher, Sci. Rep., 2016, 6, 32150 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2020 |