Automated exploration of the conformational degrees of freedom along reaction profiles - driving a FASTCAR

Abstract

This publication aims at presenting a Python-based workflow designed to enable a fully automatised and exhaustive exploration of the conformational degrees of freedom within the calculation of reaction paths in molecular systems. The proposed strategy focuses on effectively representing the lowest energy conformers for intricate, highly rotatable, and non-intuitive transition states, reagents and products, using existing computational tools. The article presents a workflow that is demonstrated through the application of five chemical reactions, chosen to be representative of the diversity and complexity of actual experimental studies, and which often prove to be challenging to study “by hand”. The proposed methodology is expected to be of a great help in the modelling of state-of-the art organic chemistry reactions, whose complexity is ever increasing.

---

1 Introduction

Theoretical modelling of molecular reactions is a challenging task considering the immense complexity of the experimental situations.^1–4 When computing reaction paths, one is always facing the issue of determining whether the lowest energy profile has been identified or not.^5,6 This is noticeably true regarding the conformational degrees of freedom, whose explicit and non-automatised exploration is only conceivable for small molecular systems. While organic chemistry is a field developing towards complexity, theoreticians often need to simplify the molecular systems they study to be able to unfold reaction paths calculations. Such a mismatch, at a time of steady increase in computational power, is an issue in itself. The course of our interactions with colleagues from experimental chemistry led us to consider it, and to set up a fully automated workflow to allow for an easier, exhaustive exploration of conformational degrees of freedom along reaction profiles. The present article is dedicated to the presentation of this solution, which we label hereafter FASTCAR (Fully Automated Sampling for Transition-state CAlculation and Reaction profiles.)

In a first section, we present the basic tools and philosophy of this Python-based workflow, which heavily relies on the CREST library of Grimme and coworkers,⁷ supplemented by an additional library, sPyRMSD,⁸ helping in rejecting equivalent structures. The second section is dedicated to an illustration of the functioning of FASTCAR.

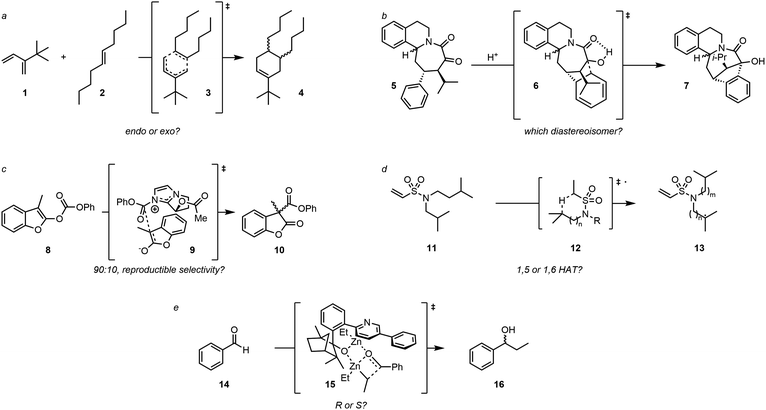
We have selected five challenging examples embodying the complexity of molecular systems (Fig. 1). The first example involves a Diels–Alder reaction between 4,4-dimethyl-3-methylenepent-1-ene (1) and (E)-dec-5-ene (2), which has a total of 6561 potential conformers due to eight rotatable bonds (Fig. 1a). The second example involves an intramolecular acid-catalysed cyclization reaction of polycyclic azocane derivative, a previously analyzed reaction in our group⁹ and whose selectivity appeared to be driven by conformation equilibria (Fig. 1b). The third example relies on an enantioselective organo-catalysed rearrangement of benzofurane derivatives (Black rearrangement), where selectivity was assumed to relate to differences in steric repulsion in the two putative transition state geometries (Fig. 1c).¹⁰ Since these are differing essentially by the relative orientation of the reaction partners, they can be seen as “non-covalent conformers” hence fall within the scope of our proposal. The fourth example involves a radical H-atom transfer reaction on flexible aliphatic molecules, thus likely to present a significant number of conformers (Fig. 1d).¹¹ The fifth example is an enantioselective dialkylzinc addition on benzaldehyde using a ligand containing flexible biaryl axes (Fig. 1e).¹²

Fig. 1 (a) Diels Alder reaction between 4,4-dimethyl-3-methylenepent-1-ene (1) and (E)-dec-5-ene (2). (b) diastereoselective intramolecular acidic cyclization. (c) enantioselective organo-catalysed Black rearrangement. (d) Regioselective intramolecular radical H-atom transfer. (e) Enantioselective dialkylzinc additions on benzaldehyde.

Finally, some development perspective for future versions of FASTCAR are proposed, noticeably related to the elimination of the dependency on the start point geometry that appeared in the case of the intramolecular cyclization reaction.

2 The FASTCAR workflow

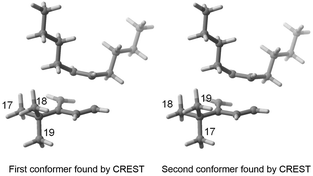
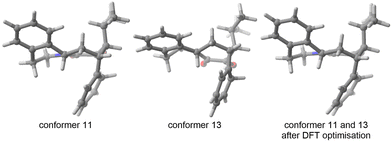
As indicated in the introduction, the aim of FASTCAR is to enable the exploration of the conformational degrees of freedom along a given reaction path calculation. It relies mostly on the use of two previously developed tools: CREST⁷ and sPyRMSD,⁸ interfaced with a DFT code (here Gaussian 16).¹³ CREST, developed by the group of S. Grimme, allows the sampling of conformers by the use of DFTB-based metadynamics calculations, either for energy minima (reagents or products) or for transition states (constrained searches). This potent tool proved extremely efficient in producing starting structures for further high-level (DFT) calculations (see for instance a the recent example in ref. 14), but in the course of our works we noticed it sometimes struggles to eliminate geometries that should be considered duplicates. Two cases are generally encountered. In the first one, the proposed geometries are actual rotamers of the same conformer with energy and/or rotational constants too high to be considered by CREST as rotamers. This situation is frequently encountered with branched alkyl and phenyl groups; see for instance the case of a tert-butyl rotation on Fig. 2.

Fig. 2 Two conformers found by CREST and considered as duplicates in FASTCAR.

In the second case, the geometries are artifacts, likely due to inaccuracies in the description of the GFN-xtb¹⁵ based potential energy surface (for instance two geometries differing by the rotation of a methyl group of an unusual angle) - and which ultimately converge to the geometry of an already encountered conformer at the DFT optimisation stage. In Fig. 3, conformers 11 and 13 both have an invariant RMSD of 0.62 (which exceeds our chosen threshold of 0.5, vide infra). However, after DFT optimization, they result in the same transition state geometry.

Fig. 3 Two conformers found by CREST leading to the same TS after DFT optimisation.

In both cases, the “incorrect” geometries are highly reminiscent of other “correct” conformers found by CREST. This similarity can then be used to set up a refinement in the selection of geometries, which is here performed using SpyRMSD (Python library for the calculation of invariant root mean square deviation (RMSD) between structures).

Overall, FASTCAR uses five interrelated Python programs which are detailed hereafter. Note that the current version of FASTCAR supports jobs submission through the Slurm system¹⁶ (version 18.08.8, as used on our local computing cluster).

Automated_CREST

This first program reads an input file, which contains the parameters to be used for the CREST search, the sPyRMSD cut-off (see below), the Gaussian calculations to be performed, and the name of a Gaussian output file for the starting geometry. This program then extracts the geometry from the indicated output, checks the nature of calculation to be performed by examining the computed frequencies (constrained TS search if the first frequency is negative, unconstrained otherwise), and starts it using the user-defined parameters and a default energy window of 6 kcal mol⁻¹. A first filter for equivalent geometries is applied through the CREGEN utility (using the recommended energy window for rotation barriers of 30 kcal mol⁻¹).

Automated_RMSD

This program further refines the conformer ensemble by applying sPyRMSD, using a user-defined threshold for rejection of rotations-equivalent geometries. This parameter is by default set to 0.5 in line with former works dealing with conformational analysis.¹⁷ It must here be noted that this value is quite arbitrary, and even though our experience showed it is usually adequate for the kind of chemistries presented herein (see Section S1 in supplementary material for an illustration in the case of the Black rearrangement reaction, ESI†), it is a quite critical parameter that the user should examine and eventually optimise. The program then initiates Gaussian calculations for each remaining conformer. To save time, frequencies are not calculated in the unconstrained search. If two-step optimisation is chosen, a smaller basis set is used first, e.g. 6-31G(d,p), and after the next part, Automated_Check_1, a larger one, e.g. 6-311++G(d,p), is used.

Automated_Check_1 (optional)

This program filters out unfinished Gaussian calculations, non-optimised geometries and those with incorrect first frequencies, <0 for geometry and >0 for TS. In the case of constrained (TS) searches, it further rejects geometries associated to comparable energies and frequencies, which are assumed to be redundant. The criterion for energy is set at 10⁻⁶ a.u., and at the matching integer value (in cm⁻¹) for frequencies. A final refinement of the TS geometries is achieved by rejection of calculations presenting imaginary frequency less than 0.5 times the one given in input. The resulting conformer ensemble is then used for a subsequent larger-basis set DFT calculation.

Automated_Check_2

This program continues the workflow by eliminating incomplete and duplicate geometries. In the case of constrained searches it sets a rejection criterion for imaginary modes (less than 0.7 times the negative frequency in the input). If selected, it then initiates an IRC calculation (both forward and backward) followed by geometry optimisation, starting from the geometry with the lowest SCF energy. In the case of unconstrained searches, it starts a frequency calculation and, if selected, additional calculations on the lowest SCF energy geometry.

Automated_EnergyExtract

This program accomplishes the workflow by extracting the energies of all final calculations. Subsequently, it compiles the extracted energies into a comprehensive text file, facilitating further analysis.

Note: during the final stages of this manuscript preparation, we noticed the publication of a related tool, Autobench, by the group of Cormanich.¹⁸ Both Autobench and FASTCAR are devised to ease the exploration of the conformational degrees of freeedom and exploit the molecular similarity (evaluated by RMSD) to reduce computational effort. They however differ in objective: in the case of Autobench, the aim is to further ease methods benchmarking, while FASTCAR aims at facilitating conformational analysis along reaction profiles. This difference of objective results in difference in the geometry pruning, as we here additionally include a selection criterion based on the norm of the imaginary mode. This allow us to avoid misguiding towards inappropriate geometries (typically local maxima associated to a methyl rotation, likely to appear for complex molecular species). We additionally noticed during our development that the use of an invariant RMSD code was extremely useful to further reject equivalent structures, hence the choice of sPyRMSD - which does not seem to be involved in AutoBench.

3 Results and discussion

3.1 Computational details and additional note

The electronic structure calculations for all examples presented below were conducted using Gaussian 16 rev B.01.38 software. All calculations were done on a CPU cluster (12-CPU calculations) managed under Slurm 18.08.8, and piloted by FASTCAR. The level of theory used in the following examples is B3LYP-D3/6-31G(d,p) for the Diels–Alder reaction, B3LYP-D3BJ/6-31G(d,p) for the acidic cyclization and IEFPCM(2-methyl-2-propanol)-B3LYP-D3/6-311++G(d,p) for the Black rearrangement, IEFPCM(dichloroethane)-ω B97wD/6-311++G(d,p) for the regioselective intramolecular radical H-atom transfer and BP86/SVP for the enantioselective dialkylzinc additions on benzaldehyde chosen as as still representative level in molecular reactivity studies.^19–23 All optimisations conducted under Gaussian were done without constraints. As indicated in the workflow (vide supra), vibrational frequencies were systematically computed in the case of the transition state search, and at the end of the search for the minimum case, to ensure in both case the proper nature of the stationary point. Molecular structure images were obtained using the CYLview2.0 software.²⁴

In addition to the examples discussed in the present publication, we additionally refer the interested reader to an additional work that was submitted nearly concomitantly to this one to ChemSusChem,²⁵ which made extensive use of the FASTCAR approach.

3.2 Diels–Alder reaction with highly rotatable bonds

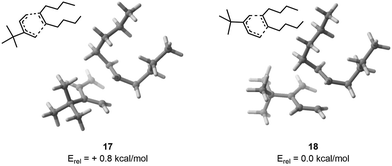
As a first example, we have selected a Diels–Alder reaction between 4,4-dimethyl-3-methylenepent-1-ene (1) and (E)-dec-5-ene (2). This reaction was chosen because 2 has 8 rotatable bonds, which generates thousands of possible conformers. Additionally, the presence of a tert-butyl moiety on 1 is expected to reverse the usual endo selectivity.²⁶ To feed FASTCAR, we have identified an arbitrary transition state (TS) for both the endo and exo geometries without any a priori.

For the endo transition state, CREST identified 1258 unique conformers. This number was reduced to 714 by initially pruning with CREGEN, and then applying the sPyRMSD code, which yielded 147 conformers for DFT calculations. Out of these, 144 transition state (TS) calculations were successfully completed within an energy window of 6.2 kcal mol⁻¹. The most stable TS was found to be 3.7 kcal mol⁻¹ lower in energy compared to the arbitrary TS.

For the exo geometry, CREST identified 1562 unique conformers, which were reduced to 909 after an initial pruning step using CREGEN. Finally, 229 conformers were selected for DFT calculation using the sPyRMSD code. A total of 229 transition state (TS) calculations were successfully carried out within an energy window of 7.0 kcal mol⁻¹. The comparison between the most stable TS and the arbitrary input TS revealed that the former was 3.0 kcal mol⁻¹ lower in energy.

Finally, upon examining the arbitrary input TS, it was found that the exo configuration demonstrated greater stability by 1.5 kcal mol⁻¹. After the procedure, it was found that the most stable exo conformer had an energy level 0.8 kcal mol⁻¹ lower than its endo counterpart (Fig. 4), showing as expected that a proper consideration of the conformational degrees of freedom is essential if one is desiring to study chemical reactivity and selectivity – used in a two-level Maxwell–Boltzmann model, a difference of activation barriers of 1.5 kcal mol⁻¹ indeed results in a selectivity at room temperature of 93 : 7, which drops to 80 : 20 at 0.8 kcal mol⁻¹. Taking into account all retained conformers, we eventually end up in a 86 : 14 (exo : endo) selectivity, which further stresses the usefulness of not restricting the analysis to the sole lowest energy geometry.

Fig. 4 On the left, lowest TS found for endo. On the right, lowest TS found for the exo.

3.3 Intramolecular cyclization of a polycyclic azocane

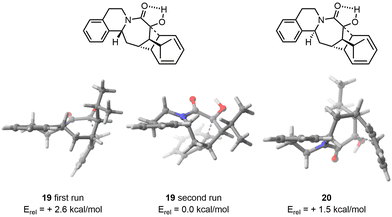
FASTCAR was then applied to an intramolecular acid-catalysed cyclization reaction of a polycyclic azocane derivative. This reaction had previously been modelled in our group using CREST on the starting materials of both diastereoisomers, to help in reducing the number of starting geometries to consider for the search of transition state (making here use of the Hammond postulate,²⁷ assuming the lowest energy transition states should relate to the lowest energy conformers for the reagents). This process provided the desired selectivity but at a high cost of human and computational resources. Our aim was to revisit this example using FASTCAR, and check whether a satisfactory reproduction of experimental selectivity was attainable at a much lower cost in terms of human resources.

In this example, CREST identified fewer conformers (19 for 19 and 15 for 20) due to more constrained geometry. CREGEN did not reduce those ensembles, while sPyRMSD reduced the number of conformers due to duplicates arising mainly from the rotation of the isopropyl group (6 for 19 and 20). In both cases, we observed a significant decrease in the TS energy compared to the arbitrary TS provided (3.2 kcal mol⁻¹ for 19 and 9.2 kcal mol⁻¹ for 20).

After FASTCAR, it was discovered that the TS for the (experimental) minor diastereoisomer was 1.1 kcal mol⁻¹ more stable. This finding does not align with the experimental observation (dr over 20 : 1 in favour of the other). We surmised this discrepancy was related to an incomplete coverage of the potential energy surface by CREST, which “missed” significant regions. Indeed, though FASTCAR found a TS 3.2 kcal mol⁻¹ more stable than the given input, it was not the most stable possible, since it could be shown to be higher in energy than the previously published one. This issue could likely be addressed by a fine tuning of the search parameters within CREST, to ensure a more thorough exploration of the potential energy surface. However this may be quite complicated to unfold, and the solution likely system-dependent, in conceptual contradiction with the philosophy of FASTCAR (thought to be a quite generic tool). Conversely, by analogy with the approach used in the case of genetic algorithm, we envisioned the possibility to correct this problem by an iterative application of the conformer search.

Two approaches were then attempted to address this discrepancy. The initial attempt was to feed FASTCAR with the most stable conformers found by CREST (without any DFT optimization). This unfortunately resulted in the same conformer ensemble being found in both cases. Subsequently, we focused on the most stable conformer after DFT optimization and selected it as the starting input. After applying FASTCAR for a second time, CREST identified new low energy conformers for the major diastereoisomer. The most stable transition state (TS) was found to be 2.6 kcal mol⁻¹ lower in energy compared to the TS found during the first iteration. In the case of the minor diastereoisomer, no variation in the conformer ensemble was observed after the reiteration, resulting in the same lowest TS geometry. As a result, a strong selectivity in line with experiment was eventually observed, the difference in activation barriers being in that case of 1.5 kcal mol⁻¹ (Fig. 5). By precaution, FASTCAR was run a third time taking the most stable TS found after the first iteration and to our delight the same lowest TS was found.

Fig. 5 On the left, lowest TS found for major diastereoisomer after the first workflow. On the middle, lowest TS found for major diastereoisomer after a second iteration of the procedure. On the right, lowest TS found for the minor diastereoisomer.

3.4 Organocatalysed rearrangement

As third example, we selected an asymmetric organocatalyzed rearrangement. This reaction has been previously reported by Zhang and et al. without a computational study being reported to the best of our knowledge.¹⁰ In this paper, the author describes an enantioselective Black rearrangement catalysed by a chiral bicyclic imidazole with excellent conversion (up to 99%) and very good enantiomeric excess (ee up to 88%). This reaction serves as a compelling example of molecular selectivity, given that the experimental ee did not exceed 99%, indicating a need for precise computational energy gaps to replicate reactivity accurately. Therefore, we decided to use the two-steps approach to afford high computational calculation at a lower cost, e.g. a first DFT optimisation at lower cost, here IEFPCM(2-methyl-2-propanol)-B3LYP-D3/6-31G(d,p), to remove duplicate and wrong TS before an optimisation using a larger basis set, IEFPCM(2-methyl-2-propanol)-B3LYP-D3/6-311++G(d,p).

In the case of the major product (resulting from TS 21), CREST identified 41 candidates without trimming from CREGEN. sPyRMSD reduced the number of conformers to 18. Following the initial DFT optimisation, 12 candidates were identified that matched the design criteria. Two were duplicates and four were deemed to be of no further use (not appropriate geometries). The selected conformers were then optimised using a larger basis set, resulting in 11 unique TS and one duplicate. In the case of the minor product (resulting from TS 22), CREST identified 19 candidates, which was subsequently reduced to 17 following CREGEN. sPyRMSD reduced the number of conformers to five. Following the initial DFT optimisation, it was found that all candidates matched the design criteria. The selected conformers were then optimised using a larger basis set, resulting in five unique TS (Fig. 6).

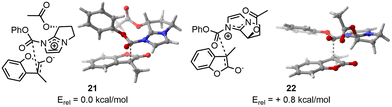Fig. 6 On the left, lowest TS found for major enantiomer. On the right, lowest TS found for the minor enantiomer.

The SCF energy difference between the major and minor products was found to be 0.4 kcal mol⁻¹ using IEFPCM(2-methyl-2-propanol)-B3LYP-D3/6-31G(d,p) and 0.8 kcal mol⁻¹ using IEFPCM(2-methyl-2-propanol)-B3LYP-D3/6-311++G(d,p) leading respectively to computational ee of 35% and 63% at 0 °C. Given an experimental ee of 81%, it is anticipated that the energy difference will be 1.2 kcal mol⁻¹,²⁸ hence the computational results modelled the right selectivity with a slightly underestimated ee.

3.5 Regioselective intramolecular radical H-atom transfer

As fourth example, and to illustrate the wide applicability of the proposed tool, we selected a recently reported radicalar H-atom transfer reaction by Herbort et al.¹¹

In this study, the authors designed a series of model substrates able to induce selective γ–C–H functionalisation through multiple H-atom transfers (HATs). A key step in the proposition is the intramolecular HAT between a sulfonylvinyl radical and a remote C–H position, which is shown to display a significant level of selectivity towards the 1,6-HAT reaction, which was further confirmed by some DFT calculations.

Herein, we propose to revisit this reaction, focusing on one example which - to our best knowledge - was not examined by computations but only through experiments: the 1,5/1,6 selectivity in the case of N-isobutyl-N-isopentylethenesulfonamide.

Here also we proceeded via a two-step approach to alleviate the computational effort: a first round of optimisation at the IEFPCM(dichloroethane)-ω B97wD/6-31++G(d,p) level, followed by reoptimisation at the IEFPCM(dichloroethane)-ω B97wD/6-311++G(d,p) level (level of theory used in the original publication).

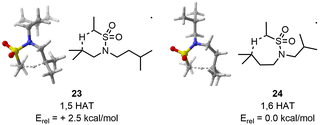
In the case of the 1,6 HAT, CREST identified 114 structures. CREGEN reduced this number to 89 candidates. sPyRMSD further reduced this number to 23 TS candidate structures. After the first optimisation, 20 unique TS and 3 duplicates were identified. The 20 TS structures were maintained at the larger level of theory.

Regarding the 1,5 HAT, CREST found 190 structures. CREGEN reduced this number to 127 candidates. sPyRMSD further reduced this number to 42 TS candidate structures. Following the first optimisation, 29 unique structures are identified, the remaining 11 being duplicates. All 29 structures are maintained at the larger level of theory.

At the low level (double-zeta), the energy difference between the lowest TS for the 1,6 and 1,5 HAT is of 2.6 kcal mol⁻¹. This value is only marginally reduced at the larger level (2.5 kcal mol⁻¹) (Fig. 7). Such an energy difference would result in a 98 : 2 selectivity in a two-levels model, which is preserved in a more complete Maxwell–Boltzmann statistical model including all conformers. The computed selectivity is thus overestimated but in good qualitative agreement with experiments.

Fig. 7 On the left, lowest TS found for 1,5 HAT. On the right, lowest TS found for 1,6 HAT.

3.6 Enantioselective dialkylzinc additions on benzaldehyde

As final example, we present an enantioselective dialkylzinc addition on benzaldehyde using chiral ligands with flexible biaryl axes, as reported by Goldfuss et al.¹² This example demonstrates the use of a metal centre in FASTCAR.

In this paper, fencholes ligands are employed in conjunction with dimethyl or diethylzinc to facilitate enantioselective addition of benzaldehyde. These ligands exhibit rotational mobility along a pyridyl phenyl axis and, upon addition of an equivalent of alkylzinc, assume a preferred (P) conformation. The yields are high (over 94%) and the ee ranges from low to excellent (24–95%).

In this study, we propose to investigate the addition of diethylzinc to benzaldehyde using a pyridyl terpenol chiral ligand. To the best of our knowledge only the addition of dimethylzinc has been studied.

We employed a one-step approach at the BP86/SVP level, similar to the approach used in the aforementioned publication.

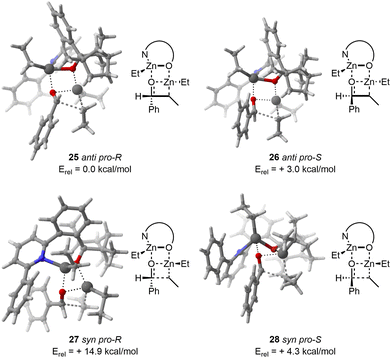
With regard to the TS 25, CREST identified 15 structures. Subsequently, CREGEN reduced this number to 14 candidate structures. sPyRMSD further reduced this number to 3 TS candidate structures. Following the DFT optimisation, 3 unique TS structures were identified.

In the case of the TS 26, the CREST analysis identified 18 distinct structures. The CREGEN step did not reduced this number. sPyRMSD further reduced this number to 4 TS candidate structures. After the DFT optimisation, 4 unique TS were localized.

Regarding the TS 27, CREST identified 20 structures. CREGEN did not refined these candidates. sPyRMSD further refined this number to 3 TS candidate structures. After the application of the DFT optimisation procedure, a total of 2 unique structures were identified, with the remaining 1 being duplicate.

With respect to the TS 28, CREST identified 160 structures. CREGEN reduced this number to 131 candidates. sPyRMSD further reduced this number to 17 TS candidate structures. Following the DFT optimisation, a total of 15 unique structures were identified, with the remaining 2 being duplicates.

The computational results are in good agreement with the experimental and computational values reported in the original publication. It is worth reiterating that the reactivity order for the dimethylzinc reactant with anti pro-R as a reference was found to be anti pro-R, anti pro-S, syn pro-S and syn pro-R (0.0, +3.3, +5.5, +13.0 kcal mol⁻¹). The order of reactivity for the diethylzinc reactant was found to be identical to that observed in the original publication, with a similar relative energy compared to the 25anti pro-R (0.0, +3.0, +4.3, +14.9 kcal mol⁻¹, Fig. 8). As in the original publication, the energy is overestimated, with the experimental ee being 95% for dimethylzinc and 92% for diethylzinc.

Fig. 8 On the top left, lowest TS found for 25anti pro-R. On the top right, lowest TS found for 26anti pro-S. On the bottom left, lowest TS found for 27syn pro-R. On the bottom right, lowest TS found for 28syn pro-S.

4 Conclusion

In conclusion, FASTCAR is designed to identify the most stable conformers within complex molecular systems using only an arbitrary geometry as a starting point. The workflow streamlines the process of conformer analysis by harnessing the capabilities of established tools, including SLURM, CREST, sPyRMSD, and Gaussian16, making it effortless, rapid, and precise.

The effectiveness of our approach is demonstrated by its successful application to various chemical systems. In the presented examples (along with other works currently under study in our group and recently published), the transition state located at the end of FASTCAR was more stable than the provided one. In one particular case, FASTCAR needed to be rerun to ensure the location of the global minimum transition state, because of an incomplete exploration of the potential energy surface at the DFTB-based metadynamics level. Nevertheless, the presented results demonstrate the ability of the proposed workflow to quickly locate transition states and determine accurate geometries, and forthcoming publications from our group will further illustrate the efficiency of FASTCAR in providing activation and reaction energies meeting experimental data, in various areas from sugar chemistry, organocatalysis and radical chemistry. We believe the solution as it stands is of value for the scientific community, helping in addressing more and more complex chemical reactions by computational methods. In the near future, we will nevertheless improve FASTCAR by the integration of several new features. These will noticeably include the integration of the iterative mode within the main frame, but also the interfacing to other quantum chemistry codes and possibility to run further additional calculations (varying the calculation level or running post-SCF analyses).

Author contributions

O. G. contributed to the initial development of the project, implementation, investigation, methodology, writing and editing. B. C. contributed to the early stages of project development, writing and editing. F. G. contributed to the conceptualisation, investigation, methodology, supervision, writing and editing.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We gratefully acknowledge the Agence Nationale de la Recherche (ANR) for funding (Catalfur project number ANR-21-CE43-0005). We additionally thank the University of Poitiers, the Centre National de la Recherche Scientifique (CNRS) for financial support. We would like to extend our thanking to the CREST development team for the continued help and support. Finally, we would also like to thank the referees for their constructive comments and suggestions, which helped to strenghthen our publication.

References

1. G.-J. Cheng, X. Zhang, L. W. Chung, L. Xu and Y.-D. Wu, J. Am. Chem. Soc., 2015, 137, 1706–1725.
2. T. Sperger, I. A. Sanhueza and F. Schoenebeck, Acc. Chem. Res., 2016, 49, 1311–1319.
3. Q. Peng, F. Duarte and R. S. Paton, Chem. Soc. Rev., 2016, 45, 6093–6107.
4. J. P. Reid and M. S. Sigman, Nat. Rev. Chem., 2018, 2, 290–305.
5. D. Yepes, F. Neese, B. List and G. Bistoni, J. Am. Chem. Soc., 2020, 142, 3613–3625.
6. M. Burns, S. Essafi, J. R. Bame, S. P. Bull, M. P. Webster, S. Balieu, J. W. Dale, C. P. Butts, J. N. Harvey and V. K. Aggarwal, Nature, 2014, 513, 183–188.
7. P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192.
8. R. Meli and P. C. Biggin, J. Cheminf., 2020, 12, 49.
9. Y. Reviriot, B. Michelet, R. Beaud, A. Martin-Mingot, F. Guégan, S. Thibaudeau, J. Rodriguez and D. Bonne, Chem. – Eur. J., 2022, 28, e202200432.
10. M. Wang, Z. Zhang, S. Liu, F. Xie and W. Zhang, Chem. Commun., 2014, 50, 1227–1230.
11. J. H. Herbort, T. N. Bednar, A. D. Chen, T. V. RajanBabu and D. A. Nagib, J. Am. Chem. Soc., 2022, 144, 13366–13373.
12. M. Leven, N. E. Schlörer, J. M. Neudörfl and B. Goldfuss, Chem. – Eur. J., 2010, 16, 13443–13449.
13. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian–Revision B.01, Gaussian Inc., Wallingford CT, 2016.
14. P. Probst, J. Groos, D. Wang, A. Beck, K. Gugeler, J. Kästner, W. Frey and M. R. Buchmeiser, J. Am. Chem. Soc., 2024, 146, 8435–8446.
15. S. Spicher and S. Grimme, Angew. Chem., Int. Ed., 2020, 59, 15665–15673.
16. A. B. Yoo, M. A. Jette and M. Grondona, in SLURM: Simple Linux Utility for Resource Management, Springer Berlin Heidelberg, 2003, p. 44–60.
17. J.-P. Ebejer, G. M. Morris and C. M. Deane, J. Chem. Inf. Model., 2012, 52, 1146–1158.
18. R. A. Cormanich and G. D. da Silva, J. Chem. Inf. Model., 2024, 64, 3322–3331.
19. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
20. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
21. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
22. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
23. P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222.
24. C. Y. Legault, CYLview20, Université de Sherbrooke, 2020, https://www.cylview.org, Accessed: 2024-06-27.
25. S. Behloul, O. Gayraud, G. Frapper, F. Guégan, K. Upitak, C. M. Thomas, Z. Yan, K. De Oliveira Vigier and F. Jérôme, ChemSusChem, 2024, e202400289.
26. Y. Li, J. Chen and Z. Yang, Chem. – Eur. J., 2024, 30, e202304371.
27. G. S. Hammond, J. Am. Chem. Soc., 1955, 77, 334–338.
28. S. T. Schneebeli, M. L. Hall, R. Breslow and R. Friesner, J. Am. Chem. Soc., 2009, 131, 3965–3973.

---

Footnote

† Electronic supplementary information (ESI) available: FASTCAR source code (Python3), structures of starting transition state geometries and output unique conformers deduced by FASTCAR in XYZ format. See DOI: https://doi.org/10.1039/d4cp01721h

---