Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Magnetic and relaxation properties of vanadium(IV) complexes: an integrated 1H relaxometric, EPR and computational study†
Valeria
Lagostina
a,
Fabio
Carniato
 b,
David
Esteban-Gómez
b,
David
Esteban-Gómez
 c,
Carlos
Platas-Iglesias
c,
Carlos
Platas-Iglesias
 *c,
Mario
Chiesa
*c,
Mario
Chiesa
 *a and
Mauro
Botta
*a and
Mauro
Botta
 *b
*b
aDepartment of Chemistry, University of Turin, Via Giuria 9, 10125 Torino, Italy. E-mail: mario.chiesa@unito.it
bDipartimento di Scienze e Innovazione Tecnologica, Università del Piemonte Orientale, Viale T. Michel 11, 15121 Alessandria, Italy. E-mail: mauro.botta@uniupo.it
cUniversidade da Coruña, Centro de Investigacións Científicas Avanzadas (CICA) and Departamento de Química, Facultade de Ciencias, 15071, A Coruña, Galicia, Spain. E-mail: carlos.platas.iglesias@udc.es
First published on 20th January 2023
Abstract
We report a detailed study of the magnetic and relaxation properties of a series of oxovanadium(IV) complexes comprising the aqua ion [VO(H2O)5]2+ and [VO(ox)2]2− (ox = oxalate), [VO(nta)]− (nta = nitrilotriacetate), [VO(dtpa)]3− (dtpa = diethylenetriaminepentaacetate) and [VO(acac)2] (acac = acetylacetonato) in solution. The complexes were characterized using continuous wave (X-band) and pulsed (Q-band) EPR measurements and 1H nuclear magnetic relaxation dispersion (NMRD) studies in the 0.01–120 MHz 1H Larmor frequency range. The 51V A-tensor parameters obtained from the analysis of EPR spectra are in good agreement with those obtained using theoretical calculations at the DFT and coupled-cluster levels (DLPNO-CCSD), while g-tensors were obtained with CASSCF/NEVPT2 calculations. EPR measurements reveal significant differences in the electronic Te1 and Tem relaxation times, with [VO(acac)2] showing a markedly different behaviour due to the trans coordination geometry. The NMRD profiles measured at different temperatures have contributions from both the outer- and inner-sphere mechanisms, with the latter showing contributions from the dipolar and scalar mechanisms. The rotational correlation times (τR) obtained from the fitting of NMRD and EPR data are in good mutual agreement. The scalar mechanism depends on the hyperfine coupling constants of the coordinated water molecule Haiso, which were obtained from the fitting of the NMRD profiles and DFT calculations. Finally, the analysis of the data provided information on the exchange rate of coordinated water molecules, which display mean residence times of ∼7–17 μs at 298 K.
Introduction
Magnetic molecules are next-generation components in many different technological areas, ranging from magnetic resonance imaging (MRI)1–3 to quantum information technologies.4,5 All of these applications require the modulation of the spin–lattice (longitudinal) relaxation time (Te1) and the phase-memory relaxation time (Tem). Te1 defines the lifetime of an excited spin state and is the upper limit of Tem. Tem is the lifetime of the electron spin superposition or coherence time, and encompasses Te2 and all other processes that cause electron spin dephasing. Applications in quantum information technology require designing systems where both these parameters are long, which is challenging due to the ubiquitous spin bath (nearby electronic spins or nuclear spins) that produces stochastic interactions that shorten both relaxation times.6 On the other hand, contrast agents for application in MRI should be efficient at shortening the nuclear relaxation times of water proton nuclei in their vicinity.7 Vanadium(IV) complexes are being actively studied as potential candidates for molecular spin qubits,8–14 and have also been proposed as potential MRI contrast agents.15 In the latter case, the paramagnetic V(IV) complex creates a local fluctuating magnetic field that increases the relaxation efficiency of nearby solvent protons. Vanadium(IV) has an electron spin S = 1/2 and a nuclear spin I = 7/2 for the stable isotope 51V, which presents a natural abundance of nearly 100%. Oxovanadium(IV) complexes, in particular, have longer electron spin decoherence times than many other first-row transition metal ions, a key property for applications in quantum information processing. The relaxivity induced by VO2+ compounds is lower than that by low molecular weight gadolinium complexes, but it still provides significant relaxation enhancement, particularly at low magnetic field strengths.15,16 Mustafi et al.17 reported the use of bis(acetylacetonato)oxovanadium(IV) ([VO(acac)2]) as a potential contrast agent and studied the interaction of the complex with serum albumin and performed in vivo experiments for imaging tumours in rats. Furthermore, vanadium(IV) complexes are used in other medical applications, such as the treatment of diabetes, anti-tumour therapy and the treatment of viral, bacterial or parasitic infections.18The study of the NMR spectra of paramagnetic species is limited by the shortening of the nuclear transverse relaxation time (Tn2) caused by the presence of unpaired electrons, which may induce extensive line-broadening. If Tn2 is long enough, it is possible to observe the NMR spectra characterized by paramagnetically shifted signals. However, short Tn2 values make signals too broad to be detected. The Fast-Field-Cycling NMR (FFC-NMR) technique was designed to overcome this limitation, as it permits one to study the structural and dynamic properties of paramagnetic complexes dissolved in a solvent (usually in H2O), by investigating the solvent magnetic properties.19 This technique is largely used for the development of new contrast agents for MRI applications.20
The effect of the paramagnetic complex on water proton relaxation is influenced by many parameters. The observed relaxation effect is the result of two main contributions: the outer-sphere contribution,21,22 arising from water molecules diffusing in the proximity of the paramagnetic centre, and the inner-sphere contribution, arising from water molecules coordinated to the paramagnetic centre that get exchanged with bulk water molecules. The theoretical description of the relaxation theory is given by the Solomon–Bloembergen–Morgan equations,7 and includes a rather large number of structural and dynamic parameters. Thus, it is very important to combine different techniques offering complementary information on the most important ones.23
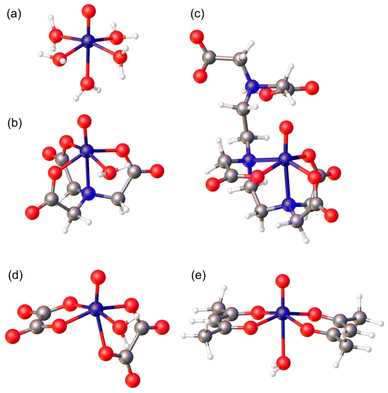
In this paper, we report a combined EPR and 1H relaxometry study on a series of oxovanadium(IV) complexes that establishes a clear relationship between their relaxation properties and their structural and dynamic parameters (electron spin relaxation times, rotational dynamics, hydration state, water exchange rate, etc.). For this purpose we re-investigated the [VO(H2O)5]2+ complex, which was characterized earlier using either FFC-NMR16 or EPR24 measurements, but not combining the two techniques. Additionally, we selected a series of complexes that contain a water molecule coordinated to the metal ion either axially ([VO(acac)2]) or equatorially ([VO(nta)]−, H3nta = nitrilotriacetic acid; [VO(ox)]2−, H2ox = oxalic acid). Furthermore, we also investigated the [VO(dtpa)]3− complex (H5dtpa = diethylenetriaminepentaacetic acid), which lacks any coordinated water molecule. Fig. 1 shows the models of the structures of the complexes investigated in this work obtained with DFT calculations. The analysis of the 1H nuclear magnetic relaxation dispersion (NMRD)25 profiles is supported by complementary information extracted by EPR (rotational correlation times (τR),26 longitudinal (Te1)27 and transverse (Tem)28 relaxations). Additionally, theoretical calculations based on DFT and wave function approaches were used as an additional source of information. This integrated approach offers, for the first time, a clear description of the relaxometric behaviour of oxovanadium(IV) complexes in solution.
Results and discussion
Continuous wave (CW) EPR experiments
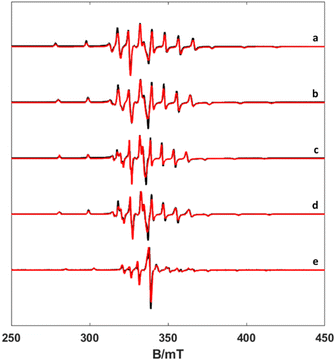
The EPR spectra of the vanadium complexes recorded in water frozen solution (77 K) show the expected eight-fold hyperfine splitting typical of VIV (51V I = 7/2, natural abundance 99.76%).29 The spectra could be simulated using the spin Hamiltonian shown in eqn (1), which considers the electronic Zeeman interaction and the hyperfine coupling of electronic and nuclear moments.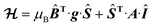 | (1) |
Here, g is the electronic anisotropic Landé tensor and A is the hyperfine coupling tensor. Computer simulation afforded the parameters reported in Table 1, while the experimental and simulated spectra are presented in Fig. 2. The [VO(H2O)5]2+ complex is characterised by axially symmetric g- and A-tensors that match well those reported previously.24,30 All other complexes show slightly rhombic tensors.
| g x | g y | g z | A x | A y | A z | τ 298R | E r | ||
|---|---|---|---|---|---|---|---|---|---|
| a Data obtained for the cis isomer. DLPNO-CCSD calculations afford Ax, Ay and Az values of −156, −148 and −509 for [VO(ox)2(H2O)]2−. b Data obtained for the trans isomer. c Value estimated from the spectrum recorded at room temperature. | |||||||||
| [VO(H2O)5]2+ | Exp. | 1.9786 | 1.9786 | 1.9344 | −206.5 | −206.5 | −546 | 47.8 ± 1.4 | 14.8 ± 0.8 |
| Calc. | 1.9830 | 1.9820 | 1.9099 | −201 | −198 | −552 | |||
| [VO(nta)]− | Exp. | 1.9820 | 1.9770 | 1.9375 | −203 | −187 | −527 | 35.5 ± 1.3 | 14.9 ± 1.0 |
| [VO(nta)(H2O)]− | Calc. | 1.9805 | 1.9751 | 1.9164 | −164 | −164 | −509 | ||
| [VO(nta)(H2O)]−·2H2O | Calc. | 1.9803 | 1.9761 | 1.9194 | −163 | −162 | −507 | ||
| [VO(dtpa)]3− | Exp. | 1.9822 | 1.9770 | 1.9444 | −184 | −176 | −507 | 86.0 ± 2.2 | 13.0 ± 0.7 |
| [VO(Hdtpa)]2− | Calc. | 1.9798 | 1.9789 | 1.9253 | −151 | −146 | −492 | ||
| [VO(ox)2]2− | Exp. | 1.9801 | 1.9760 | 1.9392 | −192 | −181 | −520 | 38.2 ± 0.9 | 16.4 ± 0.6 |
| [VO(ox)2(H2O)]2− | Calc.a | 1.9819 | 1.9777 | 1.9172 | −165 | −155 | −507 | ||
| [VO(ox)2(H2O)]2−·2H2O | Calc.a | 1.9795 | 1.9762 | 1.9173 | −155 | −149 | −500 | ||
| [VO(acac)2] | Exp. | 1.9805 | 1.9735 | 1.9444 | −161 | −176 | −498 | 77.0c | |
| [VO(acac)2(H2O)] | Calc.b | 1.9855 | 1.9743 | 1.9368 | −131 | −157 | −491 | ||
| [VO(acac)2(H2O)]·2H2O | Calc.b | 1.9817 | 1.9758 | 1.9305 | −146 | −161 | −496 | ||
As noted previously for VO2+ complexes,31 the values of gz and Az are correlated, with [VO(H2O)5]2+ displaying the most negative Az value and the lowest gz. Detailed structural studies concluded that [VO(acac)2] is present in solution as a mixture of cis and trans isomers, with the major species in solution being the trans form (∼85%), which contains a water molecule coordinated in the trans position with respect to the oxo group.32 The value of the 51V isotropic hyperfine coupling aiso determined here for [VO(acac)2] (−278 MHz) is in excellent agreement with that reported previously for the trans isomer (−276 MHz), while the cis isomer (minor) is characterized by a larger aiso value of −291 MHz.32 The X-ray crystal structures of the [VO(ox)2]2− and [VO(nta)]− complexes show that a water molecule is coordinated to the metal ion in the cis position with respect to the oxo group.33–35 The X-ray structure of the [VO(H3DTPA)] complex evidences coordination of the ligand through two amine N atoms and three oxygen atoms of carboxylate groups, and thus this complex lacks any coordinated water molecule.36
Variable temperature EPR experiments
EPR spectra were recorded in aqueous solutions in the temperature range 294–353 K. Under these circumstances, the anisotropic g- and A-tensors are averaged out depending on the rate of motion of the complex, which in turn depends on the temperature. The result is an 8-line spectrum centred at the average g factor and line separation reflecting the 51V isotropic hyperfine component aiso. Inspection of Fig. 3 shows a clear mI linewidth dependency, which is directly correlated with the rotational correlation time (τR). Using the rigid limit spin-Hamiltonian parameters reported in Table 1, τR was determined through the simulation of the spectra using the Easyspin26 routine garlic (Fig. 3, see also Fig. S1–S3, ESI†). In this way, the spectra are simulated leaving τR as a unique free parameter.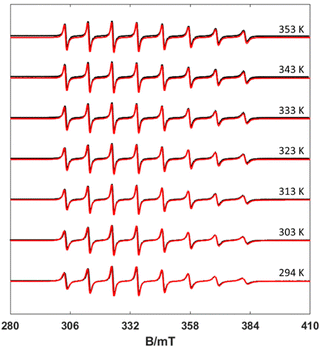 | ||
| Fig. 3 Experimental (black) and simulated (red) X-band CW EPR spectra of the [VO(nta)]− complex recorded at different temperatures (10 mW power and 0.5 mT modulation amplitude). | ||
The τR values measured at different temperatures are summarized in Table S1 (ESI).† The values of τR decrease upon increasing the temperature, as would be expected, following a simple exponential dependence according to the below equation (Fig. S4 and S5, ESI†):
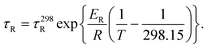 | (2) |
In eqn (2), τ298R is the rotational correlation time at 298.15 K and ER represents the corresponding activation energy for rotation. The longest τ298R value was determined for the complex with H5dtpa, as expected according to its molecular weight. The τ298R value determined for this complex is slightly lower than that determined by Chen using EPR measurements (∼105 ps).15 The [VO(ox)2]2− and [VO(nta)]− complexes present comparable molecular weights and very similar rotational correlation times. However, the [VO(acac)2] complex displays a longer τ298R value than the latter two, in spite of their similar molecular weight. The [VO(H2O)5]2+ complex presents a τ298R value somewhat longer than those of [VO(ox)2]2− and [VO(nta)]−, which can be attributed to the formation of a well-defined second-sphere hydrogen-bonding network. The activation energies for rotation (∼15 kJ mol−1) are similar to those obtained from relaxometric data for the aqua-complexes of Gd(III),37 Mn(II)38 and Fe(III)39 complexes.
Electron spin dynamics: Te1 and Tem measurements
To investigate the temperature dependence of the electronic relaxation times of the VO2+ complexes, Q-band ESE EPR spectra were recorded using a standard Hahn echo sequence. Representative spectra recorded at 10 K are shown in Fig. 4, along with the corresponding computer simulations. The spin Hamiltonian parameters obtained from the analysis of the CW-X-band EPR spectra provide a good simulation of the Q-band ESE spectra, adding confidence on the values reported in Table 1. The electron spin relaxation times were measured at a fixed magnetic field, corresponding to the maximum echo intensity. To investigate the spin relaxation times in detail and to quantify the electronic phase memory time and the spin–lattice relaxation time in frozen solutions as a function of temperature, echo decay and inversion recovery experiments were performed in the temperature range 20–200 K. The corresponding values are shown in Fig. 5. For [VO(acac)2] the echo relaxation is too fast to allow accurate measurements above 120 K. The Te1 values were obtained using inversion-recovery experiments and by subsequent fitting of the signal intensity (I) to a bi-exponential equation: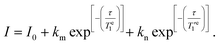 | (3) |
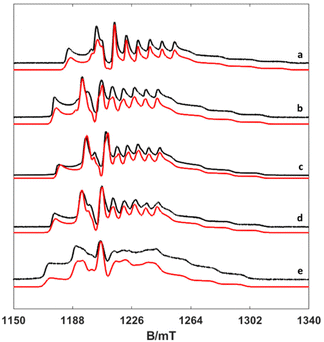 | ||
| Fig. 4 Experimental (black) and simulated (red) Q-band ESE spectra (a) [VO(H2O)5]2+, (b) [VO(nta)(H2O)]−, (c) [VO(Hdtpa)]2−, (d) [VO(ox)2(H2O)]2−, and (e) [VO(acac)2(H2O)]. | ||
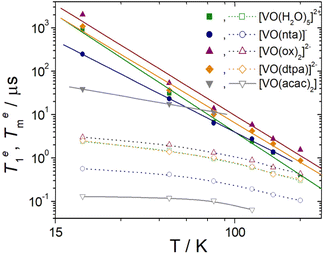
The values of the pre-exponential factors km and kn indicate that the long Te1 component dominates the inversion-recovery traces (Table S2, ESI†). The Te1 values decrease steadily on increasing the temperature, with Te1 being in the range ∼40–2100 μs at 20 K and decreasing to ca. 6–15 μs at 80 K. The plots of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Te1versus log
Te1versus log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T are linear, which indicates that relaxation is dominated by the Raman mechanism according to eqn (4), where b and n are the Raman coefficient and Raman exponent, respectively. Thus, direct relaxation appears to be negligible in the temperature range explored here.
T are linear, which indicates that relaxation is dominated by the Raman mechanism according to eqn (4), where b and n are the Raman coefficient and Raman exponent, respectively. Thus, direct relaxation appears to be negligible in the temperature range explored here.
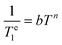 | (4) |
The fit of the data (Table 2) afforded similar n values of 3.0–3.3 for [VO(H2O)5]2+, [VO(ox)2]2− and [VO(DTPA)]3−, as can be anticipated by the similar slopes of the plots shown in Fig. 5. These n values are close to those determined for different oxovanadium(IV) complexes using magnetic susceptibility and EPR measurements.9,10,40,41 The [VO(nta)]− complex is characterised by a slightly lower n value, while [VO(acac)2] displays a very low n value of 0.88. As a result, Te1 decreases much smoothly with temperature for [VO(acac)2] compared to all other complexes studied here. As a result, [VO(acac)2] shows the shortest Te1 value (38.7 μs) among the five complexes at 20 K, but all five complexes show similar Te1 values at 80 K (6–14 μs). The different temperature dependence of Te1 observed for [VO(acac)2] is likely related to its trans coordination geometry, where the donor atoms of the acac ligands occupy equatorial positions.
| b/μs−1 K−n | n | |
|---|---|---|
| a Data obtained from frozen aqueous solutions (complex concentration ∼3 mM). | ||
| [VO(H2O)5]2+ | 6.8(5)×10−8 | 3.3(1) |
| [VO(nta)]− | 1.95(8)×10−6 | 2.57(5) |
| [VO(dtpa)]3− | 6.8(6)×10−8 | 3.1(2) |
| [VO(ox)2]2− | 1.4(2)×10−7 | 3.0(1) |
| [VO(acac)2] | 1.86(4)×10−3 | 0.88(2) |
For Tem measurements the decay traces were fitted using the stretched-exponential expression:
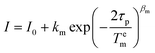 | (5) |
1H nuclear relaxation dispersion (NMRD) profiles
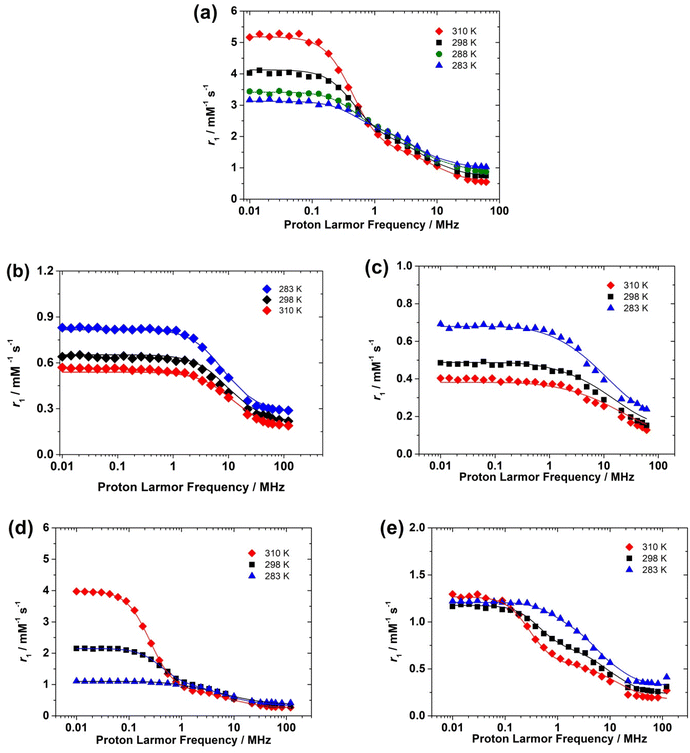
The NMRD profiles of the oxovanadium(IV) complexes were measured at various temperatures (283, 298 and 310 K) from 0.01 to 120 MHz (expressed as a function of 1H Larmor frequency). For each NMRD profile, 25 relaxation times were measured, in order to have a good definition of the curves (Fig. 6).The NMRD profiles obtained for the [VO(H2O)5]2+ complex present a similar shape to that reported by Bertini et al.16 Relaxivity (r1) is nearly constant at low fields in the range from 0.01 to 0.1–0.2 MHz. A dispersion in which r1 decreases is observed above ∼0.2 MHz until 20 MHz, followed by a region with constant r1 at frequencies above 20 MHz. The NMRD profiles recorded for the [VO(acac)2] and [VO(ox)2]2− complexes show similar shapes. The shape of the NMRD profile is however different for the [VO(nta)]− complex, which shows a broad region of constant relaxivity below 2 MHz and a dispersion in the 2–30 MHz region. This shape is characteristic of complexes where the inner-sphere contribution to relaxivity is dominated by the dipolar mechanism, such as Gd3+ and most Mn2+ complexes.20 The relaxivity increase observed below ∼1 MHz denotes the presence of a significant scalar contribution, as observed for [Mn(H2O)6]2+ and a few other Mn2+ complexes.38,42,43
The scalar contribution that dominates r1 at low fields depends on the isotropic (Fermi contact) proton hyperfine coupling constant Haiso and the correlation time 1/τsi, which is the sum of the water exchange rate constant (kex = 1/τM) and the electronic longitudinal (1/Te1) or transverse (1/Te2) relaxation rates. The electronic relaxation times are generally nearly invariant in the temperature range used for NMRD measurements. The increase of relaxivity at low frequencies observed for [VO(H2O)5]2+ and [VO(ox)2]2− as a function of temperature indicates that r1 is limited by a slow water exchange rate, as τM is longer than T1 for the coordinated water molecule. Increasing temperature decreases τM for the proton nuclei of the coordinated water, and thus r1 increases.
At high frequencies, the inner-sphere contribution to r1 is provided by the dipolar mechanism, for which the relevant correlation time involves τM, Tei (Te1, Te2) and τR. The shortest among these three correlation times is τR, which is in the ps time scale, while τM and Tei appear to be in the μs and ns time scales, respectively. Thus, the fast rotation of the complex in solution limits r1 at high fields, and therefore the trend with temperature is reversed, as τR becomes shorter with increasing temperature.
The [VO(nta)]− complex presents higher r1 values than the complex with H5DTPA over the whole range of proton Larmor frequencies. This suggests that the [VO(nta)]− complex contains a coordinated water molecule, as observed in the solid state.35 The complex with H5DTPA likely lacks any coordinated water molecule, with the observed relaxivity being a consequence of the outer-sphere mechanism. The decrease in relaxivity with temperature is therefore likely related to a faster diffusion.
Theoretical calculations
DFT calculations were carried out to gain insight into the structures of the complexes in solution and their correlation with EPR parameters. The geometries of the complexes were optimized at the TPSSh/Def2-TZVPP level incorporating bulk solvent effects with a polarized continuum model (see Computational details below). The optimized molecular geometries are presented in Fig. 1, while relevant structural features are provided in Table 3 (see also Tables S4–S11, ESI†).V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
V–O | V–OH2O | V–N | V⋯HH2O | H a iso | Ref. | ||
|---|---|---|---|---|---|---|---|---|
| a Data obtained for the cis isomer. b Data obtained for the trans isomer. c Data for equatorial water molecules. The range of experimental hyperfine couplings refers to the four inequivalent equatorial water protons obtained by DFT (this work) or determined in the ENDOR single crystal study of ref. 49. d Data for axial water molecules. The two protons of the axial water molecule are not magnetically equivalent. | ||||||||
| [VO(H2O)5]2+ | DFT | 1.565 | 2.052–2.056;c 2.212d | 2.671c/2.888d | 0.73–7.86c/0.09d | |||
| Exp. | 1.569 | 2.023–2.030;c 2.183d | −0.39–8.67c | 46 and 49 | ||||
| 1.577 | 2.026–2.027;c 2.175d | −0.04; 0.01d | 44 | |||||
| [VO(nta)(H2O)]− | DFT | 1.606 | 1.974–1.979 | 2.128 | 2.372 | 2.682 | 3.89 | |
| [VO(nta)(H2O)]−·2H2O | DFT | 1.605 | 1.988–1.999 | 2.085 | 2.368 | 2.587 | 4.90 | |
| Exp. | 1.596 | 1.997–2.022 | 2.005 | 2.322 | 35 | |||
| [VO(Hdtpa)]2− | DFT | 1.6112 | 1.987–1.994 | — | 2.209/2.356 | — | — | |
| Exp. | 1.603 | 1.981–2.032 | 2.179/2.304 | 36 | ||||
| [VO(ox)2(H2O)]2− | DFTa | 1.613 | 1.973–2.151 | 2.186 | 2.667 | 4.30; 1.34 | ||
| [VO(ox)2(H2O)]2−·2H2O | DFTa | 1.629 | 1.974–2.130 | 2.141 | 2.732 | 1.6; 1.72 | ||
| Exp.a | 1.594 | 2.006–2.184 | 2.033 | 33 | ||||
| [VO(acac)2(H2O)] | DFTb | 1.597 | 1.991–1.999 | 2.479 | — | 2.950 | 0.04 | |
| [VO(acac)2(H2O)]·2H2O | DFTb | 1.598 | 1.991–2.026 | 2.336 | — | 2.868 | 0.07 | |
| Exp.b | 1.599 | 1.982–1.998 | 2.196 | — | 50 | |||
The [VO(H2O)5]2+ system is characterized by short V–Ocis distances and a long V–Otrans distance associated with the trans influence of the V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond. The calculated distances are in excellent agreement with the experimental values obtained with X-ray diffraction measurements.44–46 The calculated V
O bond. The calculated distances are in excellent agreement with the experimental values obtained with X-ray diffraction measurements.44–46 The calculated V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O distance (1.565 Å) is also in nice agreement with the X ray data (1.57–1.58 Å). DFT calculations were also performed in the [VO(oxa)2(H2O)]2− system, for which X-ray structures were reported with the coordinated water molecule at both cis33,47 and trans48 positions with respect to the V
O distance (1.565 Å) is also in nice agreement with the X ray data (1.57–1.58 Å). DFT calculations were also performed in the [VO(oxa)2(H2O)]2− system, for which X-ray structures were reported with the coordinated water molecule at both cis33,47 and trans48 positions with respect to the V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond. The calculations on the trans isomer systematically led to square pyramidal optimized geometries, even upon the inclusion of two explicit second-sphere water molecules. The 1H NMRD data clearly show the presence of a water molecule coordinated to the VO2+ cation, and thus subsequent calculations were performed on the cis isomer (Table 3). The DFT calculations provide a V–Owater distance that is considerably longer than that observed in the solid state. The inclusion of two explicit second-sphere water molecules shortens the V–Owater distance by ∼0.04 Å, but the calculated value remains 0.11 Å longer than the X ray value.
O bond. The calculations on the trans isomer systematically led to square pyramidal optimized geometries, even upon the inclusion of two explicit second-sphere water molecules. The 1H NMRD data clearly show the presence of a water molecule coordinated to the VO2+ cation, and thus subsequent calculations were performed on the cis isomer (Table 3). The DFT calculations provide a V–Owater distance that is considerably longer than that observed in the solid state. The inclusion of two explicit second-sphere water molecules shortens the V–Owater distance by ∼0.04 Å, but the calculated value remains 0.11 Å longer than the X ray value.
Calculations performed in the [VO(nta)(H2O)]− system provide a minimum energy conformation with the coordinated water molecule in the cis position and the N atom of nitrilotriacetate occupying the trans position, which leads to a long V–N distance (2.372 Å) associated with the trans influence of the V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond. This is in good agreement with the X-ray structures reported in the literature.34,35 Again, the inclusion of explicit second-sphere water molecules causes a shortening of the V–Owater distance, as observed previously for Mn(II) and Gd(III) complexes.51,52
O bond. This is in good agreement with the X-ray structures reported in the literature.34,35 Again, the inclusion of explicit second-sphere water molecules causes a shortening of the V–Owater distance, as observed previously for Mn(II) and Gd(III) complexes.51,52
DFT calculations yield two minimum energy geometries for the [VO(acac)(H2O)] system characterized by cis and trans coordination of the water molecule. The relative Gibbs free energies calculated with DFT favour the trans isomer by 4.1 kcal mol−1. The relative energy is reversed and reduced to 0.3 kcal mol−1 upon inclusion of two second-sphere water molecules, and thus both forms likely have a significant population in solution. This is in line with EPR measurements, which evidenced the presence of the cis and trans isomers in solution.32,53 As expected, the trans isomer displays a long V–Owater distance of 2.48 Å. This distance was found to be up to ∼0.27 Å shorter in the solid state.50 Inclusion of explicit second-sphere water molecules brings this distance closer to the experimental value (Table 2). The overestimation of the V–Owater distance by DFT is likely related to a rather flat potential energy surface associated with the weak interaction, which arises from the strong trans influence of the V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond.
O bond.
An X-ray structure was reported for the [VO(H3DTPA)] complex, in which two acetate groups and one of the amine N atoms are protonated.36 However, the first protonation constant of the [VO(DTPA)]3− complex was reported to be log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 7.0, and thus the main species in solution at the pH used for 1H NMRD measurements corresponds to the mono-protonated form of the complex.54 Thus, DFT calculations were performed in the [VO(HDTPA)]2− system. The calculated structure resembles the crystal structure of the [VO(H3DTPA)] complex.
K = 7.0, and thus the main species in solution at the pH used for 1H NMRD measurements corresponds to the mono-protonated form of the complex.54 Thus, DFT calculations were performed in the [VO(HDTPA)]2− system. The calculated structure resembles the crystal structure of the [VO(H3DTPA)] complex.
The EPR measurements described above evidenced significant variations of the 51V hyperfine coupling constants for the complexes investigated in this work (Table 1). The values of Ax, Ay and Az were estimated with DFT calculations using the TPSS0 functional55 (25% HF exchange), a variant of the TPSSh functional56 (10% exchange) with increased HF exchange. The TPSS0 functional was found to perform well in the prediction of A-tensors of V(IV) complexes.57 The results obtained at the TPSS0/Def2-QZVPP level (Table 1) show that DFT predicts the experimental hyperfine coupling constants with a rather good accuracy. Test calculations performed with the coupled cluster theory, using the recently described domain based local pair natural orbital method (DLPNO-CCSD), afforded Ax, Ay and Az values for [VO(ox)2(H2O)]2−, in excellent agreement with both the experiment and DFT (Table 1). The DLPNO-CCSD method was found to provide very accurate spin densities for both organic radicals58 and transition metal complexes.59 Furthermore, our DFT calculations reported here for [VO(H2O)5]2+ and [VO(acac)(H2O)] afford very similar results to those reported recently using DLPNO-CCSD calculations.59
The [VO(H2O)5]2+ system is characterized by more negative Ax, Ay and Az values. Furthermore, the calculated absolute Az values follow the trend [VO(H2O)5]2+ > [VO(nta)(H2O)]− > [VO(ox)2(H2O)]2− > [VO(Hdtpa)]2− > [VO(acac)(H2O)], in agreement with the experimental trend. The inclusion of explicit second-sphere water molecules has a minor impact on the A-tensor values. Thus, it is possible to conclude that DFT describes rather accurately the spin density distributions in these complexes.
In contrast to A-tensors,60 the prediction of g-tensors of transition metal complexes with DFT is particularly challenging, with the results depending dramatically on the functional used and the amount of HF exchange.61,62 Good agreement between the experimental g-tensor values and those obtained with DFT was observed for some V(IV) complexes.63,64 For the complexes studied here, test calculations performed with different functionals showed that the prediction of g-tensors with DFT is particularly problematic. Thus, we turned our attention to calculations based on the complete active space self-consistent field (CASSCF) method [CAS(5,1)], with a dynamic correlation being introduced with the N-Electron Valence State Perturbation Theory (NEVPT2). The g-tensors calculated at the CASSCF/NEVPT2 level present gx and gy values close to the experimental data. The calculated gz values are somewhat lower than the experimental ones, but follow rather well the experimental trend. Indeed, [VO(acac)(H2O)] and [VO(Hdtpa)]2− display the highest gz values among the five complexes, and then decrease following the order [VO(nta)(H2O)]− > [VO(ox)2(H2O)]2− > [VO(H2O)5]2+. As observed for the A-tensors, the incorporation of explicit second-sphere water molecules has a minor impact on the calculated values. Overall, the theoretical calculations presented here capture the main features observed for EPR parameters, which indicates that the molecular geometries describe reasonably well the structures of this family of complexes in solution.
Fitting of the 1H NMRD profiles
The analysis of the NMRD profiles was initiated by attempting to fit the data recorded for the [VO(HDTPA)]2− complex, as for this system r1 is expected to be the result of the outer-sphere contribution only. A previous relaxometric study presented fitting of the data using unrealistically low distances of the closest approach of outer-sphere water molecules (aV–H ∼ 2.0 Å).15 This prompted the authors of ref. 15 to introduce a second-sphere contribution to obtain more reasonable fitting parameters. We attempted to fit the data using the diffusion translational model proposed by Freed,21 employing a distance of the closest approach of 2.45 Å. This distance corresponds to the average V⋯H distance observed in the DFT structure of [VO(ox)2(H2O)]2−·2H2O, in which a non-coordinated water molecule is involved in hydrogen bonding interaction with the V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group. A reasonably good fit was obtained using aV–H = 2.45 Å (Fig. 6c), affording values of the relative diffusion coefficient D298V–H and its activation energy ED very similar to those obtained for other small paramagnetic complexes (Table 4).37,65,66 Furthermore, the values obtained from the fits are close to those reported for the self-diffusion of water in water (D298 = 23.0 m2 s−1 and ED = 17.6 kJ mol−1).67 The fast diffusion of the small water molecule is expected to dominate the relative diffusion coefficient D298V–H, and thus these results provide confidence in the analysis. The aV–H value of 2.45 Å was subsequently used to fit the NMRD data of [VO(ox)2(H2O)]2− and [VO(H2O)5]2+, while for the [VO(nta)(H2O)]− and [VO(acac)(H2O)] complexes we had to use a somewhat longer value (2.7 Å) to obtain satisfactory fits. This may be related to the lower net electrical charges of the latter two complexes compared to the former. The aV–H value assumed for [VO(nta)(H2O)]− and [VO(acac)(H2O)] is close to the distance between the H atom of a methanol molecule involved in hydrogen bonding with the oxo group in [VO(acac)(H2O)] (2.79 Å).68 The values of D298V–H and ED obtained for the [VO(HDTPA)]2− complex were subsequently fixed for the analysis of all other complexes investigated here.
O group. A reasonably good fit was obtained using aV–H = 2.45 Å (Fig. 6c), affording values of the relative diffusion coefficient D298V–H and its activation energy ED very similar to those obtained for other small paramagnetic complexes (Table 4).37,65,66 Furthermore, the values obtained from the fits are close to those reported for the self-diffusion of water in water (D298 = 23.0 m2 s−1 and ED = 17.6 kJ mol−1).67 The fast diffusion of the small water molecule is expected to dominate the relative diffusion coefficient D298V–H, and thus these results provide confidence in the analysis. The aV–H value of 2.45 Å was subsequently used to fit the NMRD data of [VO(ox)2(H2O)]2− and [VO(H2O)5]2+, while for the [VO(nta)(H2O)]− and [VO(acac)(H2O)] complexes we had to use a somewhat longer value (2.7 Å) to obtain satisfactory fits. This may be related to the lower net electrical charges of the latter two complexes compared to the former. The aV–H value assumed for [VO(nta)(H2O)]− and [VO(acac)(H2O)] is close to the distance between the H atom of a methanol molecule involved in hydrogen bonding with the oxo group in [VO(acac)(H2O)] (2.79 Å).68 The values of D298V–H and ED obtained for the [VO(HDTPA)]2− complex were subsequently fixed for the analysis of all other complexes investigated here.
| [VO(H2O)5]2+ | [VO(dtpa)]3− | [VO(ox)2]2− | [VO(nta)]− | [VO(acac)2] | |
|---|---|---|---|---|---|
| a Parameters fixed during the fitting procedure. b Parameters fixed to the estimates obtained with DFT. c Values fixed to those obtained with EPR measurements. | |||||
| τ 298m/μs | 16.7 ± 0.8 | — | 16.7 ± 0.2 | 14.5 ± 3.4 | 6.3 ± 0.8 |
| ΔH‡/kJ mol−1 | 19.3 ± 1.1 | — | 72.6 ± 1.1 | 13.2 ± 5.0 | 8.1 ± 4.0 |
| τ 298R/ps | 46.1 ± 1.0 | — | 52.4 ± 1.1 | 35.5c | 30.9 ± 2.3 |
| E r/kJ mol−1 | 25.0 ± 1.2 | — | 22.3 ± 1.7 | 14.9c | 26.4 ± 2.7 |
| T e2981/ns | 1.08 ± 0.11 | 0.88 ± 0.06 | 0.88 ± 0.03 | 0.31 ± 0.08 | 0.62 ± 0.05 |
| E s/kJ mol−1 | 1.0a | 1.0a | 22.3 ± 2.0 | 12.0 ± 5.0 | 27.9 ± 7.6 |
| D 298V–H/10−10 m2 s−1 | 20.2a | 20.2 ± 0.1 | 20.2a | 20.2a | 20.2a |
| E D/kJ mol−1 | 17.0a | 17.0 ± 1.3 | 17.0a | 17.0a | 17.0a |
| H a iso/MHz | 3.77 ± 0.3 | — | 3.66 ± 0.03 | — | 1.75 ± 0.25 |
| r V–H/Å | 2.671b | — | 2.667b | 2.682b | 2.678b |
| a V–H/Å | 2.45a | 2.45a | 2.45a | 2.70a | 2.70a |
| q | 4 | 0 | 1 | 1 | 1 |
We next analysed the data obtained for the [VO(nta)(H2O)]− complex, which lacks dispersion at a low field indicative of a scalar relaxation mechanism. Here the relaxivity in the high-field region is limited by τR, and thus we were unable to fit the data using both τR and kex = 1/τM as the fitting parameters. Therefore, we fixed the values of τ298R and the activation parameter Er to the values obtained with EPR measurements (see above). This allowed us to obtain an estimate of τM, although with a relatively large statistical error (14.5 ± 3.4 μs). The NMRD profiles of [VO(H2O)5]2+, [VO(ox)2(H2O)]2− and [VO(acac)(H2O)] could be satisfactorily fitted considering both dipolar and scalar contributions to inner-sphere relaxivity. The number of coordinated water molecules q was fixed to 4 in the case of [VO(H2O)5]2+, since the axial water molecule is very labile, with a mean residence time estimated to be ∼1 ns.69 Thus, the axial water molecule is not expected to contribute significantly to the observed relaxivity. Finally, the distances involving the paramagnetic ion and the proton nuclei of inner-sphere water molecules were estimated from DFT calculations and fixed during the fitting procedures.
Spin density distributions
The electron spin density at a certain nucleus N, ρα−βN is directly measured by the isotropic hyperfine structure constant,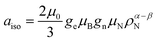 where μ0 is the vacuum permeability, ge is the electron g-factor, μB is the Bohr's magneton, gn is the nuclear g factor and μN is the nuclear magneton. The spin density at the proton, Haiso, is one of the key parameters affecting relaxivity. It is directly measured using advanced EPR techniques, such as ENDOR (electron nuclear double resonance) and ESEEM (electron spin-echo envelope modulation), and can be estimated through the fitting of the NMRD data (Table 4). Moreover, the use of computational methods can greatly enhance their interpretation. For [VO(H2O)5]2+ single crystals, ENDOR data are available, reporting small Haiso values of 0.01 and −0.04 MHz for axially coordinated water and larger values in the range from −0.39 to 8.67 MHz for equatorially coordinated water molecules. These data, corroborated by DFT calculations,31 show that the isotropic hyperfine coupling constants of the water molecule protons are very sensitive not only to the V–OH2O distance but also crucially depend on the orientation of the molecule, with respect to the vanadyl bond. The Haiso values obtained in this work for the equatorial water molecules [VO(H2O)5]2+ fall within the range 0.73–7.86 MHz (Table 3), in nice agreement with the experiment. The Haiso value for [VO(H2O)5]2+ estimated from the fitting of the NMRD data (Table 4) is of the order of 3.7 MHz and reflects an averaged value over different water orientations.
where μ0 is the vacuum permeability, ge is the electron g-factor, μB is the Bohr's magneton, gn is the nuclear g factor and μN is the nuclear magneton. The spin density at the proton, Haiso, is one of the key parameters affecting relaxivity. It is directly measured using advanced EPR techniques, such as ENDOR (electron nuclear double resonance) and ESEEM (electron spin-echo envelope modulation), and can be estimated through the fitting of the NMRD data (Table 4). Moreover, the use of computational methods can greatly enhance their interpretation. For [VO(H2O)5]2+ single crystals, ENDOR data are available, reporting small Haiso values of 0.01 and −0.04 MHz for axially coordinated water and larger values in the range from −0.39 to 8.67 MHz for equatorially coordinated water molecules. These data, corroborated by DFT calculations,31 show that the isotropic hyperfine coupling constants of the water molecule protons are very sensitive not only to the V–OH2O distance but also crucially depend on the orientation of the molecule, with respect to the vanadyl bond. The Haiso values obtained in this work for the equatorial water molecules [VO(H2O)5]2+ fall within the range 0.73–7.86 MHz (Table 3), in nice agreement with the experiment. The Haiso value for [VO(H2O)5]2+ estimated from the fitting of the NMRD data (Table 4) is of the order of 3.7 MHz and reflects an averaged value over different water orientations.
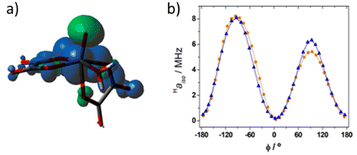
The average value obtained for equatorial water molecules with DFT (Haiso = 4.0 MHz) is in excellent agreement with the result obtained with NMRD. Similar values (Haiso ∼ 3.7 MHz) are derived for [VO(ox)2(H2O)]2− with NMRD, while for [VO(acac)(H2O)] a lower Haiso ∼ 1.7 MHz was obtained. The hyperfine coupling constants obtained from NMRD measurements for [VO(ox)2(H2O)]2− are in good agreement with those obtained with DFT (Table 3). The known angular dependence of Haiso![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31 becomes evident by comparing the values calculated for the [VO(oxa)2(H2O)]2− and [VO(oxa)2(H2O)]2−·2H2O systems (Table 3). Indeed, the [VO(oxa)2(H2O)]2−·2H2O system presents a shorter V–OH2O distance than [VO(oxa)2(H2O)]2− associated with a lower Haiso value (Table 3). Inspection of the spin density calculated for the [VO(oxa)2(H2O)]2− system (Fig. 7a) shows that the positive spin density mostly resides close to the V atom, with a spatial distribution that resembles a dxy orbital, as would be expected.70 The vanadyl oxo atom displays a negative spin density due to spin polarization, as well as the donor atoms of the metal coordination environment, although to a lesser extent. This is in agreement with the DFT and ENDOR studies performed in the 17O enriched [VO(H2O)5]2+ system.71 Spin transfer to the protons of coordinated water molecules involves the overlap of the metal dxy orbital, hosting the unpaired electron, with the molecular orbitals on the hydrogen atoms of H2O. This interaction is maximized when the H atoms lie on the xy plane leading to a large Haiso value.72 As the protons of the water molecule are rotated out of the equatorial plane the overlap with the proton molecular orbitals is negligible and Haiso becomes smaller. With this in mind, the [VO(oxa)2(H2O)]2− system was therefore further explored by running relaxed potential energy surface scans, in which the dihedral angle ϕ defined by the V
31 becomes evident by comparing the values calculated for the [VO(oxa)2(H2O)]2− and [VO(oxa)2(H2O)]2−·2H2O systems (Table 3). Indeed, the [VO(oxa)2(H2O)]2−·2H2O system presents a shorter V–OH2O distance than [VO(oxa)2(H2O)]2− associated with a lower Haiso value (Table 3). Inspection of the spin density calculated for the [VO(oxa)2(H2O)]2− system (Fig. 7a) shows that the positive spin density mostly resides close to the V atom, with a spatial distribution that resembles a dxy orbital, as would be expected.70 The vanadyl oxo atom displays a negative spin density due to spin polarization, as well as the donor atoms of the metal coordination environment, although to a lesser extent. This is in agreement with the DFT and ENDOR studies performed in the 17O enriched [VO(H2O)5]2+ system.71 Spin transfer to the protons of coordinated water molecules involves the overlap of the metal dxy orbital, hosting the unpaired electron, with the molecular orbitals on the hydrogen atoms of H2O. This interaction is maximized when the H atoms lie on the xy plane leading to a large Haiso value.72 As the protons of the water molecule are rotated out of the equatorial plane the overlap with the proton molecular orbitals is negligible and Haiso becomes smaller. With this in mind, the [VO(oxa)2(H2O)]2− system was therefore further explored by running relaxed potential energy surface scans, in which the dihedral angle ϕ defined by the V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group and the water molecule (O
O group and the water molecule (O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) V–O–H) was varied in the range from −180° to +180° (Fig. 7b). The calculated Haiso values are positive regardless of the value of ϕ, but show two well-defined maxima at ϕ = −90° and 90°, which correspond to the situations in which the H atom of the coordinated water molecule lies on the equatorial plane. The different height of the two maxima observed for Haiso is related to the variations of the V–OH2 distance during the relaxed potential energy surface scan, which changes in the range ∼2.18–2.22 Å. In contrast, Haiso reaches the minimum values when the water O–H bond is perpendicular to the equatorial plane (ϕ = 0, 180°). The Haiso values obtained by averaging those obtained for the two 1H nuclei of the coordinated water molecule were found to vary in the range 2.82–1.5 MHz, highlighting also in this case the impact of the orientation of the water molecule with respect to the xy molecular plane on the observed Haiso.
V–O–H) was varied in the range from −180° to +180° (Fig. 7b). The calculated Haiso values are positive regardless of the value of ϕ, but show two well-defined maxima at ϕ = −90° and 90°, which correspond to the situations in which the H atom of the coordinated water molecule lies on the equatorial plane. The different height of the two maxima observed for Haiso is related to the variations of the V–OH2 distance during the relaxed potential energy surface scan, which changes in the range ∼2.18–2.22 Å. In contrast, Haiso reaches the minimum values when the water O–H bond is perpendicular to the equatorial plane (ϕ = 0, 180°). The Haiso values obtained by averaging those obtained for the two 1H nuclei of the coordinated water molecule were found to vary in the range 2.82–1.5 MHz, highlighting also in this case the impact of the orientation of the water molecule with respect to the xy molecular plane on the observed Haiso.
The angular dependence shown in Fig. 7b was previously reported for [VO(H2O)5]2+, although in the latter case negative Haiso values were calculated for ϕ values close to 0, 180 and 360°. In the present case, DLPNO-CCSD calculations provided a small positive Haiso value (0.14 MHz) for ϕ = 175°, which supports the results obtained with DFT. We also note that DLPNO-CCSD calculations provide significantly lower Haiso values than DFT (the maximum value is ∼1.5 MHz), a situation that was observed earlier. In the present case DFT appears to provide Haiso values in better agreement with the experiment than DLPNO-CCSD. This is very likely related to the overestimation of the V–OH2 distances by DFT, as evidenced by inspecting Table 3. This effect is alleviated only in part by incorporating a few explicit second-sphere water molecules, as observed previously for other metal complexes.51,52
The experimental Haiso value obtained for [VO(acac)(H2O)] (Haiso ∼ 1.8 MHz) is much larger than that calculated for the dominant trans isomer (∼0.06 MHz). Thus, it is likely that the value of Haiso obtained from NMRD is related to the presence of a minor fraction of the cis isomer in solution. DFT calculations afford Haiso values of 0.47 MHz and 3.27 MHz for the cis isomer using the [VO(acac)(H2O)] and [VO(acac)(H2O)]·2H2O systems, respectively. It is important to note that the values obtained by NMRD reflect an average of the different structures present in solution. Considering the sharp dependence of Haiso with the orientation of the water molecule, it is likely that dynamic effects play an important role.
Rotational dynamics
The τ298R value obtained from the NMRD fitting for [VO(H2O)5]2+ is in excellent agreement with that estimated with EPR measurements (47.8 ps). The τ298R values obtained for [VO(ox)2(H2O)]2− by NMRD (52 ps) and EPR (38 ps) are also in reasonable agreement. A more significant discrepancy is however observed for [VO(acac)(H2O)], as the EPR value (77 ps) is about twice the value obtained with NMRD (30.9 ps). This discrepancy could arise from the rather large number of parameters that affect the relaxivity data, which introduces some uncertainties in the values of some of them. Nevertheless, we also stress that the τ298R values obtained by NMRD refer to the reorientation of the V⋯H vector involving the coordinated water molecule, while the τ298R values obtained by EPR likely reflect better the rotation of the whole molecule. For instance, the local mobility of the water molecule coordinated to Gd3+ results in shorter τ298R values for the V⋯H vector than the V⋯O one, with τ298RH/τ298RO ∼ 0.65.73 In contrast, intramolecular hydrogen bonding interactions involving the coordinated water molecule may restrict local rotation, resulting in an enhanced relaxivity.74Electron relaxation
The fitting of the NMRD data yields similar values for the electron relaxation time Te1, which are around 1 ns (Table 4). However, we have made a number of assumptions during the fitting, and thus these results should be obtained with some care. Indeed, we assumed that Te1 does not change with the applied magnetic field, and further that Te1 = Te2. Electronic relaxation in d1 complexes is likely the result of the time modulation of the g- and A-tensors,16 probably as a result of rotation and fluctuations of the metal coordination sphere caused by molecular vibrations and collisions with the solvent. For some of the complexes good fits of the data were only possible by assuming the Te1 changes with temperature following Arrhenius behaviour with an activation energy Es (Table 4). We note that the [VO(nta)(H2O)]− and [VO(acac)(H2O)] complexes show shorter Te1 values than the remaining complexes studied here, which is in qualitative agreement with the EPR relaxation data discussed above (Fig. 5). However, further experimental and theoretical studies are necessary to gain a better understanding of electron relaxation in the aqueous solutions of oxovanadium(IV) complexes.Water exchange
The τ298M for the vanadyl aqua-ion is sensibly longer compared to the values observed for [Gd(H2O)8]3+ (τ298M = 1.2 ns)37 and [Mn(H2O)6]2+ (τ298M = 35.5 ns).38 The τ298M value of 19.1 μs is also sensibly shorter than that determined for the equatorial water molecules using 17O NMR measurements (2 ms).75 This suggests that 1H exchange is faster than the exchange of the whole water molecule due to the prototropic contribution to water exchange at the acidic pH used for NMRD measurements. A similar effect was reported recently for [Fe(H2O)6]3+, which is characterized by a τ298MO value of the whole water of 25 μs, and a τ298MH value of 756 ns in 0.15 M HNO3.39The [VO(oxa)2(H2O)]2˙− and [VO(nta)(H2O)]˙− complexes show similar residence times of the coordinated water molecule (∼15 μs, Table 4), while for [VO(acac)2(H2O)] water exchange is faster. The related activation enthalpy (ΔH‡) assumes similar values for all complexes except [VO(oxa)2(H2O)]2−. The very high enthalpy barrier determined for the latter may be related to the expulsion of the coordinated water molecule from the inner-coordination sphere as a result of interconversion between the cis and trans isomers. This process would shift the coordinated water molecule to the labile trans position, facilitating water exchange. Support for this hypothesis is provided by the detection of a minor fraction of the trans isomer in solution using EPR measurements (4%).76 An 1H exchange mechanism involving the rearrangement of the water ligand from an equatorial to an axial position was suggested previously on the grounds of a TH2 NMR relaxation study. The same work reported an 1H τ298M value for [VO(oxa)2(H2O)]2− (5.4 μs) somewhat longer than that determined here. Most likely water exchange in [VO(acac)2(H2O)] also involves interconversion between the cis and anti isomers, which are both present in solution. This explains the presence of a scalar contribution to relaxivity associated with a rather large Haiso value, which is not expected for the major trans isomer.
Conclusions
We have reported an integrated EPR, 1H relaxometric and computational study that provides very detailed information on the magnetic and dynamic properties of oxovanadium(IV) complexes in solution. The structure of the complexes in aqueous solution was established by using a combination of EPR and computational studies. This allowed estimating different parameters that affect the 1H relaxation times of the solutions of these complexes in water, including the distances of the closest approach of second-sphere water molecules, the distance between the 1H nuclei of coordinated water molecules and the paramagnetic centre and rotational correlation times. The inner-sphere contribution to 1H relaxivities was found to display contributions from both the scalar and dipolar mechanisms. Water exchange in this series of complexes occurs in the μs timescale, with all complexes showing similar water exchange rates. The Haiso values obtained from NMRD were corroborated with DFT calculations, which show that the orientation of the coordinated water molecule affects dramatically the hyperfine coupling constant.The details on the magnetic and relaxation properties of oxovanadium(IV) complexes revealed here are relevant for the development of molecular probes for different applications, including molecular spin qubits and MRI contrast agents.
More generally, we believe that this methodology, which synergistically combines two complementary spectroscopic techniques and computational procedures, represents a significant advance in the characterization of paramagnetic species in solution. Compared to the traditional approach based on the measurement and analysis of data collected with a single experimental technique, this methodology provides a more complete, accurate and reliable set of structural and dynamic information.
Experimental section
Sample preparation
All the precursors were high purity reagents from Sigma Aldrich. The [VO(H2O)5]2+ complex was obtained by dissolving 8 mg of VOSO4 in 10 mL of water at pH < 2, adjusted with H2SO4. For [VO(oxa)2(H2O)]2− (ref. 67 and 76) and [VO(nta)(H2O)]− (ref. 66 and 77) complexes the procedure was similar, using a nearly 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio between the metal ion and the ligand in solution. 3 mg of nitrilotriacetic acid, or 3 mg of oxalic acid, were dissolved in 3 mL of water, and then the pH was adjusted to about 5–6 pH units with a NaOH solution and 2.5 mg of VOSO4 were added to the solution. For the [VO(dtpa)]3− complex (1
1 molar ratio between the metal ion and the ligand in solution. 3 mg of nitrilotriacetic acid, or 3 mg of oxalic acid, were dissolved in 3 mL of water, and then the pH was adjusted to about 5–6 pH units with a NaOH solution and 2.5 mg of VOSO4 were added to the solution. For the [VO(dtpa)]3− complex (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio), 10 mg of the ligand were dissolved in 2.5 mL of water containing 5 mg of VOSO4, the mixture was stirred for 1 hour and then the pH was adjusted to 7 with a 5% of NaHCO3 solution.15 The [VO(acac)2] complex was prepared according to literature protocols.78 V2O5 was dissolved in a 3
1 molar ratio), 10 mg of the ligand were dissolved in 2.5 mL of water containing 5 mg of VOSO4, the mixture was stirred for 1 hour and then the pH was adjusted to 7 with a 5% of NaHCO3 solution.15 The [VO(acac)2] complex was prepared according to literature protocols.78 V2O5 was dissolved in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 H2O
2 H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2SO4 (conc) solution. Then 5 mL of ethanol were added, and the resulting solution was heated at reflux temperature under stirring for 1 hour. Excess V2O5 was removed by filtration and acetylacetone was added under stirring at pH = 7. The concentration of the complexes in solution is tested with the Evans method,79 which afforded the following values: [VO(H2O)5]2+ = 3.5 mM, [VO(dtpa)]3− = 1.8 mM, [VO(oxa)2(H2O)]2− = 3.9 mM, [VO(nta)(H2O)]− = 12.2 mM and [VO(acac)2] = 14.1 mM. For pulse EPR measures the latter two solutions were diluted to ∼3 mM in order to have similar concentrations for all complexes.
H2SO4 (conc) solution. Then 5 mL of ethanol were added, and the resulting solution was heated at reflux temperature under stirring for 1 hour. Excess V2O5 was removed by filtration and acetylacetone was added under stirring at pH = 7. The concentration of the complexes in solution is tested with the Evans method,79 which afforded the following values: [VO(H2O)5]2+ = 3.5 mM, [VO(dtpa)]3− = 1.8 mM, [VO(oxa)2(H2O)]2− = 3.9 mM, [VO(nta)(H2O)]− = 12.2 mM and [VO(acac)2] = 14.1 mM. For pulse EPR measures the latter two solutions were diluted to ∼3 mM in order to have similar concentrations for all complexes.
1H NMRD measurements
The 1/TH11H Nuclear Magnetic Relaxation Dispersion (NMRD) profiles were measured on a Fast-Field Cycling (FFC) Stelar SmarTracer Relaxometer over a continuum of magnetic field strengths from 0.00024 to 0.25 T (corresponding to 0.01–10 MHz proton Larmor frequencies). The relaxometer operates under computer control with an absolute uncertainty in 1/TH1 of ± 1%. Additional data points in the range 20–120 MHz were obtained with a High Field Relaxometer (Stelar) equipped with the HTS-110 3T Metrology Cryogen-free Superconducting Magnet. The measurements were performed using the standard inversion recovery sequence (20 experiments, 2 scans) with a typical 90° pulse width of 3.5 μs and the reproducibility of the data was within ± 0.5%. The temperature was controlled with a Stelar VTC-91 heater airflow equipped with a copper-constantan thermocouple (uncertainty of ± 0.1 K).EPR measurements
X-band CW-EPR spectra were recorded on a Bruker EMX spectrometer (MW frequency 9.75 GHz) equipped with a cylindrical cavity. Q-band pulse EPR and Q-band CW EPR experiments were performed on a Bruker ELEXSYS E580 spectrometer (MW frequency 9.76 GHz and 34 GHz respectively) equipped with a continuous helium flow cryostat from Oxford Inc. The magnetic field was measured by means of a Bruker ER035M NMR gaussmeter. Electron–Spin-Echo (ESE)-detected EPR experiments were carried out with the pulse sequence π/2–τ–π–τ–echo. The microwave pulse lengths tπ/2 and tπ and the τ value employed are specified in the corresponding figure captions. Tem measurements were performed using a two-pulse Hahn spin echo sequence, π/2–τ–π–τ–echo and varying the inter-pulse delay τ from an initial value of 120 ns with time increments of 8 ns for 800 points. The π/2 and π lengths were set to 16 and 32 ns, respectively. Te1 measurements were performed through the inversion recovery pulse sequence, π–T–π/2–τ–π–τ–echo, where the interpulse delay T has an initial value of 1 × 105 ns, π/2 and π have a length 16 and 32 ns, respectively, and τ is fixed to 400 ns. The time increments of T and the shot-repetition rate were adjusted at each temperature. For low temperature measurements 30% glycerol solutions were prepared in order to obtain good low T glasses.Computational details
Geometry optimizations of the vanadium(IV) complexes were performed with the Gaussian 16 program package (Rev B.01)80 using unrestricted Kohn–Sham calculations with the hybrid-meta GGA functional TPSSh56 and the Def2-TZVPP81 basis set. Solvent effects were incorporated with a polarized continuum model82 using the default settings [scrf = (pcm, solvent = water)]. The integration grid was increased using the integral = superfinegrid keyword. Frequency calculations were used to confirm that the optimized structures corresponded to stationary points.The computation of A- and g-tensors was carried out using the ORCA program system (release 5.0.3).83,84 The A-tensors were computed with both the TPSSh and TPSS0 functionals,55 and the Def2-QZVPP basis set.81 The TPSS0 functional is a 25% exchange version of TPSSh. The g-tensors were computed with the N-electron valence perturbation theory to second order (SC-NEVPT2)85 on the basis of complete active space self-consisted field (CASSCF)86 calculations. The active space consisted of one electron distributed in five metal based 3d orbitals [CAS(1,5)]. All calculations were performed with the aid of the resolution of identity (RI) approximation for both Coulomb and exchange (RI-JK)87 using the Def2/JK88 auxiliary basis set. The second order contribution to the A-tensor from spin orbit coupling was considered with the spin–orbit mean-field method [SOMF(1X)].89 The integration grids were increased from the defaults using the AngularGrid 7 and IntAcc 5.0 options within the %method section. The quality of the A-tensors obtained with DFT was tested using the coupled cluster theory, including single and double excitations, with the domain based local pair natural orbital method (DLPNO-CCSD).90,91 These calculations used the default settings defined by the DLPNO-HFC1 keyword.59 Bulk water solvent effects in all ORCA calculations were introduced with the SMD model developed by Truhlar,92 which is based on the electron density of the solute and a polarized continuum.
Author contributions
V. L.: EPR data and NMRD profiles. F. C.: synthesis, purification, and characterization of the complexes, and NMRD profiles. D. E.-G.: DFT calculations. C. P.-I.: DFT calculations, NMR data analysis, conceptualization and manuscript preparation. M. C.: EPR studies, data analysis, conceptualization and manuscript preparation. M. B.: project supervision, conceptualization and manuscript preparation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. B. and F. C. acknowledge the financial support from the Ministero dell'Università e della Ricerca (PRIN 2017A2KEPL project). C. P.-I. and D. E. G. thank Ministerio de Ciencia e Innovación (PID2019-104626GB-I00) and Xunta de Galicia (Grant ED431B 2020/52) for generous financial support, and acknowledge Centro de Supercomputación de Galicia for providing access to computing facilities.References
- M. C. Heffern, L. M. Matosziuk and T. J. Meade, Lanthanide probes for bioresponsive imaging, Chem. Rev., 2014, 114, 4496–4539 CrossRef CAS PubMed
.
- J. Wahsner, E. M. Gale, A. Rodríguez-Rodríguez and P. Caravan, Chemistry of MRI Contrast Agents: Current Challenges and New Frontiers, Chem. Rev., 2019, 119, 957–1057 CrossRef CAS PubMed
.
- G. Angelovski and É. Tóth, Strategies for sensing neurotransmitters with responsive MRI contrast agents, Chem. Soc. Rev., 2017, 46, 324–336 RSC
.
- F. Troiani and M. Affronte, Molecular spins for quantum information technologies, Chem. Soc. Rev., 2011, 40, 3119 RSC
.
- M. Atzori and R. Sessoli, The Second Quantum Revolution: Role and Challenges of Molecular Chemistry, J. Am. Chem. Soc., 2019, 141, 11339–11352 CrossRef CAS PubMed
.
- J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. E. Freedman, Millisecond Coherence Time in a Tunable Molecular Electronic Spin Qubit, ACS Cent. Sci., 2015, 1, 488–492 CrossRef CAS PubMed
.
- L. Helm, Relaxivity in paramagnetic systems: Theory and mechanisms, Prog. Nucl. Magn. Reson. Spectrosc., 2006, 49, 45–64 CrossRef CAS
.
- J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. E. Freedman, Multiple Quantum Coherences from Hyperfine Transitions in a Vanadium(IV) Complex, J. Am. Chem. Soc., 2014, 136, 15841–15844 CrossRef CAS PubMed
.
- M. Atzori, L. Tesi, E. Morra, M. Chiesa, L. Sorace and R. Sessoli, Room-Temperature Quantum Coherence and Rabi Oscillations in Vanadyl Phthalocyanine: Toward Multifunctional Molecular Spin Qubits, J. Am. Chem. Soc., 2016, 138, 2154–2157 CrossRef CAS PubMed
.
- M. Atzori, E. Morra, L. Tesi, A. Albino, M. Chiesa, L. Sorace and R. Sessoli, Quantum Coherence Times Enhancement in Vanadium(IV)-based Potential Molecular Qubits: the Key Role of the Vanadyl Moiety, J. Am. Chem. Soc., 2016, 138, 11234–11244 CrossRef CAS PubMed
.
- L. Tesi, E. Lucaccini, I. Cimatti, M. Perfetti, M. Mannini, M. Atzori, E. Morra, M. Chiesa, A. Caneschi, L. Sorace and R. Sessoli, Quantum coherence in a processable vanadyl complex: new tools for the search of molecular spin qubits, Chem. Sci., 2016, 7, 2074–2083 RSC
.
- I. Gimeno, A. Urtizberea, J. Román-Roche, D. Zueco, A. Camón, P. J. Alonso, O. Roubeau and F. Luis, Broad-band spectroscopy of a vanadyl porphyrin: a model electronuclear spin qudit, Chem. Sci., 2021, 12, 5621–5630 RSC
.
- C. E. Jackson, C.-Y. Lin, S. H. Johnson, J. van Tol and J. M. Zadrozny, Nuclear-spin-pattern control of electron-spin dynamics in a series of V(iv) complexes, Chem. Sci., 2019, 10, 8447–8454 RSC
.
- C.-Y. Lin, T. Ngendahimana, G. R. Eaton, S. S. Eaton and J. M. Zadrozny, Counterion influence on dynamic spin properties in a V(iv) complex, Chem. Sci., 2019, 10, 548–555 RSC
.
- J. W. Chen, R. L. Belford and R. B. Clarkson, Second-Sphere and Outer-Sphere Proton Relaxation of Paramagnetic Complexes: From EPR to NMRD, J. Phys. Chem. A, 1998, 102, 2117–2130 CrossRef CAS
.
- I. Bertini, Z. Xia and C. Luchinat, Solvent water 1H NMRD study of oxovanadium(IV) aquo ion, J. Magn. Reson., 1992, 99, 235–246 CAS
.
- D. Mustafi, B. Peng, S. Foxley, M. W. Makinen, G. S. Karczmar, M. Zamora, J. Ejnik and H. Martin, New vanadium-based magnetic resonance imaging probes: Clinical potential for early detection of cancer, JBIC, J. Biol. Inorg. Chem., 2009, 14, 1187–1197 CrossRef CAS PubMed
.
- D. Rehder, The potentiality of vanadium in medicinal applications, Inorg. Chim. Acta, 2020, 504, 119445 CrossRef CAS
.
- E. Anoardo, G. Galli and G. Ferrante, Fast-field-cycling NMR: Applications and instrumentation, Appl. Magn. Reson., 2001, 20, 365–404 CrossRef CAS
.
- S. Aime, M. Botta, D. Esteban-Gómez and C. Platas-Iglesias, Characterisation of magnetic resonance imaging (MRI) contrast agents using NMR relaxometry, Mol. Phys., 2019, 117, 898–909 CrossRef CAS
.
- J. H. Freed, Dynamic effects of pair correlation functions on spin relaxation by translational diffusion in liquids. II. Finite jumps and independent T1 processes, J. Chem. Phys., 1978, 68, 4034–4037 CrossRef CAS
.
- P. H. Fries, C. Gateau and M. Mazzanti, Practical Route to Relative Diffusion Coefficients and Electronic Relaxation Rates of Paramagnetic Metal Complexes in Solution by Model-Independent Outer-Sphere NMRD. Potentiality for MRI Contrast Agents, J. Am. Chem. Soc., 2005, 127, 15801–15814 CrossRef CAS PubMed
.
- J. A. Peters, The reliability of parameters obtained by fitting of 1H NMRD profiles and 17O NMR data of potential Gd3+-based MRI contrast agents, Contrast Media Mol. Imaging, 2016, 11, 160–168 CrossRef CAS PubMed
.
- N. F. Albanese and N. D. Chasteen, Origin of the electron paramagnetic resonance line widths in frozen solution of the oxovanadium(IV) ion, J. Phys. Chem., 1978, 82, 910–914 CrossRef CAS
.
- I. E. Haedicke, T. Li, Y. L. K. Zhu, F. Martinez, A. M. Hamilton, D. H. Murrell, J. T. Nofiele, H.-L. M. Cheng, T. J. Scholl, P. J. Foster and X. Zhang, An enzyme-activatable and cell-permeable MnIII-porphyrin as a highly efficient T1 MRI contrast agent for cell labeling, Chem. Sci., 2016, 7, 4308–4317 RSC
.
- S. Stoll and A. Schweiger, EasySpin, a comprehensive software package for spectral simulation and analysis in EPR, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed
.
- Y. Zhou, B. E. Bowler, G. R. Eaton and S. S. Eaton, Electron spin lattice relaxation rates for S=12 molecular species in glassy matrices or magnetically dilute solids at temperatures between 10 and 300 K, J. Magn. Reson., 1999, 139, 165–174 CrossRef CAS PubMed
.
- G. R. Eaton and S. S. Eaton, Solvent and temperature dependence of spin echo dephasing for chromium(V) and vanadyl complexes in glassy solution, J. Magn. Reson., 1999, 136, 63–68 CrossRef CAS PubMed
.
- T. S. Smith, R. LoBrutto and V. L. Pecoraro, Paramagnetic spectroscopy of vanadyl complexes and its applications to biological systems, Coord. Chem. Rev., 2002, 228, 1–18 CrossRef CAS
.
- C. F. Mulks, B. Kirste and H. Van Willigen, ENDOR Study of V02+-lmidazole Complexes in Frozen Aqueous Solution, J. Am. Chem. Soc., 1982, 104, 5906–5911 CrossRef CAS
.
- A. C. Saladino and S. C. Larsen, Density Functional Theory Calculations of the Electron Paramagnetic Resonance Parameters for VO2+ Complexes, J. Phys. Chem. A, 2003, 107, 1872–1878 CrossRef CAS
.
- S. S. Amin, K. Cryer, B. Zhang, S. K. Dutta, S. S. Eaton, O. P. Anderson, S. M. Miller, B. A. Reul, S. M. Brichard and D. C. Crans, Chemistry and Insulin-Mimetic Properties of Bis(acetylacetonate)oxovanadium(IV) and Derivatives, Inorg. Chem., 2000, 39, 406–416 CrossRef CAS PubMed
.
- R. E. Oughtred, E. S. Raper and H. M. M. Shearer, The crystal structure of diammonium bis(oxalato)monoaquaoxovanadate(IV) monohydrate, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1976, 32, 82–87 CrossRef
.
- A. Tesmar, I. Inkielewicz-Stępniak, A. Sikorski, D. Wyrzykowski, D. Jacewicz, P. Zięba, J. Pranczk, T. Ossowski and L. Chmurzyński, Structure, physicochemical and biological properties of new complex salt of aqua-(nitrilotriacetato-N,O,O′,O”)-oxidovanadium(IV) anion with 1,10-phenanthrolinium cation, J. Inorg. Biochem., 2015, 152, 53–61 CrossRef CAS PubMed
.
- A. Tesmar, D. Wyrzykowski, K. Kazimierczuk, J. Kłak, S. Kowalski, I. Inkielewicz-Stępniak, J. Drzeżdżon, D. Jacewicz and L. Chmurzyński, Structure, Physicochemical and Biological Properties of an Aqua
(2,2′,2′′-Nitrilotriacetato)-oxidovanadium(IV) Salt with 4-Methylpyridinium Cation, Z. Anorg. Allg. Chem., 2017, 643, 501–510 CrossRef CAS
.
- A. B. Ilyukhin, L. M. Shkol'nikova, A. L. Poznyak and S. S. Makarevich, Crystal structure of diethylenetriaminepentaacetato(2-)vanadyl monohydrate, Koord. Khim., 1991, 17, 918–921 CAS
.
- D. H. Powell, O. M. N. Dhubhghaill, D. Pubanz, L. Helm, Y. S. Lebedev, W. Schlaepfer and A. E. Merbach, Structural and Dynamic Parameters Obtained from 17O NMR, EPR, and NMRD Studies of Monomeric and Dimeric Gd3+ Complexes of Interest in Magnetic Resonance Imaging: An Integrated and Theoretically Self-Consistent Approach, J. Am. Chem. Soc., 1996, 118, 9333–9346 CrossRef CAS
.
- D. Esteban-Gómez, C. Cassino, M. Botta and C. Platas-Iglesias, 17O and 1H relaxometric and DFT study of hyperfine coupling constants in [Mn(H2O)6]2+, RSC Adv., 2014, 4, 7094 RSC
.
- Z. Baranyai, F. Carniato, A. Nucera, D. Horváth, L. Tei, C. Platas-Iglesias and M. Botta, Defining the conditions for the development of the emerging class of FeIII-based MRI contrast agents, Chem. Sci., 2021, 12, 11138–11145 RSC
.
- M. Atzori, S. Benci, E. Morra, L. Tesi, M. Chiesa, R. Torre, L. Sorace and R. Sessoli, Structural Effects on the Spin Dynamics of Potential Molecular Qubits, Inorg. Chem., 2018, 57, 731–740 CrossRef CAS PubMed
.
- J.-L. Du, G. R. Eaton and S. S. Eaton, Electron Spin Relaxation in Vanadyl, Copper(II), and Silver(II) Porphyrins in Glassy Solvents and Doped Solids, J. Magn. Reson., Ser. A, 1996, 119, 240–246 CrossRef CAS
.
- E. Balogh, Z. He, W. Hsieh, S. Liu and É. Tóth, Dinuclear Complexes Formed with the Triazacyclononane Derivative ENOTA4−: High-Pressure 17O NMR Evidence of an Associative Water Exchange on [MnII2(ENOTA)(H2O)2], Inorg. Chem., 2007, 46, 238–250 CrossRef CAS PubMed
.
- I. Bertini, F. Briganti, Z. Xia and C. Luchinat, Nuclear Magnetic Relaxation Dispersion Studies of Hexaaquo Mn(II) Ions in Water-Glycerol Mixtures, J. Magn. Reson., Ser. A, 1993, 101, 198–201 CrossRef CAS
.
- M. Magnussen, T. Brock-Nannestad and J. Bendix, Penta-aqua-oxovanadium(IV) bis(trifluoro-methane-sulfonate), Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2007, 63, m51–m53 CrossRef CAS PubMed
.
- A. Tézé, C. Marchal-Roch, H. So, M. Fournier and G. Hervé, Synthesis, X-ray crystal structure, and EPR study of [Na(H2O)2]2[VO(H2O)5][SiW12O40]·4H2O, Solid State Sci., 2001, 3, 329–338 CrossRef
.
- J. Krakowiak, D. Lundberg and I. Persson, A Coordination Chemistry Study of Hydrated and Solvated Cationic Vanadium Ions in Oxidation States +III, +IV, and +V in Solution and Solid State, Inorg. Chem., 2012, 51, 9598–9609 CrossRef CAS PubMed
.
- L. Lin, S. Wu, C. Huang, H. Zhang, X. Huang and Z. Lian, Piperazinium aqua-bis-(oxalato)-oxovanadate(IV) sesquihydrate, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2004, 60, m631–m633 CrossRef CAS
.
- H. Sehimi, I. Chérif and M. F. Zid, Crystal structure of bis-[4-(di-methyl-amino)-pyridinium]aqua-bis-(oxalato)oxidovanadate(IV) dihydrate, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2016, 72, 1002–1005 CrossRef CAS PubMed
.
- N. M. Atherton and J. F. Shackleton, Proton ENDOR of VO(H2O)52+ in Mg(NH4)2(SO4)2)26H2O, Mol. Phys., 1980, 39, 1471–1485 CrossRef CAS
.
- R. B. P. Pesci, E. J. de Souza, E. Niquet, O. R. Nascimento, R. B. Viana and V. M. Deflon, Supramolecular structures in oxovanadium(IV) compounds with pyrid-2-one and pyrid-4-one ligands, J. Mol. Struct., 2019, 1194, 104–111 CrossRef CAS
.
- D. Esteban-Gómez, A. de Blas, T. Rodríguez-Blas, L. Helm and C. Platas-Iglesias, Hyperfine Coupling Constants on Inner-Sphere Water Molecules of GdIII-Based MRI Contrast Agents, ChemPhysChem, 2012, 13, 3640–3650 CrossRef PubMed
.
- V. Patinec, G. A. Rolla, M. Botta, R. Tripier, D. Esteban-Gómez and C. Platas-Iglesias, Hyperfine Coupling Constants on Inner-Sphere Water Molecules of a Triazacyclononane-based Mn(II) Complex and Related Systems Relevant as MRI Contrast Agents, Inorg. Chem., 2013, 52, 11173–11184 CrossRef CAS PubMed
.
- V. Nagarajan, B. Müller, O. Storcheva, K. Köhler and A. Pöppl, Coordination of solvent molecules to VO(acac)2 complexes in solution studied by hyperfine sublevel correlation spectroscopy and pulsed electron nuclear double resonance, Res. Chem. Intermed., 2007, 33, 705–724 CrossRef CAS
.
- G. Anderegg, F. Arnaud-Neu, R. Delgado, J. Felcman and K. Popov, Critical evaluation of stability constants of metal complexes of complexones for biomedical and environmental applications* (IUPAC Technical Report), Pure Appl. Chem., 2005, 77, 1445–1495 CrossRef CAS
.
- S. Grimme, Accurate Calculation of the Heats of Formation for Large Main Group Compounds with Spin-Component Scaled MP2 Methods, J. Phys. Chem. A, 2005, 109, 3067–3077 CrossRef CAS PubMed
.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Climbing the Density Functional Ladder: Nonempirical Meta–Generalized Gradient Approximation Designed for Molecules and Solids, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed
.
- D. Sanna, G. Sciortino, V. Ugone, G. Micera and E. Garribba, Nonoxido VIV Complexes: Prediction of the EPR Spectrum and Electronic Structure of Simple Coordination Compounds and Amavadin, Inorg. Chem., 2016, 55, 7373–7387 CrossRef CAS PubMed
.
- O. I. Gromov, Performance of the DLPNO-CCSD and recent DFT methods in the calculation of isotropic and dipolar contributions to 14N hyperfine coupling constants of nitroxide radicals, J. Mol. Model., 2021, 27, 194 CrossRef CAS PubMed
.
- M. Saitow and F. Neese, Accurate spin-densities based on the domain-based local pair-natural orbital coupled-cluster theory, J. Chem. Phys., 2018, 149, 034104 CrossRef PubMed
.
- G. Micera and E. Garribba, Is the spin-orbit coupling important in the prediction of the 51V hyperfine coupling constants of VIVO2+ species? ORCA versus Gaussian performance and biological applications, J. Comput. Chem., 2011, 2822–2835 CrossRef CAS PubMed
.
- S. P. de Visser, M. G. Quesne, B. Martin, P. Comba and U. Ryde, Computational modelling of oxygenation processes in enzymes and biomimetic model complexes, Chem. Commun., 2014, 50, 262–282 RSC
.
- E. Lelong, J.-M. Suh, G. Kim, D. Esteban-Gómez, M. Cordier, M. H. Lim, R. Delgado, G. Royal, C. Platas-Iglesias, H. Bernard and R. Tripier, Complexation of C-Functionalized Cyclams with Copper(II) and Zinc(II): Similarities and Changes When Compared to Parent Cyclam Analogues, Inorg. Chem., 2021, 60, 10857–10872 CrossRef CAS PubMed
.
- S. Maurelli, G. Berlier, M. Chiesa, F. Musso and F. Corà, Structure of the catalytic active sites in vanadium-doped aluminophosphate microporous materials. New evidence from spin density studies, J. Phys. Chem. C, 2014, 118, 19879–19888 CrossRef CAS
.
- R. C. R. Bottini, L. G. Fachini, G. B. Baptistella, D. Stinghen, F. S. Santana, M. Briganti, R. R. Ribeiro, J. F. Soares, E. L. Sá and G. G. Nunes, An unsymmetrical mixed-valence oxidovanadium(IV/V) binuclear complex: Synthesis, characterization, DFT studies, and bromoperoxidase activity, Inorg. Chim. Acta, 2022, 537, 120947 CrossRef CAS
.
- L. Vander Elst, A. Sessoye, S. Laurent and R. N. Muller, Can the Theoretical Fitting of the Proton-Nuclear-Magnetic-Relaxation-Dispersion (Proton NMRD) Curves of Paramagnetic Complexes Be Improved by Independent Measurement of Their Self-Diffusion Coefficients?, Helv. Chim. Acta, 2005, 88, 574–587 CrossRef CAS
.
- G. A. Rolla, C. Platas-Iglesias, M. Botta, L. Tei and L. Helm,
1H and 17O NMR Relaxometric and Computational Study on Macrocyclic Mn(II) Complexes, Inorg. Chem., 2013, 52, 3268–3279 CrossRef CAS PubMed
.
- R. Mills, Self-diffusion in normal and heavy water in the range 1-45.deg., J. Phys. Chem., 1973, 77, 685–688 CrossRef CAS
.
- D. Mustafi and M. W. Makinen, Structure and Conformation of Bis(acetylacetonato)oxovanadium(IV) and Bis(maltolato)oxovanadium(IV) in Solution Determined by Electron Nuclear Double Resonance Spectroscopy, Inorg. Chem., 2005, 44, 5580–5590 CrossRef CAS PubMed
.
- L. Helm and A. E. Merbach, Inorganic and bioinorganic solvent exchange mechanisms, Chem. Rev., 2005, 105, 1923–1960 CrossRef CAS PubMed
.
- E. Ruiz, J. Cirera and S. Alvarez, Spin density distribution in transition metal complexes, Coord. Chem. Rev., 2005, 249, 2649–2660 CrossRef CAS
.
- D. Baute and D. Goldfarb, The 17O Hyperfine Interaction in V17O(H217O)52+ and Mn(H217O)62+ Determined by High Field ENDOR Aided by DFT Calculations, J. Phys. Chem. A, 2005, 109, 7865–7871 CrossRef CAS PubMed
.
- S. C. Larsen, DFT Calculations of Proton Hyperfine Coupling Constants for [VO(H2O)5]2+: Comparison with Proton ENDOR Data, J. Phys. Chem. A, 2001, 105, 8333–8338 CrossRef CAS
.
- F. A. Dunand, A. Borel and A. E. Merbach, How Does Internal Motion Influence the Relaxation of the Water Protons in LnIIIDOTA-like Complexes?, J. Am. Chem. Soc., 2002, 124, 710–716 CrossRef CAS PubMed
.
- E. Boros, R. Srinivas, H. Kim, A. M. Raitsimring, A. V. Astashkin, O. G. Poluektov, J. Niklas, A. D. Horning, B. Tidor and P. Caravan, Intramolecular Hydrogen Bonding Restricts Gd–Aqua-Ligand Dynamics, Angew. Chem., Int. Ed., 2017, 56, 5603–5606 CrossRef CAS PubMed
.
- K. Wuethrich and R. E. Connick, Nuclear Magnetic Resonance Relaxation of Oxygen-17 in Aqueous Solutions of Vanadyl Perchlorate and the Rate of Elimination of Water Molecules from the First Coordination Sphere, Inorg. Chem., 1967, 6, 583–590 CrossRef CAS
.
- P. Buglyó, E. Kiss, I. Fábián, T. Kiss, D. Sanna, E. Garribba and G. Micera, Speciation and NMR relaxation studies of VO(IV) complexes with several O-donor containing ligands: oxalate, malonate, maltolate and kojate, Inorg. Chim. Acta, 2000, 306, 174–183 CrossRef
.
- D. Sanna, I. Bódi, S. Bouhsina, G. Micera and T. Kiss, Oxovanadium(IV) complexes of phosphonic derivatives of iminodiacetic and nitrilotriacetic acids, J. Chem. Soc., Dalton Trans., 1999, 3275–3282 RSC
.
- R. N. Rogers and G. E. Pake, Paramagnetic Relaxation in Solutions of VO++, J. Chem. Phys., 1960, 33, 1107–1111 CrossRef CAS
.
- D. M. Corsi, C. Platas-Iglesias, H. van Bekkum and J. A. Peters, Determination of paramagnetic lanthanide(III) concentrations from bulk magnetic susceptibility shifts in NMR spectra., Magn. Reson. Chem., 2001, 39, 723–726 CrossRef CAS
.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC
.
- J. Tomasi, B. Mennucci and R. Cammi, Quantum mechanical continuum solvation models, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed
.
- F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS
.
- F. Neese, Software update: the ORCA program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed
.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, Introduction of n-electron valence states for multireference perturbation theory, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS
.
- P.-Å. Malmqvist and B. O. Roos, The CASSCF state interaction method, Chem. Phys. Lett., 1989, 155, 189–194 CrossRef CAS
.
- S. Kossmann and F. Neese, Comparison of two efficient approximate Hartee–Fock approaches, Chem. Phys. Lett., 2009, 481, 240–243 CrossRef CAS
.
- F. Weigend, Hartree–Fock exchange fitting basis sets for H to Rn, J. Comput. Chem., 2008, 29, 167–175 CrossRef CAS PubMed
.
- B. A. Heß, C. M. Marian, U. Wahlgren and O. Gropen, A mean-field spin-orbit method applicable to correlated wavefunctions, Chem. Phys. Lett., 1996, 251, 365–371 CrossRef
.
- C. Riplinger and F. Neese, An efficient and near linear scaling pair natural orbital based local coupled cluster method, J. Chem. Phys., 2013, 138, 034106 CrossRef PubMed
.
- C. Riplinger, P. Pinski, U. Becker, E. F. Valeev and F. Neese, Sparse maps—A systematic infrastructure for reduced-scaling electronic structure methods. II. Linear scaling domain based pair natural orbital coupled cluster theory, J. Chem. Phys., 2016, 144, 024109 CrossRef PubMed
.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Additional EPR data and geometries obtained with DFT. See DOI: https://doi.org/10.1039/d2qi02635j |
| This journal is © the Partner Organisations 2023 |