Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
High photothermal conversion efficiency for semiconducting polymer/fullerene nanoparticles and its correlation with photoluminescence quenching†
D. C.
Grodniski
*a,
L.
Benatto
 a,
J. P.
Gonçalves
a,
J. P.
Gonçalves
 b,
C. C.
de Oliveira
b,
C. C.
de Oliveira
 b,
K. R. M.
Pacheco
b,
K. R. M.
Pacheco
 a,
L. B.
Adad
c,
V. M.
Coturi
c,
L. S.
Roman
a,
L. B.
Adad
c,
V. M.
Coturi
c,
L. S.
Roman
 a and
M.
Koehler
a and
M.
Koehler
 *a
*a
aDepartment of Physics, Federal University of Paraná, 81531-980, Curitiba, PR, Brazil. E-mail: koehler@fisica.ufpr.br
bCell Biology Department, Federal University of Paraná, 81531-980, Curitiba, PR, Brazil
cCenter for Materials Technology, Parana Institute of Technology, 81359-010, Curitiba, PR, Brazil
First published on 28th November 2022
Abstract
Semiconducting polymer nanoparticles (SPNs) have potential applications in a variety of fields due to their remarkable capacity to convert light into other forms of energy. This conversion can occur through photoluminescence (PL), photovoltaic (PV), and/or photothermal (PT) effects, and therefore SPNs can be employed in organic solar cells (OSCs) or nano agents for photothermal therapy (PTT), for instance. Here we explore those properties by studying the correlation between PT efficiency (η) enhancement and SPN PL quenching with increasing fullerene (PC71BM) doping. This correlation was observed for nanoparticles of three different conjugated polymers so that the highest PT efficiency was found for SPNs of MDMO-PPV/PC71BM (η ≈ 74.8%). Using a combination of a kinetic model with quantum chemistry calculations, it is suggested that those phenomena derive from the fast non-radiative (NR) decay of charge transfer (CT) excitons at the polymer/fullerene interface. Our analysis revealed key physical properties that mostly influence the PT effect and enabled us to determine NR rates of the systems under study. The improvement of η with doping essentially occurs because the NR deactivation of CT states is faster than the NR recombination of the Frenkel excitons in the donor. Since we observed that the CT exciton NR rate tends to follow an energy gap law, NR recombination improvement may originate from the stronger vibrational overlap between CT state and ground state. Finally, our findings are in agreement with the open circuit voltage average loss observed in bulk heterojunction OSC using the same polymers as donors. The synergetic experimental characterization of PT and PL effects together with the proper theoretical modeling can thus provide valuable information on the factors that enhance a particular kind of energy conversion in SPNs. This methodology can be a valuable tool to prospect new materials aiming at theranostic applications and/or clean energy generation.
1 Introduction
The interaction of light with matter can result in several interesting phenomena like photoluminescence, photovoltaic, photoacoustic and photothermal effects. Those phenomena are interconnected and might involve competing physical processes so that the good characterization of one of them can provide valuable information about the others and vice-versa.At this point it is important to remember some general concepts behind the possible effects that originate from light absorption:
(i) Photoluminescence (PL) is the emission of light due to the radiative recombination of the excited states.
(ii) On the other hand, the photovoltaic (PV) effect is the free charge generation upon light absorption and constitutes the basic phenomena behind the fabrication of solar cells for energy conversion. In this field, as an alternative to the conventional solar cells, organic solar cells (OSCs) have been developing rapidly over the past few years.1 OSCs are essentially based on blends of an electron donor (D), a conjugated polymer (CP) or oligomer, and an electron acceptor (A), usually a fullerene.
(iii) The photo-thermal (PT) effect is the process that converts the energy of the absorbed photon into heat. Photo-thermal energy conversion has been studied for applications comprising biomedical therapies,2–4 mechanical actuators,5,6 optical data storage,7 chemical catalysis8 and so on.9,10 In biomedicine, photo-thermal therapy (PTT), a specific type of hyperthermia therapy, has emerged as a potential therapeutic approach as an adjuvant treatment of cancer due to many of its advantages such as high specificity, low toxicity to normal tissues and minimal invasiveness.11–14
(iv) Finally, the photoacoustic (PA) effect is the conversion of the photon energy into sound waves.15 This effect can be used for PA imaging which can provide deeper tissue penetration since it detects phonons instead of photons after light excitation.16 Since the PA response is intrinsically linked to the photothermal conversion, the selection of materials for PTT is naturally compatible with the selection of materials for PA imaging applications. This makes the systems with large PA and PTT responses potential candidates for the development of theranostics agents that combine therapy and diagnosis for a low cost but more precise medicine.17 Several materials have shown photo-thermal therapeutic efficacy in vitro and in pre-clinical animal experiments, such as hybrid materials,18,19 organic molecules,20,21 noble metal materials,22,23 and again CPs.24–33
As mentioned above, CPs can be employed in OSC or as PTT agents as well. The CP are characterized by long conjugated bond structures and repeating chemical units with delocalized π-electron systems. Those features enable different arrangements of their backbone structure to properly control their optoelectronic properties like radiative and non-radiative decay pathways.34–37 In addition, CPs are organic and biologically inert which make them suitable candidates for biological and biomedical applications, such as in bio sensing,38,39 bio imaging,40,41 drug delivery and release,42,43 and photodynamic therapy.44–50 Besides, they can be easily prepared as hydrophobic nanoparticles with photo stability, biocompatibility or biodegradability.51–54 Usually for PTT applications in medicine, the CPs are employed in the form of semiconducting polymer nanoparticles (SPNs).55
In OSCs, the PV effect is enhanced when the CPs are blended with fullerene. The reason is because light absorption in organic semiconductors does not generate free charges but bound electron-hole pairs, called Frenkel-type excitons. The photogenerated exciton can then dissociate into free charges (producing the PV effect) or recombine to the ground state via radiative (producing the PL effect) or non-radiative (producing the PT effect) pathways. In the absence of the acceptor, the excitons generated in the CP tends to recombine due to the high exciton binding energy (Eb) in those materials.56 However, when the acceptor is present, the excitons can diffuse to the D/A interface where a fast electron transfer from the D to the A might take place. The electron transfer produces then a strong quench of the polymer's PL and creates an intermediary charge transfer (CT) exciton that can either recombine to the ground state or dissociate into free charges. The formation of CT excitons tends to favor the dissociation (and consequently the PV effect) because the binding energy of this excited state is lower than Eb. Currently, the state-of art OSCs are fabricated using non-fullerene acceptors and have reached efficiencies up to 18%.57 Yet there is still some debate about the mechanisms behind non-radiative (NR) recombination at the D/A heterojunction that would produce intrinsic limitations to the performance of those devices.58 The NR recombination increases the open-circuit voltage losses which decreases the photo-conversion efficiency.58
Despite the few results reported in the literature, it was observed that CP-based SPNs also showed an enhancement of the PT effect with the fullerene-doping.59 For instance, Lyu et al. made use of the enhanced NR recombination in those nanoparticles to apply them as in vivo photo-thermal therapy agents.59 The reasons behind the magnification of the photo-thermal effect induced by the fullerene are still poorly understood but it is reasonable to suppose that it is linked to non-radiative deactivation of CT excitons. This open question motivated us to investigate the heat generation of SPNs doped with fullerene after illuminating them with a green light (532 nm) laser. We employed a multiple method approach that combined the synthesis of the nanoparticles, experiments for morphological, thermal, and optical characterization, and theoretical modelling. The experimental work involved the comparison between PL measurements with photo-thermal analysis. The PT measurements were performed using an adapted differential scanning calorimetry (DSC) setup. We then developed a theoretical model to quantify the efficiency of heat generation during the experiment with the laser. The PL measurements were also explained using a kinetic model and quantum chemical calculations to obtain the characteristic rates that governs the charge transfer (or recombination) dynamics at the D/A heterojunction. The results of the optical and thermal measurements were analyzed by considering the rates for charge transfer, charge separation or recombination to compose a physical picture that relates the PT effect with intrinsic properties at the D/A heterojunction (like exciton binding energy, and driving forces for charge transfer, for instance).
The method was applied to SPNs synthetized using poly(3-hexylthiophene-2,5-diyl) (P3HT), poly[2-methoxy-5-(3′,7′-dimethyloctyloxy)-1,4-phenylenevinylene] (MDMO-PPV) and Poly[2,7-(9,9-dioctyl-dibenzosilole)-alt-4,7-bis(thiophen-2-yl)benzo-2,1,3-thiadiazole] (PSiF-DBT) as donors and the fullerene [6,6]-Phenyl C71 butyric acid methyl ester (PC71BM) as the acceptor. The use of different polymers enabled us to identify the key properties that governs the PT effect in nanoparticles of polymer/fullerene heterojunctions. In addition, since the processes that lead to heat generation compete with those to produce free charges, the characterization developed here is also useful to gain insights on the PV effect in those systems. By averaging the open circuit voltage of many OSCs reported in the literature (that employed the donors considered here), we showed that the average voltage loss observed in those devices is in general accordance with the predictions derived from our analysis.
Finally, we demonstrated that our approach can be a powerful method to investigate the photothermal effect and non-radiative recombination in D/A blends. It can also be very useful for the search of new materials aiming at PTT and solar energy conversion.
2. Experimental
2.1 Materials
In this work we used three different conjugated polymers as donors: (i) P3HT with molecular weight between 54 and 75 kDa,60 (ii) MDMO-PPV with molecular weight around 120 kDa,61 and the copolymer (iii) PSiF-DBT (molecular weight between 54 and 80 kDa).62 Those polymers were mixed with the fullerene [6,6]-Phenyl C71 butyric acid methyl ester (PC71BM, molecular weight approximately 1.031 kDa)63 as acceptor to form donor/acceptor blends. All the materials were purchased from Sigma-Aldrich and their chemical structure are illustrated in Fig. 1(a)–(d). The energy level of the frontier orbitals (HOMO, highest occupied molecular orbital, and LUMO, lowest unoccupied molecular orbitals) of the materials considered here are shown in Fig. 1(e).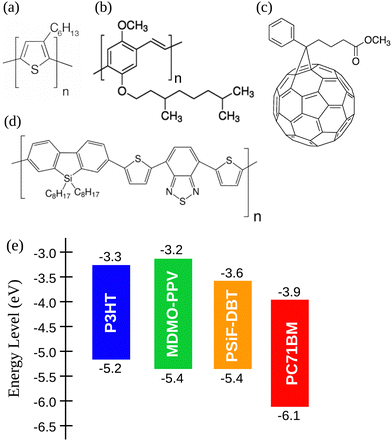 | ||
| Fig. 1 Chemical structures of (a) P3HT, (b) MDMO-PPV, (c) PC71BM and (d) PSiF-DBT. (e) Energy level diagram of the considered polymers and fullerene.60–63 | ||
2.2 Synthesis of semiconductor polymers nanoparticles
The SPNs were synthesized by nanoprecipitation.64,65 In the sequence we detail the steps to obtain those nanoparticles. (i) First, 1 mg of each conjugated polymer (either P3HT, MDMO-PPV or PSiF-DBT) were dissolved in 4 ml of tetrahydrofuran (THF) and subjected to a constant magnetic stirring until it reaches a complete dissolution of the solutes. This process took between 2 and 3 hours depending on the polymer. The same procedure was repeated to dissolve 1 mg of PC71BM in 4 ml of THF. The resulting solutions have thus a concentration of 0.25 mg ml−1. (ii) In the sequence, four additional solutions in THF were prepared for each polymer with different levels of fullerene doping: one pure sample containing only the polymer (0%), and another three solutions with fullerene amounts of 40, 70 and 100 w/w%, respectively. In order to keep the concentration of polymer constant at 0.25 mg ml−1 in all samples, PC71BM solutions were added to the polymer solutions produced in the step (i) in volumes to generate the concentrations of 0.175 mg ml−1 (40% doping), 0.1 mg ml−1 (70% doping) and 0.25 mg ml−1 (100% doping). An additional solution in THF containing only fullerene (0.25 mg ml−1) was also prepared. (iii) These solutions were rapidly injected into 0.8 ml of deionized water that was submitted to bath sonication at 25 kHz for 5 minutes. Due to the hydrophobicity of the polymers and the fullerene lateral groups they quickly condense in nanoparticles to minimize the contact surface with water.64 (iv) The solutions containing the formed nanoparticles were then placed under magnetic stirring for three hours until the complete evaporation of THF. The final aqueous solutions concentrations of the SPNs were then 0.071, 0.10, 0.12, and 0.14 mg ml−1 for the 0%, 40%, 70% and 100% fullerene doping, respectively. Those solutions are next quoted using the polymer's acronym followed by a number referring to the concentration of polymer doping. For instance, PPV-0, PPV-40, PPV-70 and PPV-100 are the samples prepared using MDMO-PPV with 0%, 40%, 70% and 100% of fullerene doping, respectively. Finally, these aqueous solutions were filtered through a polyethersulfone (PES) syringe filter of 0.22 μm to remove large aggregates of SPNs.2.3 Morphological and photophysical characterization
The morphology of the nanoparticles was characterized using transmission electron microscopy (TEM). The TEM images were obtained using a JEOL JEM 1200 transmission electron microscope at acceleration voltage of 120 kV. The SPNs aqueous solutions were dripped over copper grids and then stored until complete drying of the sample (for a period of time usually longer than 24 hours).The photophysical properties of the SPNs in aqueous solution were investigated by UV-Vis and photoluminescence measurements. The UV-Vis spectra in deionized water were obtained using the Thermo Scientific™ Evolution 201 UV-Vis spectrophotometer. The photoluminescence spectra were recorded at room temperature by employing a Fluotolog-3 Fluorescence Spectrofluorometer (Horiba Jobin Yvon). The samples were excited at wavelength of 532 nm. This wavelength is very close to the peak of the absorption spectra of the polymers studied here.
2.4 Thermal analysis of the SPNs
The measurement of the specific heat (heat capacity per unit mass) of the SPNs is essential to determine SPN temperature variations induced by laser irradiation. Heat capacity (cp) is the amount of energy (heat) that must be added to a substance to increase its temperature by 1 °C at constant pressure.66 The relation between isobaric specific heat capacity of a material and the heat absorbed during a linear temperature change is:67,68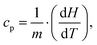 | (1) |
A usual DSC heating program generates an enthalpy curve as function of the heating temperature. Based on the areas under DSC curves measured for baseline, standard and sample, the specific heat can be obtained as:69,70
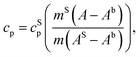 | (2) |
In this work, stepwise method for determination of the specific heat capacity was applied using a Heat Flux Differential Scanning Calorimeter DSC-3 STARe System by Mettler Toledo. Nitrogen was applied as a purge gas to minimize oxidation of the sample during measurements. Before the experiments, the thermal response and temperature were calibrated with the heat of the fusion and the melting point of pure indium. The SPNs dispersed in an aqueous solution were placed in aluminum pans at a fixed volume of 70 μl. The pans were sealed with an aluminum lid containing a small central orifice. It is important to mention that the sample pans and the reference pan were made of the same material and had approximate the same mass. Baseline, standard and samples measurements were taken sequentially following an operation program that starts by applying an isotherm for three minutes. In the sequence a succession of heating ramps of 1 °C were applied with a heating rate of 1 °C min−1, merged by isotherms of two minutes. Measurements were performed in the temperature range between 26 °C and 38 °C.
2.5 Photo-thermal heat flow measurements
After the assessment of cp, we performed photothermal measurements to quantify the heat generated when the SPNS are under laser illumination. A continuous wave laser (powered by a power supply) with wavelength of 532 nm was then adapted to the DSC equipment, in a configuration like a Photo-calorimetry (DSC)71,72 (Fig. S1, ESI† shows a picture of the apparatus employed in those measurements). The average intensity of the laser reaching the sample (measured by a potentiometer) was 30 mW. In this home-built configuration of the DSC setup, measurements were performed with the furnace temperature fixed at 27 °C (isothermal program). We followed a sequential protocol to perform those measurements: initially the DSC was started with the laser off for three minutes to stabilize heat flow between the sample and the reference. Then, the sample and reference pans were illuminated by the laser beam during 5 cycles with increasing durations of 1, 2, 3, 4 and 5 minutes, respectively. This procedure minimizes the influence of the aluminum pan on the measurements of the samples’ enthalpy. The illumination cycles correspond then to a total irradiation time of 15 minutes. Each period of illumination was followed by intervals of 2 minutes with the laser off. In those intervals the system is forced by the DSC equipment to thermalize back to the isothermal temperature of 27 °C. During the photo-thermal measurements the DSC furnace was kept sealed by a thermal insulating cover with a transparent quartz plate in such a way that the laser beam could reach the sample. 70 μL of aqueous nanoparticles were used in those measurements.Since we were following an isotherm program, any endothermic or exothermic heat change induced by the incident light will produce a variation of enthalpy dH/dT between the sample and the reference. The amount of heat (Q(J)) released by the sample in the interval between the initial time ti (when laser is turned on) until the final time tf (when it is turned off) can be obtained by:73
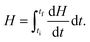 | (3) |
Once the specific heat capacity cp is known, temperature variation ΔT (°C), can be calculated using the heat balance equation:
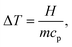 | (4) |
Using the value of H obtained from eqn (3) and considering the power of the laser radiation reaching the sample (Plaser), one can estimate the photo-thermal conversion efficiency (PCE) from:74
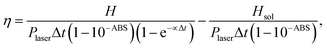 | (5) |
Since the samples tend to have different properties of light absorption depending on the kind of polymer or fullerene doping, the concentration of the solutions used for the photo-thermal measurements were adjusted to have approximately ABS = 1 at the wavelength around 532 nm. Those concentrations are reported in Section 2.2.
3. Theoretical methods
3.1 Kinetic model, photoluminescence quenching, and population of charge transfer states
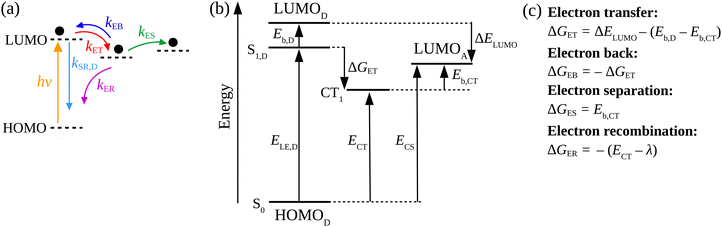
We applied a kinetic approach proposed in ref. 56 to correlate the photoluminescence (PL) measurements of the SPNs with the corresponding photo-thermal measurement obtained by DSC. This approach enabled us to identify the main physical properties of the D/A blends that influence the heat generation induced by light absorption.In Fig. 2, we illustrate the charge dynamics considered in ref. 56 with the rates assumed to describe the efficiency of PL quenching via polymer excitation. After the donor excitation, the model in ref. 56 consider all the possible processes to deactivate the singlet exciton (Fig. 2(a)) at the D/A interface: (i) it can simply recombine with a rate kSR,D or (ii) the electron can be transferred to the acceptor (with a rate kET) forming the charge transfer (CT) state. Once the CT state is created, (iii) it can be deactivated by the separation of the pair (with a rate kES), (iv) can recreate the singlet exciton in the polymer from a back transfer of the electron (with a rate kEB) or, finally, (v) recombine directly from the CT state to reestablish the ground state (with the rate kER). The photoluminescence (PL) quenching efficiency (QD) can be measured by comparing the PL of pristine donor (PL[D]) with the PL of donor/acceptor blend (PL[D/A]) in the form:75
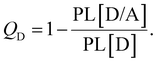 | (6) |
From computational simulations of QD, the exciton dynamics at the D/A interface can be understood more profoundly.76–78 In this work, we will follow the procedure detailed in ref. 56 to simulate QD for the three blends considered here. The model uses the molecular energies as input parameters.
Each process in Fig. 2(a) is characterized by a frequency rate (k) that can be quantified using the Marcus formalism:79,80
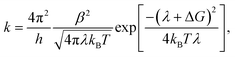 | (7) |
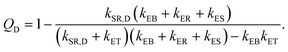 | (8) |
In eqn (8), kSR,D is the inverse of singlet exciton recombination lifetime (1/τ) of donor polymer and can be obtained from experimental data. Here we will use a typical value of τ for donor polymers of 250 ps.83 Using the exciton binding energy of the CT state (Eb,CT, see Fig. 2(c)) as fitting parameter, we use eqn (8) to reproduce the experimental PL quenching obtained from the photoluminescence measurements. We will focus our theoretical analysis on the samples with the highest fullerene doping. After the fitting, all characteristic rates illustrated in Fig. 2(a) are completely determined. We can then use those rates to calculate the population of CT excitons derived from the steady state solution of the kinetics’ model in ref. 56:
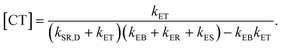 | (9) |
Eqn (9) gives the concentration of CT excitons generated by charge transfer at the heterojunction relative to the population of excitons created in the donor after light absorption. The total rate of direct CT recombination at the D/A interface (the process indicated by a purple arrow in Fig. 2(a)) is RCT = kER[CT]. We will use this parameter to investigate the influence of the CT concentration and recombination on the photothermal efficiency of the SPNs samples.
3.2 Exciton binding energy
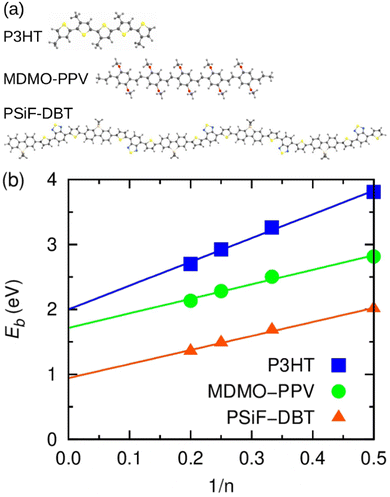
The calculation of exciton binding energy for the polymers considered in this work is fundamental to determine the driving forces for electron transfer and electron separation (ΔGET and ΔGES, respectively, see Fig. 2(c)). This parameter can be calculated by subtracting the fundamental energy gap from the optical gap.84 The method used here to calculate Eb of polymers is described in detail in ref. 85. It involves the linear extrapolation of oligomer energies in relation to the reciprocal of the number of mers (1/n). We performed this procedure to avoid deviations related to differences in the delocalization lengths along the polymeric chains. Oligomers with five mers (n = 5, pentamers) were considered in the calculations. The side chains of the oligomers were replaced by methyl groups to reduce the computational cost. The ground state geometry of oligomers was calculated by DFT with the long-range-corrected hybrid functional ωB97XD86 functional and 6-31G(d,p) basis set.87 The molecular energies were obtained using the M0688 functional and 6-31G(d,p) basis set. Results produced by this level of theory are usually in good agreement with experiment at a reasonable computational cost.85,89 Finally, the solid-state exciton binding energy of polymers was obtained in a simple way Eb/ε,90 where ε is the dielectric constant of the organic film.4. Results and discussion
4.1 Transmission electron microscopy measurements
The morphology and the SPNs size were investigated using transmission electron microscopy (TEM) for all fullerene concentrations. Since the TEM images had approximately the same general features for all levels of doping, Fig. 3(a)–(c) shows the results for polymer-100 samples. Those were the SPNs with the highest PT response. The SPNs in Fig. 3(a)–(c) had a uniform spherical morphology with average diameters of approximately ∼46 ± 17 nm (median 44.11 nm) for the P3HT-100 sample, ∼95 ± 21 nm (median 98.70 nm) for the PSiF-100 and ∼18 ± 6 nm (median 15.40 nm) for the PPV-100. Semiconductor nanoparticles with the diameter around 16 nm are very common for PPV91,92 due to the low mass of this polymer when dispersed in solution.92 It is well known in the literature that SPNs tends to agglomerate due to strong π–π interactions.91–93 This tendency restricted an accurate determination of the distribution of nanoparticles sizes in the solutions dropped over the TEM copper thin film. Hence, an extended study to measure the distribution of nanoparticles sizes was not possible. Yet Fig. S2 (ESI†) shows histograms of nanoparticles sizes obtained from a visual inspection to sections of TEM images like the ones in Fig. 3. The SPNs sizes in the histograms were manually assessed. Fig. S2 (ESI†) indicates that the distribution of SPNs sizes is broad but with a peak around the magnitude of the average diameters reported above. | ||
| Fig. 3 TEM images of conjugated polymer/PC71BM heterojunctions nanoparticles for the samples (a) P3HT-100, (b) PSiF-100, (c) PPV-100. | ||
The polymer/fullerene SPNs in Fig. 3(a) had a contrast in grey scale, with a dark core and a clearer external layer. In ref. 93 this contrast was attributed to variations in the density of the materials that form the SPNs’. Consequently, the PC71BM, that has a higher density (1.5 g cm−3),94 appeared darker than the P3HT (1.10 g cm−3)95 in the TEM images. The same contrast was also observed in MDMO-PPV/PCBM blends96 where the fullerene appearing considerably darker then the MDMO-PPV (0.910 g cm−3).97 Those results suggest that all our SPNs doped with fullerene are formed by a PC71BM rich central core covered by a polymeric outer shell.91,98
4.2 Photoluminescence measurements
The effects of fullerene doping on the photophysical properties of the SPNs were studied by comparing UV-Vis absorption and photoluminescence (PL) spectra measured in aqueous solutions. The absorption spectra of pure PC71BM nanoparticles are shown in Fig. S3 (ESI†). The fullerene nanoparticles had a broad absorption in the range between 300 nm and 700 nm, with (not well-defined peaks) at 378, 470, 564, and 685 nm. Those features are important to characterize the variations in the polymer absorption induced by the fullerene doping of the SPNs.Fig. S3a–c (ESI†) show the UV-Vis spectra of the nanoparticles as a function of the fullerene doping. The SPN absorption rises and becomes broader with increasing PC71BM concentration. This broadening is induced by the higher absorption in the range between 300 and 400 nm and between 600 and 700 nm. For P3HT(PPV)-100 samples, the fullerene characteristic peaks around 378 nm and 685 nm are clearly identified but blue shifted relative to the spectrum measured for SPNs of PC71BM. In the case of the PSIF, the fullerene contribution tends to fill the gap between the two main characteristic peaks of the polymer absorption associated to the π–π* transitions and the intramolecular charge transfer (ICT).99 This fact (together with a higher absorption over the 600 nm to 800 nm range) produces a very broad absorption band for the PSIF-100 sample. Since the PSIF is D–A block copolymer,100 the internal charge transfer (ICT) phenomena along the polymer chain tends to increase the light absorption in the visible range compared to the homopolymers P3HT and PPV. Among these two materials, the P3HT has a higher absorption coefficient than PPV101 in the range between 400 and 600 nm.
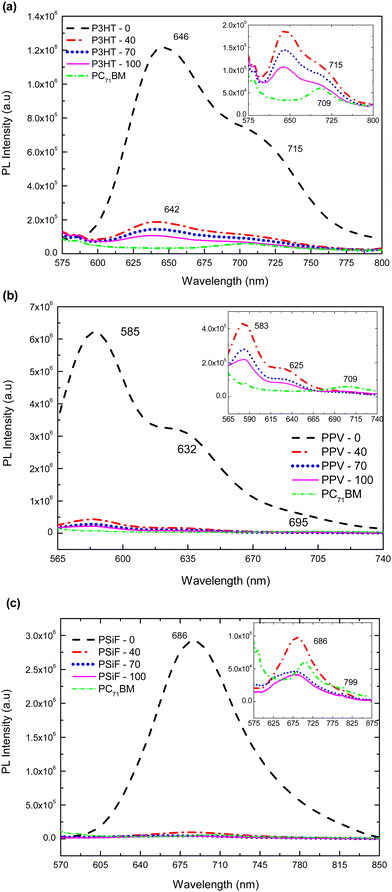
Photoluminescence response of P3HT-0 is shown in Fig. 4(a). It has a well-defined maximum emission at 646 nm, and a less energetic shoulder at 720 nm.102 The emission of the P3HT-40, P3HT-70 and P3HT-100 samples were blue-shifted and broadened compared to P3HT-0 due to the formation intermixed morphology between PC71BM and P3HT.103 Those effects are also related to the increase of the conformational disorder which tends to reduce the effective conjugation length.104 The intensity of the polymer's emission was gradually quenched with the increase amount of fullerene (for the P3HT-100 nanoparticles the PL of the SPNs is quenched by 87% compared to the emissions of the P3HT-0 sample, see Table 1).
| Heterojunctions | PL quenching efficiency (%) | ||
|---|---|---|---|
| PC71BM weight percentage (%) | |||
| 40 | 70 | 100 | |
| P3HT:PC71BM | 80.6 | 84.5 | 86.0 |
| MDMO-PPV:PC71BM | 94.8 | 96.4 | 97.0 |
| PSiF-DBT:PC71BM | 95.7 | 97.6 | 97.6 |
Photoluminescence intensity in Fig. 4(b) for PPV-0 has characteristic peaks at 585 nm, 632 nm and 695 nm, respectively.105 With the fullerene doping, 585 nm peak is blue shifted by around 2 nm relative to the same band observed in the SPNs of pure PPV. Again, those features can be explained by the reduction of the effective conjugation length due to steric effects produced by the presence of the PC71BM molecule. As it was observed for the P3HT, the PL of the MDMO-PPV nanoparticles is gradually quenched with the PC71BM concentration. This quenching reaches 97% of the PPV-0 emission for the sample with the highest amount of fullerene (PPV-100) (see Table 1). Finally, the PPV-70 and PPV-100 samples shows a small peak around 709 nm. Since the fullerene has a weak absorption around 532 nm (the wavelength used to excite the samples), this band corresponds to emissions from the PC71BM.106 It was found that the charge transfer from the fullerene to the polymer is not efficient which decreases the PL quenching efficiency when the exciton is formed in the acceptor.56
Photoluminescence emissions of PSiF-DBT nanoparticles are shown in Fig. 4(c). In contrast to the absorption spectrum that has two peaks, the PL of PSiF-DBT samples is dominated by a single broad peak at approximately 686 nm, in a broader range wavelength including the small peak around 709 nm. The presence of a single emission was also observed for PSiF-DBT films. This feature was attributed to an efficient energy transfer between the SiF segment to the DBT unit of the chain in the solid state.107 This transfer extinguishes the emission from the SiF segment at 416 nm that is observed when the PL spectrum of PSiF-DBT is measured in solution.107 As it happened for the other polymers, the emission of the PSiF-DBT nanoparticles is quenched with the PC71BM doping. This quenching is approximately 97% for the PSiF-DBT-100 sample (see Table 1). Finally, for the PSiF-70 and PSiF-100 SCNP samples there are also a weak emission band around 799 nm that probably corresponds to the PL from PC71BM.
Table 1 summarizes the efficiency of photoluminescence quenching for the different kinds of SPNs as a function of fullerene concentration. The quenching efficiency increases with the percentage of PC71BM weight specially from 40% to 70% but tends to saturate when this concentration further rises to 100%. The increasing quenching is due to the non-radiative deactivation of excitons in the donor derived from the efficient photo-induced charge transfer between the polymer and the PC71BM.59 This effect suggests that the donor and the acceptor are indeed in close contact inside the SPNs since the simple physical mixture of a polymer and the PC71BM does not produce a high percentage of fluorescence extinction.59
The PT measurements described in the next section will demonstrate that the PL quenching induced by the fullerene doping has a negative correlation with the enhancement of non-radiative heat generation after light excitation. The reasons behind this correlation will become clear in Section 4.4.
4.3 Photo-thermal measurements
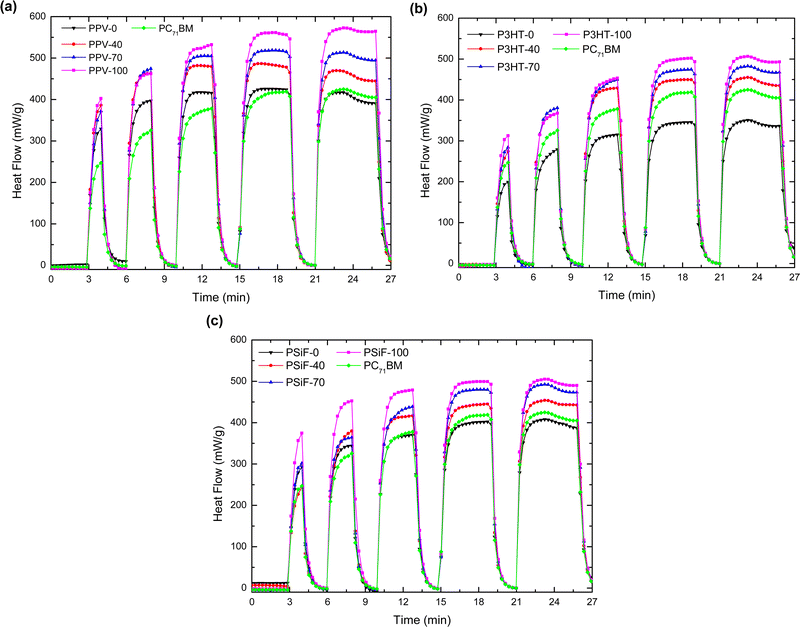
The specific heat capacity of the nanoparticles obtained using the DSC measurements are displayed in Table S1 (ESI†). Here we are going to apply those results to study the photo-thermal effect of the SPNs after laser illumination.The SPNs time-dependent heat generation dH/dt in the isothermal mode at 27 °C (measured following the experimental procedures described in Section 2.5) are shown in Fig. 5. After an initial period of 3 minutes with the laser OFF, the samples were periodically illuminated by alternating laser ON and OFF periods of 5- and 2 minutes duration, respectively, always keeping a fixed irradiation intensity of 312 mW cm−2. During the starting period of 3 minutes without illumination, the system reaches the heat flow of thermal equilibrium (0 mW). When the laser source is turned on, however, there is a sudden positive variation in dH/dt which indicates the presence of an exothermic process in the sample. The magnitude of the heat flow increases with the number of laser irradiation cycles but tends to saturate after 3 (PPV) and 4 (P3HT and PSiF) illumination periods. The pure polymer and fullerene samples followed similar dH/dt variations but the magnitude of the heat flow raised with the PC71BM doping. The dH/dt reached a steady-state magnitude of 350.54 (506.35) mW g−1 (Fig. 5(a)), 416.65 (570.62) mW g−1 (Fig. 5(b)), and 407.86 (505.26) mW g−1 (Fig. 5(c)) for the P3HT-0(100), PPV-0(100), and PSiF-0(100) samples, respectively. The higher variations of the heat flow were thus observed for the P3HT and PPV nanoparticles, but the highest magnitude was found for the PPV-100 sample. The enhancement of the heat flow with the fullerene doping is in line with the PL quenching induced by the higher concentration of PC71BM in the photoluminescence measurements described above.
It follows from eqn (3) that the increase of the area below the dH/dt × t curve in Fig. 5 corresponds to a higher amount of heat (Q) produced by laser illumination. Upon removal of the photoexcitation, the heat flow drops to values close to 0 mW within the OFF-period interval of 120 seconds. Fig. 5 shows that all the samples displayed good photostability throughout the illumination cycles. Just after 4 minutes of irradiations all the samples displayed a slight decrease of the heat flow, probably associated to some photodegradation of the materials that form the SPNs.108,109
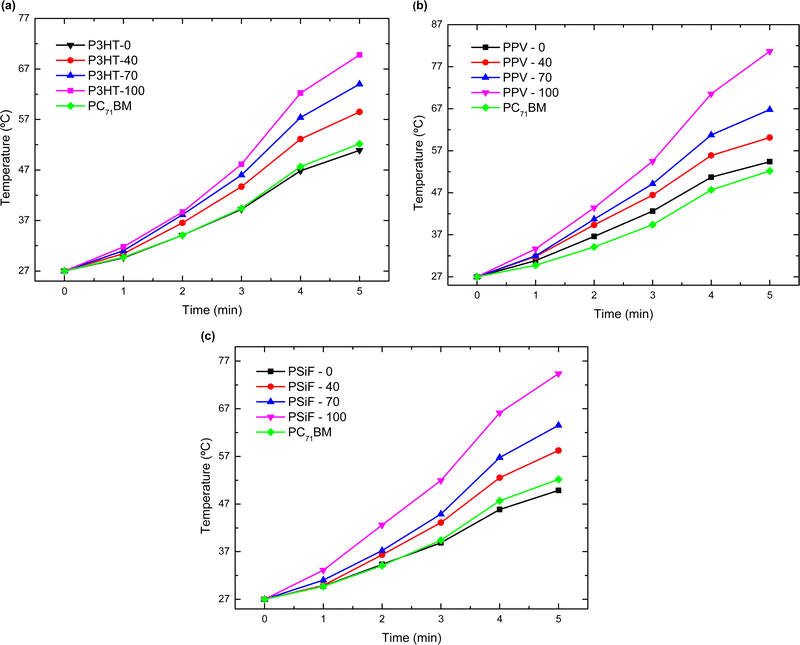
The magnitude of Q generated during the laser illumination is obtained by integrating the curves of Fig. 5. Using eqn (4), the specific heat at 27 °C in Table S2 (ESI†), and the mass of the samples in Table S3 (ESI†), one can then calculate the temperature variation (ΔT) produced by the light excitation after each cycle of laser irradiation. The final temperature (Tf) is obtained by Tf = ΔT + 27 °C (see Fig. 6). After the 5th cycle, the temperature of the solution increases by 1.88-fold for P3HT-0 (final temperature Tf = 50.9 °C), 2.0 fold for PPV-0 (Tf = 54.4 °C), and 1.84-fold for PSiF-0 samples (Tf = 49.8 °C). However, those temperature changes are significantly enhanced with the fullerene doping. After the same duration of laser irradiation, the solution temperature is elevated by 2.5-fold for P3HT-100 (Tf = 69.8 °C), 3.0-fold for PPV-100 (Tf = 80.7 °C), and 2.75-fold for PSiF-100 samples (Tf = 74.4 °C). For comparison, when the aluminum pan was filled only with water, the temperature increased by 3 °C after the 5th cycle of laser illumination. Again, the fullerene doped PPV samples showed the highest temperature variations in agreement with the heat flow measurements of Fig. 5(b).
Table 2 shows the PCE calculated using eqn (5) for Δt = 900 s (15 minutes). The value of α in eqn (5) was found by averaging the time constants of the heat flux decay observed just after switching off the laser. This average considered all cycles and curves of Fig. 5 and gave α = 0.054 ± 0.013 s−1. Fig. S4 (ESI†) exemplifies one fitting of the ensemble used to determine α. In addition, the magnitude of Qsol was assumed to be 2.3 J which is the heat generated when the photothermal procedures (depicted in Section 2.5) are repeated filling the aluminum sample pan only with water.
| Heterojunctions | Photothermal conversion efficiency (η) (%) | |||
|---|---|---|---|---|
| PC71BM weight percentage (%) | ||||
| 0 | 40 | 70 | 100 | |
| P3HT:PC71BM | 47.5 | 59.4 | 65.3 | 66.7 |
| MDMO-PPV:PC71BM | 57.8 | 64.3 | 74.5 | 74.8 |
| PSiF-DBT:PC71BM | 54.1 | 62.2 | 62.2 | 69.5 |
The photothermal efficiencies for polymer-only nanoparticles in Table 2 are comparable with the ones reported for some low-band gap copolymers (around 68%).110 The values of PCE are high (above 50% for the MDMO-PPV and PSIF-DBT systems or close to it for the P3HT SPNs) even in the absence of fullerene doping. Inter-chain interactions (that are especially strong in nanoparticles) might result in a forbidden character of the lowest optical transition of some polymers.111 Consequently, it is expected that most of the excitons undergoes a non-radiative decay under those conditions.111
As observed for other properties reported above, the PCE increases with the fullerene doping to reach a maximum for the samples with 100% PC71BM concentration. This enhancement is higher for the SPNs of P3HT (40%) and MDMO-PPV (29%) and lower for the PSiF-DBT (22%). The efficiency of photo-thermal conversions reached by the PPV-100 nanoparticles are comparable to the ones found in highly efficient systems specifically fabricated to optimize photo-thermal conversion.112
The luminescence quenching displayed in Table 1, the variations in the solution temperature showed in Fig. 6 and the PCE enhancement of Table 2, all coincide well with each other. The amplification of those effects is consistent with the photo-induced electron transfer from the polymer to the acceptor as illustrated in Fig. 2(a) that leads to the loss of luminescence intensity and a corresponding gain in heat generation from non-radiative recombination. In fact, the systems with lower (higher) PL are the systems with higher (lower) values of photothermal PCE. As long-lived triplet excited species produced by intersystem crossing are improbable in polymer/fullerene systems,113 the fluorescence emission from the polymer excitation competes with the non-radiative and radiative recombination from the CT state created after the electron transfer. Hence one can apply the kinetic approaches originally proposed to describe the charge transfer at donor/acceptor heterojunctions of OSCs to understand the results of the photo-thermal measurements. We developed these ideas in the next section.
4.4 Theoretical results
In this section we use calculations based on DFT and TDDFT methods and the kinetic model briefly described in Section 3.1 to assess key features of the donor/acceptor systems considered in the photo-thermal experiments.Fig. 7(a) shows the optimized geometry of the P3HT, MDMO-PPV and PSiF-DBT pentamers used in our DFT and TDDFT calculations. The PSiF-DBT chain is considerably longer than the chain of the other oligomers. In this context, it is important to determine the value of the exciton binding energy (a key parameter to characterize the charge transfer process) that it is not constrained by differences in lengths of the oligomer's chains. Hence, Fig. 7(b) depicts the procedure followed to determine the (1/n) extrapolation of the exciton binding energy (Eb) for those polymers. The value of Eb for very long chains was obtained after fitting a straight line to the values of Eb found for oligomers with 2, 3, 4 and 5 mers. The resulting values are in Table 3. As expected, the internal charge transfer along the PSiF-DBT chain significantly reduces the exciton binding energy compared to the Eb calculated for the other two homopolymers. The higher electron delocalization along the hexagonal rings of the PPV backbone tends to lower Eb relative to the P3HT for finite chains. Yet the difference in the exciton biding energy between these two polymers tends to decrease for longer chains.
| Blends | E b | E b/εb | E b,CT | Q D – Exp. | Q D – Theo. | R CT |
|---|---|---|---|---|---|---|
| a Binding energy of the donor exciton extrapolated to large values of n. b Solid-state exciton binding energy (ε was considered here to be equal to 2). c Adjusted from Eb/ε to best correlate the theoretical quenching with the experimental one for the 100% samples. d Those rates were calculated assuming that the total population of exciton generation in the donor is equal to 1. | ||||||
| P3HT/PC71BM | 2.00 | 1.00 | 0.76 | 85 | 85 | 0.85 |
| MDMO-PPV/PC71BM | 1.72 | 0.86 | 0.86 | 97 | 95 | 0.95 |
| PSiF-DBT/PC71BM | 0.94 | 0.47 | 0.38 | 97.6 | 96 | 0.67 |
Table 3 also shows the exciton biding energy of the CT state (Eb,CT) that is obtained from the fitting of eqn (8) to the experimental quenching efficiencies (QD) in Table 1 (for the samples with 100% fullerene doping). This table also compares the QD found from the PL experiments with the theoretical quenching calculated from eqn (8).
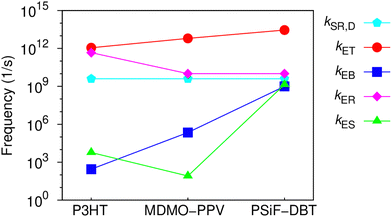
One can see that there is a reasonable agreement between theory and experiment. This result suggests that the strong dielectric stabilization of the two charges forming a CT state is more effective to compensate the coulomb binding of a Frenkel exciton in the solid state for the MDMO-PPV/PC71BM nanoparticles. Consequently, Eb ≈ Eb,CT for this system114 so that the driving force for the CT separation is considerably increased. In contrast, Eb,CT is considerably lower than Eb for the PSiF-DBT/PC71BM system. This indicates that the electron-transfer and separation processes are more effective for the PSiF nanoparticles as can be deduced from the rates in Fig. 8.
Fig. 8 compares the characteristic rates of the processes involved in the charge transfer and recombination at the D/A heterojunction (Fig. 2(a)) for the three systems considered in this work. Fig. S6 (ESI†) shows the diagrams representing the energy levels and magnitudes of transfer rates after donor photoexcitation. Those results confirm that the PSiF-DBT/PC71BM system have the higher rate for charge transfer (kET) which explains the great efficiency of those nanoparticles to quench the PL induced by laser excitation. Indeed, kET tends to be determined by the magnitude of the exciton binding energy in the donor so that it increases when Eb decreases (faster values of kET are essential to enhance QD). Due to higher binding energy of the CT exciton, kES is considerably slower for the MDMO-PPV system compared to the other rates reported in Fig. 8. Consequently, once the CT exciton is formed through the fast electron transfer from the MDMO-PPV to the fullerene, this state is not easily dissociated into free charges.
This feature increases the population of CT excitons and enhance the CT recombination at the D/A interface (RCT) calculated from eqn (4) (last column of Table 3). RCT is then higher for the MDMO-PPV/PC71BM and lower for the PSiF-DBT/PC71BM systems. In the P3HT system, RCT is relatively high due to the contribution of kER. The lower value of ECT at the P3HT/PC71BM heterojunction (see Fig. 1(e)) considerably increased the recombination rate of the CT state for this system.
At this point it is interesting to note that RCT can also be interpreted as the fraction of the excitons created in the donor that are deactivated by recombination of the CT exciton formed at the D/A interface. Following this interpretation, the fact that QD ∼ RCT for the P3HT and the MDMO-PPV systems (see Table 3) indicates that almost all excitons created in those polymers will form CT excitons that ends up by recombining at the D/A heterojunction. On the other hand, QD > RCT for the PSiF-DBT nanoparticles which suggests that a lower fraction of excitons is deactivated using the CT recombination pathway in this system. This result agrees with the fact that a higher fraction of CT excitons can dissociate into free charges at the PSiF-DBT/PC71BM interface compared to the other D/A systems considered here.
4.5 Discussion
The results reported in Sections 4.1, 4.2, and 4.3 indicates that the increase of the photo-thermal effect upon fullerene doping is related to an enhancement of the non-radiative (NR) recombination produced by the decay of the CT excitons formed at the donor/acceptor heterojunction.However, before discussing the results for nanoparticles doped with fullerene, it is important to estimate the rate of NR recombination (kSR,D-NR) for the polymer-only SPNs. The determination of this rate will help us correlate the enhancement of the photothermal conversion produced by the addition of the acceptor with the CT recombination rate found using the kinetic model. Assuming that kSR,D-NR = η·kSR,D, using the values of the PCE in Table 3 for the polymer-only samples and kSR,D = (250 ps)−1, we find that kSR,D-NR is 1.90 × 109 s−1, 2.31 × 109 s−1, and 2.16 × 109 s−1 for the P3HT, MDMO-PPV, and PSiF-DBT, respectively. Hence the MDMO-PPV has the fastest non-radiative recombination rate even in the absence of fullerene.
The NR rate of conjugated polymers/fullerene systems tend to follow the so-called energy-gap (EG) law.115,116 The EG anticipates an exponential enhancement of the probability of non-radiative exciton decay upon decreasing the band gap. This behavior originates from the higher overlap between the excited and the ground state vibrational manifolds. The three polymers considered here have different but very close HOMO–LUMO energy gaps (1.9, 2.2, and 1.8 eV for the P3HT, MDMO-PPV, and PSiF-DBT, respectively, see Fig. 1(e)) so that it is difficult to associate the small variations in the non-radiative recombination rates calculated above with the EG law. Those differences in kSR,D-NR might then derive from a complex interaction of many factors like variations in the rigidity of the molecular structure,115 the degree of exciton delocalization115,117 or changes in the intermolecular interactions determined by the chain packing inside the nanoparticles.117 Those morphological characteristics might affect that ground-state vibrational manifold or the forbidden character of the lowest optical transition.111
Let us now turn to the results for the nanoparticles doped with fullerene. In principle, not every NR decay in those systems occurs by the deactivation of the CT exciton at the D/A heterojunction. The exciton can either recombine before reaching the heterojunction (which decreases QD) or dissociate into free charges after forming the CT state (which decreases RCT). Hence, assuming that QD quantifies the proportion of exciton that effectively reach the heterojunction and are able to form the CT state, we propose that the non-radiative recombination rate of the CT state is weighted by the ratio between RCT and QD in the form
| kER-NR = (RCT/QD)·η·kER, | (10) |
Using eqn (10), the data in Table 3 and the kER rates of Fig. 8, kER-NR is 3.1 × 1011 s−1, 7.4 × 109 s−1, and 4.8 × 109 s−1 for the P3HT, MDMO-PPV, and PSiF-DBT, respectively. Since the NR rates from eqn (10) are higher compared to the NR rates for polymer-only SPNs (kER-NR > kSR,D-NR), it is then clear why the fullerene doping enhance the photo-thermal effect. kER-NR is more than two orders of magnitude faster than kSR,D-NR for the P3HT system which is in qualitative agreement with the greater enhancement of η between the P3HT-0 and the P3HT-100 samples. As mentioned above, the higher value of kER-NR for the P3HT/PC71BM nanoparticles is a direct consequence of lower value of the effective gap (Ecs = HOMOD – LUMOA) at this heterojunction.115 Despite the greater increase of η for the P3HT system, the nanoparticles of MDMO-PPV/PC71BM are the most efficient to generate heat upon laser excitation. The main reason behind this better performance of the PPV system lies in the fact that it has a faster electron transfer rate (kET) than the P3HT system. Consequently, the PPV/fullerene sample is more efficient to quench the excitons. In addition, the slower rate for charge separation (kES) at the PPV/fullerene heterojunction (see Fig. 8) increases the CT population which enhances RCT. This system is efficient to form CT excitons by the electron transfer from the polymer to the acceptor but is not efficient to dissociate them. Thus, most of the CT excitons ends up by being deactivated using the NR recombination pathway.
One important morphological factor that might contribute to the strong quenching observed for the PPV-100 samples is the shorter diameter of those nanoparticles compared to the SPNs of the other systems (see Fig. 3(c) above). Since the excitons diffusion length is around 10 nm, the reduced volume of those SPNs increases the probability that excitons created in the polymer will be able to reach the D/A heterojunction. On the other hand, after the formation of the CT state, the proximity between the electron (in the donor) and the hole (in the acceptor) tends to increase the Coulomb attraction between them. The smaller size effect can then further decrease the kES rate and favors the electron–hole recombination. It also tends to reduce the average mass of PPV-based nanoparticles compared the other systems. All those features contribute to explain the higher temperatures reached by the SPNs of MDMO-PPV/PC71BM after laser excitation.
A recent study involving a large data set of published and new material combinations of donor/fullerene heterojunctions for organic solar cells found that non-radiative voltage losses decrease with increasing ECT.58,118 This trend was in accordance with the inverted Marcus regime for non-radiative transition rates in organic donor/acceptor systems and is related to vibrational overlap between the wave functions of the CT and ground states (see discussion below).58 In principle those results could be described by assuming an effective EG law of non-radiative voltage losses:118
| kET-NR ∝ exp(−γECT), | (11) |
Inspired in Fig. 2(b), one can assume that a better approximation to ECT is ECT* = Ecs − Eb,CT. From the data in Fig. 1(e) and Table 3, ECT* is 0.54, 0.64 and 1.1 eV for the P3HT, MDMO-PPV and PSiF-DBT systems, respectively. Consequently, the values of kET-NR estimated above are in qualitative agreement with the trend reported in ref. 58 (eqn (11)) so that the NR rate decreases with increasing ECT*. In fact, the ratio between the NR rates for the PPV-100 and P3HT-100 samples calculated applying eqn (10) is kPPVER-NR/kP3HTER-NR ≈ 42. On the other hand, if one assumes that γ = (kT)−1 at room temperature in eqn (11), the ratio between those rates is exp[−γ(EP3HTCT − EPPVCT)] ≈ 47. Hence, the NR rates obtained from the application of the kinetic model and eqn (10) are in reasonable accordance with the EG law expressed in eqn (11).
However, the agreement between the kinetic model and eqn (11) fails for the PSiF-DBT system. The reason behind this deviation lies in the small energy shift between the LUMO of the polymer and the LUMO of the fullerene (ΔELUMO). For the PSiF-DBT/PC71BM system, ΔELUMO ≈ 0.3 eV which tends to decrease the energy difference between the local excited state of the donor (LE) and the CT state (ΔELE-CT). It was found that when ΔELE-CT ≤ 0.3 eV the effective EG law starts to fail for the polymer/fullerene blends since the non-radiative rate becomes dominated by the thermal population of the LE state.118
Recently some studies have evidenced the important role played by high frequency molecular modes on the intrinsic voltage loss in donor/acceptor OSCs.119 Under those circumstances the use of the simple Marcus theory is questionable since it can underestimate the NR rates. Considering a simplified two state model that involves only the CT and ground states, indeed the NR rate from the relaxed CT to a vibrationally excited ground state is proportional to the vibrational overlap between the wave functions of the two electronic configurations.58 However, the influence of this overlap on kER-NR becomes less important with increasing ECT. The systems studied here have ΔELUMO higher than 0.3 eV. In addition, when the reorganization energy is subtracted from ECT in eqn (7) (as it was done here), the rates calculated using the simple Marcus theory are similar to more sophisticated approaches like the Marcus–Levich–Jortner model.58
Finally, as an additional insight, our results can anticipate the non-radiative voltage loss (ΔVnr) of the blends under consideration. This parameter is important to gauge the photovoltaic properties of the OSCs active layer. ΔVnr is related to the external electroluminescent quantum efficiency (EQEEL) by ΔVnr = −(1/eγ)ln(EQEEL), where EQEEL depends on the radiative and non-radiative recombination rates so that EQEEL ∝ kER-R/(kER-NR + kER-R). Consequently, ΔVnr increases when kER-NR increases. If one assumes that the NR recombination is dominant over the radiative recombination at the heterojunction, we anticipate a higher open voltage loss for the P3HT/fullerene blend since kP3HTER-NR > kPPVER-NR > kPSiFER-NR. Table S5 of the ESI† surveys the values of Voc and Ecs reported in the literature for OSCs using the blends of the polymers considered here with PC61BM (the data reported in the literature for this fullerene is more abundant than the data for blends with PC71BM). We believe that the polymer/PC61BM heterojunctions retains photophysical characteristics of the polymer/PC71BM systems. The parameters showed in Table S5 (ESI†) were measured for different research groups around the world involving 24, 22, and 4 devices fabricated using the P3HT/PC61BM, MDMO-PPV/PC61BM, and PSiF/PC61BM blends, respectively. The voltage loss obtained averaging all those results is 0.71 V (P3HT), 0.66 V (MDMO-PPV), and 0.62 V (PSiF-DBT) which corresponds to the sequence of magnitudes of kER-NR derived from our analysis.
5. Nanoparticle biocompatibility: preliminary study
SPNs are considered functional nanomaterials and have a wide range of applications in different fields. Their biomedical applications are being explored specially in diseases with limited therapy efficacy, such as cancers, as photo-therapeutic agents. However, promising outcomes as therapeutic or theragnostic agents, likewise any other biomaterial, SPNs biocompatibility is crucial to the intended use. Regarding biological investigation, in vitro cytotoxicity determination is considered a gold standard to screen new therapeutic agents, biological devices, or any other material with biomedical intended use. Neutral red uptake by murine fibroblasts (Balb/3T3 cloneA31) cultivated in vitro is the main test used in this context and has been validated and standardized for this purpose by several different organizations (such as the International Organization for Standardization – ISO, the National Toxicology Program (NTP)), the Interagency Center for the Evaluation of Alternative Toxicological Methods (NICEATM), the European Centre for the Validation of Alternative Methods [ECVAM].120,121 Therefore, this methodology using this cell line was employed in this work to determine MDMO-PPV/PC71BM nanoparticles biocompatibility by screening a wide range of nanoparticles concentration (from nanograms to micrograms). Considering these nanoparticles prospective applicability in cancer therapy, we have also tested their cytotoxic effects on a highly metastatic murine melanoma cell line (B16-F10). Toxicity often leads to metabolic cells failure consequently driving to changes in cells morphology and attachment. In this context, we have also investigated MDMO-PPV/PC71BM nanoparticles effects on cell culture by comparing the cell density after treatment with cells that were not exposed to these nanoparticles. Four independent experiments for each cell line and methodology were run and concentrations that reduced 30% the viability were considered cytotoxic, as defined by ISO 10993-5:2009. Outlier data was evaluated by statistical tests, but no outliers were identified, demonstrating experimental reproducibility. Therefore, encouraged by our results, we performed initial biocompatibility experiments using MDMO-PPV/PC71BM with 1:1 fullerene (w/w%) (ESI,† 9). As observed in the Fig. S7 (ESI†), concentrations up to 30 μg ml−1 in biological protein-rich environment were not considered cytotoxic per se neither to fibroblasts nor to melanoma cells. Taken all the results together we can assume that this range of concentrations are good starting points to further testing, especially considering that one desirable characteristic is to avoid normal tissue damage induced by cytotoxicity. Nevertheless, there was a clear concentration-dependent tendency to decrease melanoma cells viability that was not observed to fibroblasts.The results indicate that these SPNs might have dual activity when combining laser application to their intrinsic effects to melanoma, and investigation of the physical processes that correlates PL quenching with PT effect in polymer/fullerene semiconducting nanoparticles in cellular environment deserves further investigation.
6. Concluding remarks
Semiconductive polymers nanoparticles (SPNs) with increasing fullerene (PC71BM) doping were produced and analyzed to determine photothermal efficiency and photoluminescence quenching. Our results clearly evidenced an increasing negative correlation between these two phenomena with doping. This negative correlation was observed to SPNs synthetized using different polymer types: two homopolymers (P3HT and MDMO-PPV) and one donor–acceptor copolymer (PSiF-DBT). P3HT/PC71BM and PSiF-DBT/PC71BM with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 fullerene (w/w%) nanoparticles showed a photothermal energy conversion efficiency of η ≈ 66.7% and 69.5%, respectively, which are typical values for conjugated systems.25,110 Meanwhile, MDMO-PPV/PC71BM with 1
1 fullerene (w/w%) nanoparticles showed a photothermal energy conversion efficiency of η ≈ 66.7% and 69.5%, respectively, which are typical values for conjugated systems.25,110 Meanwhile, MDMO-PPV/PC71BM with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 fullerene (w/w%) showed the highest photothermal energy conversion efficiency (η ≈ 74.8%). The negative correlation between the PT effect and the PL quenching (upon the fullerene doping) are produced by the photoinduced electron transfer from the donor to the acceptor to generate CT states. The fluorescence emission from polymer would then compete with the non-radiative and radiative recombination of CT excitons. As a general conclusion we found that the enhancement of the PT effect upon doping happens because the rate of non-radiative recombination of singlet excitons in the donor is slower than the deactivation NR rate of the CT states. Since we observed that these NR rates tend to follow an energy gap law,119 the improvement of the NR recombination through the CT pathway would be produced by a stronger vibrational overlap between the CT state and the ground state when ECT decreases.
1 fullerene (w/w%) showed the highest photothermal energy conversion efficiency (η ≈ 74.8%). The negative correlation between the PT effect and the PL quenching (upon the fullerene doping) are produced by the photoinduced electron transfer from the donor to the acceptor to generate CT states. The fluorescence emission from polymer would then compete with the non-radiative and radiative recombination of CT excitons. As a general conclusion we found that the enhancement of the PT effect upon doping happens because the rate of non-radiative recombination of singlet excitons in the donor is slower than the deactivation NR rate of the CT states. Since we observed that these NR rates tend to follow an energy gap law,119 the improvement of the NR recombination through the CT pathway would be produced by a stronger vibrational overlap between the CT state and the ground state when ECT decreases.
Yet other conclusions (that links the PT effect with the PL and PV effects) can be derived from our analysis.
(i) Since the driving forces for electron transfer are similar in the systems under study, it was found that the PL quenching is essentially determined by the binding energy of the singlet exciton in polymer. Since Eb is higher for the P3HT system, the SPNs of this polymer showed a lower PL quenching (85%) when compared to the quenching measured for the MDMO-PPV (95%) and PSiF-DBT (96%) systems.
(ii) Once the CT exciton is formed, its recombination or dissociation into free charges is mainly determined by the binding energy of the CT exciton (Eb,CT). Eb,CT is stronger for the MDMO-PPV system and weakest for the PSiF-DBT system. Hence, the PSiF-DBT SPNs are more effective to convert CT excitons into free charges (which favors the PV effect) compared to the other nanoparticles. In the MDMO-PPV systems, most of the CT excitons end up by recombining. This is the basic reason behind the high value of η for MDMO-PPV/PC71BM nanoparticles.
(iii) The P3HT/PC71BM nanoparticle has the highest non-radiative recombination rate of the CT state among the systems studied. Due to the low ECT, the kP3HTER-NR is almost two orders of magnitude faster than the NR recombination of the donor's singlet. This variation explains the greatest improvement of η observed for the P3HT system with the fullerene doping.
(iv) The analysis developed here using PL and PT experiments together with a kinetic theory and quantum chemistry simulations gives results that are consistent with the magnitude of the PV loss observed in OSCs. This result reasserts that those effects in D/A heterojunctions are intrinsically related to the fast electron transfer between the donor and the acceptor to form CT states.
We finally conclude that the combination of optical and thermal analysis with a simple theoretical model describing the kinetic of charge dissociation at the heterojunction (together with quantum chemistry calculations) is a powerful approach to characterize the recombination process in donor/acceptor systems. This method can be useful in the quest for more efficient organic solar cells or organic nanoparticles aiming at photothermal applications like PT therapy.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work has been partially supported by research and technological development program of the Companhia Paranaense de Energia – COPEL, through the PD2866-0470/2017 project, regulated by ANEEL. This study was also financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior-Brasil (CAPES)-Finance Code 001, PROAP/PPGBCM-UFPR and student's fellowships. Special thanks go to CAPES-PrInt-UFPR, CNPq (grant 381113/2021-3) and to LCNano/SisNANO 2.0 (grant 442591/2019-5) for financial support UFPR/PRPG – research financial support (grant approved on 04/2018 UFPR/PRPPG “Apoio a atividades de pesquisa” call). The authors would like to thank Dr Lucelia Donatti for experimental support on spectrophotometer use and LabCet (ICC/Fiocruz) for kindly providing the BALB/3T3 cells. MK specially thanks CNPq (grant 310251/2021-4), Profs. Evaldo Ribeiro, Prof. Dante H. Mosca, and Tecpar for the use of the DSC.References
- Y. Li, W. Huang and D. Zhao, et al., Recent Progress in Organic Solar Cells: A Review on Materials from Acceptor to Donor, Molecules, 2022, 27(6), 1800 CrossRef CAS PubMed.
- S. S. Grewal and W. O. Tatum, Laser thermal ablation in epilepsy, Expert Rev. Neurother., 2019, 19(12), 1211–1218 CrossRef CAS PubMed.
- A. Carmignani, M. Battaglini, E. Sinibaldi, A. Marino, V. Vighetto, V. Cauda and G. Ciofani, In Vitro and Ex Vivo Investigation of the Effects of Polydopamine Nanoparticles Size on Their Antioxidant and Photothermal Properties: Implications for Biomedical Applications, ACS Appl. Nano Mater., 2022, 5(1), 1702–1713 CrossRef CAS.
- W. Faubel, S. Heissler, U. Pyell and N. Ragozina, Photothermal trace detection in capillary electrophoresis for biomedical diagnostics and toxic materials (invited), Rev. Sci. Instrum., 2003, 74, 491–494 CrossRef CAS.
- E. Smela, Conjugated Polymer Actuators for Biomedical Applications, Adv. Mater., 2003, 15(6), 481–494 CrossRef CAS.
- B. Han, Y.-L. Zhang, Q.-D. Chen and H.-B. Sun, Carbon-Based Photothermal Actuators, Adv. Funct. Mater., 2018, 28, 1802235 CrossRef.
- T. S. Kao, S. D. Jenkins, J. Ruostekoski and N. I. Zheludev, Coherent control of nanoscale light localization in metamaterial: creating and positioning isolated subwavelength energy hot spots, Phys. Rev. Lett., 2011, 106(8), 085501 CrossRef CAS PubMed.
- J.-D. Xiao and H.-L. Jiang, Metal–Organic Frameworks for Photocatalysis and Photothermal Catalysis, Acc. Chem. Res., 2019, 52, 356–366 CrossRef CAS PubMed.
- D. T. Nga, A. D. Phan, V. D. Lam, L. M. Woods and K. Wakabayashi, Enhanced solar photothermal effect of PANi fabrics with plasmonic nanostructures, RSC Adv., 2020, 10, 28447–28453 RSC.
- P. Pallavicini, G. Chirico and A. Taglietti, Harvesting Light to Produce Heat: Photothermal Nanoparticles for Technological Application and Biomedical Devices, Chem. – Eur. J., 2021, 27, 15361–15374 CrossRef CAS PubMed.
- K. Yang, L. Hu, X. Ma, S. Ye, L. Cheng, X. Shi, C. Li, Y. Li and Z. Liu, Multimodal Imaging Guided Photothermal Therapy using Functionalized Graphene Nanosheets Anchored with Magnetic Nanoparticles, Adv. Mater., 2012, 24, 1868–1872 CrossRef CAS PubMed.
- K. Yang, J. Wan, S. Zhang, B. Tian, Y. Zhang and Z. Liu, The influence of surface chemistry and size of nanoscale graphene oxide on photothermal therapy of cancer using ultra-low laser power, Biomaterials, 2012, 33, 2206–2214 CrossRef CAS PubMed.
- J. Sun, M. Guo, H. Pang, J. Qi, J. Zhang and Y. Ge, Treatment of malignant glioma using hyperthermia, Neural Regener. Res., 2013, 8, 2775–2782 Search PubMed.
- L. C. Kennedy, L. R. Bickford, N. A. Lewinski, A. J. Coughlin, Y. Hu, E. S. Day, J. L. West and R. A. Drezek, A New Era for Cancer Treatment: Gold Nanoparticle-Mediated Thermal Therapies, Small, 2011, 7, 169–183 CrossRef CAS PubMed.
- J. Liu, J. Geng, L.-D. Liao, N. Thakor, X. Gao and B. Liu, Conjugated polymer nanoparticles for photoacoustic vascular imaging, Polym. Chem., 2014, 5, 2854–2862 RSC.
- T. F. Abelha, C. A. Dreiss, M. A. Green and L. A. Dailey, Conjugated polymers as nanoparticle probes for fluorescence and photoacoustic imaging, J. Mater. Chem. B, 2020, 8, 592–606 RSC.
- M. Ling, R. Sun and G. Li, et al., NIR-II emissive dye based polymer nanoparticle targeting EGFR for oral cancer theranostics, Nano Res., 2022, 15, 6288–6296 CrossRef CAS.
- L. Wu, S. Fang, S. Shi, J. Deng, B. Liu and L. Cai, Hybrid polypeptide micelles loading indocyanine green for tumor imaging and photothermal effect study, Biomacromolecules, 2013, 14, 3027–3033 CrossRef CAS PubMed.
- X. Y. Yang, et al., Functional Black Phosphorus Nanosheets for Mitochondria-Targeting Photothermal/Photodynamic Synergistic Cancer Therapy, Chem. Sci., 2019, 10, 3779–3785 RSC.
- B. Zhou, Y. Li, G. Niu, M. Lan, Q. Jia and Q. Liang, Near-Infrared Organic Dye-Based Nanoagent for the Photothermal Therapy of Cancer, ACS Appl. Mater. Interfaces, 2016, 8(44), 29899–29905 CrossRef CAS PubMed.
- H. S. Jung, P. Verwilst, A. Sharma, J. Shin, J. L. Sessler and J. S. Kim, Organic Molecule-Based Photothermal Agents: An Expanding Photothermal Therapy Universe, Chem. Soc. Rev., 2018, 47, 2280–2297 RSC.
- H. S. Han, et al., Gold-Nanoclustered Hyaluronan Nano-Assemblies for Photothermally Maneuvered Photodynamic Tumor Ablation, ACS Nano, 2016, 10, 10858–10868 CrossRef CAS PubMed.
- F. Liu, X.-D. Wang and S.-Y. Du, Production of gold/silver doped carbon nanocomposites for effective photothermal therapy of colon cancer, Sci. Rep., 2020, 10, 7618 CrossRef CAS PubMed.
- L. G. Xu, L. Cheng, C. Wang, R. Peng and Z. Liu, Conjugated Polymers for Photothermal Therapy of Cancer, Polym. Chem., 2014, 5, 1573–1580 RSC.
- H. Sun, F. Lv, L. Liu, Q. Gu and S. Wang, Conjugated Polymer Materials for Photothermal therapy, Adv. Ther., 2018, 1(6), 1800057 CrossRef.
- Y. Wang, H.-M. Meng, G. Song, Z. Li and X.-B. Zhang, Conjugated-Polymer-Based Nanomaterials for Photothermal Therapy, ACS Appl. Polym. Mater., 2020, 2(10), 4258–4272 CrossRef CAS.
- S. S. Kelkar, et al., Dual wavelength stimulation of polymeric nanoparticles for photothermal therapy, Lasers Surg. Med., 2016, 48, 893–902 CrossRef PubMed.
- J. B. Vines, D.-J. Lim and H. Park, Contemporary Polymer-Based Nanoparticle Systems for Photothermal Therapy, Polymers, 2018, 10(12), 1357–1372 CrossRef PubMed.
- H. Zhang, et al., Dual-Mode Antibacterial Conjugated Polymer Nanoparticles for Photothermal and Photodynamic Therapy, Macromol. Biosci., 2020, 20, 1900301 CrossRef CAS PubMed.
- F. Lin, Q.-Y. Duan and F.-G. Wu, Conjugated Polymer-Based Photothermal Therapy for Killing Microorganisms, ACS Appl. Polym. Mater., 2020, 2(10), 4331–4344 CrossRef CAS.
- Y. Wang, S. Li, L. Liu and L. Feng, Phothothermal-Responsive Conjugated Polymer Nanoparticles for the Rapid and Effective Killing of Bacteria, ACS Appl. Bio Mater., 2018, 1(1), 27–32 CrossRef CAS.
- Y. Lyu, Semiconducting Polymer Nanobioconjugates for Targeted Photo-thermal Activation of neurons, J. Am. Chem. Soc., 2016, 138(29), 9049–9052 CrossRef CAS PubMed.
- N. A. D. Yamamoto, M. E. Payne, M. Koehler, A. Facchetti, L. S. Roman and A. C. Arias, Charge transport model for photovoltaic devices based on printed polymer: Fullerene nanoparticles, Sol. Energy Mater. Sol. Cells, 2015, 141, 171–177 CrossRef CAS.
- P. Chen, et al., Facile syntheses of conjugated polymers for phototermal tumour therapy, Nat. Commun., 2019, 10, 1192–1201 CrossRef PubMed.
- Z. Zeglio, et al., Conjugated Polymers for Assessing and Controlling Biological Functions, Adv. Mater., 2019, 31, 1806712 CrossRef PubMed.
- L. Xiao, et al., Recent Advances in Polymer-Based Photothermal materials for Biological Applications, ACS Appl. Polym. Mater., 2020, 2(10), 4273–4288 CrossRef CAS.
- B. Guo, et al., Molecular Engineering of Conjugated Polymers for Biocompatible Organic Nanoparticles with Highly Efficient Photoacoustic and Photothermal Performance in Cancer Theranostics, ACS Nano, 2017, 11(10), 10124–10134 CrossRef CAS PubMed.
- Y. Lyu and K. Y. Pu, Recent Advances of Activatable Molecular Probes Based on Semiconducting Polymer Nanoparticles in Sensing and Imaging, Adv. Sci., 2017, 4, 1600481 CrossRef PubMed.
- H.-J. Jang, et al., Suppression of Ionic Doping by Molecular Dopants in Conjugated Polymers for Improving Specificity and Sensitivity in Biosensing Applications, ACS Appl. Mater. Interfaces, 2020, 12(40), 45036–45044 CrossRef CAS PubMed.
- J. Liu, et al., Conjugated polymer nanoparticles for photoacoustic vascular imaging, Polym. Chem., 2014, 5, 2854–2862 RSC.
- Y. Lyu and K. Pu, Recent Advances of Activable Molecular Probes Based on Semiconducting Polymer Nanoparticles in Sensing and Imaging, Adv. Sci., 2017, 4(6), 1600481 CrossRef PubMed.
- Z. Lu, Z. Zhang and Y. Tang, Conjugated Polymers-Based Thermal-Responsive Nanoparticles for Controlled Drug Delivery, Tracking, and Synergistic Photodynamic Therapy/Chemotherapy, ACS Appl. Bio Mater., 2019, 2(10), 4485–4492 CrossRef CAS PubMed.
- S. Sarkar and N. Levi-Polyachenko, Conjugated Polymer nano-systems for hyperthermia, imaging and drug delivery, Adv. Drug Delivery Rev., 2020, 163–164, 40–64 CrossRef CAS PubMed.
- Z. Zhang, et al., ROS-Responsive and active targeted drug delivery based on conjugated polymer nanoparticles for synergistic chemo-/photodynamic therapy, J. Mater. Chem. B, 2021, 9, 2240–2248 RSC.
- G. Feng, et al., Multifunctional Conjugated Polymer Nanoparticles for Image-Guided Photodynamic and Photothermal Therapy, Small, 2017, 13, 1602807 CrossRef PubMed.
- M. Doshi, A. Copik and A. J. Gesquiere, Development and characterization of conducting polymer nanoparticles for photodynamic therapy in vitro, Photodiagn. Photodyn. Ther., 2015, 12, 476–489 CrossRef CAS PubMed.
- Q. Jia, Q. Song and W. Huang, Rejuvenated Photodynamic Therapy for Bacterial Infections, Adv. Healthcare Mater., 2019, 8, 1900608 CrossRef PubMed.
- J. Li, et al., Near-Infrared Photoactivatable Semiconducting Polymer Nanoblockaders for Metastasis-inhibited Combination Cancer Therapy, Adv. Mater., 2019, 31, 1905091 CrossRef CAS PubMed.
- X. Shen, et al., Water-Soluble Conjugated Polymers for Simultaneous Two-Photon Cell Imaging and Two-Photon Photodynamic Therapy, Adv. Opt. Mater., 2013, 1, 92–99 CrossRef.
- F. A. Monge, et al., Highly Effective Inactivation of SARS-CoV-2 by Conjugated Polymers and Oligamers, ACS Appl. Mater. Interfaces, 2020, 12(50), 55688–55695 CrossRef CAS PubMed.
- C. M. MacNeill, E. G. Graham and N. H. Levi-Polyachenko, Soft template synsthesis of donor–acceptor conjugated polymer nanoparticles: structural effects, stability, and photothermal studies, J. Polym. Sci., Part A: Polym. Chem., 2014, 52, 1622–1632 CrossRef CAS.
- J. Li, J. Rao and K. Pu, Recent progress on semiconducting polymer nanoparticles for molecular imaging and cancer phototherapy, Biomaterials, 2018, 155, 217–235 CrossRef CAS PubMed.
- J. Zhang, et al., Biocompatible semiconducting polymer nanoparticles as robust photoacoustic and photothermal agents revealing the effects of chemical structure on high photothermal conversion efficiency, Biomaterials, 2018, 181, 92–102 CrossRef CAS PubMed.
- J. Geng, et al., Biocompatible Conjugated Polymer Nanoparticles for Efficient Photothermal Tumor Therapy, Small, 2015, 11, 1603–1610 CrossRef CAS PubMed.
- D. Jaque, et al., Nanoparticles for photothermal therapies, Nanoscale, 2014, 6, 9494–9530 RSC.
- L. Benatto, M. de, J. Bassi, L. C. W. Menezes, L. S. Roman and M. Koehler, Kinetic model for photoluminescence quenching by selective excitation of D/A blends: implications for charge separation in fullerene and non-fullerene organic solar cells, J. Mater. Chem. C, 2020, 8, 8755–8769 RSC.
- F. Liu, L. Zhou and W. Liu, et al., Organic Solar Cells with 18% Efficiency Enabled by an Alloy Acceptor: A Two-in-One Strategy, Adv. Mater., 2021, 33, 2100830 CrossRef CAS PubMed.
- J. Benduhn, et al., Intrinsic non-radiative voltage losses in fullerene-based organic solar cells, Nat. Energy, 2017, 2, 17053–17058 CrossRef CAS.
- Y. Lyu, et al., Intraparticle Molecular Orbital Engineering of Semiconducting Polymer Nanoparticles as Amplified Theranostics for In Vivo Photoacoustic Imaging and Photothermal Therapy, ACS Nano, 2016, 10(4), 4472–4481 CrossRef CAS PubMed.
- L. Valentini, M. Cardinali, M. Mladjenovic, P. Uskokovic, F. Alimenti, L. Roseli and J. Kenny, Flexible transistors exploiting P3HT on paper substrates and graphene oxide films as gate dielectrics: proof of concept, Sci. Adv. Mater., 2013, 5, 1–4 CrossRef.
- W. Hou, L. Gao, Y.-M. Tian, W.-Q. Yan, Y.-X. Hou, J. Li and G.-Y. Zhoung, Stress-induced variation of MDMO-PPV film thickness and resistance, Synth. Met., 2017, 226, 113–118 CrossRef CAS.
- Y. Garcia-Basabe, C. F. N. Marchiori, B. G. A. L. Borges, N. A. D. Yamamoto, A. G. Macedo, M. Koehler, L. S. Roman and M. L. M. Rocco, Electronic structure, molecular orientation, charge transfer dynamics and solar cells performance in donor/acceptor copolymers and fullerene: Experimental and theoretical approaches, J. Appl. Phys., 2014, 115, 134901 CrossRef.
- T. Umeyama, S. Shibata, T. Miyata, K. Igarashi, T. Koganezawa and H. Imahori, Regioisomer effects of [70]PCBM on film structures and photovoltaic properties of composite films with a crystalline conjugated polymer P3HT, RSC Adv., 2017, 7(72), 45697–45704 RSC.
- H. Fessi, et al., Nanocapsule formation by interfacial polymer deposition following solvent displacement, Int. J. Pham., 1989, 55(1), R1–R4 CrossRef CAS.
- S. Wang, A. Singh, N. Walsh and G. Redmond, Surfactant-free, low band gap conjugated polymer nanoparticles and polymer:fullerene nanohybrids with potential for organic photovoltaics, Nanotechnology, 2016, 27, 245601 CrossRef PubMed.
- B. Wunderlich, M. Pyda, J. Pak and R. Androsch, Measurement of heat capacity to gain information about time scales of molecular motion from pico to megaseconds, Thermochim. Acta, 2001, 377(1–2), 9–33 CrossRef CAS.
- ASTM E1269-11, Standard Test Method for Determining Specific Heat Capacity by Differential Scanning Calorimetry, ASTM International, West Conshohocken, PA, 2018, http://www.astm.org Search PubMed.
- H. Hao, Y. Zhang and X. Chen, Investigation on specific heat capacity and thermal behavior of sodium hydroxyethyl sulfonate, Chin. J. Chem. Eng., 2017, 25(3), 319–323 CrossRef CAS.
- International Organization for Standardization, “Plastics – Differential scanning Calorimetry (DSC) – Part 4: Determination of specific heat capacity”, (ISO 11357-4:2014), (Beuth Verlag, Berlin, 2014).
- M. A. Ryumin, et al., Heat Capacity and Thermodynamic Functions of La2Sn2O7, Inorg. Mater., 2020, 56, 97–104 CrossRef CAS.
- T. Panda and P. Naumov, Time-Dependent Photodimerization of α-trans-Cinnamic Acid Studied by Photocalorimetry and NMR Spectroscopy, Cryst. Growth Des., 2018, 18(5), 2744–2749 CrossRef CAS.
- N. Sahadev and A. A. Anappara, Enhanced photothermal effect in reduced graphene oxide in solid-state, J. Appl. Phys., 2017, 122, 185103 CrossRef.
- J. O. Hill, For Better Thermal Analysis and Calorimetry, ICTAC, 3rd edn, 1991, p. 93 Search PubMed.
- V. P. Pattani and J. W. Tunnel, Nanoparticle-mediated photothermal therapy: a comparative study of heating for different particle types, Lasers Surg. Med., 2012, 44(8), 675–684 CrossRef PubMed.
- A. Weu, T. R. Hopper, V. Lami, J. A. Kreß, A. A. Bakulin and Y. Vaynzof, Field-Assisted Exciton Dissociation in Highly Efficient PffBT4T-2OD:Fullerene Organic Solar Cells, Chem. Mater., 2018, 30(8), 2660–2667 CrossRef CAS.
- J. Kern, S. Schwab, C. Deibel and V. Dyakonov, Binding Energy of Singlet Excitons and Charge Transfer Complexes in MDMO-PPV: PCBM Solar Cells, Phys. Status Solidi RRL, 2011, 5(10–11), 364–366 CrossRef CAS.
- M. Gerhard, A. P. Arndt, M. Bilal, U. Lemmer, M. Koch and I. A. Howard, Field-Induced Exciton Dissociation in PTB7-Based Organic Solar Cells, Phys. Rev. B, 2017, 95(19), 195301 CrossRef.
- L. Benatto, C. A. M. Moraes, M. D. J. Bassi, L. Wouk, L. S. Roman and M. Koehler, Kinetic Modeling of the Electric Field Dependent Exciton Quenching at the Donor–Acceptor Interface, J. Phys. Chem. C, 2021, 125(8), 4436–4448 CrossRef CAS.
- Z. Cao, S. Yang, B. Wang, X. Shen, G. Han and Y. Yi, Multi-Channel Exciton Dissociation in D18/Y6 Complexes for High-Efficiency Organic Photovoltaics, J. Mater. Chem. A, 2020, 8(39), 20408–20413 RSC.
- G. Zhou, M. Zhang, Z. Chen, J. Zhang, L. Zhan, S. Li, L. Zhu, Z. Wang, X. Zhu and H. Chen, et al., Marcus Hole Transfer Governs Charge Generation and Device Operation in Nonfullerene Organic Solar Cells, ACS Energy Lett., 2021, 6(8), 2971–2981 CrossRef CAS.
- A. J. Ward, A. Ruseckas, M. M. Kareem, B. Ebenhoch, L. A. Serrano, M. Al-Eid, B. Fitzpatrick, V. M. Rotello, G. Cooke and I. D. W. Samuel, The Impact of Driving Force on Electron Transfer Rates in Photovoltaic Donor–Acceptor Blends, Adv. Mater., 2015, 27(15), 2496–2500 CrossRef CAS PubMed.
- K. Do, Q. Saleem, M. K. Ravva, F. Cruciani, Z. Kan, J. Wolf, M. R. Hansen, P. M. Beaujuge and J. L. Brédas, Impact of Fluorine Substituents on π-Conjugated Polymer Main-Chain Conformations, Packing, and Electronic Couplings, Adv. Mater., 2016, 28(37), 8197–8205 CrossRef CAS PubMed.
- S. D. Dimitrov, B. C. Schroeder, C. B. Nielsen, H. Bronstein, Z. Fei, I. McCulloch, M. Heeney and J. R. Durrant, Singlet Exciton Lifetimes in Conjugated Polymer Films for Organic Solar Cells, Polymers, 2016, 8(1), 14 CrossRef PubMed.
- J.-L. Bredas, Mind the Gap!, Mater. Horiz., 2014, 1(1), 17–19 RSC.
- L. Benatto and M. Koehler, Effects of Fluorination on Exciton Binding Energy and Charge Transport of π-Conjugated Donor Polymers and the ITIC Molecular Acceptor: A Theoretical Study, J. Phys. Chem. C, 2019, 123(11), 6395–6406 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Long-Range Corrected Hybrid Density Functionals with Damped Atom–Atom Dispersion Corrections, Phys. Chem. Chem. Phys., 2008, 10(44), 6615–6620 RSC.
- Z. Zheng, J.-L. Brédas and V. Coropceanu, Description of the Charge Transfer States at the Pentacene/C60 Interface: Combining Range-Separated Hybrid Functionals with the Polarizable Continuum Model, J. Phys. Chem. Lett., 2016, 7(13), 2616–2621 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Function, Theor. Chem. Acc., 2008, 120(1–3), 215–241 Search PubMed.
- L. C. W. Menezes, Y. Jin, L. Benatto, C. Wang, M. Koehler, F. Zhang and L. S. Roman, Charge Transfer Dynamics and Device Performance of Environmentally Friendly Processed Non-Fullerene Organic Solar Cells, ACS Appl. Energy Mater., 2018, 1(9), 4776–4785 Search PubMed.
- L. Benatto, C. F. N. Marchiori, C. M. Araujo and M. Koehler, Molecular Origin of Efficient Hole Transfer from Non-Fullerene Acceptors: Insights from First-Principles Calculations, J. Mater. Chem. C, 2019, 7(39), 12180–12193 RSC.
- X. Wang, J. W. Ryan, A. Singh, J. G. Beirne, E. Palomares and G. Redmond, Encapsulation of MEH-PPV:PCBM Hybrids in the Cores of Block Copolymer Micellar Assemblies: Photoinduced Electron Transfer in a Nanoscale Donor–Acceptor System, Langmuir, 2016, 32(1), 329–337 CrossRef PubMed.
- M. Peters, S. Seneca, N. Hellings, T. Junkers and A. Ethirajan, Size-dependent properties of functional PPV-based conjugated polymer nanoparticles for bioimaging, Colloids Surf., B, 2018, 169, 494–501 CrossRef CAS PubMed.
- R. M. Beal, A. Stravrinadis, J. H. Warner, J. M. Smith, H. E. Assender and A. A. R. Watt, The Molecular Structure of Polymer-Fullerene Composite Solar Cells and Its Influence on Device Performance, Macromolecules, 2010, 43, 2343–2348 CrossRef CAS.
- C. W. T. Bulle-Lieuwma, W. J. H. van Gennip, J. K. J. van Duren, P. Jonkheijm, R. A. J. Janssen and J. W. Niemantsverdriet, Characterization of polymer solar cells by TOF-SIMS depth profiling, Appl. Surf. Sci., 2003, 203, 547–550 CrossRef.
- T. J. Prosa, M. J. Winokur, J. Moulton, P. Smith and A. J. Heeger, X-ray structural studies of poly(3-alkylthiophenes): an example of an inverse comb, Macromolecules, 1992, 25, 4364–4372 CrossRef CAS.
- J. K. J. van Duren, X. Yang, J. Loos, C. W. T. Bulle-Lieuwma, A. B. Sieval, J. C. Hummelen and R. A. J. Janssen, Relating the Morphology of Poly(p-phenylene vinylene)/Methanofullerene Blends to Solar-Cell Performance, Adv. Funct. Mater., 2004, 14(5), 425–434 CrossRef CAS.
- X. Yang, J. Loos, S. C. Veenstra, W. J. H. Verhess, M. M. Wienk, J. M. Kroon, M. A. J. Michels and R. A. J. Janssen, Nanoscale morphology of high-performance polymer solar cells, Nano Lett., 2005, 5(4), 579–583 CrossRef CAS PubMed.
- F. Piersimoni, S. Chambon and K. Vandewal, Influence of Fullerene Ordering on the Energy of the Charge-transfer State and Open-Circuit Voltage in Polymer:Fullerene Solar Cells, J. Phys. Chem. C, 2011, 115, 10873–10880 CrossRef CAS.
- L. Benatto, C. F. N. Marchiori, T. Talka, M. Aramini, N. A. D. Yamamoto, S. Huotari, L. S. Roman and M. Koehler, Comparing C60 and C70 as acceptor in organic solar cells: Influence of the electronic and aggregation size on the photovoltaic characteristics, Thin Solid Films, 2020, 697, 137827 CrossRef CAS.
- L. C. W. Menezes, W. Renzi, C. F. N. Marchiori, C. K. B. Q. M. Oliveira, F. von Kieseritzky, J. L. Duarte and L. S. Roman, Nonradiative Energy Transfer between Porphyrin and Copolymer in Films Processed by Organic Solvent and Water-Dispersible Nanoparticles with Photovoltaic Applications, J. Phys. Chem. C, 2018, 122(10), 5796–5804 CrossRef.
- B. K. Abeyweera and B. W. Alphenaar, Thickness dependent red shift of the photocurrent spectrum in bulk heterojunction solar cells, Appl. Phys. Lett., 2013, 102, 0411131 CrossRef.
- O. A. Ghazy, Water-Based Blend Nanoparticles of P3HT and PCBM for the Application in Organic Solar Cells, Adv. Polym. Technol., 2015, 34, 21500–21507 CrossRef.
- P.-T. Huang, P.-F. Huang, Y.-J. Horng and C.-P. Yang, Photoluminescence Study on Charge Transfer Behavior of Poly(3-hexylthiophene) and PCBM Blends, J. Chin. Chem. Soc., 2013, 60, 467–472 CrossRef CAS.
- S. Quan, F. Teng, Z. Xu, L. Qian, Y. Hou, Y. Wang and X. Xu, Solvent and concentration effects on fluorescence emission in MEH-PPV solution, Eur. Polym. J., 2006, 42, 228–233 CrossRef CAS.
- R. A. Abumosa, B. A. Al-Asbahi and M. S. AlSalhi, Optical Properties and Amplified Spontaneous Emission of Novel MDMO-PPV/C500 Hybrid, Polymers, 2017, 7, 71–81 CrossRef PubMed.
- S. Cook, H. Ohkita, Y. Kim, J. J. Benson-Smith, D. D. C. Bradley and J. R. Durrant, A photophysical study of PCBM thin films, Chem. Phys. Lett., 2007, 445, 276–280 CrossRef CAS.
- E. Wang, C. Li, W. Zhuang, J. Peng and Y. Cao, High-efficiency red and green light-emitting polymers based on a novel wide bandgap poly(2,7-silafluorene), J. Mater. Chem., 2008, 18, 797–801 RSC.
- S. Tian, Q. Yue, C. Liu, M. Li, M. Yin, Y. Gao, F. Meng, B. Z. Tang and L. Luo, Complete Degradation of a Conjugated Polymer into Green Upcycling Products by Sunlight in Air, J. Am. Chem. Soc., 2021, 143, 10054–10058 CrossRef CAS PubMed.
- W. Yang, Z. Luo, R. Sun, J. Guo, T. Wang, Y. Wu, W. Wang, J. Guo, Q. Wu, M. Shi, H. Li, C. Yang and J. Min, Simultaneous enhanced efficiency and thermal stability in organic solar cells from a polymer acceptor additive, Nat. Commun., 2020, 11, 1218–1227 CrossRef CAS PubMed.
- L. Guo, W. Liu, G. Niu, P. Zhang, X. Zheng, Q. Jia, H. Zhang, J. Ge and P. Wang, Polymer Nanoparticles with High Photothermal Conversion Efficiency as Robust Photoacoustic and Thermal Theranostics, J. Mater. Chem. B, 2017, 5, 2832–2839 RSC.
- J. Piris, T. E. Dykstra, A. A. Bakulin, P. H. M. van Loosdrecht, W. Knulst, M. T. Trinh, J. M. Schins and L. D. A. Siebbeles, Photogeneration and Ultrafast Dynamics of Excitons and Charges in P3HT/PCBM Blends, J. Phys. Chem. C, 2009, 113, 14500–14506 CrossRef CAS.
- T. Dong, K. Wen, J. Chen, J. Xie, W. Fan, H. Ma, L. Yang, X. Wu, F. Xu, A. Peng and H. Huang, Significant Enhancement of Photothermal and Photoacoustic Efficiencies for Semiconducting Polymer Nanoparticles through Simply Molecular Engineering, Adv. Funct. Mater., 2018, 28, 1800135 CrossRef.
- M. Liedtke, A. Sperlich and H. Kraus, et al., Triplet Exciton Generation in Bulk-Heterojunction Solar Cells Based on Endohedral Fullerenes, J. Am. Chem. Soc., 2011, 133, 9088–9094 CrossRef CAS PubMed.
- S. Karuthedath, J. Gorenflot and Y. Firdaus, et al., Intrinsic efficiency limits in low-bandgap non-fullerene acceptor organic solar cells, Nat. Mater., 2021, 20, 378–384 CrossRef CAS PubMed.
- M. C. Scharber and N. S. Sariciftci, Low Band Gap Conjugated Semiconducting Polymer, Adv. Mater. Technol., 2021, 6, 2000857 CrossRef CAS.
- R. Englman and J. Jortner, The energy gap law for non-radiative decay in large molecules, J. Lumin., 1970, 1–2, 134–142 CrossRef.
- X.-K. Chen, M. K. Ravva, H. Li, S. M. Ryno and J.-L. Brédas, Effect of Molecular Packing and Charge Delocalization on the Nonradiative Recombination of Charge-Transfer States in Organic Solar Cells, Adv. Energy Mater., 2016, 6, 1601325 CrossRef.
- X.-K. Chen, D. Qian, Y. Wang, T. Kirchartz, W. Tress, H. Yao, J. Yuan and M. Hulsbeck, et al., A unified description of non-radiative voltage losses in organic solar cells, Nat. Energy, 2021, 6, 799–806 CrossRef CAS.
- F. D. Eisner, M. Azzouzi, Z. Fei, X. Hou, T. D. Anthopoulos, T. J. S. Dennis, M. Heeney and J. Nelson, Hybridization of Local Exciton and Charge-Transfer States Reduces Nonradiative Voltage Losses in Organic Solar Cells, J. Am. Chem. Soc., 2019, 141, 6362–6374 CrossRef CAS PubMed.
- ISO 10993-5:2009 – International Organization for Standardization, Biological evaluation of medical devices – Part 5: Tests for in vitro cytotoxicity, Switzerland, 2009.
- OECD 2010, Series on Testing and Assessment: Guidance document on using cytotoxicity tests to estimate starting doses for acute oral systemic toxicity tests No. 129; URL https://www.oecd.org/chemicalsafety/testing/seriesontestingandassessmenttestingforhumanhealth.htm (accessed on November 10, 2022).
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ma00912a |
| This journal is © The Royal Society of Chemistry 2023 |