Open Access Article
Open Access ArticleApplications of the octanol–air partitioning ratio: a critical review
Sivani
Baskaran†
 and
Frank
Wania
and
Frank
Wania
 *
*
Department of Physical and Environmental Sciences, Environmental Sciences and Department of Chemistry, University of Toronto Scarborough, 1265 Military Trail, Toronto, Ontario M1C 1A4, Canada. E-mail: frank.wania@utoronto.ca; Tel: +1-416-287-7225
First published on 7th June 2023
Abstract
The octanol–air partition ratio (KOA), also referred to as the octanol–air partition coefficient, has a wide range of applications in environmental chemistry. In this review, we explore the historical context of using octanol as a surrogate for various types of organic matter. We examine in detail the single-parameter linear free energy relationships (spLFERs) that rely on the KOA to describe partitioning equilibria between the gas phase and vegetation, soil, particles, dust, surfaces, materials, and animal tissues. We further use poly-parameter linear free energy relationships (ppLFERs) to estimate how well octanol approximates the partitioning properties of these divergent phases. While the availability of ppLFERs for many environmentally and biologically relevant phases has rendered some of the spLFERs based on the KOA largely obsolete, the KOA still serves a useful purpose as a single parameter describing the tendency of a neutral organic chemical to partition from the gas phase into a wide variety of organic phases. As such, it is a well-defined, easy-to-comprehend and experimentally accessible descriptor of compound volatility from organic phases.
Environmental significanceThere is a long tradition of using the solvent octan-1-ol as a surrogate for a large variety of organic matter when seeking to predict the phase distribution of organic compounds. While not as ubiquitous and common as the octanol–water partitioning ratio KOW, the octanol–air partitioning ratio KOA is widely used when studying the partitioning of organic compounds between organic matter and the gas phase. With the increasing availability and acceptance of methods for predicting the partitioning of organic vapours from air into soil organic matter, atmospheric particles, biological tissues, and polymers, that do not depend on a surrogate organic solvent phase, it is valid to explore whether there is still a role to play for simple linear regressions involving the logarithm of the KOA. This review concludes that there is continued need for a single parameter quantifying organic compound volatility from organic phases and the KOA is well suited to fulfill this role. |
1 Introduction
Phase equilibrium processes involving the gas phase have been studied for over two centuries, beginning with an effort to understand gas solubilities (e.g., Bunsen,1 Henry,2 and Ostwald3), improving drug and anesthetic delivery based on the permeability of these compounds into cells and lipids (e.g., Meyer4 and Overton5), for use in chemical separation processes and partition chromatography (e.g., Pierotti et al.6 and Porter et al.7) and understanding the behaviour and fate of chemicals in the environment.8,9 The study of chemical partitioning between gaseous, aqueous, and organic phases has since become a fundamental aspect of environmental and physical chemistry, as well as medicinal and pharmaceutical sciences.Chemical equilibrium partition ratios, K12, hereafter simply referred to as partition ratios, describe the relative chemical concentrations in two adjacent phases at equilibrium and are dependent on environmental conditions such as temperature. In many instances, partition ratios are referred to as partition coefficients; however, because this property is influenced by external conditions (i.e., temperature), IUPAC guidelines recommend the use of the term partition ratios.10 Because partition ratios of chemicals can span many orders of magnitude, they are often expressed on a base 10 logarithmic scale (i.e., log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K12).
K12).
In this review we examine the role of the octanol–air partition ratio (KOA) and its relevance to our understanding of environmental chemical fate processes. In previous work we explored the different methods used to measure and estimate the KOA of an organic chemical.11 Here, we summarize all of the different phase equilibria that have been described with the help of the KOA including partitioning between the gas phase and vegetation, soil, particles, dust, surfaces, materials (e.g., polyurethane), and animal tissue. We further evaluate how good a surrogate octan-1-ol is for these phases and highlight the limitations of simple regressions between equilibrium partitioning ratios and the KOA. We also explore the use of the KOA in bioaccumulation and chemical risk assessments and as a coordinate in chemical space plots. Considering the availability of tools for estimating environmentally relevant phase equilibria involving the gas phase that do not rely on the KOA, we further address the question of why the KOA still serves a useful purpose.
1.1 What is the KOA?
Partitioning between octanol and air has been described directly and indirectly with different physical–chemical properties. It is directly quantified using the octanol–air partition ratio (KOA), Ostwald coefficient in octanol (Loct; e.g., Boyer and Bircher12), the Gibbs energy for octanol–air phase transfer (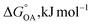 ; e.g., Berti et al.13), and Henry's law constant in octanol (koctH, Pa m3 mol−1; Roberts14). It has also been indirectly quantified by combining either a chemical's vapour pressure with the activity coefficients at infinite dilution in octanol (e.g., Hussam and Carr15) or the octanol–water (KOW) and the air–water partition ratios (KAW; e.g., Finizio et al.16).
; e.g., Berti et al.13), and Henry's law constant in octanol (koctH, Pa m3 mol−1; Roberts14). It has also been indirectly quantified by combining either a chemical's vapour pressure with the activity coefficients at infinite dilution in octanol (e.g., Hussam and Carr15) or the octanol–water (KOW) and the air–water partition ratios (KAW; e.g., Finizio et al.16).
K OA is the concentration of a chemical in octanol divided by the concentration of a chemical in air at equilibrium (eqn (1)).
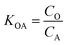 | (1) |
1.2 A brief history of partition ratios
Interest in partitioning properties and in particular the KOA grew and waned throughout the years in various sub-disciplines including physical, analytical, medicinal, pharmaceutical, and environmental chemistry. Exploration of partition ratios began with investigations into the solubility of gases in water and later other solvents. Henry's law constant,2 Bunsen absorption coefficient,1 and Ostwald coefficient3 were gas-solvent partition properties dependent on different external conditions.17,18 Partitioning into organic phases and specifically lipids became of interest after the discovery of anesthesia in 1846.19 At the turn of the 20th century, Meyer4 and Overton5 independently proposed that narcotics were being dissolved in lipids to cause narcosis rather than cholesterols and lipids dissolving into the narcotics.5 In their experiments to identify chemicals partitioning to lipids, both Meyer and Overton found it challenging to use biological lipids because of their tendency to develop emulsions. They suggested the use of a partition ratio (P) between water and another organic phase instead. Overton initially used olive oil as the reference phase as it was cheaper and easier to obtain than long chain alcohols, which were known to have solvation properties closely related to those of biological lipids. Overton also noted that the high melting points of these alcohols implies that measurements would need to be made at physiologically unrealistic temperatures. In the following decades, there were few significant advances in the study of partition ratios; physical and biological chemists focused on the solubilities of different chemicals in various solvents20 and developed manometric devices for measuring the solubilities of gases in blood.21 In 1935, Meyer and Hemmi22 returned to the idea of partition ratios and proposed the use of oleyl alcohol over olive oil, as oleyl alcohol would act as a better surrogate for body lipids when describing the partitioning of more polar compounds.It was only in the early 1950s however that the use of solvent-water partition ratios was re-popularized by the work of Collander.23–25 In 1947, Collandar published his work “On Lipoid Solubility” where he compared the solvent-water partition ratios for a number of different solvents including octan-1-ol, referred to as octanol henceforth, olive oil and oleic acid.23 In particular, he noted that research has yet to identify a solvent that can dissolve a variety of solutes and represent the lipid phase well.23 Collander found that the partition ratios in one alcohol/water system can be used to calculate the partition ratios in another alcohol/water system.24 Octanol was favoured as it was, unlike ethyl ether, not very soluble in water and while hydrophilic substances and bases were more soluble in octanol, hydrophobic solutes were equally soluble in ethyl ether and octanol.24 Over the next two decades, different solvents, including various alcohols, were considered for the organic reference phase.26 In some of their earliest work, Hansch and colleagues found partition ratios had additive–constituent properties — which allows for fragment-based estimation techniques.27–29 Hansch et al. commonly used octanol as the reference organic phase in these works.27,28 Hansch later noted that multiple works showed good correlation between the octanol–water partition ratio and various organic bio-polymers.30 They reported on these developments and the applicability of the octanol–water phase ratio in drug design in some of the very first volumes of the Annual Reports in Medicinal Chemistry.30,31 The use of partition ratios, particularly the KOW, in drug design took off after the publication of various works by Hansch and their colleagues, including one of the earliest review papers on partitioning, by Leo et al. in 1971.29
It is important to note that initial measurements for partition ratios would have been extremely challenging in the absence of modern analytical instruments; early methods included the use of manometers12 and coulometry.27 The development of partition chromatography, including gas chromatography in the 1940s and 1950s,32 led to more measurements and increased interest in gas–liquid partition ratios. In 1959, in an effort to improve understanding of separation processes, Pierotti et al.33,34 measured the infinite dilution activity coefficient of various solutes in multiple solvents using gas–liquid chromatography.
The first directly reported KOA value, albeit referred to as an Ostwald coefficient, appears to be by Boyer and Bircher in 1960, while investigating the solubility of various gases in different alcohols using a modified Van Slyke-Neill blood gas apparatus.12,21 Another set of KOA data was published 13 years later in an effort to understand characteristics of solvents used in gas chromatography.35 The next reported measurement of KOA was published in 1978.36 This work built on work by Battino and co-workers exploring gas–liquid partitioning of gaseous compounds, driven in part by the desire to find a solvent that could act as a model for partitioning of compounds (including anesthetics) between the gas phase and cell membranes.37,38
By the 1980s, environmental chemists had adopted the use of KOW from the pharmaceutical industry for use in predicting the environmental fate and behaviour of chemicals (e.g., Smith et al.8). Paterson et al.39 were perhaps the first to identify the KOA as a useful descriptor for plant–air partitioning and noted the dearth of experimental KOA values. At the same time, octanol–air partitioning became increasingly of interest to the physical chemistry community in the mid 1980s as Pollack et al.,40 Carr (e.g., Hussam and Carr15), and Cabani (e.g., Berti et al.13) and colleagues explored the thermodynamics of gas–liquid equilibria, reporting Gibbs energies of solutions and infinite dilution activity coefficients for solutes in octanol.
Exploration of the KOA and other gas–liquid partition ratios to characterize the behaviour of inhaled anesthetics was renewed in the early 1990s (e.g., Taheri et al.41,42 and Liu et al.43). In the same decade, Harner and Carr began independently reporting KOA values for various solutes. Harner's focus was on the use of KOA to understand the environmental partitioning behaviour of chemicals between air and various types of organic matter.44 Dallas and Carr45 were interested in understanding the effect that the mutual solubility of octanol and water has on the KOW. A head space sampling system developed by Carr and colleagues made measuring vapour–liquid equilibria easier.15,45 In the following two decades interest in the KOA has not waned and many more measurements of the KOA have been reported.11
2 Single-parameter linear free energy relationships involving the KOA
2.1 Phase concentration ratios involving air
In many investigations involving organic chemicals, concentrations in a phase in contact with air are measured, e.g., concentration in phase X CX in units of mol m−3. It is then quite common to calculate ratios between those concentrations and the concentration in the air, e.g., CA in mol m−3: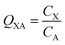 | (2) |
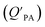 is often expressed in units of m3 air µg−1 particles. The dimensionless QPA value can be obtained as:
is often expressed in units of m3 air µg−1 particles. The dimensionless QPA value can be obtained as: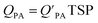 | (3) |
If phase X is a biological phase, e.g., the foliage of a plant, the concentration ratio is sometimes referred to as a bioconcentration factor (BCF).
Generally, the CA in eqn (1) refers to the concentration in the gas phase. However, in some cases, the total concentration in air CTA, i.e., concentration in both the gas and particle phase (CP) has been measured and is used for the ratio calculation:
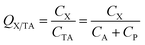 | (4) |
2.2 The types of single parameter linear energy relationships involving KOA
Many studies seek to relate the concentration ratios QXA obtained for different chemicals against the KOA of those chemicals. This typically takes the form:| QXA = aKOAm | (5) |
log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QXA = m QXA = m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA + log10 KOA + log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a | (6) |
These types of equations are called single parameter linear free energy relationships (spLFERs). The implicit assumption underlying these relationships is that phase X, or a constituent of phase X, has solvation properties that resemble those of octanol. An example, where the entirety of phase X is assumed to have octanol-resembling solvation properties, are organic surface films. More commonly, phase X has different constituents that may contribute to the uptake of chemicals. In this case, the concentration ratio may be expressed as the sum of the concentration ratios in the bulk phase constituents weighted by the constituents' abundance in the bulk phase, e.g.:
| QXA = fAX + fWXKWA + afORXKOAm + fYXKYA + aSurface/XKSurface/A | (7) |
In many cases, the assumption is then made, explicitly or implicitly, that the term afORXKmOA is larger than all of the other terms in eqn (7), in which case we obtain:
| QXA = afORXKmOA | (8) |
log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QXA = m QXA = m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA + log10 KOA + log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fORX + log10 fORX + log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a | (9) |
Examples of such composite bulk phases are soil, atmospheric particles and biological materials.
In earlier papers, when the KOA had not been well established as a concept and when few experimental KOA values were available, KOW/KAW instead of KOA was used in relationships of type 5, 6, 8, and 9, i.e., the KOA was estimated as the ratio of the KOW and the equilibrium air water partition ratio KAW. It is believed that KOW/KAW in general has far higher uncertainty than KOA values, especially if predicted properties are being used. This has been observed in some correlations between empirical KOA and KOW/KAW values with QXA.46,47
2.3 A thermodynamic look at spLFERs involving KOA
According to Goss and Schwarzenbach:48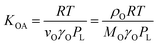 | (10) |
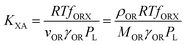 | (11) |
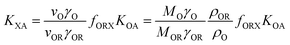 | (12) |
Incidentally, eqn (11) corresponds to a single parameter linear free energy relationship between KXA and PL. In other words, QXA can be, and often has been, related to PL in equations of the type:
| QXA = aPL−m | (13) |
log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QXA = −m QXA = −m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PL + log10 PL + log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a | (14) |
Equations involving KOA are believed to be preferable over those involving PL, because the ratio γO/γOR is less variable for different compounds than is γOR.49 Finizio et al.16 also noted that because the PL cannot be measured directly it can incur large errors for chemicals with high melting points that are solids at environmentally relevant temperatures. However, whether spLFERs involving PL or KOA are preferable may also depend on which of these two parameters can be obtained with higher reliability.50
Eqn (10) and (11) also illustrate a potential issue with spLFERs involving the KOA (or the PL). Both KOA and KXA are inversely proportional to PL. The PL varies over many orders of magnitude between different chemicals, whereas γO and γOR vary only over a small range. KXA and KOA (and also KXA and PL) are therefore bound to be highly correlated if the dataset includes chemicals of divergent volatility. This auto-correlation issue has been discussed by Paterson and Mackay51 and will be discussed further below.
2.4 Reasons why exponent/slope m in spLFERs involving KOA is not 1
There are several reasons why the exponent/slope m in equations of type 5, 6, 8, and 9 can deviate from 1.The first is that QXA does not reflect equilibrium conditions. If a chemical's KXA is large, it can take a long time to reach equilibrium. If the chemical originates in the gas phase, the measured CX is lower than it should be at equilibrium and the QXA for such high KXA compounds accordingly is lower than KXA. This leads to slopes m that are lower than 1. If, however, the chemical originates in phase X, non-achievement of equilibrium leads to a measured CA that is lower than it should be at equilibrium. QXA for high KXA compounds then is higher than KXA and slopes m are more likely to exceed 1. An example of the latter would be a dust particle that includes polymer fragments containing the chemical of interest as an additive.
The KOA threshold for non-achievement of equilibrium depends on a number of factors, such as the size, viscosity, composition and homogeneity of the octanol-resembling constituent in phase X, the mass transfer kinetics between air and that phase and the time available for equilibration. However, often several studies indicate similar threshold values. For example, vegetation is likely to reach equilibrium with gas phase chemicals with a log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA below 8.52,53 On the other hand, compounds with a log10
KOA below 8.52,53 On the other hand, compounds with a log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA in excess of 13 are unlikely to achieve equilibrium with atmospheric particles within the atmospheric lifetime of most particles.54
KOA in excess of 13 are unlikely to achieve equilibrium with atmospheric particles within the atmospheric lifetime of most particles.54
Disequilibrium may also be a result of temperature differences between air and the condensed phase X. Partitioning between gas and condensed phases are generally highly temperature dependent and the low heat capacity of air means that temperature can fluctuate far more quickly in air than in phase X. This, however, tends not to be an issue in laboratory experiments, where thermal equilibrium can typically be ensured. Some chemicals may also form non-exchangeable residues in the condensed phase, e.g., in soil organic matter, and thus are not available for partitioning but can be chemically extracted during analysis.
Another reason for slopes m being lower than 1 could be the use of total air concentrations CTA instead of gas phase concentrations CA (eqn (4)versuseqn (2)). In that case, QXA is too small (relative to KXA) for low volatility chemicals that partition to atmospheric particles.
The final reason for deviations of slopes m from 1 are differences in the solvation properties of octanol and the octanol-resembling phase. Goss and Schwarzenbach48 show that a slope of 1 is obtained if γO/γOR is constant. For substances within a compound class, slopes deviating from 1 can be obtained if γO/γOR varies proportionally with KOA.
2.5 Phase equilibria that have been described with spLFERs involving the KOA
| KVA = fA + fWKWA + fLKOA | (15) |
Subsequently, the KOA has been applied repeatedly to estimate chemical uptake in different plant species (e.g., Tremolda et al.,61 Dowdy and McKone,62 Keymeulen et al.63). Tolls and McLachlan64 reported a correlation of equation type 5 between log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KVA measured for welsh ray grass and log10
KVA measured for welsh ray grass and log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA with R2 values of 0.89 to 0.90. KOA values that were consistently lower than the KVA were attributed to differences in the temperature at which the two variables had been measured.64 Brown et al.65 also found linear correlations between the log10 of the whole pine needle–air partition ratio (log10
KOA with R2 values of 0.89 to 0.90. KOA values that were consistently lower than the KVA were attributed to differences in the temperature at which the two variables had been measured.64 Brown et al.65 also found linear correlations between the log10 of the whole pine needle–air partition ratio (log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPine/A, R2 = 0.96) and the pine needle wax–air partition ratio (log10
KPine/A, R2 = 0.96) and the pine needle wax–air partition ratio (log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KWax/A, R2 = 0.70) and the log10
KWax/A, R2 = 0.70) and the log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA. The regression coefficients a and m in eqn (6) are thus specific to the plant species (e.g., Tolls and McLachlan,64 Kömp and McLachlan,66 McLachlan,53 Nizzetto et al.67). The intercept should further be dependent on whether the concentration in vegetation is expressed on a fresh or dry weight basis. Most spLFER equations are for 25 °C but exploration of the interspecies variability of KVA in relation to the KOA showed that KVA is more temperature dependent than the KOA.66 In a modelling effort, Taylor et al.68 used eqn (6) with m equal to 0.7 and log10
KOA. The regression coefficients a and m in eqn (6) are thus specific to the plant species (e.g., Tolls and McLachlan,64 Kömp and McLachlan,66 McLachlan,53 Nizzetto et al.67). The intercept should further be dependent on whether the concentration in vegetation is expressed on a fresh or dry weight basis. Most spLFER equations are for 25 °C but exploration of the interspecies variability of KVA in relation to the KOA showed that KVA is more temperature dependent than the KOA.66 In a modelling effort, Taylor et al.68 used eqn (6) with m equal to 0.7 and log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a equal to 0.15 for clover–air partitioning as a general model for plant–air partitioning whenever no plant specific model is available. We stress that most of these studies were limited to non-polar organic contaminants.
a equal to 0.15 for clover–air partitioning as a general model for plant–air partitioning whenever no plant specific model is available. We stress that most of these studies were limited to non-polar organic contaminants.
The KOA (or KOW and KAW combined) has also been related to the partitioning between specific parts of a plant and air, including leaf–air,55,65 bark–air,69,70 tree core–air71 and cuticle–air.63 The capacity to quantify these individual partition ratios in plants has advanced passive-sampling techniques in both indoor and outdoor environments for organic pollutants. For example, in indoor air, olive trees have been used to measure polycyclic aromatic hydrocarbons72 and in outdoor environments, bark, leaf, litter, and pine needles have been used as passive samplers for PBDEs,73 chlorobenzenes,74 and various volatile organic compounds.75
In addition to partitioning between air and individual plants and plant parts, the KOA can be used to describe bulk phase partitioning between the gas phase and entire forest canopies. Horstmann and McLachlan76 measured deposition of chemicals onto deciduous and coniferous canopies in Germany and found that the distribution of chemicals with log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA < 10 approached equilibrium. Accordingly, they derived equations in the form of eqn (5) to relate pseudo canopy–air partition ratios KCanopy/A with the KOA, both for a deciduous canopy (m = 0.76, log10
KOA < 10 approached equilibrium. Accordingly, they derived equations in the form of eqn (5) to relate pseudo canopy–air partition ratios KCanopy/A with the KOA, both for a deciduous canopy (m = 0.76, log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a = 1.15) and a coniferous canopy (m = 0.69, log10
a = 1.15) and a coniferous canopy (m = 0.69, log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a = 1.58). Su et al.77 conducted a similar study in a deciduous forest in Canada and derived a similar correlation (m = 0.67, log10
a = 1.58). Su et al.77 conducted a similar study in a deciduous forest in Canada and derived a similar correlation (m = 0.67, log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a = 2.04). Many of these equations were derived from datasets comprising only a small subset of structurally related chemicals (e.g., PCBs) and thus these models likely work best when applied to chemicals of similar size and structure.
a = 2.04). Many of these equations were derived from datasets comprising only a small subset of structurally related chemicals (e.g., PCBs) and thus these models likely work best when applied to chemicals of similar size and structure.
The relationships above assume that chemical equilibrium is established between the vegetation and the atmospheric gas phase. However, as mentioned in Section 2.4, this is generally only a defensible assumption for relatively volatile chemicals, whereas for less volatile chemicals the kinetics of uptake and plant growth play a more important role in controlling plant bioaccumulation and bioconcentration.78 McLachlan53 presented a conceptual framework, which illustrates how measurements of plant uptake can be used to delineate the KOA ranges within which different processes, including wet and dry deposition, are dominant. Volatile chemicals with low log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA (<8.5) reach equilibrium and the KVA is directly correlated with the log10
KOA (<8.5) reach equilibrium and the KVA is directly correlated with the log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA. For involatile chemicals with high log10
KOA. For involatile chemicals with high log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA (>11), particle bound deposition is important which is apparent in another correlation of the log10 of the particle–air partition ratio log10
KOA (>11), particle bound deposition is important which is apparent in another correlation of the log10 of the particle–air partition ratio log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPA with log10
KPA with log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA.53 For chemicals with intermediate log10
KOA.53 For chemicals with intermediate log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA (8.5–11) uptake into plants from air is not a function of KOA, but rather a function of the kinetics of the transport from air to the plant storage compartment and the time of exposure. Later modelling work52 confirmed that non-volatile chemicals (log10
KOA (8.5–11) uptake into plants from air is not a function of KOA, but rather a function of the kinetics of the transport from air to the plant storage compartment and the time of exposure. Later modelling work52 confirmed that non-volatile chemicals (log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA > 8) do not approach equilibrium between plants and air and so the application of the KOA for estimating plant BCFs and KVA is more applicable to volatile chemicals. More volatile chemicals (log10
KOA > 8) do not approach equilibrium between plants and air and so the application of the KOA for estimating plant BCFs and KVA is more applicable to volatile chemicals. More volatile chemicals (log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA < 5) also have the potential to volatilize from a plant's stem, trunk, and leaves.79
KOA < 5) also have the potential to volatilize from a plant's stem, trunk, and leaves.79
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOC) is highly correlated with the log10
KOC) is highly correlated with the log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW, with a slope of ∼1.82KOW/KAW and the organic carbon–air partition ratio KOC/A were found to be similarly related.81 Accordingly, Hippelein and McLachlan80 extended the Karickhoff equation to soil–air partitioning:
KOW, with a slope of ∼1.82KOW/KAW and the organic carbon–air partition ratio KOC/A were found to be similarly related.81 Accordingly, Hippelein and McLachlan80 extended the Karickhoff equation to soil–air partitioning: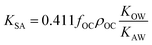 | (16) |
As more directly measured KOA became available, its role in soil–air partitioning became evident and the KOA was used directly to describe soil–air partitioning.80,83 For example, volatilization fluxes of pesticides from sludge-amended soil were found to correlate with KOA and the pesticide concentration in the sludge.84,85 He et al.86 found that when using directly measured KOA values, the predicted KSA value was ∼2.7 times greater than the experimental KSA, while KSA values predicted using experimental KOW/KAW values were in better agreement with experimental KSA values. This prompted He et al.86 to develop a modified Karickhoff equation:
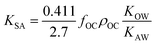 | (17) |
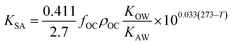 | (18) |
Contrary to expectations, Hippelein and McLachlan88 observed that the absorption of organic chemicals in organic matter showed dependence on relative humidity and proposed a semi-empirical equation for predicting KSA:
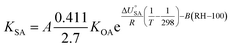 | (19) |
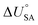 is the internal energy of soil–air phase change, which also varies with RH.88 Hippelein and McLachlan recommend an A value of 2 and a value of 0.0437 for B as they found B to be relatively constant across penta- and hexachlorobenzene and various PCBs.80 As both B and
is the internal energy of soil–air phase change, which also varies with RH.88 Hippelein and McLachlan recommend an A value of 2 and a value of 0.0437 for B as they found B to be relatively constant across penta- and hexachlorobenzene and various PCBs.80 As both B and 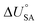 are chemical specific, or at least homologue specific, using this semi-empirical equation for predicting KSA to describe general soil–air partitioning poses some challenges with data availability.89 Instead, Davie-Martin et al.89 suggest that compound group specific multiple linear regressions using KOA, RH, and temperature be used for estimating KSA because this approach requires fewer chemical specific properties (i.e., B and
are chemical specific, or at least homologue specific, using this semi-empirical equation for predicting KSA to describe general soil–air partitioning poses some challenges with data availability.89 Instead, Davie-Martin et al.89 suggest that compound group specific multiple linear regressions using KOA, RH, and temperature be used for estimating KSA because this approach requires fewer chemical specific properties (i.e., B and 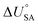 ) and performed much better than the general equation. However, there are limitations to this approach, as the fOC term is not included in the regression and KSA is assumed to be linearly correlated with RH.
) and performed much better than the general equation. However, there are limitations to this approach, as the fOC term is not included in the regression and KSA is assumed to be linearly correlated with RH.
While the relationships above all assume that partitioning of chemicals to soils from the air is solely governed by absorption on soil organic matter, this assumption is often not valid, especially in air-dry soil and soil with a low organic matter content. Under such circumstances, adsorption to mineral surfaces can become dominant.90,91 In particular, relative humidity plays a critical role in determining the relative importance of adsorption to the mineral–air interface. If only absorption processes (i.e., sorption into soil organic matter) is considered, estimates of the KSA are likely to be underestimated.91 In other words, whenever adsorption plays a role in soil–air partitioning, using octanol as a surrogate for soil will be insufficient.91,92
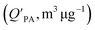 and log10
and log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PL.95
PL.95
Whereas in its original formulation, the Junge–Pankow relationship was based on the assumption that chemicals adsorb onto the surface of the particles, Pankow96 showed that the use of PL is also compatible with an absorption model of particle–air partitioning, which took the form of eqn (11) and related PL to 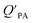 . If chemicals are absorbed into a particle's organic matter (OM) fraction, the KOA can serve as an alternative measure for estimating
. If chemicals are absorbed into a particle's organic matter (OM) fraction, the KOA can serve as an alternative measure for estimating 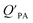 (see Section 2.3 and Finizio et al.16 for details). Assuming an octanol density (ρO) of 820 kg m−3,16 a ratio MOγO/MOMγOM equal to 1 and that all OM present in the aerosol is available for partitioning,95 simplifies eqn (11) to an equation of type 6, where log10
(see Section 2.3 and Finizio et al.16 for details). Assuming an octanol density (ρO) of 820 kg m−3,16 a ratio MOγO/MOMγOM equal to 1 and that all OM present in the aerosol is available for partitioning,95 simplifies eqn (11) to an equation of type 6, where log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a equals −11.91 and m is 1.
a equals −11.91 and m is 1.
A strong relationship between 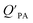 and KOA would suggest that interactions of neutral organic chemicals with the OM in the particles is similar to that in octanol, i.e., via absorption, rather than surface adsorption.16 Indeed, KOA and
and KOA would suggest that interactions of neutral organic chemicals with the OM in the particles is similar to that in octanol, i.e., via absorption, rather than surface adsorption.16 Indeed, KOA and 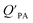 values have been found to be correlated for a number of compound classes including PAHs, PCBs, organochlorine pesticides, and PCNs16,95 and the KOA is often considered to be a better predictor than PL for particle–air partitioning,95,97,98i.e., the KOA-based model performs better than the Junge–Pankow model.95,97,99 The KOA based model is believed to act as a more universal model for
values have been found to be correlated for a number of compound classes including PAHs, PCBs, organochlorine pesticides, and PCNs16,95 and the KOA is often considered to be a better predictor than PL for particle–air partitioning,95,97,98i.e., the KOA-based model performs better than the Junge–Pankow model.95,97,99 The KOA based model is believed to act as a more universal model for 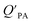 , as structurally similar compounds tended to group together when regressing
, as structurally similar compounds tended to group together when regressing 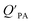 against the KOA, but this did not occur when
against the KOA, but this did not occur when 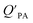 was regressed against PL.95,97,98
was regressed against PL.95,97,98
While the regressions between KOA and 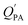 can be quite strong (R2 0.60 to 0.99), slopes of the regression are often less than 1 (e.g., Falconer and Harner,97 Finizio et al.,16 Harner and Bidleman,95 Radonic et al.100). Two explanations have been proposed to explain this: octanol and OM have different solvation properties or equilibrium has not been reached (see Section 2.4). It is likely that both explanations hold true. For example, the polarity of secondary aerosol particles can differ from octanol, such that the activity ratio of a chemical in octanol and organic matter deviates from 1, thus the slope of a KOA and
can be quite strong (R2 0.60 to 0.99), slopes of the regression are often less than 1 (e.g., Falconer and Harner,97 Finizio et al.,16 Harner and Bidleman,95 Radonic et al.100). Two explanations have been proposed to explain this: octanol and OM have different solvation properties or equilibrium has not been reached (see Section 2.4). It is likely that both explanations hold true. For example, the polarity of secondary aerosol particles can differ from octanol, such that the activity ratio of a chemical in octanol and organic matter deviates from 1, thus the slope of a KOA and 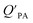 regression will also differ from 1.101 Yeo et al.102 suggested that the activity ratio assumption of 1 held true for multi-ortho PCBs but not for non/mono-ortho PCBs based on regressions of KOA and PL from Harner and Bidleman.95 Götz et al.103 noted that the KOA based model tended to overestimate the
regression will also differ from 1.101 Yeo et al.102 suggested that the activity ratio assumption of 1 held true for multi-ortho PCBs but not for non/mono-ortho PCBs based on regressions of KOA and PL from Harner and Bidleman.95 Götz et al.103 noted that the KOA based model tended to overestimate the 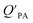 and recommended using an MO/MOM value of 0.26 in eqn (11).
and recommended using an MO/MOM value of 0.26 in eqn (11).
The presence of soot or elemental carbon can also alter the particle–air partitioning of chemicals because then adsorption to such sorbents can occur in addition to bulk phase absorption.104 In these instances a model based solely on KOA has a tendency to underestimate the 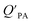 ,104–106 and a second term to describe the adsorption to soot is needed:104
,104–106 and a second term to describe the adsorption to soot is needed:104
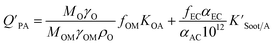 | (20) |
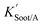 is the soot–air partitioning ratio in units of L kg−1.104 The 1012 included in the denominator is for unit conversion. However, Helm and Bidleman107 found the opposite to be true, where the
is the soot–air partitioning ratio in units of L kg−1.104 The 1012 included in the denominator is for unit conversion. However, Helm and Bidleman107 found the opposite to be true, where the 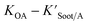 model overpredicts the
model overpredicts the 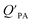 whereas using KOA alone better agreed with field measurements. The differing conclusions from the various studies do not reject the suitability of KOA as parameter for predicting
whereas using KOA alone better agreed with field measurements. The differing conclusions from the various studies do not reject the suitability of KOA as parameter for predicting 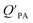 , rather suggests that better characterization of the particle phase (e.g., the polarity) is needed to better understand chemical interactions between particle and gas phase.
, rather suggests that better characterization of the particle phase (e.g., the polarity) is needed to better understand chemical interactions between particle and gas phase.
Dust–air partitioning can also be defined by 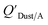 which has units of m3 mg−1 and is often used in place of QDust/A (Weschler and Nazaroff;109 see Section 2.1). Whether the equilibrium partitioning of a chemical with dust is kinetically limited depends on both the KOA and size and viscosity of the particle, whereby chemicals with higher log10
which has units of m3 mg−1 and is often used in place of QDust/A (Weschler and Nazaroff;109 see Section 2.1). Whether the equilibrium partitioning of a chemical with dust is kinetically limited depends on both the KOA and size and viscosity of the particle, whereby chemicals with higher log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA values take longer to equilibrate as do larger particles.108 Weschler and Nazaroff109 found a correlation between measured
KOA values take longer to equilibrate as do larger particles.108 Weschler and Nazaroff109 found a correlation between measured 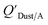 and KOA values—however they note that for some points in the regression the
and KOA values—however they note that for some points in the regression the 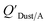 values are calculated using KOA. For chemicals with high log10KOA values, the
values are calculated using KOA. For chemicals with high log10KOA values, the 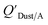 or QDust/A value is less than what would be expected which is attributed to non-equilibrium conditions (Weschler and Nazaroff,109 Zhang et al.;110 see Section 2.4).
or QDust/A value is less than what would be expected which is attributed to non-equilibrium conditions (Weschler and Nazaroff,109 Zhang et al.;110 see Section 2.4).
Similarly, Shoeib et al.111,112 found that the KOA model for QDust/A tended to under-predict the concentration in the dust phase, which could be attributed to differences in how some compounds (e.g., MeFOSE and EtFOSE) interact with octanol and organic matter or non-equilibrium conditions.112 It is possible that the dust particles contain varying levels of contaminants, depending on whether they originate from the physical degradation of polymers containing the chemical as additive or whether the chemical is being taken up in the particles from the gas phase.112 Indeed, this was observed in house dust samples, where the bromine concentration for BDE 209 contaminated samples varied highly.113
Using Weschler and Nazaroff's109 equations for 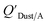 (i.e., eqn (3) and (8)) and assuming values for fOM,Dust and ρDust, Li et al.114 present an equation for
(i.e., eqn (3) and (8)) and assuming values for fOM,Dust and ρDust, Li et al.114 present an equation for 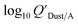 in the form of eqn (6), where m equals 1 and log10
in the form of eqn (6), where m equals 1 and log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a is −13.0.
a is −13.0.
Chemicals with log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA values between 8 and 11, had measured
KOA values between 8 and 11, had measured 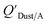 values similar to predicted values.114 Chemicals with log10
values similar to predicted values.114 Chemicals with log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA values less than 8 had predicted
KOA values less than 8 had predicted 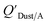 values that were higher than the measured value, likely because air concentration levels were underestimated.114 Predicted
values that were higher than the measured value, likely because air concentration levels were underestimated.114 Predicted 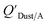 values lower than measured values for chemicals with log10KOA values greater than 11 were again attributed to disequilibrium conditions.114
values lower than measured values for chemicals with log10KOA values greater than 11 were again attributed to disequilibrium conditions.114
Recently, Wei et al.115 combined eqn (4) and (6) parameterized for both KPA and KDust as functions of KOA, to estimate a dust–total air partition ratio KDust/TA:
log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QDust/A = (m1 − m2)log10 QDust/A = (m1 − m2)log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA + log10 KOA + log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a1 − log10 a1 − log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a2 a2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − log10 TSP − log10 TSP | (21) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QDust/A and log10
QDust/A and log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QPA against log10
QPA against log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA, respectively, and log10
KOA, respectively, and log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a1 and log10
a1 and log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a2 are the intercepts of these regressions. If TSP × QPA is much less than 1, particle–air partitioning is negligible and the use of eqn (21) is redundant.115 Wei et al.115 observed good agreement between KOA and QDust/TA for phthalates, which were estimated to have TSP × QPA values less than one. Whereas PAHs which have a wider range in TSP × QPA values, showed a poorer correlation between KOA and QDust/TA.115
a2 are the intercepts of these regressions. If TSP × QPA is much less than 1, particle–air partitioning is negligible and the use of eqn (21) is redundant.115 Wei et al.115 observed good agreement between KOA and QDust/TA for phthalates, which were estimated to have TSP × QPA values less than one. Whereas PAHs which have a wider range in TSP × QPA values, showed a poorer correlation between KOA and QDust/TA.115
However, the organic film present on many surfaces is often treated as a bulk-phase, and therefore an absorption model using KOA has been applied to estimate film–air partition ratios QFilm/A (e.g., Harner and Bidleman,95 Weschler and Nazaroff108). Implicit in these approaches is either the assumption that surface adsorption is negligible or that adsorption to the film surface and absorption in the bulk film can be collectively described with one partitioning constant. The latter can be problematic, as the time scales for equilibration are often widely different for surface and bulk phase uptake. Also, adsorption scales with surface area and absorption with mass. In some instances, the term film–air partitioning has been used to describe partitioning between thin polymer films and air (e.g., ethylene vinyl acetate116); these instances are described in Section 2.5.6.
Q
Film/A values for both indoor117,118 and outdoor119 films were found to be correlated with, or similar to, KOA values. Subsequently, studies have used organic films as passive environmental samplers relating KOA and QFilm/A using eqn (8), where m and log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a are both 1.120,121 While the measured QFilm/A correlated well with KOA, Wu et al.122 observed very shallow regression slopes particularly for films obtained from rural environments.
a are both 1.120,121 While the measured QFilm/A correlated well with KOA, Wu et al.122 observed very shallow regression slopes particularly for films obtained from rural environments.
Bi et al.123 reported on the  of mirrors, plates, and windows in units of m and, assuming that organic films are present on all impervious surfaces, converted these values to dimensionless QFilm/A, by estimating a film thickness and percentage of organic material in the film. These QFilm/A values were in good agreement with KOA.
of mirrors, plates, and windows in units of m and, assuming that organic films are present on all impervious surfaces, converted these values to dimensionless QFilm/A, by estimating a film thickness and percentage of organic material in the film. These QFilm/A values were in good agreement with KOA.
Li et al.114 presented a simplified relationship between KOA and a window film–air partition ratio. As with 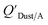 , estimated
, estimated 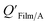 values for chemicals with log10
values for chemicals with log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA values between 8 and 11 agreed well with experimental values, chemicals with log10
KOA values between 8 and 11 agreed well with experimental values, chemicals with log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA < 8 were over-predicted, and those with log10
KOA < 8 were over-predicted, and those with log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA values > 11 were under-predicted.114
KOA values > 11 were under-predicted.114
The time needed for a chemical to reach equilibrium with a surface film is dependent on both the KOA, the thickness of the film (X; m), and the mass transfer coefficient from bulk air onto the film (MTCS in units of m h−1):108
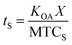 | (22) |
As discussed in Section 2.4, it can take several months for surface–air partitioning of chemicals with very high log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA values to reach equilibrium. For chemicals with log10
KOA values to reach equilibrium. For chemicals with log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA > 12, this can be upwards of 1 year.124
KOA > 12, this can be upwards of 1 year.124
While modelling film growth by SVOCs deposition, Weschler and Nazaroff125 noted that the majority of chemicals in organic film have log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA values between 10 and 13. Because chemicals with low KOA values equilibrate quickly between organic films and air, films can become enriched in chemicals with higher log10
KOA values between 10 and 13. Because chemicals with low KOA values equilibrate quickly between organic films and air, films can become enriched in chemicals with higher log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA over time.125
KOA over time.125
The KOA has also been used to estimate a time-dependent uptake coefficient (ka) for gaseous compounds by liquid organic films:
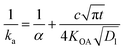 | (23) |
Ockenden and colleagues127 found that the KOA was linearly correlated with the sampling rate of PCBs into triolein containing semi-permeable membrane devices (SPMD) used as passive air samplers (PASs), thus the KOA could be used to estimate the amount of time required by non-polar substances to equilibrate with the PAS.
Multiple studies have shown correlations between KOA and the partitioning between air and polymer material used in other PASs, including polyurethane foam,128 low density polyethylene,129 ethylene vinyl acetate,130 and activated carbon and florisil.131 De Coensel132 noted that given the strong correlation between the KOA and KPDMS/A (polydimethyl siloxane–air partition ratio) for p-dichlorobenzene and naphthalene, KPDMS/A could even be used to estimate KOA. However such an approximation is likely to be limited to non-polar substances as the interactions of polar substances with PDMS and octanol is not the same.
The KOA has also been correlated with partitioning between various textile materials such as cotton and air, generally showing fairly strong correlations.133 Yu et al.134 observed that the correlation between the cotton–air partition ratio QCotton/A and KOA is specific to different homologous compound groups. However, Saini et al.135 found a low correlation between KOA and measured QCotton/A which was attributed to the irregularity and variance in the material itself, as polyester–air partition ratios KPolyester/A were more strongly correlated with KOA.
Won et al.136 also observed linear relationships between KOA and partition ratios between carpet, vinyl, and drywall material and air under different conditions. Partitioning between latex paint and air was also found to be correlated with KOA.137
Reppas-Chrysovitsinos et al.138 compiled published material–air partition ratios (KMA) and presented a general single parameter equation based on eqn (6), where m is equal to 1 and log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a equal to −1.22. They also present KOA-based equations to estimate specific material–air partitioning ratios for polyethylene, polyurethane, PDMS, carbohydrates, polyoxymethylene (POM), and nylons.138
a equal to −1.22. They also present KOA-based equations to estimate specific material–air partitioning ratios for polyethylene, polyurethane, PDMS, carbohydrates, polyoxymethylene (POM), and nylons.138
Arguably, adsorption is the most relevant sorption process to describe partitioning to non-porous and non-organic material and octanol is unlikely to be a relevant surrogate for surfaces and materials whenever adsorption is the dominant uptake process.
| KXA = KOA(fneutral lipids + 0.3fphosolipids) + KAW(fwater + 0.7fphospholipids) | (24) |
Hau and Connell correlated odour thresholds144 and nasal pungency thresholds145 of chemicals with KOW and KAW but not with KOA. This is likely because methods for measuring and estimating KOW and KAW were well-established and there were few measurements of KOA at the time. Later, Hau et al.146 showed biophase–air partitioning ratios to be related to KOA and as a result the minimum alveolar concentration (MAC), which describes the potency of anaesthetics, is also related to KOA. Slightly different correlations between KOA and MAC were observed for alkanes and alcohols, however if the MAC of chemicals with very high KOW values is corrected with the blood/brain partition ratio, then the regressions converge, and a single equation can describe the relationship between MAC and KOA:146
log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MACcorr = −1.10 MACcorr = −1.10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA + 2.41 KOA + 2.41 | (25) |
Nielsen et al.147 found the KOA to be a good proxy for sensory irritant receptor–air partitioning such that it can be used to estimate RD50, the concentration at which a chemical causes a 50% decrease in respiratory frequency in an air-breathing organism:
log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RD50 = 0.8361 RD50 = 0.8361![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA − 6.0879 KOA − 6.0879 | (26) |
Raines et al.148 similarly found a correlation between KOA and the concentration of aromatic inhaled drugs needed to inhibit the N-methyl-D-aspartate receptor by 50%.
More recently, the KOA has also been utilized in food science to estimate release behaviour of flavour compounds from an octanol–water emulsion.149,150 Measured blood–air and milk–air partition ratios151 and feces–air partition ratios152 were also shown to correlate with the KOA. KOA has also been used as a surrogate for lipid–air partitioning to predict respiratory elimination rates153 and human skin uptake108 in environmental chemical fate models. Kelly and Gobas154 noted that the estimated biomagnification factor of persistent neutral organic chemicals for wolves was correlated with KOA.
Bioaccumulation assessments based solely on octanol–water partition ratios (KOW) fail to take into account the role of respiratory elimination in air-breathing organisms.153 In fact, chemicals with log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW values less than 5, and thus not considered bioaccumulative by various regulatory agencies (e.g., the Government of Canada155), can have the potential to biomagnify in air-breathing organisms. Modelling results from Gobas et al.153 indicate that persistent chemicals with log10
KOW values less than 5, and thus not considered bioaccumulative by various regulatory agencies (e.g., the Government of Canada155), can have the potential to biomagnify in air-breathing organisms. Modelling results from Gobas et al.153 indicate that persistent chemicals with log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA greater than 5 and log10
KOA greater than 5 and log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW greater than 2 have the potential to bioaccumulate in terrestrial food chains. This was further supported by modelling work by Czub and McLachlan52 who found that in humans chemicals with log10
KOW greater than 2 have the potential to bioaccumulate in terrestrial food chains. This was further supported by modelling work by Czub and McLachlan52 who found that in humans chemicals with log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA between 6 and 10 and log10
KOA between 6 and 10 and log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW value between 2 and 9 had high environmental bioaccumulation potentials and Kelly et al.156 who noted that chemicals with log10
KOW value between 2 and 9 had high environmental bioaccumulation potentials and Kelly et al.156 who noted that chemicals with log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA values greater than 6 and log10
KOA values greater than 6 and log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW values greater than 2 can biomagnify in air-breathing organisms. Of the chemicals listed on Canada's 2003 Domestic Substances List, 57% have an estimated log10
KOW values greater than 2 can biomagnify in air-breathing organisms. Of the chemicals listed on Canada's 2003 Domestic Substances List, 57% have an estimated log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW value between 2 and 5 and an estimated KOA, value greater 5—and thus are potentially bioaccumulative.153 Providing evidence beyond modelling studies, Moses et al.157 found lipid-normalized concentrations of dieldrin, heptachlor epoxide and β-hexachlorocyclohexane to be 5–14 times higher in seals than in fish. These chemicals have log10
KOW value between 2 and 5 and an estimated KOA, value greater 5—and thus are potentially bioaccumulative.153 Providing evidence beyond modelling studies, Moses et al.157 found lipid-normalized concentrations of dieldrin, heptachlor epoxide and β-hexachlorocyclohexane to be 5–14 times higher in seals than in fish. These chemicals have log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOW values around 5 or lower and log10
KOW values around 5 or lower and log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA values greater than 8.
KOA values greater than 8.
More recent modelling studies on compounds released indoors have also shown that inhalation exposure is the primary exposure route of persistent volatile organic compounds with log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA values less than 6,158 while for chemicals with log10
KOA values less than 6,158 while for chemicals with log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA greater than 6, non-dietary ingestion (i.e., hand-to-mouth) is the primary exposure pathway, particularly in children.158,159
KOA greater than 6, non-dietary ingestion (i.e., hand-to-mouth) is the primary exposure pathway, particularly in children.158,159
3 How good a surrogate is n-octanol for various types of phases?
While many studies reviewed in Section 2 reported strong linear relationships between log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QXA (where X is an organic phase) and log10
QXA (where X is an organic phase) and log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA, it is not really possible to compare these relationships with each other, for example to assess whether the solvation properties of a particular phase more closely resemble those of octanol than those of another. This is because of divergent datasets used in those studies that include different types and numbers of chemicals and because of the unknown and variable uncertainty of the KOA and QXA values used in these relationships. Also, as mentioned before, it is not always assured that the QXA data refer to equilibrium conditions.
KOA, it is not really possible to compare these relationships with each other, for example to assess whether the solvation properties of a particular phase more closely resemble those of octanol than those of another. This is because of divergent datasets used in those studies that include different types and numbers of chemicals and because of the unknown and variable uncertainty of the KOA and QXA values used in these relationships. Also, as mentioned before, it is not always assured that the QXA data refer to equilibrium conditions.
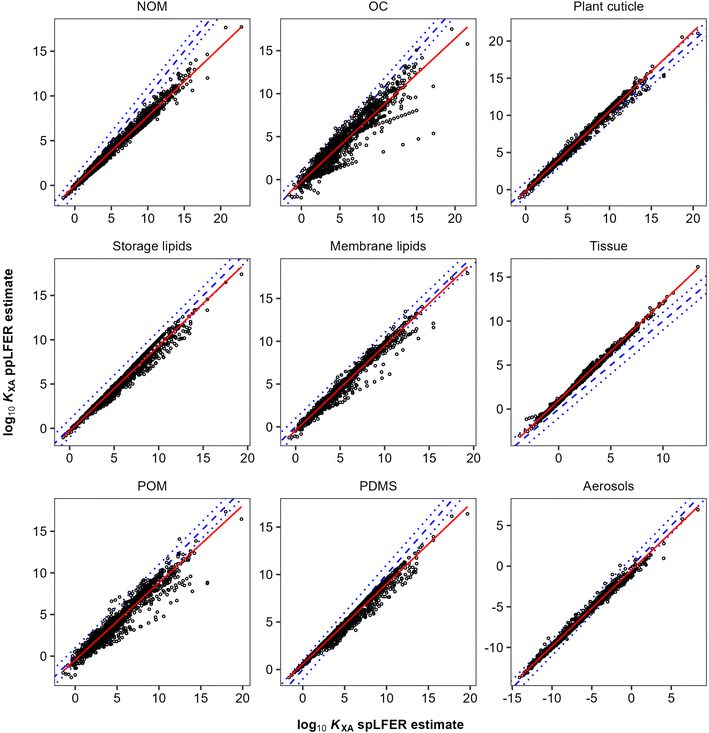
However, we can test how good a surrogate KOA is for other partitioning equilibria between an organic phase X and air by comparing KXA values that have either been obtained with a KOA-based spLFER prediction or by a poly-parameter linear free energy relationship (ppLFER) that has been calibrated directly for phase X. In some cases (i.e., plant cuticles, storage lipid, membrane lipid), we can directly compare the KOA with a ppLFER-predicted KXA. Furthermore, we sometimes have to rely on thermodynamic triangles to estimate a KXA from ppLFER-predicted KXW and KAW values (natural organic matter NOM, storage lipids, membrane lipids, tissue, POM). To avoid the uncertainty in KOA influencing the comparison, we can also predict the KOA at the appropriate temperature with ppLFERs.160,161 This approach is thus similar to the one used by Endo et al.,143 when probing the extent to which n-octanol is a good surrogate for various biomaterials. Table 1 details the partition ratios that are being compared. We used 1316 organic chemicals with complete sets of experimental solute descriptors, as supplied by the UFZ-LSER database.162 We note that this set of chemicals is limited to generally small and primarily non-polar substances. More complex multifunctional chemicals or chemicals with unusual substitutions, such as the polyflourinated alkyl substances, are not well-represented.
| Phase X | ppLFER predicted KXA | log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA spLFER based prediction KOA spLFER based prediction |
|---|---|---|
| NOM | Average log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KNOM/A for 10 different organic matter systems including humic acids, fulvic acids, and natural organic matter, predicted with ppLFER by Niederer et al.167 KNOM/A for 10 different organic matter systems including humic acids, fulvic acids, and natural organic matter, predicted with ppLFER by Niederer et al.167 |
log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOC/A predicted with spLFER by Borisover and Graber81 using KOA at 15 °C KOC/A predicted with spLFER by Borisover and Graber81 using KOA at 15 °C |
| OC | log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOC/A calculated as log10 KOC/A calculated as log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KWA + log10 KWA + log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOC, where KOC is predicted with ppLFER by Nguyen et al.168 KOC, where KOC is predicted with ppLFER by Nguyen et al.168 |
log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOC/A predicted with spLFER by Borisover and Graber81 using KOA at 25 °C KOC/A predicted with spLFER by Borisover and Graber81 using KOA at 25 °C |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Plant cuticles | log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPlant/A predicted with ppLFER by Platts and Abraham163 KPlant/A predicted with ppLFER by Platts and Abraham163 |
log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA at 25 °C KOA at 25 °C |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Storage lipid | log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KStorage-lipid/A calculated as log10 KStorage-lipid/A calculated as log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KWA + log10 KWA + log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KStorage-lipid/W where KStorage-lipid/W is predicted with ppLFER by Geisler et al.164 KStorage-lipid/W where KStorage-lipid/W is predicted with ppLFER by Geisler et al.164 |
log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA at 37 °C KOA at 37 °C |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Membrane lipid | log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMembrane-lipid/A calculated as log10 KMembrane-lipid/A calculated as log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KWA + log10 KWA + log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KMembrane-lipid/W where KMembrane-lipid/W is predicted with ppLFER by Endo et al.165 KMembrane-lipid/W where KMembrane-lipid/W is predicted with ppLFER by Endo et al.165 |
log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA at 37 °C KOA at 37 °C |
| Tissue | log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KTissue/A calculated as log10 KTissue/A calculated as log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KTissue/W + log10 KTissue/W + log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KWA where KTissue/W is predicted with a composition model by Endo et al.143 using ppLFERs for KStorage-lipid/W by Geisler et al.,164KMembrane-lipid/W by Endo et al.,165KAlbumin/W by Endo and Goss,169KProtein/W by Endo et al.170 KWA where KTissue/W is predicted with a composition model by Endo et al.143 using ppLFERs for KStorage-lipid/W by Geisler et al.,164KMembrane-lipid/W by Endo et al.,165KAlbumin/W by Endo and Goss,169KProtein/W by Endo et al.170 |
log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KTissue/A predicted using a fractional composition model with KOA to 37 °C; KTissue/A = (fStorage-lipid + fMembrane-lipid)KOA + fWKWA KTissue/A predicted using a fractional composition model with KOA to 37 °C; KTissue/A = (fStorage-lipid + fMembrane-lipid)KOA + fWKWA |
| Aerosols | Average of log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPA for aerosol sampled in Dübendorf fall & winter, Aspvretn, and Roost, predicted using ppLFERs by Arp et al.171 KPA for aerosol sampled in Dübendorf fall & winter, Aspvretn, and Roost, predicted using ppLFERs by Arp et al.171 |
log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPA predicted with spLFER by Harner and Bidleman95 using KOA at 15 °C KPA predicted with spLFER by Harner and Bidleman95 using KOA at 15 °C |
| POM | log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPOM/A calculated as log10 KPOM/A calculated as log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPOM/W + log10 KPOM/W + log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KWA where KPOM/W is predicted with ppLFER by Endo et al.172 KWA where KPOM/W is predicted with ppLFER by Endo et al.172 |
log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPOM/A predicted with spLFER by Reppas-Chrysovitsinos et al.138 using KOA at 25 °C KPOM/A predicted with spLFER by Reppas-Chrysovitsinos et al.138 using KOA at 25 °C |
| PDMS | log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPDMS/A predicted with ppLFER by Sprunger et al.173 KPDMS/A predicted with ppLFER by Sprunger et al.173 |
log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KPDMS/A predicted with spLFER by Reppas-Chrysovitsinos et al.138 using KOA at 25 °C KPDMS/A predicted with spLFER by Reppas-Chrysovitsinos et al.138 using KOA at 25 °C |
In general, there are very strong correlations (R2 > 0.89) between the KOA based spLFER and ppLFER estimated values of log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KXA (Fig. 1). Such good correlations can at least in part be attributed to a statistical issue discussed by Paterson and Mackay,51 who assert that apparently significant correlations can be obtained by inadvertently correlating a quantity with itself. In the current case, log10
KXA (Fig. 1). Such good correlations can at least in part be attributed to a statistical issue discussed by Paterson and Mackay,51 who assert that apparently significant correlations can be obtained by inadvertently correlating a quantity with itself. In the current case, log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KXA and log10
KXA and log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA are almost inevitably correlated, because of the presence of the “solubility in air” in their denominator (eqn (10) and (11)). The vapour pressure, or “solubility in air”, of substances ranges over many orders of magnitude, whereas the solubilities of substances in organic phases vary little and thus contribute little to the variation in partition ratios between chemicals. For similar reasons the KOA is very highly correlated with the liquid saturation vapour pressure.50 In order to eliminate this auto-correlation, we also plot the difference between ppLFER and spLFER estimates of KXA against the log10
KOA are almost inevitably correlated, because of the presence of the “solubility in air” in their denominator (eqn (10) and (11)). The vapour pressure, or “solubility in air”, of substances ranges over many orders of magnitude, whereas the solubilities of substances in organic phases vary little and thus contribute little to the variation in partition ratios between chemicals. For similar reasons the KOA is very highly correlated with the liquid saturation vapour pressure.50 In order to eliminate this auto-correlation, we also plot the difference between ppLFER and spLFER estimates of KXA against the log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA used to generate the spLFER estimate (Fig. 2).
KOA used to generate the spLFER estimate (Fig. 2).
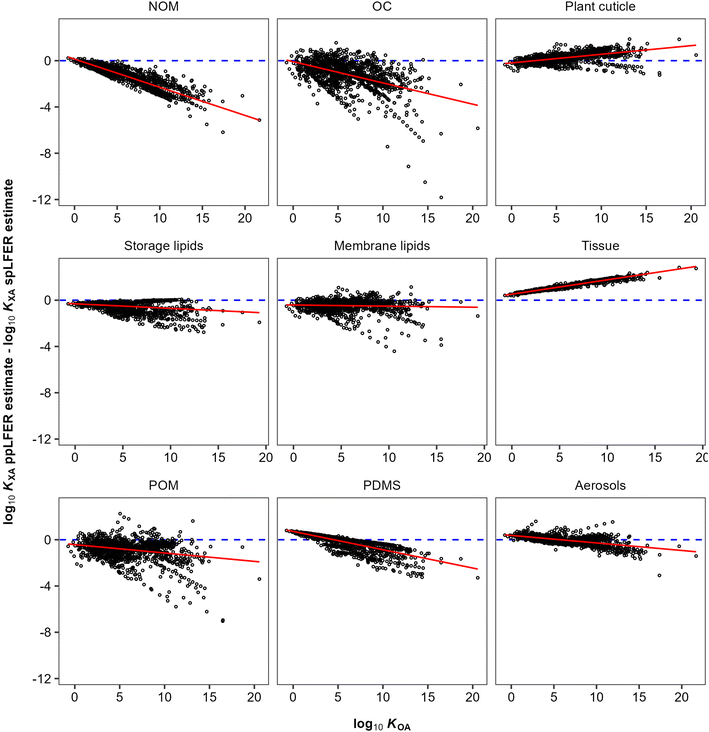 | ||
Fig. 2 The difference between ppLFER and spLFER estimates for log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KXA plotted against the log10 KXA plotted against the log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA used to derive the spLFER estimate. KOA used to derive the spLFER estimate. | ||
Thus, if the KOA is a good surrogate for a partitioning equilibrium, we expect to see a regression with a slope m of near unity in Fig. 1 (ref. 47) and a horizontal regression line in Fig. 2. By normalizing ppLFER estimated values of KXA by spLFER estimates of KXA we can better visualize the variation in KXA with KOA that is not easily observed in Fig. 1. For example, a negative slope in Fig. 2 indicates that as the KOA of a chemical increases, the KOA based estimate (i.e., the spLFER estimate) is greater than the ppLFER estimate. This suggests that when the slope is negative (<0), the activity ratio (γO/γX) is greater than 1 whereas a positive slope suggests that the activity ratio is less than 1. In Table 2 we present the slopes and intercepts of the regressions and coefficients of determination (R2) of both plots and the root mean squared error (RMSE) between the spLFER and ppLFER-based estimates.
| Phase X | Fig. 1 | Fig. 2 | RMSE | ||||
|---|---|---|---|---|---|---|---|
| Slope | Intercept | R 2 | Slope | Intercept | R 2 | ||
| NOM | 0.78 | −0.04 | 0.98 | −0.24 | 0.14 | 0.79 | 0.42 |
| OC | 0.83 | −0.22 | 0.89 | −0.18 | −0.08 | 0.25 | 1.02 |
| Plant cuticle | 1.07 | −0.19 | 0.99 | 0.07 | −0.19 | 0.28 | 0.39 |
| Storage lipids | 0.96 | −0.31 | 0.97 | −0.04 | −0.31 | 0.06 | 0.50 |
| Membrane lipids | 0.99 | −0.41 | 0.97 | −0.01 | −0.41 | 0.00 | 0.53 |
| Tissue | 1.12 | 0.97 | 0.99 | 0.12 | 0.52 | 0.95 | 0.26 |
| POM | 0.93 | −0.47 | 0.92 | −0.07 | −0.42 | 0.07 | 0.87 |
| PDMS | 0.84 | 0.58 | 0.97 | −0.16 | 0.72 | 0.57 | 0.45 |
| Aerosols | 0.93 | −0.50 | 0.99 | −0.07 | 0.37 | 0.31 | 0.33 |
Slopes near 1 in Fig. 1 and near 0 in Fig. 2 and RMSE values of 0.50 and 0.53 respectively, indicate that the KOA value is a good surrogate for the partitioning between storage and membrane lipids and the gas phase and a very good predictor for partitioning into tissue. The results for PDMS are similar to those of storage and membrane lipids. The KOA also appears to be a reasonable surrogate for the partitioning between aerosols95 and plant cuticles163 and the gas phase, with RMSE values of 0.33 and 0.39 respectively. In the case of partitioning to soil organic matter from the gas phase, the spLFERs based on the KOA have the highest RMSE and tend to give predictions that are biased low for compounds with high KOA values, indicated by the slopes in the plots in Fig. 2 being negative and the large scatter below the regression line. To a smaller extent that is also the case for the KOA-based spLFERs for POM and PDMS138 and the storage164 and membrane lipids.165 The opposite is the case for the KOA and KAW-based fractional composition model for KTissue/A where a positive slope in Fig. 2 suggest that relying on KOA to estimate partitioning into tissues leads to an overestimation for low volatility compounds.
4 Is the KOA obsolete?
4.1 Alternative means for predicting environmental phase equilibria involving the gas phase
A major motivation for introducing the KOA as an equilibrium partitioning property was to use it in the prediction of other equilibria between environmental phases and the gas phase. Accordingly, the literature is replete with linear free energy relationships that regress an environmentally relevant partitioning ratio involving the gas phase against KOA (see also Section 2). Those predictive equations suffer from the same shortcomings as other single-parameter linear free energy relationships, namely they have no universal applicability, but require different regression coefficients for different compound groups capable of undergoing a variety of intermolecular interactions.92 The longevity and popularity of those equations can be explained in part by their robustness for largely non-polar substances and the prevalence of such substances among the contaminants of historical concern.Major progress in predicting environmental phase equilibria has been made in the decades since the KOA has first been introduced. In particular, poly-parameter linear free energy relationships (ppLFERs) have become a viable method for predicting partition ratios involving environmental phases, mostly, because (i) calibrations have been performed to determine system constants (the regression constants of the ppLFER equations) for most environmentally relevant phase equilibria or can be estimated,162,174 (ii) solute descriptors for numerous contaminants have been experimentally determined.175 When carefully calibrated system constants and experimental solute descriptors are combined, ppLFERs can achieve prediction accuracy on the order of 0.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 units.176 Even for substances, for which no experimental solute descriptors exist, those descriptors can now be predicted with the help of QSPRs162,177 and still result in a prediction accuracy for environmental phase equilibria better than one order of magnitude.176KOA-based spLFERs would be hard pressed to match such accuracy, even if they were only applied to substances appropriate for a particular regression, i.e., similar to the substances used in the calibration of that spLFER. In other words, there is no longer the need for a parameter such as KOA to predict contaminant partitioning from the gas phase into organism lipids,164 soil organic matter,167 atmospheric particles,171 or sampling sorbents.178
log10 units.176 Even for substances, for which no experimental solute descriptors exist, those descriptors can now be predicted with the help of QSPRs162,177 and still result in a prediction accuracy for environmental phase equilibria better than one order of magnitude.176KOA-based spLFERs would be hard pressed to match such accuracy, even if they were only applied to substances appropriate for a particular regression, i.e., similar to the substances used in the calibration of that spLFER. In other words, there is no longer the need for a parameter such as KOA to predict contaminant partitioning from the gas phase into organism lipids,164 soil organic matter,167 atmospheric particles,171 or sampling sorbents.178
The merit of ppLFER extends beyond the provision of estimates that tend to be more precise than estimates from KOA-based spLFERs. By describing the different intermolecular interactions involved in partitioning, ppLFERs also provide a mechanistic understanding of organic chemical solvation in various phases.179
The question therefore arises whether there is still a need for the KOA. The answer is two-fold. First there are still some partitioning equilibria between air and organic phases, which need to be predicted with the help of KOA-based spLFERs. Second, the utility of the KOA is not limited to the prediction of specific environmentally relevant phase equilibria.
4.2 Continued need for KOA-based predictions of environmental phase equilibria
Currently, there are no robust ppLFERs that would be able to predict partitioning into plants. The ppLFER for plant cuticles by Platts and Abraham163 suffers from (i) a limited suitability of isolated tomato cuticles to represent plant foliage more generally and (ii) a calibration that had not a sufficiently diverse set of substances to be widely applicable with confidence. Therefore, KOA-based prediction methods are still required for the very plant–air phase equilibria, for which the KOA was first introduced.39 Important examples include the empirical KOA-based equations for predicting partitioning in forest canopies (eqn (9) and (10) in Horstmann and McLachlan,76eqn (11) in Su et al.77).While many environmentally relevant phase equilibria can now be predicted directly, the availability of tools to predict partition ratios at a variety of temperatures is much more limited. For example, while ppLFERs for predicting gas particle partitioning at 15 °C exist,171 atmospheric temperatures range over more than 60 K. The KOA for many contaminants has been determined as a function of temperature or can be predicted using a ppLFER for the internal energy of phase transfer from octanol to gas phase 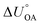 .161,180 It is thus possible to estimate an environmentally relevant equilibrium partition ratio at any temperature by either (i) applying KOA-based spLFERs by inserting (empirical or predicted) KOA values at the relevant temperatures or by (ii) adjusting the environmentally relevant partition ratio to the desired temperature using van't Hoff's equation and the (empirical or predicted)
.161,180 It is thus possible to estimate an environmentally relevant equilibrium partition ratio at any temperature by either (i) applying KOA-based spLFERs by inserting (empirical or predicted) KOA values at the relevant temperatures or by (ii) adjusting the environmentally relevant partition ratio to the desired temperature using van't Hoff's equation and the (empirical or predicted) 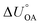 . Implicit in either approach is that the temperature dependence of the partitioning between the environmentally relevant phase and the gas phase is well described by the temperature dependence of octanol–air partitioning. Admittedly, one can obviously also adjust an equilibrium partitioning ratio derived from a ppLFER using such a
. Implicit in either approach is that the temperature dependence of the partitioning between the environmentally relevant phase and the gas phase is well described by the temperature dependence of octanol–air partitioning. Admittedly, one can obviously also adjust an equilibrium partitioning ratio derived from a ppLFER using such a 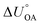 . Note, since the KOA and many other environmentally relevant phase equilibrium ratios are commonly defined using molar volumetric concentration in the gas phase (rather than a partial pressure), the
. Note, since the KOA and many other environmentally relevant phase equilibrium ratios are commonly defined using molar volumetric concentration in the gas phase (rather than a partial pressure), the 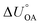 needs to be used in the van't Hoff equation.
needs to be used in the van't Hoff equation. 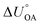 can be obtained from the enthalpy of phase transfer
can be obtained from the enthalpy of phase transfer 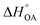 by deducting the product of the ideal gas constant and absolute temperature.
by deducting the product of the ideal gas constant and absolute temperature.
There is need to further explore the extent of agreement between the internal energy of phase transfer between various environmentally relevant phases X and the gas phase  and
and  . This is currently limited by the availability of measurements for KXA at different temperatures, but there are indications that
. This is currently limited by the availability of measurements for KXA at different temperatures, but there are indications that  can deviate from
can deviate from  .66
.66
4.3 The need for a single parameter describing partitioning from the gas phase into a wide variety of environmentally relevant organic phases
However, even if well-calibrated ppLFER equations existed for all relevant partitioning equilibria between air and organic phases at all desired temperatures, it would still be useful to have a single parameter that can serve to describe the tendency of a neutral organic chemical to partition from the gas phase into a wide variety of organic phases of environmental relevance. For such a parameter to be most useful, it needs to be (i) well-defined, (ii) directly accessible to measurement, and (iii) a reasonable surrogate for a wide variety of organic phases. The KOA is better suited to this role than other parameters:• An equilibrium partition ratio involving a real environmental organic phase is not a good choice because environmental phases are of variable composition and therefore not sufficiently well-defined.
• While the saturation vapour pressure is the traditional parameter for expressing compound volatility, the solid state vapour pressure is not an appropriate parameter to describe the volatility of a substance from any organic phase other than its own pure solid phase, because of the strong influence of the lattice energy.
• Although this can be in principle corrected by using the saturation vapour pressure of the sub-cooled liquid, it has the drawback that this parameter cannot be determined directly by experiment. It also implies that the organic reference phase is a different one for every substance.
• While other organic solvents or polymers may be equally good (and possibly even better) surrogates of environmental organic phases relative to octanol, the knowledge of how good a surrogate octanol is, is much better than for any other organic solvent (see Section 3).
As such, the KOA can still play an important role as a measure of volatility from organic phases. It is an easy to comprehend, single chemical characteristic that can be used to judge a chemical's propensity to undergo a very wide range of environmental processes. Just by knowing a compound's KOA, it is possible to infer a tremendous amount of information on its environmental behaviour. This is illustrated in Fig. 3. For example, instead of requiring separate parameters to assess a chemical's equilibrium phase distribution in atmosphere and soils, its susceptibility to evaporate or be exhaled, and the importance of processes controlling its deposition to plants, this can all be deduced from the compound's KOA. At the same time, it can inform you about the suitability of a sampling sorbent for the compound and which human exposure pathways are likely to be relevant.
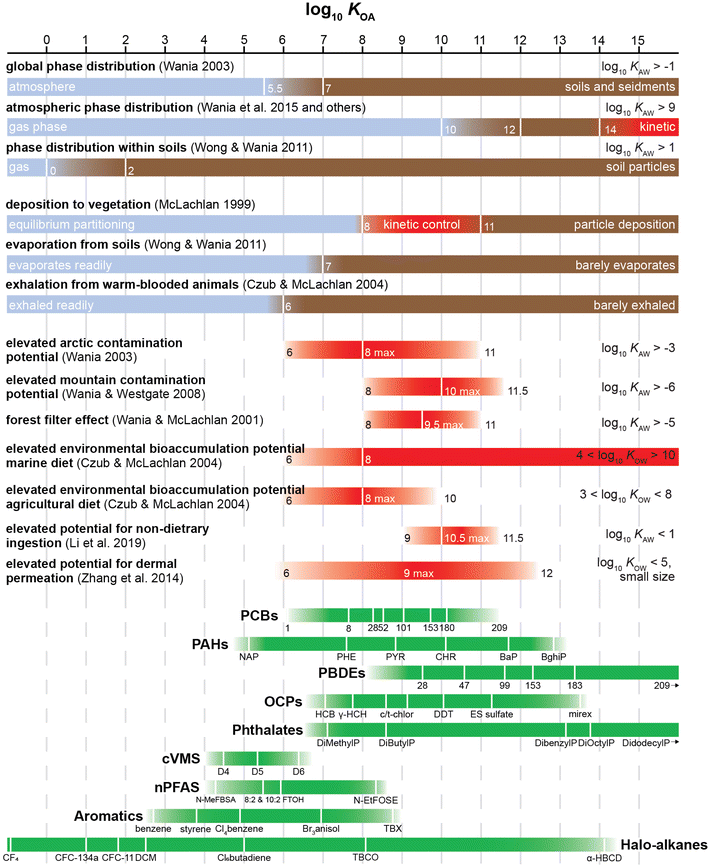 | ||
Fig. 3 Relationship between KOA range and the environmental fate of common contaminants. Vertical lines are indicative of the log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KOA, blue and brown bars indicate the relative dominant phase a chemical will be present in,52,53,181–183 red bars indicate the bioaccumulation potential of chemicals within a KOA range,52,158,181,184–186 and green bars indicate the KOA range of various compound groups. PCBs: polychorinated biphenyls; PAHs: polycyclic aromatic hydrocarbons; PBDEs: polybrominated diphenyl ethers; OCPs: organochlorine pesticides; cVMS: cyclic volatile methylsiloxanes; nPFAS: per- and poly-fluoroalkyl substances. KOA, blue and brown bars indicate the relative dominant phase a chemical will be present in,52,53,181–183 red bars indicate the bioaccumulation potential of chemicals within a KOA range,52,158,181,184–186 and green bars indicate the KOA range of various compound groups. PCBs: polychorinated biphenyls; PAHs: polycyclic aromatic hydrocarbons; PBDEs: polybrominated diphenyl ethers; OCPs: organochlorine pesticides; cVMS: cyclic volatile methylsiloxanes; nPFAS: per- and poly-fluoroalkyl substances. | ||
Another example for the utility of such a parameter is that it can serve as a volatility threshold for classification, prioritization and possibly even regulation of chemicals (Section 2.5.7). For example, KOA is being used as a threshold for the potential to bioaccumulate in air-breathing species.187
Another advantage of KOA is the possibility to use it in analyses that require the display of model results as a function of the chemical partitioning space. By taking advantage of octan-1-ol being able to represent a wide variety of organic phases reasonably well, the KOA facilitates the display of model-derived contaminant behaviour in a chemical partitioning space defined by coordinates of hydrophobicity and volatility. For example, when Czub et al.188 plotted the model calculated combined Arctic Contamination and BioAccumulation Potential (AC-BAP) of organic chemicals as a function of KOA and KAW, octan-1-ol simultaneously serves to approximate the solvation properties of soil and sedimentary organic matter, forest canopies, organic aerosol particles and lipids in a variety of organisms (plants, food animals, humans). Similarly, in Li et al.'s158 analysis of human exposure pathway, the KOA is used simultaneously to estimate partition equilibria between a very large variety of phases and the gas phase. This includes soil and sediment organic matter, atmospheric particles, house dust, various indoor surfaces, plant and animal lipids and human skin. While it would be possible to perform the type of model calculations performed by Czub et al.188 and Li et al.158 using partitioning ratios that are not estimated from KOA, it would be much more difficult to perform the systematic investigation of how the model results depend on the partitioning characteristics of an organic chemical without relying on partitioning ratios involving octan-1-ol. It would clearly be impossible to display them in a two-dimensional partitioning space.
5 Conclusion
This review examines the role of the KOA in environmental chemistry. We examined the historical context of partition ratios and the various ways the KOA is used to predict and describe gas partitioning properties in the real environment. The KOA is shown to be a reasonable surrogate for multiple environmental phases and has applications in environmental, atmospheric, physical chemical, medical, and food sciences. It is more advantageous to use the KOA to describe these partitioning processes instead of vapour pressure, because it is well defined, has broader applicability, and can be reliably estimated and measured.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the European Chemical Industry Council (CEFIC) through project ECO 41 of the Long-range Research Initiative (LRI).References
- R. Bunsen, XV. On the law of absorption of gases, London, Edinburgh Dublin Philos. Mag. J. Sci., 1855, 9, 116–130 CrossRef.
- W. Henry III., Experiments on the quantity of gases absorbed by water, at different temperatures, and under different pressures, Philos. Trans. R. Soc. London, 1803, 93, 29–42 CrossRef.
- W. Ostwald, Solutions, Longmans, Green, and Co., London, New York, 1891 Search PubMed.
- H. Meyer, Zur theorie der alkoholnarkose, Arch. Exp. Pathol. Pharmakol., 1899, 42, 109–118 CrossRef.
- C. E. Overton, Studien über die Narkose: Zugleich ein Beitrag zur allgemeinen Pharmakologie, Fischer, Jena, 1901 Search PubMed.
- G. J. Pierotti, C. H. Deal, E. L. Derr and P. E. Porter, Solvent effects in gas–liquid partition chromatography, J. Am. Chem. Soc., 1956, 78, 2989–2998 CrossRef CAS.
- P. E. Porter, C. H. Deal and F. H. Stross, The determination of partition coefficients from gas–liquid partition chromatography, J. Am. Chem. Soc., 1956, 78, 2999–3006 CrossRef CAS.
- J. H. Smith, W. R. Mabey, N. Bohonos, B. R. Holt, S. S. Lee, T. W. Chou, D. C. Bomberger and T. Mill, Environmental Pathways of Selected Chemicals in Freshwater Systems Part 1: Background and Experimental Procedures, Environmental Protection Agency, 1977, Technical Report 600778074 Search PubMed.
- D. R. Branson, Estimating the Hazard of Chemical Substances to Aquatic Life, American Society for Testing and Materials, 1978, pp. 55–70 Search PubMed.
- The IUPAC, Compendium of Chemical Terminology: the Gold Book, IUPAC, International Union of Pure and Applied Chemistry (IUPAC), Research Triangle Park, NC, 4th edn, 2019 Search PubMed.
- S. Baskaran, Y. D. Lei and F. Wania, A database of experimentally derived and estimated octanol–air partition ratios (KOA), J. Phys. Chem. Ref. Data, 2021, 50, 043101 CrossRef CAS.
- F. L. Boyer and L. J. Bircher, The solubility of nitrogen, argon, methane, ethylene and ethane in normal primary alcohols, J. Phys. Chem., 1960, 64, 1330–1331 CrossRef CAS.
- P. Berti, S. Cabani, G. Conti and V. Mollica, Thermodynamic study of organic compounds in octan-1-ol. Processes of transfer from gas and from dilute aqueous solution, J. Chem. Soc., Faraday Trans. 1, 1986, 82, 2547–2556 RSC.
- J. M. Roberts, Measurement of the Henry's law coefficient and first order loss rate of PAN in n-octanol, Geophys. Res. Lett., 2005, 32, L08803 Search PubMed.
- A. Hussam and P. W. Carr, Rapid and precise method for the measurement of vapor/liquid equilibria by headspace gas chromatography, Anal. Chem., 1985, 57, 793–801 CrossRef CAS.
- A. Finizio, D. Mackay, T. Bidleman and T. Harner, Octanol–air partition coefficient as a predictor of partitioning of semi-volatile organic chemicals to aerosols, Atmos. Environ., 1997, 31, 2289–2296 CrossRef CAS.
- R. Battino and H. L. Clever, The solubility of gases in liquids, Chem. Rev., 1966, 66, 395–463 CrossRef CAS.
- A. E. Markham and K. A. Kobe, The solubility of gases in liquids, Chem. Rev., 1941, 28, 519–588 CrossRef CAS.
- D. H. Robinson and A. H. Toledo, Historical Development of Modern Anesthesia, J. Investig. Surg., 2012, 25, 141–149 CrossRef PubMed.
- A. Seidell, Solubilities of Inorganic and Organic Compounds, a Compilation of Quantitative Solubility Data from the Periodical Literature, New York, Van Nostrand, 1919 Search PubMed.
- D. D. Van Slyke and J. M. Neill, The determination of gases in blood and other solutions by vacuum extraction and manometric measurement. i, J. Biol. Chem., 1924, 61, 523–573 CrossRef CAS.
- K. Meyer and H. Hemmi, Beitrage zur theorie der narkose. III, Biochem. Z., 1935, 39–71 CAS.
- R. Collander, On lipoid solubility, Acta Physiol. Scand., 1947, 13, 363–381 CrossRef CAS PubMed.
- R. Collander, The partition of organic compounds between higher alcohols and water, Acta Chem. Scand., 1951, 774–780 CrossRef CAS.
- R. Collander, The permeability of nitella cells to non-electrolytes, Physiol. Plant., 1954, 7, 420–445 CrossRef CAS.
- C. Hansch, Drug Design, Academic Press, New York, 1971, vol. 1, pp. 271–342 Search PubMed.
- C. Hansch, P. P. Maloney, T. Fujita and R. M. Muir, Correlation of biological activity of phenoxyacetic acids with Hammett substituent constants and partition coefficients, Nature, 1962, 194, 178–180 CrossRef CAS.
- T. Fujita, J. Iwasa and C. Hansch, A new substituent constant, π, derived from partition coefficients, J. Am. Chem. Soc., 1964, 86, 5175–5180 CrossRef CAS.
- A. Leo, C. Hansch and D. Elkins, Partition coefficients and their uses, Chem. Rev., 1971, 71, 525–616 CrossRef CAS.
- C. Hansch, Annual Reports in Medicinal Chemistry, Academic Press, 1968, vol. 3, pp. 348–357 Search PubMed.
- C. Hansch, Annual Reports in Medicinal Chemistry, Academic Press, 1967, vol. 2, pp. 347–359 Search PubMed.
- R. Wixon, Chromatography: a Century of Discovery 1900–2000: the Bridge to the Sciences/Technology, Elsevier Science, Ltd, Amsterdam; New York, 1st edn, 2001, pp. 1–38 Search PubMed.
- G. J. Pierotti, C. H. Deal and E. L. Derr, Activity coefficients and molecular structure, Ind. Eng. Chem., 1959, 51, 95–102 CrossRef CAS.
- J. Gmehling and J. Menke, Activity Coefficients at Infinite Dilution. Pt. 5: C1–C16, DECHEMA, Frankfurt/Main, 2007, vol. 9 Search PubMed.
- L. Rohrschneider, Solvent characterization by gas–liquid partition coefficients of selected solutes, Anal. Chem., 1973, 45, 1241–1247 CrossRef CAS.
- R. J. Wilcock, R. Battino, W. F. Danforth and E. Wilhelm, Solubilities of gases in liquids II. The solubilities of He, Ne, Ar, Kr, O2, N2, CO, CO2, CH4, CF4, and SF6 in n-octane 1-octanol, n-decane, and 1-decanol, J. Chem. Thermodyn., 1978, 10, 817–822 CrossRef CAS.
- R. Battino, F. D. Evans and W. F. Danforth, The solubilities of seven gases in olive oil with references to theories of transport through the cell membrane, J. Am. Oil Chem. Soc., 1968, 45, 830–833 CrossRef CAS PubMed.
- J. E. Byrne, R. Battino and W. F. Danforth, The solubility of gases in liquids 7. The solubilities of N2, O2, Ar, CO, CO2, and c-C3H6 in benzene and isobutanol solutions of cholesterol, lecithin, and cephalin at 310.65 K, J. Chem. Thermodyn., 1974, 6, 245–250 CrossRef CAS.
- S. Paterson, D. Mackay, D. Tam and W. Shiu, Uptake of organic chemicals by plants: a review of processes, correlations and models, Chemosphere, 1990, 21, 297–331 CrossRef CAS.
- G. L. Pollack, J. F. Himm and J. J. Enyeart, Solubility of xenon in liquid n-alkanols: Thermodynamic functions in simple polar liquids, J. Chem. Phys., 1984, 81, 3239–3246 CrossRef CAS.
- S. Taheri, M. J. Halsey, J. Liu, E. I. I. Eger, D. D. Koblin and M. J. Laster, What solvent best represents the site of action of inhaled anesthetics in humans, rats, and dogs?, Anesth. Analg., 1991, 72, 627–634 CrossRef CAS PubMed.
- S. Taheri, M. J. Laster, J. Liu, E. I. I. Eger, M. J. Halsey and D. D. Koblin, Anesthesia by n-alkanes not consistent with the Meyer-Overton hypothesis: Determinations of the solubilities of alkanes in saline and various lipids, Anesth. Analg., 1993, 77, 7–11 CrossRef CAS PubMed.
- J. Liu, J. Laster, S. Taheri, E.I. Eger, D. D. Koblin and M. J. Halsey, Is there a cutoff in anesthetic potency for the normal alkanes?, Anesth. Analg., 1993, 77, 12–18 CrossRef CAS PubMed.
- T. Harner and D. Mackay, Measurement of octanol–air partition coefficients for chlorobenzenes, PCBs, and DDT, Environ. Sci. Technol., 1995, 29, 1599–1606 CrossRef CAS PubMed.
- A. J. Dallas, PhD thesis, University of Minnesota, United States – Minnesota, 1995.
- H. V. Andersen and M. Frederiksen, Sorption of PCB from air to settled house dust in a contaminated indoor environment, Chemosphere, 2021, 266, 129139 CrossRef CAS PubMed.
- T. Salthammer and T. Schripp, Application of the Junge- and Pankow-equation for estimating indoor gas/particle distribution and exposure to SVOCs, Atmos. Environ., 2015, 106, 467–476 CrossRef CAS.
- K.-U. Goss and R. P. Schwarzenbach, Gas/solid and gas/liquid partitioning of organic compounds: critical evaluation of the interpretation of equilibrium constants, Environ. Sci. Technol., 1998, 32, 2025–2032 CrossRef CAS.
- J. F. Pankow, Further discussion of the octanol/air partition coefficient KOA as a correlating parameter for gas/particle partitioning coefficients, Atmos. Environ., 1998, 32, 1493–1497 CrossRef CAS.
- H. Xiao and F. Wania, Is vapor pressure or the octanol–air partition coefficient a better descriptor of the partitioning between gas phase and organic matter?, Atmos. Environ., 2003, 37, 2867–2878 CrossRef CAS.
- S. Paterson and D. Mackay, Correlation of tissue, blood, and air partition coefficients of volatile organic chemicals, Br. J. Ind. Med., 1989, 46, 321–328 CAS.
- G. Czub and M. S. McLachlan, Bioaccumulation potential of persistent organic chemicals in humans, Environ. Sci. Technol., 2004, 38, 2406–2412 CrossRef CAS PubMed.
- M. S. McLachlan, Framework for the interpretation of measurements of SOCs in plants, Environ. Sci. Technol., 1999, 33, 1799–1804 CrossRef CAS.
- F. Zhao, I. Riipinen and M. MacLeod, Steady-state mass balance model for predicting particle–gas concentration ratios of PBDEs, Environ. Sci. Technol., 2021, 55, 9425–9433 CrossRef CAS PubMed.
- E. Bacci, M. J. Cerejeira, C. Gaggi, G. Chemello, D. Calamari and M. Vighi, Bioconcentration of organic chemical vapours in plant leaves: the azalea model, Chemosphere, 1990, 21, 525–535 CrossRef CAS.
- M. Riederer, Estimating partitioning and transport of organic chemicals in the foliage/atmosphere system: discussion of a fugacity-based model, Environ. Sci. Technol., 1990, 24, 829–837 CrossRef CAS.
- M. Riederer, Plant Contamination: Modeling and Simulation of Organic Chemical Processes, 1995 Search PubMed.
- N. L. L. Steyaert, M. Hauck, S. W. H. Van Hulle and A. Jan Hendriks, Modelling bioaccumulation of semi-volatile organic compounds (SOCs) from air in plants based on allometric principles, Chemosphere, 2009, 77, 727–732 CrossRef CAS PubMed.
- D. C. G. Muir, M. D. Segstro, P. M. Welbourn, D. Toom, S. J. Eisenreich, C. R. Macdonald and D. M. Whelpdale, Patterns of accumulation of airborne organochlorine contaminants in lichens from the Upper Great Lakes Region of Ontario, Environ. Sci. Technol., 1993, 27, 1201–1210 CrossRef CAS.
- J. F. Müller, D. W. Hawker and D. W. Connell, Calculation of bioconcentration factors of persistent hydrophobic compounds in the air/vegetation system, Chemosphere, 1994, 29, 623–640 CrossRef.
- P. Tremolada, V. Burnett, D. Calamari and K. C. Jones, Spatial distribution of PAHs in the U.K. atmosphere using pine needles, Environ. Sci. Technol., 1996, 30, 3570–3577 CrossRef CAS.
- D. L. Dowdy and T. E. McKone, Predicting plant uptake of organic chemicals from soil or air using octanol/water and octanol/air partition ratios and a molecular connectivity index, Environ. Toxicol. Chem., 1997, 16, 2448–2456 CrossRef CAS.
- R. Keymeulen, G. De Bruyn and H. Van Langenhove, Headspace gas chromatographic determination of the plant cuticle–air partition coefficients for monocyclic aromatic hydrocarbons as environmental compartment, J. Chromatogr. A, 1997, 774, 213–221 CrossRef CAS.
- J. Tolls and M. S. McLachlan, Partitioning of semivolatile organic compounds between air and Lolium multiflorum (Welsh ray grass), Environ. Sci. Technol., 1994, 28, 159–166 CrossRef CAS PubMed.
- R. H. A. Brown, J. N. Cape and J. G. Farmer, Partitioning of chlorinated solvents between pine needles and air, Chemosphere, 1998, 36, 1799–1810 CrossRef CAS.
- P. Kömp and M. S. McLachlan, Interspecies variability of the plant/air partitioning of polychlorinated biphenyls, Environ. Sci. Technol., 1997, 31, 2944–2948 CrossRef.
- L. Nizzetto, C. Pastore, X. Liu, P. Camporini, D. Stroppiana, B. Herbert, M. Boschetti, G. Zhang, P. A. Brivio, K. C. Jones and A. Di Guardo, Accumulation Parameters and Seasonal Trends for PCBs in Temperate and Boreal Forest Plant Species, Environ. Sci. Technol., 2008, 42, 5911–5916 CrossRef CAS PubMed.
- M. Taylor, S. M. Lyons, C. L. Davie-Martin, T. S. Geoghegan and K. J. Hageman, Understanding trends in pesticide volatilization from agricultural fields using the pesticide loss via volatilization model, Environ. Sci. Technol., 2020, 54, 2202–2209 CrossRef CAS PubMed.
- Y. Zhao, L. Yang and Q. Wang, Modeling persistent organic pollutant (POP) partitioning between tree bark and air and its application to spatial monitoring of atmospheric POPs in mainland china, Environ. Sci. Technol., 2009, 43, 8469–8470 CrossRef CAS.
- Y. Zhao, L. Yang and Q. Wang, Modeling persistent organic pollutant (POP) partitioning between tree bark and air and its application to spatial monitoring of atmospheric POPs in mainland China, Environ. Sci. Technol., 2008, 42, 6046–6051 CrossRef CAS PubMed.
- C. Rauert, A. Kananathalingam and T. Harner, Characterization and Modeling of Polycyclic Aromatic Compound Uptake into Spruce Tree Wood, Environ. Sci. Technol., 2017, 51, 5287–5295 CrossRef CAS PubMed.
- M. F. Sari, F. Esen and Y. Tasdemir, Characterization, source apportionment, air/plant partitioning and cancer risk assessment of atmospheric PAHs measured with tree components and passive air sampler, Environ. Res., 2021, 194, 110508 CrossRef CAS PubMed.
- X. Fu, J. Wang, X. Zhou, J. Deng, Y. Liu, W. Zhang, L. Liu, L. Dong and K. Lin, Tree bark as a passive air sampler to indicate atmospheric polybrominated diphenyl ethers (PBDEs) in southeastern China, Environ. Sci. Pollut. Res., 2014, 21, 7668–7677 CrossRef CAS PubMed.
- J. Leppich, J. H. Pardue and W. A. Jackson, Wetlands & Remediation: an International Conference, Columbus, 2000, pp. 17–24 Search PubMed.
- T. A. Wetzel and W. J. Doucette, Plant leaves as indoor air passive samplers for volatile organic compounds (VOCs), Chemosphere, 2015, 122, 32–37 CrossRef CAS PubMed.
- M. Horstmann and M. S. McLachlan, Atmospheric deposition of semivolatile organic compounds to two forest canopies, Atmos. Environ., 1998, 32, 1799–1809 CrossRef CAS.
- Y. Su, F. Wania, T. Harner and Y. D. Lei, Deposition of polybrominated diphenyl ethers, polychlorinated biphenyls, and polycyclic aromatic hydrocarbons to a boreal deciduous forest, Environ. Sci. Technol., 2007, 41, 534–540 CrossRef CAS PubMed.
- W. J. Doucette, C. Shunthirasingham, E. M. Dettenmaier, R. T. Zaleski, P. Fantke and J. A. Arnot, A review of measured bioaccumulation data on terrestrial plants for organic chemicals: Metrics, variability, and the need for standardized measurement protocols, Environ. Toxicol. Chem., 2018, 37, 21–33 CrossRef CAS PubMed.
- M. Limmer and J. Burken, Phytovolatilization of organic contaminants, Environ. Sci. Technol., 2016, 50, 6632–6643 CrossRef CAS PubMed.
- M. Hippelein and M. S. McLachlan, Soil/air partitioning of semivolatile organic compounds. 1. Method development and influence of physical-chemical properties, Environ. Sci. Technol., 1998, 32, 310–316 CrossRef CAS.
- M. D. Borisover and E. R. Graber, Specific interactions of organic compounds with soil organic carbon, Chemosphere, 1997, 34, 1761–1776 CrossRef CAS.
- S. W. Karickhoff, Semi-empirical estimation of sorption of hydrophobic pollutants on natural sediments and soils, Chemosphere, 1981, 10, 833–846 CrossRef CAS.
- A. Finizio, T. Bidleman and S. Szeto, Emission of chiral pesticides from an agricultural soil in the Fraser Valley, British Columbia, Chemosphere, 1998, 36, 345–355 CrossRef CAS.
- T. F. Bidleman, Atmospheric transport and air-surface exchange of pesticides, Water, Air, Soil Pollut., 1999, 115, 115–166 CrossRef CAS.
- I. T. Cousins, N. Hartlieb, C. Teichmann and K. C. Jones, Measured and predicted volatilisation fluxes of PCBs from contaminated sludge-amended soils, Environ. Pollut., 1997, 97, 229–238 CrossRef CAS PubMed.
- X. He, S. Chen, X. Quan, Z. Liu and Y. Zhao, Temperature-dependence of soil/air partition coefficient for polychlorinated biphenyls at subzero temperatures, Chemosphere, 2009, 77, 1427–1433 CrossRef CAS PubMed.
- N. Li, F. Wania, Y. D. Lei and G. L. Daly, A comprehensive and critical compilation, evaluation, and selection of physical–chemical property data for selected polychlorinated biphenyls, J. Phys. Chem. Ref. Data, 2003, 32, 1545–1590 CrossRef CAS.
- M. Hippelein and M. S. McLachlan, Soil/air partitioning of semivolatile organic compounds. 2. Influence of temperature and relative humidity, Environ. Sci. Technol., 2000, 34, 3521–3526 CrossRef CAS.
- C. L. Davie-Martin, K. J. Hageman, Y.-P. Chin, V. Rougé and Y. Fujita, Influence of temperature, relative humidity, and soil properties on the soil–air partitioning of semivolatile pesticides: Laboratory measurements and predictive models, Environ. Sci. Technol., 2015, 49, 10431–10439 CrossRef CAS PubMed.
- K.-U. Goss, The air/surface adsorption equilibrium of organic compounds under ambient conditions, Crit. Rev. Environ. Sci. Technol., 2004, 34, 339–389 CrossRef CAS.
- K.-U. Goss, J. Buschmann and R. P. Schwarzenbach, Adsorption of Organic Vapors to Air-Dry Soils: Model Predictions and Experimental Validation, Environ. Sci. Technol., 2004, 38, 3667–3673 CrossRef CAS PubMed.
- K.-U. Goss and R. P. Schwarzenbach, Linear free energy relationships used to evaluate equilibrium partitioning of organic compounds, Environ. Sci. Technol., 2001, 35, 1–9 CrossRef CAS PubMed.
- C. Junge, Fate of Pollutants in the Air and Water Environments, Wiley, New York, 1977, vol. 1, pp. 7–26 Search PubMed.
- J. F. Pankow, Review and comparative analysis of the theories on partitioning between the gas and aerosol particulate phases in the atmosphere, Atmos. Environ., 1987, 21, 2275–2283 CrossRef CAS.
- T. Harner and T. F. Bidleman, Octanol–air partition coefficient for describing particle/gas partitioning of aromatic compounds in urban air, Environ. Sci. Technol., 1998, 32, 1494–1502 CrossRef CAS.
- J. F. Pankow, An absorption model of the gas/aerosol partitioning involved in the formation of secondary organic aerosol, Atmos. Environ., 1994, 28, 189–193 CrossRef CAS.
- R. L. Falconer and T. Harner, Comparison of the octanol–air partition coefficient and liquid-phase vapor pressure as descriptors for particle/gas partitioning using laboratory and field data for PCBs and PCNs, Atmos. Environ., 2000, 34, 4043–4046 CrossRef CAS.
- H. Kaupp and M. S. McLachlan, Gas/particle partitioning of PCDD/Fs, PCBs, PCNs and PAHs, Chemosphere, 1999, 38, 3411–3421 CrossRef CAS.
- J.-E. Oh, J.-S. Choi and Y.-S. Chang, Gas/particle partitioning of polychlorinated dibenzo-p-dioxins and dibenzofurans in atmosphere; evaluation of predicting models, Atmos. Environ., 2001, 35, 4125–4134 CrossRef CAS.
- J. Radonic, M. Vojinovic-Miloradov, M. Turk-Sekulic, J. Kiurski, M. Djogo and D. Milovanovic, The octanol–air partition coefficient KOA as a predictor of gas-particle partitioning of polycyclic aromatic hydrocarbons and polychlorinated biphenyls at industrial and urban sites, J. Serb. Chem. Soc., 2011, 76, 447–458 CrossRef CAS.
- B. Chandramouli, M. Jang and R. M. Kamens, Gas–particle partitioning of semi-volatile organics on organic aerosols using a predictive activity coefficient model: analysis of the effects of parameter choices on model performance, Atmos. Environ., 2003, 37, 853–864 CrossRef CAS.
- H.-G. Yeo, M. Choi, M.-Y. Chun and Y. Sunwoo, Gas/particle concentrations and partitioning of PCBs in the atmosphere of Korea, Atmos. Environ., 2003, 37, 3561–3570 CrossRef CAS.
- C. W. Götz, M. Scheringer, M. MacLeod, C. M. Roth and K. Hungerbühler, Alternative approaches for modeling gas–particle partitioning of semivolatile organic chemicals: Model development and comparison, Environ. Sci. Technol., 2007, 41, 1272–1278 CrossRef PubMed.
- J. Dachs and S. J. Eisenreich, Adsorption onto aerosol soot carbon dominates gas-particle partitioning of polycyclic aromatic hydrocarbons, Environ. Sci. Technol., 2000, 34, 3690–3697 CrossRef CAS.
- P. Fernández, J. O. Grimalt and R. M. Vilanova, Atmospheric gas-particle partitioning of polycyclic aromatic hydrocarbons in high mountain regions of Europe, Environ. Sci. Technol., 2002, 36, 1162–1168 CrossRef PubMed.
- N. Vardar, Y. Tasdemir, M. Odabasi and K. E. Noll, Characterization of atmospheric concentrations and partitioning of PAHs in the Chicago atmosphere, Sci. Total Environ., 2004, 327, 163–174 CrossRef CAS PubMed.
- P. Helm and T. Bidleman, Gas–particle partitioning of polychlorinated naphthalenes and non- and mono–ortho-substituted polychlorinated biphenyls in arctic air, Sci. Total Environ., 2005, 342, 161–173 CrossRef CAS PubMed.
- C. J. Weschler and W. W. Nazaroff, Semivolatile organic compounds in indoor environments, Atmos. Environ., 2008, 42, 9018–9040 CrossRef CAS.
- C. J. Weschler and W. W. Nazaroff, SVOC partitioning between the gas phase and settled dust indoors, Atmos. Environ., 2010, 44, 3609–3620 CrossRef CAS.
- X. Zhang, M. L. Diamond, M. Robson and S. Harrad, Sources, emissions, and fate of polybrominated diphenyl ethers and polychlorinated biphenyls indoors in Toronto, Canada, Environ. Sci. Technol., 2011, 45, 3268–3274 CrossRef CAS PubMed.
- M. Shoeib, T. Harner, M. Ikonomou and K. Kannan, Indoor and outdoor air concentrations and phase partitioning of perfluoroalkyl sulfonamides and polybrominated diphenyl ethers, Environ. Sci. Technol., 2004, 38, 1313–1320 CrossRef CAS PubMed.
- M. Shoeib, T. Harner, B. H. Wilford, K. C. Jones and J. Zhu, Perfluorinated sulfonamides in indoor and outdoor air and indoor dust: Occurrence, partitioning, and human exposure, Environ. Sci. Technol., 2005, 39, 6599–6606 CrossRef CAS PubMed.
- T. F. Webster, S. Harrad, J. R. Millette, R. D. Holbrook, J. M. Davis, H. M. Stapleton, J. G. Allen, M. D. McClean, C. Ibarra, M. A.-E. Abdallah and A. Covaci, Identifying transfer mechanisms and sources of decabromodiphenyl ether (BDE 209) in indoor environments using environmental forensic microscopy, Environ. Sci. Technol., 2009, 43, 3067–3072 CrossRef CAS PubMed.
- H.-L. Li, L.-Y. Liu, Z.-F. Zhang, W.-L. Ma, E. Sverko, Z. Zhang, W.-W. Song, Y. Sun and Y.-F. Li, Semi-volatile organic compounds in infant homes: levels, influence factors, partitioning, and implications for human exposure, Environ. Pollut., 2019, 251, 609–618 CrossRef CAS PubMed.
- W. Wei, C. Dassonville, S. Sivanantham, A. Gregoire, F. Mercier, B. L. Bot, L. Malingre, O. Ramalho, M. Derbez and C. Mandin, Semivolatile organic compounds in French schools: Partitioning between the gas phase, airborne particles and settled dust, Indoor Air, 2021, 31, 156–169 CrossRef CAS PubMed.
- J. B. Wilcockson and F. A. P. C. Gobas, Thin-film solid-phase extraction to measure fugacities of organic chemicals with low volatility in biological samples, Environ. Sci. Technol., 2001, 35, 1425–1431 CrossRef CAS PubMed.
- U. M. Shahin, Y.-H. Li and T. M. Holsen, Dry deposition of gas-phase polycyclic aromatic hydrocarbons to greased surrogate surfaces, Aerosol Sci. Technol., 1999, 31, 446–455 CrossRef CAS.
- Y. Wu, C. M. A. Eichler, W. Leng, S. S. Cox, L. C. Marr and J. C. Little, Adsorption of phthalates on impervious indoor surfaces, Environ. Sci. Technol., 2017, 51, 2907–2913 CrossRef CAS PubMed.
- M. L. Diamond, S. E. Gingrich, K. Fertuck, B. E. McCarry, G. A. Stern, B. Billeck, B. Grift, D. Brooker and T. D. Yager, Evidence for organic film on an impervious urban surface: characterization and potential teratogenic effects, Environ. Sci. Technol., 2000, 34, 2900–2908 CrossRef CAS.
- C. M. Butt, M. L. Diamond, J. Truong, M. G. Ikonomou, P. A. Helm and G. A. Stern, Semivolatile organic compounds in window films from lower manhattan after the september 11th World Trade Center attacks, Environ. Sci. Technol., 2004, 38, 3514–3524 CrossRef CAS PubMed.
- C. M. Butt, M. L. Diamond, J. Truong, M. G. Ikonomou and A. F. H. ter Schure, Spatial distribution of polybrominated diphenyl ethers in Southern Ontario as measured in indoor and outdoor window organic films, Environ. Sci. Technol., 2004, 38, 724–731 CrossRef CAS PubMed.
- R. Wu, T. Harner, M. Diamond and B. Wilford, Partitioning characteristics of PCBs in urban surface films, Atmos. Environ., 2008, 42, 5696–5705 CrossRef CAS.
- C. Bi, Y. Liang and Y. Xu, Fate and transport of phthalates in indoor environments and the influence of temperature: a case study in a test house, Environ. Sci. Technol., 2015, 49, 9674–9681 CrossRef CAS PubMed.
- B. Cetin and M. Odabasi, Polybrominated diphenyl ethers (PBDEs) in indoor and outdoor window organic films in Izmir, Turkey, J. Hazard. Mater., 2011, 185, 784–791 CrossRef CAS PubMed.
- C. J. Weschler and W. W. Nazaroff, Growth of organic films on indoor surfaces, Indoor Air, 2017, 27, 1101–1112 CrossRef CAS PubMed.
- D. J. Donaldson, B. T. Mmereki, S. R. Chaudhuri, S. Handley and M. Oh, Uptake and reaction of atmospheric organic vapours on organic films, Faraday Discuss., 2005, 130, 227–239 RSC.
- W. A. Ockenden, H. F. Prest, G. O. Thomas, A. Sweetman and K. C. Jones, Passive air sampling of PCBs: Field calculation of atmospheric sampling rates by triolein-containing semipermeable membrane devices, Environ. Sci. Technol., 1998, 32, 1538–1543 CrossRef CAS.
- M. Shoeib and T. Harner, Characterization and comparison of three passive air samplers for persistent organic pollutants, Environ. Sci. Technol., 2002, 36, 4142–4151 CrossRef CAS PubMed.
- M. E. Bartkow, D. W. Hawker, K. E. Kennedy and J. F. Müller, Characterizing uptake kinetics of PAHs from the air using polyethylene-based passive air samplers of multiple surface area-to-volume ratios, Environ. Sci. Technol., 2004, 38, 2701–2706 CrossRef CAS PubMed.
- K. E. Kennedy, D. W. Hawker, J. F. Müller, M. E. Bartkow and R. W. Truss, A field comparison of ethylene vinyl acetate and low-density polyethylene thin films for equilibrium phase passive air sampling of polycyclic aromatic hydrocarbons, Atmos. Environ., 2007, 41, 5778–5787 CrossRef CAS.
- S. Ly-Verdú, F. A. Esteve-Turrillas, A. Pastor and M. de la Guardia, A passive sampling-based analytical strategy for the determination of volatile organic compounds in the air of working areas, Anal. Chim. Acta, 2010, 677, 131–139 CrossRef PubMed.
- N. De Coensel, K. Desmet, T. Górecki and P. Sandra, Determination of polydimethylsiloxane-air partition coefficients using headspace sorptive extraction, J. Chromatogr. A, 2007, 1150, 183–189 CrossRef CAS PubMed.
- J.-Y. Lao, C.-C. Wu, L.-J. Bao, L.-Y. Liu, L. Shi and E. Y. Zeng, Size distribution and clothing–air partitioning of polycyclic aromatic hydrocarbons generated by barbecue, Sci. Total Environ., 2018, 639, 1283–1289 CrossRef CAS PubMed.
- J. Yu, F. Wania and J. P. D. Abbatt, A New Approach to Characterizing the Partitioning of Volatile Organic Compounds to Cotton Fabric, Environ. Sci. Technol., 2022, 56, 3365–3374 CrossRef CAS PubMed.
- A. Saini, C. Rauert, M. J. Simpson, S. Harrad and M. L. Diamond, Characterizing the sorption of polybrominated diphenyl ethers (PBDEs) to cotton and polyester fabrics under controlled conditions, Sci. Total Environ., 2016, 563–564, 99–107 CrossRef CAS PubMed.
- D. Won, R. L. Corsi and M. Rynes, Sorptive interactions between VOCs and indoor materials: Sorptive interactions between VOCs and indoor materials, Indoor Air, 2001, 11, 246–256 CrossRef CAS PubMed.
- T. Schripp, T. Salthammer, C. Fauck, G. Bekö and C. J. Weschler, Latex paint as a delivery vehicle for diethylphthalate and di-n-butylphthalate: Predictable boundary layer concentrations and emission rates, Sci. Total Environ., 2014, 494–495, 299–305 CrossRef CAS PubMed.
- E. Reppas-Chrysovitsinos, A. Sobek and M. MacLeod, Screening-level models to estimate partition ratios of organic chemicals between polymeric materials, air and water, Environ. Sci.: Processes Impacts, 2016, 18, 667–676 RSC.
- P. Poulin and K. Krishnan, A tissue composition-based algorithm for predicting tissue:air partition coefficients of organic chemicals, Toxicol. Appl. Pharmacol., 1996, 136, 126–130 CrossRef CAS PubMed.
- P. Poulin and K. Krishnan, A mechanistic algorithm for predicting blood:air partition coefficients of organic chemicals with the consideration of reversible binding in hemoglobin, Toxicol. Appl. Pharmacol., 1996, 136, 131–137 CrossRef CAS PubMed.
- P. Poulin and K. Krishnan, Molecular structure-based prediction of the partition coefficients of organic chemicals for physiological pharmacokinetic models, Toxicol. Methods, 1996, 6, 117–137 CrossRef CAS.
- L. Li, J. N. Westgate, L. Hughes, X. Zhang, B. Givehchi, L. Toose, J. M. Armitage, F. Wania, P. Egeghy and J. A. Arnot, A Model for Risk-Based Screening and Prioritization of Human Exposure to Chemicals from Near-Field Sources, Environ. Sci. Technol., 2018, 52, 14235–14244 CrossRef CAS PubMed.
- S. Endo, T. N. Brown and K.-U. Goss, General model for estimating partition coefficients to organisms and their tissues using the biological compositions and polyparameter linear free energy relationships, Environ. Sci. Technol., 2013, 47, 6630–6639 CrossRef CAS PubMed.
- K. M. Hau and D. W. Connell, Quantitative structure-activity relationships (QSARs) for odor thresholds of volatile organic compounds (VOCs), Indoor Air, 1998, 8, 23–33 CrossRef CAS.
- K. M. Hau, D. W. Connell and B. J. Richardson, Quantitative structure-activity relationships for nasal pungency thresholds of volatile organic compounds, Toxicol. Sci., 1999, 47, 93–98 CrossRef CAS PubMed.
- K. M. Hau, D. W. Connell and B. J. Richardson, A Study of the Biological Partitioning Behavior of n-Alkanes and n-Alkanols in Causing Anesthetic Effects, Regul. Toxicol. Pharmacol., 2002, 35, 273–279 CrossRef CAS PubMed.
- G. D. Nielsen, E. S. Thomsen and Y. Alarie, Sensory irritant receptor compartment properties. Equipotent vapour concentrations related to saturated vapour concentrations, octanol-water, and octanol-gas partition coefficients, Acta Pharm. Nord., 1990, 2, 31–44 CAS.
- D. E. Raines, F. Gioia, R. J. Claycomb and R. J. Stevens, The N-methyl-D-aspartate receptor inhibitory potencies of aromatic inhaled drugs of abuse: evidence for modulation by cation-pi interactions, J. Pharmacol. Exp. Ther., 2004, 311, 14–21 CrossRef CAS PubMed.
- S. Tamaru, N. Igura and M. Shimoda, Effectiveness of water–air and octanol–air partition coefficients to predict lipophilic flavor release behavior from O/W emulsions, Food Chem., 2018, 239, 712–717 CrossRef CAS PubMed.
- S. Tamaru, A. Ono, N. Igura and M. Shimoda, High correlation between octanol–air partition coefficient and aroma release rate from O/W emulsions under non-equilibrium, Food Res. Int., 2019, 116, 883–887 CrossRef CAS PubMed.
- S. Batterman, L. Zhang, S. Wang and A. Franzblau, Partition coefficients for the trihalomethanes among blood, urine, water, milk and air, Sci. Total Environ., 2002, 284, 237–247 CrossRef CAS PubMed.
- G. A. Moser and M. S. McLachlan, Partitioning of polychlorinated biphenyls and hexachlorobenzene into human faeces, Chemosphere, 2002, 46, 449–457 CrossRef CAS PubMed.
- F. A. P. C. Gobas, B. C. Kelly and J. Arnot, Quantitative structure activity relationships for predicting the bioaccumulation of pops in terrestrial food-webs, QSAR Comb. Sci., 2003, 22, 329–336 CrossRef CAS.
- B. C. Kelly and F. A. P. C. Gobas, Bioaccumulation of persistent organic pollutants in lichen-caribou-wolf food chains of Canada's Central and Western Arctic, Environ. Sci. Technol., 2001, 35, 325–334 CrossRef CAS PubMed.
- Government of Canada, Persistence and Bioaccumulation Regulations, 2022, https://laws-lois.justice.gc.ca/PDF/SOR-2000-107.pdf Search PubMed.
- B. C. Kelly, M. G. Ikonomou, J. D. Blair, A. E. Morin and F. A. P. C. Gobas, Food web-specific biomagnification of persistent organic pollutants, Science, 2007, 317, 236–239 CrossRef CAS PubMed.
- S. K. Moses, J. R. Harley, C. L. Lieske, D. C. Muir, A. V. Whiting and T. M. O'Hara, Variation in bioaccumulation of persistent organic pollutants based on octanol–air partitioning: influence of respiratory elimination in marine species, Mar. Pollut. Bull., 2015, 100, 122–127 CrossRef CAS PubMed.
- L. Li, J. A. Arnot and F. Wania, How are humans exposed to organic chemicals released to indoor air?, Environ. Sci. Technol., 2019, 53, 11276–11284 CrossRef CAS PubMed.
- N. Aurisano, L. Huang, L. Milà i Canals, O. Jolliet and P. Fantke, Chemicals of concern in plastic toys, Environ. Int., 2021, 146, 106194 CrossRef CAS PubMed.
- S. Baskaran, Y. D. Lei and F. Wania, Reliable prediction of the octanol–air partition ratio, Environ. Toxicol. Chem., 2021, 40, 3166–3180 CrossRef CAS PubMed.
- S. Baskaran, A. Podagatlapalli, A. Sangion and F. Wania, Predicting the Temperature Dependence of the Octanol–Air Partition Ratio: A New Model for Estimating ΔUOA°, J. Solution Chem., 2023, 52, 51–69 CrossRef CAS.
- N. Ulrich, S. Endo, T. Brown, G. Bronner, M. H. Abraham and K.-U. Goss, UFZ-LSER Database V 3.2 [Internet], 2017 Search PubMed.
- J. A. Platts and M. H. Abraham, Partition of volatile organic compounds from air and from water into plant cuticular matrix: an LFER analysis, Environ. Sci. Technol., 2000, 34, 318–323 CrossRef CAS.
- A. Geisler, S. Endo and K.-U. Goss, Partitioning of organic chemicals to storage lipids: Elucidating the dependence on fatty acid composition and temperature, Environ. Sci. Technol., 2012, 46, 9519–9524 CrossRef CAS PubMed.
- S. Endo, B. I. Escher and K.-U. Goss, Capacities of membrane lipids to accumulate neutral organic chemicals, Environ. Sci. Technol., 2011, 45, 5912–5921 CrossRef CAS PubMed.
- M. H. Abraham, A. Ibrahim and W. E. Acree, Partition of compounds from gas to water and from gas to physiological saline at 310 K: Linear free energy relationships, Fluid Phase Equilib., 2007, 251, 93–109 CrossRef CAS.
- C. Niederer, R. P. Schwarzenbach and K.-U. Goss, Elucidating differences in the sorption properties of 10 humic and fulvic acids for polar and nonpolar organic chemicals, Environ. Sci. Technol., 2007, 41, 6711–6717 CrossRef CAS PubMed.
- T. H. Nguyen, K.-U. Goss and W. P. Ball, Polyparameter linear free energy relationships for estimating the equilibrium partition of organic compounds between water and the natural organic matter in soils and sediments, Environ. Sci. Technol., 2005, 39, 913–924 CrossRef CAS PubMed.
- S. Endo and K.-U. Goss, Serum albumin binding of structurally diverse neutral organic compounds: data and models, Chem. Res. Toxicol., 2011, 24, 2293–2301 Search PubMed.
- S. Endo, J. Bauerfeind and K.-U. Goss, Partitioning of neutral organic compounds to structural proteins, Environ. Sci. Technol., 2012, 46, 12697–12703 CrossRef CAS PubMed.
- H. P. H. Arp, R. P. Schwarzenbach and K.-U. Goss, Ambient gas/particle partitioning. 2: the influence of particle source and temperature on sorption to dry terrestrial aerosols, Environ. Sci. Technol., 2008, 42, 5951–5957 CrossRef CAS PubMed.
- S. Endo, S. E. Hale, K.-U. Goss and H. P. H. Arp, Equilibrium partition coefficients of diverse polar and nonpolar organic compounds to polyoxymethylene (POM) passive sampling devices, Environ. Sci. Technol., 2011, 45, 10124–10132 CrossRef CAS PubMed.
- L. Sprunger, A. Proctor, W. E. Acree and M. H. Abraham, Characterization of the sorption of gaseous and organic solutes onto polydimethyl siloxane solid-phase microextraction surfaces using the Abraham model, J. Chromatogr. A, 2007, 1175, 162–173 CrossRef CAS PubMed.
- T. N. Brown, QSPRs for predicting equilibrium partitioning in solvent–air systems from the chemical structures of solutes and solvents, J. Solution Chem., 2022, 1101–1132 CrossRef CAS.
- S. Endo and K.-U. Goss, Predicting partition coefficients of polyfluorinated and organosilicon compounds using polyparameter linear free energy relationships (PP-LFERs), Environ. Sci. Technol., 2014, 48, 2776–2784 CrossRef CAS PubMed.
- A. Stenzel, K.-U. Goss and S. Endo, Prediction of partition coefficients for complex environmental contaminants: Validation of COSMOtherm, ABSOLV, and SPARC, Environ. Toxicol. Chem., 2014, 33, 1537–1543 CrossRef CAS PubMed.
- T. N. Brown, IFSQSAR – A Python Package for Applying QSARs, 1.0.1, https://github.com/tnbrowncontam/ifsqsar Search PubMed.
- I. Kamprad and K.-U. Goss, Systematic investigation of the sorption properties of polyurethane foams for organic vapors, Anal. Chem., 2007, 79, 4222–4227 CrossRef CAS PubMed.
- S. Endo and K.-U. Goss, Applications of polyparameter linear free energy relationships in environmental chemistry, Environ. Sci. Technol., 2014, 48, 12477–12491 CrossRef CAS PubMed.
- C. Mintz, K. Burton, T. Ladlie, M. Clark, W. E. Acree and M. H. Abraham, Enthalpy of solvation correlations for gaseous solutes dissolved in dibutyl ether and ethyl acetate, Thermochim. Acta, 2008, 470, 67–76 CrossRef CAS.
- F. Wania, Assessing the Potential of Persistent Organic Chemicals for Long-Range Transport and Accumulation in Polar Regions, Environ. Sci. Technol., 2003, 37, 1344–1351 CrossRef CAS.
- F. Wania, Y. D. Lei, C. Wang, J. P. D. Abbatt and K.-U. Goss, Using the chemical equilibrium partitioning space to explore factors influencing the phase distribution of compounds involved in secondary organic aerosol formation, Atmos. Chem. Phys., 2015, 15, 3395–3412 CrossRef CAS.
- F. Wong and F. Wania, Visualising the equilibrium distribution and mobility of organic contaminants in soil using the chemical partitioning space, J. Environ. Monit., 2011, 13, 1569–1578 RSC.
- F. Wania and J. N. Westgate, On the Mechanism of Mountain Cold-Trapping of Organic Chemicals, Environ. Sci. Technol., 2008, 42, 9092–9098 CrossRef CAS PubMed.
- F. Wania and M. S. McLachlan, Estimating the Influence of Forests on the Overall Fate of Semivolatile Organic Compounds Using a Multimedia Fate Model, Environ. Sci. Technol., 2001, 35, 582–590 CrossRef CAS PubMed.
- X. Zhang, J. A. Arnot and F. Wania, Model for Screening-Level Assessment of Near-Field Human Exposure to Neutral Organic Chemicals Released Indoors, Environ. Sci. Technol., 2014, 48, 12312–12319 CrossRef CAS PubMed.
- European Chemicals Agency, Guidance on Information Requirements and Chemical Safety Assessment Chapter R.7c: Endpoint Specific Guidance., 2017 Search PubMed.
- G. Czub, F. Wania and M. S. McLachlan, Combining long-range transport and bioaccumulation considerations to identify potential arctic contaminants, Environ. Sci. Technol., 2008, 42, 3704–3709 CrossRef CAS PubMed.
Footnote |
| † Current affiliation and address: Department of Environmental Engineering, Norwegian Geotechnical Institute, Sandakerveien 140, 0484, Oslo, Norway. |
| This journal is © The Royal Society of Chemistry 2023 |