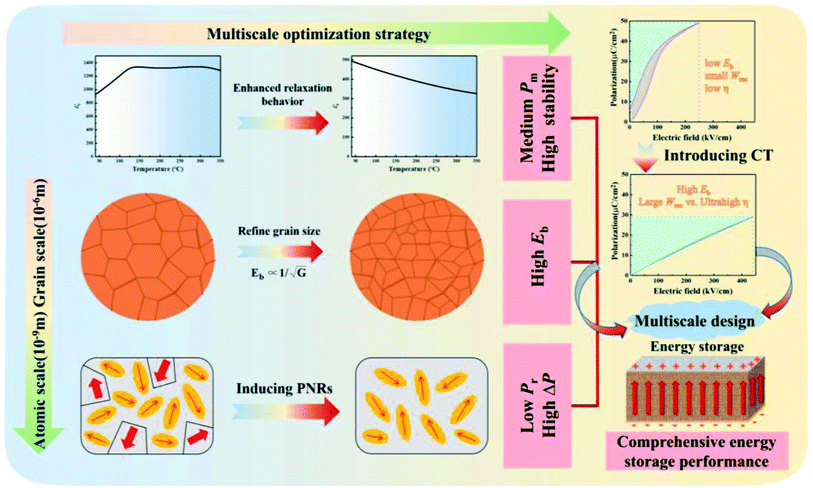
Superior energy storage performance in (Bi_0.5Na_0.5)TiO₃-based lead-free relaxor ferroelectrics for dielectric capacitor application via multiscale optimization design

Abstract

Developing environmentally friendly lead-free dielectric ceramics with ultrahigh energy storage performance is fundamental to next-generation high-power capacitors but challenging as well. Herein, a record-breaking ultrahigh energy efficiency η of 97.8% and high energy density W_rec of 5.81 J cm⁻³ are simultaneously achieved in (Bi_0.5Na_0.5)TiO₃ (BNT)-based relaxor ferroelectric ceramics by introducing linear dielectric CaTiO₃ in order to synergistically manipulate the domain structure and microstructure evolution at the multiscale, generating the existence of stable and highly-dynamic polar nanoregions, fine grain size, suppressed leakage current density, and a large band gap E_g concurrently. More excitingly, the designed ceramic shows a remarkable thermal endurance (W_rec ≈ 3.7 ± 0.2 J cm⁻³, η ≈ 96% ± 3%, 30–160 °C), frequency stability (W_rec ≈ 3.9 ± 0.2 J cm⁻³, η ≈ 98% ± 2%, 5–200 Hz), cycling reliability (W_rec ≈ 3.5 ± 0.1 J cm⁻³, η ≈ 95% ± 2%, 1–10⁵ cycles) at 350 kV cm⁻¹, and superior discharge performance (power density P_D ≈ 96.2 MW cm⁻³, discharge speed t_0.9 ≈ 37.6 ns). This study explores high performance lead-free relaxor ferroelectrics for energy storage capacitors and offers an effective strategy to tailor the dielectric of relaxor ferroelectrics.

---

1. Introduction

Energy storage devices are vital for the development of contemporary electronic techniques and electrical power systems.¹ In comparison to lithium-ion batteries and electrochemical supercapacitors, dielectric capacitors have received growing attention and research interest due to the highest power density, rapid charge–discharge capability and long lifetime,² which endows them with wide prospects in pulsed power systems.³ However, the unsatisfactory energy storage density (W_rec) and efficiency (η) seriously impede potential applications of dielectric capacitors.² In general, W_rec and η are two significant physical characteristics to assess the practicability of dielectric materials, which can be calculated by using polarization–electric field (P–E) hysteresis loops: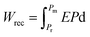 and 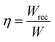, where P_m, P_r and E represent the maximum polarization, remnant polarization, and electric field, respectively.^3–5 Clearly, high dielectric breakdown strengths (E_b), large P_m and low P_r are all necessary to achieve excellent energy storage performance (ESP). A high E_b value can be obtained by refining the grain size,⁶ reducing field-induced strain,⁷ introducing high band gap E_g materials,⁸ and optimizing process conditions.⁹ The P_m value is closely associated with the species of material,¹⁰ and P_r can be tailored by domain engineering,^11,12 and introducing defect engineering or a nonpolar phase.^13–15 In consequence, multiscale optimization design should be adopted to explore dielectric materials with excellent ESP for capacitors applications.

Compared to linear dielectrics and ferroelectrics, relaxor antiferroelectrics (AFEs) and relaxor ferroelectrics (RFEs) exhibit great potential in the energy storage field because of a good combination of large ΔP (P_m − P_r), high η and E_b.^16–18 Breakthroughs in ESP were recently achieved in lead-free relaxor AFEs including AgTa_0.55Nb_0.45O₃ (W_rec ∼6.3 J cm⁻³) and 0.76NaNbO₃-0.24BNT (W_rec ∼12.2 J cm⁻³) by nanodomain engineering.^5,19 Yet, a relatively low η (large energy consumption) is still a common issue in AFEs because of the high polarization hysteresis caused by the field-induced AFE-FE phase transition.²⁰ Especially, an inferior η means that most of the energy will be transformed into thermal energy and thus produces a dramatic increase of heat, shortening the service life of dielectric capacitors.^1,2 By comparison, the polar nanoregions (PNRs) in ergodic RFEs are much smaller than the nanodomains in relaxor AFEs, which show a faster response to the applied electric field.^21,22 This can greatly reduce the P_r of ergodic RFEs while maintaining a high P_m, leading to a favorable η. Therefore, lead-free RFE ceramics have been extensively investigated in the last few years.^17,18,23 Nonetheless, the achieved W_rec and η values for most reported RFEs are commonly lower than 5 J cm⁻³ and 90%, respectively, which basically results from the relatively low E_b values and fast polarization saturation.^{20,21,24–27} Thus, the exploration of a good balance between different functional parameters with W_rec, η and stabilities in lead-free RFEs has been an inevitably increasing trend. (Bi_0.5Na_0.5)TiO₃ (BNT)-based lead-free RFEs have been always the focus of investigation on energy storage materials due to highly spontaneous polarization and strong dielectric properties derived from the A-site lone pair effect.^15,28,29 Nevertheless, poor ESP (W_rec < 5.5 J cm⁻³ and η < 95%) has been gained, although the performance of BNT-based RFEs has been significantly enhanced after extensive optimization in recent years.^30–33 Therefore, further enhancements on ESP of BNT-related RFEs are still required.

In order to construct good comprehensive ESP based on BNT RFE ceramics for practical applications, multiscale optimization design (including atomic and grain scales) was proposed, as illustrated in Fig. 1. On the 10⁻⁹ m (atomic scale), Ba(Al_0.5Ta_0.5)O₃ (BAT) was incorporated into BNT to generate non-ergodic relaxor and ergodic relaxor state (NR-ER) coexistence,³⁴ which can maintain a high P_max in a low electric field and a relatively small P_r. More importantly, the addition of BAT and CaTiO₃ (CT) into BNT can produce enhanced compositional disorder and promote strong random electric field formation.²¹ This will break the long-range polar coupling of ferroelectrics and induce small-sized and highly dynamic PNRs with a fast response to the external field, thereby leading to a large P_m value, a negligible P_r, and high η.^29,35,36 Considering that linear dielectric CT has an ultrahigh E_b predicted to be 4200 kV cm⁻¹ and a near-zero P_r, and Ta₂O₅ has a wide bandgap E_g (∼4 eV),^37,38 the addition of BAT and CT into BNT would tend to reduce P_r and increase E_b. On the 10⁻⁶ m (grain scale), introducing CT into lead-free ceramics can refine the grain size to greatly enhance E_b due to the correlation between E_b and average grain sizes (G_a): E_b ∝ (G_a)^−a,⁸ which will be beneficial to the improvement of ESP.

Fig. 1 Schematic diagram of realizing remarkable ESP via a multiscale optimization strategy.

On basis of the above multiscale optimization design, (1 − x)[0.955(Bi_0.5Na_0.5)TiO₃-0.045Ba(Al_0.5Ta_0.5)O₃]-xCaTiO₃ (BNT-BAT-xCT) RFE ceramics were especially constructed and fabricated in this study. As expected, it is encouraging that superior comprehensive ESP of a high W_rec of 5.81 J cm⁻³ and a record-breaking ultrahigh η of 97.8% is synchronously achieved in the BNT-BAT-0.4CT ceramic under 440 kV cm⁻¹, together with excellent thermal endurance, frequency stability, and cycling reliability. These features outperform most reported energy-storage ceramics and reveal the effectiveness of the multiscale optimization strategy in tailoring overall ESP in dielectric ceramic capacitors. The potential origin of improving E_b and the exceptional ESP was probed in terms of a phase-field breakdown model and ex/in situ multiscale structure characterization studies.

2. Experimental procedures

The experimental preparation process, characterization details, and computational method for BNT-BAT-xCT ceramics are provided in the ESI.†

3. Results and discussion

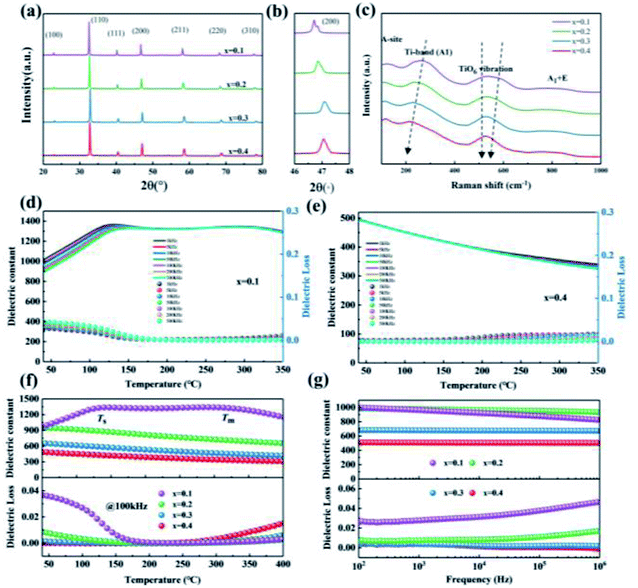
Fig. 2(a) shows X-ray diffraction (XRD) patterns for the BNT-BAT-xCT ceramics. Characteristic perovskite structures without any impurity can be found in all ceramics, indicating that CT has dissolved into the BNT-BAT lattices. A typical pseudo-cubic phase is verified by the single (200) diffraction peak with no splitting other than K_α2, which is often misapprehended as non-cubic distortion,³⁹ as shown in Fig. 2(b). Given the fact that K_α2 reflection is usually difficult to discern in the presence of rhombohedral or tetragonal symmetry, this observation of K_α2 reflections at such a small diffraction angle smaller than 50° is a forceful support for the absence of non-cubic distortion within the detection limit of the present the X-ray apparatus. Moreover, the reflection peaks gradually move to a higher degree with increasing CT content, implying a lattice shrink due to the introduction of Ca²⁺ with a smaller ionic radius at the A-site.³³ In order to more deeply identify the local structural evolution with CT addition, Raman spectroscopy (100–1000 cm⁻¹) was performed at ambient temperature, as shown in Fig. 2(c). Distinctly, similar to other BNT-based ferroelectric ceramics,^40–42 four main vibration modes appeared in the Raman spectra, that is, A-site cations (<200 cm⁻¹), B–O bond (200–400 cm⁻¹), BO₆ octahedra vibrations (400–650 cm⁻¹), and A1 + E (>700 cm⁻¹) overlapping bands. The increase of the CT content can shift Raman peaks to lower wavenumbers and produce a reduction in the intensity, which is associated with the augmentation of structure disorder and decline of unit cell polarity.^16,19,20,43 As a result, the long-range ferroelectric order was broken and PNRs with a decreased size were induced with CT incorporation,^3,15 which will generate a high P_m and a nearly negligible P_r during the charging-discharging process.

Fig. 2 (a) XRD patterns, (b) enlarged (200) peaks, and (c) Raman spectra for the BNT-BAT-xCT ceramics; temperature-dependent dielectric properties under different frequencies: (d) x = 0.1 and (e) x = 0.4; (f) temperature dependence of dielectric properties of BNT-BAT-xCT ceramics measured at 100 kHz; (g) Frequency-dependent dielectric properties for BNT-BAT-xCT ceramics measured at room temperature.

Temperature-dependent dielectric constant and loss for BNT-BAT-xCT ceramics at various frequencies are shown in Fig. 2(d), (e), and S1.† Double abnormal peaks (T_s and T_m), corresponding to the thermal evolution of rhombohedral and tetragonal discrete PNRs and to the transformation of PNRs from rhombohedral to tetragonal,^44–46 appeared in the x = 0.1 sample. No dielectric peak has been found for x ≥ 0.2. With increasing CT content, the T_m moves towards a lower temperature and becomes invisible when x ≥ 0.2 (see Fig. 2(f)), suggesting reinforced site disorder, destroyed the original long-range FE order, diminished the coupling effect of the BO₆ octahedron, and enhanced the relaxation behavior,^28,47,48 which is in line with the Raman spectral analysis. Moreover, one can see that the introduction of CT produces a declined dielectric constant and loss in the whole test temperature range. In particular, BNT-BAT-0.4CT exhibits a stable dielectric constant and ultralow loss over the wide temperature range, which are conducive to improving thermal stability and E_b. Frequency-dependent dielectric properties from 100 Hz to 1 MHz are tested, as shown in Fig. 2(g). For x = 0.1 and 0.2, the dielectric constant and loss show a decreasing and increasing trend with increasing frequency, respectively. By contrast, a stable dielectric constant (∼503, 10²–10⁶ Hz) and ultralow loss (<0.0067, 10²–10⁶ Hz) over the broad frequency range can be observed for x = 0.4 sample, which conforms to the temperature-dependent dielectric curves in Fig. 2(f). According to the empirical formula (E_b ∝ ε^−1/2_r) and previous reports,^12,49 a suitable dielectric constant and ultralow dielectric loss are more likely to achieve not only a relatively high P_m but also a high E_b value. In short, for the designed BNT-BAT-0.4CT ceramic, a suitable dielectric constant, ultralow loss, improved relaxor characteristics, and wide temperature and frequency stabilities are particularly crucial to achieve superior ESP.

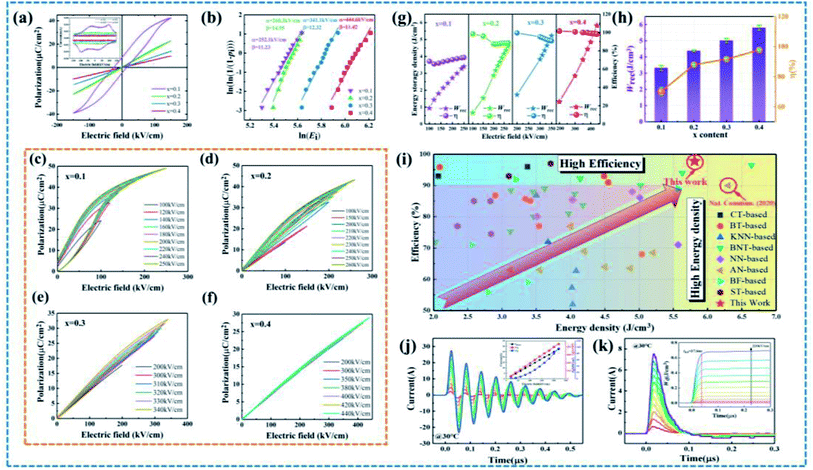
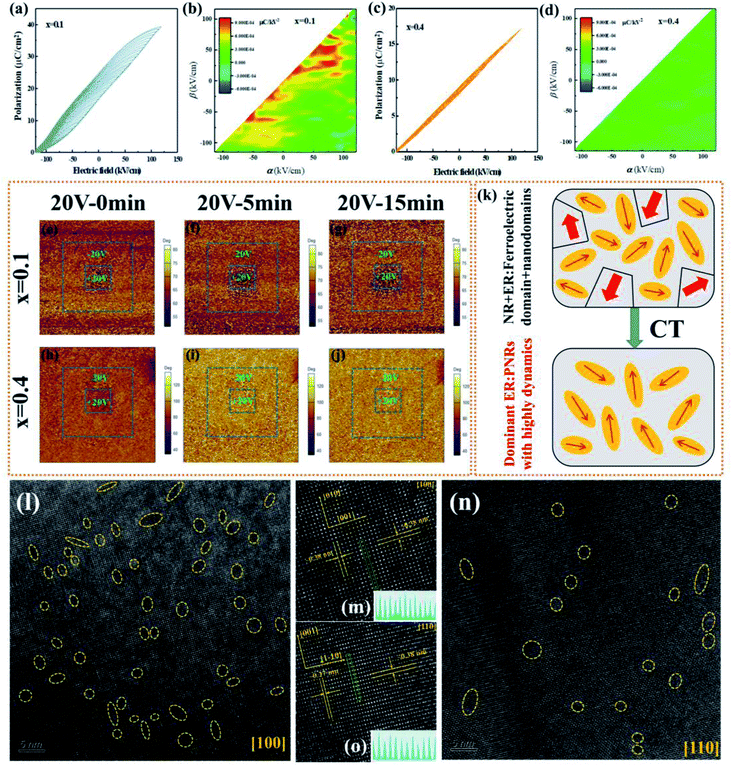
The bipolar P–E loops and current–electric field (I–E) curves for BNT-BAT-xCT ceramics were tested at 150 kV cm⁻¹ and 10 Hz to characterize the phase structure evolution, as shown in Fig. 3(a). Increasing the CT content produces an obvious transition from the pinched loop with high P_m and P_r to a nearly linear one with relatively high P_m and nearly zero P_r, indicating the interruption of ferroelectric macrodomains and the formation of PNRs.^29,30 Interestingly, a negligible P_r obtained in x ≥ 0.2 samples reveals the enhancement of ER behavior induced by the PNRs. Four current peaks can be observed for the x = 0.1 sample, which corresponds to the reversible NR-ER phase transition.⁵⁰ Notably, there was no detectable current peak for the ceramics with x ≥ 0.2, suggesting the complete ER states due to reduced PNRs sizes. The PNRs in ER ferroelectrics have high dynamic characteristics and preserve a large P_m while decreasing P_r,¹² thereby allowing for a faster response to electric field stimuli and higher η. With the addition of CT, the current intensity decreases (Fig. 3(a)), which is mainly associated with the phase transition in BNT-BAT-xCT ceramics. In detail, for the x = 0.1 ceramic, a relatively large current should be the result of the NR-ER phase coexistence evidenced by the four current peaks. With further addition of CT (x = 0.2, 0.3 and 0.4), the current intensity continues to decrease, which is caused by the gradual reduction in NR states and the emergence of the dominated ER states resulting from the decreased PNR sizes. Similar I–E behavior has been perceived in numerous BNT-related systems.^51–53

Fig. 3 (a) Bipolar P–E loops and I–E curves measured at 150 kV cm⁻¹ and room temperature and (b) Weibull distributions for BNT-BAT-xCT ceramics; unipolar P–E loops measured at 10 Hz: (c) x = 0.1, (d) x = 0.2, (e) x = 0.3, and (f) x = 0.4; (g) electric field-dependent variation of W_rec and η; (h) change of W_rec and η under respective Eb for BNT-BAT-xCT ceramics; (i) a comparison of ESP among the x = 0.4 ceramic and other recently reported dielectric ceramics; (j) underdamped and (k) overdamped discharge waveforms in different electric fields for the x = 0.4 sample, insets show the variation of I_max, C_D and P_D values and the calculated W_d curves.

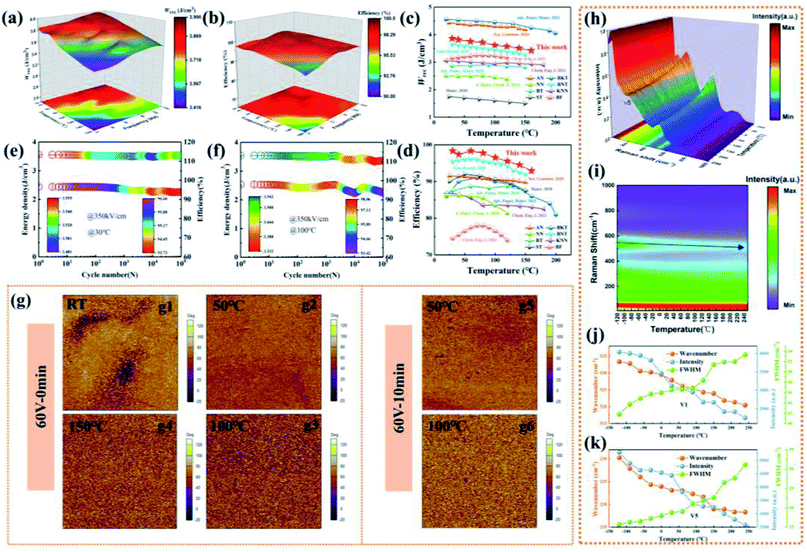
To estimate the full potential of the BNT-BAT-xCT ceramics for energy storage, statistical E_bvia Weibull distribution fitting was carried out, as shown in Fig. 3(b). Weibull modulus β is greater than 11 for all ceramics, demonstrating the high reliability of Weibull analysis. The E_b values of the ceramics increase monotonically along with the CT concentration-e.g., from ∼252.1 kV cm⁻¹ (x = 0.1) to ∼444.6 kV cm⁻¹ (x = 0.4), indicating that the addition of CT is in favor of enhancing E_b. Then we derived the evolutions of W_rec and η of the BNT-BAT-xCT ceramics (Fig. 3(g)) from the unipolar P–E loops at fields of near their E_b and 10 Hz (Fig. 3(c)–(f)). The W_rec values exhibit a nearly linear increase with the application of an electric field, meaning that a greater W_rec value can be obtained under a higher E_b. As compared to other samples (x = 0.1–0.3); the η of the x = 0.4 sample exhibits an almost electric field-insensitive feature and maintains an ultra-high value (>97%) even at high driving fields, which is attributed to its nearly linear hysteresis response due to the small-sized PNRs. The corresponding variations of W_rec and η at fields approaching E_b following CT content enhancement are plotted in Fig. 3(h). The maximum W_rec (5.81 ± 0.16 J cm⁻³) and η (97.8 ± 0.7%) were simultaneously achieved in the x = 0.4 sample, as a result of the combined effects of high polarization, ultralow hysteresis, and high E_b (Fig. 2(b) and (f)). More importantly, the marked improvement of η to >97% is extremely pivotal in addressing the energy loss of dielectrics for high-power applications, promoting reliable operation and guaranteeing service life. To verify the repeatability of ESP for BNT-BAT-xCT bulk ceramics, the P–E loops and resulting W_rec and η values of six samples are summarized in Fig. S2–S5,† measured at fields approaching the respective E_b. Distinctly, all six samples for each component exhibited a similar shape of the P–E loop and thus little difference in ESP. Especially, for the optimal composition with x = 0.4, the W_rec and η fluctuate within ±2.7% and ±0.7%, respectively, reflecting the reliable and valid ESP. A comparison of W_rec and η between BNT-BAT-0.4CT and other recently reported lead-free bulk ceramics are shown in Fig. 2(i).^{11,15,19,30,35,40,41,43,54–95} More strikingly, the combined high W_rec and ultrahigh η in the BNT-BAT-0.4CT ceramics designed by the above multiscale optimization strategy are competitive with those of the state-of-the-art lead-free AFE ceramics (W_rec of 6.3 J cm⁻³ and η of 90%),¹⁹ showing great prospects in the field of environment-friendly energy-storage capacitor applications.

The charge/discharge performance is also indispensable for dielectric capacitors in practical applications. To assess the feasibility of the BNT-BAT-0.4CT sample in a pulse power capacitor, underdamped and overdamped discharge properties under various electric fields are tested, as shown in Fig. 3(j) and (k), respectively. Similar to other lead-free energy storage materials,^8,21,96,97 the applicable maximum electric field for charge–discharge measurement is generally smaller than that for P–E loop measurement. This difference in applied electric field range may be associated with the different voltage attributes of the two methods (P–E loop, AC voltage; discharge measurement, and DC voltage). Following electric field enhancement, the maximum current (I_max), current density (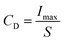, S is the electrode area), and power density 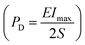exhibit a linear increasing trend, reaching the maximum values of 27.45 A, 874 A cm⁻², and 96.2 MW cm⁻³ at 220 kV cm⁻¹, respectively. As shown in Fig. 3(k), the energy density W_d (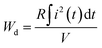, where R and V are load resistor (200 Ω) and the effective volume, respectively⁸) increases monotonically up to 0.72 J cm⁻³ at 220 kV cm⁻¹, and the discharge speed t_0.9 (the time released 90% of all energy) maintains a small value (∼37.6 ns) in a wide electric field range. It should be noted that the W_d is determined to be 0.72 J cm⁻³ at 220 kV cm⁻¹, lower than that calculated from P–E loops. This variation in values is thought to be linked with the different mechanisms of the quasistatic P–E loop (10⁻¹ s) and dynamic discharge measurement with different frequencies (10⁻⁵ s).^7,96,97 Moreover, the loss of discharged energy is also related to the equivalent series resistor, domain wall movement and measurement frequency.^19,96 Furthermore, high P_D (>44.5 MW cm⁻³) and ultrashort t_0.9 (<37 ns) can be well maintained from 30 to 160 °C at 160 kV cm⁻¹ (Fig. S6†), demonstrating good temperature stability of charge/discharge characteristics. Also, the P_D and t_0.9 remain in the vicinity of 50 MW cm⁻³ and 36 ns over wide cycle numbers (1–5000) (see Fig. S7†), respectively, which proves excellent cycling reliability. These results endow the BNT-BAT-0.4CT ceramic with good promise for pulsed-power applications under harsh field conditions.

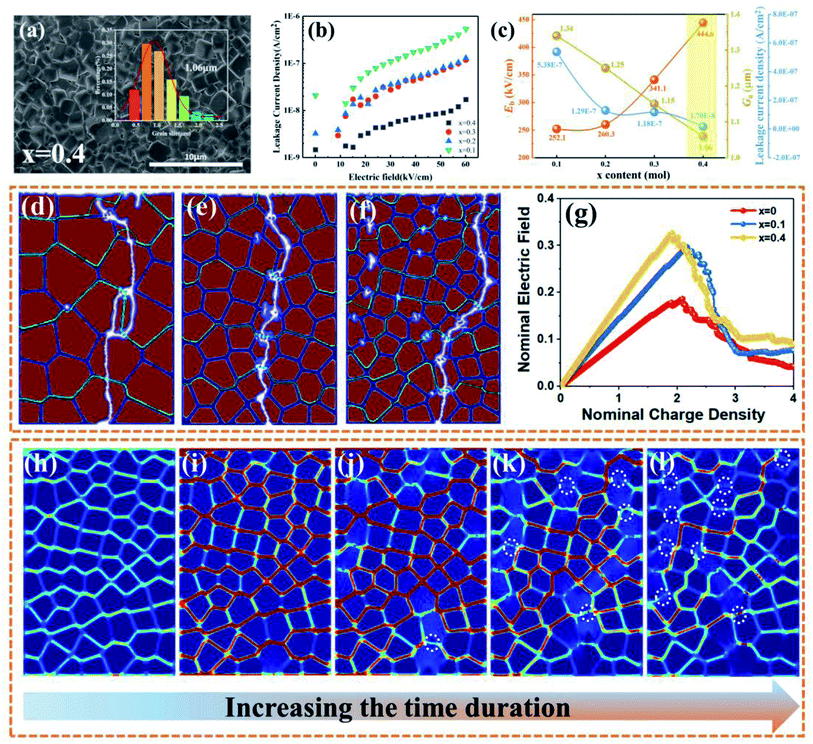
The internal and external factors affecting the E_b value are investigated to clarify the evolution law of E_b with CT addition. As shown in Fig. 4(a) and Fig. S8,† all BNT-BAT-xCT ceramics present dense and uniform microstructures with few visible pores and thus the formation of compacted grains. Based on the surface morphology of the as-sintered ceramics (Fig. S8(A)),† the G_a reduces obviously as the CT content increases (1.34 μm for x = 0.1 vs. 1.06 μm for x = 0.4). For reliable microstructure and grain size characterization, the micrographs of polished and thermally etched cross-sections of the ceramics are also shown in Fig. S8(B).† Similar to the observations of surface morphology, there is also a decline in the G_a with increasing CT content in the microstructures of the cross-sections, reaching the minimum (∼0.86 μm) for x = 0.4. The reduction of grain size can greatly produce more depletion regions due to the increased density of high resistance grain boundaries,⁹⁸ which prevents charge carrier migration, thus favoring the enhanced E_b. Furthermore, suppressed leakage current density is gained with increasing CT content, with values changing from ∼5.38 × 10⁻⁷ A cm⁻² (x = 0.1) to ∼1.7 × 10⁻⁸ A cm⁻² measured in a low electric field of 60 kV cm⁻¹ (Fig. 4(b)). The smaller leakage current density will generate fewer charged carriers,^12,99 which contributes to a higher E_b. Fig. 4(c) gives the correlation between E_b and G_a/leakage current density with CT addition. It is clear that the reductions of the G_a/leakage current density following CT content enhancement perfectly interpret the increased E_b shown in Fig. 3(g). Moreover, a high E_g of ≈3.02 eV (Fig. S9†), large electrical resistivity, a high activation energy value (Fig. S10†), low oxygen vacancy concentration (Fig. S11–S13†), and a high degree of chemical uniformity (Fig. S14†) also serve as the main intrinsic and extrinsic contributors for significantly boosted E_b value in BNT-BAT-0.4CT ceramic. It is clear that the designed materials show large potential in the achievements of intrinsic and extrinsic factors for improving E_b, which are comparable to state-of-the-art reported lead-free ceramic systems, such as BNT-based (electrical resistivity ∼150 × 10³ Ω cm at 500 °C),⁴⁸ BF-based (G_a ∼0.7 μm, E_g ∼2.8 eV, electrical resistivity (400 °C) ∼0.2 MΩ cm),⁸ NN-based (G_a ∼1 μm),^5,20 and AN-based (G_a ∼1.5–2 μm, E_g ∼2.76–2.95 eV, O_v/(O_v + O_L)∼0.12)^19,100 ceramics. These achieved good parameters are thought to be responsible for the high E_b value, as confirmed from Fig. 3(b).

Fig. 4 (a) SEM micrograph and grain size distribution of the x = 0.4 sample; (b) leakage current density as a function of the electric field with different CT contents; (c) the changes of E_b, average grain size G_a and leakage current density under 60 kV cm⁻¹ with respect to the CT content; phase-field simulations of the final breakdown paths for samples with various grain sizes: (d) x = 0, (e) x = 0.1, and (f) x = 0.4; the contour lines denote the equipotential lines of the then-current electric field. (g) The nominal electric field vs. nominal charge density for the indicated ceramics; (h–l) the nominal electric field distribution at various moments during the breakdown path growth for the x = 0.4 sample.

A phase-field breakdown model is adopted on the grain scale to deeply explore the breakdown behavior of BNT-BAT-xCT ceramics with different grain sizes, using COMSOL Multiphysics Software. The detailed simulation process is provided in the ESI.† The final breakdown paths of the specimens with different grain sizes are presented in Fig. 4(d)–(f). During the breakdown process, the breakdown path branches at the grain boundary, which possesses higher breakdown energy as compared to the grain,¹⁰¹ yielding more energy dissipation and hence improving the E_b. Generally, if ferroelectric ceramics have more branches of breakdown paths, they will exhibit higher E_b. For pure BNT-BAT ceramic with ∼1.5 μm (Fig. 4(d)), almost no detectable branches are found, while for the x = 0.4 sample with a small grain size (Fig. 4(f)), significant branches of breakdown paths are observed, leading to the highest E_b in the designed ceramics. Fig. 4(g) shows a plot of the nominal breakdown strength of samples with different grain sizes, which can be defined by the largest nominal electric field during the breakdown process.⁹ Obviously, the nominal breakdown strength is significantly promoted along with the decreased grain size. Particularly, compared with the case of the pure BNT-BAT sample, the nominal breakdown strength for the x = 0.4 sample shows 84% enhancement, which theoretically explains the great enhancement in E_b for CT-modified BNT-BAT ceramics and thus substantially supports the effect of introducing CT on the improvement of E_b. Note that, similar to the recent work on BTBZNT@SiO₂ MLCCs,⁹ a difference between the experimental results and theoretical calculations can be found. This may be attributed to the following two factors: (1) in the theoretical calculations, there is an ideal model of the microstructure by COMSOL Multiphysics. (2) Defects are present in the fabricated ceramics. Overall, this finding basically conforms to our Weibull distribution results (seeing Fig. 3(b)).

The distributions of the nominal electric field at different moments along the breakdown path growth for the x = 0.4 ceramic are shown in Fig. 4(h)–(l). It is clear that the local electric field is concentrated in the grain boundary region (Fig. 4(h)), which can delay the fast propagation of breakdown paths due to the higher breakdown energy.

Under the imposed electric field, the breakdown initiates from the grain region (Fig. 4(i)), and the growth of the breakdown path can be blocked when the breakdown path encounters the grain boundary, as marked by the white circles in Fig. 4(j)–(l). Then, the electric field concentration aggravates at the end of the growing breakdown path (Fig. 4(k)). As the applied electric field increases, the local electric field exceeds the breakdown strength of the grain boundary, and then the breakdown path runs through the entire grain and grain boundary, producing complete breakdown (Fig. 4(l)).^102,103 Overall, the number of grain boundaries plays a decisive role in increasing the breakdown strength of ferroelectric ceramics,^16,68 that is, more grain boundaries can greatly contribute to a higher dielectric breakdown strength for ferroelectric ceramics with smaller grain sizes.

To gain a deep insight into phase transformation and polarization switching from a microscopic perspective, the first-order reversal curve (FORC) distributions of the representative compositions (x = 0.1 and 0.4) are analyzed using a series of asymmetric P–E loops (Fig. 5(a) and (c)), which can give reasonable descriptions of the hysteresis feature based on the Preisach model.^12,104 On the basis of the evolution of the diagrams (Fig. 5(b) and (d)), the transition from NR-ER towards a complete ER state with the incorporation of CT has been illustrated. For the x = 0.1 sample, the diagram shows a distinctive image feature characterized by a high-intensity distribution zone (Fig. 5(b)), implying strong polarization nonlinearity with large total polarization owing to the intensive switching of microdomains at a relatively low electric field.^105,106 In sharp contrast, the highly concentered areas are almost undetectable over the entire electric field for the BNT-BAT-0.4CT ceramic, indicating significantly weakened FE nonlinearly. This homogeneous distribution reflects a shift toward the complete ER state with an almost linear polarization response, since ER features ultralow coercivity and a small switching energy barrier.^12,107

Fig. 5 FORC loops [(a) and (c)] and their evolution [(b) and (d)] for the incorporated ceramics; (e–j) PFM phase images after poling treatment and relaxation durations for x = 0.1 and 0.4 samples; (k) schematic illustration of domain evolution resulting from CT incorporation. (l–o) HR-TEM images of domain morphology and lattice fringes along [100]_c and [110]_c for the x = 0.4 ceramic.

From a microscopic perspective, the shape evolution of P–E loops is closely linked with the dynamic response of PNRs, which has been observed in lead-free RFE materials.^20,108,109 To validate the domain evolution in the BNT-BAT-CT ceramics, out-of-plane PFM phase, amplitude, and morphology characterization studies in scanning areas of 5 × 5 μm² at a voltage of 20 V and different relaxation times are employed, as shown in Fig. 5(e)–(j), S15 and S16,† respectively. A negative DC voltage of −20 V was initially imposed on a 3 × 3 μm² area and then the same positive DC voltage was applied on a 1 × 1 μm² area. One can first note that the x = 0.1 ceramic has a stable retention of polarization at 15 min after it is poled with a voltage of 20 V (Fig. 5(e)–(g)), which means a relatively strong ferroelectricity with large P_m, high P_r, and high hysteresis, and is in accordance with the observations in Fig. 3(a). As for the domain evolution in x = 0.4, the results suggest that a certain degree of the domain can still be induced after being poled with 20 V and 0 min, which provides the basis for the realization of a relatively high P_m. In stark contrast, the polarized domains revert quickly to their original state only in 5 min with the removal of the applied voltage, verifying the much improved domain switching mobility and highly-dynamic PNRs in the BNT-BAT-0.4CT ceramic.^12,40,110 Based on the FORC and PFM measurements, Fig. 5(k) vividly shows the schematic illustration of the evolution of domain configuration. Accordingly, the incorporated CT into BNT-BAT drives compositional disorder in the BNT-BAT-xCT system, destroying the NR-ER order of BNT-BAT and transforming the large-sized FE domains and nanodomains into nano-scale PNRs with high dynamics, which is thus responsible for an ER state. It is the tailored domain engineering induced by CT incorporation that has a decisive influence on the production of high ESP especially the substantial augmentation in η.

In order to directly and deeply probe domain morphology for achieving excellent ESP, high-resolution transmission electron microscopy (HR-TEM) analysis was further conducted for the x = 0.4 ceramic. As shown in Fig. 5(l) and (n), complex domain patterns with randomly scattered PNRs are clearly observed along [100]_c and [110]_c, suggesting a local-structure inhomogeneity.⁸ The randomly distributed elliptically shaped PNRs exhibit a small size range of ∼1.2–2.8 nm, which are comparable with those observed in other lead-free ceramics with high energy-storage properties.^8,20,21 The extremely small PNRs obtained not only show a quick response to the imposed electric field due to low switching energy barriers and high dynamics, as confirmed by the PFM measurements (Fig. 5(h)–(j)), but also generate an extremely low P_r, thus further resulting in a slim P–E loop and satisfactory η of the BNT-BAT-0.4CT sample. In addition, as presented in Fig. 5(m) and (o), the HR-TEM images of the lattice fringes reveal the good crystalline quality of the ceramic.

In actual applications, the temperature stability, frequency dependence, and cycling reliability of ESP are also key parameters to assess the potential of dielectric capacitors.^1,19,111 With increasing temperature, a slight decline in P_max and nearly negligible P_r can be detected, which are the results of a reduced dielectric constant (see Fig. 2(e)) and highly-dynamic PNRs (see Fig. 5). Accordingly, the W_rec and η under 350 kV cm⁻¹ slightly reduce on heating. Based on the P–E loops measured at different temperatures and frequencies (Fig. S17†), three-dimensional plots of W_rec and η for BNT-BAT-0.4CT are shown in Fig. 6(a) and (b), respectively, where a linear-like and almost hysteresis-free polarization response is involved over whole temperature and frequency range. As a consequence, temperature- and frequency-insensitive ESP is achieved, featuring high W_rec and η with minimal variations (W_rec ≈ 3.7 ± 0.2 J cm⁻³, η ≈ 96% ± 3%, 30–160 °C, W_rec ≈ 3.9 ± 0.2 J cm⁻³, andη ≈ 98% ± 2%, 5–200 Hz). In comparison with state-of-the-art thermally stable lead-free energy storage ceramics,^{19,21,41,74,86,107,112,113} the BNT-BAT-0.4CT ceramic can not only possess a high W_rec (≈3.7 ± 0.2 J cm⁻³) value but also show an ultrahigh η (≈96% ± 3%) over a wide usage temperature range, as shown in Fig. 6(c) and (d). Based on the P–E loops for various cycle numbers (Fig. S18†), the cycling reliability measured at 30 and 100 °C are presented in Fig. 6(e) and (f), respectively. At 30 °C, both W_rec and η retain nearly unchanged values at 350 kV cm⁻¹ with cycle numbers of up to 10⁵, indicating outstanding cycling reliability. This high reliability can be ascribed to the inhibition of fatigue from the domain wall.¹¹¹ At 100 °C, the W_rec and η are found to exhibit a slight fluctuation, i.e., W_rec ≈ 3.5 ± 0.2 J cm⁻³ and η ≈ 96% ± 3%, after 10⁵ charge/discharge cycles, respectively, which suggests that BNT-BAT-0.4CT still has a satisfactory high-temperature anti-fatigue character. These advantages endow the BNT-BAT-0.4CT ceramic with bright development prospects for future capacitor applications.

Fig. 6 Three-dimensional plots of (a) W_rec and (b) η with respect to temperature and frequency for BNT-BAT-0.4CT. A comparison of temperature-dependent (c) W_rec and (d) η between the BNT-BAT-0.4CT ceramic and recently reported energy-storage bulk ceramics; the variation of W_rec and η as a function of the cycle number at (e) 30 °C and (f) 100 °C; (g) temperature-dependent PFM phase images after poling treatment and relaxation durations for the x = 0.4 ceramic; (h) Raman spectra and (i) the corresponding evolution at the evaluated temperature; change in the wavenumber, peak intensity, and FWHM of (j) ν₁ and (k) ν₅ modes for the NN-0.3CT ceramic.

Then we performed in situ PFM and Raman measurements in response to the temperature to uncover the microstructure evolution for excellent stabilities of the BNT-BAT-0.4CT ceramic. Fig. 6(g) and S19† show the PFM phase and amplitude images at different temperatures after poling treatment at 60 V, respectively. At room temperature, the ceramic displays a certain number of switched nanodomains (Fig. 6(g1)), providing a guarantee for the production of relatively high P_m values (Fig. 3(a) and S17†). As the temperature rises, no obvious switching domains appear (Fig. 6(g2–g4)). After 10 min at different temperatures, the ceramic exhibits a nanodomain structure with no perceptible change in morphology (Fig. 6(g5) and (g6)), showing significant temperature-independent structural stability with a highly dynamic nanodomain. As shown in Fig. 6(h), (i) and S20,† broadened and smoothed Raman peaks are observed following the temperature increment from −120 to 250 °C. However, the number of Raman peaks remains nearly constant, uncovering no variety in local structure symmetry within a broad temperature range.²¹ Furthermore, the more detailed changes in peak position, intensity and FWHM of ν₁ and ν₅ modes are presented in Fig. 6(j) and (k), respectively. Both ν₁ and ν₅ exhibit a slight shift to lower wavenumbers, an augmentation of FWHM, and a decrease of intensity with increasing temperature, demonstrating the weakening of the bonding between the A/B-site cations and oxygen. This can generate enhanced local structural disorder and strengthened activity of PNRs, reducing the potential barrier for domain switching with an electric field and thus offering a guarantee for achieving high η on heating.²⁰ In combination with stable PNRs with highly dynamic, almost no change in local structure symmetry, and strengthened structural disorder, a linear-like polarization-field response can be achieved in BNT-BAT-0.4CT ceramic over a broad temperature range. In addition, as shown in Fig. S21,† the BNT-BAT-0.4CT ceramic shows a small leakage current density (<3 × 10⁻⁸ A cm⁻²) over a broad temperature range from 30 °C to 160 °C, indicating the suppressive hopping and concentration of thermally activated charge carriers.^114,115 This stable and low leakage current density will guarantee a high E_b and low P–E hysteresis within a broad temperature range. Moreover, stable change of the dielectric constant within a broad electric field and temperature range (Fig. S21†) would allow the BNT-BAT-0.4CT ceramic to possess high E_b and stable P_m at evaluated temperatures, which also contributes to temperature-insensitive high ESP.

4. Conclusions

In summary, the ESP of BNT-BAT-xCT relaxor ferroelectric ceramics designed by a multiscale optimization strategy is investigated for dielectric capacitor application. Due to the incorporation of CT and its synergistic effect with BNT-BAT, features including the existence of stable and highly dynamic PNRs, fine grain size, and suppressed leakage current density, as well as large E_g are obtained. As a result, BNT-BAT-0.4CT shows superior comprehensive ESP, achieving a record-breaking ultrahigh η of 97.8% and high W_rec of 5.81 J cm⁻³ under a high driving field of 440 kV cm⁻¹. Encouragingly, the remarkable energy storage thermal endurance (W_rec ≈ 3.7 ± 0.2 J cm⁻³, η ≈ 96% ± 3%, 30–160 °C), frequency stability (W_rec ≈ 3.9 ± 0.2 J cm⁻³, η ≈ 98% ± 2%, 5–200 Hz), cycling reliability (W_rec ≈ 3.5 ± 0.1 J cm⁻³, η ≈ 95% ± 2%, 1–10⁵ cycles) at 350 kV cm⁻¹, and superior discharge performance (P_D ≈ 96.2 MW cm⁻³, t_0.9 ≈ 37.6 ns) are also realized in the ceramic. The mechanism for the achieved stability is demonstrated to be the temperature-insensitive local structural symmetry and high activity PNRs are characterized by temperature-dependent PFM and Raman measurements. These findings demonstrate that the BNT-BAT-0.4CT ceramic could serve as a high performance lead-free ceramic material for future energy storage capacitors in advanced pulsed power systems.

Author contributions

Chongyang Li: investigation, methodology, conceptualization, writing – original draft. Jikang Liu: data curation, formal analysis, software. Wangfeng Bai: writing – review and editing, validation, funding acquisition, project administration, supervision, resources. Shiting Wu: validation. Peng Zheng: validation, supervision, resources, data curation, software. Jingji Zhang: validation, resources. Zhongbin Pan: data curation, validation, software. Jiwei Zhai: resources, supervision, validation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to acknowledge the Natural Science Foundation of Zhejiang Province (LY20E020008 and LY22E020006) and the National Natural Science Foundation of China (Grant No. 51802063).

References

1. J. Li, F. Li, Z. Xu and S. Zhang, Adv. Mater., 2018, 30, 1802155.
2. P. Zhao, H. Wang, L. Wu, L. Chen, Z. Cai, L. Li and X. Wang, Adv. Energy Mater., 2019, 9, 1803048.
3. J. Qian, Y. Han, C. Yang, P. Lv, X. Zhang, C. Feng, X. Lin, S. Huang, X. Cheng and Z. Cheng, Nano Energy, 2020, 74, 104862.
4. T. Zhang, W. Li, Y. Zhao, Y. Yu and W. Fei, Adv. Funct. Mater., 2018, 28, 1706211.
5. H. Qi, R. Zuo, A. Xie, A. Tian, J. Fu, Y. Zhang and S. Zhang, Adv. Funct. Mater., 2019, 29, 1903877.
6. X. Zhu, P. Shi, R. Kang, S. Li, Z. Wang, W. Qiao, X. Zhang, L. He, Q. Liu and X. Lou, Chem. Eng. J., 2021, 420, 129808.
7. J. Li, Z. Shen, X. Chen, S. Yang, W. Zhou, M. Wang, L. Wang, Q. Kou, Y. Liu, Q. Li, Z. Xu, Y. Chang, S. Zhang and F. Li, Nat. Mater., 2020, 19, 999–1005.
8. H. Qi, A. Xie, A. Tian and R. Zuo, Adv. Energy Mater., 2020, 10, 1903338.
9. P. Zhao, Z. Cai, L. Chen, L. Wu, Y. Huan, L. Guo, L. Li, H. Wang and X. Wang, Energy Environ. Sci., 2020, 13, 4882–4890.
10. R. E. Cohen, Nature, 1992, 358, 136–138.
11. Q. Yuan, G. Li, F.-Z. Yao, S.-D. Cheng, Y. Wang, R. Ma, S.-B. Mi, M. Gu, K. Wang, J.-F. Li and H. Wang, Nano Energy, 2018, 52, 203–210.
12. H. Pan, J. Ma, J. Ma, Q. Zhang, X. Liu, B. Guan, L. Gu, X. Zhang, Y.-J. Zhang, L. Li, Y. Shen, Y.-H. Lin and C.-W. Nan, Nat. Commun., 2018, 9, 1813.
13. X. Ren, Nat. Mater., 2004, 3, 91–94.
14. Y. Feng, J. Wu, Q. Chi, W. Li, Y. Yu and W. Fei, Chem. Rev., 2020, 120, 1710–1787.
15. F. Yan, K. Huang, T. Jiang, X. Zhou, Y. Shi, G. Ge, B. Shen and J. Zhai, Energy Storage Mater., 2020, 30, 392–400.
16. Z. Wang, R. Kang, W. Liu, L. Zhang, L. He, S. Zhao, H. Duan, Z. Yu, F. Kang, Q. Sun, T. Zhang, P. Mao, J. Wang and L. Zhang, Chem. Eng. J., 2022, 427, 131989.
17. G. Wang, Z. Lu, Y. Li, L. Li, H. Ji, A. Feteira, D. Zhou, D. Wang, S. Zhang and I. M. Reaney, Chem. Rev., 2021, 121, 6124–6172.
18. Z. Yang, H. Du, L. Jin and D. Poelman, J. Mater. Chem. A, 2021, 9, 18026–18085.
19. N. Luo, K. Han, M. J. Cabral, X. Liao, S. Zhang, C. Liao, G. Zhang, X. Chen, Q. Feng, J.-F. Li and Y. Wei, Nat. Commun., 2020, 11, 4824.
20. A. Xie, R. Zuo, Z. Qiao, Z. Fu, T. Hu and L. Fei, Adv. Energy Mater., 2021, 11, 2101378.
21. L. Chen, F. Long, H. Qi, H. Liu, S. Deng and J. Chen, Adv. Funct. Mater., 2022, 32, 2110478.
22. R. Huang, H. Wang, C. Tao, M. Cao, H. Hao, Z. Yao and H. Liu, Small Methods, 2021, 5, 2100787.
23. H. Qi and R. Zuo, J. Mater. Chem. A, 2019, 7, 3971–3978.
24. H. Wang, Y. Liu, T. Yang and S. Zhang, Adv. Funct. Mater., 2019, 29, 1807321.
25. Y. Tian, L. Jin, H. Zhang, Z. Xu, X. Wei, G. Viola, I. Abrahams and H. Yan, J. Mater. Chem. A, 2017, 5, 17525–17531.
26. Z. Yang, H. Du, L. Jin, Q. Hu, S. Qu, Z. Yang, Y. Yu, X. Wei and Z. Xu, J. Eur. Ceram. Soc., 2019, 39, 2899–2907.
27. V. Veerapandiyan, F. Benes, T. Gindel and M. Deluca, Materials, 2020, 13, 5742.
28. D. Li, Y. Lin, M. Zhang and H. Yang, Chem. Eng. J., 2020, 392, 123729.
29. M. Wang, Q. Feng, C. Luo, Y. lan, C. Yuan, N. Luo, C. Zhou, T. Fujita, J. Xu, G. Chen and Y. Wei, ACS Appl. Mater. Interfaces, 2021, 13, 51218–51229.
30. X. Qiao, D. Wu, F. Zhang, B. Chen, X. Ren, P. Liang, H. Du, X. Chao and Z. Yang, J. Mater. Chem. C, 2019, 7, 10514–10520.
31. Z. Jiang, H. Yang, L. Cao, Z. Yang, Y. Yuan and E. Li, Chem. Eng. J., 2021, 414, 128921.
32. P. Shi, X. Zhu, X. Lou, B. Yang, Q. Liu, C. Kong, S. Yang, L. He, R. Kang and J. Zhao, Chem. Eng. J., 2022, 428, 132612.
33. S. Bian, Z. Yue, Y. Shi, J. Zhang and W. Feng, J. Am. Ceram. Soc., 2021, 104, 936–947.
34. W. Bai, Y. Bian, J. Hao, B. Shen and J. Zhai, J. Am. Ceram. Soc., 2013, 96, 246–252.
35. D. Li, D. Zhou, W. Liu, P.-J. Wang, Y. Guo, X.-G. Yao and H.-X. Lin, Chem. Eng. J., 2021, 419, 129601.
36. Z. Shen, X. Wang, B. Luo and L. Li, J. Mater. Chem. A, 2015, 3, 18146–18153.
37. H. Y. Zhou, X. Q. Liu, X. L. Zhu and X. M. Chen, J. Am. Ceram. Soc., 2018, 101, 1999–2008.
38. T. Li, P. Chen, F. Li and C. Wang, Chem. Eng. J., 2021, 406, 127151.
39. K. Wang, A. Hussain, W. Jo and J. Rödel, J. Am. Ceram. Soc., 2012, 95, 2241–2247.
40. Y. Ding, W. Que, J. He, W. Bai, P. Zheng, P. Li, J. Zhang and J. Zhai, J. Eur. Ceram. Soc., 2022, 42, 129–139.
41. F. Yan, X. Zhou, X. He, H. Bai, S. Wu, B. Shen and J. Zhai, Nano Energy, 2020, 75, 105012.
42. C. Luo, Y. Wei, Q. Feng, M. Wang, N. Luo, C. Yuan, C. Zhou, T. Fujita and J. Xu, Chem. Eng. J., 2022, 429, 132165.
43. X. Zhao, W. Bai, Y. Ding, L. Wang, S. Wu, P. Zheng, P. Li and J. Zhai, J. Eur. Ceram. Soc., 2020, 40, 4475–4486.
44. Z. Pan, D. Hu, Y. Zhang, J. Liu, B. Shen and J. Zhai, J. Mater. Chem. C, 2019, 7, 4072–4078.
45. F. Yan, H. Bai, X. Zhou, G. Ge, G. Li, B. Shen and J. Zhai, J. Mater. Chem. A, 2020, 8, 11656–11664.
46. Z. Dai, J. Xie, X. Fan, X. Ding, W. Liu, S. Zhou and X. Ren, Chem. Eng. J., 2020, 397, 125520.
47. X. Zhou, H. Qi, Z. Yan, G. Xue, H. Luo and D. Zhang, J. Eur. Ceram. Soc., 2019, 39, 4053–4059.
48. X. Li, Y. Cheng, F. Wang, Q. Xu, Y. Chen, L. Xie, Z. Tan, J. Xing and J. Zhu, Chem. Eng. J., 2022, 431, 133441.
49. J. Xing, Y. Huang, B. Wu, H. Liu, Z. Tan, Q. Chen, W. Zhang, D. Xiao and J. Zhu, ACS Appl. Electron. Mater., 2020, 2, 3717–3727.
50. X. Liu and X. Tan, Adv. Mater., 2016, 28, 574–578.
51. S. K. Gupta, R. McQuade, B. Gibbons, P. Mardilovich and D. P. Cann, J. Appl. Phys., 2020, 127, 074104.
52. H.-S. Han, W. Jo, J.-K. Kang, C.-W. Ahn, I. Won Kim, K.-K. Ahn and J.-S. Lee, J. Appl. Phys., 2013, 113, 154102.
53. F. Wang, M. Xu, Y. Tang, T. Wang, W. Shi and C. M. Leung, J. Am. Ceram. Soc., 2012, 95, 1955–1959.
54. L. Zhao, Q. Liu, J. Gao, S. Zhang and J.-F. Li, Adv. Mater., 2017, 29, 1701824.
55. S. Li, H. Nie, G. Wang, C. Xu, N. Liu, M. Zhou, F. Cao and X. Dong, J. Mater. Chem. C, 2019, 7, 1551–1560.
56. K. Han, N. Luo, S. Mao, F. Zhuo, L. Liu, B. Peng, X. Chen, C. Hu, H. Zhou and Y. Wei, J. Mater. Chem. A, 2019, 7, 26293–26301.
57. N. Luo, K. Han, F. Zhuo, C. Xu, G. Zhang, L. Liu, X. Chen, C. Hu, H. Zhou and Y. Wei, J. Mater. Chem. A, 2019, 7, 14118–14128.
58. N. Luo, K. Han, L. Liu, B. Peng, X. Wang, C. Hu, H. Zhou, Q. Feng, X. Chen and Y. Wei, J. Am. Ceram. Soc., 2019, 102, 4640–4647.
59. N. Luo, K. Han, F. Zhuo, L. Liu, X. Chen, B. Peng, X. Wang, Q. Feng and Y. Wei, J. Mater. Chem. C, 2019, 7, 4999–5008.
60. Z. Chen, X. Bai, H. Wang, J. Du, W. Bai, L. Li, F. Wen, P. Zheng, W. Wu, L. Zheng and Y. Zhang, Ceram. Int., 2020, 46, 11549–11555.
61. Q. Li, S. Ji, D. Wang, J. Zhu, L. Li, W. Wang, M. Zeng, Z. Hou, X. Gao, X. Lu, Q. Li and J.-M. Liu, J. Eur. Ceram. Soc., 2021, 41, 387–393.
62. H. Yang, H. Qi and R. Zuo, J. Eur. Ceram. Soc., 2019, 39, 2673–2679.
63. F. Yan, Y. Shi, X. Zhou, K. Zhu, B. Shen and J. Zhai, Chem. Eng. J., 2021, 417, 127945.
64. N. Liu, R. Liang, Z. Zhou and X. Dong, J. Mater. Chem. C, 2018, 6, 10211–10217.
65. Y. Lin, D. Li, M. Zhang and H. Yang, J. Mater. Chem. C, 2020, 8, 2258–2264.
66. L. Zheng, P. Sun, P. Zheng, W. Bai, L. Li, F. Wen, J. Zhang, N. Wang and Y. Zhang, J. Mater. Chem. C, 2021, 9, 5234–5243.
67. D. Hu, Z. Pan, X. Zhang, H. Ye, Z. He, M. Wang, S. Xing, J. Zhai, Q. Fu and J. Liu, J. Mater. Chem. C, 2020, 8, 591–601.
68. X. Qiao, F. Zhang, D. Wu, B. Chen, X. Zhao, Z. Peng, X. Ren, P. Liang, X. Chao and Z. Yang, Chem. Eng. J., 2020, 388, 124158.
69. D. Li, Y. Lin, Q. Yuan, M. Zhang, L. Ma and H. Yang, J. Materiomics, 2020, 6, 743–750.
70. J. Liu, Y. Ding, C. Li, W. Bai, P. Zheng, J. Zhang and J. Zhai, J. Mater. Sci.: Mater. Electron., 2021, 32, 21164–21177.
71. Y. Ding, J. Liu, C. Li, W. Bai, S. Wu, P. Zheng, J. Zhang and J. Zhai, Chem. Eng. J., 2021, 426, 130811.
72. M. Zhou, R. Liang, Z. Zhou and X. Dong, Ceram. Int., 2019, 45, 3582–3590.
73. Z. Dai, J. Xie, W. Liu, X. Wang, L. Zhang, Z. Zhou, J. Li and X. Ren, ACS Appl. Mater. Interfaces, 2020, 12, 30289–30296.
74. Q. Yuan, F.-Z. Yao, S.-D. Cheng, L. Wang, Y. Wang, S.-B. Mi, Q. Wang, X. Wang and H. Wang, Adv. Funct. Mater., 2020, 30, 2000191.
75. G. Liu, Y. Li, B. Guo, M. Tang, Q. Li, J. Dong, L. Yu, K. Yu, Y. Yan, D. Wang, L. Zhang, H. Zhang, Z. He and L. Jin, Chem. Eng. J., 2020, 398, 125625.
76. Q. Hu, Y. Tian, Q. Zhu, J. Bian, L. Jin, H. Du, D. O. Alikin, V. Y. Shur, Y. Feng, Z. Xu and X. Wei, Nano Energy, 2020, 67, 104264.
77. H. Yang, Z. Lu, L. Li, W. Bao, H. Ji, J. Li, A. Feteira, F. Xu, Y. Zhang, H. Sun, Z. Huang, W. Lou, K. Song, S. Sun, G. Wang, D. Wang and I. M. Reaney, ACS Appl. Mater. Interfaces, 2020, 12, 43942–43949.
78. Z. Cai, C. Zhu, H. Wang, P. Zhao, Y. Yu, L. Li and X. Wang, J. Mater. Chem. A, 2019, 7, 17283–17291.
79. W. Wang, Y. Pu, X. Guo, T. Ouyang, Y. Shi, M. Yang, J. Li, R. Shi and G. Liu, Ceram. Int., 2019, 45, 14684–14690.
80. Y. Pu, W. Wang, X. Guo, R. Shi, M. Yang and J. Li, J. Mater. Chem. C, 2019, 7, 14384–14393.
81. M. Zhang, H. Yang, D. Li, L. Ma and Y. Lin, J. Mater. Chem. C, 2020, 8, 8777–8785.
82. Z. Yang, H. Du, S. Qu, Y. Hou, H. Ma, J. Wang, J. Wang, X. Wei and Z. Xu, J. Mater. Chem. A, 2016, 4, 13778–13785.
83. B. Qu, H. Du, Z. Yang and Q. Liu, J. Am. Ceram. Soc., 2017, 100, 1517–1526.
84. T. Shao, H. Du, H. Ma, S. Qu, J. Wang, J. Wang, X. Wei and Z. Xu, J. Mater. Chem. A, 2017, 5, 554–563.
85. Z. Yang, H. Du, L. Jin, Q. Hu, H. Wang, Y. Li, J. Wang, F. Gao and S. Qu, J. Mater. Chem. A, 2019, 7, 27256–27266.
86. M. Zhou, R. Liang, Z. Zhou and X. Dong, J. Mater. Chem. A, 2018, 6, 17896–17904.
87. L. Yang, X. Kong, Z. Cheng and S. Zhang, ACS Appl. Mater. Interfaces, 2020, 12, 32834–32841.
88. J. Shi, X. Chen, X. Li, J. Sun, C. Sun, F. Pang and H. Zhou, J. Mater. Chem. C, 2020, 8, 3784–3794.
89. A. Tian, R. Zuo, H. Qi and M. Shi, J. Mater. Chem. A, 2020, 8, 8352–8359.
90. W. Pan, M. Cao, A. Jan, H. Hao, Z. Yao and H. Liu, J. Mater. Chem. C, 2020, 8, 2019–2027.
91. H. Yang, F. Yan, Y. Lin and T. Wang, Appl. Phys. Lett., 2017, 111, 253903.
92. H. Yang, F. Yan, Y. Lin and T. Wang, ACS Sustainable Chem. Eng., 2017, 5, 10215–10222.
93. C. Cui and Y. Pu, J. Alloys Compd., 2018, 747, 495–504.
94. X. Kong, L. Yang, Z. Cheng and S. Zhang, J. Am. Ceram. Soc., 2020, 103, 1722–1731.
95. Y. Ding, P. Li, J. He, W. Que, W. Bai, P. Zheng, J. Zhang and J. Zhai, Composites, Part B, 2022, 230, 109493.
96. J. Li, F. Li, Z. Xu and S. Zhang, Adv. Mater., 2018, 30, 1870240.
97. J. Jiang, X. Meng, L. Li, S. Guo, M. Huang, J. Zhang, J. Wang, X. Hao, H. Zhu and S.-T. Zhang, Energy Storage Mater., 2021, 43, 383–390.
98. R. Waser, Ferroelectrics, 1992, 133, 109–114.
99. P. Lv, J. Qian, C. Yang, Y. Wang, W. Wang, S. Huang, X. Cheng and Z. Cheng, ACS Energy Lett., 2021, 6, 3873–3881.
100. Y. Xu, Z. Yang, K. Xu, Y. Cao, Y. Tian, L. Guo, J. Tian, H. Tian, X. Liu, L. Lin and G. Wang, Chem. Eng. J., 2021, 426, 131047.
101. Z. Cai, X. Wang, W. Hong, B. Luo, Q. Zhao and L. Li, J. Am. Ceram. Soc., 2018, 101, 5487–5496.
102. Y. Huan, T. Wei, X. Wang, X. Liu, P. Zhao and X. Wang, Chem. Eng. J., 2021, 425, 129506.
103. Y. H. Huang, Y. J. Wu, B. Liu, T. N. Yang, J. J. Wang, J. Li, L.-Q. Chen and X. M. Chen, J. Mater. Chem. A, 2018, 6, 4477–4484.
104. I. Fujii, S. Trolier-McKinstry and C. Nies, J. Am. Ceram. Soc., 2011, 94, 194–199.
105. D. Piazza, L. Stoleriu, L. Mitoseriu, A. Stancu and C. Galassi, J. Eur. Ceram. Soc., 2006, 26, 2959–2962.
106. M. Deluca, L. Stoleriu, L. P. Curecheriu, N. Horchidan, A. C. Ianculescu, C. Galassi and L. Mitoseriu, J. Appl. Phys., 2012, 111, 084102.
107. M. Zhang, H. Yang, Y. Yu and Y. Lin, Chem. Eng. J., 2021, 425, 131465.
108. R. Kang, Z. Wang, W. Liu, L. He, X. Zhu, P. Shi, X. Zhang, L. Zhang and X. Lou, ACS Appl. Mater. Interfaces, 2021, 13, 25143–25152.
109. H. Pan, F. Li, Y. Liu, Q. Zhang, M. Wang, S. Lan, Y. Zheng, J. Ma, L. Gu, Y. Shen, P. Yu, S. Zhang, L.-Q. Chen, Y.-H. Lin and C.-W. Nan, Science, 2019, 365, 578–582.
110. R. Dittmer, W. Jo, J. Rödel, S. Kalinin and N. Balke, Adv. Funct. Mater., 2012, 22, 4208–4215.
111. H. Pan, S. Lan, S. Xu, Q. Zhang, H. Yao, Y. Liu, F. Meng, E.-J. Guo, L. Gu, D. Yi, X. Renshaw Wang, H. Huang, L. MacManus-Driscoll Judith, L.-Q. Chen, K.-J. Jin, C.-W. Nan and Y.-H. Lin, Science, 2021, 374, 100–104.
112. G. Liu, M. Tang, X. Hou, B. Guo, J. Lv, J. Dong, Y. Wang, Q. Li, K. Yu, Y. Yan and L. Jin, Chem. Eng. J., 2021, 412, 127555.
113. X. Kong, L. Yang, Z. Cheng and S. Zhang, Materials, 2020, 13, 180.
114. P. Zhao, B. Tang, Z. Fang, F. Si, C. Yang and S. Zhang, Chem. Eng. J., 2021, 403, 126290.
115. P. Zhao, B. Tang, F. Si, C. Yang, H. Li and S. Zhang, J. Eur. Ceram. Soc., 2020, 40, 1938–1946.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d2ta00380e

---