Open Access Article
Open Access ArticleOxygen evolution reaction activity and underlying mechanism of perovskite electrocatalysts at different pH†
Bae-Jung
Kim
a,
Emiliana
Fabbri
 *a,
Mario
Borlaf
*a,
Mario
Borlaf
 b,
Daniel F.
Abbott
a,
Ivano E.
Castelli
b,
Daniel F.
Abbott
a,
Ivano E.
Castelli
 c,
Maarten
Nachtegaal
a,
Thomas
Graule
b and
Thomas J.
Schmidt
c,
Maarten
Nachtegaal
a,
Thomas
Graule
b and
Thomas J.
Schmidt
 ad
ad
aPaul Scherrer Institut, Forschungstrasse 111, 5232 Villigen PSI, Switzerland. E-mail: emiliana.fabbri@psi.ch
bLaboratory for High Performance Ceramics, Empa, Swiss Federal Laboratories for Science and Technology, 8600 Dübendorf, Switzerland
cDepartment of Energy Conversion and Storage, Technical University of Denmark, Anker Engelunds Vej 411, DK-2800, Kgs. Lyngby, Denmark
dLaboratory of Physical Chemistry, ETH Zürich, CH-8093 Zürich, Switzerland
First published on 18th November 2020
Abstract
The members of the perovskite oxide family have been vastly explored for their potential as active electrocatalysts for an efficient anodic reaction (i.e. the oxygen evolution reaction, OER) of the water splitting process. Therefore, restless effort has been invested in the development of perovskite oxides as efficient OER catalysts, while the OER mechanism is still in veil. The rational development of perovskite catalysts for practical water electrolysis is left on hold until the full comprehension of the underlying mechanism is established under real operation conditions. Up to date, primarily two different OER mechanisms – conventional and lattice oxygen evolution – have been conjectured where the former follows a reversible route while the latter leads to irreversible changes. In this present study, we present evidence which suggests that perovskite catalysts follow both mechanisms concomitantly while one is preferentially selected based on their thermodynamic and kinetic natures dependent on pH.
Introduction
As the search for environmentally sustainable energy resources continues, mainstreaming renewable energy is now becoming more urgent. In parallel, the energy storage technologies are also drawing attention for mediating inconsistent power generation from renewable energy sources. Water electrolysis utilizes hydrogen as an energy vector to store vast amounts of energy, and typically operates either in acidic or alkaline electrolytes.2,3 Particularly, operation under alkaline conditions takes advantage of a less corrosive environment, which allowed exploring abundant and low cost non-noble metals as electrocatalysts to constitute water splitting reactions.4 However, the use of KOH solution as the electrolyte creates vulnerability to carbonation during operation, which shifts the pH level towards near-neutral values and decreases the electrolyte conductivity.3,4 Carbonation occurs when CO2 is introduced into the alkaline electrolyte lowering the initially high pH level due to the equilibrium reaction between CO2 and HCO3−, in which the catalyst then functions under a near-neutral pH (7–10).3 In addition, recently developed anion exchange membranes, which exhibits comparable conductivity to that of acidic membranes, also suffers from carbonation and decreases membrane conductivity.4,5 On the other hand, these concerns actually push electrolysis application towards the direction of co-electrolysis, where at the cathode valuable fuels, such as hydrocarbons, syngas, and methanol can be directly produced.3,4As many studies have been devoted to searching for an ideal electrocatalyst for the OER, perovskite oxides have stood out as promising electrocatalysts as they offer advantages from their ability to modify easily their intrinsic properties by cation substitution.2,6–18 Meanwhile, the excitement of searching for new or possibly more active perovskite OER catalysts left the understanding of the underlying OER mechanism trail behind. The complexity of understanding the OER mechanism arises as the activity of some catalysts cannot be simply explained by considering the activity-mechanism correlations related to the well-known Sabatier principle.19,20 Recent studies have suggested that the OER activity of a perovskite catalyst may be affected by a different paradigm which involves the participation of lattice oxygen atoms in the oxygen evolution (i.e. lattice oxygen evolution reaction, LOER).1,6,21–29 The LOER involves a dynamically changing catalyst surface as it interacts with the electrolyte, and it can potentially lead to perovskite metal cation dissolution.1,6,25,30–32 Likewise, the prominence of LOER has recently been highlighted to additionally elucidate the OER mechanism of transition metal oxide catalysts.1,6,22,23,25,32–38 Generally in alkaline conditions, OER and LOER are thermodynamically coupled.31 The dissolved metal cations during LOER can either be dissolved into the electrolyte and oxidized to a higher valence state or recombined with the excessive hydroxide ions from the electrolyte promoting the formation of an oxy(hydroxide) layer. Several studies indeed report the formation of a superficial oxy(hydroxide) layer under OER conditions for highly active metal oxides.6,25,39–42
The classical OER mechanism is under the basis that the oxygen is evolved only around the metal center, whereas the mechanism that involves the participation of lattice oxygen signifies that the surface metal atom is not the only active center. Fig. 1a and b describe the conventional mechanism20,43 and the lattice oxygen participating mechanism,1 respectively. As sketched in Fig. 1b, the participation of lattice oxygen involves the construction of a surface oxy(hydroxide) layer (step 1′ and 2′ of Fig. 1b) followed by the creation of oxygen vacancies (step 3′ of Fig. 1b), which is a decoupled electron–proton transfer step. Subsequently, the created oxygen vacancy can either be subjected to surface cation dissolution where the changes at the surface of the catalyst would be irreversible. Alternatively, the oxygen vacancy could be replenished by hydroxide anions from the electrolyte.1 Recently, it has been suggested that a decoupled charge transfer would occur at the catalyst surface if the removal of the involved charge from the active site has fast kinetics; otherwise, a concerted coupled proton–electron transfer (CPET) would be expected considering the high energy of formation for charge intermediates.44–47 Considering alkaline conditions where the pKa (proton affinity) is high, a transition metal oxide catalyst would be able to delocalize charged intermediates by changing its oxidation state instead of requiring an electron transfer.47 A density functional theory calculation study23 has revealed that this process of delocalization would be thermodynamically more probable, and therefore the catalyst is likely to follow the LOER mechanism. To further understand the OER mechanism of perovskite catalysts in alkaline environment, the pH dependence of OER activity for few perovskites and other oxide catalysts has been emphasized in high alkaline conditions (pH range of 13–14.5),25,32,34,35,38,44,48 but not in a wide range of pH values and specifically in near-neutral conditions. It is important to recall that the electrolyte carbonation challenges the practical operation as the system's pH shifts to near-neutral, and therefore raises uncertainties concerning the reaction pathways of perovskite catalysts. Thus, it is necessary to understand the catalytic behavior of perovskite catalysts upon the change of pH to near-neutral. Therefore, in this present study, we provide further understanding of the OER mechanism for different perovskite catalysts, namely Ba0.5Sr0.5CoO3−δ (BSC), Ba0.5Sr0.5Co0.8Fe0.2O3−δ (BSCF), La0.5Sr0.5CoO3−δ (LSC), La0.2Sr0.8Co0.8Fe0.2O3−δ (LSCF), PrBaCo2O6−δ (PBC), and PrBaCo1.6Fe0.4O6−δ (PBCF) prepared via flame spray synthesis (refer to Fig. S1, ESI†), by comparing electrocatalytic activities at in a wide range of pH (7–14) levels. The selected ABO3 perovskite structures present different A site cations, but all contain Co or Co/Fe as B site cations. Indeed, Co-based perovskites are known to possess high OER activity, particularly when Co is partially occupied by Fe.24,49 Our recent studies24,49 show that Fe incorporation into Co-based perovskite oxides alters perovskite intrinsic properties, particularly the initial Co oxidation state. This leads to more OER active and stable catalyst compositions in alkaline environment (pH 13), particularly for BSC and LSC-based perovskites. In the present study, the OER activity and stability of Co-based perovskite catalysts with and without Fe doping are studied over a wide range of pH environments. Furthermore, the perovskite electronic and local structure changes under the different pH levels are investigated by operando X-ray absorption spectroscopy.
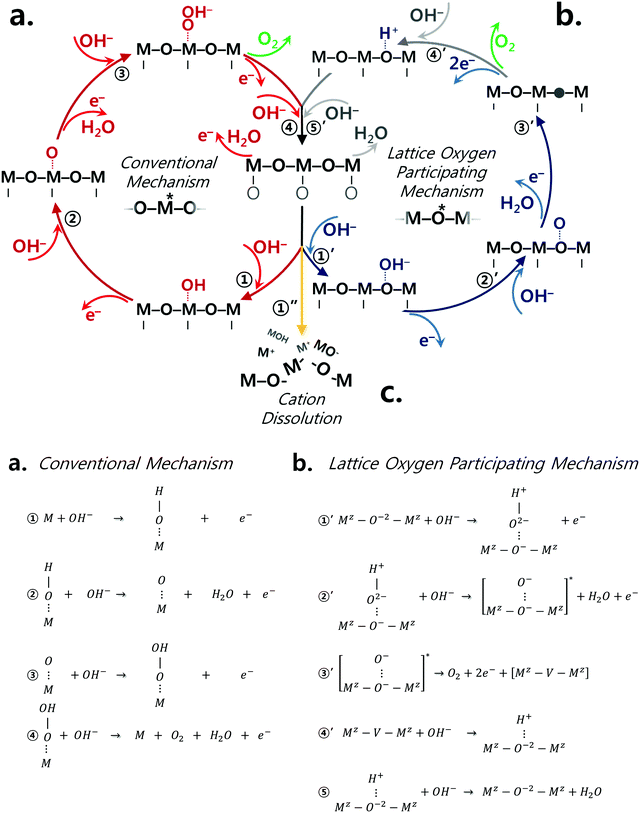 | ||
| Fig. 1 Perovskite catalysts are plausible to undergo both conventional and lattice oxygen participating mechanisms as sketched in (a) and (b), respectively.1 The conventional mechanism consists of concerted proton electron transfers while step 3′ of the lattice oxygen participating mechanism is a decoupled transfer of charges. (c) The dissolution of surface cations is another competing reaction which the catalyst may undergo due to the thermodynamic instability under the oxygen evolution reaction condition. | ||
Experimental
Material synthesis
BSC, LSC, BSCF, and LSCF have been synthesized by flame spray synthesis.50 The used precursors include barium carbonate (BaCO3, ≥99%, Sigma-Aldrich, Germany), lanthanum oxide (La2O3, >99.99%, Auer Remi, Germany) strontium nitrate (Sr(NO3)2, ≥98%, Sigma-Aldrich, Germany), cobalt nitrate hexahydrate (Co(NO3)2·6H2O, 99.9%, Auer Remy, Germany) and iron nitrate nonahydrate (Fe(NO3)3·9H2O, ≥98%, Sigma-Aldrich, Germany). Corresponding precursors for each catalyst were dissolved in a mixture of water and nitric acid (HNO3, 70%, Sigma-Aldrich, Germany). After, acetic acid (HAc, ≥99.0%, Sigma-Aldrich, Germany) was added to obtain a solvent composition of HAc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HNO3
HNO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O = 25
H2O = 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 74 in volume. For LSC and LSCF, the La2O3 was dissolved in concentrated nitric acid and the resulting product was added into a mixture of N,N-dimethylformamide (DMF, ≥99.8%, Roth, Switzerland), acetic acid and water, (final volume ratio of 50
74 in volume. For LSC and LSCF, the La2O3 was dissolved in concentrated nitric acid and the resulting product was added into a mixture of N,N-dimethylformamide (DMF, ≥99.8%, Roth, Switzerland), acetic acid and water, (final volume ratio of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30, respectively) were the other precursors were previously dissolved. For all catalyst preparation, the total metal concentration in the precursor solution was 0.2 M. For the preparation of the PrBaCo2O5+x (PBC) and PrBaCo2−yFeyO5+x (y = 0.4 and 1.0) precursor solutions, stoichiometric amounts of praseodymium oxide (Pr6O11, 99.9%, Auer Remy), barium carbonate (BaCO3, ≥99%, Sigma-Aldrich), cobalt nitrate hexahydrate (Co(NO3)2·6H2O, 99.9%, Sigma-Aldrich) and iron nitrate nonahydrate (Fe(NO3)3·9H2O, ≥98%, Sigma-Aldrich) were dissolved in a mixture of solvents composed by N,N-dimethylformamide (DMF, ≥99.8%, Roth), acetic acid (HAc, ≥99.0%, Sigma-Aldrich), nitric acid (HNO3, 70%, Sigma-Aldrich) and water in 45
30, respectively) were the other precursors were previously dissolved. For all catalyst preparation, the total metal concentration in the precursor solution was 0.2 M. For the preparation of the PrBaCo2O5+x (PBC) and PrBaCo2−yFeyO5+x (y = 0.4 and 1.0) precursor solutions, stoichiometric amounts of praseodymium oxide (Pr6O11, 99.9%, Auer Remy), barium carbonate (BaCO3, ≥99%, Sigma-Aldrich), cobalt nitrate hexahydrate (Co(NO3)2·6H2O, 99.9%, Sigma-Aldrich) and iron nitrate nonahydrate (Fe(NO3)3·9H2O, ≥98%, Sigma-Aldrich) were dissolved in a mixture of solvents composed by N,N-dimethylformamide (DMF, ≥99.8%, Roth), acetic acid (HAc, ≥99.0%, Sigma-Aldrich), nitric acid (HNO3, 70%, Sigma-Aldrich) and water in 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 volume ratio, respectively. Firstly, the Pr6O11 was dissolved in the mixture of water and nitric acid at 80 °C; when a clear green solution was obtained, the BaCO3 was added and then, when no more CO2 bubbles were observed, the Co and Fe (only for PBCF solutions) metal precursors. When all dissolved, the HAc and the DMF were added, obtaining a final total metal concentration of 0.1 M.
25 volume ratio, respectively. Firstly, the Pr6O11 was dissolved in the mixture of water and nitric acid at 80 °C; when a clear green solution was obtained, the BaCO3 was added and then, when no more CO2 bubbles were observed, the Co and Fe (only for PBCF solutions) metal precursors. When all dissolved, the HAc and the DMF were added, obtaining a final total metal concentration of 0.1 M.
The prepared precursor solutions were pumped into flame by using a three-piston pump (C-601, Büchi, Switzerland) with a flow controller (C-610, Büchi, Switzerland) with a constant flow free of pulsations of 20 mL min−1. The nozzle is assembled by a commercial flame cutter (Type 150-200, PanGas, Switzerland) modified with a centered capillary (Ø inner = 1.05 mm, Ø outer = 1.6 mm), allowing an axial injection of the liquid precursors. The capillary is surrounded by a circular gap (Ø = 3 mm) through which the dispersion gas is supplied. Pure oxygen (99.95%, Carbagas, Switzerland) was used as dispersion gas with a flow rate of 35 L min−1 (45 L min−1 for LSC and LSCF). The combustion gas was formed by acetylene (99.6%, Carbagas, Switzerland), with a flow rate of 13 L min−1, and pure oxygen (17 L min−1 for BSC and BSCF and 30 L min−1 for LSC and LSCF). Finally, the produced powders were collected in a baghouse filter (Friedli AG, Switzerland), while representative powder samples were simultaneously collected on four ashless paper filters (Whatman, Sigma-Aldrich) using a by-pass inlet with two vacuum pumps.
Material characterizations
Phase characterization of prepared materials was performed using powder X-ray diffraction (XRD, Bruker D8 system in Bragg–Brentano geometry, Cu Kα radiation (λ = 0.15418 nm)). Specific surface area was calculated by Brunauer–Emmett–Teller (BET) analysis of N2 adsorption/desorption isotherms (AUROSORB-1, Quantachrome). Transmission electron microscopy (TEM) and energy dispersive X-ray spectroscopy (EDX) (TECNAI F30 operated at 300 kV for transmission imaging) were used to study the surface morphology of the prepared materials.For ex situ and operando X-ray absorption spectroscopy (XAS) measurements, the ink was prepared by dissolving catalyst powders in a solution mixture of isopropanol and Milli-Q water in the equal volumetric ratio and sonicated for 30 min. The prepared ink was then spray coated on Kapton film. XAS spectra at the Co K-edge were recorded at the SuperXAS beamline of the Swiss Light Source (PSI, Villigen, Switzerland). The incident photon beam provided by a 2.9 T superbend magnet source was collimated by a Si-coated mirror at 2.5 mRad and subsequently monochromatized by a Si(111) channel-cut monochromator. A Rh-coated toroidal mirror at 2.5 mRad was used to focus the X-ray beam to a beam size of 1 mm by 0.2 mm maximal on the sample position. The SuperXAS beamline51 enabled the collection of 120 spectra during a measurement of 60 s (QEXAFS mode), which were then averaged. The spectra of samples were collected in transmission mode using N2 filled 15 cm long ionization chambers, where a Co foil was located between the second and third ionization chamber served to calibrate and align all spectra. Extended X-ray absorption fine structure (EXAFS) spectra were analyzed using the Demeter software package,52 which included background subtraction, energy calibration (based on the simultaneously measured Co reference foil) and edge-step normalization. The resulting spectra were converted to the photoelectron wave vector k (in units Å−1) by assigning the photoelectron energy origin, E0, corresponding to k = 0, to the first inflection point of the absorption edge. The resulting χ(k) functions were weighted with k3 to compensate for the dampening of the EXAFS amplitude with increasing k. χ(k) functions were Fourier transformed over 3–12 Å−1 and subsequently fitted. The theoretical models used for the EXAFS fittings of BSC and BSCF were generated from CoOOH53 for the Co–O coordination shell and the first Co–Co shell at ∼2.5–2.7 Å (not corrected for phase shift), and from Co(OH)254 for the second Co–Co shell at ∼2.7–3.0 Å (not corrected for phase shift) using the FEFF6.2 library.
Electrochemical characterization
Electrochemical tests were conducted in a standard three-electrode electrochemical cell using the rotating disk electrode (RDE) methodology at the standard room temperature. The setup consists of a potentiostat (Biologic VMP-300) and a rotation speed controlled motor (Pine Instrument Co., AFMSRCE). The reversible hydrogen electrode (RHE) was used as the reference electrode so that the OER overpotential is consistent at tested different pH levels.44 A piece of gold mesh was used as the counter electrode. A homemade Teflon cell was used to contain electrolytes with the working electrode immersed under the potential control. A porous thin film of materials was prepared by drop-casting a catalyst ink (0.02 mg) on a polished glassy carbon electrode (5 mm OD/0.196 cm2).55 The catalyst ink was prepared from a catalyst suspension made from sonicating (Bandelin, RM 16 UH, 300 Weff, 40 kHz) 10 mg of catalyst in a solution mixture of 4 mL isopropyl alcohol and 1 mL of Milli-Q water (ELGA, PURELAB Chorus), and 20 μL of ion-exchanged Nafion (Sigma-Aldrich, 5 wt%).56 The 0.1 M and 1.0 M KOH were used as electrolytes with pH of 13 and 14, respectively, prepared by dissolving respective KOH pellets (Sigma-Aldrich, 99.99%) in Milli-Q water. For measurements at pH 12, the pH was lowered from 0.1 M KOH (pH 13) by adding 0.1 M HClO4 solution, which was prepared by diluting concentrated HClO4 (Sigma-Aldrich, 70%) in Milli-Q water. 0.5 M KHCO3 electrolyte was saturated with synthetic air for 2 hours to attain a pH level of 9. Lastly, equal molar ratio of KH2PO4 and K2HPO4 were dissolved in Milli-Q water to preparation of pH 7 potassium phosphate buffer. Initially, 25 reverse potentiostatic sweeps of CV were performed in the synthetic air-saturated electrolyte from 1.0 to 1.7 VRHE at a scan rate of 10 mV s−1. Afterwards, series of chronoamperometry (CA) measurements were carried out holding each potential step for 30 seconds to obtain steady-state currents in the potential range from 1.2 to 1.7 VRHE while rotating the working electrode at 900 rpm. Tafel plots were constructed from the resulting polarization curves for all materials under study for an effective comparison of OER activities. The potential stability of catalyst materials was conducted using the same setup; alternating electrode potential between 1.0 VRHE and 1.6 VRHE for 500 times holding for 10 seconds each to reach steady-state at each potential. The stability plot is plotted by recording current densities at 1.6 VRHE. Five cycles of CV and electrochemical impedance spectroscopy (EIS) was carried out after every 100 cycles. All measured currents were normalized by the mass of catalyst loading, and potentials were corrected for the ohmic drop obtained from EIS.Operando flow cell test
The homemade operando XAS electrochemical flow cell used in this study was extensively described previously.57 The electrode materials were spray coated at the center of Kapton films. Black pearl (Cabot Corp.) was used as the counter electrode material. A silver chloride electrode (Ag+/AgCl) (Hugo Sachs Elektronik) was used as the reference electrode. During electrochemical testing, the electrolyte was drawn into the cell and collected in a syringe at the flow rate of 0.2 mL min−1. The CA measurement was carried out holding for 120 s at each increasing potential step from 1.2 VRHE to 1.54 VRHE (or higher), and back again to 1.2 VRHE during the reverse sequence. At each potential step, both transmission XAS spectra at the Co K-edges were collected simultaneously for 60 seconds. The energy position of the Co K-edge is determined at the half edge-step intensity.Density functional theory calculations – pourbaix diagrams
Density Functional Theory (DFT) calculations are used to help understand the experimental data. In the first set of calculations, the stability of the perovskites in an aqueous environment was investigated by means of Pourbaix diagrams. Pourbaix diagrams were constructed to show the phase diagram of solid and dissolved species as a function of pH and external potential based on the total energies for the solid bulk of perovskites and the other solids competing phases as described in the Materials Project database.58 The ion concentrations of 10−6 M were used. The dissolution energies for the dissolved species were obtained from experiments.59,60 This method is implemented in the Atomic Simulation Environment (ASE) package,61 and more details about the methodology can be found in ref. 62 and 63. All the bulk structures have been fully relaxed using the Quantum ESPRESSO code,64 PBEsol as exchange–correlation functional65 with a Hubbard +U correction of 2 eV applied to the p-orbitals of O, and d-orbitals of the transition metals and the pseudopotentials from the Standard Solid State Pseudopotential library (SSSP accuracy).66,67Results and discussion
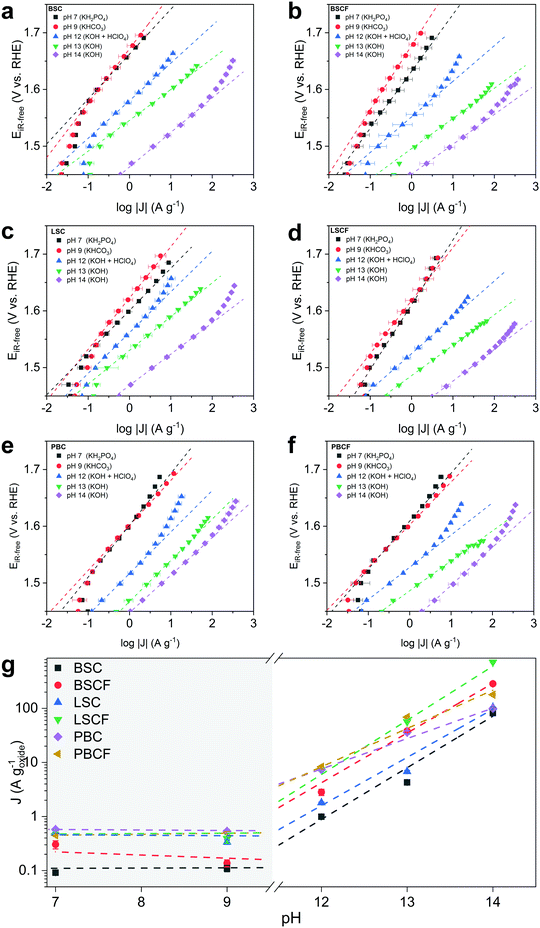
The OER activity as a function of pH is evaluated from Tafel plots (Fig. 2) constructed from series of chronoamperometry measurements at different pH levels for each prepared catalyst: BSC, BSCF, LSC, LSCF, PBC, and PBCF. Electrolyte solutions containing an appropriate concentration of KOH were prepared for pH 13 and pH 14, whereas pH 12 was prepared by titrating KOH at pH 13 with HClO4. Electrolyte solutions corresponding to pH 9 and pH 7 were prepared by using an appropriate concentration of KHCO3 and KH2PO4, respectively, and adjusting to the desired pH by titrating with either KOH or HClO4.In the region from pH 14 to 12 a linear decrease of the mass-normalized current density (A g−1) at 1.58 VRHE is observed (Fig. 2 and Table 1) for all of the investigated perovskites. Specifically, cubic perovskites – BSC, BSCF, LSC, LSCF – revealed slopes of ∂![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(J) vs. ∂pH close to unity, while double perovskites – PBC and PBCF – revealed a fractional slope (less than 1) hinting at the degradation of the perovskite structure or possible side reactions.44 The degradation of double perovskite also has been described in our previous work, for which its thermodynamic stability is held accountable.8 Previous studies20,34,44,47 postulate that the linear relationship between log of activity and pH, as observed for BSC, BSCF, LSC and LSCF, implies that the proton transfer in the LOER mechanism is the rate-determining step.34,35 Particularly, referring to the LOER mechanism sketched in Fig. 1b, the rate limiting step would be the deprotonation step of surface hydroxyl groups (step 2′ of Fig. 1b), decoupling the deprotonation from the ensuing electron transfer step (step 3′ of Fig. 1b). In other words, such a first-order relationship would indicate that the catalytic activity is dependent on the concentration of OH− in the high-alkaline region.34,68
log(J) vs. ∂pH close to unity, while double perovskites – PBC and PBCF – revealed a fractional slope (less than 1) hinting at the degradation of the perovskite structure or possible side reactions.44 The degradation of double perovskite also has been described in our previous work, for which its thermodynamic stability is held accountable.8 Previous studies20,34,44,47 postulate that the linear relationship between log of activity and pH, as observed for BSC, BSCF, LSC and LSCF, implies that the proton transfer in the LOER mechanism is the rate-determining step.34,35 Particularly, referring to the LOER mechanism sketched in Fig. 1b, the rate limiting step would be the deprotonation step of surface hydroxyl groups (step 2′ of Fig. 1b), decoupling the deprotonation from the ensuing electron transfer step (step 3′ of Fig. 1b). In other words, such a first-order relationship would indicate that the catalytic activity is dependent on the concentration of OH− in the high-alkaline region.34,68
| BSC | BSCF | LSC | LSCF | PBC | PBCF | ||
|---|---|---|---|---|---|---|---|
| pH 14 | m (mV dec−1) | 61 | 53 | 55 | 56 | 66 | 67 |
| j 0 (A g−1) | 1.46 | 1.45 | 1.47 | 1.42 | 1.45 | 1.43 | |
| J @1.58V (A g−1) | 81.7 | 285.0 | 104.1 | 715.0 | 99.4 | 180.0 | |
| pH 13 | m (mV dec−1) | 54 | 53 | 59 | 54 | 73 | 50 |
| j 0 (A g−1) | 1.55 | 1.50 | 1.53 | 1.49 | 1.47 | 1.49 | |
| J @1.58V (A g−1) | 4.3 | 38.1 | 6.8 | 56.6 | 36.0 | 68.8 | |
| pH 12 | m (mV dec−1) | 66 | 63 | 72 | 64 | 73 | 57 |
| j 0 (A g−1) | 1.58 | 1.55 | 1.56 | 1.53 | 1.52 | 1.53 | |
| J @1.58V (A g−1) | 1.0 | 2.8 | 1.8 | 7.3 | 7.3 | 8.3 | |
| pH 9 | m (mV dec−1) | 96 | 113 | 90 | 94 | 79 | 75 |
| j 0 (A g−1) | 1.67 | 1.67 | 1.62 | 1.62 | 1.60 | 1.60 | |
| J @1.58V (A g−1) | 0.1 | 0.1 | 0.3 | 0.4 | 0.5 | 0.5 | |
| pH 7 | m (mV dec−1) | 79 | 100 | 74 | 114 | 91 | 84 |
| j 0 (A g−1) | 1.66 | 1.63 | 1.60 | 1.61 | 1.60 | 1.61 | |
| J @1.58V (A g−1) | 0.1 | 0.3 | 0.5 | 0.5 | 0.6 | 0.5 | |
In the near-neural pH region (pH 7–9) relatively higher Tafel slopes (90–100 mV dec−1) were observed compared to the alkaline pH region, showing greatly reduced current densities and suggesting a different reaction mechanism. However, also the presence of different anion species in the pH 7 and 9 electrolytes should be considered. A previous study69 has attributed the decrease of activity to the poisoning of active sites by the phosphate from the electrolyte. Nevertheless, the phosphate group in solution would not disturb the proton transfer.68 Moreover in KHCO3, the side reactions involving the oxidation of carbonate species could not be excluded (refer to Table S1, ESI†) leading to less current contribution from the oxygen evolution. Overall, considering the pKa of these electrolytes, none of them provide “optimal” conditions for OER.47
More importantly, attention should be drawn towards the zeroth-order relationship between the mass activity and the proton activity in this near-neutral pH region (Fig. 2g). The similar OER activity between pH 7 and 9 signifies that the activity is independent of pH in the near-neutral pH region. Grimaud et al.34 postulated that a catalyst with its activity independent of pH would undergo a mechanism that only involves concerted proton–electron transfer (CPET) steps. Yoo et al.23 reported that thermodynamic preference of the mechanisms between conventional OER (i.e. fully-CPET) and LOER would depend on the covalency between the surface metal and the oxygenated intermediates. On the basis of these two observations, our findings suggest that a particular mechanism – either conventional OER or LOER – would be preferred depending on the pH region. Even though one mechanism would be more preferred over the other at a certain pH level, the less preferred mechanism would not be precluded. Both mechanisms would partially and proportionally occur in conjunction as their thermodynamics and kinetics are coupled.1,31
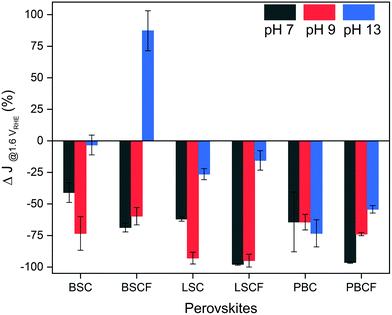
Furthermore, the perovskite catalysts revealed different current density response during the potential stability test which consists of 500 cycles of potential steps between 1.0 and 1.6 VRHE (Fig. 3 and Fig. S5, ESI†). Fig. 3 displays the changes in current density at the end of 500 cycles in percentage. All perovskite catalysts reveal a loss of current density at the selected pH level, except for BSCF at pH 13 (refer to Fig. S5b, ESI†). Such current density can be elucidated by their thermodynamic stabilities predicted from Pourbaix diagrams (which are based on density functional theory (DFT) calculations (Fig. S6, ESI†)). It is anticipated that among the selected perovskites, only BSCF is meta-stable in the entire working potential range for OER at pH 13 indicating that its perovskite structure is retained while undergoing partial cation dissolution. Particularly, Ba and Sr cations are mostly prone to dissolution compared to the Co and Fe cations,6 but the latter cations could also undergo dissolution and re-deposition process, as also recently observed by Chung and co-workers for Fe–MOxHy oxyhydroxides.30 Thereby, BSCF is able to support the formation of OER active Co/Fe-oxy(hydroxide) layer at its surface, preserving high OER activity and stability.24 It has recently been reported by performing DFT calculations70 that metastable perovskites are actually the most promising OER catalysts due to the possibility of having diverse surface reaction sites. However, metastable materials under OER conditions, such as BSCF, can represent the optimal OER catalysts only if the cation dissolution process is kinetically slow enough to prevent severe material loss.70 Specifically for BSCF, the working potential is out of the meta-stable region at pH levels lower than 13 (which is highlighted in blue in Fig. S6b, ESI†). Such thermodynamic instability at lower pH region is manifested by the decreasing stability of BSCF at near-neutral pH, where ∼60% of initial current density was lost at the end of 500 cycles (Fig. 3). Similarly, severe loss of current density at near-neutral pH is also seen for BSC, LSC and LSCF. Particularly, LSC and LSCF clearly revealed significant current density loss at pH 13. In case of double perovskites, PBC and PBCF, severe loss of current densities were observed in all pH ranges. The decrease of current densities can also for these perovskites be related to their Pourbaix diagrams, which show no meta-stable regions (Fig. S6e and f, ESI†), but not entirely. It should be noted that the degradation mechanism (such as cation dissolution) is always thermodynamically coupled to the OER/LOER process31 (Fig. 1c), but it is also kinetically controlled. For instance, the Pourbaix diagrams of BSC and LSCF (Fig. S6a and d, ESI†) describe its thermodynamic instability at pH 13, yet they demonstrated increasing current density within the first 100 cycles, followed by a decrease after 100 cycles (Fig. S5a and d, ESI†). Therefore, besides the thermodynamic stability, the cation dissolution kinetics, as well as possible surface reconstruction can contribute to hinder catalyst performance degradation. Furthermore, it should be mentioned that most of the investigated perovskites show severe current lost under near-neutral pH values, where the conventional OER mechanism is supposed to be more favoured than LOER, suggesting that fast material degradation is not always necessarily associated with LOER. Thus, these results suggest that the thermodynamic stability predicted by Pourbaix diagrams and the relationship between OER, LOER, and metal cation dissolutions cannot provide a full picture of the catalyst stability, but the reaction kinetics play also a big role. Based on these findings, we speculate that there are parallel processes concurring during the OER processes: the potential-induced oxygen evolution and the dissolution of surface cations, where the dissolution varies among catalysts due to their thermodynamics and surface kinetics, yet is inevitable.
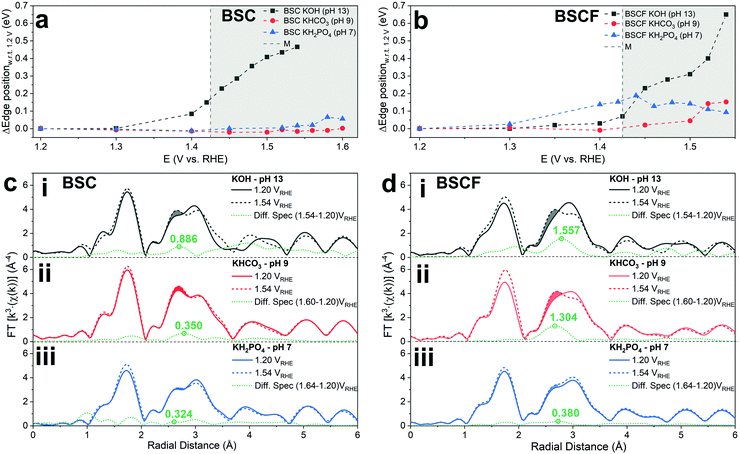
In order to assess the electronic and structural changes of the perovskites during the OER process at various pH conditions, operando X-ray absorption spectroscopy (XAS) was carried out at pH 7, 9, and 13. Fig. 4a and b plots the extent of the shift in the Co K-absorption edge energy positions of normalized X-ray absorption near edge structure (XANES) spectra of BSC and BSCF, respectively, at the half height maximum recorded during anodic polarization as was shown in their CV (refer to Fig. S4, ESI†). A shift of Co K-edge position of XANES spectra to higher incident energies indicates an increase in Co oxidation state. Previously, the potential-induced increase in the Co oxidation state, together with specific changes in the extended X-ray absorption fine structure (EXAFS) spectra for BSCF has been attributed to the formation of a Co/Fe-oxy(hydroxide) phase.6,8,24 In alkaline condition (i.e. pH 13), both BSC and BSCF revealed accelerated shifts in their Co K-edge energy position when polarized above the OER onset potential (>1.4 VRHE), which is ascribable to the growth of Co/Fe-oxy(hydroxide) layer.6,24 The formation of Co/Fe-oxy(hydroxide) layer can result from the LOER, which not only leads to evolution of oxygen molecules but is also known to cause irreversible surface changes,25,30,32,71,72 such as the formation of a Co/Fe-oxy(hydroxide) layer on BSCF as was shown in ref. 6 and 24 and elucidated in eqn (1).
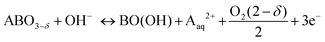 | (1) |
Fig. 4c and d clearly illustrate the insignificant development of this FT-EXAFS peak (highlighted) for both BSC and BSCF at pH 7 signifying the inactive formation of Co/Fe-oxy(hydroxide) at near-neutral pH regime. In parallel, the best fit to the FT-EXAFS spectra of BSC and BSCF taken at the highest anodic potential show progressively smaller increases in their Co–Co/Fe coordination number as the pH decreases (i.e. 13, 9, and 7); for example, BSCF shows an increase in Co–Co coordination number of ∼0.4 at pH 13, while at lower pHs the increase is almost insignificant (∼0.2 at pH 9 and ∼0.1 at pH 7, respectively, refer to Table S2, ESI†). This further supports that the development of Co/Fe-oxy(hydroxide) layer is suppressed in the near-neutral pH region. As reported by many studies, the surface reconstruction during OER and the formation of a superficial oxyhydroxide layer is not necessarily synonym of material instability.6,25,30,32 Indeed, as discussed in ref. 6 and 30, a dynamic self-reconstruction of the catalyst surface during OER can be seen also as a “dynamic stability”30 where metal cations can in principle dissolve and re-deposit on the catalyst surface, leading to an oxyhydroxide phase with superior OER activity and also stable performance. Differently, in near-neutral pH values, where the conventional CPET OER mechanism seems to dominate and any surface reconstruction is observed, all the investigated perovskites undergo substantial activity loss over potential cycles.
Finally, it should be also mentioned that the Co/Fe-oxyhydroxide formed under alkaline pH level can also undergoes LOER. Recently, while the conventional CPET OER mechanism has been reported to take place on the surface of CoOOH catalyst, the introduction of Zn into the catalyst structure leads to a change in the reaction mechanism, favouring the LOER.35 Similarly, the Fe substitution into CoAl2O4 facilitates the reconstruction of the catalyst surface towards an active Co oxyhydroxide under OER conditions and activates the occurrence of the LOER.32 Likewise, the of Co/Fe-oxy(hydroxide) formed in alkaline region on the surface of BSCF can provide high OER activity and a dynamically stable surface.
In light of all the above findings, the following reactions are all concurrently conceivable for perovskites during the OER process: (i) OH− adsorption on the surface metal atom (i.e. conventional mechanism), adsorption on lattice oxygen (LOER mechanism), and cation dissolution. Although one reaction seems to be preferred more than the other depending on the pH as it affects the kinetics of adsorbate species and the thermodynamic stability of the catalyst, yet, none of these reactions would be obsolete. This realization introduces an additional aspect which needs to be carefully thought of and integrated in the course of catalyst development and optimization.
Conclusions
In summary, fruitful information could be obtained from the study of perovskite OER activity and stability versus different pH levels and from the changes in perovskite structure during the OER process, from which certain aspects regarding the mechanism could be inferred. The studied perovskites showed a first-order relationship between activity and pH in the high alkaline region while revealing zeroth-order in the near-neutral pH region. Differences in the OER activity versus pH, order of activity between alkaline and near-neutral pH regions suggest that different mechanisms are predominant in the different pH regions. From monitoring the changes in the energy position of the Co K absorption edge during the OER process, the potential-induced increase of Co oxidation state was found only in alkaline pH (i.e. pH 13) for BSC and BSCF. Combined with the results of operando FT-EXAFS spectra, this increase of Co oxidation state is related to the development of Co/Fe-oxy(hydroxide) species, which is a result of the LOER mechanism. Differently, in the near neutral region the development of a Co/Fe-oxy(hydroxide) surface layer was not clearly observed. Thus, perovskite catalysts would seemingly be more inclined to evolve oxygen through the LOER mechanism in a highly alkaline condition, and the level of affinity towards facilitating LOER would diminish as the system's pH decreases to near-neutral, in accordance with the previous analysis of slopes of ∂![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(J) vs. ∂pH−1. Nevertheless, a catalyst would not perform oxygen evolution through only one of the two mechanisms discussed in here, but it would rather preferentially and proportionally take both paths of plausible mechanisms (conventional and LOER) as they are thermodynamically entangled as shown in ref. 33. In addition, the effect of cation dissolution must not be forgotten as it is also thermodynamically intertwined with OER.33 Interestingly, for most of the investigated perovskite compositions the highest stability was observed at higher pH levels where the LOER seems to dominate over the conventional OER mechanism. This result suggests that the A-site cation dissolution generally induced by LOER can actually lead to a dynamically stable surface, mostly composed by an oxyhydroxide phase and having both higher OER activity and good stability.
log(J) vs. ∂pH−1. Nevertheless, a catalyst would not perform oxygen evolution through only one of the two mechanisms discussed in here, but it would rather preferentially and proportionally take both paths of plausible mechanisms (conventional and LOER) as they are thermodynamically entangled as shown in ref. 33. In addition, the effect of cation dissolution must not be forgotten as it is also thermodynamically intertwined with OER.33 Interestingly, for most of the investigated perovskite compositions the highest stability was observed at higher pH levels where the LOER seems to dominate over the conventional OER mechanism. This result suggests that the A-site cation dissolution generally induced by LOER can actually lead to a dynamically stable surface, mostly composed by an oxyhydroxide phase and having both higher OER activity and good stability.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the Swiss National Science Foundation through its Ambizione Program and the NCCR Marvel, the Swiss Competence Center for Energy Research (SCCER) Heat & Electricity Storage through Innosuisse, Switzerland, and Paul Scherrer Institute for financial contributions to this work, respectively. The authors thank the Swiss Light Source for providing beamtime at the SuperXAS beamline.Notes and references
- E. Fabbri and T. J. Schmidt, ACS Catal., 2018, 8, 9765–9774 CrossRef CAS.
- E. Fabbri, M. Nachtegaal, X. Cheng and T. J. Schmidt, Adv. Energy Mater., 2015, 5, 1402033 CrossRef.
- J. Durst, A. Rudnev, A. Dutta, Y. C. Fu, J. Herranz, V. Kaliginedi, A. Kuzume, A. A. Permyakova, Y. Paratcha, P. Broekmann and T. J. Schmidt, Chimia, 2015, 69, 769–776 CrossRef CAS.
- J. Herranz, J. Durst, E. Fabbri, A. Patru, X. Cheng, A. A. Permyakova and T. J. Schmidt, Nano Energy, 2016, 29, 4–28 CrossRef CAS.
- C. C. Pavel, F. Cecconi, C. Emiliani, S. Santiccioli, A. Scaffidi, S. Catanorchi and M. Comotti, Angew. Chem., Int. Ed., 2014, 53, 1378–1381 CrossRef CAS.
- E. Fabbri, M. Nachtegaal, T. Binninger, X. Cheng, B. J. Kim, J. Durst, F. Bozza, T. Graule, R. Schaublin, L. Wiles, M. Pertoso, N. Danilovic, K. E. Ayers and T. J. Schmidt, Nat. Mater., 2017, 16, 925 CrossRef CAS.
- J. Suntivich, K. J. May, H. A. Gasteiger, J. B. Goodenough and Y. Shao-Horn, Science, 2011, 334, 1383–1385 CrossRef CAS.
- B. J. Kim, X. Cheng, D. F. Abbott, E. Fabbri, F. Bozza, T. Graule, I. E. Castelli, L. Wiles, N. Danilovic, K. E. Ayers, N. Marzari and T. J. Schmidt, Adv. Funct. Mater., 2018, 28, 1804355 CrossRef.
- J. Suntivich, H. A. Gasteiger, N. Yabuuchi, H. Nakanishi, J. B. Goodenough and Y. Shao-Horn, Nat. Chem., 2011, 3, 546–550 CrossRef CAS.
- B. J. Kim, D. F. Abbott, X. Cheng, E. Fabbri, M. Nachtegaal, F. Bozza, I. E. Castelli, D. Lebedev, R. Schaublin, C. Coperet, T. Graule, N. Marzari and T. J. Schmidt, ACS Catal., 2017, 7, 3245–3256 CrossRef CAS.
- X. Cheng, E. Fabbri, B. Kim, M. Nachtegaal and T. J. Schmidt, J. Mater. Chem. A, 2017, 5, 13130–13137 RSC.
- X. Cheng, E. Fabbri, Y. Yamashita, I. E. Castelli, B. Kim, M. Uchida, R. Haumont, I. Puente-Orench and T. J. Schmidt, ACS Catal., 2018, 8, 9567–9578 CrossRef CAS.
- J. O. Bockris and T. Otagawa, J. Electrochem. Soc., 1984, 131, 290–302 CrossRef CAS.
- J. Suntivich, K. J. May, H. A. Gasteiger, J. B. Goodenough and Y. Shao-Horn, Science, 2011, 334, 1383–1385 CrossRef CAS.
- Y. Matsumoto, S. Yamada, T. Nishida and E. Sato, J. Electrochem. Soc., 1980, 127, 2360–2364 CrossRef CAS.
- E. Fabbri, A. Habereder, K. Waltar, R. Kotz and T. J. Schmidt, Catal. Sci. Technol., 2014, 4, 3800–3821 RSC.
- C. Su, W. Wang, Y. Chen, G. Yang, X. Xu, M. O. Tadé and Z. Shao, ACS Appl. Mater. Interfaces, 2015, 7, 17663–17670 CrossRef CAS.
- J. Yu, J. Sunarso, Y. Zhu, X. Xu, R. Ran, W. Zhou and Z. Shao, Chem. – Eur. J., 2016, 22, 2719–2727 CrossRef CAS.
- J. Rossmeisl, Z. W. Qu, H. Zhu, G. J. Kroes and J. K. Norskov, J. Electroanal. Chem., 2007, 607, 83–89 CrossRef CAS.
- I. C. Man, H. Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martinez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Norskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165 CrossRef CAS.
- J. T. Mefford, X. Rong, A. M. Abakumov, W. G. Hardin, S. Dai, A. M. Kolpak, K. P. Johnston and K. J. Stevenson, Nat. Commun., 2016, 7, 11053 CrossRef CAS.
- J. S. Yoo, Y. S. Liu, X. Rong and A. M. Kolpak, J. Phys. Chem. Lett., 2018, 9, 1473–1479 CrossRef CAS.
- J. S. Yoo, X. Rong, Y. S. Liu and A. M. Kolpak, ACS Catal., 2018, 8, 4628–4636 CrossRef CAS.
- B.-J. Kim, E. Fabbri, D. F. Abbott, X. Cheng, A. H. Clark, M. Nachtegaal, M. Borlaf, I. E. Castelli, T. Graule and T. J. Schmidt, J. Am. Chem. Soc., 2019, 141, 5231–5240 CrossRef CAS.
- Y. Pan, X. Xu, Y. Zhong, L. Ge, Y. Chen, J.-P. M. Veder, D. Guan, R. O’Hayre, M. Li, G. Wang, H. Wang, W. Zhou and Z. Shao, Nat. Commun., 2020, 11, 2002 CrossRef CAS.
- X. Li, H. Wang, Z. Cui, Y. Li, S. Xin, J. Zhou, Y. Long, C. Jin and J. B. Goodenough, Sci. Adv., 2019, 5, eaav6262 CrossRef CAS.
- Y. Zhu, Q. Lin, Z. Hu, Y. Chen, Y. Yin, H. A. Tahini, H.-J. Lin, C.-T. Chen, X. Zhang, Z. Shao and H. Wang, Small, 2020, 16, 2001204 CrossRef CAS.
- R. P. Forslund, W. G. Hardin, X. Rong, A. M. Abakumov, D. Filimonov, C. T. Alexander, J. T. Mefford, H. Iyer, A. M. Kolpak, K. P. Johnston and K. J. Stevenson, Nat. Commun., 2018, 9, 3150 CrossRef.
- Y. Zhu, H. A. Tahini, Z. Hu, Z.-G. Chen, W. Zhou, A. C. Komarek, Q. Lin, H.-J. Lin, C.-T. Chen, Y. Zhong, M. T. Fernández-Díaz, S. C. Smith, H. Wang, M. Liu and Z. Shao, Adv. Mater., 2020, 32, 1905025 CrossRef CAS.
- D. Y. Chung, P. P. Lopes, P. Farinazzo Bergamo Dias Martins, H. He, T. Kawaguchi, P. Zapol, H. You, D. Tripkovic, D. Strmcnik, Y. Zhu, S. Seifert, S. Lee, V. R. Stamenkovic and N. M. Markovic, Nat. Energy, 2020, 5, 222–230 CrossRef.
- T. Binninger, R. Mohamed, K. Waltar, E. Fabbri, P. Levecque, R. Kötz and T. J. Schmidt, Sci. Rep., 2015, 5, 12167 CrossRef CAS.
- T. Wu, S. Sun, J. Song, S. Xi, Y. Du, B. Chen, W. A. Sasangka, H. Liao, C. L. Gan, G. G. Scherer, L. Zeng, H. Wang, H. Li, A. Grimaud and Z. J. Xu, Nat. Catal., 2019, 2, 763–772 CrossRef CAS.
- T. Binninger, R. Mohamed, K. Waltar, E. Fabbri, P. Levecque, R. Kotz and T. J. Schmidt, Sci. Rep., 2015, 5, 12167 CrossRef CAS.
- A. Grimaud, O. Diaz-Morales, B. H. Han, W. T. Hong, Y. L. Lee, L. Giordano, K. A. Stoerzinger, M. T. M. Koper and Y. Shao-Horn, Nat. Chem., 2017, 9, 457–465 CrossRef CAS.
- Z.-F. Huang, J. Song, Y. Du, S. Xi, S. Dou, J. M. V. Nsanzimana, C. Wang, Z. J. Xu and X. Wang, Nat. Energy, 2019, 4, 329–338 CrossRef CAS.
- J. T. Mefford, X. Rong, A. M. Abakumov, W. G. Hardin, S. Dai, A. M. Kolpak, K. P. Johnston and K. J. Stevenson, Nat. Commun., 2016, 7, 11053 CrossRef CAS.
- W. G. Hardin, J. T. Mefford, D. A. Slanac, B. B. Patel, X. Q. Wang, S. Dai, X. Zhao, R. S. Ruoff, K. P. Johnston and K. J. Stevenson, Chem. Mater., 2014, 26, 3368–3376 CrossRef CAS.
- Y. Zhu, H. A. Tahini, Z. Hu, Y. Yin, Q. Lin, H. Sun, Y. Zhong, Y. Chen, F. Zhang, H.-J. Lin, C.-T. Chen, W. Zhou, X. Zhang, S. C. Smith, Z. Shao and H. Wang, J. Mater. Chem. A, 2020, 8, 6480 RSC.
- C. Spori, J. T. H. Kwan, A. Bonakdarpour, D. P. Wilkinson and P. Strasser, Angew. Chem., Int. Ed., 2017, 56, 5994–6021 CrossRef.
- T. Reier, Z. Pawolek, S. Cherevko, M. Bruns, T. Jones, D. Teschner, S. Selve, A. Bergmann, H. N. Nong, R. Schlogl, K. J. J. Mayrhofer and P. Strasser, J. Am. Chem. Soc., 2015, 137, 13031–13040 CrossRef CAS.
- M. Risch, A. Grimaud, K. J. May, K. A. Stoerzinger, T. J. Chen, A. N. Mansour and Y. Shao-Horn, J. Phys. Chem. C, 2013, 117, 8628–8635 CrossRef CAS.
- K. J. May, C. E. Carlton, K. A. Stoerzinger, M. Risch, J. Suntivich, Y. L. Lee, A. Grimaud and Y. Shao-Horn, J. Phys. Chem. Lett., 2012, 3, 3264–3270 CrossRef CAS.
- J. O. Bockris, J. Chem. Phys., 1956, 24, 817–827 CrossRef CAS.
- L. Giordano, B. H. Han, M. Risch, W. T. Hong, R. R. Rao, K. A. Stoerzinger and Y. Shao-Horn, Catal. Today, 2016, 262, 2–10 CrossRef CAS.
- J. J. Warren, T. A. Tronic and J. M. Mayer, Chem. Rev., 2010, 110, 6961–7001 CrossRef CAS.
- M. T. M. Koper, Phys. Chem. Chem. Phys., 2013, 15, 1399–1407 RSC.
- M. T. M. Koper, Chem. Sci., 2013, 4, 2710–2723 RSC.
- C. Yang, M. Batuk, Q. Jacquet, G. Rousse, W. Yin, L. Zhang, J. Hadermann, A. M. Abakumov, G. Cibin, A. Chadwick, J.-M. Tarascon and A. Grimaud, ACS Energy Lett., 2018, 3, 2884–2890 CrossRef CAS.
- B.-J. Kim, E. Fabbri, I. E. Castelli, M. Borlaf, T. Graule, M. Nachtegaal and T. J. Schmidt, Catalysts, 2019, 9, 263 CrossRef CAS.
- A. Heel, P. Holtappels, P. Hug and T. Graule, Fuel Cells, 2010, 10, 419–432 CrossRef CAS.
- O. Muller, M. Nachtegaal, J. Just, D. Lutzenkirchen-Hecht and R. Frahm, J. Synchrotron Radiat., 2016, 23, 260–266 CrossRef.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef CAS.
- R. G. Delaplane, J. A. Ibers, J. R. Ferraro and J. J. Rush, J. Chem. Phys., 1969, 50, 1920–1927 CrossRef CAS.
- F. Pertlik, Monatsh. Chem., 1999, 130, 1083–1088 CAS.
- T. J. Schmidt, H. A. Gasteiger, G. D. Stab, P. M. Urban, D. M. Kolb and R. J. Behm, J. Electrochem. Soc., 1998, 145, 2354–2358 CrossRef CAS.
- J. Suntivich, H. A. Gasteiger, N. Yabuuchi and Y. Shao-Horn, J. Electrochem. Soc., 2010, 157, B1263–B1268 CrossRef CAS.
- T. Binninger, E. Fabbri, A. Patru, M. Garganourakis, J. Han, D. F. Abbott, O. Sereda, R. Kotz, A. Menzel, M. Nachtegaal and T. J. Schmidt, J. Electrochem. Soc., 2016, 163, H906–H912 CrossRef CAS.
- The Materials Project, https://materialsproject.org/, accessed Nov. 2017, 2017.
- J. W. Johnson, E. H. Oelkers and H. C. Helgeson, Comput. Geosci., 1992, 18, 899–947 CrossRef.
- M. Pourbaix, Atlas of electrochemical equilibria in aqueous solutions, Pergamon Press, 1966 Search PubMed.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dulak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiotz, O. Schutt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. H. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef.
- K. A. Persson, B. Waldwick, P. Lazic and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235438 CrossRef.
- I. E. Castelli, K. S. Thygesen and K. W. Jacobsen, J. Mater. Chem. A, 2015, 3, 12343–12349 RSC.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. L. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef.
- Standard Solid State Pseudopotential Library, http://materialscloud.org/sssp.
- G. Prandini, A. Marrazzo, I. E. Castelli, N. Mounet and N. Marzari, Precision and efficiency in solid-state pseudopotential calculations, Cornell University, 2018 Search PubMed.
- Y. Surendranath, M. W. Kanan and D. G. Nocera, J. Am. Chem. Soc., 2010, 132, 16501–16509 CrossRef CAS.
- B. H. Han, M. Risch, Y. L. Lee, C. Ling, H. F. Jia and Y. Shao-Horn, Phys. Chem. Chem. Phys., 2015, 17, 22576–22580 RSC.
- N. Vonrüti and U. Aschauer, Phys. Chem. Chem. Phys., 2019, 21, 24354–24360 RSC.
- B. Han, K. A. Stoerzinger, V. Tileli, A. D. Gamalski, E. A. Stach and Y. Shao-Horn, Nat. Mater., 2016, 16, 121 CrossRef.
- M. Risch, A. Grimaud, K. J. May, K. A. Stoerzinger, T. J. Chen, A. N. Mansour and Y. Shao-Horn, J. Phys. Chem. C, 2013, 117, 8628–8635 CrossRef CAS.
- J. H. Huang, Q. C. Shang, Y. Y. Huang, F. M. Tang, Q. Zhang, Q. H. Liu, S. Jiang, F. C. Hu, W. Liu, Y. Luo, T. Yao, Y. Jiang, Z. Y. Pan, Z. H. Sun and S. Q. Wei, Angew. Chem., Int. Ed., 2016, 55, 2137–2141 CrossRef CAS.
- J. H. Huang, Q. H. Liu, T. Yao, Z. Y. Pan and S. Q. Wei, J. Phys.: Conf. Ser., 2016, 712, 012128 CrossRef.
- D. Totir, Y. B. Mo, S. Kim, M. R. Antonio and D. A. Scherson, J. Electrochem. Soc., 2000, 147, 4594–4597 CrossRef CAS.
- P. D. Battle, T. C. Gibb and R. Strange, J. Solid State Chem., 1989, 81, 217–229 CrossRef CAS.
- T. C. Gibb, J. Mater. Chem., 1992, 2, 387–393 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ma00661k |
| This journal is © The Royal Society of Chemistry 2021 |