Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Photoluminescence modal splitting via strong coupling in hybrid Au/WS2/GaP nanoparticle-on-mirror cavities†
Merve
Gülmüs
a,
Thomas
Possmayer
 a,
Benjamin
Tilmann
a,
Benjamin
Tilmann
 a,
Paul
Butler
a,
Paul
Butler
 bc,
Ian D.
Sharp
bc,
Ian D.
Sharp
 bc,
Leonardo de S.
Menezes
bc,
Leonardo de S.
Menezes
 ad,
Stefan A.
Maier
ad,
Stefan A.
Maier
 ef and
Luca
Sortino
ef and
Luca
Sortino
 *a
*a
aChair in Hybrid Nanosystems, Nanoinstitute Munich, Faculty of Physics, Ludwig-Maximilians-Universität München, 80539 Munich, Germany. E-mail: luca.sortino@physik.uni-muenchen.de
bWalter Schottky Institute, Technische Universität München, Am Coulombwall 4, 85748 Garching, Germany
cPhysics Department, TUM School of Natural Sciences, Technische Universität München, Am Coulombwall 4, 85748 Garching, Germany
dDepartamento de Física, Universidade Federal de Pernambuco, 50670-901 Recife, PE, Brazil
eSchool of Physics and Astronomy, Monash University, Clayton, Victoria 3800, Australia
fThe Blackett Laboratory, Department of Physics, Imperial College London, London, SW7 2BW, UK
First published on 18th September 2024
Abstract
By integrating dielectric and metallic components, hybrid nanophotonic devices present promising opportunities for manipulating nanoscale light–matter interactions. Here, we investigate hybrid nanoparticle-on-mirror optical cavities, where semiconductor WS2 monolayers are positioned between gallium phosphide (GaP) nanoantennas and a gold mirror, thereby establishing extreme confinement of optical fields. Prior to integration of the mirror, we observe an intermediate coupling regime from GaP nanoantennas covered with WS2 monolayers. Upon introduction of the mirror, enhanced interactions lead to modal splitting in the exciton photoluminescence spectra, spatially localized within the dielectric-metallic gap. Using a coupled harmonic oscillator model, we extract an average Rabi splitting energy of 22.6 meV at room temperature, at the onset of the strong coupling regime. Moreover, the characteristics of polaritonic emission are revealed by the increasing Lorentzian linewidth and energy blueshift with increasing excitation power. Our findings highlight hybrid nanophotonic structures as novel platforms for controlling light–matter coupling with atomically thin materials.
Introduction
Nanoscale gaps focus light into sub-nm regions between closely spaced optically resonant surfaces,1,2 providing atomic-scale interactions driving the emergence of quantum features in nanoscale electromagnetism,3–5 and strong field confinement for efficient light–matter coupling and surface-enhanced spectroscopies.6,7 Within this context, the exceptional optoelectronic properties of two-dimensional (2D) materials make them appealing for integration into nanophotonic gaps featuring extreme light confinement.8,9 In particular, 2D semiconductors, such as transition metal dichalcogenides (TMDCs), are promising active materials for nanophotonic devices.10–12 At the single layer limit, they offer stable excitonic resonances and can be deterministically manipulated for device fabrication.13 2D semiconductors placed between a reflective metallic mirror and a resonant plasmonic nanoparticle, in a so-called nanoparticle-on-mirror geometry, have served as the basis for numerous studies of strong light–matter coupling under ambient conditions,14–18 nonlinear optics,19,20 and for deterministic coupling of single photon sources.21,22 While such structures represent a viable platform for achieving strong coupling, observation of photoluminescence (PL) emission from polaritonic states in plasmonic systems is hindered by low quantum efficiencies and the dissipative nature of plasmonic resonances. Thus, signatures of strongly coupled systems based on embedded 2D semiconductors have primarily been studied by means of scattering and non-linear optical processes.23 Polaritonic PL emission has been reported from plasmonic nanoparticle-on-mirror cavities with embedded organic molecules at cryogenic temperatures24 and PL signatures of strong coupling were observed for 2D semiconductors in tip-enhanced plasmonic nanogaps,25 however, the detection of polaritonic luminescence signatures in particle-on-mirror geometries remains extremely challenging owing to high optical losses, broad spectral overlap, spatial and temporal fluctuations in the local field environment and quenching mechanisms at metal–dielectric interfaces.15,23,26 For this purpose, hybrid nanocavities combining Mie resonant dielectric nanoparticles with metallic mirrors offer a new approach to overcome the limitations of plasmonic systems, usually suffering from intrinsic ohmic losses.27 The inclusion of a dielectric component helps to mitigate these losses, while providing greater flexibility in tuning the optical properties of the nanocavity through the careful selection of materials and their geometry. Although such optical cavities have been the subject of theoretical investigations,28,29 experimental demonstrations have so far been restricted to the use of random dispersions of spherical dielectric nanoparticles30–32 and evidence of polaritonic PL emission has only been partially observed.33In this work, we investigated the interaction between top-down lithographically defined cylindrical gallium phosphide (GaP) dielectric nanoparticle-on-mirror cavities and excitons in a WS2 TMDC monolayer. We first transfer the monolayer onto GaP nanoantenna arrays, observing strain signatures and PL emission enhancement, confirming an intermediate light–matter coupling regime in the scattering response. By introducing a reflective gold mirror, we enhance the light–matter coupling strength via extreme field confinement in the nanometer-sized gap. The effective coupling is observed as a modal splitting in the WS2 PL emission spectra, spatially localized within the nanoscale gap cavity. We employ a coupled oscillator model (COM) to describe the coherent interaction between excitons and cavity modes and extract Rabi splitting energies in the range of 20–24 meV, placing the system at the onset of the strong coupling regime. Furthermore, the strain-dependent emission from the monolayer allows us to disentangle the roles of different excitonic states to the coupling, with spectral analysis revealing a prominent Lorentzian character of the polaritonic emission from the nanocavity. With increased optical excitation power, we observe a blueshift of the coupled exciton emission, further indicating non-linear polariton interactions. Our results hold promise for the development of hybrid nanophotonic structures, emphasizing the synergistic potential of combining dielectric and metallic nanocavities for enhanced light–matter interactions with 2D materials.
Results
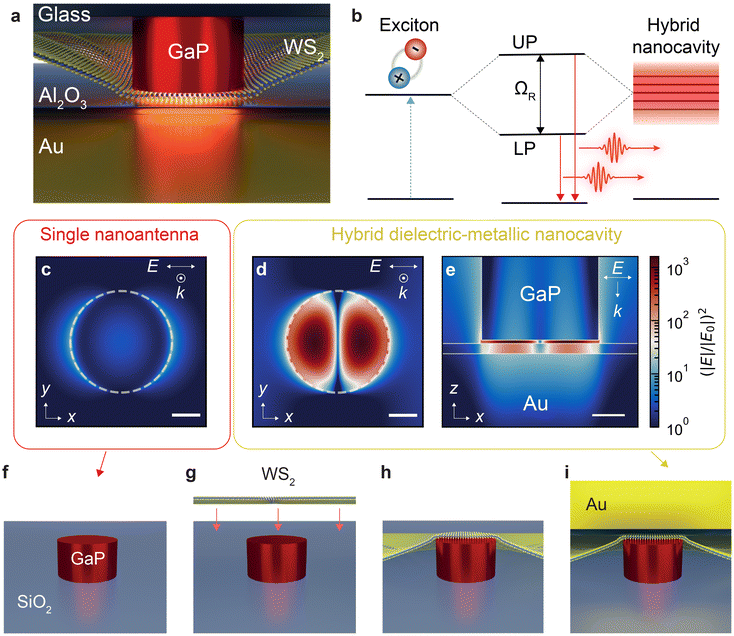
The hybrid dielectric-on-mirror nanocavity (Fig. 1a) is composed of a Mie resonant GaP antenna and a gold mirror. An additional thin (3 nm) dielectric spacer of alumina (Al2O3) is grown on the gold surface using atomic layer deposition (ALD) to preserve the optical efficiency of the 2D semiconductor. By embedding a WS2 monolayer within the gap, the enhanced interaction of excitons with the strongly confined field pushes the system towards the strong light–matter coupling regime via hybridization of the photon–exciton coupled system (Fig. 1b). By modelling a single photon and an exciton as coupled harmonic oscillators, the interaction between light and matter can be described using the following Hamiltonian:12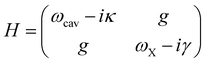 | (1) |
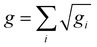 is the coupling strength defined by the superposition of all the excitons taking part in the strong coupling condition. The off-diagonal terms introduce the coupling strength between the two oscillators. When the coupling strength overcomes the dissipative losses (|g| ≫ |γ|, |κ|), the system enters the strong coupling regime and two distinct eigenmodes, or dressed states, are created. These are known as the lower (LP) and upper (UP) polariton branches, separated by the Rabi energy (ΩR), and exhibit mixed light–matter properties, with energies defined by:12
is the coupling strength defined by the superposition of all the excitons taking part in the strong coupling condition. The off-diagonal terms introduce the coupling strength between the two oscillators. When the coupling strength overcomes the dissipative losses (|g| ≫ |γ|, |κ|), the system enters the strong coupling regime and two distinct eigenmodes, or dressed states, are created. These are known as the lower (LP) and upper (UP) polariton branches, separated by the Rabi energy (ΩR), and exhibit mixed light–matter properties, with energies defined by:12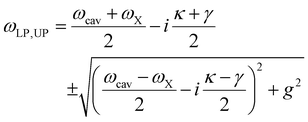 | (2) |
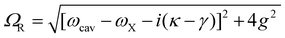 . When the condition
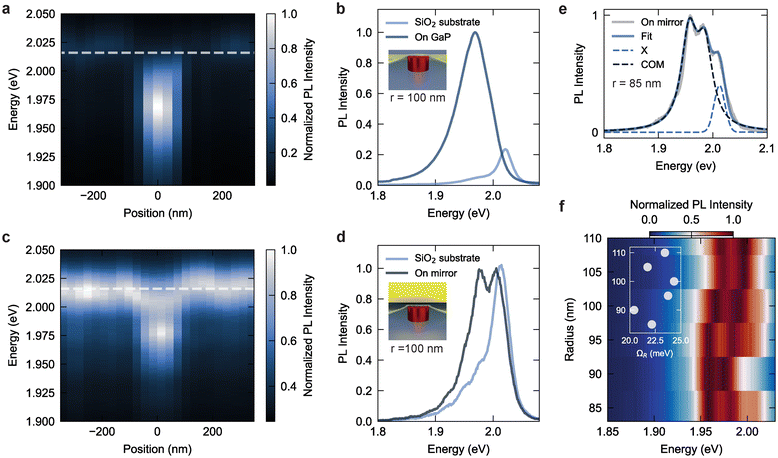
. When the condition 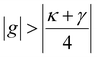 is satisfied, such that the splitting exceeds the combined spectral widths of both resonances, the coupled system overcomes the threshold needed to enter the strong coupling regime. We then define a normalized strong coupling condition threshold: 4g/(κ + γ) = 1. When the coupling strength approaches this condition, and satisfies 4g/(κ + γ) > 0.5, we define the intermediate light–matter coupling regime.23,34
is satisfied, such that the splitting exceeds the combined spectral widths of both resonances, the coupled system overcomes the threshold needed to enter the strong coupling regime. We then define a normalized strong coupling condition threshold: 4g/(κ + γ) = 1. When the coupling strength approaches this condition, and satisfies 4g/(κ + γ) > 0.5, we define the intermediate light–matter coupling regime.23,34
Several key factors contribute to the realization of the strong coupling regime, most notably the need for strong electromagnetic field intensities (∼|E|2) in resonance with material emitters possessing strong transition dipole moments, all confined within a small effective modal volume. For this purpose, 2D TMDC semiconductors are especially versatile, with atomic scale thicknesses suitable for probing the confined optical fields in nanoparticle-on-mirror geometries.35 WS2 stands out due to its large exciton binding energies and oscillator strengths that arise from reduced dielectric screening and increased quantum confinement, as well as its transition to direct bandgap at the monolayer limit, which facilitates the coupling with light.13 Additionally, single atomic TMDC layers can be deterministically manipulated and transferred on top of optically resonant dielectric nanostructures,36,37 or integrated in vertical van der Waals heterostructures,38 further extending the design opportunities for hybrid nanophotonic devices.
In this work, we first designed our nanoparticle-on-mirror cavities with finite-difference time-domain (FDTD) numerical simulations. Fig. 1c–e shows the results of the simulated electric field enhancement (|E|/|E0|)2 of both a single GaP nanoantenna and the hybrid dielectric-metallic mirror nanocavity. The electric field intensity of the scattered radiation, |E|2, is normalized to the intensity of the linearly polarized normal incidence plane wave, |E0|2, at a wavelength of 619 nm, which is resonant with WS2 exciton emission. Fig. 1c presents the simulated intensity at the top surface of a single GaP nanoantenna with 90 nm radius and 100 nm height, showing a 10-fold increase of the scattered field intensity. This enhancement is particularly concentrated at the edges and is influenced by the geometry of the nanoantenna.36 As expected, the addition of the gold mirror enhances the field intensity by a factor of 103 (Fig. 1d and e), owing to the extreme confinement within the 1 nm gap.
Considering the promising results predicted from simulation, we proceeded with fabrication of the hybrid nanocavity following the steps shown in Fig. 1f–i (see also ESI note 1†). First, arrays of GaP nanoantennas (height of 100 nm and radius spanning from 85 nm to 135 nm) were fabricated on SiO2 substrates with standard top-down lithography processes. We then mechanically exfoliated, aligned, and transferred WS2 monolayers on top of the nanoantennas using an all-dry stamping method (Fig. 1g and h). To finalize the mirror component, a gold film was sputtered onto a fused silica substrate and a 3 nm thick Al2O3 dielectric spacer was deposited onto the gold film resulting in a surface roughness below 1 nm (see ESI note 1†). Finally, the hybrid nanocavity was completed by positioning the gold mirror, as shown in Fig. 1i, thereby creating the nanoscale gap.
Fig. 2a displays the experimental dark field scattering data from the fabricated GaP nanoantenna array, along with a comparison with numerical FDTD calculations for the same antenna geometry. The fabricated structures exhibit excellent agreement with the calculated results, with the predicted resonance redshift in larger structures. A maximal spectral overlap with the WS2 exciton emission (dashed white line in Fig. 2a) is observed for a radius of approximately 90 nm. After transferring the WS2 monolayer onto selected nanoantennas, we performed PL and dark field scattering spectroscopy. The reference darkfield scattering and PL spectra of a WS2 monolayer on a GaP nanoantenna with radius of 90 nm are shown in Fig. 2b. Here, the scattering profile exhibits a noticeable dip at the WS2 exciton resonance, arising from the resonant coupling between excitons and the spectrally broad Mie modes of the GaP nanoantenna. The interaction between the 2D excitons and the nanoantenna can be described by a COM in the form:12,23
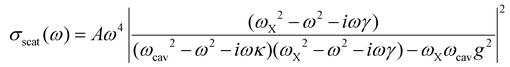 | (3) |
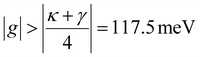 , our system falls in an intermediate light–matter coupling regime prior to the introduction of the metallic mirror.34
, our system falls in an intermediate light–matter coupling regime prior to the introduction of the metallic mirror.34
 | ||
| Fig. 2 (a) Experimental measurements (left) and numerical FDTD simulations (right) of the dark field scattering cross-section, presented as the normalized scattering intensity as a function of radius for GaP nanoantennas with fixed height 100 nm, on silica substrates. The resonance wavelength of WS2 monolayer exciton emission is indicated by the dashed white line. (b) PL emission and dark field scattering spectra of a WS2 monolayer coupled to a GaP nanoantenna with radius of 90 nm. The dashed line is a fit with the coupled oscillator model described in eqn (3) (see also ESI note 6†). Inset: Illustration of the WS2 monolayer/GaP nanoantenna system. (c) PL spectra of monolayer WS2 coupled to GaP nanoantennas with different radii, compared with the reference PL emission from WS2 on a bare SiO2 substrate. (d) Relative strain values extracted from the exciton peak position, using the empirical dependence of −50 meV/%.39 | ||
We further extract the tensile strain present in our WS2 layers as a function of the GaP resonator radius by analysis of the exciton spectral shifts in the PL profiles. Fig. 2c shows the PL emission spectra for WS2 on GaP nanoantennas with different radii, showing increasing red shifts with reduced structure dimensions. The redshift of the PL peak can be translated into an effective strain value with the empirical relationship of −50 meV/%.39Fig. 2d shows the tensile strain values extracted from the PL spectra, reaching values of approximately 1%, with the expected increase for smaller nanostructures.40 We note that, the magnitude of the shift for the maximum strain still lies well within the total width of the cavity scattering resonance, and inhomogeneities in the nanoscale strain profile induce a broadening of the exciton linewidths, directly affecting the coupling strength of each nanocavity.
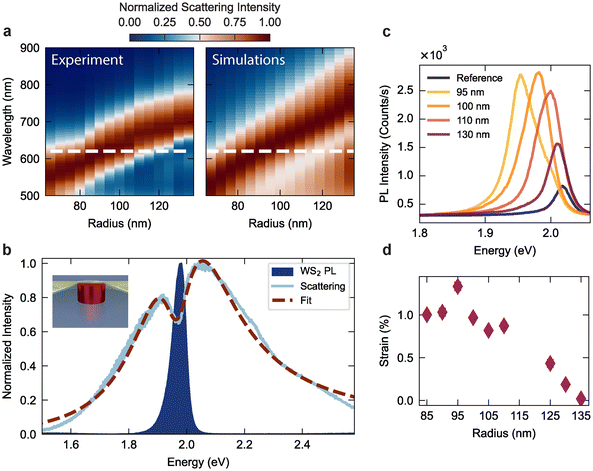
For comprehensive comparison of changes in the PL spectral profile, we conducted spatially dependent PL measurements, where the diffraction-limited excitation laser spot was linearly scanned across the nanoantenna position. Fig. 3a shows the hyperspectral PL emission map for a WS2 monolayer on a single GaP nanoantenna, collected by scanning the diffraction-limited 532 nm laser spot across the position of the antenna, centered at x = 0 nm. The PL signal was collected from the nanoantenna side, in a back reflection geometry, through the same excitation objective (NA = 0.9). From the spatial emission, we find that the co-localization of tensile strain and near-field enhancement at the nanoantenna position induces a substantial exciton redshift40 and a strong PL enhancement.36Fig. 3b shows the PL spectra, extracted from vertical profiles in Fig. 3a, for WS2 coupled to the nanoantenna (x = 0 nm) and on the bare SiO2 substrate (x = 250 nm). The coupled WS2 spectrum exhibits a broadening, owing to inhomogeneous strain profiles in the deformed monolayer, along with the redshift due to tensile strain.
 | ||
| Fig. 3 (a) Room-temperature hyperspectral PL emission map for a WS2 monolayer coupled to a GaP nanoantenna with 100 nm radius. The excitation laser is scanned linearly across the nanoantenna position, centered at x = 0 nm. (b) Comparison of PL spectra for the uncoupled exciton on a SiO2 substrate to that from the exciton coupled to the GaP nanoantenna, with the latter exhibiting the expected strain-induced red shift and broadening. The spectra are normalized to the coupled emission intensity maximum. (c) WS2 hyperspectral PL emission map from the same nanoantenna shown in (a) but with the presence of the gold mirror to generate the nanocavity gap. (d) PL spectrum for the uncoupled exciton on the SiO2 substrate (at x = 250 nm) compared to the emission at the nanogap position (at x = 0), revealing characteristic splitting for the coupled exciton emission. The spectra are normalized to the coupled emission intensity maximum. (e) PL spectrum from monolayer WS2 embedded in a hybrid nanocavity with GaP nanoantenna radius of 85 nm. The spectrum is fitted with a coupled oscillator model (COM) following eqn (4) (black dashed line), along with a Gaussian peak (blue dashed line) that accounts for the uncoupled and unstrained exciton emission peak (X) (see also ESI note 6†). (f) PL emission from monolayer WS2 in hybrid nanocavities comprising GaP nanoantennas with radii from 85 to 110 nm. Inset: Rabi energy (ΩR) values extracted with the COM model in eqn (4). | ||
Following the characterization of the WS2 on the isolated GaP nanoantenna, we incorporated the gold mirror to form a complete nanoparticle-on-mirror resonator. Fig. 3c and d presents the hyperspectral PL map of the same nanoantenna discussed above, but after the mirror integration. The PL signal is now collected from the SiO2 substrate side. Compared to the previous case, we observe an overall increase in the relative PL intensity between excitons outside the cavity region and the nanocavity-coupled excitons, which can be ascribed to reflections of the mirror, leading to higher excitation and collection efficiency of PL emission from the uncoupled area. Importantly, at the nanoantenna position, the PL spectrum is characterized by a doublet, redshifted from the unstrained exciton and spatially localized within the nanogap (Fig. 3c). Fig. 3d shows a comparison of the spectral emission collected on and off the nanocavity. Both spectral contributions to the doublet appear at energies below the neutral exciton resonance. Considering the origin of the doublet from within the nanoparticle-on-mirror cavity, we note that no PL emission peak splitting is observed from antennas that are spectrally off-resonance from the WS2 exciton (ESI Fig. S2a†). In addition, we detect a blueshift in the exciton resonance when introducing the mirror (see ESI Fig. S2b†), ascribed to changes in dielectric screening induced by the metallic surface. As the field confinement in the nanogap is found to be mainly independent of the radius of the investigated nanoantenna (see ESI note 3†), we consider the possibility that the lack of splitting in off-resonant cavities could be related to nanoscale variations in the distance between antenna and mirror, as well as inhomogeneous strain, both of which could vary with nanoantenna size and impact, for example, the formation of trions in the 2D semiconductor.41 However, we can rule out dark excitons and trions as the origin of the PL peak splitting since these are usually observed at cryogenic temperatures, and at energies between 40 and 60 meV below the neutral exciton resonance,32,42–46 larger than the splitting observed in our experiments (< 25 meV). Similarly, we can rule out defect states as these are commonly observed as a broad emission peak at lower energies.47,48 We thus find that the PL emission doublet is a signature of polaritonic emission induced by the interaction between excitons located at the top of the nanoantenna and the confined optical field in the nanometer-sized gap between the nanoantenna and mirror. We further probed the scattering of the nanoparticle-on-mirror cavity, however, the signal exhibits pronounced fringes due to multiple reflections within the 150 μm thick coverslip above the particle-on-mirror cavity, hindering the evidence of strong coupling in the scattering spectra (see ESI note 4†). We note, however, that we observe larger splitting in the scattering spectra with values above 50 meV, twice than those observed in PL emission.
The PL intensity emitted by the exciton–polariton system, IX(ω), can be modelled within a COM using the following formula:23,25
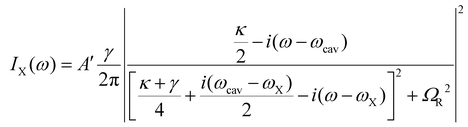 | (4) |
To further unveil the nature of the hybrid nanocavity PL emission, we investigated the individual contributions of the PL peak components as a function of excitation power. As shown in Fig. 3f, for several nanoantennas we observed a splitting in the PL emission of the redshifted strained exciton, along with an additional peak from the uncoupled exciton. Fig. 4a shows a fit of such a PL spectrum with three Voigt profiles (see also ESI note 5†), corresponding to the LP and UP peaks of the coupled excitons and, at higher energies, the emission of unstrained excitons (X). The redshifted polariton doublet in the PL spectrum is co-located with the strained area in the WS2 monolayer and the gap formed with the metallic mirror. We note that deformations in the strained region could lead to a distribution of out-of-plane orientations of the excitonic dipoles, promoting an effective enhancement of the light–matter interaction and facilitating the coupling with 2D excitons.
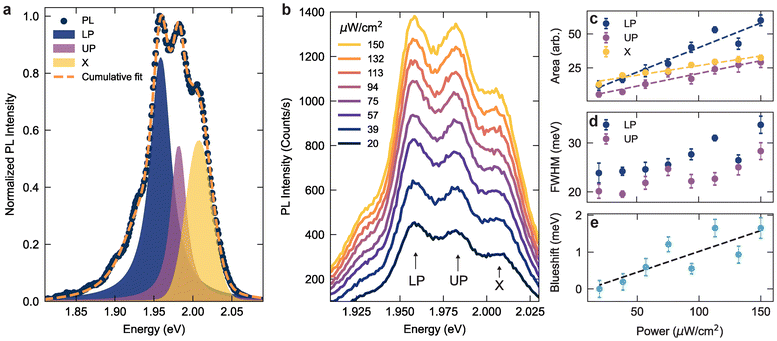
Fig. 4b shows the PL emission spectra as a function of excitation power, from which we extracted the relative peak areas and linewidths, as well as Lorentzian and Gaussian weights. Fig. 4c shows the integrated area for each peak as a function of excitation power, which reveals a stronger linear dependence for the polaritonic branches compared to uncoupled excitons. Namely, the excitation power dependence of the emission intensity is 1.3 times larger for the UP peak and 2.5 times larger for the LP peak. From the Voigt profiles, we also extract an increase in linewidth and a predominant Lorentzian line shape at higher intensities for the polaritonic branches, as predicted from the more coherent PL emission of polaritonic states compared to bare excitons.49 In ESI Fig. S6† we show the relative weights of the Gaussian and Lorentzian fits for each of the component peaks. At high excitation power, the polaritonic emission can be fitted with a Lorentzian function, while the neutral exciton exhibits a predominant Gaussian character, independent of the excitation power. Moreover, while UP emission is usually hindered in the PL emission, the small energy splitting comparable to thermal excitations, could promote recombination from the UP state even in the presence of relaxation processes. We further fitted the dip in the PL doublet with a Gaussian function50 and plotted the extracted energy minima in Fig. 4e. This observed energy blueshift with increasing excitation power provides further support for the picture of strongly interacting exciton–polaritons, confined within the small nanocavity gap volume.
Conclusions
In summary, we investigated hybrid dielectric nanoparticle-on-mirror nanocavities, incorporating WS2 monolayers between GaP Mie-resonant dielectric nanoantennas and a reflective gold mirror, to manipulate light–matter interactions in 2D semiconductors. Optical spectroscopy revealed an intermediate coupling regime of WS2 coupled to single nanoantennas. After introducing the mirror, we observed a modal splitting in the PL signal of coupled excitons arising from the strong interaction between 2D confined excitons and the optical fields within the nanogap. Using a coupled harmonic oscillator model, we extracted Rabi splitting values ranging from 20 to 24 meV at room temperature. The origin of the splitting was confirmed by analysis of spatial and spectral PL emission data, which demonstrated a Lorentzian profile of the polaritonic peaks and a blueshift with increasing excitation power. These findings hold promise for the application of 2D hybrid nanophotonic structures for polaritonic devices at room temperature.51 Moreover, the use of piezoelectric or phase change materials as dielectric resonators could provide a route to tailor the strain magnitude in the 2D materials, fixed in our approach during the transfer process. Our approach aimed to develop a top-down route for nanoparticle-on-mirror cavities, and while the current design is not yet suitable for practical applications, establishing a higher degree of control and stability by optimizing the contact between lithographically defined particles and the reflective mirror, for instance via micromanipulation,52 as well as the use of monocrystalline metallic mirrors, could potentially provide enhanced control over light–matter interactions, towards the implementation of 2D single photon sources,53 van der Waals heterostructures,54 and Moiré superlattices55 in hybrid nanophotonic platforms.Author contributions
M. G. and B. T. fabricated the GaP samples. M. G. transferred the WS2 monolayers. P. B. performed the ALD deposition. M. G., T. P., and L. S. carried out optical spectroscopic measurements. M. G. and L. S. analysed the data. L. d. S. M., I. D. S. and S. A. M. managed various aspects of the project. L. S. conceived the idea and supervised the project. The manuscript was written through the contributions of all authors. All authors have given approval to the final version of the manuscript.Data availability
The data that support the findings of this study are available from https://doi.org/10.5281/zenodo.13120851.Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. A. M. acknowledges the Lee Lucas chair in physics and the Australian Research Council (Centre of Excellence in Future Low-Energy Electronics Technologies – CE 170100039). L. S. acknowledges funding support through a Humboldt Research Fellowship from the Alexander von Humboldt Foundation. Our studies were partially supported by the Center for NanoScience (CeNS) – Faculty of Physics, Ludwig-Maximilians University Munich. I. D. S. and P. B. acknowledge support from Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy – EXC 2089/1–390776260, and TUM. Solar in the context of the Bavarian Collaborative Research Project Solar Technologies Go Hybrid (SolTech).References
- J. J. Baumberg, J. Aizpurua, M. H. Mikkelsen and D. R. Smith, Nat. Mater., 2019, 18, 668–678 CrossRef CAS PubMed.
- J. Jeong, H. W. Kim and D. S. Kim, Nanophotonics, 2022, 11, 1231–1260 CrossRef CAS.
- Y. Yang, D. Zhu, W. Yan, A. Agarwal, M. Zheng, J. D. Joannopoulos, P. Lalanne, T. Christensen, K. K. Berggren and M. Soljačić, Nature, 2019, 576, 248–252 CrossRef CAS.
- C. Ciracì, R. T. Hill, J. J. Mock, Y. Urzhumov, A. I. Fernández-Domínguez, S. A. Maier, J. B. Pendry, A. Chilkoti and D. R. Smith, Science, 2012, 337, 1072–1074 CrossRef.
- K. J. Savage, M. M. Hawkeye, R. Esteban, A. G. Borisov, J. Aizpurua and J. J. Baumberg, Nature, 2012, 491, 574–577 CrossRef CAS.
- J. Sun, Y. Li, H. Hu, W. Chen, D. Zheng, S. Zhang and H. Xu, Nanoscale, 2021, 13, 4408–4419 RSC.
- G.-C. Li, Q. Zhang, S. A. Maier and D. Lei, Nanophotonics, 2018, 7, 1865–1889 CrossRef CAS.
- A. Reserbat-Plantey, I. Epstein, I. Torre, A. T. Costa, P. A. D. Gonçalves, N. A. Mortensen, M. Polini, J. C. W. Song, N. M. R. Peres and F. H. L. Koppens, ACS Photonics, 2021, 8, 85–101 CrossRef CAS.
- Y. Koo, T. Moon, M. Kang, H. Joo, C. Lee, H. Lee, V. Kravtsov and K.-D. Park, Light: Sci. Appl., 2024, 13, 30 CrossRef CAS PubMed.
- A. Krasnok, S. Lepeshov and A. Alú, Opt. Express, 2018, 26, 15972 CrossRef CAS PubMed.
- Y. Meng, J. Feng, S. Han, Z. Xu, W. Mao, T. Zhang, J. S. Kim, I. Roh, Y. Zhao, D.-H. Kim, Y. Yang, J.-W. Lee, L. Yang, C.-W. Qiu and S.-H. Bae, Nat. Rev. Mater., 2023, 8, 498–517 CrossRef.
- L. Huang, A. Krasnok, A. Alú, Y. Yu, D. Neshev and A. E. Miroshnichenko, Rep. Prog. Phys., 2022, 85, 046401 CrossRef CAS.
- G. Wang, A. Chernikov, M. M. Glazov, T. F. Heinz, X. Marie, T. Amand and B. Urbaszek, Rev. Mod. Phys., 2018, 90, 021001 CrossRef CAS.
- D. Zheng, S. Zhang, Q. Deng, M. Kang, P. Nordlander and H. Xu, Nano Lett., 2017, 17, 3809–3814 CrossRef CAS PubMed.
- J. Qin, Y. H. Chen, Z. Zhang, Y. Zhang, R. J. Blaikie, B. Ding and M. Qiu, Phys. Rev. Lett., 2020, 124, 63902 CrossRef CAS.
- J. Wen, H. Wang, W. Wang, Z. Deng, C. Zhuang, Y. Zhang, F. Liu, J. She, J. Chen, H. Chen, S. Deng and N. Xu, Nano Lett., 2017, 17, 4689–4697 CrossRef CAS PubMed.
- B.-Y. Wen, J.-Y. Wang, T.-L. Shen, Z.-W. Zhu, P.-C. Guan, J.-S. Lin, W. Peng, W.-W. Cai, H. Jin, Q.-C. Xu, Z.-L. Yang, Z.-Q. Tian and J.-F. Li, Light: Sci. Appl., 2022, 11, 235 CrossRef CAS PubMed.
- D. O. Sigle, J. Mertens, L. O. Herrmann, R. W. Bowman, S. Ithurria, B. Dubertret, Y. Shi, H. Y. Yang, C. Tserkezis, J. Aizpurua and J. J. Baumberg, ACS Nano, 2015, 9, 825–830 CrossRef CAS PubMed.
- X. Liu, J. Yi, S. Yang, E.-C. Lin, Y.-J. Zhang, P. Zhang, J.-F. Li, Y. Wang, Y.-H. Lee, Z.-Q. Tian and X. Zhang, Nat. Mater., 2021, 20, 1210–1215 CrossRef CAS PubMed.
- C. Li, X. Lu, A. Srivastava, S. D. Storm, R. Gelfand, M. Pelton, M. Sukharev and H. Harutyunyan, Nano Lett., 2021, 21, 1599–1605 CrossRef CAS PubMed.
- Y. Luo, G. D. Shepard, J. V. Ardelean, D. A. Rhodes, B. Kim, K. Barmak, J. C. Hone and S. Strauf, Nat. Nanotechnol., 2018, 13, 1137–1142 CrossRef CAS PubMed.
- X. Xu, A. B. Solanki, D. Sychev, X. Gao, S. Peana, A. S. Baburin, K. Pagadala, Z. O. Martin, S. N. Chowdhury, Y. P. Chen, T. Taniguchi, K. Watanabe, I. A. Rodionov, A. V. Kildishev, T. Li, P. Upadhyaya, A. Boltasseva and V. M. Shalaev, Nano Lett., 2023, 23, 25–33 CrossRef CAS PubMed.
- M. Pelton, S. D. Storm and H. Leng, Nanoscale, 2019, 11, 14540–14552 RSC.
- M. Wersäll, J. Cuadra, T. J. Antosiewicz, S. Balci and T. Shegai, Nano Lett., 2017, 17, 551–558 CrossRef.
- K.-D. Park, M. A. May, H. Leng, J. Wang, J. A. Kropp, T. Gougousi, M. Pelton and M. B. Raschke, Sci. Adv., 2019, 5, 1–8 Search PubMed.
- J. Sun, H. Hu, D. Zheng, D. Zhang, Q. Deng, S. Zhang and H. Xu, ACS Nano, 2018, 12, 10393–10402 CrossRef CAS.
- M. Caldarola, P. Albella, E. Cortés, M. Rahmani, T. Roschuk, G. Grinblat, R. F. Oulton, A. V. Bragas and S. A. Maier, Nat. Commun., 2015, 6, 7915 CrossRef CAS.
- S. Shen, Y. Wu, Y. Li, P. Xie, Q. Ding, X. Kuang, W. Wang and W. Wang, Phys. Rev. B, 2022, 105, 155403 CrossRef CAS.
- K. As'ham, I. Al-Ani, M. Alaloul, S. Abdo, A. Abdulghani, W. Lei, H. T. Hattori, L. Huang and A. E. Miroshnichenko, Phys. Rev. Appl., 2023, 19, 054049 CrossRef.
- H. Sugimoto and M. Fujii, ACS Photonics, 2018, 5, 1986–1993 CrossRef CAS.
- F. Deng, H. Huang, J.-D. Chen, S. Liu, H. Pang, X. He and S. Lan, Nano Lett., 2022, 22, 220–228 CrossRef CAS PubMed.
- S. Liu, F. Deng, W. Zhuang, X. He, H. Huang, J.-D. Chen, H. Pang and S. Lan, ACS Nano, 2022, 16, 14390–14401 CrossRef CAS PubMed.
- J. Fang, K. Yao, M. Wang, Z. Yu, T. Zhang, T. Jiang, S. Huang, B. A. Korgel, M. Terrones, A. Alù and Y. Zheng, Nano Lett., 2023, 23, 9803–9810 CrossRef CAS PubMed.
- L. Sortino, M. Gülmüs, B. Tilmann, L. de S. Menezes and S. A. Maier, Light: Sci. Appl., 2023, 12, 202 CrossRef CAS PubMed.
- M.-E. Kleemann, R. Chikkaraddy, E. M. Alexeev, D. Kos, C. Carnegie, W. Deacon, A. C. de Pury, C. Große, B. de Nijs, J. Mertens, A. I. Tartakovskii and J. J. Baumberg, Nat. Commun., 2017, 8, 1296 CrossRef PubMed.
- L. Sortino, P. G. Zotev, S. Mignuzzi, J. Cambiasso, D. Schmidt, A. Genco, M. Aßmann, M. Bayer, S. A. Maier, R. Sapienza and A. I. Tartakovskii, Nat. Commun., 2019, 10, 5119 CrossRef CAS PubMed.
- T. Bucher, A. Vaskin, R. Mupparapu, F. J. F. Löchner, A. George, K. E. Chong, S. Fasold, C. Neumann, D.-Y. Choi, F. Eilenberger, F. Setzpfandt, Y. S. Kivshar, T. Pertsch, A. Turchanin and I. Staude, ACS Photonics, 2019, 6, 1002–1009 CrossRef CAS.
- Y. Liu, N. O. Weiss, X. Duan, H.-C. Cheng, Y. Huang and X. Duan, Nat. Rev. Mater., 2016, 1, 16042 CrossRef CAS.
- I. Niehues, R. Schmidt, M. Drüppel, P. Marauhn, D. Christiansen, M. Selig, G. Berghäuser, D. Wigger, R. Schneider, L. Braasch, R. Koch, A. Castellanos-Gomez, T. Kuhn, A. Knorr, E. Malic, M. Rohlfing, S. Michaelis de Vasconcellos and R. Bratschitsch, Nano Lett., 2018, 18, 1751–1757 CrossRef CAS PubMed.
- L. Sortino, M. Brooks, P. G. Zotev, A. Genco, J. Cambiasso, S. Mignuzzi, S. A. Maier, G. Burkard, R. Sapienza and A. I. Tartakovskii, ACS Photonics, 2020, 7, 2413–2422 CrossRef CAS.
- M. G. Harats, J. N. Kirchhof, M. Qiao, K. Greben and K. I. Bolotin, Nat. Photonics, 2019, 14, 324–329 CrossRef.
- J. Shi, J. Zhu, X. Wu, B. Zheng, J. Chen, X. Sui, S. Zhang, J. Shi, W. Du, Y. Zhong, Q. Wang, Q. Zhang, A. Pan and X. Liu, Adv. Opt. Mater., 2020, 8, 1–9 Search PubMed.
- Z. Wang, Y. Liu, D. Chen, Z. Wang, M. Asbahi, S. D. Rezaei, J. Deng, J. Teng, A. T. S. Wee, W. Zhang, J. K. W. Yang and Z. Dong, Sci. Rep., 2022, 12, 15861 CrossRef CAS PubMed.
- N. S. Mueller, R. Arul, G. Kang, A. P. Saunders, A. C. Johnson, A. Sánchez-Iglesias, S. Hu, L. A. Jakob, J. Bar-David, B. de Nijs, L. M. Liz-Marzán, F. Liu and J. J. Baumberg, Nat. Commun., 2023, 14, 5726 CrossRef CAS PubMed.
- K.-D. Park, T. Jiang, G. Clark, X. Xu and M. B. Raschke, Nat. Nanotechnol., 2018, 13, 59–64 CrossRef CAS PubMed.
- T. W. Lo, X. Chen, Z. Zhang, Q. Zhang, C. W. Leung, A. V. Zayats and D. Lei, Nano Lett., 2022, 22, 1915–1921 CrossRef CAS.
- P. K. Chow, R. B. Jacobs-Gedrim, J. Gao, T.-M. Lu, B. Yu, H. Terrones and N. Koratkar, ACS Nano, 2015, 9, 1520–1527 CrossRef CAS PubMed.
- Z. Wu, W. Zhao, J. Jiang, T. Zheng, Y. You, J. Lu and Z. Ni, J. Phys. Chem. C, 2017, 121, 12294–12299 CrossRef CAS.
- F. P. Laussy, E. del Valle and C. Tejedor, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 1–17 CrossRef.
- E. Maggiolini, L. Polimeno, F. Todisco, A. Di Renzo, B. Han, M. De Giorgi, V. Ardizzone, C. Schneider, R. Mastria, A. Cannavale, M. Pugliese, L. De Marco, A. Rizzo, V. Maiorano, G. Gigli, D. Gerace, D. Sanvitto and D. Ballarini, Nat. Mater., 2023, 22, 964–969 CrossRef CAS PubMed.
- D. Sanvitto and S. Kéna-Cohen, Nat. Mater., 2016, 15, 1061–1073 CrossRef CAS.
- P. G. Zotev, Y. Wang, D. Andres-Penares, T. Severs-Millard, S. Randerson, X. Hu, L. Sortino, C. Louca, M. Brotons-Gisbert, T. Huq, S. Vezzoli, R. Sapienza, T. F. Krauss, B. D. Gerardot and A. I. Tartakovskii, Laser Photonics Rev., 2023, 17(8), 2200957 CrossRef CAS.
- L. Sortino, P. G. Zotev, C. L. Phillips, A. J. Brash, J. Cambiasso, E. Marensi, A. M. Fox, S. A. Maier, R. Sapienza and A. I. Tartakovskii, Nat. Commun., 2021, 12, 6063 CrossRef CAS.
- M. Kremser, M. Brotons-Gisbert, J. Knörzer, J. Gückelhorn, M. Meyer, M. Barbone, A. V. Stier, B. D. Gerardot, K. Müller and J. J. Finley, npj 2D Mater. Appl., 2020, 4, 8 CrossRef CAS.
- L. Du, M. R. Molas, Z. Huang, G. Zhang, F. Wang and Z. Sun, Science, 2023, 379, eadg0014 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr03166k |
| This journal is © The Royal Society of Chemistry 2024 |