Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
On the multiphoton ionisation photoelectron spectra of phenol†
Diptesh
Dey
 *ab,
Joanne L.
Woodhouse
ac,
Marcus P.
Taylor
a,
Helen H.
Fielding
*ab,
Joanne L.
Woodhouse
ac,
Marcus P.
Taylor
a,
Helen H.
Fielding
 a and
Graham A.
Worth
a and
Graham A.
Worth
 *a
*a
aDepartment of Chemistry, University College London, 20 Gordon Street, London WC1H 0AJ, UK. E-mail: diptesh.de@gmail.com; g.a.worth@ucl.ac.uk
bDepartment of Chemistry, Northwestern University, Evanston, Illinois 60208, USA
cDepartment of Chemistry, University of Southampton, Southampton, SO17 1BJ, UK
First published on 5th January 2024
Abstract
The phenol molecule is a prototype for non-adiabatic dynamics and the excited-state photochemistry of biomolecules. In this article, we report a joint theoretical and experimental investigation on the resonance enhanced multiphoton ionisation photoelectron (REMPI) spectra of the two lowest ionisation bands of phenol. The focus is on the theoretical interpretation of the measured spectra using quantum dynamics simulations. These were performed by numerically solving the time-dependent Schrödinger equation using the multi-layer variant of the multiconfiguration time-dependent Hartree algorithm together with a vibronic coupling Hamiltonian model. The ionising laser pulse is modelled explicitly within the ionisation continuum model to simulate experimental femtosecond 1+1 REMPI photoelectron spectra. These measured spectra are sensitive to very short lived electronically excited states, providing a rigorous benchmark for our theoretical methods. The match between experiment and theory allows for an interpretation of the features of the spectra at different wavelengths and shows that there are features due to both ‘direct' and ‘indirect' ionisation, resulting from non-resonant and resonant excitation by the pump pulse.
1 Introduction
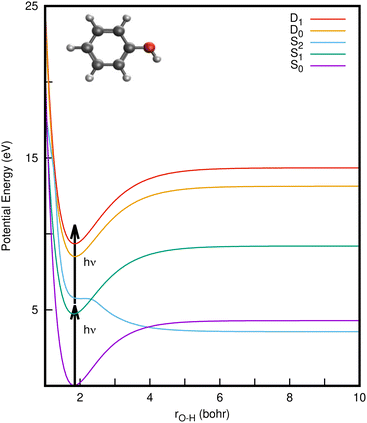
Phenol (C6H5OH) is an important molecular motif in many biologically relevant molecules, for example the amino acid tyrosine, where it plays a key role in the catalysis of the water-splitting reaction in photosystem II,1 and the green fluorescent and photoactive yellow proteins chromophores.2–4 As a result, the photophysics and photochemistry of phenol have attracted considerable attention as prototypes for understanding the photochemistry of important biomolecules.5–25Ultraviolet (UV) photoexcitation of phenol results in cleavage of the O–H bond to produce the phenoxyl radical (C6H5O˙) and a H atom,
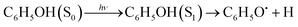 | (1) |
CIs and non-radiative decay mechanisms are ubiquitous in the photochemistry of polyatomic molecules.26 Interestingly, both the S2/S1 and S2/S0 CIs involve the same coupling coordinates: the O–H stretch (rO–H) and CCOH dihedral angle (θ).8 Electronic structure calculations have revealed that the S2 (1πσ*) state corresponds to a Rydberg-type 3s orbital in the Franck–Condon (FC) region with significant antibonding σ* character with respect to the O–H bond that eventually opens the pathway for hydrogen abstraction.5,6 With UV-excitation below the S2/S1 CI (for excitation wavelengths 275 nm > λ > 248 nm), nonadiabatic tunneling-facilitated O–H bond fission persists, accounting for a much slower timescale for photodissociation.16,17,20 The excited state dynamics of phenol thus represent a classic example of nonadiabatic transitions between adiabatic electronic states mediated by CIs, in which the relative position of the 1πσ* state with respect to 1ππ* state governs the dynamics, as also found in the photodissociation of other heteroatomic molecules.6,11,12
Although numerous studies have focused on the photodissociation of phenol following photoexcitation to the bright S1 and dark S2 states,5–20,24,25 relatively little attention has been paid to the photoionisation dynamics. Experimentally, the most direct way of probing ionisation is to use photoelectron spectroscopy (PES), where measurement of the electron kinetic energy (eKE) distribution provides a direct measure of the binding energy of the molecular orbital from which the electron is removed, as well as information about the vibrational energy distribution, both prior to and after photoionisation. In this regard, multiphoton ionisation27 has emerged as a powerful tool. In particular, resonance-enhanced multiphoton ionisation (REMPI) PES provides valuable insight into the electronically excited states that are involved in the UV photochemistry and photophysics27,28 and can reveal excited-state dynamics of short-lived states.29
In a conventional REMPI-PES experiment, a molecule is ionised by sequential absorption of two (or more) photons. In 1+1 REMPI, the first photon promotes the molecule to specific vibrational levels of an excited electronic state and a second photon ionises the molecule (as illustrated by arrows in Fig. 1). The spectra are often reported as a function of electron binding energy (eBE) defined as the difference between the total photon energy and the measured eKE. Analyzing the eBE distribution of photoelectrons can shed light on the electronic structure, electronic character and relaxation dynamics of the resonance-enhancing state; e.g., the S2 → S1 internal conversion is reported to be the dominant relaxation pathway in the two-photon ionisation of phenol at ∼207 nm, while increasing the duration of the ionising pulse led to increases in photoelectron yield at high electron binding energy.29
Here, we present calculated photoelectron spectra determined using numerical quantum wavepacket dynamics simulations to solve the time-dependent Schrödinger equation with an explicit treatment of the light-field. The results are compared with measured photoelectron spectra obtained following 1+1 REMPI with UV femtosecond laser pulses at six different wavelengths, most of which were reported in earlier work,22 spanning the two UV absorption bands.
Since vibronic (electron-vibrational) coupling plays a crucial role in the electronic spectra of molecules,30,31 we model the ionisation spectra by taking into account the vibronic coupling effects which in turn can help understand the experimental spectrum. To do this, the theoretical simulations are based on constructing a vibronic coupling Hamiltonian31 and carefully investigating the associated nonadiabatic dynamics using the multi-layer variant of the multi-configurational time-dependent Hartree (ML-MCTDH) algorithm.32,33 The model includes five electronic states: S0, S1, S2, D0 and D1. An ionisation continuum model is invoked in conjunction with photoelectron cross-section calculations to model the photoelectron spectra in the presence of a laser pulse. From the model Hamiltonian, eighteen vibrations are found to be required for the treatment of the short-time dynamics. These include the O–H bond stretch and C–C–O–H torsion that contain CIs in the singlet manifold along with the modes that provide couplings to at least first-order. Of these 18 modes, from an analysis of the coupling strengths (both inter- and intra-state) it was found that the key dynamics can be treated with only 10 vibrations.
The motivation for this work was: (i) to shed light on the participation of intermediate states in the two-photon excitation process, (ii) to quantify the power of our theoretical model in reproducing the energy-resolved photoelectron spectra, and (iii) to provide a preliminary understanding prior to measuring and computing future time-resolved photoelectron spectra of phenol.
The remainder of the paper is organized as follows. The vibronic coupling Hamiltonian model and the quantum dynamical simulations are described in Section 2.1. The experimental details are presented in Section 2.2. The 1+1 REMPI spectra obtained experimentally and theoretically are then presented and discussed in Section 3. Finally, we summarize and conclude with future prospects in Section 4.
2 Methodology
2.1 Theoretical framework
The molecular Hamiltonian Hmol for a set of N electronic states is an N × N matrix which can be written as a sum of terms
| Hmol = H(0) + W(0) + W(1) + W(2) | (2) |
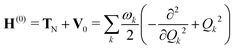 | (3) |
The set of diabatic potential matrices W describe the changes in the excited-state surfaces with respect to the ground state by including the effects of electronic excitation and vibronic coupling. The model contains N = 5 states. These are the ground and lowest two excited singlet states, along with the lowest two cation states. To this end, the zeroth-order matrix W(0) is a diagonal matrix containing the vertical excitation and ionisation energies Ek at Q0
| W(0) = Ek. | (4) |
Since we choose the diabatic and adiabatic basis to coincide at the FC geometry, there is no off-diagonal counterpart of Ek. The values for these energies were taken from different sources and ultimately adjusted so that the calculated absorption and photoelectron spectra match experiment. Table 1 lists the vertical excitation energy values for the different states. These compare well with other studies.16
| Vertical excitation (eV) | Osc. strength | |||||
|---|---|---|---|---|---|---|
| CASSCFa | CCSDb | Expt. | Model | CCSDb (a.u.) | ||
| a SA(3)-CAS(8,8)/6-31+G* for the singlet and SA(2)-CAS(7,8)/6-31+G* for the doublet states. b EOM-CCSD/6-31+G* for the singlet and IP-EOM-CCSD/6-31+G* for the doublet states. c Bist, Brand and Williams, J. Mol. Spectrosc., 1966, 21, 76. d Bist, Brand and Williams, J. Mol. Spectrosc., 1967, 24, 413. e Lipert and Colson JCP, 1990, 92, 3240. f Palmer et al., J. Mol. Struct., 1979, 52, 293. | ||||||
| 1 | S0(1A1) | 0.0 | 0.0 | 0.0 | 0.0 | |
| 2 | S1(1B2ππ*) | 4.82 | 4.93 | 4.51c | 4.859 | 0.0205 |
| 3 | S2(1B1πσ*) | 5.94 | 5.75 | 5.12d | 5.379 | 0.0002 |
| 4 | D0(2B1) | 7.986 | 8.333 | 8.508e | 8.608 | — |
| 5 | D1(2A2) | 8.670 | 9.164 | 9.280f | 9.380 | — |
The first-order matrix elements are expressed as
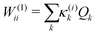 | (5) |
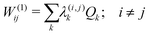 | (6) |
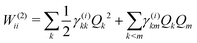 | (7) |
Consideration of molecular symmetry simplifies the model by imposing restrictions on the modes that will appear in the summations. For non-vanishing interstate coupling constants λ(i,j)k, the product of symmetries of the two states (Γi and Γj) and the vibrational mode (Γk) must contain the totally symmetric irreducible representation of the point group of the molecule (ΓA), i.e.,
| λ(i,j)k ≠ 0, if ΓI ⊗ Γk ⊗ Γj ⊃ ΓA. | (8) |
| γ(i)km ≠ 0, if Γk ⊗ Γm ⊗ Γi ⊃ ΓA | (9) |
| κ(j)k ≠ 0, if Γk ⊃ ΓA | (10) |
The linear intrastate κ(i)k and interstate λ(i,j)k coupling constants, along with the bilinear interstate coupling constants γ(i,j)km are reported in the ESI.†
For vibrational modes exhibiting significant anharmonicity, a harmonic approximation to the diabatic potentials can be a poor description in which case they should be replaced by anharmonic potentials such as Morse or quartic functions.21,37,38 An anharmonic description to the intersecting singlet potential surfaces (S0, S1, and S2) was constructed by replacing vibration ν33 with the O–H bond stretch, rOH and the vibration ν2 with the C–C–O–H bond torsion angle, θ. The diabatic potentials for these modes were then taken from the work of Lan et al.8 For S0 and S1 this was a Morse potential for rOH, while for S2 an avoided-crossing potential was used to provide the barrier. These were combined with cosine series for θ. For the cationic states (D0 and D1), which are states 4 and 5 in the model, the following diabatic potentials were constructed
V4(r,θ) = v40(r) + J1 − J2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2θ) − J3 cos(2θ) − J3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ | (11) |
| v40(r) = D4e[1 − exp(−a4(r − r4))]2 + a40, | (12) |
V5(r,θ) = v50(r) + K1 − K2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(2θ) − K3 cos(2θ) − K3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cosθ cosθ | (13) |
| v50(r) =D5e[1 − exp(−a5(r − r5))]2 + a50. | (14) |
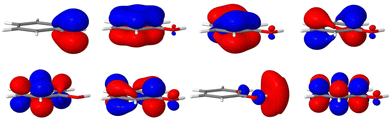
The remaining coupling parameters entering the model Hamiltonian are obtained by fitting the ab initio energy points along each normal mode to the adiabatic form of the diabatic electronic Hamiltonian through a least-squares fitting procedure. This is done by using the VCHAM program39 of the Quantics package.40,41 Ten modes were found to have significant coupling (the mode numbers are given in Fig. 3). The ab initio energies were calculated at the CASSCF level of theory, employing an active space of either 7 or 8 electrons in 8 orbitals, i.e., CAS(7,8) or CAS(8,8) with a 6-31+G* basis set. The active space comprises the oxygen lone pair, 1ππ, 1ππ*, and 1πσ* orbitals as shown in Fig. 2. The electronic structure calculations were carried out using the Gaussian 09 program.42 The model for the cation states is similar to that previously published in a study of the photoelectron spectrum of phenol.21 These parameters then underwent some minor adjustments to make the calculated absorption and photoelectron spectra match experiments. The final values are listed in the ESI.†
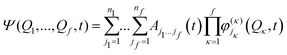 | (15) |
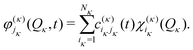 | (16) |
In the ML-MCTDH scheme, the wavefunction ansatz corresponds to a hierarchical expansion of SPFs in a recursive way to form an ML-tree structure where each layer l acts as a set of SPFs for the layer above (l − 1) as
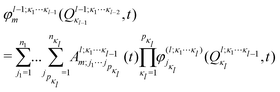 | (17) |
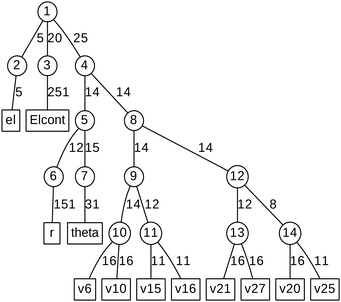
ML expansion of the wavepacket can be intuitively visualized using ML-tree diagrams.33Fig. 3 depicts the ML-tree structure used in the present work, in which a circle represents a node that stands for a set of A-coefficients and a square represents a set of time-independent primitive basis functions. The number in the circles denotes the node number in the layered structure, while within nodes, the number next to the link lines represent the numbers of SPFs used on the node. The number on the lines between a circle and a square represent the number of primitive functions or grid points used for that particular degree of freedom. Primitive basis functions are usually chosen as discrete variable representation (DVR) functions. Herein, we adopted Hermite DVRs for the vibrational modes. The depth of the tree is four layers where the first layer separates the electronic (el) and vibrational (r, theta, and vx) degrees of freedom. The electronic continuum (Elcont) is added to model the kinetic energy of the ejected electron. The electronic degree of freedom represents the manifold of electronic states; the wavefunction is expanded in the set of electronic states where each electronic state-dependent component is expanded in the ML-MCTDH form. The particular choice of ML-tree strongly influences the numerical effort.
The ML-MCTDH equations of motion (EOMs) for the SPFs and expansion coefficients are derived variationally using the Dirac–Frenkel variational principle and applying the recursive algorithm of Manthe.33,48 This leads to an optimal description of the evolving wavepacket for a given choice of basis and layering scheme. The EOMs are integrated following variable mean field technique with Adams–Bashforth–Moulton predictor–corrector integrator of order 6 and accuracy 10−5. Standard convergence tests were carried out to assess the precision of the integrator and the number of SPFs and primitive basis functions used. This is usually done by monitoring the population of the natural orbitals – the largest population of the least occupied natural orbital was noted to be ∼10−3. The ground state wavepacket is obtained by relaxation method49 following imaginary time propagation of an initial wavepacket.45,50 All ML-MCTDH simulations were performed using the Quantics suite of programs.40
Within Fermi's golden-rule limit,51 assuming a direct transfer of the initial wavepacket to the final state, a spectrum can be directly obtained as the Fourier transform of the autocorrelation function C(t) as
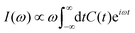 | (18) |
| C(t) =〈Ψ(0)|Ψ(t)〉 = 〈Ψ(t/2)*|Ψ(t/2)〉. | (19) |
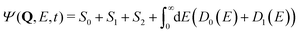 | (20) |
| I(E) ∝ |〈Ψ(t → ∞)|D0(E)〉|2 + |〈Ψ(t → ∞)|D1(E)〉|2. | (21) |
The light field is added to the molecular Hamiltonian to get the full Hamiltonian for the system
| H = Hmol + HL(t) | (22) |
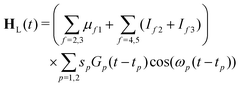 | (23) |
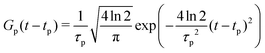 | (24) |
The maximum amplitude of each pulse is thus at tp and the time delay between them is t2 − t1.
In these simulations, both pulses are centred at t1 = t2 = 0. The width of the pulses is given by the FWHM, τp. Here, both pulses use τp = 50 fs. It should be noted that this is shorter than the experimental pulse widths, which were 200 fs. This was chosen to keep the simulations short, and means that the bandwidth is slightly broader than the experiment, but this should be insignificant for the overall dynamics seen. The strength parameters for both pulses were set to 0.01 a.u., i.e. a weak pulse. The strength of the interaction is then modulated by the values of the transition dipoles and ionisation propensities. The transition dipole from S0 to S1 is the dominant factor for the excitation. μ21 was taken to be 1.0. The transition dipole from the ground state to S2 is a factor of 10 smaller than that of the S1 state, as reflected in the oscillator strengths listed in Table 1 which depend on the square of the transition dipole. For this reason a value for μ31 = 0.1 was taken. Due to the symmetry of the states, the transition dipoles are in different directions, with the S1 transition dipole in the x, y plane and the S2 along the z-axis. The model thus assumes unpolarised light.
The ionisation propensity from the S0 and S1 states to the D0 and D1 cationic states can be obtained by computing the photoionisation cross-section.22 This is done by using ezDyson code56,57 (version 5.0) where the photoionisation matrix elements 〈ϕDIα|μ|ψk〉 (for each transition at the FC point) are evaluated numerically on a grid and averaged isotropically over all molecular orientations. ψk is the initial state wavefunction, μ is the molecular dipole operator and ϕDIα is the Dyson orbital. The Dyson orbitals are one-electron functions defined as the overlap between the neutral and cationic states as58
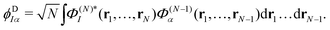 | (25) |
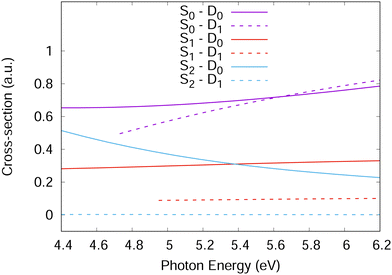
For accurate simulations, ionisation propensities should be used in simulations as a propensity surface to take into account the geometry dependence of the dipole moment and Dyson orbitals. However, for simplicity, the propensities used here were taken as constants based on the values in Fig. 4 calculated at the Franck–Condon point. This is equivalent to the Condon approximation used for the simulation of excitation spectra and should be a good approximation in the diabatic picture used for the Hamiltonian in this work as the orbitals should change slowly with changing nuclear geometry. For the Hamiltonian, the S1 and S2 ionisation propensities were taken to be equal and given a value of 1.0, except for the S2–D1 ionisation which was given a value of 0.0.
2.2 Experimental details
Our molecular beam velocity-map imaging (VMI) photoelectron spectrometer has been described in detail elsewhere.62 Briefly, a molecular beam of phenol was created by expanding 1.8 bar of helium carrier gas through phenol heated to 70 °C in the sample tube of a pulsed Even-Lavie valve, operating at a repetition rate of 500 Hz. The molecular beam was collimated by a 1 mm skimmer as it couples into the differentially pumped VMI chamber where it is intersected with UV femtosecond laser pulses in the range 275–200 nm. Wavelengths in the range 275–235.5 nm were generated by sum frequency mixing the output of an optical parametric amplifier (Coherent Opera-F) with the fundamental of a Ti:sapphire regenerative amplifier (Coherent Legend) to produce tunable visible radiation, which was subsequently frequency doubled. The full-width at half-maximum (FWHM) sech2 pulse durations have been measured to be in the range of around 175 fs at the relevant wavelengths through autocorrelation measurements using the nonresonant ionisation of butadiene at 235.5 nm. The 200 nm light was generated using a Coherent 4th harmonic generation system and previous measurements have suggested the sech2 pulse duration is on the order of 200 fs FWHM. Pulse energies are <2 μJ per pulse.63 The photon flux was attenuated to keep the photoelectron count-rates below 5 photoelectrons per pulse to avoid detector saturation and multiphoton processes. The known binding energy of phenol64 was used to confirm the absence of space-charge effects. Photoelectron images were recorded for 600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 laser shots. Background images (without phenol) were also recorded for 600
000 laser shots. Background images (without phenol) were also recorded for 600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 laser shots and subtracted from the photoelectron images. Photoelectron spectra were recovered from the background-subtracted data using the pBASEX image inversion algorithm,65 and the energy scale was calibrated by recording the 2+1 resonance-enhanced multiphoton ionisation (REMPI) spectrum of Xe at 249.6 nm for spectra recorded using wavelengths in the range 275–235.5 nm. The resolution was ΔE/E ≈ 3%. For the 200 nm spectrum, the 3-photon ionisation of xenon at 200 nm was used to calibrate the detector, and the resolution was ΔE/E ≈ 6%.
000 laser shots and subtracted from the photoelectron images. Photoelectron spectra were recovered from the background-subtracted data using the pBASEX image inversion algorithm,65 and the energy scale was calibrated by recording the 2+1 resonance-enhanced multiphoton ionisation (REMPI) spectrum of Xe at 249.6 nm for spectra recorded using wavelengths in the range 275–235.5 nm. The resolution was ΔE/E ≈ 3%. For the 200 nm spectrum, the 3-photon ionisation of xenon at 200 nm was used to calibrate the detector, and the resolution was ΔE/E ≈ 6%.
3 Results and discussion
Since the intermediate electronic state plays a crucial role in the 1+1 REMPI spectra, we first calculate the UV absorption spectra to check that the bound excited states are well described by the model. Fig. 5(a) shows the gas-phase experimental absorption spectrum and a calculated absorption spectrum corresponding to S1 ← S0 excitation. In the simulation, a Franck–Condon excitation of the initial wavepacket to the S1 state was assumed and a damping time of 150 fs applied to the resultant autocorrelation function. The S2(πσ*) state is dark, with a much smaller oscillator strength than S1 and does not provide significant intensity. The S1 band has a strong 000 transition at 275.1 nm (4.5 eV) followed by another relatively strong absorption at 268.2 nm (experiment) or 267.3 nm (theory). The band origin and the relative spacing of the simulated spectrum matches well with the experimental spectrum, which suggest that the vibronic coupling Hamiltonian model can capture the excited-state dynamics involving the intermediate electronic state.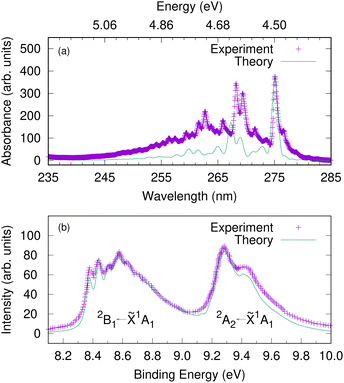 | ||
| Fig. 5 The gas-phase UV-vis absorption spectrum of phenol plotted against a calculated spectrum corresponding to S1(1B2) ← S0 excitation (upper panel). An energy scale (in eV) is added corresponding to the wavelength (in nm) as a guide to the eye. The photoelectron spectra of phenol corresponding to D0 ← S0 and D1 ← S0 excitations (lower panel). The experimental photoelectron spectrum is a single photon He(I) spectrum adapted from ref. 66. Here we assume a vertical excitation in the theoretical simulations and damping times of 150 fs, 27 fs and 35 fs, respectively are considered. | ||
Before investigating the REMPI-PES, we simulated the photoelectron spectra assuming a vertical excitation of the initial wavepacket to each of the ionic states D0 and D1. The resulting spectrum is given as a sum of individual spectrum from separate wavepacket propagations on the cationic states. This gives the vibrational fine structure associated with the photoelectron spectrum and checks the accuracy of the vibronic coupling model. Fig. 5(b) shows the resulting photoelectron spectra of these two lowest energy bands – the band between 8.2 and 9.0 eV corresponds to the D0(2B1) ← S0(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1) transition, and the band between 9.2 and 10.0 eV corresponds to the D1(2A2) ← S0(
1A1) transition, and the band between 9.2 and 10.0 eV corresponds to the D1(2A2) ← S0(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1) transition. It is to be noted that both the spectral bands have been shifted to account for the zero point energy of the neutral molecule, and damping times of 27 fs and 35 fs were chosen for the 2B1 and 2A2 bands, respectively. The spectrum indicates the 2B1 band to be well-structured with progressions from several vibrational modes, while the 2A2 band is mostly broad and lacks structure. The experimental photoelectron spectrum of phenol at 21 eV of Debies and Rabalais66 is superimposed as this experiment used a single-photon ionisation scheme and the spectrum will therefore only contain signal from direct photoionisation from the ground electronic state. A good match between experiment and theory is noted with respect to the band origins 000 located at 8.37 eV and 9.3 eV and the relative spacing between the peaks.
1A1) transition. It is to be noted that both the spectral bands have been shifted to account for the zero point energy of the neutral molecule, and damping times of 27 fs and 35 fs were chosen for the 2B1 and 2A2 bands, respectively. The spectrum indicates the 2B1 band to be well-structured with progressions from several vibrational modes, while the 2A2 band is mostly broad and lacks structure. The experimental photoelectron spectrum of phenol at 21 eV of Debies and Rabalais66 is superimposed as this experiment used a single-photon ionisation scheme and the spectrum will therefore only contain signal from direct photoionisation from the ground electronic state. A good match between experiment and theory is noted with respect to the band origins 000 located at 8.37 eV and 9.3 eV and the relative spacing between the peaks.
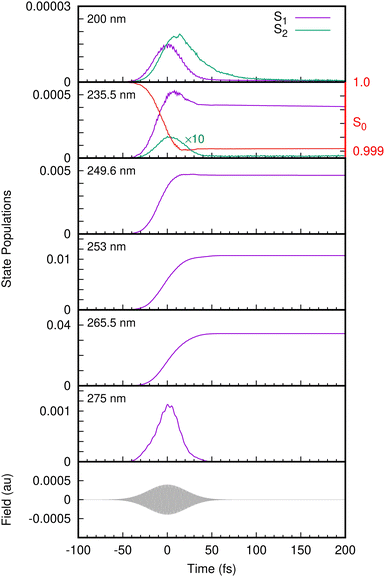
With the benchmarked model Hamiltonian for the valence and cation states, we then simulated the one-colour two-photon REMPI spectra following excitation with UV femtosecond laser pulses. The laser pulse is now explicitly included in the simulations using the light–matter Hamiltonian of eqn (23). The state populations from the simulations with different laser pulse frequencies are shown in Fig. 6. At 275 nm, only the S1 state is populated, and the population follows the envelope of the laser pulse. This is typical of non-resonant excitation. Previous experiments have found a long-lived state at this excitation energy, but in our model the lowest state in S1 lies just above 275 nm in energy. In contrast, for pulses with wavelengths 265.5 nm to 249.6 nm the population of S1 rises and remains fairly constant after the pulse finishes, consistent with the very long decay lifetimes (around 1 nanosecond) observed experimentally in this wavelength range and previously assigned to tunneling under the S2/S1 CI.17,67 This is resonant excitation. No population of S2 is seen in any of these simulations as the energy is too low for direct excitation, and also too low for the molecule to access the S2/S1 CI. For this reason the only contributions in the photoelectron spectra arise from ionisation from S1, going to either D0 or D1.
The spectra obtained from the simulations from the populations of the continuum states using eqn (21), are plotted as a function of two-photon electron binding energy (eBE), i.e.
| eBE = 2hν − eKE | (26) |
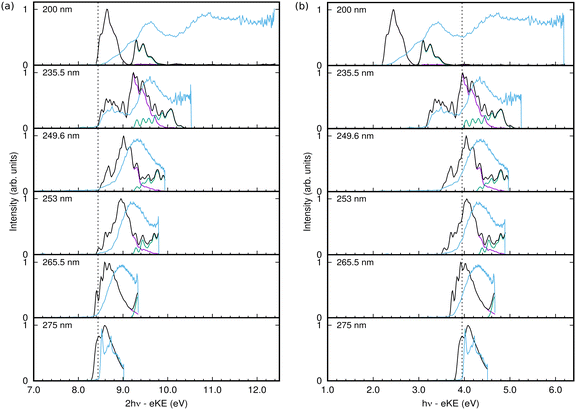
The 1+1 REMPI-PES at 275 nm (∼4.5 eV) comprises a two-peak structure which corresponds to D0 ← S0 excitation via the intermediate excited state. But for shorter wavelengths, the 2-photon excitation energy becomes sufficient to include a contribution from the D1 state. The calculated spectra in Fig. 7 are also broken down into contributions from the final cation states. Starting from 265.5 nm, spectral signatures from both D0 ← S0 (in purple lines) and D1 ← S0 (in green lines) are observed.
In general the shape and widths of the calculated spectra qualitatively match those of the experimental signals. The calculated spectra are, however, slightly red-shifted by approximately 0.1 eV and the calculated spectra have more structure. The lack of quantitative agreement is due to the simplicity of the model used in the calculations. For efficiency, the simulations only included 10 vibrational modes, which leads to a more structured spectra due to the missing intramolecular vibrational relaxation. The model is able to reproduce the vertical absorption and photoelectron spectra quite well, but the energies and vibrational frequencies do not match exactly the real values resulting in discrepancies in the relative intensities of spectral peaks that may become significant in the more sensitive calculations including a pulse. The use of the Condon approximation for the excitation may also be significant in the latter case where the excitation process must be described accurately. It is also possible that the simple pulse used in the calculations does not adequately match the experimental pulse.
The calculated spectrum at 200 nm is clearly not a good match. This is because the S3 state was not incorporated in our vibronic coupling Hamiltonian for simplicity, and for excitation wavelengths shorter than 200 nm it becomes relevant since the vertical excitation energy to bound S3 (2 ππ*) state is around 203 nm (∼6.1 eV). The missing spectral features at higher energies in the simulated spectrum compared to the experimental spectrum reflect the omission of this state.
Despite the lack of quantitative agreement, the main features of the calculated spectra allow an analysis of the experimental spectra, and in particular allow the assignment of features due to resonant and non-resonant ionisation. Returning to the spectra in Fig. 7, from 275 nm to 249.6 nm, the photoelectron spectrum peak moves to higher energy with higher pulse energy. In the experimental spectrum, a shoulder grows in at a fairly constant energy at the low end of the spectrum, and this is seen as a peak around 8.6 eV that becomes more intense with increasing frequency in the calculated spectra. This peak and the main peak are due to ionisation to D0, while the ionisation to D1 is much lower in intensity, growing in at the high energy side with increasing pulse frequency.
At 235.5 nm, there are clearly two peaks that are both due to ionisation to D0. One is centred around 8.6 eV with the higher energy peak at 9.2 eV. Looking at the state populations in Fig. 6, at this frequency there is now some direct, non-resonant, excitation of the S2 state, but it is very small and does not contribute significantly to the photoelectron spectrum. The low energy peak, as well as the low energy shoulders at lower photon energies, are thus the signals from non-resonant ionisation of S1. The larger peak that shifts with photon energy is due to the resonant ionisation from S0via S1.
The resonant ionisation peak shifts due to the vibrational energy carried over from the neutral excitation to the ion. This energy is Evib = hν − Sn, where Sn is the ground vibrational state energy for the neutral state being excited. Thus the electron kinetic energy is eKE = 2hν − (Dn + Evib), where Dn is the ground vibrational state energy for the cation state being ionised into. This leads to the one-photon binding energy
| Dn − Sn = hν − eKE | (27) |
As mentioned, at energies below 248 nm the S2/S1 conical intersection is not accessible and no dissociation is seen on the time-scale of the simulations (200 fs). At 235.5 nm, some population enters the S2(πσ*) state and dissociation is observed with this small amount of nuclear density associated with S2 moving out along the O–H coordinate. At 200 nm, Fig. 6 shows that the S2 state becomes populated after the S1 state due to internal conversion through the intersection. The S1 population in fact decays through the conical intersection entirely into S2, which then decays as the O–H bond breaks.
4 Conclusions
We have performed a joint theoretical and experimental study to probe the excited-state dynamics of phenol from 1+1 REMPI spectra of the first two ionisation bands, carrying out quantum wavepacket calculations to model and interpret the experimental spectra.Building on our earlier work modelling the photoelectron spectrum of phenol,21 we constructed a new vibronic coupling Hamiltonian in normal mode coordinates for the lowest two valence states of phenol. The electronic structure calculations were carried out using the CASSCF method and the model parameters entering the Hamiltonian were determined by least-square fitting of the ab initio points. The absorption and photoelectron spectrum calculated using the two model Hamiltonians and quantum dynamics simulations show an excellent agreement with experimental spectra while considering a vertical excitation in the FC region.
To model the REMPI spectra, the Hamiltonians for the valence and ionised states of phenol were combined and laser pulses with different frequencies explicitly included in the simulations. The outgoing electron is modelled by the ionisation continuum model which populates electron kinetic energy states and allows the excitation energy dependent photoelectron spectra to be calculated. The calculated spectra are in good agreement with the experimental spectra, except at 200 nm where the model needs to be further improved by including the S3 state, which dominates the experimental spectrum at this wavelength.
From an analysis of the state populations, it is clear that the photoelectron signal is entirely due to ionisation from the S1(ππ*) state. Ionisation takes place to both D0 and D1 cation states. The lower D0 band has regions that can be assigned to high energy ‘direct’, non-resonant, ionisation that gives rise to a peak with constant electron binding energy and ‘indirect’ ionisation due to ionising S1 after resonant excitation that gives to a peak which shifts with excitation energy.28
Femtosecond time-resolved photoelectron spectroscopy (TRPES) is a powerful tool to track the evolution of electronic structure following photoexcitation and it is particularly advantageous when multiple excited states are involved in the dynamics.28,68–71 Here, we used femtosecond 1+1 REMPI at a series of wavelengths to see the photon energy dependence of the photoelectron signal and thus probe the short time dynamics. Adding in time delays between the excitation and ionisation pulses would gain further information by following the relaxation dynamics as a function of time.
Finally, although understanding the electronic structure and relaxation dynamics of isolated molecular chromophores in the gas-phase lies at the heart of photochemical reactions, the environment can also tune the dynamics. To that end, studies have also looked into the role of an aqueous environment and highlighted the possibility of formation of solvated electrons on ultrafast timescales.22 Currently, liquid-jet photoelectron spectroscopy experiments are becoming feasible that can reveal the effect of complex environments.72 The present work strengthens our understanding on the UV photoresponse of phenol in the gas-phase and will serve as a benchmark to study the effect of complex environments in which the chromophores are usually embedded. This work will also serve as a test-bed to conduct TRPES studies on phenol.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
D. D. is thankful to Dr Michael Parkes for helpful discussions with ezDyson calculations. The research leading to these results has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie Grant agreement No. 892554 (D. D.), and the EPSRC under the COSMOS programme grant (EP/X026973/1) (G. W.). J. W. acknowledges funding from UCL, and M. T. from the University of Birmingham.References
- B. A. Barry, Photochem. Photobiol., 1993, 57, 179–188 CrossRef CAS PubMed.
- J. J. van Thor, Chem. Soc. Rev., 2009, 38, 2935–2950 RSC.
- A. Acharya, A. M. Bogdanov, B. L. Grigorenko, K. B. Bravaya, A. V. Nemukhin, K. A. Lukyanov and A. I. Krylov, Chem. Rev., 2017, 117, 758–795 CrossRef CAS PubMed.
- A. Henley and H. H. Fielding, Int. Rev. Phys. Chem., 2019, 38, 1–34 Search PubMed.
- A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2001, 105, 9275–9283 CrossRef CAS.
- A. L. Sobolewski, W. Domcke, C. Dedonder-Lardeux and C. Jouvet, Phys. Chem. Chem. Phys., 2002, 4, 1093–1100 RSC.
- C.-M. Tseng, Y. T. Lee and C.-K. Ni, J. Chem. Phys., 2004, 121, 2459–2461 CrossRef CAS PubMed.
- Z. Lan, W. Domcke, V. Vallet, A. L. Sobolewski and S. Mahapatra, J. Chem. Phys., 2005, 122, 224315 CrossRef PubMed.
- M. Abe, Y. Ohtsuki, Y. Fujimura, Z. Lan and W. Domcke, J. Chem. Phys., 2006, 124, 224316 CrossRef PubMed.
- M. G. D. Nix, A. L. Devine, B. Cronin, R. N. Dixon and M. N. R. Ashfold, J. Chem. Phys., 2006, 125, 133318 CrossRef PubMed.
- M. N. R. Ashfold, B. Cronin, A. L. Devine, R. N. Dixon and M. G. D. Nix, Science, 2006, 312, 1637–1640 CrossRef CAS PubMed.
- M. N. R. Ashfold, A. L. Devine, R. N. Dixon, G. A. King, M. G. D. Nix and T. A. A. Oliver, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 12701–12706 CrossRef CAS PubMed.
- M. G. D. Nix, A. L. Devine, R. N. Dixon and M. N. R. Ashfold, Chem. Phys. Lett., 2008, 463, 305–308 CrossRef CAS.
- M. L. Hause, Y. H. Yoon, A. S. Case and F. F. Crim, J. Chem. Phys., 2008, 128, 104307 CrossRef PubMed.
- A. Iqbal, M. S. Y. Cheung, M. G. D. Nix and V. G. Stavros, J. Phys. Chem. A, 2009, 113, 8157–8163 CrossRef CAS PubMed.
- R. N. Dixon, T. A. A. Oliver and M. N. R. Ashfold, J. Chem. Phys., 2011, 134, 194303 CrossRef PubMed.
- G. M. Roberts, A. S. Chatterley, J. D. Young and V. G. Stavros, J. Phys. Chem. Lett., 2012, 3, 348–352 CrossRef CAS PubMed.
- K. R. Yang, X. Xu, J. Zheng and D. G. Truhlar, Chem. Sci., 2014, 5, 4661–4680 RSC.
- X. Zhu and D. R. Yarkony, J. Chem. Phys., 2016, 144, 024105 CrossRef PubMed.
- C. Xie, J. Ma, X. Zhu, D. R. Yarkony, D. Xie and H. Guo, J. Am. Chem. Soc., 2016, 138, 7828–7831 CrossRef CAS PubMed.
- M. P. Taylor and G. A. Worth, Chem. Phys., 2018, 515, 719–727 CrossRef CAS.
- J. W. Riley, B. Wang, J. L. Woodhouse, M. Assmann, G. A. Worth and H. H. Fielding, J. Phys. Chem. Lett., 2018, 9, 678–682 CrossRef CAS PubMed.
- A. Henley, J. W. Riley, B. Wang and H. H. Fielding, Faraday Discuss., 2020, 221, 202–218 RSC.
- G. Christopoulou, T. Tran and G. A. Worth, Phys. Chem. Chem. Phys., 2021, 23, 23684–23695 RSC.
- N. Giri and S. Mahapatra, J. Chem. Phys., 2022, 156, 094305 CrossRef CAS PubMed.
- S. Matsika and P. Krause, Annu. Rev. Phys. Chem., 2011, 62, 621–643 CrossRef CAS PubMed.
- M. N. R. Ashfold and J. D. Howe, Annu. Rev. Phys. Chem., 1994, 45, 57–82 CrossRef CAS.
- H. H. Fielding and G. A. Worth, Chem. Soc. Rev., 2018, 47, 309–321 RSC.
- C. P. Schick, S. D. Carpenter and P. M. Weber, J. Phys. Chem. A, 1999, 103, 10470–10476 CrossRef CAS.
- L. S. Cederbaum, W. Domcke, H. Köppel and W. Von Niessen, Chem. Phys., 1977, 26, 169–177 CrossRef CAS.
- H. Köppel, W. Domcke and L. S. Cederbaum, Adv. Chem. Phys., 1984, 57, 59–246 CrossRef.
- H. Wang and M. Thoss, J. Chem. Phys., 2003, 119, 1289–1299 CrossRef CAS.
- U. Manthe, J. Chem. Phys., 2008, 128, 164116 CrossRef PubMed.
- G. A. Worth, H. D. Meyer, H. Köppel, L. S. Cederbaum and I. Burghardt, Int. Rev. Phys. Chem., 2008, 27, 569–606 Search PubMed.
- M. Baer, Chem. Phys., 2000, 259, 123–147 CrossRef CAS.
- G. A. Worth and L. S. Cederbaum, Annu. Rev. Phys. Chem., 2004, 55, 127–158 CrossRef CAS PubMed.
- A. Lehr, S. Gómez, M. A. Parkes and G. A. Worth, Phys. Chem. Chem. Phys., 2020, 22, 25272–25283 RSC.
- S. Faraji, M. Vazdar, V. Sivaranjana Reddy, M. Eckert-Maksic, H. Lischka and H. Köppel, J. Chem. Phys., 2011, 135, 154310 CrossRef CAS PubMed.
- C. Cattarius, A. Markmann and G. A. Worth, The VCHAM program, 2007, https://www.pci.uni-heidelberg.de/tc/usr/mctdh/ Search PubMed.
- G. A. Worth, K. Giri, G. W. Richings, I. Burghardt, M. H. Beck, A. Jäckle and H.-D. Meyer, The Quantics Package, Version 1.2, University of Birmingham, Birmingham, UK, 2016 Search PubMed.
- G. A. Worth, Comput. Phys. Commun., 2020, 248, 107040 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, et al., Gaussian 09, Revision A.02, Gaussian, Inc., 2009 Search PubMed.
- O. Vendrell and H.-D. Meyer, J. Chem. Phys., 2011, 134, 044135 CrossRef PubMed.
- H.-D. Meyer, U. Manthe and L. S. Cederbaum, Chem. Phys. Lett., 1990, 165, 73–78 CrossRef CAS.
- M. H. Beck, A. Jäckle, G. A. Worth and H.-D. Meyer, Phys. Rep., 2000, 324, 1–105 CrossRef CAS.
- T. Westermann, R. Brodbeck, A. B. Rozhenko, W. Schoeller and U. Manthe, J. Chem. Phys., 2011, 135, 184102 CrossRef PubMed.
- J. Schulze, M. F. Shibl, M. J. Al-Marri and O. Kühn, J. Chem. Phys., 2016, 144, 185101 CrossRef PubMed.
- U. Manthe, J. Chem. Phys., 2009, 130, 054109 CrossRef PubMed.
- R. Kosloff and H. Tal-Ezer, Chem. Phys. Lett., 1986, 127, 223–230 CrossRef CAS.
- H.-D. Meyer and G. A. Worth, Theor. Chem. Acc., 2003, 109, 251–267 Search PubMed.
- R. Schinke, Photodissociation Dynamics, Cambridge University Press, Cambridge, 1991 Search PubMed.
- A. Raab, G. A. Worth, H.-D. Meyer and L. S. Cederbaum, J. Chem. Phys., 1999, 110, 936–946 CrossRef CAS.
- M. Seel and W. Domcke, J. Chem. Phys., 1991, 95, 7806–7822 CrossRef CAS.
- G. A. Worth, R. E. Carley and H. H. Fielding, Chem. Phys., 2007, 338, 220–227 CrossRef CAS.
- D. Dey, A. I. Kuleff and G. A. Worth, Phys. Rev. Lett., 2022, 129, 173203 CrossRef CAS PubMed.
- S. Gozem and A. I. Krylov, ezDyson, https://iopenshell.usc.edu/downloads/ezdyson. Search PubMed.
- S. Gozem, A. O. Gunina, T. Ichino, D. L. Osborn, J. F. Stanton and A. I. Krylov, J. Phys. Chem. Lett., 2015, 6, 4532–4540 CrossRef CAS PubMed.
- G. Wu, S. P. Neville, O. Schalk, T. Sekikawa, M. N. R. Ashfold, G. A. Worth and A. Stolow, J. Chem. Phys., 2015, 142, 074302 CrossRef PubMed.
- A. I. Krylov, Ann. Rev. Phys. Chem., 2008, 59, 433–462 CrossRef CAS PubMed.
- R. A. Kendall, T. H. Dunning Jr. and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng and X. Feng, et al. , Mol. Phys., 2015, 113, 184–215 CrossRef CAS.
- A. R. McKay, M. E. Sanz, C. R. S. Mooney, R. S. Minns, E. M. Gill and H. H. Fielding, Rev. Sci. Instrum., 2010, 81, 123101 CrossRef CAS PubMed.
- O. M. Kirkby, M. A. Parkes, S. P. Neville, G. A. Worth and H. H. Fielding, Chem. Phys. Lett., 2017, 683, 179–185 CrossRef CAS.
- K. Fuke, H. Yoshiuchi, K. Kaya, Y. Achiba, K. Sato and K. Kimura, Chem. Phys. Lett., 1984, 108, 179–184 CrossRef CAS.
- G. A. Garcia, L. Nahon and I. Powis, Rev. Sci. Instrum., 2004, 75, 4989–4996 CrossRef CAS.
- T. Debies and J. Rabalais, J. Electron Spectrosc. Relat. Phenom., 1972, 1, 355–370 CrossRef.
- R. A. Livingstone, J. O. F. Thompson, M. Iljina, R. J. Donaldson, B. J. Sussman, M. J. Paterson and D. Townsend, J. Chem. Phys., 2012, 137, 184304 CrossRef PubMed.
- D. M. Neumark, Annu. Rev. Phys. Chem., 2001, 52, 255–277 CrossRef CAS PubMed.
- A. Stolow and J. G. Underwood, Adv. Chem. Phys., 2008, 139, 497–583 CrossRef CAS.
- P. Chakraborty, Y. Liu, S. McClung, T. Weinacht and S. Matsika, J. Phys. Chem. Lett., 2021, 12, 5099–5104 CrossRef CAS PubMed.
- M. S. Schuurman and V. Blanchet, Phys. Chem. Chem. Phys., 2022, 24, 20012–20024 RSC.
- W. G. Fortune, M. S. Scholz and H. H. Fielding, Acc. Chem. Res., 2022, 55, 3631–3640 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Parameters of model Hamiltonian. See DOI: https://doi.org/10.1039/d3cp05559k |
| This journal is © the Owner Societies 2024 |