Fragmentation channels of non-fullerene cationic carbon clusters
Piero
Ferrari†
 a,
Klavs
Hansen
a,
Klavs
Hansen
 *bc,
Ozan
Lacinbala
a,
Ewald
Janssens
*bc,
Ozan
Lacinbala
a,
Ewald
Janssens
 a and
Peter
Lievens
a and
Peter
Lievens
 a
a
aQuantum Solid-State Physics, Department of Physics and Astronomy, KU Leuven, 3001 Leuven, Belgium
bCenter for Joint Quantum Studies and Department of Physics, School of Science, Tianjin University, 92 Weijin Road, Tianjin 300072, China. E-mail: klavshansen@tju.edu.cn
cLanzhou Center for Theoretical Physics, Key Laboratory of Theoretical Physics of Gansu Province, Lanzhou University, Lanzhou, Gansu 730000, China
First published on 4th November 2023
Abstract
The unimolecular fragmentation channels of highly excited small cationic carbon clusters have been measured with a time-of-flight mass spectrometer after photofragmentation. The dominant channel is loss of the neutral trimer, for all CN+N = 10–27 clusters except for N = 11, 12 which decay by monomer emission, and C25+ which shows competing loss of C2 and C3. The results permit to quantify the role of the rotational entropy in the competition between monomer and trimer decays with the help of energies calculated with density functional theory.
1. Introduction
The ability of carbon atoms to form stable single, double and triple bonds gives, together with bond hybridization, rise to a number of allotropic forms of the element, including graphite, diamond, amorphous carbon, graphene,1 carbon nanotubes2 and fullerenes.3 The bonding flexibility is also reflected in the variety of structures carbon clusters possess in the gas phase, each with their own homologous series of electronic and thermodynamic properties and reactivities of importance for e.g. the energy dissipation processes by radiative cooling, fragmentation, and electron emission.4 The structural diversity of carbon clusters has been demonstrated in ion mobility experiments,5 which showed that small carbon clusters are linear chains up to around CN+ with N = 10, cyclic and bicyclic for 10 < N < 31 and fullerene structures for larger sizes.5–7In astrochemical context, carbon is a particularly relevant element, given its high relative abundance in the interstellar medium and its ability to form stable extended covalent bonds. To date, many carbon-based molecules8,9 and some carbon clusters have been detected in space, such as C2,10 C311–13 and C5.14 Laboratory spectroscopic investigations have been performed for this purpose on carbon chains.15–17
In an application context, carbon clusters are suspected to play a role in combustion. The nature of the species that ultimately form molecular compounds, e.g. polycyclic aromatic hydrocarbons and soot particles in flames, is still unclear,18 although various nucleation and growth mechanisms have been proposed.19–22
In the present article we report experiments of unimolecular decays on time scales of a time-of-flight mass spectrometer, i.e. from several to tens of microseconds. This is beyond the time required for the onset of thermal equilibrium. Internal conversion, for example, requires23,24 ∼10−14–10−8 s and intramolecular vibrational transitions23,25 ∼10−13–10−7 s. As the experiments reported here concern highly excited clusters at their limit of stability, the shortest time scales in the above ranges are most likely the most relevant. The internal energy is thus expected to be statistically distributed among accessible rovibronic states. This allows a description of the unimolecular reactions as arising from a completely equilibrated microcanonical system (the ergodic assumption). Several experimental results about fragmentation patterns of small carbon clusters have been interpreted successfully with statistical theories (such as phase space theory26 and Weisskopf theory27), indicating that the ergodic assumption is indeed valid. A combination of the Metropolis Monte Carlo method and Weisskopf theory, with input from ab initio quantum calculations, allowed to explain the experimental branching ratios of neutral C5, C7 and C9.28 Detailed balance rate constants have also been successfully used to describe a range of experiments on the electron emission and thermal radiation of anionic carbon clusters; see e.g. ref. 29 and 30 for a few examples.
A statistical description of the decays does not, however, define the outcome entirely. As a first approximation the application of statistical theories mixing assumption make observed decay channels the lowest energy channels. It will be shown in the analysis of the data presented here that the ordering may change due to differences in rotational entropy.
The fragmentation of cationic carbon clusters has been investigated previously by several excitation methods, such as UV-visible (multi-)photon absorption,31–36 low-energy collision-induced dissociation,37 fast beam photo-fragment translational spectroscopy,26 dissociative electron impact ionization,38 surface-induced dissociation39 and dissociation recombination.40 The dominant fragmentation channel for neutral, cationic, and anionic carbon clusters is the release of a neutral trimer C3 for the non-fullerene clusters of N < 32 and C2 release for the fullerenes, which define the molecular structures for N > 32.41–44
The general agreement from these studies is that emission of the neutral C3 (‘the α particle of carbon clusters’) is the dominant channel for the non-fullerene clusters. However, authors have reported differing observations for the fragmentation of several cluster sizes. O’Brien et al.45 identified only C3 as the loss channel of CN+, N < 32. Besides the C3 primary dissociation channel, Radi et al.46 detected a number of different fragmentation channels, i.e. loss of C1, C5, C10 and C14 from CN+ (N ≲ 30).46 These experiments are of particular interest because they were performed on mass-selected ions, and a delayed measurement eliminates the prompt ions, which can be produced before internal equilibrium is established. Unfortunately the equipment used in the experiments is plagued by the presence of the artefact called ghost peaks (see ref. 47 for details), which makes it uncertain if this elimination was actually accomplished in these experiments. Other workers48 observed that loss of C5 is the major fragmentation channel for C15+, and in particular for C16+ and C19+, with C3 loss appearing as a minor channel.
In summary, the presence of the prompt fragmentation channels in these studies leaves some questions as to the decay channels of statistically well mixed clusters, and as yet there is no consensus about the fragmentation channels of metastable carbon clusters. In the present work, we investigate the metastable decay of cationic clusters, excited and ionized by a laser pulse. The delayed extraction in time-of-flight mass spectrometry eliminates the problem of detecting the prompt products in photo-excitation experiments and in collision-induced fragmentation (see e.g. the analogous case for silicon clusters in ref. 49). In other words, it allows a more system specific characterization of the processes, without the contamination from excitation specific reactions.
2. Experimental procedure
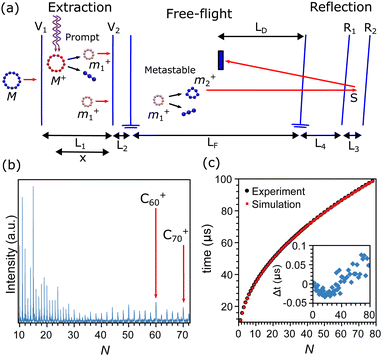
The carbon clusters were produced in a Smalley-type laser ablation source, which is described in detail in ref. 50. Briefly, the second harmonic of a focused Nd:YAG laser (532 nm) was used to ablate a graphite target. The formed plasma was cooled by He gas which was injected into the source through a pulsed valve, operated with a backing pressure of 7 bar and at room temperature. The helium gas carrying the clusters underwent a supersonic expansion into vacuum through a conical nozzle, forming a directional molecular beam of the carbon clusters. The mass distribution of the clusters was characterized after ionization by a reflectron time-of-flight mass spectrometer, depicted in the scheme of Fig. 1a. An example of a mass spectrum recorded after ionization and excitation as described below is presented in Fig. 1b, showing a wide distribution of CN+ clusters, up to N = 72, and higher intensities for certain sizes.Ions produced in the source are rejected from the beam by a static electric field and only neutral clusters enter the extraction region of the mass spectrometer, where they are exposed to the light from a focused F2 excimer laser (157 nm). During the laser pulse the clusters absorb a number of photons, resulting in a rapid ionization and fragmentation. A large fraction of the fragmentation caused by this excitation will occur practically instantaneously compared with the microsecond timescales of acceleration in the mass spectrometer, and will therefore occur when the clusters are still in the extraction region of the mass spectrometer. Following the literature we denote this type of fragmentation as “prompt”.
Knowledge of the dimensions and applied potentials of the mass spectrometer, depicted by the double arrows in Fig. 1a, allows us to calculate the flight times of the prompt fragments from the moment of laser excitation until detection. After prompt fragmentation occurred, clusters may still have sufficient internal energies to fragment. If the additional fragmentation event takes place within the free-flight region of the mass spectrometer (LF in Fig. 1a), the fragment is denoted as “metastable”. Prompt and metastable fragments can be distinguished in a mass spectrum with suitable settings of the reflectron potentials. The metastable clusters will then appear as a series of peaks interleaved with the promptly fragmented peaks. Details of the procedure for the apparatus used here can be found in ref. 49. A summary on the flight times of the prompt peaks is presented in Fig. 1c, where the measured flight times (black squares) are compared with the calculations (red circles), showing agreement between measurements and calculations within the width of the peaks. In this calculation, the main uncertainty is the exact position where the clusters are excited by the pulse from the F2 laser, denoted as x in Fig. 1a. This value is fitted on the measured flight times where the voltages and lengths are known inputs.
3. Quantum calculations
Complementary density functional theory (DFT) calculations were performed for CN+ clusters in the N = 10 to 27 size range, focusing in particular on the dissociation energies for the neutral monomer C, dimer C2 and trimer C3 emission channels. The calculations were performed with the ORCA 5.03 software package,51 employing the PBE exchange–correlation functional52 together with the Def2-TZVPP basis set.53 In addition, the effect of dispersion forces was included using the D3BJ dispersion correction.54 This level of theory was shown to correctly predict the transition from linear to ring configurations in small cationic carbon clusters.55 The geometries of the clusters were obtained from the work in ref. 56 and consist of single rings.The ion mobility experiments showed single-ring geometries from N = 10, and competition with double rings starting at N = 21, which then becomes dominant above N = 28.7 Each geometry was first optimized at the PBE(D3BJ)/Def2-SVP level, after which a second geometry optimization was performed, using the larger Def2-TZVPP basis set. Harmonic vibrational frequencies were computed for all CN+ clusters, obtaining only positive vibrational frequencies. Hence, the optimized geometries are confirmed as true minima on the potential energy surface.
The dissociation energies of the neutral monomer (D1), dimer (D2), and trimer (D3) emission channels are computed based on eqn (1), with E the zero-point-corrected absolute energy of the cluster in parenthesis and i = 1, 2, 3.
| Di = E(CN−i+) + E(Ci) − E(CN+). | (1) |
4. Results and discussion
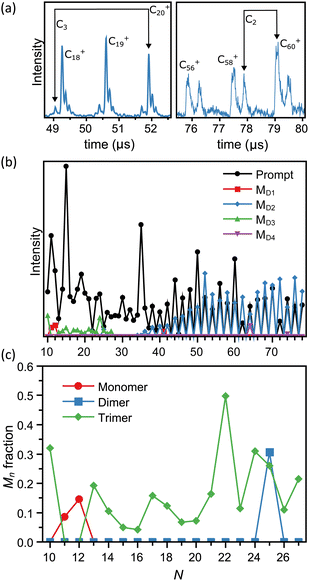
As outlined in the Experimental procedure section, the flight times of the metastable fragments can be calculated and the fragmentation channels unambiguously identified. We see emission of neutral monomers (CN+ → CN−1+ + C), dimers (CN+ → CN−2+ + C2), and trimers (CN+ → CN−3+ + C3). This is illustrated with two examples in Fig. 2a. A summary of the analysis is shown in Fig. 2b, presenting the intensities in mass spectra of the prompt and metastable fragments corresponding to each size N.The intensities of the prompt fragments in Fig. 1b show several well-known features, such as the high intensity of the peaks of C50+, C60+ and C70+. Generally, the intensities of hot clusters result from a combination of intrinsic stabilities, stabilization caused by radiative cooling, and the mass spectrum reshuffling due to evaporation events prior to mass selection. These effects have been discussed elsewhere (see e.g. ref. 55 for small carbon cations) and we will not elaborate on the subject of intensities here.
Fig. 2b confirms the loss of dimers for the fullerene structures. This pattern is well-known for large carbon clusters,59 and agrees with the equally well known pattern seen in the intensities of the promptly produced clusters, where only even-numbered species are seen.
The main subject of this article is the emission channels of the clusters of sizes N < 28. With three exceptions the C3 channel is dominant with no traces of other channels at the level of 4% in our data, based on the level of noise on the mass spectra. The exceptions to the trimer emission pattern are C25+, where both C2 and C3 emissions are observed, and C11+ and C12+, where only monomer emission occurs. Notably, no larger fragments than the trimer were seen, in strong contrast to a number of the studies mentioned in the Introduction where also the loss of five atoms and occasionally even larger fragments were reported. As shown in ref. 49 for silicon clusters, such large fragments can be detected with the device used in the present study.
The dissociation energies of the C, C2, and C3 loss channels, calculated with density functional theory (DFT), are shown in Fig. 3. The channels seen experimentally agree well for most cluster sizes with the expectations from the computed DN values when one assumes that the observed fragmentation channel is the one with the lowest dissociation energy. This holds also for the two monomer emitters C11+ and C12+.
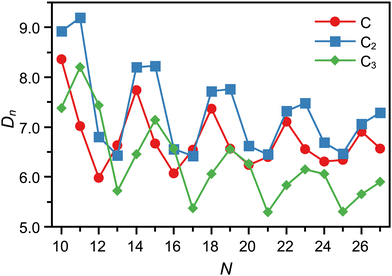 | ||
| Fig. 3 Dissociation energies computed for CN+ clusters in the N = 10–27 size range. The fragmentation channels of neutral C, C2 and C3 are shown. | ||
There are, however, a few disagreements with this simple picture. A simple correlation between lower dissociation energy and observed fragmentation channel cannot explain the dominance of the C3 emission channel for C15+ and C16+, and neither the competition between C2 and C3 loss observed for C25+. Likewise, neither the absence of two competing channels for N = 19, 20 is understandable by the simple energetic argument.
Considerations of the rotational entropy of the emitted neutral provides an understanding of the systematics of most of these cases. The number of rotational degrees of freedom of the product differs by two when a dimer or a trimer is emitted, compared with atom emission. The detailed balance rate constants for dimer or trimer emission will then get a contribution from the summation over these extra degrees of freedom. This adds a factor for those channels, which is on the order of the thermal average over the rotational degree of freedom. This calculation has been discussed in some detail for the slightly different case of dimer loss from fullerenes.60 A complete derivation here would require consideration of both attachment cross sections and a rigorous treatment of angular momentum conservation, including the role of angular momentum of the vibrational motion of the linear molecules (see e.g. ref. 61). This is beyond the scope of this work, and we limit the considerations to the leading order terms, with the limitations this will give to the conclusions.
The monomer emission rate constant of cluster size N can be written to a reasonable approximation as62
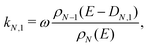 | (2) |
| 3N − 6 → 3(N − 1) − 6 = 3N − 9 | (3) |
| 3N − 6 → 3(N − 3) − 6 + 3 × 3 − 5 = 3N − 11, | (4) |
| ρN−3(E) ≈ ρN−1(E). | (5) |
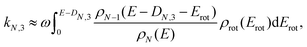 | (6) |
| ρN−1(E − DN,3 − Erot) ≈ ρN−1(E − DN,3)e−Erot/T, | (7) |
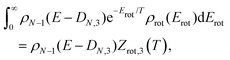 | (8) |
| Z = e−F/T = e−Ē/T+S, | (9) |
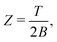 | (10) |
| Z ≈ eS, | (11) |
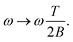 | (12) |
For decays on the microsecond time scale the microcanonical temperature is given as a fraction of the activation energy, less the so-called finite heat capacity correction. The first term is essentially the reciprocal of the logarithm of the frequency factor multiplied by the experimental time. In the present case, this is about 1/25 to 1/30 and the finite heat bath correction about 1/2 to 1/3 of this, with a negative sign. For details of these estimates, please see ref. 64.
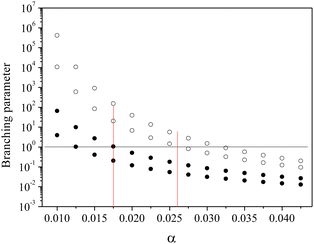
Motivated by these considerations we parametrize the microcanonical temperature by the parameter α as T = αD, where D is the dissociation energy pertaining to the observed decay. With δD the difference in activation energy for trimer and monomer loss, D3 − D1, this makes trimer decays dominant if
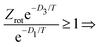 | (13) |
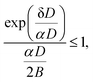 | (14) |
Fig. 4 shows the calculation of the left-hand side of eqn (14) for the four sizes N = 11, 12, 15 and 16 for which the monomer dissociation energy is less than that of the trimer. Points above the ordinate 1 line correspond to monomer emission. The expected value of the parameter α that defines the microcanonical temperatures for each of the four sizes is seen to fall in this region, between the two vertical red lines, where all sizes behave theoretically as experimentally observed.
5. Conclusions
We have measured the carbon trimer to be the dominant decay channel for non-fullerene carbon clusters up to size 31. The detection limit of the decay channels is 4% of the total amount of metastable decay. The loss of larger neutral fragments reported in earlier studies is absent in these experiments at this level. Clusters of three different sizes emit smaller fragments and in two of those cases, the behavior is consistent with the calculated ground state energies of the species. The dominant channels of the four clusters that energetically show monomer–trimer competition can all be rationalized in terms of the trimer rotational entropy contribution to the evaporative frequency factor. Although the dominant channel is explained correctly this way, the contrast in the experimentally observed monomer–trimer branching ratios is actually much stronger than the theoretical prediction. The reason for this is not clear. A remaining significant discrepancy between experiment and theory is the dimer decay of N = 25. We suggest that the presence of isomers can cause this. Finally, we would like to reiterate the observation that previous experiments applying collision induced fragmentation may involve processes of a more direct nature and that problems caused by such interferences are eliminated by considering delayed processes, as done here.Author contributions
PF performed the experiments and DFT calculations. KH conducted the analysis on rotational entropy effects. PF, OL and KH wrote the first version of the manuscript. PF, EJ and PL envisioned the study. All authors participated in the writing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the Research Foundation Flanders (FWO, G.0A05.19N), and the KU Leuven Research Council (project C14/22/103). PF acknowledges the FWO for a senior postdoctoral grant. KH acknowledges support from the National Science Foundation of China with the grant ‘NSFC no. 12047501’ and the Ministry of Science and Technology of People's Republic of China with the 111 Project under Grant no. B20063. The computational resources and services used in this work were provided by the VSC (Flemish Supercomputer Center), funded by the FWO and the Flemish government. This article is based upon work from COST Action CA18212 – Molecular Dynamics in the GAS phase (MD-GAS), supported by COST (European Cooperation in Science and Technology).Notes and references
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- S. Iijima, Nature, 1991, 354, 56–58 CrossRef CAS.
- H. W. Kroto, J. R. Heath, S. C. O’Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163 CrossRef CAS.
- P. Ferrari, E. Janssens, P. Lievens and K. Hansen, Int. Rev. Phys. Chem., 2019, 38, 405–440 Search PubMed.
- G. Von Helden, M.-T. Hsu, P. R. Kemper and M. T. Bowers, J. Chem. Phys., 1991, 95, 3835–3837 CrossRef CAS.
- S. Yang, K. Taylor, M. Craycraft, J. Conceicao, C. Pettiette, O. Cheshnovsky and R. Smalley, Chem. Phys. Lett., 1988, 144, 431–436 CrossRef CAS.
- G. von Helden, M. T. Hsu, N. Gotts and M. T. Bowers, J. Phys. Chem., 1993, 97, 8182–8192 CrossRef CAS.
- A. Tielens, Rev. Mod. Phys., 2013, 85, 1021 CrossRef CAS.
- B. A. McGuire, Astrophys. J., Suppl. Ser., 2018, 239, 17 CrossRef CAS.
- S. P. Souza and B. L. Lutz, Astrophys. J., 1977, 216, L49–L51 CrossRef CAS.
- K. W. Hinkle, J. J. Keady and P. F. Bernath, Science, 1988, 241, 1319–1322 CrossRef CAS PubMed.
- J. P. Maier, N. M. Lakin, G. A. Walker and D. A. Bohlender, Astrophys. J., 2001, 553, 267 CrossRef CAS.
- T. F. Giesen, B. Mookerjea, G. W. Fuchs, A. A. Breier, D. Witsch, R. Simon and J. Stutzki, Astron. Astrophys., 2020, 633, A120 CrossRef CAS.
- P. F. Bernath, K. H. Hinkle and J. J. Keady, Science, 1989, 244, 562–564 CrossRef CAS PubMed.
- J. P. Maier, J. Phys. Chem. A, 1998, 102, 3462–3469 CrossRef CAS.
- J. Rademacher, E. S. Reedy and E. K. Campbell, J. Phys. Chem. A, 2022, 126, 2127–2133 CrossRef CAS PubMed.
- J. T. Buntine, M. I. Cotter, U. Jacovella, C. Liu, P. Watkins, E. Carrascosa, J. N. Bull, L. Weston, G. Muller, M. S. Scholz and E. Bieske, J. Chem. Phys., 2021, 155, 214302 CrossRef CAS PubMed.
- J. W. Martin, M. Salamanca and M. Kraft, Prog. Energy Combust. Sci., 2022, 88, 100956 CrossRef.
- M. Frenklach and L. B. Ebert, J. Phys. Chem., 1988, 92, 561–563 CrossRef CAS.
- J. Ahrens, M. Bachmann, T. Baum, J. Griesheimer, R. Kovacs, P. Weilmünster and K.-H. Homann, Int. J. Mass Spectrom., 1994, 138, 133–148 CrossRef CAS.
- K.-H. Homann, Angew. Chem., Int. Ed., 1998, 37, 2434–2451 CrossRef PubMed.
- Z. Mansurov, J. Eng. Phys. Thermophys., 2011, 84, 125–159 CrossRef CAS.
- E. S. Medvedev and V. I. Osherov, Radiationless transitions in polyatomic molecules, Springer, 1995, vol. 57 Search PubMed.
- V. L. Ermolaev, Russ. Chem. Rev., 2001, 70, 471–490 CrossRef CAS.
- D. J. Nesbitt and R. W. Field, J. Phys. Chem., 1996, 100, 12735–12756 CrossRef CAS.
- H. Choi, R. T. Bise, A. A. Hoops, D. H. Mordaunt and D. M. Neumark, J. Phys. Chem. A, 2000, 104, 2025–2032 CrossRef CAS.
- G. Martinet, M. Chabot, K. Wohrer, S. Della Negra, D. Gardes, J. Scarpaci, P. Desesquelles, V. Lima, S. Díaz-Tendero and M. Alcamí, et al. , Eur. Phys. J. D, 2003, 24, 149–152 CrossRef CAS.
- S. Díaz-Tendero, P.-A. Hervieux, M. Alcamí and F. Martín, Phys. Rev. A, 2005, 71, 033202 CrossRef.
- N. Kono, T. Furukawa, H. Tanuma, J. Matsumoto, H. Shiromaru, T. Azuma, K. Najafian, M. S. Pettersson, B. Dynefors and K. Hansen, Phys. Chem. Chem. Phys., 2015, 17, 24732 RSC.
- Y. Ebara, T. Furukawa, J. Matsumoto, H. Tanuma, T. Azuma, H. Shiromaru and K. Hansen, Phys. Rev. Lett., 2016, 117, 133004 CrossRef PubMed.
- M. Geusic, T. McIlrath, M. Jarrold, L. Bloomfield, R. Freeman and W. Brown, J. Chem. Phys., 1986, 84, 2421–2422 CrossRef CAS.
- P. P. Radi, T. L. Bunn, P. R. Kemper, M. E. Molchan and M. T. Bowers, J. Chem. Phys., 1988, 88, 2809–2814 CrossRef CAS.
- K. Hansen and E. E. B. Campbell, J. Chem. Phys., 1996, 104, 5012–5018 CrossRef CAS.
- B. P. Pozniak and R. C. Dunbar, Int. J. Mass Spectrom., 1997, 165, 299–313 CrossRef.
- K. Koyasu, T. Ohtaki, N. Hori and F. Misaizu, Chem. Phys. Lett., 2012, 523, 54–59 CrossRef CAS.
- P. Fischer, P. F. Giesel and L. Schweikhard, Eur. Phys. J. D, 2023, 77, 27 CrossRef CAS.
- S. W. McElvany, B. I. Dunlap and A. O’Keefe, J. Chem. Phys., 1987, 86, 715–725 CrossRef CAS.
- C. Lifshitz, T. Peres and I. Agranat, Int. J. Mass Spectrom., 1989, 93, 149–163 CrossRef CAS.
- R. L. Whetten, C. Yeretzian and P. M. S. John, Int. J. Mass Spectrom., 1994, 138, 63–76 CrossRef CAS.
- O. Heber, K. Seiersen, H. Bluhme, A. Svendsen, L. Andersen and L. Maunoury, Phys. Rev. A, 2006, 73, 022712 CrossRef.
- S. Tomita, J. Andersen, C. Gottrup, P. Hvelplund and U. Pedersen, Phys. Rev. Lett., 2001, 87, 073401 CrossRef CAS PubMed.
- C. Lifshitz, Int. J. Mass Spectrom., 2000, 198, 1–14 CrossRef CAS.
- K. Głuch, S. Matt-Leubner, O. Echt, B. Concina, P. Scheier and T. Märk, J. Chem. Phys., 2004, 121, 2137–2143 CrossRef PubMed.
- B. Concina, K. Głuch, S. Matt-Leubner, O. Echt, P. Scheier and T. Märk, Chem. Phys. Lett., 2005, 407, 464–470 CrossRef CAS.
- S. C. O’Brien, J. R. Heath, R. F. Curl and R. E. Smalley, J. Chem. Phys., 1988, 88, 220–230 CrossRef.
- P. P. Radi, T. L. Bunn, P. R. Kemper, M. E. Molchan and M. T. Bowers, J. Chem. Phys., 1988, 88, 2809–2814 CrossRef CAS.
- D. Schröder and D. Sülzle, J. Chem. Phys., 1991, 94, 6933 CrossRef.
- M. B. Sowa-Resat, P. A. Hintz and S. L. Anderson, J. Phys. Chem., 1995, 99, 10736–10741 CrossRef CAS.
- P. Ferrari, E. Janssens, P. Lievens and K. Hansen, J. Chem. Phys., 2015, 143, 224313 CrossRef PubMed.
- P. Ferrari, J. Vanbuel, Y. Li, T.-W. Liao, E. Janssens and P. Lievens, The Double-Laser Ablation Source Approach in Gas-Phase Synthesis of Nanoparticles, Wiley-VCH, 2017, pp. 59–78 Search PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- F. Q. Chen, N. Kono, R. Suzuki, T. Furukawa, H. Tanuma, P. Ferrari, T. Azuma, H. Shiromaru, V. Zhaunerchyk and K. Hansen, Phys. Chem. Chem. Phys., 2019, 21, 1587–1596 RSC.
- S. Iida, W. Hu, R. Zhang, P. Ferrari, K. Masuhara, H. Tanuma, H. Shiromaru, T. Azuma and K. Hansen, Mon. Not. Royal Astrom. Soc., 2022, 514, 844–851 CrossRef CAS.
- P. P. Radi, M. E. Rincon, M. T. Hsu, J. Brodbelt-Lustig, P. Kemper and M. T. Bowers, J. Phys. Chem., 1989, 93, 6187–6197 CrossRef CAS.
- C. Lifshitz, P. Sandler, H.-F. Griitzmacher, J. Sun, T. Weiske and H. Schwarz, J. Phys. Chem., 1993, 97, 6592–6597 CrossRef CAS.
- P. Barran, S. Firth, A. Stace, H. Kroto, K. Hansen and E. Campbell, Int. J. Mass Spectrom., 1997, 167, 127–133 CrossRef.
- K. Hansen, E. E. B. Campbell and O. Echt, Int. J. Mass Spectrom., 2006, 252, 79 CrossRef CAS.
- K. Hansen and P. Ferrari, Chem. Phys. Lett., 2021, 768, 138385 CrossRef CAS.
- K. Hansen, Statistical Physics of Nanoparticles in the Gas Phase, Springer, Dordrecht, 2018, vol. 73 Search PubMed.
- J. U. Andersen, E. Bonderup and K. Hansen, J. Chem. Phys., 2001, 114, 6518–6525 CrossRef CAS.
- K. Hansen, Mass Spectrom. Rev., 2021, 40, 725–740 CrossRef PubMed.
Footnote |
| † Present address: Institute for Molecules and Materials, Radboud University, HFML-FELIX, 6525 ED Nijmegen, The Netherlands. |
| This journal is © the Owner Societies 2023 |