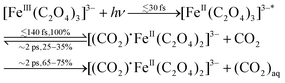Ultrafast photoelectron spectroscopy of photoexcited aqueous ferrioxalate†
L.
Longetti
 a,
T. R.
Barillot
a,
M.
Puppin
a,
J.
Ojeda
a,
L.
Poletto
b,
F.
van Mourik
a,
C. A.
Arrell‡
a,
T. R.
Barillot
a,
M.
Puppin
a,
J.
Ojeda
a,
L.
Poletto
b,
F.
van Mourik
a,
C. A.
Arrell‡
 a and
M.
Chergui
a and
M.
Chergui
 *a
*a
aLaboratory of Ultrafast Spectroscopy and the Lausanne Centre for Ultrafast Science, ISIC, Ecole Polytechnique Fédérale de Lausanne, CH-1015 Lausanne, Switzerland. E-mail: majed.chergui@ep.ch
bNational Research Council of Italy – Institute of Photonics and Nanotechnologies (CNR-IFN), via Trasea 7, 35131 Padova, Italy
First published on 21st October 2021
Abstract
The photochemistry of metal–organic compounds in solution is determined by both intra- and inter-molecular relaxation processes after photoexcitation. Understanding its prime mechanisms is crucial to optimise the reactive paths and control their outcome. Here we investigate the photoinduced dynamics of aqueous ferrioxalate ([FeIII(C2O4)3]3−) upon 263 nm excitation using ultrafast liquid phase photoelectron spectroscopy (PES). The initial step is found to be a ligand-to-metal electron transfer, occuring on a time scale faster than our time resolution (≲30 fs). Furthermore, we observe that about 25% of the initially formed ferrous species population are lost in ∼2 ps. Cast in the contest of previous ultrafast infrared and X-ray spectroscopic studies, we suggest that upon prompt photoreduction of the metal centre, the excited molecules dissociate in <140 fs into the pair of CO2 and [(CO2)FeII(C2O4)2]3− fragments, with unity quantum yield. About 25% of these pairs geminately recombine in ∼2 ps, due to interaction with the solvent molecules, reforming the ground state of the parent ferric molecule.
Introduction
Photoinduced electron transfer in transition metal complexes is often the initial process that drives their photophysics and photochemistry. Iron complexes are of great practical interest,1–3 in part motivated by the abundance of the metallic element. Their rich photophysics has been the focus of several ultrafast spectroscopic studies aimed at unravelling the electronic and structural dynamics on femtosecond to picosecond time scales.4–6 Here we focus on the prototypical case of Ferric tris-oxalate ([FeIII(C2O4)3]3−) for which a complete picture of the initial reaction steps is still lacking. While the photoreaction intermediates and products are well known,7,8 there is no consensus yet on the initial electron transfer mechanisms, which are considered to play a pivotal role in the photochemistry of this class of compounds.The molecular structure of ferrioxalate is shown in Fig. 1a. The iron atom (orange) is six-fold coordinated to oxalate (ox = (C2O4)2−) ligands, bound to the metal by chelation in a helical chiral geometry. The molecule has octahedral symmetry and belongs to the D3 point group. Exposure to ultraviolet (UV) light induces a photoreaction whose final products are bi-oxalate ferrous species.9–15 The UV-visible absorption spectrum of ferrioxalate8,13,14,16 shows two main bands: a ligand-field band originating from d–d transitions at wavelengths >500 nm, and a more intense band at λ < 440 nm, assigned to a ligand-to-metal charge transfer (LMCT) excitation.14,17–19 The quantum yield (QY) of the final photoproduct ([FeII(C2O4)2]2−) for excitation wavelengths between 440 and 270 nm is constant and greater than unity (about 1.25),8,14,16,20 making this molecule a “gold standard” for actinometry.13,21
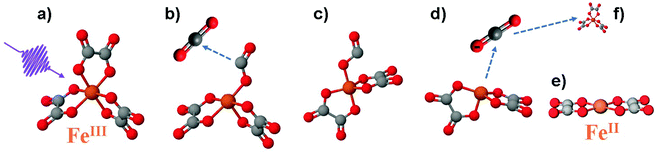 | ||
| Fig. 1 Photoreaction sequence of the [FeIII(C2O4)3] molecule proposed in ref. 8. (a) Ferrioxalate 3D steady-state structure: iron in orange, oxygen in red, carbon in grey. It is still debated if the impulsive photoexcitation triggers a charge transfer at this stage. (b) CO2 detachment within 0.5 ps. (c) Molecule isomerisation upon fragmentation. (d) CO2˙− radical detachment (approx. 1 ns). (e) [FeII(C2O4)2] product in its final configuration. (f) The radical triggers a new redox reaction with an unphotolysed ground state ferric molecule on a longer time scale, completing the ferrioxalate photochemistry. | ||
The photoreaction has been described in two steps: first UV excitation leads to the creation of ferrous species and a carbonaceous radical as photoproducts, second on the ns time scale this radical then reduces another ferrioxalate molecule. Whether the initial metal reduction takes place upon photoexcitation (i.e. an LMCT state is promptly excited) or upon ligand dissociation is still a matter of debate. Flash photolysis experiments by Parker and Hatchard put forward the hypothesis of a prompt iron reduction on the nanosecond time scale.14 This was further supported by optical spectroscopy by DeGraff et al.,22 who investigated the ferrioxalate photoproduct kinetics. A further study of intermediate photoproducts by Patterson and co-workers23 suggested a different scenario, in which the C–C oxalate bond is homolytically cleaved and FeII species are produced in a subsequent redox process, implying a delayed iron reduction picture. Chen et al. performed ultrafast UV-visible transient absorption (TA) and Fe K-edge X-ray absorption spectroscopy (XAS) on ferrioxalate aqueous solutions upon 266 nm excitation.24–26 In these studies, the Fe K post-edge features were related to the iron-oxygen bond length and their changes were attributed to an increase, from 2.01 Å up to 2.21 Å within 2 ps,24 in an excited ferric tris-oxalate molecule, i.e. with no reduction of the metal atom. At later times (>4 ps) a bond shrinkage (1.92 Å) was reported and interpreted as fingerprint of homolytic cleavage of the Fe–O bond. In their scenario, no electron transfer occurs within 140 ps24 while oxalate ligand fragmentation has started by 5 ps, producing two CO2˙− radicals. According to their optical TA results, a strong transient signal due to the solvated electrons was observed and attributed to a charge transfer to solvent (CTTS) process.24,25 Thus, this interpretation supports the hypothesis of ligand dissociation followed by metal centre reduction at later times. In contrast, an optical TA study by Pozdnyakov et al.27 reported formation of reaction intermediates (CO2˙− radicals) as a consequence of intramolecular electron transfer.
More recently, an Fe K-edge XAS study of aqueous ferrioxalate was carried out with femtosecond resolution at the SACLA X-ray free electron laser (XFEL).28 It showed an initial red-shift by over 4 eV of the K-edge, occurring within the temporal resolution of 140 fs, which then decreases and stabilises to a value of ∼3 eV within ∼3 ps, with no further subsequent evolution at least up to 100 ps. The authors proposed that CO2 is released within 140 fs (their experimental temporal resolution) and the second ligand moiety (CO2)˙− is detached within 3 ps.28 Such a reaction mechanism is explained by assuming a prompt charge transfer scenario, which is clearly supported by the red shift of over 4 eV observed within the cross-correlation of their experiment. However, while tr-XAS experiments are sensitive to changes of the oxidation states, the associated edge shifts also depend on bond elongation29 and on the fraction of excited species.30
Time-resolved infrared (IR) TA spectroscopy studies of photoexcited ferrioxalate by Straub et al.8 reported new bands, attributed to solvated CO2 fragments appearing within the experimental temporal resolution of 0.5 ps. This supports the scenario of an early ligand fragmentation of the neutral carbon dioxide as in ref. 28, compatible with a prompt metal reduction. A second radical CO2˙− was found to detach from the ferrous complex within 1 ns, subsequent to a molecular isomerisation. Based on these IR TA results, the picture of the ferrioxalate photochemistry that emerges is summarised in Fig. 1. UV photon absorption (a) triggers CO2 release within 0.5 ps (b). After structural rearrangement of the molecule (c) towards the square-planar geometry of the ferrous bioxalate final product (e), the remaining CO2˙− ligand moiety is released within 1 ns (d). The next step of the reaction is triggered by this free radical on ns time scales, which reacts with a ground state ferrioxalate molecule (f) to generate an additional [FeII(C2O4)2]2− product.
As mentioned above, the time scale of the initial electron transfer is still a matter of debate. Furthermore, while the studies by Chen et al.,24–26 Ogi et al.28 and Straub et al.8 all report a 2–3 ps component in their results, its interpretation is radically different in these three studies. Here, we apply for the first time ultrafast photoelectron spectroscopy (PES) on ferric tris-oxalate in aqueous solutions, to investigate the initial photoinduced events. In particular, PES is very sensitive to the oxidation state of the metal and any changes it undergoes, as recently demonstrated in a study on ferric hexacyanide.31 We find that photoexcitation induces a prompt ligand-to-metal charge transfer (LMCT). We also find that ∼25% of the photoreduced molecules decay in about ∼2 ps. In line with the high photochemical yield of the reaction, we conclude that the initial photoreduction triggers dissociation of all molecules but, due to the interaction with solvent molecules, about 25% of these recombine in ∼2 ps into the ground state of the parent ferric molecule. The interaction of the fragments with the solvent can however not be cast in the context of the so-called cage effect32 in which recoiling fragments recombine.
The article proceeds as follows: we first present the steady-state PE spectrum of the solvated complex and discuss it. The iron electronic structure after photoexcitation is then identified and discussed. The temporal evolution of the transient signal reveals the kinetics of the photogenerated ferrous species. These results are discussed in the framework of previous ultrafast experimental studies.
Methods
The ferrioxalate aqueous solution was prepared by dissolving (NH4)3[FeIII(C2O4)3] salt (CAS no. 13268-42-3, supplier ACROS) in MilliQ water (resistivity = 18.2 MΩ cm) from a Millipore machine. The sample was steered, filtered and kept in the dark to avoid photodegradation. A 500 mM concentration was used to maximise the solute PES signal and avoid crystal growth on the nozzle tip (we found the saturation concentration at room temperature to be ∼700 mM).The experimental setup for tr-PES of liquid solutions is described in details elsewhere.33–35 In brief, ultrashort monochromatised vacuum-ultraviolet (VUV) pulses with a duration <50 fs and a photon energy ∼35 eV were focussed on a liquid micro jet (μ-jet) of 17 μm-diameter. The μ-jet flow rate of 0.30 ml min−1 ensures that the sample is refreshed for each pulse at a laser repetition rate of 6 kHz. The ferrioxalate solution has enough charge carriers (ions and counterions) to compensate for the streaming potential33,36 and no spectral distortions were observed. To avoid this effect also in the pure water reference sample (solvent-only, Fig. 2), we added NaCl to have 25 mM concentration. Compared to previous reports,31,33,34,37,38 an improved collection efficiency (×20) of the photoelectron analyzer was achieved by the addition of electrostatic lenses to the time of flight (TOF) electron spectrometer. Steady-state PE spectra were acquired in field-free mode (lenses grounded) and in an enhancing mode (lenses on) for time-resolved measurements. To compensate for an additional energy dependence in the photoelectron distribution, spectra collected in the enhancing mode were calibrated to the static PES reference acquired in field-free mode by eventually correcting an energy offset of few hundreds of meV.
The third harmonic (263 nm) of the Ti:Sapphire laser was used as pump and focussed on the μ-jet onto a focal spot of 200 μm diameter (full width at half-maximum – FWHM), at a fluence between 0.6 and 1.4 mJ cm−2. Temporal overlap between pump and probe pulses was calibrated with a precision of 10 fs by measuring the laser-assisted photoelectric effect (LAPE)37 signal from water. The temporal cross correlation between the pump and probe pulses is measured to be 96 ± 4 fs FWHM. More details are reported in the ESI.†
Results
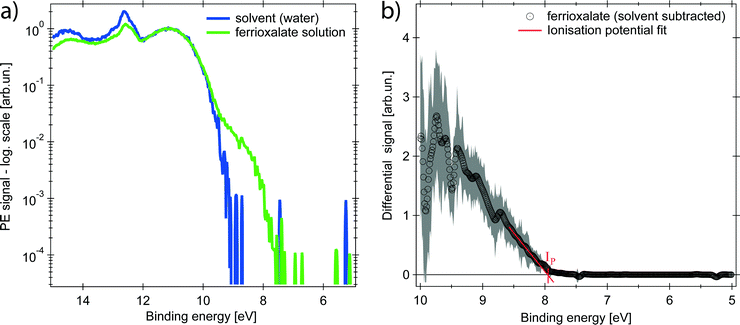
The PE spectrum of the aqueous ferrioxalate solution is shown in Fig. 2 (green trace, in logarithmic scale) and is compared to the PE spectrum of the pure solvent (blue trace). The bands at binding energies EB > 10 eV originate from liquid- and gas-phase water molecular orbitals,39 which dominate the spectra. The contribution of the solute can be clearly distinguished at EB < 10 eV, below the water's ionisation threshold, in a background-free spectral range (green trace at 8–10 eV). Further solute contributions due to occupied orbitals at EB > 10 eV overlap with the water's PE signal and cannot be distinguished.The PE spectrum of the solute is the difference between the solution PE spectrum (green) and the water one (blue), as shown in the right panel of Fig. 2 (black trace) on a linear scale. The observed band is centred at EB = (9.5 ± 0.2) eV and the solvated molecule ionisation potential is Ip = (7.9 ± 0.2) eV, retrieved as x-intercept of the linear fit of the band tail (Fig. 2). To assign the spectral feature of the ferrioxalate PE signal we compared our results with previous PES studies of similar ferric (Fe3+) compounds in aqueous solutions. Seidel et al.40 reported PES of octahedral ferric hexa-aquo complex. Its PE spectrum shows close resemblance to the trace in the right panel of Fig. 2 (see Fig. S2 in the ESI†), though the ferrioxalate's Ip is slightly smaller than that of the hexa-aquo complex, whose metal orbitals are strongly mixed with the water ones.40 This stands for a weaker, though not negligible, metal–solvent interaction because of the presence of the surrounding oxalate ligands. We therefore assign the solute band in Fig. 2 to the Fe3+3d5 HOMO orbitals of ferrioxalate.
Upon excitation with the 263 nm pump pulse, we observe a new spectral feature in the PE spectrum at lower EB than the ionisation potential of the unexcited molecule, as shown by the orange trace in Fig. 3 (plotted on logarithmic scale), whereas the green trace is the PE spectrum at negative time delays. The experimental uncertainty of all the traces here presented is computed, per point, as the standard deviation within the single dataset, whose average defines the single point amplitude (see Section S3 in the ESI†). This is reported as shaded area corresponding to 2σ. The PE signal for 6 < EB < 7.5 eV increases upon photoexcitation and is clearly distinct from the PE spectrum of the unexcited molecule.
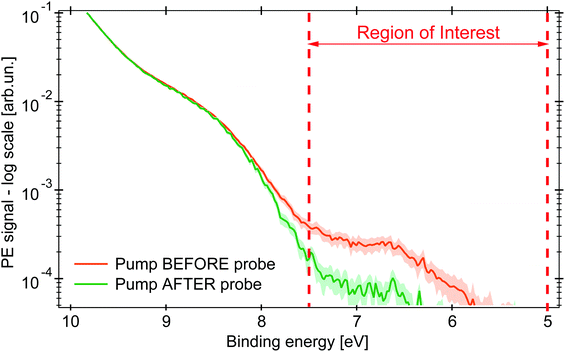 | ||
| Fig. 3 PE spectra in logarithmic scale of an aqueous solution of 0.5 M (NH4)3[FeIII(C2O4)3] under 263 nm excitation (probe photon energy 34.0 eV). The green PE spectrum for pump pulse hitting the sample 0.2 ps after the probe pulse (negative time delay), in orange the pump arrives 1 ps before (positive time delay). The shaded area represents the uncertainty range of 2σ. Between the dashed red lines is the RoI whose integrated signal is represented by the kinetic traces (in Fig. 4). | ||
The amplitude of the transient feature at EB ∼ 7 eV is ∼2% that of the steady-state ferric HOMO band, compatible with the calculated excitation yield (∼3%, see Table S1 in the ESI†). The ionisation potential (Ip) of the photoexcited sample is ∼6.0 eV, analogous to the hexa-aquo ferrous compound reported by Seidel et al.,40 who also showed that ferrous compounds (Fe2+) have an Ip lower than the oxidised counterpart (Fe3+). Furthermore, photoexcited aqueous ferricyanide shows a similar transient PE signal at lower EB, which was related to a photoreduced ferrous species.31 We hence assign the transient PE feature in the photoexcited ferrioxalate (Fig. 3) to a photogenerated ferrous Fe2+3d6 species. Its Ip decreases by ∼2 eV EB with respect to the steady-state ferrioxalate because of a reduction of the metal oxidation state. We use this feature to follow the subsequent electronic dynamics in photoexcited ferrioxalate.
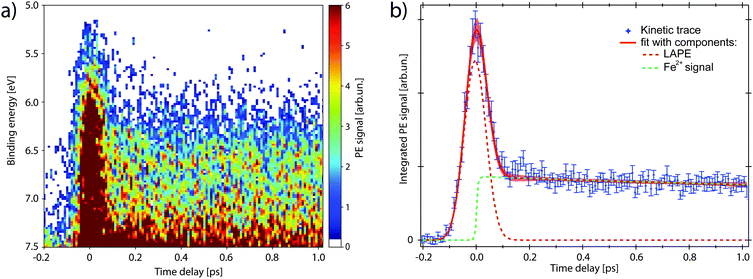
The map in Fig. 4a shows the PE spectra with colour-coded intensity within the energy range defined as Region of Interest (RoI, 5.0 < EB < 7.5 eV), acquired for time delays between −0.2 and 1.0 ps (10 fs step). The transient PE signal from ferrous species appears in the RoI already at t = 0 and overlaps with the intense feature due to the Laser-Assisted Photoelectric Effect (LAPE). This is attributed to the first-order replica at 6.5 eV of the water HOMO peak (EB = 11.16 eV).37 The LAPE signal was characterised in a tr-LPES measurement on pure water under the same experimental conditions, from which the instrumental response function (IRF) of 96 ± 4 fs (FWHM) was determined (more information in the ESI†).
Kinetic traces of the transient PE signal are calculated as the integrated PE signal within the RoI highlighted in Fig. 3 and are plotted as a function of pump–probe time delay (Fig. 4b and 5) to display the transient PE signal dynamics. The average of the signal amplitude for t < −200 fs was taken as background level and subtracted from the kinetic trace. The error bars correspond to the experimental standard deviation σ per single delay point and are taken into account in the fit procedure. The trace in Fig. 5a has the LAPE signal subtracted.
We now investigate the hypothesis that this transient has an exponential rise (1 − e−t/τr), with time constant τr. The fit function (full expression in Section S4 of the ESI†) is shown as a red trace in Fig. 4b and its fit components are displayed as dashed traces: the LAPE in orange and the ferrous PE signal in green. The rise time that results from the least square minimisation is τr = 30 ± 40 fs, about three times smaller than the IRF. Such value with its confidence interval, compared with the experimental time resolution, indicates that the signal rise is instantaneous and we can consider the generation of ferrous species to happen in ≲30 fs. Moreover, no evidence of intermediate electronic state is detected, corroborating the picture of a prompt iron photoreduction upon 263 nm excitation.28
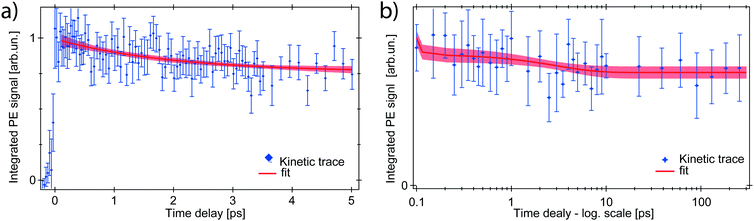
The ferrous PE signal dynamics is better displayed by the kinetic trace in Fig. 5a (LAPE contribution subtracted), which shows a decreasing trend up to ∼5 ps. Given the initial amplitude A0 at t = 0, we observe a partial decrease and then a stabilisation of the signal, which is also seen in Fig. 5b as an asymptotic value (at least up to 250 ps). A two-component fit with an exponentially decreasing signal A1e−t/τ1 and a plateau (asymptotic amplitude A∞) is performed to infer these parameters from the kinetic trace of Fig. 5a. The values from the best fit are
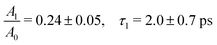 | (1) |
To explain this observation we take into account the two most plausible scenarios which could justify the integrated intensity drop within the RoI. These can be either a decrease in the population of ferrous species, or a shift of their PE band towards higher EB. The latter is excluded by comparing kinetic traces of the RoI sliced in 4 consecutive energy regions, that do not show a consecutive spectral intensity reduction of a slice after the next, but instead a homogeneous intensity drop (Fig. S3 in the ESI†). Concerning the first scenario, given the nature of the photoionisation process, the PE intensity is directly proportional to the orbital occupancy and to the amount of probed ferrous species. Therefore it can change if the latter varies in the probed volume, or if the occupancy decreases. This would correspond to a metal oxidation with consequent band shift to the EB of steady-state ferrioxalate HOMO (ferric) and a homogeneous signal drop. The former case can be discarded because the liquid jet can be seen as stationary on the picosecond time scale and diffusion is not fast enough for the photoexcited molecules to leave the probed volume in hundreds of ps. So the drop of the PE signal within the RoI is due to a population loss of reduced species which, as will be discussed below, is a return to the parent ferric species form.
Discussion
The prompt (≲30 fs) reduction of the ferrioxalate metal centre upon photoexcitation, here reported, demonstrates for the first time that the nature of the electronic excited state of ferrioxalate reached at 263 nm reflects a ligand-to-metal-charge-transfer (LMCT) character. The previously proposed delayed intermolecular reduction of the metal26 is not supported by our results, which on the other hand confirm the conclusions of the fs-XAS study.28 This is also consistent with the previous assignments that the absorption at wavelengths shorter than 440 nm is due to an LMCT state, based on the detected ferrous products14,17 and on the typical photochemistry of such a class of metal–organic compounds.18,19The next issue concerns the ∼2 ps kinetics (Fig. 5), whose signal corresponds to a loss of ∼1/4 of the photoreduced molecules. This time constant is reminiscent of the 1.5–2.5 ps component reported by Straub et al.8 in their infrared TA study of photoexcited ferrioxalate. They monitored the infrared CO single- and double-bond stretch bands of the oxalate in the parent molecule that lie in the 1300–1800 cm−1 region, but also the 2200–2400 cm−1 region, where the antisymmetric ν3 stretch mode of the CO2 fragment is expected. They observed a bleach (negative) signal of all ferrioxalate parent bands, which partially recovers in less than 10 ps, while a broad absorption appears in the 2200–2340 cm−1 region within their temporal resolution of 0.5 ps, which in ∼2 ps evolves into a triplet of bands centred at 2290, 2315 and 2341 cm−1. Among these lines, the first two are attributed to hot ν3 band transitions, showing that the CO2 fragments are released with a high internal energy content. Their results suggest that in less than 0.5 ps a vibrationally-hot CO2 is born, but within the first 2 ps neither the parent molecule is fully reformed, nor the free CO2 species are fully created.
Straub et al.8 attributed the 1–2 ps time components to a branching due to a fast internal conversion, which involves roughly 25% to 35% of the initially photoexcited complexes, as inferred from the amplitude of the bleach recovery at 10 ps. This is remarkably close to the ∼25% loss of photoreduced molecules that we observe in our photoemission data, whose ∼2 ps time scale is observed on a purely electronic signal. Thus, based on ref. 8, one could conclude that right after excitation a branching occurs with ∼25–35% of the photoreduced molecules reforming the parent ferric species in ∼2 ps, followed by intramolecular electronic relaxation. We will see below that this is not the case.
Moreover, we note that the ∼2 ps time scale is also close to the ∼3 ps reported in the fs-XAS study by Ogi et al.,28 who observed a slight decrease of the edge red shift after its initial prompt shift of over 4 eV. Based on their results and on simulations, they proposed that photoexcitation of the LMCT state creates [FeII(C2O4)3]3−* which loses CO2 within 140 fs and then CO2˙− within 3 ps to generate a [FeII(C2O4)2]2− product. However, as mentioned by the same authors, if the photoexcited complex is vibrationally cooled on ultrafast time scales in the form of [(CO2˙)FeII(C2O4)2]3− it may not dissociate CO2 immediately. Since this species cannot be distinguished from [FeII(C2O4)2]2−, owing to similarities in their Fe K-edge shifts and Fe(II)–O bond lengths, the observed spectrum of long-lived components may contain some contribution from this radical complex. A possible loss of the second CO2˙− fragment within 2–3 ps is however excluded by the IR TA results of Straub et al.,8 since it would not result in a bleach recovery, but on the contrary it would double its amplitude. In addition, the mechanism suggested by Ogi et al.28 would not lead to any change of Fe(II)-related PES signals, which contradicts the present results.
The above scenario by Straub et al.8 might suggest that part (25–35%) of the formed Fe(II)-complexes remains long enough (∼2 ps) in a non-dissociative excited state to allow them to transfer the electron back to the ligand, reforming the parent ferric species, followed by ultrafast intramolecular electronic relaxation. This is reminiscent of the ultrafast PES results on ferric Fe(CN)6 in solution,31 in which the prompt LMCT (<80 fs) was followed by a much slower back electron transfer in ∼500 fs. However, in the following we exclude that the ∼2 ps component is an actual back electron transfer of the photoreduced molecules because: (a) it would imply a branching to two channels for which one (dissociation) is overwhelming. The ratio of rates of these two channels (<140 fs/2000 fs) should lead to a <7% population of the ∼2 ps channel, which is not borne out by the present and the transient IR results;8 (b) the scenario of a long-lived excited state (∼2 ps) is very unlikely as the general pattern for all transition metal complexes is that of an extremely fast intramolecular relaxation.4
Rather, in order to reconcile the IR and X-ray studies and our results, we propose that after prompt photoreduction of the Fe centre, the initial loss of CO2 from the reduced molecules occurs with unity quantum yield in <140 fs (based on the XAS studies by Ogi et al.28), and that 25–35% geminately recombine on a ∼2 ps time scale due the effects of the solvent.32 This is clear from the IR TA studies,8 as the free CO2 bands show a rise time of 1.5 to 2.5 ps and the ground state bleach recovers in about the same time scale. In this scenario, the ∼2 ps time constant is a rate determining step due to geminate recombination, which leads to a return to the ground state of the parent ferrioxalate molecule after ultrafast intermolecular relaxation. This is also consistent with the fs-XAS studies, as in time-resolved XAS the magnitude of the ionization edge shift depends on the excitation yield,28,30 therefore a decrease of 25–35% of the initially excited molecules will inevitably lead to a decrease of the edge red shift, as actually observed.
In the above picture, it is clear that photoreduction precedes and triggers release of the CO2 ligand fragment. The latter necessitates the rupture of two bonds, namely, one of the two Fe–O bonds and the intra-oxalate ligand C–C bond. The 263 nm excitation deposits a total energy of 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (450 kJ mol−1) into the system and the observation of vibrationally hot CO2 fragments, carrying away ∼7000 cm−1 in the form of internal vibrational (probably also rotational) energy, implies that there is still a large surplus of energy for impulsive bond breaking. Density functional theory (DFT) geometry optimization were carried out on the LMCT state by Ogi et al.,28 indicating that the C–C bond of the reduced ligand weakens and dissociates, while the Fe(II)–O bond is elongated to arrive at the surface crossing between the excited and the ground electronic states. They considered other intermediates but they seem unlikely in view of the rearrangements they imply prior to releasing the CO2 ligand, which would not be compatible with a fast dissociation.
000 cm−1 (450 kJ mol−1) into the system and the observation of vibrationally hot CO2 fragments, carrying away ∼7000 cm−1 in the form of internal vibrational (probably also rotational) energy, implies that there is still a large surplus of energy for impulsive bond breaking. Density functional theory (DFT) geometry optimization were carried out on the LMCT state by Ogi et al.,28 indicating that the C–C bond of the reduced ligand weakens and dissociates, while the Fe(II)–O bond is elongated to arrive at the surface crossing between the excited and the ground electronic states. They considered other intermediates but they seem unlikely in view of the rearrangements they imply prior to releasing the CO2 ligand, which would not be compatible with a fast dissociation.
The effect of the solvent is not trivial here as it is unlikely to form a “cage” with clear-cut contours around the solute. Indeed, in the case of aqueous [Ru(bpy)3]2+ or [Fe(bpy)3]2+ (bpy = bipyridine) complexes, the first aqueous solvation shell was shown by Quantum Mechanical/Molecular Mechanics (QMMM) simulations to consist of intercalated water molecules.41 Ferrioxalate has a similar structure and is bulkier, as the Fe–O bond distances28 are larger than the Fe–N ones. In addition, the metal is ferric, while in [Fe(bpy)3]2+ it is ferrous. It is therefore highly likely that the same intercalation of solvent molecules occurs in the case of ferrioxalate. Therefore, the conventional view of the cage effect where departing fragments recoil against the cage walls and recombine is not applicable here.42 Although rapid fragment release into the solvent in the case of photoexcited molecular complexes with possible intercalated solvent molecules have been reported for ferrous Fe(CN)6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ,43,44 Mn(CO)3(Rbpy)Br (ligand Rbpy, where R = tBu, H, CF3, NO2)45 and Mn2(CO)10,46 the present case shows that the CO2 fragments, although promptly generated in <140 fs, require ∼2 ps to appear in the solvent. Rather, the latter time scale implies that some form of rearrangement of the solvent species occurs around the photoexcited solute prior to fragment release into the solvent. The nature of this rearrangement is unclear and the fact that the initial excitation is an LMCT one may play a role, as it generates a dipole in the solvent. This is reminiscent of the observations47 on solvated [Re(Cl)(CO)3(N,N)] and [Re(imidazole)(CO)3(N,N)]+ for which time scales of several ps were reported in the build-up of the final MLCT state, even though the electron transfer process is in itself prompt.
,43,44 Mn(CO)3(Rbpy)Br (ligand Rbpy, where R = tBu, H, CF3, NO2)45 and Mn2(CO)10,46 the present case shows that the CO2 fragments, although promptly generated in <140 fs, require ∼2 ps to appear in the solvent. Rather, the latter time scale implies that some form of rearrangement of the solvent species occurs around the photoexcited solute prior to fragment release into the solvent. The nature of this rearrangement is unclear and the fact that the initial excitation is an LMCT one may play a role, as it generates a dipole in the solvent. This is reminiscent of the observations47 on solvated [Re(Cl)(CO)3(N,N)] and [Re(imidazole)(CO)3(N,N)]+ for which time scales of several ps were reported in the build-up of the final MLCT state, even though the electron transfer process is in itself prompt.
In summary, combining our results and those of transient IR8 and ultrafast X-ray absorption spectroscopy,28 we propose the following initial sequence of events in the reaction scheme of photoexcited ferrioxalate:
Conclusions
We have performed ultrafast photoelectron spectroscopy (PES) on aqueous ferrioxalate solution to study its electronic dynamics upon 263 nm excitation. Photoemission signals from the Fe 3d orbitals were characterised in steady-state and transient PES. Clear spectral features are assigned to ferric and to photogenerated ferrous species. The oxidation state change of the metal centre has been monitored with femtosecond resolution, pointing to a prompt (<30 fs) metal photoreduction by electron transfer from the ligand. This demonstrates the LMCT nature of the photoexcited electronic state of the solvated ferrioxalate. Following this, we observe a loss of about 25% of the population of reduced species in ∼2 ps. This observation cannot be attributed to a back electron transfer, which follows a reaction branching. Rather, combining the results from recent ultrafast X-ray absorption spectroscopy28 and transient infrared absorption,8 we propose a picture of the ensuing dynamics which assumes that: (a) photoreduced molecules undergo CO2 ligand dissociation with unity quantum yield; (b) about 25–35% of these undergo geminate recombination due to solvent effects, but we rule out a simple caging of fragments. Because the fragments have translationally thermalised during the ∼2 ps time lag, the recombination must most likely populate the ground state of the ferric parent species. This interpretation lifts some of the discrepancies regarding the initial events that arose between the fs X-ray and the infrared TA studies. The ensuing processes at later times are well captured by these methods, in particular, concerning the structural transformations. The origin of the above-unity quantum yield of the photoinduced reaction lies in the fact that the 65–75% of dissociated molecules survive over long time, releasing CO2˙− fragments in less than 1 ns,8 which undergo subsequent reduction reaction with unphotolysed ferrioxalate molecules. The present work shows how the combination of ultrafast PES, sensitive to the electronic structure, and ultrafast X-ray and IR tools, sensitive to the electronic and molecular structure, allow a complete picture of the dynamics characterising metal complexes.Data availability
The analysed data related to the figures here displayed are available through this Repository http://10.24435/materialscloud:n8-5e.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We want to thank Oliviero Cannelli for interesting and fruitful discussions. This work was supported by the Swiss NSF via the NCCR:MUST and grants 206021_145057 and 206021_182994, and by the European Research Council Advanced Grant H2020 ERCEA 695197 DYNAMOX.References
- J. J. Pignatello, E. Oliveros and A. MacKay, Advanced Oxidation Processes for Organic Contaminant Destruction Based on the Fenton Reaction and Related Chemistry, Crit. Rev. Environ. Sci. Technol., 2006, 36, 1–84 CrossRef CAS.
- I. Pozdnyakov, P. Sherin, N. Bazhin, V. Plyusnin and V. V. Voevodsky, [Fe(Ox)3]3− complex as a photodegradation agent at neutral pH: Advances and limitations, Chemiosphere, 2018, 195, 839–846 CrossRef CAS PubMed.
- J. Chen and W. R. Browne, Photochemistry of iron complexes, Coord. Chem. Rev., 2018, 374, 15–35 CrossRef CAS.
- M. Chergui, Ultrafast Photophysics of Transition Metal Complexes, Acc. Chem. Res., 2015, 48, 801–808 CrossRef CAS PubMed.
- E. Zhang and K. J. Gaffney, Mechanistic studies of photoinduced spin crossover and electron transfer in inorganic complexes, Acc. Chem. Res., 2015, 48, 1140–1148 CrossRef PubMed.
- M. Chergui, Ultrafast photophysics and photochemistry of iron hexacyanides in solution: Infrared to X-ray spectroscopic studies, Coord. Chem. Rev., 2018, 372, 52–65 CrossRef CAS.
- C. Weller, S. Horn and H. Herrmann, Photolysis of Fe(III) carboxylato complexes: Fe(II) quantum yields and reaction mechanisms, J. Photochem. Photobiol., A, 2013, 268, 24–36 CrossRef CAS.
- S. Straub, P. Brünker, J. Lindner and P. Vöhringer, Femtosecond infrared spectroscopy reveals the primary events of the ferrioxalate actinometer, Phys. Chem. Chem. Phys., 2018, 20, 21390 RSC.
- A. J. Allmand and W. W. Webb, The Photolisis of Potassium Ferraioxalate Solutions. Part I. Experimental, J. Chem. Soc., 1929, 1518–1531 RSC.
- R. Livingston, Photochemical oxidation of oxalic acid sensitized by ferric ion, J. Chem. Phys., 1940, 44, 601–611 CrossRef CAS.
- C. A. Parker, A new sensitive chemical actinometer - I. Some trials with potassium ferrioxalate, Proc. R. Soc. London, Ser. A, 1953, 220, 104–116 Search PubMed.
- C. A. Parker, Induced autoxidation of oxalate in relation to the photolysis of potassium ferrioxalate, Trans. Faraday Soc., 1954, 50, 1213–1221 RSC.
- C. G. Hatchard and C. A. Parker, A new sensitive chemical actinometer. Potassium ferrioxalate as a standard chemical actinometer, Proc. R. Soc. London, Ser. A, 1956, 235, 518–536 CAS.
- C. A. Parker and C. G. Hatchard, Photodecomposition of Complex Oxalates. Some Preliminary Experiments by Flash Photolysis, J. Phys. Chem., 1959, 63, 22–26 CrossRef CAS.
- G. C. O'neil, et al., Ultrafast Time-Resolved X-ray Absorption Spectroscopy of Ferrioxalate Photolysis with a Laser Plasma X-ray Source and Microcalorimeter Array, J. Phys. Chem. Lett., 2017, 8, 1099–1104 CrossRef PubMed.
- S. Goldstein and J. Rabani, The ferrioxalate and iodide-iodate actinometers in the UV region, J. Photochem. Photobiol., A, 2008, 193, 50–55 CrossRef CAS.
- J. Lee and H. H. Seliger, Quantum Yield of the Ferrioxalate Actinometer, J. Chem. Phys., 1964, 40, 519–523 CrossRef CAS.
- B. P. Lever, Charge Transfer Spectra of Transition Metal Complexes, J. Chem. Educ., 1974, 51, 612–616 CrossRef.
- J. Šima and J. Makáňová, Photochemistry of iron(III) complexes, Coord. Chem. Rev., 1997, 160, 161–189 CrossRef.
- S. G. Ionescu and T. Oncescu, Photolisis of K3[Fe(C204)3] in Dimethylformamide, J. Photochem., 1983, 23, 45–50 CrossRef CAS.
- H. J. Kuhn, S. E. Braslavsky and R. Schmidt, Chemical Actinometry (IUPAC Technical Report), Pure Appl. Chem., 2004, 76, 2105–2146 CAS.
- B. A. DeGraff and G. D. Cooper, On the Photochemistry of the Ferrioxalate System, J. Phys. Chem., 1971, 75, 2897–2902 CrossRef CAS.
- J. I. H. Patterson and S. P. Perone, Spectrophotometric and electrochemical studies of flash-photolyzed trioxalatoferrate(III), J. Phys. Chem., 1973, 77, 2437–2440 CrossRef CAS.
- J. Chen, H. Zhang, I. V. Tomov and P. M. Rentzepis, Electron Transfer Mechanism and Photochemistry of Ferrioxalate Induced by Excitation in the Charge Transfer Band, Inorg. Chem., 2008, 47, 2024–2032 CrossRef CAS PubMed.
- H. Zhang, J. Chen, I. V. Tomov, A. S. Dvornikov and P. M. Rentzepis, Photoelectron Detachment and Solvated Electron Dynamics of the Cobalt(III) and Iron(III) Oxalato Complexes, J. Phys. Chem. A, 2007, 111, 11584–11588 CrossRef CAS PubMed.
- J. Chen, H. Zhang, I. V. Tomov and P. M. Rentzepis, Electron Transfer Mechanism and Photochemistry of Ferrioxalate Induced by Excitation in the Charge Transfer Band, Inorg. Chem., 2008, 47, 2024–2032 CrossRef CAS PubMed.
- I. P. Pozdnyakov, O. V. Kel, V. F. Plyusnin, V. P. Grivin and N. M. Bazhin, New Insight into Photochemistry of Ferrioxalate, J. Phys. Chem. A, 2008, 112, 8316–8322 CrossRef CAS PubMed.
- Y. Ogi, et al., Ultraviolet photochemical reaction of ferrioxalate in aqueous solutions studied by femtosecond time-resolved X-ray absorption spectroscopy using an X-ray free electron laser, Struct. Dyn., 2015, 2, 034901 CrossRef CAS PubMed.
- M. Kubin, et al., Probing the oxidation state of transition metal complexes: a case study on how charge and spin densities determine Mn L-edge X-ray absorption energies, Chem. Sci., 2018, 9, 6813–6829 RSC.
- C. Bressler, R. Abela and M. Chergui, Exploiting EXAFS and XANES for time-resolved molecular structures in liquids, Z. Kristallogr., 2008, 223, 307–321 CAS.
- J. Ojeda, C. A. Arrell, L. Longetti, M. Chergui and J. Helbing, Charge-transfer and impulsive electronic-to-vibrational energy conversion in ferricyanide: Ultrafast photoelectron and transient infrared studies, Phys. Chem. Chem. Phys., 2017, 19, 17052–17062 RSC.
- J. Franck and E. Rabinowitsch, Some remarks about free radicals and the photochemistry of solutions, Trans. Faraday Soc., 1934, 120–130 RSC.
- C. A. Arrell, et al., A simple electron time-of-flight spectrometer for ultrafast vacuum ultraviolet photoelectron spectroscopy of liquid solutions, Rev. Sci. Instrum., 2014, 85, 103117 CrossRef CAS PubMed.
- J. Ojeda, C. A. Arrell, J. Grilj, F. Frassetto, L. Mewes, H. Zhang, F. van Mourik, L. Poletto and M. Chergui, Harmonium: A pulse preserving source of monochromatic extreme ultraviolet (30–110 eV) radiation for ultrafast photoelectron spectroscopy of liquids, Struct. Dyn., 2016, 3, 023602 CrossRef CAS PubMed.
- C. A. Arrell, J. Ojeda, L. Longetti, A. Crepaldi, S. Roth, G. Gatti, A. Clark, F. Van Mourik, M. Drabbels, M. Grioni and M. Chergui, Harmonium: An Ultrafast Vacuum Ultraviolet Facility, Chimia, 2017, 71, 268–272 CrossRef CAS PubMed.
- N. Preissler, F. Buchner, T. Schultz and A. Lübcke, Electrokinetic charging and evidence for charge evaporation in liquid microjets of aqueous salt solution, J. Phys. Chem. B, 2013, 117, 2422–2428 CrossRef CAS PubMed.
- C. Arrell, J. Ojeda, L. Mewes, J. Grilj, F. Frassetto, L. Poletto, F. van Mourik and M. Chergui, Laser-Assisted Photoelectric Effect from Liquids, Phys. Rev. Lett., 2016, 117, 143001 CrossRef CAS PubMed.
- L. Longetti, et al., Photoemission from non-polar aromatic molecules in the gas and liquid phase, Phys. Chem. Chem. Phys., 2020, 22, 3965–3974 RSC.
- B. Winter, R. Weber, W. Widdra, M. Dittmar, M. Faubel and I. V. Hertel, Full Valence Band Photoemission from Liquid Water Using EUV Synchrotron Radiation, J. Phys. Chem. A, 2004, 108, 2625–2632 CrossRef CAS.
- R. Seidel, S. Thürmer, J. Moens, P. Geerlings, J. Blumberger and B. Winter, Valence photoemission spectra of aqueous Fe2+/3+ and [Fe(CN)6]4−/3− and their interpretation by DFT calculations, J. Phys. Chem. B, 2011, 115, 11671–11677 CrossRef CAS PubMed.
- M. E. Moret, I. Tavernelli, M. Chergui and U. Rothlisberger, Electron localization dynamics in the triplet excited state of [Ru(bpy)3]2+ in aqueous solution, Chem. – Eur. J., 2010, 16, 5889–5894 CrossRef CAS PubMed.
- V. A. Apkarian and N. Schwentner, Molecular Photodynamics in Rare Gas Solids, Chem. Rev., 1999, 99, 1481–1514 CrossRef CAS PubMed.
- T. J. Penfold, M. Reinhard, M. H. Rittmann-Frank, I. Tavernelli, U. Rothlisberger, C. J. Milne, P. Glatzel and M. Chergui, X-ray Spectroscopic Study of Solvent Effects on the Ferrous and Ferric Hexacyanide Anions, J. Phys. Chem. A, 2014, 118, 9411–9418 CrossRef CAS PubMed.
- M. Reinhard, G. Auböck, N. A. Besley, I. P. Clark, G. M. Greetham, M. W. Hanson-Heine, R. Horvath, T. S. Murphy, T. J. Penfold, M. Towrie, M. W. George and M. Chergui, Photoaquation Mechanism of Hexacyanoferrate(II) Ions: Ultrafast 2D UV and Transient Visible and IR Spectroscopies, J. Am. Chem. Soc., 2017, 139, 7335–7347 CrossRef CAS PubMed.
- W. C. Henke, C. J. Otolski, W. N. Moore, C. G. Elles and J. D. Blakemore, Ultrafast Spectroscopy of [Mn(CO)3] Complexes: Tuning the Kinetics of Light-Driven CO Release and Solvent Binding, Inorg. Chem., 2020, 59, 2178–2187 CrossRef CAS PubMed.
- J. Z. Zhang and C. B. Harris, Photodissociation dynamics of Mn2(CO)10 in solution on ultrafast time scales, J. Chem. Phys., 1991, 95, 4024–4032 CrossRef CAS.
- A. El Nahhas, C. Consani, A. M. Blanco-Rodríguez, K. M. Lancaster, O. Braem, A. Cannizzo, M. Towrie, I. P. Clark, S. Záliš, M. Chergui and A. Vlček, Ultrafast excited-state dynamics of rhenium(I) photosensitizers Re(Cl)(CO)3(N,N) and [Re(imidazole)(CO)3(N,N)]+: Diimine effects, Inorg. Chem., 2011, 50, 2932–2943 CrossRef CAS PubMed.
- M. Chergui, Ultrafast molecular photophysics in the deep-ultraviolet, J. Chem. Phys., 2019, 150, 070901 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp02872c |
| ‡ Current address: Laboratory for Condensed Matter, Paul Scherrer Institut, CH-5232 Villigen, Switzerland. |
| This journal is © the Owner Societies 2021 |