DOI:
10.1039/D4RA04300F
(Review Article)
RSC Adv., 2024,
14, 23184-23203
Computational study of the dimerization of glyphosate: mechanism and effect of solvent†
Received
12th June 2024
, Accepted 9th July 2024
First published on 23rd July 2024
Abstract
A computational study on the structure and stability of different series of glyphosate (Glyph) dimers comprising nonionized (N) and zwitterionic structures (Z) for neutral monomers, followed by an analysis of energetics of Glyph dimerization process have been performed by means of quantum chemical calculations in different media. Optimized geometries for energy minima, as well as relative potential and free energies of the possible various conformers of each series of Glyph dimer were computed as a function of the medium at B3LYP-D3/6-311++G(2d,2p) level. The solvation model based on density (SMD) is employed for all solution phase computations. Non-ionized dimers (DN), anion–cation (AC) and either zwitterion–zwitterion (DZP and DZC) or non-ionized-phosphonate zwitterion (NZP) ionized neutral forms of Glyph dimer are predicted to exist in the gas phase and in solution in large contrast to Glyph monomers. The DZC dimer form exhibiting a centrosymmetric arrangement of two carboxylate zwitterion units was found to be the most stable dimer structure in all media. In aqueous solution, the DZP and AC dimer type structures are significantly stabilized by hydration. The tautomerisms between DZC, DZP and AC dimer type structures have been investigated in the gas phase and in solution. The DZC type structures are more prone to experience proton transfer in water than in the gas phase and in cyclohexane. The mechanism for the tautomerization process in neutral ionized Glyph dimers proceeds via two direct proton transfer paths: DZP ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC
AC ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC. Results show that solvents play a key role in modulating the energetics of the dimerization process of Glyph. Solvation in cyclohexane, favors the dimerization process however, hydration opposed it. In aqueous solution, the mechanism of the dimerization of Glyph from its phosphonate zwitterionic monomer form (ZP) could be described by a set of equilibria including direct proton transfer paths as follows: 2ZP
DZC. Results show that solvents play a key role in modulating the energetics of the dimerization process of Glyph. Solvation in cyclohexane, favors the dimerization process however, hydration opposed it. In aqueous solution, the mechanism of the dimerization of Glyph from its phosphonate zwitterionic monomer form (ZP) could be described by a set of equilibria including direct proton transfer paths as follows: 2ZP ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZP
DZP ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC
AC ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC. According to our results, in aqueous solution, DZC Glyph dimers and their corresponding DZP and AC tautomers should be present in higher concentration than phosphonate zwitterionic Glyph monomers for high Glyph concentration, a fact that seems controversial in the literature.
DZC. According to our results, in aqueous solution, DZC Glyph dimers and their corresponding DZP and AC tautomers should be present in higher concentration than phosphonate zwitterionic Glyph monomers for high Glyph concentration, a fact that seems controversial in the literature.
1. Introduction
Glyphosate [N-(phosphonomethyl)glycine] (Scheme 1), is known to be the world's most successful commercial broad spectrum herbicide, being the active ingredient of the widely used weed control agent Roundup (registered mark Monsanto Co).1–7 Numerous physiological, biochemical and genetic experiments have demonstrated that Glyph inhibits the activity of the enzyme 5-enolpyruvylshikimate EPSPS, the key enzyme in the shikimate acid pathway.2,8–10 This biochemical mode of action was shown to be unique for Glyph-based herbicides and no other classes of commercial herbicides are known to inhibit EPSP Synthase or other enzymes in this important pathway. The key component of the biological activity of Glyph as EPSPS inhibitor was suggested to be due to its conformational flexibility in accordance with extensive structure–activity relationship studies.11 A fully understanding of the structural chemistry of Glyph is, thus, of significant importance not only from the point of view of fundamental research but also for the development and the rational design of Glyph-tolerant variants and for the target synthesis of new herbicides. Moreover, knowing the behavior of Glyph at a molecular level is important to be able to design new removal techniques and new detection methods taking into account the serious consequences of water pollution12 and the deleterious Glyph-induced oxidative stress in plants.13–15 In this context, considerable knowledge on the molecular structure and complex chemistry of Glyph was gained through the determination and harnessing of X-ray crystallography data of Glyph16,17 and some of its complexes derivatives18–25 over the four last decades. This compound was determined to exist in the zwitterionic form with a phosphonate proton delocalized on the amino nitrogen.16,17 As a ligand for metal complexation, the glyphosate molecule was shown to be ambivalent with the potential for formation of unidentate,21,22 bidentate and tridentate co-ordination19,22 via 5-membered chelate rings, and additionally for polymer association through the peripheral carboxylate and phosphonate groups.18,22–25 Experimental studies addressing the solution nature of Glyph were scares.26–31 A number of studies showed that Glyph forms a pH-dependent zwitterion structure in aqueous solution.27,28,32 The salts18,20,25,33,34 and coordination complexes of Glyph have been the subject of some interest in solution and several examples are available in the literature.8,16,19,22,34–36 The affinities of Glyph for metal ions,36 the stoichiometries of the metal chelates formed36 and their equilibrium constant of formation in solution have been investigated in solution.34–36 These studies have established the tendency of Glyph to form 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 chelates and dimer species with most divalent metal ions when the ligand concentration is doubled.36 The interaction of the herbicide with soil components37–39 such as clay minerals,40–43 oil organic matter44 and soil humic45 molecules has been also the matter of a number of studies. Phosphonate group was found to be mainly responsible for the hydrogen-bonding interaction between Glyph and soil components.39 When the herbicide is in contact with water-soluble HA, IR and fluorescence spectroscopies provided evidence for the formation of HA–Glyph complexes at different pH.28,46 All these experimental studies have provided valuable information on the coordination modes of Glyph in solution but a thorough understanding the behavior of Glyph and its aggregation state in water solution is still lacking. Likewise, several studies focused on the application of the IR spectroscopic techniques27,28,33 to study the acid solution equilibrium of Glyph in water solution have suggested the presence of both monomer and dimer of Glyph at low pH values, however structural molecular details of the dimer are not known. Additionally, corona discharge ion mobility spectrometry (CD-IMS)47 recently applied for direct analysis of Glyph in drinking water at different temperatures have detected the presence of a pic which was attributed to the Glyph dimer, but this attribution had not been clearly confirmed up to now in the literature. As a consequence, the presence of dimers in aqueous solution is still experimentally under debate and data related to dimer complexes of the most widespread herbicide in aqueous solution is poorly known if not absent. Moreover, several recent studies48,49 have pointed out the existence of a close relationship between properties of some herbicide dimers and their bioactivity. They demonstrated that herbicide dimers had higher bioactivities and/or dual modes of action than their corresponding monomers.49 The properties of Glyph dimeric herbicide are not studied till now and therefore, the presence of a structure–activity relationships for Glyph dimer could not be excluded. Theoretically, several investigations have been devoted to study the structure of Glyph monomer either in the gas phase and in aqueous solution.50–59 In particular, the relative stability of neutral (non-ionized) and zwitterionic (ionized) forms has been the object of intense debate. Perhaps, the most systematic and detailed structural study on the Glyph monomer was reported by our researcher group60 at various quantum chemical levels of ab initio and DFT theories, in the gas phase and in aqueous solution. We showed that non-ionized neutral structures exist only in the gas phase but the zwitterionic form is unstable in vacuo at all levels of theory. In aqueous solution, the integral equation formalism polarizable continuum model (IEFPCM) using the standard UFF radii cavity failed to correctly predict the stabilization of the zwitterionic form with respect to the non-ionized neutral form in aqueous solution. However, calculation with the density based solvation model (SMD) was well consistent with the experimental findings and led to the identification of the phosphonate zwitterionic (ZP) structure as the global minimum energy in aqueous solution.29–31,61,62 Our own results have been confirmed, subsequently, by a more recent paper55 dealing with the Glyph deprotonation in solution. The latter study had supported the use of the SMD-B3LYP-D3/6-311++G(2d,2p) as the most reliable level of calculation to predict accurately the structure of Glyph monomer and its deprotonation reaction sites in water solution. Regarding Glyph dimers, they have received some theoretical attention too,47,63 although much less than the monomer. Previous quantum chemical studies on Glyph dimers were restricted to proton-bound Glyph dimer in the gas phase.47 An other recent investigation63 motivated by the observation of two high pressure phase transitions by Raman spectroscopy, allowed the prediction of a new crystal structure of Glyph consisting of periodic repetition of pairs of zwitterion forms sustained by N–H⋯O H-bonds using crystal modeling. Moreover, other theoretical studies57,58 concluded that dimers of Glyph are stabilized by divalent and trivalent metal cations, which is feasible in biological systems. But, most of them considered the cationic and/or the mono-anion dimer complex structures57 with Glyph molecule as anion and dianion in the gas phase and/or in solution. Despite these few reports, theoretical or experimental structural studies dealing with the homo- and heterodimers neutral forms of Glyph with non-ionized and/or zwitterion forms in the gas phase and in solution are absent. In this work, quantum mechanical calculations were carried out trying to address the following fundamental questions: (1) are there energy minima for ionized forms of Glyph dimers (zwitterion–zwitterion, non-ionized–zwitterion, anion–cation) and if yes, what are the relative stabilities of the ionized and non-ionized forms, (2) what is the influence of the medium (gas phase, nonpolar solvent, water) on both structure and stability, and (3) what is the free energy and the mechanism of dimer association of Glyph in vacuum and in solution?
1 chelates and dimer species with most divalent metal ions when the ligand concentration is doubled.36 The interaction of the herbicide with soil components37–39 such as clay minerals,40–43 oil organic matter44 and soil humic45 molecules has been also the matter of a number of studies. Phosphonate group was found to be mainly responsible for the hydrogen-bonding interaction between Glyph and soil components.39 When the herbicide is in contact with water-soluble HA, IR and fluorescence spectroscopies provided evidence for the formation of HA–Glyph complexes at different pH.28,46 All these experimental studies have provided valuable information on the coordination modes of Glyph in solution but a thorough understanding the behavior of Glyph and its aggregation state in water solution is still lacking. Likewise, several studies focused on the application of the IR spectroscopic techniques27,28,33 to study the acid solution equilibrium of Glyph in water solution have suggested the presence of both monomer and dimer of Glyph at low pH values, however structural molecular details of the dimer are not known. Additionally, corona discharge ion mobility spectrometry (CD-IMS)47 recently applied for direct analysis of Glyph in drinking water at different temperatures have detected the presence of a pic which was attributed to the Glyph dimer, but this attribution had not been clearly confirmed up to now in the literature. As a consequence, the presence of dimers in aqueous solution is still experimentally under debate and data related to dimer complexes of the most widespread herbicide in aqueous solution is poorly known if not absent. Moreover, several recent studies48,49 have pointed out the existence of a close relationship between properties of some herbicide dimers and their bioactivity. They demonstrated that herbicide dimers had higher bioactivities and/or dual modes of action than their corresponding monomers.49 The properties of Glyph dimeric herbicide are not studied till now and therefore, the presence of a structure–activity relationships for Glyph dimer could not be excluded. Theoretically, several investigations have been devoted to study the structure of Glyph monomer either in the gas phase and in aqueous solution.50–59 In particular, the relative stability of neutral (non-ionized) and zwitterionic (ionized) forms has been the object of intense debate. Perhaps, the most systematic and detailed structural study on the Glyph monomer was reported by our researcher group60 at various quantum chemical levels of ab initio and DFT theories, in the gas phase and in aqueous solution. We showed that non-ionized neutral structures exist only in the gas phase but the zwitterionic form is unstable in vacuo at all levels of theory. In aqueous solution, the integral equation formalism polarizable continuum model (IEFPCM) using the standard UFF radii cavity failed to correctly predict the stabilization of the zwitterionic form with respect to the non-ionized neutral form in aqueous solution. However, calculation with the density based solvation model (SMD) was well consistent with the experimental findings and led to the identification of the phosphonate zwitterionic (ZP) structure as the global minimum energy in aqueous solution.29–31,61,62 Our own results have been confirmed, subsequently, by a more recent paper55 dealing with the Glyph deprotonation in solution. The latter study had supported the use of the SMD-B3LYP-D3/6-311++G(2d,2p) as the most reliable level of calculation to predict accurately the structure of Glyph monomer and its deprotonation reaction sites in water solution. Regarding Glyph dimers, they have received some theoretical attention too,47,63 although much less than the monomer. Previous quantum chemical studies on Glyph dimers were restricted to proton-bound Glyph dimer in the gas phase.47 An other recent investigation63 motivated by the observation of two high pressure phase transitions by Raman spectroscopy, allowed the prediction of a new crystal structure of Glyph consisting of periodic repetition of pairs of zwitterion forms sustained by N–H⋯O H-bonds using crystal modeling. Moreover, other theoretical studies57,58 concluded that dimers of Glyph are stabilized by divalent and trivalent metal cations, which is feasible in biological systems. But, most of them considered the cationic and/or the mono-anion dimer complex structures57 with Glyph molecule as anion and dianion in the gas phase and/or in solution. Despite these few reports, theoretical or experimental structural studies dealing with the homo- and heterodimers neutral forms of Glyph with non-ionized and/or zwitterion forms in the gas phase and in solution are absent. In this work, quantum mechanical calculations were carried out trying to address the following fundamental questions: (1) are there energy minima for ionized forms of Glyph dimers (zwitterion–zwitterion, non-ionized–zwitterion, anion–cation) and if yes, what are the relative stabilities of the ionized and non-ionized forms, (2) what is the influence of the medium (gas phase, nonpolar solvent, water) on both structure and stability, and (3) what is the free energy and the mechanism of dimer association of Glyph in vacuum and in solution?
 |
| | Scheme 1 Schematic representation of Glyph molecule: N is the non-ionized form, ZP and ZC are the phosphonate and the carboxylate zwitterionic neutral forms, respectively. | |
2. Computational methods
Quantum chemical calculations were carried out using the Gaussian09 software package (revision D.01).64 A wide set of suitable geometries of neutral Glyph dimers were built with the most stable non-ionized (N) and the ionized zwitterionic monomers (ZP and ZC) optimized in aqueous solution in our previous work.60 We considered the 13 lowest energy structures of Glyph monomer60 (comprising 5 ZP and 4 of each ZC and N structure-types) that are within a relative Gibbs free energy (ΔG) not exceeding 1.5 kcal mol−1 between conformers of the same structure-type. Initial geometries of ionized and non-ionized neutral Glyph dimers were built by joining the 13 selected lowest energy structures of Glyph monomers in all combinations: nonionized–nonionized (DN), nonionized-phosphonate zwitterion (NZP), nonionized-carboxylate zwitterion (NZC), phosphonate zwitterion-phosphonate zwitterion (DZP), carboxylate zwitterion-carboxylate zwitterion (DZC), phosphonate zwitterion-carboxylate zwitterion (ZPZC) and anion–cation (AC). For each of these dimers, we have built up to 50 different geometries, ensuring the maximum number of hydrogen bonded interactions between the carboxylic, phosphonate and amine acid groups when possible. We have taken into account: (i) different possibilities to form diverse kinds of inter-monomeric H-bonds: (OP)O–H⋯−O(CO), (OP)O–H⋯O(CO), (OP)O–H⋯−O(PO), (OC)O–H⋯−O(PO), (OC)O–H⋯O(CO), N+–H⋯−O(CO), N+–H⋯−O(PO) and N+–H⋯O(OC) and (ii) internal rotations around P–C, N–C and C–C bonds in each monomer. Since the number of degrees of freedom is relatively large, we cannot rigorously exclude the existence of other energy minima on the potential energy surface. Nevertheless, the dimer structures reported here appear to be the most plausible ones, since we took a range of a maximum of 6 kcal mol−1 on the relative stability between conformers for each structure-type. Calculations have been performed at the Density functional level of theory (DFT) by means of B3LYP functional and using the 6-311++G(2d,2p) basis set. The dispersion correction to DFT is modelled by the well-established Grimme's D3 empirical dispersion scheme.65 Computations in solution were performed in three different environments: in vacuum, in cyclohexane solution, and in aqueous solution. The implicit solvation model based on density (SMD)66 with the corresponding default radii, the so-called intrinsic Coulomb radii (iC) was employed to account for solvation effects. The SMD SCRF model combined with B3LYP-D3/6-311++G(2d,2p) level represents an excellent approach to model structure of Glyph in solution, as it has been shown60 to provide (i) results comparable to MP2/6-311++(2d,2p) calculations and (i) accurate values on calculated energy differences between non-ionized (N) and zwitterionic (ZP) Glyph monomer, in accordance with experimental findings.29–31 Concerning the choice of the basis set, the use of the more extended 6-311++G(2d,2p) basis set is shown to be highly efficient in accurately predicting the experimentally observed structures of Glyph in aqueous solution. The performance of smaller basis set basis-set functions was tested and evaluated for Glyph monomer.60 Basis sets of double-ζ and triple-ζ quality used in a test run on geometry optimizations were less satisfactory. The addition of diffuse functions to a triple-ζ basis set was shown to be important and necessary to obtain accurate results on calculated energy differences between non-ionized and zwitterionic Glyph conformers, in agreement with experimental findings.29–31 The structures of all dimer systems were fully optimized in the gas phase, in aqueous and in cyclohexane solution. Geometry optimizations have been followed by harmonic vibrational frequencies computations, confirming the nature of the stationary points either as a minimum or transition state. Non-electrostatic solvent contributions arising from short-range interactions between the solute and solvent molecules in the first solvation shell, called the cavity–dispersion–solvent-structure (CDS) term, were taken in to account in the calculation since the computed energies of monomers60 were shown to be dependent on the cavity size, one of the major components of the non-electrostatic terms. The proton transfer mechanism between ionized species of Glyph dimers (DZC, DZP and AC) is studied at SMD-B3LYP-D3/6-311++G(2d,2p) level in the different environments (in the gas phase and in solution). We used the TS theory67 in order to estimate the forward and reverse barriers of the investigated intermolecular tautomerization processes between DZC and AC and between AC and DZP tautomers. IRC calculations68 were performed for all the pathways at the B3LYP-D3/6-311++G(2d,2p) level to confirm the reaction coordinates from transition states to stable products in the gas phase and in solution using the SMD66 solvation model. In order to compute dimerization energies, the structures for the non-ionized and zwitterionic Glyph monomer in the gas phase and water solution were taken from our previous work.60 A detailed conformational analysis of Glyph monomer in cyclohexane was performed at SMD-B3LYP-D3/6-311++G(2d,2p) in this work for the first time. The structures and energies of the most stable ionized (ZP and ZC) and non-ionized (N) neutral forms of Glyph monomer, optimized in cyclohexane were reported in ESI Fig. S1 and S5–S12.† Relative energies between ionized and non-ionized neutral Glyph monomer conformers in the gas phase, in cyclohexane and in aqueous solution were summarized in Table S1, in ESI.† The free energy of dimerization in solution (ΔG) was determined by the addition of the value of the free energy of dimerization in the gas phase (ΔGg) to the difference in the free energy of solvation between the monomers and the dimer (δΔGsolv). A correction term accounting for the change of reference state from gas phase to 1 M solution is added at last.
ΔG = ΔGg + δΔGsolv + RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(1/22.4) ln(1/22.4) |
| δΔGsolv = Gsolv. (dimer) − 2Gsolv. (monomer) |
3. Results and discussion
3.1. Conformers, energetics and solvation effects
The most stable structures obtained for each phase (gas, cyclohexane and water solution) and group of dimers (DN, NZ, DZC, DZP and AC) at the B3LYP-D3/6-311++G(2d,2p) level are depicted in Fig. 1–3. Their relative energies are listed in Table 1 and represented in Fig. 4a. Cartesian coordinates and energies of each Glyph dimer optimized in the gas phase and in cyclohexane and aqueous solution are reported in ESI, S13–S25, S26–S40 and S41–S71.† As it is shown from Table 1, energy minima for the neutral ionized zwitterion–zwitterion (DZ), nonionized–nonionized neutral (DN) and nonionized–zwitterion (NZ) structures of Glyph dimer are obtained in all media, even in the gas phase. A common structural feature of these dimers is that all the minima are head-to-tail dimers where the faces of Glyph molecules expose phosphonate groups and carboxylate functionality, as was shown in Fig. 1–3. The preferred geometries are significantly different depending on the media. Moreover, the striking result from these calculations is the fact that the carboxylate zwitterion–zwitterion (DZC1) homodimer is the most stable Glyph dimer structure both in the gas phase and in solution. These results obtained for the dimer are in contrast with those predicted for Glyph monomer60 which have predicted that the latter exist only in a non-ionized neutral (N) form in the gas phase. Note that there is a great resemblance between the gas phase and the nonpolar medium. Calculation produce the same DZC, DZP, AC, NZP and DN preferred structures in the gas phase and in cyclohexane solution. The electronic energy sequence of stability for the series of Glyph dimers in the gas phase is: DZC > DN > AC > NZP > DZP. SMD-B3LYP-D3 optimizations in cyclohexane reverse the stability of ionized NZP and non-ionized DN and provide an opposite trend in energy sequence as follows: DZC > AC ≅ DZP > NZP > DN. It is worth noting that the relative energies between non-ionized (DN) and ionized forms (either DZP or NZ and or AC) are quite different. Both the non-ionized DN and NZP forms are significantly disfavored with respect to the most stable DZC1 in cyclohexane. The opposite trends in the order of stability between the ionized and the non-ionized dimers in cyclohexane, could be caused by the large differences in the free solvation energy values (ΔGsolv.tot.). As it is seen from Table 2, all the ionized and non-ionized structures studied have favorable solvation free energy in cyclohexane (ΔGsolv.tot < 0), indicating a stabilization effect of solvent with respect to vacuum. The magnitudes of free solvation energies of ionized dimers (DZC, DZP and AC) are much larger than those of non-ionized neutral (DN) forms and are dominated by large electrostatic contributions. This is likely to be ascribed to the cyclohexane (C6H12) large molecular polarizability, a fundamental player of London dispersion interactions. As cyclohexane is non-polar solvent, the negative ΔGsolv.tot. values are due to the action of van der Waals electrostatic attractions among the solute molecule and surrounding solvent molecules whose magnitude overcomes the free energy cost for creating the cavity. We are not aware of any previous computational study providing estimates of ΔGsolv.tot. for Glyph in hydrophobic medium, so only limited comparisons69–73 can be carried out. Our calculation at SMD-B3LYP-D3/6-311++G(2d,2p) can be supported by the experimental findings and theoretical results on nonpolar solvation of many polar solutes in organic solvents.71–73 Interestingly, the behavior Glyph monomer and its dimer resembles that of several amino acid side chains solutes which indicates a favorable solvation (ΔGsolv.tot. < 0) in cyclohexane.70–73 Especially, our estimates of the solvation free energy in cyclohexane of carboxylate zwitterionic Glyph dimers (ΔGsolv.tot. in the range −16–19 kcal mol−1) are found in quantitative agreement with that (ΔGsolv.tot. = −20.5 kcal mol−1) computed for carboxylate zwitterionic glycine dimer69 at B3LYP and MP2 levels of theory using the 6-31+G(2df,2p) basis set. However, significant differences between aqueous phase-optimized structures and those obtained in the gas phase and cyclohexane solution are detected. As indicated in Table 1 and shown in Fig. 2 and 3, calculations provide more energy conformational minima for zwitterionic carboxylate (DZC), for zwitterionic phosphonate (DZP) and for anion–cation (AC) type structures of Glyph dimer in aqueous solution than in the gas phase and in non-polar medium (cyclohexane). New DZC, DZP and AC conformers, are found to be significantly populated in aqueous solution as shown in Fig. 4b. Several DZC type structures undergo reorientation of O–H and/or rotation around a bond skeleton of one Glyph monomer when going from gas phase and/or cyclohexane to aqueous solution and the reverse is also true. This is the case of DZC3 which collapses to DZC13 in aqueous solution by hydrogen reorientation. DZC6 also gives DZC8 in aqueous solution by rotation around C–N bond. However, DZC10, DZC11 and DZC12, all give DZC6 in the gas phase. A number of conformational minima display close energies in each DZC, DZP and AC series in aqueous solution, in contrast to the gas phase and nonpolar solution. Table 1 illustrates the dependency of the relative stability between ionized and non-ionized Glyph dimers on the dielectric constant of the solvent. As it is shown, the values obtained tend to increase in magnitude as the dielectric constant increase. Especially, the free energy difference between DZC and DN and between DZC and those containing N and Z monomers (NZP) increase significantly in absolute value, in aqueous solution (about twice with regard to those in cyclohexane). Despite these differences, all the ionized neutral dimers DZC, DZP, AC and NZP type structures tend to remain more stable than the non-ionized (DN) Glyph dimer structure in aqueous solution as also detected in cyclohexane. Comparison between solvation free energies in both solvents, we note, that there are several trends in the data that are immediately obvious. In all cases, the solvation energy rises (becomes more negative) as the dielectric constant of the solvent increases. All these quantities tend to be higher in magnitude than those corresponding in cyclohexane, being more than the thrice. This can be due to the fact that water is a polar solvent able to form hydrogen bonds in contrast to cyclohexane. Not surprisingly, the largest |ΔGsolv.| values are associated with ionized neutral zwitterion–zwitterion (DZC and DZP) and anion–cation (AC) type structures which can be engaged in multiple hydrogen bonds with water molecules. All the more, the absolute value of free hydration energies is significantly larger in ionized neutral Glyph dimers containing zwitterionic monomers (ZC and/or ZP or AC) than in non-ionized ones. This indicates that zwitterion-containing dimers are more stabilized by hydration than their non-ionized counterparts. The partitioning of the different contributions to solvation free energy reported in Table 2 confirm these findings. In fact, the results reveal the leading role of polarization represented by the electrostatic contribution (ΔGsolv.el.). The latter consists of a van der Waals contribution, essentially of the same magnitude in the two liquids, and a hydrogen bond contribution, whose magnitude is large in H2O and zero in cyclohexane (C6H12). The sequence of polarization of the different type structure of Glyph in water can be explained considering two main factors: (i) the charge separation within the system, favoring zwitterionic forms over non-ionic ones; and (ii) the geometry of the dimer, producing larger polarization energies when the most charged groups are external. The largest hydration energy corresponds to DZP dimers containing phosphonate ZP monomers, with anionic phosphonate group (POO−) are external. This allows solvation of phosphonate groups by water molecules, increasing dimer stability of dimer complex because of more favorable intermolecular interactions with water molecules. The situation is different for the ionized AC and DZC type structures (Fig. 2 and 3). Whereas two external phosphonates (POO−) appear in the most preferred geometries of DZP dimers, only one is displayed outside in AC structures and which disappear in DZC type structures (Fig. 2). This explains why the polarization energy is larger for the most stable conformer of DZP dimers than for DZC and AC ones (Table 2). All the ionized zwitterionic
and anion–cation dimer structures are more solvated than the non-ionized DN and NZP dimer structures. This is because NZP displays one charged (POO−) outside in contrast to DN which exhibits two externals non charged P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups. It may be noted that, all the calculated Glyph dimer free energies of hydration are seen very negative and fall within the range −42.4 kcal mol−1 (for non-ionized) to −81 kcal mol−1 (for ionized DZP). Of some importance is the comparable behavior of the zwitterionic glycine dimer69 and several zwitterionic amino acids70,73,74 in water solution. The data corresponding to the carboxylate zwitterion dimers, reported in Table 2, are remarkably similar to the value (ΔGsolv. = −66.3 kcal mol−1) computed for carboxylate zwitterionic glycine dimer in water solution.69 One may notes that these values obtained in the range −42–81 kcal mol−1 are in consonant to the estimate of −59 kcal mol−1 from the Onsager formula75,76 for the solvation free energy of a dipolar sphere. Our calculations showed that solvation properties are related in a very nearly fashion to the Onsager function, Fo, that in turn relates to the properties of the solvent.75,76 In fact, the increase of ΔGsolv.tot. by about more than the thrice of any species of DZC Glyph dimer from cyclohexane to water can be correlated is nearly a linear function of with the rise in the Onsager function Fo = (ε − 1)/(ε + 2),75,76 which is itself magnified by a factor of 3.4 when increases from 2 to 78. There is hence every reason to believe that the solvation model being applied here, while certainly not absolutely accurate in a quantitative sense, provide very reasonable approximations to the environments they are meant to reproduce. It may be noted that the estimation of non-electrostatic contribution arising from short-range interactions between the solute and solvent molecules in the first solvation shell, called the cavity–dispersion–solvent-structure (CDS) term, differ from cyclohexane to water. While Enonel. terms are negative and low in cyclohexane, they are positive and largely expected (in absolute values) in water solution. These results can be easily rationalized by the fact that water molecules are the smallest (a cyclohexane molecule has a van der Waals volume roughly 5 times larger than that of a water molecule) and so liquid water is characterized by the largest number density, which in turn increases the entropy loss associated with cavity creation, due to the solvent-excluded volume effect. As a consequence, the energy associated to cavity creation is larger to that in cyclohexane and thus non-electrostatic (CDS) contribution is positive and larger in water. Nevertheless, solvation free energy ΔGsolv in H2O (see Table 2) are found negative for all dimers, paralleling the situation in nonpolar medium C6H12. This may indicate that the free energy cost of cavity creation is not so large and the attractive solute–solvent energetic interactions (accounting also for hydrogen bonds) are able to overcome the free energy cost of cavity creation. These results are in line with experimental data71,77,78 and previous computational investigations of several polar amino acid side chain equivalents in cyclohexane solution and in water.70,72–74 Nonetheless, calculation reveal that the highest values of free energy of solvation (|ΔGsolv.| values) are not associated to the most stable solute in aqueous solution and in cyclohexane. As is shown in Table 1, the carboxylate zwitterionic dimer form DZC1 which is the most stable Glyph dimer do not experience the largest solvation (or polarization) in water and in cyclohexane solution. This indicates that several effects in addition to the polarization term are involved and counteract each other, even when effects on solvent are not considered explicitly. Among these effects, non-covalent intermolecular and intra-moleculecular hydrogen-bondings (H-bonds) may be important for structure selection and stability of Glyph dimers in different media. To elucidate the role of H-bonds, their structural features are inspected and criticized in the series of the five types of Glyph dimer structures displayed in Fig. 1–3. Structural analysis of the equilibrium structures affords a total of a maximum of seven short contacts characterizing H-bonds of each series of type of structure (DZC, DZP, AC, NZP, DN), which are classified in chemical classes belonging to three fundamental types: neutral H-bonds (HB) between two neutral groups, ionic H-bonds (IHB) between a neutral and charged group and zwitterionic H-bonds (ZHB) between two oppositely charged groups. Fig. 1–3, show that both O–H⋯−O and N+–H⋯O ionic H-bonds participate in stabilizing the IHB pattern which result in the formation of 8-membered rings (displaying O–H⋯−O) and 9-membered rings (establishing O–H⋯−O and N+–H⋯O) with different arrangements. ZHB consist of intramolecular and intermolecular N+–H⋯−O H-bonds through which 5- and 10- membered rings are formed. In Table 3 are collected the intermolecular and intramolecular bond distances (dO⋯H) characterizing the IHB, ZHB and HB for the most stable structures of each type (DZC, DZP, AC, NZP, DN) of Glyph dimer in different media. From the results obtained in Table 3, it is clear that the largest contributors to the stabilization of the glyphosate dimers are IHB and ZHB in the ionized Glyph dimers, HB and IHB in NZ and only HB in DN dimer structures in the gas phase and in solution. As pointed out in previous experimental79,80 and theoretical81 reports, the bond strength of these H-bonds should follow the ranking HB < IHB ≤ ZHB. For Glyph dimer, our computation at B3LYP-D3/6-311++G(2d,2p) give bond strengths of 24.0 kcal mol−1 for O–H⋯−O IHB, of 31.8 kcal mol−1 for N+–H⋯−O ZHB and of 5.1 kcal mol−1 for O–H⋯O HB, in quantitative agreement with the experimental data79,80 (a bond strength on the order of ∼5 kcal mol−1 for HB and bond strengths typically between 5–35 kcal mol−1 for IHB and ZHB). Therefore, the energetic competition between ionized and non-ionized isomers of Glyph dimer is due to the high stabilization energy of the ionic hydrogen bond (IHB) network in the ionized structures compared to that in NZ and DN isomers. The presence of four high bond energy of O–H⋯−O IHB and 2N+–H⋯−O ZHB impart a greater stability to the carboxylate zwitterionic units in DZC dimers in comparison with phosphonate zwitterion pairs in DZP and anion–cation pairs in AC and non-ionized pairs (DN). The effect of multiple IHB and ZHB on the stabilization of DZC with respect to the other isomers is visible even in the gas phase. A double carboxylate zwitterion (such as in DZC structures) without additional solvent molecules attached are stabilized both by the attractive coulomb interaction between opposite charges and by enhanced IHB and ZHB H-bonding networks. As shown in Table 3, all the dO⋯H are in the range 1.490–2.437 Å significantly inferior to the sum of the vander Walls radii (2.72 Å),82 indicating that all the primary intermolecular and intramolecular (O–H⋯−O and N+–H⋯−O) interactions in the DZC types of structures are very strong in the gas phase. Whenever, calculation show that solvents have significantly effects on the properties of these H-bonds. The upper set of data indicates a distinction between the IHB, ZHB and HB. Whereas the increasing polarity of the solvent has a significant effect on the two former sort of H-bonds, only a smaller effect upon the length of the latter is detected. The bond strengths of the neutral O–H⋯O and N–H⋯O H-bonds are maintained in a cyclohexane solution having a low dielectric constant. However, opposite solvent effects are detected on IHB and ZHB when ε rises. While the length of O–H⋯−O decreased, the N+–H⋯−O elongates quickly in a uniform fashion such that the N+–H⋯−O all become significantly weaker than OH⋯−O H-bonds in water solution. The perturbation effect of N+–H⋯−O zwitterionic H-bonds by hydration can be due to the fact that the random orientation of the dipolar interaction of the water polar solvent cannot be as effective as the amine groups with a readily formable orientation as was explained in previous works on low-barrier hydrogen bonding.83,84 The most important feature, is that the N+–H⋯−O H-bond weakening coupled to a shortening of the inter-subunit separation, facilitate in aqueous solution the proton transfer between the hydroxide group (O–H) and oxygen ions (O−) of carboxylate group in DZC. In effect, the equilibrium distance between donor and acceptor is in the range 1.564–1.719 Å in gas phase. This is too large as compared to 1.528–1.574 Å in aqueous solution, and hence the proton transfer in this position is strongly unfavorable. Remarkably notes are the fact that most of the DZC type structure Glyph dimer (DZC1 to DZC5), can entirely be isomerized to their AC tautomers and DZP form in aqueous solution. However, no proton transfer was achieved in the gas phase and in cyclohexane for the five most stable DZC structure. All DZP and AC structures tautomers of DZC1 found in aqueous solution are not stable in the gas phase and most of them collapse after optimization to their DZC or to one of the DZC conformers already optimized in gas phase. Therefore, characteristics and structural features of Glyph dimers, established for the gas phase and non-polar solvent, are different fundamentally from that for aqueous solution. The differences detected has a great deal with structural properties which are coupled to the medium reorganization as was pointed above. More specifically, the principal discrepancies detected in solution result mainly from differences in solvation energies between ionized and non-ionized species which exceed four times in water. Obviously, these solvation effects on ionized and non-ionized dimer species can change dramatically the relative acidity/basicity determined in the gas phase. As a consequence, the intermolecular proton-transfer could be affected in ionized species and therefore changes in prototropic conversion equilibria may be involved in different media. In the following section, we will try to study the tautomerism in Glyph dimer by outlying the main feature of the proton transfer mechanism between ionized species of Glyph dimers in the different environments. We will show if a possible proton transfer could take place in the gas phase and in cyclohexane since DZP and AC ionized species are stable in these media?
O groups. It may be noted that, all the calculated Glyph dimer free energies of hydration are seen very negative and fall within the range −42.4 kcal mol−1 (for non-ionized) to −81 kcal mol−1 (for ionized DZP). Of some importance is the comparable behavior of the zwitterionic glycine dimer69 and several zwitterionic amino acids70,73,74 in water solution. The data corresponding to the carboxylate zwitterion dimers, reported in Table 2, are remarkably similar to the value (ΔGsolv. = −66.3 kcal mol−1) computed for carboxylate zwitterionic glycine dimer in water solution.69 One may notes that these values obtained in the range −42–81 kcal mol−1 are in consonant to the estimate of −59 kcal mol−1 from the Onsager formula75,76 for the solvation free energy of a dipolar sphere. Our calculations showed that solvation properties are related in a very nearly fashion to the Onsager function, Fo, that in turn relates to the properties of the solvent.75,76 In fact, the increase of ΔGsolv.tot. by about more than the thrice of any species of DZC Glyph dimer from cyclohexane to water can be correlated is nearly a linear function of with the rise in the Onsager function Fo = (ε − 1)/(ε + 2),75,76 which is itself magnified by a factor of 3.4 when increases from 2 to 78. There is hence every reason to believe that the solvation model being applied here, while certainly not absolutely accurate in a quantitative sense, provide very reasonable approximations to the environments they are meant to reproduce. It may be noted that the estimation of non-electrostatic contribution arising from short-range interactions between the solute and solvent molecules in the first solvation shell, called the cavity–dispersion–solvent-structure (CDS) term, differ from cyclohexane to water. While Enonel. terms are negative and low in cyclohexane, they are positive and largely expected (in absolute values) in water solution. These results can be easily rationalized by the fact that water molecules are the smallest (a cyclohexane molecule has a van der Waals volume roughly 5 times larger than that of a water molecule) and so liquid water is characterized by the largest number density, which in turn increases the entropy loss associated with cavity creation, due to the solvent-excluded volume effect. As a consequence, the energy associated to cavity creation is larger to that in cyclohexane and thus non-electrostatic (CDS) contribution is positive and larger in water. Nevertheless, solvation free energy ΔGsolv in H2O (see Table 2) are found negative for all dimers, paralleling the situation in nonpolar medium C6H12. This may indicate that the free energy cost of cavity creation is not so large and the attractive solute–solvent energetic interactions (accounting also for hydrogen bonds) are able to overcome the free energy cost of cavity creation. These results are in line with experimental data71,77,78 and previous computational investigations of several polar amino acid side chain equivalents in cyclohexane solution and in water.70,72–74 Nonetheless, calculation reveal that the highest values of free energy of solvation (|ΔGsolv.| values) are not associated to the most stable solute in aqueous solution and in cyclohexane. As is shown in Table 1, the carboxylate zwitterionic dimer form DZC1 which is the most stable Glyph dimer do not experience the largest solvation (or polarization) in water and in cyclohexane solution. This indicates that several effects in addition to the polarization term are involved and counteract each other, even when effects on solvent are not considered explicitly. Among these effects, non-covalent intermolecular and intra-moleculecular hydrogen-bondings (H-bonds) may be important for structure selection and stability of Glyph dimers in different media. To elucidate the role of H-bonds, their structural features are inspected and criticized in the series of the five types of Glyph dimer structures displayed in Fig. 1–3. Structural analysis of the equilibrium structures affords a total of a maximum of seven short contacts characterizing H-bonds of each series of type of structure (DZC, DZP, AC, NZP, DN), which are classified in chemical classes belonging to three fundamental types: neutral H-bonds (HB) between two neutral groups, ionic H-bonds (IHB) between a neutral and charged group and zwitterionic H-bonds (ZHB) between two oppositely charged groups. Fig. 1–3, show that both O–H⋯−O and N+–H⋯O ionic H-bonds participate in stabilizing the IHB pattern which result in the formation of 8-membered rings (displaying O–H⋯−O) and 9-membered rings (establishing O–H⋯−O and N+–H⋯O) with different arrangements. ZHB consist of intramolecular and intermolecular N+–H⋯−O H-bonds through which 5- and 10- membered rings are formed. In Table 3 are collected the intermolecular and intramolecular bond distances (dO⋯H) characterizing the IHB, ZHB and HB for the most stable structures of each type (DZC, DZP, AC, NZP, DN) of Glyph dimer in different media. From the results obtained in Table 3, it is clear that the largest contributors to the stabilization of the glyphosate dimers are IHB and ZHB in the ionized Glyph dimers, HB and IHB in NZ and only HB in DN dimer structures in the gas phase and in solution. As pointed out in previous experimental79,80 and theoretical81 reports, the bond strength of these H-bonds should follow the ranking HB < IHB ≤ ZHB. For Glyph dimer, our computation at B3LYP-D3/6-311++G(2d,2p) give bond strengths of 24.0 kcal mol−1 for O–H⋯−O IHB, of 31.8 kcal mol−1 for N+–H⋯−O ZHB and of 5.1 kcal mol−1 for O–H⋯O HB, in quantitative agreement with the experimental data79,80 (a bond strength on the order of ∼5 kcal mol−1 for HB and bond strengths typically between 5–35 kcal mol−1 for IHB and ZHB). Therefore, the energetic competition between ionized and non-ionized isomers of Glyph dimer is due to the high stabilization energy of the ionic hydrogen bond (IHB) network in the ionized structures compared to that in NZ and DN isomers. The presence of four high bond energy of O–H⋯−O IHB and 2N+–H⋯−O ZHB impart a greater stability to the carboxylate zwitterionic units in DZC dimers in comparison with phosphonate zwitterion pairs in DZP and anion–cation pairs in AC and non-ionized pairs (DN). The effect of multiple IHB and ZHB on the stabilization of DZC with respect to the other isomers is visible even in the gas phase. A double carboxylate zwitterion (such as in DZC structures) without additional solvent molecules attached are stabilized both by the attractive coulomb interaction between opposite charges and by enhanced IHB and ZHB H-bonding networks. As shown in Table 3, all the dO⋯H are in the range 1.490–2.437 Å significantly inferior to the sum of the vander Walls radii (2.72 Å),82 indicating that all the primary intermolecular and intramolecular (O–H⋯−O and N+–H⋯−O) interactions in the DZC types of structures are very strong in the gas phase. Whenever, calculation show that solvents have significantly effects on the properties of these H-bonds. The upper set of data indicates a distinction between the IHB, ZHB and HB. Whereas the increasing polarity of the solvent has a significant effect on the two former sort of H-bonds, only a smaller effect upon the length of the latter is detected. The bond strengths of the neutral O–H⋯O and N–H⋯O H-bonds are maintained in a cyclohexane solution having a low dielectric constant. However, opposite solvent effects are detected on IHB and ZHB when ε rises. While the length of O–H⋯−O decreased, the N+–H⋯−O elongates quickly in a uniform fashion such that the N+–H⋯−O all become significantly weaker than OH⋯−O H-bonds in water solution. The perturbation effect of N+–H⋯−O zwitterionic H-bonds by hydration can be due to the fact that the random orientation of the dipolar interaction of the water polar solvent cannot be as effective as the amine groups with a readily formable orientation as was explained in previous works on low-barrier hydrogen bonding.83,84 The most important feature, is that the N+–H⋯−O H-bond weakening coupled to a shortening of the inter-subunit separation, facilitate in aqueous solution the proton transfer between the hydroxide group (O–H) and oxygen ions (O−) of carboxylate group in DZC. In effect, the equilibrium distance between donor and acceptor is in the range 1.564–1.719 Å in gas phase. This is too large as compared to 1.528–1.574 Å in aqueous solution, and hence the proton transfer in this position is strongly unfavorable. Remarkably notes are the fact that most of the DZC type structure Glyph dimer (DZC1 to DZC5), can entirely be isomerized to their AC tautomers and DZP form in aqueous solution. However, no proton transfer was achieved in the gas phase and in cyclohexane for the five most stable DZC structure. All DZP and AC structures tautomers of DZC1 found in aqueous solution are not stable in the gas phase and most of them collapse after optimization to their DZC or to one of the DZC conformers already optimized in gas phase. Therefore, characteristics and structural features of Glyph dimers, established for the gas phase and non-polar solvent, are different fundamentally from that for aqueous solution. The differences detected has a great deal with structural properties which are coupled to the medium reorganization as was pointed above. More specifically, the principal discrepancies detected in solution result mainly from differences in solvation energies between ionized and non-ionized species which exceed four times in water. Obviously, these solvation effects on ionized and non-ionized dimer species can change dramatically the relative acidity/basicity determined in the gas phase. As a consequence, the intermolecular proton-transfer could be affected in ionized species and therefore changes in prototropic conversion equilibria may be involved in different media. In the following section, we will try to study the tautomerism in Glyph dimer by outlying the main feature of the proton transfer mechanism between ionized species of Glyph dimers in the different environments. We will show if a possible proton transfer could take place in the gas phase and in cyclohexane since DZP and AC ionized species are stable in these media?
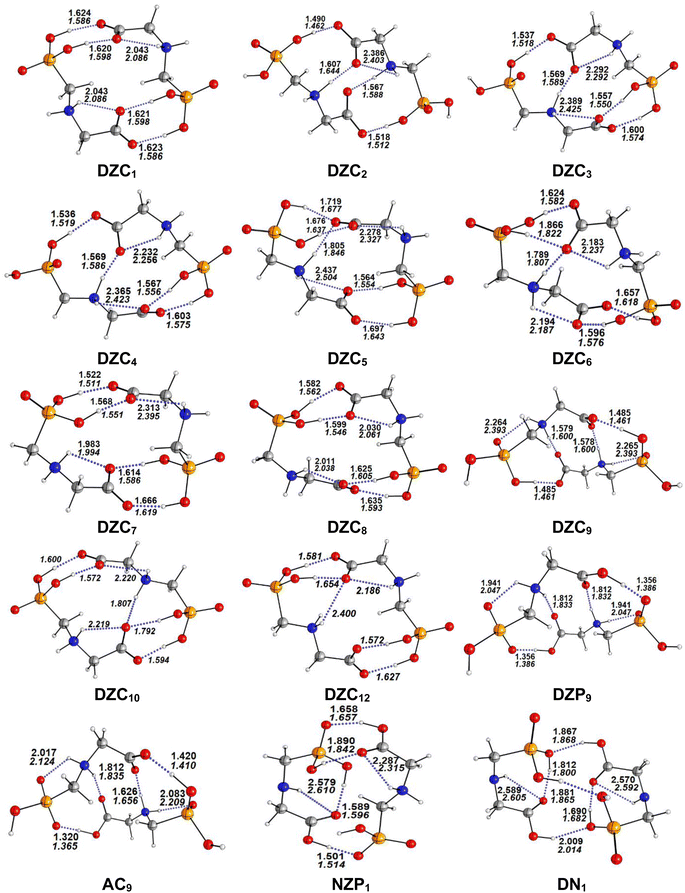 |
| | Fig. 1 Optimized structures of non-ionized and ionized forms of Glyph dimers in the gas phase and in cyclohexane solution at SMD-B3LYP-D3/6-311++G(2d,2p) level. Interatomic distances (in Å) are shown for H-bonds in the gas phase (in plane text) and in cyclohexane (in italics). | |
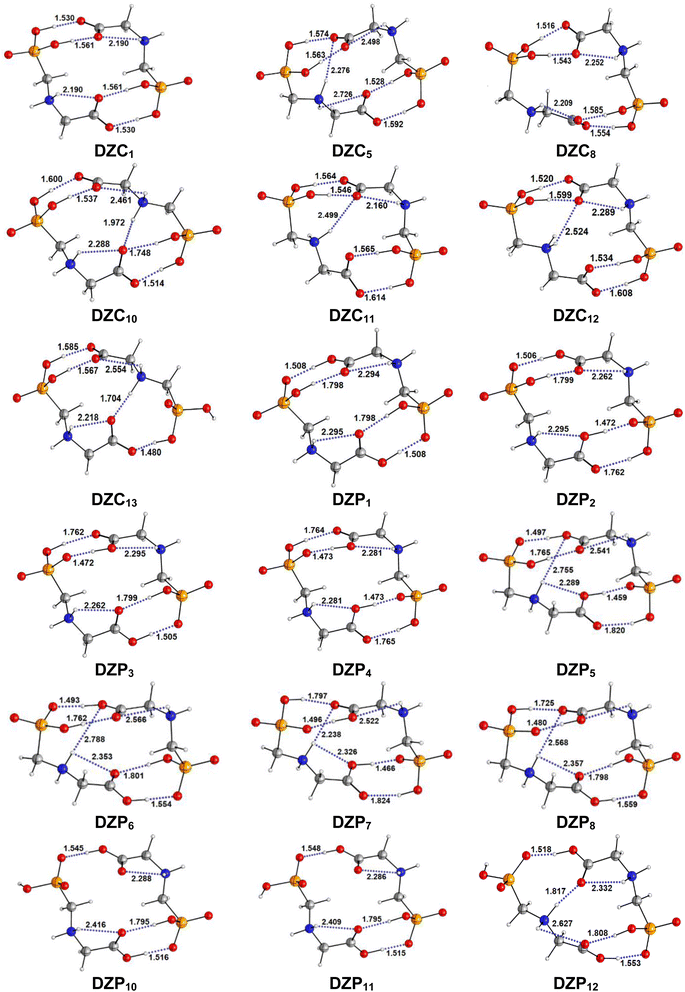 |
| | Fig. 2 Optimized structures of DZC and DZP forms of Glyph dimers in aqueous solution at SMD-B3LYP-D3/6-311++G(2d,2p) level. Interatomic distances in Å. | |
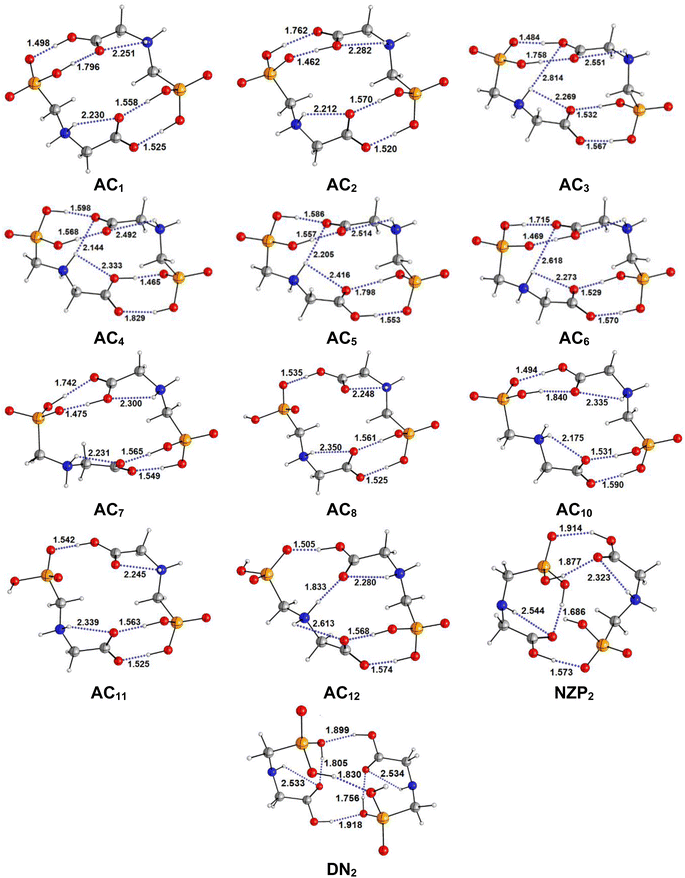 |
| | Fig. 3 Optimized structures of AC, NZP and DN forms of Glyph dimers in aqueous solution at SMD-B3LYP-D3/6-311++G(2d,2p) level. Interatomic distances in Å. | |
Table 1 Computed energies [kcal mol−1] for the diverse conformers of ionized and non-ionized forms of neutral Glyph dimer relative to the most stable one in the gas phasea and in solution.b ΔE is the relative electronic energy and ΔG refers to relative free energy at 298.15 K
| Conformer |
Gas phase |
Cyclohexane |
Water |
| ΔE |
ΔG |
ΔE |
ΔG |
ΔE |
ΔG |
| Calculations at B3LYP-D3/6-311++G(2d,2p) level. Calculation at SMD-B3LYP-D3/6-311++G(2d,2p) level. |
| DZC1 |
0.0 |
0.0 |
0.0 |
0.0 |
0.3 |
0.0 |
| DZC2 |
2.3 |
0.6 |
4.8 |
2.5 |
— |
— |
| DZC3 |
2.3 |
0.9 |
3.0 |
1.3 |
— |
— |
| DZC4 |
2.5 |
1.1 |
3.1 |
1.1 |
— |
— |
| DZC5 |
1.0 |
2.5 |
1.0 |
1.6 |
1.3 |
0.1 |
| DZC6 |
2.1 |
2.7 |
2.1 |
2.7 |
— |
— |
| DZC7 |
3.4 |
3.5 |
2.6 |
1.3 |
— |
— |
| DZC8 |
3.2 |
3.6 |
2.1 |
1.9 |
2.3 |
1.0 |
| DZC9 |
5.9 |
3.9 |
9.3 |
7.1 |
— |
— |
| DZC10 |
— |
— |
2.6 |
2.4 |
3.4 |
2.8 |
| DZC11 |
— |
— |
— |
— |
3.6 |
3.1 |
| DZC12 |
— |
— |
3.3 |
4.2 |
2.8 |
2.3 |
| DZC13 |
|
— |
|
— |
5.5 |
3.3 |
| DZP1 |
— |
— |
— |
— |
0.0 |
0.1 |
| DZP2 |
— |
— |
— |
— |
1.5 |
1.2 |
| DZP3 |
— |
— |
— |
— |
1.5 |
1.2 |
| DZP4 |
|
— |
|
— |
3.0 |
1.9 |
| DZP5 |
— |
— |
— |
— |
1.9 |
2.3 |
| DZP6 |
|
— |
|
— |
1.1 |
2.6 |
| DZP7 |
— |
— |
— |
— |
2.6 |
3.4 |
| DZP8 |
|
— |
|
— |
2.0 |
3.6 |
| DZP9 |
7.2 |
5.7 |
9.6 |
6.8 |
— |
— |
| DZP10 |
— |
— |
— |
— |
3.6 |
2.6 |
| DZP11 |
— |
— |
— |
— |
3.8 |
2.6 |
| DZP12 |
|
— |
|
— |
4.3 |
3.7 |
| AC1 |
— |
— |
— |
— |
0.3 |
0.2 |
| AC2 |
— |
— |
— |
— |
1.8 |
1.1 |
| AC3 |
— |
— |
— |
— |
1.0 |
1.2 |
| AC4 |
— |
— |
— |
— |
2.2 |
1.7 |
| AC5 |
— |
— |
— |
— |
1.7 |
1.7 |
| AC6 |
— |
— |
— |
— |
2.0 |
2.4 |
| AC7 |
|
— |
|
— |
3.1 |
2.0 |
| AC8 |
— |
— |
— |
— |
4.0 |
2.4 |
| AC9 |
7.1 |
4.1 |
9.7 |
6.8 |
— |
— |
| AC10 |
— |
— |
— |
— |
2.5 |
2.8 |
| AC11 |
— |
— |
— |
— |
4.1 |
2.8 |
| AC12 |
— |
— |
— |
— |
4.3 |
3.1 |
| NZP1 |
5.1 |
4.6 |
9.2 |
8.2 |
— |
— |
| NZP2 |
— |
— |
— |
— |
14.0 |
12.3 |
| DN1 |
5.2 |
3.4 |
12.8 |
10.1 |
— |
— |
| DN2 |
|
— |
|
— |
23.5 |
21.2 |
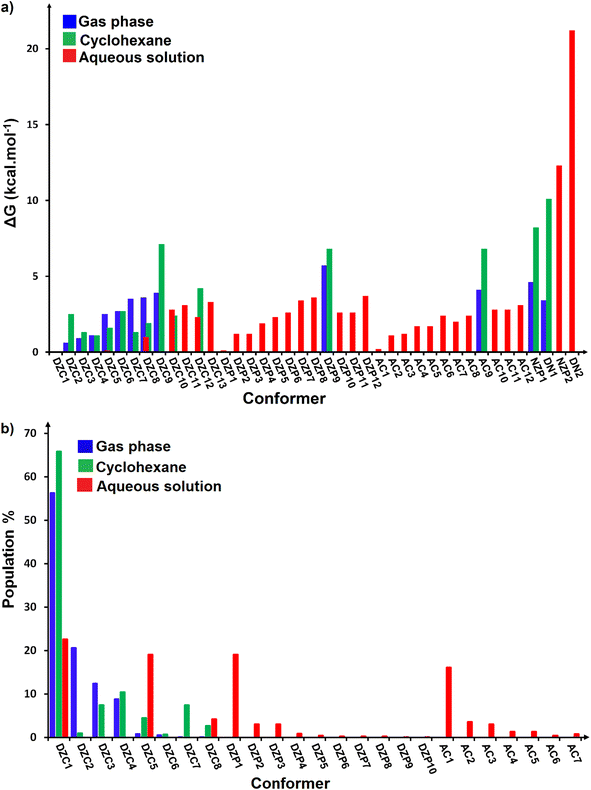 |
| | Fig. 4 (a) Comparison of relative Gibbs free energies (ΔG) in the gas phase and in solution at SMD-B3LYP-D3/6-311++G(2d,2p) level. (b) Boltzmann population values for stable conformers of ionized forms of neutral Glyph dimer in the gas phase and in solution at SMD-B3LYP-D3/6-311++G(2d,2p) level. | |
Table 2 Gibbs free energy of solvation, ΔGsolv.a,b,c (kcal mol−1), of the diverse conformers of ionizedd,e and non-ionizedd,e forms of neutral Glyph dimer in cyclohexane and in aqueous solution at SMD-B3LYP-D3/6-311++G(2d,2p) level
| Conformer |
Cyclohexane |
Water |
| ΔGsolv.tot.a |
ΔGsolv.el.b |
Enonel.c |
ΔGsolv.tot.a |
ΔGsolv.el.b |
Enonel.c |
| ΔGsolv,tot. represents the total Gibbs free energy of solvation: ΔGsolv.tot. = Gs − Gg where Gs is the total Gibbs free energy in solution (the free energy sommation of the electrostatic and non-electrostatic terms) and Gg is the Gibbs free energy in the gas phase. ΔGsolv,el. is the electrostatic Gibbs free energy of solvation: ΔGsolv.el. = Gel − Gg where Gel is the Gibbs free energy in solution including only the electrostatic term. Enonel. is the non-electrostatic contribution. DZC10, DZC11, DZC12, DZC13, NZP2 and all DZP and AC (except DZP9 and AC9) ionized structures are not stable in the gas phase. Thus, the gas-phase computation was done using the geometry optimized in solution. Thermal contributions were taken from calculations in solution. DN2 non-ionized structure is not stable in the gas phase. The gas-phase computation was done using the geometry optimized in solution. Thermal contributions were taken from calculations in solution. |
| DZC1 |
−17.9 |
−14.2 |
−3.7 |
−55.0 |
−67.4 |
12.4 |
| DZC2 |
−16.0 |
−11.8 |
−4.2 |
— |
— |
— |
| DZC3 |
−17.5 |
−13.6 |
−3.9 |
— |
— |
— |
| DZC4 |
−17.8 |
−13.9 |
−3.9 |
— |
— |
— |
| DZC5 |
−18.8 |
−15.2 |
−3.6 |
−57.4 |
−69.7 |
12.3 |
| DZC6 |
−17.9 |
−14.1 |
−3.8 |
— |
— |
— |
| DZC7 |
−20.0 |
−16.6 |
−3.5 |
— |
— |
— |
| DZC8 |
−19.6 |
−16.0 |
−3.6 |
−57.6 |
−70.1 |
12.5 |
| DZC9 |
−14.7 |
−10.7 |
−4.1 |
— |
— |
— |
| DZC10 |
−19.5 |
−15.6 |
−3.8 |
−64.0 |
−76.6 |
12.6 |
| DZC11 |
— |
— |
— |
−68.5 |
−80.8 |
12.3 |
| DZC12 |
−19.6 |
−15.7 |
−3.9 |
−65.1 |
−77.6 |
12.5 |
| DZC13 |
— |
— |
— |
−61.6 |
−74.6 |
13.0 |
| DZP1 |
— |
— |
— |
−78.7 |
−90.9 |
12.3 |
| DZP2 |
— |
— |
— |
−78.7 |
−91.2 |
12.5 |
| DZP3 |
— |
— |
— |
−78.7 |
−91.2 |
12.4 |
| DZP4 |
— |
— |
— |
−78.8 |
−91.5 |
12.7 |
| DZP5 |
— |
— |
— |
−79.0 |
−91.2 |
12.3 |
| DZP6 |
— |
— |
— |
−80.8 |
−92.9 |
12.2 |
| DZP7 |
— |
— |
— |
−78.4 |
−90.6 |
12.2 |
| DZP8 |
— |
— |
— |
−80.5 |
−92.6 |
12.1 |
| DZP9 |
−16.8 |
−12.9 |
−3.8 |
— |
— |
— |
| DZP10 |
— |
— |
— |
−79.9 |
−92.7 |
12.9 |
| DZP11 |
— |
— |
— |
−81.0 |
−93.8 |
12.8 |
| DZP12 |
— |
— |
— |
−76.4 |
−89.2 |
12.9 |
| AC1 |
— |
— |
— |
−72.4 |
−84.7 |
12.3 |
| AC2 |
— |
— |
— |
−72.1 |
−84.7 |
12.6 |
| AC3 |
— |
— |
— |
−73.4 |
−85.6 |
12.2 |
| AC4 |
— |
— |
— |
−69.9 |
−82.1 |
12.2 |
| AC5 |
— |
— |
— |
−71.8 |
−84.0 |
12.2 |
| AC6 |
— |
— |
— |
−73.4 |
−85.6 |
12.2 |
| AC7 |
— |
— |
— |
−71.9 |
−84.4 |
12.5 |
| AC8 |
— |
— |
— |
−73.5 |
−86.4 |
12.9 |
| AC9 |
−15.2 |
−11.2 |
−3.9 |
— |
— |
— |
| AC10 |
— |
— |
— |
−74.7 |
−87.1 |
12.4 |
| AC11 |
— |
— |
— |
−74.4 |
−87.3 |
12.9 |
| AC12 |
— |
— |
— |
−71.5 |
−84.4 |
12.9 |
| NZP1 |
−14.3 |
−10.8 |
−3.5 |
— |
— |
— |
| NZP2 |
— |
— |
— |
−56.5 |
−65.2 |
8.7 |
| DN1 |
−11.2 |
−8.1 |
−3.1 |
— |
— |
— |
| DN2 |
— |
— |
— |
−42.4 |
−47.7 |
5.4 |
Table 3 Interatomic distances (in Å) for H-bonds computed in the gas phase (in plane text), in cyclohexane solution (in italics) and in aqueous solution (in bold) for the diverse conformers of ionized and non-ionized forms of neutral Glyph dimer
| Conformer |
IHB |
ZHB |
HB |
| O–H⋯−O |
N+–H⋯O |
N+–H⋯−O |
O–H⋯O |
N–H⋯O |
| DZC1 |
1.624 |
1.586 |
1.530 |
— |
2.043 |
2.086 |
2.190 |
— |
— |
| |
1.620 |
1.598 |
1.561 |
2.043 |
2.086 |
2.190 |
| |
1.621 |
1.598 |
1.561 |
|
|
|
| |
1.623 |
1.586 |
1.530 |
|
|
|
| DZC2 |
1.490 |
1.462 |
|
— |
2.386 |
2.403 |
|
— |
— |
| |
1.518 |
1.512 |
|
1.607 |
1.644 |
|
| |
|
|
|
1.567 |
1.588 |
|
| DZC3 |
1.537 |
1.518 |
|
— |
2.292 |
2.292 |
|
— |
— |
| |
1.557 |
1.550 |
|
2.389 |
2.425 |
|
| |
1.600 |
1.574 |
|
1.569 |
1.589 |
|
| DZC5 |
1.719 |
1.677 |
1.574 |
— |
2.278 |
2.327 |
2.498 |
— |
— |
| |
1.676 |
1.637 |
1.563 |
2.437 |
2.504 |
2.726 |
| |
1.564 |
1.554 |
1.528 |
1.805 |
1.846 |
2.276 |
| |
1.697 |
1.643 |
1.592 |
|
|
|
| DZP9 |
1.356 |
1.386 |
|
1.812 |
1.832 |
|
1.941 |
2.047 |
|
— |
— |
| |
1.356 |
1.386 |
|
1.812 |
1.833 |
|
1.941 |
2.047 |
|
| DZP1 |
|
|
1.508 |
|
|
2.294 |
|
|
1.798 |
— |
— |
| |
|
|
1.508 |
|
|
2.295 |
|
|
1.798 |
| DZP5 |
|
|
1.497 |
|
|
2.541 |
|
|
1.765 |
— |
— |
| |
|
|
1.459 |
|
|
2.289 |
|
|
1.820 |
| |
|
|
|
|
|
2.755 |
|
|
|
| AC9 |
1.320 |
1.365 |
|
1.812 |
1.835 |
|
1.626 |
1.656 |
|
— |
— |
| |
1.420 |
1.410 |
|
2.083 |
2.209 |
|
2.017 |
2.124 |
|
| AC1 |
|
|
1.498 |
|
|
2.251 |
|
|
2.230 |
|
|
1.796 |
— |
| |
|
|
1.558 |
|
|
|
|
|
|
|
|
|
| |
|
|
1.525 |
|
|
|
|
|
|
|
|
|
| AC3 |
|
|
1.484 |
|
|
2.551 |
|
|
2.269 |
|
|
1.758 |
_ |
| |
|
|
1.532 |
|
|
2.814 |
|
|
|
|
|
|
| |
|
|
1.567 |
|
|
|
|
|
|
|
|
|
| NZP1 |
1.501 |
1.514 |
|
2.287 |
2.315 |
|
— |
1.658 |
1.657 |
|
2.579 |
2.610 |
|
| |
|
|
|
|
|
|
1.890 |
1.842 |
|
|
|
|
| |
|
|
|
|
|
|
1.589 |
1.596 |
|
|
|
|
| NZP2 |
|
|
1.573 |
|
|
2.323 |
— |
|
|
1.914 |
|
|
2.544 |
| |
|
|
|
|
|
|
|
|
1.877 |
|
|
|
| |
|
|
|
|
|
|
|
|
1.686 |
|
|
|
| DN1 |
— |
— |
— |
2.009 |
2.014 |
|
2.589 |
2.605 |
|
| |
1.881 |
1.865 |
|
2.570 |
2.592 |
|
| |
1.867 |
1.868 |
|
|
|
|
| |
1.690 |
1.682 |
|
|
|
|
| |
1.812 |
1.800 |
|
|
|
|
| DN2 |
— |
— |
— |
|
|
1.918 |
|
|
2.533 |
| |
|
|
1.830 |
|
|
2.534 |
| |
|
|
1.899 |
|
|
|
| |
|
|
1.756 |
|
|
|
| |
|
|
1.805 |
|
|
|
3.2. Tautomerism in neutral ionized Glyph dimers
Calculations in the gas phase show that the proton can be spontaneously transferred from a gaseous phosphonate zwitterionic dimer (DZP9) to a gaseous anion–cation dimer (AC9). The latter isomerizes via a direct proton transfer in to a gaseous carboxylate tautomer (DZC9). The stationary structures, together with the corresponding transition states involved in the two proton transfer steps of the tautomerization process are presented in Fig. 5a. Cartesian coordinates of the transition states (TS) for DZP9 and AC9 conversions are reported in ESI S72–S73.† The energy profile for the whole process is plotted in Fig. 5b. As shown in Fig. 5a, the structure of the tautomers in the gas phase involves a three monocyclic geometry with a ten membered ring in the middle adopting a boat conformation. The results suggest that the proton transfer in the gas phase is favored by the existence of the second intermolecular N+–H⋯O H-bond which helps to stabilize the DZP9 system as a cyclic structure, to eliminate the proton transfer barrier of the strongest OH⋯−O(PO) H-Bond. This can be understood in terms of the acid–base model previously proposed in litterature85 which takes into account that each monomer in the DZP9 dimer behaves simultaneously as a H-bond donor and H-bond acceptor. In other words, the H-bond donor character of the carboxylic acid group (COOH) of the Glyph monomer in DZP9 is enhanced because it behaves also as a hydrogen bond acceptor, while the H-bond acceptor character of the −OPO(C2O2H4N+) monomer is enhanced because it behaves also as a H-bond donor due to the presence of the amine group (NH2+) in the monomer. The conjunction of both effects makes the spontaneous proton transfer possible. Even though, the proton transfer observed in the gas phase is favored by the strong intermolecular coulombic interactions between the cation +NH2 and the anion COO− produced in the process, which is absent in the most stable DZC1 type structure. The energetics reported in Table 4 indicate that, in the gas phase, phosphonate zwitterionic DZP9 type structure undergoes a very fast and exothermic conversion to its corresponding AC9 form, suggesting a very small energy barrier of about 0.2 kcal mol−1. For the AC9 conversion to its DZC9 tautomer, the energy barrier is of only 0.05 kcal mol−1. The anion–cation AC9 structure, is expected to have a very small life and therefore, needs to reorganize into a more kinetically stable carboxylate DZC9 dimer structure as shown in Fig. 5a. As a result, the tautomerization process in the gas phase, could be roughly represented by the following kinetic scheme: DZP ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC
AC![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC. The anion–cation AC species can be considered as a reaction intermediate in equilibrium with phosphonate (DZP) and carboxylate (DZC) tautomers. In cyclohexane, calculation have predicted the same mechanism of intermolecular proton transfer between DZP9 and its corresponding anion–cation AC9 and carboxylate DZC9 tautomers (Fig. 5a). Cartesian coordinates of the transition states (TS) DZC and AC and between AC and DZP tautomers for DZP9 and AC9 conversions, in cyclohexane are reported in ESI S74–75.†
DZC. The anion–cation AC species can be considered as a reaction intermediate in equilibrium with phosphonate (DZP) and carboxylate (DZC) tautomers. In cyclohexane, calculation have predicted the same mechanism of intermolecular proton transfer between DZP9 and its corresponding anion–cation AC9 and carboxylate DZC9 tautomers (Fig. 5a). Cartesian coordinates of the transition states (TS) DZC and AC and between AC and DZP tautomers for DZP9 and AC9 conversions, in cyclohexane are reported in ESI S74–75.†
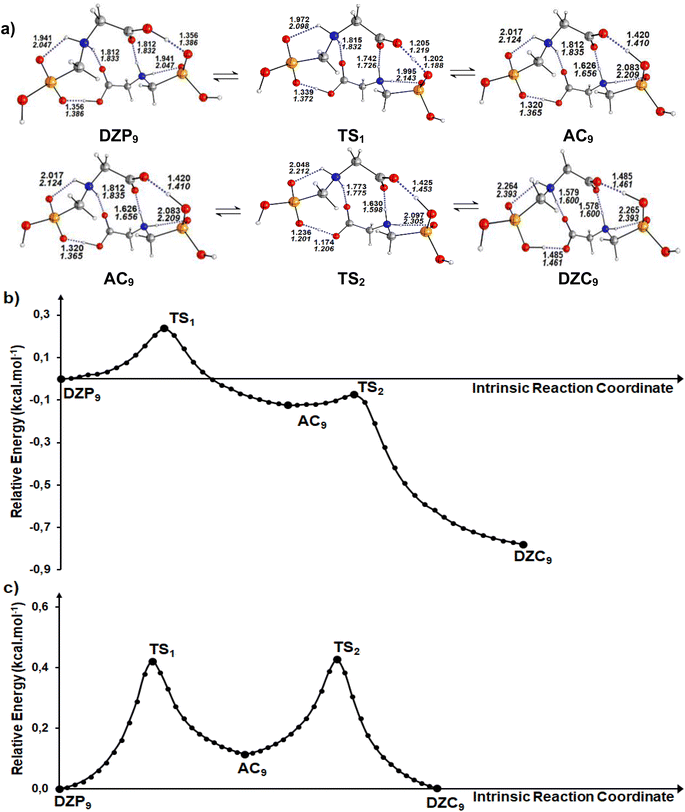 |
| | Fig. 5 (a) Structures of DZP, DZC and AC tautomers involved in the intermolecular proton transfer reaction of Glyph, together with the corresponding transition states (TS), optimized in the gas phase and in cyclohexane solution at SMD-B3LYP-D3/6-311++G(2d,2p) level. Interatomic distances (in Å) are shown for H-Bonds in the gas phase (in plane text) and in cyclohexane (in italics). (b) and (c) Reaction pathways following intrinsic reaction coordinate (IRC) calculations in the forward and reverse directions from each TS involved in the intermolecular tautomerization processes of the ionized forms of neutral Glyph dimer (b) in the gas phase at B3PLYP-D3/6-311++G(2d,2p) level and (c) in cyclohexane solution at SMD-B3LYP-D3/6-311++G(2d,2p) level. | |
Table 4 Energetics and activation parameters (kcal mol−1) of the tautomerism of the most stable ionized forms of neutral Glyph dimer in the gas phase and in solutiona,b
| |
ΔE0 |
ΔH298 |
TΔS |
ΔG298 |
ΔE‡0 |
ΔG‡298 |
| Calculations at B3LYP-D3/6-311++G(2d,2p) in the gas phase and at SMD-B3LYP-D3/6-311++G(2d,2p) in solution. Meanings of symbols are as follows: ΔE0, ΔH298 and ΔG298 are the tautomerization electronic energies (at 0 K), enthalpies (at 298 K) and Gibbs free energies (at 298 K). ΔE‡0 and ΔG‡298 are the electronic (at 0 K) and free activation energies (at 298 K), respectively. The values in parentheses are the activation energies for the reverse conversion processes. |
| Gas phase |
DZP9 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) TS1 TS1 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC9 AC9 |
−0.2 |
−0.6 |
0.9 |
−1.6 |
0.2(0.4) |
−1.7(−0.1) |
AC9 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) TS2 TS2 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC9 DZC9 |
−1.1 |
−0.3 |
−0.1 |
−0.2 |
0.05(1.2) |
−1.2(−1.0) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Cyclohexane |
DZP9 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) TS1 TS1 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC9 AC9 |
0.1 |
−0.4 |
−0.4 |
0.0 |
0.5(0.4) |
−0.8(−0.8) |
AC9 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) TS2 TS2 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC9 DZC9 |
−0.4 |
−0.1 |
−0.4 |
0.2 |
0.4(0.8) |
−2.6(−2.8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Aqueous solution |
DZP1 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) TS1 TS1 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC1 AC1 |
0.3 |
−0.6 |
−0.6 |
0.0 |
1.4(1.1) |
−0.9(−1.0) |
AC1 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) TS2 TS2 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC1 DZC1 |
0.0 |
−0.6 |
−0.4 |
−0.2 |
1.2(1.2) |
−1.3(−1.1) |
DZP2 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) TS3 TS3 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC1 AC1 |
−1.2 |
−1.8 |
−0.7 |
−1.1 |
0.6(1.9) |
−0.9(0.1) |
DZP3 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) TS4 TS4 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC2 AC2 |
0.3 |
−0.4 |
−0.3 |
−0.1 |
1.4(1.0) |
−0.8(−0.7) |
AC2 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) TS5 TS5 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC1 DZC1 |
−1.6 |
−1.9 |
−0.8 |
−1.1 |
0.5(2.1) |
−2.1(−0.9) |
DZP4 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) TS6 TS6 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC2 AC2 |
−1.2 |
−1.9 |
−1.1 |
−0.8 |
0.7(1.8) |
−0.5(0.3) |
The energetic profile of the tautomerism is depicted in Fig. 5c. The energetic reported in Table 4 show that solvation of the ionized and zwitterionic DZP9 and DZC9 tautomers by non-polar cyclohexane solvent increases the energetic barriers with respect to the gas phase for the intermolecular proton transfers from DZP9 to AC9 and from AC9 to DZC9 and makes the full proton transfer from the ZDP9 to DZC9 through AC as a slightly endergonic. Only this class of tautomers including a ten-membered ring with N+–H⋯O H-bonds undergo proton transfer. As was suggested in the gas phase, the reorientation of the +NH2 group and the formation of intermolecular N+–H⋯O bonding in the dimer structure is also a prerequisite for proton transfer from AC to DZP, in cyclohexane. The situation changes in aqueous solution, where both the DZP and AC dimers are stabilized by hydration. Water stabilizes the phosphonate zwitterions DZP1 complex more than the AC and DZC, up to the point that it becomes the global minimum on the proton transfer path. We report in Fig. 6, the DZP and AC tautomers structures, which were obtained starting with the most stable DZC1 structure within the transition structures (TS) involved in the six-proton transfer processes. The Fig. 7 shows the energy profiles for the interconversion between the most stable DZC1 and its corresponding DZP and AC tautomers in aqueous solution. Cartesian coordinates of all the transition states (TS) for conversions between DZC1 and their DZP and AC tautomers, in aqueous solution are reported in ESI S76–S81.† Table 4 also included the energetics of the six calculated tautomerization processes between DZC1 Glyph dimer and their corresponding anion–cation (AC) and phosphonate zwitterionic (DZP) tautomers. As it is seen in the Fig. 7, from DZC to AC path, the most preferred DZC1 structure interconverts to two ionized structures noted as AC1 and AC2 via two direct proton transfer mechanisms. These tautomerism processes involve the transfer of a peripheral (H1) and an internal (H2) proton, along an intermolecular pathway. Due to the fact that DZC1 structure is a centrosymmetric arrangement of two carboxylate zwitterion units associated with four (H1H2H3H4) intermolecular ionic O–H⋯−O H-bonds, transfer of H3 and H4 protons (Fig. 6) enable degenerate tautomerization processes leading to two anion–cation (AC) tautomers isoenergetic to AC1 and AC2, respectively. Each one of the ionized AC structures exhibits a non-degenerate HH transfer leading to two phosphonate zwitterionic dimer structures (DZP). As shown in Fig. 7, AC1 isomerizes to DZP1 and DZP2 phosphonate tautomers via two direct proton transfers of H4 and H3, respectively. In the same way (similarly), AC2 isomerizes to DZP3 and DZP4 phosphonate zwitterionic tautomers. Both DZP3 and DZP2 are isoenergetic and so equally populated owing to the centrosymmetric arrangement of OH⋯−O. From the energetics reported in Table 4, it appears that the most preferred phosphonate (DZP1), the anion cation AC1 and the carboxylate zwitterionic (DZC1) tautomers, are almost isoenergetic on the ΔE0, ΔH298, and ΔG298 surfaces. The equilibrium proton transfer paths leading from DZP Glyph dimers to their corresponding AC and DZC tautomers are quite favorable with small activation barriers (0.5–1.4 kcal mol−1) on the ΔE0. The transitions between DZP and AC as well as among AC and DZC tautomeric forms are found barrierless on the ΔG298 surface as was detected in the gas phase and in cyclohexane solution. Most importantly, from DZC to AC paths, the lowest energy barriers of 1.2 kcal mol−1 are obtained for the transfer of the protons in the peripheric chemical positions such as H4 and H1. The values of energy barriers of proton transfer of H3 and H2 in central positions are roughly twice those corresponding to protons in the peripheral positions as shown in Fig. 7. This indicates that the tautomerism process is substantially faster for the peripheric protons than for protons in central positions. Remarkably, the reverse is true for the transition from DZP to AC and from AC to DZC. Proton transfer of internal (H2, H3) protons are faster than peripheral ones (H4, H1) as the values of corresponding activation energies are smaller (lesser). All the more, the spontaneous intermolecular proton transfer paths are those leading from DZP Glyph dimers to their corresponding AC and from AC to their DZC tautomers. This indicates that the deprotonation site is the carboxyl group which releases the proton to the phosphonate (POO−) group as also detected in the gas phase and in non-polar solvent. Therefore, two direct proton transfers from the carboxyl to the phosphonate group seems to be the most plausible mechanism for the intermolecular tautomerization process in Glyph dimers in aqueous solution as well as in gas phase and bon polar medium. In this postulated mechanism, the Glyph phosphonate dimer deprotonation leads to an anion–cation (AC), and the subsequent proton transfer leads to the carboxylate dimer product according to a set of the following two tautomerism equilibria: DZP![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC
AC ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC. It is to be noted that DZC5 (Fig. 2) which is nearly isoenergetic to DZC1 (ΔG = 0.1 kcal mol−1) exhibits similar mechanism of interconversion to its corresponding AC and DZP tautomers as DZC1. However, the number of its tautomers differ from that of DZC1. Calculation predicts that DZC5 interconverts to four AC structures by (HHHH) proton transfers noted as AC3, AC4, AC5 and AC6. Each of the AC dimer structure interconverts to two DZP tautomers by (HH) non-degenerated tautomerism proton transfer giving in all eight DZP tautomers (with four isoenergetic identical to the other) as shown in ESI, Fig. S2.† Relative free energies (ΔG) between tautomers are roughly about 1–2 kcal mol−1 and thus a rapid interconversion between them could be predicted as was also proposed for the most stable DZC1 structure in aqueous solution.
DZC. It is to be noted that DZC5 (Fig. 2) which is nearly isoenergetic to DZC1 (ΔG = 0.1 kcal mol−1) exhibits similar mechanism of interconversion to its corresponding AC and DZP tautomers as DZC1. However, the number of its tautomers differ from that of DZC1. Calculation predicts that DZC5 interconverts to four AC structures by (HHHH) proton transfers noted as AC3, AC4, AC5 and AC6. Each of the AC dimer structure interconverts to two DZP tautomers by (HH) non-degenerated tautomerism proton transfer giving in all eight DZP tautomers (with four isoenergetic identical to the other) as shown in ESI, Fig. S2.† Relative free energies (ΔG) between tautomers are roughly about 1–2 kcal mol−1 and thus a rapid interconversion between them could be predicted as was also proposed for the most stable DZC1 structure in aqueous solution.
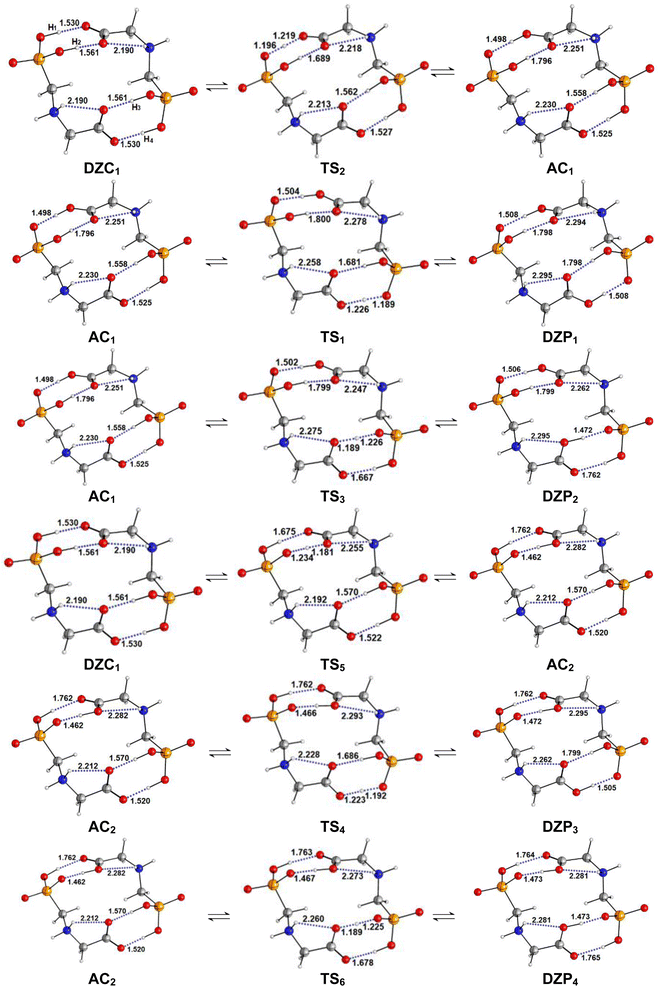 |
| | Fig. 6 Structures of DZP, DZC and AC tautomers involved in the intermolecular proton transfer reaction of Glyph, together with the corresponding transition states (TS), optimized in aqueous solution at SMD-B3LYP-D3/6-311++G(2d,2p) level. Interatomic distances are given in Å. | |
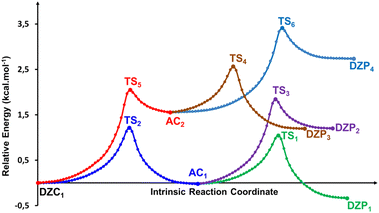 |
| | Fig. 7 Reaction pathways following intrinsic reaction coordinate (IRC) calculations in the forward and reverse directions from each TS involved in the intermolecular tautomerization processes of the most stable ionized forms of neutral Glyph dimer in aqueous solution at SMD-B3LYP-D3/6-311++G(2d,2p). | |
3.3. Dimerization process of Glyph
Table 5 lists the complete set of dimerization energies, calculated for Glyph pairs, in the gas phase and in two different solvents (water and cyclohexane). For each medium, we considered the most stable tautomer for the monomer and the dimer (in water we consider the three tautomers of the most stable DZC1 dimer). Solvent effects on the dimerization energies estimated by δΔG(solv.,tot.) are included in Table 5. The results obtained shows that the dimerization energies are strongly negative, ranging from −23.7 to −29.6 kcal mol−1, depending on the medium. In the gas phase, computation predicted a strong zwitterion–zwitterion interaction energy for the dimer formation of DZC1 from the non-ionized N1 conformer of Glyph monomer of about −23.7 kcal mol−1. The free energy of dimerization at 298.15 K remains quite negative (about −5.5 kcal mol−1) in spite of a large entropy contribution. In cyclohexane (the same structures are considered), dimerization process is more favorable relative to the vacuum phase (−29.6 vs. −23.7 kcal mol−1). The value of free dimerization energy at 298 K (ΔG = −12.1 kcal mol−1) is more than twice the value calculated in vacuum, indicating that dimerization of Glyph is highly exergonic in cyclohexane. In aqueous solution, where zwitterion tautomers (ZP) have to be considered for the Glyph monomer, the calculations predict similar trends for the interaction energy. Dimerization energies are also more negative than the gas phase (ΔE decreased by 3.6 kcal mol−1), but differences with respect to cyclohexane are substantially smaller, about 2.3 kcal mol−1. The zwitterion–zwitterion interaction energy is clearly slightly stronger in DZP1 dimer (less negative by 0.3 kcal mol−1), however, the resultant free energies, for the DZP1 and AC1 dimer geometries, respectively, are about approximately 0.1–0.2 kcal mol−1 less favorable than for the overall minimum DZC1 dimer structure. Calculation shows that the free energy of the dimer formation of DZC1 from ZP1 is increased by 1.5 kcal mol−1 in water with respect to its value in cyclohexane. Most of the differences in estimating ΔG in solution comes from differences in the free solvation energy (δΔGsolv.). As indicated in Table 5, free solvation energy contributions calculated in both media deviate significantly. In water solution, hydration opposes (disfavors) dimerization as all δΔGsolv.tot. values are highly positive. However, free solvation contribution in cyclohexane, is slightly favorable (by 4.7 kcal mol−1). Further analysis shows that solvation effects in water are significantly larger in magnitude for the monomers relative to the dimer (i.e., the values listed in the δΔGsolv.tot column in Table 2 is highly positive) in comparison with the results in cyclohexane. These discrepancies detected among cyclohexane and water solvent effects could be caused by the large differences in the free solvation energy values (ΔGsolv.) among the phosphonate zwitterionic (ZP) and non-ionized neutral (N) monomers. The magnitudes of free solvation energies of ZP1 zwitterions (ΔGsolv = −53.6 kcal mol−1) are much larger (about the thrice) than that (ΔGsolv = −19.9 kcal mol−1)60 of non-ionized N1 conformer in water solution.
Table 5 Energetics (kcal. mol−1) for Glyph dimerization process in the gas phase and in solutiona,b
| |
ΔE |
δΔGsolv.tot. |
ΔG |
Calculations at B3LYP-D3/6-311++G(2d,2p) in the gas phase and at SMD-B3LYP-D3/6–311++G(2d,2p) in solution. Meanings of symbols are as follows: ΔE and ΔG are the total energies and free energies at 298.15 K, respectively. δΔGsolv.tot. standards for the difference in total solvation energies and is defined as: 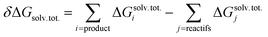 . Note that ΔG in solution also includes the concentration correction, as explained in the method of calculation. . Note that ΔG in solution also includes the concentration correction, as explained in the method of calculation. |
| Gas phase |
2N1 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC1 DZC1 |
−23.7 |
— |
−5.5 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Cyclohexane |
2N1 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC1 DZC1 |
−29.6 |
−4.7 |
−12.1 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Aqueous solution |
2ZP1 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC1 DZC1 |
−27.0 |
52.2 |
−10.6 |
2ZP1 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZP1 DZP1 |
−27.3 |
28.5 |
−10.5 |
2ZP1 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC1 AC1 |
−27.0 |
34.8 |
−10.4 |
Calculation leads to largely much higher difference in solvation energy between the zwitterion ZP1 and the non-ionized N1 forms (δΔGsolv.tot. = 33.7 kcal mol−1) in water than in cyclohexane (δΔGsolv,tot. = 17.4 kcal mol−1). From these obtained results, additional insights can also be made by computing the free energy transfer between the two solvents (water and cyclohexane) (δΔGw–c = ΔGsolv. (H2O) − ΔGsolv. (C6H12) from H2O to C6H12). We find that δΔGw–c < 0 for N1 and ZP1 monomers as well as for DZC1 dimer, indicating their decreased propensities in being solvated by cyclohexane rather than H2O. Calculation reveals that ZP1 present the highest free energy of transfer from water to cyclohexane. The strong tendency of ZP1 monomers to be solvated by water rather than cyclohexane may be due to the greater exposure of chemical groups in the two phosphonate zwitterionic Glyph monomers relative to the non-ionized N1 form and to the carboxylate DZC1 Glyph dimer. Moreover, more important than the solvation energies of any of the individual species, are the differences between the dimer complex and the sum of its constituents. We note that the solvation energy of any of the H-bonded (DZP1, DZC1 and AC1) dimer complexes is substantially less than the combined value of the pair of separated ZP1 monomers. It is this lesser stabilization of the dimer complex by solvation that results in the diminished H-bond energies in water with respect to cyclohexane solution so evident in Table 5. Despite that hydration disfavors significantly the dimer formation of neutral ionized H-bond Glyph dimer complexes, the dimerization process remains strongly exergonic in water solution. Dimer formation of DZC1 it is found slightly more favorable in water than its counterparts AC1 and DZP1. Therefore, in aqueous solution, the mechanism of the dimerization of Glyph from its phosphonate zwitterionic (ZP) monomer could be described by a set of equilibria (1) and (2) including direct proton transfers: 2ZP ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC (1) and DZP
DZC (1) and DZP ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC
AC ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC (2). The Combination of eqn (1) and (2) gives eqn (3) represented by the following set of equilibria: 2ZP
DZC (2). The Combination of eqn (1) and (2) gives eqn (3) represented by the following set of equilibria: 2ZP ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZP
DZP![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC
AC ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC (3). Hence, in aqueous solution, a mixture of DZC1 and their phosphonate zwitterions (DZP) and anion–cation (AC) tautomers, might be abundant in supersaturated aqueous solution, a fact that remains controversial in the literature. Note, finally, that there are some comments on the accuracy of our free energy calculations in solution. A principal source of concern about the presented results had to do with the modeling of solvation of not only the H-bonded dimer complexes, but of the isolated subunits monomers as well. That is, implicit in evaluation of the energetics of the dimerisation process is an assessment of the solvation energy of each of the subunits monomers, as well as the dimer complex. It is readily apparent that a homogenous continuum solvation model which deals with the solvent as a structureless dielectric medium, serves as an inexact model for a solvent with its discrete solvent molecules and the lack of explicit dynamic time dependence in these methods. Nonetheless, continuum models have achieved what is now a long history of successful applications to a range of chemical problems86–88 and even specifically to conventional H-bonds89–92 and to peptides and dipeptides93–96 which are representatives of glycine, the simplest amino acid derivative of Glyph. It is encouraging also that, despite the approximate nature of our treatment of solvation, our findings within the implicit solvation model based on density (SMD) of a 5.1 kcal mol−1 endothermicity for conventional O–H⋯O and of 24.0 kcal mol−1 and 31.8 kcal mol−1 bond strengths for O–H⋯−O and N+–H⋯−O, respectively, are in striking coincidence with the experimental data79,80 and with the computed results obtained97 by applying a more sophisticated treatment of solvation. It is hence concluded that the findings in the present models of H-bond formation in different media are far less subject to inaccuracies introduced by the particular means of including solvation phenomena. Furthermore, it was shown that the pure continuum, while certainly not absolutely accurate in a quantitative sense, allowed to provide very reasonable approximations to the environments they are meant to reproduce. In fact, numerous studies89,98 using a variety of homogenous continuum models had demonstrated that various solvation properties are related in a very nearly fashion to the Onsager function, Fo, that in turn relates to the properties of the solvent.75,76 Fortunately, calculation within the SMD implicit model applied here, had revealed similar trends for Fo, as indicated above in Section 3.1. Indeed, of some importance that these findings are not entirely without experimental support. Our own work on Glyph monomer60 had demonstrated that the implicit solvation model based on density (SMD) combined applied at B3LYP-D3/6-311++G(2d,2p) level is able to provide accurate results on relative energies between zwitterion and non-ionized forms of Glyph monomer in water solution in good accord with the experimental results observed in crystal phase16,17 and in solution.29–31,61,62 Moreover, the hybrid discrete-continuum approach with a water molecule in the first solvation shell had been applied to study the conformational equilibria between ionized and non-ionized tautomers of Glyph monomer in water solution at SMD-B3LYP-D3/6-311++G(2d,2p) level,60 but we found only small changes from the results derived from a pure continuum. The explicit consideration of a large water molecules in the first solvation shell is important to stabilize99–101 as has been established by many studies on amino acids in water using hybrid discrete–continuum approach.102–113 However, for the dimeric system studied herein, statistical analysis of conformations is a fundamental question. Application of classical MD simulations are inappropriate due to limitations of classical force fields in describing proton transfer between Glyph monomers, while ab initio MD simulations are computationally too expensive. Further work will consider a combined QM/MM (quantum mechanics/molecular mechanics) MD methods, which represents an intermediate and promising approach to obtain the free energy of association.
DZC (3). Hence, in aqueous solution, a mixture of DZC1 and their phosphonate zwitterions (DZP) and anion–cation (AC) tautomers, might be abundant in supersaturated aqueous solution, a fact that remains controversial in the literature. Note, finally, that there are some comments on the accuracy of our free energy calculations in solution. A principal source of concern about the presented results had to do with the modeling of solvation of not only the H-bonded dimer complexes, but of the isolated subunits monomers as well. That is, implicit in evaluation of the energetics of the dimerisation process is an assessment of the solvation energy of each of the subunits monomers, as well as the dimer complex. It is readily apparent that a homogenous continuum solvation model which deals with the solvent as a structureless dielectric medium, serves as an inexact model for a solvent with its discrete solvent molecules and the lack of explicit dynamic time dependence in these methods. Nonetheless, continuum models have achieved what is now a long history of successful applications to a range of chemical problems86–88 and even specifically to conventional H-bonds89–92 and to peptides and dipeptides93–96 which are representatives of glycine, the simplest amino acid derivative of Glyph. It is encouraging also that, despite the approximate nature of our treatment of solvation, our findings within the implicit solvation model based on density (SMD) of a 5.1 kcal mol−1 endothermicity for conventional O–H⋯O and of 24.0 kcal mol−1 and 31.8 kcal mol−1 bond strengths for O–H⋯−O and N+–H⋯−O, respectively, are in striking coincidence with the experimental data79,80 and with the computed results obtained97 by applying a more sophisticated treatment of solvation. It is hence concluded that the findings in the present models of H-bond formation in different media are far less subject to inaccuracies introduced by the particular means of including solvation phenomena. Furthermore, it was shown that the pure continuum, while certainly not absolutely accurate in a quantitative sense, allowed to provide very reasonable approximations to the environments they are meant to reproduce. In fact, numerous studies89,98 using a variety of homogenous continuum models had demonstrated that various solvation properties are related in a very nearly fashion to the Onsager function, Fo, that in turn relates to the properties of the solvent.75,76 Fortunately, calculation within the SMD implicit model applied here, had revealed similar trends for Fo, as indicated above in Section 3.1. Indeed, of some importance that these findings are not entirely without experimental support. Our own work on Glyph monomer60 had demonstrated that the implicit solvation model based on density (SMD) combined applied at B3LYP-D3/6-311++G(2d,2p) level is able to provide accurate results on relative energies between zwitterion and non-ionized forms of Glyph monomer in water solution in good accord with the experimental results observed in crystal phase16,17 and in solution.29–31,61,62 Moreover, the hybrid discrete-continuum approach with a water molecule in the first solvation shell had been applied to study the conformational equilibria between ionized and non-ionized tautomers of Glyph monomer in water solution at SMD-B3LYP-D3/6-311++G(2d,2p) level,60 but we found only small changes from the results derived from a pure continuum. The explicit consideration of a large water molecules in the first solvation shell is important to stabilize99–101 as has been established by many studies on amino acids in water using hybrid discrete–continuum approach.102–113 However, for the dimeric system studied herein, statistical analysis of conformations is a fundamental question. Application of classical MD simulations are inappropriate due to limitations of classical force fields in describing proton transfer between Glyph monomers, while ab initio MD simulations are computationally too expensive. Further work will consider a combined QM/MM (quantum mechanics/molecular mechanics) MD methods, which represents an intermediate and promising approach to obtain the free energy of association.
4. Conclusion
In conclusion, we have presented the first theoretical evidence for the formation of a zwitterionic Glyph dimer in vacuum and in solution based on the use of highly accurate computational approach. We have demonstrated that the Glyph dimer predominantly forms a carboxylate zwitterion pair DZC type structure in all media. Our study points out the crucial influence of specific pattern of ionic (O–H⋯−O) and zwitterionic (N+–H⋯−O) H-bonds on the relative stability of different series of ionized and non-ionized Glyph dimers and their various conformers. The DZC1 Glyph dimer structure type involving a centrosymmetric arrangement of carboxylate zwitterion pairs held together by ionic O–H⋯−O Hydrogen bonding network has been shown to process the highest stability, making them one of the most efficient Glyph dimer system in all media. It could be shown that most of the carboxylate zwitterion (DZC) type structure undergo proton transfer in aqueous solution unlike what happens in the gas phase and in cyclohexane. The thermodynamic and kinetic aspects of the intermolecular tautomerism equilibria between the ionized species of Glyph dimers have been determined. Two direct proton transfers from the carboxyl to the phosphonate groups seem to be the most plausible mechanism for the tautomerization process in ionized Glyph dimers. In this postulated mechanism, the Glyph phosphonate (DZP) dimer tautomerization leads to an anion–cation (AC), and the subsequent proton transfer leads to the carboxylate dimer (DZC) product according to the following equilibria: DZP![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC
AC ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC. The solely Glyph phosphonate zwitterion dimer pair sustained by N+–H⋯O H-bonding patter, stable in the gas phase and in cyclohexane solution, isomerize to their DZC tautomers with essentially two pathways identical to those determined in aqueous solution. The calculated thermodynamic parameters of the dimerization process of Glyph monomer show that dimer formation of the most stable carboxylate DZC1 dimer structure is exergonic in vacuum and even in cyclohexane and aqueous solution. Solvents have been shown to play a key role in modulating the energetics of the dimerization of Glyph. Dimerization process in cyclohexane is found more favorable relative to the vacuum phase; this is because the solvation contribution to dimerization in cyclohexane relative to vacuum is small and negative. In aqueous solution, however, hydration opposes dimerization of zwitterionic Glyph monomers as all δΔGsolv.tot. quantities are found highly positive in water. The dimerization process in water is slightly less favorable than in cyclohexane due to the very large disturbing effect of water solvation. It is suggested that a mixture of predominantly carboxylate DZC and their DZP and AC tautomeric species should be present for high Glyph concentrations and that the dimerization process in water, may occur through a set of equilibria including direct proton transfers paths: 2ZP
DZC. The solely Glyph phosphonate zwitterion dimer pair sustained by N+–H⋯O H-bonding patter, stable in the gas phase and in cyclohexane solution, isomerize to their DZC tautomers with essentially two pathways identical to those determined in aqueous solution. The calculated thermodynamic parameters of the dimerization process of Glyph monomer show that dimer formation of the most stable carboxylate DZC1 dimer structure is exergonic in vacuum and even in cyclohexane and aqueous solution. Solvents have been shown to play a key role in modulating the energetics of the dimerization of Glyph. Dimerization process in cyclohexane is found more favorable relative to the vacuum phase; this is because the solvation contribution to dimerization in cyclohexane relative to vacuum is small and negative. In aqueous solution, however, hydration opposes dimerization of zwitterionic Glyph monomers as all δΔGsolv.tot. quantities are found highly positive in water. The dimerization process in water is slightly less favorable than in cyclohexane due to the very large disturbing effect of water solvation. It is suggested that a mixture of predominantly carboxylate DZC and their DZP and AC tautomeric species should be present for high Glyph concentrations and that the dimerization process in water, may occur through a set of equilibria including direct proton transfers paths: 2ZP ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZP
DZP![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC
AC ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC.
DZC.
Data availability
The data supporting this article have been included as part of the ESI.†
Conflicts of interest
There are no conflicts to declare.
References
- G. M. Dill, R. D. Sammons, P. C. C. Feng, F. Kohn, K. Kretzmer, A. Mehrsheikh, M. Bleeke, J. L. Honegger, D. Farmer, D. Wright and E. A. Haupfear, Glyphosate: Discovery, development, applications, and properties. in Glyphosate Resistance in Crops and Weeds: History, Development, and Management, ed. Nandula V. K., John Wiley and Sons, Inc., Hoboken, 2010, pp. 1–33 Search PubMed
 .
. - J. E. Franz, in Discovery, Development and Chemistry of Glyphosate. The Herbicide Glyphosate, ed. E. Grossbard and D. Atkinson, Butterworth and Co., Ltd, Boston, MA, USA, 1985, pp. 3–17 Search PubMed
 .
. - C. Fest and K.-J. Schmidt, The Chemistry of Organo-Phosphorus Pesticides, Springer-Verlag Berlin Heidelberg, New York, 2nd edn, 1982, ch. 3.3 Search PubMed
 .
. - J. E. Franz, M. K. Mao and J. A. Sikorski, Am. Chem. Soc. Monogr., 1997, 189, 653 Search PubMed
 .
. - M. A. Dhansay, P. W. Linder, R. G. Torrington and T. A. Modro, J. Phys. Org. Chem., 1990, 3, 248 CrossRef CAS
 .
. - E. A. Smith and F. W. Oehme, A literature review, Vet. Hum. Toxicol., 1992, 34, 531–543 CAS
 .
. - G. M. Williams, R. Kroes and I. C. Munro, Regul. Toxicol. Pharmacol., 2000, 31, 117–165 CrossRef CAS
 .
. - C. F. B. Coutinho and L. H. Mazo, Quim. Nova, 2005, 28(6), 1038–1045 CrossRef CAS
 .
. - A. S. Silva, I. V. Toth, L. Pezza, H. R. Pezza and J. L. F. C. Lima, Anal. Sci., 2011, 27, 1031–1036 CrossRef CAS PubMed
 .
. - H. C. Steinrücken and N. Amrhein, Eur. J. Biochem., 1984, 143, 351–357 CrossRef PubMed
 .
. - T. Funke, H. Han, L. Martha Healy-Fried, M. Fischer and E. Schönbrunn, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 13010–13015 CrossRef CAS
 .
. - E. Funari, L. Donati, D. Sandroni and M. Vighi, Pesticide levels in groundwater: value and limitation of monitoring. Pesticide Risk in Groundwater, CRC Press, 2019, pp. 3–44 Search PubMed
 .
. - G. S. Johal and D. M. Huber, Eur. J. Agron., 2009, 31, 144–152 CrossRef CAS
 .
. - M. P. Gomes, E. Smedbol, A. Chalifour, L. Hénault-Ethier, M. Labrecque, L. Lepage, M. Lucotte and P. Juneau, J. Exp. Bot., 2014, 65, 4691–4703 CrossRef CAS
 .
. - M. P. Gomes, S. G. Le Manac’h, S. Maccario, M. Labrecque, M. Marc Lucotte and P. Juneau, Pestic. Biochem. Physiol., 2016, 130, 65–70 CrossRef CAS PubMed
 .
. - P. Knuuttila and H. Knuuttila, Acta Chem. Scand., Ser. B, 1979, 33, 623–626 CrossRef
 .
. - H. Krawczyk and T. J. Bartczaks, Phosphorus, Sulfur Silicon Relat. Elem., 1993, 82, 117–125 CrossRef CAS
 .
. - P. H. Smith and K. N. Raymond, Inorg. Chem., 1988, 27, 1056–1061 CrossRef CAS
 .
. - T. G. Appleton, K. A. Byriel, J. R. Hall, C. H. L. Kennard, D. E. Lynch, J. A. Sinkinson and G. Smith, Inorg. Chem., 1994, 33, 444–455 CrossRef CAS
 .
. - D. Heineke, S. J. Franklin and K. N. Raymond, Inorg. Chem., 1994, 33, 2413–2421 CrossRef CAS
 .
. - E. T. Clarke, P. R. Rudolf, A. E. Martell and A. Clearfield, Inorg. Chim. Acta, 1989, 164, 59–63 CrossRef CAS
 .
. - D. S. Sagatys, C. Dahlgren, G. Smith, R. C. Bott and J. M. White, J. Chem. Soc., Dalton
Trans., 2000, 3404–3410 RSC
 .
. - D. S. Sagatys, C. Dahlgren, G. Smith, R. C. Bott and A. C. Willis, Aust. J. Chem., 2000, 53, 77–81 CrossRef CAS
 .
. - P. R. Rudolf, E. T. Clarke, A. E. Martell and A. Clearfield, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1988, 44, 796–799 CrossRef
 .
. - P. H. Smith, F. E. Hahn, A. Hugi and K. N. Raymond, Inorg. Chem., 1989, 28, 20522061 Search PubMed
 .
. - D. Wauchope, J. Agric. Food Chem., 1976, 24, 717 CrossRef CAS
 .
. - A. Piccolo and G. Celano, J. Environ. Sci. Health, Part B, 1993, 28, 447–457 CrossRef
 .
. - A. Piccolo and G. Celano, Environ. Toxicol. Chem., 1994, 13, 1737–1741 CAS
 .
. - B. Liu, L. Dong, Q. Yu, X. Li, F. Wu, Z. Tan and S. Luo, J. Phys. Chem. B, 2016, 120, 2132–2137 CrossRef CAS
 .
. - W. Yan and C. Jing, Environ. Sci. Technol., 2018, 52(4), 1946–1953 CrossRef CAS
 .
. - L. M. Rodríguez, M. L. Pedano, M. Albornoz, J. D. Fuhr, M. L. Martiarena and G. Zampieri, Mater. Today: Proc., 2019, 14, 117–121 Search PubMed
 .
. - P. M. L. Sandercock, Can. Soc. Forensic Sci. J., 1997, 30(4), 191–197 CrossRef
 .
. - S. Shoval and S. Yariv, Agrochimica, 1981, 25(5–6), 377–386 CAS
 .
. - T. G. Appleton, J. R. Hall and I. J. McMahon, Inorg. Chem., 1986, 25, 726–734 CAS
 .
. - H. E. L. Madsen, H. H. Christensen and C. Gottlieb-Petersen, Acta Chem. Scand., Ser. A, 1978, 32, 79 CrossRef
 .
. - R. J. Motekaitis and A. E. Martell, J. Coord. Chem., 1985, 14, 139–149 CAS
 .
. - W. E. Dubbin, G. Sposito and M. Zavarin, Soil Sci., 2000, 165, 699–707 CrossRef CAS
 .
. - J. Sheals, S. Sjöberg and P. Persson, Environ. Sci. Technol., 2002, 36, 3090–3095 CrossRef CAS
 .
. - L. Torstensson, Behaviour of Glyphosate in Soils and its Degradation, in The Herbicide Glyphosate, ed. E. Grossbard and D. Atkinson, Butterworths, London, 1985, pp. 137–150 Search PubMed
 .
. - P. Sprankle, W. F. Meggitt and D. Penner, Weed Sci., 1975, 23, 224–228 CAS
 .
. - R. L. Glass and J. Agric, Food Chem., 1987, 35, 497–500 CAS
 .
. - S. Shoval and S. Yariv, Clays Clay Miner., 1979, 21, 19–23 CrossRef
 .
. - E. Morillo, T. Undabeytia and C. Maqueda, Environ. Sci. Technol., 1997, 31, 3588–3592 CrossRef CAS
 .
. - P. Sprankle, W. F. Meggitt and D. Penner, Weed Sci., 1975, 23, 229–234 CrossRef CAS
 .
. - J. B. Weber, and C. T. Miller, Organic chemical movement over and through soil, in Reactions and Movement of Organic Chemical in Soils, ed. B L Showney and K Brown, Soil Science Society of America, Madison, WI, 1989, pp. 305–334 Search PubMed
 .
. - G. Celano, and A. Piccolo, An infrared spectroscopy approach to the study of the interactions of the herbicide Glyphosate with a purified humic acid Proceedings, Second Inter National Workshop on Pesticides and Soils, University of Alicante, Alicante, Spain, May 31-June 2, 1989, 1991, pp 143–149 Search PubMed
 .
. - S. M. Seyed Khademi, U. Telgheder, Y. Valadbeigi, V. Ilbeigi and M. Tabrizchi, Int. J. Mass Spectrom., 2019, 442, 29–34 CrossRef CAS
 .
. - Q. Zhao, R. Xie, T. Zhang, J. Fang, X. Mei, J. Ning and Y. Tang, Bioorg. Med. Chem. Lett., 2011, 21, 6404–6408 CrossRef CAS PubMed
 .
. - G. Ding, J. Tang, W. Zhang, Y. Li, J. Niu, W. Wang, H. Huo, J. Li and Y. Cao, Crop Prot., 2020, 132, 105111 CAS
 .
. - P. Kaliannan, M. M. N. Ali, T. Seethalakshmi and P. Venuvanalingam, J. Mol. Struct.: THEOCHEM, 2002, 618, 117–125 CrossRef CAS
 .
. - P. Kaliannan, M. M. N. Ali and P. Venuvanalingam, Mol. Phys., 2003, 101, 3073–3083 CrossRef CAS
 .
. - M. M. N. Ali, P. Kaliannan and P. Venuvanalingam, J. Mol. Struct.: THEOCHEM, 2005, 714, 99–108 CrossRef
 .
. - M. M. Peixoto, G. F. Bauerfeldt, M. H. Herbst, M. S. Pereira and C. O. da Silva, J. Phys. Chem. A, 2015, 119(21), 5241–5249 CrossRef CAS
 .
. - G. Ruano, M. L. Pedano, M. Albornoz, J. D. Fuhr, M. L. Martiarena and G. Zampieri, Appl. Surf. Sci., 2021, 567, 150753 CrossRef CAS
 .
. - A. G. Albesa and M. E. F. Hermosilla, Chem. Phys., 2023, 100140 Search PubMed
 .
. - G. Obeid, G. O. Moraes, T. C. Penna, L. A. Schenberg, L. C. Ducati and T. C. Correraa, J. Chem. Phys., 2023, 158, 054306 CrossRef CAS
 .
. - M. Purgel, Z. Takács, C. M. Jonsson, L. Nagy, I. Andersson, I. Bányai, I. Pápai, P. Persson, S. Sjöberg and I. Tóth, J. Inorg. Biochem., 2009, 103, 1426–1438 CrossRef CAS PubMed
 .
. - M. S. Caetano, T. C. Ramalho, D. F. Botrel, E. F. F. da Cunha and W. C. de Mello, Int. J. Quantum Chem., 2012, 112, 2752–2762 CrossRef CAS
 .
. - P. Gros, A. A. Ahmed, O. Kühn and P. Leinweber, Environ. Monit. Assess., 2019, 191, 244 CrossRef
 .
. - O. Fliss, K. Essalah and A. Ben Fredj, Phys. Chem. Chem. Phys., 2021, 23, 26306–26323 RSC
 .
. - B. C. Barja and M. D. S. Afonso, Environ. Sci. Technol., 1998, 32, 3331–3335 CrossRef CAS
 .
. - J. Sheals, P. Persson and B. Hedman, Inorg. Chem., 2001, 40, 4302–4309 CrossRef CAS
 .
. - C. J. G. Wilson, P. A. Wood and S. Parson, CrystEngComm, 2023, 25, 988–997 RSC
 .
. - M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 (Revision D.01), Gaussian, Inc., Wallingford CT, 2009 Search PubMed
 .
. - S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104–154119 CrossRef
 .
. - A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS
 .
. - P. Pechukas, Annu. Rev. Phys. Chem., 1981, 32, 159–177 CrossRef CAS
 .
. - K. Fukui, J. Phys. Chem., 1970, 74, 4161–4163 CrossRef CAS
 .
. - P. Friant-Michel and M. F. Ruiz-Lopez, ChemPhysChem, 2010, 11, 3499–3504 CrossRef CAS
 .
. - C. J. D. Foumthuim, M. Carrer, M. Houvet, T. Škrbić, G. Graziano and A. Giacometti, Phys. Chem. Chem. Phys., 2020, 22, 25848–25858 RSC
 .
. - A. Radzicka and R. Wolfenden, Biochemistry, 1988, 27, 1664–1670 CrossRef CAS
 .
. - A. Villa and A. Mark, J. Comput. Chem., 2002, 23, 548–553 CrossRef CAS
 .
. - J. Chang, A. M. Lenhoff and S. I. Sandler, J. Phys. Chem. B, 2007, 111, 2098–2106 CrossRef CAS PubMed
 .
. - S. Dixit, R. Bhasin, E. Rajasekaran and B. Jayaram, J. Chem. Soc., Faraday Trans., 1997, 93, 1105–1113 RSC
 .
. - L. Onsager, J. Am. Chem. Soc., 1936, 58, 1486–1493 CrossRef CAS
 .
. - M. W. Wong, M. J. Frisch and K. B. Wiberg, J. Am. Chem. Soc., 1991, 113, 4776–4782 CrossRef CAS
 .
. - D. Sitkoff, K. A. Sharp and B. Honig, J. Phys. Chem., 1994, 98, 1978 CrossRef CAS
 .
. - R. Wolfenden, L. Andersson, P. M. Cullis and C. C. B. Southgate, Biochemistry, 1981, 20, 849 CrossRef CAS PubMed
 .
. - C. L. Perrin and J. B. Nielson, Annu. Rev. Phys. Chem., 1997, 48, 511–544 CrossRef CAS
 .
. - M. Meot-Ner Mautner, Chem. Rev., 2012, 112, PR22103 Search PubMed
 .
. - S. Heiles, R. J. Cooper, G. Berden, J. Oomens and E. R. Williams, Phys. Chem. Chem. Phys., 2015, 17, 30642–30647 RSC
 .
. - J. E. Huheey, E. A. Keiter and R. L. Keiter, Inorganic Chemistry : Principles of Structure and Reactivity, New York, 4th edn, 1997 Search PubMed
 .
. - A. Warshel and A. Papazyan, Proc. Natl. Acad. Sci. U.S.A., 1996, 93, 13665–13670 CrossRef CAS
 .
. - A. Onoda, Y. Yamada, J. Takeda, Y. Nakayama, T. Okamura, M. Doi, H. Yamamoto and N. Ueyama, Bull. Chem. Soc. Jpn., 2004, 77, 321–329 CrossRef CAS
 .
. - O. Mó, M. Yáñez, L. Gonzâlez and J. Elguero, ChemPhysChem, 2001, 7, 465–467 CrossRef
 .
. - J. Tomasi, Theor. Chem. Acc., 2004, 112, 184–203 Search PubMed
 .
. - P. Winget, C. J. Cramer and D. G. Truhlar, Theor. Chem. Acc., 2004, 112, 217–227 Search PubMed
 .
. - Y. Moreau, P.-F. Loos and X. Assfeld, Theor. Chem. Acc., 2004, 112, 228–239 Search PubMed
 .
. - S. Scheiner and T. Kar, J. Phys. Chem. B, 2005, 109, 3681–3689 CrossRef CAS
 .
. - C. E. Cannizzaro and K. N. Houk, J. Am. Chem. Soc., 2002, 124, 7163–7169 CrossRef CAS PubMed
 .
. - P. J. A. Ribeiro-Claro and P. D. Vaz, Chem. Phys. Lett., 2004, 390, 358–361 CrossRef CAS
 .
. - S. M. Melikova, K. S. Rutkowski, P. Rodziewicz and A. Koll, J. Mol. Struct., 2004, 705, 49–61 CrossRef CAS
 .
. - Z.-X. Wang and Y. Duan, J. Comput. Chem., 2004, 25, 1699–1716 CrossRef CAS PubMed
 .
. - H. Zhang, Z. Zhou and Y. Shi, J. Phys. Chem. A, 2004, 108, 6735–6743 CrossRef CAS
 .
. - X. Gong, Z. Zhou, D. Du, X. Dong and S. Liu, Int. J. Quantum Chem., 2005, 103, 105–117 CrossRef CAS
 .
. - M. Wen, J. Jiang, Z.-X. Wang and C. Wu, Theor. Chem. Acc., 2014, 133, 1471 Search PubMed
 .
. - N. Ben-Tal, D. Sitkoff, I. A. Topol, A.-S. Yang, S. K. Burt and B. Honig, J. Phys. Chem. B, 1997, 101, 450–475 CrossRef CAS
 .
. - S. Scheiner, J. Phys. Chem. B, 2005, 109, 16132–16141 CrossRef CAS PubMed
 .
. - S. Chalmet, W. Harb and M. F. Ruiz-L pez, J. Phys. Chem. A, 2001, 105, 11574–11581 CrossRef CAS
 .
. - P. I. Nagy and K. Takacs-Novak, Phys. Chem. Chem. Phys., 2004, 6, 2838–2848 RSC
 .
. - A. Lambert, J.-B. Regnouf-de-Vains and M. F. Ruiz-López, Chem. Phys. Lett., 2007, 442, 281–284 CrossRef CAS
 .
. - F. R. Tortonda, J. L. Pascual-Ahuir, E. Silla and I. Tuñón, Chem. Phys. Lett., 1996, 260, 21–26 CrossRef CAS
 .
. - P. Bandyopadhyay and M. S. Gordon, J. Chem. Phys., 2000, 113, 1104–1109 CrossRef CAS
 .
. - P. Bandyopadhyay, M. S. Gordon, B. Mennucci and J. Tomasi, J. Chem. Phys., 2002, 116, 5023–5032 CrossRef CAS
 .
. - N. Benbrahim, A. Rahmouni and M. F. Ruiz-López, Phys. Chem. Chem. Phys., 2008, 10, 5624–5632 RSC
 .
. - H. S. Rzepa and M. Y. Yi, J. Chem. Soc., Perkin Trans., 1991, 2, 531–537 RSC
 .
. - M. S. Gordon and J. H. Jensen, Acc. Chem. Res., 1996, 29, 536–543 CrossRef CAS
 .
. - E. Tajkhorshid, K. J. Jalkanen and S. Suhai, J. Phys. Chem. B, 1998, 102, 5899–5913 CrossRef CAS
 .
. - K. Frimand, H. Bohr, K. J. Jalkanen and S. Suhai, Chem. Phys., 2000, 255, 165–194 CrossRef CAS
 .
. - E. Kassab, J. Langlet, E. Evleth and Y. Akacem, J. Mol. Struct.: THEOCHEM, 2000, 531, 267–282 CrossRef CAS
 .
. - M. N. Blom, I. Compagnon, N. C. Polfer, G. von Helden, G. Meijer, S. Suhai, B. Paizs and J. Oomens, J. Phys. Chem. A, 2007, 111, 7309–7316 CrossRef CAS
 .
. - S. Tiwari, P. C. Mishra and S. Suhai, Int. J. Quantum Chem., 2008, 108, 1004–1016 CrossRef CAS
 .
. - I. Degtyarenko, K. J. Jalkanen, A. A. Gurtovenko and R. M. Nieminen, J. Comput. Theor. Nanosci., 2008, 5, 277 CrossRef CAS
 .
.
Footnote |
| † Electronic supplementary information (ESI) available: Structures and energetics of the most stable conformers of each series of ionized and non-ionized neutral Glyph dimer at B3LYP-D3/6-311++G(2d,2p) level of calculation and using the solvation model based on density (SMD) in different media. Structures and energies of the most stable ionized and non-ionized of neutral Glyph monomer in cyclohexane at SMD-B3LYP-D3/6-311++G(2d,2p) level. It still contains geometry and energy values of the transition states involved in the tautomerization processes of ionized neutral Glyph dimers in vacuum, in cyclohexane and in aqueous solution. See DOI: https://doi.org/10.1039/d4ra04300f |
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *
*
![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC
AC ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC. Results show that solvents play a key role in modulating the energetics of the dimerization process of Glyph. Solvation in cyclohexane, favors the dimerization process however, hydration opposed it. In aqueous solution, the mechanism of the dimerization of Glyph from its phosphonate zwitterionic monomer form (ZP) could be described by a set of equilibria including direct proton transfer paths as follows: 2ZP
DZC. Results show that solvents play a key role in modulating the energetics of the dimerization process of Glyph. Solvation in cyclohexane, favors the dimerization process however, hydration opposed it. In aqueous solution, the mechanism of the dimerization of Glyph from its phosphonate zwitterionic monomer form (ZP) could be described by a set of equilibria including direct proton transfer paths as follows: 2ZP ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZP
DZP ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC
AC ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC. According to our results, in aqueous solution, DZC Glyph dimers and their corresponding DZP and AC tautomers should be present in higher concentration than phosphonate zwitterionic Glyph monomers for high Glyph concentration, a fact that seems controversial in the literature.
DZC. According to our results, in aqueous solution, DZC Glyph dimers and their corresponding DZP and AC tautomers should be present in higher concentration than phosphonate zwitterionic Glyph monomers for high Glyph concentration, a fact that seems controversial in the literature.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 chelates and dimer species with most divalent metal ions when the ligand concentration is doubled.36 The interaction of the herbicide with soil components37–39 such as clay minerals,40–43 oil organic matter44 and soil humic45 molecules has been also the matter of a number of studies. Phosphonate group was found to be mainly responsible for the hydrogen-bonding interaction between Glyph and soil components.39 When the herbicide is in contact with water-soluble HA, IR and fluorescence spectroscopies provided evidence for the formation of HA–Glyph complexes at different pH.28,46 All these experimental studies have provided valuable information on the coordination modes of Glyph in solution but a thorough understanding the behavior of Glyph and its aggregation state in water solution is still lacking. Likewise, several studies focused on the application of the IR spectroscopic techniques27,28,33 to study the acid solution equilibrium of Glyph in water solution have suggested the presence of both monomer and dimer of Glyph at low pH values, however structural molecular details of the dimer are not known. Additionally, corona discharge ion mobility spectrometry (CD-IMS)47 recently applied for direct analysis of Glyph in drinking water at different temperatures have detected the presence of a pic which was attributed to the Glyph dimer, but this attribution had not been clearly confirmed up to now in the literature. As a consequence, the presence of dimers in aqueous solution is still experimentally under debate and data related to dimer complexes of the most widespread herbicide in aqueous solution is poorly known if not absent. Moreover, several recent studies48,49 have pointed out the existence of a close relationship between properties of some herbicide dimers and their bioactivity. They demonstrated that herbicide dimers had higher bioactivities and/or dual modes of action than their corresponding monomers.49 The properties of Glyph dimeric herbicide are not studied till now and therefore, the presence of a structure–activity relationships for Glyph dimer could not be excluded. Theoretically, several investigations have been devoted to study the structure of Glyph monomer either in the gas phase and in aqueous solution.50–59 In particular, the relative stability of neutral (non-ionized) and zwitterionic (ionized) forms has been the object of intense debate. Perhaps, the most systematic and detailed structural study on the Glyph monomer was reported by our researcher group60 at various quantum chemical levels of ab initio and DFT theories, in the gas phase and in aqueous solution. We showed that non-ionized neutral structures exist only in the gas phase but the zwitterionic form is unstable in vacuo at all levels of theory. In aqueous solution, the integral equation formalism polarizable continuum model (IEFPCM) using the standard UFF radii cavity failed to correctly predict the stabilization of the zwitterionic form with respect to the non-ionized neutral form in aqueous solution. However, calculation with the density based solvation model (SMD) was well consistent with the experimental findings and led to the identification of the phosphonate zwitterionic (ZP) structure as the global minimum energy in aqueous solution.29–31,61,62 Our own results have been confirmed, subsequently, by a more recent paper55 dealing with the Glyph deprotonation in solution. The latter study had supported the use of the SMD-B3LYP-D3/6-311++G(2d,2p) as the most reliable level of calculation to predict accurately the structure of Glyph monomer and its deprotonation reaction sites in water solution. Regarding Glyph dimers, they have received some theoretical attention too,47,63 although much less than the monomer. Previous quantum chemical studies on Glyph dimers were restricted to proton-bound Glyph dimer in the gas phase.47 An other recent investigation63 motivated by the observation of two high pressure phase transitions by Raman spectroscopy, allowed the prediction of a new crystal structure of Glyph consisting of periodic repetition of pairs of zwitterion forms sustained by N–H⋯O H-bonds using crystal modeling. Moreover, other theoretical studies57,58 concluded that dimers of Glyph are stabilized by divalent and trivalent metal cations, which is feasible in biological systems. But, most of them considered the cationic and/or the mono-anion dimer complex structures57 with Glyph molecule as anion and dianion in the gas phase and/or in solution. Despite these few reports, theoretical or experimental structural studies dealing with the homo- and heterodimers neutral forms of Glyph with non-ionized and/or zwitterion forms in the gas phase and in solution are absent. In this work, quantum mechanical calculations were carried out trying to address the following fundamental questions: (1) are there energy minima for ionized forms of Glyph dimers (zwitterion–zwitterion, non-ionized–zwitterion, anion–cation) and if yes, what are the relative stabilities of the ionized and non-ionized forms, (2) what is the influence of the medium (gas phase, nonpolar solvent, water) on both structure and stability, and (3) what is the free energy and the mechanism of dimer association of Glyph in vacuum and in solution?
1 chelates and dimer species with most divalent metal ions when the ligand concentration is doubled.36 The interaction of the herbicide with soil components37–39 such as clay minerals,40–43 oil organic matter44 and soil humic45 molecules has been also the matter of a number of studies. Phosphonate group was found to be mainly responsible for the hydrogen-bonding interaction between Glyph and soil components.39 When the herbicide is in contact with water-soluble HA, IR and fluorescence spectroscopies provided evidence for the formation of HA–Glyph complexes at different pH.28,46 All these experimental studies have provided valuable information on the coordination modes of Glyph in solution but a thorough understanding the behavior of Glyph and its aggregation state in water solution is still lacking. Likewise, several studies focused on the application of the IR spectroscopic techniques27,28,33 to study the acid solution equilibrium of Glyph in water solution have suggested the presence of both monomer and dimer of Glyph at low pH values, however structural molecular details of the dimer are not known. Additionally, corona discharge ion mobility spectrometry (CD-IMS)47 recently applied for direct analysis of Glyph in drinking water at different temperatures have detected the presence of a pic which was attributed to the Glyph dimer, but this attribution had not been clearly confirmed up to now in the literature. As a consequence, the presence of dimers in aqueous solution is still experimentally under debate and data related to dimer complexes of the most widespread herbicide in aqueous solution is poorly known if not absent. Moreover, several recent studies48,49 have pointed out the existence of a close relationship between properties of some herbicide dimers and their bioactivity. They demonstrated that herbicide dimers had higher bioactivities and/or dual modes of action than their corresponding monomers.49 The properties of Glyph dimeric herbicide are not studied till now and therefore, the presence of a structure–activity relationships for Glyph dimer could not be excluded. Theoretically, several investigations have been devoted to study the structure of Glyph monomer either in the gas phase and in aqueous solution.50–59 In particular, the relative stability of neutral (non-ionized) and zwitterionic (ionized) forms has been the object of intense debate. Perhaps, the most systematic and detailed structural study on the Glyph monomer was reported by our researcher group60 at various quantum chemical levels of ab initio and DFT theories, in the gas phase and in aqueous solution. We showed that non-ionized neutral structures exist only in the gas phase but the zwitterionic form is unstable in vacuo at all levels of theory. In aqueous solution, the integral equation formalism polarizable continuum model (IEFPCM) using the standard UFF radii cavity failed to correctly predict the stabilization of the zwitterionic form with respect to the non-ionized neutral form in aqueous solution. However, calculation with the density based solvation model (SMD) was well consistent with the experimental findings and led to the identification of the phosphonate zwitterionic (ZP) structure as the global minimum energy in aqueous solution.29–31,61,62 Our own results have been confirmed, subsequently, by a more recent paper55 dealing with the Glyph deprotonation in solution. The latter study had supported the use of the SMD-B3LYP-D3/6-311++G(2d,2p) as the most reliable level of calculation to predict accurately the structure of Glyph monomer and its deprotonation reaction sites in water solution. Regarding Glyph dimers, they have received some theoretical attention too,47,63 although much less than the monomer. Previous quantum chemical studies on Glyph dimers were restricted to proton-bound Glyph dimer in the gas phase.47 An other recent investigation63 motivated by the observation of two high pressure phase transitions by Raman spectroscopy, allowed the prediction of a new crystal structure of Glyph consisting of periodic repetition of pairs of zwitterion forms sustained by N–H⋯O H-bonds using crystal modeling. Moreover, other theoretical studies57,58 concluded that dimers of Glyph are stabilized by divalent and trivalent metal cations, which is feasible in biological systems. But, most of them considered the cationic and/or the mono-anion dimer complex structures57 with Glyph molecule as anion and dianion in the gas phase and/or in solution. Despite these few reports, theoretical or experimental structural studies dealing with the homo- and heterodimers neutral forms of Glyph with non-ionized and/or zwitterion forms in the gas phase and in solution are absent. In this work, quantum mechanical calculations were carried out trying to address the following fundamental questions: (1) are there energy minima for ionized forms of Glyph dimers (zwitterion–zwitterion, non-ionized–zwitterion, anion–cation) and if yes, what are the relative stabilities of the ionized and non-ionized forms, (2) what is the influence of the medium (gas phase, nonpolar solvent, water) on both structure and stability, and (3) what is the free energy and the mechanism of dimer association of Glyph in vacuum and in solution?

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(1/22.4)
ln(1/22.4)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups. It may be noted that, all the calculated Glyph dimer free energies of hydration are seen very negative and fall within the range −42.4 kcal mol−1 (for non-ionized) to −81 kcal mol−1 (for ionized DZP). Of some importance is the comparable behavior of the zwitterionic glycine dimer69 and several zwitterionic amino acids70,73,74 in water solution. The data corresponding to the carboxylate zwitterion dimers, reported in Table 2, are remarkably similar to the value (ΔGsolv. = −66.3 kcal mol−1) computed for carboxylate zwitterionic glycine dimer in water solution.69 One may notes that these values obtained in the range −42–81 kcal mol−1 are in consonant to the estimate of −59 kcal mol−1 from the Onsager formula75,76 for the solvation free energy of a dipolar sphere. Our calculations showed that solvation properties are related in a very nearly fashion to the Onsager function, Fo, that in turn relates to the properties of the solvent.75,76 In fact, the increase of ΔGsolv.tot. by about more than the thrice of any species of DZC Glyph dimer from cyclohexane to water can be correlated is nearly a linear function of with the rise in the Onsager function Fo = (ε − 1)/(ε + 2),75,76 which is itself magnified by a factor of 3.4 when increases from 2 to 78. There is hence every reason to believe that the solvation model being applied here, while certainly not absolutely accurate in a quantitative sense, provide very reasonable approximations to the environments they are meant to reproduce. It may be noted that the estimation of non-electrostatic contribution arising from short-range interactions between the solute and solvent molecules in the first solvation shell, called the cavity–dispersion–solvent-structure (CDS) term, differ from cyclohexane to water. While Enonel. terms are negative and low in cyclohexane, they are positive and largely expected (in absolute values) in water solution. These results can be easily rationalized by the fact that water molecules are the smallest (a cyclohexane molecule has a van der Waals volume roughly 5 times larger than that of a water molecule) and so liquid water is characterized by the largest number density, which in turn increases the entropy loss associated with cavity creation, due to the solvent-excluded volume effect. As a consequence, the energy associated to cavity creation is larger to that in cyclohexane and thus non-electrostatic (CDS) contribution is positive and larger in water. Nevertheless, solvation free energy ΔGsolv in H2O (see Table 2) are found negative for all dimers, paralleling the situation in nonpolar medium C6H12. This may indicate that the free energy cost of cavity creation is not so large and the attractive solute–solvent energetic interactions (accounting also for hydrogen bonds) are able to overcome the free energy cost of cavity creation. These results are in line with experimental data71,77,78 and previous computational investigations of several polar amino acid side chain equivalents in cyclohexane solution and in water.70,72–74 Nonetheless, calculation reveal that the highest values of free energy of solvation (|ΔGsolv.| values) are not associated to the most stable solute in aqueous solution and in cyclohexane. As is shown in Table 1, the carboxylate zwitterionic dimer form DZC1 which is the most stable Glyph dimer do not experience the largest solvation (or polarization) in water and in cyclohexane solution. This indicates that several effects in addition to the polarization term are involved and counteract each other, even when effects on solvent are not considered explicitly. Among these effects, non-covalent intermolecular and intra-moleculecular hydrogen-bondings (H-bonds) may be important for structure selection and stability of Glyph dimers in different media. To elucidate the role of H-bonds, their structural features are inspected and criticized in the series of the five types of Glyph dimer structures displayed in Fig. 1–3. Structural analysis of the equilibrium structures affords a total of a maximum of seven short contacts characterizing H-bonds of each series of type of structure (DZC, DZP, AC, NZP, DN), which are classified in chemical classes belonging to three fundamental types: neutral H-bonds (HB) between two neutral groups, ionic H-bonds (IHB) between a neutral and charged group and zwitterionic H-bonds (ZHB) between two oppositely charged groups. Fig. 1–3, show that both O–H⋯−O and N+–H⋯O ionic H-bonds participate in stabilizing the IHB pattern which result in the formation of 8-membered rings (displaying O–H⋯−O) and 9-membered rings (establishing O–H⋯−O and N+–H⋯O) with different arrangements. ZHB consist of intramolecular and intermolecular N+–H⋯−O H-bonds through which 5- and 10- membered rings are formed. In Table 3 are collected the intermolecular and intramolecular bond distances (dO⋯H) characterizing the IHB, ZHB and HB for the most stable structures of each type (DZC, DZP, AC, NZP, DN) of Glyph dimer in different media. From the results obtained in Table 3, it is clear that the largest contributors to the stabilization of the glyphosate dimers are IHB and ZHB in the ionized Glyph dimers, HB and IHB in NZ and only HB in DN dimer structures in the gas phase and in solution. As pointed out in previous experimental79,80 and theoretical81 reports, the bond strength of these H-bonds should follow the ranking HB < IHB ≤ ZHB. For Glyph dimer, our computation at B3LYP-D3/6-311++G(2d,2p) give bond strengths of 24.0 kcal mol−1 for O–H⋯−O IHB, of 31.8 kcal mol−1 for N+–H⋯−O ZHB and of 5.1 kcal mol−1 for O–H⋯O HB, in quantitative agreement with the experimental data79,80 (a bond strength on the order of ∼5 kcal mol−1 for HB and bond strengths typically between 5–35 kcal mol−1 for IHB and ZHB). Therefore, the energetic competition between ionized and non-ionized isomers of Glyph dimer is due to the high stabilization energy of the ionic hydrogen bond (IHB) network in the ionized structures compared to that in NZ and DN isomers. The presence of four high bond energy of O–H⋯−O IHB and 2N+–H⋯−O ZHB impart a greater stability to the carboxylate zwitterionic units in DZC dimers in comparison with phosphonate zwitterion pairs in DZP and anion–cation pairs in AC and non-ionized pairs (DN). The effect of multiple IHB and ZHB on the stabilization of DZC with respect to the other isomers is visible even in the gas phase. A double carboxylate zwitterion (such as in DZC structures) without additional solvent molecules attached are stabilized both by the attractive coulomb interaction between opposite charges and by enhanced IHB and ZHB H-bonding networks. As shown in Table 3, all the dO⋯H are in the range 1.490–2.437 Å significantly inferior to the sum of the vander Walls radii (2.72 Å),82 indicating that all the primary intermolecular and intramolecular (O–H⋯−O and N+–H⋯−O) interactions in the DZC types of structures are very strong in the gas phase. Whenever, calculation show that solvents have significantly effects on the properties of these H-bonds. The upper set of data indicates a distinction between the IHB, ZHB and HB. Whereas the increasing polarity of the solvent has a significant effect on the two former sort of H-bonds, only a smaller effect upon the length of the latter is detected. The bond strengths of the neutral O–H⋯O and N–H⋯O H-bonds are maintained in a cyclohexane solution having a low dielectric constant. However, opposite solvent effects are detected on IHB and ZHB when ε rises. While the length of O–H⋯−O decreased, the N+–H⋯−O elongates quickly in a uniform fashion such that the N+–H⋯−O all become significantly weaker than OH⋯−O H-bonds in water solution. The perturbation effect of N+–H⋯−O zwitterionic H-bonds by hydration can be due to the fact that the random orientation of the dipolar interaction of the water polar solvent cannot be as effective as the amine groups with a readily formable orientation as was explained in previous works on low-barrier hydrogen bonding.83,84 The most important feature, is that the N+–H⋯−O H-bond weakening coupled to a shortening of the inter-subunit separation, facilitate in aqueous solution the proton transfer between the hydroxide group (O–H) and oxygen ions (O−) of carboxylate group in DZC. In effect, the equilibrium distance between donor and acceptor is in the range 1.564–1.719 Å in gas phase. This is too large as compared to 1.528–1.574 Å in aqueous solution, and hence the proton transfer in this position is strongly unfavorable. Remarkably notes are the fact that most of the DZC type structure Glyph dimer (DZC1 to DZC5), can entirely be isomerized to their AC tautomers and DZP form in aqueous solution. However, no proton transfer was achieved in the gas phase and in cyclohexane for the five most stable DZC structure. All DZP and AC structures tautomers of DZC1 found in aqueous solution are not stable in the gas phase and most of them collapse after optimization to their DZC or to one of the DZC conformers already optimized in gas phase. Therefore, characteristics and structural features of Glyph dimers, established for the gas phase and non-polar solvent, are different fundamentally from that for aqueous solution. The differences detected has a great deal with structural properties which are coupled to the medium reorganization as was pointed above. More specifically, the principal discrepancies detected in solution result mainly from differences in solvation energies between ionized and non-ionized species which exceed four times in water. Obviously, these solvation effects on ionized and non-ionized dimer species can change dramatically the relative acidity/basicity determined in the gas phase. As a consequence, the intermolecular proton-transfer could be affected in ionized species and therefore changes in prototropic conversion equilibria may be involved in different media. In the following section, we will try to study the tautomerism in Glyph dimer by outlying the main feature of the proton transfer mechanism between ionized species of Glyph dimers in the different environments. We will show if a possible proton transfer could take place in the gas phase and in cyclohexane since DZP and AC ionized species are stable in these media?
O groups. It may be noted that, all the calculated Glyph dimer free energies of hydration are seen very negative and fall within the range −42.4 kcal mol−1 (for non-ionized) to −81 kcal mol−1 (for ionized DZP). Of some importance is the comparable behavior of the zwitterionic glycine dimer69 and several zwitterionic amino acids70,73,74 in water solution. The data corresponding to the carboxylate zwitterion dimers, reported in Table 2, are remarkably similar to the value (ΔGsolv. = −66.3 kcal mol−1) computed for carboxylate zwitterionic glycine dimer in water solution.69 One may notes that these values obtained in the range −42–81 kcal mol−1 are in consonant to the estimate of −59 kcal mol−1 from the Onsager formula75,76 for the solvation free energy of a dipolar sphere. Our calculations showed that solvation properties are related in a very nearly fashion to the Onsager function, Fo, that in turn relates to the properties of the solvent.75,76 In fact, the increase of ΔGsolv.tot. by about more than the thrice of any species of DZC Glyph dimer from cyclohexane to water can be correlated is nearly a linear function of with the rise in the Onsager function Fo = (ε − 1)/(ε + 2),75,76 which is itself magnified by a factor of 3.4 when increases from 2 to 78. There is hence every reason to believe that the solvation model being applied here, while certainly not absolutely accurate in a quantitative sense, provide very reasonable approximations to the environments they are meant to reproduce. It may be noted that the estimation of non-electrostatic contribution arising from short-range interactions between the solute and solvent molecules in the first solvation shell, called the cavity–dispersion–solvent-structure (CDS) term, differ from cyclohexane to water. While Enonel. terms are negative and low in cyclohexane, they are positive and largely expected (in absolute values) in water solution. These results can be easily rationalized by the fact that water molecules are the smallest (a cyclohexane molecule has a van der Waals volume roughly 5 times larger than that of a water molecule) and so liquid water is characterized by the largest number density, which in turn increases the entropy loss associated with cavity creation, due to the solvent-excluded volume effect. As a consequence, the energy associated to cavity creation is larger to that in cyclohexane and thus non-electrostatic (CDS) contribution is positive and larger in water. Nevertheless, solvation free energy ΔGsolv in H2O (see Table 2) are found negative for all dimers, paralleling the situation in nonpolar medium C6H12. This may indicate that the free energy cost of cavity creation is not so large and the attractive solute–solvent energetic interactions (accounting also for hydrogen bonds) are able to overcome the free energy cost of cavity creation. These results are in line with experimental data71,77,78 and previous computational investigations of several polar amino acid side chain equivalents in cyclohexane solution and in water.70,72–74 Nonetheless, calculation reveal that the highest values of free energy of solvation (|ΔGsolv.| values) are not associated to the most stable solute in aqueous solution and in cyclohexane. As is shown in Table 1, the carboxylate zwitterionic dimer form DZC1 which is the most stable Glyph dimer do not experience the largest solvation (or polarization) in water and in cyclohexane solution. This indicates that several effects in addition to the polarization term are involved and counteract each other, even when effects on solvent are not considered explicitly. Among these effects, non-covalent intermolecular and intra-moleculecular hydrogen-bondings (H-bonds) may be important for structure selection and stability of Glyph dimers in different media. To elucidate the role of H-bonds, their structural features are inspected and criticized in the series of the five types of Glyph dimer structures displayed in Fig. 1–3. Structural analysis of the equilibrium structures affords a total of a maximum of seven short contacts characterizing H-bonds of each series of type of structure (DZC, DZP, AC, NZP, DN), which are classified in chemical classes belonging to three fundamental types: neutral H-bonds (HB) between two neutral groups, ionic H-bonds (IHB) between a neutral and charged group and zwitterionic H-bonds (ZHB) between two oppositely charged groups. Fig. 1–3, show that both O–H⋯−O and N+–H⋯O ionic H-bonds participate in stabilizing the IHB pattern which result in the formation of 8-membered rings (displaying O–H⋯−O) and 9-membered rings (establishing O–H⋯−O and N+–H⋯O) with different arrangements. ZHB consist of intramolecular and intermolecular N+–H⋯−O H-bonds through which 5- and 10- membered rings are formed. In Table 3 are collected the intermolecular and intramolecular bond distances (dO⋯H) characterizing the IHB, ZHB and HB for the most stable structures of each type (DZC, DZP, AC, NZP, DN) of Glyph dimer in different media. From the results obtained in Table 3, it is clear that the largest contributors to the stabilization of the glyphosate dimers are IHB and ZHB in the ionized Glyph dimers, HB and IHB in NZ and only HB in DN dimer structures in the gas phase and in solution. As pointed out in previous experimental79,80 and theoretical81 reports, the bond strength of these H-bonds should follow the ranking HB < IHB ≤ ZHB. For Glyph dimer, our computation at B3LYP-D3/6-311++G(2d,2p) give bond strengths of 24.0 kcal mol−1 for O–H⋯−O IHB, of 31.8 kcal mol−1 for N+–H⋯−O ZHB and of 5.1 kcal mol−1 for O–H⋯O HB, in quantitative agreement with the experimental data79,80 (a bond strength on the order of ∼5 kcal mol−1 for HB and bond strengths typically between 5–35 kcal mol−1 for IHB and ZHB). Therefore, the energetic competition between ionized and non-ionized isomers of Glyph dimer is due to the high stabilization energy of the ionic hydrogen bond (IHB) network in the ionized structures compared to that in NZ and DN isomers. The presence of four high bond energy of O–H⋯−O IHB and 2N+–H⋯−O ZHB impart a greater stability to the carboxylate zwitterionic units in DZC dimers in comparison with phosphonate zwitterion pairs in DZP and anion–cation pairs in AC and non-ionized pairs (DN). The effect of multiple IHB and ZHB on the stabilization of DZC with respect to the other isomers is visible even in the gas phase. A double carboxylate zwitterion (such as in DZC structures) without additional solvent molecules attached are stabilized both by the attractive coulomb interaction between opposite charges and by enhanced IHB and ZHB H-bonding networks. As shown in Table 3, all the dO⋯H are in the range 1.490–2.437 Å significantly inferior to the sum of the vander Walls radii (2.72 Å),82 indicating that all the primary intermolecular and intramolecular (O–H⋯−O and N+–H⋯−O) interactions in the DZC types of structures are very strong in the gas phase. Whenever, calculation show that solvents have significantly effects on the properties of these H-bonds. The upper set of data indicates a distinction between the IHB, ZHB and HB. Whereas the increasing polarity of the solvent has a significant effect on the two former sort of H-bonds, only a smaller effect upon the length of the latter is detected. The bond strengths of the neutral O–H⋯O and N–H⋯O H-bonds are maintained in a cyclohexane solution having a low dielectric constant. However, opposite solvent effects are detected on IHB and ZHB when ε rises. While the length of O–H⋯−O decreased, the N+–H⋯−O elongates quickly in a uniform fashion such that the N+–H⋯−O all become significantly weaker than OH⋯−O H-bonds in water solution. The perturbation effect of N+–H⋯−O zwitterionic H-bonds by hydration can be due to the fact that the random orientation of the dipolar interaction of the water polar solvent cannot be as effective as the amine groups with a readily formable orientation as was explained in previous works on low-barrier hydrogen bonding.83,84 The most important feature, is that the N+–H⋯−O H-bond weakening coupled to a shortening of the inter-subunit separation, facilitate in aqueous solution the proton transfer between the hydroxide group (O–H) and oxygen ions (O−) of carboxylate group in DZC. In effect, the equilibrium distance between donor and acceptor is in the range 1.564–1.719 Å in gas phase. This is too large as compared to 1.528–1.574 Å in aqueous solution, and hence the proton transfer in this position is strongly unfavorable. Remarkably notes are the fact that most of the DZC type structure Glyph dimer (DZC1 to DZC5), can entirely be isomerized to their AC tautomers and DZP form in aqueous solution. However, no proton transfer was achieved in the gas phase and in cyclohexane for the five most stable DZC structure. All DZP and AC structures tautomers of DZC1 found in aqueous solution are not stable in the gas phase and most of them collapse after optimization to their DZC or to one of the DZC conformers already optimized in gas phase. Therefore, characteristics and structural features of Glyph dimers, established for the gas phase and non-polar solvent, are different fundamentally from that for aqueous solution. The differences detected has a great deal with structural properties which are coupled to the medium reorganization as was pointed above. More specifically, the principal discrepancies detected in solution result mainly from differences in solvation energies between ionized and non-ionized species which exceed four times in water. Obviously, these solvation effects on ionized and non-ionized dimer species can change dramatically the relative acidity/basicity determined in the gas phase. As a consequence, the intermolecular proton-transfer could be affected in ionized species and therefore changes in prototropic conversion equilibria may be involved in different media. In the following section, we will try to study the tautomerism in Glyph dimer by outlying the main feature of the proton transfer mechanism between ionized species of Glyph dimers in the different environments. We will show if a possible proton transfer could take place in the gas phase and in cyclohexane since DZP and AC ionized species are stable in these media?


![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC
AC![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC. The anion–cation AC species can be considered as a reaction intermediate in equilibrium with phosphonate (DZP) and carboxylate (DZC) tautomers. In cyclohexane, calculation have predicted the same mechanism of intermolecular proton transfer between DZP9 and its corresponding anion–cation AC9 and carboxylate DZC9 tautomers (Fig. 5a). Cartesian coordinates of the transition states (TS) DZC and AC and between AC and DZP tautomers for DZP9 and AC9 conversions, in cyclohexane are reported in ESI S74–75.†
DZC. The anion–cation AC species can be considered as a reaction intermediate in equilibrium with phosphonate (DZP) and carboxylate (DZC) tautomers. In cyclohexane, calculation have predicted the same mechanism of intermolecular proton transfer between DZP9 and its corresponding anion–cation AC9 and carboxylate DZC9 tautomers (Fig. 5a). Cartesian coordinates of the transition states (TS) DZC and AC and between AC and DZP tautomers for DZP9 and AC9 conversions, in cyclohexane are reported in ESI S74–75.†
![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) TS1
TS1 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC9
AC9![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) TS2
TS2 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC9
DZC9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) TS1
TS1 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC9
AC9![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) TS2
TS2 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC9
DZC9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) TS1
TS1 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC1
AC1![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) TS2
TS2 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC1
DZC1![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) TS3
TS3 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC1
AC1![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) TS4
TS4 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC2
AC2![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) TS5
TS5 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC1
DZC1![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) TS6
TS6 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC2
AC2![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC
AC ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC. It is to be noted that DZC5 (Fig. 2) which is nearly isoenergetic to DZC1 (ΔG = 0.1 kcal mol−1) exhibits similar mechanism of interconversion to its corresponding AC and DZP tautomers as DZC1. However, the number of its tautomers differ from that of DZC1. Calculation predicts that DZC5 interconverts to four AC structures by (HHHH) proton transfers noted as AC3, AC4, AC5 and AC6. Each of the AC dimer structure interconverts to two DZP tautomers by (HH) non-degenerated tautomerism proton transfer giving in all eight DZP tautomers (with four isoenergetic identical to the other) as shown in ESI, Fig. S2.† Relative free energies (ΔG) between tautomers are roughly about 1–2 kcal mol−1 and thus a rapid interconversion between them could be predicted as was also proposed for the most stable DZC1 structure in aqueous solution.
DZC. It is to be noted that DZC5 (Fig. 2) which is nearly isoenergetic to DZC1 (ΔG = 0.1 kcal mol−1) exhibits similar mechanism of interconversion to its corresponding AC and DZP tautomers as DZC1. However, the number of its tautomers differ from that of DZC1. Calculation predicts that DZC5 interconverts to four AC structures by (HHHH) proton transfers noted as AC3, AC4, AC5 and AC6. Each of the AC dimer structure interconverts to two DZP tautomers by (HH) non-degenerated tautomerism proton transfer giving in all eight DZP tautomers (with four isoenergetic identical to the other) as shown in ESI, Fig. S2.† Relative free energies (ΔG) between tautomers are roughly about 1–2 kcal mol−1 and thus a rapid interconversion between them could be predicted as was also proposed for the most stable DZC1 structure in aqueous solution.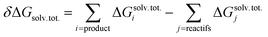 . Note that ΔG in solution also includes the concentration correction, as explained in the method of calculation.
. Note that ΔG in solution also includes the concentration correction, as explained in the method of calculation.![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC1
DZC1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC1
DZC1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC1
DZC1![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZP1
DZP1![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC1
AC1![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC (1) and DZP
DZC (1) and DZP ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC
AC ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC (2). The Combination of eqn (1) and (2) gives eqn (3) represented by the following set of equilibria: 2ZP
DZC (2). The Combination of eqn (1) and (2) gives eqn (3) represented by the following set of equilibria: 2ZP ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZP
DZP![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC
AC ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC (3). Hence, in aqueous solution, a mixture of DZC1 and their phosphonate zwitterions (DZP) and anion–cation (AC) tautomers, might be abundant in supersaturated aqueous solution, a fact that remains controversial in the literature. Note, finally, that there are some comments on the accuracy of our free energy calculations in solution. A principal source of concern about the presented results had to do with the modeling of solvation of not only the H-bonded dimer complexes, but of the isolated subunits monomers as well. That is, implicit in evaluation of the energetics of the dimerisation process is an assessment of the solvation energy of each of the subunits monomers, as well as the dimer complex. It is readily apparent that a homogenous continuum solvation model which deals with the solvent as a structureless dielectric medium, serves as an inexact model for a solvent with its discrete solvent molecules and the lack of explicit dynamic time dependence in these methods. Nonetheless, continuum models have achieved what is now a long history of successful applications to a range of chemical problems86–88 and even specifically to conventional H-bonds89–92 and to peptides and dipeptides93–96 which are representatives of glycine, the simplest amino acid derivative of Glyph. It is encouraging also that, despite the approximate nature of our treatment of solvation, our findings within the implicit solvation model based on density (SMD) of a 5.1 kcal mol−1 endothermicity for conventional O–H⋯O and of 24.0 kcal mol−1 and 31.8 kcal mol−1 bond strengths for O–H⋯−O and N+–H⋯−O, respectively, are in striking coincidence with the experimental data79,80 and with the computed results obtained97 by applying a more sophisticated treatment of solvation. It is hence concluded that the findings in the present models of H-bond formation in different media are far less subject to inaccuracies introduced by the particular means of including solvation phenomena. Furthermore, it was shown that the pure continuum, while certainly not absolutely accurate in a quantitative sense, allowed to provide very reasonable approximations to the environments they are meant to reproduce. In fact, numerous studies89,98 using a variety of homogenous continuum models had demonstrated that various solvation properties are related in a very nearly fashion to the Onsager function, Fo, that in turn relates to the properties of the solvent.75,76 Fortunately, calculation within the SMD implicit model applied here, had revealed similar trends for Fo, as indicated above in Section 3.1. Indeed, of some importance that these findings are not entirely without experimental support. Our own work on Glyph monomer60 had demonstrated that the implicit solvation model based on density (SMD) combined applied at B3LYP-D3/6-311++G(2d,2p) level is able to provide accurate results on relative energies between zwitterion and non-ionized forms of Glyph monomer in water solution in good accord with the experimental results observed in crystal phase16,17 and in solution.29–31,61,62 Moreover, the hybrid discrete-continuum approach with a water molecule in the first solvation shell had been applied to study the conformational equilibria between ionized and non-ionized tautomers of Glyph monomer in water solution at SMD-B3LYP-D3/6-311++G(2d,2p) level,60 but we found only small changes from the results derived from a pure continuum. The explicit consideration of a large water molecules in the first solvation shell is important to stabilize99–101 as has been established by many studies on amino acids in water using hybrid discrete–continuum approach.102–113 However, for the dimeric system studied herein, statistical analysis of conformations is a fundamental question. Application of classical MD simulations are inappropriate due to limitations of classical force fields in describing proton transfer between Glyph monomers, while ab initio MD simulations are computationally too expensive. Further work will consider a combined QM/MM (quantum mechanics/molecular mechanics) MD methods, which represents an intermediate and promising approach to obtain the free energy of association.
DZC (3). Hence, in aqueous solution, a mixture of DZC1 and their phosphonate zwitterions (DZP) and anion–cation (AC) tautomers, might be abundant in supersaturated aqueous solution, a fact that remains controversial in the literature. Note, finally, that there are some comments on the accuracy of our free energy calculations in solution. A principal source of concern about the presented results had to do with the modeling of solvation of not only the H-bonded dimer complexes, but of the isolated subunits monomers as well. That is, implicit in evaluation of the energetics of the dimerisation process is an assessment of the solvation energy of each of the subunits monomers, as well as the dimer complex. It is readily apparent that a homogenous continuum solvation model which deals with the solvent as a structureless dielectric medium, serves as an inexact model for a solvent with its discrete solvent molecules and the lack of explicit dynamic time dependence in these methods. Nonetheless, continuum models have achieved what is now a long history of successful applications to a range of chemical problems86–88 and even specifically to conventional H-bonds89–92 and to peptides and dipeptides93–96 which are representatives of glycine, the simplest amino acid derivative of Glyph. It is encouraging also that, despite the approximate nature of our treatment of solvation, our findings within the implicit solvation model based on density (SMD) of a 5.1 kcal mol−1 endothermicity for conventional O–H⋯O and of 24.0 kcal mol−1 and 31.8 kcal mol−1 bond strengths for O–H⋯−O and N+–H⋯−O, respectively, are in striking coincidence with the experimental data79,80 and with the computed results obtained97 by applying a more sophisticated treatment of solvation. It is hence concluded that the findings in the present models of H-bond formation in different media are far less subject to inaccuracies introduced by the particular means of including solvation phenomena. Furthermore, it was shown that the pure continuum, while certainly not absolutely accurate in a quantitative sense, allowed to provide very reasonable approximations to the environments they are meant to reproduce. In fact, numerous studies89,98 using a variety of homogenous continuum models had demonstrated that various solvation properties are related in a very nearly fashion to the Onsager function, Fo, that in turn relates to the properties of the solvent.75,76 Fortunately, calculation within the SMD implicit model applied here, had revealed similar trends for Fo, as indicated above in Section 3.1. Indeed, of some importance that these findings are not entirely without experimental support. Our own work on Glyph monomer60 had demonstrated that the implicit solvation model based on density (SMD) combined applied at B3LYP-D3/6-311++G(2d,2p) level is able to provide accurate results on relative energies between zwitterion and non-ionized forms of Glyph monomer in water solution in good accord with the experimental results observed in crystal phase16,17 and in solution.29–31,61,62 Moreover, the hybrid discrete-continuum approach with a water molecule in the first solvation shell had been applied to study the conformational equilibria between ionized and non-ionized tautomers of Glyph monomer in water solution at SMD-B3LYP-D3/6-311++G(2d,2p) level,60 but we found only small changes from the results derived from a pure continuum. The explicit consideration of a large water molecules in the first solvation shell is important to stabilize99–101 as has been established by many studies on amino acids in water using hybrid discrete–continuum approach.102–113 However, for the dimeric system studied herein, statistical analysis of conformations is a fundamental question. Application of classical MD simulations are inappropriate due to limitations of classical force fields in describing proton transfer between Glyph monomers, while ab initio MD simulations are computationally too expensive. Further work will consider a combined QM/MM (quantum mechanics/molecular mechanics) MD methods, which represents an intermediate and promising approach to obtain the free energy of association.![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC
AC ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC. The solely Glyph phosphonate zwitterion dimer pair sustained by N+–H⋯O H-bonding patter, stable in the gas phase and in cyclohexane solution, isomerize to their DZC tautomers with essentially two pathways identical to those determined in aqueous solution. The calculated thermodynamic parameters of the dimerization process of Glyph monomer show that dimer formation of the most stable carboxylate DZC1 dimer structure is exergonic in vacuum and even in cyclohexane and aqueous solution. Solvents have been shown to play a key role in modulating the energetics of the dimerization of Glyph. Dimerization process in cyclohexane is found more favorable relative to the vacuum phase; this is because the solvation contribution to dimerization in cyclohexane relative to vacuum is small and negative. In aqueous solution, however, hydration opposes dimerization of zwitterionic Glyph monomers as all δΔGsolv.tot. quantities are found highly positive in water. The dimerization process in water is slightly less favorable than in cyclohexane due to the very large disturbing effect of water solvation. It is suggested that a mixture of predominantly carboxylate DZC and their DZP and AC tautomeric species should be present for high Glyph concentrations and that the dimerization process in water, may occur through a set of equilibria including direct proton transfers paths: 2ZP
DZC. The solely Glyph phosphonate zwitterion dimer pair sustained by N+–H⋯O H-bonding patter, stable in the gas phase and in cyclohexane solution, isomerize to their DZC tautomers with essentially two pathways identical to those determined in aqueous solution. The calculated thermodynamic parameters of the dimerization process of Glyph monomer show that dimer formation of the most stable carboxylate DZC1 dimer structure is exergonic in vacuum and even in cyclohexane and aqueous solution. Solvents have been shown to play a key role in modulating the energetics of the dimerization of Glyph. Dimerization process in cyclohexane is found more favorable relative to the vacuum phase; this is because the solvation contribution to dimerization in cyclohexane relative to vacuum is small and negative. In aqueous solution, however, hydration opposes dimerization of zwitterionic Glyph monomers as all δΔGsolv.tot. quantities are found highly positive in water. The dimerization process in water is slightly less favorable than in cyclohexane due to the very large disturbing effect of water solvation. It is suggested that a mixture of predominantly carboxylate DZC and their DZP and AC tautomeric species should be present for high Glyph concentrations and that the dimerization process in water, may occur through a set of equilibria including direct proton transfers paths: 2ZP ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZP
DZP![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) AC
AC ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) DZC.
DZC.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.





