Gas-phase electronic spectra of HC2n+1H+ (n = 2–6) chains†
Samuel J. P.
Marlton
 ,
Chang
Liu
,
Chang
Liu
 ,
Patrick
Watkins
and
Evan J.
Bieske
,
Patrick
Watkins
and
Evan J.
Bieske
 *
*
School of Chemistry, University of Melbourne, Parkville 3010, Australia. E-mail: evanjb@unimelb.edu.au
First published on 9th April 2024
Abstract
Highly unsaturated carbon chains are generated in combustion processes and electrical discharges, and are confirmed constituents of the interstellar medium. In hydrogen-rich environments smaller carbon clusters tend to exist as linear chains, capped on each end by hydrogen atoms. Although the HC2nH+ polyacetylene chains have been extensively characterized spectroscopically, the corresponding odd HC2n+1H+ chains have received far less attention. Here we use two-colour resonance enhanced photodissociation spectroscopy to measure electronic spectra for HC2n+1H+ (n = 2–6) chains contained in a cryogenically cooled quadrupole ion trap. The HC2n+1H+ chains are formed either top-down by ionizing and fragmenting pyrene molecules using pulsed 266 nm radiation, or bottom-up by reacting cyclic carbon cluster cations with acetylene. Ion mobility measurements confirm that the HC2n+1H+ species are linear, consistent with predictions from electronic structure calculations. The HC2n+1H+ electronic spectra exhibit three band systems in the visible/near infrared spectral range, which each shifts progressively to longer wavelength by ≈90 nm with the addition of each additional C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C subunit. The strongest visible HC11H+ band has a wavelength (λ = 545.1 nm) and width (1.5 nm) that match the strong λ 5450 diffuse interstellar band (DIB). However, other weaker HC11H+ bands do not correspond to catalogued DIBs, casting doubt on the role of HC11H+ as a carrier for the λ 5450 DIB. There are no identifiable correspondences between catalogued DIBs and bands for the other HC2n+1H+ chains, allowing upper limits to be established for their column densities in diffuse interstellar clouds.
C subunit. The strongest visible HC11H+ band has a wavelength (λ = 545.1 nm) and width (1.5 nm) that match the strong λ 5450 diffuse interstellar band (DIB). However, other weaker HC11H+ bands do not correspond to catalogued DIBs, casting doubt on the role of HC11H+ as a carrier for the λ 5450 DIB. There are no identifiable correspondences between catalogued DIBs and bands for the other HC2n+1H+ chains, allowing upper limits to be established for their column densities in diffuse interstellar clouds.
1 Introduction
Polyynes and highly unsaturated carbon chains (CnHm, CnHm+, CnHm−, with m = 1, 2) are confirmed constituents of the interstellar medium (ISM), particularly in molecular clouds such as the starless core TMC-1, where they have been detected through their microwave and infrared transitions.1–5 Although carbon chain molecules are prevalent in molecular clouds, they are typically less abundant in hot molecular cores, translucent clouds, and diffuse clouds.6 Highly unsaturated carbon chains were also proposed as potential carriers of diffuse interstellar bands (DIBs), discrete spectral features occurring across the visible and near infrared spectral ranges that are presumed to arise from the absorptions of molecules in diffuse molecular clouds.7–9 Although more than 500 DIBs have been identified, the only known carrier is the C60+ fullerene, which is associated with five DIBs.10,11The widespread importance of carbon chains and the ease with which they can be generated has motivated several laboratory investigations of their infrared and electronic transitions.6,12–17 Electronic spectra for bare carbon chains have been recorded for neutral,18–21 cation,22–24 and anion species.25–27 For hydrogenated species, electronic spectra have been measured for neutral CnH chains up to n = 16,27 CnH+ chains up to n = 17,28 and CnH− chains up to n = 24.14,29 Neutral CnH (n = 2–9) chains have also been characterized through photoelectron spectra of anion CnH− chains.30,31 Electronic spectra have been measured for polyacetylene cations as large as HC14H+.32,33 In work related to the current study, the A3Σ−u ← X3Σ−g electronic band systems of neutral HC2n+1H (n = 3–6) chains have been measured using cavity ring down spectroscopy, confirming that these species have linear, centro-symmetric structures.34 The visible electronic transitions of neutral HC2n+1H (n = 3–6) chains have also been studied using resonance enhanced two-colour photoionization spectroscopy.35
Here we examine the HC2n+1H+ chains through their electronic absorptions in a cryogenically cooled ion trap, extending our earlier spectroscopic studies of bare and hydrogenated carbon clusters, including Cn+ cyclocarbons,36,37 and singly hydrogenated carbon chains and rings C2n+1H+.28 As they lack a permanent dipole moment, the HC2n+1H+ chains cannot easily be detected using microwave spectroscopy so their investigation in the ISM necessarily relies on either their electronic or infrared transitions. The only previously reported electronic spectra for the HC2n+1H+ chains (n = 2–7) are for ions embedded in a neon matrix.19,22,38 These matrix spectra exhibited several different band systems, that were interpreted with the aid of multireference electronic structure calculations.39,40 Although the Ne matrix spectra are useful for identifying relevant transitions and assessing their relative intensities, the lines are broadened and shifted in wavelength due to ion-matrix interactions. Potentially, there are also contributions to the spectra from neutral molecules in the matrix. The higher resolution gas-phase spectra reported here provide the first opportunity for comparisons with astronomical data and for gauging the presence of HC2n+1H+ chains in the ISM.
Although HC2n+1H+ chains are yet to be detected in space, they may be produced in different regions through ion–molecule reactions. For example, flow tube studies show that C5H2+ is generated efficiently from the reaction of C3H+ and C4H2.41 This and similar reactions may occur in protoplanetary disks in which diacetylene has recently been detected.42 Other formation mechanisms could involve protonation of neutral C2n+1H molecules by H3+ or HCO+. Laboratory studies show that HC2n+1H+ ions are also produced through reactions of carbon cluster cations with acetylene, such as:43
| Cn+ + C2H2 → Cn−1H2+ + C3 |
| Cn+ + C2H2 → Cn+2H2+ |
The first reaction occurs for C4+, C6+ and C8+, which are presumably mainly linear molecules, and is favoured by the stability of the C3 co-fragment. The second reaction occurs over a size range for which the carbon cluster population consists of linear and cyclic isomers (C7+, C8+, C9+) or only cyclic isomers (C10+, C11+, C12+ C13+, C14+).43 The reactivity of small cyclo-carbon cations with acetylene stands in contrast to their unreactivity with many other molecules, including H2, D2,44 O2,44 CH4,44 N2O,45 and HCN.46 Hydrogenated carbon chains might also be formed top-down through photodissociation of PAHs or other large hydrocarbon molecules.47–49 In the current study, we mimic this route by generating HC2n+1H+ chains by ionizing and dissociating pyrene molecules using pulsed 266 nm radiation.
2 Experimental methods
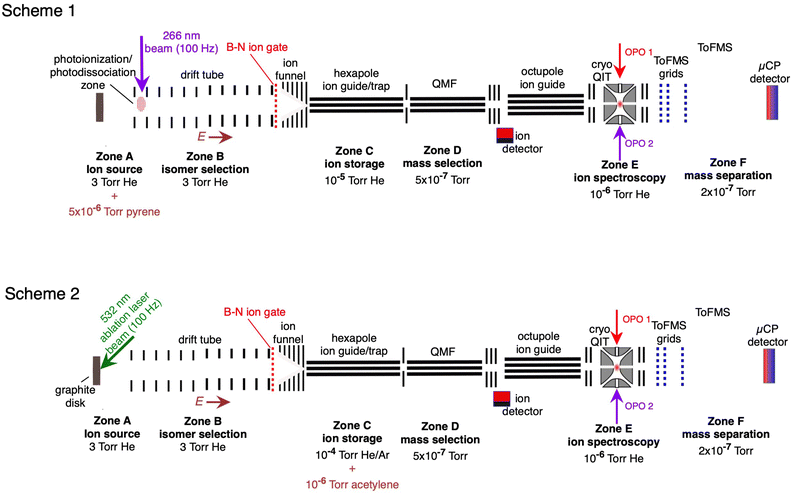
The experimental setup has been described previously.28,36,50 The apparatus, shown in Fig. 1, consists of several linked stages that include an ion source, an ion mobility drift tube, a hexapole ion guide/pretrap where the ions were accumulated, a quadrupole mass filter, an octopole ion guide, a cryogenically cooled quadrupole ion trap (QIT), and a time-of-flight mass spectrometer. The HC2n+1H+ ions were generated in two ways, which are illustrated in Fig. 1 (Schemes 1 and 2). First, as shown in Fig. 1 (Scheme 1), the HC2n+1H+ ions were produced by exposing vapour emanating from a solid pyrene sample (vapor pressure P ≈ 5× 10−6 torr at 300 K) with the fourth harmonic of a pulsed Nd:YAG laser (λ = 266 nm, 50 μJ per pulse, 100 Hz). The ions passed through a drift tube ion mobility spectrometer (IMS) containing He buffer gas at ≈3 torr, propelled by a ≈10 V cm−1 electric field. The drift tube IMS served to separate the ions spatially and temporally according to their collision cross sections with He buffer gas. When required, an electrostatic Bradbury–Nielsen ion gate positioned at the end of the drift region was used to select ions with a particular range of collision cross sections. Following the drift region the ion packet was compressed radially by an RF ion funnel and passed through a 1 mm orifice in a differential wall and then into an RF hexapole ion guide. Ions were accumulated in the hexapole for 50 shots of the ablation laser, then released to travel through a quadrupole mass filter (QMF). Ions then passed through an octupole ion guide and into a three-dimensional quadrupole ion trap (QIT) connected to a cryohead, where they were cooled to ≈10 K through collisions with He gas introduced through a pulsed nozzle operating at 2 Hz.Electronic action spectra of HC2n+1H+ ions were recorded using two-colour resonance enhanced photodissociation (REPD) by monitoring C2n+1H+ and C2n+1+ photofragments (corresponding to loss of H, 2H, or H2), and also for HC13H+ the C11+ photofragment (loss of HCCH). After 400 ms in the QIT, ions were exposed to a single pulse of light from a tunable optical parametric oscillator (OPO, EKSPLA NT342B, 6 ns pulse, bandwidth ≈4 cm−1) followed 10 ns later by a pulse of fixed-wavelength light from a second OPO (EKSPLA NT340, 6 ns pulse width, bandwidth ≈4 cm−1). The spectra in the visible region were normalised with respect to the laser power at each wavelength. The wavelength of the OPO output was measured using a wavemeter (Ångstrom High Finesse). The wavelength of the second OPO output was chosen to maximise the resonant two-colour photofragment signal, while minimising the signal produced by the second OPO alone, and was 440 nm for HC5H+, 500 nm for HC7H+, 550 nm for HC9H+, 450 nm for HC11H+, and 235 nm for HC13H+.
The HC2n+1H+ chains were also synthesised by reacting carbon cluster cations with acetylene as shown in Fig. 1 (Scheme 2). The carbon cluster cations were generated by laser ablation of a graphite disk with the second-harmonic of the Nd:YAG ablation laser (λ = 532 nm) and passed through the IMS stage. Specific carbon cluster isomers were selected by their arrival time (ta) using the Bradbury–Nielson ion gate. Ion mobility arrival time distributions were measured by scanning the delay between firing the ablation laser and opening the Bradbury–Nielsen ion gate. The mobility-selected ions then passed into the hexapole ion guide where they were stored for up to 500 ms. The hexapole region contained a 2% acetylene in argon gas mixture (P ≈ 2 × 10−4 torr, acetylene number density ≈1011 cm−3). Ions exiting the hexapole passed through the QMF and octupole ion guide and into the QIT where they were probed spectroscopically as described above for Scheme 1.
It should be emphasized that the HC2n+1H+ molecules do not dissociate directly following excitation to the lower electronic states (Ã, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) and
and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) states), but require absorption of an additional photon or photons from the second laser. Without the second laser pulse, there was essentially no photodissociation. This is consistent with bond dissociation energies (D0) calculated for C5H2+ at the CCSD(T)/cc-pVTZ level of theory using optimized geometries found at the TPSSh/def2-TZVP level of theory. The calculated dissociation energies are:
states), but require absorption of an additional photon or photons from the second laser. Without the second laser pulse, there was essentially no photodissociation. This is consistent with bond dissociation energies (D0) calculated for C5H2+ at the CCSD(T)/cc-pVTZ level of theory using optimized geometries found at the TPSSh/def2-TZVP level of theory. The calculated dissociation energies are:
(a) C5H+(1Σ+) + H(2S1/2) 4.28 eV
(b) l-C5+(2Σ+u) + H2(1Σ+g) 6.28 eV
(c) c-C3+(2B2) + C2H2 (1Σ+g) 6.65 eV
(d) l-C3+(2Σ+u) + C2H2 (1Σ+g) 6.99 eV
Therefore, the lowest energy dissociation channel (H-loss) should have a single-photon onset at around 290 nm, at a shorter wavelength than investigated in the current study. A similar situation should prevail for the larger HC2n+1H+ chains for which the Ã, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) and
and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) states progressively shift to lower energies. The photodissociation yields did not depend on the delay between the first and second laser pulses (out to 10 μs) indicating that the molecules undergo rapid internal conversion following excitation to the Ã,
states progressively shift to lower energies. The photodissociation yields did not depend on the delay between the first and second laser pulses (out to 10 μs) indicating that the molecules undergo rapid internal conversion following excitation to the Ã, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) and
and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) states and that the second photon delivers sufficient additional energy to take the vibrationally excited ions above the dissociation threshold.
states and that the second photon delivers sufficient additional energy to take the vibrationally excited ions above the dissociation threshold.
3 Quantum chemical calculations
The HC2n+1H+ chains were investigated computationally using the CAM-B3LYP density functional theory method51 including empirical dispersion (D3BJ)52 and the triple zeta def2-TZVP basis set.53 These geometries were employed for electronic structure calculations using the complete active space self consistent field (CASSCF)54 method with the def2-TZVP basis set taking spin–orbit coupling into account as implemented in the ORCA/5.0.2 program package.55 CASSCF calculations were undertaken for HC5H+, HC7H+, and HC9H+ using the active spaces recommended in ref. 39 with averaging over eight doublet and eight quartet states. We tested this approach by calculating the spin–orbit coupling constants of C7− and HC4H+. For C7−, the active space was comprised of nine electrons in two σ and eight π orbitals, which yielded spin–orbit constants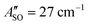 (experimental value 27.4 cm−1) and
(experimental value 27.4 cm−1) and 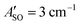 (experimental value 0.6 cm−1).56 For HC4H+, the active space was comprised of seven electrons in eight π orbitals, which yielded spin–orbit constants
(experimental value 0.6 cm−1).56 For HC4H+, the active space was comprised of seven electrons in eight π orbitals, which yielded spin–orbit constants 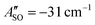 (experimental value −31.1 cm−1) and
(experimental value −31.1 cm−1) and 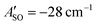 (experimental value −30 cm−1).33,57 The equilibrium geometry and ground state rotational constant of HC5H+ were calculated using the CCSD(T) method58 with the TZVP basis set59 in the ORCA program package.55
(experimental value −30 cm−1).33,57 The equilibrium geometry and ground state rotational constant of HC5H+ were calculated using the CCSD(T) method58 with the TZVP basis set59 in the ORCA program package.55
4 Results and discussion
4.1 Electronic structure of HC2n+1H+ chains
Before reporting and discussing the electronic spectra it is worth briefly reviewing the electronic states and transitions of the HC2n+1H+ linear molecules. As described previously,38–40,60 the![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πu/g ground state of the linear HC2n+1H+ molecules is described by the …(n/2)π4u (n/2)π4g (n/2 + 1)π1u electronic configuration for n even, and …((n − 1)/2)π4g ((n + 1)/2)π4u ((n + 1)/2)π1g configuration for n odd. These configurations give rise to
2Πu/g ground state of the linear HC2n+1H+ molecules is described by the …(n/2)π4u (n/2)π4g (n/2 + 1)π1u electronic configuration for n even, and …((n − 1)/2)π4g ((n + 1)/2)π4u ((n + 1)/2)π1g configuration for n odd. These configurations give rise to ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πu and
2Πu and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πg ground states for even and odd n, respectively.
2Πg ground states for even and odd n, respectively.
There are three excited electronic states that are relevant for transitions in the 200–2000 nm range – the 12Πg/u, 22Πg/u and 32Πg/u states.39 As explained in ref. 39, for HC2n+1H+ chains with n even, the 1Πg and 2Πg states have predominantly …(n/2)π4u (n/2)π3g (n/2 + 1)π2u configurations, whereas the 3Πg state is an admixture of …(n/2)π4u (n/2)π3g (n/2 + 1)π2u and …(n/2)π4u (n/2)π3g (n/2 + 1)π0u (n/2 + 1)π1g configurations. For HC2n+1H+ chains with n odd, the 12Πu and 22Πu states have predominantly …((n − 1)/2)π4g ((n + 1)/2)π3u ((n + 1)/2)π2g configurations, whereas the 32Πu state is an admixture of …((n − 1)/2)π4g ((n + 1)/2)π3u ((n + 1)/2)π2g and …((n − 1)/2)π4g ((n + 1)/2)π4u ((n + 1)/2)π0g ((n + 3)/2)π1u configurations. In other words, the à and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) states, are best described as SOMO ← SOMO−1 excitations, whereas SOMO ← SOMO−1 and LUMO ← SOMO excitations are important for the C state. The 12Πg/u ← X2Πu/g and 22Πg/u ← X2Πu/g transitions are predicted to be relatively weak compared to the 32Πg/u ← X2Πu/g transition.39 There is also an adjacent 2Φg/u state that is not optically coupled to the ground state. However, transitions to this state potentially gain intensity through vibronic coupling with the excited Πg/u states.38 Previously Fulara et al. labelled the three lowest excited Πu/g states as Ã2Πu/g,
states, are best described as SOMO ← SOMO−1 excitations, whereas SOMO ← SOMO−1 and LUMO ← SOMO excitations are important for the C state. The 12Πg/u ← X2Πu/g and 22Πg/u ← X2Πu/g transitions are predicted to be relatively weak compared to the 32Πg/u ← X2Πu/g transition.39 There is also an adjacent 2Φg/u state that is not optically coupled to the ground state. However, transitions to this state potentially gain intensity through vibronic coupling with the excited Πg/u states.38 Previously Fulara et al. labelled the three lowest excited Πu/g states as Ã2Πu/g, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2Πu/g and
2Πu/g and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2Πu/g states,38 a convention we retain in this paper.
2Πu/g states,38 a convention we retain in this paper.
4.2 Electronic spectra
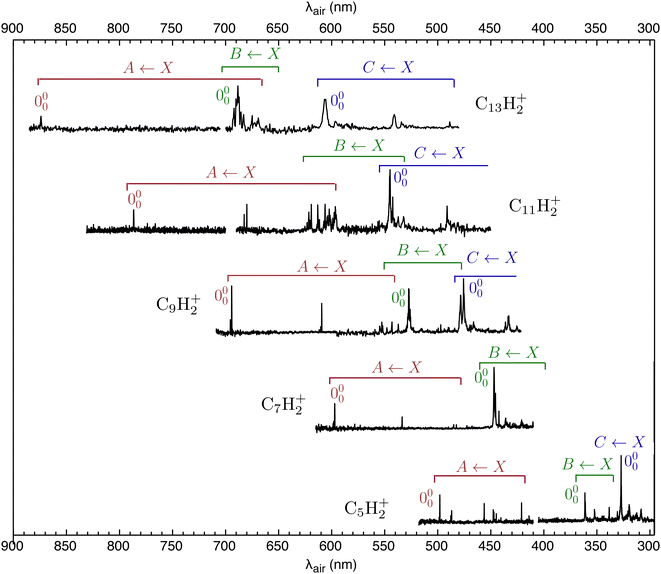
The REPD spectra of HC2n+1H+ molecules (n = 2–6) are presented in Fig. 2. Wavelengths (λair), widths and assignments for the bands are given in Tables S2 and S3 in the ESI.† The HC2n+1H+ spectra are similar to Ne matrix absorption spectra measured by Maier and coworkers,19,22,38 except that peaks in the gas-phase spectra are sharper and are displaced slightly to the blue from the Ne matrix peaks. Peak intensities in the REPD spectra depend on the photodissociation efficiency resulting from the 2-colour excitation scheme and are therefore probably less reliable than the relative intensities of peaks in the Ne matrix absorption spectra.Maier and coworkers assigned most HC2n+1H+ transitions in the visible and UV regions to Ã2Πu/g ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πg/u,
2Πg/u, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2Πu/g ←
2Πu/g ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πg/u and
2Πg/u and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2Πu/g ←
2Πu/g ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πg/u band systems, with the latter system carrying the highest oscillator strength.38 Complications in the spectra of HC9H+, HC11H+, HC13H+ and HC15H+ led them to invoke transitions to another electronic state, possibly the 2Φg/u state, which may derive intensity through vibronic coupling.38 The gas-phase spectra are broadly consistent with this previous interpretation, although some of our assignments differ from those in ref. 38, particularly for HC9H+, HC11H+ and HC13H+. In our interpretation, the spectra are affected by vibronic interactions, particularly between overtone vibrational levels in the à state manifold and the vibrationless level of the
2Πg/u band systems, with the latter system carrying the highest oscillator strength.38 Complications in the spectra of HC9H+, HC11H+, HC13H+ and HC15H+ led them to invoke transitions to another electronic state, possibly the 2Φg/u state, which may derive intensity through vibronic coupling.38 The gas-phase spectra are broadly consistent with this previous interpretation, although some of our assignments differ from those in ref. 38, particularly for HC9H+, HC11H+ and HC13H+. In our interpretation, the spectra are affected by vibronic interactions, particularly between overtone vibrational levels in the à state manifold and the vibrationless level of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state. Vibronic mixing of zero-order Ã2Πu/g and
state. Vibronic mixing of zero-order Ã2Πu/g and ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2Πu/g levels leads to sharing of intensity between the strong
2Πu/g levels leads to sharing of intensity between the strong ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2Πu/g ←
2Πu/g ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πg/u origin transition and weaker Ã2Πu/g ←
2Πg/u origin transition and weaker Ã2Πu/g ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πg/u overtone transitions. Depending on the size of the chains, the consequence is that instead of the
2Πg/u overtone transitions. Depending on the size of the chains, the consequence is that instead of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2Πu/g ←
2Πu/g ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πg/u origin transition appearing as a single band it is manifested as several peaks. Furthermore, for some chain sizes, higher vibronic levels of the
2Πg/u origin transition appearing as a single band it is manifested as several peaks. Furthermore, for some chain sizes, higher vibronic levels of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2Πu/g state are resonant with the lower levels of the
2Πu/g state are resonant with the lower levels of the ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2Πu/g state, further complicating the spectrum. This mixing is particularly evident for HC11H+ for which the interacting zero-order levels are nearly resonant. The nature of the vibronic coupling between the A, B and C states is not clear at this stage, but, given that all three electronic states share the same symmetry, the coupling is probably mediated by totally symmetric CC or CH stretch vibrational modes.
2Πu/g state, further complicating the spectrum. This mixing is particularly evident for HC11H+ for which the interacting zero-order levels are nearly resonant. The nature of the vibronic coupling between the A, B and C states is not clear at this stage, but, given that all three electronic states share the same symmetry, the coupling is probably mediated by totally symmetric CC or CH stretch vibrational modes.
The lowest energy Ã2Πg/u ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πu/g band systems exhibit sharp peaks, whose widths are limited by the bandwidth of the OPO (≈5 cm−1). The à ←
2Πu/g band systems exhibit sharp peaks, whose widths are limited by the bandwidth of the OPO (≈5 cm−1). The à ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) transitions are predicted to be relatively weak with calculated oscillator strengths of 0.0005, 0.0002, 0.0012, 0.0009, and 0.0019 for HC5H+, HC7H+, HC9H+, HC11H+ and HC13H+, respectively.39 The band shift induced by the Ne matrix for the à ←
transitions are predicted to be relatively weak with calculated oscillator strengths of 0.0005, 0.0002, 0.0012, 0.0009, and 0.0019 for HC5H+, HC7H+, HC9H+, HC11H+ and HC13H+, respectively.39 The band shift induced by the Ne matrix for the à ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) origin transition is −110 cm−1 for HC5H+, −71 cm−1 for HC7H+, −9 cm−1 for HC9H+, −37 cm−1 for HC11H+, and −33 cm−1 for HC13H+. The à ←
origin transition is −110 cm−1 for HC5H+, −71 cm−1 for HC7H+, −9 cm−1 for HC9H+, −37 cm−1 for HC11H+, and −33 cm−1 for HC13H+. The à ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) band systems of the HC2n+1H+ chains exhibit a progression in the acetylenic C
band systems of the HC2n+1H+ chains exhibit a progression in the acetylenic C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C stretch mode, extending to one or two quanta, with a spacing of ≈2000 cm−1. For HC5H+, a progression in even quanta of the ν8 mode (the lowest frequency πg mode) is also observed. As shown in Fig. 3, the wavelength of the Ã2Πg/u ←
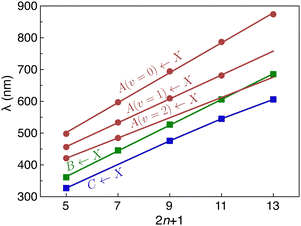
C stretch mode, extending to one or two quanta, with a spacing of ≈2000 cm−1. For HC5H+, a progression in even quanta of the ν8 mode (the lowest frequency πg mode) is also observed. As shown in Fig. 3, the wavelength of the Ã2Πg/u ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πu/g origin transition increases linearly with the number of carbon atoms in the chain (by ≈94 nm for each additional C2 subunit), akin to other carbon chain series.13,14,16,17
2Πu/g origin transition increases linearly with the number of carbon atoms in the chain (by ≈94 nm for each additional C2 subunit), akin to other carbon chain series.13,14,16,17
Our assignments for the origins of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2Πg/u ←
2Πg/u ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πu/g and
2Πu/g and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2Πg/u ←
2Πg/u ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πu/g band systems for HC5H+ and HC7H+ agree with those of Fulara et al.38 However, for HC9H+, HC11H+ and HC13H+, the bands originally assigned to the
2Πu/g band systems for HC5H+ and HC7H+ agree with those of Fulara et al.38 However, for HC9H+, HC11H+ and HC13H+, the bands originally assigned to the ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2Πg/u ←
2Πg/u ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πu/g origin transitions are reassigned as origins of the
2Πu/g origin transitions are reassigned as origins of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2Πg/u ←
2Πg/u ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πu/g band systems, while strong peaks following the linear trend between wavelength and chain length established for the
2Πu/g band systems, while strong peaks following the linear trend between wavelength and chain length established for the ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2Πg/u ←
2Πg/u ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πu/g origin transitions for HC5H+ and HC7H+ are assigned as the
2Πu/g origin transitions for HC5H+ and HC7H+ are assigned as the ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2Πg/u ←
2Πg/u ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πu/g origins for HC9H+, HC11H+ and HC13H+. As noted above, it seems that overtones and combinations of vibrational modes associated with the Ã2Πg/u state interact with the vibrationless level of the
2Πu/g origins for HC9H+, HC11H+ and HC13H+. As noted above, it seems that overtones and combinations of vibrational modes associated with the Ã2Πg/u state interact with the vibrationless level of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2Πg/u state, leading to mixing and sharing of oscillator strength. These interactions particularly affect the spectrum of HC11H+, and are responsible for a cluster of peaks near 600 nm. Assuming that the zero-order oscillator strength of the
2Πg/u state, leading to mixing and sharing of oscillator strength. These interactions particularly affect the spectrum of HC11H+, and are responsible for a cluster of peaks near 600 nm. Assuming that the zero-order oscillator strength of the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2Πg/u ←
2Πg/u ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πu/g origin transition greatly exceeds the oscillator strengths for the Ã2Πg/u ←
2Πu/g origin transition greatly exceeds the oscillator strengths for the Ã2Πg/u ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πu/g overtone transitions, one can estimate the deperturbed energies for the
2Πu/g overtone transitions, one can estimate the deperturbed energies for the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2Πg/u state from the centre-of-gravity of the transitions in the origin region (the corresponding wavelengths are plotted in Fig. 3). If this is done, the wavelengths for the deperturbed origin transitions of the three band systems follow linear trends with chain size (see Fig. 3). Significantly, with this new set of assignments there is no need to invoke an additional electronic state to explain the spectra of HC9H+, HC11H+ and HC13H+ in the visible region as was done in ref. 38.
2Πg/u state from the centre-of-gravity of the transitions in the origin region (the corresponding wavelengths are plotted in Fig. 3). If this is done, the wavelengths for the deperturbed origin transitions of the three band systems follow linear trends with chain size (see Fig. 3). Significantly, with this new set of assignments there is no need to invoke an additional electronic state to explain the spectra of HC9H+, HC11H+ and HC13H+ in the visible region as was done in ref. 38.
A weak band appears approximately 27 cm−1 to the red of the Ã2Πu/g ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πg/u origin transitions in the HC5H+, HC7H+, and HC9H+ spectra. The two transitions can be assigned to the 2Π1/2 ← 2Π1/2 sub-band (strong) and 2Π3/2 ← 2Π3/2 sub-band (weak), which are separated by the difference in the spin–orbit splittings for the ground and excited states
2Πg/u origin transitions in the HC5H+, HC7H+, and HC9H+ spectra. The two transitions can be assigned to the 2Π1/2 ← 2Π1/2 sub-band (strong) and 2Π3/2 ← 2Π3/2 sub-band (weak), which are separated by the difference in the spin–orbit splittings for the ground and excited states 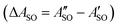 . Using the SOC + CASSCF/def2-TZVP method, we calculated spin–orbit splittings for HC5H+
. Using the SOC + CASSCF/def2-TZVP method, we calculated spin–orbit splittings for HC5H+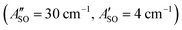 , HC7H+
, HC7H+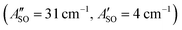 , and HC9H+
, and HC9H+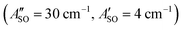 . The calculated ΔASO values agree with the observed peak separations for HC5H+ (26 cm−1), HC7H+ (29 cm−1), and HC9H+ (27 cm−1). The spin–orbit coupling constants for the HC2n+1H+ ions are similar to those measured for the
. The calculated ΔASO values agree with the observed peak separations for HC5H+ (26 cm−1), HC7H+ (29 cm−1), and HC9H+ (27 cm−1). The spin–orbit coupling constants for the HC2n+1H+ ions are similar to those measured for the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Π and Ã2Π states of the isoelectronic C7− anion
2Π and Ã2Π states of the isoelectronic C7− anion 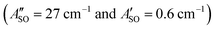 .56 The relative intensity for the 2Π3/2 ← 2Π3/2 sub-band compared to the 2Π1/2 ← 2Π1/2 sub-band (10–20%) is consistent with predicted thermal populations of the 2Π3/2 and 2Π1/2 levels for molecules in the cryotrap (12% at T = 20 K, assuming a Boltzmann distribution). An alternative assignment of the lower energy peak as a vibrational hot band is less convincing as the vibrational modes should be effectively cooled in the cryotrap. For example, the lowest frequency πu bend mode (ν11) for HC5H+ has a calculated frequency of 128 cm−1;39 at T = 30 K less than 0.4% of the molecules would have a single quantum of ν11.
.56 The relative intensity for the 2Π3/2 ← 2Π3/2 sub-band compared to the 2Π1/2 ← 2Π1/2 sub-band (10–20%) is consistent with predicted thermal populations of the 2Π3/2 and 2Π1/2 levels for molecules in the cryotrap (12% at T = 20 K, assuming a Boltzmann distribution). An alternative assignment of the lower energy peak as a vibrational hot band is less convincing as the vibrational modes should be effectively cooled in the cryotrap. For example, the lowest frequency πu bend mode (ν11) for HC5H+ has a calculated frequency of 128 cm−1;39 at T = 30 K less than 0.4% of the molecules would have a single quantum of ν11.
To better understand the formation of linear HC11H+ through the bimolecular reaction of C9+ and acetylene we constructed a potential energy surface describing the most important reaction steps (Fig. 4). Following the initial encounter, the C9+ + C2H2 reaction proceeds through a series of bicyclic and cyclic intermediates without any prohibitive barrier. The last step involves ring opening to yield the HC11H+ chain, which, in the absence of collisions would have an internal energy above the Ã, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) and
and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) excited states. Therefore, it is possible that the nascent HC11H+ product ions are stabilized under low pressure conditions through inverse internal conversion and radiative emission from an excited electronic state (Poincaré fluorescence),61 or alternatively through emission of infrared radiation. Although we believe that Fig. 4 illustrates a credible mechanism for C11H2+ chain formation directly from a bimolecular collision, we cannot discount the possibility that a nascent Cn+…C2H2 complex is initially formed by a three body collision in the hexapole, and is collisionally transformed into a linear C11H2+ chain either in the heaxapole, en route to the QIT, or in the QIT itself. It is also unclear at this stage whether any of the intermediates shown in Fig. 4 are formed in the hexapole and stabilized by collisions with Ar gas (P ≈ 2 × 10−4 torr), making their way, along with the linear C11H2+ chains, into the QIT.
excited states. Therefore, it is possible that the nascent HC11H+ product ions are stabilized under low pressure conditions through inverse internal conversion and radiative emission from an excited electronic state (Poincaré fluorescence),61 or alternatively through emission of infrared radiation. Although we believe that Fig. 4 illustrates a credible mechanism for C11H2+ chain formation directly from a bimolecular collision, we cannot discount the possibility that a nascent Cn+…C2H2 complex is initially formed by a three body collision in the hexapole, and is collisionally transformed into a linear C11H2+ chain either in the heaxapole, en route to the QIT, or in the QIT itself. It is also unclear at this stage whether any of the intermediates shown in Fig. 4 are formed in the hexapole and stabilized by collisions with Ar gas (P ≈ 2 × 10−4 torr), making their way, along with the linear C11H2+ chains, into the QIT.
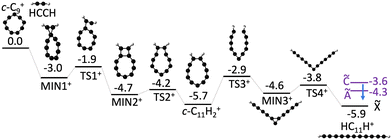 | ||
| Fig. 4 Proposed formation mechanism for HC11H+ from c-C9+ + C2H2 reaction. Ground state energies (black bars) are calculated using DFT (ωB97X-D/def2-SVP). Excited state energies (purple bars) for HC11H+ are determined from the spectra shown in Fig. 2. Putative deactivation of HC11H+ product ions by fluorescence from excited electronic states is indicated by a blue arrow. All values are in units of eV. | ||
4.3 Astronomical implications
It is relevant to consider briefly whether any of the HC2n+1H+ chains are DIB carriers. We first consider the relatively narrow à ←![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) transitions, which occur in the visible or near infrared regions for HC2n+1H+ (n = 2–6). The stronger
transitions, which occur in the visible or near infrared regions for HC2n+1H+ (n = 2–6). The stronger ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ←
← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) and
and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) ←
← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) origin transitions either do not occur in the visible (C5H2+), or are broad (C7H2+, C9H2+, C13H2+). The exception is the intense
origin transitions either do not occur in the visible (C5H2+), or are broad (C7H2+, C9H2+, C13H2+). The exception is the intense ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) ←
← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) origin transition of C11H2+, which we discuss later.
origin transition of C11H2+, which we discuss later.
We first consider HC5H+, noting that its strongest band in the visible region, the Ã2Π1/2 ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Π1/2 origin transition at 498.0 ± 0.2 nm, is reasonably close to DIBs at 497.961 nm and 498.214 nm in spectra for HD 204827.62 To investigate the possible correspondence between the HC5H+ absorption and these nearby DIBs, we recorded the à ←
2Π1/2 origin transition at 498.0 ± 0.2 nm, is reasonably close to DIBs at 497.961 nm and 498.214 nm in spectra for HD 204827.62 To investigate the possible correspondence between the HC5H+ absorption and these nearby DIBs, we recorded the à ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) origin band at higher resolution using a pulsed dye laser (bandwidth 0.04 cm−1). The spectrum exhibits partial resolution of rotational substructure with an R-branch maximum at 498.02 nm (see Fig. 5). The band was best simulated assuming a temperature of 12 K, a calculated ground state rotational constant B′′ = 0.07477 cm−1 (computed using CCSD(T)/TZVP), and an excited state rotational constant of B′ = 0.07193 cm−1 that was adjusted to give the best match between the simulated and measured spectra. It is apparent that the HC5H+ band does not correspond to either of the adjacent DIBs and that the match would not improve at higher temperatures. The origin bands for the à ←
origin band at higher resolution using a pulsed dye laser (bandwidth 0.04 cm−1). The spectrum exhibits partial resolution of rotational substructure with an R-branch maximum at 498.02 nm (see Fig. 5). The band was best simulated assuming a temperature of 12 K, a calculated ground state rotational constant B′′ = 0.07477 cm−1 (computed using CCSD(T)/TZVP), and an excited state rotational constant of B′ = 0.07193 cm−1 that was adjusted to give the best match between the simulated and measured spectra. It is apparent that the HC5H+ band does not correspond to either of the adjacent DIBs and that the match would not improve at higher temperatures. The origin bands for the à ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) transitions of HC7H+, HC9H+ and HC11H+, which occur across the visible region, also do not match tabulated DIBs for HD 183143 or HD 204827 sight-lines.62,63
transitions of HC7H+, HC9H+ and HC11H+, which occur across the visible region, also do not match tabulated DIBs for HD 183143 or HD 204827 sight-lines.62,63
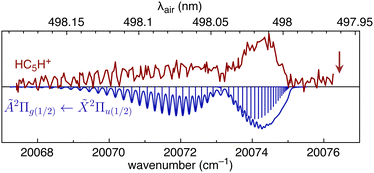 | ||
Fig. 5 REPD spectrum of the HC5H+ Ã2Π1/2 ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Π1/2 band origin measured using a dye laser (bandwidth 0.04 cm−1). The spectrum is compared with a simulation generated using B′′ = 0.07477 cm−1, B′ = 0.07193 cm−1, and T = 12 K. The vertical arrow indicates the position of the 497.961 nm DIB (data from ref. 62). 2Π1/2 band origin measured using a dye laser (bandwidth 0.04 cm−1). The spectrum is compared with a simulation generated using B′′ = 0.07477 cm−1, B′ = 0.07193 cm−1, and T = 12 K. The vertical arrow indicates the position of the 497.961 nm DIB (data from ref. 62). | ||
The absence of à ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) origin transitions for HC5H+, HC7H+, HC9H+ and HC11H+ in the HD 183143 or HD 204827 spectra allows one to estimate upper limits for column densities for these sight-lines using the relationship:64
origin transitions for HC5H+, HC7H+, HC9H+ and HC11H+ in the HD 183143 or HD 204827 spectra allows one to estimate upper limits for column densities for these sight-lines using the relationship:64
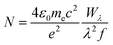 | (1) |
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) transitions are relatively large because the oscillator strengths for these transitions are small.
transitions are relatively large because the oscillator strengths for these transitions are small.
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) transitions in the visible region and astronomical data for HD 183143.63Nmax values are based on a 10 mÅ minimum detectable equivalent width (Wλ), and use calculated (fcalc) and experimental (fexp) oscillator strengths from ref. 39 and ref. 38, respectively. Band positions and widths are taken from the current work. Nmax values based on fcalc are given first and those based on fexp are given second in parentheses
transitions in the visible region and astronomical data for HD 183143.63Nmax values are based on a 10 mÅ minimum detectable equivalent width (Wλ), and use calculated (fcalc) and experimental (fexp) oscillator strengths from ref. 39 and ref. 38, respectively. Band positions and widths are taken from the current work. Nmax values based on fcalc are given first and those based on fexp are given second in parentheses
| Species | λ nm | f calc (fexp) | N max 1012 cm−2 |
|---|---|---|---|
| HC5H+ | 498.0 | 0.00046 (0.00075) | 100(60) |
| HC7H+ | 597.1 | 0.00022 (0.0018) | 140(18) |
| HC9H+ | 694.3 | 0.00118 (0.004) | 20(6) |
| HC11H+ | 786.8 | 0.00089 (0.0046) | 20(4) |
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2Πu ←
2Πu ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πg origin transition of HC11H+ corresponds in position and width to the λ 5450 DIB measured in several astronomical surveys. This can be seen in Fig. 6(a) where the HC11H+ REPD spectrum is plotted together with a synthetic spectrum generated using data for HD 183143.63 Assuming for the moment that the
2Πg origin transition of HC11H+ corresponds in position and width to the λ 5450 DIB measured in several astronomical surveys. This can be seen in Fig. 6(a) where the HC11H+ REPD spectrum is plotted together with a synthetic spectrum generated using data for HD 183143.63 Assuming for the moment that the ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2Πu ←
2Πu ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πg origin transition is responsible for the λ 5450 DIB, a column density of ≈8 × 1012 cm−2 is estimated using eqn (1) with λ = 5450 Å, Wλ = 0.3595 Å (from ref. 63) and fcalc = 0.18 (from ref. 39). A somewhat larger column density of ≈5 × 1013 cm−2 is estimated employing the Ne matrix oscillator strength (fmatrix = 0.025).
2Πg origin transition is responsible for the λ 5450 DIB, a column density of ≈8 × 1012 cm−2 is estimated using eqn (1) with λ = 5450 Å, Wλ = 0.3595 Å (from ref. 63) and fcalc = 0.18 (from ref. 39). A somewhat larger column density of ≈5 × 1013 cm−2 is estimated employing the Ne matrix oscillator strength (fmatrix = 0.025).
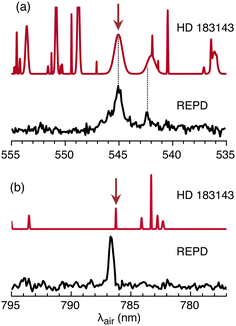 | ||
Fig. 6 REPD spectra for HC11H+ in the visible/NIR range for: (a) ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2Πu ← 2Πu ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πg origin transition; (b) Ã2Πu ← 2Πg origin transition; (b) Ã2Πu ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πg origin transition. In each case, a synthetic astronomical DIB spectrum for HD 183143 generated using data from ref. 63 is shown above the REPD spectrum. Arrows indicate DIBs close to HC11H+ absorptions. 2Πg origin transition. In each case, a synthetic astronomical DIB spectrum for HD 183143 generated using data from ref. 63 is shown above the REPD spectrum. Arrows indicate DIBs close to HC11H+ absorptions. | ||
If HC11H+ is responsible for the λ 5450 DIB, then other weaker HC11H+ bands should also appear in astronomical spectra. The nearby HC11H+ transition at 542.3 nm may contribute to the broad DIB at 542.001 nm (see Fig. 6(a)). Comparisons for other transitions over the 600–700 nm range are difficult because the HC11H+ bands are broad and there is a high density of DIBs in this region. However, the Ã2Πu ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πg origin transition at 786.8 nm is relatively narrow and occurs in a region where DIBs are sparse, with the nearest DIB at 786.243 nm (see Fig. 6(b)).63 The Ã2Πu ←
2Πg origin transition at 786.8 nm is relatively narrow and occurs in a region where DIBs are sparse, with the nearest DIB at 786.243 nm (see Fig. 6(b)).63 The Ã2Πu ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πg transition is estimated to be weaker than the
2Πg transition is estimated to be weaker than the ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2Πu ←
2Πu ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πg transition by a factor of five based on the matrix oscillator strengths,38 or by a factor of 200 based on the calculated oscillator strengths.39 If the matrix oscillator strengths are correct, then the Ã2Πu ←
2Πg transition by a factor of five based on the matrix oscillator strengths,38 or by a factor of 200 based on the calculated oscillator strengths.39 If the matrix oscillator strengths are correct, then the Ã2Πu ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πg origin transition would have an equivalent width of Wλ = 70 mÅ, making it 4–5 times more intense than the λ 7862 DIB in the HD 183143 spectrum reported in ref. 63 (Wλ = 16 mÅ). In this case the transition should certainly be apparent in existing astronomical spectra. However, if the calculated oscillator strengths are correct, then the Ã2Πu ←
2Πg origin transition would have an equivalent width of Wλ = 70 mÅ, making it 4–5 times more intense than the λ 7862 DIB in the HD 183143 spectrum reported in ref. 63 (Wλ = 16 mÅ). In this case the transition should certainly be apparent in existing astronomical spectra. However, if the calculated oscillator strengths are correct, then the Ã2Πu ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πg origin transition would have an equivalent width of Wλ = 2 mÅ, probably making it difficult to detect.
2Πg origin transition would have an equivalent width of Wλ = 2 mÅ, probably making it difficult to detect.
If HC11H+ exists in the ISM one might expect similar or greater abundances of HC5H+, HC7H+ and HC9H+, although the relative amounts may depend sensitively on their formation mechanisms and the stability of their precursors. If the Ne matrix oscillator strengths are correct, then their column densities should probably exceed 5 × 1013 cm−2, which, according to the upper limits reported in Table 1, would imply that the Ã2Πu ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πg origin transitions of HC7H+, HC9H+ and perhaps HC5H+ should be apparent in existing astronomical spectra. On the other hand, if the calculated oscillator strengths are correct, the column densities would exceed 8 × 1012 cm−2 and the Ã2Πu ←
2Πg origin transitions of HC7H+, HC9H+ and perhaps HC5H+ should be apparent in existing astronomical spectra. On the other hand, if the calculated oscillator strengths are correct, the column densities would exceed 8 × 1012 cm−2 and the Ã2Πu ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πg origin transitions of HC5H+, HC7H+, HC9H+ may be too weak to detect.
2Πg origin transitions of HC5H+, HC7H+, HC9H+ may be too weak to detect.
On balance, the correspondence between the ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) ←
← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) origin transition of HC11H+ and the λ 5450 DIB should probably be viewed as a coincidence. Confirmation would require the discovery of other weaker HC11H+ bands in astronomical spectra. As well, one might also expect to observe visible bands for the smaller HC5H+, HC7H+ and HC9H+ species, which would presumably be formed by similar chemical pathways to HC11H+.
origin transition of HC11H+ and the λ 5450 DIB should probably be viewed as a coincidence. Confirmation would require the discovery of other weaker HC11H+ bands in astronomical spectra. As well, one might also expect to observe visible bands for the smaller HC5H+, HC7H+ and HC9H+ species, which would presumably be formed by similar chemical pathways to HC11H+.
5 Conclusions
Electronic spectra of HC5H+, HC7H+, HC9H+, HC11H+, and HC13H+ have been measured in a cryogenically cooled ion trap. The spectra exhibit sharp bands over the NIR, visible and UV ranges, associated with the Ã2Πu/g ←![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πg/u,
2Πg/u, ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2Πu/g ←
2Πu/g ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πg/u and
2Πg/u and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2Πu/g ←
2Πu/g ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πg/u band systems. Regular red-shifts of 70–94 nm in wavelength for the origin transitions of these band systems accompanying addition of each C
2Πg/u band systems. Regular red-shifts of 70–94 nm in wavelength for the origin transitions of these band systems accompanying addition of each C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C unit are disrupted and obscured by vibronic resonances, particularly for the
C unit are disrupted and obscured by vibronic resonances, particularly for the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2Πu/g ←
2Πu/g ← ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Πg/u transitions of HC9H+, HC11H+, and HC13H+.
2Πg/u transitions of HC9H+, HC11H+, and HC13H+.
We find no correspondences between catalogued DIBs and the electronic absorption bands of HC5H+, HC7H+, HC9H+ and HC13H+. However, the strongest HC11H+ band matches the broad λ 5450 DIB. There are two points counting against HC11H+ being a carrier for the λ 5450 DIB. First, less intense bands in the 600–900 nm range in the HC11H+ REPD spectrum are absent from astronomical spectra, although this may be because these bands are much weaker than the 545.1 nm band. Second, there is no evidence in the astronomical spectra for the visible bands of HC5H+, HC7H+, HC9H+ which would presumably have similar or greater abundances than HC11H+. The most promising HC11H+ band for future astronomical detection is probably the A ← X origin transition at 786.8 nm, which, if HC11H+ is the carrier, should be detectable for sight lines that give a strong signal for the λ 5450 DIB. Better estimates for upper limits of the column densities for HC5H+, HC7H+, HC9H+ and HC11H+ require reliable oscillator strengths for the electronic transitions. Hopefully, fresh experiments or calculations will help resolve the discrepancies between computed and measured oscillator strengths.
The HC2n+1H+ chains may also be detectable in the ISM through their infrared transitions, particularly given the recent advances in IR astronomy with the James Webb Space Telescope. The requisite laboratory infrared spectra should be obtainable using various mass-selective action spectroscopy techniques, including He droplet ion spectroscopy,65–67 rare gas tagging,67 or leak-out spectroscopy.68
The current study demonstrates that laser ionization/fragmentation of PAHs is an effective strategy for forming highly unsaturated carbon chains. Although C13H2+ is the largest chain generated from pyrene, even longer species will presumably be produced by ionizing and dissociating larger PAHs. Ultimately, it will be interesting to see whether there is a progressive transition from linear to monocyclic C2n+1H2+ structures with increasing size, as occurs for C2n+1H+ ions, for which cyclic isomers dominate for species larger than C15H+.28 Ion mobility measurements for hydrogenated carbon ions generated through laser ablation of graphite in a He/H2 supersonic expansion suggest that linear and monocyclic isomers are present in roughly equal proportions for C15H2+ and C17H2+, and that the monocyclic isomer dominates for C19H2+ and C21H2+.69 Another avenue for future research involves spectroscopically characterizing carbon chains terminated with O or N atoms that are generated using appropriate heterocyclic or substituted PAHs as precursors.
Finally, we note that the strategy of reacting isomer-selected carbon cluster cations with other neutral molecules in the hexapole ion guide has promise for generating exotic molecular ions that can be spectroscopically probed in the cryo-QIT. In the current work the viability of this approach was demonstrated by producing HC2n+1H+ chains as products of the reaction between cyclic carbon cluster cations and acetylene molecules. Although, cyclocarbon cations are relatively stable and do not react with most molecules, the smaller linear carbon chains react with a range of molecules, including H2, D2,44 O2,44 CH4,44 N2O,45 and HCN.46 It should be relatively straightforward to investigate product ions from these reactions, some of which have astrophysical relevance, using electronic spectroscopy.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported under the Australian Research Council's Discovery Project funding scheme (Project Numbers DP150101427 and DP160100474). The authors thank Richard Mathys from the Science Faculty Workshop for his contributions to the design and construction of the apparatus used in this study.Notes and references
- J. Pety, P. Gratier, V. Guzmán, E. Roueff, M. Gerin, J. R. Goicoechea, S. Bardeau, A. Sievers, F. Le Petit, J. Le Bourlot, A. Belloche and D. Talbi, Astron. Astrophys., 2012, 548, A68 CrossRef
.
- S. Brünken, L. Kluge, A. Stoffels, O. Asvany and S. Schlemmer, Astrophys. J., Lett., 2014, 783, L4 CrossRef
.
- J. Cernicharo, M. Agúndez, C. Cabezas, R. Fuentetaja, B. Tercero, N. Marcelino, Y. Endo, J. Pardo and P. de Vicente, Astron. Astrophys., 2022, 657, L16 CrossRef CAS
.
- J. Cernicharo, A. M. Heras, A. Tielens, J. R. Pardo, F. Herpin, M. Guélin and L. Waters, Astrophys. J., 2001, 546, L123 CrossRef CAS
.
- M. McCarthy, C. Gottlieb, H. Gupta and P. Thaddeus, Astrophys. J., 2006, 652, L141–L144 CrossRef CAS
.
- K. Taniguchi, P. Gorai and J. C. Tan, arXiv, 2023, preprint, arXiv:2303.15769 [astro-ph.GA] DOI:10.48550/arXiv.2303.15769.
- A. E. Douglas, Nature, 1977, 269, 130–132 CrossRef CAS
.
- J. P. Maier, G. A. Walker and D. A. Bohlender, Astrophys. J., 2004, 602, 286 CrossRef CAS
.
-
The Diffuse Interstellar Bands, ed. A. G. G. M. Tielens and T. P. Snow, Kluwer, Dordrecht, 1995 Search PubMed
.
- E. K. Campbell, M. Holz, D. Gerlich and J. P. Maier, Nature, 2015, 523, 322–323 CrossRef CAS PubMed
.
- H. Linnartz, J. Cami, M. Cordiner, N. Cox, P. Ehrenfreund, B. Foing, M. Gatchell and P. Scheier, J. Mol. Spectrosc., 2020, 367, 111243 CrossRef CAS
.
- A. Van Orden and R. J. Saykally, Chem. Rev., 1998, 98, 2313–2357 CrossRef CAS PubMed
.
- E. B. Jochnowitz and J. P. Maier, Proc. Int. Astron. Union, 2008, 4, 395–402 CrossRef
.
- R. Nagarajan and J. P. Maier, Int. Rev. Phys. Chem., 2010, 29, 521–554 Search PubMed
.
- M. A. Duncan, J. Phys. Chem. A, 2012, 116, 11477–11491 CrossRef CAS PubMed
.
- C. Rice and J. Maier, J. Phys. Chem. A, 2013, 117, 5559–5566 CrossRef CAS PubMed
.
- L. N. Zack and J. P. Maier, Chem. Soc. Rev., 2014, 43, 4602–4614 RSC
.
- P. Freivogel, J. Fulara, D. Lessen, D. Forney and J. P. Maier, Chem. Phys., 1994, 189, 335–341 CrossRef CAS
.
- J. Fulara, P. Freivogel, D. Forney and J. P. Maier, J. Chem. Phys., 1995, 103, 8805–8810 CrossRef CAS
.
- D. Forney, P. Freivogel, M. Grutter and J. P. Maier, J. Chem. Phys., 1996, 104, 4954–4960 CrossRef CAS
.
- X. Chen, M. Steglich, V. Gupta, C. A. Rice and J. P. Maier, Phys. Chem. Chem. Phys., 2014, 16, 1161–1165 RSC
.
- P. Freivogel, J. Fulara, D. Lessen, D. Forney and J. P. Maier, Chem. Phys., 1994, 189, 335–341 CrossRef CAS
.
- E. K. Campbell and P. W. Dunk, Rev. Sci. Instrum., 2019, 90, 1–7 CrossRef
.
- J. E. Colley, D. S. Orr and M. A. Duncan, J. Chem. Phys., 2022, 157, 121102 CrossRef CAS PubMed
.
- D. W. Arnold, S. E. Bradforth, T. N. Kitsopoulos and D. M. Neumark, J. Chem. Phys., 1991, 95, 8753–8764 CrossRef CAS
.
- P. Freivogel, J. Fulara, M. Jakobi, D. Forney and J. P. Maier, J. Chem. Phys., 1995, 103, 54–59 CrossRef CAS
.
- D. A. Kirkwood, M. Tulej, M. V. Pachkov, M. Schnaiter, F. Güthe, M. Grutter, M. Wyss, J. P. Maier and G. Fischer, J. Chem. Phys., 1999, 111, 9280–9286 CrossRef CAS
.
- S. J. Marlton, J. T. Buntine, C. Liu, P. Watkins, U. Jacovella, E. Carrascosa, J. N. Bull and E. J. Bieske, J. Phys. Chem. A, 2022, 126, 6678–6685 CrossRef CAS PubMed
.
- H. Linnartz, T. Motylewski and J. P. Maier, J. Chem. Phys., 1998, 109, 3819–3823 CrossRef CAS
.
- T. R. Taylor, C. Xu and D. M. Neumark, J. Chem. Phys., 1998, 108, 10018–10026 CrossRef CAS
.
- E. Garand, T. I. Yacovitch, J. Zhou, S. M. Sheehan and D. M. Neumark, Chem. Sci., 2010, 1, 192–201 RSC
.
- J. Fulara, M. Grutter and J. P. Maier, J. Phys. Chem. A, 2007, 111, 11831–11836 CrossRef CAS PubMed
.
- A. Dzhonson, E. B. Jochnowitz and J. P. Maier, J. Phys. Chem. A, 2007, 111, 1887–1890 CrossRef CAS PubMed
.
- C. D. Ball, M. C. McCarthy and P. Thaddeus, J. Chem. Phys., 2000, 112, 10149–10155 CrossRef CAS
.
- H. Ding, T. W. Schmidt, T. Pino, A. E. Boguslavskiy, F. Güthe and J. P. Maier, J. Chem. Phys., 2003, 119, 814–819 CrossRef CAS
.
- J. T. Buntine, M. I. Cotter, U. Jacovella, C. Liu, P. Watkins, E. Carrascosa, J. N. Bull, L. Weston, G. Muller, M. S. Scholz and E. J. Bieske, J. Chem. Phys., 2021, 155, 214302 CrossRef CAS PubMed
.
- S. J. Marlton, J. T. Buntine, P. Watkins, C. Liu, U. Jacovella, E. Carrascosa, J. N. Bull and E. J. Bieske, J. Phys. Chem. A, 2023, 127, 1168–1178 CrossRef CAS PubMed
.
- J. Fulara, A. Nagy, I. Garkusha and J. P. Maier, J. Chem. Phys., 2010, 133, 024304 CrossRef PubMed
.
- J. Zhang, X. Guo and Z. Cao, Int. J. Mass Spectrom., 2010, 290, 113–119 CrossRef CAS
.
- M. Mühlhäuser, J. Haubrich and S. D. Peyerimhoff, Int. J. Quantum Chem., 2004, 100, 53–58 CrossRef
.
- S. Dheandhanoo, L. Forte, A. Fox and D. K. Bohme, Can. J. Chem., 1986, 64, 641–648 CrossRef CAS
.
- B. Tabone, G. Bettoni, E. F. van Dishoeck, A. M. Arabhavi, S. Grant, D. Gasman, T. Henning, I. Kamp, M. Güdel and P. O. Lagage,
et al.
, Nat. Astron., 2023, 1–10 CAS
.
- S. W. McElvany, J. Chem. Phys., 1988, 89, 2063–2075 CrossRef CAS
.
- S. W. McElvany, B. I. Dunlap and A. O'Keefe, J. Chem. Phys., 1998, 86, 715–725 CrossRef
.
- M. S. Resat, J. N. Smolanoff, I. B. Goldman and S. L. Anderson, J. Chem. Phys., 1994, 100, 8784–8794 CrossRef CAS
.
- D. C. Parent and S. W. McElvany, J. Am. Chem. Soc., 1989, 111, 2393–2401 CrossRef CAS
.
- B. West, F. Useli-Bacchitta, H. Sabbah, V. Blanchet, A. Bodi, P. M. Mayer and C. Joblin, J. Phys. Chem. A, 2014, 118, 7824–7831 CrossRef CAS PubMed
.
- H. R. Hrodmarsson, J. Bouwman, A. G. Tielens and H. Linnartz, Int. J. Mass Spectrom., 2022, 476, 116834 CrossRef CAS
.
- H. R. Hrodmarsson, J. Bouwman, A. G. Tielens and H. Linnartz, Int. J. Mass Spectrom., 2023, 485, 116996 CrossRef CAS
.
- J. T. Buntine, E. Carrascosa, J. N. Bull, U. Jacovella, M. I. Cotter, P. Watkins, C. Liu, M. S. Scholz, B. D. Adamson, S. J. P. Marlton and E. J. Bieske, Rev. Sci. Instrum., 2022, 93, 043201 CrossRef CAS PubMed
.
- M. Saitow, U. Becker, C. Riplinger, E. F. Valeev and F. Neese, J. Chem. Phys., 2017, 146, 164105 CrossRef PubMed
.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed
.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC
.
- B. O. Roos, P. R. Taylor and P. E. Siegbahn, Chem. Phys., 1980, 48, 157–173 CrossRef CAS
.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed
.
- N. M. Lakin, M. Pachkov, M. Tulej, J. P. Maier, G. Chambaud and P. Rosmus, J. Chem. Phys., 2000, 113, 9586–9592 CrossRef CAS
.
- U. Jacovella and F. Merkt, Phys. Chem. Chem. Phys., 2017, 19, 23524–23531 RSC
.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS
.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef
.
- M. Mühlhäuser, J. Haubrich, G. Mpourmpakis, A. Mavrandonakis and G. E. Froudakis, Internet Electron. J. Mol. Des., 2003, 2, 578–588 Search PubMed
.
- A. Léger, P. Boissel and L. d'Hendecourt, Phys. Rev. Lett., 1988, 60, 921 CrossRef PubMed
.
- L. M. Hobbs, D. G. York, T. P. Snow, T. Oka, J. A. Thorburn, M. Bishof, S. D. Friedman, B. J. McCall, B. Rachford and P. Sonnentrucker, Astrophys. J., 2008, 680, 1256 CrossRef CAS
.
- L. M. Hobbs, D. G. York, J. A. Thorburn, T. P. Snow, M. Bishof, S. D. Friedman, B. J. McCall, T. Oka, B. Rachford, P. Sonnentrucker and D. E. Welty, Astrophys. J., 2009, 705, 32 CrossRef CAS
.
- T. Motylewski, H. Linnartz, O. Vaizert, J. P. Maier, G. A. Galazutdinov, F. A. Musaev, J. Krełowski, G. A. H. Walker and D. A. Bohlender, Astrophys. J., 2000, 531, 312–320 CrossRef CAS
.
- C. J. Moon, S. Erukala, A. J. Feinberg, A. Singh, M. Y. Choi and A. F. Vilesov, J. Chem. Phys., 2023, 158, 224307 CrossRef CAS PubMed
.
- S. Erukala, A. Feinberg, A. Singh and A. F. Vilesov, J. Chem. Phys., 2021, 155, 084306 CrossRef CAS PubMed
.
- S. Brünken, F. Lipparini, A. Stoffels, P. Jusko, B. Redlich, J. Gauss and S. Schlemmer, J. Phys. Chem. A, 2019, 123, 8053–8062 CrossRef PubMed
.
- P. C. Schmid, O. Asvany, T. Salomon, S. Thorwirth and S. Schlemmer, J. Phys. Chem. A, 2022, 126, 8111–8117 CrossRef CAS PubMed
.
- S. Lee, N. Gotts, G. von Helden and M. T. Bowers, J. Phys. Chem. A, 1997, 101, 2096–2102 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00625a |
| This journal is © the Owner Societies 2024 |