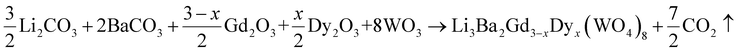Open Access Article
Open Access ArticleStructure and luminescence properties of Dy3+ doped quaternary tungstate Li3Ba2Gd3(WO4)8 for application in wLEDs†
Abir Douziab,
Sami Slimi a,
Eduard Madirovc,
Andrey Turshatov
a,
Eduard Madirovc,
Andrey Turshatov c,
Bryce S. Richards
c,
Bryce S. Richards c,
Rosa Maria Solé
c,
Rosa Maria Solé a,
Magdalena Aguilóa,
Francesc Díaza,
Ezzedine Ben Salemb and
Xavier Mateos
a,
Magdalena Aguilóa,
Francesc Díaza,
Ezzedine Ben Salemb and
Xavier Mateos *a
*a
aUniversitat Rovira i Virgili (URV, ), Física i Cristal lografia de Materials (FiCMA), Marcel·li Domingo 1, 43007, Tarragona, Spain. E-mail: xavier.mateos@urv.cat
bI.P.E.I. of Monastir, Unit of Materials and Organic Synthesis, University of Monastir, 5019, Tunisia
cInstitute of Microstructure Technology, Karlsruhe Institute of Technology, Hermann-von-Helmholtz-Platz 1, 76344 Eggenstein-Leopoldshafen, Germany
First published on 8th August 2023
Abstract
Quaternary tungstates with the composition Li3Ba2Gd3(WO4)8 doped with different concentrations of Dy3+ (from 0.5 to 10 at%) were prepared by the solid-state reaction method at 900 °C. Their structural, spectroscopic and optical properties were studied systematically in this work. X-ray diffraction analysis confirmed the crystallization of Li3Ba2Gd3(WO4)8 to have a monoclinic structure (sp. gr. C2/c); the lattice constants for 1 at% doping concentration of Dy3+ are a = 5.2126(2) Å, b = 12.7382(1) Å, c = 19.1884(3) Å, Vcalc = 1273,40(4) Å3 and β = a × c = 91.890(9)°. The first principles calculations for the undoped crystal revealed a direct bandgap of 2.45 eV, which is very close to the experimental one. The identified broad, and strong excitation peak at 450 nm indicates that Li3Ba2Gd3(WO4)8:Dy3+ phosphors are suitable to be pumped by a blue laser diode (LD). Under excitation at 445 nm, the phosphor showed a stronger luminescence peak at 575 nm which corresponds to the Dy3+:4F9/2 → 6H13/2 transition, and three weaker emissions peaks at 477, 661, and 750 nm. Meanwhile, the effect of different Dy3+ contents on the luminescence properties was investigated. The optimum concentration to minimize the quenching effect was 4 at% and the critical distance is 31.209 Å. The phosphor emitted strong greenish-yellow light situated at (0.425, 0.472) in CIE coordinates with a color temperature of 3652 K. All the measured luminescence lifetime curves exhibited a single-exponential nature. Excellent thermal stability was found for this tungstate phosphor (the activation energy is 0.352 ± 0.01 eV). The measured absolute photoluminescence quantum yield was around 10.5%. The results presented in this work show that Li3Ba2Gd3(WO4)8:Dy3+ phosphors with strong yellow emission are promising candidates for white-light emitting LED (wLED) applications.
1. Introduction
In recent years, white light-emitting diodes (wLEDs) in the field of solid-state lighting have gained growing attention due to their outstanding advantages, such as high reliability, high luminous efficiency, good material stability and environmental sustainability.1–5 Presently, one of the most common approaches to achieve white light is to blend commercial blue LED chips with yellow phosphors such as the well-known Ce3+-doped yttrium aluminum garnet (YAG:Ce3+).6,7 It shows high stability and performance (high PhotoLuminescence Quantum Yield, PLQY), absorbing blue light and emitting yellow persistent luminescence, as well as combining efficiently those blue and yellow photons to yield white light in a compact wLED.8 However, the YAG material has a high melting point (∼1970 °C9) which makes the industrial exploitation of this material expensive. It is therefore relevant to search for new effective luminescent materials that radiate yellow light with cheaper industrial fabrication cost (e.g. lower melting temperature). The performance of such wLEDs highly depends on the luminescence performance of the phosphors which are doped with different rare-earth ions (RE).10,11 The host matrix and activator ions are two factors that influence the luminescence properties of the phosphor.Among the activator ions (RE), dysprosium ions (Dy3+) are of interest to produce yellow emission. The 4F9/2 → 6H15/2 and 4F9/2 → 6H13/2 transitions in Dy3+ ions are located in the blue and yellow spectral regions, respectively. It is known that the 4F9/2 → 6H13/2 transition is hypersensitive to the crystal field (according to the selection rules ΔL = 2, ΔJ = 2).12–14 Therefore, the relative intensity of the yellow emission is responsive to the surrounding local environment of the Dy3+ ions and it is possible to change the ratio of yellow to blue (Y/B) emission intensities and produce white light using Dy3+ doped luminophores.15,16 The Y/B ratio depends on the level of Dy3+ doping and the structure of the host matrix (i.e., the symmetry of the point group for the Dy3+ ion sites).17 The emission intensity of the 4F9/2 → 6H13/2 transition is greater than that of the 4F9/2 → 6H15/2 transition (resulting in yellow luminescence) for the case where Dy3+ ions localize to the low-symmetry sites, and vice versa. Among the many crystals that have been reported, tungstate crystals exhibit a much higher Y/B intensity ratio compared to other crystals, due to the high level of covalency of the metal–ligand binding.18–20
Tungstate crystals are an important class of oxide host matrix for doping with RE ions. These crystals have received much interest due to their stable chemical properties, rich crystal chemistry, and potential applications in areas such as laser systems, electrochemistry, and photonics.21–23 As a member of the tungstate family of materials, the quaternary compound Li3Ba2RE3(WO4)8 (RE = La–Lu, Y), which is isostructural with Li3Ba2RE3(MoO4)8, has been explored as a host for solid-state lasers, and its crystal structure has been solved by Pan et al.24,25 It shows a monoclinic system with C2/c space group symmetry. Due to the occurrence of a statistical distribution of rare-earth and lithium atoms, these crystals exhibit high structural disorder, which results in homogeneous broadening of the absorption and emission lines when rare-earth ions are doped and fill the positions of RE3+ ions.26 So far, several studies were dedicated to Li3Ba2RE3(WO4)8 type-phosphors for applications in wLED. Li3Ba2Y3(WO4)8:Tb3+/Eu3+ emits white light, which is composed of three typical emission bands: green from Tb3+, red from Eu3+, and blue from the substrate. The luminescent colors can be tuned by adjusting the relative doping ratios of Eu3+ and Tb3+ in Li3Ba2Y3(WO4)8 phosphor, resulting in changes in the spectral components.27 Thus, Li3Ba2Y3(WO4)8:Eu3+ was synthesized by a high temperature solid-state reaction method. The color purity (97.2%) and thermal stability (activation energy ΔE = 0.27 eV) were found to be better than that of the commercial Y2O2S:Eu3+ phosphor.28 For the past few years, less attention has been paid to isostructural Gd-based compounds, e.g., lithium barium gadolinium quaternary tungstate Li3Ba2Gd3(WO4)8. Few studies predicted the suitability of the single crystal Li3Ba2Gd3(WO4)8 doped with Nd3+ (ref. 29) and Yb3+/Er3+ (ref. 30) for application in diode pumped lasers. Guo et al. reported on the characteristic of the green emission with high color purity collected from the phosphor Li3Ba2Gd3(WO4)8:Tb3+.31 Nevertheless, to the best of our knowledge, based on this tungstate host, the preparation of new types of phosphors for solid-state lighting is still relatively rare.
Herein, in this work, new Dy3+ ions-doped Li3Ba2Gd3(WO4)8 phosphors have been successfully synthesized by the conventional solid-state method. The structural, morphological, photoluminescence, and colorimetric properties were discussed in detail to yield that the Li3Ba2Gd3(WO4)8:Dy3+ is a promising yellow light emitting phosphor for solid-state lighting applications.
2. Experimental and methods
2.1. Materials synthesis
A new family of tungsten, Li3Ba2Gd3(WO4)8 doped with Dy3+ was synthesized using the traditional solid-state reaction method to explore and develop new phosphors. Li2CO3 (>99%, VWR Chemicals), BaCO3 (99.9%, chemPUR), Gd2O3 (99.99%, Treibacher AG), Dy2O3 (99.99%, Treibacher AG) and WO3 (99.9%, Honeywell Fluka) were used as reagents. They were first weighed in stoichiometric proportions, then transferred with ethanol to an agate mortar and carefully ground for 2 h to obtain a homogeneous mixture. After complete evaporation of the alcohol, they were placed directly into an alumina crucible, placed in a muffle furnace and sintered at 700 °C for one day in air to remove the CO2. Then, to obtain single-phase samples of Li3Ba2Gd3−xDyx(WO4)8 (x being from 1 at% to 10 at% in the raw materials mixture) we had to repeat the process again but keeping the temperature at 900 °C to achieve the pure phase while handling the mixture comfortably without melting. This was in air atmosphere for 24 h to ensure the adequate chemical reaction.The Li3Ba2Gd3−xDyx(WO4)8 samples were prepared using the following chemical reaction:
2.2. Experimental measurements
Structural characterization of the synthesized Li3Ba2Gd3(WO4)8:xDy3+ powders was performed by X-ray powder diffraction. Measurements were performed using a Bruker-AXS D8-Advance diffractometer with a vertical θ–θ goniometer with Cu Kα radiation (1.5406 Å). To detect the diffracted X-rays, a position sensitive detector (LynxEye-XE-T) was employed with an opening angle of 2.94°. For Rietveld refinement, the recording conditions were step size of 0.02° and step time of 2 s in the 2θ range from 5° to 80°. The support of the sample was Si(510), which has low background. The Rietveld refinement was computed using GSAS II software.The infrared (IR) spectra were recorded using a Fourier transform infrared spectrometer (FTIR, model FI/IR 6700, Jasco). Raman spectra were taken with a Renishaw InVia confocal Raman microscope that was equipped with an edge filter, a 50× objective, and an Ar+ ion laser as the excitation source (with λex = 514 nm). Differential thermal analysis (DTA) was performed using a MOM Q-1500 D derivatograph, using a Pt–Rh thermocouple and a Pt crucible. The heating and cooling rates were both 15 °C min−1 and under 140 cm3 min−1 of nitrogen flow. The sample weight was 3.5 mg. The accuracy of the temperature measurement was approximately ±5 °C. The composition of the samples was determined using electron dispersive X-ray spectroscopy (EDX) and was performed using a FEI Quanta 600 environmental scanning electron microscope (SEM) connected to an microanalyzer (Oxford Inca 3.0).
A spectrophotometer (Varian Cary 5000 UV-visible-IR), equipped with an integrating sphere, was employed to record the reflectance spectra at room temperature (RT, 20 °C) from 200 nm to 700 nm, on 12 mm diameter pellet samples, with a data interval of 0.5 nm and an integration time of 1 s. The photoluminescence (PL) spectroscopy under 445 nm excitation was performed using an in-house setup based on a diode laser (FC-445-2W) with a power of 1.1 W, coupled to an optical fiber and collimating lens to focus the light on the sample, and a spectral analyzer (OSA, Ando AQ6315-E) for detection. The excitation and emission (under λex = 350 nm) spectra were obtained using the spectrofluorometer (FS5, Edinburgh Instruments), with a built-in xenon lamp serving as the excitation source. PL lifetime measurements were performed using a photomultiplier tube (R928P, Hamamatsu), mounted in a temperature-cooling housing (CoolOne, Horiba), with the PLwavelength being selected with a double monochromator (Bentham, DTMS300). The excitation source was a 445 nm laser diode (Roithner) mounted in a temperature stabilized mount (TCLDM9, Thorlabs) and driven by a laser diode controller (ITC4001, Thorlabs). The photoluminescence quantum yield PLQY value is estimated with an optical setup built around an integrating sphere (Labsphere, 6′′Ø, 3 P-LPM-060-SL). The sample is placed in the middle of a sphere and is excited with a CW LED operating at 445 nm (Thorlabs, M450LP2) that is driven with a laser diode controller (Thorlabs, ITC4001).
The theoretical calculations of energy band structures were carried out using the density functional theory (DFT) plane-wave pseudopotential method via the Cambridge Serial Total Energy Package (CASTEP) code.32 The bandgap and electron structure of the host Li3Ba2Gd3(WO4)8 were calculated using the Perdew–Burke–Ernzerhof function within the generalized gradient approximation. The crystal parameters were taken from ref. 29. For the Brillouin zone, the Monkhorst–Pack scheme k-points grid sampling was set at 5 × 5 × 5, while a kinetic energy cutoff of 910 eV was used during calculations. The convergence tolerances of the maximum energy change, maximum force, and maximum displacement for the geometry optimization were 1.0 × 10−5 Hartree, 0.03 Hartree Å−1, and 0.001 Å, respectively. Pseudopotential = Norm conserving, FFT density = 54 × 54 × 144, SCF tolerance = 10−5 eV per atom, Monkhorst-Pack grid = 1/0.03 Å × 1/0.03 Å × 1/0.03 Å, k points set = 1/0.002 Å and the Brillouin zone path is: L(−0.5, 0, 0.5) → M(−0.5, 0.5, 0.5) → A(−0.5, 0, 0) → G(0, 0, 0) → Z(0, −0.5, 0.5) → V(0, 0, 0.5).
3. Results and discussion
3.1. Crystal structure analysis
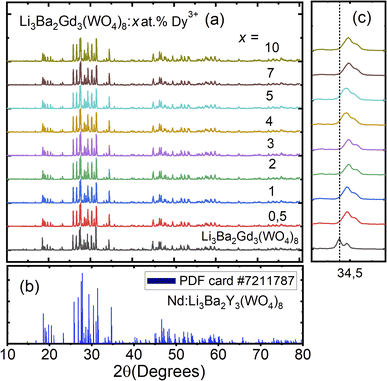
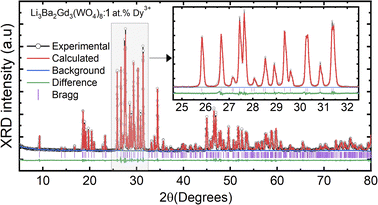
The crystal structure and phase purity of the prepared powders were confirmed by XRD. Fig. 1(a) shows the XRD profiles of the prepared Li3Ba2Gd3−x(WO4)8:xDy3+ phosphors for x in the range 0–10 at%. The relative intensity and position of the diffraction peaks of the synthesized powders are in good agreement with the JCPDS (Joint Committee on Powder Diffraction Standards) #7211787 for the 5 at% Nd:Li3Ba2Y3(WO4)8 crystal displayed in Fig. 1(b). No other diffraction peaks from impurities are detectable, indicating that the prepared samples are single-phase. Li3Ba2Gd3−x(WO4)8:x at% Dy3+ phosphors crystallize in the monoclinic class with the C2/c space group (2/m point group). The doping levels studied with Dy3+ ions do not change the structure of the material (same monoclinic phase), although the positions of the XRD diffraction peaks slightly shift to higher angles with respect to the undoped sample (Fig. 1(c)). This, according to Bragg's law, indicates a change in lattice constants. In addition, the sharp and intense peaks indicate that the samples have high crystallinity, which is advantageous for improving the luminous efficiency of the phosphors. According to the Shannon reference, the ionic radii of Dy3+, Li+, Ba2+ and Gd3+ are as follows: Dy3+ (1.027 Å, coordination number (CN) = VIIl), Li+ (0.92 Å, CN = VIIl), Ba2+ (1.42 Å, CN = VIIl) and Gd3+ (1.053 Å, CN = VIIl).33 It can be noted that Gd3+ has the closest radius and has the same charge number as Dy3+. The Dy3+ ions in Li3Ba2Gd3(WO4)8 are expected to replace the trivalent host-forming cations, Gd3+, in the 8f site type. The replacement of Gd3+ by Dy3+ is expected to induce a change in the lattice parameters. Indeed, a decrease in lattice constants has been noticed previously. The replacement of Gd3+ ions in the lattice by Dy3+ is supported by the % difference in ionic radii (Dr) between the activator (Dy3+) and the host ion (Gd3+), determined using eqn (1):34
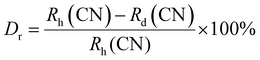 | (1) |
| Data | Li3Ba2Gd3(WO4)8: 1 at% Dy3+ |
|---|---|
| Chemical formula | Li3Ba2Gd2.97Dy0.03(WO4)8 |
| Crystal system | Monoclinic |
| Space group (IT number, Z) | C2/c (15, 2) |
| Laue class | 2/m |
| Calculated density (g cm−3) | 7.4045 |
| Lattice constant a, b, c (Å) | 5.2126(2), 12.7382(1), 19.1884(3) |
| α, β, γ (deg.) | 90, 91.8906(9), 90 |
| Volume (Å3) | 1273.40(4) |
| 2θ range (deg.) | 5–80 |
| 2θ step (deg.) | 0.02 |
| Radiations | Cu Kα1 (λ = 1.5418 Å) |
| Refinement software | GSAS II |
| Reduced χ2 | 2.25 |
| Goodness of fit (GOF) | 1.50 |
| Rw (%) | 8.092 |
The atomic coordinates, sites, occupancy factors (O. F.) and isotropic displacement parameters (Biso) obtained for the Li3Ba2Gd3(WO4)8: 1 at% Dy3+ sample are summarized in Table 2. From the results of the Rietveld refinement, a fragment of the Li3Ba2Gd3(WO4)8:Dy3+ structure in projection on the two crystallographic planes b–c and a–b was drawn, as shown in Fig. 3. The metal–oxygen (M−O) interatomic distances in the [Gd|Li1|Dy]O8, [Li2]O6, and [Ba]O10 polyhedra determined by VESTA analysis of the .cif file are shown in Table 3 and plotted in Fig. 4. Ba2+ cations are coordinated with 10 oxygen atoms to form the distorted [Ba]O10 polyhedra in which the interatomic distances are determinated to be between 2.6878(1) and 3.0371(5) Å. Li+ ions are located in two crystallographic sites, one called Li2 where the are atoms located in a special crystallographic position with the 4th Wyckoff symbol coordinated by 6 oxygen atoms, and the other called Li1 statistically distributed with Gd3+|Dy3+ ions. Each Gd|Li1|Dy is coordinated by eight oxygen atoms to form a distorted polyhedron, the interatomic distances Gd|Li1|Dy–O vary between 2.1345(1) and 2.6146(5) Å. This structure contains [Gd|Li1|Dy]O8, [Li2]O6 and [Ba]O10 polyhedra which are further interconnected by sharing oxygen atoms. The nearby [Gd|Li1|Dy]O8 polyhedron leading to a 2-dimensional layered structure parallel to (b–c) plan. [Ba]O10 polyhedron are connected to the adjacent [Gd|Li1|Dy]O8–[Gd|Li1|Dy]O8 layer to form a three-dimensional (3D) network, which results in a one-layer polyhedron structure.
| Atoms | Sites | x/a | y/b | z/c | O. F. | Biso (Å2) |
|---|---|---|---|---|---|---|
| W1 | 8f | 0.4887(7) | 0.4403(3) | 0.4052(7) | 1.000 | 1.224(7) |
| W2 | 8f | 0.5013(8) | 0.7437(6) | 0.3510(3) | 1.000 | 0.884(1) |
| Ba | 4e | 1.0000(0) | 0.5318(8) | 0.2500(0) | 1.000 | 1.684(1) |
| Gd|Li1|Dy | 8f | 0.9666(1) | 0.6532(4) | 0.4564(2) | 0.742|0.250|0.008 | 0.779(4) |
| Li2 | 4e | 0.5000(0) | 0.3220(0) | 0.2500(0) | 1.000 | 1.554(2) |
| O1 | 8f | 0.6296(7) | 0.4145(8) | 0.3215(0) | 1.000 | 2.921(1) |
| O2 | 8f | 0.2547(2) | 0.5490(9) | 0.3926(9) | 1.000 | 2.843(7) |
| O3 | 8f | 0.7456(8) | 0.4830(5) | 0.4636(3) | 1.000 | 2.264(1) |
| O4 | 8f | 0.3402(9) | 0.3321(3) | 0.4530(5) | 1.000 | 3.054(9) |
| O5 | 8f | 0.2892(4) | 0.70776(6) | 0.2864(1) | 1.000 | 2.737(5) |
| O6 | 8f | 0.7328(4) | 0.6524(9) | 0.3632(8) | 1.000 | 3.053(4) |
| O7 | 8f | 0.6621(5) | 0.8621(2) | 0.3220(4) | 1.000 | 2.580(5) |
| O8 | 8f | 0.3267(0) | 0.7626(0) | 0.4312(0) | 1.000 | 2.501(2) |
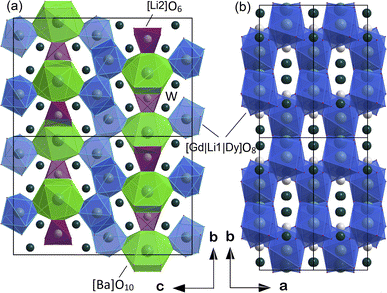 | ||
| Fig. 3 Fragment of structure of Li3Ba2Gd3(WO4)8:Dy3+ in projection to the (a) b–c crystallographic plane and (b) a–b plane. | ||
| M−O distances (Å) × numbers | ||
|---|---|---|
| [Gd|Li1|Dy]O8 | [Li2]O6 | [Ba]O10 |
| Gd|Li1|Dy–O | Li2–O | Ba–O |
| Gd|Li1|Dy–O6 = 2.1345(1) × 1 | Li2–O1 = 1.9154(3) × 2 | Ba–O7 = 2.6878(1) × 2 |
| Gd|Li1|Dy–O4 = 2.3721(6) × 1 | Li2–O5 = 2.1930(5) × 2 | Ba–O5 = 2.7768(9) × 2 |
| Gd|Li1|Dy–O2 = 2.3896(2) × 1 | Li2–O7 = 2.3310(9) × 2 | Ba–O1 = 2.8312(7) × 2 |
| Gd|Li1|Dy–O8 = 2.4021(6) × 1 | Ba–O2 = 3.0112(7) × 2 | |
| Gd|Li1|Dy–O4′ = 2.4078(6) × 1 | Ba–O6 = 3.0371(5) × 2 | |
| Gd|Li1|Dy–O3 = 2.4603(7) × 1 | ||
| Gd|Li1|Dy–O3′ = 2.4646(7) × 1 | ||
| Gd|Li1|Dy–O8′ = 2.6146(5) × 1 | ||
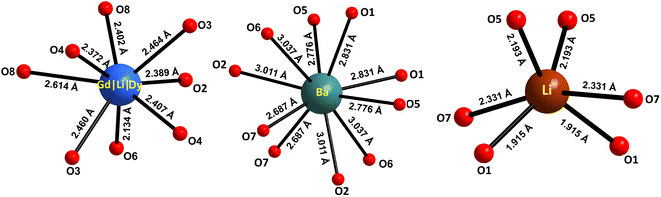 | ||
| Fig. 4 Oxygenated environment of [Gd|Li1|Dy]O8, [Li2]O6 and [Ba]O10 polyhedra in Li3Ba2Gd3(WO4)8: 1 at% Dy3+. The values indicate the interatomic distances. | ||
3.2. Differential thermal analysis
The DTA curves for the Li3Ba2Gd3(WO4)8: 10 at% Dy3+ sample corresponding to the heating and cooling of the sample are presented in Fig. S1.† A single strong and reversible endothermic (on heating) and exothermic (on cooling) effect can be observed, which corresponds to the congruent melting and crystallization processes. Moreover, the starting temperature of melting corresponds well to 1029 °C, which is a little bit lower than the melting point of the pure host, i.e. 1034 °C.29 Upon cooling the sample, we found an exothermic peak at 1023 °C which could be due to the crystallization of the monoclinic phase. Finally, the absence of additional thermal effects well reflects the absence of polymorphic phase transformations of the first type below the melting point for this composition.3.3. FTIR & Raman spectroscopy
The FTIR spectra of Li3Ba2Gd3−x(WO4)8:xDy3+ with 0 ≤ x ≤ 10 at% phosphors were recorded and presented in Fig. S2(a),† and they indicate that there is no significant change in the FTIR spectra with increasing Dy3+ concentrations. Several intense and sharp peaks can be observed in the range of 400–1500 cm−1 which belong to the characteristic absorption of WO42−. Precursor and calcined samples show absorption peaks corresponding to the appearance of (WO4)2− groups between 400 and 1000 cm−1.35,36 Among them, the intense absorption bands around 682, 756 and 783 cm−1 originate from the double-bridge stretching mode (WOOW). While the least intense peak located at 918 cm−1 can be attributed to the band stretching mode (W–O). The peaks at 829 and 423 cm−1 are attributed to the band stretching and bending (WOW) modes, respectively.36 The Raman spectra of Li3Ba2Gd3(WO4)8:xDy3+ with x = 0, 1, 3, 5, 7 and 10 at% measured between 100 and 1000 cm−1 under ambient conditions are shown in Fig. S2(b).† Nine modes are observed, the modes centred at 913, and 886 cm−1 are assigned to the symmetric stretching of the (WO4)2− tetrahedra, the modes 840, 795 and 747 cm−1 to the asymmetric stretching, the one at 395 cm−1 to the asymmetric bending of WO4, the one at 325 cm−1 to the symmetrical bending, and the ones at 212 and 128 cm−1 to lattice modes.37–393.4. Morphology and composition
Fig. 5(a) shows a SEM micrograph of Li3Ba2Gd3−x(WO4)8: 1 at% Dy3+ annealed at 900 °C. We observe that the particles have a more or less spherical shape morphology, block-shaped and with a non-uniform size distribution. The composition of the samples studied was determined by line-scan EDX analysis and element mapping. Typical EDX spectra of the Dy-doped sample (with x = 1 at%) are shown in Fig. 5(b) and the element mapping of the doped sample is shown in Fig. 5(c). For the Dy-doped sample, we can clearly confirm the presence of Dy as an additional element. The element mapping of Dy and Gd suggests an uniform distribution of the dopant in the host matrix, as also derived from the conclusion of the XRD results.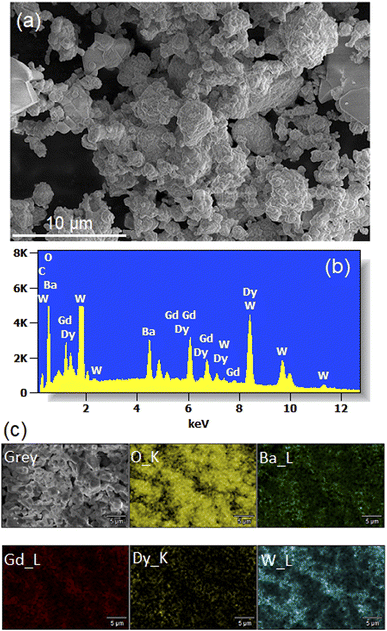 | ||
| Fig. 5 (a) SEM image (b) Energy-dispersive X-ray (EDX) spectra (c) elemental mapping for the Li3Ba2Gd3 (WO4)8: 1 at% Dy3+. | ||
3.5. Bandgap and electronic structure
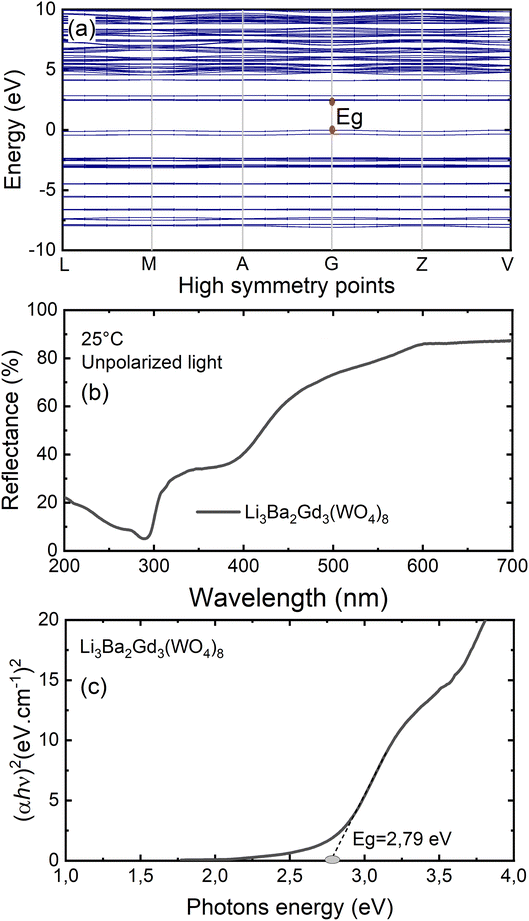
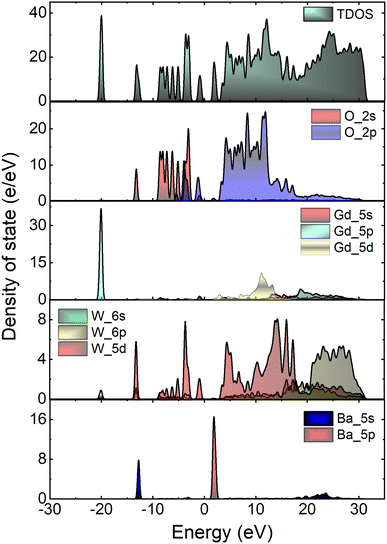
To gain insight into the electronic structure of Li3Ba2Gd3(WO4)8, DFT calculations were performed, and the results are shown in Fig. 6(a). The energy gap between the conduction band (CB) minimum and the valence band (VB) maximum was determined to be 2.45 eV. One can find that the band structure is direct band gap where the maximum of VB and the minimum of CB are located along the same vertical line G. Owing to a relatively large energy gap which can accommodate the ground and excited states of the doped activator, the host was considered to be a suitable matrix for phosphors application. In order to evaluate the experimental optical band gap of the host, diffuse reflectance spectra were recorded in the range of 200–700 nm at room temperature as shown in Fig. 6(b). A broad absorption band with a maximum value at about 300 nm was observed for the undoped sample, this corresponds to the charge transition band (CTB) of oxygen to tungsten O2− → W6+.The Kubelka–Munk (K–M) relation is employed to evaluate the optical band gap value of the studied host.40 More details about the K–M calculations could be found in the ESI file.† We plot [F(R∞)hν]2 as a function of hν, the bandgap value Eg can be obtained by deducing the fitted regions at the abscissae, as shown in Fig. 6(c). The experimental value of the optical band gap of the host Li3Ba2Gd3(WO4)8 was found to be equal to 2.79 eV, which is very close to the theoretical one. This underestimation of the theoretical result could be explained by the fact that the Perdew–Burke–Ernzerhof function of the generalized gradient approximation was adopted to deal with exchange correlation interactions.41,42Fig. 7 depicts the total and atom-resolved partial density of states (DOS) of Li3Ba2Gd3(WO4)8. From the figure we know that the conduction band is caused by the p-state of Ba, the d-state of W and p-state of Gd atoms, while all of the elements contribute to the valence band. The VB with energy stretching from the Fermi energy level around 0 eV to −9.27 eV is mainly caused by the O-2p state and the W-6p, 5d states. The deeper valence band with energy around −20.02 eV is derived from the 5p-state of the Gd atom.
3.6. Optical properties
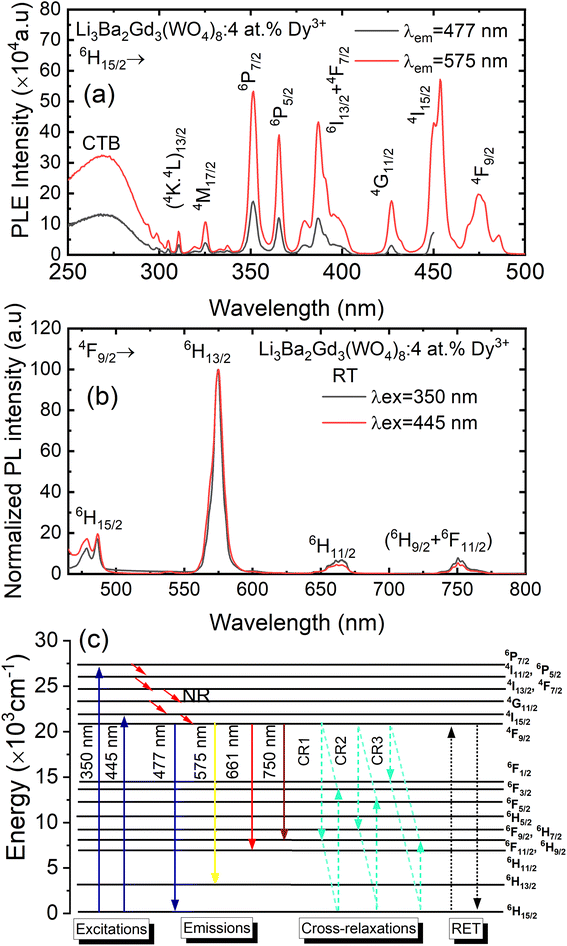
Fig. 8(a) depicts the photoluminescence excitation (PLE) spectra of Li3Ba2Gd3(WO4)8: 4 at% Dy3+ phosphor. There is no difference between the excitation bands under different monitoring wavelengths (λem = 477 and 575 nm), except the excitation intensity. It can be seen that the excitation spectra consist of an intense broad band and some narrow peaks. Among them, the broad excitation band in the UV region from 250 to 310 nm centered at 269 nm is mainly ascribed to the CTB of WO42− groups and corresponds to electrons which are excited from the oxygen 2p states to tungsten 5d states through the absorption of photons within the WO42− group.43 The existence of the strong CTB of the WO42− group in the excitation spectra indicates the presence of energy transfer from the WO42− group to the Dy3+ ions in Li3Ba2Gd3(WO4)8:Dy3+ phosphors. It is similar to the previous reported cases for other tungstate phosphors, NaY(WO4)2:Dy3+.44 In the longer wavelength region from 310 to 500 nm, some sharp lines due to the f–f transitions of Dy3+ are observed, which are assigned to the electronic transitions 6H15/2 → (4K13/2 + 4L13/2) at 311 nm, 6H15/2 → 4M17/2 at 325 nm, 6H15/2 → 6P7/2 at 351 nm, 6H15/2 → 6P5/2 at 365 nm, 6H15/2 → (4I13/2 + 4F7/2) at 386 nm, 6H15/2 → 4G11/2 at 427 nm, 6H15/2 → 4I15/2 at 453 nm and 6H15/2 → 4F9/2 at 475 nm,45,46 in which there are two stronger absorption peaks, one in the UV at 350 and the second is in the blue at 450 nm. The intensity of the blue excitation peak is higher with 7.5 nm of excitation bandwidth.The emission spectra of Dy3+ as shown in Fig. 8(b) can be ascribed to the change from excited energy level to a lower energy level. The PL spectra of the phosphors excited at 445 nm are very similar to those excited at 350 nm. The emission characteristics of the Dy3+ doped sample consisted of multiple sharp peaks with multiple wavelengths due to the unique electronic transition in the system. The compact manifolds of energy levels in the upper parts of the activator cause electrons that are excited to decay only through the 4F9/2 level to the lower 6Hj/2 (j = 15, 13, 11,9) levels at 477, 575, 661, and 750 nm respectively. The large energy difference between each lower level causes the emission spectra to be separated at a distance. By comparing the emission spectra of the sample Li3Ba2Gd3(WO4)8: 4 at% Dy3+ collected under two different excitation wavelengths, we conclude that the emssion peaks do not change with λex. Furthermore, the ratio Y/B of emission at 575 nm (yellow) and 477 nm (blue), is almost the same for both cases, 5.17. This indicates that in this synthesized series, the predominant color is yellow. That ratio is known to be highly dependent on the site occupied by Dy3+. In the compound Li3Ba2Gd3(WO4)8, the low symmetry of the site occupied by Dy3+ increases the 575 nm emission in comparison to the 477 nm emission.47 Fig. 8(c) shows the energy transfer processes of Dy3+ ions in Li3Ba2Gd3(WO4)8: x at% Dy3+ phosphors. Under the 350 nm and 445 nm excitation, Dy3+ ions absorb the photon energy and transfers it from the ground state 6H15/2 to the metastable excited states. During this process, the excited populations are rapidly released at the 4F9/2 energy level by a non-radiative (NR) process that occurs between the excited states. The transitions 4F9/2 → 6H15/2, 4F9/2 → 6H13/2, 4F9/2 → 6H11/2 and 4F9/2 → 6H9/2 + 6F11/2, are radiative and produce the emission peaks at 477, 575, 661 and 750 nm, respectively. Due to the resonance energy between energy levels, the nonradiative energy transfer (ET) and concentration quenching may take place between 4F9/2 + 6H15/2 and 6H15/2 + 4F9/2, and the cross-relaxation (CR) mechanisms may also take place among neighboring Dy3+ ions. Considering the energy match rule, the possible ET and three CR channels are: CR1: 4F9/2 + 6H15/2 → 6F11/2,6H9/2 + 6F3/2, CR2: 4F9/2 + 6H15/2 → 6F9/2,6H7/2 + 6F5/2 and CR3: 4F9/2 + 6H15/2 → 6F1/2 + 6F11/2,6H9/2.44
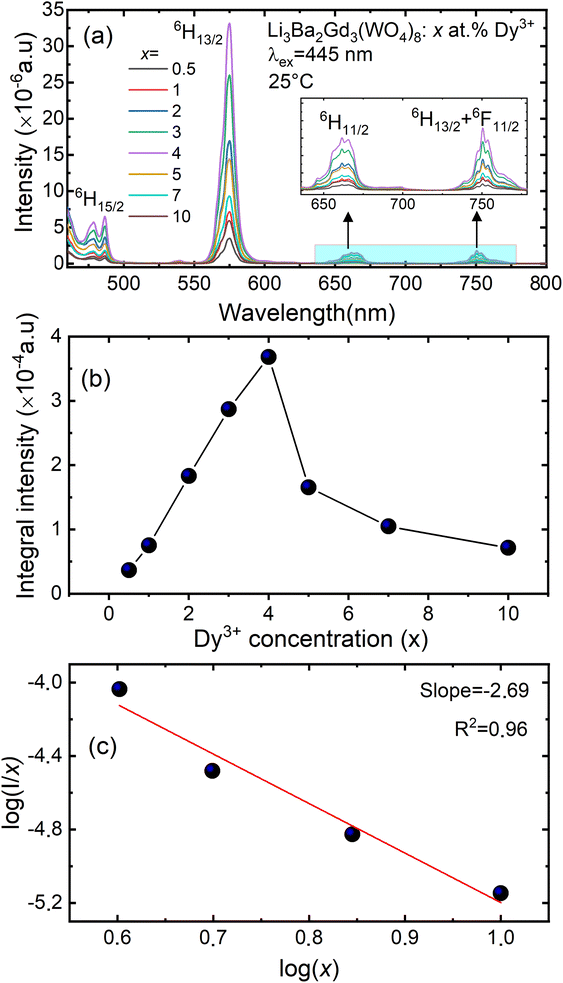
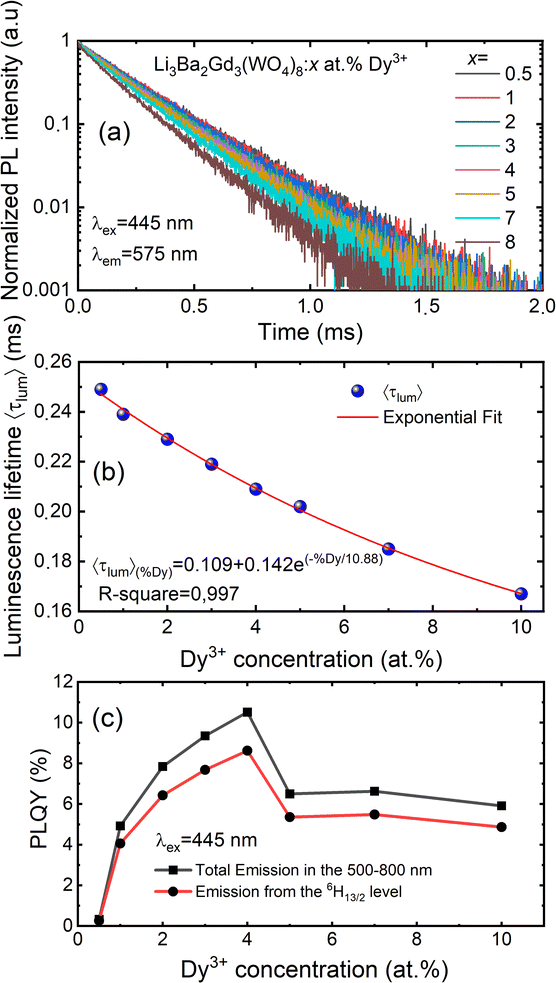
Fig. 9(a) shows the concentration of Dy3+ ions influences on the PL intensities ofLi 3Ba2Gd3(WO4)8: x at% Dy3+ phosphor (x = 0.5, 1, 2, 3, 4, 5, 7, and 10) under excitation of 445 nm. The ratio Y/B of the yellow and the blue emission is increased from 4.49 for 0.5 at% sample to 5.58 when the concentration of Dy3+ ions is 10 at%. The maximum PL emission intensity was found when the Dy3+ doping concentration was 4 at%. Thereafter, the intensity decreases due to concentration-dependent fluorescence quenching. As the concentration of Dy3+ doping ions increases, the average distance between Dy3+ ions decreases. Cross-relaxation mechanism between adjacent Dy3+ ions become more probable. As reported in Fig. 9(b), it is evident that the intensity 4F9/2 → 6Hj/2 (j = 15, 13, 11, 9) transitions steadily increases with increasing the Dy3+ concentration up to 4 at% of Dy3+ ions concentration and then quenches for 4 at%. This type of concentration quenching phenomenon can be attributed to the exchange interaction or the multipolar electrical interaction.48 It is known that when the energy transfer results from the exchange interaction, the critical distance between Dy3+ and the quenching site must be less than 4 Å.49 As suggested by Blasse,50 the average critical distance of exchange transfer (Rc) can be determined as follows:
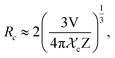 | (2) |
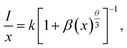 | (3) |
 represents the emission intensity per activator (x), k and β are constants for a given host lattice, θ is the type of interaction between the emitting ions, here θ = 6, 8, 10 corresponding to dipole–dipole (d–d), dipole–quadrupole (d–q) and quadrupole–quadrupole (q–q) interaction, respectively. Fig. 9(c) shows I/x as a function of x on a logarithmic scale for Li3Ba2Gd3(WO4)8: x at% Dy3+phosphors. The dependence of
represents the emission intensity per activator (x), k and β are constants for a given host lattice, θ is the type of interaction between the emitting ions, here θ = 6, 8, 10 corresponding to dipole–dipole (d–d), dipole–quadrupole (d–q) and quadrupole–quadrupole (q–q) interaction, respectively. Fig. 9(c) shows I/x as a function of x on a logarithmic scale for Li3Ba2Gd3(WO4)8: x at% Dy3+phosphors. The dependence of 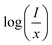 on log(x) is relatively linear, and the slope (θ/3) is determined to be 2.69. The value of θ is equal to 8.07, indicating that the concentration quenching in Li3Ba2Gd3(WO4)8 is attributed to the dipole–quadrupole (d–q) interaction.
on log(x) is relatively linear, and the slope (θ/3) is determined to be 2.69. The value of θ is equal to 8.07, indicating that the concentration quenching in Li3Ba2Gd3(WO4)8 is attributed to the dipole–quadrupole (d–q) interaction.
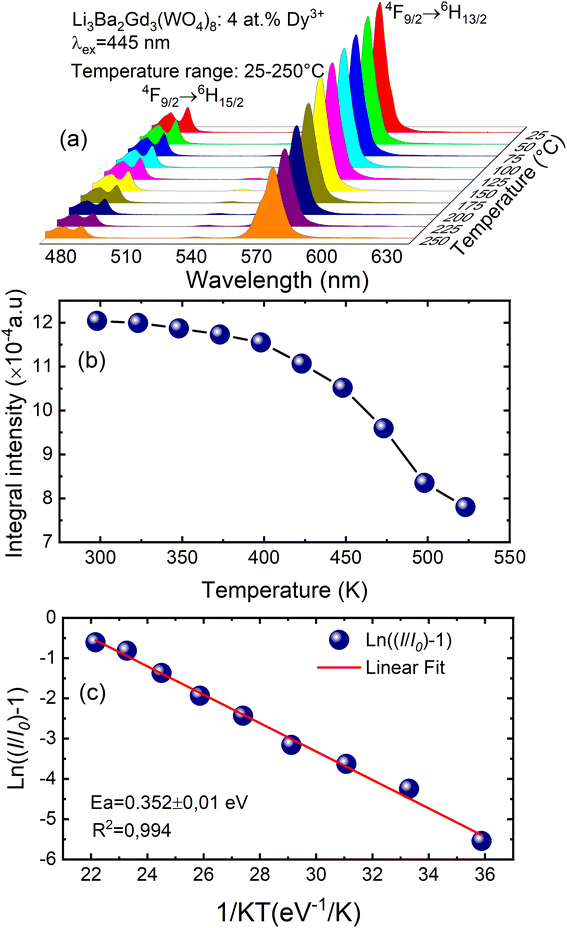
To examine the effects of high temperature at real work conditions of wLEDs on the luminescent properties of the prepared Li3Ba2Gd3(WO4)8: x at% Dy3+ luminophores, a series of PL emission spectra in the temperature range of 25–250 °C was acquired for the particular sample with x = 4 at% (corresponding to the maximum emission intensity at room temperature), using excitation at 445 nm, see Fig. 10(a). The emission peaks show a similar spectral profile to each other. The position of the emission peaks does not change with increasing temperature. However, the emission intensities of all peaks gradually decrease with temperature. In the spectra, a double-peaked feature is clearly apparent for the 4F9/2 → 6H15/2 transition from about 488 nm. On the other hand, the samples also do not reach the thermal quenching temperature, indicating high thermal stability at high temperature. Note that the decrease in luminescence intensity with temperature is not monotonic. Thus, at 100 °C the emission intensity is reduced to ∼8.5%, at 150 °C it is reduced to ∼12.4%, and at 250 °C the integral intensity is around 62% less than of its value at RT, see Fig. 10(b). All Li3Ba2Gd3(WO4)8 samples doped with Dy3+ showed high thermal stability at high temperature. This behavior is attributed to a temperature-induced redistribution of Dy3+ ions across the lattice sites. In order to understand the thermal suppression of luminescence of the synthesized materials and to determine the activation energy value of this process, a modified Arrhenius equation was applied:53
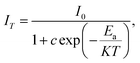 | (4) |
In order to determine the color parameters, the CIE coordinates (x,y) and the correlated color temperature parameter (CCT) were obtained using the standard formula. The chromaticity coordinates can be calculated from the tri-stimulus values of CIE 1931-XYZ tri-chromatic system,55,56 more details about this calculation is presented in the ESI file.† CIE chromaticity coordinates are generally used to check the exact emission color and color purity. The emission spectra of Li3Ba2Gd3(WO4)8: x at% Dy3+ phosphors were used to calculate the CIE chromaticity coordinates. The calculated chromaticity for different concentration levels are displayed in Fig. 11 and their numerical values are shown in Table 4. The small shifting in the (x,y) coordinates when the concentration of the Dy3+ increases is explained by the change of the ratio Y/B mentioned above.
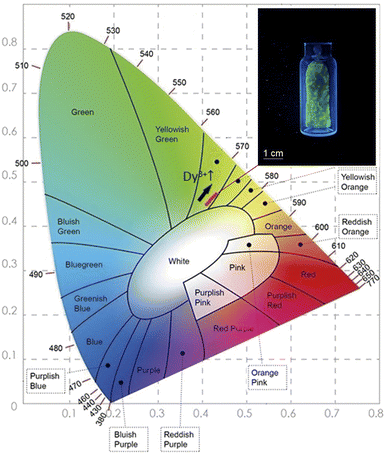 | ||
| Fig. 11 The CIE chromaticity diagram of the Dy3+ doped Li3Ba2Gd3(WO4)8 phosphors at 445 nm of Excitation; (inset) a photograph of the greenish-yellow phosphor under blue light illumination. | ||
| Dy3+ concentration (at%) | x | y | CCT (K) | Color purity (%) |
|---|---|---|---|---|
| 0.5 | 0.417 | 0.467 | 3756 | 95 |
| 1 | 0.418 | 0.466 | 3736 | 96.4 |
| 2 | 0.421 | 0.471 | 3701 | 96.8 |
| 3 | 0.424 | 0.471 | 3663 | 97.1 |
| 4 | 0.425 | 0.472 | 3652 | 98 |
| 5 | 0.424 | 0.474 | 3668 | 98.2 |
| 7 | 0.428 | 0.477 | 3619 | 98.5 |
| 10 | 0.430 | 0.481 | 3621 | 98.3 |
From Fig. 11, it can be seen that all the coordinates are located in the greenish-yellow color region of the CIE diagram, demonstrating that the Dy3+-doped Li3Ba2Gd3(WO4)8 phosphors have potential for white LED applications. The same color found by calculating the CIE chromaticity coordinates, can be seen when we illuminate the sample with blue light at 450 nm, see the inset in Fig. 12. After obtaining the chromaticity coordinates, the CCT can be calculated using the following empirical McCamy formula:57
| CCT = −449n3 + 3525n2 − 6823.3n + 5520.33, | (5) |
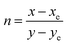 , while xe and ye correspond to the epicenter, the values of xe and ye are 0.332 and 0.186 respectively. The CCT values were calculated as 3756, 3736, 3701, 3663, 3652, 3668, 3619 and 3621 K for the eight synthesized phosphors. The results exhibited the characteristics of low color correlated temperature. The color purity of phosphors is also a key factor in producing a better light source for LED applications.58 To determine this factor, the following formula is used:
, while xe and ye correspond to the epicenter, the values of xe and ye are 0.332 and 0.186 respectively. The CCT values were calculated as 3756, 3736, 3701, 3663, 3652, 3668, 3619 and 3621 K for the eight synthesized phosphors. The results exhibited the characteristics of low color correlated temperature. The color purity of phosphors is also a key factor in producing a better light source for LED applications.58 To determine this factor, the following formula is used:
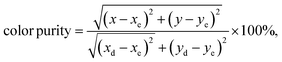 | (6) |
The luminescence decay curves of Li3Ba2Gd3(WO4)8: x at% Dy3+ phosphors at RT are shown in Fig. 12(a), (λex = 445 nm and λem = 575 nm). The decay process can be well fitted by single exponential function the eqn (7) as follows:
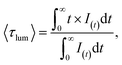 | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−x/10.88), as shown in Fig. 12(b).
exp(−x/10.88), as shown in Fig. 12(b).
By monitoring within the luminescence range of 500–800 nm and excited with 445 nm blue radiation, the absolute photoluminescence quantum yield, PLQY was obtained for different concenrtaion levels of Dy3+ ions. It was directly measured using a QE Pro-Ocean Insight spectrofluorimeter with an integrating sphere. The PLQY can be calculated as follows59: PLQY = LS/(ER − ES), where LS is the integrated intensity of the luminescence emission spectrum of the sample, ES is the integrated intensity of the spectrum of light used for exciting the sample, and ER is the integrated intensity of the spectrum of excitation light without the sample in the sphere. The result of the calculation are shown in Fig. 12(c). We can see that the doping concentration of Dy3+ ion has a great impact on the PLQY. The value for the sample with the strongest emission, 4 at% Dy3+, was found to be 10.5%. However, the PLQY of Li3Ba2Gd3(WO4)8:Dy3+ can be enhanced by controlling the particle size, size distribution, morphology, and crystalline defects through optimization of the processing conditions and composition. Hence, Li3Ba2Gd3(WO4)8:Dy3+ can be a good candidate for the yellow component applied in wLEDs.
Table 5 provides a comparative view of the emission properties of several yellow-emitted Dy3+-activated inorganic phosphors materials studied so far. The chromatic coordinates (x,y) of the yellow emission vary from material to another, depending on the actual composition of the host phosphor and the excitation wavelength. In our case, the yellow/blue emission ratio (Y/B) under 445 nm-blue excitation is relatively high compared to other phosphors, resulting in a strong greenish-yellow luminescence.
| Phosphor | λex (nm) | x | y | CCT (K) | τlum (ms) | PLQY (%) | Ref. |
|---|---|---|---|---|---|---|---|
| Li3Ba2Gd3(WO4)8 | 445 | 0.425 | 0.472 | 3652 | 0.209 | 10.5 | This work |
| NaLi9(SiO4)O9 | 445 | 0.469 | 0.495 | 3150 | 0.630 | — | 16 |
| Sr3LaNb3O12 | 352 | 0.425 | 0.450 | 3252 | — | 18.24 | 60 |
| Ca3TeO6 | 349 | 0.417 | 0.461 | 3735 | 0.506 | — | 61 |
| NaLa(MoO4)2 | 352 | 0.345 | 0.386 | — | 0.150 | 22 | 62 |
| (Ca,Sr)7(SiO3)6Cl2 | 380 | 0.350 | 0.502 | — | — | 24.6 | 63 |
| NaLaMgWO6 | 388 | 0.441 | 0.475 | — | 0.133 | 15.8 | 17 |
| SrAl2O4 | 350 | 0.300 | 0.345 | — | 0.930 | 9.52 | 64 |
4. Conclusions
New quaternary tungstate Li3Ba2Gd3(WO4)8:Dy3+ phosphors were successfully synthesized by the solid-state reaction, and its microstructural, spectroscopic and opticals properties were investigated in detail. X-ray diffraction Rietveld analysis revealed that the prepared luminophores crystallize in the monoclinic system with the C2/c space group and that the dopant ions Dy3+ replace the cations Gd3+ occupying the crystallographic site 8f. The FE-SEM micrograph revealed that the as-synthesized powder particles had micron size with irregular shape. The DFT calculations for the undoped sample showed a direct band gap of 2.45 eV. The excitation spectra indicated that this phosphor could be effectively excited with blue laser diode emitting at 445 nm. The PL spectra of the luminophores are dominated by the 4F9/2 → 6H13/2 band at 575 nm that determines a strong greenish-yellow emission color. The optimum concentration of Dy3+ is 4 at%, and the dipole-quadrupole is the dominant mechanism for concentration quenching. The decay curves were single exponential in nature and the decay time value decreases with increasing Dy3+ ion concentration, which suggests energy transfer between adjacent Dy3+ ions. The absolute photoluminescence quantum yield was found to be stronlgly dependent on the concentration of Dy3+ ions and its 10.5% for the sample with the strongest emission. The temperature dependent PL revealed good thermal stability of the as-synthesized phosphor with an appreciable activation energy of 0.352 eV. The combination of the findings mentioned above suggests the prospective utility of the synthesized phosphors for applications in wLEDs under the excitation of blue LED chips.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research article has been possible with the support of the Secretaria d’Universitats i Recerca del Departament d’Empresa i Coneixement de la Generalitat de Catalunya, the European Union (UE), and the European Social Fund (ESF) (2021 FI_B1 00170). Grant PID2019-108543RB-I00 funded by MCIN/AEI/10.13039/501100011033. The authors from KIT gratefully acknowledge the financial support provided by the Helmholtz Association, in particular Research Field Energy – Program Materials and Technologies for the Energy Transition – Topic 1 Photovoltaics (38.01.05).References
- H. Guo, X. Wang, J. Chen and F. Li, Opt. Mater. Express, 2010, 18, 1513–1515 Search PubMed.
- W. Yang, C. Liu, S. Lu, J. Du, Q. Gao, R. Zhang, Y. Liu and C. Yang, J. Mater. Chem. C, 2018, 6, 290–298 RSC.
- H. Li, H. M. Noh, B. K. Moon, B. C. Choi, J. H. Jeong, K. Jang, H. S. Lee and S. S. Yi, Inorg. Chem., 2013, 52, 11210–11217 CrossRef CAS PubMed.
- W. Lu, N. Guo, Y. Jia, Q. Zhao, W. Lv, M. Jiao, B. Shao and H. You, Inorg. Chem., 2013, 52, 3007–3012 CrossRef CAS PubMed.
- H. Guo and X. Huang, J. Alloys Compd., 2018, 764, 809–814 CrossRef CAS.
- V. Bachmann, C. Ronda and A. Meijerink, Chem. Mater., 2009, 21, 2077–2084 CrossRef CAS.
- R. Zhang, T. Maeda, R. Maruta, S. Kusaka, B. Ding, K.-I. Murai and T. Moriga, J. Solid State Chem., 2010, 183, 620–623 CrossRef CAS.
- W. Li, G. Fang, Y. Wang, Z. You, J. Li, Z. Zhu, C. Tu, Y. Xu and W. Jie, Vacuum, 2021, 188, 110215 CrossRef CAS.
- V. J. Fratello and C. D. Brandle, J. Cryst. Growth, 1993, 128, 1006–1010 CrossRef CAS.
- L. Zhao, F. Fan, X. Chen, Y. Wang, Y. Li and B. Deng, J. Mater. Sci.: Mater. Electron., 2018, 29, 5975–5981 CrossRef CAS.
- F. Fan, L. Zhao, Y. Shang, J. Liu, W. Chen and Y. Li, J. Lumin., 2019, 211, 14–19 CrossRef CAS.
- H. Chen, P. Loiseau and G. Aka, J. Lumin., 2018, 199, 509–515 CrossRef CAS.
- H. Liu, L. Liao, Q. Guo, D. Yang and L. Mei, J. Lumin., 2017, 181, 407–410 CrossRef CAS.
- R. Mi, J. Chen, Y. Liu, L. Mei, J. Yuan, Y. Xia, Z. Huang and M. Fang, Mater. Res. Bull., 2017, 86, 146–152 CrossRef CAS.
- Q. Liu, J. Guo, M. Fan, Q. Zhang, S. Liu, K. L. Wong, Z. Liu and B. Wei, J. Mater. Chem. C, 2020, 8, 2117–2122 RSC.
- S. Slimi, P. Loiko, K. Bogdanov, A. Volokitina, R. M. Solé, M. Aguiló, F. Díaz, E. Ben Salem and X. Mateos, J. Alloys Compd., 2022, 896, 163109 CrossRef CAS.
- B. Han, Y. Dai, J. Zhang and H. Shi, Mater. Lett., 2017, 204, 145–148 CrossRef CAS.
- Y. Wei, C. Tu, H. Wang, F. Yang, G. Jia, Z. You, X. Lu, J. Li, Z. Zhu and Y. Wang, J. Alloys Compd., 2007, 438, 310–316 CrossRef CAS.
- W. W. Zhou, B. Wei, W. Zhao, G. F. Wang, X. Bao, Y. H. Chen, F. W. Wang, J. M. Du and H. J. Yu, Opt. Mater., 2011, 34, 56–60 CrossRef CAS.
- W. Zhao, W. W. Zhou, B. Wei, Y. Yu, G. F. Wang, J. M. Du, H. J. Yu, Z. C. Lv and Y. H. Chen, J. Alloys Compd., 2012, 538, 136–143 CrossRef CAS.
- Y. C. Chang, C. H. Liang, S. A. Yan and Y. S. Chang, J. Phys. Chem. C, 2010, 114, 3645–3652 CrossRef CAS.
- M. Shang, G. Li, X. Kang, D. Yang and J. Lin, J. Electrochem. Soc., 2011, 158, H565 CrossRef CAS.
- K. Subbotin, P. Loiko, S. Slimi, A. Volokitina, A. Titov, D. Lis, E. Chernova, S. Kuznetsov, R. M. Solé, U. Griebner, V. Petrov, M. Aguiló, F. Díaz, P. Camy, E. Zharikov and X. Mateos, J. Lumin., 2020, 228, 117601 CrossRef CAS.
- Y. Pan, Y. Chen, Y. Lin, X. Gong, J. Huang, Z. Luo and Y. Huang, CrystEngComm, 2012, 14, 3930–3935 RSC.
- G. Q. Wang, X. H. Gong, Y. J. Chen, J. H. Huang, Y. F. Lin, Z. D. Luo and Y. D. Huang, Opt. Mater., 2014, 36, 1255–1259 CrossRef CAS.
- B. Xiao, Z. Lin, L. Zhang, Y. Huang and G. Wang, PLoS One, 2012, 7, 40631 CrossRef PubMed.
- W. Guo, Y. Tian, P. Huang, L. Wang, Q. Shi and C. Cui, Ceram. Int., 2016, 42, 5427–5432 CrossRef CAS.
- J. Hu, X. Gong, J. Huang, Y. Chen, Y. Lin, Z. Luo and Y. Huang, Opt. Mater. Express, 2016, 6, 181 CrossRef CAS.
- H. Li, L. Zhang and G. Wang, J. Alloys Compd., 2009, 478, 484–488 CrossRef CAS.
- Y. Zhao, Y. Huang, L. Zhang, Z. Lin and G. Wang, Optoelectron. Adv. Mater., Rapid Commun., 2012, 6, 357–362 CAS.
- W. L. Guo, Y. T. Jiao, P. S. Wang, Q. Liu, S. Liu and F. Hou, Solid State Phenom., 2018, 281, 686–691 Search PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570 CAS.
- R. D. Shannon, Acta Crystallogr., 1976, 32, 751–767 CrossRef.
- Y. Han, S. Wang, H. Liu, L. Shi, A. Song, X. Lu, J. Wei, Z. Mao, D. Wang, Z. Mu, Z. Zhang and S. Niu, J. Alloys Compd., 2020, 844, 156070 CrossRef CAS.
- S. P. S. Porto and J. F. Scott, Phys. Rev., 1967, 157, 716–719 CrossRef CAS.
- L. Macalik, J. Hanuza and A. A. Kaminskii, J. Raman Spectrosc., 2002, 33, 92–103 CrossRef CAS.
- P. Tarte and M. Liegeois-Duyckaerts, Spectrochim. Acta, Part A, 1972, 28, 2029–2036 CrossRef CAS.
- J. Hanuza, A. Haznar, M. A. Pietraszko, A. Lemiec, J. H. Van Der Maas3, M. Czka and E. T. G. Lutz3, J. Raman Spectrosc., 1997, 28, 953–963 CrossRef CAS.
- J. Hanuza and L. Macalik, Spectrochim. Acta, Part A, 1987, 43, 361–373 CrossRef.
- A. S. Rajashekharaiah, G. P. Darshan, R. B. Basavaraj, Y. V. Naik, D. Kavyashree, S. C. Sharma and H. Nagabhushana, Opt. Mater., 2019, 95, 109237 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- V. N. Staroverov, G. E. Scuseria, J. P. Perdew, E. R. Davidson and J. Katriel, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 74, 1–4 CrossRef.
- C. A. Kodaira, H. F. Brito and M. C. F. C. Felinto, J. Solid State Chem., 2003, 171, 401–407 CrossRef CAS.
- X. Liu, W. Xiang, F. Chen, Z. Hu and W. Zhang, Mater. Res. Bull., 2013, 48, 281–285 CrossRef CAS.
- J. Wang, Y. Xu, M. Hojamberdiev, Y. Cui, H. Liu and G. Zhu, J. Alloys Compd., 2009, 479, 772–776 CrossRef CAS.
- G. Jia, Y. Song, M. Yang, Y. Huang, L. Zhang and H. You, Opt. Mater., 2009, 31, 1032–1037 CrossRef CAS.
- J. Zhang, Z. Yu, J. Guo, W. Yan and W. Xue, J. Alloys Compd., 2017, 703, 156–162 CrossRef CAS.
- J. S. Kim, P. E. Jeon, Y. H. Park, J. C. Choi, H. L. Park, G. C. Kim and T. W. Kim, Appl. Phys. Lett., 2004, 85, 3696–3698 CrossRef CAS.
- Y. Zhang, D. Geng, M. Shang, X. Zhang, X. Li, Z. Cheng, H. Lian and J. Lin, Dalton Trans., 2013, 42, 4799–4808 RSC.
- G. Blasse, Phys. Lett. A, 1968, 28, 444–445 CrossRef CAS.
- P. B. Devaraja, D. N. Avadhani, H. Nagabhushana, S. C. Prashantha, S. C. Sharma, B. M. Nagabhushana, H. P. Nagaswarupa and B. Dharuka Prasad, Mater. Charact., 2014, 97, 27–36 CrossRef CAS.
- D. L. Dexter and J. H. Schulman, J. Chem. Phys., 1954, 22, 1063–1070 CrossRef CAS.
- J. Zhou, Z. Xia, M. Yang and K. Shen, J. Mater. Chem., 2012, 22, 21935–21941 RSC.
- C. D. S. Brites, P. P. Lima, N. J. O. Silva, A. Millán, V. S. Amaral, F. Palacio and L. D. Carlos, New J. Chem., 2011, 35, 1177–1183 RSC.
- K. V. Krishnaiah, K. U. Kumar and C. K. Jayasankar, Mater. Express, 2013, 3, 61–70 CrossRef CAS.
- B. Shanmugavelu and V. V. R. K. Kumar, J. Lumin., 2014, 146, 358–363 CrossRef CAS.
- I. E. Ashdown, Proceeding of the SPIE, Solid State Lighting II, 2002, vol. 4776, p. 51 Search PubMed.
- Y. J. Yun, J. K. Kim, J. Y. Ju, S. K. Choi, W. I. Park, J. Y. Suh, H. K. Jung, Y. Kim and S. Choi, Phys. Chem. Chem. Phys., 2017, 19, 11111–11119 RSC.
- Z. Xia, J. Zhuang and L. Liao, Inorg. Chem., 2012, 51, 7202–7209 CrossRef CAS PubMed.
- Y. Zhang, Z. Liang, W. Wang, Y. Lin, R. Tang, J. Wang, D. He, J. Liu, Z. Zhang, L. Zhao, B. Deng, D. Zhang and R. Yu, J. Mater. Sci.: Mater. Electron., 2022, 33, 26619–26632 CrossRef CAS.
- G. Zhang, L. Zhao, F. Fan, Y. Bai, B. Ouyang, W. Chen, Y. Li and L. Huang, Spectrochim. Acta, Part A, 2019, 223, 117343 CrossRef CAS PubMed.
- H.-N. Huang, J. Zhou, H.-F. Zhou, Z.-C. Yu, Y.-Q. Wu and G.-J. Zhou, J. Nanosci. Nanotechnol., 2018, 18, 5433–5440 CrossRef CAS PubMed.
- F. Liu, Y. Fang, N. Zhang, J. Hou, L. Zhang, S. Yu and S. Liu, J. Rare Earths, 2014, 32, 812–816 CrossRef CAS.
- B. C. Jamalaiah and Y. Ramesh Babu, Mater. Chem. Phys., 2018, 211, 181–191 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra02501b |
| This journal is © The Royal Society of Chemistry 2023 |