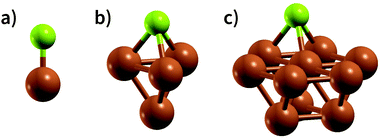Open Access Article
Open Access ArticleA transferable prediction model of molecular adsorption on metals based on adsorbate and substrate properties†
Paolo
Restuccia
 *,
Ehsan A.
Ahmad
and
Nicholas M.
Harrison
*,
Ehsan A.
Ahmad
and
Nicholas M.
Harrison
Department of Chemistry, Imperial College London, 82 Wood Lane, London, W12 0BZ, UK. E-mail: p.restuccia@imperial.ac.uk
First published on 22nd June 2022
Abstract
Surface adsorption is one of the fundamental processes in numerous fields, including catalysis, the environment, energy and medicine. The development of an adsorption model which provides an effective prediction of binding energy in minutes has been a long term goal in surface and interface science. The solution has been elusive as identifying the intrinsic determinants of the adsorption energy for various compositions, structures and environments is non-trivial. We introduce a new and flexible model for predicting adsorption energies to metal substrates. The model is based on easily computed, intrinsic properties of the substrate and adsorbate, which are the same for all the considered systems. It is parameterised using machine learning based on first-principles calculations of probe molecules (e.g., H2O, CO2, O2, N2) adsorbed to a range of pure metal substrates. The model predicts the computed dissociative adsorption energy to metal surfaces with a correlation coefficient of 0.93 and a mean absolute error of 0.77 eV for the large database of molecular adsorption energies provided by Catalysis-Hub.org which have a range of 15 eV. As the model is based on pre-computed quantities it provides near-instantaneous estimates of adsorption energies and it is sufficiently accurate to eliminate around 90% of candidates in screening study of new adsorbates. The model, therefore, significantly enhances current efforts to identify new molecular coatings in many applied research fields.
1 Introduction
Control of the chemical and physical properties of surfaces and interfaces is both of fundamental interest and vital in a very wide range of technologies including catalysis, the environment, energy and medicine. Given the current pressing need for innovation in areas such as energy supply, energy distribution and transport there is a pressing need to develop technologies that can both extend the working lifetime of existing infrastructure and facilitate the development of new sustainable approaches to production and consumption. This has led to the wide acknowledgment of the importance of controlling material surfaces and coatings.1,2 Common phenomena, such as corrosion and friction, cause substantial economic losses every year and severely impact the environment. For example, in extending the lifetime of current infrastructure, the worldwide costs of prevention, detection and mitigation of metal corrosion alone are estimated to be 2.5 trillion US dollars per year.3 In addition, when considering the innovation of new devices, the development of micro- and nano-electromechanical systems requires new approaches for friction reduction in limited dimensions which leads to reduced efficiency and failure.4 The ability to deposit molecular and nanostructured coatings with advanced functional properties is primed to have a profound effect on such diverse technologies as wearable electronics, corrosion inhibitors and lubricant additives. One of the challenges in molecular science is therefore the need to find novel, earth-abundant, inexpensive and environmentally friendly materials that adsorb in a controlled manner to surfaces and interfaces. Historically, innovation of new materials has been a time-consuming and challenging task; it typically takes 20 to 70 years to progress from laboratory conception to widespread commercial use.5 Developments have also been mainly based on the incremental evolution of existing systems with the oft reported outcome that newly discovered solutions are based on exactly the same underlying mechanisms as their predecessors; to find something radical and innovative has usually been a matter of luck.Extensive use is made of molecular additives for friction and corrosion reduction. A fundamental step in discovering new classes of these surfaces modifiers is a predictive understanding of the thermodynamics for both molecular and dissociative adsorption on different substrates.6–12 For this purpose, it is essential to be able to compute the binding energy (BE) of different adsorption modes with sufficient accuracy to be able to predict the molecular level adhesion of the self assembling coating. In principle this is achievable using modern atomistic simulations but in practice is problematic as the parameter space of factors that affect the BE is very large.13 There has therefore been a significant and sustained effort aimed at identifying a small number of easily computed descriptors that can accurately capture the nature of the molecule–surface interaction, and thus facilitating a simple and efficient predictive model of adsorption. In recent years the combination of high-throughput density functional theory (DFT) calculations and machine learning techniques has opened a new era of informatics-based approach to materials design, from which a number of simple models for predicting adsorption energies have emerged.14–32 Similar approaches have also been used for predicting other figures of merit, like the inhibition efficiency of molecules.33 These models are usually based on linear relationships using simple descriptors for both the substrate and the adsorbed molecule (e.g., the number of valence electrons, the electronegativity of the substrate15 and the ionization potential of the molecule16). Despite their simplicity, these models have been demonstrated to be quite effective in predicting adsorption energies, especially when machine learning techniques are employed.14,16 However, in the past such models have been limited in their transferability. For instance, any given model may be limited to the adsorption of molecules in one specific adsorption site (i.e., on-top or hollow). For a more extensive employment of these predictive calculations, one would like to extend the possible range of adsorption sites to model a broader array of realistic configurations, such as stepped edges or grain boundaries at the surface, and include a wide range of molecular adsorbates.
In the current work we present a new predictive linear model that uses appropriate physical descriptors to predict in minutes the adsorption of a wide range of molecules to multiple substrates in a variety of surface adsorption sites. The model is based on a combination of systematic DFT calculations and machine learning. The model reported here accurately predicts the different dissociative adsorption energies of a range of probe molecules over simple homogeneous metallic substrates. Despite its simplicity, the model provides a good estimate of molecular BE in different configuration sites with limited computational effort, and it is devised in a form that facilitates its extension to more complicated structures (e.g., oxides, carbonates or defective surfaces). Moreover, the margin of error in the BE prediction is sufficiently small that provides a sufficiently accurate estimate of fully optimised first principles calculations, saving time and facilitating the rapid screening of a broader range of systems. Therefore, the model is accurate enough to guide the discovery and optimisation of molecular adsorbates in order to improve the functionality of corrosion inhibitors and lubricant additives and is likely to find application in fields such as catalysis, molecular electronics and biomedicine,34–36 where the adsorption of molecules and molecular films underpins many important processes.
2 Method
2.1 BE calculation in slab configuration
For the adsorption energies of the training set (i.e., the slab systems) and the calculation of the later defined Molecule-Bulk Energy (MBE) terms, spin-polarized DFT calculations were performed using the projector-augmented wave method (PAW) as implemented in the plane-wave code QUANTUM ESPRESSO (QE)37 to have a proper description of the core electrons. We used the PAW pseudopotentials38 from the PSLibrary 1.0.039 within the generalised gradient approximation (GGA) of Perdew, Burke and Ernzerhof (PBE)40 for the exchange–correlation energy. The electronic wave functions are expanded as a linear combination of plane waves up to a kinetic energy of 95 Ry, which we find is sufficient to converge the total energies (1 meV per atom) and equilibrium lattice constant (0.1 mÅ) for the considered substrates.For the cell structure, we considered different configurations for the slab and the MBE calculations: for the former, we employed supercells with a 2 × 2 in-plane size in order to reduce the interaction between adsorbate replicas and 5 of 6 layers, depending of the substrate of the different materials. For the latter, all the clusters were computed in a 20 Å × 20 Å × 20 Å cubic cell, so the self interaction between the cluster replicas is negligible. All the input and output geometries for both the slab and the MBE calculations are provided as ESI.†
The Monkhorst–Pack grid41 is used for sampling the Brillouin zone, but different k-mesh for each structure under study were considered. In particular, we selected the optimal k-point grid for each slab geometry, whereas all the calculations involving clusters had a sampling at Gamma point due to the large cell dimensions. To improve the convergence, the Marzari–Vanderbilt cold smearing42 method is used for the sampling of the Fermi surface, with a width of 0.27 eV in order to obtain accurate forces. The convergence criteria of forces and energy are 0.003 eV Å−1 and 10−2 eV.
2.2 HOMO, LUMO and HOMO–LUMO gap calculation for molecule in gas phase
For the calculation of the HOMO, LUMO and HOMO–LUMO gap, we performed DFT calculations using the CRYSTAL17 computational suite,43,44 in which the crystalline orbitals are expanded as a linear combination of a local basis set composed by atom-centered Gaussian orbitals with s, p, or d symmetry. For all the elements employed in the molecular calculations (namely, H, C, N, O, F, S, Cl), we used the 6-31G** basis sets.45–51The approximation electronic exchange and correlation for these calculations is based on the Becke, 3-parameter, Lee–Yang–Parr (B3LYP) hybrid functional incorporating 20% Hartree–Fock exchange.52–54 This global hybrid corrects effectively for self-interaction and thus generally better formation energies and energy levels than GGA approaches.55,56 Moreover, the efficiency of Crystal17 code and the relatively small size of the considered molecules allows to compute effectively the electronic properties within hybrid scheme without a significant increase of the computational time. The Coulomb and exchange series are summed directly and truncated using strict overlap criteria with thresholds of 10−10, 10−10, 10−10, 10−20, 10−30 as described elsewhere.44,57
3 Results and discussion
The general definition for the computed BE to a surface may be written as:| BE = Etot − (Esub + Emol) | (1) |
The total BE can be analysed in terms of many contributions that may be related to properties of the molecule and the surface.58–60 Defining a comprehensive model for the BE is challenging. A recent approach proposed by Dean et al.16 succeeded in predicting the BE of probe molecules to metal nano-particles. This model is based on the idea that BE can be adequately represented by stability descriptors for the adsorbate, the adsorption site, the substrate and a simply computed estimate of the interaction between the molecule and the surface. These assumptions led to the following linear equation for the BE:
| BE =a + b × CElocal + c × IPEA + d × MADs | (2) |
In order to overcome these limitations, we present here a model using suitable descriptors for the adsorption of molecules over flat substrates. In particular, we propose the following equation for the prediction of BE:
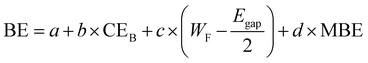 | (3) |
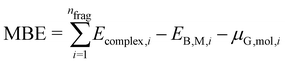 | (4) |
In the current work, ordinary least squares (OLS) linear regressions were used to determine the coefficients in eqn (3) from a training set of first principles energies using the statsmodels library67 provided in Python 3.68 For the OLS regression, we adopted a training set of eight different probe molecules, namely Cl2, CO2, F2, H2, H2O, H2S, N2 and O2, adsorbed over ten different metal substrates, namely Ag(111), Al(111), Au(111), Cu(111), Fe(100), Fe(110), Ir(111), Pt(111), V(100) and V(110). In each case the energy of the most stable adsorption configuration was used. Where possible standard reference data was used for each of the terms of eqn (3): for CEB, we used the observed formation energies of the transition metals provided by ref. 69, for the work function, we employed the DFT computed values provided by the Materials Project database.70 The HOMO–LUMO gap of the molecules was estimated from first principles calculations, with the computational details provided in the Methods section. The MBE was also computed using a small cluster which will be discussed below.
3.1 Analysing contributions to the MBE
An appropriate calculation of the MBE is essential for the efficiency and accuracy of the proposed model. The simplest level of approximation used here is that proposed by Dean et al. in which the MBE is computed as eqn (4), i.e., the binding energy is the energy difference in the gas phase of a specific fragment obtained during the dissociative process and one metal atom of the substrate.16 An example of this possible configuration to calculate MBE is shown in Fig. 1a for the case of Cl adsorbed to a Cu atom. The regression statistics are shown in Table 1a, while Fig. 2 shows the parity plot of the model training against the DFT computed adsorption energies for the predicted BE.| (a) First approach for MBE, as shown in Fig. 1a. R2 = 0.21, MAE = 1.97 eV, RMSE = 2.52 eV | |||
|---|---|---|---|
| Coefficient estimate | SE | P-Value | |
| a | 2.2460 | 1.6048 | 0.167 |
| b | −0.7268 | 0.3114 | 0.023 |
| c | 0.8900 | 0.2721 | 0.002 |
| d | −0.0886 | 0.0970 | 0.365 |
| (b) Second approach for MBE, as shown in Fig. 1b. R2 = 0.83, MAE = 0.89 eV, RMSE = 1.17 eV | |||
|---|---|---|---|
| Coefficient estimate | SE | P-Value | |
| a | 1.5812 | 0.7064 | 0.029 |
| b | −0.2925 | 0.1461 | 0.050 |
| c | 0.1793 | 0.1122 | 0.116 |
| d | 1.0163 | 0.0691 | 3 × 10−21 |
| (c) Third approach for MBE, as shown in Fig. 1c. R2 = 0.94, MAE = 0.52 eV, RMSE = 0.69 eV | |||
|---|---|---|---|
| Coefficient estimate | SE | P-Value | |
| a | 0.7426 | 0.4208 | 0.083 |
| b | −0.1735 | 0.0874 | 0.052 |
| c | 0.1844 | 0.0659 | 0.007 |
| d | 0.9927 | 0.0370 | 3 × 10−34 |
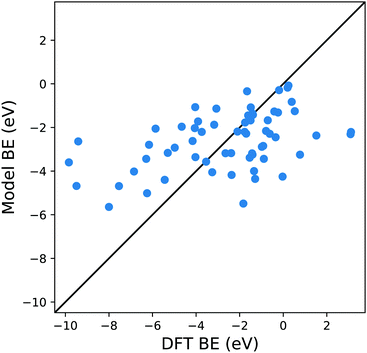 | ||
| Fig. 2 Parity plot for the training of the model against the DFT BE calculations with the MBE approach proposed in eqn (4) and the system shown in Fig. 1a. The black solid line represents the parity between the computed DFT BE and the predicted value. | ||
This approximation provides a rather poor prediction of the BE: the correlation coefficient R2 is around 0.21 (an R2 of 0 corresponds to no correlation and of 1.0 to a perfect set of predictions) and the mean absolute error (MAE) is almost 2 eV. The parity plot in Fig. 2 confirms that the linear regression does not provide a good description of the BE. Although Dean et al. have shown convincingly that this approach reproduces the energy of adsorption to metallic nanoparticles in an on-top configuration of several radical groups (namely, CH3, CO and OH), it evidently fails to do so when the molecules are adsorbed on a wide range of substrates.
A possible explanation for this discrepancy is that the variations of the interactions in the hollow and bridge adsorption sites considered here are not captured by binding to a single metal atom. This suggests that a somewhat larger cluster is required to take into account the different adsorption site configurations in the calculation of MBE such as that represented in Fig. 1b. Here the Cl is adsorbed to a four atom cluster based on the hollow site presented by the Cu(111). The idea is to perform the training of the model in a geometry that is congruous with that used in a periodic surface calculation: hence, if we want to train the model with the data of Cl adsorption over a hollow site of the Cu(111) geometry, we create the smallest cluster, for this specific substrate, which retains the symmetry of the surface adsorption site. We conveniently create these clusters that resemble the surface adsorption sites for all the considered substrates in our training set and the geometries employed for these calculations are provided as ESI.† Another essential advantage of this approach is the possibility to easily explore sites with lower coordination numbers that resemble substrates containing defects or stepped edges. In particular, one can adsorb the molecular fragments over different cluster sites to resemble the adsorption site of interest. The calculation of these configurations with a periodic slab structure is achieved by using large supercells with hundreds of atoms requiring computational resources that are significantly larger than those needed for the few atoms of a reasonable cluster. We, therefore, can reduce the computational effort by several orders of magnitudes, especially for magnetic systems. In creating our training dataset, we noted that, even for the very simple surface geometries studied, the computational time required to compute clusters containing iron and vanadium was around one order of magnitude lower than the corresponding slab calculations. This reduction in the computational effort is then enhanced as the results of cluster calculations for many common molecular fragments can be computed once and then stored in a database.
With the use of this approach, we change the definition of MBE as follows:
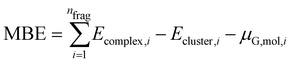 | (5) |
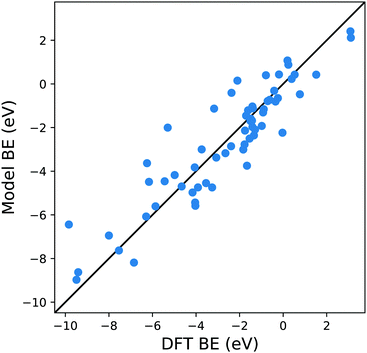 | ||
| Fig. 3 Parity plot for the training of the model against the DFT BE calculations with the MBE cluster approach proposed in eqn (5) and the system shown in Fig. 1b. The black solid line represents the parity between the computed DFT BE and the predicted value. | ||
Extending this approach, one can compute the MBE from adsorption to the 10 atom cluster displayed in Fig. 1c for the case Cl adsorbed to a hollow site on Cu. Therefore, it is possible to explore more complicated adsorption geometries than the smaller cluster, maintaining the adsorption site symmetry.
From Fig. 4 it is evident that the model based on this MBE provides a satisfactory description of the adsorption energetics with a correlation coefficient of 0.94, and a more significant reduction of the MAE to 0.5 eV.
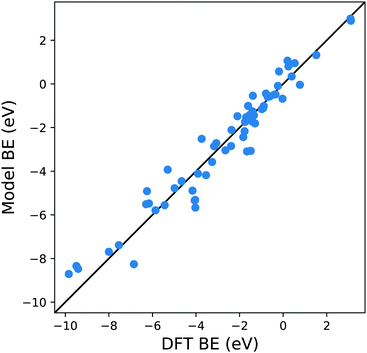 | ||
| Fig. 4 Parity plot for the training of the model against the DFT BE calculations with the MBE cluster approach proposed in eqn (5) and the system shown in Fig. 1c. The black solid line represents the parity between the computed DFT BE and the predicted value. | ||
In addition, all of the fitted parameters have a P-value equal or smaller than 0.05, which is the threshold to obtain a confidence level of 95% in the predictions of the model. Even if this threshold should not be seen as a sharp edge for statistical significance,71 the obtained values for both the P-value and the standard errors provide a rigorous test for the effectiveness of our model.
It is possible to perform a more quantitative analysis of the accuracy of the proposed models by considering the residuals distribution as shown in Fig. 5: each panel presents this distribution as a histogram counter of the errors for the MBE calculation approaches proposed in this work. As expected, the errors follow a normal distribution, and every time the description of the MBE is improved, the residuals range is almost halved, further validating our approach. It is also interesting to notice that moving from the smaller to larger cluster leads to a notable reduction in the MAE of around 40%, but the correlation coefficients are similar (0.83 for the smaller clusters, 0.94 for the larger ones). Therefore, one can adjust the model for convenience: it is possible to either lose a bit of predictive accuracy with the advantage of realising a database with smaller clusters (which usually requires around half the time for the actual calculation) or retain a better precision with the cost of longer computational time to build the database of the MBE coefficients. From now on, our analysis will focus on the predictive model employing the larger clusters since they provide the most accurate results.
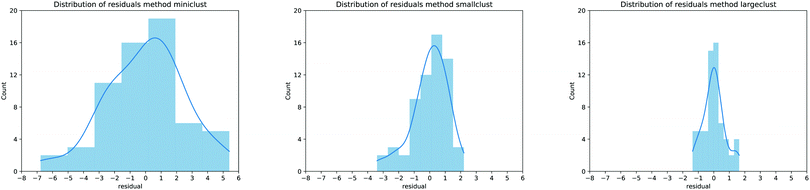 | ||
| Fig. 5 Residual distribution for the MBE calculation as proposed in Fig. 1a (left panel), Fig. 1b (center panel) and Fig. 1c (right panel). The blue curve represents a smoothing interpolation of the residual data. | ||
In addition to the analysis of residuals it is interesting to evaluate the effectiveness of the proposed model by considering the learning curves, shown in Fig. 6, of the three different approaches proposed in our study. These curves show how well defined the learning is during the training of the model when we vary the training dataset and we normalise both the training and the cross-validation scores. The best results are obtained when these values approach 1. As shown in the panels of Fig. 6, the best learning curve is obtained when we consider the MBE using the larger cluster model, further indicating that this approach provides the most accurate results. Moreover, this curve also shows that a training set of around half the size can provide a similar accuracy as the original dataset, further validating the effectiveness of the MBE calculation with a larger cluster even if the initial sample size is not particularly wide.
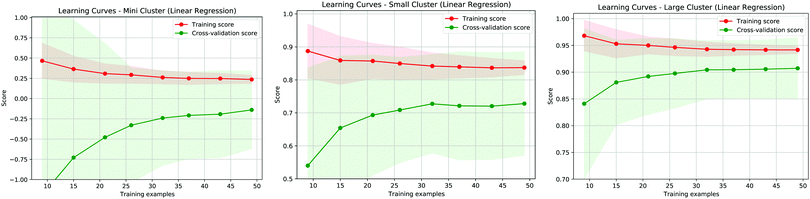 | ||
| Fig. 6 Learning curve for the three fitting methods referring to Fig. 1a (left panel), Fig. 1b (center panel) and Fig. 1c (right panel). The red (green) curves represent the training (validation) score for the proposed predictive models. | ||
We can conclude that the simple model proposed here can predict BE with reasonable accuracy, although with a slightly larger error than the current state-of-the-art, for various adsorption geometries and adsorbates. The MAE for the training set is somewhat higher than the model reported by Dean et al. of around 0.1 eV. However, our training dataset provides a more extensive range of BE (from −10 to +3 eV), so the associated relative error is comparable. With this approach, we are not looking for a perfect BE prediction of few meV, but to have an accuracy sufficient to eliminate around 90% of candidates in the screening study of new adsorbates, which can be a useful starting point for refinement or for technological application.
Before proceeding with the model validation analysis, it is interesting to note the importance of MBE in calculating the BE since its OLS regression coefficient d is the one with the smallest relative error and P-value. To understand how relevant this term is in calculating the predicted BE, we compare two different types of dataset training. The first is the one we discussed in the previous paragraph and is shown in Fig. 4. The second is based on a simple OLS regression of the MBE values of the considered reaction paths against the computed DFT BE. The results are shown in Fig. 7 and Table 2. It is apparent that qualitatively the first training approach (blue dots) provides similar results to the one based solely on MBE (red squares), highlighting the greater importance of the MBE term in the definition of the model. A deeper analysis involving the regression coefficients, such as R2, MAE and the root mean square error (RMSE), shows us a clearer picture. Although R2 is similar in both scenarios (0.94 vs. 0.93), we notice an increase in both MAE and RMSE when considering in training only MBE by 8% and 14%, respectively. Therefore, even if the MBE is an essential part of the definition of this new model, it is important to consider all the physical terms we have identified in the definition of eqn (3), in order to minimize the average error in the BE.
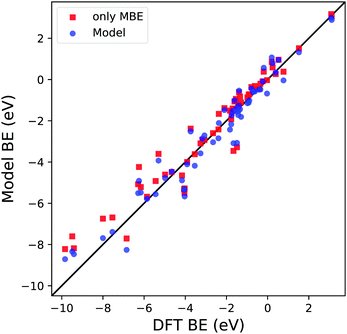 | ||
| Fig. 7 Parity plot for the trained model BE (blue dots) with the coefficients reported in Table 1c and MBE values (red squares) against the DFT BE calculations. | ||
| Model | MBE | |
|---|---|---|
| R 2 | 0.94 | 0.93 |
| MAE (eV) | 0.52 | 0.56 |
| RMSE (eV) | 0.69 | 0.79 |
After the training, the following step is to validate the model for use in predicting new dissociation paths for larger molecules. To do so, we compared its predictions to reaction energies computed and tabulated in previous work.
3.2 Validation of the model
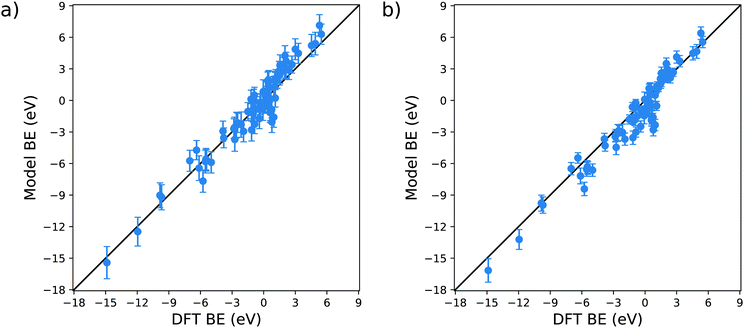
The validation of the proposed model is essential for its employment in actual technological applications. To do so, we compare the BE predicted by the model with the parameters provided in Table 1c with the DFT reaction energies available on the Catalysis-Hub.org database22,23 for 80 different surface reactions. In particular, we chose twelve different molecules, namely CH4, C2H6, CO2, H2, H2O, H2S, N2, NH3, NO, N2O, NO2 and O2, adsorbed over eleven different metal substrates, namely Ag(111), Al(111), Au(111), Co(111), Cu(111), Ir(111), Ni(111), Pd(111), Pt(111), Sc(111), Y(111). The specific reaction geometries employed for the validation are provided as ESI.† All the DFT reaction energies retrieved from the Catalysis-Hub.org database had been computed within the BEEF-vdW approximation to electronic exchange and correlation.72The parity plots resulting from this comparison are shown in Fig. 8. The error bars present in the plots are computed using standard error propagation based on the errors obtained from the OLS regressions.
From Fig. 8a, it is clear that the model captures to a reasonable level of accuracy the variation in BE in these systems: the correlation coefficient of the parity plot is 0.93, the MAE is 0.77 eV and the RMSE is 1.02 eV. When searching for a molecule with a specific adsorption energy with a typical range of 20 eV the MAE of 0.77 eV is sufficient to reduce the number of candidate molecules by well over an order of magnitude. It is, nevertheless, interesting to note that there are outliers to this general trend. For example, the model predicts a favourable adsorption energy for several molecules (C2H6, H2O, NH3 and N2O) on Pd(111) (data provided in the ESI†), whereas the DFT data predicts unfavourable adsorption energies. In all of these cases, the BE is in the region of ±1 eV, which is consistent with the MAE found in the training of the model. We can tentatively conclude from this that the current model is less reliable in describing the dissociative adsorption in this weak bonding region. Another possible explanation for this behaviour can also be found in the different exchange and correlation functional employed in our study: as explained in the Method section, we used the generalized gradient approximation (GGA) for the MBE calculation, whereas the data retrieved from Catalysis-Hub.org were all computed within the BEEF-vdW approximation, which has specific corrections to take into account the dispersion interactions. The absence of the latter in our model can explain the differences arising from the weakly bonded systems.
Apart from these outliers, the prediction of tabulated values is remarkably accurate. As for the original fit to the training set, the intercept of the model has a significant associated error and P-value. It is therefore interesting to test the performance of the model when this parameter is neglected, this data is displayed in Fig. 8b. It is notable that (i) without a there is only a slight offset in the predicted BE which does not affect the general behaviour of the parity plot, with R2, MAE and RMSE essentially unchanged, and (ii) the estimated error bars for each energy are substantially reduced. This latter observation is explained by the fact that half of the error in the predicted BE is due to the uncertainty of a, which is the coefficient with the highest relative error and P-value.
The discussion above demonstrates that the current model provides a low-cost prediction of the BE to homogeneous metal substrates using a single set of parameters for all the adsorbates. Having just one set of parameters is rather convenient, compared to other models proposed in the literature,15 to have a general predictive model independent of the adsorbed species over the substrate, allowing the use of just one formula for any system of interest.
It is interesting also to speculate on the extension of the model to a more general framework for predicting adsorption to a wider range of substrates. A natural extension would be to design a simple MBE cluster calculation for the alloy, oxide and carbonate substrates, which are essential in many technological applications and for which there is currently a lack of predictive models regarding molecular adsorption. Moreover, the proposed model could predict the adsorption of more complicated adsorbate, such as self-assembling monolayer, by considering the addition of dispersion interactions (e.g., PBE-D3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 73) within the DFT calculation of the MBE term. This type of adsorbate is relevant in different research fields, and the prediction of their adsorption energy could help tailor their performances.
73) within the DFT calculation of the MBE term. This type of adsorbate is relevant in different research fields, and the prediction of their adsorption energy could help tailor their performances.
3.3 Comparison with SISSO approach
A possible concern in using the proposed approach is that our model only uses OLS regressions, which might be considered simplistic when compared to state-of-the-art approaches. In particular, one of the most advanced methods in extracting effective descriptors to predict materials properties is the so-called Sure Independence Screening and Sparsifying Operator (SISSO) algorithm.74 SISSO can identify the best descriptors among a set of physical properties, determining the optimal subset. Moreover, it can also identify the most accurate mathematical expressions to obtain the optimised relationship for the available data. It is, therefore, natural to benchmark the results shown in the previous sections with the ones obtained by employing the SISSO algorithm.The first step is to identify whether our approach provides an accurate set of descriptors in a linear relationship. With SISSO, it is possible to perform this by using the so-called Φ0 space, in which all the descriptors are formed into linear combinations. In this way, it is possible to understand if the descriptors we identify are the most relevant for describing the molecular adsorption process over metallic substrates and to quantify the error in predicting the energies in the training dataset. Therefore, alongside the three descriptors employed in the previous sections, we added eight additional physical and chemical properties of the molecule and the metallic substrate to increase the set of descriptors, among which SISSO would determine the optimal ones. Namely, we choose the number of valence electrons of the atomic specie in the metallic substrate (Nve), the surface energy of the metal (γmet), the first ionization potential of the metal (I1), the volume of a single atom in the metallic substrate (Vmet), the metal electronegativity (χmet), the HOMO (HOMOmol), LUMO (LUMOmol) and molar mass (Mmol) of the molecule as additional physical/chemical descriptors to process in the SISSO algorithm. These data have been gathered as tabulated values (namely, Nve, I1, Vmet, χmet and Mmol), by DFT values provided by the Materials Project database (γmet)70 and by performing DFT calculations (HOMOmol and LUMOmol) as detailed in the Method section.
Applying the SISSO algorithm to the training data shown in Fig. 4, we obtained a best fit with three coefficients by using the following equation (the data obtained by the SISSO algorithm are provided as ESI†):
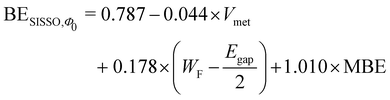 | (6) |
However, the power of SISSO is the possibility to explore different features space and combine the descriptors with different mathematical operations to minimize the error during the training of the model. This approach has been performed in the past24,25,27,75–77 and very accurate models for the adsorption energy prediction have been created without using a simple linear relationship. To understand whether this could lead to a more accurate and transferable predictive model we expanded the training beyond the simple Φ0 feature space, namely using Φ1, Φ2 and Φ3, to obtain a more sophisticated combination of the presented descriptors. Unsurprisingly, the SISSO approach to broader features space leads to a more complicated equation for the adsorption energy. For example, performing a SISSO training over the Φ3 using three coefficients (i.e., Φ3-3D approach), which is the one with the lowest RMSE of 0.30 eV, yields the following as the optimal formula for the BE:
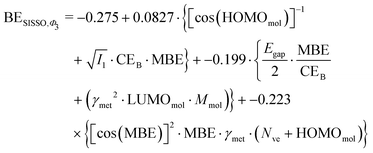 | (7) |
Similar equations have been obtained when performing the training within the Φ1 and Φ2 features space with 3D descriptors. The difference between eqn (3) and (7) is notable with the latter depending on many more descriptors than the former, and a significant reduction of the RMSE for the training set is obtained; it is halved when we use the Φ3-3D training. All the RMSE obtained from the training of the dataset and the validation of the model are reported in Table 3.
| Model | Train RMSE (eV) | Validation RMSE (eV) |
|---|---|---|
| Eqn (3) | 0.69 | 1.02 |
| Φ 0-3D | 0.68 | 1.09 |
| Φ 1-3D | 0.55 | 1.48 |
| Φ 2-3D | 0.40 | 1.13 |
| Φ 3-3D | 0.30 | 1.00 |
The reduced training error suggests that the physically motivated model is performing significantly worse then the SISSO approach. However, the validation of the model is based on its predictive power in a variety of systems and we tested this by attempting to predict the binding energies reported in the https://Catalysis-Hub.org database. When we performed this validation, we obtained comparable RMSE. The significance of this observation is that the significantly simpler and physically motivated model proposed here has been demonstrated to predict the BE of a variety of reactions path with an error similar to that obtained with the more complex relationships identified by SISSO. This result is promising, as the current work has identify a different way to interpret the problem of predicting BE: instead of seeking the optimal mathematical combinations of descriptors that can optimise the data fitting, we can identify simple physical and chemical properties that can adequately describe the most relevant terms for predicting the molecular BE over metallic substrates.
4 Conclusion
In summary, we report a new model of molecule–surface binding based on the combination of first principles calculations with machine learning algorithms, such as ordinary least squares regression. This model provides in minutes and with little computational effort, a reasonable estimate of the adsorption of small molecules to metal substrates by using easily computed descriptors for all the considered systems, which is essential for its transferability and application to more complicated compounds. Moreover, using a single set of parameters for all adsorbates is particularly effective because the predictive formula is independent of the adsorbed molecule or functional group.The model distinguishes different reaction sites and between molecular and dissociative adsorption accurately, especially for larger adsorption energies (values greater than ±1 eV). We found that the most relevant term in predicting the adsorption energy is the molecule–substrate interaction described by MBE. This result is not surprising: several works performed in the past have shown the effectiveness of the cluster model in the description of the adsorption energy.78–80 The relevant point in our study is that, with simple corrections, we can improve the prediction provided by the cluster model by adding relevant physical and chemical properties that can accurately describe the adsorption process. Compared with an independent and well established database of computed adsorption energies, the predicted values suggest that the model is transferable in that it can provide equally accurate BE predictions for a variety of functional groups and surfaces from outside the training set. We have also benchmarked our model against the SISSO algorithm. Even though the proposed model in eqn (3) is quite far from the best-case scenario in the training part, with an RMSE twice larger than the one for the model of eqn (7), we verified that the validation test using the dataset from Catalysis-Hub provides promising results for our prediction, with an RMSE comparable to any model obtained through the SISSO approach. This result is a good validation for our proposed simple linear relationship.
The model is constructed so that its extension to different substrates (e.g., oxides and carbonates) and technically relevant functional groups is straightforward. We expect the model to find widespread use in a variety of applications. For example, the innovation of new coatings for friction and corrosion reduction and the development of novel anti-pathogen coatings to reduce disease transmission via surfaces.
Author contributions
Paolo Restuccia: methodology, investigation, formal analysis, writing – original draft. Ehsan A. Ahmad: investigation, writing – review & editing. Nicholas M. Harrison: methodology, formal analysis, writing – review & editing, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work made use of the high performance computing facilities of Imperial College London. The authors thankfully acknowledge the funding and technical support from BP through the BP International Centre for Advanced Materials (BP-ICAM). The authors want also to thank Dr Giuseppe Mallia for the fruitful discussions. The pictures present in this article are generated thanks to XCrySDen81,82 and Matplotlib.83Notes and references
- J. V. Barth, G. Costantini and K. Kern, Nature, 2005, 437, 671–679 CrossRef CAS PubMed.
- K. Choy, Prog. Mater. Sci., 2003, 48, 57–170 CrossRef CAS.
- G. Koch, J. Varney, N. Thompson, O. Moghissi, M. Gould and J. Payer, NACE Impact, 2016.
- K. Komvopoulos, Wear, 1996, 200, 305–327 CrossRef CAS.
- R. Gross, R. Hanna, A. Gambhir, P. Heptonstall and J. Speirs, Energy Policy, 2018, 123, 682–699 CrossRef.
- M. Finšgar and J. Jackson, Corros. Sci., 2014, 86, 17–41 CrossRef.
- Y. Zhu, M. L. Free, R. Woollam and W. Durnie, Prog. Mater. Sci., 2017, 90, 159–223 CrossRef CAS.
- K. Kousar, M. Walczak, T. Ljungdahl, A. Wetzel, H. Oskarsson, P. Restuccia, E. Ahmad, N. Harrison and R. Lindsay, Corros. Sci., 2021, 180, 109195 CrossRef CAS.
- A. Neville, A. Morina, T. Haque and M. Voong, Tribol. Int., 2007, 40, 1680–1695 CrossRef CAS.
- I. Minami, Appl. Sci., 2017, 7, 445 CrossRef.
- G. Fatti, P. Restuccia, C. Calandra and M. C. Righi, J. Phys. Chem. C, 2018, 122, 28105–28112 CrossRef CAS.
- S. Peeters, P. Restuccia, S. Loehlé, B. Thiebaut and M. C. Righi, J. Phys. Chem. A, 2019, 123, 7007–7015 CrossRef CAS PubMed.
- J. K. Nørskov, T. Bligaard, B. Hvolbæk, F. Abild-Pedersen, I. Chorkendorff and C. H. Christensen, Chem. Soc. Rev., 2008, 37, 2163–2171 RSC.
- E.-J. Ras, M. J. Louwerse, M. C. Mittelmeijer-Hazeleger and G. Rothenberg, Phys. Chem. Chem. Phys., 2013, 15, 4436–4443 RSC.
- W. Gao, Y. Chen, B. Li, S.-P. Liu, X. Liu and Q. Jiang, Nat. Commun., 2020, 11, 1196 CrossRef CAS PubMed.
- J. Dean, M. G. Taylor and G. Mpourmpakis, Sci. Adv., 2019, 5, eaax5101 CrossRef CAS PubMed.
- L. T. Roling and F. Abild-Pedersen, ChemCatChem, 2018, 10, 1643–1650 CrossRef CAS.
- L. T. Roling, L. Li and F. Abild-Pedersen, J. Phys. Chem. C, 2017, 121, 23002–23010 CrossRef CAS.
- Z. Yan, M. G. Taylor, A. Mascareno and G. Mpourmpakis, Nano Lett., 2018, 18, 2696–2704 CrossRef CAS PubMed.
- C. Liu, Y. Li, M. Takao, T. Toyao, Z. Maeno, T. Kamachi, Y. Hinuma, I. Takigawa and K.-I. Shimizu, J. Phys. Chem. C, 2020, 124, 15355–15365 CrossRef CAS.
- F. Calle-Vallejo, J. I. Martínez, J. M. García-Lastra, P. Sautet and D. Loffreda, Angew. Chem., Int. Ed., 2014, 53, 8316–8319 CrossRef CAS PubMed.
- K. T. Winther, M. J. Hoffmann, J. R. Boes, O. Mamun, M. Bajdich and T. Bligaard, Sci. Data, 2019, 6, 75 CrossRef PubMed.
- O. Mamun, K. T. Winther, J. R. Boes and T. Bligaard, Sci. Data, 2019, 6, 76 CrossRef PubMed.
- O. Mamun, K. T. Winther, J. R. Boes and T. Bligaard, npj Comput. Mater., 2020, 6, 177 CrossRef CAS.
- M. Andersen, S. V. Levchenko, M. Scheffler and K. Reuter, ACS Catal., 2019, 9, 2752–2759 CrossRef CAS.
- A. J. Chowdhury, W. Yang, E. Walker, O. Mamun, A. Heyden and G. A. Terejanu, J. Phys. Chem. C, 2018, 122, 28142–28150 CrossRef CAS.
- C. S. Praveen and A. Comas-Vives, ChemCatChem, 2020, 12, 4611–4617 CrossRef CAS.
- Y. Zhang and X. Xu, Machine Learning with Applications, 2021, 3, 100010 CrossRef.
- C. Chang and A. J. Medford, J. Phys. Chem. C, 2021, 125, 18210–18216 CrossRef CAS.
- V. Fung, G. Hu, P. Ganesh and B. G. Sumpter, Nat. Commun., 2021, 12, 88 CrossRef CAS PubMed.
- Z. Li, B. J. Bucior, H. Chen, M. Haranczyk, J. I. Siepmann and R. Q. Snurr, J. Chem. Phys., 2021, 155, 014701 CrossRef CAS PubMed.
- R. Anderson, A. Biong and D. A. Gómez-Gualdrón, J. Chem. Theory Comput., 2020, 16, 1271–1283 CrossRef CAS PubMed.
- C. T. Ser, P. Žuvela and M. W. Wong, Appl. Surf. Sci., 2020, 512, 145612 CrossRef.
- T. Bligaard, J. Nørskov, S. Dahl, J. Matthiesen, C. Christensen and J. Sehested, J. Catal., 2004, 224, 206–217 CrossRef CAS.
- C. Joachim and M. A. Ratner, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 8801–8808 CrossRef CAS PubMed.
- B. Kasemo, Surf. Sci., 2002, 500, 656–677 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- A. Dal Corso, Comput. Mater. Sci., 2014, 95, 337–350 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- N. Marzari, D. Vanderbilt, A. De Vita and M. C. Payne, Phys. Rev. Lett., 1999, 82, 3296–3299 CrossRef CAS.
- R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1360 Search PubMed.
- R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D'Arco, M. Llunell, M. Causà, Y. Noël, L. Maschio, A. Erba, M. Rérat and S. Casassa, CRYSTAL17 User's Manual, University of Torino, 2017 Search PubMed.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665 CrossRef CAS.
- M. S. Gordon, J. S. Binkley, J. A. Pople, W. J. Pietro and W. J. Hehre, J. Am. Chem. Soc., 1982, 104, 2797–2803 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- G. W. Spitznagel, T. Clark, P. V. R. Schleyer and W. J. Hehre, J. Comput. Chem., 1987, 8, 1109–1116 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- D. Jacquemin, E. A. Perpète, G. Scalmani, M. J. Frisch, R. Kobayashi and C. Adamo, J. Chem. Phys., 2007, 126, 144105 CrossRef PubMed.
- J. Muscat, A. Wander and N. Harrison, Chem. Phys. Lett., 2001, 342, 397–401 CrossRef CAS.
- C. Pisani, R. Dovesi and C. Roett, Hartree-Fock Ab Initio Treatment of Crystalline Systems, Springer Verlag, 1st edn, 1988, vol. 48 Search PubMed.
- J. Scaranto, G. Mallia and N. Harrison, Comput. Mater. Sci., 2011, 50, 2080–2086 CrossRef CAS.
- C. Morin, D. Simon and P. Sautet, J. Phys. Chem. B, 2004, 108, 5653–5665 CrossRef CAS.
- B. Wang, S. Günther, J. Wintterlin and M.-L. Bocquet, New J. Phys., 2010, 12, 043041 CrossRef.
- K. Fukui, T. Yonezawa and H. Shingu, J. Chem. Phys., 1952, 20, 722–725 CrossRef CAS.
- R. Hoffmann, Rev. Mod. Phys., 1988, 60, 601–628 CrossRef CAS.
- H. Ishii, K. Sugiyama, E. Ito and K. Seki, Adv. Mater., 1999, 11, 605–625 CrossRef CAS.
- N. G. Hörman, O. Andreussi and N. Marzari, J. Chem. Phys., 2019, 150, 041730 CrossRef PubMed.
- N. G. Hörmann, N. Marzari and K. Reuter, npj Comput. Mater., 2020, 6, 136 CrossRef.
- N. G. Hörmann and K. Reuter, J. Chem. Theory Comput., 2021, 17, 1782–1794 CrossRef PubMed.
- S. Seabold and J. Perktold, 9th Python in Science Conference, 2010, pp. 92–96.
- G. Van Rossum and F. L. Drake, Python 3 Reference Manual, CreateSpace, 2009.
- C. Kittel, Introduction to Solid State Physics, John Wiley & Sons, 8th edn, 2004 Search PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- Analytical Methods Committee AMCTB No. 93, Anal. Methods, 2020, 12, 872–874 RSC.
- J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235149 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- R. Ouyang, S. Curtarolo, E. Ahmetcik, M. Scheffler and L. M. Ghiringhelli, Phys. Rev. Mater., 2018, 2, 083802 CrossRef CAS.
- A. J. Chowdhury, W. Yang, A. Heyden and G. A. Terejanu, J. Phys. Chem. C, 2021, 125, 17742–17748 CrossRef CAS.
- D. Roy, S. C. Mandal and B. Pathak, ACS Appl. Mater. Interfaces, 2021, 13, 56151–56163 CrossRef CAS PubMed.
- M. M. Montemore, C. F. Nwaokorie and G. O. Kayode, Catal. Sci. Technol., 2020, 10, 4467–4476 RSC.
- C. Lacaze-Dufaure, J. Roques, C. Mijoule, E. Sicilia, N. Russo, V. Alexiev and T. Mineva, J. Mol. Catal. A: Chem., 2011, 341, 28–34 CrossRef CAS.
- P. Hejduk, M. Witko and K. Hermann, Top. Catal., 2009, 52, 1105–1115 CrossRef CAS.
- S. Zygmunt, R. Mueller, L. Curtiss and L. Iton, THEOCHEM, 1998, 430, 9–16 CrossRef CAS.
- A. Kokalj, J. Mol. Graphics Modell., 1999, 17, 176–179 CrossRef CAS PubMed.
- A. Kokalj, Comput. Mater. Sci., 2003, 28, 155–168 CrossRef CAS.
- J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp01572b |
| This journal is © the Owner Societies 2022 |