Predicting differential ion mobility behaviour in silico using machine learning

Abstract

Although there has been a surge in popularity of differential mobility spectrometry (DMS) within analytical workflows, determining separation conditions within the DMS parameter space still requires manual optimization. A means of accurately predicting differential ion mobility would benefit practitioners by significantly reducing the time associated with method development. Here, we report a machine learning (ML) approach that predicts dispersion curves in an N₂ environment, which are the compensation voltages (CVs) required for optimal ion transmission across a range of separation voltages (SVs) between 1500 to 4000 V. After training a random-forest based model using the DMS information of 409 cationic analytes, dispersion curves were reproduced with a mean absolute error (MAE) of ≤ 2.4 V, approaching typical experimental peak FWHMs of ±1.5 V. The predictive ML model was trained using only m/z and ion-neutral collision cross section (CCS) as inputs, both of which can be obtained from experimental databases before being extensively validated. By updating the model via inclusion of two CV datapoints at lower SVs (1500 V and 2000 V) accuracy was further improved to MAE ≤ 1.2 V. This improvement stems from the ability of the “guided” ML routine to accurately capture Type A and B behaviour, which was exhibited by only 2% and 17% of ions, respectively, within the dataset. Dispersion curve predictions of the database's most common Type C ions (81%) using the unguided and guided approaches exhibited average errors of 0.6 V and 0.1 V, respectively.

---

The orthogonal separations provided by differential mobility spectrometry (DMS) are becoming an increasingly valuable technique in the analytical chemist's toolkit.^1,2 Capable of operation as either standalone device or in tandem with other separation techniques, the ease with which DMS couples to mass spectrometers (MS) has been especially useful for the separation and characterization of isobaric/isomeric analytes.^3–8 However, the current lack of predictability of DMS behaviour presents a challenge for its seamless implementation within some analytical workflows. For example, performing complete scans of DMS parameters to identify the optimal conditions for analyte separation and transmission may not be possible within narrow-band elution times of liquid chromatography (LC). Accurate a priori predictions of optimal DMS conditions would benefit DMS practitioners, particularly those working in DMS-based proteomics,^9–13 lipidomics,^14–17 and metabolomics analyses.^1,2,18

The separation of ions within any ion mobility spectrometry (IMS) device depends on the ion's field-dependent mobility [K(E)] through a neutral buffer gas,^19,20 which is specific to the identity of the gas as well as the electric field strength (E) as per eqn (1):

v = K(E)·E (1)

where v is the ion's steady-state drift velocity through the IMS cell. This relationship is linear when IMS experiments are conducted in the so-called ‘low-field limit’ of 2–10 Td (1 Td = 10–21 V m²),^19,21 where field-heating does not perturb the ion's thermal velocity. In other words, the internal energy of the ion (i.e., its thermal energy, 3/2·k_b·T) is significantly larger than any internal energy increase caused by acceleration in the electric field. Structural information can be obtained in this regime by correlating the linear dependence of an ion's mobility with the applied electric field using the stepped field method.²² Linear regression yields the ion's mobility, which is assumed to correspond to the zero-field mobility [K(0)] when the field strengths used fall within the low-field limit.^23,24K(0) is related to the ion-neutral collision cross section (CCS) by means of the Mason–Schamp relationship shown in eqn (2):where μ is the reduced mass of the ion and drift gas species, z is the charge, e is the elementary charge, k_b is the Boltzmann constant, T is the temperature, N is the number density of the gas, and Ω is the CCS (or, more appropriately, the momentum transfer cross section). CCSs correspond to the orientationally-averaged collision area between the charged analyte and its gaseous collision partner, providing insight into the ion's gas-phase structure when coupled with theoretical modelling of CCSs.^25,26 Direct CCS measurements above the low-field limit are not possible without empirical calibration strategies^27–30 due to the non-linear dependence of ion mobility on field-strength (eqn (3)),^31,32 where the value of the alpha function α(E/N) at a specific E/N defines the ratio of an ion's high- and low-field mobility (eqn (4)).

Separations in DMS,^33,34 a term used synonymously with field asymmetric waveform ion mobility spectrometry (FAIMS),^31,35 harness the field-dependence of ion mobility to achieve a spatial separation of ions (Fig. S1†). The DMS waveform, denoted as the separation voltage (SV), consists of an electric field that oscillates between its high- and low-field phases. Due to the non-linear dependence of ion mobility on field strength, the SV causes the ion to adopt trajectories that divert from the transmission axis. The field-dependent mobility of an ion is encoded within the compensation voltage (CV) required for transmission through the DMS cell, as the CV is related to the alpha function,³⁴ and by association, the ion's CCS.

Based on this first-principles consideration, mapping the field-dependent mobility should be feasible using only the intrinsic properties associated with the ion's mobility (i.e., mass and CCS). Haack and coworkers made a first step in this regard by reproducing the DMS behaviour of the tetramethylammonium³⁶ and tricarbastannatrane ([N(CH₂CH₂CH₂)₃Sn]⁺)³⁷ cations using only temperature dependent CCS calculations in the free molecular regime. Given the reasonable accuracy of this approach, we hypothesized that dispersion plots could be generated in silico using machine learning (ML) models trained only with CCS and m/z as inputs. This follows the absence of a closed-form expression that can relate the ion-neutral interaction potential with the ion's field-dependent mobility. Using ML to complete this connection would enable predictions of dispersion plots using only intrinsic ion properties that are accessible via CCS libraries^38–45 or calculation packages.^46–48 This would be of tremendous utility for method development within the various ‘omics realms’, where the CV space occupied by the desired analytes could be mapped prior to data acquisition with minimal effort. The methodology simply requires a “reverse-engineering” of the ML-model used to obtain CCSs from DMS-MS data.⁴⁹ However, broadly applicable predictions of an ion's dispersion behaviour necessitate the use of a calibration set spanning several chemical classes, CCSs, and m/z ratios. As a first step in our endeavour to globally map differential ion mobility, we report on the ML-based in silico generation of dispersion plots in an N₂ environment for a compendium containing 409 molecular cations. Since the interaction potential between N₂ and a protonated analyte differs from cationic adducts (e.g., [M + Na]⁺), we chose to model protonated species ([M + H]⁺), which were present in significantly greater quantities.

Methods

A SelexION DMS cell (SCIEX, Canada) with a 1 mm gap between the planar electrodes was mounted in the atmospheric region between the orifice of a QTRAP 5500 hybrid triple quadrupole linear ion trap mass spectrometer and a Turbospray (SCIEX) electrospray ionization (ESI) source (Fig. S2†).³⁴ Analytes were solubilized into mixtures containing 10 ng mL⁻¹ in either a 50 : 50 MeOH : H₂O or MeCN : H₂O ESI solvent mixture, both of which contained 0.1% formic acid. Analyte mixtures were infused into the ESI source (positive mode) at a flow rate of 10 μL min⁻¹. DMS-MS measurements were conducted using N₂ as both the curtain gas (20 psi) and as the collision gas (ca. 7 mTorr) for data acquisition in multiple reaction monitoring (MRM) mode. MRM transitions (available in the ESI†) were monitored as the SV was stepped from 1500 to 4000 V in 500 V increments, with additional data taken at SV = 3250 V and 3750 V to ensure thorough mapping of the dispersion curves at high field strengths. At each SV, the ion current was recorded while ramping the CV from −30 V to 30 V in increments of 0.1 V to produce an ionogram. Each ionogram was fit with a Gaussian distribution, for which the centroid was taken as the CV required for maximum ion transmission. The m/z and CCS of the parent ion, as calculated using MobCal-MPI,⁴⁸ were used as the inputs for training the ML model to predict SV/CV pairs. Full details of experimental parameters related to data acquisition are provided in Table S1.† Details concerning CCS calculations are available in the ESI in section S1.† The ML source-code, which employs the Random Forest Regression model as implemented in the Python Sci-kit Learn package, and associated benchmarking data is available on the Hopkins Laboratory GitHub repository (https://github.com/HopkinsLaboratory).

Results and discussion

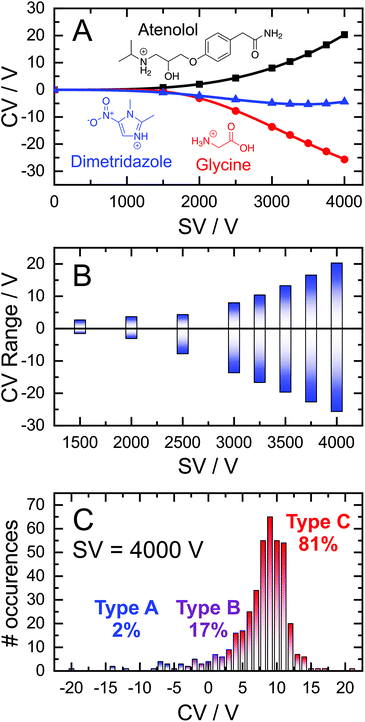
The field-dependent nature of the interaction potential between the analyte and DMS carrier gas is an important metric to consider when modelling an ion's field-dependent mobility. Qualitative insights in this regard can be inferred from a dispersion curve (i.e., plots of the CV required for optimal ion transmission as a function of SV)^50,51 depending on the relationship between SV and CV.^33,52 For example, three dispersion curves from the 409 molecules used in this study are shown in Fig. 1A; these represent the most common behaviours observed in DMS experiments. In a dry N₂ environment, dispersion curves are predominantly Type C in nature, whereby the ion-neutral interaction potential results in a hard-sphere scattering event upon collision. Type C ions are characterized by increasingly positive CV shifts for optimal ion transmission as the SV increases (e.g., protonated atenolol; black curve). As the molecular weight of the ion decreases or charge sites become “exposed”, the interactions between the analyte and carrier gas become stronger and shift toward behaviour associated with dynamic clustering. The clustering phenomenon can manifest in one of two ways depending on the binding strength of the adduct formed. Type B behaviour is characterized by CVs that initially decrease with increasing SV before reaching a minimum, upon which CVs trend towards more positive values. This is interpreted as arising from weak clustering interactions under low-field conditions, which are eventually overcome at high-field. Dimetridazole (blue trace) is a representative Type B ion that exhibits weak ion-neutral interactions with the carrier gas due to greater charge density within the analyte. Cluster formation can be long-lived in cases when the ion's charge is highly localized, resulting in Type A dispersion curves. In a dry N₂ environment, Type A behaviour is only observed in rare cares for low molecular weight ions and is characterized by continually decreasing CV shifts as the SV increases (e.g., Fig. 1A; glycine, red trace).

Fig. 1 (A) Dispersion curves for protonated atenolol (black squares), protonated dimetridazole (blue triangles), and protonated L-glycine (red circles). (B) The range of CV values for given SV values for the 409 molecules in our dataset and their distributions (C) at SV = 4000 V according to their Type A (blue), B (purple) or C (red).

The range of CVs adopted by the 409 cations are shown in Fig. 1B. At low SVs, the CVs of Type A, B, and C ions are similar. However, differential mobilities become more pronounced at higher SVs due to the field-dependence of ion mobility. At SV = 4000 V, the optimum CV for ion elution ranges from −26 V for glycine to +20 V for atenolol. Untargeted analysis would necessitate sampling this entire window to ensure adequate coverage of the chemical space even though most ions are Type C and elute within the CV = 0–15 V window (Fig. 1C). As it stands, there are no “rules” for predicting an ion's DMS behaviour, which presents a significant challenge for coupling DMS-MS to some front-end interfaces (e.g., LC). Introduction of the desired analytes to the DMS cell within a short time window precludes a full scan of the CV range, necessitating predictive technologies to facilitate method development in tandem separation workflows the incorporate DMS.

Modelling the dispersion curves (i.e., the DMS behaviour) of an ion requires metrics that capture the ion-neutral interaction potential. This is especially important in the case of the dataset used here, where 331 ions exhibit Type C behaviour, but only 72 and 6 ionic species exhibit Type B and A behaviours, respectively. The interaction potential is heavily influenced by the charge density and conformation of the ion, both of which can be reasonably captured through the ion's m/z and CCS.^36,37 However, the broad distributions of m/z and CCS within this dataset (Fig. S3†) requires an ML framework to incorporate these properties in the prediction of an ion's differential mobility.⁵³ One must also be cognisant of bias, variance, and overfitting in the chosen ML model, all of which contribute to poor predictive capabilities for systems outside of the training set. Random Forest Regression (RFR), an unbiased decision-tree-based model, has demonstrated low variance and low susceptibility to overfitting.^54,55 The resistance to overfitting stems from the law of large numbers, which states that the average obtained from many trials will become closer to the expected (real) value as more trials are performed. As such, we employed a RFR algorithm to create a predictive model for DMS dispersion curve data utilizing 200 randomized decision trees as implemented in the scikit-learn Python package. To train the RFR framework, our DMS-MS database was randomly split into a training set and an “out-of-the-bag” external validation set using only analyte m/z and CCSs as inputs.

The mean absolute error (MAE) of the RFR predictions, averaged across 100 randomized training/validation set splits, is plotted as a function of training set size (i.e., a learning curve) for SV = 4000 V in the top panel of Fig. 2. Since the CV window occupied by the analytes is largest at SV = 4000 V, the associated MAE can be thought of as the upper limit of error for the RFR model. Training the RFR model using 95% of the database at SV = 4000 V predicts the corresponding CV with a MAE of 2.4 V. This is an encouraging result considering the relatively small size of the dataset and the limited number of parameters used in the ML framework. This model is especially accuare for the lower SVs, for which optimal CVs can be predicted with even lower MAEs (Fig. S4†). Moreover, the MAEs associated with CV predictions typically lie within the full-width half-maximum (FWHM) range of a DMS peak (±1.5 V). It is also worth noting that the unguided learning curve shown in the top panel of Fig. 2 does not plateau at large training set sizes. This implies that more accurate predictions using the unguided approach are to be expected as the DMS-MS dataset expands with the addition of information for more analytes.

Fig. 2 (Top) Learning curve depicting the mean absolute error (MAE) for CV predictions as a function of training set size with inputs of m/z and CCS (unguided; red) and including CV values at SV = 1500, 2000 V (guided; blue). (Bottom) Boxplot of CV error according to dispersion plot type for 1000 predictions at SV = 4000 using a randomized 95 : 5 training/validation split. The mean and median are shown as a black circle/square and solid black line, respectively. Boxes correspond to the 25th and 75th percentile; whiskers extend to the 10th and 90th percentile. The mean CV error and one standard deviation are shown as text. The green highlighted region corresponds to the typical FWHM of a peak in a DMS ionogram (±1.5 V).

Recalling that the proportion of Type A, B, and C ions within the database are 2%, 17%, and 81%, respectively, it is necessary to investigate the accuracy of model predictions for each different DMS behaviour. If a validation set is disproportionately composed of Type A or B ions, the MAE for the data set can be especially high. Conversely, if the validation set is entirely composed of Type C ions, the associated MAE will be low and not representative of the global accuracy. To ensure adequate validation, we performed an additional 1000 randomized trials using a 95 : 5 partition of the dataset for training/validation. The deviations of calculated versus experimental CV values at SV = 4000 V are shown as a boxplot in the bottom panel of Fig. 2 according to their classification as a Type A, B, or C ions. For the unguided ML model (i.e., just using m/z and CCS as input), dispersion curve predictions for Type A, B, or C ions exhibit average errors of −7.9, −2.3, and 0.6 V, respectively. The low errors for Type C ions from the out-of-the-bag external validation set demonstrates that the ML model is accurate to within the day-to-day variance in SV/CV pairs (typically the peak's FWHM).

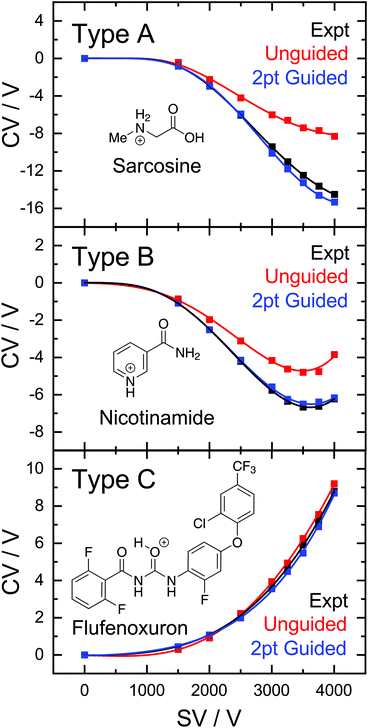
While predictions of Type C curves lie within the FHWM of the associated ionogram peak, the predictions for Type A and B ions are consistently at more positive CV values than those observed experimentally. It should be noted that the RFR-predicted Type A and B dispersion curves only deviate appreciably from experiment at SV > 2000 V. Therefore, we hypothesized that a “guided” ML model supplemented with CV values measured at SV = 1500 and 2000 V would provide the curvature required to capture Type A and B behaviour. Indeed, this was the case as demonstrated by the two-point guided learning curve and the distribution of errors in Fig. 2. Although this procedure had only a marginal improvement on Type C curve predictions (average error 0.1 V), the overall predictive capability when all species were considered improved by a factor of two (Fig. 2, top panel; 1.2 V MAE for guided model). This improvement stems from the considerable error reduction in predictions of Type A and B behaviour, which exhibit average errors of −4.4 V and 0.2 V, respectively, for the guided model (see bottom panel of Fig. 2).

The success of the ML-approach in predicting an ion's DMS behaviour is further exemplified by analysis of the experimental and predicted dispersion curves. Fig. 3 shows three representative Type A, B, and C dispersion plots taken from a single validation set. Predicted dispersion plots for the remaining molecules of the validation set are provided in section S2 of the ESI.† The Type C behaviour of flufenoxuron is captured almost exactly by both the guided and unguided RFR approach, which is true for nearly all Type C ions in this study. Although the unguided ML model captures the shape of the Type A and B dispersion curves, the predicted CV values are ca. 2 V more positive at the high SV region of the curves. This shift to more positive CV values is consistently observed for predictions of the other Type A and B ions, likely arising from their under-representation in the training set (and thus positive skewing due to over-representation of Type C). The 2-point guided approach substantially improves predictions of Type B ions (e.g., niacin) and, in some instances, produced a near exact prediction of Type A dispersion curves (e.g., sarcosine). Overall, the ability of RFR to replicate an ion's DMS behaviour is impressive and is expected to improve further with the addition of more examples to the database.

Fig. 3 Experimental (black), unguided ML (red) and 2-point guided ML (blue) dispersion curves for (top) sarcosine, (middle) nicotinamide, and (bottom) flufenoxuron. The validation data was generated from a randomized 95 : 5 training/validation data split.

Conclusions

In this work, we demonstrate how DMS behaviour can be predicted using machine learning. Using only m/z and CCS as inputs, random forest regression can accurately predict experimental dispersion curves following training with a set of 409 molecular cations. Prediction of the optimal CV required for ion elution at SV = 4000 V (i.e., the DMS condition most difficult to predict) was accomplished with a MAE of 2.4 V. The accuracy of these predictions is excellent considering the relatively small size of the training set and that the ions within the dataset exhibit a large CV range (−26 to +22 V) at this separation field strength. The greatest factor contributing to the MAE is the under-represented Types A and B species in the dataset, which account for only 2% and 17% of the data, respectively, and exhibit respective average errors of −7.9 V and −2.4 V. Because dispersion curve predictions deviate from experiment only at SV > 2000, one can adopt a method whereby CVs at SV = 1500 V and 2000 V are first predicted and measured, then introduced as input features for a “guided” ML model. Doing so results in a model with an overall MAE of 1.2 V at SV = 4000 V and average errors of 0.1 V for Type C ions, 0.2 V for Type B ions, and −4.4 V for Type A ions.

Accurate prediction of DMS behaviour will streamline method development for practitioners interested in adding an orthogonal separation dimension to their workflows. The unguided approach requires only m/z and CCS as input features, both of which can be found in published repositories^38–45 or determined by calculation.^46–48 Since the MAE for Type C ions (1.6 V) aligns with the typical FWHM of an ionogram peak (±1.5 V), employing this ML model to inform experiment will generally result in transmission of the desired analyte. Targeted approaches, in which the identity of the analyte is known, will benefit the most from predictions of DMS behaviour since the ability to set a specific SV/CV pair for a desired analyte will cut down on the time required for method development and mitigate redundant data acquisition. Extension of the predictive capabilities towards other common MS adducts (e.g., [M + Na]⁺, [M + NH₄]⁺) and negative ions [M − H]⁻ will become possible as more data is acquired. For untargeted approaches, it would be fruitful to utilize the dispersion plot as an additional metric for compound identification. Specifically, one could implement a characterization methodology whereby an ion's CCS could be inferred from its dispersion plot to enhance confidence in unknown compound identifications. The work reported here is intended to serve as the framework for these future endeavours, which will be reported on in due course.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to acknowledge Dr J. C. Yves Le Blanc and Dr Bradley B. Schneider (SCIEX) for helpful discussions as well as the high-performance computing support from Compute Canada. WSH would like to acknowledge the financial support provided by the Natural Sciences and Engineering Research Council (NSERC) of Canada in the form of Discovery, Engage, and Alliance grants, the Ontario Centres of Excellence in the form of a VIP-II grant, as well as the government of Ontario for an Ontario Early Researcher Award. C. I. acknowledges financial support from the Government of Canada for the Vanier Canada Graduate Scholarship.

References

1. K. L. Arthur, M. A. Turner, J. C. Reynolds and C. S. Creaser, Anal. Chem., 2017, 89, 3452–3459.
2. S. Wernisch and S. Pennathur, Anal. Bioanal. Chem., 2019, 411, 6297–6308.
3. W. Jin, M. Jarvis, M. Star-Weinstock and M. Altemus, Anal. Bioanal. Chem., 2013, 405, 9497–9508.
4. A. T. Maccarone, J. Duldig, T. W. Mitchell, S. J. Blanksby, E. Duchoslav and J. L. Campbell, J. Lipid Res., 2014, 55, 1668–1677.
5. C. Liu, G. A. Gómez-Ríos, B. B. Schneider, J. C. Y. Le Blanc, N. Reyes-Garcés, D. W. Arnold, T. R. Covey and J. Pawliszyn, Anal. Chim. Acta, 2017, 991, 89–94.
6. A. Cohen, N. W. Ross, P. M. Smith and J. P. Fawcett, Rapid Commun. Mass Spectrom., 2017, 31, 842–850.
7. K. H. B. Lam, J. C. Y. Le Blanc and J. L. Campbell, Anal. Chem., 2020, 92, 11053–11061.
8. P. Pathak, M. A. Baird and A. A. Shvartsburg, J. Am. Soc. Mass Spectrom., 2020, 31, 1603–1609.
9. H. Zhao, A. J. Creese and H. J. Cooper, Methods Mol. Biol., 2016, 1355, 241–250.
10. H. J. Cooper, J. Am. Soc. Mass Spectrom., 2016, 27, 566–577.
11. A. J. Creese, N. J. Shimwell, K. P. B. Larkins, J. K. Heath and H. J. Cooper, J. Am. Soc. Mass Spectrom., 2013, 24, 431–443.
12. P. V. Shliaha, V. Gorshkov, S. I. Kovalchuk, V. Schwämmle, M. A. Baird, A. A. Shvartsburg and O. N. Jensen, Anal. Chem., 2020, 92, 2364–2368.
13. L. K. Muehlbauer, A. S. Hebert, M. S. Westphall, E. Shishkova and J. J. Coon, Anal. Chem., 2020, 92, 15959–15967.
14. A. A. Shvartsburg, G. Isaac, N. Leveque, R. D. Smith and T. O. Metz, J. Am. Soc. Mass Spectrom., 2011, 22, 1146–1155.
15. T. P. I. Lintonen, P. R. S. Baker, M. Suoniemi, B. K. Ubhi, K. M. Koistinen, E. Duchoslav, J. L. Campbell and K. Ekroos, Anal. Chem., 2014, 86, 9662–9669.
16. T. Baba, J. L. Campbell, J. C. Y. Le Blanc, P. R. S. Baker and K. Ikeda, J. Lipid Res., 2018, 59, 910–919.
17. A. P. Bowman, R. R. Abzalimov and A. A. Shvartsburg, J. Am. Soc. Mass Spectrom., 2017, 28, 1552–1561.
18. Z. Chen, S. L. Coy, E. L. Pannkuk, E. C. Laiakis, A. J. Fornacejr and P. Vouros, J. Am. Soc. Mass Spectrom., 2018, 29, 1650–1664.
19. E. A. Mason and E. W. McDaniel, Transport properties of ions in gases, John Wiley and Sons, New York, 1988.
20. C. Larriba-Andaluz and F. Carbone, J. Aerosol Sci., 2021, 151, 105659.
21. H. E. Revercomb and E. A. Mason, Anal. Chem., 1975, 47, 970–983.
22. J. A. McLean, J. A. Schultz and A. S. Woods, in Electrospray and MALDI Mass Spectrometry: Fundamentals, Instrumentation, Practicalities, and Biological Applications, ed. R. B. Cole, New York, 2nd edn, 2011, pp. 411–439.
23. S. M. Stow, T. J. Causon, X. Zheng, R. T. Kurulugama, T. Mairinger, J. C. May, E. E. Rennie, E. S. Baker, R. D. Smith, J. A. McLean, S. Hann and J. C. Fjeldsted, Anal. Chem., 2017, 89, 9048–9055.
24. V. Gabelica, A. A. Shvartsburg, C. Afonso, P. Barran, J. L. P. Benesch, C. Bleiholder, M. T. Bowers, A. Bilbao, M. F. Bush, J. L. Campbell, I. D. G. Campuzano, T. Causon, B. H. Clowers, C. S. Creaser, E. De Pauw, J. Far, F. Fernandez-Lima, J. C. Fjeldsted, K. Giles, M. Groessl, C. J. Hogan, S. Hann, H. I. Kim, R. T. Kurulugama, J. C. May, J. A. McLean, K. Pagel, K. Richardson, M. E. Ridgeway, F. Rosu, F. Sobott, K. Thalassinos, S. J. Valentine and T. Wyttenbach, Mass Spectrom. Rev., 2019, 38, 291–320.
25. C. Larriba and C. J. Hogan, J. Phys. Chem. A, 2013, 117, 3887–3901.
26. C. Larriba-Andaluz and J. S. Prell, Int. Rev. Phys. Chem., 2020, 39, 569–623.
27. K. M. Hines, J. C. May, J. A. McLean and L. Xu, Anal. Chem., 2016, 88, 7329–7336.
28. C. B. Lietz, Q. Yu and L. Li, J. Am. Soc. Mass Spectrom., 2014, 25, 2009–2019.
29. M. Chai, M. N. Young, F. C. Liu and C. Bleiholder, Anal. Chem., 2018, 90, 9040–9047.
30. J. A. Silveira, M. E. Ridgeway and M. A. Park, Anal. Chem., 2014, 86, 5624–5627.
31. A. A. Shvartsburg, Differential ion mobility spectrometry: Nonlinear ion transport and fundamentals of FAIMS, CRC Press, Boca Raton, 2008.
32. A. A. Shvartsburg and R. D. Smith, Anal. Chem., 2008, 80, 9689–9699.
33. R. W. Purves and R. Guevremont, Anal. Chem., 1999, 71, 2346–2357.
34. B. B. Schneider, E. G. Nazarov, F. Londry, P. Vouros and T. R. Covey, Mass Spectrom. Rev., 2016, 35, 687–737.
35. R. Guevremont, J. Chromatogr. A, 2004, 1058, 3–19.
36. A. Haack, J. Crouse, F. J. Schlüter, T. Benter and W. S. Hopkins, J. Am. Soc. Mass Spectrom., 2019, 30, 2711–2725.
37. J. Crouse, A. Haack, T. Benter and W. S. Hopkins, J. Am. Soc. Mass Spectrom., 2020, 31, 796–802.
38. X. Zheng, N. A. Aly, Y. Zhou, K. T. Dupuis, A. Bilbao, V. L. Paurus, D. J. Orton, R. Wilson, S. H. Payne, R. D. Smith and E. S. Baker, Chem. Sci., 2017, 8, 7724–7736.
39. Z. Zhou, J. Tu, X. Xiong, X. Shen and Z. J. Zhu, Anal. Chem., 2017, 89, 9559–9566.
40. Z. Zhou, X. Shen, J. Tu and Z. J. Zhu, Anal. Chem., 2016, 88, 11084–11091.
41. K. M. Hines, D. H. Ross, K. L. Davidson, M. F. Bush and L. Xu, Anal. Chem., 2017, 89, 9023–9030.
42. G. Paglia, J. P. Williams, L. Menikarachchi, J. W. Thompson, R. Tyldesley-Worster, S. Halldórsson, O. Rolfsson, A. Moseley, D. Grant, J. Langridge, B. O. Palsson and G. Astarita, Anal. Chem., 2014, 86, 3985–3993.
43. A. R. Shah, K. Agarwal, E. S. Baker, M. Singhal, A. M. Mayampurath, Y. M. Ibrahim, L. J. Kangas, M. E. Monroe, R. Zhao, M. E. Belov, G. A. Anderson and R. D. Smith, Bioinformatics, 2010, 26, 1601–1607.
44. J. A. Picache, B. S. Rose, A. Balinski, K. L. Leaptrot, S. D. Sherrod, J. C. May and J. A. McLean, Chem. Sci., 2019, 10, 983–993.
45. J. C. May, C. B. Morris and J. A. McLean, Anal. Chem., 2017, 89, 1032–1044.
46. S. A. Ewing, M. T. Donor, J. W. Wilson and J. S. Prell, J. Am. Soc. Mass Spectrom., 2017, 28, 587–596.
47. T. Wu, J. Derrick, M. Nahin, X. Chen and C. Larriba-Andaluz, J. Chem. Phys., 2018, 148, 074102.
48. C. Ieritano, J. Crouse, J. L. Campbell and W. S. Hopkins, Analyst, 2019, 144, 1660–1670.
49. C. Ieritano, A. Lee, J. Crouse, Z. Bowman, N. Mashmoushi, P. M. Crossley, B. P. Friebe, J. L. Campbell and W. S. Hopkins, Anal. Chem., 2021, 93, 8937–8944.
50. D. S. Levin, R. A. Miller, E. G. Nazarov and P. Vouros, Anal. Chem., 2006, 78, 5443–5452.
51. B. B. Schneider, T. R. Covey, S. L. Coy, E. V. Krylov and E. G. Nazarov, Int. J. Mass Spectrom., 2010, 298, 45–54.
52. R. Guevremont and R. W. Purves, Rev. Sci. Instrum., 1999, 70, 1370–1383.
53. S. W. C. Walker, A. Anwar, J. M. Psutka, J. Crouse, C. Liu, J. C. Y. Le Blanc, J. Montgomery, G. H. Goetz, J. S. Janiszewski, J. L. Campbell and W. S. Hopkins, Nat. Commun., 2018, 9, 5096.
54. L. Breiman, Mach. Learn., 2001, 45, 5–32.
55. J. R. Quinlan, Mach. Learn., 1986, 1, 81–106.

---

Footnote

† Electronic supplementary information (ESI) available: Supplementary Fig. S1–S25, Table S1, and Supplementary sections S1 and S2 (PDF). DMS-MS database used for model training, MRM transitions, and ClassyFire molecular classifications (XLSX). See DOI: 10.1039/d1an00557j

---