Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
From megahertz to terahertz qubits encoded in molecular ions: theoretical analysis of dipole-forbidden spectroscopic transitions in N2+
Kaveh
Najafian
,
Ziv
Meir
 and
Stefan
Willitsch
and
Stefan
Willitsch
 *
*
Department of Chemistry, University of Basel, Klingelbergstrasse 80, 4056 Basel, Switzerland. E-mail: stefan.willitsch@unibas.ch
First published on 13th October 2020
Abstract
Recent advances in quantum technologies have enabled the precise control of single trapped molecules on the quantum level. Exploring the scope of these new technologies, we studied theoretically the implementation of qubits and clock transitions in the spin, rotational, and vibrational degrees of freedom of molecular nitrogen ions including the effects of magnetic fields. The relevant spectroscopic transitions span six orders of magnitude in frequency, illustrating the versatility of the molecular spectrum for encoding quantum information. We identified two types of magnetically insensitive qubits with very low (“stretched”-state qubits) or even zero (“magic” magnetic-field qubits) linear Zeeman shifts. The corresponding spectroscopic transitions are predicted to shift by as little as a few mHz for an amplitude of magnetic-field fluctuations on the order of a few mG, translating into Zeeman-limited coherence times of tens of minutes encoded in the rotations and vibrations of the molecule. We also found that the Q(0) line of the fundamental vibrational transition is magnetic-dipole allowed by interaction with the first excited electronic state of the molecule. The Q(0) transitions, which benefit from small systematic shifts for clock operation and is thus well suited for testing a possible variation in the proton-to-electron mass ratio, were so far not considered in single-photon spectra. Finally, we explored possibilities to coherently control the nuclear-spin configuration of N2+ through the magnetically enhanced mixing of nuclear-spin states.
1 Introduction
Over the past two decades, a range of different methods have been devised for the generation of cold trapped molecules in the gas phase. These include molecular-beam slowing and trapping,1–3 direct laser cooling,4–6 assembly from ultracold atoms,7 and sympathetic cooling.8,9 In this context, experiments in which single molecular ions are co-trapped with single atomic ions10–15 show excellent prospects for achieving the long-standing goal of gaining full control over the quantum state and dynamics of single isolated molecules. In these experiments, a quantum-logic approach16 is pursued in which the co-trapped atomic ion is used to cool the external motion of the molecular ion to the quantum ground state and to non-destructively detect its internal quantum state. Coherent Rabi and Ramsey spectroscopy,11,13 quantum-non demolition state detection10,12,15 and atom-molecule entanglement14 have recently been demonstrated.A full control over the quantum states of cold and trapped molecules will enable improved experiments in the realm of precision spectroscopy. Applications range from precisely validating existing physical theories such as quantum electrodynamics,17–19 testing fundamental concepts20,21 such as a possible time variation of physical constants22,23 and the putative existence of new forces of nature,24 benchmarking molecular-structure theory,13,25 performing controlled chemical reactions,26,27 to implementing new time standards based on narrow rovibrational molecular transitions in the mid-infrared spectral domain.28–30
In many sensitive approaches to the spectroscopy of molecular ions, the molecule is destroyed in the process of detection.28,31 The newly developed methods for non-destructive detection and coherent manipulation of molecular ions promise an increase of several orders of magnitude in the experimental duty cycle.12,32 This increase will result in a markedly improved spectroscopic sensitivity and, therefore, precision. Another exciting aspect of this technology is the implementation of molecular qubits which can be used for applications in quantum computation,33 simulation,34 metrology,35 and communication.36
Here, we studied theoretically the implementation of molecular qubits and their prospective application for spectroscopic precision measurements in the homonuclear 14N2+ molecular ion. We chose this molecule due to its prospects for investigating a possible time variation of the electron-to-proton mass ratio37 and for serving as a mid-infrared (MIR) frequency standard.29,30,38 These applications are enabled by the lack of a permanent dipole moment of the molecule such that rovibrational transitions within the same electronic state are electric-dipole forbidden. These transitions only become allowed in higher order and thus exhibit very narrow natural linewidths28,39 and low to vanishing susceptibility to external perturbations such as blackbody radiation and stray electric fields.37,38 These qualities also make N2+ an excellent system for encoding qubits in its rovibrational state manifold in which radiative lifetimes of excited states are estimated to be on the order of months to years.39
While electric perturbations are inherently small in N2+ (see discussion in ref. 37 and in Appendix A), the molecular states are strongly coupled to external magnetic fields due to the doublet electron-spin character of the molecule.38 Finite magnetic fields are present in a typical experimental apparatus, especially in ion-trapping experiments in which they are a perquisite for operation. Moreover, an external magnetic field is used to lift the degeneracy of Zeeman states and to define the quantization axis of qubits realized in atomic systems. Therefore, there is a need for a comprehensive theoretical analysis of the influence of external magnetic fields on the rovibrational states of N2+.
Here, we expanded the theory of the hyperfine structure of N2+ in ref. 40 to include the Zeeman effect. We numerically diagonalized the effective molecular Hamiltonian of N2+ in the electronic ground state, X 2Σ+g, including the interaction with magnetic fields. From the energy-level structure thus derived, we analyzed several classes of spectroscopic transitions from the radio (MHz) to mid-infrared (THz) domains. The different types of transitions (Zeeman, hyperfine-structure, fine-structure, rotational and vibrational) are discussed with respect to their applications as qubits and in precision spectroscopy.
Magnetic-field insensitive transitions are important since magnetic-field fluctuations are amongst the dominant effects causing decoherence of qubit superpositions. The use of magnetic-field-insensitive transitions for molecular qubits can dramatically increase their coherence time.41 We identified “magic” transitions42 for which the relative Zeeman shift between the energy levels involved cancels to first order at an experimentally practicable magnetic-field strength of a few Gauss. These transitions allow for magnetic-field-limited coherence times of tens of minutes in rotational and vibrational qubits at realistic levels of magnetic field noise without the need for magnetic shielding or active magnetic-noise cancellation. We also identified transitions in which the linear Zeeman shift is only on the order of 10 Hz G−1 irrespective of the magnetic-field strength. The latter are transitions between “stretched” states of different rovibrational manifolds in the electronic ground state for which the contribution of the electron spin to the Zeeman shift largely cancels.37,43 These “stretched” magnetic-insensitive transitions are unique to molecular qubits.
Previous experimental and theoretical works on N2+ analyzed the S(0) rotational component of the fundamental vibrational transition,28,38i.e., the transition from the vibrational and rotational ground state to first vibrationally and second rotationally excited state. This transition is single-photon allowed by electric-quadrupole (E2) selection rules. The corresponding Q(0) transition, i.e., the pure vibrational transition with no excitation of the rotation, was predicted to exhibit superior properties for clock and precision-spectroscopy applications due to smaller systematic shifts.37 Here, we show that the Q(0) transitions, which were previously considered to be forbidden in single-photon excitation in the present system,38 are actually magnetic-dipole (M1) allowed through the anisotropy of the interaction of the electron spin with the magnetic field. This is enabled by a mixing of the first excited electronic state, A 2Πu, with the electronic ground-state, X 2Σ+g, of the nitrogen ion.44
In addition, we identified avoided crossings of energy levels originating from two different nuclear-spin configurations with nuclear-spin quantum numbers I = 0 and I = 2. The avoided crossings occur at low, experimentally accessible magnetic-field strengths of a few tens of Gauss. Around these avoided crossings, the molecular eigenstates have a mixed character of the I = 0 and I = 2 spin states. This magnetically enhanced nuclear-spin mixing opens up opportunities for transmuting molecular-spin states on demand by coherent two-photon processes, e.g., stimulated Raman pumping,45 through the highly mixed states around the avoided crossings.
Finally, we found that for some transitions, M1 coupling dominates the spectrum while for others E2 coupling prevails due to selection rules forbidding M1 coupling. We also found that hyperfine mixing terms in the Hamiltonian allow for otherwise forbidden transitions which significantly changes the spectra compared to zeroth-order expectations.
2 Theory
2.1 Basis states
The molecular nitrogen ion, N2+, in the electronic ground state, X 2Σ+g, is adequately described within the Hund's case (bβJ) angular momentum coupling scheme46 given by,| N + S = J, | (1) |
| J + I = F. | (2) |
| |ϕi〉 = |v,N,S,J,I,F,m〉. | (3) |
Since each 14N atom has a nuclear spin of 1, the total nuclear spin, I, of the 14N2+ molecule can take the values of I = 0, 1, 2. This gives rise to different nuclear-spin-symmetry isomers with even (odd) I denoted as ortho (para). In N2+, even (odd) values of I allow for only even (odd) rotational quantum numbers N due to the total permutation symmetry of the molecular wavefunction imposed by the generalized Pauli principle. While our results are applicable for both spin isomers of N2+, in this manuscript, we mainly focus on the ortho nuclear-spin isomer with I = 0, 2 which is associated with the rotational ground state of particular interest in experiments.
2.2 Effective Hamiltonian
We considered the following effective Hamiltonian for the electronic ground state, X 2Σ+g, of N2+,40,47,49![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) = = ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) vib + vib + ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) rot + rot + ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) fs + fs + ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) hfs + hfs + ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) z. z. | (4) |
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) vib,ii = Gv,
vib,ii = Gv, ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) rot,ii = BvN(N + 1) − Dv(N(N + 1))2, and
rot,ii = BvN(N + 1) − Dv(N(N + 1))2, and ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) fs,ii = γv,N(J(J + 1) − N(N + 1) − S(S + 1))/2. Here, the subscript v indicates that the molecular constants are effective values for a given vibrational and Born–Oppenheimer electronic state, Gv is the vibrational energy, Bv is the rotational constant, Dv is the centrifugal-distortion constant and γv,N is the electron spin-rotation coupling constant which includes a centrifugal correction term γv,N = γv + γDvN(N + 1).40 The relevant spectroscopic constants are listed in Table 1. Note that our notation of the constants differs in places from the one found in the literature40 to render it unambiguous in the present context.
fs,ii = γv,N(J(J + 1) − N(N + 1) − S(S + 1))/2. Here, the subscript v indicates that the molecular constants are effective values for a given vibrational and Born–Oppenheimer electronic state, Gv is the vibrational energy, Bv is the rotational constant, Dv is the centrifugal-distortion constant and γv,N is the electron spin-rotation coupling constant which includes a centrifugal correction term γv,N = γv + γDvN(N + 1).40 The relevant spectroscopic constants are listed in Table 1. Note that our notation of the constants differs in places from the one found in the literature40 to render it unambiguous in the present context.
| v = 0 | v = 1 | |
|---|---|---|
| G v − G0 (cm−1) | 0 | 2174.746(1)55 |
| B v (cm−1) | 1.9223897(53)56 | 1.90330(2)57 |
| D v (×106 cm−1) | 5.9748(50)56 | 5.904(21)57 |
| γ v (MHz) | 280.25(45)58 | 276.92253(13)40 |
| γ D v (kHz) | 0 | −0.39790(23)40 |
| b F v (MHz) | 102.4(1.1)58 | 100.6040(15)40 |
| t v (MHz) | 23.3(1.0)58 | 28.1946(13)40 |
| t D v (Hz) | 058 | −73.5(2.7)40 |
| eqQ v (MHz) | — | 0.7079(60)40 |
| c Iv (kHz) | — | 11.32(85)40 |
| g s μ B (MHz G−1) | 2.802538,59 | 2.802538,59 |
| g r μ B (Hz G−1) | 50.10738 | 49.54738 |
| g n μ N (Hz G−1) | 307.9238 | 307.9238 |
| g l μ B (Hz G−1) | −379344 | −382144 |
The effective hyperfine-interaction Hamiltonian takes the form,40
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) hfs = hfs = ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) bF + bF + ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) t + t + ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) eqQ + eqQ + ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) cI. cI. | (5) |
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) bF represents the Fermi-contact interaction which has off-diagonal matrix elements in the J quantum number,
bF represents the Fermi-contact interaction which has off-diagonal matrix elements in the J quantum number, ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) t is the dipolar hyperfine interaction with off-diagonal matrix elements in N and J,
t is the dipolar hyperfine interaction with off-diagonal matrix elements in N and J, ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) eqQ is the electric-quadrupole hyperfine interaction with off-diagonal matrix elements in N, J and I and
eqQ is the electric-quadrupole hyperfine interaction with off-diagonal matrix elements in N, J and I and ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) cI is the magnetic nuclear spin-rotation interaction which mixes states of different quantum number, J. All matrix elements are given in Appendix B, and the effective coupling constants are given in Table 1. A schematic of the resulting energy levels is shown in Fig. 1.
cI is the magnetic nuclear spin-rotation interaction which mixes states of different quantum number, J. All matrix elements are given in Appendix B, and the effective coupling constants are given in Table 1. A schematic of the resulting energy levels is shown in Fig. 1.
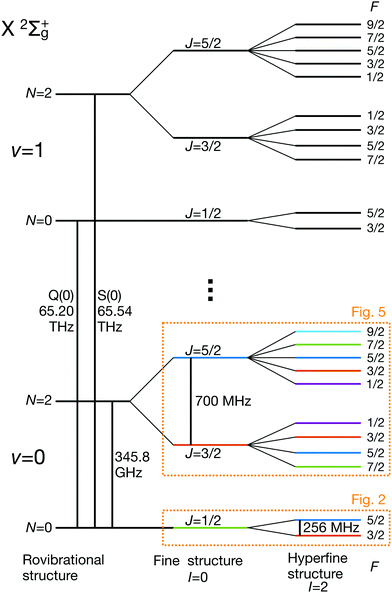 | ||
| Fig. 1 Partial schematic of the field-free energy levels of N2+ in the electronic ground state, X 2Σ+g (not to scale). The states are labeled using the Hund's case (bβJ) basis eqn (3). The dotted boxes indicate the level subspaces shown in Fig. 2 and 5 where the relevant Zeeman manifolds are displayed. The color coding of the levels is identical with the one used in these figures. | ||
In the X 2Σ+g ground state of N2+, the effective Zeeman Hamiltonian, ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) z, neglecting relativistic and radiative corrections,50 has four first-order contributions corresponding to the interaction of the magnetic field B with the magnetic moments of the electron spin, rotation and nuclear spin,47,48,51,52
z, neglecting relativistic and radiative corrections,50 has four first-order contributions corresponding to the interaction of the magnetic field B with the magnetic moments of the electron spin, rotation and nuclear spin,47,48,51,52
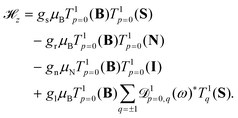 | (6) |
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) z represents the anisotropic correction to the electron-spin Zeeman interaction and gl is the corresponding effective g-factor. T1p denotes a spherical tensor operator of rank 1 in the space-fixed (subscript p) coordinate system,
z represents the anisotropic correction to the electron-spin Zeeman interaction and gl is the corresponding effective g-factor. T1p denotes a spherical tensor operator of rank 1 in the space-fixed (subscript p) coordinate system, ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 1pq(ω) is a Wigner rotation-matrix element, and the subscript q denotes spherical tensor components in the molecule-fixed coordinate system. The p = 0 component of the space-fixed coordinate system is taken to be aligned with the direction of the magnetic field, T1p=0(B) = BZẐ. The rotational and anisotropic spin g-factors, gr and gl, show a non-negligible dependence on the vibrational state (see Table 1). Diagonal terms in the interaction of the magnetic field with the electronic orbital angular momentum (L) vanish in a Σ state and terms of higher order in the magnetic field (∝B2)47,53 are neglected in our analysis.
1pq(ω) is a Wigner rotation-matrix element, and the subscript q denotes spherical tensor components in the molecule-fixed coordinate system. The p = 0 component of the space-fixed coordinate system is taken to be aligned with the direction of the magnetic field, T1p=0(B) = BZẐ. The rotational and anisotropic spin g-factors, gr and gl, show a non-negligible dependence on the vibrational state (see Table 1). Diagonal terms in the interaction of the magnetic field with the electronic orbital angular momentum (L) vanish in a Σ state and terms of higher order in the magnetic field (∝B2)47,53 are neglected in our analysis.
The interaction of the magnetic field with the electron spin mixes states with different J and F quantum numbers. The matrix elements are given by,
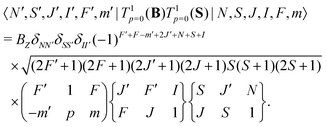 | (7) |
The same type of mixing occurs also for the interaction with the rotational magnetic moment,
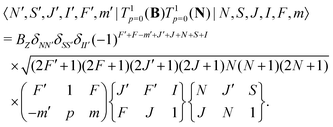 | (8) |
Interaction with the nuclear spin only mixes states with different F quantum numbers,
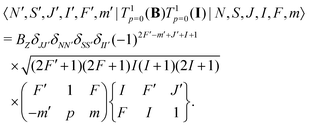 | (9) |
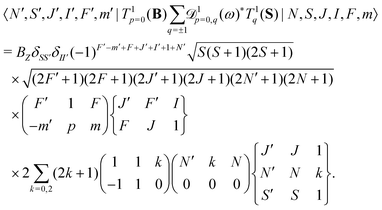 | (10) |
The complete Hamiltonian given in eqn (4) was diagonalized numerically by solving ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (BZ)|ψk〉 = Ek(BZ)|ψk〉 in the Hund's case (bβJ) basis eqn (3) to obtain the energies, Ek(BZ), and mixing-coefficients, cki(BZ),
(BZ)|ψk〉 = Ek(BZ)|ψk〉 in the Hund's case (bβJ) basis eqn (3) to obtain the energies, Ek(BZ), and mixing-coefficients, cki(BZ),
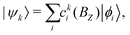 | (11) |
2.3 Transition moments
In homonuclear diatomic molecules, transitions within the same Born–Oppenheimer electronic state are electric-dipole (E1) forbidden due to the permutation symmetry of the two nuclei. We therefore derived general expressions for magnetic-dipole (M1) and electric-quadrupole (E2) transitions and calculated their strengths under the influence of an external magnetic field.In the basis set of eqn (3), the square of the transition moment Skl between different Zeeman levels can be separated into angular (A) and radial (R) parts as,60
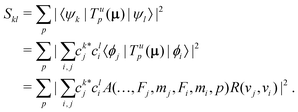 | (12) |
2.4 Magnetic-dipole transitions within the same vibrational state
For magnetic-dipole transitions, the operators that couple to the radiation have the same form as the Zeeman Hamiltonian for coupling with an external magnetic field given in eqn (7) with the substitution BZ → B(t).47 Therefore, the angular part of the transition moment eqn (12) for M1 transitions can be obtained from the matrix elements eqn (7)–(10) where p is now the polarization index of the magnetic-field of the radiation, B(t). Transitions induced by isotropic and anisotropic interaction with the electron spin and interaction with the rotation and nuclear spin are denoted by M1S, M1aS, M1N and M1I. From the angular part of the transition moment, the following selection rules can be derived,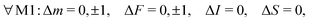 | (13) |
| M1S: S ≠ 0, ΔN = 0, | (14) |
| M1aS: S ≠ 0, ΔN = 0, 2, | (15) |
| M1N: N ≠ 0, ΔN = 0, | (16) |
| M1I: I ≠ 0, ΔN = 0, ΔJ = 0. | (17) |
For transitions within the same vibrational state, Δv = 0, the radial part of the transition moment is given by the expectation value of the magnetic moment, R(v,v) ≡ g, where the values of the g-factors are determined by the underlying interaction (Table 1).
2.5 Electric-quadrupole transitions within the same vibrational state
For E2 transitions, the coupling operator is T2p(Q) in spherical tensor notation where Q is the electric-quadrupole-moment tensor.61 The matrix elements for the E2 transition moments are given by,61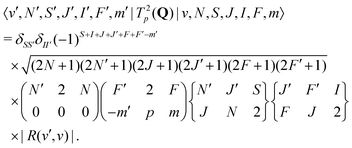 | (18) |
From the angular part of the transition moment, the following selection rules can be derived for E2 transitions,
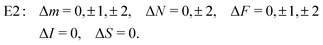 | (19) |
For transitions within the same vibrational level Δv = 0, the radial part of the transition moment is given by the permanent electric quadrupole moment, R(v,v) = Qv = 1.86 ea02,44 for low vibrational states.
2.6 Vibrational transitions
The transition strength between different vibrational levels was estimated by expanding the radial part of the transition moment to first order around the equilibrium bond length (Re),60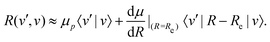 | (20) |
From eqn (20), it seems that the first term only contributes to transitions within the same vibrational manifold, since 〈v′|v〉 = δvv′. However, rovibrational mixing, which is not explicitly apparent in the effective Hamiltonian approach taken here, introduces a non-zero overlap between different vibrational states.49 Therefore, the first term in eqn (20) allows for vibrational transitions according to eqn (12).
The second term in eqn (20) introduces vibrational transitions through the change in the transition moment with internuclear distance. The vibrational matrix element for the fundamental vibrational transition within the harmonic approximation is given by,
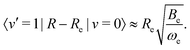 | (21) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55 and Be ≈ 1.93 cm−1
55 and Be ≈ 1.93 cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58 are the harmonic vibration wavenumber and the equilibrium rotational constant.
58 are the harmonic vibration wavenumber and the equilibrium rotational constant.
For low rotational states, we found that the strongest (M1S) transitions caused by the first term in eqn (20) are 4–5 orders of magnitude weaker than those originating from the second term for E2 and M1aS coupling. Transitions due to vibrational mixing are therefore neglected in the following. The reader is referred to Appendix C for further details.†
The couplings can be estimated from the change in the relevant g-factors with the effective bond length upon vibrational excitation given in Table 1 yielding Δgr/ΔR ≈ 4 × 10−5μB/a0 and Δgl/ΔR ≈ 2 × 10−3μB/a0. The difference in averaged bond lengths, ΔR, between v = 0 and v = 1 is estimated from the relation of the rotational constant to the equilibrium positions, Bv=1/Bv=0 = Rv=02/Rv=12, such that ΔR ≈ 0.01 a0.
For E2 transitions, the change in the electric quadrupole moment with the internuclear distance is given by dQ/dR = 2.63 ea0.44
2.7 Einstein A coefficients
The relative importance of M1 and E2 transitions to the spectra was assessed by comparing their Einstein A coefficients. For M1 transitions,65 one obtains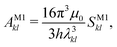 | (22) |
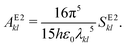 | (23) |
3 Results and discussion
3.1 Hyperfine and Zeeman qubits in the rotational ground state, N = 0
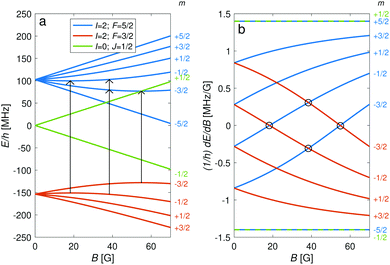
The hyperfine-Zeeman energy levels of the rovibronic ground-state manifold, X 2Σ+g (v = 0, N = 0), of N2+ as function of the strength of an external magnetic field are displayed in Fig. 2a.For the I = 0 isomer, the situation is similar to the ground state of bosonic alkaline-earth ions (e.g., 88Sr+) which are also used as qubits.66 The total angular momentum J = 1/2 results in two Zeeman levels which are separated by (gs + 2/3gl)μB ≈ 2.8 MHz G−1 (green traces in Fig. 2). All terms in the Zeeman Hamiltonian are zero except for the isotropic and anisotropic electron-spin terms. Thus, the situation is formally identical (apart from negligible mixing terms to higher rotational states) to the atomic 2S1/2 case. Transitions between the two Zeeman levels can be driven by M1S coupling (green stick in Fig. 3).
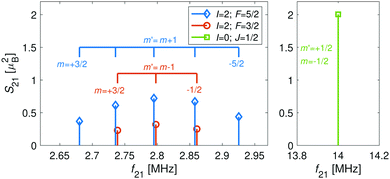 | ||
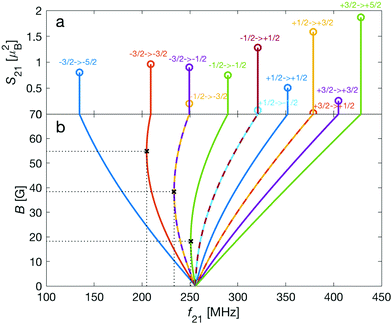
| Fig. 3 Strengths, S21, of M1S transitions, m → m′, between Zeeman levels within the hyperfine manifolds of the rovibronic ground state, X 2Σ+g (v = 0, N = 0), of the I = 0 (green) and I = 2 (blue and red) nuclear-spin species of N2+ as a function of transition frequency, f21. The abscissa indicates the transition frequencies at a magnetic field of 5 G. The color code is the same as in Fig. 2. | ||
For the I = 2 isomer, the hyperfine interaction splits the rovibronic ground state into two hyperfine manifolds with total angular-momentum quantum numbers F = 3/2 and F = 5/2 (red and blue traces in Fig. 2). The relatively small splitting of 5/2bF,v=0 ≈ 256 MHz (for B = 0 G), together with the strong magnetic coupling, M1S, leads to a deviation of the Zeeman splittings from the weak coupling regime (linear Zeeman effect) to the intermediate coupling regime already at relatively low magnetic fields of few tens of Gauss. The full decoupling of the spin and orbital angular momenta (Paschen–Back regime) occurs already at magnetic fields of a few hundreds of Gauss.
As a consequence, Zeeman transitions within each hyperfine manifold are not equally spaced (Fig. 3, blue and red bars). The unequal spacing can be used to address Zeeman transitions individually and to allow for optical pumping and state readout as was demonstrated with polar CaH+ molecules.11 The transitions are dominated by M1S coupling (see Fig. 3 for the transition strengths). M1 transitions arising from the anisotropic-spin, rotational and nuclear-spin terms were found to be 3–5 orders of magnitude weaker due to the difference in magnitude between gs and gr, gn, and gl.
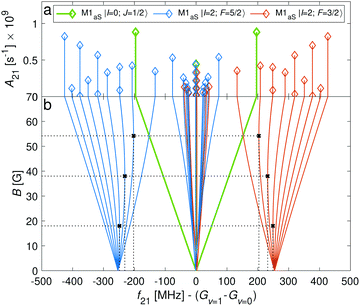
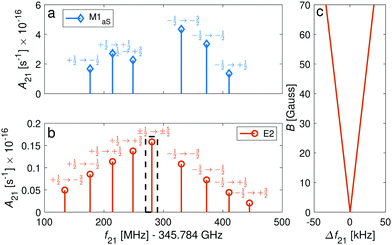
Transition between the two hyperfine manifolds, |F = 3/2〉 → |F′ = 5/2〉, are also allowed by M1S coupling. These transitions are commonly used as long-lived qubits in atomic ions.42 Here, we identified transitions in which the dependence of the energy levels on the magnetic field is equal for both the lower and upper states for specific values of the magnetic field (see arrows in Fig. 2a, circles in Fig. 2b and dotted lines in Fig. 4b). This equal dependency results in an insensitivity of the transitions to magnetic field fluctuations to first order. Insensitive transitions at “magic” magnetic fields are used in atomic systems42,67 to encode qubits with improved coherence times and to circumvent the need for magnetic shielding. Due to the small hyperfine splittings in N2+, the “magic” magnetic field occurs at small and easily accessible values. The second-order Zeeman susceptibility of the transitions around the “magic” values is ∼16 mHz mG−2 (for all the hyperfine “magic” transitions in Fig. 4b) from which we estimated a shift as low as ΔE/h = Δf ≈ 16 mHz in the transition frequencies for a magnetic-field fluctuation of 1 mG. Thus, these transitions are ideally suited for encoding qubits with magnetic-field-limited coherence times of up to 1/Δf ≈ 60 s68 as well as for applications in precision spectroscopy. Typical strengths for these hyperfine transitions are given in Fig. 4a.
3.2 Hyperfine and Zeeman qubits in the rotationally excited state, N = 2
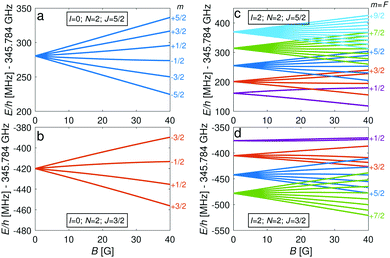
The energy levels of the second rotationally excited state in the vibronic ground state, X 2Σ+g (v = 0, N = 2), of the ortho nuclear-spin isomer, are displayed in Fig. 5. The rotational excitation shifts the spectrum by 6Bv=0 − 36Dv=0 ≈ 345.784 GHz compared to the rotationless case. The spin-rotation coupling,![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) fs, splits the levels into J = 3/2 and J = 5/2 manifolds which are separated by 5/2γv=0 ≈ 700 MHz (for B = 0 G). For the I = 0 species, this coupling generates an energy-level structure which is qualitatively similar to that of the I = 2 configuration within N = 0 (Fig. 2). However, because of the large spin-rotation splitting, the deviation from a linear Zeeman effect occurs at higher magnetic fields compared to the situation in Fig. 2. For instance, the first “magic” magnetic field for the |J = 3/2, m = −1/2〉 → |J′ = 5/2, m′ = −1/2〉 transition occurs at ∼49 G compared to ∼18 G for the |F = 3/2, m = −1/2〉 → |F′ = 5/2, m′ = −1/2〉 transition in the N = 0, I = 2 state.
fs, splits the levels into J = 3/2 and J = 5/2 manifolds which are separated by 5/2γv=0 ≈ 700 MHz (for B = 0 G). For the I = 0 species, this coupling generates an energy-level structure which is qualitatively similar to that of the I = 2 configuration within N = 0 (Fig. 2). However, because of the large spin-rotation splitting, the deviation from a linear Zeeman effect occurs at higher magnetic fields compared to the situation in Fig. 2. For instance, the first “magic” magnetic field for the |J = 3/2, m = −1/2〉 → |J′ = 5/2, m′ = −1/2〉 transition occurs at ∼49 G compared to ∼18 G for the |F = 3/2, m = −1/2〉 → |F′ = 5/2, m′ = −1/2〉 transition in the N = 0, I = 2 state.
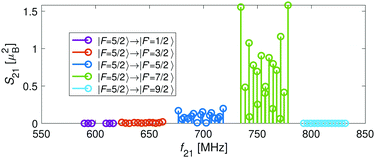
For the I = 2 nuclear-spin species in the N = 2 rotational state, the levels are further split by the hyperfine interaction which is dominated by the Fermi-contact (![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) bF) and dipolar (
bF) and dipolar (![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) t) terms. Thus, the energy levels split into F = 9/2,…,1/2 and F = 7/2,…,1/2 for the J = 5/2 (Fig. 5c) and J = 3/2 (Fig. 5d) spin-rotation manifolds, respectively. M1S coupling is again dominant. For spin-rotation transitions, we found that ΔF = 1 components are prevalent, as can be seen in the spectrum displayed in Fig. 6. “Magic” transitions can be found at magnetic fields as low as few Gauss (e.g., the |F = 5/2, m = +1/2〉 → |F′ = 7/2, m′ = −1/2〉 at ∼756.3 MHz and B = 1.55 G) with second-order Zeeman-shifts as low as ∼8 mHz mG−2 (see Appendix D for a partial list of the strongest “magic” transitions below 70 G).
t) terms. Thus, the energy levels split into F = 9/2,…,1/2 and F = 7/2,…,1/2 for the J = 5/2 (Fig. 5c) and J = 3/2 (Fig. 5d) spin-rotation manifolds, respectively. M1S coupling is again dominant. For spin-rotation transitions, we found that ΔF = 1 components are prevalent, as can be seen in the spectrum displayed in Fig. 6. “Magic” transitions can be found at magnetic fields as low as few Gauss (e.g., the |F = 5/2, m = +1/2〉 → |F′ = 7/2, m′ = −1/2〉 at ∼756.3 MHz and B = 1.55 G) with second-order Zeeman-shifts as low as ∼8 mHz mG−2 (see Appendix D for a partial list of the strongest “magic” transitions below 70 G).
An interesting effect in N2+ as exemplified here with the N = 2 manifold is the coupling between nuclear-spin states through the electric-quadrupole hyperfine interaction, ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) eqQ, which mixes levels with even (or odd) total nuclear spin I. In 14N2+, there is only a single para nuclear-spin state with I = 1 such that only the ortho species with I = 0, 2 exhibit this coupling. This interaction results in avoided crossings of energy levels originating from the different ortho spin states. As an example, Fig. 7a shows such an avoided crossing between the |F = 3/2, m = −3/2〉 states originating from the I = 0 (red) and I = 2 (blue) species. This avoided crossing occurs at a relatively low magnetic field of ∼54 G. Around the crossing point, the levels exhibit a strong mixing of the I = 0 and I = 2 basis states (see Fig. 7b). This magnetically enhanced nuclear-spin mixing is interesting as it opens up possibilities to manipulate the nuclear-spin configuration of the molecule on demand (see Fig. 12 and the accompanying discussion further below).
eqQ, which mixes levels with even (or odd) total nuclear spin I. In 14N2+, there is only a single para nuclear-spin state with I = 1 such that only the ortho species with I = 0, 2 exhibit this coupling. This interaction results in avoided crossings of energy levels originating from the different ortho spin states. As an example, Fig. 7a shows such an avoided crossing between the |F = 3/2, m = −3/2〉 states originating from the I = 0 (red) and I = 2 (blue) species. This avoided crossing occurs at a relatively low magnetic field of ∼54 G. Around the crossing point, the levels exhibit a strong mixing of the I = 0 and I = 2 basis states (see Fig. 7b). This magnetically enhanced nuclear-spin mixing is interesting as it opens up possibilities to manipulate the nuclear-spin configuration of the molecule on demand (see Fig. 12 and the accompanying discussion further below).
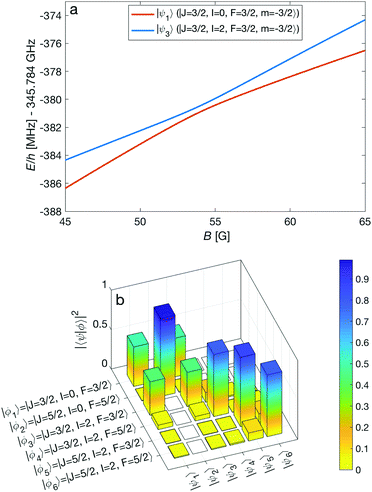 | ||
| Fig. 7 (a) Adiabatic level energies, E, as a function of the magnetic field strength, B, showing an avoided crossing between two states originating from two different nuclear-spin states (I = 0, 2) in the X 2Σ+g (v = 0, N = 2) level. The states indicated in the legend represent the dominant contributions at zero magnetic field. (b) Overlap of the eigenstates eqn (11) with the basis vectors eqn (3), |〈ϕi|ψk〉|2 = |cki|2, at a magnetic field of 54 G. Here, |〈ϕi|ψk〉|2 ≈ δik for zero magnetic field. | ||
3.3 Rotational qubits
We now consider transitions from the rotational ground state N = 0 to the second excited rotational state N′ = 2 at frequencies around ∼345 GHz. The sensitivity of these transitions to the proton-to-electron mass ratio69 renders them interesting for testing a possible time variation of these fundamental constants as they are within the reach of stabilized THz sources.70In general, M1S transition selection rules do not permit a change of rotational quantum numbers by ΔN = 2, but this mechanism must still be considered due to mixing of rotational states. In addition, the anisotropy of the electron-spin g-factor tensor allows for ΔN = 2 transitions through M1aS coupling. We also consider electric-quadrupole (E2) transitions which also permit such a change in the rotational quantum number. In addition, E2 transitions permit changes in the angular-momentum-projection quantum number Δm = ±2, ±1, 0. Thus, magnetic-dipole and electric-quadrupole rotational spectra will show different signatures as illustrated in Fig. 8a and b. For the |J = 1/2〉 → |J′ = 3/2〉 transitions, M1aS coupling was found to be ∼3 orders of magnitude stronger than the E2 coupling while for the |J = 1/2〉 → |J′ = 5/2〉, it was only found to be about 1 order of magnitude stronger (Fig. 8a and b).
 | ||
| Fig. 8 Spectrum of Zeeman components of the spin-rotational transition |N = 0, J = 1/2〉 → |N′ = 2, J′ = ±5/2〉 for the I = 0 isomer. The intensities of the transitions are given in the form of Einstein A coefficients (eqn (23) and (22)) for comparison of (a) M1aS coupling with (b) E2 coupling. The magnetic field was assumed to be 70 G. Labels indicate the Zeeman components of the transitions. (c) Magnification of the dashed rectangle in (b) showing the stretched transitions, |J = 1/2, m = ±1/2〉 → |J′ = 5/2, m′ = ±5/2〉, which show a very small dependence on the magnetic field and are only separated by 66.5 kHz at 70 G. The frequency axis in (c) is referenced to the field-free line positions. | ||
The Δm = ±2 and ΔJ = 2 lines are allowed for E2 coupling opening up opportunities to exploit transitions between “stretched” states, e.g., |J = 1/2, m = ±1/2〉 → |J′ = 5/2, m′ = ±5/2〉 in the I = 0 nuclear-spin isomer and |F = 5/2, m = ±5/2〉 → |F′ = 9/2, m′ = ±9/2〉 in the I = 2 nuclear-spin isomer. These transitions show a very small linear dependence on the magnetic field due to cancellation of the major contribution from the isotropic Zeeman Hamiltonian eqn (7) in the ground and excited “stretched” states. The remaining susceptibility of these levels to magnetic field is attributed to the rotational dependence of the anisotropic (eqn (10)) and rotational (eqn (8)) Zeeman Hamiltonians. The isotropic term (eqn (7)) still has a small effect due to mixing of the rotational states. Thus, precise measurements of the magnetic dependence of these transitions can be used for an accurate determination of the anisotropic electron-spin and rotational g-factors.
The “stretched” transitions depend linearly on the magnetic field in the range considered here (up to 70 G) as can be seen in Fig. 8c. The frequencies of these transitions will change by ΔE/h = Δf ≈ 475 mHz for magnetic field fluctuations of 1 mG. Therefore, they can be exploited for encoding THz qubits with coherence times of up to 1/Δf ≈ 2 s68 and for precision THz spectroscopy. The rotational spectrum of the I = 2 nuclear-spin species also exhibits “magic” magnetic-field insensitive transitions with second-order shifts as low as ∼3 mHz mG−2 (Appendix D). Magnetic field fluctuations on the order of ∼1 mG still permit qubits with Zeeman-limited coherence times of up to 1/Δf ≈ 5 min.
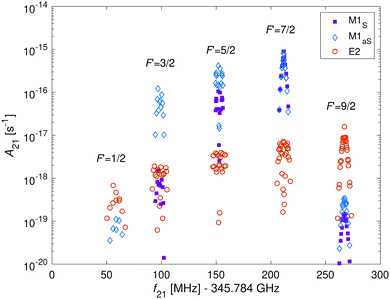
In Fig. 9, the hyperfine components of the transition |N = 0, J = 1/2, F = 5/2〉 → |N′ = 2, J′ = 5/2, F′〉 in the I = 2 nuclear-spin state due to M1 and E2 coupling are shown. The M1S rotational transitions are allowed by rotational mixing induced by the dipolar hyperfine interaction, ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) t. The strongest M1S lines are on par with the strongest M1aS lines and are up to two order of magnitude stronger than the E2 lines. However, in some cases the strengths for both types of transitions are similar and in other cases, only E2 transitions are allowed due to quadrupole selections rules. Thus, one should consider both types of transitions when analyzing the molecular spectrum. To directly compare the strength of both types of couplings with eqn (12), we calculated the relevant Einstein A coefficients using eqn (22) and (23).
t. The strongest M1S lines are on par with the strongest M1aS lines and are up to two order of magnitude stronger than the E2 lines. However, in some cases the strengths for both types of transitions are similar and in other cases, only E2 transitions are allowed due to quadrupole selections rules. Thus, one should consider both types of transitions when analyzing the molecular spectrum. To directly compare the strength of both types of couplings with eqn (12), we calculated the relevant Einstein A coefficients using eqn (22) and (23).
3.4 Rovibrational qubits
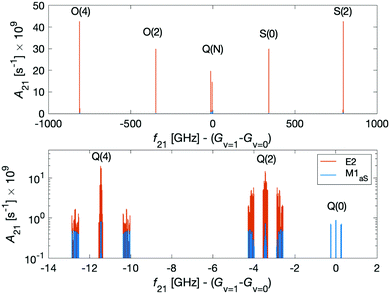
Dipole-forbidden rovibrational lines in N2+ were first observed by Germann et al.28 Vibrational transitions are promising for tests of a possible temporal variation of the proton-to-electron mass ratio because of their sensitivity to these constants. Also, they benefit from higher transition frequencies than rotational lines and thus allow for a better relative spectroscopic precision.37Fig. 10 shows the O(N), Q(N) and S(N) branches of the fundamental vibrational spectrum, i.e., transitions with |v = 0, N〉 → |v′ = 1, N′ = N + (−2, 0, +2)〉 and N = 0, 2, 4 and for the two ortho nuclear-spin species.Transitions within the Q(0) manifold, |v = 0, N = 0〉 → |v′ = 1, N′ = 0〉, are usually considered to be forbidden for single photon excitation within a Σ electronic state.37 E2 selection rules forbid transitions from N = 0 to N′ = 0. However, the anisotropic electron-spin interaction eqn (10) permits N = 0 to N′ = 0 transitions and it varies considerably with the internuclear distance (eqn (20)). This leads to the appearance of Q(0) lines in the spectrum which, to the best of our knowledge, were so far not considered for the present vibrational spectrum.
In Fig. 11, components of the Q(0) transition, i.e. |v = 0, N = 0, J = 1/2〉 → |v′ = 1, N′ = 0, J′ = 1/2〉, of both the I = 0 and I = 2 species is shown. For both nuclear-spin configurations, the “stretched” transitions, i.e. |J = 1/2, m = ±1/2〉 → |J′ = 1/2, m′ = ±1/2〉 and |F = 5/2, m = ±5/2〉 → |F′ = 5/2, m′ = ±5/2〉 are allowed by M1aS coupling and show very small linear Zeeman shifts of Δgl/3 ≈ 9.3 mHz mG−1. This dependency is ∼50 times smaller than for transitions between “stretched” states in the S(0) (|N = 0〉 → |N′ = 2〉) manifold. Precise measurements of the magnetic dependence of these transitions constitute a direct measurement of the anisotropy of the electron-spin g-factor tensor.
The Q(0) spectrum also exhibits “magic” transitions for the I = 2 species (indicated by black crosses in Fig. 11) at relatively low magnetic fields of a few 10 G. The second-order Zeeman susceptibility of these transitions is ∼16 mHz mG−2. Note that there are no “magic” transitions for the I = 0 nuclear-spin configuration when driving a transition from the rotational ground state, N = 0. This is due to the linear Zeeman shifts of the rotational ground state at the magnetic field values considered here (see Fig. 2a green lines).
We now turn to discuss S(0) transitions, i.e. |v = 0, N = 0〉 → |v′ = 1, N′ = 2〉. The S(0) spectrum is predicted to be ∼30 times stronger (see Fig. 10 red lines) than the Q(0) spectrum due to E2 transitions (eqn (20)). The second largest contribution to the S(0) spectrum is due to M1aS coupling (Fig. 10 blue lines). All other coupling mechanisms were found to be more than 5 orders of magnitude smaller. Q(2) transitions, |v = 0, N = 2〉 → |v′ = 1, N′ = 2〉, are also dominated by E2 coupling.
The S(0) spectrum is predicted to exhibit “magic” transitions at low magnetic fields of a few Gauss and with second-order Zeeman susceptibilities as low as ∼1 mHz mG−2 (see Appendix D). With magnetic field fluctuations on the order of ∼1 mG, they can be used for encoding vibrational qubits with coherence times of up to ≈15 min. This corresponds to a relative Zeeman shift of ΔE/E ≈ 1 × 10−17 without any active or passive magnetic field stabilization. The S(0) spectrum also features “stretched” transitions that have a low linear Zeeman shift of ∼480 mHz mG−1.
The S(0) transitions at 4.574 μm with A ≈ 3 × 10−8 Hz can be driven using commercial quantum-cascade lasers as demonstrated in ref. 28. With typical values for the laser power of 100 mW and a 1/e beam radius of 50 μm at the position of the molecule, Rabi frequencies71 of Ω ∼ (2π)10 kHz are estimated yielding π-pulse times of tπ ∼ 50 μs thus enabling an efficient coherent manipulation of the rovibrational levels of the molecule. For the Q(0) transitions, A ≈ 4 × 10−10 Hz. With the same laser parameters, Ω ∼ (2π)0.5 kHz and tπ ∼ 1 ms are estimated.
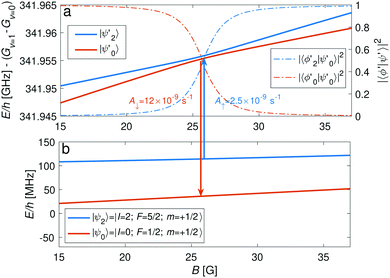
The |v′ = 1, N′ = 2〉 rotational manifold of the first excited vibrational state exhibits avoided crossings between levels of the two ortho-nuclear-spin species as illustrated in Fig. 12. The mixing is again induced by the quadrupole hyperfine interaction, ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) eqQ. At a magnetic field of ∼25.8 G, the states labeled
eqQ. At a magnetic field of ∼25.8 G, the states labeled 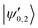 in Fig. 12 are composed of a 50–50 mixture of the |I′ = 2, F′ = 3/2, m′ = −3/2〉 and |I′ = 0, J′ = 3/2, m′ = −3/2〉 basis states. This opens up the possibility of coupling two distinct molecular states of different nuclear-spin character, for instance the |ψ2〉 = |I = 2, F = 5/2, m = 1/2〉 and |ψ0〉 = |I = 0, J = 1/2, m = 1/2〉 in the rovibrational ground state, v = 0, N = 0. These states show negligible nuclear-spin mixing. Fig. 12 illustrates how these two states in the vibrational ground state can be interconverted by excitation and deexcitation to either of the mixed states
in Fig. 12 are composed of a 50–50 mixture of the |I′ = 2, F′ = 3/2, m′ = −3/2〉 and |I′ = 0, J′ = 3/2, m′ = −3/2〉 basis states. This opens up the possibility of coupling two distinct molecular states of different nuclear-spin character, for instance the |ψ2〉 = |I = 2, F = 5/2, m = 1/2〉 and |ψ0〉 = |I = 0, J = 1/2, m = 1/2〉 in the rovibrational ground state, v = 0, N = 0. These states show negligible nuclear-spin mixing. Fig. 12 illustrates how these two states in the vibrational ground state can be interconverted by excitation and deexcitation to either of the mixed states 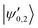 in v = 1. Alternatively, interconversion of the nuclear-spin states can be achieved by populating one of the mixed state in v = 1 and appropriately tuning the magnetic field across the crossing region.
in v = 1. Alternatively, interconversion of the nuclear-spin states can be achieved by populating one of the mixed state in v = 1 and appropriately tuning the magnetic field across the crossing region.
4 Summary and conclusions
In this paper, we presented a theoretical study of dipole-forbidden spectroscopic transitions in N2+ considering the complete hyperfine, rovibrational and Zeeman level structure. We identified magnetic-field insensitive transitions which are promising for encoding qubits because of their excellent coherence properties and for clock operation because of their weak dependence on magnetic fields. We calculated the strengths of magnetic-dipole and electric-quadrupole allowed spectroscopic transitions showing the importance of both in the radiofrequency, microwave and infrared spectrum of the nitrogen molecular ion. We found that pure vibrational transitions, Q(0), are allowed by M1 coupling induced by the anisotropic spin-magnetic field interaction. These transitions, which benefit from the lowest systematic shifts for clock operation, were not considered in the single-photon spectrum of N2+ so far. Finally, we showed that the electric-quadrupole hyperfine interaction causes avoided crossings between states of the two ortho nuclear-spin configurations of nitrogen. This magnetically enhanced nuclear-spin mixing opens the possibility to coherently transmute the nuclear-spin state on demand.It is instructive to make a quantitative comparison between the magnetic insensitivity of clock transitions embedded in N2+ to other clock systems, e.g., Al+ quantum-logic clocks which currently exhibit among the lowest systematic uncertainties.72 The Al+ clock is based on the 1S0 ↔ 3P0 electronic transition which is first-order magnetically sensitive due to the nuclear spin, I = 5/2, of 27Al+. By averaging two stretched Zeeman transitions, the first-order shift is canceled, and the clock only depends on second-order Zeeman shifts.73 This averaging technique is not an option for qubit applications. The second-order sensitivity of Al+, ∼7.2 × 10−4 mHz mG−2, is five orders of magnitude smaller than the sensitivity of N2+ “magic” transitions analysed here. However, since the Al+ clock works at a finite magnetic field of 1.2 G,72 the clock transition acquires an effective first-order sensitivity of ∼1.7 mHz mG−1. This first-order sensitivity is five times smaller than that of the Q(0) “stretched” transitions in N2+. However, for the “magic” transitions in N2+, which have a vanishing first-order sensitivity, the magnetic-field sensitivity breaks even with the Al+ clock transition at a fluctuating magnetic field value of ∼0.1 mG which is a typical value for a system with actively stabilized magnetic field. Below this value, the N2+ “magic” transitions are less sensitive than the Al+ clock while above they are more sensitive to magnetic field fluctuations.
Data and materials availability
The codes used for diagonalizing the molecular Hamiltonian and generating the plots of this study are available on the Zenodo repository at http:/www.doi.org/10.5281/zenodo.4006578.Conflicts of interest
There are no conflicts to declare.Appendix
A Electric-field induced systematic shifts
In the main text, we have considered the usefulness of different types of spectroscopic transitions for clock applications and as qubits in terms of their sensitivity to magnetic fields which causes the dominant systematic shifts in N2+. In addition, viable clock candidates should also have low susceptibilities to electric fields. For completeness, we consider here the AC-Stark and electric quadrupole shifts, complementing the discussion in ref. 37.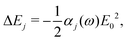 | (24) |
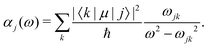 | (25) |
Different types of AC-Stark shifts contribute to the present problem. The AC-Stark shift from the RF drive of an ion trap with frequency ω ≈ (2π)20 MHz can be estimated in the limit ω → 0 in eqn (25). For vibrational transitions with f ≈ 65.2 THz, one obtains a relative shift of ΔfAC/(fE02) = 7 × 10−24 (m V−1)2. Typically, the electric field amplitude vanishes at the position of the ions in a Paul trap. However, trap imperfections can lead to a non-zero electric-field amplitude. These fields will cause a relative shift of 1.26 × 10−18 at a field amplitude of 300 V m−1 for the fundamental vibrational transition. It should be noted that such a field amplitude is excessive for an ion in a typical ion trap built for quantum-logic experiments. For other classes of transitions, e.g., hyperfine or rotational excitations, the corresponding shift is smaller as the energy spacing decreases and the cancellation of the AC-Stark shift between the upper and the lower state is more significant.
The AC-Stark shift induced by ambient blackbody radiation can also be estimated in the limit of ω → 0 because the maximum of the thermal spectral energy density at a temperature of 300 K is situated around 31 THz which is small compared to the frequencies of electronic transitions from the vibrational ground-state. The time-averaged value of the quadratic electric-field amplitude of a 300 K radiator is E02/2 = 〈E02〉 ≈ (831.9 V m−1)2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 75 yielding a relative shift of ΔfAC/f = 1.0 × 10−17 for vibrational transitions. Transitions within a vibrational state will have smaller shifts due to cancellation between the upper and lower levels. The N2+ molecular clock is therefore suitable for operation in a room-temperature environment.
75 yielding a relative shift of ΔfAC/f = 1.0 × 10−17 for vibrational transitions. Transitions within a vibrational state will have smaller shifts due to cancellation between the upper and lower levels. The N2+ molecular clock is therefore suitable for operation in a room-temperature environment.
AC-Stark shifts from the probe laser can be eliminated by using the Hyper-Ramsey spectroscopic method76 or through a balanced Raman scheme.77 In a Rabi- or Ramsey-type clock experiment, the laser power is reduced in order to minimize power broadening. In order to obtain a Rabi frequency of Ω ∼ (2π)1 Hz on the S(0) branch of the fundamental vibrational transition, 1 nW of laser power focused to a beam radius of 50 μm is required. The intensity is thus I = 0.26 W m−2 corresponding to an electric field of 13.9 V m−1. The AC-Stark shift obtained from eqn (24) is then ΔfAC/f = 8.9 × 10−22. With a laser power more suitable for driving qubits of ∼100 mW, the intensity is I = 2.55 × 107 W m−2 and an AC-Stark shift of 5.8 Hz or ΔfAC/f = 8.9 × 10−14 is obtained.
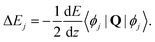 | (26) |
All the Zeeman- and hyperfine transitions in N = 0 are therefore immune to electric-quadrupole shifts to first order. Rotational transitions of the form N = 0 → (N′ = 2, F= 1/2), among which several “magic” transitions were identified (see Appendix D), are also not affected by this shift, as is the Q(0) branch of vibrational transitions. The Q(0) transitions of the I = 0 nuclear-spin configuration are therefore especially suitable for clock operation because they are immune from the quadrupole shift and feature stretched-state transitions which have a low susceptibility to magnetic fields. Q(2) transitions can also be chosen with F = F′ = 1/2 such that the quadrupole shift cancels. For S(0) transitions, the quadrupole shift vanishes in the lower states N = 0 and the upper state can be chosen as F′ = 1/2.
The differential shift of the fine-structure transitions with ΔJ = 1 within the N = 2 manifold was calculated for the “magic” transitions listed in Appendix D. The differential shift ranges between 1.13–5.65 Hz for the “magic” transitions with the exception of |J = 3/2, I = 2, F = 7/2, MF = −1/2〉 → |J = 5/2, I = 2, F = 9/2, MF = −3/2〉 for which an accidental cancellation leads to a vanishing shift. Therefore, suitable clock transitions with a low sensitivity to magnetic fields and vanishing quadrupole shifts were identified in every class of transitions examined in this paper.
B The effective hyperfine Hamiltonian
The effective hyperfine-interaction Hamiltonian takes the form,![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) hfs = hfs = ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) bF + bF + ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) t + t + ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) eqQ + eqQ + ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) cI. cI. | (27) |
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) hfs and their matrix elements have been discussed in ref. 40 and are reproduced here for convenience.
hfs and their matrix elements have been discussed in ref. 40 and are reproduced here for convenience. ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) bF represents the Fermi-contact interaction which has off-diagonal matrix elements in J,
bF represents the Fermi-contact interaction which has off-diagonal matrix elements in J,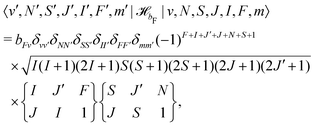 | (28) |
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) t is the dipolar hyperfine interaction with off-diagonal matrix elements in N and J,
t is the dipolar hyperfine interaction with off-diagonal matrix elements in N and J,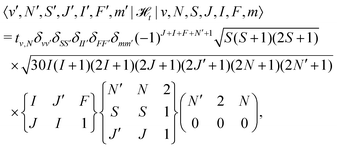 | (29) |
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) eqQ is the electric-quadrupole hyperfine interaction with off-diagonal matrix elements in N, J and I,
eqQ is the electric-quadrupole hyperfine interaction with off-diagonal matrix elements in N, J and I,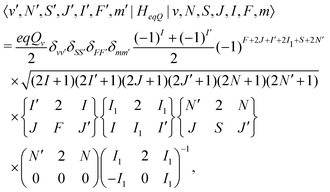 | (30) |
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) cI is the magnetic nuclear spin-rotation interaction which mixes states of different quantum number, J,
cI is the magnetic nuclear spin-rotation interaction which mixes states of different quantum number, J,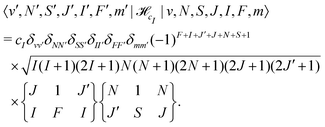 | (31) |
All effective coupling constants are given in Table 1.
C Rovibrational interactions
The rovibrational mixing was estimated in the same way as in ref. 49 and 79, i.e., as a result of the dependence of the rotational constant, B, on the bond length, R, within the harmonic approximation for the vibration. The rotational constant, B(R) ∝ R−2, was expanded in a Taylor series to first order around the equilibrium internuclear distance R = Re,| B(R) = Be[1 − 2ξ + O(ξ2)]. | (32) |
Inserting eqn (32) in the rotational Hamiltonian, B(R)N2, the rigid-rotor Hamiltonian, BeN2, and the rotation–vibration coupling Hamiltonian to first order,
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) ro-vib = −2Beξ ro-vib = −2Beξ![[N with combining circumflex]](https://www.rsc.org/images/entities/b_char_004e_0302.gif) 2. 2. | (33) |
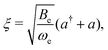 | (34) |
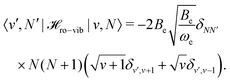 | (35) |
The combined vibrational and rigid-rotor Hamiltonians, ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) vib = Gv and
vib = Gv and ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) rot = BeN2, respectively, were diagonalized including the rovibrational interaction
rot = BeN2, respectively, were diagonalized including the rovibrational interaction ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) ro-vib numerically using the v = 0, 1, 2, 3, 4 vibrational and N = 0, 2, 4, 6, 8, 10 rotational states as a basis set to obtain the mixing coefficients. In this treatment, we found
ro-vib numerically using the v = 0, 1, 2, 3, 4 vibrational and N = 0, 2, 4, 6, 8, 10 rotational states as a basis set to obtain the mixing coefficients. In this treatment, we found 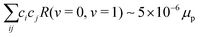 in N = 2 according to eqn (20). For E2 transitions, this corresponds to transition moment of ∼10−5 ea02. The second term in eqn (20), however, leads to a much stronger transition moment of ∼10−1 ea02. Therefore, the effect of rovibrational mixing in the calculation of the transition moments for low-lying rotational states can be neglected.
in N = 2 according to eqn (20). For E2 transitions, this corresponds to transition moment of ∼10−5 ea02. The second term in eqn (20), however, leads to a much stronger transition moment of ∼10−1 ea02. Therefore, the effect of rovibrational mixing in the calculation of the transition moments for low-lying rotational states can be neglected.
D “Magic” magnetic-field-insensitive transitions
| (A) Hyperfine transitions: (I = 2) M1S | |v = 0, N = 0〉 → |v′ = 0, N′ = 0〉 | B [G] | A [s−1] | f − f0 [MHz] | a [mHz mG−2] |
|---|---|---|---|---|---|
| |J = 1/2, I = 2, F = 3/2, m = −3/2〉 → | |J = 1/2, I = 2, F = 5/2, m = −3/2〉 | 54.85 | 8.6 × 10−18 | 204.80 | 19.1 |
| |J = 1/2, I = 2, F = 3/2, m = −1/2〉 → | |J = 1/2, I = 2, F = 5/2, m = −3/2〉 | 38.40 | 6.1 × 10−18 | 233.51 | 16.1 |
| |J = 1/2, I = 2, F = 3/2, m = −3/2〉 → | |J = 1/2, I = 2, F = 5/2, m = −1/2〉 | 38.42 | 6.1 × 10−18 | 233.48 | 16.1 |
| |J = 1/2, I = 2, F = 3/2, m = −1/2〉 → | |J = 1/2, I = 2, F = 5/2, m = −1/2〉 | 18.28 | 1.6 × 10−17 | 250.83 | 15.6 |
| (B) Fine-structure transitions: (I = 0, 2) M1S | |v = 0, N = 2〉 → |v′ = 0, N′ = 2〉 | B [G] | A [s−1] | f − f0 [MHz] | a [mHz mG−2] |
|---|---|---|---|---|---|
| |J = 3/2, I = 0, F = 3/2, m = −1/2〉 → | |J = 5/2, I = 0, F = 5/2, m = −1/2〉 | 49.20 | 3.1 × 10−16 | 686.52 | 8.9 |
| |J = 3/2, I = 2, F = 3/2, m = −1/2〉 → | |J = 5/2, I = 2, F = 5/2, m = −1/2〉 | 17.15 | 2.2 × 10−16 | 656.74 | 12.0 |
| |J = 3/2, I = 2, F = 3/2, m = +1/2〉 → | |J = 5/2, I = 2, F = 5/2, m = −1/2〉 | 3.81 | 1.0 × 10−16 | 660.16 | 10.5 |
| |J = 3/2, I = 2, F = 5/2, m = −1/2〉 → | |J = 5/2, I = 2, F = 7/2, m = −3/2〉 | 48.30 | 1.9 × 10−16 | 738.06 | 8.0 |
| |J = 3/2, I = 2, F = 5/2, m = −3/2〉 → | |J = 5/2, I = 2, F = 7/2, m = −1/2〉 | 48.72 | 1.6 × 10−16 | 739.40 | 7.0 |
| |J = 3/2, I = 2, F = 5/2, m = −1/2〉 → | |J = 5/2, I = 2, F = 7/2, m = −1/2〉 | 22.31 | 3.9 × 10−16 | 752.31 | 8.2 |
| |J = 3/2, I = 2, F = 5/2, m = +1/2〉 → | |J = 5/2, I = 2, F = 7/2, m = −1/2〉 | 1.55 | 1.9 × 10−16 | 756.33 | 7.9 |
| |J = 3/2, I = 2, F = 7/2, m = −1/2〉 → | |J = 5/2, I = 2, F = 9/2, m = −3/2〉 | 49.84 | 2.8 × 10−16 | 832.14 | 6.3 |
| |J = 3/2, I = 2, F = 7/2, m = −3/2〉 → | |J = 5/2, I = 2, F = 9/2, m = −1/2〉 | 49.39 | 2.7 × 10−16 | 832.67 | 6.2 |
| |J = 3/2, I = 2, F = 7/2, m = −1/2〉 → | |J = 5/2, I = 2, F = 9/2, m = −1/2〉 | 24.06 | 5.9 × 10−16 | 843.94 | 6.3 |
| (C) Rotational transitions: (I = 2) M1aS | |v = 0, N = 0〉 → |v′ = 0, N′ = 2〉 | B [G] | A [s−1] | f − f0 [MHz] | a [mHz mG−2] |
|---|---|---|---|---|---|
| |J = 1/2, I = 2, F = 3/2, m = −3/2〉 → | |J = 3/2, I = 2, F = 1/2, m = −1/2〉 | 45.57 | 2.2 × 10−15 | −244.08 | 9.4 |
| |J = 1/2, I = 2, F = 3/2, m = −1/2〉 → | |J = 3/2, I = 2, F = 1/2, m = −1/2〉 | 15.80 | 9.3 × 10−15 | −225.74 | 12.3 |
| |J = 1/2, I = 2, F = 3/2, m = −1/2〉 → | |J = 3/2, I = 2, F = 1/2, m = +1/2〉 | 9.37 | 2.7 × 10−15 | −223.57 | 9.3 |
| |J = 1/2, I = 2, F = 3/2, m = −3/2〉 → | |J = 3/2, I = 2, F = 3/2, m = −3/2〉 | 29.85 | 9.8 × 10−15 | −257.50 | 7.3 |
| |J = 1/2, I = 2, F = 3/2, m = −1/2〉 → | |J = 3/2, I = 2, F = 3/2, m = −1/2〉 | 36.99 | 1.2 × 10−15 | −254.73 | 3.8 |
| |J = 1/2, I = 2, F = 5/2, m = −3/2〉 → | |J = 3/2, I = 2, F = 3/2, m = −1/2〉 | 38.86 | 1.4 × 10−15 | −488.22 | −12.1 |
| |J = 1/2, I = 2, F = 5/2, m = −1/2〉 → | |J = 3/2, I = 2, F = 3/2, m = −1/2〉 | 15.30 | 1.9 × 10−15 | −504.42 | −14.9 |
| |J = 1/2, I = 2, F = 3/2, m = −1/2〉 → | |J = 3/2, I = 2, F = 3/2, m = +1/2〉 | 48.51 | 7.4 × 10−15 | −264.22 | 5.3 |
| |J = 1/2, I = 2, F = 3/2, m = +1/2〉 → | |J = 3/2, I = 2, F = 3/2, m = +3/2〉 | 17.64 | 5.9 × 10−15 | −253.71 | 5.4 |
| |J = 1/2, I = 2, F = 3/2, m = −3/2〉 → | |J = 3/2, I = 2, F = 5/2, m = −3/2〉 | 44.15 | 7.7 × 10−15 | −297.86 | 5.9 |
| |J = 1/2, I = 2, F = 5/2, m = −3/2〉 → | |J = 3/2, I = 2, F = 5/2, m = −3/2〉 | 60.07 | 1.9 × 10−15 | −501.62 | −12.6 |
| |J = 1/2, I = 2, F = 5/2, m = −1/2〉 → | |J = 3/2, I = 2, F = 5/2, m = −3/2〉 | 35.38 | 5.4 × 10−15 | −531.06 | −10.9 |
| |J = 1/2, I = 2, F = 3/2, m = −1/2〉 → | |J = 3/2, I = 2, F = 5/2, m = −1/2〉 | 16.71 | 7.1 × 10−15 | −289.93 | 3.4 |
| |J = 1/2, I = 2, F = 5/2, m = −3/2〉 → | |J = 3/2, I = 2, F = 5/2, m = −1/2〉 | 43.39 | 7.8 × 10−15 | −521.55 | −13.8 |
| |J = 1/2, I = 2, F = 3/2, m = −1/2〉 → | |J = 3/2, I = 2, F = 5/2, m = +1/2〉 | 60.74 | 6.2 × 10−15 | −302.52 | 3.2 |
| |J = 1/2, I = 2, F = 5/2, m = −1/2〉 → | |J = 3/2, I = 2, F = 5/2, m = +1/2〉 | 4.82 | 6.8 × 10−15 | −544.71 | −11.7 |
| |J = 1/2, I = 2, F = 3/2, m = +1/2〉 → | |J = 3/2, I = 2, F = 5/2, m = +3/2〉 | 30.76 | 7.5 × 10−15 | −292.22 | 3.0 |
| |J = 1/2, I = 2, F = 5/2, m = −3/2〉 → | |J = 3/2, I = 2, F = 7/2, m = −3/2〉 | 58.94 | 1.4 × 10−14 | −539.71 | −12.8 |
| |J = 1/2, I = 2, F = 5/2, m = −1/2〉 → | |J = 3/2, I = 2, F = 7/2, m = −3/2〉 | 33.79 | 9.0 × 10−15 | −568.41 | −10.6 |
| |J = 1/2, I = 2, F = 5/2, m = −3/2〉 → | |J = 3/2, I = 2, F = 7/2, m = −1/2〉 | 46.34 | 6.2 × 10−15 | −556.10 | −12.8 |
| |J = 1/2, I = 2, F = 5/2, m = −1/2〉 → | |J = 3/2, I = 2, F = 7/2, m = −1/2〉 | 19.49 | 1.4 × 10−14 | −576.51 | −11.1 |
| |J = 1/2, I = 2, F = 5/2, m = −1/2〉 → | |J = 3/2, I = 2, F = 7/2, m = +1/2〉 | 6.12 | 7.4 × 10−15 | −580.31 | −10.9 |
| (D) Rovibrational transitions: (I = 2): M1aS | |v = 0, N = 0〉 → |v′ = 1, N′ = 0〉 | B [G] | A [s−1] | f − f0 [MHz] | a [mHz mG−2] |
|---|---|---|---|---|---|
| |J = 1/2, I = 2, F = 5/2, m = −3/2〉 → | |J = 1/2, I = 2, F = 3/2, m = −3/2〉 | 54.37 | 4.4 × 10−10 | −202.56 | −19.3 |
| |J = 1/2, I = 2, F = 5/2, m = −1/2〉 → | |J = 1/2, I = 2, F = 3/2, m = −3/2〉 | 38.05 | 2.1 × 10−10 | −230.99 | −16.3 |
| |J = 1/2, I = 2, F = 5/2, m = −3/2〉 → | |J = 1/2, I = 2, F = 3/2, m = −1/2〉 | 38.10 | 2.1 × 10−10 | −231.01 | −16.2 |
| |J = 1/2, I = 2, F = 5/2, m = −1/2〉 → | |J = 1/2, I = 2, F = 3/2, m = −1/2〉 | 18.12 | 4.4 × 10−10 | −248.18 | −15.8 |
| |J = 1/2, I = 2, F = 3/2, m = −3/2〉 → | |J = 1/2, I = 2, F = 5/2, m = −3/2〉 | 54.37 | 4.4 × 10−10 | 203.45 | 19.3 |
| |J = 1/2, I = 2, F = 3/2, m = −1/2〉 → | |J = 1/2, I = 2, F = 5/2, m = −3/2〉 | 38.03 | 2.1 × 10−10 | 231.91 | 16.3 |
| |J = 1/2, I = 2, F = 3/2, m = −3/2〉 → | |J = 1/2, I = 2, F = 5/2, m = −1/2〉 | 38.12 | 2.1 × 10−10 | 231.88 | 16.2 |
| |J = 1/2, I = 2, F = 3/2, m = −1/2〉 → | |J = 1/2, I = 2, F = 5/2, m = −1/2〉 | 18.12 | 4.4 × 10−10 | 249.07 | 15.8 |
| (E) Rovibrational transitions: (I = 2): E2 | |v = 0, N = 0〉 → |v′ = 1, N′ = 2〉 | B [G] | A [s−1] | f − f0 [MHz] | a [mHz mG−2] |
|---|---|---|---|---|---|
| |J = 1/2, I = 2, F = 5/2, m = −1/2〉 → | |J = 3/2, I = 2, F = 1/2, m = −1/2〉 | 30.06 | 5.8 × 10−9 | −480.97 | −5.2 |
| |J = 1/2, I = 2, F = 5/2, m = −1/2〉 → | |J = 3/2, I = 2, F = 3/2, m = −3/2〉 | 47.64 | 8.5 × 10−9 | −491.42 | −8.0 |
| |J = 1/2, I = 2, F = 5/2, m = +1/2〉 → | |J = 3/2, I = 2, F = 3/2, m = −3/2〉 | 14.87 | 3.8 × 10−9 | −508.36 | −6.7 |
| |J = 1/2, I = 2, F = 3/2, m = −1/2〉 → | |J = 3/2, I = 2, F = 3/2, m = −1/2〉 | 36.60 | 1.8 × 10−9 | −257.19 | 3.9 |
| |J = 1/2, I = 2, F = 5/2, m = −3/2〉 → | |J = 3/2, I = 2, F = 3/2, m = −1/2〉 | 39.07 | 6.7 × 10−9 | −490.68 | −11.5 |
| |J = 1/2, I = 2, F = 3/2, m = −1/2〉 → | |J = 3/2, I = 2, F = 3/2, m = +1/2〉 | 46.75 | 4.2 × 10−9 | −265.99 | 5.6 |
| |J = 1/2, I = 2, F = 5/2, m = −3/2〉 → | |J = 3/2, I = 2, F = 3/2, m = +1/2〉 | 33.59 | 3.3 × 10−9 | −498.86 | −9.9 |
| |J = 1/2, I = 2, F = 5/2, m = −1/2〉 → | |J = 3/2, I = 2, F = 3/2, m = +1/2〉 | 4.28 | 5.6 × 10−9 | −509.68 | −13.1 |
| |J = 1/2, I = 2, F = 3/2, m = −1/2〉 → | |J = 3/2, I = 2, F = 3/2, m = +3/2〉 | 61.63 | 1.1 × 10−9 | −275.92 | 4.3 |
| |J = 1/2, I = 2, F = 3/2, m = +1/2〉 → | |J = 3/2, I = 2, F = 3/2, m = +3/2〉 | 16.85 | 5.0 × 10−9 | −255.67 | 5.6 |
| |J = 1/2, I = 2, F = 5/2, m = −1/2〉 → | |J = 3/2, I = 2, F = 5/2, m = −5/2〉 | 64.93 | 8.9 × 10−9 | −506.02 | −7.5 |
| |J = 1/2, I = 2, F = 3/2, m = −3/2〉 → | |J = 3/2, I = 2, F = 5/2, m = −3/2〉 | 44.62 | 3.2 × 10−9 | −294.67 | 6.0 |
| |J = 1/2, I = 2, F = 5/2, m = −3/2〉 → | |J = 3/2, I = 2, F = 5/2, m = −3/2〉 | 59.97 | 6.0 × 10−9 | −498.49 | −12.5 |
| |J = 1/2, I = 2, F = 5/2, m = +1/2〉 → | |J = 3/2, I = 2, F = 5/2, m = −3/2〉 | 10.74 | 5.4 × 10−9 | −540.42 | −10.3 |
| |J = 1/2, I = 2, F = 5/2, m = −1/2〉 → | |J = 3/2, I = 2, F = 5/2, m = −1/2〉 | 18.34 | 3.8 × 10−9 | −537.47 | −12.5 |
| |J = 1/2, I = 2, F = 5/2, m = −3/2〉 → | |J = 3/2, I = 2, F = 5/2, m = +1/2〉 | 31.36 | 6.0 × 10−9 | −530.66 | −11.9 |
| |J = 1/2, I = 2, F = 3/2, m = +1/2〉 → | |J = 3/2, I = 2, F = 5/2, m = +5/2〉 | 65.10 | 5.2 × 10−9 | −300.92 | 2.3 |
| |J = 1/2, I = 2, F = 3/2, m = −3/2〉 → | |J = 3/2, I = 2, F = 7/2, m = −5/2〉 | 14.88 | 1.5 × 10−8 | −314.32 | 4.0 |
| |J = 1/2, I = 2, F = 5/2, m = −1/2〉 → | |J = 3/2, I = 2, F = 7/2, m = −5/2〉 | 51.30 | 3.5 × 10−9 | −543.57 | −9.2 |
| |J = 1/2, I = 2, F = 3/2, m = −3/2〉 → | |J = 3/2, I = 2, F = 7/2, m = −3/2〉 | 48.10 | 1.3 × 10−8 | −324.81 | 6.1 |
| |J = 1/2, I = 2, F = 5/2, m = −1/2〉 → | |J = 3/2, I = 2, F = 7/2, m = −3/2〉 | 33.18 | 2.0 × 10−9 | −557.44 | −10.9 |
| |J = 1/2, I = 2, F = 5/2, m = +1/2〉 → | |J = 3/2, I = 2, F = 7/2, m = −3/2〉 | 8.04 | 2.2 × 10−9 | −568.88 | −10.1 |
| |J = 1/2, I = 2, F = 3/2, m = −1/2〉 → | |J = 3/2, I = 2, F = 7/2, m = −1/2〉 | 16.21 | 1.3 × 10−8 | −314.63 | 4.2 |
| |J = 1/2, I = 2, F = 5/2, m = −3/2〉 → | |J = 3/2, I = 2, F = 7/2, m = −1/2〉 | 45.32 | 1.8 × 10−9 | −545.49 | −13.1 |
| |J = 1/2, I = 2, F = 3/2, m = −1/2〉 → | |J = 3/2, I = 2, F = 7/2, m = +1/2〉 | 54.89 | 1.4 × 10−8 | −324.78 | 2.9 |
| |J = 1/2, I = 2, F = 5/2, m = −3/2〉 → | |J = 3/2, I = 2, F = 7/2, m = +1/2〉 | 33.85 | 2.3 × 10−9 | −557.16 | −12.0 |
| |J = 1/2, I = 2, F = 5/2, m = −1/2〉 → | |J = 3/2, I = 2, F = 7/2, m = +1/2〉 | 5.95 | 1.7 × 10−9 | −569.15 | −11.1 |
| |J = 1/2, I = 2, F = 3/2, m = +1/2〉 → | |J = 3/2, I = 2, F = 7/2, m = +3/2〉 | 22.93 | 1.5 × 10−8 | −315.33 | 2.9 |
| |J = 1/2, I = 2, F = 3/2, m = +3/2〉 → | |J = 3/2, I = 2, F = 7/2, m = +7/2〉 | 41.67 | 2.7 × 10−8 | −316.98 | 1.3 |
| |J = 1/2, I = 2, F = 3/2, m = −3/2〉 → | |J = 5/2, I = 2, F = 3/2, m = −1/2〉 | 56.95 | 4.7 × 10−9 | 322.93 | 10.7 |
| |J = 1/2, I = 2, F = 3/2, m = −1/2〉 → | |J = 5/2, I = 2, F = 3/2, m = −1/2〉 | 25.65 | 8.1 × 10−9 | 348.66 | 9.7 |
| |J = 1/2, I = 2, F = 3/2, m = −3/2〉 → | |J = 5/2, I = 2, F = 3/2, m = +1/2〉 | 16.17 | 1.1 × 10−8 | 352.02 | 15.4 |
| |J = 1/2, I = 2, F = 5/2, m = +1/2〉 → | |J = 5/2, I = 2, F = 3/2, m = +3/2〉 | 52.04 | 2.0 × 10−9 | 117.76 | −4.6 |
| |J = 1/2, I = 2, F = 5/2, m = +3/2〉 → | |J = 5/2, I = 2, F = 3/2, m = +3/2〉 | 16.39 | 4.2 × 10−9 | 101.77 | −5.8 |
| |J = 1/2, I = 2, F = 3/2, m = −1/2〉 → | |J = 5/2, I = 2, F = 5/2, m = −3/2〉 | 48.87 | 3.3 × 10−9 | 383.90 | 9.3 |
| |J = 1/2, I = 2, F = 3/2, m = +1/2〉 → | |J = 5/2, I = 2, F = 5/2, m = −3/2〉 | 23.68 | 5.3 × 10−9 | 403.02 | 8.8 |
| |J = 1/2, I = 2, F = 3/2, m = −3/2〉 → | |J = 5/2, I = 2, F = 5/2, m = −1/2〉 | 44.96 | 8.3 × 10−9 | 382.72 | 13.3 |
| |J = 1/2, I = 2, F = 5/2, m = −1/2〉 → | |J = 5/2, I = 2, F = 5/2, m = −1/2〉 | 6.98 | 4.1 × 10−9 | 152.46 | −2.4 |
| |J = 1/2, I = 2, F = 3/2, m = −3/2〉 → | |J = 5/2, I = 2, F = 5/2, m = +1/2〉 | 25.75 | 4.0 × 10−9 | 400.41 | 12.9 |
| |J = 1/2, I = 2, F = 3/2, m = −1/2〉 → | |J = 5/2, I = 2, F = 5/2, m = +1/2〉 | 1.26 | 4.8 × 10−9 | 408.33 | 12.7 |
| |J = 1/2, I = 2, F = 5/2, m = +3/2〉 → | |J = 5/2, I = 2, F = 5/2, m = +5/2〉 | 60.47 | 8.4 × 10−9 | 162.26 | −1.8 |
| |J = 1/2, I = 2, F = 3/2, m = −1/2〉 → | |J = 5/2, I = 2, F = 7/2, m = −5/2〉 | 67.42 | 3.0 × 10−9 | 423.69 | 7.8 |
| |J = 1/2, I = 2, F = 3/2, m = −3/2〉 → | |J = 5/2, I = 2, F = 7/2, m = −3/2〉 | 63.13 | 2.9 × 10−9 | 416.02 | 12.8 |
| |J = 1/2, I = 2, F = 3/2, m = −1/2〉 → | |J = 5/2, I = 2, F = 7/2, m = −3/2〉 | 39.26 | 3.8 × 10−9 | 447.47 | 10.6 |
| |J = 1/2, I = 2, F = 5/2, m = −3/2〉 → | |J = 5/2, I = 2, F = 7/2, m = −3/2〉 | 36.74 | 5.9 × 10−9 | 213.99 | −5.3 |
| |J = 1/2, I = 2, F = 3/2, m = −1/2〉 → | |J = 5/2, I = 2, F = 7/2, m = −1/2〉 | 20.54 | 3.3 × 10−9 | 459.46 | 11.7 |
| |J = 1/2, I = 2, F = 3/2, m = −1/2〉 → | |J = 5/2, I = 2, F = 7/2, m = +1/2〉 | 3.88 | 2.1 × 10−9 | 464.18 | 11.3 |
| |J = 1/2, I = 2, F = 5/2, m = −1/2〉 → | |J = 5/2, I = 2, F = 7/2, m = +1/2〉 | 67.69 | 4.6 × 10−9 | 222.96 | −2.0 |
| |J = 1/2, I = 2, F = 5/2, m = +3/2〉 → | |J = 5/2, I = 2, F = 7/2, m = +5/2〉 | 31.84 | 1.5 × 10−9 | 210.01 | −1.0 |
| |J = 1/2, I = 2, F = 5/2, m = −3/2〉 → | |J = 5/2, I = 2, F = 9/2, m = −5/2〉 | 9.72 | 1.7 × 10−8 | 259.28 | −3.7 |
| |J = 1/2, I = 2, F = 5/2, m = −3/2〉 → | |J = 5/2, I = 2, F = 9/2, m = −3/2〉 | 43.36 | 1.3 × 10−8 | 268.40 | −6.2 |
| |J = 1/2, I = 2, F = 5/2, m = −3/2〉 → | |J = 5/2, I = 2, F = 9/2, m = −1/2〉 | 68.91 | 7.8 × 10−9 | 286.49 | −6.1 |
| |J = 1/2, I = 2, F = 5/2, m = −1/2〉 → | |J = 5/2, I = 2, F = 9/2, m = −1/2〉 | 13.68 | 1.5 × 10−8 | 259.82 | −4.7 |
| |J = 1/2, I = 2, F = 5/2, m = −1/2〉 → | |J = 5/2, I = 2, F = 9/2, m = +1/2〉 | 47.59 | 1.2 × 10−8 | 269.15 | −3.9 |
| |J = 1/2, I = 2, F = 5/2, m = +1/2〉 → | |J = 5/2, I = 2, F = 9/2, m = +3/2〉 | 23.35 | 1.5 × 10−8 | 261.01 | −3.3 |
Acknowledgements
We thank Prof. Timothy Steimle (Arizona State University) for his critical reading of the manuscript and for his comments. This work has been supported by the Swiss National Science Foundation as part of the National Centre of Competence in Research, Quantum Science and Technology (NCCR-QSIT), grant nr. CRSII5_183579, and by the University of Basel.Notes and references
- S. D. Hogan, M. Motsch and F. Merkt, Phys. Chem. Chem. Phys., 2011, 13, 18705 RSC.
- S. Y. T. van de Meerakker, H. L. Bethlem, N. Vanhaecke and G. Meijer, Chem. Rev., 2012, 112, 4828 CrossRef CAS.
- Y. Segev, M. Pitzer, M. Karpov, N. Akerman, J. Narevicius and E. Narevicius, Nature, 2019, 572, 189 CrossRef CAS.
- L. Anderegg, B. L. Augenbraun, Y. Bao, S. Burchesky, L. W. Cheuk, W. Ketterle and J. M. Doyle, Nat. Phys., 2018, 14, 890 Search PubMed.
- D. J. McCarron, M. H. Steinecker, Y. Zhu and D. DeMille, Phys. Rev. Lett., 2018, 121, 013202 CrossRef CAS.
- L. Caldwell, J. Devlin, H. Williams, N. Fitch, E. Hinds, B. Sauer and M. Tarbutt, Phys. Rev. Lett., 2019, 123, 033202 CrossRef CAS.
- S. A. Moses, J. P. Covey, M. T. Miecnikowski, D. S. Jin and J. Ye, Nat. Phys., 2017, 13, 13 Search PubMed.
- K. Mølhave and M. Drewsen, Phys. Rev. A: At., Mol., Opt. Phys., 2000, 62, 011401 CrossRef.
- X. Tong, A. H. Winney and S. Willitsch, Phys. Rev. Lett., 2010, 105, 143001 CrossRef.
- F. Wolf, Y. Wan, J. C. Heip, F. Gebert, C. Shi and P. O. Schmidt, Nature, 2016, 530, 457 CrossRef CAS.
- C. W. Chou, C. Kurz, D. B. Hume, P. N. Plessow, D. R. Leibrandt and D. Leibfried, Nature, 2017, 545, 203 CrossRef CAS.
- M. Sinhal, Z. Meir, K. Najafian, G. Hegi and S. Willitsch, Science, 2020, 367, 1213–1218 CrossRef CAS.
- C. Chou, A. Collopy, C. Kurz, Y. Lin, M. Harding, P. Plessow, T. Fortier, S. Diddams, D. Leibfried and D. Leibrandt, Science, 2020, 367, 1458–1461 CrossRef CAS.
- Y. Lin, D. R. Leibrandt, D. Leibfried and C.-W. Chou, Nature, 2020, 581, 273–277 CrossRef CAS.
- K. Najafian, Z. Meir, M. Sinhal and S. Willitsch, Nat. Commun., 2020, 11, 4470 CrossRef CAS.
- P. O. Schmidt, T. Rosenband, C. Langer, W. M. Itano, J. C. Bergquist and D. J. Wineland, Science, 2005, 309, 749 CrossRef CAS.
- L. Semeria, P. Jansen, G.-M. Camenisch, F. Mellini, H. Schmutz and F. Merkt, Phys. Rev. Lett., 2020, 124, 213001 CrossRef CAS.
- S. Alighanbari, M. G. Hansen, V. Korobov and S. Schiller, Nat. Phys., 2018, 14, 555 Search PubMed.
- J. Biesheuvel, J. P. Karr, L. Hilico, K. S. E. Eikema, W. Ubachs and J. C. J. Koelemeij, Nat. Commun., 2016, 7, 10385 Search PubMed.
- M. S. Safronova, D. Budker, D. DeMille, D. F. J. Kimball, A. Derevianko and C. W. Clark, Rev. Mod. Phys., 2018, 90, 025008 CrossRef CAS.
- D. DeMille, J. M. Doyle and A. O. Sushkov, Science, 2017, 357, 990–994 CrossRef CAS.
- S. Schiller and V. Korobov, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 71, 032505 CrossRef.
- V. Flambaum and M. Kozlov, Phys. Rev. Lett., 2007, 99, 150801 CrossRef CAS.
- E. J. Salumbides, J. C. J. Koelemeij, J. Komasa, K. Pachucki, K. S. E. Eikema and W. Ubachs, Phys. Rev. D, 2013, 87, 112008 CrossRef.
- N. Hölsch, M. Beyer, E. J. Salumbides, K. S. E. Eikema, W. Ubachs, Ch Jungen and F. Merkt, Phys. Rev. Lett., 2019, 122, 103002 CrossRef.
- T. Sikorsky, Z. Meir, R. Ben-shlomi, N. Akerman and R. Ozeri, Nat. Commun., 2018, 9, 920 CrossRef.
- A. D. Dörfler, P. Eberle, D. Koner, M. Tomza, M. Meuwly and S. Willitsch, Nat. Commun., 2019, 10, 5429 CrossRef.
- M. Germann, X. Tong and S. Willitsch, Nat. Phys., 2014, 10, 820 Search PubMed.
- J.-Ph. Karr, J. Mol. Spectrosc., 2014, 300, 37 CrossRef CAS.
- S. Schiller, D. Bakalov and V. I. Korobov, Phys. Rev. Lett., 2014, 113, 023004 CrossRef CAS.
- S. Willitsch, Handbook of High-Resolution Spectroscopy, John Wiley & Sons, Chichester, 2011, vol. 3, p. 1691 Search PubMed.
- Z. Meir, G. Hegi, K. Najafian, M. Sinhal and S. Willitsch, Faraday Discuss., 2019, 217, 561–583 RSC.
- D. DeMille, Phys. Rev. Lett., 2002, 88, 067901 CrossRef CAS.
- J. A. Blackmore, L. Caldwell, P. D. Gregory, E. M. Bridge, R. Sawant, J. Aldegunde, J. Mur-Petit, D. Jaksch, J. M. Hutson, B. E. Sauer, M. R. Tarbutt and S. L. Cornish, Quantum Sci. Technol., 2018, 4, 014010 CrossRef.
- T. Manovitz, R. Shaniv, Y. Shapira, R. Ozeri and N. Akerman, Phys. Rev. Lett., 2019, 123, 203001 CrossRef CAS.
- H. J. Kimble, Nature, 2008, 453, 1023 CrossRef CAS.
- M. Kajita, G. Gopakumar, M. Abe, M. Hada and M. Keller, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 89, 032509 CrossRef.
- M. Kajita, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 92, 043423 CrossRef.
- M. Germann, PhD thesis, University of Basel, 2016.
- N. B. Mansour, C. Kurtz, T. Steimle, G. Goodman, L. Young, T. Scholl, S. Rosner and R. Holt, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, 4418 CrossRef CAS.
- Y. Wang, M. Um, J. Zhang, S. An, M. Lyu, J.-N. Zhang, L.-M. Duan, D. Yum and K. Kim, Nat. Photonics, 2017, 11, 646 CrossRef CAS.
- C. Langer, R. Ozeri, J. D. Jost, J. Chiaverini, B. DeMarco, A. Ben-Kish, R. B. Blakestad, J. Britton, D. B. Hume, W. M. Itano, D. Leibfried, R. Reichle, T. Rosenband, T. Schaetz, P. O. Schmidt and D. J. Wineland, Phys. Rev. Lett., 2005, 95, 060502 CrossRef CAS.
- L. Caldwell, H. Williams, N. Fitch, J. Aldegunde, J. M. Hutson, B. Sauer and M. Tarbutt, Phys. Rev. Lett., 2020, 124, 063001 CrossRef CAS.
- P. J. Bruna and F. Grein, J. Mol. Spectrosc., 2004, 227, 67 CrossRef CAS.
- U. Gaubatz, P. Rudecki, S. Schiemann and K. Bergmann, J. Chem. Phys., 1990, 92, 5363–5376 CrossRef CAS.
- R. A. Frosch and H. M. Foley, Phys. Rev., 1952, 88, 1337 CrossRef CAS.
- J. M. Brown and A. Carrington, Rotational Spectroscopy of Diatomic Molecules, Cambridge University Press, Cambridge, 2003 Search PubMed.
- J. Brown, M. Kaise, C. Kerr and D. Milton, Mol. Phys., 1978, 36, 553–582 CrossRef CAS.
- T. Balasubramanian, V. Bellary and K. N. Rao, Can. J. Phys., 1994, 72, 971–978 CrossRef CAS.
- J.-P. Karr, V. I. Korobov and L. Hilico, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 77, 062507 CrossRef.
- T. Ma, C. Butler, J. M. Brown, C. Linton and T. C. Steimle, J. Phys. Chem. A, 2009, 113, 8038–8044 CrossRef CAS.
- J. Chen, J. Gengler, T. Steimle and J. M. Brown, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 73, 012502 CrossRef.
- L. Schiff and H. Snyder, Phys. Rev., 1939, 55, 59 CrossRef CAS.
- M. Beyer and F. Merkt, J. Chem. Phys., 2018, 149, 214301 CrossRef.
- F. Michaud, F. Roux, S. P. Davis, A.-D. Nguyen and C. O. Laux, J. Mol. Spectrosc., 2000, 203, 1–8 CrossRef CAS.
- Y.-D. Wu, J.-W. Ben, B. Li, L.-J. Zheng, Y.-Q. Chen and X.-H. Yang, Chin. J. Chem. Phys., 2007, 20, 285 CrossRef.
- D. Collet, J.-L. Destombes, I. H. Bachir and T. Huet, Chem. Phys. Lett., 1998, 286, 311–316 CrossRef CAS.
- T. J. Scholl, R. A. Holt and S. D. Rosner, J. Mol. Spectrosc., 1998, 192, 424 CrossRef CAS.
- E. Tiesinga, P. J. Mohr, D. B. Newell and B. N. Taylor, The 2018 CODATA Recommended Values of the Fundamental Physical Constants (Web Version 8.1), 2020.
- D. Papoušek, Collect. Czech. Chem. Commun., 1989, 54, 2555–2630 CrossRef.
- M. Germann and S. Willitsch, Mol. Phys., 2016, 114, 769 CrossRef CAS.
- G. Karl and J. D. Poll, J. Chem. Phys., 1967, 46, 2944 CrossRef CAS.
- A. Goldman, R. Tipping, Q. Ma, C. Boone, P. Bernath, P. Demouline, F. Hase, M. Schneider, J. Hannigan, M. Coffey and C. Rinsland, J. Quant. Spectrosc. Radiat. Transfer, 2007, 103, 168 CrossRef CAS.
- M. Dang-Nhu, R. Zander, A. Goldman and C. P. Rinsland, J. Mol. Spectrosc., 1990, 144, 366 CrossRef CAS.
- G. W. F. Drake, Springer Handbook of Atomic, Molecular and Optical Physics, Springer, New York, 2006, p. 192 Search PubMed.
- A. Keselman, Y. Glickman, N. Akerman, S. Kotler and R. Ozeri, New J. Phys., 2011, 13, 073027 CrossRef.
- T. P. Harty, D. T. C. Allcock, C. J. Ballance, L. Guidoni and H. A. Janacek, Phys. Rev. Lett., 2014, 113, 220501 CrossRef CAS.
- B. E. A. Saleh and M. C. Teich, Fundamentals of Photonics, Wiley-Interscience, Hoboken, 2nd edn, 2007 Search PubMed.
- D. Hanneke, R. Carollo and D. Lane, Phys. Rev. A, 2016, 94, 050101 CrossRef.
- S. Schiller, B. Roth, F. Lewen, O. Ricken and M. Wiedner, Appl. Phys. B: Lasers Opt., 2008, 95, 55–61 CrossRef.
- D. Leibfried, R. Blatt, C. Monroe and D. Wineland, Rev. Mod. Phys., 2003, 75, 281 CrossRef CAS.
- S. M. Brewer, J.-S. Chen, A. M. Hankin, E. R. Clements, C. W. Chou, D. J. Wineland, D. B. Hume and D. R. Leibrandt, Phys. Rev. Lett., 2019, 123, 033201 CrossRef CAS.
- S. Brewer, J.-S. Chen, K. Beloy, A. Hankin, E. Clements, C. Chou, W. McGrew, X. Zhang, R. Fasano and D. Nicolodi, et al. , Phys. Rev. A, 2019, 100, 013409 CrossRef CAS.
- A. Lofthus and P. H. Krupenie, J. Phys. Chem. Ref. Data, 1977, 6, 113 CrossRef CAS.
- F. Riehle, Frequency Standards, Basics and Applications, Wiley-VCH Verlag GmbH, 2005 Search PubMed.
- V. Yudin, A. Taichenachev, C. Oates, Z. Barber, N. D. Lemke, A. D. Ludlow, U. Sterr, C. Lisdat and F. Riehle, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 82, 011804 CrossRef.
- C. Sanner, N. Huntemann, R. Lange, C. Tamm and E. Peik, Phys. Rev. Lett., 2018, 120, 053602 CrossRef CAS.
- W. M. Itano, J. Res. Natl. Inst. Stand. Technol., 2000, 105, 829–837 CrossRef CAS.
- T. Balasubramanian, V. Bellary, R. D'Cunha and K. N. Rao, J. Mol. Spectrosc., 1992, 153, 26–31 CrossRef CAS.
Footnote |
| † While for rovibrational E2 transitions it is well established to calculate the transition moment via the second term in eqn (20),28,62,63 the situation is less clear for rovibrational transitions of M1 type. Such transitions were first reported in ref. 64 for the 3Σ−g ground electronic state of the O2 molecule. In ref. 49, two types of mechanisms were elaborated to rationalize the M1 rovibrational transition intensities observed in ref. 64. One is rovibrational mixing and the other is due to coupling of different Born–Oppenheimer states. The former, analyzed in Appendix C, was found to be small in the present case, the latter is included in the anisotropic electron spin Zeeman coupling which was found to give the dominant contribution to the rovibrational M1 transition intensities studied here. |
| This journal is © the Owner Societies 2020 |