Maximum likelihood estimations of force and mobility from single short Brownian trajectories†
Raphael
Sarfati
a,
Jerzy
Bławzdziewicz
b and
Eric R.
Dufresne
 *c
*c
aDepartment of Applied Physics, Yale University, New Haven, CT 06520, USA
bDepartment of Mechanical Engineering, Texas Tech University, Lubbock, TX 79409, USA
cDepartment of Materials, ETH Zürich, 8092 Zürich, Switzerland. E-mail: ericd@ethz.ch
First published on 20th February 2017
Abstract
We describe a method to extract force and diffusion parameters from single trajectories of Brownian particles. The analysis, based on the principle of maximum likelihood, is well-suited for out-of-equilibrium trajectories, even when a limited amount of data is available and the dynamical parameters vary spatially. We substantiate this method with experimental and simulated data, and discuss its practical implementation, strengths, and limitations.
1 Introduction
Brownian particles are ubiquitous in soft matter and biological sciences, from colloidal particles to fluorescently-tagged molecules. The trajectories of these particles contain precious information about their structure and interactions. For example, particle sizes are routinely quantified by measuring diffusion coefficients of a dilute suspension in a well-characterized fluid.1,2 Alternatively, when the particles are well-characterized, the trajectory of a Brownian particle can probe the solvent's rheological properties.3 Analysis of Brownian trajectories can also reveal the conservative and dissipative forces acting on particles due to external fields4 or interactions with other particles.5Since Brownian trajectories are stochastic, their analysis is necessarily statistical. The physical theory describing the statistics of Brownian particles is well-established.6 When particles fluctuate near an equilibrium position, conservative forces acting on them are readily extracted using Boltzmann statistics.7 In the absence of external forces, the dissipative forces acting on particles can be calculated from their diffusion coefficient using the Stokes–Einstein relation. More generally, the Smoluchowski equation describes the trajectory of Brownian particles when conservative forces and diffusion coefficients vary over space.8 In this case, conservative and dissipative forces can simultaneously be determined from the distribution of displacements at each configuration.
Importantly, this requires the measurement of many trajectories through the same system configuration. This approach has been successfully implemented for micron-sized colloidal particles, which can be repeatedly trapped in the desired configuration and released using optical traps.5,9–11 However, in some cases Brownian particles cannot be manipulated with optical traps, and in others the laser will perturb the rest of the system. In such situations, one requires a method to determine the forces with less data, typically a single trajectory.
Maximum likelihood estimators have recently been shown to be powerful tools for measuring the diffusion coefficient of Brownian particles.12–14 They are more efficient and more accurate than the conventional approach, where one determines a diffusion coefficient by calculating a mean-squared displacement and fitting. Given a discretely sampled trajectory, maximum likelihood estimators provide an explicit analytical expression for the best estimate of the diffusion coefficient. This approach explicitly accounts for common experimental artifacts such as localization error from exposure time-induced blurring,12 finite trajectory length,13 or limited photon statistics.14
We recently introduced a method, based on the same principle, to estimate force and diffusion parameters from single Brownian trajectories.15 Our numerical approach allows one to efficiently estimate spatially varying dynamical parameters. It can provide useful results for even short trajectories, because it assumes a specific functional form for the spatial dependence of the dynamical parameters. One can readily characterize the statistical error and bias in these estimates through the analysis of ensembles of simulated data. Here, we provide a detailed description of our numerical maximum likelihood analysis (MLA) of Brownian trajectories. First, we provide a simple review of the principles of Brownian motion and maximum likelihood. Second, we demonstrate the method based on simulations and experimental data, including the analysis of strong interactions between pairs of paramagnetic particles. Finally, we discuss the practical implementation of the method, and provide the corresponding MATLAB code in the ESI.†
2 Theoretical background
In this section, we briefly review the solution to the Smoluchowski equation and the principle of maximum likelihood. We illustrate how to combine these two concepts with a simple example.Let us consider the one-dimensional position x of a particle over time, and call F the applied force and D the diffusion coefficient. In general, F and D may depend on x. However, on sufficiently short time intervals Δt the particle samples a region where F and D are uniform. In this case, the solution of the Smoluchowski equation states that the displacements δx = x(t + Δt) − x(t) over Δt follow a Gaussian distribution
 | (1) |
μ = ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) Δt, Δt, | (2) |
| σ2 = 2DΔt, | (3) |
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) is the drift velocity:
is the drift velocity:![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) = bF + ∇D. = bF + ∇D. | (4) |
| D = bkBT, | (5) |
The time evolution of the probability distribution for a constant force and diffusion coefficient is illustrated in Fig. 1a. From an experimental trajectory X = {x1,…,xN+1} with time interval Δt, F and D can be directly calculated from the mean and variance of the displacements, δxi = xi+1 − xi, according to eqn (2) and (3).
In contrast, the principle of MLA is to identify the set of dynamical parameters, α, that are most likely to describe an observed set of displacements, δ = {δxi}i=1…N. The likelihood 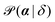 that α describes the observed displacements δ can be expanded as
that α describes the observed displacements δ can be expanded as
 | (6) |
Smoluchowski's theory provides the probability of observing a specific displacement given a set of parameters, p(δxi|α). Using Bayes' theorem, we can determine p(α|δxi):
 | (7) |
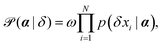 | (8) |
For numerical stability, it is more convenient to work with log-likelihood functions. For an observed trajectory X of corresponding set of displacements δ, we define the log-likelihood function of argument α as
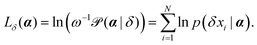 | (9) |
The determination of α = (F,D) from a single Brownian trajectory is illustrated in Fig. 1. A simulated trajectory for a room-temperature Brownian particle with D = 10−13 m2 s−1 and F = 50 fN is super-imposed over the probability distribution as the black curve in Fig. 1a. The log-likelihood landscape associated to this trajectory in the α = (F,D) phase space is plotted in Fig. 1b. The log-likelihood function is maximized at the appropriate values of F and D, as visible in Fig. 1b and mathematically supported in the ESI.†
The utility and limitations of this approach are made apparent in the following sections.
3 Illustrative examples
3.1 Experimental trajectory of a single particle with constant F and D
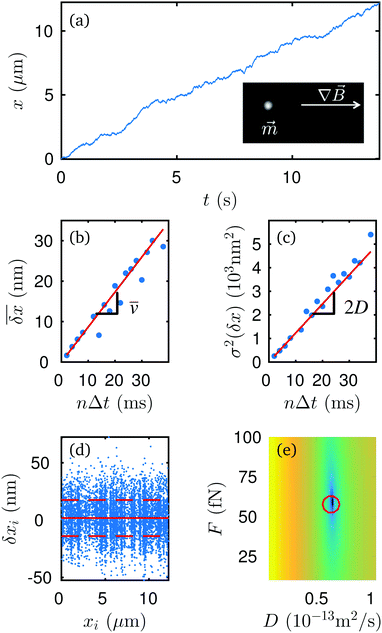
We compare measurements of the force and diffusion coefficient of a single Brownian particle using two different methods: (1) direct calculation of the time-dependent mean and variance of the trajectory,9 and (2) MLA. Paramagnetic spheres (2.8 μm diameter) are suspended in water and sediment against a glass coverslip. A permanent magnet is positioned next to the sample to create a locally uniform gradient of the magnetic field B along the x-direction. The field gradient drives the paramagnetic particle with constant external force. Further experimental details are provided in the ESI.† A representative trajectory, x(t), of the particle is shown in Fig. 2a. Here, the frame-to-frame time interval is Δt = 2 ms, and the exposure time is τex = 0.5 ms.From this trajectory, we calculate ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) (Fig. 2b) and D (Fig. 2c) from (respectively) the mean and variance of the displacements at different lag times δx = xi+n − xi = x(ti + nΔt) − x(ti). We obtain the following estimations: F = 58 ± 3 fN and D = 6.16 ± 0.14 × 10−14 m2 s−1.
(Fig. 2b) and D (Fig. 2c) from (respectively) the mean and variance of the displacements at different lag times δx = xi+n − xi = x(ti + nΔt) − x(ti). We obtain the following estimations: F = 58 ± 3 fN and D = 6.16 ± 0.14 × 10−14 m2 s−1.
Alternatively, we can apply MLA to the distribution of the frame-to-frame displacements {δxi = xi+1 − xi}, using parametrization α = (F,D). The results for the MLA fits of the mean and standard deviation are presented in Fig. 2d. The log-likelihood landscape for this trajectory in the (F,D) plane is represented in Fig. 2e. It shows a maximum at (F,D) = (59 ± 2 fN, 6.28 ± 0.15 × 10−14 m2 s−1), which corresponds to the values obtained from the conventional statistical analysis. This demonstrates that MLA is reliable in this simple case of constant F and D.
3.2 Simulated trajectories of pair interactions
We focus now on the more complex case of pair interactions. We assume that both the interparticle force, F, and the relative diffusion coefficient, D, depend on the center-to-center distance r (Fig. 3a-inset). We perform simulations corresponding to pairs of micron-sized particles interacting through capillary interaction with a rough contact-line. The force profile is given by| F(r) = −ϕ(x/a)−β, | (10) |
 | (11) |
 | ||
| Fig. 3 Testing MLA for spatially varying force and diffusion coefficients with simulated trajectories. (a) Sample trajectory (green line), and corresponding MLA fit (black line) from a simulation of colloidal spheres interacting via (inset) force F(r) and diffusion D(r) as described in eqn (10) and (11). (b) All simulated trajectories. Darker shades signify a higher density of curves. (c–f) Probability density function (PDF) of the fit parameters obtained from MLA. Red curves correspond to trajectories with Δt = 0.1 ms and τex = 0 ms. Blue curves correspond to trajectories with Δt = 4 ms and τex = 1 ms. (g and h) Fitted displacement (g) and force (h) profiles obtained from MLA for all trajectories. Black curves correspond to input profiles. | ||
We perform Ns = 1000 simulations with timestep of Δts = 0.1 ms. These trajectories depend on 4 parameters α = {ϕ, β, D0, R0}. The input values are {1.2 × 10−40 N, 5, 5.5 × 10−14 m2 s−1, 1 × 10−6 m}. A single simulated trajectory is shown in Fig. 3a, along with its corresponding MLA fit. It is important to note that due to the stochastic nature of Brownian motion, each trajectory is different. We plot a superposition of all trajectories in Fig. 3b to show this variability.
We estimate the underlying physical parameters for each trajectory using MLA. Details on the numerical optimization are given in the ESI.† As shown in Fig. 3c–f, MLA estimates (red histograms) agree very well with the input parameters (vertical black line). The spatial dependence of the particle displacements and the force are also accurately captured by MLA, as shown in Fig. 3g and h. The red bands are a super-position of all the fitted profiles, and the black lines show the input to the simulation. The estimated profiles match very well the input profiles, with most of the deviations not exceeding about 10% of the actual profiles. We discuss the effect of trajectory blurring, present in video microscopy experiments, on the accuracy of MLA estimates in Section 4.1.
These results show that MLA gives a very good estimation of the actual force profile and dynamic parameters for simulated trajectories.
3.3 Experimental trajectory of magnetic dipole–dipole pair interactions
We now investigate the reliability of MLA on experimental trajectories of isolated pairs of paramagnetic spheres in a magnetic field B. The magnetic field induces a magnetic dipole in both spheres, causing them to attract each other. Neglecting the mutual induced dipoles effect occurring at short distances, the interaction is well described by a power-law force (eqn (10)) with exponent18β = 4. Because the beads are heavy and sedimented, their hydrodynamic coupling should also include a contribution from the bottom surface of the observation chamber. For the diffusion coefficient of the separation, we use a three-parameter functional form:| D(r) = (Dr−1(r, D0, R0) + (Dh−1 − D0−1)/2)−1 | (12) |
We apply MLA to a pair trajectory using functional forms described in eqn (10) and (12), hence α = {ϕ, β, D0, R0, Dh}. The raw trajectory and displacement profile are shown in Fig. 4a and b. The fitted trajectory, diffusion profile and force profile are shown in Fig. 4a, c and d.
We investigate the reliability of the fits in two ways. First, we compare the diffusion profile obtained from this single trajectory to an independent measurement. Second, we look at how the MLA fit is modified when a few points of the trajectory are artificially removed: a robust fit ought to be resilient to small changes in the trajectory.
The displacements δri as a function of separation r for the part of the trajectory before contact (Fig. 4a, t ≤ 2.8 s) are presented in Fig. 4b. The large displacements at small separations (colored points in Fig. 4b) may be expected to dominate the force profile. To test this hypothesis, we manually removed some of these (ri, δri) points, and performed MLA of the truncated trajectories. The resulting force profiles are compared in Fig. 4d, where the full trajectory is dark red and the line colors approach yellow as the trajectory is more strongly truncated (the colors correspond to the last points included in Fig. 4b). Truncation of the data at small separations does change the estimated force profile, but the effects are very small (of the order of a few percents), even for the shortest trajectory (light yellow), where most of data points close to contact have been removed. This shows that MLA provides a robust fit, in the sense that small changes in a trajectory have only small effects on the results from the fit.
4 Practical considerations
In this section, we present some general guidelines regarding the practical implementation of MLA.4.1 Data acquisition
Experimental trajectories of Brownian particles are typically acquired using video microscopy, which involves two key temporal parameters: the frame-to-frame time interval Δt, and the exposure time τex. Finite exposure times are well known to cause systematic errors in the observed variance of displacements at short time intervals.22,23 To mimic realistic experimental conditions, we undersample and blur the simulated trajectories of Section 3.2. We use a readily accessible time interval Δt = 4 ms and an exposure time τex = 1 ms. (To emulate finite exposure times, we simply average the simulated positions over a 1 ms interval.) The results of MLA estimates of the parameters from these trajectories are shown as blue histograms in Fig. 3c–f. They agree reasonably well with the input parameters, with small but significant systematic errors. Similarly, blurring causes small but significant systematic errors in the displacement and force profiles, shown by the blue bands in Fig. 3g and h. The displacements tend to be more dispersed near contact, and the forces are systematically overestimated. To minimize these systematic errors due to finite camera exposure time, it is important that τex be significantly smaller than Δt. More generally, typical particle displacements over the considered time interval, Δt, should be large compared to uncertainties in measuring the particle displacement.4.2 Statistical error estimates
Statistical errors for a force profile obtained by MLA can be evaluated by simulating trajectories. Consider an experimental trajectory fitted using functional forms Fe(r) and De(r), where MLA has returned α0 as the most likely estimate of the parameters. One can then perform a Brownian dynamics simulation to simulate a large number of trajectories with the same time interval, length and spatial domains as the real experiments, using Fe(r), De(r), and α0. Each simulated trajectory can be analyzed to provide estimates of the parameters as well as the force and diffusion profiles. The spreads in these values and fits capture the statistical uncertainty on the MLA estimates. To illustrate, we plot in Fig. 5a the local density of force profile curves corresponding to the 1000 simulations described in Section 3.2. From this two-dimensional histogram, we can calculate the 5th and 95th percentiles at each separation r (black dashed lines), and hence recover a 90% confidence interval. The MATLAB code at the core of such analyses is included in the ESI.†4.3 Functional form choice and resilience
When the force and diffusion profiles vary with position, MLA requires functional forms for each. In some cases, these functional forms may be known exactly from the literature, but in other cases, they are not. In the latter case, one must use approximate functional forms F*(r) and D*(r). Reasonable ones can be chosen based on some basic knowledge of the underlying physics, such as continuity, monotony, and limiting behavior. To characterize the impact of using an incorrect but physically reasonable functional form, we analyzed trajectories from Section 3.2 using functional forms different from the ones used for the simulations, eqn (10) and (11). MLA estimates of the force profile using an incorrect force profile F*(r) = −ϕ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) exp(−r/β) are shown in Fig. 5b. Although they agree well with the input profile in the far-field, they significantly underestimate the force in the near-field. Similarly, estimates of the force profile using an incorrect functional form for the diffusion profile D*(r) = 2D0(1 − (3/2)r0/r), shown in Fig. 5c, lead to small but significant errors in the force estimate. However, in both cases we see that even with these wrong functional forms, the fitted force profiles remain essentially confined to the 90% confidence interval, except maybe at very small separations with the exponential force profile, where the fitted profiles are on average ∼20% below what they should be (Fig. 5b).
exp(−r/β) are shown in Fig. 5b. Although they agree well with the input profile in the far-field, they significantly underestimate the force in the near-field. Similarly, estimates of the force profile using an incorrect functional form for the diffusion profile D*(r) = 2D0(1 − (3/2)r0/r), shown in Fig. 5c, lead to small but significant errors in the force estimate. However, in both cases we see that even with these wrong functional forms, the fitted force profiles remain essentially confined to the 90% confidence interval, except maybe at very small separations with the exponential force profile, where the fitted profiles are on average ∼20% below what they should be (Fig. 5b).
5 Conclusions
Maximum likelihood analysis is a powerful method to extract forces and diffusion coefficients from individual Brownian trajectories. It is fast and easy to implement. Our numerical approach to MLA is particularly useful when the amount of data is limited and the force and diffusion profiles vary over space. It can be very efficient, achieving small statistical uncertainties with a modest amount of data, by exploiting the smooth spatial dependence of the force and diffusion profiles. It can be very accurate, when the correct forms for the spatial dependence are employed and the typical particle displacements are large compared to any static or dynamic particle locating errors.In this paper and our previous implementation of the method,15 we considered experimental trajectories of micron-sized colloidal particles. Fundamentally, this technique could also be employed with much smaller objects, such as fluorescently labeled proteins. Advanced microscopic techniques now allow for measurements of molecule positions with spacial resolution around 10 nm and time resolution better than 1 ms.24 However, due to photobleaching and other experimental difficulties, the recorded trajectories are typically very short, hence making the study of molecular interactions very difficult. We believe that extension of MLA in the domain of single molecule tracking could not only be useful for measuring diffusion coefficients, as already established, but also help to understand long-range interactions between biological components, hence clarifying the molecular cell processes which work by an interplay of diffusion and interaction.
This work was supported by the National Science Foundation (CBET 12-36086). We would like to thank Jason Merrill, Robert Style, and Larry Wilen for helpful discussions.
References
- N. A. Clark, J. A. Lunacek and G. B. Benedek, Am. J. Phys., 1970, 38, 575 CrossRef.
- B. J. Berne and R. Pecora, Dynamic Light Scattering, Dover Publications, Inc., Mineola, New York, 2000 Search PubMed.
- T. G. Mason, K. Ganesan, J. H. van Zanten, D. Wirtz and S. C. Kuo, Phys. Rev. Lett., 1997, 79, 3282 CrossRef CAS.
- Y. Roichman, B. Sun, Y. Roichman, J. Amato-Grill and D. G. Grier, Phys. Rev. Lett., 2008, 100, 013602 CrossRef PubMed.
- J. C. Crocker and D. G. Grier, Phys. Rev. Lett., 1994, 73, 352 CrossRef CAS PubMed.
- J. Perrin, Atoms, D. Van Nostrand company, New York, 1916 Search PubMed.
- D. C. Prieve and N. A. Frej, Langmuir, 1990, 6, 396 CrossRef CAS.
- S. Chandrasekhar, Rev. Mod. Phys., 1943, 15, 1 CrossRef.
- S. K. Sainis, V. Germain and E. R. Dufresne, Phys. Rev. Lett., 2007, 99, 018303 CrossRef PubMed.
- J. W. Merrill, S. K. Sainis, J. Bławzdziewicz and E. R. Dufresne, Soft Matter, 2010, 6, 2187 RSC.
- D. J. Evans, A. D. Hollingsworth and D. G. Grier, Phys. Rev. E, 2016, 93, 042612 CrossRef PubMed.
- A. J. Berglund, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 011917 CrossRef PubMed.
- X. Michalet and A. J. Berglund, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 061916 CrossRef PubMed.
- C. L. Vestergaard, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2016, 94, 022401 CrossRef PubMed.
- R. Sarfati and E. R. Dufresne, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2016, 94, 012604 CrossRef PubMed.
- D. Stamou, C. Duschl and D. Johannsmann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2000, 62, 5263 CrossRef CAS.
- P. L. Biancaniello and J. C. Crocker, Rev. Sci. Instrum., 2006, 77, 113702 CrossRef.
- D. Du, F. Toffoletto and S. L. Biswal, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 043306 CrossRef PubMed.
- E. R. Dufresne, T. M. Squires, M. P. Brenner and D. G. Grier, Phys. Rev. Lett., 2000, 85, 3317 CrossRef CAS PubMed.
- S. Bhattacharya, J. Bławzdziewicz and E. Wajnryb, Physica A, 2005, 356, 294 CrossRef.
- S. Bhattacharya, J. Bławzdziewicz and E. Wajnryb, J. Fluid Mech., 2005, 541, 263 CrossRef.
- W. P. Wong and K. Halvorsen, Opt. Express, 2006, 14, 12517 CrossRef PubMed.
- T. Savin and P. S. Doyle, Biophys. J., 2005, 88, 623 CrossRef CAS PubMed.
- A. Kusumi, T. A. Tsunoyama, K. M. Hirosawa, R. S. Kasai and T. K. Fujiwara, Nat. Chem. Biol., 2014, 10, 524–532 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Materials & methods, and mathematical derivations. See DOI: 10.1039/c7sm00174f |
| This journal is © The Royal Society of Chemistry 2017 |