Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
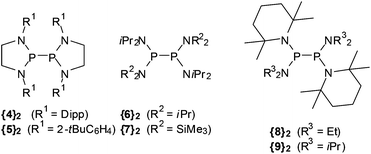
On the energetics of P–P bond dissociation of sterically strained tetraamino-diphosphanes†
M.
Blum
a,
O.
Puntigam
a,
S.
Plebst
a,
F.
Ehret
a,
J.
Bender
a,
M.
Nieger
b and
D.
Gudat
*a
aInstitut für Anorganische Chemie, University of Stuttgart, Pfaffenwaldring 55, 70550 Stuttgart, Germany. E-mail: gudat@iac.uni-stuttgart.de
bLaboratory of Inorganic Chemistry, Dept. of Chemistry, University of Helsinki, P.O. Box 55, 00014 University of Helsinki, Finland
First published on 28th August 2015
Abstract
The homolytic P–P bond fission in a series of sterically congested tetraaminodiphosphanes (R2N)2P–P(NR2)2 ({4}2–{9}2, two of which were newly synthesized and fully characterized) into diaminophosphanyl radicals (R2N)2P˙ (4–9) was monitored by VT EPR spectroscopy. Determination of the radical concentration from the EPR spectra permitted to calculate free dissociation energies ΔG295Diss as well as dissociation enthalpies ΔHDiss and entropies ΔSDiss, respectively. Large positive values of ΔG295Diss indicate that the degree of dissociation is in most cases low, and the concentration of persistent radicals – even if they are spectroscopically observable at ambient temperature – remains small. Appreciable dissociation was established only for the sterically highly congested acyclic derivative {9}2. Analysis of the trends in experimental data in connection with DFT studies indicate that radical formation is favoured by large entropy contributions and the energetic effect of structural relaxation (geometrical distortions and conformational changes in acyclic derivatives) in the radicals, and disfavoured by attractive dispersion forces. Comparison of the energetics of formation for CC-saturated N-heterocyclic diphosphanes and the 7π-radical 3c indicates that the effect of energetic stabilization by π-electron delocalization in the latter is visible, but stands back behind those of steric and entropic contributions. Evaluation of spectroscopic and computational data indicates that diaminophosphanyl radicals exhibit, in contrast to aminophosphenium cations, no strong energetic preference for a planar arrangement of the (R2N)2P unit.
Introduction
Kinetic stabilisation by sterically demanding substituents is an immensely useful concept which has played a key role in the advancement of modern organometallic and molecular inorganic chemistry and permitted the preparation of many new classes of isolable or persistent compounds.1 A distinct example of previously unknown, kinetically stabilised species in main-group element chemistry are long-lived neutral pnictyl radicals R2E˙ (E = P, As).2 The first specimens, 1 and 2 (Scheme 1), were generated in 1976 by Lappert et al. via reduction of chlorophosphane or chloroarsane precursors and identified as persistent radicals with half-lives t1/2 > 1 month at 20 °C by EPR spectroscopy.3 Building on this pioneering work, to date arsanyl and phosphanyl radicals with a wider selection of bulky alkyl, aryl or amino substituents have been characterized.4,5 | ||
| Scheme 1 Examples of persistent pnictyl radicals and a dimerization reaction under E–E bond formation. | ||
Apart from some recent reports on stable phosphanyl radicals that were isolated and fully characterized in the crystalline state,4f,h,i the monomers exist generally only in the gas phase or in solution but are dimerized when solid.4c,d,g,j,l,6 In several cases, temperature dependent equilibria between phosphanyl radicals and their dimers (Scheme 1) were detected spectroscopically in solution, and the observed prevalence of diphosphanes at low temperatures was interpreted as reflecting the gain in enthalpy and the loss in entropy associated with the dimerization under P–P bond formation.4c,e,g,j–l
Detailed studies on the structural aspects of the dimerization of persistent pnictyl radicals were performed on 1 and the N-heterocyclic phosphanyl radical 3c. Comparison of the molecular geometries of 1P, 1As (as determined by gas phase electron diffraction) and their dimers {(Me3Si)2CH}2E–E{CH(SiMe3)2}2 ({1P}2, E = P and {1As}2, E = As) revealed that the dimerization is accompanied by bond angle distortions in the alkyl groups and a reorientation of the CH(SiMe3)2 substituents in a R2E unit from a syn,syn-conformation in the radicals to a syn,anti-conformation in the dimers. Backed by computational studies,6,7 these changes were interpreted as indicating that the dimers in the crystal are loaded with a substantial amount of steric strain energy. The possibility to discharge the strain upon release of the molecule from the crystal lattice was seen as a strong driving force for the formation of monomers in solution or the gas phase, and led to a description of 1 as “Jack-in-the-box molecules”.6 In a recent computational analysis8 of the dimerization of 1 it was emphasized that a realistic description of the energetics of this process requires also the consideration of dispersion forces: neglecting dispersion, the energy required for P–P bond homolysis was predicted insufficient to offset the stabilizing effect of structural relaxation in the radicals, and it is only due to the dispersive attraction between the radicals that dimer formation is energetically favoured.
A different source of energetic stabilization was discussed for the N-heterocyclic radicals 3: based on a comparison of EPR hyperfine couplings to the 31P and 14N nuclei and computational evidence, Wright et al.4g concluded that the spin density is not mainly phosphorus-based as in other phosphanyl radicals, but rather delocalized over the heterocycle. They described these species consequently as 7π-radicals and postulated that their creation from the corresponding dimers should be facilitated by a combination of steric effects (repulsion between bulky substituents) and electronic stabilization by π-delocalization. In accord with this hypothesis, formation of persistent radicals 3c from dissociation of the isolable dimer {3c}2 was observed at exceedingly mild conditions (room temperature) in solution,4g and an experimental evaluation of the energetics of the P–P bond homolysis of the dimer {3c}2 gave a dissociation enthalpy ΔHDiss of 79 kJ mol−1,4k well below the average P–P bond enthalpy of 201 kJ mol−1.9 Computationally, the dissociation energies were greatly underestimated when dispersion forces were neglected (cf. an unrealistically low calculated dissociation energy of ≈3 kJ mol−1 for a N-Me substituted model dimer {3d}2),4g and overestimated when dispersion effects were included (cf. ΔHdiss,calc = 95.8 kJ mol−1 for {3d}2 and 129.9 kJ mol−1 for {3c}2 at the ωB97X-D/cc-pVDZ level of theory).4k
Summarizing the available knowledge on persistent phosphanyl (and arsanyl) radicals, it becomes clear that their common property is the stabilization against dimer formation or further reaction4k by sterically crowded substituents. The factors controlling this stabilization have been extensively studied for a few representatives (mainly 1), but there are still many open questions which address, e.g., the interplay of steric and electronic stabilizing effects in 3 and related cyclic or open diaminophosphanyl radicals. Improving our understanding of these factors is needed in order make better use of the still underdeveloped potential of the persistent radicals in synthesis, but also to deepen our insight into the reactivity and thermal stability of E–E-bonded frameworks, and the tuning of these qualities by steric strain. Furthermore, considering that the results of computational studies seem to depend strongly on the computational model applied,4g,k,8 an experiment based research approach seems highly desirable in order to provide an unbiased reference point. We report here on the extension of a previous experimental study on the dissociation energetics of the diphosphane {3c}2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4k to include compounds featuring both N-heterocyclic ({4}2, {5}2, Scheme 2) and acyclic ({6}2–{9}2) molecular frameworks, and a discussion of the results in the light of computational studies.
4k to include compounds featuring both N-heterocyclic ({4}2, {5}2, Scheme 2) and acyclic ({6}2–{9}2) molecular frameworks, and a discussion of the results in the light of computational studies.
Results and discussion
Synthesis and characterization of sterically crowded tetraaminodiphosphanes and diaminophosphanyl radicals
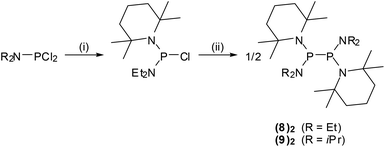
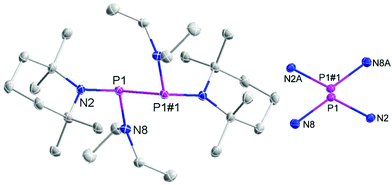
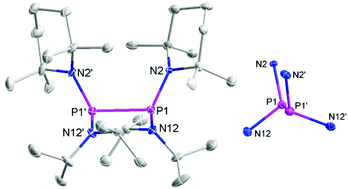
Diphosphanes {4}2–{6}2 were prepared by reductive coupling of appropriate chlorophosphane precursors using previously published procedures.4j,k,10 In case of {7}2, the reported protocol4c was modified by using sodium naphthalenide instead of potassium graphite as reducing agent. Finally, {8}2 and {9}2 were obtained analogously by reduction of the chlorophosphane precursors with magnesium or sodium (Scheme 3). Both new compounds were characterized by elemental analyses, spectral data, and single-crystal X-ray diffraction studies.‡The individual molecules in crystalline {8}2 (Fig. 1) display crystallographic Ci-symmetry and exhibit therefore a staggered conformation in which both the two R2P moieties as a whole and the two pairs of Et2N and TMP substituents are mutually trans to each other. The nitrogen atoms adopt planar or near planar coordination geometries (sum of bond angles 360.0(4)° at N8 and 353.5(4)° at N2), and the coordination planes around these atoms are strongly twisted with respect to the central NPN plane (skew angles§ 62° for the TMP and 80° for the Et2N substituent). The molecules in crystalline {9}2 feature a pseudo-ecliptic alignment of the R2P units (Fig. 2) in which the P–N bonds to the TMP substituents lie nearly in one plane (dihedral angle N(2)–P(1)–P(1′)–N(2′) 1.2(3)°) and the piperidine rings are adjacent to each other. The resulting arrangement comes close to C2-symmetry. As in {8}2, the coordination geometry at the nitrogen atoms is quasi-planar (sum of bond angles 357.0(9)–359.2(9)°). The skew angles between the NPN unit and the iPr2N-substituent of ca. 83° are similar as in {8}2 whereas the skew of the TMP ring is less pronounced (skew angles ca. 53°).
The P–P distance in {8}2 falls into the range known for other strained symmetrical diphosphanes (Table 1) whereas that in {9}2 exceeds even the longest distances reported so far (2.320–2.321 Å in {3c}2 and {4}2)4j,k by more than 3 pm. A reasonable explanation for the extreme bond lengthening may be seen in the pseudo-ecliptic conformation which is most likely enforced by the steric requirements of the substituents and maximizes the Pauli-repulsion between P–N bonds and lone-pairs¶ at adjacent phosphorus atoms.
The 31P spectra of {8}2 display two singlets with slightly unequal intensity, and the 1H and 13C NMR spectra contain two sets of signals of Et2N and tetramethylpiperidyl (TMP) substituents. Similar features had also been observed for {7}2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4c and indicate the presence of a mixture of meso- and rac-diastereomers with different stereochemical configuration at the phosphorus atoms in solution. A 31P NMR spectrum of {9}2 recorded at −80 °C shows likewise two signals which coalesce, however, to a single line at higher temperature. The 1H and 13C NMR spectra display also intricate temperature dependent coalescence phenomena. In addition, a new, extremely broad resonance (Δν1/2 = 7100 Hz at r.t., cf. Fig. S3 in the ESI†) grows in when the temperature is raised and reversibly disappears upon cooling. We attribute this signal to radical 9, the presence of which was independently proven by EPR spectroscopy (see below). Altogether, the observed spectral changes indicate the simultaneous occurrence of two dynamic processes, viz. reversible equilibration between {9}2 and two radicals 9 (which enables also interconversion between rac- and meso-{9}2), and freezing of the TMP ring inversion at low temperature. It should be noted that there is ample literature precedence for the spectroscopic observation of equilibration between persistent phosphanyl radicals and their dimers,4c,e,j–l but {9}2 is to the best of our knowledge the first example where the coexistence of both reactants has been established by NMR spectroscopy.
4c and indicate the presence of a mixture of meso- and rac-diastereomers with different stereochemical configuration at the phosphorus atoms in solution. A 31P NMR spectrum of {9}2 recorded at −80 °C shows likewise two signals which coalesce, however, to a single line at higher temperature. The 1H and 13C NMR spectra display also intricate temperature dependent coalescence phenomena. In addition, a new, extremely broad resonance (Δν1/2 = 7100 Hz at r.t., cf. Fig. S3 in the ESI†) grows in when the temperature is raised and reversibly disappears upon cooling. We attribute this signal to radical 9, the presence of which was independently proven by EPR spectroscopy (see below). Altogether, the observed spectral changes indicate the simultaneous occurrence of two dynamic processes, viz. reversible equilibration between {9}2 and two radicals 9 (which enables also interconversion between rac- and meso-{9}2), and freezing of the TMP ring inversion at low temperature. It should be noted that there is ample literature precedence for the spectroscopic observation of equilibration between persistent phosphanyl radicals and their dimers,4c,e,j–l but {9}2 is to the best of our knowledge the first example where the coexistence of both reactants has been established by NMR spectroscopy.
Direct characterization of radicals was feasible by recording EPR spectra of solutions of {4}2–{9}2 in inert solvents (hexane, toluene). The signals of the radicals were readily observed at ambient (4, 9) or elevated temperature (5–8) and analysed by simulation using the EasySpin12 program (Table 2).
| g | a(31P) [G] | a(14N)a [G] | Further splittingsa | Ref. | |
|---|---|---|---|---|---|
| a Number of interacting nuclear spins given in parentheses. b Published data from ref. 4a and c: g = 2.0046–2.007, a(31P) = 75.9–77.2 G, a(14N) = 5.2–5.95 G. | |||||
| 3c | 2.0248 | 42 | 5.4 (2 N) | — | 4g |
| 4 | 2.0031 | 60.9 | 3.7 (2 N) | a(1H) = 2.9 G (4 H) | 4j |
| 5 | 2.014 | 63.8 | 4.3 (2 N) | a(1H) = 3.8 G (2 H) | 4l |
| 6 | 2.0055 | 75.5 | 3.8 (2 N) | — | This work |
| 7 | 2.0047 | 76.2 | 5.6 (1 N) | a(29Si) = 12.2 G | This workb |
| 8 | 2.0045 | 83.5 | 5.8 (1 N) | a(1H) = 2.6 G (4 H) | This work |
| 9 | 2.0047 | 84.7 | 5.7 (1 N) | a(1H) = 1.2 G (2 H) | This work |
The spectral parameters of 4, 5 and 7 match previously published data.4a,c,j,l All signals are split into multiplets due to hyperfine coupling with the nuclear spins of the 31P (I = 1/2) and one (7–9) or two (4–6) 14N (I = 1) nuclei. In some cases, additional couplings to remote 1H or 29Si nuclei are resolved. The hyperfine couplings to phosphorus (60–84 G) are larger than in 3c (a(31P) = 42 G![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4k) and cover roughly the lower half of the range of couplings (63–108 G
4k) and cover roughly the lower half of the range of couplings (63–108 G![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2a) in known phosphanyl radicals. The absence of resolved hyperfine coupling to one 14N nucleus in 7 had been previously noted and was attributed to the fact that couplings to nitrogen atoms in silylamino-groups are usually unobservable,4a,c presumably since their steric bulk prevents a coplanar orientation of the phosphorus and nitrogen coordination planes.2a The spectra of 8, 9 reveal, however, that unequal a(14N) couplings are also observable in dialkylamino-substituted phosphanyl radicals and the absence of resolved coupling to 14N is thus not specific for silylamino groups.
2a) in known phosphanyl radicals. The absence of resolved hyperfine coupling to one 14N nucleus in 7 had been previously noted and was attributed to the fact that couplings to nitrogen atoms in silylamino-groups are usually unobservable,4a,c presumably since their steric bulk prevents a coplanar orientation of the phosphorus and nitrogen coordination planes.2a The spectra of 8, 9 reveal, however, that unequal a(14N) couplings are also observable in dialkylamino-substituted phosphanyl radicals and the absence of resolved coupling to 14N is thus not specific for silylamino groups.
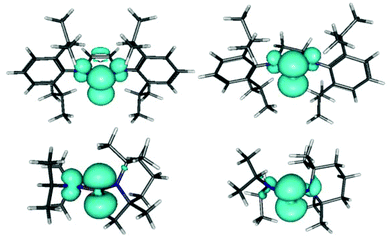
Computational studies on different conformers of 6–9 confirm the expectation2a,4a that the spin density resides mainly in the phosphorus p-orbital and reveal further that its delocalization on the nitrogen atoms shows a marked conformational dependence that is largely independent of substituent type (Fig. 3 and Table 3): maximum values of the spin density, and hence the hyperfine coupling constant (a(14N) 5–6 G), are found when the coordination planes at the phosphorus and nitrogen atoms are coplanar, and minimum values (|a(14N)| < 1 G) when they are close to perpendicular.
| a(31P)a [G] | a(14N)a,b [G] | Skew anglea [°] | ||
|---|---|---|---|---|
| a Numbers in parentheses denote the percentage of NPA spin density on the appropriate atom. b A plot of a(14N) vs. skew angle is shown in Fig. S2 in the ESI. c Two identical NR2 moieties. | ||||
| 3c | 56.4 (59) | 6.6 (18)c | 5c | |
| 4 | 75.9 (76) | 5.8 (11) | 8 | |
| 3.9 (11) | 9 | |||
| 5 | 74.6 (76) | 5.7 (11) | 5 | |
| 5.5 (10) | 8 | |||
| 6 | 77.2 (76) | 5.1 (10)c | 44c | |
| 7 | NiPr2 | 81.1 (77) | 5.9 (18) | 21 |
| N(SiMe3)2 | 0.4 (1) | 73 | ||
| 8 | NEt2 | 96.5 (80) | 5.9 (14) | 16 |
| TMP | −0.8 (1) | 82 | ||
| 9 | NiPr2 | 87.7 (86) | 6.1 (6) | 15 |
| TMP | −1.1 (2) | 82 | ||
Based on this correlation, we can confirm the association of the large hyperfine coupling in 7 with the NiPr2 group4a,c and conclude further that the splittings in the spectra of 8,9 arise from interaction with the NR2 (R = Et, iPr) groups and the coupling to the TMP substituent is unresolved. The observation that a(14N) in 4–6 is smaller than in 7–9 (Table 2) may be attributable to the presence of librational motion of the R2N-groups in the real molecules which cannot be reproduced computationally. However, the calculations support the earlier conjecture4g that the reduction of a(31P) and simultaneous increase of a(14N) in 3c coincides with extended delocalization of the spin density over the complete ring (Fig. 3).
Thermochemistry of diphosphane dissociation
Thermochemical parameters for the dissociation of the diphosphanes according to R2P–PR2 ⇄ 2 R2P˙ may be derived from the temperature dependent variation of the equilibrium constant K = c(R2P˙)2/c(R2P–PR2). The latter can be determined by measuring the radical concentration in a sample prepared by dissolution of a known amount of solid diphosphane, and then back-calculating the actual concentration of the diphosphane in solution. The radical concentration is readily obtained from the double integral of the EPR signal in relation to that of a reference sample with a known number of spins.12 Following this approach, we determined the concentration of radicals 4–9 in solutions of {4}2–{9}2 against a calibrated sample of ultramarine blue by using a previously published procedure.4k A summary of the thermochemical parameters derived from these measurements is given in Table 4, and a detailed account is contained in the ESI.†| Diphosphane | ΔG295Diss [kJ mol−1] | pK295Diss![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
ΔHDiss [kJ mol−1] | ΔSDiss [J (mol K)−1] |
|---|---|---|---|---|
| a pK295Diss = −lg(KDiss(295 K)/[mol l−1]). b Data from ref. 4k. | ||||
{3c}2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
26.8(8) | 4.8(8) | 78.8(8) | 176(15) |
| {4}2 | 69.4(21) | 12.3(22) | 102.3(11) | 112(4) |
| {5}2 | 88.6(17) | 15.7(28) | 104.9(10) | 55(3) |
| {6}2 | 70.2(21) | 12.4(4) | 108.9(12) | 131(4) |
| {7}2 | 69.6(28) | 12.3(5) | 95.4(14) | 87(5) |
| {8}2 | 66.9(23) | 11.9(4) | 99.5(12) | 110(4) |
| {9}2 | 13(7) | 2.3(12) | 64.2(30) | 174(13) |
Evaluation of the data in Table 4 reveals that although the radicals 4–9 are spectroscopically readily observable as persistent species at ambient or elevated temperature, the dissociation equilibria lie in all cases but {9}2 extensively on the side of the diphosphanes, and the dissociation affects generally far less than 1% of the dimers even at temperatures as high as 120 °C. In case of {9}2, the calculated degree of dissociation for a solution of 1 mM initial concentration of 0.65(5) at 295 K clearly exceeds the value of 0.063(7) for 3c, and attests that radicals predominate under these conditions.
The observation of a large variability in ΔHDiss and ΔSDiss reveals, however, that structural changes have nonetheless a significant impact on the energetics of the bond fission. Comparing the dissociation energetics of {4}2 and {5}2 with that of {3c}2 shows that introduction of the CC double bond goes along with a decrease in ΔHDiss by some 23–25 kJ mol−1. In view of the presence of identical or at least similar substituents in all species, attractive dispersion forces between the two R2P fragments in the dimers are not expected to change greatly, and the lower dissociation enthalpy for {3c}2 is thus considered to reflect mainly the postulated4g extra stabilization of radical 3c by π-delocalization effects.
It should be noted, however, that the exceptional dissociation tendency of {3c}2 (as evidenced by the drastic decrease of ΔG295Diss as compared to {4}2 and {5}2) is not attributable to the enthalpy lowering alone, but is assisted by a simultaneous large increase in the entropic term. Since the translational contribution to the reaction entropy is identical in all cases, this change implies that the loss of internal conformational flexibility associated with radical dimerization must increase significantly from 5 over 4 to 3c. Without going into detail, we presume that the difference between the last two species owes to the rigidity of the unsaturated heterocyclic ring in 3c, which severely reduces the conformational freedom of the N-aryl groups. The further shift of the dissociation equilibrium to the side of the dimer in case of {5}2 is exclusively attributable to the change in ΔSDiss and may be qualitatively explained by assuming that the restrictions in the conformational freedom upon dimerization decrease with the number of bulky o-alkyl substituents in the N-aryl moieties.
Aggravating conformational restrictions with increasing steric demand of substituents may also help to rationalize the observation that the values of ΔSDiss in the acyclic diphosphanes {7}2–{9}2 exhibit comparable changes as in the heterocycles 3c–5. Apart from that, the dissociation enthalpies are for {7}2, {8}2 by some 5–10 kJ mol−1 lower than for {4}2, {5}2, and display a further sharp decrease in case of {9}2 where ΔHDiss is even smaller than for {3c}2. While this last finding is deemed to reflect the exceptional degree of strain that had already become evident in the extreme P–P bond lengthening and enforcement of the energetically unfavourable pseudo-ecliptic conformation, the reason for the low dissociation enthalpies in {7}2 and {8}2 is at first glance less obvious. We assume, however, that their increased conformational flexibility enables the acyclic (R2N)2P moieties to yield to the steric congestion upon dimerization as in the case of {1P}2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 and {7}2
6 and {7}2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4d by a distortion of dihedral angles that loads the dimers with some extra steric strain energy. Since the release of this energy during dissociation in a “Jack-in-the-box” manner6 amounts to a relative stabilization of the radicals, this effect is suitable to explain the reduction of ΔHDiss in comparison to the cyclic derivatives where the conformational constraints of the ring render such structural relaxation unfeasible.
4d by a distortion of dihedral angles that loads the dimers with some extra steric strain energy. Since the release of this energy during dissociation in a “Jack-in-the-box” manner6 amounts to a relative stabilization of the radicals, this effect is suitable to explain the reduction of ΔHDiss in comparison to the cyclic derivatives where the conformational constraints of the ring render such structural relaxation unfeasible.
Last, but not least, {6}2 shows the largest value of ΔHDiss of all derivatives in this study which is, however, compensated by an unusually high entropic contribution that must be seen as main driving force of the dissociation. Whereas the large dissociation enthalpy is not unexpected if one considers that the moderately sized N-alkyl groups seem inappropriate for loading the dimer with a large amount of strain energy, we have currently no good explanation for the atypically large entropy term.
Computational studies
In order to validate our hypotheses on the origin of the trends in dissociation enthalpies and improve our understanding of the bond fission process, we performed computational studies of the dissociation reactions of {4}2–{9}2. Acknowledging that a realistic description of molecular structures and energetics requires inclusion of long-range and dispersion interactions,4k,8 all calculations were carried out at the ωB97x-D/cc-pVDZ level which had been previously shown to give an appropriate description of the molecular structure of {3c}2.4k Molecular geometries of dimers and radicals were first energy optimized using the solid-state structures as starting points, and the nature of the final geometries as local minima on the energy hypersurface was then validated by frequency calculations. In case of the radicals 7–9 and the diphosphanes {4}2, {6}2, and {8}2, we located alternative conformers that were likewise local minima on the energy hypersurface but proved energetically less stable (ΔE 19.5 kJ mol−1 for trans-{4}2vs. gauche-{4}2, 65.9 kJ mol−1 for trans-{6}2vs. gauche-{6}2, and 13.2 kJ mol−1 for gauche-{8}2vs. trans-{4}2) and were not considered further. Computed and experimental geometries of the dimers are generally in good agreement, with the single exception that the P–P distance in {4}2 is significantly overestimated. Comparison of calculated (Table 5) and experimental (Table 1) P–P distances for the remaining compounds yields a liner relation P–Pcalc = 0.95 P–Pexp + 0.11 Å (R2 = 0.93). The computations reproduce also the molecular conformation of 7 determined by gas phase electron diffraction.4d Comparing the geometries of the (R2N)2P units in radicals and diphosphanes reveals that formation of N-heterocyclic radicals is mainly associated with a deformation of bond angles at the nitrogen atoms, whereas formation of acyclic species involves also appreciable conformational changes (see Fig. S12†).| P–P | ΔEzpe | ΔErelax | ΔEfrag |
E
D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
ΔH298 | ΔG298 | |
|---|---|---|---|---|---|---|---|
| a E D = contribution from empirical dispersion terms. b Data from ref. 4k. | |||||||
| {3c}2 | 3.323b | 120.5b | 59.5 | 196.4 | 153.3 | 129.9b | 5.9b |
| {4}2 | 2.317 | 155.3 | 41.2 | 208.9 | 147.1 | 158.4 | 66.4 |
| {5}2 | 2.301 | 156.8 | 51.4 | 219.2 | 100.9 | 157.4 | 79.7 |
| {6}2 | 2.296 | 119.0 | 79.9 | 214.8 | 79.8 | 123.3 | 39.0 |
| {7}2 | 2.278 | 98.6 | 106.4 | 234.8 | 102.2 | 105.6 | 9.5 |
| {8}2 | 2.296 | 85.5 | 121.7 | 223.2 | 75.8 | 19.9 | 0.4 |
| {9}2 | 2.348 | 51.5 | 121.3 | 193.8 | 97.3 | 10.3 | −9.4 |
Energies (including corrections for zero point vibrational energy, ΔEzpe) and (free) enthalpies (ΔH298, ΔG298) for the dissociation reactions were computed with the inclusion of basis set superposition errors as determined from counterpoise calculations and are listed in Table 5. In addition, we computed also a decomposition13 of the total reaction energy into a fragmentation energy ΔEfrag (the negative of the interaction energy13Eint between two radical fragments having the same geometry as the R2P units in the dimer) and a relaxation energy ΔErelax (the energy released upon relaxation of the distorted radicals to their equilibrium geometry, i.e. the negative of the preparation energy13 ΔEprep).
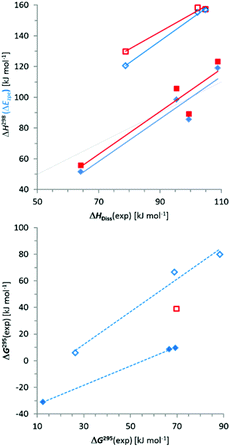
Comparison of absolute values and trends in computed (ΔH298) and experimental (ΔHDiss) dissociation enthalpies (Fig. 4) reveals a reasonable match for N-alkyl-/silyl-substituted diphosphanes ({6}2–{9}2) while the dissociation enthalpies of N-aryl derivatives ({3c}2–{5}2) are clearly overestimated in the computations (as had already been noted for 3c4k).|| A similar result emerges for comparison of ΔEzpe with ΔHDiss (Fig. 4). While it is known that most density functionals have problems with a proper description of the difference in intermolecular binding energies between aromatic and aliphatic moieties,14 a deviation of some 50 kJ mol−1 as found here is far too large to refer to this explanation, and we are currently unable to provide a consistent rationalization for this effect.
Computed free enthalpies ΔG298 (Table 5) are generally much smaller than the experimental values (Table 4), which is mainly due to the fact that the computations heavily overestimate the entropy terms. This deviation may in part reflect the difference between gas phase and solution (it has been claimed that the entropy contribution to ΔG in solution at room temperature is roughly half of that in the gas phase15) and had been noted previously.4k With the exception of {6}2, which we consider an outlier, a comparison between computed and experimental free enthalpies gives a similar result as had already been observed for the enthalpies (Fig. 4).
The results of the energy decomposition analysis listed in Table 5 indicate that the variations in ΔEfrag are not only much smaller than those of the total energy term (ΔEzpe or ΔH298), but show also a different response to structural changes. With the exception of {3c}2 (where a contribution from electronic stabilization by π-delocalization must be taken into account), ΔEfrag in both N-heterocyclic and acylic compounds dwindles with increasing steric demand of the substituents, which suggests that its variation reflects mainly the bond weakening or strengthening associated with the modulation of repulsive interactions between bulky peripheral groups. Given that the P–P bond lengthening in sterically congested diphosphanes is commonly ascribed to the same origin,8 it is not surprising that the changes in ΔEfrag – unlike those in the total energy terms (ΔEzpe or ΔH298) or experimentally determined enthalpies ΔHDiss – correlate with the variation in P–P distances (Fig. 5). Even if a clear-cut partitioning between ‘intrinsic’ bond energy and strain energy in congested molecules is not a trivial task,7 we conclude that ΔEfrag can serve as an – at least approximate – measure of P–P bond strength. Since the values of ΔEfrag come close to the average P–P bond enthalpy9 of 201 kJ mol−1 and approach the dissociation energies of sterically uncongested diphosphanes (239–368 kJ mol−1 for R2P–PR2 with R = H, Et, F, Cl, I16), the P–P bonds in {3c}2–{9}2 cannot be considered as intrinsically particularly weak. It must be conceded, however, that as in case of 18 attractive dispersion forces (epitomized by the empirical dispersion term ED) make a considerable contribution to the total adhesion energy. This contribution is clearly dominant for {3c}2 and {4}2 where it represents 70–80% of the fragmentation energy.
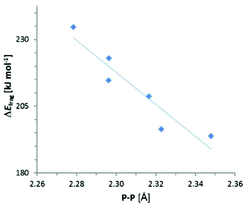 | ||
| Fig. 5 Plot of computed fragmentation energies ΔEfragvs. bond distances. The straight line is the result of a linear regression analysis (R2 = 0.89). | ||
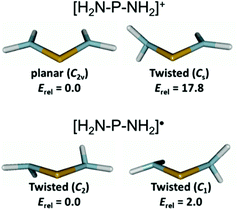
The relaxation energies ΔErelax which stabilize the radicals 3c–9 through structural adaptation and conformation changes are, like in 1P,8 smaller than the fragmentation energies, but with 20–60% of the magnitude of ΔEfrag still substantial. Furthermore, the variation between different radicals (ΔΔErelax = 80.5 kJ mol−1) is twice as large as that of the fragmentation energies (ΔΔEfrag = 41.0 kJ mol−1) and must thus be seen as the dominant energetic contribution in explaining the trend in dissociation energies between different diphosphanes. Structural relaxation of the acyclic radicals 6–9 provides generally a larger energy release (ΔErelax 80–122 kJ mol−1) than relaxation of the N-heterocyclic species 3c–5 (ΔErelax 41–60 kJ mol−1) and is associated with additional conformational changes (Fig. S12 in the ESI†). These findings support at first glance the perception of the dimers {6}2–{9}2 as sterically strained “Jack-in-the-box” molecules which can release their strain energy by undergoing geometrical and conformational adaptation during dissociation. However, we must also consider that the variation in skew angles or the pyramidalization of NR2 groups associated with a conformational change may affect the spin density delocalization, and thus the electronic stability, of the radicals. In order to assess the importance of these effects, we analysed the conformational preferences of the parent diaminophosphanyl radical (H2N)2P˙ (10˙) and the appropriate cation [(H2N)2P+] (10+), assuming that the impact of steric constraints is in these species negligible and any changes will be dominated by electronic effects. Geometry optimizations were carried out using DFT (B3LYP with (aug)-cc-pVDZ and aug-cc-pVTZ basis sets) and coupled cluster (CCSD/aug-cc-pvdz) methods. The results did not differ significantly, and we will only discuss those of the CCSD calculations (Fig. 6).
The cation 10+ exhibits, as expected, a C2v-symmetrical planar geometry with rather short PN distances of 1.643 Å. Geometry optimization of a conformer obtained by rotation of one NH2 group by 90° led to the localization of a transition state 17.8 kJ mol−1 higher in energy than the ground state. The ‘orthogonal’ amino substituent is characterized by a lengthened PN bond (1.715 vs. 1.632 Å for the ‘in plane’ NH2 group) and a slightly pyramidal geometry at the N-atom. The computational results are in accord with the established view of aminophosphenium ions17,18 as delocalized, allyl-anion analogue π-systems in which rotation of NR2 groups (which partially disrupts the π-delocalization) is impeded by a significant energy barrier. In contrast, radical 10˙ features a non-planar, C2-symmetrical ground state geometry with twisted orientation of the NH2 groups (skew angle 30°), pyramidal coordination at the N-atoms (sum of bond angles 343°) and lengthened PN bonds (1.752 Å). The search for a rotational transition state yielded a C1-symmetrical geometry in which the average PN distance remains essentially unchanged (PN 1.773, 1.737 Å, average 1.755 Å) and the pyramidalization in the ‘orthogonal’ NH2 group increases further (sum of bond angles at N 331°). The transition state energy lies by merely 2.0 kJ mol−1 above that of the ground state, indicating that the energetic barrier to NH2-group rotation is negligible and the geometrical changes associated with this process do not affect radical stability. This pronounced difference to the cation is easily rationalized if one considers that placement of an extra electron in the (PN-antibonding) LUMO of the cation reduces the π-bond order, and thus the available stabilization from π-delocalization. Consequently, the remaining interaction between an unpaired electron on the P-atom and the nitrogen lone-pairs in aminophosphanyl radicals should be better described as hyperconjugative, and its tuning by rotational reorientation of NH2 (or NR2) groups offers – unlike as in aminophosphenium ions17 – only minor opportunities for electronic (de)stabilization.
The computational studies on 10+ and 10˙ imply that the orientational preorganisation of phosphorus p-orbitals and nitrogen lone-pairs which arises from embedding of an NPN into a five-membered heterocycle18,19 offers an energetic advantage for aminophosphenium cations, but not for radicals, and that the NPN unit of the latter provides, apart from possible constraints imposed by a cyclic molecular structure, no further restoring force to maintain local planarity. We are thus prompted to conclude that the structural reorganization of the radicals formed during dissociation of tetraamino-diphosphanes is not associated with any extra electronic stabilization of the unpaired electron, but is essentially driven by steric factors. In turn, the inhibition of structural relaxation by a geometrical constraining cyclic structure must be considered to have an adverse effect on dissociation enthalpies, which helps to explain why P–P bond fission is slightly more endothermic for the heterocyclic dimers {3c}2–{5}2 than for {7}2–{9}2.
Conclusions
Thermochemical data for the homolytic P–P bond fission of a series of sterically congested diphosphanes (two of which were newly synthesized and fully characterized) were determined. The values of free reaction energies ΔG295Diss and pK295Diss indicate that the dissociation affects in most cases only a small fraction of the diphosphanes, and the concentration of persistent radicals – even if they may be spectroscopically observable at ambient temperature – remains small. A notable exemption is {9}2 where the degree of dissociation (for a 1 mM solution at 295 K) is by an order of magnitude larger than for the N-heterocyclic diphosphane {3c}2. The acyclic radical 9 must thus be considered as even more stable than 3c which benefits from electronic stabilization by π-delocalization.4gAnalysis of trends in experimental data in connection with computational studies allowed us to relate the variations in ΔG295Diss/pK295Diss to both enthalpy and entropy effects. Stabilization of radicals relative to dimers with a concomitant decrease in dissociation enthalpies ΔHDiss is mainly due to structural relaxation (adaptation of bond angles and – for the acyclic species 6–9 – conformational changes) and driven by the need to minimize steric congestion. Electronic stabilization by P,N-π-conjugation, which is crucial for aminophosphenium cations,17,18 is hardly of importance for aminophosphanyl radicals, and the energetic effect of cyclic π-delocalization in 3c is visible but stands back. The radical stabilizing influences are offset by strong attractive dispersion forces, which are once more8 confirmed as crucial for the prevalence of diphosphanes. Entropic factors driving the dissociation can be qualitatively related to the gain of conformational flexibility in the radicals, although their origin is not yet understood in detail and cannot be adequately modelled computationally. Still, the supplement of the enthalpic stabilization of the radicals by a particularly large entropic contribution must be seen as decisive for the extensive dissociation of {9}2 (and {3c}2).
It should be noted that our results are in principle in accord with the results of a computational study on the dimerization of the radicals 18 stating that the monomer – dimer equilibrium is predominantly governed by the balance of attractive dispersion forces and entropic factors. However, the results presented here emphasize that the different aspects of structural relaxation (in particular the conformational changes enabling “Jack-in-the-box” behaviour6) are also vital for the explanation of the trends in dissociation enthalpies and entropies between different molecules. Furthermore, it appears that computational models tend to overestimate the entropy term associated with the diphosphane dissociation, and yield thus free reaction energies which are systematically too low.
Experimental
Materials and methods
All manipulations were carried out under dry argon. Solvents were dried by standard procedures. NMR spectra were recorded on Bruker Avance AV 400 or AV 250 instruments (1H: 400.1/250.0 MHz, 13C: 100.5/62.9 MHz, 31P: 161.9/101.2 MHz); chemical shifts were referenced to ext. TMS (1H, 13C), 85% H3PO4 (Ξ = 40.480747 MHz, 31P). Elemental analyses were carried out using an Elementar Micro Cube. Melting Points were determined with a Büchi B-545 melting point apparatus in sealed capillaries. EPR spectra were measured with a Bruker EMX X-band spectrometer. Hyperfine splittings were determined by spectral simulation with the program EasySpin.12 Quantitative EPR measurements and evaluation of thermochemical data from the spectral data were carried out using the same protocol that had been applied in case of {3c}2. A detailed description has been given elsewhere.4kChlorophosphane precursors (iPr2NPCl2,19 (Me3Si)2N(iPr2N)PCl,4a (iPr2N)2PCl,20 and (TMP)(iPr2N)PCl21) and the diphosphanes {4}2,4j {5}2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4l and {6}2,10 were prepared as described elsewhere. Diphosphane {7}2 was prepared by a modification of the reported procdure,4c using sodium naphthalenide instead of potassium graphite as reducing agent.
4l and {6}2,10 were prepared as described elsewhere. Diphosphane {7}2 was prepared by a modification of the reported procdure,4c using sodium naphthalenide instead of potassium graphite as reducing agent.
Synthetic procedures
Crystal structure determinations
Diffraction studies were carried out using a Bruker diffractometer equipped with an Kappa APEX II Duo CCD-detector and a KRYO-FLEX cooling device with Mo-Kα radiation (λ = 0.71073 Å) at T = 100 K. The structures were solved by direct methods (SHELXS-9722a) and refined with a full-matrix least-squares scheme on F2 (SHELXL-201422b). Semi-empirical absorption corrections were applied for all structures. Non-hydrogen atoms were refined anisotropically, and H atoms with a riding model, on F2. Details of the crystal structure determinations are listed in Table 6. For {9}2, the absolute structure parameter22c was refined as x = 0.00(10). Details of the crystal structure determinations are listed in Table 6 (for 9_Cl in the ESI†).| {8}2 | {9}2 | |
|---|---|---|
| CCDC | 1414815 | 1414816 |
| Formula | C26H56N4P2 | C30H64N4P2 |
| Formula weight | 486.69 | 542.79 |
| Crystal size (mm) | 0.21 × 0.08 × 0.07 | 0.12 × 0.11 × 0.10 |
| T [K] | 100(2) | 100(2) |
| Crystal system | Monoclinic | Orthorhombic |
| Space group | P21/n | P21212 |
| a (Å) | 8.3594(6) | 16.522(2) |
| b (Å) | 9.0786(6) | 17.526(2) |
| c (Å) | 18.6456(12) | 11.2185(15) |
| β (°) | β = 92.968(3) | 90 |
| V (Å3) | 1413.15(17) | 3248.5(7) |
| Density (Mg m−3) | 1.144 | 1.110 |
| F(000) | 540 | 1208 |
| Z | 2 | 4 |
| Abs. coeff. μ (mm−1) | 0.174 | 0.158 |
| Absorption correction | Semiempirical from equivalents | Numerical |
| Data collected | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 704 704 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 756 756 |
| Unique data | 2901 | 5756 |
| Observed data with I > 2σ(I) | 2248 | 3419 |
| Restraints | 0 | 0 |
| Variables | 145 | 325 |
| R 1 (I > 2σ(I)) | 0.041 | 0.066 |
| wR2 | 0.108 | 0.113 |
| GOF | 1.034 | 0.992 |
| Max. diff. dens. (e Å−3) | 0.483 | 0.329 |
| Min. diff. dens. (e Å−3) | −0.302 | −0.313 |
Computational studies
Computational studies were performed with the Gaussian0923 suite of programs. Computations on 4–9 and {4}2–{9}2 were carried out using the ωB97X-D functional by Head-Gordon24 with cc-pVDZ basis sets. Explorative calculations were also carried out with Truhlar's M06-2X functional25 and the same basis. Attempts to use larger basis sets (i.e. including diffuse funtions or of triple zeta quality) failed due to numerical or computation time problems. Numerical integrations were performed on an ultrafine grid. Since an attempt to model the dissociation of {6}2 in solution showed that inclusion of solvent effects by a PCM model had no significant effect (ΔΔEzpe < 3 kJ mol−1 for the reaction and <3.3 kJ mol−1 for individual reactants), we further resigned from using a solvation model. Molecular structures were first energy optimized without symmetry constraints using the XRD data as starting points. Harmonic frequencies and zero-point energies (ZPE) at optimized gas phase structures were calculated at the same levels and showed all molecular geometries to present local minima (only positive eigenvalues of the Hessian matrix) on the potential energy surface. Energies (including vibrational zero-point correction), enthalpies, and free enthalpies calculated for the dissociation reactions are corrected for basis set superposition errors (BSSE), the necessary corrections being obtained by counterpoise calculations. Computations on 10+/10˙ were carried out at the B3LYP/(aug)-cc-pVDZ and CCSD/(aug)-cc-pVDZ levels; both approaches gave similar results, and only the CCSD results will be discussed. MOLDEN26 and GABEDIT27 were used for visualization, and NPA spin densities were computed with the program AOMIX.28Acknowledgements
We the bw-grid project29 for computational resources and Dr W. Frey (Institute of Organic Chemistry, University of Stuttgart) for the collection of X-ray data sets.Notes and references
- P. P. Power, J. Organomet. Chem., 2004, 689, 3904 CrossRef CAS.
- For reviews on this topic, see: (a) P. P. Power, Chem. Rev., 2003, 103, 789 CrossRef CAS PubMed; (b) C. D. Martin, M. Soleilhavoup and G. Bertrand, Chem. Sci., 2013, 4, 3020 RSC.
- M. J. S. Gynane, A. Hudson, M. F. Lappert, P. P. Power and H. J. Goldwhite, Chem. Soc., Chem. Commun., 1976, 623 RSC.
- (a) M. J. S. Gynane, A. Hudson, M. F. Lappert, P. P. Power and H. Goldwhite, Dalton Trans., 1980, 2428 RSC; (b) B. Cetinkaya, A. Hudson, M. F. Lappert and H. Goldwhite, J. Chem. Soc., Chem. Commun., 1982, 609 RSC; (c) J.-P. Bezombes, P. B. Hitchcock, M. F. Lappert and J. E. Nycz, Dalton Trans., 2004, 499 RSC; (d) J.-P. Bezombes, K. B. Borisenko, P. B. Hitchcock, M. F. Lappert, J. E. Nycz, D. W. H. Rankin and H. E. Robertson, Dalton Trans., 2004, 1980 RSC; (e) A. Dumtrescu, V. L. Rudzench, V. D. Romanenko, A. Mari, W. W. Schoeller, D. Bourissou and G. Bertrand, Inorg. Chem., 2004, 43, 6546 CrossRef PubMed; (f) P. Agarwal, N. A. Piro, K. Meyer, P. Müller and C. C. Cummins, Angew. Chem., Int. Ed., 2007, 46, 3111 CrossRef CAS PubMed; (g) R. Edge, R. J. Less, E. J. L. McInnes, K. Müther, V. Naseri, J. M. Rawson and D. S. Wright, Chem. Commun., 2009, 1691 RSC; (h) S. Ishida, F. Hirakawa and T. Iwamoto, J. Am. Chem. Soc., 2011, 133, 12968 CrossRef CAS PubMed; (i) O. Back, B. Donnadieu, M. van Hopffgarten, S. Klein, R. Tonner, G. Frenking and G. Bertrand, Chem. Sci., 2011, 2, 858 RSC; (j) N. A. Giffin, A. D. Hendsbee, L. L. Roemmele, M. D. Lumsden, C. C. Pye and J. D. Masuda, Inorg. Chem., 2012, 51, 837 CrossRef PubMed; (k) D. Förster, H. Dilger, F. Ehret, M. Nieger and D. Gudat, Eur. J. Inorg. Chem., 2012, 3989 CrossRef; (l) O. Puntigam, D. Förster, N. A. Giffin, S. Burck, J. Bender, F. Ehret, A. D. Hendsbee, M. Nieger, J. D. Masuda and D. Gudat, Eur. J. Inorg. Chem., 2013, 2041 CrossRef CAS.
- For a persistent phosphanyl radical stabilised by bulky aryl and phosphanyl groups see: (a) M. Cattani-Lorente and M. Geoffroy, J. Chem. Phys., 1989, 91, 1498 CrossRef CAS; (b) S. Loss, A. Magistrato, L. Cataldo, S. Hoffmann, M. Geoffroy, U. Röthlisberger and H. Grützmacher, Angew. Chem., Int. Ed., 2001, 40, 723 CrossRef CAS.
- (a) S. L. Hinchley, C. A. Morrison, D. W. H. Rankin, C. L. B. Macdonald, R. J. Wiacek, A. H. Cowley, M. F. Lappert, G. Gundersen, J. A. C. Clyburne and P. P. Power, Chem. Commun., 2000, 2045 RSC; (b) S. L. Hinchley, C. A. Morrison, D. W. H. Rankin, C. L. B. Macdonald, R. J. Wiacek, A. Voigt, A. H. Cowley, M. F. Lappert, G. Gundersen, J. A. C. Clyburne and P. P. Power, J. Am. Chem. Soc., 2001, 123, 9045 CrossRef CAS PubMed.
- K. B. Borisenko and D. W. H. Rankin, Inorg. Chem., 2003, 42, 7129 CrossRef CAS PubMed.
- J.-D. Guo, S. Nagase and P. P. Power, Organometallics, 2015, 34, 2028 CrossRef CAS.
- W. Kutzelnigg, Angew. Chem., Int. Ed. Engl., 1984, 96, 262 CAS.
- H. R. G. Bender, E. Niecke, M. Nieger and H. Westermann, Z. Anorg. Allg. Chem., 1994, 620, 1194 CrossRef CAS.
- R. Grubba, Ł. Ponikiewski, J. Chojnacki and J. Pikies, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2009, 65, o2214 CrossRef CAS PubMed.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42 CrossRef CAS PubMed; G. R. Eaton, S. S. Eaton, D. P. Barr and R. T. Weber, in Quantitative EPR – A practitioner's guide, Springer, Wien, 2010 Search PubMed.
- (a) K. Kitaura and K. Morokuma, Int. J. Quantum Chem., 1976, 10, 324 CrossRef; (b) T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1558 CrossRef CAS.
- K. S. Kim, S. Karthikeyan and N. J. Singh, J. Chem. Theory Comput., 2011, 7, 3471 CrossRef CAS PubMed.
- R. Robiette, V. K. Aggarwal and J. N. Harvey, J. Am. Chem. Soc., 2007, 129, 15513 CrossRef CAS PubMed.
- (a) A. Finch, A. Hameed, P. J. Gardner and N. Paul, J. Chem. Soc. C, 1969, 391 CAS; (b) A. A. Sandoval, H. C. Moser and R. W. Kiser, J. Phys. Chem., 1963, 67, 124 CrossRef CAS; (c) F. E. Saalfeld and H. J. Svec, Inorg. Chem., 1964, 3, 1442 CrossRef CAS; (d) N. N. Grishin, G. M. Bogolyubov and A. A. Petrov, J. Gen. Chem. USSR, 1968, 38, 2595 Search PubMed; (e) C. S. Dean, A. Finch, P. J. Gardner and D. W. Payling, J. Chem. Soc., Faraday Trans., 1973, 1921 Search PubMed.
- Reviews on phosphenium ions: (a) A. H. Cowley and R. A. Kemp, Chem. Rev., 1985, 85, 367 CrossRef CAS; (b) M. Sanchez, M. R. Mazières, L. Lamandé and R. Wolf, Multiple Bonds and Low Coordination Chemistry in Phosphorus Chemistry, ed. M. Regitz and O. J. Scherer, Thieme, Stuttgart, 1990, p. 129ff Search PubMed; (c) D. Gudat, Coord. Chem. Rev., 1997, 163, 71 CrossRef CAS; (d) H. Nakazawa, Adv. Organomet. Chem., 2004, 50, 107 CrossRef; (e) L. Rosenberg, Coord. Chem. Rev., 2012, 256, 606 CrossRef CAS.
- D. Gudat, Eur. J. Inorg. Chem., 1998, 1087 CrossRef CAS.
- H. H. Karsch, in Synthetic Methods of Organometallic and Inorganic Chemistry, ed. G. Brauer and W. W. Herrmann, Thieme, Stuttgart, 1996, vol. 3, p. 110 Search PubMed.
- D. J. Dellinger, D. M. Sheehan, N. K. Christensen, J. G. Lindberg and M. H. Caruthers, J. Am. Chem. Soc., 2003, 125, 940 CrossRef CAS PubMed.
- G. R. Gillette, A. Igau, A. Baceiredo and G. Bertrand, New J. Chem., 1991, 15, 393 CAS.
- (a) G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2008, 64, 112 CrossRef CAS PubMed; (b) G. M. Sheldrick, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2015, 71, 3 Search PubMed; (c) S. Parsons, H. D. Flack and T. Wagner, Acta Crystallogr., Sect. B: Struct. Sci., 2013, 69, 249 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, GAUSSIAN 09 (Revision B01), Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615 RSC.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215 Search PubMed.
- G. Schaftenaar and J. H. Noordik, J. Comput.-Aided Mol. Des., 2000, 14, 123 CrossRef CAS PubMed.
- A. R. Allouche, J. Comput. Chem., 2011, 32, 174 CrossRef CAS PubMed.
- (a) S. I. Gorelsky and A. B. P. Lever, J. Organomet. Chem., 2001, 635, 187 CrossRef CAS; (b) S. I. Gorelsky, AOMix: Program for Molecular Orbital Analysis, University of Ottawa, 2012, http://www.sg-chem.net/ Search PubMed.
- bwGRiD (http://www.bw-grid.de), member of the German D-Grid initiative, funded by Federal Ministry for Education and Research and the Ministry for Science, Research and Arts, Baden-Württemberg.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental and simulated EPR spectra of 6–9; plot of computed hyperfine couplings vs. skew angles; 1H NMR spectra of 9/{9}2; results and evaluation of VT EPR measurements; energies and coordinates of calculated molecular structures of radicals 4–9 and diphosphanes {4}2–{9}2; graphical representation of the structural relaxation; crystallographic data. CCDC 1414814 (9_Cl), 1414815 {8}2 and 1414816 {9}2. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5dt02854j |
| ‡ Crystallographic data of the chlorophosphane 9_Cl (the precursor of {9}2) are found in the ESI.† |
| § We define the skew angle as a dihedral angle ANPB where A and B are points on the normal vectors of the NPN and CNC/CNSi planes. |
| ¶ Even if the electron density of the phosphorus lone-pairs is not visible in the crystal structure, the conformation of {9}2 suggests an ecliptic orientation of the lone-pairs and the P1–N12/P1′–N12′ bonds. |
| || A similar deviation between calculated bond enthalpies/energies of N-alkyl/silyl- and N-aryl-substituted diphosphanes was also found at the M06-2X/cc-pVDZ level. |
| This journal is © The Royal Society of Chemistry 2016 |