A Li-rich strategy towards advanced Mn-doped triphylite cathodes for Li-ion batteries

Abstract

Triphylite-structured lithium iron/manganese phosphates have captured rapt attention as prospective positive electrodes for Li-ion batteries, targeted to automotive applications. Here we report on a strategy to improve the power characteristics of Mn-doped LiFePO₄ cathode materials by introducing extra Li at the transition metal site (Li-rich) via a facile solvothermal synthesis route. The crystal structure refinement based on joint synchrotron and neutron powder diffraction data unambiguously confirmed the formation of a Li-rich phase, with additional validation coming from scanning transmission electron microscopy, electron energy loss spectroscopy, and ⁵⁷Fe Mössbauer spectroscopy. The particularly created defect structure of the Li-rich Li_1+δ(Fe_0.5Mn_0.5)_1−δPO₄ with additional Li⁺ ions residing at the 3d-metal site enables the extended solid solution region of the Li ion de/intercalation mechanism established using operando synchrotron X-ray powder diffraction. The suggested strategy offers an advanced electrochemical behavior of the materials that exhibit specific capacities of over 158 mAh g⁻¹ at C/10 and 120 mAh g⁻¹ at 10C, with retention of 84 ± 4% after 500 cycles at 10C.

---

Introduction

The triphylite-structured LiFePO₄ (LFP) as a positive electrode (cathode) material for Li-ion batteries (LIBs) was first suggested by Goodenough's group.¹ It has an attractive theoretical capacity of 170 mAh g⁻¹, a high chemical and thermal stability due to covalently bonded oxygen in the PO₄ groups, a relatively low volume change during Li⁺ de/intercalation, and low cost owing to the abundancy of iron.¹ At the same time, the pristine LFP material reveals a medium working potential of 3.43 V vs. Li⁺/Li, low but tunable Li⁺ diffusion coefficient (10⁻¹⁵–10⁻¹² cm² s⁻¹)^2,3 and poor electronic conductivity (10⁻⁹ S⋅cm⁻¹)⁴ resulting in sluggish kinetics of Li⁺ de/insertion limiting high-power applications. The main reason for the hindered kinetics in LFP is a significant contribution of the two phase mechanism with a slow phase boundary propagation that occurs via a hybrid regime of slow diffusion and charge transfer process.³ In this sense, the improved Li⁺ de/intercalation kinetics can be reached by extending the solid solution regions of Li ion de/insertion.

The LFP crystal structure is formally represented as a hexagonal oxygen close-packing where Li is located in edge-sharing octahedra (the M1 site) and Fe is positioned in corner-sharing octahedra (the M2 site).⁵ This structure easily accommodates various point defects: lithium (V_Li) and iron (V_Fe) vacancies, Fe_Li and Li_Fe antisite pairs, hydroxyl defects associated with the P substitution, or a combination of these,^7–10 with all of them drastically influencing the electrochemical performance.¹¹ The antisite defects are the most abundant due to their low formation energy.⁶ On the one hand, the anti-site defects might block the main diffusion pathway of Li ions along the b axis¹² thus significantly deteriorating the electrochemical properties. On the other hand, recent computational studies have revealed that in a highly disordered LFP, the defects reduce the ‘diffusion anisotropy’ and activate the so-called 2D diffusion mechanism with enhanced migration along the [100] direction.¹³ As a comparison, diffusion coefficients for the [010] and [100] directions containing 0.5% of Fe/Li antisite defects differ by four orders of magnitude, while introducing up to 25% of the defects results in almost equalizing the diffusion coefficients along the two directions.¹³ Experimentally, the 2D-diffusion mechanism was confirmed by means of operando transmission electron microscopy tomography coupled with XANES in single-crystal LFP microrods.¹⁴ In the case of the 2D-diffusion mechanism, the preferred orientation of particles (and their shape) has fewer effects on the electrochemical performance compared to the 1D diffusion case.

Taking into account the role of antisite defects in Li-ion diffusion, the partial Li substitution at the d-metal site could be beneficial to overall Li⁺ diffusion coefficients. According to the computational studies, it is possible to introduce up to 12.5% of additional Li ions at the M2 site with oxidation of the d-metal for charge compensation in the triphylite structure.¹⁵ This results not only in a higher concentration and diffusivity of charge carriers, but also in switching the diffusion network dimensionality from 1D to 2D or even 3D depending on the degree of substitution.¹⁵ In a recent study, the energy barriers for three different directions were calculated and compared between those of a conventional LFP and Li-rich LFP material manifesting a reduction by 15% and 63% for the [001] and [101] directions, respectively, for the latter material.¹⁶ Thus, the presence of additional Li ions at the M2 site might improve both Li-ion diffusion and kinetics.

The attempts of synthesizing Li-rich materials resulted in Li_1.05Fe_0.95PO₄ (Li-rich LFP) obtained via solvothermal synthesis, which demonstrates an attractive electrochemical performance at high C rates (140 mAh g⁻¹ at fast charge – 10C and slow discharge mode – C/10). An extended solid solution region related to the presence of additional Li ions in the structure inhibits nucleation of the FePO₄ heterosite during charge/discharge.¹⁷ A similar effect was described in ref. 18: it was possible to alter significantly the de/intercalation mechanism from a conventional two-phase to a full-range solid solution in Li-rich Mn spinels via changing the Li content.

In order to enhance the operating potential, electronic and ionic conductivities of LFP, a partial substitution for the 3d-metal at the M2 site is applied.^19,20 The Mn²⁺/Mn³⁺ pair having its working potential of 4.1 V vs. Li⁺/Li in the triphylite-type structure seems to be a prospective candidate. Among various chemical compositions of LiFe_xMn_1−xPO₄ (0 < x < 1), LiFe_0.5Mn_0.5PO₄ (LFMP) is worth mentioning as it demonstrates the synergetic effect of the Mn substitution resulting in a higher operation potential, and the presence of Fe reducing the impact of Jahn–Teller distortion and sluggish kinetics at the Mn^2+/3+ redox transition.^21,22 LFMP has the lowest charge transfer resistance among the LiFe_xMn_1−xPO₄ solid solutions and, as a result, the most attractive electrochemical performance and cycling stability.²³ For this reason, a number of LFMP materials have been synthesized exhibiting specific capacity close to the theoretical one.²⁴ However, no data on Li-rich LFMP can be found in the literature to the best of our knowledge.

In this work, we report on a novel Li-rich Li_1+δ(Fe_0.5Mn_0.5)_1−δPO₄ (Li-rich LFMP) positive electrode material prepared by an easily scalable solvothermal method with attractive electrochemical performance due to an extended solid solution region of Li⁺ de/intercalation. To validate the formation of a Li-rich system we performed a multi-modal analysis of the crystal structure and chemical composition by synchrotron X-ray (SXRD), electron (ED) and neutron diffraction (ND), scanning transmission electron microscopy, and Fourier transform infrared (FTIR) and ⁵⁷Fe Mössbauer spectroscopies. The de/intercalation mechanism was studied by a combination of the diffraction (SXRD) and electrochemical (PIT) techniques. Both methods revealed the prolonged solid solution regions during Li⁺ de/insertion compared to the published research results for stoichiometric LFMP samples.

Experimental part

Li-rich LFMP was synthesized via solvothermal treatment of a Li₃PO₄ precursor followed by high-temperature annealing of the resulting product. Prior to the synthesis, the water content of the crystal hydrates was measured by means of thermogravimetric analysis. In a typical procedure, LiOH·H₂O (Komponent reactive, 99%, 3.5405 g) was dissolved in 40 ml of an H₂O–ethylene glycol mixture (3 : 7 volume ratio). After the complete dissolution, 1.8 ml of H₃PO₄ (Komponent reactive, 85% aqueous solution) was added. This led to immediate formation of a white suspension of Li₃PO₄. At the same time, ascorbic acid (Ruskhim, 99%, 0.45 g), MnSO₄·0.99H₂O (Komponent reactive, 98%, 2.3808 g), and FeSO₄·6.97H₂O (Komponent reactive, 98%, 3.9272 g) were dissolved in 10 ml of deionized water and mixed with the Li₃PO₄ suspension. The concentration of ascorbic acid is much lower compared to the Mn²⁺ and Fe²⁺ concentrations so that, along with the excess of Li⁺ from the Li₃PO₄ precursor in the reaction media, enables the formation of a Li-rich material. The mixture was transferred to a 125 ml stainless-steel reactor (Parr Instruments), and then it was sealed and kept at 190 °C for 1 hour with stirring. The obtained material was mixed with glucose in a 10 : 1 mass ratio in ethanol and dried at 40 °C for 1 hour using a rotating evaporator (Heidolph Instruments). The resulting powder was heated up to 650 °C and annealed for 3 hours under a purified Ar flow to get the carbon-coated Li-rich LFMP.

The chemical composition was determined by means of ICP-OES analysis with an Agilent 720 spectrometer. For the experiment, a weighed sample (ca. 20 mg) of material was placed in a volumetric flask of 50.0 ml, and 15 ml of aqua regia (concentrated nitric (HNO₃) and concentrated hydrochloric (HCl) acid (Panreac) (1 : 3) by volume) was added. All the samples were vigorously shaken for 2 min and deionized water was added to the mark.

Synchrotron X-ray powder diffraction (SXRD) experiments were carried out at the PETRA III synchrotron facility (beamline P02.1)²⁵ at the Deutsches Elektronen-Synchrotron (DESY) in Hamburg at a wavelength of 0.20736 Å. The powder data were collected between 1 and 21° 2θ at 298 K in rotating glass capillaries. 2D images obtained from a Varex XRD 4343CT detector (2880 × 2880 pixels with 150 × 150 μm pixel size) were integrated in the pyFAI software.²⁶ The calibrant was LaB₆ (660a NIST powder). The neutron powder diffraction (ND) patterns were collected with the high-resolution powder diffractometer SPODI²⁷ in Forschungs-Neutronenquelle Heinz Maier-Leibnitz (FRMII) at Technical University of Munich at a wavelength of 1.5482 Å. The data were collected in the 2–152° 2θ range at room temperature. Si standard data were used for calibration. The joint Rietveld refinement was performed with the use of TOPAS software with routines of the TOPAS-Academic package.²⁸ X-ray diffraction can distinguish between Mn/Fe and Li, whereas neutron diffraction helps in contrasting Mn and Fe and locating Li. A combination of these methods makes it possible to determine the accurate atomic composition on both crystallographic sites. Both M1 and M2 sites were allowed to contain any amounts of Li, Mn, and Fe with total occupancy per each site constrained to 1. The P site occupancy was refined freely. Anisotropic atomic displacement parameters were used.

⁵⁷Fe Mössbauer experiments were carried out in a transmission geometry with a 1500 MBq γ-source of ⁵⁷Co(Rh) mounted on a conventional constant acceleration drive. The spectra were fitted using the SpectrRelax program.²⁹ The isomer shift (δ) values are referred to that of α-Fe at room temperature.

The Fourier transform infrared (FTIR) spectra were collected with an ALPHA II compact FT-IR spectrometer. The spectra were recorded in the 4000–400 cm⁻¹ range with 2 cm⁻¹ resolution and averaging 3 scans. The reproducibility was checked by probing different spots of the same powder sample.

For transmission electron microscopy (TEM) investigation, a small amount of the powder sample was ground with an agate mortar and pestle in ethyl alcohol followed by depositing the suspension onto a carbon film supported by a copper grid. The selected area electron diffraction (SAED) patterns, high angle annular dark field scanning transmission electron microscopy (HAADF-STEM) images, and energy-dispersive X-ray (EDX) and electron energy loss (EELS) spectra were acquired on a probe aberration-corrected Titan Themis Z (ThermoFisher Scientific) electron microscope at 200 kV equipped with a Super-X system for EDX analysis and with a Gatan Quantum ER965 spectrometer. The EELS maps were recorded in STEM-mode with 1 eV energy resolution. To measure the Mn oxidation state, the core-loss EELS spectra of Mn were recorded using a monochromated electron beam with the energy resolution of 0.15–0.17 eV at 120 kV.

The slurry for electrode preparation was produced by mixing the active material (90%), PVDF (5%), carbon black (5%) and N-methylpyrrolidone (NMP) as a solvent in a SPEX 8000M ball mill and then applied on a carbon-coated aluminum foil using an automatic film applicator ZAA 2300 (Zehntner) with thickness of 150 μm and calendered at 70 °C. Round-shaped electrodes with an area of 1.54 cm² and an average mass loading of active material of 4–5 mg cm⁻² were cut and dried in a vacuum oven at 120 °C overnight. The two-electrode CR2032 coin-type half cells were assembled in an Ar-filled glovebox (MBraun, p(O₂) = 0.1 ppm, p(H₂O) = 0.1 ppm) with Li metal (Gelon Lib, 99.9%) as an anode and a commercial electrolyte consisting of 1 M LiPF₆ dissolved in a mixture of EC : DEC (1 : 1 by vol). Galvanostatic cycling was carried out in the potential range of 2.5–4.3 V vs. Li⁺/Li using a battery testing system (Neware). For high C-rate and long-term cycling experiments a CC-CV charge protocol was used with a current cutoff of C/10. For 1C and 10C-rate experiments, a set of 5 coin cells were used. Potentiostatic intermittent titration (PIT) measurements were performed in three-electrode cells with Li metal as counter and reference electrodes in the potential range of 2.5–4.3 V vs. Li⁺/Li with a step voltage of 10 mV, and a cutoff current equal to C/50 using a potentiostat-galvanostat (Biologic VMP-3) for the experiments of one-time measurements was considered. Li⁺ diffusion coefficients were determined as it was discussed elsewhere.^30,31 The current transients were analyzed in the single phase regions (3.52–3.55 V and 3.60–3.65 V vs. Li⁺/Li during charge and 3.53–3.56 V and 3.60–3.65 V vs. Li⁺/Li during discharge processes). All electrochemical measurements were conducted at room temperature.

For the operando SXRD experiments, modified CR2032 coin cells with Kapton windows were assembled in an Ar-filled glovebox (MBraun, p(O₂) = 0.1 ppm, p(H₂O) = 0.1 ppm). The electrochemical cycling was carried out at a constant current density (C/5) for both charge and discharge. The data were collected between 1 and 21° 2θ at 298 K (Varex XRD 4343CT detector). The background was subtracted from the integrated data using Derivative Peak-Screening Asymmetric Least Squares Algorithm (derpsalsa)³² as implemented in pybaselines.³³ The sequential Rietveld refinement was done in GSAS II software.³⁴

Results and discussion

1. Structure refinement and morphology

According to ICP-OES measurements, the Fe : Mn ratio is equal to 1 : 1 (Table S1, ESI†), while STEM-EDX shows slightly higher Fe concentration over Mn (1.05 : 1). The d-metal ratio was obtained by averaging a set of 5 spectra (Table S2, ESI†), the typical EDX spectrum is depicted in Fig. S1 (ESI†). The room temperature ⁵⁷Fe Mössbauer spectrum of the Li-rich LFMP sample (Fig. 1a) shows a dominant symmetric doublet Fe(1) with isomer shift (δ) and quadrupole splitting (Δ) (Table 1) corresponding to the high-spin ferrous Fe²⁺ ions in an octahedral oxygen environment.³⁵ These parameters are in agreement with the literature data for Fe²⁺ in the triphylite LiFePO₄.^36,37 In addition, we notice another paramagnetic doublet Fe(2) with asymmetric and broadened components indicative of a non-uniform crystal environment of iron ions. The isomer shift for the Fe(2) doublet corresponds to the ferric ions with a formal oxidation state of 3+. The large average quadrupole splitting suggests that the Fe³⁺ ions are distributed over positions with a strong electric field gradient at ⁵⁷Fe nuclei. Thus, ⁵⁷Fe Mössbauer spectroscopy suggests a noticeable amount of Fe³⁺ (11.8(4) %), which can be deduced to 0.06 Fe³⁺ per chemical formula if all ferric ions are considered to be oxidized to restore the electroneutrality upon Li substitution at the M2 site. No presence of characteristic bands of –OH or H₂O was observed by means of FTIR spectroscopy, which in combination with chemical analysis validates the absence of hydroxyl defects in place of the PO₄ groups. The wide signal around 1600 cm⁻¹ can be assigned to the C=C stretching band attributed to carbon coating of the composite (Fig. 1b).

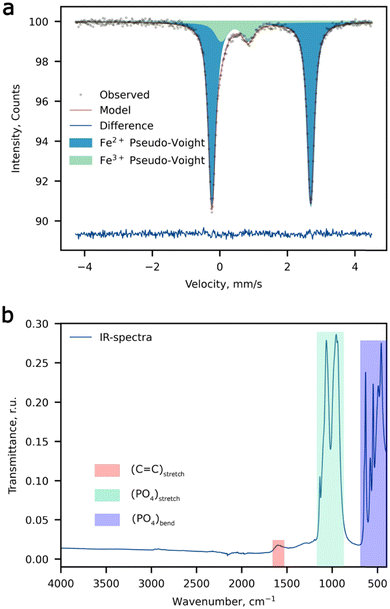Fig. 1 Spectroscopic measurements. (a) The ⁵⁷Fe Mössbauer spectrum, and (b) the FTIR spectrum of Li-rich LFMP.

Table 1 Material characterization by ⁵⁷Fe Mössbauer spectroscopy

Component	δ, mm s^−1	Δ, mm s^−1	Γ, mm s^−1	I, %
Fe(1) Fe^2+	1.22(1)	2.94(1)	0.25(1)	88.2(4)
Fe(2) Fe^3+	0.43(1)	0.77(1)	0.58(3)	11.8(4)

---

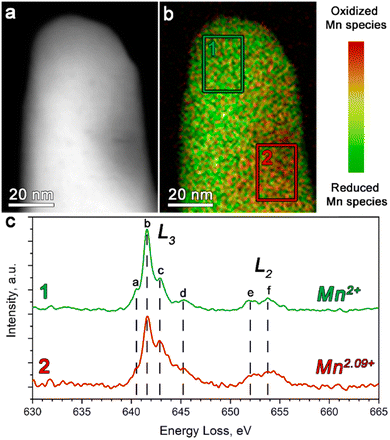
The STEM-EELS measurements were performed to estimate the oxidation state of Mn in Li_1+δ(Fe_0.5Mn_0.5)_1−δPO₄ (Fig. 2).

Fig. 2 (a) The ADF-STEM image of Li_1+δ(Fe_0.5Mn_0.5)_1−δPO₄ particles with (b) the corresponding color-coded STEM-EELS Mn oxidation state map. (c) The Mn-L_2,3 edge EELS spectra for Li_1+δ(Fe_0.5Mn_0.5)_1−δPO₄ integrated over the regions 1 and 2, outlined on the image in (b) with green and red rectangles, respectively.

The Mn L-edge demonstrates two well-resolved maxima corresponding to the L₂ and L₃ transitions (see Fig. 2c). In addition, both the L₂ and L₃ peaks reveal a complex multiplet structure, whereas each component was assigned in Fig. 2c as a–d and e–f for the L₃ and L₂ transitions, respectively. It can be clearly seen that as the concentration of the oxidized Mn species increases, the c-component of the L₃ line gains its intensity, while the b-component keeps the same intensity. Thereby, we used the 641–642 eV and 642.5–643.5 eV energy loss windows, corresponding to the b- and c-components of the L₃ line, to map the location of the reduced and oxidized Mn species, respectively. The corresponding color-coded maps were superimposed to generate the Mn valence maps presented in Fig. 2b.

Moreover, in order to get a quantitative estimation of the Mn oxidation state, we used the Mn L₃/L₂ “white line” intensity ratio as was suggested by Tan, H. et al.³⁸ As a result, the Mn oxidation state was estimated to vary from 2+ (region 1 in Fig. 2b) to 2.09+ (region 2 in Fig. 2b). This once again indirectly confirmed the presence of extra Li in the M2 positions, which is caused by partial oxidation of both Fe and Mn, albeit also revealing the slight local inhomogeneity of the Li/Mn³⁺ distribution at the atomic scale.

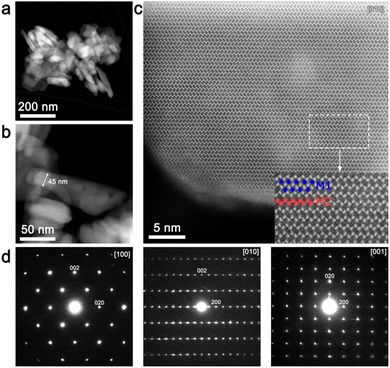
An overview HAADF-STEM image (Fig. 3a and b) demonstrates rod-like crystallites of the as-prepared material with a thickness of ∼45–50 nm. [010] high-resolution HAADF-STEM imaging (Fig. 3c) was performed in order to directly analyze the Li_Fe/Mn antisite defects. Due to the large difference between Li and Mn/Fe atomic masses, the bright dots in the HAADF-STEM image (Fig. 3c) correspond to the Fe/Mn/Li atomic columns at the M2 sites, whereas the dark area between them represents atomic columns of Li at the M1 site. Since no HAADF signal is observed at the M1 site, the number of Fe/Mn atoms in the M1 columns (antisite defects) is supposed to be negligible. The indexation of the three SAED patterns (Fig. 3d) clearly demonstrates 0kl:k + l = 2n, hk0:h = 2n and hk0:h = 2n reflection conditions, in agreement with the space group Pnma.

Fig. 3 (a) An overview and (b) the [100] HAADF-STEM image of Li-rich LFMP particles. The minimal thickness along the b-axis (denoted with a double sided arrow) is ∼45 nm. (c) The low-pass filtered [010] HAADF-STEM image of a Li-rich LFMP crystal; in the magnified area, Fe/Mn atomic columns and Li positions are represented as red and blue circles respectively. (d) The [100], [010] and [001] SAED patterns for Li-rich LFMP.

The crystal structure was refined using the Rietveld method using the joint powder SXRD and ND data (Fig. 4a and b). Taking into account the results of ⁵⁷Fe Mössbauer and FTIR spectroscopy as well as HAADF-STEM imaging, a model with Li at the M2 site was chosen as the most probable. For the refinement procedure, the Li fraction at the M2 site was refined and Fe and Mn had the total site occupancy equal to 1, while the P and Li at the M1 site occupancies were set to 1. Atomic displacement parameters were refined anisotropically. The model converged at R_wp = 1.15% and GOF of 4.94. This model suggests a 7.23(16)% excess of Li at the M2 position resulting in the Li_1.07Mn_0.46Fe_0.47PO₄ chemical formula (Tables 2–4). Additionally, a Li-stoichiometric model was chosen for comparison, and the model results in the following chemical composition LiFe_0.52Mn_0.48PO₄ and reliability factor R_wp = 1.396%, which makes it less plausible. Furthermore, neither ⁵⁷Fe Mössbauer spectroscopy experimental results, nor EELS data on the Mn-L_2,3 edge corroborate with the Li-stoichiometric model.

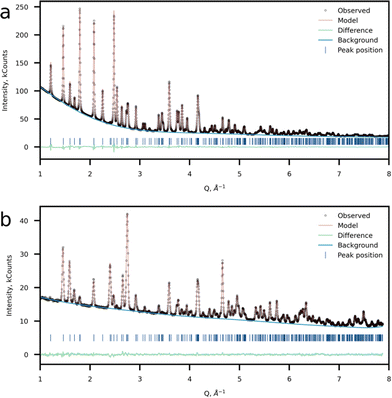Fig. 4 Crystal structure refinement results. Observed, calculated and difference plots of (a) SXRD and (b) NPD refinement of Li-rich LFMP.

Table 2 Cell parameters and refined composition for Li-rich LFMP determined by joint ND and SXRD refinement

Formula	Li1.07(2)Mn0.456(3)Fe0.473(2)PO4
Space group	Pnma
a, Å	10.3853(6)
b, Å	6.0507(3)
c, Å	4.7187(3)
V, Å^3	296.515(3)
Z	4
GOF	4.94
R exp, %	0.52
R p, Rwp, %	0.84,1.15

---

Table 3 Structural parameters obtained for Li-rich LFMP from joint refinement on SXRD and ND data

Atom	Wyckoff position	x/a	y/b	z/c	Occupancy
Li1	4a	0	0	0	1
Li2	4c	0.28204(4)	1/4	0.97386(11)	0.0723(16)
Fe2	4c	0.28204(4)	1/4	0.97386(11)	0.474(2)
Mn2	4c	0.28204(4)	1/4	0.97386(11)	0.454(3)
O1	4c	0.09724(17)	1/4	0.7377(3)	1
O2	4c	0.45537(15)	1/4	0.2077(3)	1
O3	8d	0.16361(13)	0.04790(16)	0.2812(2)	1
P1	4c	0.09407(8)	1/4	0.41261(15)	1

---

Table 4 Atomic displacement parameters (Ų) obtained for Li-rich LFMP from joint refinement on XRD and ND data

Atom	U 11	U 22	U 33	U 12	U 13	U 23
Li1	0.020(2)	0.019(2)	0.028(3)	−0.0058(16)	−0.005(2)	0.002(2)
Li2	0.0040(3)	0.0061(3)	0.0071(3)	0	0.0001(3)	0
Fe2	0.0040(3)	0.0061(3)	0.0071(3)	0	0.0001(3)	0
Mn2	0.0040(3)	0.0061(3)	0.0071(3)	0	0.0001(3)	0
O1	0.0145(8)	0.0095(8)	0.0102(10)	0	0.0018(8)	0
O2	0.0087(9)	0.0126(8)	0.0113(9)	0	0.0008(7)	0
O3	0.0119(6)	0.0061(5)	0.0102(6)	0.0046(5)	0.0012(7)	0.0025(5)
P1	0.0078(5)	0.0072(4)	0.0100(5)	0	−0.0036(4)	0

---

SXRD and ND (Fig. 4a and b) data confirmed the formation of a single-phase orthorhombic triphylite-type material (S.G. Pnma), thus validating the SAED data, which reveals the Pnma space group. The morphology of the as-prepared material represents rod-like nanoparticles with the mean particle length of 50–100 nm and thickness of ∼50 nm according to the SEM observations (Fig. S2 and S3, ESI†). In the case of the triphylite-type cathode, such morphology is beneficial due to shortened mobile ion diffusion pathways along the b-axis having the lowest activation barriers in the structure.¹²

2. Electrochemistry

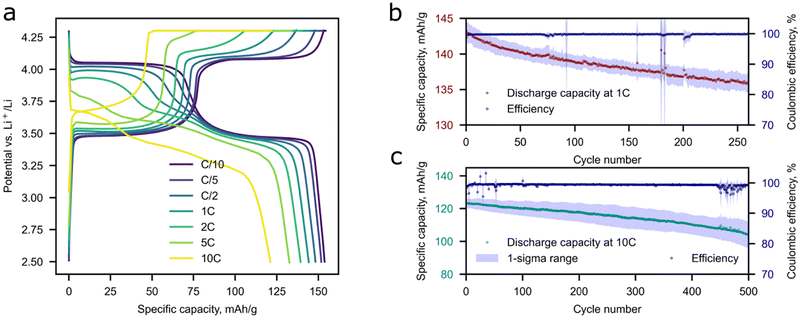
The prepared composites demonstrate a decent electrochemical performance and exhibit 158 mAh g⁻¹ at C/10 and 120 mAh g⁻¹ at 10C at discharge as depicted in Fig. 5a. The maximum achieved discharge capacity is close to the theoretical value (158 mAh g⁻¹). The theoretical capacity was calculated with consideration of the decreased concentration of active M²⁺ ions caused by the charge compensation of Li⁺ excess. Two distinct plateaus can be observed in the galvanostatic curves, which are attributed to the Fe^2+/3+and Mn^2+/3+ transitions during the charge process.³⁹ As for discharge, an additional plateau appears at approximately 3.6 V and becomes more pronounced at current densities higher than C/5. This phenomenon was observed for the first-time by Wang et al.,⁴⁰ where the authors relied on a phase-separated model and claimed that the possible reason behind this is an electrochemical–chemical reaction between delithiated MnPO₄ and lithiated LiFePO₄ since the Li⁺ intercalation in MnPO₄ displays slower kinetics compared to that of FePO₄. The speculation was made by analyzing GIT curves, where the additional plateau was attributed to the Mn³⁺ reduction. An alternative opinion was later expressed by researchers in ref. 41 where DFT calculations were performed for phase-separated and solid solution LiFe_0.5Mn_0.5PO₄ cases. The authors argue that only for a true solid solution material without domain structures is this appearance of the third plateau legit.

Fig. 5 The electrochemical performance of Li-rich LFMP in Li half-cells. (a) Charge–discharge profiles of Li-rich LFMP at different C-rates, cycling stability of Li-rich LFMP at 1C (b) and 10C (c). The standard deviations (1-Sigma range) and mean values of discharge specific capacity and coulombic efficiency are calculated from five experiments (b and c).

The capacity retention of Li-rich LFMP of 80–88% was observed during long-term cycling for 500 cycles at 10C and 92–97% at 1C during 280 cycles (Fig. 5b and c), which is highly beneficial for practical implementation of the material in high-power application areas. A slight deviation in the electrochemical response is observed as the discharge capacity and coulombic efficiency decrease during cycling. The possible reason behind this is Li dendrite crystallization-dissolution during a high current density loading. Extraction of the maximum amount of Li during charge is possible by a combination of CC and CV charging protocols.

As it can be deduced from the processed experimental PIT data (Fig. S4, ESI†), the de/intercalation process occurs via a solid solution mechanism covering state of charge (SOC) regions of (0–0.03, 0.31–0.7, and 0.96–1) during the charge and (1–0.93, 0.76–0.39, and 0.02–0) SOC during the discharge, correspondingly (Fig. S5, ESI†). Li⁺ de/intercalation undergoing via a two-phase mechanism was extracted by summing up the charge values accumulated during a phase transition and divided by the total charge amount during insertion or extraction of Li⁺. The two-phase region boundaries were established by analyzing the shape of the current transients (Fig. S6, ESI†) during charge and discharge near the phase transitions. Current transients in the solid solution region could be recognized by a characteristic fast decrease of current in the short time region in current vs. time coordinates. When a phase transition occurs during the chronoamperometric measurements, the current transients typically show very slow current decays corresponding to a large charge passing through the electrode at the phase transformation potential, and sometimes a characteristic nucleation-induced maximum can be detected.⁴² Taking into account the above-discussed features, transients at 3.48–3.49 V vs. Li⁺/Li are assigned to the two-phase phase transitions that accompany the Fe^2+/3+ redox. Applying the same concept, the potential for the Fe^3+/2+ transition is observed at 3.47 V vs. Li⁺/Li. Taking into account PIT conditions, the experimental error of the phase transition potential determination lies within 10 mV. As the potential range of Li⁺ de/intercalation was extracted, the exact SOC values for the solid-state and two-phase mechanism were calculated as the charge accumulated during the process divided by the total charge.

Li⁺ diffusion coefficients were determined in the single phase regions near the phase transition potential, where the intercalation charges were high enough to allow for a quantitative data treatment. For the Mn^2+/3+ transition it was impossible to extract reasonable transients for diffusion coefficient estimation as the kinetics of Li⁺ de/insertion in the Mn activity region is extremely sluggish and the insertion/extraction process requires too much time.⁴³ The diffusion coefficients for Li_xFMP obtained from the PIT data were 2 × 10⁻¹² cm² s⁻¹ for the charge process and 2 × 10⁻¹¹ cm² s⁻¹ for the discharge, which are comparable with the recently reported values for LFP and LFMP.^13,44

3. Operando SXRD

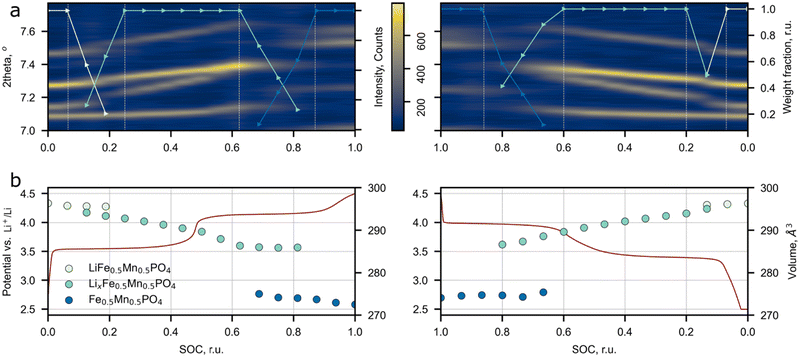
The influence of the Li⁺ excess on the phase transitions and Li⁺ de/intercalation mechanism was studied by means of operando synchrotron X-ray diffraction (Fig. 6). The Pnma space group was assigned to each SXRD scan in the whole range of Li concentrations during cycling, which is in agreement with the SAED analysis and the previous works on LFMP.^45,46 The material experiences two-phase transitions during (dis)charge designated by jump-like shifts of the peak positions (Fig. 6a and Fig. S7, ESI†). According to the results, the two-phase regions are enclosed between 0.94 (0.93) and 0.75 (0.80) and between 0.38 (0.40) and 0.13 (0.14) SOC during charge (discharge) leading to 57 (61)% of solid solution mechanism during cycling. A less pronounced volume change during the intermediate phase L_xFMP to the lithiated LFMP phase transition was observed for the discharge process. This slight asymmetry can be explained by mechanical strain and defect accumulation during operation of the material and by different nucleation rates of the corresponding phases.⁵ As it was stated by Ravnsbæk et al., the volume mismatch between Li_xFMP and FMP and the resulting mechanical strain are much higher than those for LFMP and Li_xFMP, stabilizing the solid solution behavior of Li⁺ insertion during discharge,⁴⁷ while for the lower LFMP and Li_xFMP volume mismatch the nucleation of an intermediate phase is more preferable than the solid solution behavior.⁴⁷

Fig. 6 Synchronized results of operando SXRD study of Li-rich LFMP. (a) Evolution of peak positions and phase weights during cycling. (b) The unit cell volume change during cycling and charge–discharge profile at C/5.

The previous research on conventional LFMP reported a similar phase transformation behavior, but narrower solid solution regions were observed.^45–47 The comparison between the solid solution ranges extracted from the SXRD and PIT data for LFMP and Li-rich LFMP is presented in Fig. S8 (ESI†). The main difference between the current work and the published data is a larger overall length of the solid solution regions: the operando SXRD detected the presence of solid solutions near lithiated (LFMP, 0.00–0.07 SOC) and delithiated (FMP, 0.9–1.0 SOC) phases. Although, in the paper⁴⁵ where the stoichiometric LiFe_0.5Mn_0.5PO₄ was studied, the PIT experiment also discerns short solid solution ranges near the LFMP and FMP phases. The solid solution range retrieved from the PIT experiment is less extended than the one defined from the operando SXRD data. The reason behind this is that in contrast to the SXRD experiments, the redox processes during the PIT measurements are closer to the equilibrium pathway and thus the mechanism of Li⁺ de/intercalation during material operation could be determined more precisely.

No assumption on the defect chemistry influence on the Li de/intercalation mechanism was made in most of the operando LFMP experiments, which makes this paper a good reference for the estimation of additional Li⁺ effects on the de/intercalation mechanism.^45–47 Ravnsbæk et al.⁴⁷ carried out an operando SXRD study of LiFe_0.4Mn_0.6PO₄ composites with various particle sizes prepared via a solid-state reaction. Such a synthesis scheme inevitably results in negligible amount of Fe(Mn)/Li antisite defects,⁴⁸ and hence one may consider the reported material as close to the stoichiometric one. The authors stated that the reduction of particle size from 106 to 50 nm increases the propagation of the single-phase mechanism from 17% to 51% of the total Li⁺ insertion process.⁴⁷ Though the particle length of Li-rich LFMP obtained in our work is larger than 50 nm (∼80 nm) the observed solid solution range is comparable with the reported results for 52 nm particles, Fig. S8 (ESI†). The only significant difference between the compared materials is the Li-rich structure. Thus we may conclude that additional Li ions at the M2 site could be a significant factor affecting the solid solution propagation upon Li de/intercalation in the material. A supportive confirmation of our hypothesis is provided by Drozhzhin et al.,¹⁷ where it was speculated that additional Li at the M2 site in Li-rich LFP prevents nucleation of the heterosite phase thus increasing the contribution of the solid solution mechanism to the overall process. It seems that the same effect is reasonable for the Mn-containing Li-rich LFMP system. Further supporting evidence comes from ref. 18 where a similar effect was described for Li-rich Mn spinels. It was possible to switch the de/intercalation mechanism from a conventional two-phase to a full-range solid solution by introducing additional Li ions in the spinel structure. Despite the positive role of additional Li⁺ ions on the increase of the solid solution range, the drawback of the current approach is that the Li-rich phase's electronic conductivity falls-off. In order to reduce the impact of the conductivity drop, the material's particles were covered with a conductive carbon coating produced by glucose decomposition. The TEM images and EELS mapping of the carbon coating are presented in Fig. S9 (ESI†).

The above-mentioned role of Li-rich defects in spinel- and triphylite-type structures confirms that the extended solid-solution region in the Li-rich LFMP material is affected by introducing additional Li ions at the M2 site.

Conclusion

In a quest for a commercially viable, safe, low-cost positive electrode material for high-power batteries, we designed a novel Li-rich Li_1+δ(Fe_0.5Mn_0.5)_1−δPO₄ cathode material and synthesized it via a facile solvothermal route. The crystal structure of the obtained material was precisely refined based on the joint neutron and synchrotron X-ray diffraction data. The refined amount of additional Li⁺ at the M2 site was found to be 7%, which corroborates with the results of ⁵⁷Fe Mössbauer spectroscopy, clearly identifying the presence of Fe³⁺ and EELS data yielding slight oxidation of Mn²⁺. At the same time, according to the HAADF-STEM imaging and IR spectroscopy, no Fe(Mn)/Li antisite defects were detected and no phosphorous non-stoichiometry was revealed. It is assumed that creating the defect structure with additional “off-stoichiometric” Li ions residing at the M2 site improves the high-C rate capabilities of the material extending the solid solution de/intercalation regions for both charge and discharge processes. The possible explanation behind this could be that (i) Li⁺ can migrate along more than one crystallographic direction due to lowered energy barriers resulting in a pseudo-2D diffusion mechanism, (ii) extra Li⁺ at the M2 site prevents nucleation of the heterosite-type Fe_0.5Mn_0.5PO₄, hence extending the solid solution region of Li de/intercalation. The synthesized material demonstrates a superior cycling stability corresponding to 80–88% capacity retention after 500 cycles at 10C. The future steps for enhancing the properties of the material should include modifying the morphology with the production of microspherical secondary particles in order to increase the volumetric energy density and surface modification with the optimization of the carbon coating technique for ramping up the capacity retention even more during high current density load. To sum up, substituting d-metals at the M2 site in LFMP with Li comprises a viable strategy in either modification or optimization of triphylite-type cathode materials for high-power applications.

Author contributions

Eugene E. Nazarov: conceptualization, data curation, formal analysis, investigation, validation, methodology, visualization, writing – original draft. Artem D. Dembitskiy: methodology, data curation, formal analysis, visualization, software, writing – original draft. Ivan A. Trusov: methodology, validation, formal analysis, writing – review & editing. Oleg A. Tyablikov: resources, methodology, writing – review & editing. Iana S. Glazkova: methodology, vizualization, data curation. Alexey V. Sobolev: methodology, vizualization, data curation. Igor A. Presniakov: methodology, data curation, writing – review & editing. Ivan V. Mikheev: methodology, data curation, writing – review & editing. Anatolii V. Morozov: methodology, data curation, vizualization. Victoria A. Nikitina: conceptualization, validation, writing – review & editing. Artem M. Abakumov: conceptualization, writing – review & editing. Evgeniy V. Antipov: conceptualization, writing – review & editing, supervision. Stanislav S. Fedotov: conceptualization, visualization, formal analysis, writing – original draft, writing – review & editing, funding acquisition, supervision.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

E. E. N. and S. S. F. acknowledge financial support from RFBR (grant 20-33-90291). The authors thank DESY (Hamburg, Germany), a member of the Helmholtz Association HGF, for providing access to the experimental facilities at Petra III and we would like to thank Dr Volodymyr Baran and Dr Martin Etter personally for their kind assistance at the beamline P02.1 and valuable advice (the beamtime was allocated for the proposal I-20200707). The authors are grateful to Heinz Maier-Leibnitz Zentrum (MLZ) for granting time at SPODI (Proposal 16308) and warmly thank Dr Anatoliy Senyshyn for support with the neutron powder diffraction experiments and for fruitful discussions. The authors also acknowledge AICF of Skoltech.

References

1. A. K. Padhi, K. S. Nanjundaswamy and J. B. Goodenough, J. Electrochem. Soc., 1997, 144, 1188.
2. S. Y. Chung, J. T. Bloking and Y. M. Chiang, Nat. Mater., 2002, 1, 123–128.
3. V. D. Sumanov, O. A. Tyablikov, A. V. Morozov, S. S. Fedotov, S. Y. Vassiliev and V. A. Nikitina, Electrochim. Acta, 2021, 368, 137627.
4. A. V. Churikov, A. V. Ivanishchev, I. A. Ivanishcheva, V. O. Sycheva, N. R. Khasanova and E. V. Antipov, Electrochim. Acta, 2010, 55, 2939–2950.
5. Y. Z. Dong, Y. M. Zhao and H. Duan, Mater. Chem. Phys., 2011, 129, 756–760.
6. K. Hoang and M. Johannes, Chem. Mater., 2011, 23, 3003–3013.
7. H. Liu, M. J. Choe, R. Enrique, B. Orvananos, L. Zhou, T. Liu, K. Thornton and C. Grey, J. Phys. Chem. C, 2017, 121, 12025–12036.
8. R. Amisse, M. T. Sougrati, L. Stievano, C. Davoisne, G. Drazi, B. Budic, R. Dominko and C. Masquelier, Chem. Mater., 2015, 27, 4261–4273.
9. D. A. Aksyonov, I. Varlamova, I. A. Trussov, A. A. Savina, A. Senyshyn, K. J. Stevenson, A. M. Abakumov, A. Zhugayevych and S. S. Fedotov, Inorg. Chem., 2021, 60, 5497–5506.
10. V. D. Sumanov, D. A. Aksyonov, O. A. Drozhzhin, I. Presniakov, A. V. Sobolev, I. Glazkova, A. A. Tsirlin, D. Rupasov, A. Senyshyn, I. V. Kolesnik, K. J. Stevenson, E. Antipov and A. M. Abakumov, Chem. Mater., 2019, 31, 5035–5046.
11. A. M. Abakumov, S. S. Fedotov, E. V. Antipov and J. M. Tarascon, Nat. Commun., 2020, 11, 4976.
12. S. Kandhasamy, K. Nallathamby and M. Minakshi, Prog. Solid State Chem., 2012, 40, 1–5.
13. L. Hong, K. Yang and M. Tang, npj Comput. Mater., 2019, 5, 118.
14. L. Hong, L. Li, Y. K. Chen-Wiegart, J. Wang, K. Xiang, L. Gan, W. Li, F. Meng, F. Wang, J. Wang, Y.-M. Chiang, S. Jin and M. Tang, Nat. Commun., 2017, 8, 1194.
15. H. Zeng, Y. Gu, G. Teng, Y. Liu, J. Zheng and F. Pan, Phys. Chem. Chem. Phys., 2018, 20, 17497–17503.
16. K.-Y. Park, I. Park, H. Kim, G. Yoon, H. Gwon, Y. Cho, Y. Soo Yun, J. J. Kim, S. Lee, D. Ahn, Y. Kim, H. Kim, I. Hwang, W. S. Yoon and K. Kang, Energy Environ. Sci., 2016, 9, 2902–2915.
17. O. A. Drozhzhin, A. V. Sobolev, V. D. Sumanov, I. S. Glazkova, D. A. Aksyonov, A. D. Grebenshchikova, O. A. Tyablikov, A. M. Alekseeva, I. V. Mikheev, I. Dovgaliuk, D. Chernyshov, K. J. Stevenson, I. A. Presniakov, A. M. Abakumov and E. V. Antipov, J. Phys. Chem. C, 2020, 124, 126–134.
18. M. Bianchini, E. Suard, L. Croguennec and C. Masquelier, J. Phys. Chem. C, 2014, 118, 25947–25955.
19. J. Hu, J. Xie, X. Zhao, H. Yu, X. Zhou, G. Cao and J. Tu, J. Mater. Sci. Technol., 2009, 25(3), 405–409.
20. H. H. Ryu, H. H. Sun, S. T. Myung, C. S. Yoon and Y. K. Sun, Energy Environ. Sci., 2021, 14, 844–852.
21. B. Ding, P. Xiao, G. Ji, Y. Ma, L. Lu and J. Y. Lee, ACS Appl. Mater. Interfaces, 2013, 5, 12120–12126.
22. M. V. Zakharkin, O. A. Drozhzhin, I. V. Tereshchenko, D. Chernyshov, A. M. Abakumov, E. V. Antipov and K. J. Stevenson, Appl. Energy Mater., 2018, 1, 5842–5846.
23. T. F. Yi, P. P. Peng, Z. Fang, Y. R. Zhu, Y. Xie and S. Luo, Composites, Part B, 2019, 175, 107067.
24. Y. Deng, C. Yang, K. Zou, X. Qin, Z. Zhao and G. Chen, Adv. Energy Mater., 2017, 7, 1601958.
25. A. C. Dippel, H. P. Liermann, J. T. Delitz, P. Walter, H. Schulte-Schrepping, O. H. Seeck and H. Franz, J. Synchrotron Radiat., 2015, 22, 675–687.
26. J. Kieffer and J. P. Wright, Powder Diffr., 2013, 28, S339–S350.
27. M. Hoelzel, A. Senyshyn, N. Juenke, H. Boysen, W. Schmahl and H. Fuess, Nucl. Instrum. Methods Phys. Res., Sect. A, 2012, 667, 32–37.
28. A. A. Coelho, J. Appl. Crystallogr., 2018, 51, 210–218.
29. M. E. Matsnev and V. S. Rusakov, AIP Conf. Proc., 2012, 1489, 178–185.
30. E. E. Levin, S. Yu Vassiliev and V. A. Nikitina, Electrochim. Acta, 2017, 228, 114–124.
31. C. Montella, Electrochim. Acta, 2006, 51, 3102–3111.
32. V. I. Korepanov, J. Raman Spectrosc., 2020, 51, 2061–2065.
33. D. Erb, derb12/pybaselines, Zenodo, 2021.
34. B. H. Toby and R. B. Von Dreele, J. Appl. Crystallogr., 2013, 46, 544–549.
35. T. Glaser, Angew. Chem., Int. Ed., 2011, 50, 10019–10020.
36. I. Bezza, M. Kaus, R. Heinzmann, M. Yavuz, M. Knapp, S. Mangold, S. Doyle, C. P. Grey, H. Ehrenberg, S. Indris and I. Saaduone, J. Phys. Chem. C, 2015, 119(17), 9016–9024.
37. A. Perea, L. Castro, L. Aldon, L. Stievano, R. Dedryvère, D. Gonbeau, N. Tran, G. Nuspl, J. Breger and C. Tessier, J. Solid State Chem., 2012, 192, 201–209.
38. H. Tan, J. Verbeeck, A. Abakumov and G. Van Tendeloo, Ultramicroscopy, 2012, 116, 24–33.
39. N. V. Kosova, O. A. Podgornova and A. K. Gutakovskii, J. Alloys Compd., 2018, 742, 454–465.
40. K. Wang, M. Hou, S. Yuan, Y. Hongchuan, Y. Wang, C. Wang and Y. Xia, Electrochem. Commun., 2015, 55, 6–9.
41. K. Wang, T. Shen, D. Chen and W. Wang, Chin. J. Chem. Phys., 2019, 32, 687–692.
42. A. R. Iarchuk, V. A. Nikitina, E. A. Karpushkin, V. G. Sergeyev, E. V. Antipov, K. J. Stevenson and A. M. Abakumov, ChemEletroChem, 2019, 6, 5090–5100.
43. L. F. J. Piper, N. F. Quackenbush, S. Sallis, D. O. Scanlon, G. W. Watson, K. W. Nam, X. Q. Yang, K. E. Smith, F. Omenya, N. A. Chernova and M. S. Whittingham, J. Phys. Chem. C, 2013, 117, 10383–10396.
44. H. Yang, C. Fu, Y. Sun, L. Wang and T. Liu, Carbon, 2020, 158, 102–109.
45. O. A. Drozhzhin, V. D. Sumanov, O. M. Karakulina, A. M. Abakumov, J. Hadermann, A. N. Baranov, K. J. Stevenson and E. V. Antipov, Electrochim. Acta, 2016, 191, 149–157.
46. A. Yamada, Y. Kudo and K.-Y. Liu, J. Electrochem. Soc., 2001, 148, A1153–A1158.
47. D. B. Ravnsbæk, K. Xiang, W. Xing, O. J. Borkiewicz, K. M. Wiaderek, P. Gionet, K. W. Chapman, P. J. Chupas and Y. M. Chiang, Nano Lett., 2014, 14, 1484–1491.
48. J. Biendicho and A. West, Solid State Ionics, 2011, 203, 33–36.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ya00292b

---