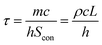Electrically driven liquid crystal network actuators
Yao-Yu
Xiao
,
Zhi-Chao
Jiang
,
Jun-Bo
Hou
,
Xin-Shi
Chen
and
Yue
Zhao
 *
*
Département de Chimie, Université de Sherbrooke, Sherbrooke, Québec, Canada. E-mail: yue.zhao@usherbrooke.ca
First published on 31st May 2022
Abstract
Soft actuators based on liquid crystal networks (LCNs) have aroused great scientific interest for use as stimuli-controlled shape-changing and moving components for robotic devices due to their fast, large, programmable and solvent-free actuation responses. Recently, various LCN actuators have been implemented in soft robotics using stimulus sources such as heat, light, humidity and chemical reactions. Among them, electrically driven LCN actuators allow easy modulation and programming of the input electrical signals (amplitude, phase, and frequency) as well as stimulation throughout the volume, rendering them promising actuators for practical applications. Herein, the progress of electrically driven LCN actuators regarding their construction, actuation mechanisms, actuation performance, actuation programmability and the design strategies for intelligent systems is elucidated. We also discuss new robotic functions and advanced actuation control. Finally, an outlook is provided, highlighting the research challenges faced with this type of actuator.
1. Introduction
Liquid crystal networks (LCNs), including liquid crystal elastomers (LCEs), are well-known as anisotropic materials that combine the characteristics of the ordered structure of liquid crystals and the entropy elasticity of polymer networks.1–5 LCNs are usually explored as soft actuators to perform stimuli-controlled deformation with full reversibility, rapid response and large amplitude. Thanks to their outstanding actuation performance and actuation-programmability, recently developed LCN actuators can exhibit complex macroscopic deformation, biomimetic locomotion, task execution capabilities and intelligent functions.6–9 Therefore, they have been explored in a variety of potential applications, including soft robots, biomimetic devices, energy generators, intelligent textiles, sensors, optical devices and some fields of modern engineering.10–22The characteristic features of the LCN materials and actuators reside in their anisotropy and their anisotropy-determined deformation. The programming of LCN actuators usually involves first arranging rod-shaped mesogens into a uniaxial, 2D or 3D alignment, through mechanical stretching, surface effects, shear extrusion, or electric or magnetic fields, and then carrying out polymer chain crosslinking to lock the orientation state of the LCNs.23,24 Their anisotropy originates from the anisotropic alignment of anisotropic mesogenic units, manifesting in their stimuli-induced actuation responses, and mechanical, electrical, optical and thermal properties, among others.1,3 When looking at actuation applications, the most conspicuous is the stimuli-induced anisotropic actuation responses, that is, LCNs can change their shape and/or exert force directionally in response to external stimuli. In most cases, the actuation mechanism relies on the liquid crystal-isotropic (LC-iso) phase transition of LCNs. Taking a monodomain main-chain nematic LCN as an example (Fig. 1), upon external stimuli, the aligned LCN actuator undergoes a phase transition from the nematic (ordered) phase to the isotropic (disordered) phase, triggering the change from the anisotropic (stretched) chain conformation to a random-coil (relaxed) chain conformation. This generates a macroscopic shrinkage along the LC director (the molecular axis of LCs) and an expansion in the transversal direction. Turning off or changing the stimuli could reverse the process of phase transition and deformation. The disrupted order of mesogens restores spontaneously (isotropic-to-nematic) and the LCN recovers to its initial shape, because of the memory effect derived from crosslinked polymer networks. In addition to the prevailing mechanism based on order–disorder phase transition, anisotropic mechanical, electrical or thermal properties can also be exploited to achieve pre-designed actuation behaviors.11,25
 | ||
| Fig. 1 An illustration of the reversible shape changing mechanism in LCNs based on the transition between the nematic monodomain and isotropic states. | ||
The actuation behavior of LCNs can be triggered by different stimuli, such as heat, light, humidity and electrical energy.26–33 Among various stimuli-responsive soft actuators, electrically driven polymer actuators are appealing and promising for practical applications. This is because electrical stimulation is the most prevailing type of energy form and has a high degree of controllability. Depending on the actuation mechanisms, electrically driven soft actuators have been extensively studied and developed into various categories, such as dielectric elastomer actuators, piezo-materials, electrothermal actuators, ionic electroactive polymers, etc.34–37 Coupling electrical stimulation with LCN materials, the accessibility and controllability of their actuation behaviours benefit from both the electrical manipulation (voltage magnitude, signal waveform, and multi-circuit control) and the actuating material design of LCNs. Several mechanisms have been developed for electrically driven LCN (ELCN) actuators. Arguably, the most widely explored is the electrothermal mechanism, which involves electrically controlling the temperature of the actuating systems to induce an order–disorder phase transition and thereby triggering a thermomechanical actuation response. A strong electric field can produce a dielectric torque to rotate the mesogens due to dielectric anisotropy and induce a direct electromechanical response. The anisotropic mechanical properties of LCNs have also been exploited in the dielectric elastomer actuation mechanism. In this report, we will review the progress in the electrically driven liquid crystal networks (ELCNs). The synergistic effect of LCN material properties and electro-actuation mechanisms provides diverse possibilities for the realization of new robotic functions and advanced actuation control.
2. Electrothermal ELCNs
Electrothermal heating offers an alternative solution to the low-efficiency, time-consuming and slow ambient heating method by providing local and internal heating within an actuator. This enables a faster temperature change process by circumventing the heating/cooling of the bulk surrounding medium (air or liquid), which leads to higher efficiency and faster response, and facilitates the practical application of LCN actuators. Since most of the LCN actuators are based on thermotropic liquid crystals,38 meaning that their order–disorder phase transition and the accompanying actuation motion are temperature-dependent, this indirect heating strategy is expected to be universally applicable to most LCN materials in principle. Compared with other electro-actuation mechanisms, their prominent merits include low driving voltage, and solvent- and electrolyte-free actuation.39 In addition, unlike photothermal actuation where heating is limited to the surface area of the actuator, electrothermal actuation can be implemented in 3D, thick and complex structures when rationally designed. Therefore, this actuation mechanism could have fewer restrictions on the form factor of LCN actuators.The mechanism of electrothermal ELCN actuators is simple: Joule heating and order–disorder phase transition. On applying voltage or current, the electrically conductive element generates Joule heat while transmitting electric current, which increases the temperature to trigger the LC-to-iso (order-to-disorder) phase transition to display the corresponding shape change and motion. On retrieving the electrical energy, the temperature drops so as to induce the disorder-to-order phase transition and the accompanying shape recovery process. Therefore, the manufacturing, characterization, design and actuation-programming of electrothermal ELCN actuators mainly revolve around these two aspects.
2.1 Construction of electrothermal ELCNs
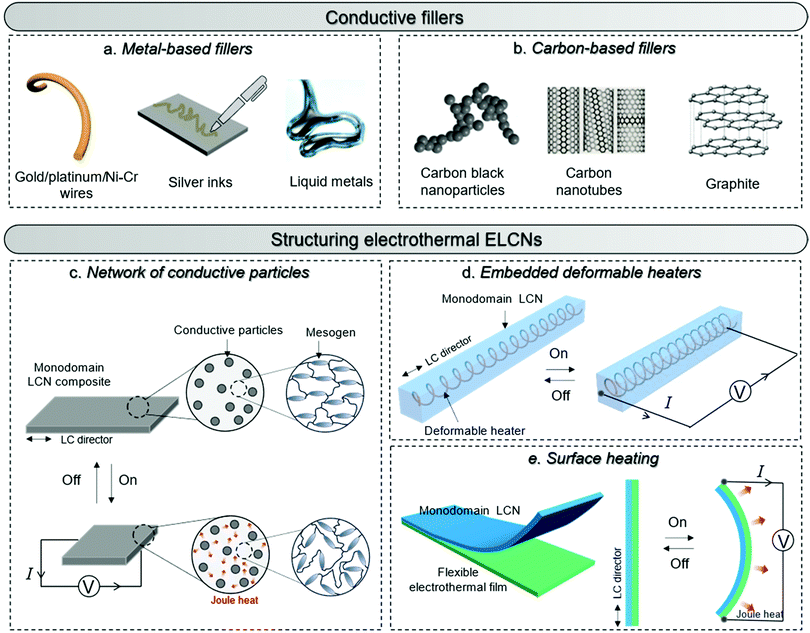
When constructing an electrothermal ELCN actuator, the selection of heating elements and how they are integrated with the LCN are fundamental aspects of the actuator design. The heating elements employed are responsible for imparting electrical conductivity and converting electrical energy into Joule heat. They can be divided into metal-based (Fig. 2a),40,41 such as gold/platinum/nickel–chromium wires, silver ink, and liquid metal, and carbon-based (Fig. 2b),42 such as carbon black nanoparticles, carbon nanotubes, and graphite circuits. Depending on the form of the heating elements and their incorporation methods, electrothermal ELCN actuators can be constructed as macroscopically homogeneous or heterogeneous. The homogeneous type includes LCN-based micro- or nano-composites, in which conductive micro- or nano-fillers are evenly distributed within the LCN matrix and form a conductive network to render the entire composite material electrically conductive (Fig. 2c).43 The heterogeneous type includes numerous examples. In these cases, the electrically conductive component is macroscopically separated from the LCN serving as the actuating component. For example, metal-based deformable heating wires can be fabricated into serpentine shapes via photolithography and etching procedures or machined into spring shapes, and then directly embedded inside the LCN substrate (Fig. 2d), or alternatively, introduced into the surface of the LCN with or without a support layer (Fig. 2e). Conductive inks can be locally printed, sprayed or coated on the surface of the actuator, or filled into the micro-channels to form line patterns or mesh-like circuits.44 Carbon-based conductive sheets/nanofillers can be introduced as surface heating elements. For example, carbon black particles can migrate into the surface region of a highly swollen LCN and achieve surface heating when electricity is applied.45Table 1 summarizes various actuator materials, and their electric input, electrically conductive properties, actuation temperatures, performances, and applications, to overview a variety of electrothermal ELCNs.| Materials | Electrical propertiesa | Stimulus inputb | Actuation temperature, time required | Performancec | Actuation or applications | Ref. |
|---|---|---|---|---|---|---|
| a Ω, Ω mm−1, kΩ □−1, mΩ sq−1 m−1: resistance; S m−1: conductivity. b V, V cm−1: voltage; A: current; mW, W, mW mm−2: power. c %: actuation strain; MPa, kPa, MPa: actuation stress; kJ m−3, J kg−1: work capacity; Hz: actuation frequency; mm: displacement; s: response time; °: bending angle; mm−1: bending curvature; mm s−1: locomotion rate. | ||||||
| Dispersed fillers forming a percolated conductive network | ||||||
| LCE/CB (bulk + surface) | 0.13 S m−1 | 40 V | 75 °C, 30 s | 22.5%/10.5 s | Uniaxial, active cell culture | 59 |
| LCE/LM (83 wt%) | 1 × 104 to 2 × 104 S m−1 | 10 W | — | 50%/30.5 J kg−1/8 & 35 s | Uniaxial, muilticone-flat, walking | 54 |
| LCE/LM (60 vol%) | — | 20.3 W | — | 15.5%/2 Hz (in water) | Uniaxial | 61 |
| Multimaterial-printed LCE–LM (0 and 88 wt%) | 2.86 × 103–2.63 × 104 S m−1 | 8.9 W cm−3 | — | 12%/15 s | Uniaxial, bending | 62 |
| Embedded deformable heaters | ||||||
| LCE/PI-based Pt heater | 3200 Ω | 50 V | — | Diameter: 2.7 mm and 3.8 mm/21 s & 22 s | Radial deformation | 47 |
| LCE tube/PI-based Cu | — | 3 V | 120 °C/30 s | 41%/0.35 MPa/30 & 270 s | Bending, gripping, walking | 51 |
| Disulfide-LCE/PI-based Cu wire | — | 3 V | ∼140 °C, 45 s | 23%/45 s/0.2 MPa/0.75% s−1 | Uniaxial, shearing, bending | 72 |
| LCE/Ni–Cr/Kapton | 1.25 Ω mm−1 | 0.04–0.2 A | 70 °C, 10 s at 0.2 A | 39%/1.36 N/20 s (for LCE/Ni–Cr) or −0.010 mm−1/0.014 mm−1 (for robotic surface) | Surface curvature change | 74 |
| LCE/PI-based Pt | 600 Ω | 430 mW | 137 °C, ∼26 s | 30%/20 s & 10 s | Uniaxial, integrated temperature sensor | 76 |
| LCE/LM channels | 3.4 × 106 S m−1 | — | 122 °C | 15 mm | Uniaxial, closed-loop control | 77 |
| LCE/LM (core) | 3.58 × 106 S m−1 | 40 mW mm−2 | 178.7 °C | 50%/40.7 J kg−1 | Uniaxial, 3D deformation, closed-loop control | 78 |
| Layered with heating elements (surface heating) | ||||||
| LCE/MWCNT–AgNW/PDMS | — | 6.5 V | ∼130 °C, 20 s | 0.46 MPa/9.97 kJ m−3/18 s | Bending, gripping | 44 |
| LCE/CB (surface) | 1.4 S m−1 | 78 mW | ∼80 °C | 50%/∼1.5 s & ∼4.5 s | Uniaxial | 45 |
| LCE/CNT sheets | 0.3 ± 0.1 kΩ □−1 | 15.1 V cm−1 | 150 °C, 5 s | 12%/97 kJ m−3/5 s | Uniaxial | 46 |
| LCE/silver ink/passive framework | <200 mΩ sq−1 m−1 | 1.5 A | — | 140°/180 s | Bending, sequential folding, walking | 50 |
| LCE–CNT/Cu wires | 5.87 × 108 S m−1 | 8 V, 1.6 A | — | ∼1000% stroke for cone-flat deformation | Uniaxial, cone-flat, swinging | 58 |
| LCE/LM-MiniGNR-COOH | 3.2 × 105 S m−1 | 1.5 V | 53 °C | 34°/3.0 s & 2 s | Bending, photothermal actuation | 63 |
| LCN/Ni–Cr wire/Kapton | 102.7 Ω | 8.2 V | 78 °C, 5 s | 760°/0.38 MPa/5 s & 15 s | Bending, walking, gripping, 3D–3D deformation | 73 |
| LCE–CB/PI-based Cr–Au layers/Kapton | 281.8 Ω | 8.2 V | 80 °C | 24%/15 s | Uniaxial, bending, walking, photo-sensing | 75 |
| LCE/LM/silicone | 3.7–4.2 Ω | 0.6 A | ∼80 °C, 10 s | 250°/10 s (or ∼50°/0.8 A, 75 kPa) | Bending, gripping, helical | 79 |
| LCE/CB/Cu track | — | 50 V | — | 90°/20 s & 35 s, rolling at 1.6 mm s−1 | Bending, rolling | 80 |
Apart from the heating elements, actuation-programming of electrothermal ELCNs, taking advantage of the programmability of LCN materials, is also crucial. The programming of ELCN actuators, which involves aligning the mesogens macroscopically and locking the orientation by chain crosslinking, is to, on the one hand, guarantee their spontaneous actuation in response to stimuli cues without external load, and, on the other hand, determine their deformation complexity. As a comparison, an unprogrammed polydomain ELCN can only contract/extend with the help of sufficient external load.1 For pure LCN actuators, their LC director and deformation can be programmed via surface alignment, photoalignment, magnetic or electric fields, or mechanical forces. Each mesogen-aligning method has its own strengths and limitations, which determine their applicability in preparing electrothermal ELCNs. It should be noted that, in order to provide sufficient actuation forces and/or to enable the incorporation of the heating elements, the thickness of electrothermal ELCN actuators is typically about several hundreds of microns or even up to millimeters. This is quite larger than that of most light-responsive LCN actuators which are usually tens of microns thick. As a result, surface-induced alignment and photoalignment are seldomly used in the preparation of the electrothermally driven ELCNs, because their fine control of the LC directors is typically limited to films thinner than 100 μm.46 Besides, upon adding heating elements, competing surface orientations and scattering effects caused by the heaters may occur. Nevertheless, Ware and coworkers utilized highly-aligned, forest-drawn CNT sheets as both the alignment layer in preparation and the surface heating element in electro-actuation, and thereby obtaining an ELCN actuator by surface alignment strategy.46 The CNT sheets can align the LCN precursors along their oriented nanogrooves. Therefore, programming of the LC director and thus the resulting actuation behavior can be achieved by layering and patterning CNT sheets on the cell surfaces as alignment layers prior to polymerization and photocrosslinking. Magnetic fields can orient mesogens in bulk volume, based on which a radially oriented ELCN has been created in a radial magnetic field as reported by Schuhladen and coworkers.47 The resulting annular ELCN can implement radial contraction/extension in the plane, imitating the deformation of the human iris. The most facile and common method for mesogen alignment in ELCNs is by mechanical stretching. This mesogen-aligning strategy is applicable to a variety of homogenous and heterogeneous ELCNs. To further break through the limitations in programming mesogen alignment of ELCNs, 4D-printing is a promising strategy. It offers a way to create centimetre-scale actuators with programmable LC directors and actuator geometries, as the mesogens can be aligned along the print path by the shear/extensional forces during ink extrusion.48,49
2.2 Actuation performance
Generally, the actuation performance of LCN-based actuators depends on their chemical composition and manufacturing process. When the chemical composition is fixed, the actuation performance of pure LCN actuators is mainly determined by the crosslinking density and the order of mesogen arrangement. On this basis, electrothermal ELCN actuators can at best maintain the actuation performance of their original LCN counterparts or show some performance deterioration.In a simplified system where the mesogens in the LCN actuating component are uniaxially aligned, the ELCN composite with dispersed fillers forming a percolated conductive network and the ELCN with embedded flexible heaters can shrink and extend along the LC director during actuation, whereas the ELCN actuator containing a passive layer can exert bending or twisting motion (Fig. 2c–e). The actuation performance (such as the actuation strain, actuation force and actuation speed) depends on the intrinsic thermo-actuation characteristics of ELCN materials, the Joule heat-controlled temperature change and thermal diffusion.
The intrinsic thermomechanical response of the ELCNs, as reflected by the actuation temperature determined by LC-iso phase transition temperature (TLC-iso) and the attainable maximum actuation degree/force, is the basis and reference for the electrothermally induced mechanical response. Joule heat is generated to elevate the temperature until the ELCN completely converts into the isotropic phase (above TLC-iso), where the actuation saturates. Alternatively, a set of temperatures below TLC-iso but within the LC-isotropic phase transition temperature range can also be acquired, at which a gradual change of the actuation strain from 0 to the maximum can be produced.
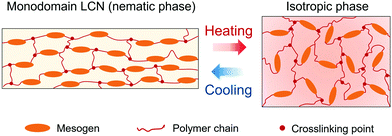
On these bases, controlling temperature oscillations electrically is important in the actuation of electrothermal ELCNs. When the power-on time is sufficiently long, the temperature (T) increases first before reaching an equilibrium stage. Assuming that, when powered on, the Joule heat produced (I2R × dt) is either absorbed by the actuator (mc × dT) or dissipated through convection (h(T − Troom)Scon × dt), and when powered off, energy absorbed (mc × dT) is dissipated by the convection process (h(T − Troom)Scon × dt), Yuan et al. proposed temperature (T)–time (t) relations for the power-on process from t = 0 to t = t1 (eqn (1)), and the power-off process from t = t1 to t = t2 (eqn (2)):50
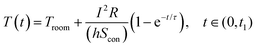 | (1) |
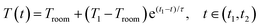 | (2) |
where I is the current, R is the resistance, m is the mass, c is the specific heat, L is the film thickness, ρ is the density, Scon is the convection surface area, and h is the convective heat transfer coefficient of the surrounding medium. According to the eqn (1), for a specific ELCN under fixed ambient conditions (i.e., τ, Troom, h and Scon are fixed), the temperature rise rate and the equilibrium temperature increase with the increasing electrical power input (I2R).
With the power-dependent temperature increase in mind, the magnitude and duration of the input electrical power can be customized to produce the desired temperature oscillation which dictates the actuation response and speed. For example, high power input and short duration can be exploited to realize fast actuation cycles by retaining the temperature increase in the rapid-heating stage, or low power input and long duration can be adopted to achieve steady deformation relying on the temperature-equilibrium stage. In the former case, increasing the magnitude of the input electrical power can effectively increase the actuation speed in the heating process to a certain extent due to the faster heating rate. This mode of electrical actuation generates rapid actuation cycles which are generally preferred in most applications (such as locomotive devices). In the latter case, the actuator can still reach the same actuation amplitude, but at a lower power input and a longer power duration, resulting in a temperature-equilibrium stage and the corresponding steady deformation over a long power-on time. It should be noted that continuing to increase the temperature above the isotropic phase (out of the actuation temperature range) does not boost the actuation degree but causes energy waste and a slow cooling process.44,51
One actuation cycle of electrothermal actuation usually takes a few seconds to several hundred seconds in the reported cases. Further improving the actuation speed is hindered by the inherent low thermal conductivity and slow thermal diffusion of LCN materials.52,53 As a result, cycling frequency of ELCN actuators is limited, e.g., less than ∼2 Hz.54 It should be noted that the problem mentioned above in fact occurs in any type of thermo-responsive polymer actuators.51 In electrothermal ELCN composites, the time frame of thermal diffusion (τ) can be approximated by considering both internal conduction and external convection processes (as proposed by Ford et al.) as follows:54
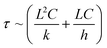 | (3) |
Apart from actuation stroke and actuation speed, force output is another important consideration when selecting an actuator for practical applications.55 Soft materials typically lack the desired actuation stress due to their softness (modulus in the range of 104–109 Pa).56 As the actual force is proportional to the cross-sectional area of the actuator, ELCN actuators can be scaled up during fabrication and actuated throughout the volume of the actuators via electrothermal mechanism for the purpose of greater force. Stacking of several layers of LCNs has been demonstrated to be effective in enlarging the force exerted and the work capacity while maintaining the actuation strain.55,57 It should be mentioned that increasing the size of the actuator may complicate the fabrication process or adversely affect the actuation speed; all these factors should be considered to provide an optimal design. Additionally, other structures, such as interpenetrating networks,27 and LCNs loaded with carbon nanotubes (CNTs) or laminated with CNT sheets have also been proved to have enhanced work capability.58
2.3 Conductive heaters: separately embedded vs. dispersed and rigid vs. soft
The criteria for incorporated heaters include high electrical conductivity, good deformability and robust structure. ELCNs with separated heating elements can rely on the selection of highly conductive heating elements, such as metal wires, printed metal traces or CNT sheets, to ensure high electrical conductivity and low driving voltage. Meanwhile, another critical aspect is to employ geometrical techniques to render these high-conductivity heaters to be also highly flexible and stretchable in the actuating materials, e.g., by film pre-buckling, coil or serpentine structures, which can reduce their constrain on the actuation performance to a negligible level. Therefore, both low voltage-driven electrical heating and non-affected actuation performance are ensured. The main drawback of these heterogeneously configured systems is the non-uniform heating and thus the uneven actuation of the LCN actuators in the plane and/or across the thickness, due to the inherent low thermal conductivity and slow thermal diffusion of LCN materials.52,53Attempts have been made to incorporate carbon-based conductive nanofillers to endow the LCN matrix with electrical conductivity and uniform heating, where the entire ELCN functions as both the heater and the actuator. To obtain an electrically conductive nanocomposite for Joule heating, carbon-based nanofillers, such as carbon black, carbon nanotubes and graphite, should be incorporated at sufficiently high content to form a percolated conductive network. However, in most cases, before satisfactory conductivity can be provided, high content of rigid nanofillers may already have caused detrimental effects like agglomeration, material stiffening, constrained LC phase transition and actuation strain reduction. For example, it was reported that CNTs of up to 2 wt% dispersed within an extruded LCN fibre actuator are insufficient to afford electrical conductivity.58 The addition of 15 wt% carbon black nanoparticles to LCN composites can yield an ELCN with an electrical conductivity of ∼1 S m−1, but the actuation strain is reduced from 35% for the unfilled LCN to 5.2% for the loaded one.59 Moreover, ELCN nanocomposites with rigid fillers generally require a higher voltage for actuation because of their lower electrical conductivity, when compared with those constructed from metal wires or CNT sheets. These cases reflect the trade-off between the actuation properties and the electrical conductivity in ELCN actuators dispersed with rigid nanofillers.
In recent years, a new type of soft fillers, liquid metals, were introduced into LCNs which makes a big difference. Eutectic gallium–indium (EGaIn), a liquid metal (LM) alloy, is commonly used due to its high fluidity and low viscosity (1.99 × 10−3 Pa s) at room temperature, high electrical conductivity (3.4 × 106 S m−1), self-healing, and low toxicity.60 As a fluidic metallic conductor, LM can be incorporated into LCNs to achieve fully soft actuators unlike those with rigid nanofillers or external metal heaters. In 2019, Majidi and co-workers reported the first LCN actuator with fluidic EGaIn LMs as the Joule heating elements (Fig. 3a).54 This system, unlike previous electrothermal ELCNs, combines enhanced thermal and electrical conductivity, largely retaining softness and actuation performance, and unaffected nematic-to-isotropic phase transition. In their study, 50 vol% (83 wt%) of EGaIn microparticles (∼200 to 500 μm in size) are dispersed throughout the LCN. By mechanical sintering (pressing) the as-prepared LM–LCNs, the EGaIn droplets with an insulating, native oxide shell rupture and coalesce to form percolating EGaIn pathways, yielding an electrical conductivity between 1 × 104 and 2 × 104 S m−1. The actuation of the polydomain LM–LCNs under bias loading shows a maximum L/Lo (normalized length, Lo represents length in the contracted state) of ∼1.62, comparable to that of neat LCNs (∼1.74). The deformation is resilient to mechanical damage as the entire sample is conductive (Fig. 3b). Conductive traces can be selectively activated by partial pressing to allow for sequential and local activation, and can self-heal by autonomously forming new conductive traces when mechanically damaged. The actuator can also be programmed via photocrosslinking to perform 2D-to-3D deformations, as shown in Fig. 3c. The same group later found that the size of the EGaIn droplets can be controlled to tune the actuation performance of the polydomain LM–LCN artificial muscles.61 LM–LCNs with smaller EGaIn particles possess higher stiffness and greater force output but reduced actuation strain due to the larger total interfacial area (also interfacial energy) between the LCN matrix and LM particles. For example, under a 70 kPa load, their intrinsic thermal actuation strain decreases from >50% when LM particles are larger (ca. >100 μm) to <5% when LM particles are ca. 10 μm or less. Ware and coworkers reported 4D-printed LM–LCNs where EGaIn droplets (93 ± 30 μm) are dispersed throughout the LCN substrate (Fig. 3d).62 In this study, the printed, monodomain LM–LCN actuators with 88 wt% LM loading possess an electrical conductivity of 2.86 × 103–2.63 × 104 S m−1, and demonstrated ∼11.4% contraction under the voltage and current of 1.6 V and 0.4 A. A decrease in actuation strain and an increase in actuation temperature were reported, which might arise from the hindered photocrosslinking process due to high EGaIn loading. Additionally, multimaterial printing was also exploited to prepare monolithic structures with spatially varied electrical conductivity. Due to the exceptional features of LMs, more and more LM–LCN actuators have been developed in recent years. Not limited to the evenly dispersed LM–LCN composites, LMs can also be incorporated as separate conductive coatings, cores or traces into the LCN matrix to endow the ELCNs new actuation control and multifunctionality.63
 | ||
| Fig. 3 (a) Schematic illustration of LCN/LM composites. (b) Damage-tolerant properties of LCN/LM composites. The LCN/LM film maintains electrothermal actuation performance with self-healed conducting traces of LMs in the composites. (c) Optical images of the shape changes of a programmed LCN/LM. The preprogrammed initial morphology of the LCN/LM film was obtained in the photoinitiated crosslinking stage. (d) 3D-printing LCN/LM actuators with electrothermal and photothermal activation. (a–c) Reproduced with permission.54 Copyright 2019. National Academy of Sciences. (d) Reproduced with permission.62 Copyright 2020, American Chemical Society. | ||
2.4 Actuation-programming of electrothermal LCN actuators
The great potential of electrothermal ELCN actuators in soft robotics applications relies on the multi-faceted programmability of the actuation material system and the high degree of controllability of electrical signals. For electrothermal ELCNs, their actuation behaviors can be programmed via material manufacturing, actuator devising, and/or electrical stimulation control. First, the LC director can be programmed and locked within the ELCN actuators (e.g., by mechanical stress, magnetic field or 4D printing), resulting in a specific molecular arrangement that produces a designated actuation mode (as described in Section 2.1). Second, reprogrammable LCNs based on dynamic covalent bonds are promising materials for ELCNs, as they enable advanced systems combining reprogrammability and electric actuation. Third, for laminated ELCN structures with passive layers, their deformation depends on the layout and distribution of the active/passive components, or the shape memory effect of the passive layers. Fourth, the control of multiple independent circuits specifically patterned in the actuator can also be used for actuation control and programming. To accomplish complex actuation modes and multifunctionality, several kinds of actuation-programming elements can be involved simultaneously. Examples are given below.For instance, Cai and coworkers demonstrated a reprogrammable electro-LCE system.72 The actuator was constructed by sandwiching a heating wire between two pieces of disulfide LCE (ss-LCE) films which can strongly bind together through disulfide bonds. The ss-LCEs are reprogrammable by heating up (180 °C, 20 min) for debonding the network, cooling down (room temperature) for deforming, and holding the deformation for shape fixation and mesogen-alignment locking (Fig. 4a). On the other hand, since shape reprogramming and electrical actuation involve stretching of the actuator, to ensure good stretchability in these processes, a heating wire of half-and-half Peano shape fabricated via photolithography was adopted to guarantee stretchability in arbitrary directions. Meanwhile, the ss-LCE films were pre-stretched biaxially prior to wire-integration so as to attain a biaxially-compressed heating wire in the as-prepared polydomain actuator, which further enhanced the stretchability. Based on this design, a single actuator can be reprogrammed repeatedly to fulfil uniaxial length changes along different directions. Distinct actuation modes, i.e., contraction, bending and shearing, can also be encoded in the actuator (Fig. 4b).
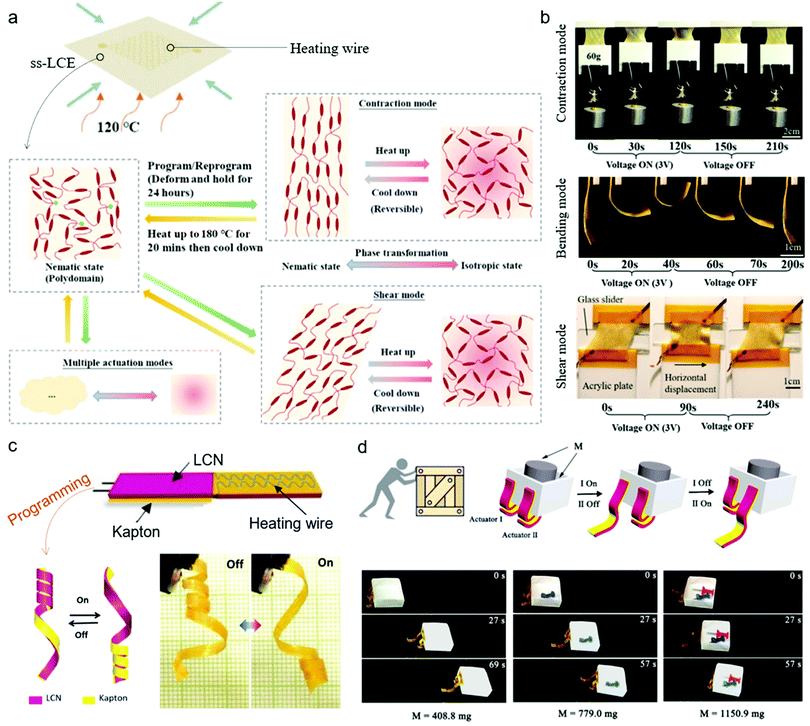 | ||
| Fig. 4 (a) Schematic illustration of the reprogrammable ss-LCE actuator based on disulfide exchange reaction. (b) Images of electro-driven contraction, bending and shear actuation modes that can be programmed in the same ss-LCE actuator. (c) A helical “Janus” ELCN actuator displaying twisting–untwisting motion simultaneously on its two parts. (d) A “Janus” soft robot walking while pushing a box. (a and b) Reproduced under the terms of the CC-BY 4.0 License,72 Copyright 2020, John Wiley and Sons. (c and d) Reproduced with permission.73 Copyright 2019, John Wiley and Sons. | ||
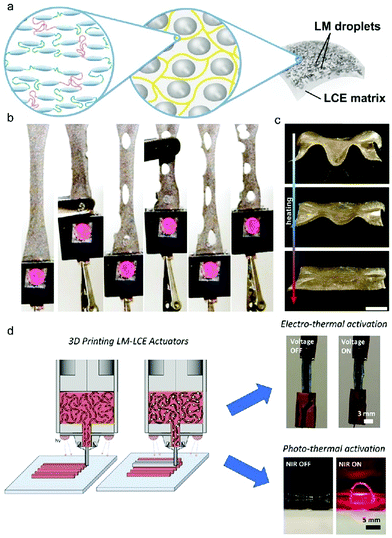
A good example is the versatile tubular actuator reported by Cai and coworkers.51 With three sets of heating wires to control a single tubular actuator, it can bend/unbend toward six different directions or homogeneously contract (∼40%)/extend. Daraio and colleagues recently developed a flexible and deformable robotic surface controlled by multiple circuits.74 In their work, they created an assembled and layered soft robot, structured as two active LCN grids (serving as 1D contractile artificial muscles) sandwiching a passive Kapton grid in between (serving as a foldable skeleton) (Fig. 5a). Additionally, Kapton cover scales were attached on the nodes of the 3 × 3 grid to act as an artificial skin with sufficient mechanical stiffness. As shown in Fig. 5b, each active LCN grid contains two sets of stretchable heating coil arrays placed orthogonally, with each array being controlled by an independent current source. The total four control channels of the assembled system can be programmed with specific current evolution at will, so as to spatiotemporally control the relative length of top and bottom strips that dictate the surface curvature. Therefore, a wide range of surface deformation and real-time control were achieved for manipulating objects on it (Fig. 5c). Another related example is the complex 3D-printed actuator assisted by LCNs.50 The structure contains 3D-printed non-active components, where the elastomeric Tangoblack is for laminating with the separately prepared monodomain LCN strip, and the plastic Verowhite functions as the rigid framework. Silver conductive wires were printed by direct ink writing (DIW) between the elastomer and the LCN. By Joule heating, bending of the laminated actuators is driven by the uniaxial deformation of the LCN strip. Thus, it can serve as active hinges in the printed and integrated composites to induce the folding and unfolding of a morphing airplane, a miura-ori structure, and a crawler. By employing multiple conductive wires, the authors realized addressable heating and thus sequential folding of a cubic box through the independent control of multiple laminated hinges. Multiple-circuit control is also utilized in soft walking devices. While for the widely explored light-guided LCN-based walkers the walking direction could be tuned by the light scanning direction, in the electro-driven LCNs, the walking direction of a single device can be changed by electrical signal-programming, as demonstrated by Wang and coworkers.75
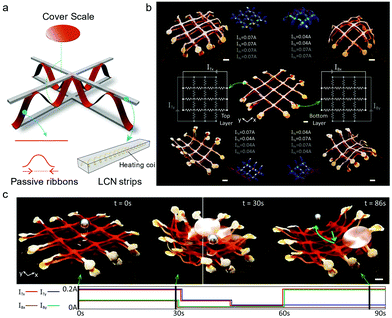 | ||
| Fig. 5 (a) Illustration of the layered soft robot including the cover scales, heating coil-embedded LCN strips, and passive Kapton ribbons. (b) Different attainable shapes of the robotic surface controlled by four independent current sources. (c) Robotic surface performing different tasks. Reproduced with permission.74 Copyright 2021, AAAS. | ||
2.5 Advanced control and functions in electrothermal ELCNs
In other cases, the incorporated conductive elements can function as both the heater and the sensor concomitantly when judiciously designed, permitting self-sensing capability which means that the actuator can detect and sense the actuation process by itself instead of relying on an additional sensing element/chip. Majidi and coworkers built an LCN actuator in which the LM (eutectic gallium–indium) channels are embedded within the LCN matrix.77 Through this structure, the content of LMs is reduced, compared with their previously reported LM–LCN composites containing uniformly dispersed LM throughout the LCN matrix. More importantly, the LM channels not only serve as a soft and compliant Joule heater, but also exhibit concomitant resistance changes during shape morphing. In this case, the changes in resistance can be correlated to changes in the actuation strain, i.e., electromechanical coupling. Consequently, self-sensing capability and closed-loop control can be realized. Toward this end, the resistance threshold value as a function of time is set in a control program, with which closed-loop control is operated by delivering and monitoring the voltage and current inputs while simultaneously calculating the resistance through the same power-supply unit under the control of MATLAB. The actuator is powered on/off automatically according to the resistance feedback when the specified thresholds are reached, achieving closed-loop control for repeatable and programmable actuation.
In a recent report, Kotikian et al. encapsulated LM into LCE actuators by core (LM)–shell (LCE) 3D printing technology.78 The resulting innervated liquid crystal elastomer (iLCE) was endowed with prescribed thermal responses, up to ∼50% actuation strain, self-sensing capability and closed-loop control (Fig. 6a). These advanced properties are attributed to several aspects of the material system. First, different voltages can be applied to reach the target actuation temperature within the LC-iso phase transition range to control the degree of contraction, corresponding to its prescribed actuation responses. Second, as the fibre length (L/L0) changes, a concomitant change in the actuator resistance (R/R0) can be quantified. The ultimate R/R0 is positively related to L/L0 and temperature (T):
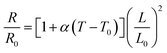 | (4) |
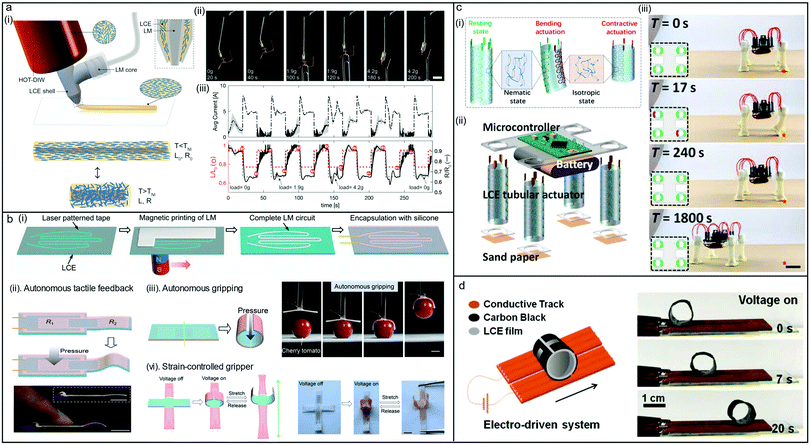 | ||
| Fig. 6 (a) (i) Schematic illustration of core–shell 3D printing of iLCE fibers composed of an LM core surrounded by an LCE shell, whose LC director is aligned along the printing direction. (ii and iii) Images and curves of a representative iLCE fiber with closed-loop control and self-adjusting actuation under different loading conditions. (b) (i) Schematic illustration of the magnetic printing of LM on the LCE film. Proprioception capability of the LM-LCE actuator: (ii) autonomous tactile feedback, (iii) autonomous gripping and (vi) strain-controlled gripping. (c) (i) Multi-direction deformation of electro-driven LCE tubular actuators. (ii and iii) Composition and locomotion of an assembled, untethered ELCN soft robot. (d) Illustration and images of a CB–LCE cylinder rolling on a conductive track. (a) Reproduced with permission.78 Copyright 2021, John Wiley and Sons. (b) Reproduced with permission.79 Copyright 2021, American Chemical Society. (c) Reproduced under the terms of the CC-BY 4.0 License.51 Copyright 2019, AAAS. (d) Reproduced with permission.80 Copyright 2020, American Chemical Society. | ||
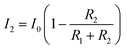 | (5) |
Intriguingly, another strategy to get rid of electric wires was demonstrated by Yang and coworkers utilizing a set-up comprising a mobile LCN-based cylinder with patterned conductive regions and a stationary conductive track (Fig. 6d).80 This design is inspired by electric locomotives for which the electrical energy is supplied by a conductive track instead of the directly contacted electric wires. The actuator is a closed cylindrical LCN band with a uniaxial mesogen alignment, and on its outer surface, four U-shaped carbon black (CB) conductive regions were patterned. When it was placed on a conductive copper track powered by a 50 V DC supply, it can roll continuously at the rate of 1.6 mm s−1. The mechanism is based on the dynamic connection between the four conductive regions of the rolling actuator and the static conductive track, which generates intermittent and local Joule heat to change the local curvature of the cylindrical actuator and thereby shifts its center of gravity continuously.
3. Direct electromechanical response of ELCNs
Electric field can induce orientation of reactive mesogenic monomers and has been utilized for LCN preparation. For nematic LCs, this resides on the dielectric anisotropy of LC molecules: Δε = ε‖ − ε⊥, ε‖ and ε⊥ being the dielectric constants parallel and perpendicular to the long axis of the mesogens, respectively. The mesogens employed typically have Δε > 0 and they align along the electric field direction; otherwise they align perpendicularly when Δε < 0.81,82 This also applies to mesogens incorporated into a crosslinked polymer network, although with much larger resistance and constraints from the network. Consequently, the electric field-induced mesogen reorientation in polymeric LCs can concomitantly generate a deformation of the soft solid materials. Generally, this actuation mechanism produces small strains while requiring high electric field strength.83 The actuation is often enhanced by increasing Δε or reducing the elastic modulus of the material. These conditions are required so that the dielectric torque exerted on the mesogens, proportional to ΔεE2 (E: electric field strength), can overcome the resistance, proportional to elastic modulus.84For example, under a lateral alternating electric field (7.5 V μm−1, 900 kHz) provided by interdigitated electrodes (IDE), Broer and coworkers realized oscillating surface topographies on a homeotropic nematic LCE with a ∼6% height change at 41 °C.85 Liu and co-workers further reported on a chiral nematic LCE that forms surface corrugations due to its helicoidal molecular organization along the film plane.86 The alternating homeotropic and planar LC alignments within the molecular helices produce hills and valleys, respectively. Under an alternating electric field of 16.1 Vrms μm−1 (900 kHz) generated by IDE, corrugation inversion (6% of the initial coating thickness), where the hills (or valleys) invert into valleys (or hills), was elicited at room temperature with a response time of ∼10 s (Fig. 7a–c). This deformation was utilized for sand removal and self-cleaning (Fig. 7d). In these highly crosslinked dry elastomers, mesogen reorientation is prohibited, but the dielectric torque causes a loss of the LC order that leads to anisotropic stress and surface deformation. Considering the low dielectric constant of the typical nematic LCEs, a small amount of CNTs was incorporated into nematic LCEs to enhance their electromechanical response. The large polarizability anisotropy of CNTs greatly increases the effective dielectric anisotropy of the composite material. In a uniaxially stretched LCE composite with ∼0.02% CNTs, a stress of ∼4.5 kPa was produced in response to E ≈ 1.9 V μm−1 at room temperature. White and coworkers further added single-walled carbon nanotubes (SWNTs, 0.02 wt%) to nematic LCEs, and achieved alignment of both the mesogens and SWNTs by the photoalignment method. On this basis, programming of the LC alignment and thus the deformation under an electric field is permitted. For example, a complex cone-like shape was formed by LCE-SWNT with a radial LC alignment under a DC field of 1.2 V μm−1 at an elevated temperature of 90 °C (Fig. 7e).87 The electromechanical response can be attributed to the rotation of SWNTs and mesogens due to the interfacial polarization between SWNTs and the matrix. The actuation can also be improved by elevating temperature or preparing LC gels to reduce the material's modulus. In particular, in LC gels, the intermolecular friction and rotation barrier are greatly reduced, allowing the realization of larger strain at lower electric field strength, as demonstrated by a series of LC gels reported by Urayama and coworkers.88,89
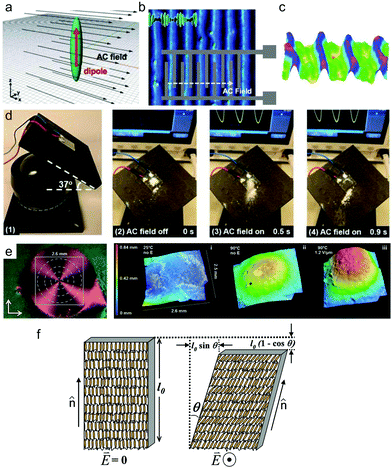 | ||
| Fig. 7 (a) Schematic showing a LC molecule with positive dielectric anisotropy experiencing torque when placed in a perpendicular electric field. (b) Optical microscope image of the formed line patterns perpendicular to the electric field observed between crossed polarizers. Insets present the rotating direction of the helix and the IDE substrate. (c) 3D images of the activated topographies of (b). (d) Self-cleaning based on AC field-driven surface topographies change. (e) Electric-field-induced shape changes of an LCE/CNT composite film: (i) before heating, (ii) after heating to 90 °C, and (iii) after applying an electric field of 1.2 VDC μm−1 (right). In this composite, 0.02 wt% CNT was dispersed in an LCE matrix with a +1 defect and azimuthal orientation (left). (f) Schematic depicting of the contraction and shearing response of a chiral SmA* LCE under an applied electric field due to the electroclinic effect. LC molecules tilt in the opposite direction upon reversal of the field polarity. (a–d) Reprinted with permission.86 Copyright 2018, John Wiley and Sons. (e) Reprinted with permission.87 Copyright 2018, American Chemical Society. (f) Reprinted with permission.94 Copyright 2007, American Institute of Physics. | ||
Ferroelectric LCE represents a type of LCE with a chiral smectic C (SmC*) phase, in which the chiral rod-like mesogens in the smectic layers tilt away from the layer normal.90,91 The symmetry-breaking caused by the chirality of LC molecules in the SmC* phase yields a spontaneous polarization perpendicular to the plane formed by the molecular axis (i.e., LC director) and the layer normal.3,92 A macroscopic uniform orientation for ferroelectric LCEs can be induced by electrical field or shear deformation, and subsequently be locked in the polar state by crosslinking. For example, they can be crosslinked in the smectic A (SmA*) phase where mesogens are parallel to the layer normal, which results in a polar axis in the layer plane; or they can be crosslinked in the SmC phase, resulting in a tilted polar axis.93 In monodomain SmA* elastomers, the coupling of the electric field along the layer plane direction and the lateral dipole of the mesogens can cause the mesogens to tilt perpendicular to the electric field, i.e., the electroclinic effect (Fig. 7f).94 This results in an in-plane shear deformation: a decrease in the smectic layer thickness and an expansion in the layer plane direction. Therefore, depending on the LC alignment within a film, different deformations can occur in an AC field. When the smectic layers are parallel to the film surface, the electroclinic effect can induce a film thickness reduction; when the smectic layers are perpendicular to the film surface, the electroclinic effect can produce an in-plane contraction along the director and an extension normal to the director. As a soft material, ferroelectric LCEs can provide a relatively larger strain compared to that of the rigid piezoelectrics. Nevertheless, their strain is generally much smaller than the typical values of LCN actuators relying on temperature-controlled nematic–isotropic phase transition, and the high electric field strength used is also a limitation for practical applications.
4. Dielectric ELCNs
The actuation mechanism of the widely explored dielectric elastomer actuator (DEA) has also been applied to LCN materials. DEA is typically made by sandwiching a passive elastomer between two compliant electrodes coated on it. Applying a high voltage can induce Maxwell stress (stress caused by the electrostatic attraction of the two electrodes), which compresses the DEA along the vertical direction of the two electrodes and expands it in the plane (Fig. 8a). This mechanism can provide highly efficient and fast actuation. However, traditionally, it usually requires pre-strain and the realization of complex deformation is difficult or involves complex manufacturing procedures. In this regard, Davidson and coworkers utilized anisotropic LCEs and developed dielectric LCE actuators.95 These actuators possess high energy conversion efficiency and fast actuation rate ascribed to the DEA actuation mechanism, as well as shape programmability brought by the LCE. The actuation behavior relies on the anisotropic stiffness and Poisson's ratio of the LCEs, both of which are determined by the orientation of the mesogens. Under Maxwell stress, the thickness of the LCE can be compressed, and the expansion in-plane is preferentially along the direction perpendicular to the LC director (i.e., the soft direction), as shown in Fig. 8b. The actuation is confined in the linear strain range to ensure elastic recovery and requires no temperature change. Furthermore, the dielectric LCE actuators can bear loads 700 times heavier and respond at a frequency of 30 Hz. It also possesses high shape programmability via the photoalignment method. As shown in Fig. 8c, director configuration of an azimuthal defect type yields a positive Gaussian curvature (cone), while the radial director configuration results in a negative Gaussian curvature (saddle-like anti-cone). Further patterning the LC director into a pixelated array of radial and azimuthal defects, the monolith can display complex out-of-plane buckling when actuated electrically (Fig. 8d and e). Another strength is the high actuation efficiency of the dielectric LCE actuator of ∼20%, which is attributed to the anisotropy of the elastic modulus and Poisson's ratio. As a comparison, the actuation efficiency of other LCE actuators reported is much lower, e.g., 0.05% for an LM-loaded LCE.61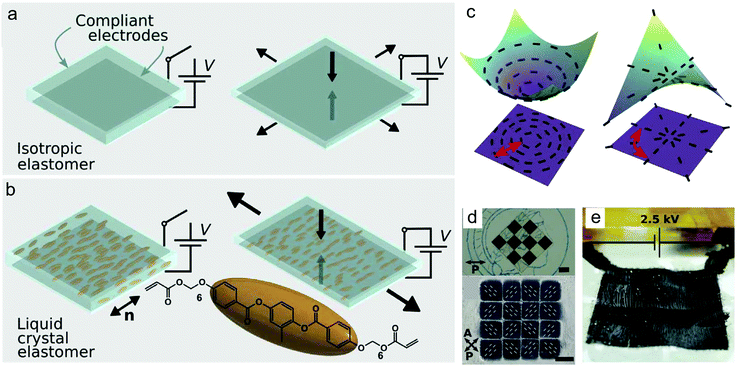 | ||
| Fig. 8 Schematics of (a) a traditional isotropic dielectric elastomer actuator and (b) an aligned dielectric LCE actuator (DLCEA) in the electric field-off and electric field-on states. (c) Illustration showing an azimuthal defect-type DLCEA deforming into a cone with locally positive Gaussian curvature (left), and a radial defect-type DLCEA deforming into an anti-cone with locally negative Gaussian curvature (right). (d) LC alignment patterns of DLCEA and (e) a large visible deformation of the DLCEA's surface upon 2.5 kV charging. Reproduced under the terms of the CC-BY 4.0 License,95 Copyright 2020, AAAS. | ||
5. Conclusions and outlook
Electrical energy could easily be one of the most favoured stimuli because of its availability, controllability, programmability and electronic circuit-based computing functionality. Light for actuating, such as laser, UV light, etc., is usually not so readily attainable. Humidity is an easily accessible stimulus, but more difficult to control. Besides, since most other non-electrical stimuli may rely on auxiliary electronics96 (e.g., light sources or humidity controllers) for their generation, amplitude-control or even the pre-programming of stimulation patterns, it seems more efficient and easier to actuate soft robots directly by electrical energy in most practical cases. In this article, we review recent ELCN actuators developed based on different electro-actuation mechanisms: electrothermally driven order–disorder phase transition, electromechanical effects based on the coupling of a strong electric field and dielectric anisotropy/intrinsic polarization, and Maxwell stress-induced actuation of dielectric LCNs. Among them, the electrothermal ELCN actuator is the type that has been studied extensively because of its high actuation degree and low driving voltage. Complex mesogen-alignment profiles can also be created within LCN substrates for electrothermal ELCN actuators by mechanical forces, network reconnection, 3D-printing technology or magnetic fields. In addition to this, structural design, device configuration, and electrical signal-programming can be further exploited for programming actuation behaviours, which ultimately leads to various complex shape changes, locomotion, and object-manipulating functions. Extensive research on them also extends to the advanced actuation control (closed-loop control), intelligent actuation behaviours (force-perceptive soft robot) and fully untethered soft robotic systems. The main disadvantage of these actuators stems from the significant heat production and slow heat diffusion. The former may make them unsuitable for heat-intolerant applications, for example, some biomedical applications. The latter leads to their low energy efficiency and low actuation frequency. Furthermore, dielectric ELCNs have also gained increasing attention due to (1) their excellent actuation performance (high strain rate, large force output, and high energy efficiency) determined by their actuation mechanism and (2) their large and programmable anisotropy in stiffness and dielectric constant dictated by the mesogen alignment in LCN materials.97 Dielectric ELCNs can be particularly superior for providing high actuation frequency (up to 30 Hz)95 and athermal actuation, but their main limitation is their high drive voltages, typically up to several kilovolts. In comparison, directly using an electrical field to induce the mesogen (re)orientation and generate a macroscopic shape change or movement could be more difficult (e.g., both high voltage in the kilovolt range as well as elevated temperatures may be required), and the outcomes (e.g., small strain) are generally less satisfactory when compared to those of other types of ELCNs. To date, relevant studies have rarely reported the application of these actuators and are more important from a fundamental research perspective. Table 2 summarizes the main features of different ELCNs. Readers can find more comparison between various electro-active polymer actuators in ref. 56, 96 and 98.| Electrothermal ELCNs | ELCNs with direct electromechanical responses | Dielectric ELCNs | |
|---|---|---|---|
| Working mechanism | Joule heat induced LC-isotropic phase transition | Electric field induced re-orientation of mesogens | Electrostatic force induced anisotropic strain |
| Stimulus input | Low voltage (mostly ≤10 V) | High voltage (kV range)/electric field (MV m−1 range) | High voltage (KV range)/electric field (100–150 MV m−1) |
| Actuation strain | Large (12–50%) | Small (0.8–8.2%)94 | 20%,97 possible to be larger |
| Actuation speed | Low (actuation frequency ≤2 Hz)61 | Fast (actuation frequency 0.2–20 Hz)94 | Fast (actuation frequency up to 30 Hz)95 |
| Efficiency | Mostly ≤0.05%61 | — | ∼20%95 |
| Strain–voltage relationship | Non-linear | Quadratic relationship between voltage and strain | Quadratic relationship between voltage and strain |
| Operating temperature | Room temperature; internal temperature 53–180 °C | Room temperature or elevated temperature (90 °C)87 | Room temperature |
| Strategies for mesogen alignment | Mechanical stretching, magnetic field, 3D-printing | All strategies for pure LCNs are possible | All strategies for pure LCNs are possible |
| Motion type | Programmed shape changes, griping, walking, rolling | Surface morphology changes, contraction/extension | Programmed shape changes |
Although electrical energy is seen as a practical and promising stimulus for powering and controlling LCN actuators, the development of ELCNs is still at an early stage and still faces a number of challenges. In terms of preparation, particularly for electrothermal ELCNs, there are two main challenges. The first is to further improve the design of conducting networks and construct a flexible, highly conductive, interference-free, robust and stable electrically conductive system that can resist large strain changes, e.g., 50% when actuated or hundreds of percent when stretched for mesogen-aligning. For stretchable electronics (e.g., sensors and power supplies), a major issue is the trade-off between stretchability (also compliance) and electrical conductivity.96 Likewise, for electrothermal ELCNs, there is a trade-off between actuation strain (or actuation capability) and conductivity. As seen in many existing cases, the actuation performance is often sacrificed more or less for the sake of a good and robust conducting network. The deterioration of actuation performance is caused by some side effects such as imposed mechanical constraints, materials hardening, and phase transition suppression brought about by the introduction of high content of conductive elements. Thus, novel conductive ELCN actuators with high electrical conductivity, compliance, largely preserved actuation capability, low conductive filler content and high homogeneity are highly pursued. Secondly, the limitations on the programmability and form factor of ELCN actuators need to be further lifted, especially when material conductivity is also an essential consideration. To date, the general shapes and sizes of the existing LCN actuators (e.g., thin films of centimetre-scale or fibres) greatly limit their scalability and integration in soft robotic applications.58 Therefore, strategies are being explored intensively to expand the achievable geometry and actuation modes of LCN actuators, such as reprogrammable LCNs and 4D-printing LCNs. These strategies, along with the well-established mesogen alignment methods, including surface alignment, photoalignment, and magnetic/electric field-induced alignment, can all be applied to the processing and programming of dielectric ELCNs or ELCNs based on direct electromechanical responses. When it comes to electrothermal ELCNs, the device fabrication and mesogen-alignment processes can be more complicated. For example, very thin electrothermal ELCNs are hard to be obtained if high stability and conductivity are to be imparted; establishing specific 2D/3D LC director profiles for thick electrothermal ELCNs is challenging; the opacity caused by fillers also significantly affects the photocrosslinking degree; all of these could limit the preparation and actuation-programmability of ELCN actuators and remain to be addressed. Therefore, in the future, innovations in techniques, strategies, and materials/device designs are expected to reconcile between building a good conducting system and the desired form factor and mesogen alignment of ELCNs. 4D printing of a thermally (re)programmable LCN, along with electrically conductive soft metal inks, is a possible solution to eliminate the limitations mentioned above. This approach is very promising for future ELCNs, as 4D printing technology, novel LCN materials, and soft metal conductors (LMs) all together hold great potential for making more advanced and intelligent systems for practical applications, possibly in a scalable manner.
In addition to the challenges faced by the ELCNs in the preparation process, other major challenges to be addressed are about their actuation properties. Electro-actuation provides an effective solution for activating actuators with complex shapes and arbitrary sizes. Different from the light stimulation having an effect on the surface regions, the electro-actuation can be induced inside the complex structure and throughout the entire volume of the actuator. In this regard, ELCN offers the possibility to actuate sophisticated, 3D, bulky structures including those emulating various 3D creatures. This could be further developed as one of the main strengths of ELCNs compared to other responsive LCN actuators. Furthermore, to fully unleash the potential of the programmable and anisotropic LCN materials for electrical actuation, other electro-actuation mechanisms99,100 can be further explored with LCN-based materials, e.g., the ion motion-induced deformation for ionic electroactive polymers.56 Jákli and coworkers reported the bending actuation of ionic liquid-incorporated LCN materials driven by a voltage below 1 V.101 Taking advantage of the superior features such as the small driving voltages (typically below 5 V) and athermal actuation, ionic ELCN actuators with preprogrammed actuation patterns could be developed for wearable applications.102 More importantly, related studies on wireless actuation, advanced auto-control and actuating system-intelligence are still quite limited but highly desired. More effort is needed to develop such advanced ELCN actuating systems, preferably by improving materials intelligence, such as molecular order-determined actuation complexity, self-sensing capability and self-regulating capability, so as to also allow neat design and simple control.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Y. Z. acknowledges the financial support from the Natural Sciences and Engineering Research Council of Canada (NSERC), le Fonds de recherche du Quebec: Nature et technologies (FRQNT) and the Quebec Centre for Advanced Materials. Y. X., Z. J. and J. H. are grateful to China Scholarship Council (CSC) and FRQNT for awarding them scholarships. X. C. thanks CSC for awarding her a scholarship.Notes and references
- T. J. White and D. J. Broer, Nat. Mater., 2015, 14, 1087–1098 CrossRef CAS PubMed
.
- F. Lancia, A. Ryabchun and N. Katsonis, Nat. Rev. Chem., 2019, 3, 536–551 CrossRef CAS
.
- C. Ohm, M. Brehmer and R. Zentel, Adv. Mater., 2010, 22, 3366–3387 CrossRef CAS PubMed
.
- D. Mistry, N. A. Traugutt, K. Yu and C. M. Yakacki, J. Appl. Phys., 2021, 129, 130901 CrossRef CAS
.
- D. Liu and D. J. Broer, Langmuir, 2014, 30, 13499–13509 CrossRef CAS PubMed
.
- Z. C. Jiang, Y. Y. Xiao, X. Tong and Y. Zhao, Angew. Chem., Int. Ed., 2019, 58, 5332–5337 CrossRef CAS PubMed
.
- H. Shahsavan, A. Aghakhani, H. Zeng, Y. Guo, Z. S. Davidson, A. Priimagi and M. Sitti, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 5125–5133 CrossRef CAS PubMed
.
- M. Pilz da Cunha, S. Ambergen, M. G. Debije, E. F. Homburg, J. M. den Toonder and A. P. Schenning, Adv. Sci., 2020, 7, 1902842 CrossRef CAS PubMed
.
- H. Zeng, H. Zhang, O. Ikkala and A. Priimagi, Matter, 2020, 2, 194–206 CrossRef PubMed
.
- Y. Y. Xiao, Z. C. Jiang, L. Yin, J. Jiang and Y. Zhao, J. Mater. Chem. C, 2021, 9, 16566–16575 RSC
.
- O. M. Wani, H. Zeng and A. Priimagi, Nat. Commun., 2017, 8, 15546 CrossRef CAS PubMed
.
- D. J. Roach, C. Yuan, X. Kuang, V. C.-F. Li, P. Blake, M. L. Romero, I. Hammel, K. Yu and H. J. Qi, ACS Appl. Mater. Interfaces, 2019, 11, 19514–19521 CrossRef CAS PubMed
.
- W. Wei, Z. Zhang, J. Wei, X. Li and J. Guo, Adv. Optical Mater., 2018, 6, 1800131 CrossRef
.
- R. Tang, Z. Liu, D. Xu, J. Liu, L. Yu and H. Yu, ACS Appl. Mater. Interfaces, 2015, 7, 8393–8397 CrossRef CAS PubMed
.
- M. Rogóż, H. Zeng, C. Xuan, D. S. Wiersma and P. Wasylczyk, Adv. Optical Mater., 2016, 4, 1689–1694 CrossRef
.
- M. Wang, X.-B. Hu, B. Zuo, S. Huang, X.-M. Chen and H. Yang, Chem. Commun., 2020, 56, 7597–7600 RSC
.
- M. Cheng, H. Zeng, Y. Li, J. Liu, D. Luo, A. Priimagi and Y. J. Liu, Adv. Sci., 2021, 2103090 Search PubMed
.
- M. del Pozo, C. Delaney, M. Pilz da Cunha, M. G. Debije, L. Florea and A. P. Schenning, Small Struct., 2021, 2100158 Search PubMed
.
- Z. Wang, K. Li, Q. He and S. Cai, Adv. Mater., 2019, 31, 1806849 CrossRef PubMed
.
- Z.-Z. Nie, B. Zuo, M. Wang, S. Huang, X.-M. Chen, Z.-Y. Liu and H. Yang, Nat. Commun., 2021, 12, 2334 CrossRef CAS PubMed
.
- J. Kloos, N. Jansen, M. Houben, A. Casimiro, J. Lub, Z. Borneman, A. P. Schenning and K. Nijmeijer, Chem. Mater., 2021, 33, 8323–8333 CrossRef CAS PubMed
.
- L. Lei, L. Han, H. Ma, R. Zhang, X. Li, S. Zhang, C. Li, H. Bai and Y. Li, Macromolecules, 2021, 54, 2691–2702 CrossRef CAS
.
- Y.-Y. Xiao, Z.-C. Jiang and Y. Zhao, Adv. Intell. Syst., 2020, 2, 2000148 CrossRef
.
- Z. Wang and S. Cai, J. Mater. Chem. B, 2020, 8, 6610–6623 RSC
.
- H. Kim, J. Gibson, J. Maeng, M. O. Saed, K. Pimentel, R. T. Rihani, J. J. Pancrazio, S. V. Georgakopoulos and T. H. Ware, ACS Appl. Mater. Interfaces, 2019, 11, 19506–19513 CrossRef CAS PubMed
.
- R. Yang and Y. Zhao, ACS Macro Lett., 2018, 7, 353–357 CrossRef CAS PubMed
.
- H.-F. Lu, M. Wang, X.-M. Chen, B.-P. Lin and H. Yang, J. Am. Chem. Soc., 2019, 141, 14364–14369 CrossRef CAS PubMed
.
- L. Dong, X. Tong, H. Zhang, M. Chen and Y. Zhao, Mater. Chem. Front., 2018, 2, 1383–1388 RSC
.
- S. Serak, N. Tabiryan, R. Vergara, T. J. White, R. A. Vaia and T. J. Bunning, Soft Matter, 2010, 6, 779–783 RSC
.
- A. H. Gelebart, D. J. Mulder, M. Varga, A. Konya, G. Vantomme, E. Meijer, R. L. Selinger and D. J. Broer, Nature, 2017, 546, 632–636 CrossRef CAS PubMed
.
- Y. Y. Xiao, Z. C. Jiang, J. B. Hou and Y. Zhao, Nat. Commun., 2021, 12, 624 CrossRef CAS PubMed
.
- Y. Liu, B. Xu, S. Sun, J. Wei, L. Wu and Y. Yu, Adv. Mater., 2017, 29, 1604792 CrossRef PubMed
.
- C. Feng, C. P. H. Rajapaksha, J. M. Cedillo, C. Piedrahita, J. Cao, V. Kaphle, B. Lüssem, T. Kyu and A. Jákli, Macromol. Rapid Commun., 2019, 40, 1900299 CrossRef CAS PubMed
.
- R. Pelrine, R. Kornbluh, Q. Pei and J. Joseph, Science, 2000, 287, 836–839 CrossRef CAS PubMed
.
- Y. Wu, J. K. Yim, J. Liang, Z. Shao, M. Qi, J. Zhong, Z. Luo, X. Yan, M. Zhang and X. Wang, Sci. Robot., 2019, 4, eaax1594 CrossRef PubMed
.
- Y. Hu, J. Liu, L. Chang, L. Yang, A. Xu, K. Qi, P. Lu, G. Wu, W. Chen and Y. Wu, Adv. Funct. Mater., 2017, 27, 1704388 CrossRef
.
- H. S. Wang, J. Cho, D. S. Song, J. H. Jang, J. Y. Jho and J. H. Park, ACS Appl. Mater. Interfaces, 2017, 9, 21998–22005 CrossRef CAS PubMed
.
- M. P. Da Cunha, M. G. Debije and A. P. Schenning, Chem. Soc. Rev., 2020, 49, 6568–6578 RSC
.
- Q. Li, C. Liu, Y.-H. Lin, L. Liu, K. Jiang and S. Fan, ACS Nano, 2015, 9, 409–418 CrossRef CAS PubMed
.
- A. Sánchez-Ferrer, T. Fischl, M. Stubenrauch, H. Wurmus, M. Hoffmann and H. Finkelmann, Macromol. Chem. Phys., 2009, 210, 1671–1677 CrossRef
.
- C. P. Frick, D. R. Merkel, C. M. Laursen, S. A. Brinckmann and C. M. Yakacki, Macromol. Rapid Commun., 2016, 37, 1912–1917 CrossRef CAS PubMed
.
- M. Shahinpoor, Smart Structures and Materials 2000: Electroactive Polymer Actuators and Devices (EAPAD), International Society for Optics and Photonics, 2000, vol. 3987, pp. 187–192 Search PubMed.
- M. Chambers, H. Finkelmann, M. Remškar, A. Sánchez-Ferrer, B. Zalar and S. Žumer, J. Mater. Chem., 2009, 19, 1524–1531 RSC
.
- H. Liu, H. Tian, J. Shao, Z. Wang, X. Li, C. Wang and X. Chen, ACS Appl. Mater. Interfaces, 2020, 12, 56338–56349 CrossRef CAS PubMed
.
- M. Chambers, B. Zalar, M. Remškar, S. Žumer and H. Finkelmann, Appl. Phys. Lett., 2006, 89, 243116 CrossRef
.
- H. Kim, J. A. Lee, C. P. Ambulo, H. B. Lee, S. H. Kim, V. V. Naik, C. S. Haines, A. E. Aliev, R. Ovalle-Robles, R. H. Baughman and T. H. Ware, Adv. Funct. Mater., 2019, 29, 1905063 CrossRef CAS
.
- S. Schuhladen, F. Preller, R. Rix, S. Petsch, R. Zentel and H. Zappe, Adv. Mater., 2014, 26, 7247–7251 CrossRef CAS PubMed
.
- X. Lu, C. P. Ambulo, S. Wang, L. K. Rivera-Tarazona, H. Kim, K. Searles and T. H. Ware, Angew. Chem., Int. Ed., 2021, 60, 5536–5543 CrossRef CAS PubMed
.
- C. Zhang, X. Lu, G. Fei, Z. Wang, H. Xia and Y. Zhao, ACS Appl. Mater. Interfaces, 2019, 11, 44774–44782 CrossRef CAS PubMed
.
- C. Yuan, D. J. Roach, C. K. Dunn, Q. Mu, X. Kuang, C. M. Yakacki, T. Wang, K. Yu and H. J. Qi, Soft Matter, 2017, 13, 5558–5568 RSC
.
- Q. He, Z. Wang, Y. Wang, A. Minori, M. T. Tolley and S. Cai, Sci. Adv., 2019, 5, eaax5746 CrossRef CAS PubMed
.
- M. Wang, J. Wang, H. Yang, B.-P. Lin, E.-Q. Chen, P. Keller, X.-Q. Zhang and Y. Sun, Chem. Commun., 2016, 52, 4313–4316 RSC
.
- S.-J. Ge, T.-P. Zhao, M. Wang, L.-L. Deng, B.-P. Lin, X.-Q. Zhang, Y. Sun, H. Yang and E.-Q. Chen, Soft Matter, 2017, 13, 5463–5468 RSC
.
- M. J. Ford, C. P. Ambulo, T. A. Kent, E. J. Markvicka, C. Pan, J. Malen, T. H. Ware and C. Majidi, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 21438–21444 CrossRef CAS PubMed
.
- T. Guin, M. J. Settle, B. A. Kowalski, A. D. Auguste, R. V. Beblo, G. W. Reich and T. J. White, Nat. Commun., 2018, 9, 2531 CrossRef PubMed
.
- L. Hines, K. Petersen, G. Z. Lum and M. Sitti, Adv. Mater., 2017, 29, 1603483 CrossRef PubMed
.
- C. M. Spillmann, J. Naciri, B. D. Martin, W. Farahat, H. Herr and B. R. Ratna, Sens. Actuators, A, 2007, 133, 500–505 CrossRef CAS
.
- J. Liu, Y. Gao, H. Wang, R. Poling-Skutvik, C. O. Osuji and S. Yang, Adv. Intell. Syst., 2020, 2, 1900163 CrossRef
.
- A. Agrawal, H. Chen, H. Kim, B. Zhu, O. Adetiba, A. Miranda, A. Cristian Chipara, P. M. Ajayan, J. G. Jacot and R. Verduzco, ACS Macro Lett., 2016, 5, 1386–1390 CrossRef CAS PubMed
.
- L. Yu, R. Peng, G. Rivers, C. Zhang, P. Si and B. Zhao, J. Mater. Chem. A, 2020, 8, 3390–3396 RSC
.
- M. J. Ford, M. Palaniswamy, C. P. Ambulo, T. H. Ware and C. Majidi, Soft Matter, 2020, 16, 5878–5885 RSC
.
- C. P. Ambulo, M. J. Ford, K. Searles, C. Majidi and T. H. Ware, ACS Appl. Mater. Interfaces, 2020, 13, 12805–12813 CrossRef PubMed
.
- P. Lv, X. Yang, H. K. Bisoyi, H. Zeng, X. Zhang, Y. Chen, P. Xue, S. Shi, A. Priimagi and L. Wang, Mater. Horiz., 2021, 8, 2475–2484 RSC
.
- Y. Yang, Z. Pei, Z. Li, Y. Wei and Y. Ji, J. Am. Chem. Soc., 2016, 138, 2118–2121 CrossRef CAS PubMed
.
- Z. Pei, Y. Yang, Q. Chen, E. M. Terentjev, Y. Wei and Y. Ji, Nat. Mater., 2014, 13, 36–41 CrossRef CAS PubMed
.
- T. Ube, K. Kawasaki and T. Ikeda, Adv. Mater., 2016, 28, 8212–8217 CrossRef CAS PubMed
.
- L. Chen, D. Chu, Z.-A. Cheng, M. Wang and S. Huang, Polymer, 2020, 208, 122962 CrossRef CAS
.
- S. Huang, Y. Shen, H. K. Bisoyi, Y. Tao, Z. Liu, M. Wang, H. Yang and Q. Li, J. Am. Chem. Soc., 2021, 143, 12543–12551 CrossRef CAS PubMed
.
- M. K. McBride, A. M. Martinez, L. Cox, M. Alim, K. Childress, M. Beiswinger, M. Podgorski, B. T. Worrell, J. Killgore and C. N. Bowman, Sci. Adv., 2018, 4, eaat4634 CrossRef CAS PubMed
.
- Y. Wu, Y. Yang, X. Qian, Q. Chen, Y. Wei and Y. Ji, Angew. Chem., Int. Ed., 2020, 59, 4778–4784 CrossRef CAS PubMed
.
- Z. C. Jiang, Y.-Y. Xiao, R.-D. Cheng, J.-B. Hou and Y. Zhao, Chem. Mater., 2021, 33, 6541–6552 CrossRef CAS
.
- Y. Wang, Z. Wang, Q. He, P. Iyer and S. Cai, Adv. Intell. Syst., 2020, 2, 1900177 CrossRef
.
- Y. Y. Xiao, Z. C. Jiang, X. Tong and Y. Zhao, Adv. Mater., 2019, 31, 1903452 CrossRef PubMed
.
- K. Liu, F. Hacker and C. Daraio, Sci. Robot., 2021, 6, eabf5116 CrossRef PubMed
.
- C. Wang, K. Sim, J. Chen, H. Kim, Z. Rao, Y. Li, W. Chen, J. Song, R. Verduzco and C. Yu, Adv. Mater., 2018, 30, 1706695 CrossRef PubMed
.
- S. Petsch, R. Rix, B. Khatri, S. Schuhladen, P. Müller, R. Zentel and H. Zappe, Sens. Actuators, A, 2015, 231, 44–51 CrossRef CAS
.
- T. A. Kent, M. J. Ford, E. J. Markvicka and C. Majidi, Multifunct. Mater., 2020, 3, 025003 CrossRef CAS
.
- A. Kotikian, J. M. Morales, A. Lu, J. Mueller, Z. S. Davidson, J. W. Boley and J. A. Lewis, Adv. Mater., 2021, 33, 2101814 CrossRef CAS PubMed
.
- B. Ma, C. Xu, L. Cui, C. Zhao and H. Liu, ACS Appl. Mater. Interfaces, 2021, 13, 5574–5582 CrossRef CAS PubMed
.
- M. Wang, Z.-W. Cheng, B. Zuo, X.-M. Chen, S. Huang and H. Yang, ACS Macro Lett., 2020, 9, 860–865 CrossRef CAS PubMed
.
- K. Urayama, S. Honda and T. Takigawa, Macromolecules, 2006, 39, 1943–1949 CrossRef CAS
.
- G. Skačej and C. Zannoni, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 10193–10198 CrossRef PubMed
.
- T. Okamoto, K. Urayama and T. Takigawa, Soft Matter, 2011, 7, 10585–10589 RSC
.
- S. Courty, J. Mine, A. Tajbakhsh and E. Terentjev, EPL, 2003, 64, 654 CrossRef CAS
.
- D. Liu, N. B. Tito and D. J. Broer, Nat. Commun., 2017, 8, 1526 CrossRef PubMed
.
- W. Feng, D. J. Broer and D. Liu, Adv. Mater., 2018, 30, 1704970 CrossRef PubMed
.
- T. Guin, B. A. Kowalski, R. Rao, A. D. Auguste, C. A. Grabowski, P. F. Lloyd, V. P. Tondiglia, B. Maruyama, R. A. Vaia and T. White, ACS Appl. Mater. Interfaces, 2018, 10, 1187–1194 CrossRef CAS PubMed
.
- K. Urayama, Macromolecules, 2007, 40, 2277–2288 CrossRef CAS
.
- K. Urayama, H. Kondo, Y. O. Arai and T. Takigawa, Phys. Rev. E, 2005, 71, 051713 CrossRef PubMed
.
- M. Rössle, R. Zentel, J. Lagerwall and F. Giesselmann, Liq. Cryst., 2004, 31, 883–887 CrossRef
.
- K. Hiraoka, W. Sagano, T. Nose and H. Finkelmann, Macromolecules, 2005, 38, 7352–7357 CrossRef CAS
.
- W. Lehmann, H. Skupin, C. Tolksdorf, E. Gebhard, R. Zentel, P. Krüger, M. Lösche and F. Kremer, Nature, 2001, 410, 447–450 CrossRef CAS PubMed
.
- K. Hiraoka, M. Kobayasi, R. Kazama and H. Finkelmann, Macromolecules, 2009, 42, 5600–5604 CrossRef CAS
.
- C. M. Spillmann, B. R. Ratna and J. Naciri, Appl. Phys. Lett., 2007, 90, 021911 CrossRef
.
- Z. S. Davidson, H. Shahsavan, A. Aghakhani, Y. Guo, L. Hines, Y. Xia, S. Yang and M. Sitti, Sci. Adv., 2019, 5, eaay0855 CrossRef CAS PubMed
.
- S. I. Rich, R. J. Wood and C. Majidi, Nat. Electron., 2018, 1, 102–112 CrossRef
.
- H. E. Fowler, P. Rothemund, C. Keplinger and T. J. White, Adv.
Mater., 2021, 33, 2103806 CrossRef CAS PubMed
.
- X. Zhu, Y. Hu, G. Wu, W. Chen and N. Bao, ACS Nano, 2021, 15, 9273–9298 CrossRef PubMed
.
- G. Wu, S. Sun, X. Zhu, Z. Ma, Y. Zhang and N. Bao, Angew. Chem., Int. Ed., 2022, 61, e202115559 CAS
.
- Y. Hu, A. Xu, J. Liu, L. Yang, L. Chang, M. Huang, W. Gu, G. Wu, P. Lu, W. Chen and Y. Wu, Adv. Mater. Technol., 2019, 4, 1800674 CrossRef
.
- C. Feng, C. P. H. Rajapaksha, J. M. Cedillo, C. Piedrahita, J. Cao, V. Kaphle, B. Lüssem, T. Kyu and A. Jákli, Macromol. Rapid Commun., 2019, 40, 1900299 CrossRef CAS PubMed
.
- D. Chen and Q. Pei, Chem. Rev., 2017, 117, 11239–11268 CrossRef CAS PubMed
.
| This journal is © The Royal Society of Chemistry 2022 |