Magnetically induced stress birefringence in stimuli-responsive hydrogels†
M. A.
Arranz
 *a,
C. M.
Andreu
*a,
C. M.
Andreu
 bc,
J.
Román
b and
E.
Vázquez
bc,
J.
Román
b and
E.
Vázquez
 bc
bc
aDepartamento de Física Aplicada, Universidad de Castilla-La Mancha, Av/Camilo José Cela 10, 13071 Ciudad Real, Spain. E-mail: MiguelAngel.Arranz@uclm.es
bFacultad de Ciencias y Tecnologías Químicas, Universidad de Castilla-La Mancha, 13005 Ciudad Real, Spain
cInstituto Regional de Investigación Cientfica Aplicada (IRICA), 13005 Ciudad Real, Spain
First published on 22nd November 2024
Abstract
We report the appearance of stress birefringence induced by an external magnetic field in stimuli-responsive hydrogels containing magnetic nanoparticles (Fe3O4). The measurement of the magneto-optical Faraday effect confirmed the superparamagnetic behaviour of those nanoparticles (NPs), its magnitude depending on the NP concentration. The results obtained from both magneto-optical Faraday and Voigt effects showed that the magnetic field induced a stress birefringence in the non-rigid structure of the magnetic hydrogel. The additional ellipsometric characterization of the transmitted light allowed us to fully characterize its polarization state, revealing the magnetic field direction to be the optic axis of that birefringent system. These results are discussed in the frame of a local rearrangement and stretching of polymeric chains parallel to the magnetic coupling direction of NPs. Such an induced alignment would break the inherent optical isotropy of the hydrogel, providing an axis of anisotropy that is responsible for turning its disordered polymeric structure into a birefringent system.
1 Introduction
Stimuli-responsive hydrogels are garnering wide interest as new functional materials with a large number of technical applications within many multidisciplinary research studies.1–3 These non-rigid systems show a skeleton structure formed by polymeric chains in a water swollen medium. The cross links between these chains are mediated generally by covalent bonds, providing a stable gel structure. Under an external stress, hydrogels are easily deformed, showing a large yield strength which arises from the interplay between the watery medium and the intense covalent bonds. Besides their great elasticity, hydrogels are also biocompatible, which turns them into excellent candidates to be considered in biomechanics or biomedicine applications.4In the case of hydrogels containing an additional amount of metallic particles, their mechanical elasticity can also be controlled by different external stimuli such as electric or magnetic fields, turning them into another class of functional materials.5–7 Hydrogels doped with electrical impurities or graphene nanofoils have been reported to show a correlated stress-electrical conductivity, a certain resemblance to the piezoelectric effect.8,9 Recently, the influence of DC or AC magnetic fields in hydrogels with different magnetic nanoparticle concentrations has also been investigated to check the magnitude of the spatial distortion of their skeleton structure.10 After applying the magnetic field, H, the magnetically coupled nanoparticles (NPs) are aligned along the H direction. This magnetic ordering inside a non-rigid structure enables a reduction of the relative distances between NPs, and consequently, an induced stretching of the polymeric chains along the H direction. Under some conditions, this effect can be extended to the macroscopic scale and even the form of that magnetically responsive hydrogel (MRH) could be controlled by external magnetic signals subsequently. These results would support the use of such a material to replace damaged human tissues, or to build micro magnetic-actuators, both applications based on external magnetic signals to generate the driving force for shaping the MRH.4,6,11
In some research areas such as biophysics and pharmacology, MRHs are being studied to produce templates at the pill scale, capable of storing and releasing drugs in a controlled way for subsequent medical treatments.11 The skeleton structure of those systems provides a huge number of cavities (pockets) deep inside, which are available to be filled with the prescribed medicament. According to previous paragraphs, an alternating magnetic field would deform periodically and elastically the structure of the MRH, and therefore, the size of its pockets. That periodic stress on the pocket volume would facilitate the drug release outside, its rate being controlled via both amplitude and frequency of an AC magnetic field.
From the physical point of view, those elastic deformations of the MRH structure, responding to an external magnetic field, arise from an induced magnetic driving force which alters the intrinsic disorder of the polymeric chains, and consequently, the inherent isotropy of the dielectric permittivity tensor of the MRH, ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) . This effect would lead us to include a magnetic-field term in
. This effect would lead us to include a magnetic-field term in ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) , i.e. ε(H), following a similar approach to that for magnetic rigid systems.12,13 For non-rigid MRHs, on(off)-diagonal components of ε(H) should be related to the effective stiffness of the skeleton structure measured along parallel and perpendicular directions to the applied H field. For transmitting light through the MRH structure, the argumentation suggests the possibility of finding two different propagation velocities as the electromagnetic wave travels with its electrical field parallel or perpendicular to H. Recent studies have investigated that possibility in transparent hydrogels containing magnetic nanoflakes, which were previously embedded into that matrix with a preferential orientation.14–16 An external H field was applied to rotate those bidimensional magnetic particles, showing two dissimilar intensities for the emerging light as its electrical field was parallel or perpendicular to the nanoflake plane.
, i.e. ε(H), following a similar approach to that for magnetic rigid systems.12,13 For non-rigid MRHs, on(off)-diagonal components of ε(H) should be related to the effective stiffness of the skeleton structure measured along parallel and perpendicular directions to the applied H field. For transmitting light through the MRH structure, the argumentation suggests the possibility of finding two different propagation velocities as the electromagnetic wave travels with its electrical field parallel or perpendicular to H. Recent studies have investigated that possibility in transparent hydrogels containing magnetic nanoflakes, which were previously embedded into that matrix with a preferential orientation.14–16 An external H field was applied to rotate those bidimensional magnetic particles, showing two dissimilar intensities for the emerging light as its electrical field was parallel or perpendicular to the nanoflake plane.
In this work, we have carried out a magneto-optical study of MRHs, focusing our efforts on investigating the capability of the disordered structure of MRH to change the polarization state of transmitting light under the effect of an external magnetic field. The results for the magneto-optical Faraday effect (MOFE) confirmed the superparamagnetic coupling of magnetic NPs, being strong enough to rotate the polarization plane of the light. Additionally, that collective magnetic behaviour was shown to stretch the polymeric chains, yielding an anisotropic axis in the MRH for the light transmission. The obtained results from both polarimetry and magneto-optical Voigt effect (MOVE) experiments allowed us to report here the appearance of birefringence in MRHs, as a response to the external magnetic stimulus. The occurrence of such sort of birefringence would add a novel functionality to MRH systems, i.e. magneto-optical functionality (MOF), where an external magnetic field (stimulus) induces the skeleton structure to evolve into a birefringent medium (response). This additional MOF would put those magnetic responsive hydrogels forward as smart materials to fabricate different photonics devices, e.g. polarization rotators or birefringent retarders, just as optical sensors in the biophysics field.
2 Materials and methods
2.1 Sample fabrication
2.2 Characterization
| C (M) | 0 | 2.5 × 10−3 | 5 × 10−3 | 10−2 | 2.5 × 10−2 | 5 × 10−2 | 10−1 |
| Suffix | PR | A | B | C | D | E | F |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 105 extinction ratio) and rotated optionally with a λ/2 -retarder, prior to reaching the sample. Therein, the sample holder consisted of a transparent crystal cuvette, whose parallel plates ensured light transmission with a negligible diffusion through the hydrogel. The external H field was supplied by an electromagnet with bored magnetic poles, being connected to an adjustable AC/DC power source (0–30 V/5 A), which enabled us to attain Hmax = ±0.6 T. The relative orientation between the H direction and the light path (y-axis in Fig. 1) could be easily changed from parallel to perpendicular, ready to investigate MOFE or MOVE, respectively.18,19 After, the polarization state of the transmitted light was optically characterized with two interchangeable devices: (a) a polarization analyzing system (Thorlabs PAX5710) or (b) a fast photodiode detector followed by an amplifier circuit. The choice for those two options depended on the specific requirements of each experiment along this work and will be detailed in the following sections.
105 extinction ratio) and rotated optionally with a λ/2 -retarder, prior to reaching the sample. Therein, the sample holder consisted of a transparent crystal cuvette, whose parallel plates ensured light transmission with a negligible diffusion through the hydrogel. The external H field was supplied by an electromagnet with bored magnetic poles, being connected to an adjustable AC/DC power source (0–30 V/5 A), which enabled us to attain Hmax = ±0.6 T. The relative orientation between the H direction and the light path (y-axis in Fig. 1) could be easily changed from parallel to perpendicular, ready to investigate MOFE or MOVE, respectively.18,19 After, the polarization state of the transmitted light was optically characterized with two interchangeable devices: (a) a polarization analyzing system (Thorlabs PAX5710) or (b) a fast photodiode detector followed by an amplifier circuit. The choice for those two options depended on the specific requirements of each experiment along this work and will be detailed in the following sections.
3 Results and discussion
3.1 TEM characterization
The study of the size, polydispersity and distribution of the magnetic NPs within the MRH structure was carried out by means of TEM. In the ESI,† we have included some selected TEM results (Fig. S1 and S2, ESI†). First, a clear difference between the MRH-F sample (S1, right) and the MRH-A sample (S1, left) is easily shown, noting that the most concentrated hydrogel contains a higher quantity of NPs. Secondly, Fig. S2a (ESI†) illustrates the distribution of the nanoparticles in the MRH hydrogel with 0.05 M as an example, i.e. MRH-E sample. As observed, there is no aggregation among the NPs. The estimated average size of the NPs in that hydrogel is 6.25 ± 0.75 nm, as shown in Fig. S2c (ESI†). That value is quite similar to all MRH samples and is confirmed by X-ray diffraction studies in the next section. Additionally, Fig. S2b (ESI†) presents clear images of a single Fe3O4 crystal in the MRH hydrogels with 0.05 M as an example, displaying clean lattice patterns.3.2 Powder X-ray diffraction
PXRD provides information on the crystalline structure and size of the nanoparticles formed into the MRH structure. Spectra were obtained for MRH samples at different concentrations and for the hydrogel without nanoparticles. The results of this preliminary characterization have been included in the ESI† (Fig. S3a), retaining here the relevant information. The pristine gel (MRH-PR) exhibits the typical broad bands corresponding to an amorphous structure. For doped MRH samples, peaks are observed at the angular positions corresponding to the respective crystalline planes Fe3O4 NPs (see their XRD diffraction spectra also in Fig. S3a, ESI†), confirming that the magnetic nature of our system is due to Fe3O4. Therein, the dashed lines correspond to the angular position of indexed diffraction peaks of the Fe3O4 phase.20 Additional information regarding the spectrum data for the MRH-F sample can be found in the Table S3b of the ESI.† Finally, the crystal size of the magnetic nanoparticles within the hydrogel was calculated using the Scherrer equation.21 The average size for all the magnetic hydrogels is 10.03 ± 1.04 nm, which is within the range of the value measured using the TEM technique.3.3 DC magnetometry
The results of this preliminary characterization have been included in Fig. S4 of the ESI.† As seen there, the data confirm the expected superparamagnetic behaviour of magnetic nanoparticles diluted into a disordered matrix. Their RT magnetization, M, follows a closed cycle in the measured H range, whose saturation values, MS, increase proportionally to the NP concentration in the hydrogel. Additionally, the absence of coercive field enables us to consider these nanoparticles as magnetic monodomains, reversing their magnetization collectively and coherently between both ±MS directions. From those results, the magnetic coupling of NPs seems to be irrespective of the skeleton structure, which points to an foreseeable isotropic contribution to the magneto-optic effects in MRH. For MRH-PR sample, the measured data clearly show a diamagnetic behaviour, which arises from the water swollen polymeric structure. Its effect on the overall M is particularly visible for MRH samples with low NP concentration (lower graph in Fig. S4, ESI†) and will bring about a relevant role also in the following magneto-optical effects.3.4 Magnetic circular birefringence in MRHs
The first experiment concerning magneto-optics in MRH samples focused on measuring the Faraday effect, with the aim of showing the capability of magnetic NPs to alter the polarization state of transmitting light through the hydrogel. For this configuration, the linearly polarized radiation can be studied as the superposition of two waves with circular polarization, whose respective electrical field vectors rotate in opposite directions around the y-axis. These right and left-handed circular polarizations are usually characterized with corresponding frequencies ω+ and ω−. As the light transverses a physical media, those quantities are dependent on its refractive index, n. For isotropic or non-magnetic systems, there is no difference between those frequencies, and the outcoming radiation preserves its original linear polarization. In the case of a magnetized media exhibiting circular double refraction, that equality is no longer applicable strictly, as those circularly polarized waves propagate with different refractive indices, i.e. n+ and n−. That yields a phase shift between both waves, δF = (π/λ)|n+ − n−|l, where l is the light path across the sample.13 Accordingly, the state of polarization for the transmitted light will be elliptical, with its major axis rotated a θF angle with respect to the polarization plane of the incoming radiation.The physical origin of this effect in magnetizable media proceeds from the response of their permittivity tensor, ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) , to an external H field. In the case of H parallel to the y-axis within an isotropic medium, the cylindrical symmetry around that direction allows us to write
, to an external H field. In the case of H parallel to the y-axis within an isotropic medium, the cylindrical symmetry around that direction allows us to write ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) as follows:
as follows:
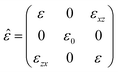 | (1) |
![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) are non-zero in magnetizable systems and can be expressed as εxz = −εzx = −ig, where g corresponds to the y-projection of the complex gyration vector. Finally, the field dependence of g can be approximated to a simple linear proportionality (g = g′H), provided the magnetic medium responds isotropically to H direction.12
are non-zero in magnetizable systems and can be expressed as εxz = −εzx = −ig, where g corresponds to the y-projection of the complex gyration vector. Finally, the field dependence of g can be approximated to a simple linear proportionality (g = g′H), provided the magnetic medium responds isotropically to H direction.12
According to previous paragraph and eqn (1), a wave propagating along y-axis satisfies the Maxwell equations for the following solutions, n± = n ∓(g/2n), where n is the refractive index at zero H field. These indices of refraction correspond respectively to two transverse waves with right and left-handed circular polarization, as introduced above. Thus, the δF phase shift can be now related to a magnetic circular birefringence, arising from the magnetization of the medium along the y-axis, i.e. My component in Fig. 1:
| δF = (π/λ)|n± − n−|l = (π/nλ)g′Hl | (2) |
This fact inevitably complicates the evaluation of the MOFE only coming from the NPs, θF,NPs, and requires a careful discussion and further analysis of θ data for the MRH-F sample. The obtained results are shown in the upper row of Fig. 2. The occurrence of the superparamagnetic contribution to the overall MOFE is visible therein by comparing the dissimilar trends of θ upon increasing H in the low field range (see circled data in Fig. 2). At low H fields, the increasing NP magnetization is able to rotate the light polarization plane, yielding an small contribution to θ, still noticeable in spite of the presence of the diamagnetic term. Once the NPs magnetization reaches its saturation value, the diamagnetic contribution of water dominates the field dependence of θ entirely. The coexistence of these competing magnetic sources can be also seen in the additional plots of θ(H) in the ESI† (S5), where the time dependence has been withdrawn. While for MRH-PR, θ(H) depends linearly on H through the whole measured range, two antisymmetric kinks can be seen at low fields for MRH-F, indicating the small contribution of superparamagnetic nanoparticles to the overall MOFE in the MRH. Correspondingly, the determination of θF,NPs for MRH-F sample was accomplished by subtracting the θF,Dia contribution. The same procedure was followed for all MRH samples listed in the Table 1. A detailed description of the full analysis of experimental data for θ has been included in the ESI† (S5). The field dependence of θF,NPs for all NP concentrations is displayed in the Fig. 3. For samples MRH-(A–C), the low concentration of magnetic nanoparticles in the hydrogel is too small to yield a significant and reliable MOFE, within the experimental resolution. However, for samples MRH-(D–F), the small MOFE is well visible and reproduces the field dependence of My, as was predicted in the preceding paragraphs. Such higher concentrations of magnetic nanoparticles enable the hydrogel to be sensitive to the action of an external H field, rotating the polarization of transmitted light despite of the strong diamagnetic environment. Prior to reaching the magnetic saturation regime, the highest Faraday rotation angle due to those NPs is ∼0.2 deg at a magnetic field around 0.2 T, that leads us to estimate a Verdet constant at 633 nm, V ∼ 2 × 102 deg Tm−1. This value is one or two orders of magnitude smaller than metal oxide glasses commonly used for Faraday rotators, e.g. terbium gallium garnet (TGG).23 MRH consists of NPs embedded in a non-rigid and water swollen matrix. These structural characteristics strongly weak and reduce the MOFE arising from the magnetic nanoparticles. For our next research study, we are aiming to design optical devices containing thin slabs of MRH with a notable increase of their Verdet constant, with the objective of approaching the reported values in thin films of NP-doped polymers.23
 | ||
| Fig. 3 Field dependence of the MOFE arising from the magnetic NPs, θF,NPs in MRH samples. Their corresponding NP concentrations correlate with their names in the legend (see also the Table 1). Lines are a guide to the eye. | ||
The plotted data in Fig. 2 for MRH-PR show a negligible field dependence of η, indicating that the diamagnetic response of water molecules does not alter the hydrogel structure. Contrarily, the results for MRH-F evidence a significant ellipticity, first increasing at low H values and finally reaching a steady field dependence. The initial rise of η coincides with the progressive superparamagnetic order of NP along H direction. As introduced above, these nanoparticles are allocated at the chains of the skeleton structure of the hydrogel.5,10 Thus, that collective magnetic alignment of NPs provides a magnetic driving force strong enough to stretch the polymeric chains parallel to the applied field. The resulting effect into the MRH is the appearance of an anisotropy axis in the hydrogel structure, which breaks its inherent optical isotropy. Once the NP saturation magnetization is achieved, the magnitude of η tends to be constant in spite of the strongly increasing diamagnetic response of MRH. This fact would confirm again the absence of ellipticity for the transmitted light through the pristine hydrogel. That magnetically induced structural anisotropy has been shown here to modify the state of polarization of the transmitted light, pointing on a novel magneto-optical functionality of MRH systems. The confirmation and relevance of these results are detailed further in the following section.
3.5 Magnetic linear birefringence in MRH
The possibility of inducing a structural anisotropy in magnetically responsive hydrogels leads us to investigate their optical birefringence power, tuned by the external H field. This new magneto-optical functionality of MRH systems is essential for further applications in flat optics or photonics devices. The origin of birefringence in crystal systems lies in the existence of an anisotropy axis within their crystallographic structure, the so-called optic axis.24 In this uniaxial materials, e.g. calcite crystals, the propagation velocity of polarized light depends on the relative orientation of its electrical field, E, and that anisotropy axis. According to cylindrical symmetry around the optic axis, any polarized wave with E perpendicular to that optic axis will be affected with the same (ordinary) refractive index, no. However, a different (extraordinary) refractive index, ne determines the propagation velocity of the polarized light with E parallel to the optic axis. For an arbitrary propagation direction, the E vector can be split into its perpendicular and parallel components to the optic axis, and the transmitted light will be a superposition of two rays (ordinary and extraordinary) traversing the medium with no and ne, respectively.12,24Beyond uniaxial crystals, the birefringence phenomenon can also appear in optically isotropic materials, provided that an optic axis is induced within their structure. For that purpose, an obvious approach is to apply an external force to distort uniaxially the relative atomic distances of a rigid system. That elastic deformation reaches the macroscopic scale in the case of non-rigid materials, as polymeric media, resulting in a non-permanent stress birefringence.3,25,26 A substantial and permanent alteration of the medium shape along a determined direction is another choice to induce birefringence in optically isotropic materials.27–30 For instance, this form birefringence was found to appear first in rippled magnetic films,31 and recently also in polymeric foil,32,33 whose respective surfaces had been previously nanopatterned along a preferential direction.
In our MRH samples, the effect of an external H field has previously shown to stretch the polymeric chains along H direction (Section 3.4.2). This uniaxial distortion would yield an optic axis in the MRH structure, and consequently, a magnetically tuned stress birefringence. Also in that section, we have found that uniaxial distortion to depend on H amplitude, and more explicitly on NP magnetization, which hints at ε and ε0 to be functions of H. To investigate that stress birefringence in MRH, we are enforced to modify the experimental setup, applying the external H field along x-axis (shown in Fig. 1). In this configuration, MOFE is absent for a polarized light propagating along y-axis, focusing our study only on the eventual birefringence occurring in the xz-plane of the MRH sample. Once the magnetic field was applied, our MRH sample would resemble an uniaxial crystal with its optic axis parallel to H direction, mainly affecting ε0 in comparison with ε in terms of H. This stress birefringence is expected to be a small perturbation of the isotropic optical behaviour of the hydrogel structure. Thus, ε0 (H) can be expanded into H powers, limiting ourselves to the quadratic term.12,34 For any linearly polarized light propagating along y-axis, its E vector can be decomposed into its Ex and Ez components, corresponding to two electromagnetic waves with parallel and perpendicular polarization with respect to the optic axis, respectively. In the view of the different components of ![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) , these waves will propagate with different velocities, yielding a phase shift between them:
, these waves will propagate with different velocities, yielding a phase shift between them:
| δV = (2π/λ)|n‖ − n⊥|l = clH2 | (3) |
The measurement of MOVE in our MRH samples was accomplished with an incoming light whose polarization plane was orientated 45° with respect to the H direction. After, the field dependence of the resulting signal was recorded with the same polarization analyzing device as in Section 3.4, also monitoring its both η and θ elliptical parameters. As an example, the obtained results for MRH-F are shown in the Fig. 4. The same field and time dependence is reproduced in other MRH samples, only differing in the decreasing amplitude of η upon lowering the NP concentration. As seen there, the effect of stepping H field is only noticeable in the ellipticity of the transmitted light. This would confirm the dispersive origin of δV in MRH systems, only concerning the imaginary part of both n‖ and n⊥. Upon the external H field, the driving force arising from magnetically coupled NPs distorts the hydrogel structure, providing the necessary anisotropy for the occurrence of MOVE. That inelastic process yields a change in the state of light polarization from linear to elliptical, leaving unaffected θ parameter. The field dependence of the MOVE can be easily obtain from η(H,t) graphs, once the time dependence is removed. Again, a detailed description of the full analysis of these experimental data has been also included in the ESI† (S5). The resulting MOVE for MRH-(C–F) samples is displayed in Fig. 5. The plotted data for the MRH-F sample indicate a strong MOVE, whose amplitude is monotonously increasing along the whole H range. These results would indicate the magnitude of the mentioned driving force and consequently the MOVE, to be only dependent on H and NP concentration. As a consequence, the diamagnetic contribution of water dipoles is irrelevant for this stress birefringence, as they have no mechanical connection to the skeleton structure. The even dependence of MOVE on H field confirms the predicted quadratic behaviour in the eqn (3). Unfortunately, the obtained results for the MOVE in MRH samples with lower NP concentrations were too small and within our experimental error, similarly to MOFE measurement. In any case, the maximum birefringence, Δn = n‖ − n⊥, can be easily estimated from Fig. 5 and the eqn (3), resulting in Δn ∼ 3 × 10−6 at H = 0, 6 T for the MRH-F sample. This value is already similar or greater than the reported results at H > 5 T for hydrogels containing bidimensional35,36 or unidimensional37 magnetic particles, respectively. Following this comparison, the intrinsic optical anisotropy factor of our NPs, ΔgNPs, can be estimated to gain insight about the true responsible for that significant birefringence in our samples. That magnitude is calculated from the expression ΔgNPs = 2ne0Δn/Cvol, where n is the sample refractive index and e0 the vacuum dielectric constant, respectively.16 From the analysis of TEM data, the volume concentration of NPs in the MRH-F sample is Cvol ∼ 0, 06, yielding an ΔgNPs ∼ 1.3 × 10−15 C2 J−1 m−1. This value is four or five orders of magnitude smaller than reported values in liquids and suspensions with 2D magnetic particles,14–16 clearly discarding Fe3O4 nanoparticles to be responsible by themselves for the strong birefringence measured in our MRHs. This confirmation was foreseeable in view of the isotropic magnetic coupling of our NPs (for instance, see the discussion in Section 3.3), in contrast to the strong shape magnetic anisotropy of 2D/1D particles of the above references.
 | ||
| Fig. 5 Field dependence of the ellipticity in the SOP of the transmitted light through different MRH samples. Their corresponding NP concentrations correlate with their names in the legend (see also the Table 1). Lines are a guide to the eye. | ||
Consequently, that leads us to point to the polymeric chains stretching parallel to H as the real source of the occurrence of birefringence in our MRHs. That alignment forces the disordered MRH to undergo a structural transition to a uniaxial anisotropy system, providing the necessary optical axis for yielding n‖ and n⊥. In short, the results of the MOVE shown in Fig. 5 support the capability of our MRH to behave as a birefringent material under a low magnetic field, which adds a magneto-optical functionality to these smart materials, being only based on a disordered polymeric structure with magnetic nanoclusters.
By analogy with crystal and polymeric systems exhibiting birefringence, a further characterization of the induced optic axis in our MRH is required to evaluate their birefringence power. As commented previously, the magnetic linear birefringence is related to the existence of two different refractive indices, ne and no, in an anisotropic medium, which splits the incident light into respective extraordinary and ordinary rays. The strength of that birefringent medium to separate those rays would be determined, first, by the relative difference between ne and no, and secondly, by the precise spatial orientation of the optical axis.32,38 This last point is relevant for accurate technical applications, as that splitting in the transmitted light depends on the orthogonal projections of the E vector of the incoming light relative to the optical axis. 6 for α ranging between ±90°. In this sense, we have studied the dependence of η of the outcoming light on that relative orientation, α, between the polarization plane of the incoming light and the optical axis. This measurement was accomplished in the MRH-F sample under Hmax = 0.6 T for gaining the maximal resolution. In this experiment, the polarization plane was rotated by means of a λ/2-retarder, being inserted in the light path between the linear polarizer and the sample. The corresponding angular dependence of η is shown in the upper plot of Fig. 6 for α ranging between ±90°. A periodic behaviour of η within the angular range and symmetric with respect to α = 0 is readily seen. Minimal values of the ellipticity correspond to linearly polarized light reaching the MRH surface with its E vector parallel or perpendicular to the optical axis, i.e. α = 0, ±90°. In both cases, the transmitted light propagates with only a refractive index, n‖ or n⊥, and there is no phase shift to affect the SOP of the incoming light. As α deviates from those boundary values, the optical axis begins to split the transmitted light into the mentioned extraordinary and ordinary rays, whose relative phase shift yields the observed increasing ellipticity in Fig. 6. This distortion of the SOP observed in the transmitted light attains its highest value around α = 45°. At this point, both orthogonal components of the incident light are maximum simultaneously, and therefore, the optical axis brings about the highest phase shift in eqn (3) for a constant H. The shown results of the angular behaviour of η are in accordance with the expected dependence for a birefringent system with its anisotropy axis lying in the x-axis.32 In the view of the sharp maxima of η(α), the angular uncertainty to locate the optic axis of our MRH at α = 0 is exceedingly small, thus suggesting the existence of an anisotropic structure precisely defined in the xyz-coordinate system.
The gradient of this stress birefringence induced by an external H field in MRH can be evaluated by determining its retardation factor, δ, similarly to the procedure reported in rippled polymeric foil exhibiting form birefringence.32 This parameter is related to the transmitted intensity by a birefringent medium placed between two crossed polarizers, T.39,40 As outlined in the previous paragraph, the SOP of the polarized light changes from linear to elliptical after traversing the hydrogel, yielding an angular dependence of the ellipticity, η(α). With those two crossed polarizers, the emerging light is reduced only to the E component along the minor axis of the elliptical SOP, and therefore, proportional to the birefringent power of the MRH. In our experimental setup, the polarization analyzing device was substituted by a high response photodiode to measure T. In this configuration, the relation between T, α and the retardation factor can be found in the following equation:
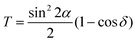 | (4) |
The measurement of T was carried out in the MRH-F sample under an applied Hmax and in the angular range of α = ±90°. The obtained results are shown in the lower plot of Fig. 6. The plotted data follows the expected sin22α behaviour for T in the eqn (4). As the magnitude T arises directly from the magneto-optical power of the birefringent structure; the angular position (α = 45°) of its maximum, Tmax, coincides with the results concerning the distorted SOP of the transmitted light (see the η(α) behaviour in Fig. 6). The measured Tmax enables us to estimate the retardation factor of MRH-F sample according to the eqn (4), yielding a δmax ∼ 0.16 rad. This retardation factor is around eight times smaller than reported δ values in rippled polymeric systems exhibiting form birefringence.32 This modest retardation factor of non-rigid MRH comes from the partial screening of NP magnetization by water magnetic dipoles. Although this diamagnetic source is not responsible for stretching the polymeric chains, it locally reduces the effective magnetization of the NPs located at the MRH skeleton structure, weakening the magnetic driving force which generates the stress birefringence. Nevertheless, the occurrence of this novel magneto-optical response in MRH already deserves further research to optimize their birefringence power, with the aim of providing a reliable alternative to glass materials in many photonics applications.
4 Conclusions
In summary, we have successfully fabricated swollen AM hydrogels containing different concentrations of magnetic nanoparticles which ranged from 0 to 0.1 M. This sort of magnetically doped hydrogel was preliminarily characterized with TEM and X-rays diffraction techniques, showing dispersed distributions of NPs embedded in the polymeric matrix. The results of SQUID magnetometry revealed a superparamagnetic behaviour of NPs with a saturation magnetization proportional to their concentration. In view of that magnetic sensitivity, we have investigated here the capability of these hydrogels to manipulate the SOP of transmitting light from the magneto-optical point of view. The measurement of the MOFE showed those hydrogels to rotate its polarization plane and distort the polymeric structure in a preferential direction parallel to H field. Those facts enabled us to consider an additional magneto-optical functionality in these MRH materials. The measurement of the MOVE confirmed the existence of uniaxial anisotropy in the MRH structure, coming from the stretching of the polymeric chains along the H direction. This breakdown of the inherent optical isotropy of hydrogels yielded the appearance of two different refractive indexes, n‖ or n⊥, for polarized light transmitting with its E vector parallel or perpendicular to H direction, respectively. Further characterization of that optical axis showed MRHs to behave as birefringent materials, whose birefringence power can be modulated by the external H field. Both MOFE and MOVE results have enabled us to extend the magnetic sensitivity of MRHs into the magneto-optical research field. From the technical point of view, this novel functionality of MRH puts these systems forward as a promising and affordable alternative to glass materials in many optical applications.Author contributions
M. A. Arranz: conceptualization, methodology, software, validation, formal analysis, investigation, data curation, writing and visualization. C. M. Andreu: validation, formal analysis, investigation, data curation, resources, writing and visualization. J. Román: investigation. E. Vázquez: resources, writing, supervision, project administration and funding acquisition.Data availability
(1) Data for this article, embedded in a full manuscript are available at [RUIDERA] at [https://ruidera.uclm.es/handle/10578/598, Author: Arranz]. (2) The data supporting this article and crystallographic data have been included as part of the ESI.† (3) This study was carried out using publicly available data from [RUIDERA] at [https://ruidera.uclm.es/handle/10578/598, Author: Arranz]. (4) Data for this article are available at [RUIDERA] at [https://ruidera.uclm.es/handle/10578/598, Author: Arranz].Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful for financial support from the Spanish Government (projects PID2020-113080RB-I00 and AEI/10.13039/501100011033), the Junta de Comunidades de Castilla-La Mancha, Spain (SBPLY/21/180501/000135/1 and MATERIALES-PCOMPLEM) and the University of Castilla-La Mancha, Spain (2022-GRIN-34076). Carlos M. Andreu acknowledges the Spanish Ministry of Universities for his FPU Fellowship (FPU21/05210). Finally, the authors would like to offer special thanks to the instrumentation team at the IRICA centre for their valuable help with sample preparation and analysis.Notes and references
- Z. Li, Y. Li, C. Chen and Y. Cheng, J. Controlled Release, 2021, 335, 541–556 CrossRef CAS PubMed.
- Z. Li, Y. Zhou, T. Li, J. Zhang and H. Tian, View, 2022, 3, 20200112 CrossRef CAS.
- F. Zhao, G. Li, X. Ji, Y. Fu, M. Qin and Z. Yuan, Appl. Surf. Sci., 2021, 539, 148228 CrossRef CAS.
- S. Z. M. Madani, A. Reisch, D. Roxbury and S. M. Kennedy, ACS Biomater. Sci. Eng., 2020, 6, 1522–1534 CrossRef CAS.
- B. P. Nowak, M. Niehues and B. J. Ravoo, Soft Matter, 2021, 17, 2857–2864 RSC.
- F. Downs, D. Lunn, M. J. Booth, J. B. Sauer, W. J. Ramsay, R. G. Klemperer, C. J. Hawker and H. Bayley, Nat. Chem., 2020, 12, 363–371 CrossRef CAS PubMed.
- L. Chen, F. Liu, T. Abdiryim and X. Liu, Mater. Today Phys., 2024, 40, 101281 CrossRef CAS.
- A. Servant, V. Leon, D. Jasim, L. Methven, P. Limousin, E. Vázquez, M. Prato and K. Kostarelos, Adv. Healthcare Mater., 2014, 3(8), 1334–1343 CrossRef CAS PubMed.
- Z. Deng, R. Yu and B. Guo, Mater. Chem. Front., 2021, 5, 2092–2123 RSC.
- J. Leganés, A. Rodríguez, M. Arranz, C. Castillo-Sarmiento, I. Ballesteros-Yáñez, A. Migallón, S. Merino and E. Vázquez, Mater. Today Chem., 2022, 23, 100702 CrossRef.
- A. Pourjavadi, R. Heydarpour and Z. M. Tehrani, New J. Chem., 2021, 45, 15705–15717 RSC.
- A. Sokolov, Optical Properties of Metals, Blackie, London, 1st edn, 1967, p. 262 Search PubMed.
- A. Vinogradov, A. Dorofeenko, A. Merzlikin, Y. Strelniker, A. Lisyansky, A. Granovsky and D. Bergman, Magnetophotonics: From Theory to Applications, Springer, Berlin, 3rd edn, 2013, p. 24 Search PubMed.
- Y. Xu, B. Ding, Z. Huang, L. Dai, P. Liu, B. Li, W. Cail, H.-M. Cheng and B. Liu, Light: Sci. Appl., 2023, 12, 3542–3547 Search PubMed.
- H. Xu, B. Ding, Y. Xu, Z. Huang, D. Wei, S. Chen, T. Lan, Y. Pan, H.-M. Cheng and B. Liu, Nat. Nanotechnol., 2022, 17, 1091–1096 CrossRef CAS PubMed.
- B. Ding, P. Zeng, Z. Huang, L. Dai, T. Lan, H. Xu, Y. Pan, Y. Luo, Q. Yu, H.-M. Cheng and B. Liu, Nat. Commun., 2022, 13, 1212 CrossRef CAS.
- G. Beaune and C. Ménager, J. Colloid Interface Sci., 2010, 343, 396–399 CrossRef CAS PubMed.
- E. D. Palik, Appl. Opt., 1963, 2, 527–539 CrossRef.
- R. Carey and B. W. J. Thomas, J. Sci. Instrum., 1971, 4, 545–547 CrossRef.
- E. Bertolucci, A. M. R. Galletti, C. Antonetti, M. Marracci, B. Tellini, F. Piccinelli and C. Visone, 2015 IEEE International Instrumentation and Measurement Technology Conference (I2MTC) Proceedings, 2015, pp. 1492–1496 Search PubMed.
- A. L. Patterson, Phys. Rev., 1939, 56, 978–982 CrossRef CAS.
- M. Arranz, E. H. Sánchez, Y. Moreno, V. Ruiz-Díez, J. Sánchez-Rojas and J. M. Colino, J. Magn. Magn. Mater., 2022, 547, 168888 CrossRef CAS.
- K. J. Carothers, R. A. Norwood and J. Pyun, Chem. Mater., 2022, 34, 2531–2544 CrossRef CAS.
- M. Born and E. Wolf, Principles of Optics, Pergamon Press, Oxford, 5th edn, 1975 Search PubMed.
- S. Shams Es-haghi, I. Offenbach, D. Debnath, R. Weiss and M. Cakmak, Polymer, 2017, 115, 239–245 CrossRef CAS.
- Z. L. Wu, D. Sawada, T. Kurokawa, A. Kakugo, W. Yang, H. Furukawa and J. P. Gong, Macromolecules, 2011, 44, 3542–3547 CrossRef CAS.
- E. Rebollar, M. Castillejo and T. Ezquerra, Eur. Polym. J., 2015, 73, 162–174 CrossRef CAS.
- M. Castillejo, T. A. Ezquerra, M. O. Margarita Martn, S. Péreza and E. Rebollar, AIP Conf. Proc., 2012, 1464, 372–380 CrossRef CAS.
- R. Moroni, D. Sekiba, F. B. de Mongeot, G. Gonella, C. Boragno, L. Mattera and U. Valbusa, Phys. Rev. Lett., 2003, 91, 7027–7030 CrossRef.
- P. Slepička, O. Nedĕla, J. Siegel, R. Krajcar, Z. Kolská and V. Švorčík, eXPRESS Polym. Lett., 2014, 8, 459–466 CrossRef.
- M. A. Arranz and J. M. Colino, Appl. Phys. Lett., 2015, 106, 3102–3105 CrossRef.
- M. A. Arranz, E. H. Sánchez, E. Rebollar, M. Castillejo and J. M. Colino, Opt. Express, 2019, 27, 21285–21294 CrossRef CAS PubMed.
- E. Bricchi, B. G. Klappauf and P. G. Kazansky, Opt. Lett., 2004, 29, 119–121 CrossRef PubMed.
- R. Carey, B. W. J. Thomas, I. V. F. Viney and G. H. Weaver, J. Phys. D, 1968, 1, 1679–1684 CrossRef.
- M. Liebi, S. Kuster, J. Kohlbrecher, T. Ishikawa, P. Fischer, P. Walde and E. J. Windhab, ACS Appl. Mater. Interfaces, 2014, 6, 1100–1105 CrossRef CAS.
- P. van Rhee, R. Rikken, L. Abdelmohsen, J. Maan, R. Nolte, J. van Hest, P. Christianen and D. Wilson, Nat. Commun., 2014, 5, 5010 CrossRef CAS.
- A. Mori, T. Kaito, H. Furukawa, M. Yamato and K. Takahashi, Mater. Res. Express, 2014, 1, 045202 CrossRef CAS.
- M. A. Arranz and J. M. Colino, J. Phys. D: Appl. Phys., 2016, 49, 5306–5313 CrossRef.
- P. Yang, G. R. Burns, J. Guo, T. S. Luk and G. A. Vawter, J. Appl. Phys., 2004, 95, 5280–5283 CrossRef CAS.
- S. Richter, C. Miese, S. Döring, F. Zimmermann, M. J. Withford, A. Tünnermann and S. Nolte, Opt. Mat. Express, 2013, 3, 1161–1166 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc04115a |
| This journal is © The Royal Society of Chemistry 2025 |




