Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Cu3Ru6Sb8—a new ternary antimonide with a new structure type†
Jai
Prakash
 a,
Nian-Tzu
Suen
a,
Minseong
Lee
b,
Eun Sang
Choi
b,
James A.
Ibers
c and
Svilen
Bobev
*a
a,
Nian-Tzu
Suen
a,
Minseong
Lee
b,
Eun Sang
Choi
b,
James A.
Ibers
c and
Svilen
Bobev
*a
aDepartment of Chemistry and Biochemistry, University of Delaware, Newark, DE 19716, USA. E-mail: bobev@udel.edu
bDepartment of Physics and National High Magnetic Field Laboratory, Florida State University, Tallahassee, FL 32310, USA
cDepartment of Chemistry, Northwestern University, Evanston, IL 60208, USA
First published on 26th October 2016
Abstract
The new ternary transition metal antimonide, Cu3Ru6Sb8, has been synthesized by a solid-state reaction of the elements at 1023 K. Its crystal structure has been established by single-crystal X-ray diffraction methods. It crystallizes in a new structure type in the trigonal crystal system (Pearson index hP17) in space group P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1. The asymmetric unit of this structure contains six crystallographically independent sites: one Cu (site symmetry .2/m.), three Ru (Ru1 (.2/m.), Ru2 (3m.), and Ru3 (
m1. The asymmetric unit of this structure contains six crystallographically independent sites: one Cu (site symmetry .2/m.), three Ru (Ru1 (.2/m.), Ru2 (3m.), and Ru3 (![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m.)), and two Sb sites (Sb1 (.m.) and Sb2 (3m.)). Two of the Ru atoms and the Cu atom are coordinated to six Sb atoms in a distorted octahedral fashion; the third Ru atom is found in a trigonal bipyramidal environment of five Sb atoms. The structure can be viewed as a hexagonal closed-packed array of Sb atoms, with Ru and Cu atoms in the interstices, representing a lattice that is an ordered variant of the NiAs structure. Electronic structure calculations provide insight into the chemical bonding in this transition metal antimonide. From magnetic and resistivity measurements on polycrystalline material, the compound is metallic and exhibits magnetic response that shows an effective moment smaller than any free-ion values, suggestive of weak itinerant magnetism.
m.)), and two Sb sites (Sb1 (.m.) and Sb2 (3m.)). Two of the Ru atoms and the Cu atom are coordinated to six Sb atoms in a distorted octahedral fashion; the third Ru atom is found in a trigonal bipyramidal environment of five Sb atoms. The structure can be viewed as a hexagonal closed-packed array of Sb atoms, with Ru and Cu atoms in the interstices, representing a lattice that is an ordered variant of the NiAs structure. Electronic structure calculations provide insight into the chemical bonding in this transition metal antimonide. From magnetic and resistivity measurements on polycrystalline material, the compound is metallic and exhibits magnetic response that shows an effective moment smaller than any free-ion values, suggestive of weak itinerant magnetism.
Introduction
Over the years, antimonides based on the transition metals have attracted much attention because of their interesting properties. For example, such compounds are known as superconductors,1–4 topological insulators,5 and magneto-resistive materials.6–8 This wide range of physical properties can be correlated with their various crystal structures and bonding interactions.9–16 Consequently, the structural aspects of antimonides have also been extensively studied—a recurring theme in the literature is the tendency of antimony atoms to form homoatomic bonds in the forms of dimers, trimers, squares, infinite chains, and planes.9–11,15–18 The added complexity to their crystal structures from the stabilization of such polyanionic units, and the availability of variable oxidation states in the transition metals have resulted in many compounds with intricate crystal structures. Some of them show very low thermal conductivity, while maintaining good electrical conductivity. Such combination of properties opens the possibility for applications as thermoelectric materials, which has been explored already for Yb14MnSb11,19,20 and other related antimonides.21–24Despite the considerable progress, still little is known about systems with more than one transition metal, not only among the antimonides, but among arsenides and bismuthides too. Such compounds could exhibit unusual magnetism owing to the presence of two or more transition metals with different electronegativities and d-electrons. Some specific examples include Ti5FeSb2,25 TiFe2Sb,26 Ti1−xMoxSb4,27 HfMoSb4,28 and Zr2V6Sb9,29 among others. Many of the known phases are substitutional derivatives of binary antimonides, i.e., the transition metals are not crystallographically ordered, but rather are mixed on the same sites.
A literature survey of the ternary Ru–M–Sb systems (M = 3d transition metals) shows that they are relatively unexplored, and only a handful of compounds are known. Examples include TiRuSb,30 VRuSb,30 Cr1–xRuxSb2,31 Ni0.5Ru0.5Sb3,23 and Zn7Ru9Sb8.32 Hence, our groups decided to explore Ru–M–Sb systems in which the M atoms have differing electronegativities and d-electrons in their valence shells.
In this report, we detail the synthesis and structural characterization of a new ordered ternary antimonide, Cu3Ru6Sb8, which also represents a new structure type. Additionally, we discuss the electronic structure and the magnetic response of Cu3Ru6Sb8.
Experimental
As a general practice in our laboratories, all starting materials were stored and handled inside an Ar-filled dry box, despite the fact that oxidation of the Cu, Ru, and Sb metals is not a concern. Elemental Ru (powder), Cu (shot), and Sb (shot), all with stated purity 99.5 wt%, were used as obtained.Synthetic procedures
Small crystals of Cu3Ru6Sb8 were first obtained at Northwestern University from a reaction of Cu (9.4 mg, 0.148 mmol), Ru (15.0 mg, 0.148 mmol), and Sb (18.0 mg, 0.148 mmol). The reactants were weighed and transferred into carbon-coated fused-silica tubes that were then evacuated to ca. 10−4 Torr, flame sealed, and placed in a computer-controlled furnace for heat treatment. The reaction mixture was initially heated to 973 K in 24 h and held constant at this temperature for 24 h. The temperature of the furnace was then raised to 1073 K at 4.1 K h−1, and the reaction mixture was annealed for 96 h. Finally, the reaction mixture was allowed to cool to 298 K by switching off the furnace. The reaction product consisted of Cu3Ru6Sb8 and Cu2Sb crystals, both of the same habit and appearance (silver colored).Through examination of several crystals one was found that had a unit cell different from that of Cu2Sb. After the structure and composition of Cu3Ru6Sb8 were established from single-crystal X-ray diffraction work and the chemical make-up of the new phase was verified by semi-quantitative EDX analysis, the synthesis was repeated at the University of Delaware from a stoichiometric solid-state reaction. A two-step process was needed to obtain a homogeneous product. In the first step, stoichiometric amounts of Ru powder, Cu chunks, and Sb powder with total mass of approx. 0.5 g were loaded in an alumina crucible. The crucible was put into a silica tube, which was then evacuated and flame sealed. The heat treatment in step one was the following—heating to 973 K in 15 h, followed by homogenization at 973 K for 96 h, and cooling to 573 K in 96 h. After that, the furnace was switched off. The resulting product was then ground into fine powder using an agate mortar and pestle, and compacted into a pellet of 5 mm diameter under 250 MPa of pressure. In the second step, the pellet was transferred into an alumina crucible, which was then jacketed inside a silica tube before flame sealing the tube under vacuum (ca. 10−4 Torr). The pellet was then heated to 1273 K in 12 h, kept there for 10 h, and then cooled to 1023 K in 14 h, followed by annealing for 72 h. Finally, the sample was cooled to 298 K over a period of 6 h. The resulting pellet was silver-metallic in color.
The stability of polycrystalline Cu3Ru6Sb8 in laboratory air was checked by X-ray powder diffraction (XRPD). It was found that the XRPD pattern of Cu3Ru6Sb8 remains unchanged for at least one month, suggesting that the compound is stable in air.
Crystallography
The crystal structure of Cu3Ru6Sb8 was determined from single-crystal X-ray diffraction data collected with the use of graphite-monochromatized Mo Kα radiation (λ = 0.71073 Å) at 100(2) K on a Bruker APEX2 diffractometer. The algorithm COSMO implemented in the program APEX2 was used to establish the data collection strategy with a series of 0.3° scans in φ and ω. The exposure time was 15 s per frame and the crystal to detector distance was 60 mm. The collection of intensity data as well as cell refinement and data reduction were carried out with the use of the program APEX2.33 A semi-empirical absorption correction based on symmetry equivalent reflections was performed with the use of the program SADABS.34 Precession images of the data set provided no evidence for a super cell, twinning, or for modulation. The structure was solved and refined in a straightforward manner with the use of the SHELX-14 algorithms of the SHELXTL program package.35The ADDSYM routine in PLATON did not indicate any missing symmetry.36 The program STRUCTURE TIDY was used to standardize the atomic positions.37 Further details are given in Table 1 and in the ESI.†
| Empirical formula | Cu3Ru6Sb8 |
|---|---|
| a R 1 = ∑||Fo| − |Fc||/∑|Fo|; wR2 = [∑[w(Fo2 − Fc2)2]/∑[w(Fo2)2]]1/2, where w = 1/[σ2Fo2 + (0.007P)2 + 1.225P] and P = (Fo2 + 2Fc2)/3. For additional information, please see the CIF in the ESI of this article. CIF has also been deposited with the Fachinformations zentrum Karlsruhe, 76344 Eggenstein-Leopoldshafen, Germany (Fax: +49-7247-808-666; E-mail: E-mail: crysdata@fiz-karlsruhe.de), with a depository number CSD 432019. | |
| Formula weight | 2169.52 |
| Space group, Z |
P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 (no. 163), 1 m1 (no. 163), 1 |
| Radiation, λ | Mo Kα, 0.71073 Å |
| T (K) | 100(2) |
| a (Å) | 8.1833(2) |
| c (Å) | 5.3835(2) |
| V (Å3) | 312.21(1) |
| ρ cal (g cm−3) | 9.42 |
| μ (cm−1) | 289.4 |
| Goodness-of-fit on F2 | 1.16 |
| R 1 (I > 2σI)a | 0.012 |
| wR2 (I > 2σI)a | 0.026 |
X-ray powder diffraction data were collected at 298 K on a Rigaku MiniFlex powder diffractometer, operated at 0.45 kW and using Ni-filtered Cu Kα radiation. Data were collected in a θ–2θ mode (2θ range of 5° to 70°) with a step size of 0.02° and 1 s per step scan speed. Data analysis was carried out using the JADE 6.5 software package.
Additional characterization and property measurements
Energy-dispersive X-ray analyses were obtained with the use of a Hitachi S-3400 SEM microscope. Multiple spots on several crystallites were analyzed. The averaged results were in good quantitative agreement with the refined composition.Four-probe resistivity measurements on the pellet of polycrystalline Cu3Ru6Sb8 were done with the use of a Quantum Design Physical Property Measurement System (PPMS). The measurements were carried out in the range of 5 K to 300 K with an excitation current of 5 mA. Four platinum wires were connected to the sintered pellet using EPO TEK H20 silver epoxy.
Magnetization measurements were carried out using a Quantum Design MPMS. Raw data were corrected for the diamagnetic contribution from the gel-cap holder, and converted to magnetic susceptibility. Field dependent magnetization (field-sweep) was measured at 2 K and 10 K by gradually increasing the applied magnetic field up to 70 kOe.
Electronic structure calculation
The electronic structure of Cu3Rb6Sb8 was computed with the Stuttgart TB-LMTO 4.7 program.38 The total and the partial Density of States (DOS), as well as the Crystal Orbital Hamilton Populations (COHP) of selected interactions are presented here. The local density approximation (LDA) was the method of choice to treat the exchange and correlation.39 All relativistic effects except spin–orbit coupling were included and estimated by using a scalar relativistic approximation.40 The symmetry of the potential is considered spherical inside each Wigner–Seitz (WS) sphere,41 and the radii of WS spheres were determined by an automatic procedure and were as follows: Cu = 1.51 Å; Ru = 1.50–1.62 Å, and Sb = 1.43–1.47 Å. The basis sets included 4s, 4p, and 3d orbitals for Cu; 5s, 5p, 4d, and 4f orbitals for Ru; 5s, 5p, and 5d orbitals for Sb. The Ru 4f and Sb 5d orbitals were handled by the Löwdin downfolding technique.42 A total of 394 irreducible k-points in the Brillouin zone were used, and the k-space integrations were done using the tetrahedron method.Results and discussion
Synthesis
As mentioned in the Introduction, there are very few pnictides that are based on Ru and another transition metal.23,30–32 A search of the ICSD database43 shows that ternary pnictides formed between the metals of groups 8 and 11 are largely unknown, with CuFeAs (Cu2Sb type) being the only structurally characterized example.44The antimonide Cu3Ru6Sb8 is the first compound of these three elements. That it crystallizes in a new structure type should pave the way for further synthetic and structural work in groups 8–11–15 phases. We tried to expand our studies into the Cu–Ru–As system, but the preliminary results indicate that an arsenide Cu3Ru6As8 cannot be easily made. If the phase does exist, then for it to be synthesized, the experimental conditions used for the Sb-archetype will have to be significantly modified. Another synthetic complication is the tendency of As to sublime. Thus, instead of an open crucible, the solid-state reactions involving As must be carried out in sealed containers. This requirement is difficult to meet as As reacts readily with Nb, the common metal of choice for sealed-tube containers. Evidence for this is the compound NbRuAs (TiNiSi type)45 that was inadvertently obtained from such a reaction. The CIF for it is provided as ESI† (ICSD depository number CSD 432020).
Structure description
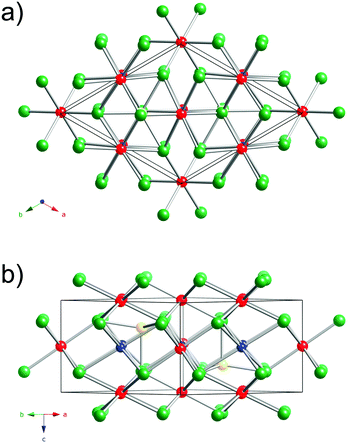
A view of the Cu3Ru6Sb8 structure is presented in Fig. 1. This new ternary compound crystallizes in what appears to be a previously unseen structure type in the centrosymmetric space group P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 (Pearson index hP17).
m1 (Pearson index hP17).
The structure has one formula unit per cell, and boasts a very small volume of 312 Å3. Thus, it is very surprising that this crystallographic arrangement is without a precedent so far.43,45 The asymmetric unit comprises six independent sites: Cu(1) with site symmetry .2/m.; Ru(1)—site symmetry .2/m., Ru(2)—site symmetry 3m.; Ru(3)—site symmetry ![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m.; Sb(1)—site symmetry .m.; and Sb(2)—site symmetry 3m. (Table 2).
m.; Sb(1)—site symmetry .m.; and Sb(2)—site symmetry 3m. (Table 2).
| Atom | Site | x | y | z |
U
eq![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a (Å2) a (Å2) |
|---|---|---|---|---|---|
| a U eq is defined as one-third of the trace of the orthogonalized Uij tensor. | |||||
| Cu(1) | 3e | 1/2 | 0 | 0 | 0.0092(1) |
| Ru(1) | 3f | 1/2 | 0 | 1/2 | 0.0078(1) |
| Ru(2) | 2d | 1/3 | 2/3 | 0.20120(9) | 0.0077(1) |
| Ru(3) | 1a | 0 | 0 | 0 | 0.0061(1) |
| Sb(1) | 6i | 0.15285(1) |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif)
|
0.27676(4) | 0.0070(1) |
| Sb(2) | 2d | 1/3 | 2/3 | 0.72741(7) | 0.0070(1) |
The best way to describe the crystal structure of Cu3Ru6Sb8 is by recognizing its close relationship with the hexagonal NiAs structure type.45 Recall that NiAs can be dubbed as the “hexagonal analogue” of the cubic rock-salt structure; that is, the As-atoms form a hcp-lattice, with the Ni-atoms filling all octahedral holes. This means that all metal atoms are coordinated octahedrally by As, while the latter are found in a trigonal prismatic environment.
Following this notion, one can visualize the structure of Cu3Ru6Sb8 as a hexagonal close-packed array of Sb atoms, with the transition metal atoms in both octahedral and tetrahedral holes. Thus, the structure is not a simple derivative of NiAs.
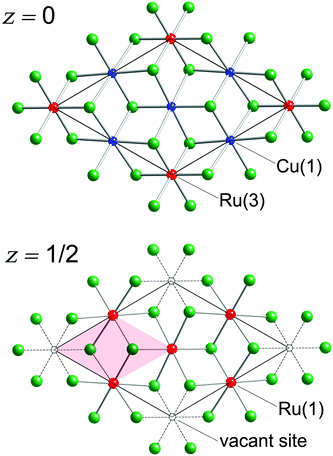
There are eight Sb atoms in one unit cell; thus, there are eight octahedral voids and sixteen tetrahedral voids per formula. The Ru(1), Ru(3), and Cu(1) atoms occupy 3/8th, 1/8th, and 3/8th of the available octahedral voids, respectively. This arrangement of atoms leaves 1/8th of the total octahedral sites vacant (Fig. 2). Thus, extending the analogy to NiAs, the Cu3Ru4□Sb8 sub-structure (the symbol □ denotes the vacant metal sites) depicted in the figure can be considered as a defect version (super-structure) of the NiAs-type spatial arrangement, where two different transition metals are ordered on the octahedral sites, while 1/8th of them are void of fillers (vide supra). This host Cu3Ru4□Sb8 lattice is, in turn, filled with two additional Ru atoms (Ru(2) in our nomenclature), that fill 1/8th of the available tetrahedral sites. The resultant Cu3Ru6□Sb8 total structure can therefore be rationalized as a “stuffed” derivative of the NiAs structure.
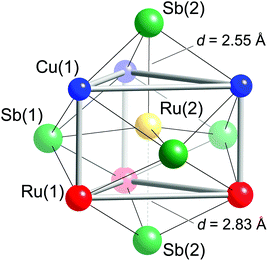
Taking a careful look at the coordination of the tetrahedral fillers provides some interesting observations. First, the Ru(2) atoms are not necessarily in tetrahedral holes—they can also be seen as being in a trigonal bipyramidal environment of five nearest Sb atoms, as shown in Fig. 3. Second, the Ru(2) atoms also have other metals in their first coordination sphere—Fig. 3 shows Ru(2) occupying the center of a trigonal prism formed from three Ru(1) and three Cu(1) atoms. The Sb trigonal bipyramid and the Cu/Ru trigonal prism are “overlayed” in a way that the faces of the metal-based trigonal prism are capped by Sb atoms—three Sb(1) atoms capping the rectangular faces and two Sb(2) atoms capping the triangular faces. The disparity between the axial Ru(2)–Sb(2) distances is obvious (the two Ru(2)–Sb(2) contacts differ by almost 0.3 Å; Table 3). Nevertheless, when compared to the sum of the Pauling single-bonded radii of Sb (1.391 Å) and Ru (1.246 Å),46 it is clear that on average, all Ru(2)–Sb bonds are very strong.
| Atom pair | Distance (Å) | Atom pair | Distance (Å) |
|---|---|---|---|
| Cu(1)–Sb(1) | 2.8812(2) × 4 | Ru(2)–Sb(1) | 2.5901(2) × 3 |
| Cu(1)–Sb(2) | 2.7810(2) × 2 | Ru(2)–Sb(2) | 2.5507(6) |
| Cu(1)–Ru(1) | 2.6918(2) × 2 | Ru(2)–Sb(2) | 2.8329(6) |
| Cu(1)–Ru(2) | 2.5986(2) × 2 | Ru(2)–Cu(1) | 2.5986(2) × 3 |
| Ru(1)–Sb(1) | 2.7432(1) × 4 | Ru(2)–Ru(1) | 2.8578(3) × 3 |
| Ru(1)–Sb(2) | 2.6605(2) × 2 | Ru(3)–Sb(1) | 2.6292(2) × 6 |
| Ru(1)–Cu(1) | 2.6918(2) × 2 | ||
| Ru(1)–Ru(2) | 2.8578(3) × 2 |
Having discussed Ru(2)–Sb distances to its nearest neighbors, it is useful to compare and contrast all Ru–Sb interactions. The NiAs structure provides dense packing; therefore, it is reasonable to expect that a “stuffed” version of this arrangement of hcp layers of Sb atoms with Ru and Cu atoms in between will result in unusual interactions. For example, the octahedral units of Ru(1)Sb6 are slightly distorted and have shorter apical than equatorial distances. The apical Ru(1)–Sb(2) distances (2.66 Å) are nearly at the mid-point of the previously discussed Ru(2)–Sb(2) contacts. The four equatorial Ru(1)–Sb(1) distances are about 2.74 Å, i.e., 3% longer.
The shortest distance between Ru(1) and Cu(1) atoms is 2.6918(2) Å, which is only longer by ca. 0.08 Å than the sum of the Pauling metallic radii of Cu (1.276 Å) and Ru (1.336 Å).46 There are not many intermetallics with ordered Cu and Ru atoms, with which to compare these numbers. Only one compound, Ti9Cu2Ru18B8, can be found in the ICSD database,43,47 that has similar distances between Cu and Ru atoms (dCu–Ru = 2.64 Å). In the structure of Cu3Ru6Sb8, every Ru(1)Sb6 octahedron shares four edges with neighboring Ru(1)Sb6 octahedra resulting in the formation of [RuSb8/3] layers as shown in Fig. 2.
The Ru(1)–Ru(2) distance of 2.8578(3) Å is longer than the sum of the metallic radii of two Ru atoms; hence this interaction can be considered very weak. The shortest Ru(1)⋯Ru(1) and Ru(1)⋯Ru(3) distances in this structure are 4.092(1) Å and 4.453(1) Å, respectively, and do not signify bonding interactions.
The Ru(3) atoms in this structure are sandwiched between the two layers that are created by sharing of the Ru(1)Sb6 octahedra. As mentioned earlier, the Ru(3) atoms are also octahedrally coordinated by six Sb atoms. The longer Ru(1)–Sb and Ru(3)–Sb distances (compared with the four very short Ru(2)–Sb distances) are consistent with the smaller coordination number of Ru(2) as compared with those of Ru(1) and Ru(3). Unlike the Ru(1)Sb6 units, the Ru(3)Sb6 octahedra are not involved in any sharing of their Sb atoms with other neighboring Ru-octahedra within the same slab (Fig. 2). However, the Ru(3)Sb6 octahedra are fused by six Cu(1)Sb6 octahedra into a Cu3[Ru(3)]1Sb4 layer (Fig. 2). The shortest Ru(3)⋯Ru(3) distance (5.384 Å) is indicative of a non-bonding interaction.
The Cu(1) atoms in this structure are surrounded by four Sb(1) and two Sb(2) atoms in a slightly distorted octahedral fashion. The Cu(1)Sb6 octahedra are axially compressed, similar to the Ru(1)Sb6 units, but the median Cu–Sb distance is longer than any of the Ru–Sb distances (Table 3). Given that the Cu radius is smaller than the Ru radius, such long contacts indicate weak interactions. Comparable Cu–Sb distances are reported in other known compounds with Cu in octahedral coordination of Sb, such as Cu3V2Sb4 (average Cu–Sb distance = 2.845 Å).48
In addition to the six Sb atoms within their coordination sphere, the Cu(1) atoms also have two Ru(1) and two Ru(2) closest neighbors at distances 2.6918(2) Å and 2.5986(2) Å, respectively (Table 3). Emphasizing metal–metal interactions among the Ru(1), Ru(2), and Cu(1) atoms, we show them as forming a hexagonal channel-like structure, where Cu(1) and Ru(1) form chains parallel to the c-axis (Fig. 4). Each Cu(1) atom in these chains is also connected to two Ru(2) atoms giving rise to the step-like units that are the building block of hexagonal cages. These hexagonal channels are filled by the Ru(3) atoms.
Electronic structure
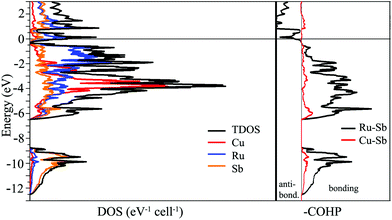
The simplest approach towards understanding the electronic structure of Cu3Ru6Sb8 is to assign oxidation numbers to the elements as follows: (Cu2+)3(Ru3+)6(Sb3−)8, which leads to a charge balanced composition, akin to a semiconductor. This notion, of course, is an exaggeration, and clearly contradicts the metallic behavior of Cu3Ru6Sb8 deduced from the resistivity measurements (ESI†). One might assign different oxidation numbers to Cu and Ru, for example (Cu+)3(Ru3+)5(Ru4+)(Sb3−)8(h+)2, and (Cu+)3(Ru3+)3(Ru4+)3(Sb3−)8, leaving some electrons/holes in the conduction band to account for the experimentally observed metallicity. However, the weak itinerant magnetism and the effective moment that is much smaller than any of the possible free-ion values (vide infra) do not support such formulations.To investigate the nature of the interactions in Cu3Ru6Sb8, electronic band-structure calculations on the basis of TB-LMTO-ASA method were carried out; the total density of states (TDOS), partial density of states (PDOS) and Crystal Orbital Hamilton Populations (COHP) curves for Cu3Ru6Sb8 are plotted in Fig. 5. As seen, there is no band gap between the valence band and the conduction band; the Fermi level is located in a region of relatively high DOS, fully consistent with the metallic behavior of Cu3Ru6Sb8.
The electronic band structure can be separated into two distinct energy ranges. The first comprises lower energy bands in the window from ca. −12.5 eV to −9 eV; these are mainly contributions of the Sb 5s orbitals, which are fairly well localized. The second, much broader region spans over 6 eV; it starts from ca. −6.5 eV and extends to just below the Fermi level. The bands that are contributing the most here originate from the admixture of Ru 4d, Cu 3d, and Sb 5p orbitals. The distribution of these bands is very similar and the substantial overlapping is suggestive of strong bonding interactions between the corresponding elements. This is consistent with the COHP curves of the Ru–Sb and Cu–Sb interactions that show them as nearly optimized around the Fermi level. Note that the interactions between Ru and Sb atoms appear to dominate the overall bonding. The electronic structure calculations do not show any significant homoatomic Sb- or Ru-bonding. Specifically, there are Sb⋯Sb contacts in Cu3Ru6Sb8 that measure 3.236(1) Å, which in other antimonides can be interpreted as an indication of hypervalent interactions. Their vanishingly small integrated COHP values in this case, however, does not support such bonding description.
Lastly, we would like to comment on the hypothesis that the structural chemistry of many transition-metal intermetallics can be explained through isolobal analogies to molecular transition-metal complexes.49 It is speculated that the transition metals tend to achieve 18 electrons (expanded octets) around them; therefore the structures could be rationalized by applying the 18 − n “rule” (n is the number of covalent bonds with other metals in which a given transition metal participates).49 Taking into account the Ru–Cu bonding and the multiplicities of the atoms in the crystal structure (vide supra), one can propose the ideal number of valance electrons per formula unit to be 126, based on the breakdown: [3 × 16 = 48 for Ru(1)] + [2 × 15 = 30 for Ru(2)] + [1 × 18 = 18 for Ru(3)] + [2 × 3 = 6 for Cu] + [3 × 8 = 24 for Sb] = 126. The available overall number of electrons in Cu3Ru6Sb8 is 121 (3 × 11 + 6 × 8 + 8 × 5). Possible explanations for the apparent electron imbalance include (1) the Ru(1)–Ru(2) interactions, which were not considered in the above-mentioned 18 − n electron partitioning, are important to the bonding; (2) the actual number of valence electrons for Cu3Ru6Sb8 is short of that predicted because although the 18 − n “rule” applies well to simpler binaries, our ordered ternary structure with competing metal–metal interactions requires an augmented electron count; and (3) atomic packing constraints may play a significant role in the stabilization of this bonding pattern, as this structure is a filled version of a hexagonal closed-packed structure.
Further indication of the delicate interplay between electronic and geometric factors in this structure is the fact that both DOS and COHP (Fig. 5) show two regions of potentially enhanced electronic stability—slightly above and below the Fermi level, evidenced by the very small DOS and COHP values at ca. +1 eV, and ca. −0.4 eV, respectively. Given that, it will be interesting to attempt synthesizing electron richer and poorer versions of Cu3Ru6Sb8 by substitution of Cu and/or Ru with other transition metals.
Magnetism
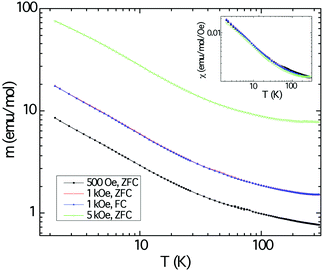
The magnetic response of polycrystalline Cu3Ru6Sb8 as a function of the temperature is shown in Fig. 6. The background from the sample holder and the core electrons were obtained from separate measurements. These were subtracted from the raw data. The sample was measured under applied fields of 500, 1000, and 5000 Oe and the three plots in the main panel show an increase of the magnetic moment (normalized per mol) as the temperature is lowered, but reveal no ordering down to 2 K. Field-cooled and zero field-cooled data show no divergence. The response appears to be typical for paramagnets.Plotting the inverse magnetic susceptibility against temperature indicates Curie–Weiss behavior in a relatively wide temperature region, confirming the notion that the material is paramagnetic. The effective moment peff and the paramagnetic Weiss temperature θW obtained from the linear regression are ca. 0.7 μB and ca. −10 K, respectively. A better and more accurate fit to the data was obtained using the modified Curie–Weiss law (ESI†), whereby a temperature independent term (χ0) was introduced, and its value estimated from a non-linear fitting procedure. This resulted in the following numerical parameters: χ0 = 0.0012 emu mol−1 Oe−1, peff = 0.78 μB, and θW = −8.8 K, respectively. Note that the value for χ0 is larger than usual and the effective moment is far smaller than the spin-only values expected for free-ion Cu2+ (3d9, S = 1/2, 1.73 μB) and the low-spin configuration of Ru3+ (4d5, S = 1/2, 1.73 μB).50 The discrepancy is even larger if one considers different spin-states for Ru and the fact that there are multiple metal sites per formula unit. We also note that the temperature-independent term is positive and fairly large compared with the diamagnetic temperature independent term (by one order of magnitude).
The magnetization data at 2 K and 10 K are shown in Fig. 7. The magnetization curves resemble those that are typically attributed to polarization of local moments owing to the external magnetic fields, with tendency for saturation more evident at 2 K. However, the projected saturation value is far less than the estimated effective moment obtained by applying the modified Curie–Weiss procedure to the susceptibility data.
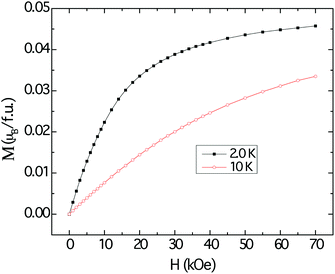 | ||
| Fig. 7 Field dependent magnetization of Cu3Ru6Sb8, measured at 10 K (red trace) and 2 K (black trace). | ||
Despite the apparent Curie–Weiss characteristic of the magnetic susceptibility, the very low effective moment and the vanishingly small saturation value suggest that the magnetism observed in Cu3Ru6Sb8 arises from itinerant electrons, rather than localized ones. The itinerant magnetism in d-electron materials has long been a subject of extensive studies and the current consensus is that the effect of spin fluctuation is the origin of Curie–Weiss-like susceptibility.51 It follows then, that the large positive χ0 can be explained by the Pauli paramagnetic contribution of the itinerant electrons. The metallic temperature dependence of the resistivity of Cu3Ru6Sb8 also supports this itinerant magnetism picture (ESI†).
Conclusions
The ternary antimonide Cu3Ru6Sb8, obtained by a direct fusion of the respective elements, was described for the very first time. Its structure was established from X-ray single-crystal diffraction method and found to crystallize in its own structure type. The structure is best viewed as a derivative of the NiAs structure type, recognizing the hexagonal close-packed array of Sb atoms, with the transition metal atoms in both octahedral and tetrahedral holes. Specifically, it is a super-structure of the NiAs-type spatial arrangement, where two different transition metals are ordered on the octahedral sites, while 1/8th of them are vacant and 1/8th of the available tetrahedral sites are filled. The resultant Cu3Ru6□Sb8 total structure can therefore be rationalized as a “stuffed” derivative of the NiAs structure.Cu3Ru6Sb8 is a metal, both from experimental and computational points of view. The delocalized nature of the interactions precludes the straightforward application of the valence rules, and as a result, certain aspects of the chemical bonding in this new structure type, are yet to be fully understood. Metal–metal bonding, in particular, appears to be very strong and further exploratory work to find other isotypic or structurally-related phases with different transition metals is warranted. Such studies are presently ongoing.
Acknowledgements
This work was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, under Award # DE-SC0008885. Use was made of the IMSERC X-ray Facility at Northwestern University, supported by the International Institute of Nanotechnology (IIN). The authors thank Prof. D. Fredrickson (UW-Madison) for useful discussion. The authors congratulate Mercouri Kanatzidis on the occasion of his 60th birthday and for his remarkable contributions to solid-state chemistry and materials.Notes and references
- M. Imai, S. Emura, M. Nishio, Y. Matsushita, S. Ibuka, N. Eguchi, F. Ishikawa, Y. Yamada, T. Muranaka and J. Akimitsu, Supercond. Sci. Technol., 2013, 26, 075001–075004 CrossRef.
- M. Wakeshima, C. Sakai and Y. Hinatsu, J. Phys.: Condens. Matter, 2007, 19, 16218 CrossRef.
- M. Imai, S. Ibuka, N. Kikugawa, T. Terashima, S. Uji, T. Yajima, H. Kageyama and I. Hase, Phys. Rev. B: Condens. Matter, 2015, 91, 14513 CrossRef.
- E. E. M. Chia, D. Vandervelde, M. B. Salamon, D. Kikuchi, H. Sugawara and H. Sato, J. Phys.: Condens. Matter, 2005, 17, l303–l310 CrossRef CAS.
- S. Chadov, X. Qi, J. Kübler, G. H. Fecher, C. Felser and S. C. Zhang, Nat. Mater., 2010, 9, 541–545 CrossRef CAS PubMed.
- K. Wang and C. Petrovic, Appl. Phys. Lett., 2012, 101, 152102 CrossRef.
- J. Y. Chan, S. M. Kauzlarich, P. Klavins, R. N. Shelton and D. J. Webb, Chem. Mater., 1997, 9, 3132–3135 CrossRef CAS.
- L. Deakin and A. Mar, Chem. Mater., 2003, 15, 3343–3346 CrossRef CAS.
- W. Schweika, R. P. Hermann, M. Prager, J. Perßon and V. Keppens, Phys. Rev. Lett., 2007, 99, 125501 CrossRef CAS PubMed.
- G. Cordier, H. Schäfer and M. Stelter, Z. Anorg. Allg. Chem., 1984, 519, 183–188 CrossRef CAS.
- H. Kleinke, Chem. Commun., 1998, 2219–2220 RSC.
- S.-Q. Xia and S. Bobev, J. Am. Chem. Soc., 2007, 129, 4049–4057 CrossRef CAS PubMed.
- S.-Q. Xia and S. Bobev, Inorg. Chem., 2008, 47, 1919–1921 CrossRef CAS PubMed.
- J. Prakash, S. Stoyko, L. Voss and S. Bobev, Eur. J. Inorg. Chem., 2016, 2016, 2912–2922 CrossRef CAS.
- M. Guch, C. R. Sankar, A. Assoud and H. Kleinke, Chem. Mater., 2010, 22, 6433–6437 CrossRef CAS.
- G. Papoian and R. Hoffmann, J. Solid State Chem., 1998, 139, 8–21 CrossRef CAS.
- R. Wang and H. Steinfink, Inorg. Chem., 1967, 6, 1685–1692 CrossRef CAS.
- A. Assoud, K. M. Kleinke, N. Soheilnia and H. Kleinke, Angew. Chem., Int. Ed., 2004, 43, 5260–5262 CrossRef CAS PubMed.
- S. R. Brown, S. M. Kauzlarich, F. Gascoin and G. J. Snyder, Chem. Mater., 2006, 18, 1873–1877 CrossRef CAS.
- E. S. Toberer, S. R. Brown, T. Ikeda, S. M. Kauzlarich and G. J. Snyder, Appl. Phys. Lett., 2008, 93, 62110 CrossRef.
- E. S. Toberer, A. Zevalkink, N. Crisosto and G. J. Snyder, Adv. Funct. Mater., 2010, 20, 4375–4380 CrossRef CAS.
- A. C. Sklad, M. W. Gaultois and A. P. Grosvenor, J. Alloys Compd., 2010, 505, L6–L9 CrossRef CAS.
- J. Navrátil, F. Laufek, T. Plecháček and Č. Drašar, J. Solid State Chem., 2012, 193, 2–7 CrossRef.
- S. M. Kauzlarich, S. R. Brown and G. J. Snyder, Dalton Trans., 2007, 2099–2107 RSC.
- G. Melnyk and W. Tremel, J. Alloys Compd., 2003, 349, 164–171 CrossRef CAS.
- H. Luo, G. Liu, F. Meng, J. Li, E. Liu and G. Wu, J. Magn. Magn. Mater., 2012, 324, 3295–3299 CrossRef CAS.
- S. Derakhshan, A. Assoud, K. M. Kleinke and H. Kleinke, Inorg. Chem., 2007, 46, 1459–1463 CrossRef CAS PubMed.
- S. Derakhshan, K. M. Kleinke, E. Dashjav and H. Kleinke, Chem. Commun., 2004, 2428–2429 RSC.
- H. Kleinke, Eur. J. Inorg. Chem., 1998, 1998, 1369–1375 CrossRef.
- C. B. H. Evers, C. G. Richter, K. Hartjes and W. Jeitschko, J. Alloys Compd., 1997, 252, 93–97 CrossRef CAS.
- T. Harada, T. Kanomata, Y. Takahashi, O. Nashima, H. Yoshida and T. Kaneko, J. Alloys Compd., 2004, 383, 200–204 CrossRef CAS.
- D. B. Xiong, Y. Zhao, N. L. Okamoto, C. Pietzonka, T. Waki and H. Inui, Inorg. Chem., 2010, 49, 10536–10542 CrossRef CAS PubMed.
- Bruker APEX2 Version 2009.5-1, Data Collection and Processing Software, Bruker Analytical X-Ray Instruments, Inc., Madison, WI, USA, 2009 Search PubMed.
- G. M. Sheldrick, SADABS, Department of Structural Chemistry, University of Göttingen, Göttingen, Germany, 2008 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed.
- A. L. Spek, PLATON, A Multipurpose Crystallographic Tool, Utrecht University, Utrecht, The Netherlands, 2014 Search PubMed.
- L. M. Gelato and E. Parthe, J. Appl. Crystallogr., 1987, 20, 139–143 CrossRef.
- O. Jepsen and O. K. Andersen, The Stuttgart TB-LMTO Program, Version 4.7, Max Planck Institut für Festkörper-forschung, Stuttgart, Germany, 1998 Search PubMed.
- U. von Barth and L. Hedin, J. Phys. C: Solid State Phys., 1972, 5, 1629–1642 CrossRef CAS.
- D. D. Koelling and B. N. Harmon, J. Phys. C: Solid State Phys., 1977, 10, 3107–3114 CrossRef CAS.
- O. K. Andersen, O. Jepsen and D. Glötzel, in Highlights of Condensed Matter Theory, ed. F. Bassani, F. Fumi and M. Tosi, North-Holland, New York, 1985 Search PubMed.
- W. R. L. Lambrecht and O. K. Andersen, Phys. Rev. B: Condens. Matter, 1986, 34, 2439–2449 CrossRef CAS.
- https://icsd.fiz-karlsruhe.de/search/index.xhtml , accessed September 2016.
- G. S. Thakur, Z. Haque, L. A. Gupta and A. K. Ganguli, J. Phys. Soc. Jpn., 2014, 83, 54706 CrossRef.
- Pearson's Handbook of Crystallographic Data for Intermetallic Compounds, ed. P. Villars and L. D. Calvert, American Society for Metals, Materials Park, OH, USA, 2nd edn, 1991, and the desktop edition, 1997 Search PubMed.
- L. Pauling, The Nature of the Chemical Bond, Cornel University, Ithaca, NY, 1960.
- B. P. T. Fokwa, C. Goerens and M. Gilleßen, Z. Kristallogr., 2010, 225, 180–186 CAS.
- M. Konyk, L. Romaka, P. Demchenko, V. V. Romaka, Y. Stadnyk and A. Horyn, J. Alloys Compd., 2014, 589, 200–206 CrossRef CAS.
- V. J. Yannello and D. C. Fredrickson, Inorg. Chem., 2015, 54, 11385–11398 CrossRef CAS PubMed.
- Introduction to Solid State Physics, ed. C. Kittel, John Wiley & Sons, Hoboken, 8th edn, 2005 Search PubMed.
- T. Moriya and T. Y. Takahashi, Annu. Rev. Mater., 1984, 14, 1–25 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Crystallographic information files (CIF) for the title compound Cu3Ru6Sb8 (CSD 432019) and for NbRuAs (CSD 432020), which was inadvertently obtained from a reaction aimed at the arsenide Cu3Ru6As8, carried out in a sealed Nb-container; a plot of the linear fit to the inverse magnetic susceptibility data for Cu3Ru6Sb8; a plot of the temperature dependence of the resistivity of polycrystalline Cu3Ru6Sb8; the experimental and simulated X-ray powder diffraction pattern of Cu3Ru6Sb8. See DOI: 10.1039/c6qi00418k |
| This journal is © the Partner Organisations 2016 |