Mechanism and regulation of tensile-induced degradation of flexible perovskite solar cells

Abstract

Flexible perovskite solar cells (FPSCs) are promising next-generation photovoltaic devices, but the poor mechanical stability issue is still a huge obstacle to their commercialization. In this work, we investigate the mechanism of tensile-induced degradation of FPSCs through experiment and theoretical analysis. We demonstrate that the cracks of the indium tin oxide electrode layer (ITO) and perovskite (PVK) layer induced by tensile stress play a major role in the efficiency degradation of FPSCs. To relieve the internal stress concentration, a polyelectrolyte layer (D-PAA/C-EA modified SnO₂) is proposed for strain engineering, which is confirmed by both numerical simulation and experiment. The threshold strain of device failure for D-PAA/C-EA modified FPSCs is nearly twice that of the original FPSCs, signifying its potential in enhancing the mechanical stability of the devices.

---

Introduction

Flexible perovskite solar cells (FPSCs) are considered some of the most promising photoelectric devices for wearable electronic applications due to their high power-conversion efficiency (PCE) and intrinsic mechanical flexibility.^1–7 Over the past decade, researchers have achieved a substantial leap in PCE for FPSCs through a functional layer material optimization strategy.^8–11 Nevertheless, as flexible photovoltaic devices, poor mechanical stability is still a significant concern regarding FPSCs, hindering their commercialization.^12–18 Mechanical stability mainly refers to the stability of FPSCs under large deformation and long-term cyclic loading. Due to the external mechanical load, cracks accumulate on the functional layers of FPSCs and affect the device performance greatly.^19,20 Thus, strategies aimed at improving the mechanical stability and investigating the mechanical-photoelectric coupled behavior in perovskite solar cells have been reported.^21,22

Several approaches have been suggested to enhance the mechanical stability of various components. These include strategies such as augmenting the inherent ductility of major constituents, introducing buffer layers (BLs) to alleviate stress, and optimizing the external structure of the device.^23–26 In a study by Sun et al.,²⁷ it was observed that the Young's moduli of CH₃NH₃PbX₃ (X = I, Br, and Cl) ranged from 10 to 20 GPa, with investigations into the mechanical stability of perovskites conducted in relation to the halide used. Hu et al.²⁸ proposed that sulfonated graphene oxide (s-GO) could be incorporated into the perovskite film, and the resulting complex s-GO–[Pb₆]⁴⁻ would effectively improve the flexibility and ductility of the perovskite film owing to the tough grain boundaries. Furthermore, the presence of cracks and delamination between different layers necessitates the use of buffer layers (BLs) to safeguard against stress-induced damage. Li et al.²⁹ introduced a soluble hydrophobic polymer as a BL to obtain more excellent mechanical stability. Moreover, double cantilever beam (DCB) test results proved that adding polyethyleneimine (PEl) as a compatibilizer could significantly improve the mechanical stability of FPSCs by enhancing the perovskite/HTL interface adhesion. An external structure optimization strategy has also emerged as a highly efficient strategy. Dauskardt et al.³⁰ introduced a new concept: perovskite compound solar cells with close-packed hexagonal or honeycomb structures, which addressed the intrinsic fragility of the functional layers through the incorporation of internal scaffolds that provide mechanical reinforcement. Li et al.³¹ also proposed kirigami structure FPSCs that exhibited high stretchability and mechanical stability under 150% stretching strain.

Furthermore, additional research has been completed on in-depth studying the mechanical behaviors and photoelectric degradation of FPSCs. Seong et al.³² first discussed that the value of (E/G_C)^1/2 would better reflect the intrinsic flexibility of FPSCs, as it governs the critical bending radius of FPSCs. In addition to mechanical properties, the mechanical degradation behaviors of the devices are also in urgent need of further research. Davis et al.¹⁹ reported a robust predictive model to accurately simulate the stress distribution and mechanical deformation of perovskite layers, to make up for the defect that the internal stress and crack in the layer cannot be studied by experimental methods. In order to further discuss the electromechanical multifield coupling in perovskite solar cells, a number of researchers concentrated on the impact of strain on the electronic band structure and the optoelectronic properties of perovskites.^33–36 Zhu et al.³⁷ calculated the band structure of FAPbI₃ through first principles, demonstrating that the band gap increases under tensile strain; this increase can impact the optical properties to some extent. Berdiyorov et al.³⁸ found an increase in charge transport of the perovskite under compressive strain due to the enhanced overlap of the atomic orbitals. Jones et al.³⁹ demonstrated a direct relation between lattice strain and the increment of defect concentration and non-radiative recombination sites, which can hinder the optical properties such as open circuit voltage. While researchers have focused on a strategy to improve mechanical stability and the electromechanical multifield coupled behaviors in perovskite layers, the coupled mechanical-photoelectric degradation mechanism and synergy among the main layers for FPSCs have been ignored.^40–42

In this work, the coupled mechanical-optoelectronic degradation mechanism for FPSCs and the associated experimental and theoretical methods are investigated. A series of in-situ quasi-static tensile tests were conducted to analyze the failure behaviors of FPSCs under high strain levels. The prepared samples exhibited an ultimate tensile strength of 200 MPa. Subsequent scanning electron microscopy (SEM) analysis of the functional layers post-tensile test revealed a significant impact of mechanical stress on the electrical properties of these layers, underscoring the critical role of mechanical factors in the performance of FPSCs. Informed by the experimental data, we developed a mechanical-photovoltaic coupled simulation model for the failure prediction of the FPSCs with COMSOL Multiphysics. Comparison with experimental results proved the accuracy of the developed simulation model. To achieve an enhancement in the mechanical stability of the functional layers, in this research, we synthesized a water-soluble and adhesive polyelectrolyte binder (D-PAA/C-EA) and added it to SnO₂ to prepare a hybrid organic–inorganic ETL for high-performance PSCs. The addition of the polyelectrolyte layer was proposed to alleviate the internal stress concentration, a hypothesis that was subsequently confirmed through comparative experiments. The D-PAA/C-EA-modified device demonstrated a threshold strain level of 5.5%, an increase of 83.3% compared to the original devices. This significant improvement indicates the potential of our approach for large-area applications. This research achieves a significant method to clarify the qualitative mechanism between the mechanical behavior and the photovoltaic performance, so as to provide more practical guidance for the design of FPSCs with high efficiency and mechanical stability.

Experimental

Sample preparation

The tested FPSC samples were produced using the same procedures as described in the authors’ previous published paper.⁴³ To synthesize the D-PAA/C-EA water-soluble polyelectrolyte binder, we adhered to the methodology outlined in Li et al.'s paper.⁴⁴ The binder was synthesized by combining PAA (from Sigma-Aldrich, molecular weight approximately 450 000, used as received without modification) with ethanolamine in a methanol solution. In a typical procedure, 10 mL of an 11 wt% ethanolamine solution in methanol was gradually introduced into 30 mL of a 4.4 wt% PAA solution in methanol, resulting in immediate precipitation. The precipitate was isolated and thrice rinsed with methanol. The final product was acquired post drying in a vacuum oven at 50 °C for a duration of 10 hours.

In situ tensile experiment platform

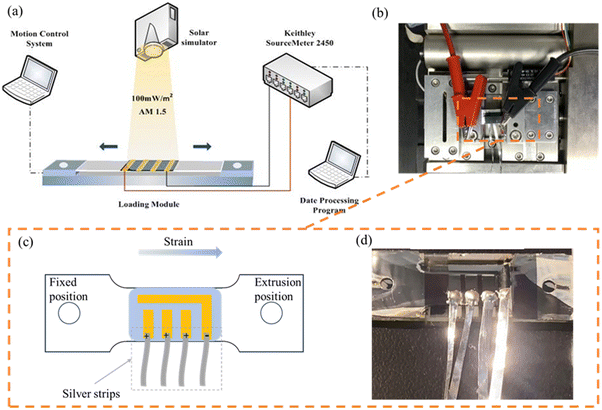
In order to clarify the qualitative mechanism between the mechanical behavior and the photovoltaic performance, a real-time mechanical-photoelectric coupled test was carried out on the multi-physical field test platform, as shown in Fig. 1a. This multi-physical field test platform consists of an in-situ tensile test machine (Fig. 1b), a Keithley 2450 source meter and a solar simulator, to simultaneously record the data on the load, displacement, and photoelectric performance of FPSCs during the tensile loading process. In order to record test data stably and accurately, we prepared FPSCs on a dog-bone substrate as tensile samples, and silver strips were bonded to the original electrodes of the FPSCs with 8821X bi-component silver glue (Fig. 1c and d). 8821X bi-component silver glue has been proven to have lower resistance and be easier to cure than conductive silver paste, and the infiltration and decomposition of silver into perovskite are also reduced.

Fig. 1 Mechanical and electrical test of FPSCs. (a) Schematic diagram of the in-situ mechanical-photoelectrical testing platform; (b) the in situ tensile test apparatus; (c) and (d) the tensile testing sample of FPSCs prepared on a dog-bone shape flexible substrate.

Results and discussion

The photoelectric degradation of FPSCs

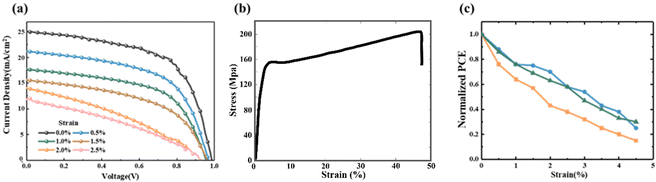
The experimentally measured J–V curve presented in Fig. 2a showed that under tensile strain from 0% to 2.5%, the short-circuit current density J_SC of FPSCs shows a clear decrease from 25 mA cm⁻² to about 12.5 mA cm⁻². Compared with the J_SC, the open-circuit voltage V_OC does not decrease significantly. It can also be observed that the fill factor (FF) of the FPSC is relatively high under 0% tensile strain, but decreases obviously under 2.5% tensile strain, and J–V curve approaches a straight line. Fig. 2cdemonstrates the degradation of the PCE under increasing tensile strains. First of all, the FPSC shows inherent ductility owing to the polyethylene naphthalate (PEN) substrate and the elongation rate of the FPSC reaches about 45%. Meanwhile the mechanical stability of the FPSC under tensile deformation decreases obviously. During the elastic deformation stage (0–4.0%), the normalized power conversion efficiency (PCE) experiences a significant decline, dropping sharply from 1.0 to approximately 0.3. This indicates a substantial loss in the photoelectric performance of the FPSC.

Fig. 2 (a) The J–V curves of the solar cell under 0–2.5% tensile strains. (b) The stress–strain of the tested perovskite solar cell. (c) The normalized PCE variations of three tested solar cells under 0–4.5% tensile strains, reflecting the degradation of photovoltaic performance.

The decrease of J_SC is often caused by the increase of the series resistance (R_S, contact resistance between layers). The larger R_S is, the smaller J_SC is, and the response of fill factor FF is reduced. Therefore, it can be inferred that the degradation of the photovoltaic performance of FPSCs under tensile load may also be caused by poor contact between the functional layers and electrodes, open circuit in some areas, a sharp increase in contact resistance and electrode resistance. Thus, finding out the main influencing factors and clarifying the mechanism of FPSCs' mechanical-photoelectric coupled behavior plays an important role in improving the mechanical stability.

The mechanism of mechanical-photoelectric coupled behavior

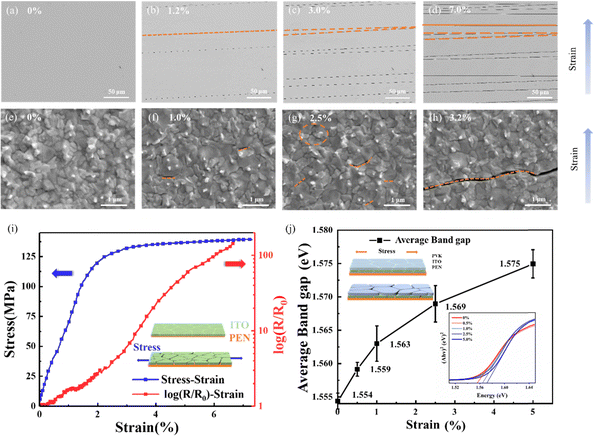
In order to clarify the mechanism of mechanical-photoelectric coupled behavior of FPSCs, in situ tensile tests were carried out on the indium tin oxide (ITO) electrode layer and the perovskite layer (PVK) via an in situ tensile platform and scanning electron microscope. The morphologies at the microscale of ITO/PEN under different tensile strains are shown in Fig. 3a–d. The first crack of ITO was observed at a very small strain level (about 1.2%). Upon the initiation of the first micro crack, there was a rapid increase of the length and number of micro cracks with the increase of the strain (Fig. 3c). Up to 7.0%, almost every micro crack extended to long cracks, and the crack density tended to be saturated, followed by an increase in crack width.

Fig. 3 The morphology at the microscale of ITO/PEN under different tensile strains: (a) 0%, (b) 1.2%, (c) 3.0%, and (d) 7.0%; the morphology at the microscale of PVK/ITO/PEN under different tensile strains: (e) 0%, (f) 1.0%, (g) 2.5% and (h) 3.2%; (i) the mechanical–electrical behavior of ITO: stress–strain curves and fractional change in resistance–strain curves; (j) the electronic properties of the polycrystalline halide perovskite film as a function of strain are shown as black points and ultraviolet-absorption spectra for the Tauc plots by Kubelka–Munk transformation are shown as colored lines.

For polycrystalline perovskite crystals, the grain boundaries are where cracks are most likely to occur under stretching deformation. The morphologies at the microscale of PVK/ITO/PEN under different tensile strains are shown in Fig. 3e–h. The first micro defect appeared at the grain boundary at a strain of 1.0%. As the strain increases, for instance, at about 2.5% strain, a new type of defect crossing the crystal was observed. Intergrain and intragrain defects were connected to form a crack as shown in Fig. 3h at about 3.2% strain.

The sharp increase in resistance of ITO can be considered a major cause of FPSCs’ photoelectric performance degradation under large stretching deformation. The resistance of ITO as a function of uniaxial strain was measured in situ using a standard four-point measurement technique. The resistance and load were recorded during uniaxial tensile elongation, and the results are presented in Fig. 3i. It is observed that the resistance increased sharply at some threshold strain, which depended on the cracking of ITO. Upon the initiation of the first micro crack, there was less than two times increase in resistance for a tensile strain below 2%. As the tensile strain increased, the ITO resistance first raised gradually and then shot up dramatically at the stage of elastic deformation. There was nearly a 150-time increase in resistance under the tensile strain of 7.0%.

It is reported that the electronic properties of the polycrystalline halide perovskite film are highly subject to macroscopic strain, which can also be considered another major cause of FPSCs’ photoelectric performance degradation. The calculated band gap average as a function of strain level and Ultraviolet-absorption spectra for the Tauc plots by Kubelka–Munk transformation are shown in Fig. 3j. As the applied tensile strain increases, the band gap first raised rapidly, and then the growing tendency slowed down. The original band gap of the polycrystalline halide perovskite film is 1.554 eV, and when the tensile strain is 1%, 2.5%, and 5.0%, the band gap rises to 1.563 eV, 1.569 eV and 1.575 eV, respectively.

Through the above-mentioned in situ tests and electromechanical behavior analysis, we can initially draw a conclusion that the main components of the FPSCs: ITO and PVK, have an important effect on the photoelectric performance. The resistance of ITO and the electrical properties of PVK all exhibit a function with strain, which provides basic experimental data support for designing the mechanical-photoelectric coupled model and revealing the mechanism of the mechanical-photoelectric coupled behavior of FPSCs.

The mechanical-photoelectric coupled model

In order to clarify the mechanical-photoelectric coupled mechanism of FPSCs, a two-dimensional model was built in COMSOL Multiphysics by means of the solid mechanics module, semiconductor module, and AC/DC module, in which the coupled relationship of multiple physical fields is built by sequential coupling.⁴⁵ The simulation model included three layers: PEN, ITO, and perovskite, which were placed sequentially, as shown in Fig. 4a. The simulation model consists of 1920 domain elements and 512 boundary elements, all of which are structured elements obtained by mapping. Table 1 shows the geometric parameters and mechanical–electrical parameters of the simulation model. Table 2 shows the photoelectric performance parameters of perovskite materials used in the semiconductor module.

Fig. 4 (a) Two-dimensional geometric model and boundary conditions of the model; (b) the concentration distribution of electrons and holes in the perovskite layer; (c) the FPSCs’ normalized PCE of experiment and simulation as a function of strain; (d) the simulated J–V curves of FPSCs under tensile strains from 0% to 2.5%; (e) the terminal current density as a function of the tensile strain under the scanning voltages of 0.1 V, 0.2 V, 0.3 V and 0.6 V.

Table 1 The geometric parameters and mechanical–electrical parameters of the simulation model

Materials	PEN	ITO	PVK
Thickness (nm)	800	200	600
Young's modulus (GPa)	8	250	15
Density (g cm^−3)	1.38	6.8	4.1
Poisson's ratio	0.28	0.25	0.27
Electrical conductivity (S m^−1)	—	2 × 10^−3	1 × 10^−3

---

Table 2 The photoelectric performance parameters of perovskite materials

Parameters	MAPbI3
χ (eV)	3.93
E g (eV)	1.555
ε r	6.5
N C (cm^−3)	2.2 × 10^18
N V (cm^−3)	1.8 × 10^19
N A (cm^−3)	1.0 × 10^16
N D (cm^−3)	1.0 × 10^18
μ n (cm^2 V^−1 s)	0.5
μ p (cm^2 V^−1 s)	0.5
τ e/τh (ns)	8/8

---

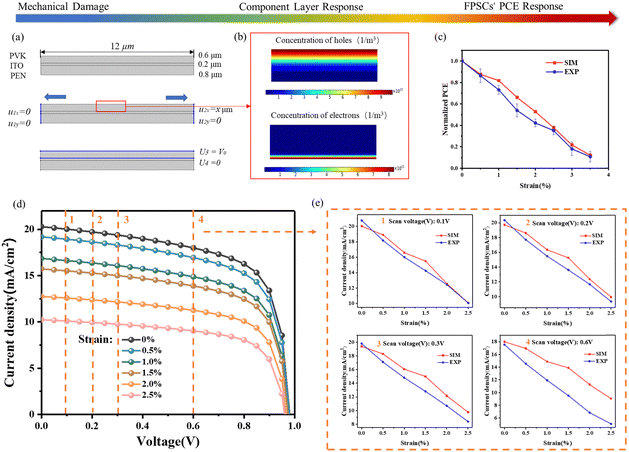
Mechanical boundary conditions restricting movement in the x-direction were assigned on the left edge and in the y-direction were assigned on the left and right edges of the sample, while a displacement was applied on the right edge, as shown in Fig. 4a. The semiconductor boundary conditions of the model are as follows: donor (N-type) doping is applied to the whole perovskite layer, and acceptor (P-type) doping is applied to a measured boundary, which will increase the number of electrons entering the conduction band and improve the perovskite conductivity. Shockley–Read–Hall recombination is added to the whole perovskite layer. The electron generation rate and the hole generation rate are defined in the whole perovskite layer, which greatly affects the initial photovoltaic performance of perovskite solar cells. In order to obtain the corresponding J–V curve of the solar cells, this model applies a scanning voltage V₀ at boundary 3 (U3 in Fig. 4a) of the perovskite layer, sets a voltage of 0 V at boundary 4 (U4 in Fig. 4a), and sets a boundary probe at boundary 4 to obtain the current density at each scanning voltage, as shown in Fig. 4a. The concentration distribution of electrons and holes in the perovskite layer is shown in Fig. 4b. Because the N-type doping is applied in the whole region and the P-type doping is applied at boundary 3, the hole concentration at boundary 3 is relatively high, whereas the electron concentration at boundary 4 is relatively high.

Parametric scanning and steady-state solver were utilized for the mechanical-photoelectric coupled simulations to simplify the calculation process and shorten the calculation time to the greatest extent. Meanwhile, by inputting the experimental function of the electromechanical behavior with the strain of ITO and PVK layers into the model, the partial differential equations are solved by the full coupling method, and the final response results of the FPSCs under different strains are obtained, as shown in Fig. 4c–e.

Fig. 4d shows the J–V curves of the FPSC model under tensile strains from 0% to 2.5%. It is observed that the J–V curves obtained from the model are consistent with the experimental results, showing that the current density first decreases relatively slowly and then suddenly decreases after reaching a voltage threshold. This is because when the applied scanning voltage is less than the turn-on voltage of the device, the current density decreases slowly, while when the applied scanning voltage is greater than the turn-on voltage of the device, the current density decreases rapidly. Moreover, the short-circuit current shows a rapid decreasing tendency, while the open-circuit voltage only shows a slight decrease with increasing tensile strain, which is basically consistent with the experimental results shown in the previous section. The terminal current density as a function of the tensile strain under the scanning voltages of 0.1 V, 0.2 V, 0.3 V, and 0.6 V are given in Fig. 4e. It can be seen that the simulation results of photovoltaic current density are in good agreement with the experimental results under the scanning voltages of 0.1 V, 0.2 V and 0.3 V, while a clear error occurs under 0.6 V. The reason for this error is that the perovskite is likely to decompose due to environmental factors during the tensile test, such as water and oxygen, which makes the output photovoltaic current density unable to reach saturation. In addition, published results focusing on the numerical simulation of perovskite solar cells reported similar disparities between experimental and simulation outcomes.^46,47 Fahsyar et al. concluded that the uncertainty or unavoidable variation during the repeated fabrication process could be the reason for the high relative error value between simulation and experiment results.⁴⁸ Anyway, it is worth noting that the short-circuit current and open-circuit voltage calculated from this model are in good agreement with the experimental results and the FPSCs’ PCE response also proves the availability of this mechanical-photoelectric coupled model (see Fig. 4c).

D-PAA/C-EA modified FPSCs

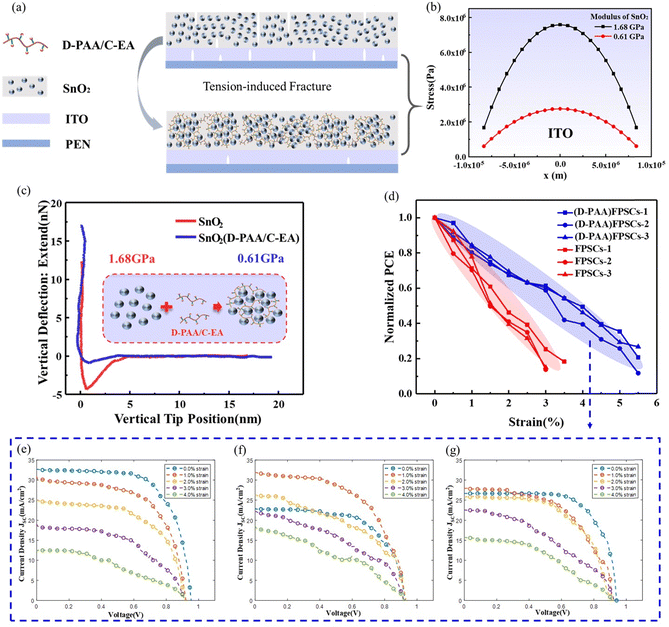
There are few reports on modifying the interface layer from the mechanics aspect to improve the mechanical stability of FPSCs. Herein, we synthesized a polyelectrolyte chain (D-PAA/C-EA) with a 3D cross-linked network structure through neutralizing acrylic acid with small molecular ethanolamine. Polyelectrolyte-modified SnO₂ was obtained as an electron transport layer by mixing SnO₂ nanoparticles with D-PAA/C-EA. This modified SnO₂ exhibits high viscosity, electrical conductivity, and mechanical flexibility, which enhances the adhesive ability and protects the brittle ITO electrode and perovskite crystals, as shown in Fig. 5a.

Fig. 5 (a) A schematic diagram showing the stress reduction role of D-PAA/C-EA under the tensile area; (b) the stress in the ITO layer was reduced due to the decrease of Young's modulus of SnO₂; (c) Young's modulus of original SnO₂ and modified SnO₂ measured by AFM peak force quantitative-nanoscale mechanical characterization; (d) normalized PCE–strain curves of D-PAA modified FPSCs and the original FPSCs; the J–V curves reflecting the degradation of photoelectric performance of D-PAA modified FPSCs under increasing tensile strain: (e) sample 1, (f) sample 2, (g) sample 3.

In order to further explain the influence of D-PAA/C-EA on the mechanical properties of SnO₂, the morphologies and Young's moduli of the original SnO₂ and modified SnO₂ were measured by atomic force microscopy (AFM) peak force quantitative-nanoscale mechanical characterization.⁴⁹Fig. 5c shows that the Young's modulus on the surface of the modified SnO₂ is 0.61 GPa, which is smaller than the Young's modulus of the original SnO₂ (1.68 GPa). Meanwhile, we also test the root mean square (RMS) roughness of the original SnO₂ and modified SnO₂, as shown in Fig. 5. The results show that the RMS of the modified SnO₂ is improved (3.0 nm), which is related to the high adhesion of the 3D cross-linked network in polyelectrolyte. The increase of RMS can properly enhance the contact between the ETL and the perovskite layer and improve the extraction and transmission ability of electrons. Fig. 5b shows that D-PAA/C-EA modified SnO₂ reduces the stress in the ITO layer referring to the elastic-plastic solution model for brittle coating on a polymer substrate proposed by Zhang et al.⁵⁰ We further test the mechanical stability of the D-PAA modified FPSCs during stretching (see Fig. 5d–g). It is observed that the wear threshold strain of the D-PAA modified FPSC was optimized from 3.0% to 5.5%. The J–V curves are also presented in Fig. 5e–g. The D-PAA modified FPSC can still maintain high FF and PCE under 2.5% strain, although its J_SC shows a slight degradation, the degradation rate of J_SC is much slower than that of the original FPSC. This result is broadly in line with expectations of stress reduction in the ITO layer. Furthermore, it indicates that the introduction of the D-PAA/C-EA modified SnO₂ can improve the tensile resistance and mechanical stability.

Conclusions

In summary, we have demonstrated that the real-time monitoring test platform of the mechanical-photoelectric field can be effectively suitable for testing and analyzing the mechanical-photoelectric coupled behavior of FPSCs under tensile load. To clarify the mechanism of mechanical-photoelectric coupled behavior, in situ tensile tests and electromechanical behavior tests were carried out. It has been proved that the increasing resistance of ITO and the decreasing electrical properties of PVK as a function of tensile strain had a major influence on performance degradation. Moreover, a mechanical-photoelectric coupled model of FPSCs based on COMSOL Multiphysics is developed for the analysis and design of high mechanical stability FPSCs, which is validated with the existing experimental results. This model proposed adding a polyelectrolyte material to SnO₂ as a modified ETL to reduce the stress in the ITO layer and PVK layer from the aspect of mechanics to improve the mechanical stability of FPSCs.

The qualitative mechanism between the mechanical behavior and the photoelectric performance of FPSCs proposed in this paper will provide a significant way to improve the mechanical stability of FPSCs, and a reasonable prediction of the coupled model of FPSCs will be an important direction for future research.

Author contributions

Meihe Zhang: software, validation, formal analysis, writing – original draft, data curation, visualization. Yuzhao Qiang: writing – review & editing, validation, visualization. Zhihao Li: writing – review & editing, formal analysis. Zhen Li: writing – review & editing, supervision. Chao Zhang: conceptualization, methodology, funding acquisition, project administration.

Conflicts of interest

All authors declared that there are no conflicts of interest.

Acknowledgements

The authors would like to acknowledge funding from the National Natural Science Foundation of China (Grant no. 12172303) and the Shaanxi Key Research and Development Program for International Cooperation and Exchanges (Grant no. 2022KWZ-23).

References

1. G. Tang and F. Yan, Nano Today, 2021, 39, 101155.
2. J. Ling, P. K. Kizhakkedath, T. M. Watson, I. Mora-Seró, L. Schmidt-Mende, T. M. Brown and R. Jose, Sol. RRL, 2021, 5, 2170113.
3. Y. Rong, Y. Hu, A. Mei, H. Tan, M. I. Saidaminov, S. I. Seok, M. D. McGehee, E. H. Sargent and H. Han, Science, 2018, 361, eaat8235.
4. J. Y. Kim, J.-W. Lee, H. S. Jung, H. Shin and N.-G. Park, Chem. Rev., 2020, 120, 7867–7918.
5. C. Zuo, H. J. Bolink, H. Han, J. Huang, D. Cahen and L. Ding, Adv. Sci., 2016, 3, 1500324.
6. H. Zhou, Q. Chen, G. Li, S. Luo, T. Song, H. Duan, Z. Hong, J. You, Y. Liu and Y. Yang, Science, 2014, 345, 542–546.
7. H. J. Snaith, Nat. Mater., 2018, 17, 372–376.
8. W. Peng, K. Mao, F. Cai, H. Meng, Z. Zhu, T. Li, S. Yuan, Z. Xu, X. Feng, J. Xu, M. D. McGehee and J. Xu, Science, 2023, 379, 683–690.
9. S. A. Hashemi, S. Ramakrishna and A. G. Aberle, Energy Environ. Sci., 2020, 13, 685–743.
10. G. Murugadoss, R. Thangamuthu, M. Rajesh Kumar and R. Ravishankar, Micro Nano Lett., 2019, 14, 1385–1387.
11. Y. Yang, S. Yu, Y. Cao and W. Li, Micro Nano Lett., 2020, 15, 732–735.
12. N. Rolston, K. A. Bush, A. D. Printz, A. Gold-Parker, Y. Ding, M. F. Toney, M. D. McGehee and R. H. Dauskardt, Adv. Energy Mater., 2018, 8, 1802139.
13. X. Hu, X. Meng, L. Zhang, Y. Zhang, Z. Cai, Z. Huang, M. Su, Y. Wang, M. Li, F. Li, X. Yao, F. Wang, W. Ma, Y. Chen and Y. Song, Joule, 2019, 3, 2205–2218.
14. Y. R. Shi, C. H. Chen, Y. H. Lou and Z. K. Wang, Mater. Chem. Front., 2021, 5, 7467–7478.
15. S. J. Sung, J. Im, G. Kim, C. S. Moon, J. J. Yoo, S. S. Shin, N. J. Jeon, B. S. Ma, D. J. Kim, T. Kim and J. Seo, Adv. Energy Mater., 2022, 12, 2200758.
16. N. Jiang, B. Xing, Y. Wang, H. Zhang, D. Yin, Y. Liu, Y. Bi, L. Zhang, J. Feng and H. Sun, Sci. Bull., 2022, 67, 794–802.
17. Z. Chen, Q. Cheng, H. Chen, Y. Wu, J. Ding, X. Wu, H. Yang, H. Liu, W. Chen, X. Tang, X. Lu, Y. Li and Y. Li, Adv. Mater., 2023, 35, 2300513.
18. D. Yang, R. Yang, S. Priya and S. Liu, Angew. Chem., Int. Ed., 2018, 58, 4466–4483.
19. M. A. Davis, R. Sweat and Z. Yu, IEEE J. Flex. Electron., 2022, 1, 231–235.
20. K. Fan, Y. Dai, J. Wang, R. Wang, Z. Lu, Y. Lou and G. Zou, Org. Electron., 2023, 117, 106778.
21. J. Yang, W. Sheng, X. Li, Y. Zhong, Y. Su, L. Tan and Y. Chen, Adv. Funct. Mater., 2023, 33, 2214984.
22. J. Dou, Q. Song, Y. Ma, H. Wang, G. Yuan, X. Wei, X. Niu, S. Ma, X. Yang, J. Dou, S. Liu, H. Zhou, C. Zhu, Y. Chen, Y. Li, Y. Bai and Q. Chen, J. Energy Chem., 2023, 76, 288–294.
23. D. Pérez-del-Rey, P. P. Boix, M. Sessolo, A. Hadipour and H. J. Bolink, J. Phys. Chem. Lett., 2018, 9, 1041–1046.
24. S. Guarnera, A. Abate, W. Zhang, J. M. Foster, G. Richardson, A. Petrozza and H. J. Snaith, J. Phys. Chem. Lett., 2015, 6, 432–437.
25. Y. Zhang, Y. Yang, M. T. Mbumba, M. W. Akram, E. K. Rop, L. Bai and M. Guli, Sol. RRL, 2022, 6, 2200823.
26. H. Ji, J. Huang, W. Zhang, X. Chen, Y. Lu, C. Ding, J. Fang, W. Song and L. Ai, Adv. Mater. Interfaces, 2022, 9, 2200483.
27. S. Sun, Y. Fang, G. Kieslich, T. J. White and A. K. Cheetham, J. Mater. Chem. A, 2015, 3, 18450–18455.
28. X. Hu, X. Meng, X. Yang, Z. Huang, Z. Xing, P. Li, L. Tan, M. Su, F. Li, Y. Chen and Y. Song, Sci. Bull., 2021, 66, 527–535.
29. Z. Li, X. Kong, Y. Jiang, X. Lu, X. Gao, C. Tan, Y. Chen, G. Zhou, J.-M. Liu and J. Gao, Soft Sci., 2021, 1, 4.
30. B. L. Watson, N. Rolston, A. D. Printz and R. H. Dauskardt, Energy Environ. Sci., 2017, 10, 2500–2508.
31. H. Li, W. Wang, Y. Yang, Y. Wang, P. Li, J. Huang, J. Li, Y. Lu, Z. Li, Z. Wang, B. Fan, J. Fang and W. Song, ACS Nano, 2020, 14, 1560–1568.
32. S. Seong, Y. Liu and X. Gong, Opt. Mater. Express, 2022, 12, 772.
33. H.-S. Kim and N.-G. Park, NPG Asia Mater., 2020, 12, 78.
34. M. Dailey, Y. Li and A. D. Printz, ACS Omega, 2021, 6, 30214–30223.
35. J. Wu, S.-C. Liu, Z. Li, S. Wang, D.-J. Xue, Y. Lin and J.-S. Hu, Natl. Sci. Rev., 2021, 8, 8.
36. Y. Chen, Y. Lei, Y. Li, Y. Yu, J. Cai, M.-H. Chiu, R. Rao, Y. Gu, C. Wang, W. Choi, H. Hu, C. Wang, Y. Li, J. Song, J. Zhang, B. Qi, M. Lin, Z. Zhang, A. E. Islam, B. Maruyama, S. Dayeh, L.-J. Li, K. Yang, Y.-H. Lo and S. Xu, Nature, 2020, 577, 209–215.
37. C. Zhu, X. Niu, Y. Fu, N. Li, C. Hu, Y. Chen, X. He, G. Na, P. Liu, H. Zai, Y. Ge, Y. Lu, X. Ke, Y. Bai, S. Yang, P. Chen, Y. Li, M. Sui, L. Zhang, H. Zhou and Q. Chen, Nat. Commun., 2019, 10, 815.
38. G. R. Berdiyorov, M. A. Carignano and M. E. Madjet, Comput. Mater. Sci., 2017, 137, 314–317.
39. T. W. Jones, A. Osherov, M. Alsari, M. Sponseller, B. C. Duck, Y.-K. Jung, C. Settens, F. Niroui, R. Brenes, C. V. Stan, Y. Li, M. Abdi-Jalebi, N. Tamura, J. E. Macdonald, M. Burghammer, R. H. Friend, V. Bulović, A. Walsh, G. J. Wilson, S. Lilliu and S. D. Stranks, Energy Environ. Mater., 2019, 12, 596–606.
40. M. Rasukkannu, D. Velauthapillai and P. A. Vajeeston, Mater. Lett., 2018, 218, 233–236.
41. R. He, X. Huang, H. Chee, F. Hao and P. Dong, Carbon Energy, 2019, 1, 109–123.
42. R. Rhee, S. Im, H. Lee, J. H. Lee, Y. Kim, D. H. Chun, C. Park, S. Lee, J. H. Kim and J. H. Park, ACS Sustainable Chem. Eng., 2020, 8, 8004–8010.
43. Z. Li, Z. Wan, C. Jia, M. Zhang, M. Zhang, J. Xue, J. Shen, C. Li, C. Zhang and Z. Li, J. Energy Chem., 2023, 85, 335–342.
44. M. Li, J. Zhang, Y. Gao, X. Wang, Y. Zhang and S. Zhang, J. Mater. Chem. A, 2021, 9, 2375–2384.
45. P. Fahsyar, N. Ludin, N. Ramli, S. Sepeai, M. Suait, M. Ibrahim, M. Teridi and K. Sopian, Appl. Phys. A: Mater. Sci. Process., 2021, 127, 383.
46. J. Jebakumar, D. Moni, D. Gracia and M. Daphny Shallet, Appl. Nanosci., 2022, 12, 1507–1518.
47. G. Haidari, AIP Adv., 2019, 9, 085028.
48. H. Li, B. Liu, D. Zhou and C. Zhang, J. Electrochem. Soc., 2020, 167, 120501.
49. M. E. Dokukin and I. Sokolov, Langmuir, 2012, 28, 16060–16071.
50. C. Zhang, F. Chen, M. H. Gray, R. Tirawat and R. E. Larsen, Int. J. Solids Struct., 2017, 120, 125–136.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ya00086b

---