Open Access Article
Open Access ArticleFrom material properties to device metrics: a data-driven guide to battery design†
Kevin W.
Knehr
 *a,
Joseph J.
Kubal
a,
Abhas
Deva
*a,
Joseph J.
Kubal
a,
Abhas
Deva
 a,
Mohammed B.
Effat
a,
Mohammed B.
Effat
 ab and
Shabbir
Ahmed
ab and
Shabbir
Ahmed
 a
a
aChemical Sciences and Engineering Division, Argonne National Laboratory, 9700 S. Cass Ave., Lemont, IL 60439, USA. E-mail: knehrkw@anl.gov
bDepartment of Mechanical Power Engineering, Assiut University, Assiut Governorate, Egypt
First published on 3rd August 2023
Abstract
The suitability of a battery for a given application depends on its metrics for energy (W h kg−1 and/or W h L−1), power (W kg−1 and/or W L−1), cost ($ per kWh), lifetime (cycles and/or years), and safety. This paper provides a data-driven perspective explaining how material properties, cell design decisions, and manufacturing costs influence and control these metrics. Insights drawn from the literature and past experience are supported by 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000+ Monte Carlo simulations, which were conducted for lithium-ion batteries using the Battery Performance and Cost Model (BatPaC). A cell with optimal energy, power, and cost is best achieved with a high voltage and a low area specific impedance. If the focus is only on optimal energy and/or cost (i.e., where power is less critical), cells also benefit from active materials with high specific capacities. For example, the energy metric of 500 W h kg−1 can be met in cells with open circuit voltages less than 4 V only if the average specific capacity of the positive and negative materials is at least ∼500 mA h g−1. The values of other parameters (e.g., thicknesses, densities, and material costs) are shown to have less influence on achieving cell metrics. It is suggested that the best way to achieve optimal energy, power, and/or cost while maintaining long lifetimes and safe operation is through modification of these other parameters to facilitate the stable operation of materials with high voltage, high capacity, and low area specific impedance. It is also shown that new negative active materials must produce cells with an area specific impedance less than 85 Ω cm2 to be cost-competitive in all electric vehicles.
000+ Monte Carlo simulations, which were conducted for lithium-ion batteries using the Battery Performance and Cost Model (BatPaC). A cell with optimal energy, power, and cost is best achieved with a high voltage and a low area specific impedance. If the focus is only on optimal energy and/or cost (i.e., where power is less critical), cells also benefit from active materials with high specific capacities. For example, the energy metric of 500 W h kg−1 can be met in cells with open circuit voltages less than 4 V only if the average specific capacity of the positive and negative materials is at least ∼500 mA h g−1. The values of other parameters (e.g., thicknesses, densities, and material costs) are shown to have less influence on achieving cell metrics. It is suggested that the best way to achieve optimal energy, power, and/or cost while maintaining long lifetimes and safe operation is through modification of these other parameters to facilitate the stable operation of materials with high voltage, high capacity, and low area specific impedance. It is also shown that new negative active materials must produce cells with an area specific impedance less than 85 Ω cm2 to be cost-competitive in all electric vehicles.
1. Introduction
Modern society depends on batteries to power and store energy in key devices used for a range of applications, including consumer electronics, power tools, medical devices, vehicles, spacecraft, and grid-level energy storage.1 Each battery application has a unique set of performance requirements and constraints, which makes it difficult for any single battery technology to dominate all applications.2 Therefore, the vast range of battery applications is served by a range of battery technologies. Key metrics for characterizing batteries are defined in Section 2. All battery technologies operate from the same principles: energy is stored in two physically separated active materials and released when electrical and ionic connections are made between the two materials, facilitating a redox reaction.3,4 The active materials are the foundation of any battery technology. The development of new active materials that can improve the cost and performance of applications is a major focus of the battery field.5–10 Predicting the success of new active materials and determining their target applications can be challenging. The properties of the active materials provide only the theoretical performance of the battery.11 The practical performance depends on the way the materials are packaged and operated to facilitate the redox reactions while guaranteeing the battery is stable and safe.12–18 The goal of this perspective paper is to provide insight into the major factors dictating how material properties and cell design choices translate into device-level performance and cost. This paper is intended to aid researchers doing fundamental research by providing information on how the basic properties and performance measured at lab scale translate into commercial cells.Most batteries use solid active materials (i.e., lead-acid, lithium-ion, and zinc-alkaline batteries), but an emerging set of batteries designed for the electric grid use liquid active materials (i.e., redox-flow and liquid-metal batteries).19–26 Lithium-ion batteries are the most widely used technology because they have high energy and power densities, which make them suitable for a range of major applications such as cell phones, laptop computers, and electric vehicles.3,11,27 The large size of the lithium-ion battery market also creates a cost advantage, due to increased research and development efforts and economies of scale, which has driven their rapid adoption for grid-level energy storage applications.28,29 Lithium-ion batteries are the state-of-the-art technology for most applications and are commonly used as the benchmark when developing emerging technologies. For this reason, we will take a dual approach by rooting the discussion in lithium-ion batteries while also investigating a broad range of parameters to make the discussion applicable to other battery technologies. Note that the nomenclature, manufacturing methods, performance assumptions, cell architectures, cell form factors, and material properties will be most consistent with the lithium-ion battery field.
We begin with an overview of the key battery metrics and a discussion of their relevance in key applications. Next, we present an overview of the steps used to transform active materials into commercial battery cells. This section provides the groundwork for understanding the design decisions and manufacturing steps required to build a viable commercial cell from the active materials. The next section introduces a set of Monte Carlo simulations that were conducted using the Battery Performance and Cost Model (BatPaC) developed by our group.12 These simulations provide a data-driven tool with which to evaluate various perspectives on cell design drawn from traditional practice, the literature, and personal experience. The simulations were used to sample the entire parameter space associated with material properties, cell design, and manufacturing. The simulations provide statistical data that highlight the parameters that are important when attempting to transform active materials into cells that achieve desired performance targets. These data are used to ground the next three sections, which outline the key parameters that influence the energy, power, and cost targets, respectively. The final two sections discuss the ramifications of including lifetime and safety concerns when designing a cell. Overall, this paper seeks to provide insight into the complications of translating research-scale materials into commercially viable battery cells. The discussion focuses on identifying bottlenecks in achieving cell metrics and describing current and potential pathways for achieving desired cell performance. The simulation results allow us to add a new dimension to this discussion of the main property effects. Whereas researchers do understand such effects qualitatively, we are able to offer some quantitative effects here.
2. Battery metrics
The set of performance and cost requirements for a particular application is usually specified by a set of metrics related to the energy, power, cost, lifetime, and safety of the battery.1 Researchers are generally aware of these battery metrics when investigating new active materials or new battery chemistries. However, a quantitative awareness of the metrics can help researchers more easily identify promising materials/chemistries and guide research efforts toward battery technologies that meet some or all the important metrics for a given application. Table 1 lists the applications that are, in our view, most and least sensitive to each of the five main battery metrics. The goal of the table is to introduce the metrics and provide a baseline understanding of how the target application influences the desired metrics of a battery. In the rest of this section, we define and discuss each metric in turn.| Metric category | Most sensitive applications | Least sensitive applications |
|---|---|---|
| Energy (W h L−1, W h kg−1) | Vehicles, consumer electronics, aviation | Grid-level applications (W h kg−1), non-urban grid-level applications (W h L−1) |
| Power (W L−1, W kg−1) | Hybrid-electric vehicles, power tools | All-electric vehicles, grid-level applications |
| Cost ($ per kWh, $ per kW) | Grid-level applications, passenger/commercial vehicles | Aerospace, medical, military |
| Lifetime (cycles, years) | Aerospace, grid-level applications, vehicles | Consumer electronics |
| Safety | Medical | None |
Energy metrics are classified by either the amount of energy stored per battery volume (i.e., energy density in W h L−1) or the amount of energy stored per battery mass (i.e., specific energy in W h kg−1). The amount of energy is determined by (i) the voltage difference between the active materials and (ii) the number of electrons stored in their charged states, which is often reported as the specific capacity in units of mA h g−1.11,30,31 The applications most sensitive to these energy metrics are those requiring long discharge times and involving physical transportation of the battery. Representative applications include vehicles (e.g., scooters, e-bicycles, passenger vehicles, and commercial trucks), consumer electronics (e.g., laptops, cell phones, wearable electronics, and drones), and aviation (including emerging all-electric aerial vehicles).3,32,33 The applications least sensitive to specific energy (W h kg−1) are stationary, grid-level applications (e.g., renewable energy shifting, energy arbitrage, ramping, and frequency regulation). As for energy density (W h L−1), only non-urban, grid-level applications are insensitive to this metric because they tend to exist in remote locations where land constraints are minimal. Urban battery installations or installations in land-constrained substations would have volumetric restrictions.4
Power metrics are classified by either the amount of power supplied per battery volume (i.e., power density in W L−1) or the amount of power supplied per battery mass (i.e., specific power in W kg−1). The most sensitive applications are those requiring brief periods (seconds to minutes) of high power and involving physical transportation of the battery. “High power” refers to instances when the power-to-energy ratio (P/E ratio) is greater than ∼10, where the P/E ratio is the peak power divided by the available energy in the system and has units of inverse time (h−1). Sensitive applications include power tools and hybrid-electric vehicles, where the battery is mainly used for regenerative braking and acceleration.34,35 The least sensitive applications are all-electric vehicles and grid-level applications. Power metrics are unimportant in all-electric vehicles because the energy requirement associated with the need for a long range forces vehicles to contain larger batteries, which have no issue meeting power demands.11 Power metrics are unimportant on the grid, where batteries are typically used in longer-duration (low P/E) applications.36
Cost is reported in $ per kWh or $ per kW, depending on whether the application is energy- or power-sensitive, respectively. The unit $ per kWh is significantly more common because most battery applications have discharge-time requirements that make $ per kWh a more informative metric. Most applications benefit from lower cost, but many applications can accommodate some tradeoff of cost for improved performance. The most sensitive applications, where low cost is vital, are all grid-level applications and passenger/commercial vehicles.32,37 Grid-level applications are sensitive to cost because they operate in a market where the main commodity (electricity) is fairly inexpensive and margins for profitability can be thin.38 Vehicles are sensitive to battery cost because the battery can be a large fraction of the total vehicle cost (15–25%), which impacts the total cost of ownership of the vehicle.39 The least sensitive applications are those where the size, lifetime/reliability, and safety of the battery far outweigh any cost concerns. These correspond to aerospace, medical, and military applications.
Lifetime is measured in number of cycles or years of operation before the energy or power capability of the battery degrades below an allowable level. Lifetime is an important consideration for most applications because it also impacts the energy, power, and cost metrics. The energy (Wh) and/or power (W) performance of a cell degrades over its operating lifetime, so cell manufacturers rate the energy and power based on performance at the end of the warranty period. To guarantee these ratings, manufacturers over-design the cell for the beginning of life based on known or expected degradation rates. Over-designing the cell negatively impacts the other cell metrics because it requires excess material. Minimizing the degradation rates to minimize the degree of cell over-design is commercially advantageous, because it enables manufacturers to extend the warranty period in applications requiring long life. The most sensitive applications include all grid-level applications and electric vehicles, where both may require thousands of cycles and/or 10 to 20+ years of operation are required.32,40 For instance, grid-level energy storage technologies are often compared based on their levelized cost of energy stored (LCOS), which has units of $ per kWhlife, where kWhlife is the total energy throughput during the warrantied life.38,41 Lifetime is also synonymous with reliability and reflects the ability of a battery technology to operate in its designated environment without unexpected failures. In that context, the most sensitive applications also include aerospace applications, where reliable operation of the battery is necessary to guarantee success of the mission, especially when battery replacement is impossible, as in satellites and extraterrestrial rovers.42 The least sensitive applications for lifetime are consumer electronics, where 3–5 years and <1800 cycles are sufficient to match the typical lifecycle of a cell phone, laptop computer, or smart watch.27
The final metric is safety, which can be defined as the likelihood of the battery causing harm to individuals or the environment. The most sensitive applications are medical applications where batteries can be located on or inside an individual, providing no opportunity for the individual to remove themselves from the situation if an issue arises. There are no least sensitive applications when it comes to safety. It is paramount for all batteries to operate without endangering the user and the environment.32,43
3. Transforming active materials into cells
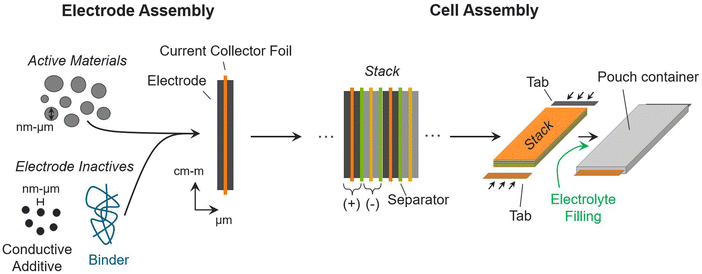
Understanding the commercial cell fabrication process is critical for understanding how material properties and design decisions translate into cell metrics. Active materials must undergo electrode and cell assembly processes to function in working commercial batteries.12,44,45Fig. 1 provides a schematic overview of the processes used to transform active materials into a commercial pouch cell. The processes in Fig. 1 are directly applicable to most battery chemistries. The figure includes the inactive materials that are added to commercial cells to facilitate, control, and contain the electrochemical reactions between the active materials. This discussion (and the Monte Carlo simulations introduced in the next section) focus on the pouch cell format, which is a common format used in electric vehicles and consumer electronics. Cylindrical, prismatic, and button/coin formats are also widely used in battery applications.44,46 These cells are assembled with modifications to the process described herein, but they still require the same inactive components. The conclusions and insights provided here are kept broad to ensure applicability for all cell formats.The left side of Fig. 1 shows the process for building one electrode assembly. The positive and negative electrode assemblies are the building blocks of a commercial pouch cell. The process is the same for both positive and negative electrodes. To form an electrode, the active materials are first mixed with inactive components, which improve the connectivity, conductivity, and stability of the active materials.44 In lithium-ion batteries, carbonaceous conductive additives (e.g., carbon black, carbon nanotubes, graphene, etc.) are included to improve the electrical connectivity between active material particles, which improves the utilization of the active materials and the electrical conductivity of the electrodes.47,48 Polymer binders are also included as inactive components to join the particles together and provide structural support.49,50 Some electrodes may require additional additives to improve performance and longevity. For instance, silicon electrodes in lithium-ion batteries can benefit from lithium-containing additives to help with capacity loss during initial cycling.51,52 Next, a slurry of the active and inactive materials is deposited (electrode layer) onto current collectors, which provide electrical connections from the active materials to similar electrodes and to external portions of the cell. Fig. 1 shows the electrode-foil architecture used in lithium-ion batteries, where the same electrode materials are coated on both sides of a thin current-collector foil (e.g., aluminum or copper).
Next, positive and negative electrode assemblies are stacked in alternating layers with separators in between.44,46 This layering is repeated tens to hundreds of times to generate a dense mass of battery materials, called a stack. The separators keep the positive and negative materials electrically isolated while allowing for ionic transport in between. For this reason, they typically overhang the electrode slightly to prevent shorting. The current-collector foils also extend past the electrodes (in Fig. 1 the extensions are not shown); to provide external electrical connections, the current-collector foils are welded to tabs (in Fig. 1 the tabs are not to scale). The stack is placed into a pouch, which is then filled with electrolyte and sealed.
4. Monte Carlo method for determining correlations
The perspectives presented here are supported by data generated from Monte Carlo simulations. These simulations were conducted over the range of commercially relevant material properties, designs, and costs using the BatPaC model.12 BatPaC is a freely available, spreadsheet-based tool developed by our group at Argonne National Laboratory over the last 15 years. BatPaC employs a bottom-up calculation, whereby the size, mass, and cost of battery cells and packs are determined from inputs related to the battery chemistry, battery design, and manufacturing specifications. The Monte Carlo simulations in this study were conducted by randomly selecting the values for input parameters within plausible ranges. The outputs from BatPaC (i.e., power, energy, and cost metrics) for the random sets of input parameters were collected into a database for statistical analysis. The database was generated from 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 simulations, with each simulation employing a random selection of all the input parameters listed in Tables 2 and 3. The simulations all assume 2 cm-thick pouch cells with a length-to-width aspect ratio of 3
000 simulations, with each simulation employing a random selection of all the input parameters listed in Tables 2 and 3. The simulations all assume 2 cm-thick pouch cells with a length-to-width aspect ratio of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
| Input parameter | Symbol | Min. value | Max. value | Units |
|---|---|---|---|---|
| Positive active material capacity | Q +,act | 100 | 2000 | mA h g−1 |
| Positive active material weight percent | f +,act | 50 | 100 | % |
| Positive active material density | ρ +,act | 1 | 5 | g cm−3 |
| Positive binder weight percent | f +,binder | 0 | 50 | % |
| Positive binder density | ρ +,binder | 0.5 | 1.5 | g cm−3 |
| Positive carbon additive weight percent | f +,ca | 0 | 50 | % |
| Positive carbon additive density | ρ +,ca | 1 | 2.5 | g cm−3 |
| Positive electrode porosity | ε + | 15 | 50 | % |
| Positive electrode thickness | δ + | 20 | 250 | μm |
| Positive current collector thickness | δ +,CC | 5 | 20 | μm |
| Negative active material capacity | Q −,act | 100 | 3000 | mA h g−1 |
| Negative active material weight percent | f −,act | 50 | 100 | % |
| Negative active material density | ρ −,act | 1 | 5 | g cm−3 |
| Negative binder weight percent | f −,binder | 0 | 50 | % |
| Negative binder density | ρ −,binder | 0.5 | 1.5 | g cm−3 |
| Negative carbon additive weight percent | f −,ca | 0 | 50 | % |
| Negative carbon additive density | ρ −,ca | 1 | 2.5 | g cm−3 |
| Negative electrode porosity | ε − | 15 | 50 | % |
| Negative current collector thickness | δ −,CC | 5 | 20 | μm |
| Separator density | ρ sep | 0.5 | 4 | g cm−3 |
| Separator porosity | ε sep | 5 | 50 | % |
| Separator thickness | δ sep | 10 | 30 | μm |
| Electrolyte density | ρ elyte | 0.5 | 4 | g cm−3 |
| Average open circuit voltage |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif)
|
1 | 5 | V |
| Negative-to-positive capacity ratio | N/P | 1.0 | 1.3 | — |
| Cell energy | E cell | 50 | 750 | Wh |
| Area specific impedance | ASI | 4 | 100 | Ω cm2 |
| Input parameter | Symbol | Min. value | Max. value | Units |
|---|---|---|---|---|
| Positive active material cost | C +,act | 1 | 200 | $ per kg |
| Positive binder cost | C +,binder | 1 | 100 | $ per kg |
| Positive conductive additive cost | C +,ca | 1 | 100 | $ per kg |
| Positive current collector cost | C +,CC | 0.1 | 10 | $ per m2 |
| Negative active material cost | C −,act | 1 | 200 | $ per kg |
| Negative binder cost | C −,binder | 1 | 100 | $ per kg |
| Negative conductive additive cost | C −,ca | 1 | 100 | $ per kg |
| Negative current collector cost | C −,CC | 0.1 | 10 | $ per m2 |
| Separator cost | C sep | 0.5 | 10 | $ per m2 |
| Electrolyte cost | C elyte | 1 | 100 | $ per L |
| Cell yield | Y cell | 70 | 100 | % |
| Cells manufactured per year | N cells | 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
— |
| Building and land costs | C building,land | 100 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
$ per m2 |
| Labor costs | C labor | 1 | 100 | $ per h |
| Electrode processing costs |
C
etrode![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) processing processing
|
0.1× | 5× | Multiplier on baseline values |
| Cell assembly costs | C assembly | 0.1× | 5× | |
| Cell formation costs | C formation | 0.1× | 5× | |
| Building support costs |
C
building![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) support support
|
0.1× | 5× | |
Table 2 lists the material property and cell design inputs used in the Monte Carlo simulations. For each simulation, a random value for each parameter was chosen between the minimum and maximum values listed in the table. The minimum and maximum values were chosen to represent commercially relevant property values for current and promising technologies. The range of positive active material capacities (Q+,act) in Table 2 accounts for commercially relevant, spinel materials at the low end (e.g., lithium iron phosphate [LFP] and lithium manganese dioxide [LMO]) and promising materials under development at the high end (i.e., lithium sulfur).11,53 The range of negative active material capacities (Q−,act) accounts for such low-capacity commercial materials as lithium titanate (LTO) at the low end and a practical, yet ambitious, value for lithium metal at the high end.54,55 The separator and electrolyte properties (ρsep, εsep, δsep, and ρelyte) and area specific impedance values (ASI) were chosen to represent both current liquid-electrolyte systems and future all-solid-state batteries.56,57 The range for the average open circuit voltage (![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) ) includes aqueous, solvent, ionic liquid, and solid-state electrolytes.31,58 To put these numbers into perspective, Fig. 2 shows the Ragone space (specific energy versus specific power) for all 200
) includes aqueous, solvent, ionic liquid, and solid-state electrolytes.31,58 To put these numbers into perspective, Fig. 2 shows the Ragone space (specific energy versus specific power) for all 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 simulations in gray.18 The figure also overlays subspaces for several commercial and emerging lithium-ion technologies. The subspaces were generated from additional Monte Carlo simulations run over the parameter ranges in Table S4 (ESI†). The figure confirms that current and emerging technologies are accounted for in the database of 200
000 simulations in gray.18 The figure also overlays subspaces for several commercial and emerging lithium-ion technologies. The subspaces were generated from additional Monte Carlo simulations run over the parameter ranges in Table S4 (ESI†). The figure confirms that current and emerging technologies are accounted for in the database of 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 simulations. It also indicates that the database contains a significant number of permutations with the potential to improve upon existing technologies. These combinations of variables are important because they will direct the subsequent discussion of methods for improving battery performance.
000 simulations. It also indicates that the database contains a significant number of permutations with the potential to improve upon existing technologies. These combinations of variables are important because they will direct the subsequent discussion of methods for improving battery performance.
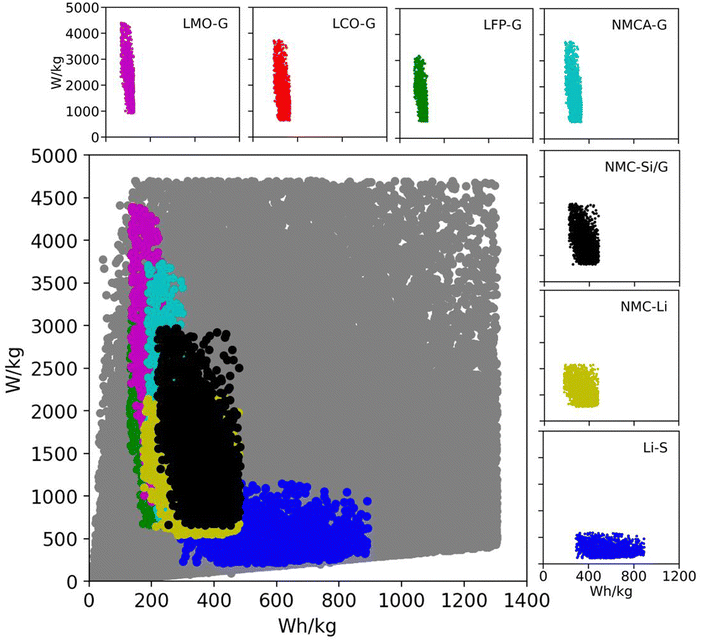 | ||
Fig. 2 Ragone space as spanned by the database generated from 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Monte Carlo simulations in BatPaC.12 The gray points correspond to the entire dataset spanned by the variable ranges in Table 2. The colored subspaces correspond to data spanned by commercial and emerging lithium-ion technologies whose variable ranges are listed in Table S4 (ESI†). 000 Monte Carlo simulations in BatPaC.12 The gray points correspond to the entire dataset spanned by the variable ranges in Table 2. The colored subspaces correspond to data spanned by commercial and emerging lithium-ion technologies whose variable ranges are listed in Table S4 (ESI†). | ||
Table 3 provides the cell and manufacturing cost inputs used in the Monte Carlo simulations. The material costs target values ∼10× lower and higher than typical commercial values. The lower values represent advances in current state-of-the-art processing. The higher values represent potential cost increases resulting from the adoption of newer, higher-performing materials, which may require more expensive raw materials or manufacturing techniques. To put the numbers in Table 3 into perspective, state-of-the-art lithium-ion cells typically have active material costs between 10 and 50 $ per kg, binder and carbon additive costs between 5 and 15 $ per kg, current collector and separator costs between 0.5 and 1.5 $ per m2, and electrolyte costs between 10 and 15 $ per L (including salt and solvent).12,59 The ranges reflect changes in composition for unique battery chemistries and changing market conditions. The minimum value of 70% for cell yield (Ycell) reflects a newly commissioned plant, while most mature plants target >90%. The number of cells manufactured per year corresponds to total annual production of 0.2 to 300 GWh y−1, when combined with the cell energy range in Table 2. The building and land cost includes site preparation and engineering and construction fees. The manufacturing process costs (i.e., Cetrode![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) processing, Cassembly, Cformation, and Cbuilding
processing, Cassembly, Cformation, and Cbuilding![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) support) were adjusted by applying multiplication factors between 0.1 to 5 to the baseline area, capital equipment cost, and labor values listed in BatPaC for all steps in the process.12 BatPaC determines the manufacturing cost of a given cell by scaling the baseline values depending on the production volumes of the cell in question. Details on the baseline manufacturing plant and the manufacturing processes can be found in the BatPaC manual.12
support) were adjusted by applying multiplication factors between 0.1 to 5 to the baseline area, capital equipment cost, and labor values listed in BatPaC for all steps in the process.12 BatPaC determines the manufacturing cost of a given cell by scaling the baseline values depending on the production volumes of the cell in question. Details on the baseline manufacturing plant and the manufacturing processes can be found in the BatPaC manual.12
Table 4 provides several composite parameters that are output from the BatPaC simulations. These parameters provide further information on the cell design and will be referenced in the remaining sections. They are not inputs to BatPaC because they are calculated during the cell design process used by BatPaC. The composite parameters are the electrode loadings (positive and negative), negative electrode thickness, and mass fraction of inactive materials. Table 4 also lists the input parameters from Table 2 which most influence each composite parameter. Details on the calculations can be found in BatPaC and its accompanying manual.12 In addition to these composite parameters, we will also reference one composite performance output: the power to energy ratio (P/E). This is the ratio of the cell power to the cell energy. The cell energy is an input parameter from Table 2. The cell power is calculated based on a 10 second pulse at 50% state of charge. The cell power is kept constant at 750 W, which corresponds to P/E ratios from 1 to 15. BatPaC calculates the power at 80% of the cell's open circuit voltage, which corresponds to a slight overdesign of the cell to account for degradation.12
| Parameter | Symbol | Units | Main dependency |
|---|---|---|---|
| Positive electrode loading | q +,loading | mA h cm−2 | δ +, Q+,act, ρ+,elyte, f+,act, ε+ |
| Negative electrode loading | q −,loading | mA h cm−2 | q +,loading, N/P |
| Negative electrode thickness | δ − | μm | q −,loading, Q−,act, ρ−,elyte, f−,act, ε− |
| Mass fraction of inactives | f inactives | % | All separator, electrolyte, current collector, binder, and carbon additive properties |
The Monte Carlo database was analyzed using correlation plots, which provide a way to quantify the extent to which a given material property, cell design, or cost parameter plays a role in achieving a given target cell metric. The correlation plots are introduced in detail in the next section. Details on the methodology used to generate the correlation plots are provided in the supplementary material.
5. Energy
5.1. Specific energy correlation plots
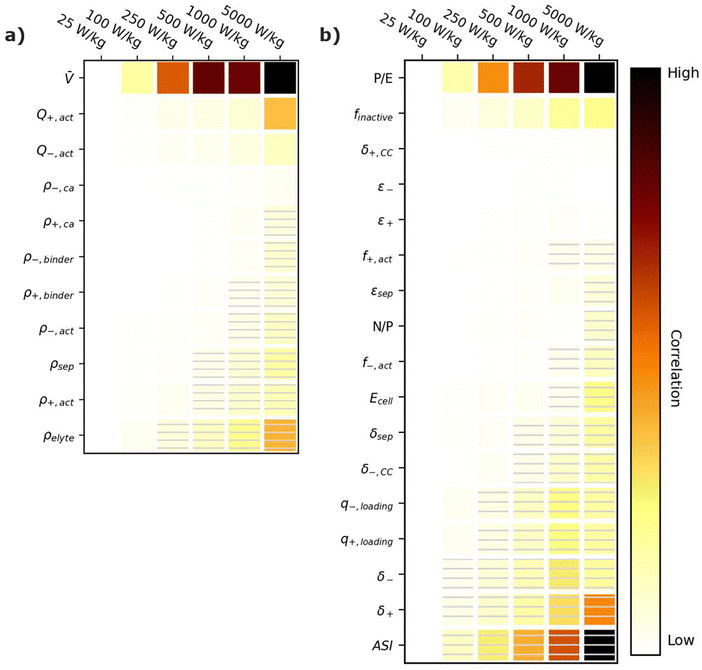
Energy-sensitive devices require batteries that can store large amounts of energy per a given mass or volume. This goal corresponds to packing the most energy into a given space with the least materials. Fig. 3 provides correlation plots that show the relative importance of material properties (Fig. 3a) and cell design decisions (Fig. 3b) when attempting to achieve certain specific energy (W h kg−1) targets. In the figure, darker colors indicate a high degree of correlation: that is, the value of the variable has a strong impact on achieving the metric. Lighter colors indicate a lower degree of correlation: the value of the variable has less impact on achieving the metric. Solid squares indicate positive correlations, where increasing the value of the parameter increases the ability to achieve the metric. Hatched squares indicate negative correlations, where increasing the value of the parameter decreases the ability to achieve the metric. For brevity, the results in Fig. 3 and the discussion in this section are restricted to specific energy. Results for energy density (W h L−1) can be found in Fig. S2 (ESI†). Most of the conclusions drawn in this section are also valid for energy density. Explanations for any discrepancies between specific energy and energy density are provided in the discussion of Fig. S2 (ESI†).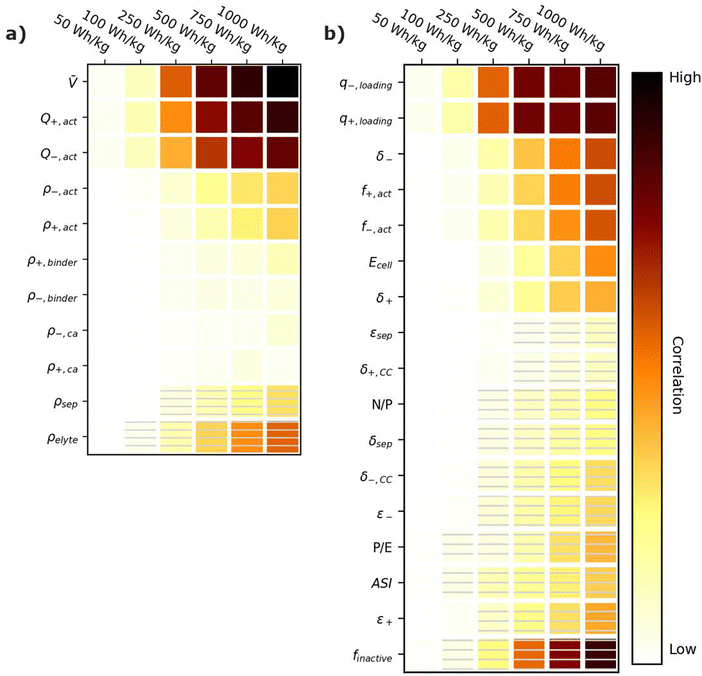 | ||
| Fig. 3 Correlation plots showing the relative importance of (a) material properties and (b) battery design parameters to achieving selected specific energy targets, for the input ranges given in Tables 2 and 4. Solid darker colors indicate the variable has a high degree of positive correlation, where higher values are necessary to achieve the goal. Hatched darker colors indicate strong negative correlation, where lower values are needed to meet the target. Light colors indicate the variable has minimal or no correlation, and its value has a limited impact on achieving the target. | ||
According to Fig. 3a, the most important material property is the average cell open circuit voltage (![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) ), as indicated by its darker values. The voltage is the most important material property because increasing the voltage decreases the amounts of all materials in the cell required to achieve a given energy target (i.e., active materials, additives, current collectors, and separators). This change increases the specific energy (W h kg−1) by decreasing the cell mass. Research and development of high-voltage positive electrode materials is a major focus of lithium-ion battery research for this reason.60–62 The most notable successes are layered oxides containing nickel, cobalt, and/or manganese, whose high voltages (
), as indicated by its darker values. The voltage is the most important material property because increasing the voltage decreases the amounts of all materials in the cell required to achieve a given energy target (i.e., active materials, additives, current collectors, and separators). This change increases the specific energy (W h kg−1) by decreasing the cell mass. Research and development of high-voltage positive electrode materials is a major focus of lithium-ion battery research for this reason.60–62 The most notable successes are layered oxides containing nickel, cobalt, and/or manganese, whose high voltages (![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) ∼ 3.6 to ∼3.8 V vs. Li/Li+) are a major reason for their adoption as positive active materials in commercial lithium-ion batteries.11
∼ 3.6 to ∼3.8 V vs. Li/Li+) are a major reason for their adoption as positive active materials in commercial lithium-ion batteries.11
The specific capacities (mA h g−1) of the active materials (Q+,act and Q−,act) are the next most important parameters. Their importance is associated with the fact that these are the dominant materials responsible for the redox reactions within the cell. State-of-the-art lithium-ion cells contain ∼40% positive active materials and ∼30% negative active materials, by weight.12 Increasing the specific capacity of an active material reduces the total mass of that active material required to achieve the same cell capacity. Reducing the amounts of active materials also reduces the required mass of additives, separators, and current collectors. As a result, for next-generation lithium-ion batteries, the industry is attempting to shift from graphite to lithium metal or silicon as the negative active materials due to their higher specific capacities.55,63 Significant research efforts are also focused on shifting the positive active material from layered oxides (lithium cobalt oxide [LCO], nickel cobalt aluminum oxide [NCA], and nickel manganese cobalt oxide [NMC]) and spinels (LFP and LMO) to high-capacity conversion materials (fluorides and alternative metal oxides), sulfur, or low-cobalt layered oxides.7,11,63–66 Sulfur, in particular, has routinely been explored because it offers specific capacities almost an order of magnitude larger than other commercial materials.53,66 These specific capacity differences are so significant that Li–S batteries deliver an energy density higher than other commercial chemistries (see Fig. 2), despite operating at a lower voltage (∼2.5 V).
The rest of the parameters in Fig. 3a are material densities. Fig. 3a indicates that the densities of most materials have a minimal influence on achieving specific energy targets. The only exception is the electrolyte density (ρelyte). This parameter has a high negative correlation because the electrolyte occupies all void space within the cell, which can be a sizeable fraction of the total electrode and separator volume (up to 50% based on the porosities in Table 2). Increases in electrolyte density add significant mass to the cell that can hinder the ability to achieve specific energy targets. There is significant work in the lithium-ion battery field focused on replacing the liquid electrolytes with solid materials to improve safety and to facilitate the use of high-energy materials that are unstable in liquid electrolytes (e.g., lithium metal or high-voltage positive materials).58,67 Although this approach is intended to unlock higher energy densities, the correlation for ρelyte suggests that increases in energy density resulting from the introduction of solid-state separators could be tempered or even outweighed by decreases in energy density caused by increases in ρelyte. This suggests that lower-density solid-state electrolytes, whose density is not significantly greater than the ∼1.2 g cm−3 of traditional liquid electrolytes, may be better suited for achieving high specific energy (W h kg−1) targets in next-generation solid-state batteries.
Fig. 3b shows the correlation of the specific energy to battery design parameters. Overall, these parameters are less strongly correlated with specific energy than they are with voltage and specific capacity (Fig. 3a), highlighting the importance of research and development of high-voltage cells and high-capacity materials. The most important positively correlated cell design parameter is the electrode loadings (i.e., q+loading and q−,loading). The loadings are positively correlated with specific energy because higher loadings correspond to fewer separators and current collectors for a given amount of active material. They are influenced by the electrode thicknesses (δ+ and δ−), which also have a positive correlation. The most important negatively correlated cell design parameter is the mass fraction of inactive materials in the cell, finactive. This composite parameter incorporates the mass of all inactive components (i.e., electrolyte, carbon additive, binder, current collectors, separators, packaging, and tabbing). Its dark color indicates a high correlation with specific energy targets. Several ways of reducing the mass of inactives have already been discussed (i.e., increasing the cell voltage, increasing the specific capacities of the active materials, increasing the loading, and using low-density electrolytes). Most additional ways to reduce the inactive mass have less impact on the energy density, according to Fig. 3b. Such options include reducing the current collector thicknesses (δ+,CC and δ−,CC), reducing the separator thickness (δsep), and/or decreasing the electrode and separator porosities (ε+, ε−, and εsep), which reduce the amount of electrolyte. The only exceptions are the mass fractions of the active materials in the electrodes (f+,act and f−,act), which have significant positive correlations with the energy density. Increasing the mass fractions decreases the amounts of binder and carbon additive in the electrode. It also helps increase the electrode loading. Overall, unpacking the influence of finactive suggests that moderate increases in the amounts of some inactive materials do not outweigh the benefits of adopting new materials with higher voltages and/or capacities. For instance, silicon negative electrodes improve the energy density over traditional graphite electrodes in lithium-ion batteries even though they require lower active mass fractions (∼90% vs. ∼96%) and higher porosities (∼40% vs. ∼25%).68–71
Fig. 3b also provides correlations for cell performance parameters. The total amount of energy of the cell (Ecell) has a positive correlation, suggesting higher-energy cells are better for achieving high energy targets. This correlation is associated with trends in cell size and cell tabbing. For instance, the pouch cells simulated in BatPaC tend to increase in mass and size as the cell energy increases. The tabs and the excess current collector foils for tab connections also increase with cell energy but at a slower rate than the rest of the cell. As a result, the tabs and excess foil contribute smaller percent values to the total cell mass as the energy increases. The mass of tabs and excess foil does not increase at the same rate as overall cell mass because there are minimum lengths required to ensure proper electrical connection, and there is no incentive to increase the tabs and excess foils past these lengths as the cell energy increases. This trend highlights the importance of using similarly sized cells when comparing energy density metrics. Note that most research cells are small to improve reproducibility and accommodate limited materials. Research cell metrics should be corrected for excess tabbing before being compared to larger, commercial-grade cells.
The remaining two performance parameters (power-to-energy ratio, P/E, and area specific impedance, ASI) are negatively correlated to the specific energy. Thinner electrodes with lower loadings are typically required for higher P/E ratios (see Section 6). This constraint makes it more difficult to achieve specific energy targets with higher P/E ratios. The ASI is a measure of the resistive losses during battery operation. Higher ASI values lead to increased resistive losses and lower cell voltages, thus negatively impacting the overall specific energy. Note that the specific energy in this work was sized based on a 3 h discharge rate, which closely approximates electric vehicle and stationary applications. Shorter discharge times will result in higher resistive losses because the losses are directly proportional to the cell current (see eqn (2) in Section 6). Therefore, the ASI will be more negatively correlated to the energy density as the discharge time is reduced.
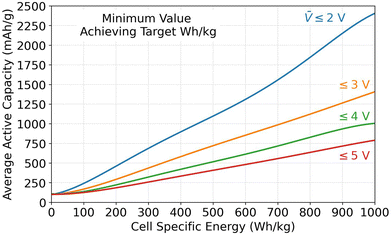
5.2. Minimum capacity and voltage requirements
The Monte Carlo database can also provide insight into the parameter values required for achieving specific energy targets. This subsection analyzes the required values for the average specific capacity, where Qavg,act is the average of Q+,act and Q−,act, and the average open circuit voltage (![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) ) because they were identified as the most important parameters in Fig. 3. Fig. 4 shows combinations of Qavg,act and
) because they were identified as the most important parameters in Fig. 3. Fig. 4 shows combinations of Qavg,act and ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) that must be met to achieve specific energy targets. The figure plots the minimum Qavg,act that can achieve a given specific energy target. Each result corresponds to the database entry with the lowest Qavg,act that achieved the target. Four sets of data are included in the plot. Each set corresponds to results for different maximum allowable
that must be met to achieve specific energy targets. The figure plots the minimum Qavg,act that can achieve a given specific energy target. Each result corresponds to the database entry with the lowest Qavg,act that achieved the target. Four sets of data are included in the plot. Each set corresponds to results for different maximum allowable ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) (i.e., 2, 3, 4, or 5 V). Due to the strong correlation between specific energy and
(i.e., 2, 3, 4, or 5 V). Due to the strong correlation between specific energy and ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) , the datasets correspond to
, the datasets correspond to ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) ∼ 2, ∼3, ∼4, and ∼5 V even though the database was filtered based on
∼ 2, ∼3, ∼4, and ∼5 V even though the database was filtered based on ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) ≤ 2, ≤3, ≤4, and ≤5 V. According to Fig. 4, a 500 W h kg−1 target can be met in cells with open circuit voltages of 2, 3, 4, or 5 V only if the average specific capacity is at least ∼1100, ∼750, ∼500, or ∼400 mA h g−1, respectively. Assuming graphite as the negative active material with an optimistic capacity of 360 mA h g−1, this constraint corresponds to positive capacity requirements of ∼1860, ∼1140, ∼640, and ∼440 mA h g−1 for the various voltages. Assuming a layered oxide as the positive active material with a forward-looking capacity of 250 mA h g−1, this constraint corresponds to negative capacity requirements of ∼1950, ∼1250, ∼750, and ∼550 mA h g−1 for the various voltages. These capacities highlight the advantage of using lithium metal as a negative electrode because it has a theoretical capacity of 3860 mA h g−1. Note that these values correspond to database entries where all other parameters are highly optimized (i.e., maximum electrode loadings and minimum inactive materials, etc.). Therefore, it would still be difficult, although not impossible, to achieve these targets with the capacity/voltage combinations shown in Fig. 4.
≤ 2, ≤3, ≤4, and ≤5 V. According to Fig. 4, a 500 W h kg−1 target can be met in cells with open circuit voltages of 2, 3, 4, or 5 V only if the average specific capacity is at least ∼1100, ∼750, ∼500, or ∼400 mA h g−1, respectively. Assuming graphite as the negative active material with an optimistic capacity of 360 mA h g−1, this constraint corresponds to positive capacity requirements of ∼1860, ∼1140, ∼640, and ∼440 mA h g−1 for the various voltages. Assuming a layered oxide as the positive active material with a forward-looking capacity of 250 mA h g−1, this constraint corresponds to negative capacity requirements of ∼1950, ∼1250, ∼750, and ∼550 mA h g−1 for the various voltages. These capacities highlight the advantage of using lithium metal as a negative electrode because it has a theoretical capacity of 3860 mA h g−1. Note that these values correspond to database entries where all other parameters are highly optimized (i.e., maximum electrode loadings and minimum inactive materials, etc.). Therefore, it would still be difficult, although not impossible, to achieve these targets with the capacity/voltage combinations shown in Fig. 4.
6. Power
Power-sensitive devices typically require batteries that can rapidly charge and discharge at high power while maintaining a minimal mass or volume. Fig. 5 provides correlation plots that indicate the relative importance of optimizing material properties (Fig. 5a) and cell design decisions (Fig. 5b) when attempting to achieve certain specific power (W kg−1) targets. Similar trends are observed for power density targets (W L−1) and are provided in Fig. S3 (ESI†). Compared to the energy targets in Fig. 3, the power targets in Fig. 5 have fewer variables with high correlation. The remaining discussion in this section will show that, while specific energy targets are impacted by the total mass of all the components in the cell (actives and inactives), specific power targets are mainly impacted by the ability to charge and discharge the active materials rapidly and efficiently, with minimal regard to most material properties.Consider the following equation for cell power, which is used to ground the discussion:
Pcell = IV = I(![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) − IR), − IR), | (1) |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) is the average open circuit voltage as defined in Table 2, and R is the cell resistance in Ω. This equation can be written in terms of the total current collector area in the cell (ACC, cm2), the current density flowing between the electrodes through the separator (i, A cm−2), and the area specific impedance (ASI, Ω cm2) as follows:
is the average open circuit voltage as defined in Table 2, and R is the cell resistance in Ω. This equation can be written in terms of the total current collector area in the cell (ACC, cm2), the current density flowing between the electrodes through the separator (i, A cm−2), and the area specific impedance (ASI, Ω cm2) as follows:Pcell = iACC(![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) − i × ASI). − i × ASI). | (2) |
Eqn (2) indicates that increasing ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) will increase the power of the cell. Therefore,
will increase the power of the cell. Therefore, ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) has a high positive correlation to achieving power targets, as shown in Fig. 5a. Cells designed for power benefit from increases in voltage in the same way as cells designed for energy. That is, for a fixed power, increasing voltage decreases the materials needed to supply current, which reduces the total mass of the cell and improves the W kg−1. Achieving a high voltage is the most important material property for achieving high power.
has a high positive correlation to achieving power targets, as shown in Fig. 5a. Cells designed for power benefit from increases in voltage in the same way as cells designed for energy. That is, for a fixed power, increasing voltage decreases the materials needed to supply current, which reduces the total mass of the cell and improves the W kg−1. Achieving a high voltage is the most important material property for achieving high power.
Eqn (2) also shows that increasing the ASI will always decrease the power of the cell. Fig. 5b confirms that ASI is negatively correlated with the power targets. The darker color for ASI implies a strong correlation, highlighting the importance of reducing resistances to achieve higher powers. This goal is a particular concern in next-generation solid-state batteries, where solid electrolytes often have lower conductivities and higher interfacial resistances than their liquid counterparts.58 The higher ASI of solid-state batteries may prevent them from achieving power targets unless they are designed with higher cell voltages. The next most negatively correlated design variables are the electrode thicknesses (δ+ and δ−) and electrode loadings (q+,loading and q−,loading). The thicknesses and loadings have negative correlations because thinner, lower-loading cells are better at achieving high power.70,72,73 Making an electrode thinner corresponds to spreading the same amount of material over a larger surface area (ACC). The benefits can be understood in the context of eqn (2). For cells operated at the same net current and/or C-rate (i.e., constant iACC), cells with thinner electrodes and larger ACC will have lower current densities (i). This helps reduce resistive losses (i.e., the negative term in eqn (2)), which increases the power of the cell. The negative correlation with loading and thickness is less dramatic than the other parameters discussed in this section because decreasing these values also has a drawback. The drawback occurs because cells with thinner electrodes (i.e., lower loadings) require the same amount of active material to be spread over a larger surface area, which requires more current collectors and separators. These additional components add mass, which limits the advantages of thinner electrodes achieved by decreasing the current density.
Fig. 5b also indicates that higher specific power targets are easier to achieve with higher power-to-energy ratios (P/E) of the cell. This correlation can be interpreted in two ways, depending on the duration requirement for maintaining power. In the first case, when the cell is rated based on sustained, constant power, a higher P/E ratio corresponds to a shorter discharge time, which can be achieved with less active mass. This change can significantly reduce the total mass of the cell because the mass of several inactive materials is also tied to the active mass (see Section 5.1). However, the cell power is often rated based on the peak pulse power. For instance, the power of an all-electric vehicle is rated on a 10- to 30-second pulse to meet acceleration demands.74 In this case, for a fixed energy, the higher P/E ratio corresponds to better power delivery from the same amount of active materials, typically through thinner electrodes. The specific energies in Fig. 3 have the opposite trend, namely, lower P/E ratios are beneficial for increasing the specific energy. These opposing trends are behind one of the tradeoffs that make it difficult to design cells for both high power and high energy metrics. Another tradeoff exists in the loading and electrode thicknesses: cells designed for energy tend to have highly loaded, thick electrodes, while cells designed for power have lightly loaded, thin electrodes. This second tradeoff also explains the opposite trends in finactive, where, counterintuitively, Fig. 5b shows that power metrics are easier to achieve with more inactives because thinner electrodes require more current collector and separator materials. The only similarities between the parameter analyses for specific energy and specific power are seen for the cell voltage and ASI, suggesting the best route to achieving both high power and high energy is through high cell voltages and low ASI.
Finally, note that no other material properties or cell design features (e.g., material densities, specific capacities, thicknesses, porosities, or mass fractions) have a significant correlation with achieving the power targets in Fig. 5. Of note are the specific capacities of the active materials (Q+,act and Q−,act), which have little correlation to the power metrics. Materials discoveries over the past decades have focused on high-capacity materials to address the energy requirements of the battery.75–77 However, for power-sensitive applications, it may be beneficial to examine or reexamine materials with lower capacities that offer lower resistances and higher voltages. Also, note that, while most of the other material properties and cell design features have minimal correlation, they can still be important based on how they impact the ASI. For instance, increasing the porosity will improve the ASI by reducing electrolyte resistance;78,79 however, this type of coupled behavior is not accounted for in the BatPaC simulations because all resistance-related information is contained in the input ASI value.
7. Cost
7.1. Impact of material and cell design on cost
Fig. 6 provides correlation plots that indicate the relative importance of optimizing material properties (Fig. 6a) and cell design decisions (Fig. 6b) when attempting to achieve certain cost ($ per kWh) targets. Comparing Fig. 6 to Fig. 3, most of the material properties and parameters that are important for increasing the energy density of the cell are also important for reducing the cell cost. This similarity is reasonable because increases in specific energy often correspond to reductions in material quantities, which also decrease the cell cost. The only exception is the electrolyte density, which has no impact on the cost. Summarizing the important parameters, the most highly correlated material properties are the average cell open circuit voltage (![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) ) and the specific capacities of the active materials (Q+,act and Q−,act). These properties are positively correlated with achieving cost targets because increasing their values reduces the amount of all materials (i.e., active materials, carbon additives, binders, electrolytes, current collectors, and separators) for a given cell energy. Less materials correspond to less cost. The cell design features with the highest positive correlations are the electrode loading (q+,loading and q−,loading), the electrode thicknesses (δ+ and δ−), the active material weight fractions (f+,act and f−,act), and the energy of the cell (Ecell). Electrode loadings (q+,loading and q−,loading) and electrode thicknesses (δ+ and δ−) are positively correlated with cost targets because increasing their value decreases the amount of current collectors and separators required for a given cell energy. The active material weight fractions (f+,act and f−,act) are positively correlated because increasing their values decreases the amount of carbon additives and binders in the cell. The energy of the cell (Ecell) is positively correlated because higher energy cells typically have smaller relative amounts of foil, tabbing, and packaging. The cell design features with the highest negative correlations are the area specific impedance (ASI), the total mass fraction of inactive materials (finactive), and the power-to-energy ratio (P/E). The area specific impedance (ASI) is negatively correlated because it reduces the amount of energy that can be discharged from a given amount of cell materials. The total mass fraction of inactive materials (finactive) is negatively correlated because increasing the mass fraction of inactives increases the amounts of materials that do not contribute to the energy stored in the cell. Finally, the power-to-energy ratio (P/E) is negatively correlated because increasing the P/E typically requires designs with thinner electrodes, yielding higher amounts of current collectors and separators.
) and the specific capacities of the active materials (Q+,act and Q−,act). These properties are positively correlated with achieving cost targets because increasing their values reduces the amount of all materials (i.e., active materials, carbon additives, binders, electrolytes, current collectors, and separators) for a given cell energy. Less materials correspond to less cost. The cell design features with the highest positive correlations are the electrode loading (q+,loading and q−,loading), the electrode thicknesses (δ+ and δ−), the active material weight fractions (f+,act and f−,act), and the energy of the cell (Ecell). Electrode loadings (q+,loading and q−,loading) and electrode thicknesses (δ+ and δ−) are positively correlated with cost targets because increasing their value decreases the amount of current collectors and separators required for a given cell energy. The active material weight fractions (f+,act and f−,act) are positively correlated because increasing their values decreases the amount of carbon additives and binders in the cell. The energy of the cell (Ecell) is positively correlated because higher energy cells typically have smaller relative amounts of foil, tabbing, and packaging. The cell design features with the highest negative correlations are the area specific impedance (ASI), the total mass fraction of inactive materials (finactive), and the power-to-energy ratio (P/E). The area specific impedance (ASI) is negatively correlated because it reduces the amount of energy that can be discharged from a given amount of cell materials. The total mass fraction of inactive materials (finactive) is negatively correlated because increasing the mass fraction of inactives increases the amounts of materials that do not contribute to the energy stored in the cell. Finally, the power-to-energy ratio (P/E) is negatively correlated because increasing the P/E typically requires designs with thinner electrodes, yielding higher amounts of current collectors and separators.
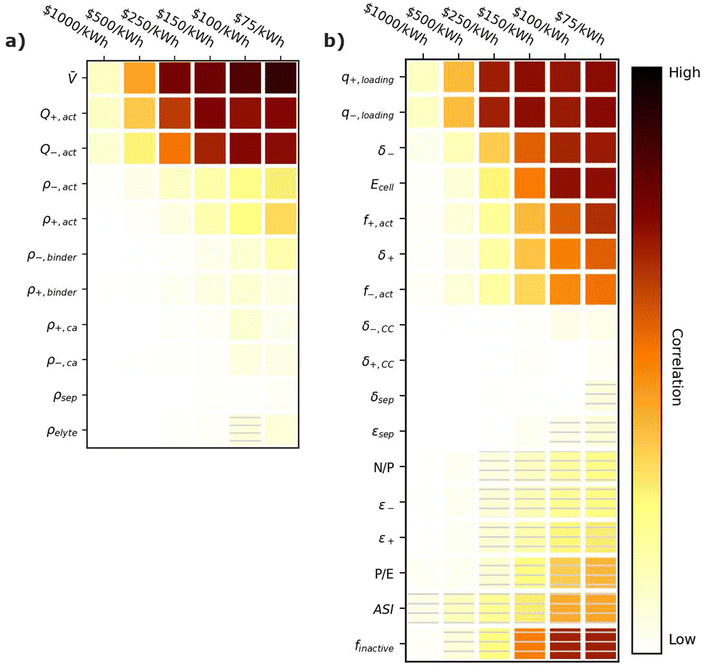 | ||
| Fig. 6 Correlation plots showing the importance of optimizing (a) material properties and (b) cell design parameters to achieving cell cost targets, for the input ranges in Tables 2 and 4. Solid darker colors indicate the variable has a high degree of positive correlation, where higher values are necessary to achieve the goal. Hatched darker colors indicate strong negative correlation, where lower values are needed to meet the target. Light colors indicate the variable has minimal or no correlation, and its value has a limited impact on achieving the target. | ||
7.2. Material and manufacturing costs
Fig. 7 shows correlation values for the cost of materials (Fig. 7a) and manufacturing parameters (Fig. 7b). All parameters in Fig. 7a have negative correlations, indicating that if a material becomes more expensive, it becomes harder to achieve the given cost targets. The most important cost parameters are the active material costs (C+,act and C−,act), the separator cost (Csep), and the electrolyte costs (Celyte). The active materials have the highest correlation because they typically make up 60–80% of the cell by weight.12 The separator cost has the next highest correlation. Its correlation is higher than that of the current collectors (C+,CC and C−,CC) despite the fact that all three materials scale with the active area of the cell. This result is reasonable because a given unit cell, which represents the smallest functioning unit of a battery, contains one positive electrode, one negative electrode, one separator, half a positive current collector, and half a negative current collector. The half current collectors result from the double-side coating of the electrodes on a current collector (see Fig. 1). Therefore, cells contain twice as many separators as positive or negative current collectors, which explains why the separator cost is more important than either current collector cost. The electrolyte cost (Celyte) is also important since it fills all the void spaces in the electrodes and separators. The binders and carbon additives have relatively little importance even over the range from 1 to 100 $ per kg because they make up only a small fraction of commercial electrodes.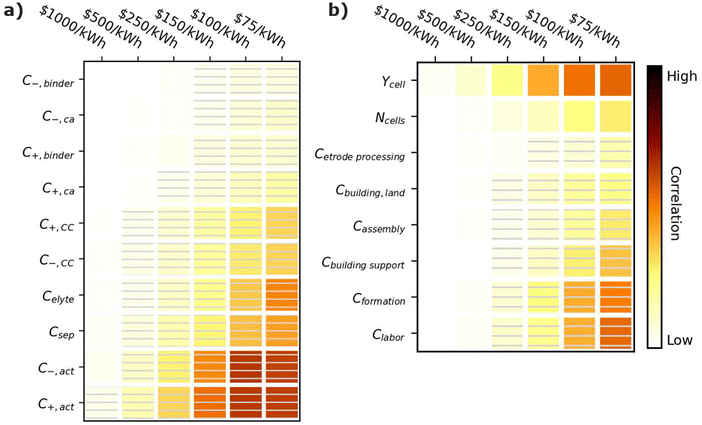 | ||
| Fig. 7 Correlation plots showing the importance of (a) material costs and (b) manufacturing parameters to achieving cell cost targets, for the input values in Table 3. Solid darker colors indicate the variable has a high degree of positive correlation, where higher values are necessary to achieve the goal. Hatched darker colors indicate strong negative correlation, where lower values are needed to meet the target. Light colors indicate the variable has minimal or no correlation, and its value has a limited impact on achieving the target. | ||
One interesting takeaway is that the material properties and cell design parameters (Fig. 6) have a greater overall correlation with target cost than the costs of the materials (Fig. 7a), as signified by the preponderance of darker squares in Fig. 6. This difference is reasonable because changing the electrochemical properties of a material impacts more than the quantity of that given material. It also impacts the size of the cell and the quantities of inactive materials. The reduction in the quantities of both active and inactive materials reduces the total cell cost. In contrast, changing the cost of an individual component (Fig. 7a) only changes the cost contribution of that one component.
Achieving cost targets also depends on reducing the manufacturing cost. Fig. 7b provides correlation plots for the parameters impacting the manufacturing cost in the BatPaC model.12 The cell yield (Ycell) is the most important positively correlated manufacturing parameter. The yield is the percentage of cells that pass final inspection. It is important because each failed cell wastes manufacturing throughput that does not result in a final product. Conversations with industrial collaborators suggest that mature plants target 90–95% yields, while newly commissioned plants can suffer from yields as low as 70% until the manufacturing conditions are optimized. The cost of the formation process (Cformation) is the most important negatively correlated manufacturing parameter. Formation corresponds to the aging and cycling of the cells after they are fully assembled to condition the interfaces between materials and generate protective corrosion layers on some of the materials.80,81 The details of specific formation processes used in industry are highly proprietary. Most formation processes take days, which requires large amounts of capital equipment, increasing the manufacturing cost. The next most important parameter is the labor cost (Clabor in $ per h). Labor can have a significant impact despite the high degree of automation in most modern manufacturing plants. This correlation is reasonable because cell manufacturing can require up to 20 process steps, resulting in significant labor even if most of the steps are highly automated.12,45 The building support costs (Cbuilding![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) support) have the next highest correlation. These costs include equipment not specific to battery assembly, such as air handling, piping, chillers, boilers, warehouse space, recycling facilities, and a solvent recovery system for the solvents used to prepare the positive electrodes.12 They also include additional air-handling costs for the dry room used to assemble the cells due to the moisture sensitivity of the commonly used Li-ion electrolytes.82 The number of cells per year produced at the plant (Ncell) has a moderate impact on the final cost (compared to the other parameters) due to improved costs resulting from higher efficiencies in labor and equipment when operating at larger scales. Finally, the electrode processing cost (Cetrode
support) have the next highest correlation. These costs include equipment not specific to battery assembly, such as air handling, piping, chillers, boilers, warehouse space, recycling facilities, and a solvent recovery system for the solvents used to prepare the positive electrodes.12 They also include additional air-handling costs for the dry room used to assemble the cells due to the moisture sensitivity of the commonly used Li-ion electrolytes.82 The number of cells per year produced at the plant (Ncell) has a moderate impact on the final cost (compared to the other parameters) due to improved costs resulting from higher efficiencies in labor and equipment when operating at larger scales. Finally, the electrode processing cost (Cetrode![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) processing, which includes mixing, coating, calendering, notching, and drying), cell assembly cost (Cassembly, which includes slitting, stacking/winding, tab welding, container insertion, and filling, and the cost of the building and land (Cbuilding,land) have a minimal correlation compared to the other parameters.
processing, which includes mixing, coating, calendering, notching, and drying), cell assembly cost (Cassembly, which includes slitting, stacking/winding, tab welding, container insertion, and filling, and the cost of the building and land (Cbuilding,land) have a minimal correlation compared to the other parameters.
7.3. Cost case study
Improving the cost of a battery is not as simple as improving one of the parameters highlighted in Fig. 6 and 7 because changing the value of one parameter usually has implications for another. Therefore, tradeoff and optimization studies are required to determine whether a new material, with all its new properties and performance ramifications, improves upon the state-of-the-art technology. A case study was conducted to provide additional insight into the underlying tradeoffs associated with materials discoveries. The case study was conducted by running a parametric sweep for a baseline, state-of-the-art lithium-ion cell with a LiNi0.8Mn0.1Co0.1O2 (NMC811) positive electrode and a graphite (G) negative electrode with the properties listed in Table 5. These properties are representative of an advanced pouch cell used in an electric vehicle. They are the default values in version 5 of BatPaC for an electric vehicle (EV) with the “NMC811-G (Energy)” electrode couple.12| Parameters | Symbol | Baseline value | Units |
|---|---|---|---|
| Positive active material capacity | Q +,act | 214 | mA h g−1 |
| Positive active material weight percent in electrode | f +,act | 96 | % |
| Positive active material cost | C +,act | 26 | $ per kg |
| Negative active material capacity | Q −,act | 360 | mA h g−1 |
| Negative active material weight percent in electrode | f −,act | 98 | % |
| Negative active material cost | C −,act | 10 | $ per kg |
| Average cell open circuit voltage |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif)
|
3.71 | V |
| Cell area specific resistance | ASI | 17.5 | Ω cm2 |
| Targets | Value | Units | |
| Cell power-to-energy ratio | P/E | 3 | h−1 |
| Cell energy | E cell | 0.25 | kWh |
| Cell cost | 88.65 | $ per kWh | |
| Maximum allowable positive electrode thickness | δ +,max | 70 | μm |
The case study was conducted using the BatPaC software to design cells that met the target power, energy, and cost requirements specified in Table 5. Cells were designed for an EV: that is, the energy was sized for a 3 h discharge (C/3), and the power was sized to achieve the target power after 10 seconds into a high-power pulse.74 The designs were also limited by a maximum positive electrode thickness of 70 μm, which accounts for coating and manufacturing yield limits and integrity of electrode layers over cycle life.83,84 The study analyzes tradeoffs that may occur when attempting to adopt active materials with new specific capacities. The case study was conducted by adjusting the specific capacity of one of the active materials—i.e., NMC811 or G—and then adjusting the value of a second parameter – i.e., ![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) , C±,act, f±,act, or ASI – until the modified cell achieved the same baseline cell cost as the default NMC811-G case. The second parameters are italicized in Table 5. This method makes it possible to show the allowable tradeoffs associated with changes in the specific capacities of active materials.
, C±,act, f±,act, or ASI – until the modified cell achieved the same baseline cell cost as the default NMC811-G case. The second parameters are italicized in Table 5. This method makes it possible to show the allowable tradeoffs associated with changes in the specific capacities of active materials.
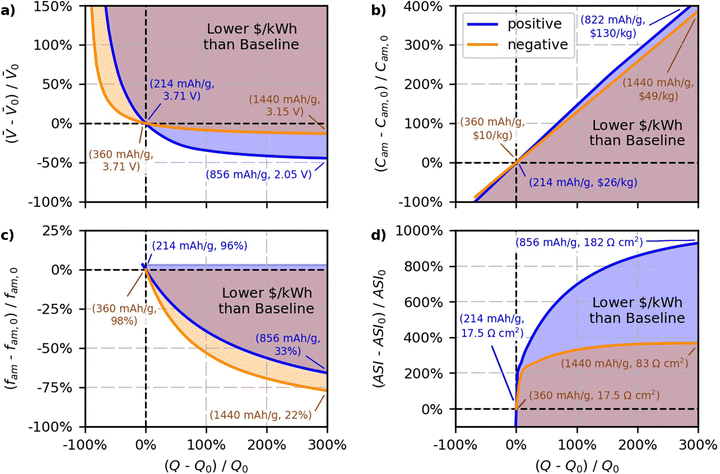
The results of the case study are shown in Fig. 8. The blue and orange lines in the figure reflect percent changes in the parameters that maintain the baseline $ per kWh, and the shaded regions reflect percent changes in the parameters that produce cells with $ per kWh lower than the baseline value. Blue lines and shaded regions in Fig. 8a correspond to results for changing the positive specific capacity and the average open circuit voltage of the cell. The blue in Fig. 8b corresponds to results for changing the positive specific capacity and the positive active material cost (C+,act). The blue in Fig. 8c corresponds to results for changing the positive specific capacity and the positive active mass fraction (f+,act). The blue in Fig. 8d corresponds to results for changing the positive specific capacity and the area specific impedance of the cell. Orange lines and shaded regions in Fig. 8a correspond to results for changing the negative specific capacity and the average open circuit voltage of the cell. The orange in Fig. 8b corresponds to results for changing the negative specific capacity and the negative active material cost (C−,act). The orange in Fig. 8c corresponds to results for changing the negative specific capacity and the negative active mass fraction (f−,act). The orange in Fig. 8d corresponds to results for changing the negative specific capacity and the area specific impedance of the cell. The objective of the figure is to study the break-even point where costs remain constant. Therefore, the figure does not attempt to quantify the degree to which costs decrease for various regions within the shaded areas. Nevertheless, note that the $ per kWh of the regions in the shaded areas will decrease with increasing distance away from the solid lines.
Fig. 8a shows the results for the average open circuit voltage of the cell, which is an important tradeoff consideration since new materials with different capacities tend to have different voltages. Both sets of lines in Fig. 8a show that increasing the specific capacity, Q±,act, will lower the cost if it is accompanied by a zero or slight decrease in the voltage of the cell. Both electrode materials show an asymptotic behavior, whereby the allowable decrease in the voltage approaches a constant value for increasing values of Q±,act. The negative and positive lines have asymptotes close to −15% and −45% of the voltage, respectively. This result indicates that new negative electrode materials will lower the cost of the cell with respect to graphite only if their voltage is greater than −15% of the voltage of the graphite-containing cell. That is, a new negative electrode material will not lower the cost of the cell if its voltage is 0.56 V (vs. Li/Li+) or higher above graphite (and at the same $ per kg as graphite). Lithium metal is promising because it increases the specific capacity while also increasing the cell voltage.55,85 Silicon is also promising because composite graphite-silicon electrodes have been shown to increase the capacity by up to 450% with <15% decreases in the cell voltage.86,87 Decreases in the voltage with increases in the positive specific capacity are more acceptable because positive materials have a higher baseline cost ($26 per kg) than negative materials ($10 per kg). Because positive materials cost more, a given percent change in positive specific capacity will have more impact to lower overall cell cost than the same percent change in the negative specific capacity. The results indicate that for new positive electrode materials with higher specific capacity to successfully lower the cost of lithium-ion cells, their voltages must be greater than −45% of the NMC811-G cell voltage (and at the same $ per kg of NMC811). This criterion translates to positive electrode materials needing voltages greater than ∼2.05 V vs. graphite (or ∼2.15 V vs. Li/Li+) to improve cost without additional reduction in active material cost. Note that sulfur is a promising positive electrode material because its voltage is just above this boundary (2.1 to 2.4 V vs. Li/Li+) and it has a potential capacity that is 300% to 500% higher than the baseline NMC value.53,66,88
Fig. 8b provides insight into the allowable increases in active material cost that can accommodate increases in specific capacity while still maintaining the baseline $ per kWh. The trends in the figure are not exactly linear since increasing the specific capacity provides additional improvements by also lowering the amounts of inactive materials. For example, a specific capacity increase of 200% can lead to a lower $ per kWh, even if the positive or negative active materials are ∼300% or ∼250% more expensive, respectively. This insight is important, as it indicates that when material costs increase, there does not need to be a one-to-one increase in capacity. That is, there is a window in which slightly more expensive materials with higher specific capacities can compete with NMC811-G. Fig. 8b also shows that the impact of active material cost is asymmetric. The positive line has a slightly greater slope than the negative line because of the different active mass weight fractions assumed in the baseline case (96% for the positive and 98% for the negative electrode). The additional inactives in the positive electrode means that reducing the amount of actives (by increasing the specific capacity) will have proportionally more impact. Therefore, the positive case can maintain the baseline cell cost at higher active materials costs, as indicated by the fact the positive line is slightly higher than the negative line.
Fig. 8c demonstrates the allowable decreases in active material weight percent in the electrode that can accommodate increases in specific capacity. This tradeoff is being explored with such new materials as silicon negative electrodes, which require higher proportions of binder and carbon additives in the electrodes to overcome structural issues associated with the expansion of the active materials.89,90 The positive and negative lines in the figure both show the extent to which materials with higher specific capacity can achieve lower costs even if it is necessary to decrease the active material weight percent in the electrode. The figure shows that the negative electrode has a higher allowable decrease in weight percent than the positive electrode, as indicated by the lines having lower values for all relative changes in capacity, Q±,act. This result is reasonable because the negative electrode is made with a water-based binder ($10 per kg in this case study) that is less expensive than the solvent-based binder used in the positive electrode ($15 per kg).12 The case study assumes a 50/50 split between the weight percentages for the conductive additive and binder. The figure demonstrates that a considerable decrease in weight percent is allowable with increasing specific capacity. For example, in the positive case, doubling the specific capacity—i.e., x-axis equal to 100% in Fig. 8c—will maintain the baseline $ per kWh with a 40% reduction in the active weight percent, which corresponds to a new weight percent of 58%. For the negative case, doubling the specific capacity will maintain the baseline $ per kWh with a 55% reduction in the active weight fraction, for a new weight percent of 44%. This relationship highlights a huge opportunity for new materials with high specific capacities that may require excess inactives to overcome structural issues (e.g., silicon and lithium metal in the negative electrode). It suggests that having a significant amount of inactives in the electrodes does not necessarily make it difficult to lower costs.
The final set of results (Fig. 8d) provides insight into the allowable increases in area specific impedance (ASI, Ω cm2) of the cell. Some of the more intriguing parts of the curves are the initial regions, where both the negative and positive lines rapidly rise to ∼200% of the ASI with minimal changes in the specific capacities, Q±,act. This result indicates that any slight increase in the specific capacity of the materials will lower the cost, as long as ASI increases by less than ∼200%. Fig. 8d highlights that, for the EV targets specified in Table 5 (i.e., energy based on a 3-hour discharge and P/E = 3), the ASI has little impact on the cost if it is <200% higher than the baseline value (i.e., <50 Ω cm2). The positive case is more accommodating of increases in ASI than the negative case. In the positive case, lower costs can be achieved over a wider range of ASI values because the higher cost of the active material means there is more benefit from increases in Q+,act. For instance, Fig. 8d shows that the positive case will yield lower costs for increases in Q+,act up to 200%, as long as ASI does not increase by more than 800%. For the negative case, the ASI increase must be below 350% to still achieve cost reductions at a 200% increase in Q−,act. Fig. 8d also shows that the ASI reaches an asymptote at ∼400% for the negative electrode, indicating that, regardless of the increase in Q−,act, the cell will not achieve lower costs versus the state-of-the-art Li-ion battery if its ASI is above 400% of the baseline (i.e., >83 Ω cm2). This tradeoff occurs because higher ASI values require thinner electrodes to achieve power targets, which require more separators and current collectors, which in turn increase the cost.
This relationship between ASI and Q−,act is a critical result that has implications for the development of next-generation solid-state lithium batteries, where a major focus of current research is targeted at increasing the conductivity of the solid-electrolyte materials and reducing interfacial resistances that occur at the solid-solid contacts in the system.91,92 The results in Fig. 8d provide a target for this research, indicating that solid-state systems may be able to compete with lithium-ion batteries on cost for EVs if the total cell ASI is below 85 Ω cm2. Note that this is an optimistic number because it assumes the costs of all components and manufacturing methods are equal to the lithium-ion case. In reality, costs for next-generation systems will likely be higher than for lithium-ion systems for the foreseeable future because lithium metal costs more than graphite and solid-state electrolytes cost more than traditional solvent-based electrolytes with polymer separators.93 Thus, the ASI ceiling may be significantly lower than 85 Ω cm2 for near-term pricing. Also note that the ASI ceilings and tradeoffs presented here are valid only for all-electric vehicles with low P/E ratios. The ceilings will be lower for any application requiring higher P/E ratios or sustained discharges shorter than 3 hours.
8. Lifetime
8.1. Degradation mechanisms
Cells with optimal energy, power, and cost metrics have degradation issues because the best methods for optimizing these metrics often cause instabilities within the cell. For instance, maximizing the voltage of the cell and the specific capacities of the active materials is crucial for achieving optimal metrics (Fig. 3a, 5a, and 6a). Unfortunately, increasing the voltage and specific capacities causes several degradation issues because these changes correspond to increasing the reactivity and mass-specific utilization of the materials, respectively, where mass-specific utilization refers to the fact that higher specific capacity (mA h g−1) corresponds to reacting more electrons per mass of material.7,61,94 Increases in voltage and capacity can lead to interfacial, material, and electrode-structural changes that negatively impact the performance of the cell.95 The key challenge for improving lifetime involves solving these issues with strategies that require the least sacrifice in energy, power, and cost.The main way to combat electrolyte instability without sacrificing voltage is to engineer the interface to form stable, ion- and electron-permeable decomposition layers that protect the active material from reaction with the electrolyte while facilitating the preferred electrochemical reactions. This approach includes tailoring electrolyte compositions (by engineering the additives, salts, and solvents) and applying coatings to the electrode surfaces.98–103 The use of engineered electrolytes has been employed successfully in lithium-ion batteries, where organic solvents are paired with graphite negative electrodes, resulting in the formation of a stable solid-electrolyte interface (SEI).102 The SEI protects the graphite from excessive corrosion and allows it to operate for thousands of cycles and >10 years within an aggressive voltage regime.40 Similar methods are being employed to stabilize lithium-metal negative electrodes, which have worse stability issues than graphite due to their lower electrochemical potential.98 Promising results have also been observed using surface coatings to stabilize lithium-metal electrodes.99,100 Electrolyte engineering and surface coatings are also employed at high-voltage positive electrodes to create a stable cathode–electrolyte interface (CEI) in lithium-ion batteries, where electrolyte oxidation can be an issue.101,104 Wide voltage windows can also induce corrosion at the electrolyte|current collector interfaces. Such corrosion can cause loss of contact with the active material and lower the energy of the cell. It is important to use a current collector suitable for the operating voltage of the electrode. Lithium-ion batteries use copper current collectors at the low-voltage negative electrode and aluminum current collectors at the high-voltage positive electrode.105 Electrolyte engineering is also employed to create a protective layer on the current collector.106
Engineered interfaces are attractive because their potential drawbacks (i.e., increases in electrolyte cost, electrolyte density, active material costs via coatings, current collector costs, and/or current collector densities) are outweighed by the advantages of using higher-voltage materials (see Fig. 3, 5, 6, and 7). Caution should be used if the methods significantly increase the density of the electrolyte or the cost of the active materials, as these increases can make it difficult to achieve W h kg−1 and $ per kWh targets, respectively (Fig. 3a and 7a). The drawback with the highest likelihood of outweighing these advantages is a significant increase in the ASI of the cell caused by an increase in the interfacial resistances. Such resistance can hinder the ability to achieve high power density targets (Fig. 5b). Therefore, efforts should be focused on developing stable, low-resistive interfaces for high power-density applications.
Irreversible phase changes or atomistic rearrangements can also be an issue in some materials. These irreversible phases occur when the oxidation state of a material has been overmodified in an attempt to maximize specific capacity. It is a common issue in conversion-type electrodes in lithium-ion batteries and in reversible zinc-manganese dioxide aqueous batteries.7,21,109 The easiest way to prevent formation of these phases is to restrict the capacity window during cycling. However, such restriction reduces the specific capacity of the material. Attempts to maintain a high specific capacity while preventing formation of irreversible phases involve adding dopants within the material or synthesizing nano-structured electrode materials. Both methods can shift the preferred thermodynamic states at high specific capacities away from irreversible phases.110,111
Volume expansion is an inherent issue in many battery materials with high specific capacities.63–65,112,113 Volume expansion can fracture the active material particles or break the protective interfacial layers. Both types of failure lead to increased side reactions with the electrolyte. Volume expansion can also impact the structural integrity of the electrode (see next sub-section). The most common examples are high-capacity silicon negative electrodes in lithium-ion batteries and systems employing metal negative electrodes (e.g., lithium and zinc).112–115 Attempts to address the issue in silicon focus on nano-sizing the material to prevent fracture, sythensizing composite active materials in which silicon is hosted in a protective carbon matrix, and using interfacial engineering methods (i.e., coatings and electrolytes) to produce stable, stretchable interfaces.112,113
In metal electrodes, volume expansion can also cause another type of failure: the formation of unwanted structures, such as mossy materials and dendrites.114,116,117 Mossy materials increase the surface area and can lead to excessive electrolyte side reactions. Dendrites can short-circuit the cell, resulting in catastrophic failure.116 In theory, metal electrodes are attractive because of their low operating voltage and high specific capacity, but in practice, significant effort is needed to control expansion effects. Interfacial engineering techniques have been employed to prevent electrolyte side reactions in metal electrodes and provide resistance to mossy and dendrite growth.98–100,117 Separators are also modified to prevent dendrites through the use of coatings or the adoption of all-solid-state materials.67,99,100,118–121 All-solid-state designs also offer the potential to reduce side reactions because the solid-state electrolyte does not infiltrate fractured active material to the same extent that a traditional liquid electrolyte would.
The modifications used to address the degradation that arises from material changes can be broadly characterized into three classes depending on whether they target the electrolyte, active material, or separator. Many of the electrolyte and active material modifications discussed in this section are similar to those employed for addressing electrolyte/interface instability issues (i.e., electrolyte engineering and surface coatings). The conclusions drawn in Section 8.1.1 about their potential drawbacks still apply. Some of the active material modifications introduced to address material changes (i.e., ion substitution, nano-sizing, and composite-material sythesis) have the potential to reduce the specific capacity and/or significantly increase the cost of the active material. Reductions in the specific capacity may decrease the ability to meet energy (Fig. 3a) and cost (Fig. 6a) targets, while increases in the active material cost can have negative ramifications for cell cost (Fig. 7a). The biggest drawback for separator modifications is an increase in area specific impedance that has large implications for meeting power targets (Fig. 5b) and can even influence cost (Fig. 8d).
Methods to prevent structural change amount to reducing volume expansion, preventing corrosion, and/or making more robust, cohesive composite electrodes.124–127 Reducing volume expansion and preventing corrosion can be achieved using the methods discussed previously (i.e., interfacial engineering and active material modifications). Robust electrodes can be made by increasing the fraction of inactive materials in the electrode, but this approach can reduce the ability to achieve energy and cost targets (Fig. 3b and 6b). The development of chemically resistant, mechanically stable inactive materials (e.g., binders and carbon additives) is a more promising approach to make robust electrodes without sacrificing energy or cost.47,90 The promise comes from the fact that the costs of inactive materials in the electrode are poorly correlated to achieving cost targets (Fig. 7a). Therefore, increasing the cost of the inactive materials to achieve better properties and higher active mass fractions is unlikely to hinder the ability to achieve cost targets.
8.2. Factors accelerating degradation
8.3. Lifetime-centric designs
Situations and applications may arise where lifetime is the most important metric. Examples include extraterrestrial applications or remote stationary applications, where replacement of the battery is impractical or impossible. The discussion in Sections 8.1.1, 8.1.2, and 8.2.2 suggests that batteries with the longest lifetime requirements should employ moderate voltages, active materials with low capacities, and low ASI. In conventional lithium-ion batteries, the negative graphite electrode is typically the lifetime-limiting electrode. Long-life batteries can be achieved by substituting graphite with lithium titanate (LTO). Lithium titanate is highly stable because it operates at ∼1.5 V vs. Li/Li+, which is well above the electrolyte reduction and lithium plating potentials. It also undergoes minimal volume expansion when lithiated to ∼150 mA h g−1 and is readily available in <100 nm particles sizes, which reduces the ASI.139,140 This negative electrode material is often paired with LMO or NMC positive electrodes to produce a stable cell (3000 to 7000 cycles) with a moderate voltage ∼2.4 V.141 Extremely long-lasting batteries can also be developed using LFP positive electrodes with LTO.142,143 Lithium iron phosphate is highly stable because it operates at ∼3.3 V vs. Li/Li+, which is below the electrolyte oxidation potential. It is also highly reversible when operated at ∼160 mA h g−1 and is readily available in <100 nm particle sizes.144,145 Despite their long life, LFP-LTO cells are seldom used in energy storage applications due to their low voltage (1.8 V), which significantly hinders their energy, power, and cost metrics.In batteries in which one electrode degrades faster than the other (e.g., the graphite electrode in conventional lithium-ion batteries), overdesigning the poor-performing electrode can be a useful method for improving the lifetime without a large sacrifice in the other metrics. This strategy is supported by the relatively low correlation between the energy and cost metrics in Fig. 3b and 6b and the N/P ratio, which is the ratio of negative to positive electrode loading and always has a value greater than one in this work.146 This form of selective overdesign suggests that complete optimization of both electrodes for performance may not guarantee long life and good metrics.
9. Safety
Safety issues occur when one or more of the degradation issues discussed in Section 8 lead to excessive temperature or pressure buildup, creating the potential of a catastrophic failure, such as a thermal runaway or chemical exposure.147–151 The first step toward ensuring safety is to reduce degradation in the cell. This includes operating the cell only within its warranty period, thereby ensuring it is removed from service before significant degradation occurs. When safety is the only metric that matters, the same lifetime-centric designs discussed in Section 8.3 are the best options, namely, choosing moderate voltages, active materials with low capacities, and cells with low ASI. In most applications, energy, power, and cost metrics are also important. Reducing degradation while maintaining optimal cell metrics can be achieved by using the strategies discussed in Section 8 to minimize electrolyte/interface instabilities, reduce material changes, prevent electrode structural changes, minimize inhomogeneous reactions, and reduce heat generation in the cell. Operation-level strategies can also be implemented to reduce degradation and improve safety. These include setting appropriate current and voltage limits on the cell during operation and using thermal management systems to maintain the cell within a stable temperature.152 Note that the thermal management system will have influences on the device-level metrics, which are out of scope with the cell-level metrics that are the focus of this perspective.Reducing degradation is not enough to achieve the goal of 100% safe battery operation. The second step is to modify the materials and design of the cell to prevent the known mechanisms of catastrophic failure. The best example is in lithium-ion batteries, where catastrophic failure caused by thermal runaway can result in batteries bursting into flames.132,153,154 Such flaming disintegration can occur through a combination of events. First, thermal runaway reactions can begin at temperatures of ∼80 °C at the graphite negative electrode.155 These reactions are followed by decomposition of the electrolyte and then release of oxygen from the positive active material at over ∼150 °C.147,148 The oxygen will further react with H2, COx, and/or light hydrocarbons within the cell to generate additional heat and accelerate thermal runaway. Hydrogen may be present because the common electrolyte salt, LiPF6, reacts with any moisture in the cell to produce H2 and highly corrosive HF. Oxides of carbon and light hydrocarbon compounds may be present because the organic solvent in the electrolyte decomposes at elevated temperatures. Thermal runaway is initiated when cell abuse or degradation causes excessive heat, which triggers the steps just described. The common causes are overcharging, short circuits (caused by lithium dendrites penetrating the separator), and loss of activity in local pathways (which creates channels of high lithium-ion transport, which in turn results in high resistance and heat).147–149
Remedies for preventing thermal runaway are undertaken in the design and manufacturing of the cell and system. One option is to use temperature-resistant positive electrode materials, which have a higher temperature threshold for oxygen release. The temperature resistance has been shown to increase with decreasing voltage and specific capacity of the material.156 This relationship presents a drawback since materials with lower voltage and capacity make it more difficult to achieve targets for energy, power, and cost (see Fig. 3a, 5a, and 6a). Another option is to reduce the flammability of the electrolytes by modifying the solvent, the salt, and the additives to reduce the flash point.102 Only slight drawbacks are expected with this option since electrolyte properties and cost are not the major drivers for achieving energy, power, and cost metrics (see Fig. 3a, 5a, 6a, and 7a). Replacing the flammable liquids with solid-state electrolytes and separators offers significant promise for improving safety. The ramifications of solid-state designs on the other parameters have been discussed previously in Sections 5.1, 6, and 7.3. Another important remedy is the removal of impurities (e.g., water) during the manufacturing of the cell. This strategy includes the effective use of dry rooms during cell assembly and proper degassing during the formation process.82 Refining these methods may impact the cell cost (see Fig. 7b), but this drawback will likely be outweighed by concomitant improvements in cell yield and lifetime.
The next two remedies are methods that “kill” the cell to prevent the thermal runaway process. The first method involves the use of temperature-sensitive separators whose pores collapse at elevated temperatures, shutting down the cell by stopping lithium transport. These separators are often lined with ceramic coatings to also provide structural stability and prevent dendrite penetration.157 This method likely has limited drawbacks since the properties and cost of the separator are only moderately correlated to the energy, power, and cost metrics (Fig. 3, 5, and 6). The second method is applied on the system level and involves the use of a battery management system to detect and isolate cells that have the potential for safety issues.153,154 It involves the use of temperature sensors, pressure sensors, and current/voltage monitoring to detect anomalies in operation that may correspond to a failing cell. Recent studies have also shown that the thickness of the cell may serve as a good proxy for a cell's state of health, which would be useful in pouch-cell designs.158 System-level methods are used in all applications, but they are particularly useful in large battery installations (i.e., electric vehicles and grid-level applications) where the mass and volume of the hardware required to monitor the cells can be distributed among many cells. Distributing battery management in this way lessens the impact on the mass, size, and cost of the total installation (on a percent basis). System-level methods also include modifications to the final system design to allow for venting of the cells to expel flammable gas.154 In electric vehicles, this solution requires modifications to the cell, module, and pack designs, which penalize the mass, volume, and cost. Grid-level and stationary applications also require the addition of ventilation systems to prevent gas from building up within the structures housing the batteries.159
10. Conclusions and outlook
We have presented a data-driven perspective that used Monte Carlo simulations to identify the material properties, cell designs, and manufacturing costs that most influence energy, power, cost, lifetime, and safety metrics. Table 6 provides an overview of the main findings by listing the parameters that most influence each cell metric. The results indicated that the best route for achieving high specific energy (W h kg−1) targets was through maximizing the cell voltage and specific capacities of the active materials. For example, 500 W h kg−1 could be met in cells with voltages of 2, 3, 4, or 5 V only if the average specific capacities of the positive and negative materials was at least ∼1100, ∼750, ∼500, or ∼400 mA h g−1, respectively. Most of the other physical properties (i.e., densities and thicknesses) of the materials and components in the cell had minimal impact when compared to voltage and capacity. The only exception was the electrolyte density, which had a moderate negative correlation with specific energy, indicating it may limit the specific energy if its value is too large. Another important strategy for reaching specific energy targets was to minimize the inactive materials in the cell (i.e., current collectors, separators, binders, carbon additives, etc.) by increasing the cell loading and increasing the active material mass fraction in the electrode.| Metric category | Parameters to maximize | Parameters to minimize |
|---|---|---|
| Energy (W h L−1, W h kg−1) |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) , Q±,act, q±,loading, f±,act , Q±,act, q±,loading, f±,act |
ASI |
| Power (W L−1, W kg−1) |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif)
|
ASI, q±,loading |
| Cost ($ per kWh) |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) , Q±,act, q±,loading, f±,act, Ycell , Q±,act, q±,loading, f±,act, Ycell |
ASI, C±,act, Clabor, Cformation |
| Lifetime (cycles, years) | — |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) , Q±,act, ASI , Q±,act, ASI |
| Safety | — |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) , Q±,act, ASI , Q±,act, ASI |
The best route for achieving high specific power (W kg−1) targets was through maximizing the cell voltage and minimizing the area specific impedance (ASI). It was also important to reduce the current density between the electrodes by reducing the electrode loading, which increases the number of separators and current collectors. This trend was opposite to that observed for achieving high specific energy targets, which highlighted the fact that cells for high specific energy and high specific power often require fundamentally different designs. Cell designs with high specific energy maximize the amount of material packed into a given area, while cell designs for high specific power spread the material out over a large area. This tradeoff makes it difficult to design cells for both high power and high energy. The most direct route to achieve a cell with high specific energy and high specific power was through maximizing the cell voltage and reducing the ASI.
Results for the cell cost ($ per kWh) indicated that the best methods for reducing this metric were the same as the methods for increasing the specific energy (i.e., higher voltages, higher specific capacities, higher loadings, higher active mass fractions, and lower area specific impedance). The methods are the same because they reduce the amount of material in the cell, which lowers the cost. It was also shown that changes to material properties and cell designs had more impact than changes to the costs of individual components. This relationship is reasonable because changing the cost of a component only impacted one component, whereas changing the value of a material or design parameter (i.e., voltage, capacity, loading, or active mass fraction) impacted multiple components. The most correlated cost and manufacturing parameters were shown to be the active material cost, the cell yield, and the cost of the cell formation manufacturing step.
This work also included a discussion of the tradeoffs required to maintain optimal energy, power, and cost metrics while also preventing degradation that can hurt lifetime and safety. The main strategy was to modify the properties and costs of the components to facilitate the safe operation of high-voltage and high-capacity materials. The simulation results supported this strategy because increases in the cost or density of the electrolyte, separator, additives, and active materials had weaker correlation with cell metrics than the voltage and capacity did. Thus, the best way to guarantee long, safe operation was to adopt active materials with low voltages, low specific capacities, and low ASIs; however, such choices would be detrimental to the other cell metrics (excluding low ASIs, which were beneficial for all metrics).
In addition, this work highlighted a tradeoff associated with solid-state electrolytes. The results indicated the potential of high ASI, high electrolyte density, and high separator cost to negatively impact one or more of the cell metrics. Note that these are three of the most common drawbacks associated with solid-state electrolytes. The results also highlighted the importance to cell metrics of high voltages and high specific capacities, which are the most common benefits of cells with solid-state electrolytes. These competing effects present an intriguing tradeoff that will ultimately influence the adoption of solid-state electrolytes. This tradeoff suggests that research to develop new solid-sate materials should be accompanied by parametric studies to identify the target values of material properties, cell designs, and cost factors that are required to surpass lithium-ion metrics.
For all the cases discussed in this work, the directionality provided for improving metrics was broad in scope. The goal was to provide a general sense of the best directions to take research when trying to understand the true promise of a new material or novel chemistry. Case-specific parametric studies should be conducted to confirm the best research direction for a specific chemistry and application. Such studies can be conducted using either models developed in-house or freely available software tools such as BatPaC.12 An example parametric study was provided in this work using the cost (in $ per kWh) of LiNi0.8Mn0.1Co0.1O2/graphite (NMC811-G) energy cells as a baseline. The study indicated that new negative and positive active materials will produce cost-competitive cells only if the resulting voltages are greater than 3.15 V or 2.05 V, respectively. This conclusion was true regardless of the increase in specific capacity (assuming constant $ per kg). The case study also indicated that new negative electrode materials will be cost-competitive only if they produce cells with an ASI less than 85 Ω cm2, regardless of the increase in specific capacity (assuming cell power and energy suitable for EVs).
In summary, this work supports the overall conclusion that the battery field is moving in the correct direction, with significant effort focused on developing high-voltage cells and high specific capacity active materials.160 These attributes benefited most of the energy, power, and cost metrics. The only exception was that power had minimal correlation to the specific capacity. This result suggests a potential opportunity to reexamine or refocus investigations on materials with low specific capacity that may possess other properties important for power metrics (i.e., high voltage and low ASI). This work also highlighted the importance of low ASI for energy, power, and cost targets and the importance of high electrode loadings for energy and cost. These two parameters are investigated less often during material discovery research than are voltage, specific capacity, and cycle life.161 It would be beneficial to develop and adopt consistent benchmarking and testing strategies to determine how new materials impact the ASI and/or the performance at high loadings. We acknowledge the difficulty in achieving reliable research-scale results and the uncertainty in comparing research performance to commercial cells.162–165 This difficulty is particularly acute for the ASI and rate capability at high loadings, where significant optimization can be done in the development stage. These shortcomings likely point to the importance of comparing data from new materials against cells containing commercially adopted materials (e.g., graphite, LFP, or NMC) fabricated under the same conditions (i.e., mixing, casting, calendering, and filling methods). Such a comparison would provide a method for benchmarking the ASI or high-loading performance of new materials against commercial competitors in a manner that is independent of fabrication conditions.
Author contributions
Kevin W. Knehr: conceptualization, investigation, data curation, formal analysis, methodology, visualization, writing – original manuscript, writing – review & editing. Joseph J. Kubal: conceptualization, investigation, data curation, formal analysis, methodology, visualization, writing – original manuscript, writing – review & editing. Abhas Deva: conceptualization, investigation, data curation, visualization, writing – original manuscript, writing – review & editing. Mohammed B. Effat: writing – original manuscript, writing – review & editing. Shabbir Ahmed: conceptualization, writing – original manuscript, writing – review & editing, supervision.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge Dennis Dees, Jane Andrew, and Gary Henriksen for their input. The authors gratefully acknowledge support from Brian Cunningham, Samuel Gillard, and David Howell at the Vehicle Technologies Office (VTO), Office of Energy Efficiency and Renewable Energy (OEERE), U.S. Department of Energy (DOE). This work was supported by the DOE, OEERE, VTO under contract number DE-AC-02-06CH11357.References
- K. W. Beard, Linden's Handbook of Batteries, McGraw Hill, 5th edn, 2019 Search PubMed.
- J. Ma, Y. Li, N. S. Grundish, J. B. Goodenough, Y. Chen, L. Guo, Z. Peng, X. Qi, F. Yang, L. Qie, C.-A. Wang, B. Huang, Z. Huang, L. Chen, D. Su, G. Wang, X. Peng, Z. Chen, J. Yang, S. He, X. Zhang, H. Yu, C. Fu, M. Jiang, W. Deng, C.-F. Sun, Q. Pan, Y. Tang, X. Li, X. Ji, F. Wan, Z. Niu, F. Lian, C. Wang, G. G. Wallace, M. Fan, Q. Meng, S. Xin, Y.-G. Guo and L.-J. Wan, J. Phys. D: Appl. Phys., 2021, 54, 183001 CrossRef CAS.
- M. Armand and J.-M. Tarascon, Nature, 2008, 451, 652–657 CrossRef CAS.
- B. Dunn, H. Kamath and J.-M. Tarascon, Science, 2011, 334, 928–935 CrossRef CAS.
- M. D. Slater, D. Kim, E. Lee and C. S. Johnson, Adv. Funct. Mater., 2013, 23, 947–958 CrossRef CAS.
- M. S. Whittingham, Chem. Rev., 2004, 104, 4271–4301 CrossRef CAS PubMed.
- A. Kraytsberg and Y. Ein-Eli, J. Solid State Electrochem., 2017, 21, 1907–1923 CrossRef CAS.
- M. M. Thackeray, C. Wolverton and E. D. Isaacs, Energy Environ. Sci., 2012, 5, 7854–7863 RSC.
- Z.-Y. Gu, J.-Z. Guo, Z.-H. Sun, X.-X. Zhao, X.-T. Wang, H.-J. Liang, X.-L. Wu and Y. Liu, Cell Rep. Phys. Sci., 2021, 2, 100665 CrossRef CAS.
- Z. Su, J. Huang, R. Wang, Y. Zhang, L. Zeng, Y. Zhang and H. Fan, J. Colloid Interface Sci., 2023, 639, 7–13 CrossRef CAS.
- D. Andre, S.-J. Kim, P. Lamp, S. F. Lux, F. Maglia, O. Paschos and B. Stiaszny, J. Mater. Chem. A, 2015, 3, 6709–6732 RSC.
- K. W. Knehr, J. J. Kubal, P. A. Nelson and S. Ahmed, Battery Performance and Cost Modeling for Electric-Drive Vehicles: A Manual for BatPaC v5.0, Argonne National Lab. (ANL), Argonne, IL (United States), 2022 Search PubMed.
- J. T. Frith, M. J. Lacey and U. Ulissi, Nat. Commun., 2023, 14, 420 CrossRef CAS PubMed.
- T. Waldmann, R.-G. Scurtu, K. Richter and M. Wohlfahrt-Mehrens, J. Power Sources, 2020, 472, 228614 CrossRef CAS.
- D. A. J. Rand and P. T. Moseley, in Electrochemical Energy Storage for Renewable Sources and Grid Balancing, ed. P. T. Moseley and J. Garche, Elsevier, Amsterdam, 2015, pp. 201–222 Search PubMed.
- R. E. Ciez and D. Steingart, Joule, 2020, 4, 597–614 CrossRef CAS.
- Y. Cao, M. Li, J. Lu, J. Liu and K. Amine, Nat. Nanotechnol., 2019, 14, 200–207 CrossRef CAS PubMed.
- C. Heubner, K. Voigt, P. Marcinkowski, S. Reuber, K. Nikolowski, M. Schneider, M. Partsch and A. Michaelis, Adv. Energy Mater., 2021, 11, 2102647 CrossRef CAS.
- D. Pavlov, Lead-acid Batteries: Science and Technology: a Handbook of Lead-acid Battery Technology and Its Influence on the Product, Elsevier Science Limited, Amsterdam, 2011 CAS.
- M. S. Whittingham, Proc. IEEE, 2012, 100, 1518–1534 CAS.
- N. D. Ingale, J. W. Gallaway, M. Nyce, A. Couzis and S. Banerjee, J. Power Sources, 2015, 276, 7–18 CrossRef.
- M. Skyllas-Kazacos, M. H. Chakrabarti, S. A. Hajimolana, F. S. Mjalli and M. Saleem, J. Electrochem. Soc., 2011, 158, R55 CrossRef CAS.
- K. W. Knehr, E. Agar, C. R. Dennison, A. R. Kalidindi and E. C. Kumbur, J. Electrochem. Soc., 2012, 159, A1446–A1459 CrossRef CAS.
- S. Biswas, A. Senju, R. Mohr, T. Hodson, N. Karthikeyan, K. W. Knehr, A. G. Hsieh, X. Yang, B. E. Koel and D. A. Steingart, Energy Environ. Sci., 2017, 10, 114–120 RSC.
- J. L. Sudworth, J. Power Sources, 2001, 100, 149–163 CrossRef CAS.
- H. Kim, D. A. Boysen, J. M. Newhouse, B. L. Spatocco, B. Chung, P. J. Burke, D. J. Bradwell, K. Jiang, A. A. Tomaszowska, K. Wang, W. Wei, L. A. Ortiz, S. A. Barriga, S. M. Poizeau and D. R. Sadoway, Chem. Rev., 2013, 113, 2075–2099 CrossRef CAS PubMed.
- G. Zubi, R. Dufo-López, M. Carvalho and G. Pasaoglu, Renewable Sustainable Energy Rev., 2018, 89, 292–308 CrossRef.
- M. S. Ziegler, J. Song and J. E. Trancik, Energy Environ. Sci., 2021, 14, 6074–6098 RSC.
- D. Choi, N. Shamim, A. Crawford, Q. Huang, C. K. Vartanian, V. V. Viswanathan, M. D. Paiss, M. J. E. Alam, D. M. Reed and V. L. Sprenkle, J. Power Sources, 2021, 511, 230419 CrossRef CAS.
- J. B. Goodenough and K.-S. Park, J. Am. Chem. Soc., 2013, 135, 1167–1176 CrossRef CAS PubMed.
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603 CrossRef CAS.
- A. Masias, J. Marcicki and W. A. Paxton, ACS Energy Lett., 2021, 6, 621–630 CrossRef CAS.
- X.-G. Yang, T. Liu, S. Ge, E. Rountree and C.-Y. Wang, Joule, 2021, 5, 1644–1659 CrossRef.
- W. Weydanz, in Encyclopedia of Electrochemical Power Sources, ed. J. Garche, C. Dyer, P. T. Moseley, Z. Ogumi, D. A. J. Rand, B. Scrosati, 2009, pp. 46–52 Search PubMed.
- P. A. Nelson, S. Ahmed, K. G. Gallagher and D. W. Dees, J. Power Sources, 2015, 283, 506–516 CrossRef CAS.
- J. Eyer and G. Corey, Energy Storage for the Electricity Grid: Benefits and Market Potential Assessment Guide, Sandia National Laboratories, 2010 Search PubMed.
- R. M. Darling, K. G. Gallagher, J. A. Kowalski, S. Ha and F. R. Brushett, Energy Environ. Sci., 2014, 7, 3459–3477 RSC.
- O. Schmidt, S. Melchior and A. Hawkes, Joule, 2019, 3, 81–100 CrossRef.
- Z. Liu, J. Song, J. Kubal, N. Susarla, K. W. Knehr, E. Islam, P. Nelson and S. Ahmed, Energy Policy, 2021, 158, 112564 CrossRef.
- H. Chen, T. N. Cong, W. Yang, C. Tan, Y. Li and Y. Ding, Prog. Nat. Sci., 2009, 19, 291–312 CrossRef CAS.
- K. W. Knehr, R. Buline, T. Baldwin, E. Guzman, H. Huynh, R. E. Ciez and D. A. Steingart, J. Electrochem. Soc., 2018, 165, A4041 CrossRef CAS.
- F. C. Krause, J. P. Ruiz, S. C. Jones, E. J. Brandon, E. C. Darcy, C. J. Iannello and R. V. Bugga, J. Electrochem. Soc., 2021, 168, 040504 CrossRef CAS.
- F. H. Gandoman, J. Jaguemont, S. Goutam, R. Gopalakrishnan, Y. Firouz, T. Kalogiannis, N. Omar and J. Van Mierlo, Appl. Energy, 2019, 251, 113343 CrossRef CAS.
- J. Li, J. Fleetwood, W. B. Hawley and W. Kays, Chem. Rev., 2022, 122, 903–956 CrossRef CAS PubMed.
- F. Degen and M. Schütte, J. Clean. Prod., 2022, 330, 129798 CrossRef CAS.
- J. M. Tarascon and M. Armand, Nature, 2001, 414, 359–367 CrossRef CAS.
- H. Zheng, R. Yang, G. Liu, X. Song and V. S. Battaglia, J. Phys. Chem. C, 2012, 116, 4875–4882 CrossRef CAS.
- X. Qi, B. Blizanac, A. DuPasquier, M. Oljaca, J. Li and M. Winter, Carbon N. Y., 2013, 64, 334–340 CrossRef CAS.
- J. Landesfeind, A. Eldiven and H. A. Gasteiger, J. Electrochem. Soc., 2018, 165, A1122–A1128 CrossRef CAS.
- G. Liu, H. Zheng, X. Song and V. S. Battaglia, J. Electrochem. Soc., 2012, 159, A214–A221 CrossRef CAS.
- W. M. Dose, C. Villa, X. Hu, A. R. Dunlop, M. J. Piernas-Muñoz, V. A. Maroni, S. E. Trask, I. Bloom, V. Dravid and C. S. Johnson, J. Electrochem. Soc., 2020, 167, 160543 CrossRef CAS.
- W. Zhu, J. Zhou, S. Xiang, X. Bian, J. Yin, J. Jiang and L. Yang, Front. Chem., 2021, 9, 712225 CrossRef CAS.
- X. Liang, C. Hart, Q. Pang, A. Garsuch, T. Weiss and L. F. Nazar, Nat. Commun., 2015, 6, 5682 CrossRef PubMed.
- Y. Ha, A. M. Colclasure, S. E. Trask, S. Ahmed, K. L. Gering, A. N. Jansen, A. Burrell and K. Park, J. Electrochem. Soc., 2021, 168, 110536 CrossRef CAS.
- J. Qian, W. A. Henderson, W. Xu, P. Bhattacharya, M. Engelhard, O. Borodin and J.-G. Zhang, Nat. Commun., 2015, 6, 6362 CrossRef CAS PubMed.
- H. Zhu, A. Prasad, S. Doja, L. Bichler and J. Liu, Nanomaterials, 2019, 9, 1086 CrossRef CAS.
- K. V. Kravchyk, D. T. Karabay and M. V. Kovalenko, Sci. Rep., 2022, 12, 1177 CrossRef CAS PubMed.
- K. J. Kim, M. Balaish, M. Wadaguchi, L. Kong and J. L. M. Rupp, Adv. Energy Mater., 2020, 2002689 Search PubMed.
- M. Wentker, M. Greenwood and J. Leker, Energies, 2019, 12, 504 CrossRef CAS.
- W. Li, B. Song and A. Manthiram, Chem. Soc. Rev., 2017, 46, 3006–3059 RSC.
- S. Ahmed, S. E. Trask, D. W. Dees, P. A. Nelson, W. Lu, A. R. Dunlop, B. J. Polzin and A. N. Jansen, J. Power Sources, 2018, 403, 56–65 CrossRef CAS.
- J. Ahn, J. Im, H. Seo, S. Yoon and K. Y. Cho, J. Power Sources, 2021, 512, 230513 CrossRef CAS.
- B. Zhu, X. Wang, P. Yao, J. Li and J. Zhu, Chem. Sci., 2019, 10, 7132–7148 RSC.
- A. Moscatelli, Nat. Nanotechnol., 2022, 17, 1237 CrossRef CAS.
- K. Turcheniuk, D. Bondarev, V. Singhal and G. Yushin, Nature, 2018, 559, 467–470 CrossRef CAS PubMed.
- A. Manthiram, Y. Fu, S.-H. Chung, C. Zu and Y.-S. Su, Chem. Rev., 2014, 114, 11751–11787 CrossRef CAS PubMed.
- C. Yang, K. Fu, Y. Zhang, E. Hitz and L. Hu, Adv. Mater., 2017, 29, 1701169 CrossRef PubMed.
- D. Vidal, C. Leys, B. Mathieu, N. Guillet, V. Vidal, D. Borschneck, P. Chaurand, S. Genies, E. De Vito, M. Tulodziecki and W. Porcher, J. Power Sources, 2021, 514, 230552 CrossRef CAS.
- M.-T. F. Rodrigues, J. A. Gilbert, K. Kalaga and D. P. Abraham, J. Phys. Energy, 2020, 2, 024002 CrossRef CAS.
- M. J. Lain, J. Brandon and E. Kendrick, Batteries, 2019, 5, 64 CrossRef CAS.
- T. Bond, R. Gauthier, A. Eldesoky, J. Harlow and J. R. Dahn, J. Electrochem. Soc., 2022, 169, 020501 CrossRef CAS.
- K. G. Gallagher, S. E. Trask, C. Bauer, T. Woehrle, S. F. Lux, M. Tschech, P. Lamp, B. J. Polzin, S. Ha, B. Long, Q. Wu, W. Lu, D. W. Dees and A. N. Jansen, J. Electrochem. Soc., 2015, 163, A138 CrossRef.
- W. Mei, H. Chen, J. Sun and Q. Wang, Sustainable Energy Fuels, 2018, 3, 148–165 RSC.
- United States Advanced Battery Consortium (USABC), LLC., USABC Goals for Low-Cost/Fast-Charge Advanced Batteries for EVs-CY 2023, United States Council for Automotive Research (USCAR), LLC., 2017.
- J. K. Seo, H.-M. Cho, K. Takahara, K. W. Chapman, O. J. Borkiewicz, M. Sina and Y. Shirley Meng, Nano Res., 2017, 1–13 Search PubMed.
- J. Cabana, L. Monconduit, D. Larcher and M. R. Palacín, Adv. Mater., 2010, 22, E170–E192 CrossRef CAS PubMed.
- P. Rozier and J. M. Tarascon, J. Electrochem. Soc., 2015, 162, A2490 CrossRef CAS.
- A. M. Colclasure, T. R. Tanim, A. N. Jansen, S. E. Trask, A. R. Dunlop, B. J. Polzin, I. Bloom, D. Robertson, L. Flores, M. Evans, E. J. Dufek and K. Smith, Electrochim. Acta, 2020, 337, 135854 CrossRef CAS.
- C. Heubner, A. Nickol, J. Seeba, S. Reuber, N. Junker, M. Wolter, M. Schneider and A. Michaelis, J. Power Sources, 2019, 419, 119–126 CrossRef CAS.
- S. J. An, J. Li, C. Daniel, D. Mohanty, S. Nagpure and D. L. Wood, Carbon N. Y., 2016, 105, 52–76 CrossRef CAS.
- D. L. Wood, J. Li and C. Daniel, J. Power Sources, 2015, 275, 234–242 CrossRef CAS.
- S. Ahmed, P. A. Nelson and D. W. Dees, J. Power Sources, 2016, 326, 490–497 CrossRef CAS.
- H. Zheng, J. Li, X. Song, G. Liu and V. S. Battaglia, Electrochim. Acta, 2012, 71, 258–265 CrossRef CAS.
- W. B. Hawley and J. Li, J. Energy Storage, 2019, 25, 100862 CrossRef.
- B. Liu, J.-G. Zhang and W. Xu, Joule, 2018, 2, 833–845 CrossRef CAS.
- E. Moyassari, T. Roth, S. Kücher, C.-C. Chang, S.-C. Hou, F. B. Spingler and A. Jossen, J. Electrochem. Soc., 2022, 169, 010504 CrossRef.
- M. Graf, C. Berg, R. Bernhard, S. Haufe, J. Pfeiffer and H. A. Gasteiger, J. Electrochem. Soc., 2022, 169, 020536 CrossRef CAS.
- X. Tao, J. Wang, C. Liu, H. Wang, H. Yao, G. Zheng, Z. W. Seh, Q. Cai, W. Li, G. Zhou, C. Zu and Y. Cui, Nat. Commun., 2016, 7, 11203 CrossRef CAS PubMed.
- M.-T. F. Rodrigues, A. Y. R. Prado, S. E. Trask, S. Ahmed, A. N. Jansen and D. P. Abraham, J. Power Sources, 2020, 477, 229029 CrossRef CAS.
- A. N. Preman, H. Lee, J. Yoo, I. T. Kim, T. Saito and S.-K. Ahn, J. Mater. Chem. A, 2020, 8, 25548–25570 RSC.
- A. M. Bates, Y. Preger, L. Torres-Castro, K. L. Harrison, S. J. Harris and J. Hewson, Joule, 2022, 6, 742–755 CrossRef CAS.
- X.-B. Cheng, C.-Z. Zhao, Y.-X. Yao, H. Liu and Q. Zhang, Chem, 2019, 5, 74–96 CAS.
- P. Albertus, S. Babinec, S. Litzelman and A. Newman, Nat. Energy, 2017, 3, 16–21 CrossRef.
- M. B. Effat, Z. Lu, A. Belotti, J. Yu, Y.-Q. Lyu and F. Ciucci, J. Power Sources, 2019, 436, 226802 CrossRef CAS.
- C. R. Birkl, M. R. Roberts, E. McTurk, P. G. Bruce and D. A. Howey, J. Power Sources, 2017, 341, 373–386 CrossRef CAS.
- M. B. Effat, J. Liu, Z. Lu, T. H. Wan, A. Curcio and F. Ciucci, ACS Appl. Mater. Interfaces, 2020, 12, 55011–55022 CrossRef CAS PubMed.
- P. Ramadass, B. Haran, P. M. Gomadam, R. White and B. N. Popov, J. Electrochem. Soc., 2004, 151, A196 CrossRef CAS.
- T. Li, X.-Q. Zhang, P. Shi and Q. Zhang, Joule, 2019, 3, 2647–2661 CrossRef CAS.
- H. Zhou, S. Yu, H. Liu and P. Liu, J. Power Sources, 2020, 450, 227632 CrossRef CAS.
- J. Lopez, A. Pei, J. Y. Oh, G.-J. N. Wang, Y. Cui and Z. Bao, J. Am. Chem. Soc., 2018, 140, 11735–11744 CrossRef CAS PubMed.
- J. Xu, Nanomicro Lett., 2022, 14, 166 CAS.
- K. Xu, Chem. Rev., 2004, 104, 4303–4417 CrossRef CAS PubMed.
- K. Xu, Chem. Rev., 2014, 114, 11503–11618 CrossRef CAS PubMed.
- H. Maleki Kheimeh Sari and X. Li, Adv. Energy Mater., 2019, 9, 1901597 CrossRef CAS.
- J. W. Braithwaite, A. Gonzales, G. Nagasubramanian, S. J. Lucero, D. E. Peebles, J. A. Ohlhausen and W. R. Cieslak, J. Electrochem. Soc., 1999, 146, 448 CrossRef CAS.
- S.-T. Myung, Y. Hitoshi and Y.-K. Sun, J. Mater. Chem., 2011, 21, 9891–9911 RSC.
- O. C. Harris, S. E. Lee, C. Lees and M. Tang, J. Phys. Energy, 2020, 2, 032002 CrossRef CAS.
- A. Hebert and E. McCalla, Mater. Adv., 2021, 2, 3474–3518 RSC.
- Q. Liu, X. Su, D. Lei, Y. Qin, J. Wen, F. Guo, Y. A. Wu, Y. Rong, R. Kou, X. Xiao, F. Aguesse, J. Bareño, Y. Ren, W. Lu and Y. Li, Nat. Energy, 2018, 3, 936–943 CrossRef CAS.
- C. N. Lininger, A. M. Bruck, D. M. Lutz, L. M. Housel, K. J. Takeuchi, E. S. Takeuchi, A. Huq, A. C. Marschilok and A. C. West, Adv. Funct. Mater., 2020, 30, 1907337 CrossRef CAS.
- G. G. Yadav, J. W. Gallaway, D. E. Turney, M. Nyce, J. Huang, X. Wei and S. Banerjee, Nat. Commun., 2017, 8, 14424 CrossRef PubMed.
- M. N. Obrovac and L. Christensen, Electrochem. Solid-State Lett., 2004, 7, A93 CrossRef CAS.
- M. T. McDowell, S. W. Lee, W. D. Nix and Y. Cui, Adv. Mater., 2013, 25, 4966–4985 CrossRef CAS PubMed.
- Y. Ito, M. Nyce, R. Plivelich, M. Klein, D. Steingart and S. Banerjee, J. Power Sources, 2011, 196, 2340–2345 CrossRef CAS.
- Y. Dai, C. Zhang, W. Zhang, L. Cui, C. Ye, X. Hong, J. Li, R. Chen, W. Zong, X. Gao, J. Zhu, P. Jiang, Q. An, D. J. L. Brett, I. P. Parkin, G. He and L. Mai, Angew. Chem., Int. Ed., 2023, 62, e202301192 CrossRef CAS PubMed.
- X.-B. Cheng, R. Zhang, C.-Z. Zhao and Q. Zhang, Chem. Rev., 2017, 117, 10403–10473 CrossRef CAS PubMed.
- H. Li, M. Murayama and T. Ichitsubo, Cell Rep. Phys. Sci., 2022, 3, 100907 CrossRef CAS.
- X. Lin, J. Yu, M. B. Effat, G. Zhou, M. J. Robson, S. C. T. Kwok, H. Li, S. Zhan, Y. Shang and F. Ciucci, Adv. Funct. Mater., 2021, 2010261 CrossRef CAS.
- A. Manthiram, X. Yu and S. Wang, Nat. Rev. Mater., 2017, 2, 1–16 Search PubMed.
- D. T. Hallinan and N. P. Balsara, Annu. Rev. Mater. Res., 2013, 43, 503–525 CrossRef CAS.
- J. C. Bachman, S. Muy, A. Grimaud, H.-H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Chem. Rev., 2016, 116, 140–162 CrossRef CAS PubMed.
- Y. Ma, J. Ma and G. Cui, Energy Storage Mater., 2019, 20, 146–175 CrossRef.
- J. M. Foster, X. Huang, M. Jiang, S. J. Chapman, B. Protas and G. Richardson, J. Power Sources, 2017, 350, 140–151 CrossRef CAS.
- A. Mukhopadhyay and B. W. Sheldon, Prog. Mater. Sci., 2014, 63, 58–116 CrossRef CAS.
- J. Saint, M. Morcrette, D. Larcher, L. Laffont, S. Beattie, J.-P. Pérès, D. Talaga, M. Couzi and J.-M. Tarascon, Adv. Funct. Mater., 2007, 17, 1765–1774 CrossRef CAS.
- Z. Chen, L. Christensen and J. R. Dahn, J. Electrochem. Soc., 2003, 150, A1073 CrossRef CAS.
- W. Guoping, Z. Qingtang, Y. Zuolong and Q. MeiZheng, Solid State Ionics, 2008, 179, 263–268 CrossRef.
- R. Zhao, J. Liu and J. Gu, Appl. Energy, 2015, 139, 220–229 CrossRef CAS.
- Y.-T. Cheng and M. W. Verbrugge, J. Electrochem. Soc., 2010, 157, A508 CrossRef CAS.
- C. Sauter, R. Zahn and V. Wood, J. Electrochem. Soc., 2020, 167, 100546 CrossRef CAS.
- T. F. Fuller, M. Doyle and J. Newman, J. Electrochem. Soc., 1994, 141, 1–10 CrossRef CAS.
- H. Liu, Z. Wei, W. He and J. Zhao, Energy Convers. Manage, 2017, 150, 304–330 CrossRef CAS.
- K. W. Knehr and S. Ahmed, J. Electrochem. Soc., 2023, 170, 020515 CrossRef.
- R. Zhao, S. Zhang, J. Liu and J. Gu, J. Power Sources, 2015, 299, 557–577 CrossRef CAS.
- M. Keyser, A. Pesaran, Q. Li, S. Santhanagopalan, K. Smith, E. Wood, S. Ahmed, I. Bloom, E. Dufek, M. Shirk, A. Meintz, C. Kreuzer, C. Michelbacher, A. Burnham, T. Stephens, J. Francfort, B. Carlson, J. Zhang, R. Vijayagopal, K. Hardy, F. Dias, M. Mohanpurkar, D. Scoffield, A. N. Jansen, T. Tanim and A. Markel, J. Power Sources, 2017, 367, 228–236 CrossRef CAS.
- A. Samba, N. Omar, H. Gualous, O. Capron, P. Van den Bossche and J. Van Mierlo, Electrochim. Acta, 2014, 147, 319–329 CrossRef CAS.
- S. Li, N. Kirkaldy, C. Zhang, K. Gopalakrishnan, T. Amietszajew, L. B. Diaz, J. V. Barreras, M. Shams, X. Hua, Y. Patel, G. J. Offer and M. Marinescu, J. Power Sources, 2021, 492, 229594 CrossRef CAS.
- A. Frank, J. Sturm, M. Steinhardt, A. Rheinfeld and A. Jossen, ECS Adv., 2022, 1, 040502 CrossRef.
- T. Yuan, Z. Tan, C. Ma, J. Yang, Z.-F. Ma and S. Zheng, Adv. Energy Mater., 2017, 7, 1601625 CrossRef.
- M. M. Thackeray and K. Amine, Nat. Energy, 2021, 6, 683 CrossRef CAS.
- N. Takami, H. Inagaki, Y. Tatebayashi, H. Saruwatari, K. Honda and S. Egusa, J. Power Sources, 2013, 244, 469–475 CrossRef CAS.
- S. Stewart, P. Albertus, V. Srinivasan, I. Plitz, N. Pereira, G. Amatucci and J. Newman, J. Electrochem. Soc., 2008, 155, A253 CrossRef CAS.
- M. E. Sotomayor, C. de la Torre-Gamarra, B. Levenfeld, J.-Y. Sanchez, A. Varez, G.-T. Kim, A. Varzi and S. Passerini, J. Power Sources, 2019, 437, 226923 CrossRef CAS.
- B. Kang and G. Ceder, Nature, 2009, 458, 190–193 CrossRef CAS PubMed.
- S.-Y. Chung, J. T. Bloking and Y.-M. Chiang, Nat. Mater., 2002, 1, 123–128 CrossRef CAS PubMed.
- J. Kasnatscheew, T. Placke, B. Streipert, S. Rothermel, R. Wagner, P. Meister, I. C. Laskovic and M. Winter, J. Electrochem. Soc., 2017, 164, A2479 CrossRef CAS.
- D. P. Abraham, E. P. Roth, R. Kostecki, K. McCarthy, S. MacLaren and D. H. Doughty, J. Power Sources, 2006, 161, 648–657 CrossRef CAS.
- S. Zheng, L. Wang, X. Feng and X. He, J. Power Sources, 2018, 378, 527–536 CrossRef CAS.
- J. Liu, Z. Wang and J. Bai, J. Mater. Chem. A, 2022, 70, 531–541 CAS.
- Y. Chen, Y. Kang, Y. Zhao, L. Wang, J. Liu, Y. Li, Z. Liang, X. He, X. Li, N. Tavajohi and B. Li, J. Mater. Chem. A, 2021, 59, 83–99 CAS.
- K. Liu, Y. Liu, D. Lin, A. Pei and Y. Cui, Sci. Adv., 2018, 4, eaas9820 CrossRef PubMed.
- A. G. Olabi, H. M. Maghrabie, O. H. K. Adhari, E. T. Sayed, B. A. A. Yousef, T. Salameh, M. Kamil and M. A. Abdelkareem, Int. J. Thermofluids, 2022, 15, 100171 CrossRef CAS.
- R. Zhang, B. Xia, B. Li, L. Cao, Y. Lai, W. Zheng, H. Wang and W. Wang, Energies, 2018, 11, 1820 CrossRef.
- X. Feng, D. Ren, X. He and M. Ouyang, Joule, 2020, 4, 743–770 CrossRef CAS.
- X. Feng, S. Zheng, D. Ren, X. He, L. Wang, H. Cui, X. Liu, C. Jin, F. Zhang, C. Xu, H. Hsu, S. Gao, T. Chen, Y. Li, T. Wang, H. Wang, M. Li and M. Ouyang, Appl. Energy, 2019, 246, 53–64 CrossRef CAS.
- Q. Huang, L. Ma, A. Liu, X. Ma, J. Li, J. Wang and J. R. Dahn, J. Power Sources, 2018, 390, 78–86 CrossRef CAS.
- H. Lee, M. Yanilmaz, O. Toprakci, K. Fu and X. Zhang, Energy Environ. Sci., 2014, 7, 3857–3886 RSC.
- L. K. Willenberg, P. Dechent, G. Fuchs, D. U. Sauer and E. Figgemeier, Sustain. Sci. Pract. Policy, 2020, 12, 557 CAS.
- H. C. Hesse, M. Schimpe, D. Kucevic and A. Jossen, Energies, 2017, 10, 2107 CrossRef.
- A. Manthiram, ACS Cent. Sci., 2017, 3, 1063–1069 CrossRef CAS PubMed.
- K. Xu, Commun. Mater., 2022, 3, 1–7 CrossRef.
- A. Tornheim, D. C. O’Hanlon, A. Vu, J. Gim, D. P. Abraham and J. R. Croy, J. Electrochem. Soc., 2023, 170, 010507 CrossRef.
- B. R. Long, S. G. Rinaldo, K. G. Gallagher, D. W. Dees, S. E. Trask, B. J. Polzin, A. N. Jansen, D. P. Abraham, I. Bloom, J. Bareño and J. R. Croy, J. Electrochem. Soc., 2016, 163, A2999 CrossRef CAS.
- J. J. Kubal, K. W. Knehr, N. Susarla, A. Tornheim, A. R. Dunlop, D. D. Dees, A. N. Jansen and S. Ahmed, J. Power Sources, 2022, 543, 231864 CrossRef CAS.
- G. Bridgewater, M. J. Capener, J. Brandon, M. J. Lain, M. Copley and E. Kendrick, Batteries, 2021, 7, 38 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ya00137g |
| This journal is © The Royal Society of Chemistry 2023 |