 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Recent trends in computational tools and data-driven modeling for advanced materials
Varshika
Singh
abc,
Santanu
Patra
ab,
Natarajan Arul
Murugan
 de,
Dana-Cristina
Toncu
af and
Ashutosh
Tiwari
de,
Dana-Cristina
Toncu
af and
Ashutosh
Tiwari
 *a
*a
aInstitute of Advanced Materials, Gammalkilsvägen 18, 590 53 Ulrika, Sweden. E-mail: director@iaam.se; Tel: +46 1313-2424
bVBRI Innovation Centre, 7/16 Kalkaji Extn, New Delhi, 110019, India
cUniversity Institute of Biotechnology, Chandigarh University, Mohali, 140413, India
dDepartment of Computer Science, School of Electrical Engineering and Computer Science, KTH Royal Institute of Technology, SE-100 44 Stockholm, Sweden
eDepartment of Computational Biology, Indraprastha Institute of Information Technology, New Delhi 110020, India
fSchool of Chemistry, University College Dublin, Belfield, Dublin 4, Ireland
First published on 25th March 2022
Abstract
The paradigm of advanced materials has grown exponentially over the last decade, with their new dimensions including digital design, dynamics, and functions. Materials modeling such as that of their properties and behavior in various environments using ab initio approaches, force-field methods and machine learning represents a key step in advanced research. Computational techniques and theoretical models pave the way for establishing the structure–property relationship for designing advanced materials with novel properties and improving their performances. Likewise, high accuracy and fewer computational resources of machine-learning approaches have been widely considered for materials design in the recent years. Furthermore, the information derived from materials studies needs to be properly stored and re-analyzed, making big data analysis an essential requirement for further investigations. The information thus generated has also led to the evolution of the genome of materials for the fostering of advanced materials. Thus, various theoretical and computational approaches provide useful predictions about materials properties and efficiency, ultimately leading to the substantial improvements for new-age devices.
1. Introduction
Advanced materials sustain their enhanced structural and functional properties such as biological, electrical, magnetic, and optical at the macro- and nano-scales, whether they are polymers, glasses, metals, ceramics, or composites. The computational studies of such materials mainly focus on their atomic interactions, to understand their unique structure-derived properties for new technology developments.1–4 The realistic models used in computer simulation both confirm and complement experiments. The computational methods allow the study of the structure, dynamics and properties of materials and establish useful structural relationships to assist the design of materials with improved properties.5 The behaviour of materials at the macroscopic level is generally governed by atomic interactions and its simulations facilitate a better understanding of the materials architecture.Material simulations of larger length and time scales under different external conditions such as temperature, pressure, pH and electric and magnetic fields have become a common tool for technological innovations.6Ab initio and Monte Carlo simulations have been widely used for studying the electronic structure and understanding the key intermolecular forces that dictate the structure and dynamic properties of materials. By applying computational methods during initial design and study, the cost and time of manufacturing, and product testing and production steps of materials are significantly reduced.7 Recent progress in machine learning, deep learning, the internet of things (IoT), big data, and intelligent optimization has deeply transformed the computational methodologies used for materials design and innovation, providing a better understanding of their fundamental properties and behavior.8
Materials modeling offers significant information at the microscopic level and explains their compositional, structural, and multifunctional properties and, along with the generation of multidimensional datasets, enables advancements in materials discovery and application for sustainable energy and environmental technologies.9 It further provides useful insight into materials design and fabrication strategies for novel and improved properties. Nevertheless, such indispensable computational tools, offering prediction of structure and even elements, as well as interesting properties, are limited by their accuracy and therefore under continuous investigation.10
The quantum mechanics and computational methods allow the identification of interatomic interactions, while other data-driven techniques help with knowledge-based models to understand structural properties and their role in the functional properties of materials.11,12 All these data and analysis procedures reduce time and cost to gain an insight into materials discovery. In 2011, the Materials Genome Initiative (MGI) announced the identification of faster, more efficient research methods that integrate theory, computation, synthesis, and characterization and accelerate new materials discovery, design, and deployment.13 Huge datasets of materials are generated in the process, which can be used to analyze and share information among the researchers worldwide, to identify the respective features, which are responsible for the materials functions in the minute time span.14Fig. 1 explains how computational methodologies allow structure modeling and function prediction of materials while generating big data and speed up the process from theory to experiment. Computational approaches provide information from the microscopic level of materials, relate to their macroscopic properties, and help modeling and engineering of materials.15
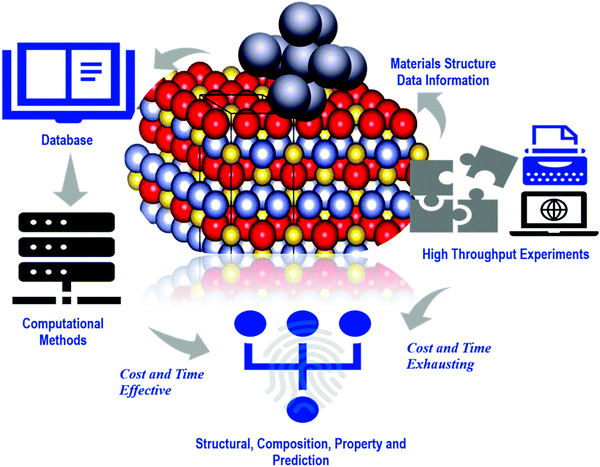 | ||
| Fig. 1 The fundamental approaches of computational procedures for structure modeling and property prediction of materials. Computational tools are faster and cheaper than the high throughput laboratory experiments for assessing the same (Inside atomic structure has been reproduced with permission from ref. 11). | ||
In this review article, we have highlighted the cutting-edge materials research in the light of computational methods and modeling by focusing on the developments of advanced and innovative properties and applications. In silico studies enable design modification, and functional prototyping would otherwise imply time-consuming and expensive iteration and fabrication steps in the case of many materials. Numerous reviews on computational materials modeling have been published in the last few decades (Table 1). Nevertheless, most of these reviews focus on a particular computational method or materials. This article enlists many in silico developments and important technological innovations in advanced materials that were not discussed or mentioned in any of the previous reviews.
| Literature review | Focus area of research |
|---|---|
| 16 | Commonly used methods of electronic structure calculation: ab initio methods, density functional theory (DFT), some semi-empirical methods |
| 17 | Ab initio calculations of optically excited states in 2D materials |
| 18 | Fundamental topics of Hartree–Fock theory in quantum chemistry |
| 19 | Machine learning in solid-state materials science |
| 20 | Density functional theory in materials science |
| 21 | Density functional theory in materials research |
| 22 | Monte Carlo simulation of microstructural evolution in metals |
| 6 | Molecular dynamics computational method in shock wave solid simulation and biopolymers |
| 23 | Molecular dynamics in steel performance |
| 24 | Multiscale materials modeling |
| 25 | Data-driven materials science |
| 26 | Artificial intelligence in materials science |
| 27 | Artificial intelligence in materials science |
| 28 | Advances in modelling and simulation of halide perovskites for solar cell applications |
2. Computational modeling for materials properties
Materials are the essential part of technology and development and they have revolutionized the way we live today. The human life is becoming more and more comfortable thanks to various materials with useful properties. The computational modeling of materials provides information about their structures, dynamics, and properties and also how these materials respond to external variables like temperature, pressure and electric and magnetic fields. Such properties of materials to respond to external conditions make them useful for design of smart materials and sensors. Successful modeling of materials properties can be used to establish various structure–property relationships which then can be used to design materials with novel properties. Some of the useful materials properties are listed as follows: (i) optical properties, (ii) magnetic properties, (iii) thermal conduction, (iv) electronic conductivity, (v) negative thermal expansion, (vi) non-linear optical properties, (vii) energy efficiency in relevance to DSSC application, (viii) superionic conductors (NASICON like materials), and (ix) thermally and pH responsive materials. We have theories such as classical mechanics, quantum mechanics and continuum mechanics to model these properties. There are many detailed studies reported in the literature to study these properties. With the use of classical mechanics, one can follow the time evolution of any system and any thermodynamic properties can be computed from the stored positions and velocities. For example, transport properties such as the diffusion coefficient of ions in superionic materials can be computed from the root mean square displacement or from the velocity autocorrelation function.The response of materials to external temperature, pressure and pH can be modeled by running the simulations in appropriate ensembles such as the constant temperature constant volume ensemble and the constant pH ensemble, and the systems in these cases are connected to thermostats, barostats and acidostats. However, the electronic (i.e., absorption and emission spectra) and magnetic properties can not be computed from the classical mechanics but rather one needs to employ electronic structure theory which treats electrons explicitly. The response of materials to light and other fields can be modeled using time dependent density functional theory. So, depending on the system of interest and properties to be modeled one needs to choose the right level of theory. For example, we studied a hybrid system made of graphene, sodium dodecylbenzene sulfonate and glucose oxidase using force-field molecular dynamics simulations29 (Fig. 2). Since, this study investigated the stabilizing interactions of this hybrid system, and given that the length scale of the system was quite larger, we chose this approach which is computationally less demanding but still able to provide insight into the microscopic interactions responsible for the stability of the system. Based on the force-field molecular dynamics, it was found that the graphene–SDBS interface was stabilized by hydrophobic interactions, while the SDBS–glucose oxidase interface was stabilized by hydrophilic interactions. Further, this also explains why the GOx cannot be immobilized directly on the graphene surface.
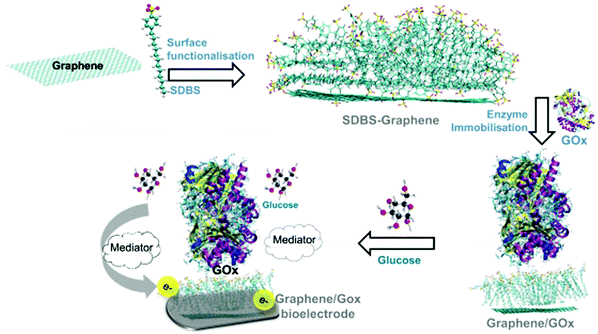 | ||
| Fig. 2 Immobilization of glucose oxidase (GOx) on the graphene: sodium dodecylbenzene sulfonate (SDBS) surface for glucose sensing applications (reproduced with permission from ref. 29). | ||
Similarly, the temperature responsive behavior of poly(N-isopropylacrylamide) (PNIPAM) and its interaction with Troponin-T were modeled successfully using force-field molecular dynamics. The force-field MD was able to successfully reproduce the coil-globular structural change in PNIPAM with increasing temperature.30,31 The pH responsive behavior of a generation-5 poly(amidoamine)-graft-poly(ethyleneglycol methacrylate) (PAMAM(G5)–PEGMA) based drug delivery system was studied by Zeng et al. using dissipative particle dynamics simulations32 (Fig. 3). The authors showed that PAMAM(G5)–PEGMA spontaneously forms unicellular micelles at normal pH and central hydrophobic core can be loaded with doxorubicin like drug molecules and the drug molecules can be released under acidic pH condition present in the cancer cell like microenvironment.
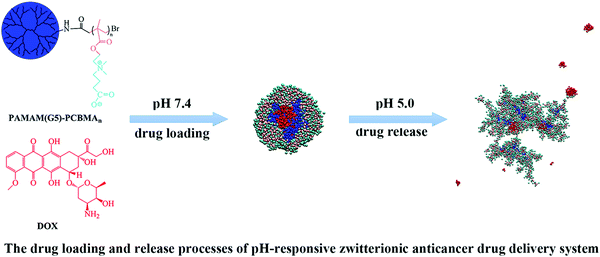 | ||
| Fig. 3 pH responsive PAMAM(G5)–PCBA polymer for drug delivery for cancer treatment (reproduced with permission from ref. 32). | ||
Therefore, computer simulations can provide valuable insight into the working mechanism of various biosensor molecules and to understand the pH and thermally responsive behavior of smart polymeric materials for various biosensor–bioelectronic applications. Also, in recent years machine learning approaches have been applied to establish the relationships between the structural properties, electronic properties, and macroscopic properties and the power conversion efficiency of dye molecules for DSSC applications. With the established relationships, it is possible to design novel materials with improved power efficiency.
3. Computational methods in materials research
Computational methods are driving advanced materials towards engineering high-performance materials. Nowadays, computational methods and tools are key components of research for the design and development of a new class of materials with advanced applications and properties. They help in planning and optimizing materials synthesis processes, including chemical reactions and required routes to follow. In addition, they also help in the analysis and interpretation of experimental data regarding materials structure and properties, offering meaningful insight into energy devices, composite materials, automobiles, and chemical and biological sciences.333.1. Materials modeling
The materials modeling approach is routinely applied as a cost-effective and complementary tool for extracting information about materials at the microscopic level and for explaining their electrical, optical, and magnetic properties. It also provides an understanding into design principles and strategies for the fabrication of materials with novel and improved properties. Therefore, the use of materials modeling along with experimental validation opens the possibilities for designing extremely useful materials that are relevant for various applications such as energy and healthcare at the industrial level. Materials properties are highly dependent on structure and hence structure prediction is considered to be the center of computational materials research.34 Materials of different length scales (i.e., nano- and micro- materials) have been developed with better properties like superplasticity and enhanced toughness and strength.35–37 Predicting the structure and properties of these materials using computational tools before performing experiments has become common practice in materials research. The development of reliable quantum/molecular mechanics approaches and atomistic scale calculations allows such projections. Materials modeling has been performed by three well-studied modeling approaches, i.e., ab initio methods, density functional theory (DFT) semi-empirical methods and force-field methods.The core knowledge achieved through ab initio methods arises from the computational solution of the electronic Schrödinger equation and helps in calculating and identifying the electronic energy, electron density, electron transfer, thermal relaxation, energy transfer, and charge recombination processes for applications in the development of cells, batteries, and other energy devices.39Ab initio methods can also help in modeling the relatively small region of materials at the quantum chemistry level, where other modeling methods are treated on an approximation basis. In drug delivery, for example, ab initio molecular dynamics simulation followed by geometry optimization was performed in the gas phase for determining the binding energies of drug–polymer complexes, leading to the finding that drug molecules interact with the polymer through hydrogen bonding, while quantum mechanics/molecular mechanics simulation showed that ciprofloxacin and metronidazole release patterns follow the zero order kinetic model.40
The remarkable advances in ab initio methods provide benchmark accuracy, used routinely to complement experimental studies, and effectively calculate a wide variety of properties such as structure, thermochemistry, various types of spectroscopic quantities and response to external perturbations. This type of calculation has practical application in industry for relevant catalytic processes, semiconductor processing, and modeling of conductivity for microelectronics applications. In addition, ab initio methods provide a wealth of details that are not available from experiments and a degree of confidence in the results that are not available from a more empirical approach.41
Ab initio calculations of optically excited states in 2D materials derived from the nature of two- and multi-particle excited states such as strongly bound Wannier excitons and charged excitons gave valuable insight into many interesting properties, for instance enhanced light–matter coupling, gate-tunable photoluminescence, and unusual excitonic optical selection rules (Table 2).42
| Method | Advantage(s) | Disadvantage(s) | Application(s) |
|---|---|---|---|
| Ab initio methods | Provide very accurate predictions based on quantum mechanics using wave functions | Intensive computational requirements | Prediction of structures, thermodynamics, spectroscopic quantities, external force responses |
| Density functional theory (DFT) | Electronic structure calculations, less extensive computational requirements | Too many approximations | Calculation of materials’ interaction properties and other kinetics calculations |
| Semi-empirical methods | Faster computation | Less accurate | Modeling of the structure and dynamics of large systems |
| Monte Carlo (MC) simulation | Probability calculations of different outcomes | Large computational resources required | Calculation of the thermodynamic properties of systems |
| Molecular mechanics (MM) | Less complicated, fast, calculates equilibrium equations of the atomistic system | Can’t predict accurate bond making and breaking geometries | Prediction of accurate structures and energies for molecules |
| Molecular dynamics (MD) | Predicts materials properties by analyzing atomic level behavior, visualizes the motion of the atoms at the nanosecond level | Based on Newtonian mechanics, lack quantum effects | Prediction of materials properties like hardness, dissolution rate, toughness, and reversibility |
| Quantum mechanics (QM) | Can model chemical bonds | Require extensive computational facilities; thus applications are limited to smaller systems | Prediction of macroscopic properties of materials |
| Finite element methods | Beer accuracy, faster, modeling of the entire structural system rather than components | Reproduce macrostructure levels but not the atomistic parameters | Analysis of stress, vibration, heat transfer and other physical analyses |
| Probabilistic materials simulation | Predicts variance in materials properties due to variance in micro-structural properties | Limited accuracy | Machine learning, data mining, pattern recognition |
| Multiscale simulation | Combines the strengths of different mechanical techniques for predicting the microscopic model and for macroscale analysis | Noise or fluctuations in microscale models | New materials design and modeling |
| Data science | Hidden correlations inferred from already available large datasets | Integration of data from experimental and computational sources, data standardization | New materials design |
Further, DFT gives estimations for the total energy and potential energy of molecules and organic complexes, and band gaps and optical transitions for metals, semiconductors, and, with modifications, insulators. This method also allows studying surface phenomena, such as oxidation and catalytic reactions and modeling of nanoparticles and nanocomposites. DFT has limitations in simulating more than few thousand atoms, which can be overcome by using empirical potentials. DFT is based on the Hohenberg–Kohn theorem that states that the potential of a quantum system can be identified by the functional of its electronic density and an additional constant.43 This theorem was extended for external potentials in an open set and established as a function of the electronic density for Coulomb potentials.44
The basic formalism needed for the ground-state quantum chemical calculations that are typically performed in DFT analysis comprises the molecular Hamiltonian with a special set of atomic units that are convenient for simplifying the equations, the Born–Oppenheimer approximation for electronic and nuclear problems, and the Hartree and Hartree–Fock equations for the electronic problem.45 DFT limitations can be overcome by using a new method called holomorphic Hartree−Fock theory, where the equations are modified to avoid the disappearance of the solutions. When applied to the simplest chemical system H2, the properties of the solutions resulted without their disappearance with geometry.46
DFT methods have been used for the modeling and simulation of new functional materials for various applications as energy storage devices, conductors, catalysts, and sensors.47–50 Coupled with experimental study, they assisted the development of advanced materials for their respective applications in the energy, environmental and health sectors.49 DFT calculations also helped in analyzing possibilities of using hydrogen as a fuel with new materials enabling catalysis and hydrogen production.51,52 Nowadays, DFT is actively used for required property prediction of materials and screening before synthesis.53
Recently, DFT calculation of electronic properties contributing to a nanomaterials integrated “on/off” switchable aptasensor system has been reported. The DFT study on the structural contribution of the monomer of poly(N-isopropylacrylamide) (PNIPAM) grafted onto a graphene oxide (GO) surface and the effective adsorption of the nucleobases on it has explained the effect of PNIPAM on the adsorption of the nucleobases as well as its biomolecular integration with the GO surface. While the experimental study proved that the PNIPAM on the nanomaterials surface does not contribute much to the full electronic feature of the system due to the insulating nature of the polymer, the DFT study showed that the bandgap energy distribution before and after the functionalization of the PNIPAM monomer remained unchanged. The optimized structures of all nucleobases, GO, the PNIPAM monomer and the GO/NIPAM structure are presented in Fig. 4.47
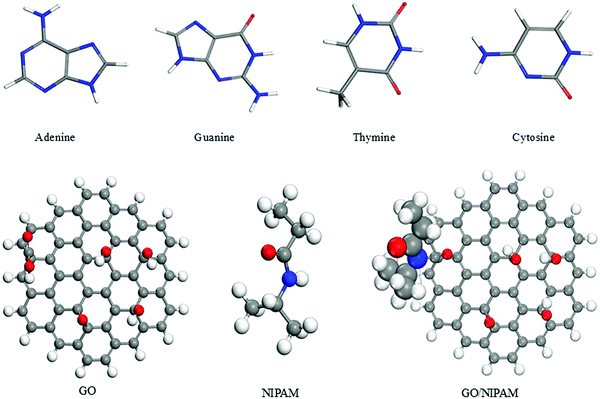 | ||
| Fig. 4 The optimised structures of the nucleobases, GO, NIPAM, and GO/NIPAM (reproduced with permission from ref. 47). | ||
Likewise, DFT has also been applied for anionic engineering of heteroanionic materials,11 mainly incorporating anions with different properties for designing heteroanionic materials (Fig. 5). A functional heteroanionic materials is computationally designed by sampling the structural phase space based on the electronic structure and, as such, the thermodynamic stability of the materials is further identified. The DFT can unravel the composition–structure–property relationships in materials science, contributing significantly to the understanding of the relationship between fundamental physical and chemical properties governing processes at the atomistic scale on one hand, and typically macroscopic properties required in engineering applications, on the other hand. For a range of materials, specifically polycrystalline bulk semiconductor materials, metals and ceramics, the physio-chemical relationships are determined in both chemical compositions and microstructures. Wisely chosen process conditions (e.g., mechanical forming and annealing in metallurgy or epitaxial growth in semiconductor technology) lead to the desired microstructure.20
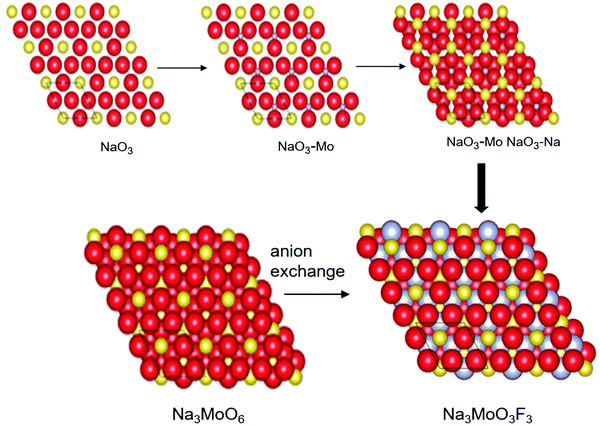 | ||
| Fig. 5 Construction of the heteroanionic materials Na3MoO3F3. Computational analysis helps in predicting building units NaO3F3 and MoO3F3 and their arrangements in the cluster. This type of heteroanionic arrangement alters the electronic, magnetic, and optical properties of molecules (reproduced with permission from ref. 11). | ||
By describing the interactions between atoms and electrons governed by the laws of quantum mechanics, DFT has become an accurate and efficient technique for solving the basic quantum-mechanical equations for complex many-atom and many-electron systems, such as structural materials, catalysis and surface science, nanomaterials, and biomaterials and geophysics. Despite its challenges in designing, simulations meaningfully represent physical and chemical properties using modeling processes including chemical reactions and phase transformation in materials. DFT is successfully used in alloy analysis, especially low-modulus, high-strength titanium alloys, high-strength steels, and aluminium cast alloys with improved processing and enhanced properties.21
The information obtained by DFT contributed to the creation of various materials–property databases like the Materials Project, AFLOWLIB, OQMD (Open Quantum Materials Database), AiiDA (Automated Interactive Infrastructure and Database for Computational Science), JARVIS-DFT, OMDB (Organic Materials Database), and QM9. A useful system to predict novel 2D materials using DFT databases was generated54 as shown in Fig. 6.
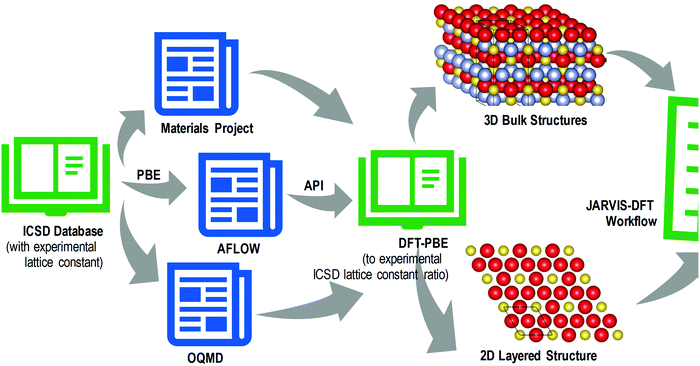 | ||
| Fig. 6 Screening of 2D materials using DFT databases. Materials with reasonably high PBE (Perdew–Burke–Ernzerhof) functionals to experimental lattice constant difference were filtered and their layered counterparts were prepared manually. Both were used for various DFT calculations and 2D property prediction (redrawn with permission from,54 inside atomic structure has been reproduced with permission from ref. 11). | ||
Semi-empirical methods represent an efficient computational tool for fast quantitative estimations of many properties, particularly useful for correlating large sets of experimental and theoretical data, for establishing trends in classes of related molecules, and for scanning a computational problem before proceeding with higher-level treatments. Compared with ab initio or density functional methods, semiempirical calculations are much faster, but less accurate, with less systematic, therefore harder to correct errors. They need improvement in accuracy and the range of applicability, without compromising their computational efficiency. In addition, they need new algorithms for modern computer architectures and extension to larger molecules.55 The well-known semi-empirical methods are the underlying theoretical approach, integral approximation, integral evaluation, and parametrization.
3.2. Computational simulation
With the advancement of supercomputers and the continuous development of efficient algorithms, computer simulations have become an integrated part of research and innovation. Though in silico simulation will never replace the experiment, it is playing an important role in the analysis, design, and optimization of engineering systems. Computer simulations help in validating theories and predicting expected outcomes under extreme physical conditions, by reducing the time and cost for extensive laboratory experiments, including trial and error steps.56–58 To achieve the full potential of computational simulation, researchers are confident to get an accurate representation of reality. A model for an expected real-world system is designed and optimized for its performance under different conditions. Simulations for novel design and testing are readily done owing to the efficient computational tools available.59 Some of the common simulation tools, along with their applied methods and applications, are listed in Table 3.| Software | Simulation procedures | Applications |
|---|---|---|
| Materials Studio | DFT, hybrid QM/MM and semi-empirical methods | Predict the atomic and molecular structures and properties of materials |
| ABINIT | DFT | Calculate the optical, mechanical, vibrational, and other observable properties of materials |
| NAMD | Molecular dynamics | Simulation |
| GROMACS | Molecular dynamics | Simulation |
| LAMMPS | Molecular dynamics | Modeling and simulation at the atomic, meso, or continuum scale |
| Gaussian | DFT, molecular mechanics | Modeling |
| VASP | DFT | Atomic scale materials modelling |
| SIESTA | DFT/molecular dynamics | Electronic structure calculations and ab initio molecular dynamics |
| CHARMM | QM/MM | Modeling and simulation |
| OpenMM | Molecular dynamics | Simulation |
| YASARA | Molecular dynamics | Molecular graphics, modeling, and simulation |
| TINKER | Molecular mechanics Molecular dynamics | Modeling and simulation |
| Amber | Molecular dynamics | Modeling and simulation |
| Quantum Espresso | DFT calculations | Materials modeling and simulation |
| CPMD | Ab initio molecular dynamics | Modeling & simulation |
| Dalton | Electronic structure theory | Modeling and simulation |
| DESMOND | Molecular dynamics | Simulation |
The most common simulation techniques for advanced materials modeling are molecular mechanics, molecular dynamics, Monte-Carlo simulation, quantum mechanical calculations, probabilistic materials simulation, and multiscale simulation techniques (Fig. 7). They have been used in various studies to identify materials behavior under adverse conditions, such as high-temperature,60,61 wearing and friction,62 welding, joining,63 and crash simulations of composite materials,64,65 leading to materials design.66
The conventional MC simulation draws samples from a probability distribution, in most cases the classical Boltzmann distribution, to obtain thermodynamic properties and minimum energy structures,69 while dynamic MC simulation calculates non-equilibrium properties like crystallization70–72 and quantum MC simulation computes various electronic properties of materials.73,74 All these MC simulations are vastly used in materials design and engineering, with strong examples being a valuable python library employing Tree Search (MDTS) and a database for large silicon–germanium (Si–Ge) alloy structures.66
MC simulations of lattice models are widely used to compute the thermodynamic properties of substitutional alloys, despite their difficulty in obtaining the desired quantities. High-level algorithms that serve as interfaces between the user and a traditional MC code, allowing the user to postulate the goals and determine the free energy of an alloy phase over its entire region of stability within a specified accuracy, without requiring any user intervention during the calculations, enable the direct determination of composition–temperature phase boundaries without requiring the calculation of the whole free energy surface of the alloy system.75 The MC simulation of metal grain growth based on the Potts model provides important information, such as the kinetics of interface migration in atomistic ordering of f.c.c., to an LI2 structure in Ni based alloy.22
MM atomistic simulations are based on empirical inter-atomic potentials and can describe the small-amplitude vibrations, torsions, elastic deformation, and electrostatic interactions in materials systems.77 A MM model helped analyze single layer graphene sheets taking into consideration binary, ternary and quaternary interactions between the atoms: by solving the equilibrium equations of the atomistic system through the arc-length strategy, the critical and post-critical behavior of graphene under compression in zigzag and armchair directions and shear was highlighted.78 In another MM model, the equilibrium paths and critical behavior are shown in comparison with available solutions for thin plates.79 MM nanostructure modeling has been widely applied.80,81
MD and MC simulations are frequently used for atomic scale lattice configuration and conformation analysis based on physical potentials or force fields, derived from the Schrödinger equations. Major force fields used for MD simulation are CHARMM, AMBER, OPLS-AA, DREIDING, UFF, GROMS, OPLS, and COMPASS, which differ in several properties. MD simulation allows atoms and molecules to interact for a period and provides a trajectory view of the motion of the atoms at the nanosecond level. MD simulations along with topological concepts are used to predict materials properties like hardness, dissolution rate, toughness, and reversibility.85 MD simulation helps in the development of an analytical model of macroscopic properties of materials to facilitate calculations of electronic band-structure, elastic properties, and piezoelectric, dielectric, and ferroelectric properties. Several applications such as thermoelectrics, catalysts, and energy devices have been designed making use of the MD simulation approach. MD analysis helps in assessing the stability and interaction of materials with various types of interfaces for the development of sensors and batteries.86
Furthermore, the MD approach helps in identifying atomic scale mechanisms controlling structure–property relationships in materials which would be experimentally exhausting to identify.87–91 The MD approach was used to understand the structure–property relationship of supramolecular polymers and establish the internal structures of the monomers of the polymers, which are responsible for the adaptivity and stimuli-responsiveness behavior of the polymers. The simulation results showed that the re-organization of the supramolecular structure occurs due to monomer diffusion on the dynamic fiber surface. Modifying the structure of the monomers results in the variation in supramolecular configuration and their response to the respective stimulus (Fig. 8).84
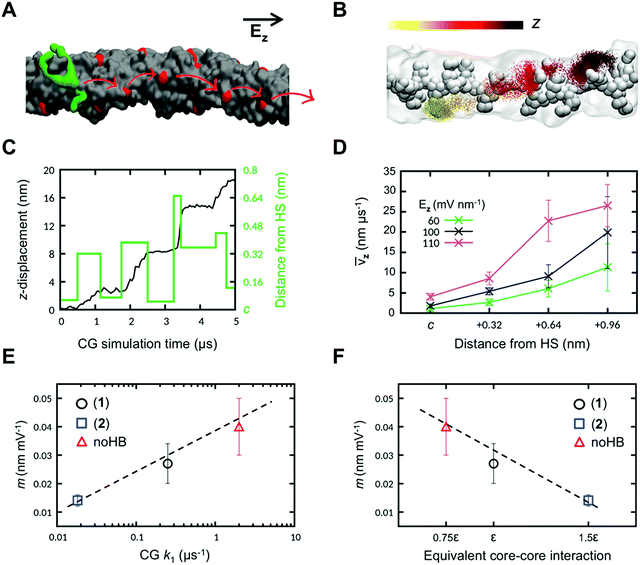 | ||
| Fig. 8 Obtaining structure–dynamics–property relationships for BTA(1)3+ supramolecular polymers. (A) The BTA monomer (green) diffuses along the z-direction, the monomer stops on accessible cores (hot spots) on the fiber surface. (B) Movement of the BTA(1)3+ core (points) onto fiber 1 at each step of the CG-MD simulation. The core is colored based on its z-displacement. The average configuration of the fiber during the CG-MD is shown in transparent gray (solid beads represent the monomer cores). High-density points identify regions where the diffusing monomer stations for longer times. (C) The z-displacement (black) of BTA (1)3+ onto fiber 1, the minimum distance between the BTA(1)3+ core, and the closest hot spot (HS) in the fiber (green) with Ez = 60 mV nm−1. (D) The average BTA(1) drift velocity (vz) as a function of the minimum distance from the closest HS for different intensities of Ez. (E) Relationship between the relative rate of stimuli-responsiveness (m) and the average exchange rate of monomers on the surface (k1) for the different fibers. (F) Linear relationship between stimuli-responsiveness rates (m) and the equivalent relative strengths of core−core interaction in the different fibers (reproduced with permission from ref. 84). | ||
Optimized coarse-grained MD methods are great exploration tools in complex topological polymer structures including star-polymers and biomacromolecules such as polyelectrolytes and polymers with intrinsic stiffness, thus contributing to an improved understanding of medical applications such as non-invasive extracorporeal shock wave lithotripsy or tumor treatment.56 MD in materials microscopic-sized dynamic simulation and its subsequent application of macro-characteristics and microstructure to steel organization performance control describes the mechanical behavior of such materials, especially crack, dislocation, and grain boundaries and their interaction.23
Computational quantum mechanics brought a high demand for new techniques in theoretical condensed matter physics that facilitates the understanding of solid materials properties with details down to the atomic level, bringing theoretical studies to a higher, though practicable level. Particularly, the Exact Muffin-Tin Orbitals (EMTO) or Kohn−Sham method allows establishing a theoretical insight into the electronic structure of complex engineering materials such as binary, iron–chromium–nickel, and stainless-steel alloys. The single-electron Schrödinger equations are solved separately within the units defined around the lattice sites. The unit cells are chosen in such a way that they should give a proper description of the local surroundings for every lattice site.92
In recent decades, the Crystal Plasticity Finite Element Method (CPFEM) has become an extremely versatile tool for describing the mechanical response of crystalline materials on all length scales from single crystals to engineering parts. Crystalline matter being mechanically anisotropic, its deformation depends on the direction of the mechanical loads and geometrical constraints imposed through the anisotropy of the elastic tensor and orientation dependence of the activation of the crystallographic deformation mechanisms (dislocations, twins, martensitic transformations).
In consequence, associated mechanical phenomena such as materials strength, shape change, ductility, strain hardening, deformation-induced surface roughening, damage, wear, and abrasion are also orientation-dependent, and, for single-crystal elastic–plastic anisotropy, macroscopically directional properties are also produced when the orientation distribution (crystallographic texture) of the grains in a polycrystal is not random. Therefore, finite element approximations have become relevant for crystal mechanical modeling, as they are based on the variational solution of the equilibrium of the forces and the compatibility of the displacements using a weak form of the principle of virtual work in each finite-volume element. The entire sample volume under consideration is discretized into such elements.
The essential step which renders the deformation kinematics of this approach a crystal plasticity formulation is the fact that the velocity gradient is written in dyadic form. This reflects the tensorial crystallographic nature of the underlying defects that lead to shear and, consequently, to both shape changes (symmetric part) and lattice rotations (skew-symmetric part), with meaningful results in solving crystal mechanical problems under complicated internal and/or external boundary conditions.97 The FEM proves to be an extremely useful tool when the problems solved are either boundary value problems or initial-value problems or both, and the solution of most of these problems by exact methods of analysis is not possible. In the FEM problem formulation, the least squares, collocation, Rayleigh–Ritz and Galerkin methods are well-established and provide solution to many engineering problems.98
The main advantage of multiscale modeling is that it combines the strengths of different computational mechanics techniques like quantum mechanics, molecular dynamics, and FE for micro- and macroscale analysis. While MS materials modeling combines existing and emerging methods from diverse scientific disciplines to bridge the wide range of time and length scales that are inherent in a number of essential phenomena and processes in materials science and engineering, it needs to be properly linked to the electronic structure theory and statistical methods to describe the physics and chemistry that govern the properties and processes of materials under realistic temperature and pressure conditions.105 The effect of MS transformation on materials science is well represented by its ability to discover new materials and their phenomena for acquiring insight into the processes that rule the materials behavior, as well as for quantitative predictions useful in materials design, completing the experimental synthesis and characterization.24
4. Data science
Data science methods are heavily promoted in materials science and data storage, re-shaping analysis. Materials discovery through conventional research including experimental, theoretical or computational implies long times and high costs, while data science accelerates the process from materials discovery to deployment.25 It includes data management with the help of reliable storage and retrieval databases and data analytics comprising data mining and analysis.106 For materials, data can include experimental information with details of test conditions. The common data science methods in materials research, i.e., big data analytics, machine learning algorithms and artificial intelligence, are discussed below.4.1. Big data analysis
Big Data usually refers to a large dataset, structured or unstructured, that can be used to extract information about definite patterns or parameters using computational algorithms. It is defined by large magnitudes of five vs. volume, velocity, variety, veracity, and value.106,107 Due to advanced computational and experimental studies, a large amount of materials data is available, leading materials research into the big data domain. Big data research of materials is relatively new and requires more robust approaches and databases for analysis, as well as huge computer data storage capability.The peer-reviewed journals are now demanding the materials science community to provide data availability statement for publications, allowing data accessibility and reuse by the community.108 Data can be submitted in standard databases, such as the NoMaD repository for materials property calculations, caNanoLab for nanomaterials in biomedical applications, the Cambridge Structural Database for crystallographic data, and PubChem for characterization of chemical substances.
In materials research, most of the information on quantum mechanics remains unutilized and is ultimately discarded, but storing this detail helps in big data analysis and allows learning more about materials properties and processes. New tools, algorithms and approaches are required to access trends or patterns among materials and their properties, and for comparing different data. Big data approaches lead to efficient structure–property relationship analysis at different length or time scales. Progress in large materials databases and machine learning algorithms helps materials research tremendously.
The development and incorporation of mathematical and statistical methods for the study of high dimensional, sparse, and noisy big data and extraction of patterns from them are now major challenges of materials research.109 These methods can be used for materials discovery by identification of key factors and exploration of their functionality in design and processing. Big data analysis of materials mainly involves extracting patterns and determining relationships between data with the aid of data mining, evolutionary algorithms, and other statistical methods. It is expected that, with recent advances in experiment and in silico, big data will result in significant materials advancements as they did for genomics, revolutionizing not only the outstanding outcomes, but also the way researchers work.110 The big data contribute to a significant acceleration in the design of new materials, from discovery to market release and even patenting such innovations, becoming a platform for the scientific practice of systematically extracting knowledge from materials datasets (Fig. 9). As such, it ultimately benefits the quality of life for the public.25,111
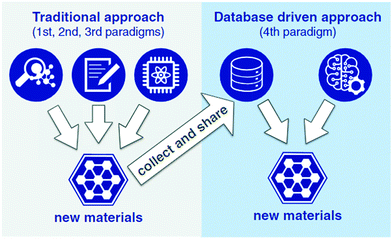 | ||
| Fig. 9 Materials discovery schematic, differentiating between the traditional approach, based on experimentation, theory, or computation, and the data-driven approach (reproduced with permission from ref. 25). | ||
4.2. Artificial intelligence
Artificial intelligence involves acquiring information and using it with reasoning and self-correction, like human intelligence with the help of computer systems. In the case of materials science, AI makes use of the data derived from theoretical and experimental works and stored in various materials databases like AFLOWLIB, JARVIS-DFT, Polymer Genome, Citrination, and Materials Innovation Network. This helps in accelerating the synthesis and optimization processes, and in identifying materials with similar behavior.112 The Materials Genome Initiative helped accelerating materials discovery and the development of databases from theoretical studies, which further catalyzed the progress. AI tools consist of machine-learning, deep-learning and other optimization techniques, and algorithms to evaluate materials performance. AI is a very active area, with many challenges, accelerating research in design, synthesis, characterization and application of molecules and materials in the near future.AI overcame the inherent limitations of the human cognitive ability with its primary algorithm framework, powerful hardware foundation, and excellent data mining ability. Its applications in materials science and engineering accelerated the simulation of the structure-related performance of materials, though with discrepancies from the experimental findings, towards a superior level, reduced the amount of computation in nano-clustered alloys, predicted properties for new materials in mapping the structure–property relationship, and allowed new technologies for innovative materials synthesis.26,113
Despite being described as the next scientific paradigm in materials discovery and optimization, the recent success of AI came from the combination with experimental research, with subsequent creation of new and creative modes of measuring properties and visualizing and interpreting data. Nevertheless, the next step in AI development requires closing the gap with a robust system that combines ML techniques with physical mechanisms within innovative scientific application.27,114
4.3. Machine learning
ML models help in predicting complex materials properties with advantageous accuracy.115 They benefit modeling and optimization for heat treatment, resistance, microstructure models, etc., for materials by using data from previous experimental and theoretical studies.116 ML methods use atoms as vectors for algorithms input, to design and predict materials properties with significant accuracy.117 ML techniques extract knowledge and insight from datasets and identify correlations and patterns. Data from both successful and failed experiments are used to train ML models and extract information, to further predict new properties of materials. These include prediction of crystalline structures, vibrational properties, transition temperatures, mechanical properties, band gaps, total energy, the enthalpy of formation, decomposition energies, etc. The ML approach was successfully used to discover the bandgap transition from indirect to direct and semiconductor to metal transition in silicon, by combining machine learning and ab initio calculations.118The most commonly applied ML approach in materials research is supervised learning that requires a good amount of quality data. Regression models like LASSO (least absolute shrinkage and selection operator), Gaussian process regression, support vector regression, artificial neural networks, and kernel ridge regression stimulate discovery of new materials with the desired structures and properties by utilizing established relationships between properties and input descriptors.19,119 For properties with defined categories, like crystal structure types and magnetic property type, classification learning methods are used. These include support vector machines, decision trees, random forests, and Bayesian inference. All ML methods can be used for both regression and classification learning for materials physics problems.12,120
The high-impact research areas in ML for materials science, which simultaneously represent remarkable opportunities for research, have been identified as: validation by experiment of physics-based simulations (useful in predicting new materials properties), ML approaches tailored for materials data and applications (regarding both small and big-scale materials problems, with immediate applicability in new materials design), high-throughput data acquisition capabilities (accelerating materials synthesis, characterization and simulation), ML that makes better scientists (relevant for progress in materials characterization), and integration of physics within ML, and ML with physics-based simulations (by developing desirable methods, reducing discrepancies between simulation and experiments, and linking physics-based models).121
In solid-state materials science, ML has led to numerous quantitative structure–property relationships, such as crystal graphs and chemical composition, building or pair-block polymers, band gap calculations, component and structure predictions, anticipation of materials properties (such as dielectric breakdown strength, glass transition temperature, thermal expansion coefficient, magnetocaloric effects, and interface energy).122
The potential of coupling approaches from materials science, modeling, and simulation with data mining and machine learning offers exciting perspectives for solving challenging problems, such as decoding and computational modeling of complex structure–process–property relationships, replacement of computationally demanding submodels in multiscale simulations, and classification and interpretation of imaging data.107
5. Materials Genome Initiative
The Materials Genome Initiative (MGI) is a US multi-agency initiative for creating resources and infrastructure to discover, manufacture, and deploy advanced materials.13,14 Advanced materials have applications in energy, security, and human development, and are crucial for national economy. The MGI realizes that these developments, if fostered, can lead to a rapid shift in the time required to find and boost new materials. Its purpose is to facilitate “discovery, development, manufacturing, and deployment of advanced materials at least twice as fast as possible today, at a fraction of the cost”.123It takes more than a decade to bring a new materials to market and commercial use.124,125 Accelerating the pace of discovery and deployment of advanced materials is the goal of the MGI, as it promotes the use of data generated through numerous mathematical modeling and statistical analysis studies. These data range from atomic coordinates and structural features to physical and other properties, and result during the development of numerous databases generated from the significant advancement of materials science. In the same way that the genome of a species or individual holds all the secrets of its existence and benefits mankind, decoding a materials genome will help in identifying every single aspect of microscopic buildup, leading to all its properties.126
The MGI stimulates use of data science for faster processes of discovery and storage of new materials information.127,128 As exemplified in Fig. 10, data sharing can significantly curtail the materials research phase by (i) lowering the problem of data collection for specific research groups and (ii) allowing more economical progress of scientific suppositions and property projection standards.127
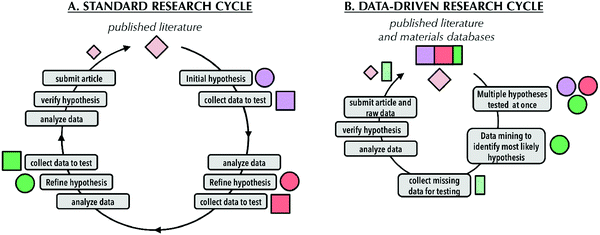 | ||
| Fig. 10 Representation to demonstrate differences between standard, single-group research (left) and new opportunities afforded by large materials databases (right) (Reproduced with permission from ref. 127). | ||
Promotion and funding for the MGI by the US government have led to the speed up of the process for new materials discovery everywhere.129 With the launch of the MGI, other organizations and worldwide committees, like The European Commission and the Psi-k Community, started investing in and promoting materials discovery through computational modeling.130,131 It fostered collaborations throughout Europe for developing computational methods for materials research among industrialists, theoreticians, and software developers.132
6. Conclusions and outlook
With the progress in high computational facilities, hardware, and new algorithms, innovation in materials science has significantly progressed in the last decade. Initially, computational methods dealt with single to fewer atoms and molecules to study their properties and interactions, but now simulate thousands of atoms with high throughput calculations and algorithms. Materials research has now shifted to data science. One of the first computational methods in materials science was density functional theory (DFT), followed by better simulation techniques for multiatomic systems. DFT determines the electronic density of a system and predicts the energy of the system. Other simulation and molecular dynamics methods allow exploration of the structure, space, and composition of systems more efficiently. Simulation and experimental studies generated a huge amount of data, bringing data science approaches to materials science. Large databases are rapidly developed for vast information storage so that they can be further analyzed and classified using big data analysis approaches. The current theoretical methods reveal the internal properties of materials without taking into consideration their actual environment. The development of ML approaches will allow the identification of better descriptors.Although various modeling and simulation tools are available, materials research still requires more advanced and efficient tools for screening millions of compositions of new materials with desirable properties to reduce the time and cost of production for individual compositions. Most of the available tools lack efficiency in dealing with materials properties at varying length and time scales. Further advances in computational capabilities, the development of novel algorithms, and the availability of data storage infrastructures present promising progress for new materials discovery and a reduced time to reach market. Materials modeling is now a key step in shortening the manufacturing time of advanced materials, further boosting the industrial and economic developments through innovation of new improved applications. It helps tailor and design new materials for various structures and systems. Nevertheless, most of these modeling and designing processes are computationally extensive and expensive, needing hours to weeks for the desired results. Hence improvement and upgrading are further necessary.
The developments of synthetic and composite materials will diversify advanced applications. Materials innovation is also critical for socio-economic development and big data and AI will accelerate the design, synthesis, and characterization of new materials. The huge amount of materials data from theoretical, in silico and experimental studies is stored and regularly analyzed. Further modeling and simulation of complex networks and systems will assist the prediction of materials for renewable energy and other applications. The multiscale, multi-physics modeling at several different scales and levels will encourage novel engineering applications. It is necessary to develop precise computational models for multiscale modeling and simulations, as well as new descriptors for multiscale problems in ML and more databases for materials properties. When produced, newly discovered materials will benefit from the internet of things, which enables empowered connection between manufacturers and machines, smarter business decision-making, and improved management of the global supply chain, but is not without its challenges in needs, security, standards, and human interfaces.120
Conflicts of interest
The authors declare that there is no conflict of interest.Acknowledgements
The authors gratefully acknowledge the financial support from the International Association of Advanced Materials.References
- M. Bonek, A. Śliwa and J. Mikuła, Computer simulation of the relationship between selected properties of laser remelted tool steel surface layer, Appl. Surf. Sci., 2016, 388(A), 174–179 CrossRef CAS.
- J.-C. Du and J. M. Rimsza, Atomistic computer simulations of water interactions and dissolution of inorganic glasses, npj Mater. Degrad., 2017, 1(1), 16 CrossRef.
- J. Zhao, L. Wu, C. Zhan, Q. Shao, Z. Guo and L. Zhang, Overview of polymer nanocomposites: Computer simulation understanding of physical properties, Polymer, 2017, 133, 272–287 CrossRef CAS.
- E. R. Homer, High-throughput simulations for insight into grain boundary structure-property relationships and other complex microstructural phenomena, Comput. Mater. Sci., 2019, 161, 244–254 CrossRef CAS.
- A. El-Azab, Why Materials Theory?, Mater. Theory, 2017, 1, 1 CrossRef.
- M. O. Steinhauser and S. Hiermaier, A Review of Computational Methods in Materials Science: Examples from Shock-Wave and Polymer Physics, Int. J. Mol. Sci., 2009, 10(12), 5135–5216 CrossRef CAS PubMed.
- A. V. Shymchenko, V. V. Tereshchenko, Y. A. Ryabov, S. V. Salkutsan and A. I. Borovkov, Review of the computational approaches to advanced materials simulation in accordance with modern advanced manufacturing trends, Mater. Phys. Mech., 2017, 32, 328–352 CAS.
- A. Mosavi, T. Rabczuk and A. Varkonyi-Koczy, Reviewing the Novel Machine Learning Tools for Materials Design. Recent Advances in Technology Research and Education, Springer Nature, 2017 Search PubMed.
- A. Ludwig, Discovery of new materials using combinatorial synthesis and high-throughput characterization of thin-film materials libraries combined with computational methods, npj Comput. Mater., 2019, 5, 70 CrossRef.
- T. S. Hofer and S. P. de Visser, Editorial: Quantum Mechanical/Molecular Mechanical Approaches for the Investigation of Chemical Systems – Recent Developments and Advanced Applications. Recent Developments and Advanced Applications, Front. Chem., 2018, 6, 357 CrossRef PubMed.
- J. K. Harada, N. Charles, K. R. Poeppelmeier and J. M. Rondinelli, Heteroanionic Materials by Design: Progress Toward Targeted Properties, Adv. Mater., 2019, 31, 1805295 CrossRef PubMed.
- Y. Liu, T. Zhao, W. Ju and S. Shi, Materials discovery and design using machine learning, J. Materiomics, 2017, 3(3), 159–177 CrossRef.
- J. J. de Pablo, B. Jones, C. L. Kovacs, V. Ozolins and A. P. Ramirez, The materials genome initiative, the interplay of experiment, theory and computation, Curr. Opin. Solid State Mater. Sci., 2014, 18, 99–117 CrossRef.
- J. J. de Pablo, N. E. Jackson, M. A. Webb, L.-Q. Chen, J. E. Moore, D. Morgan, R. Jacobs, T. Pollock, D. G. Schlom, E. S. Toberer, J. Analytis, I. Dabo, D. M. DeLongchamp, G. A. Fiete, G. M. Grason, G. Hautier, Y. Mo, K. Rajan, E. J. Reed, E. Rodriguez, V. Stevanovic, J. Suntivich, K. Thornton and J.-C. Zhao, New frontiers for the materials genome initiative, npj Comput. Mater., 2019, 5, 41 CrossRef.
- Y. Song, J. H. Dai and R. Yang, Application of First Principles Theory to the Design of Advanced Titanium Alloys, Adv. Eng. Mater. Model., 2016, 203–228 CAS.
- M. P. Johansson, V. R. I. Kaila and D. Sundholm, Ab Initio, Density Functional Theory, and Semi-Empirical Calculations, in Biomolecular Simulations. Methods in Molecular Biology (Methods and Protocols), ed. L. Monticelli, E Salonen, Humana Press, Totowa, NJ, 2013, vol 924, pp. 3–27 DOI:10.1007/978-1-62703-017-5_1.
- K. Xie, X. Li and T. Cao, Theory and Ab Initio Calculation of Optically Excited States—Recent Advances in 2D Materials, Adv. Mater., 2021,(33), 1904306 CrossRef CAS PubMed.
- P. Echenique and J. L. Alonso, A mathematical and computational review of Hartree–Fock SCF methods in quantum chemistry, Mol. Phys., 2007, 105(23–24), 3057–3098 CrossRef CAS.
- J. Schmidt, M. R. G. Marques, S. Botti and M. A. L. Marques, Recent advances and applications of machine learning in solid-state materials science, npj Comput. Mater., 2019, 5, 83 CrossRef.
- J. Neugebauer and T. Hickel, Density functional theory in materials science, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 438–448 CAS.
- J. Hafner, C. Wolverton and G. Ceder, Toward Computational Materials Design: The Impact of Density Functional Theory on Materials Research, MRS Bull., 2006,(31), 659–668 CrossRef.
- Y. Saito, The Monte Carlo simulation of microstructural evolution in metals, Mater. Sci. Eng., A, 1997, 223, 114–124 CrossRef.
- Y. Peng, S. Wang, Y. Zhang and Y. Gao, Simulation and Application of Molecular Dynamics in Materials Science, Adv. Mater. Res., 2012, 572, 232–236 Search PubMed.
- E. van der Giessen, et al., Roadmap on multiscale materials modeling, Modell. Simul. Mater. Sci. Eng., 2020, 28, 043001 CrossRef.
- L. Himanen, A. Geurts, A. S. Foster and P. Rinke, Data-Driven Materials Science: Status, Challenges, and Perspectives, Adv. Sci., 2019,(6), 1900808 CrossRef PubMed.
- X. Sha, et al., Artificial Intelligence to Power the Future of Materials Science and Engineering, Adv. Intell. Syst., 2020,(2), 1900143 CrossRef.
- B. L. DeCost, et al., Scientific AI in materials science: a path to a sustainable and scalable paradigm, Mach. Learn.: Sci. Technol., 2020, 1, 033001 Search PubMed.
- C.-J. Yu, Advances in modelling and simulation of halide perovskites for solar cell applications, J. Phys.: Energy, 2019, 1, 022001 CAS.
- A. O. Osikoya, O. Parlak, N. A. Murugan, E. D. Dikio, H. Moloto, L. Uzun, A. P. F. Turner and A. Tiwari, Acetylene-sourced CVD-synthesised catalytically active graphene for electrochemical biosensing. Acetylene-sourced CVD-synthesised catalytically active graphene for electrochemical biosensing, Biosens. Bioelectron., 2017, 89, 496–504 CrossRef CAS PubMed.
- M. Ashaduzzaman, et al., Studies on an on/off-switchable immunosensor for troponin T, Biosens. Bioelectron., 2015, 73, 100–107 CrossRef CAS PubMed.
- O. Parlak, et al., Programmable bioelectronics in a stimuli-encoded 3D graphene interface, Nanoscale, 2016, 8, 9976–9981 RSC.
- S. Zeng, et al., Computer Simulations on a pH-Responsive Anticancer Drug Delivery System Using Zwitterion-Grafted Polyamidoamine Dendrimer Unimolecular Micelles, Langmuir, 2021, 37(3), 1225–1234 CrossRef CAS PubMed.
- G. R. Schleder, A. C. M. Padilha, C. M. Acosta, M. Costa and A. Fazzio, From DFT to machine learning: recent approaches to materials science–a review, J. Phys.: Mater., 2019, 2(3), 032001 CAS.
- A. R. Oganov, C. J. Pickard, Q. Zhu and R. J. Needs, Structure prediction drives materials discovery, Nat. Rev. Mater., 2019, 4, 331–348 CrossRef.
- G. M. Odegard, T. S. Gates, L. M. Nicholson and K. E. Wise, Equivalent continuum modeling of nanostructured materials, Compos. Sci. Technol., 2002, 62, 1869–1880 CrossRef CAS.
- N. M. Ghoniemy, E. P. Busso, N. Kioussis and H. Huang, Multiscale modelling of nanomechanics and micromechanics: an overview, Philos. Mag., 2003, 83(31–34), 3475–3528 CrossRef.
- J. D. Lee, X. Wang and Y. Chen, Multiscale Computation for Nano/Micromaterials, J. Eng. Mech., 2009, 135(3), 192–202 CrossRef.
- K. Yang, C. Oses and S. Curtarolo, Modeling Off-Stoichiometry Materials with a High-Throughput Ab-Initio Approach, Chem. Mater., 2016, 28(18), 6484–6492 CrossRef CAS.
- J. Wang, Y. Ueda, H. Murakawa, M. G. Yuan and H. Q. Yang, Improvement in numerical accuracy and stability of 3-D FEM analysis in welding, Weld. J., 1996, 129–134 Search PubMed.
- P. Patra, V. S. Seesala, S. R. Soni, R. K. Roy, S. Dhara, A. Ghosh, N. Patra and S. Pal, Biopolymeric pH-responsive fluorescent gel for in vitro and in vivo colon specific delivery of metronidazole and ciprofloxacin, Eur. Polym. J., 2019, 114, 255–264 CrossRef CAS.
- R. A. Friesner, Ab initio quantum chemistry: Methodology and applications, Proc. Natl. Acad. Sci. U. S. A., 2005, 102(19), 6648–6653 CrossRef CAS PubMed.
- G. Tirimbò and B. Baumeier, Ab initio modeling of excitons: from perfect crystals to biomaterials, Adv. Phys.: X, 2021, 6, 1, DOI:10.1080/23746149.2021.1912638.
- E. H. Lieb, Density functionals for coulomb systems, Int. J. Quantum Chem., 1983, 24, 243–277, DOI:10.1002/qua.560240302.
- A. Zhou, A mathematical aspect of Hohenberg-Kohn theorem, Sci. China Math., 2019, 62, 63–68 CrossRef.
- S. Nasiri, et al., Treating the motion of nuclei and electrons in atomic and molecular quantum mechanical calculations on an equal footing: Non-Born–Oppenheimer quantum chemistry, Adv. Quantum Chem., 2020, 81, 143–166 CrossRef CAS.
- H. G. Hiscock and A. J. W. Thom, Holomorphic Hartree−Fock Theory and Configuration Interaction, J. Chem. Theory Comput., 2014, 10, 4795–4800 CrossRef CAS PubMed.
- A. D. Putri, B. Tri Murti, S. Kanchi, M. I. Sabela, K. Bisetty, A. Tiwari, Inamuddin and A. M. Asiri, Computational studies on the molecular insights of aptamer induced poly(N-isopropylacrylamide)-graft-graphene oxide for on/off- switchable whole-cell cancer diagnostics, Sci. Rep., 2019, 9, 7873 CrossRef PubMed.
- J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, Materials Design and Discovery with High-Throughput Density Functional Theory: The Open Quantum Materials Database (OQMD), JOM, 2013, 65(11), 1501–1509 CrossRef CAS.
- A. Jain, Y. Shin and K. A. Persson, Computational predictions of energy materials using density functional theory, Nat. Rev. Mater., 2016, 1, 15004 CrossRef CAS.
- X. Wu, F. Kang, W. Duan and J. Li, Density functional theory calculations: A powerful tool to simulate and design high-performance energy storage and conversion materials, Prog. Nat. Sci.: Mater. Int., 2019, 29(3), 247–255 CrossRef CAS.
- J. Greeley, T. F. Jaramillo, J. Bonde, I. B. Chorkendorff and J. K. Nørskov, Computational high-throughput screening of electrocatalytic materials for hydrogen evolution, Nat. Mater., 2006, 5, 909–913 CrossRef CAS PubMed.
- C. Wolverton, D. J. Siegel, A. R. Akbarzadeh and V. Ozolins, Discovery of novel hydrogen storage materials: an atomic scale computational approach, J. Phys.: Condens. Matter, 2008, 20, 064228 CrossRef CAS PubMed.
- A. Hospital, J.-R. Goñi, M. Orozco and J.-L. Gelpí, Molecular dynamics simulations: advances and applications, Adv. Appl. Bioinf. Chem., 2015, 8, 37–47 Search PubMed.
- K. Choudhary, et al., High-throughput Identification and Characterization of Two-dimensional Materials using Density functional theory, Sci. Rep., 2017, 7, 5179, DOI:10.1038/s41598-017-05402-0.
- W. Thiel, Semiempirical Methods, Modern Methods and Algorithms of Quantum Chemistry, Proceedings, NIC Series, ed. J. Grotendorst, John von Neumann Institute for Computing, Julich, 2nd edn, 2000, vol. 3, pp. 261–283, ISBN 3-00-005834-6 Search PubMed.
- M. O. Steinhauser, Multiscale Computational Materials Science, in Computational Multiscale Modeling of Fluids and Solids, Springer, Berlin, Heidelberg, 2017 Search PubMed.
- J. Meller, Molecular Dynamics, Encyclopedia of life science, Nature Publishing Group, 2001 Search PubMed.
- M. C. Zwier and L. T. Chong, Reaching biological timescales with all-atom molecular dynamics simulations, Curr. Opin. Pharmacol., 2010, 10(6), 745–752 CrossRef CAS PubMed.
- C. J. Roy, Review of code and simulation verification procedures for computational simulation, J. Comput. Phys., 2005, 205, 131–156 CrossRef.
- M. Murugesan and D. W. Jung, Johnson Cook Material and Failure Model Parameters Estimation of AISI-1045 Medium Carbon Steel for Metal Forming Applications, Materials, 2019, 12(4), 609 CrossRef CAS PubMed.
- J. C. Osorio-Pinzon, S. Abolghasem and J. P. Casas-Rodriguez, Predicting the Johnson Cook constitutive model constants using temperature rise distribution in plane strain machining, Int. J. Adv. Manuf. Technol., 2019, 1–16 Search PubMed.
- M. O. Robbins and M. H. Müser Johannes, Computer Simulations of Friction, Lubrication, and Wear, CRC Press LLC, 2001 Search PubMed.
- I. Montava, R. Irles, J. Segura, J. M. Gadea and E. Juliá, Numerical Simulation of Steel Reinforced Concrete (SRC) Joints, Metals, 2019, 9(2), 131 CrossRef CAS.
- J. Sliseris, L. Yan and B. Kasal, Numerical Simulation and Experimental Verification of Hollow and Foam-Filled Flax-Fabric-Reinforced Epoxy Tubular Energy Absorbers Subjected to Crashing, Mech. Compos. Mater., 2017, 53(4), 487–496 CrossRef.
- M. Guida, F. Marulo and S. Abrate, Advances in crash dynamics for aircraft safety, Prog. Aerosp. Sci., 2018, 98, 106–123 CrossRef.
- T. M. Dieb, S. Ju, K. Yoshizoe, Z. Hou, J. Shiomi and K. Tsuda, MDTS: automatic complex materials design using Monte Carlo tree search, Sci. Technol. Adv. Mater., 2017, 18(1), 498–503 CrossRef PubMed.
- K. Binder, Atomistic modeling of materials properties by Monte Carlo Simulation, Adv. Mater., 1992, 4(9), 540–547 CrossRef CAS.
- S. A. Adcock and J. A. McCammon, Molecular Dynamics: Survey of Methods for Simulating the Activity of Proteins, Chem. Rev., 2006, 106(5), 1589–1615 CrossRef CAS PubMed.
- K. V. Zakharchenko, J. H. Los, M. I. Katsnelson and A. Fasolino, Atomistic simulations of structural and thermodynamic properties of bilayer graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 235439 CrossRef.
- Y. Nie, Z. Gu, Q. Zhou, Y. Wei, T. Hao, Y. Liu, R. Liu and Z. Zhou, Controllability of Polymer Crystal Orientation Using Heterogeneous Nucleation of Deformed Polymer Loops Grafted on Two-Dimensional Nanofiller, J. Phys. Chem. B, 2017, 121(27), 6685–6690 CrossRef CAS PubMed.
- Y. Nie, R. Zhang, K. Zheng and Z. Zhou, Nucleation details of nanohybrid shish-kebabs in polymer solutions studied by molecular simulations, Polymer, 2015, 76, 1–7 CrossRef CAS.
- Z.-Z. Gu, R. Yang, J. Yang, X.-Y. Qiu, R.-J. Liu, Y. Liu, Z. Zhou and Y. Nie, Dynamic Monte Carlo simulations of effects of nanoparticle on polymer crystallization in polymer solutions, Comput. Mater. Sci., 2018, 147, 217–226 CrossRef CAS.
- G. J. Wagner and W. K. Liu, Coupling of atomistic and continuum simulations using a bridging scale decomposition, J. Comput. Phys., 2003, 190, 249–274 CrossRef.
- J. Kolorenč and L. Mitas, Applications of Quantum Monte Carlo Methods in Condensed Systems, Rep. Prog. Phys., 2001, 74, 026502 CrossRef.
- M. A. Van de Walle and, Self-driven lattice-model Monte Carlo simulations of alloy thermodynamic properties and phase diagrams, Modell. Simul. Mater. Sci. Eng., 2002, 10, 521–538 CrossRef.
- K. Vanommeslaeghe, O. Guvench and A. D. J. MacKerell, Molecular Mechanics, Curr. Pharm. Des., 2014, 20(20), 3281–3292 CrossRef CAS PubMed.
- X. Zhang, Y. Zhao and G. Lu, Recent development in quantum mechanics/molecular mechanics modeling for materials, Int. J. Multiscale Comput. Eng., 2012, 10(1), 65–82 CAS.
- A. Genoese, A. Genoese, N. L. Rizzi and G. Salerno, Buckling Analysis of Single-Layer Graphene Sheets Using Molecular Mechanics, Front. Mater., 2019, 6, 26 CrossRef.
- S. P. Timoshenko and J. M. Gere, Theory of Elastic Stability, McGraw-Hill, New York, NY, 1963 Search PubMed.
- T. Chang and H. Gao, Size-dependent elastic properties of a single-walled carbon nanotube via a molecular mechanics model, J. Mech. Phys. Solids, 2003, 51(6), 1059–1074 CrossRef CAS.
- R. Rafiee and R. M. Moghadam, On the modeling of carbon nanotubes: a critical review, Composites, Part B, 2014, 56, 435–449 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graphics, 1996, 14(1), 33–38 CrossRef CAS PubMed.
- C. Massobrio and P. Blandin, Classical and First Principles Molecular Dynamics Simulations in Material Science: Application to Structural and Dynamical Properties of Free and Supported Clusters, in Stability of Materials. NATO ASI Series (B: Physics), ed. A. Gonis, P. E. A. Turchi and J. Kudrnovský, Springer, Boston, MA, 1996, p. 355 Search PubMed.
- A. Torchi, D. Bochicchio and G. M. Pavan, How the Dynamics of a Supramolecular Polymer Determines Its Dynamic Adaptivity and Stimuli-Responsiveness: Structure–Dynamics–Property Relationships from Coarse-Grained Simulations, J. Phys. Chem. B, 2018, 122(14), 4169–4178 CrossRef CAS PubMed.
- M. Bauchy, Deciphering the atomic genome of glasses by topological constraint theory and molecular dynamics: A review, Comput. Mater. Sci., 2019, 159, 95–102 CrossRef CAS.
- M. Ashaduzzaman, S. R. Deshpande, N. A. Murugan, Y. K. Mishra, A. P. F. Turner and A. Tiwari, On/off-switchable LSPR nano- immunoassay for troponin-T, Sci. Rep., 2017, 7, 44027 CrossRef CAS PubMed.
- J. Liang, R. Tcygana and T. Malam, Molecular dynamics simulation of the structure and properties of lithium phosphate glasses, J. Non-Cryst. Solids, 2000, 263 & 264, 167–179 Search PubMed.
- V. Yamakov, D. Wolf, S. R. Phillpot, A. K. Mukherjee and H. Gleiter, Dislocation processes in the deformation of nanocrystalline aluminium by molecular-dynamics simulation, Nat. Mater., 2002, 1, 45–49 CrossRef CAS PubMed.
- V. A. Bershtein, L. M. Egorova, P. N. Yakushev, P. Pissis, P. Sysel and L. Brozova, Molecular dynamics in nanostructured polyimide–silica hybrid materials and their thermal stability, J. Polym. Sci., Part B: Polym. Phys., 2002, 40(10), 1056–1069 CrossRef CAS.
- J. Du, L. Kokou, J. L. Rygel, Y. Chen, C. G. Pantano, R. Woodman and J. Belcher, Structure of Cerium Phosphate Glasses: Molecular Dynamics Simulation, J. Am. Ceram. Soc., 2011, 94(8), 2393–2401 CrossRef CAS.
- M. Montorsi, G. Broglia and C. Mugoni, Structural Insight into Transition Metal Oxide Containing Glasses by Molecular Dynamic Simulations, in Molecular Dynamics Simulations of Disordered Materials. Springer Series in Materials Science, ed. C. Massobrio, J. Du, M. Bernasconi and P. Salmon, Springer, Cham, 2015, p. 215 Search PubMed.
- L. Vitos, Computational quantum mechanics for materials engineers: the EMTO method and applications, Engineering Materials and Processes, Springer-Verlag London, Limited, 2007, ISBN-13: 9781846289507 Search PubMed.
- T. Belytschko, R. Gracie and G. Ventura, A review of extended/generalized finite element methods for material modeling, Modell. Simul. Mater. Sci. Eng., 2009, 17, 043001 CrossRef.
- T. Belytschko, W. Liu and B. Moran, Nonlinear Finite Elements for Continua and Structures, John Wiley & Sons, 2001 Search PubMed.
- R. D. Cook, D. S. Malkus and M. E. Plesha, Concepts and Applications of Finite Element Analysis, John Wiley & Sons, 1989 Search PubMed.
- S. P. Xiao and T. Belytschko, A bridging domain method for coupling continua with molecular dynamics, Comput. Methods Appl. Mech. Eng., 2004, 193, 1645–1669 CrossRef.
- F. Roters, P. Eisenlohr, T. R. Bieler and D. Raabe, Crystal Plasticity Finite Element Methods in Materials Science and Engineering, WILEY-VCH Verlag GmbH & Co. KGaA Weinheim, 2010, ISBN 978-3-527-32447-7 Search PubMed.
- O. Oluwole, Finite Element Modeling for Materials Engineers Using MATLAB, Springer London Dordrecht HeidelbergNew York, 2011, ISBN 978-0-85729-660-3 Search PubMed.
- J. Hohe, H. Paul and C. Beckmann, A probabilistic elasticity model for long fiber reinforced thermoplastics with uncertain microstructure, Mech. Mater., 2018, 122, 118–132 CrossRef.
- F. Gottschalk, R. W. Scholza and B. Nowack, Probabilistic material flow modeling for assessing the environmental exposure to compounds: Methodology and an application to engineered nano-TiO2 particles, Environ. Model. Softw., 2010, 25(3), 320–332 CrossRef.
- F. F. Abraham, J. Q. Broughton, N. Bernstein and E. Kaxiras, Spanning the continuum to quantum length scales in a dynamic simulation of brittle fracture, Europhys. Lett., 1998, 44, 783–787 CrossRef CAS.
- E. B. Tadmor, M. Ortiz and R. Phillips, Quasicontinuum analysis of defects in solids, Philos. Mag. A, 1996, 73, 1529–1563 Search PubMed.
- R. E. Rudd and J. Q. Broughton, Coarse-grained molecular dynamics and the atomic limit of finite elements, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, R5893–R5896 CrossRef CAS.
- H. S. Park and W. K. Liu, An introduction and tutorial on multiple-scale analysis in solids, Comput. Methods Appl. Mech. Eng., 193, 1733–1772 CrossRef.
- S. Nikolov, M. Petrov, L. Lymperakis, M. Friák, C. Sachs, H.-O. Fabritius, D. Raabe and J. Neugebauer, Revealing the Design Principles of High-Performance Biological Composites Using Ab initio and Multiscale Simulations: The Example of Lobster Cuticle, Adv. Mater., 2010, 22, 519–526, DOI:10.1002/adma.200902019.
- S. R. Kalidindi and M. De Graef, Materials Data Science: Current Status and Future Outlook, Annu. Rev. Mater. Res., 2015, 45, 171–193 CrossRef CAS.
- N. Huber, S. R. Kalidindi, B. Klusemann and C. J. Cyron, Editorial: Machine Learning and Data Mining in Materials Science, Front. Mater., 2020, 7, 51, DOI:10.3389/fmats.2020.00051.
- Dealing with data, Nat. Mater., 2017, 16, 1 DOI:10.1038/nmat4841.
- K. Rajan, Materials Informatics: The Materials “Gene” and Big Data, Annu. Rev. Mater. Res., 2015, 45, 153–169 CrossRef CAS.
- S. Leonelli, Scientific Research and Big Data, The Stanford Encyclopedia of Philosophy, ed. E. N. Zalta, Summer 2020 edn, May 29, 2020, https://plato.stanford.edu/archives/sum2020/entries/science-big-data/ Search PubMed.
- Y. Chaowei, H. Qunying, L. Zhenlong, L. Kai and H. Fei, Big Data and cloud computing: innovation opportunities and challenges, Int. J. Digit. Earth, 2017, 10(1), 13–53, DOI:10.1080/17538947.2016.1239771.
- R. K. Vasudevan, K. Choudhary and A. Mehta, et al., Materials Science in the AI age: high-throughput library generation, machine learning and a pathway from correlations to the underpinning physics, MRS Commun., 2020, 9(3) DOI:10.1557/mrc.2019.95.
- Y. Xu, et al., Artificial intelligence: A powerful paradigm for scientific research, The Innovation, 2021, 2, 100179 CrossRef PubMed.
- J. Kimmig, S. Zechel and U. S. Schubert, Digital Transformation in Materials Science: A Paradigm Change in Material's Development, Adv. Mater., 2021, 33, 2004940, DOI:10.1002/adma.202004940.
- B. Kailkhura, B. Gallagher and S. Kim, et al., Reliable and explainable machine-learning methods for accelerated material discovery, npj Comput. Mater., 2019, 5, 108, DOI:10.1038/s41524-019-0248-2.
- A. Suzuki, C. Shen and N. C. Kumar, Application of computational tools in alloy design, MRS Bull., 2019, 44, 247–251, DOI:10.1557/mrs.2019.70.
- Q. Zhou, P. Tang, S. Liu, J. Pan, Q. Yan and S.-C. Zhang, Learning atoms for materials discovery, Proc. Natl. Acad. Sci. U. S. A., 2018, 115(28), E6411–E6417 CrossRef CAS PubMed.
- Z. Shi, E. Tsymbalov, M. Dao, S. Suresh, A. Shapeev and J. Li, Deep elastic strain engineering of bandgap through machine learning, Proc. Natl. Acad. Sci. U. S. A., 2018, 116(10), 4117–4122 CrossRef PubMed.
- X. Li, et al., A Comparative Assessment of Six Machine Learning Models for Prediction of Bending Force in Hot Strip Rolling Process, Metals, 2020, 10, 685, DOI:10.3390/met10050685.
- S. Chibani and F. X. Coudert, Machine learning approaches for the prediction of materials properties, APL Mater., 2020, 8, 080701, DOI:10.1063/5.0018384.
- B. Meredig, Editorial: Five High-Impact Research Areas in Machine Learning for Materials Science, Chem. Mater., 2019, 31, 9579–9581 CrossRef CAS.
- D. Packwood, et al., Machine Learning in Materials Chemistry: An Invitation, Mach. Learn. Appl., 2022, 8, 100265 Search PubMed.
- A. White, The materials genome initiative: One year on, MRS Bull., 2012, 37, 715–716 CrossRef.
- J. F. Rodrigues, L. Florea and M. C. F. de Oliveira, et al., Big data and machine learning for materials science, Discovery Mater., 2021, 1, 12, DOI:10.1007/s43939-021-00012-0.
- A. Tiwari, Advanced Materials Research and Innovation Priorities for Accomplishing the Sustainable Development Goals, Adv. Mater. Lett., 2021, 12, 1–6, DOI:10.5185/amlett.2021.061633.
- S. A. M. Tofail, Additive manufacturing: scientific and technological challenges, market uptake and opportunities, Mater. Today, 2018, 21, 22–37 CrossRef.
- A. Jain, et al., Research Update: The materials genome initiative: Data sharing and the impact of collaborative ab initio databases, APL Mater., 2016, 4, 053102, DOI:10.1063/1.4944683.
- A. A. Ashley, Big data are shaping the future of materials science, MRS Bull., 2013, 38, 594–595 CrossRef.
- S. A. Schlueter, Designing materials and devices to revolutionize and engineer the future of electronics and photonics through computationally led and data-driven approaches. Proceedings Volume 10639, Micro- and Nanotechnology Sensors, Systems, and Applications X; 106390B (2018) DOI:10.1117/12.2305496.
- Boosting materials modelling, Nat. Mater., 2016, 15, 365 DOI:10.1038/nmat4619.
- A. Agrawal and A. Choudhary, Perspective: Materials informatics and big data: Realization of the “fourth paradigm” of science in materials science, APL Mater., 2016, 4(5), 053208 CrossRef.
- A. Tiwari, Priority of Materials Research for Reaching Climate Neutrality Goals, Adv. Mater. Lett., 2022, 13, 22011683, DOI:10.5185/amlett.2022.011683.
| This journal is © The Royal Society of Chemistry 2022 |

