Accurate location of hydrogen atoms in hydrogen bonds of tizoxanide from the combination of experimental and theoretical models

Abstract

To obtain detailed information about the position of hydrogen atoms in hydrogen bonds, HBs, of crystalline organic molecular compounds is not an easy task. In this work we propose a combination of ssNMR experimental data with theoretical procedures to get such information. Furthermore, the combination of experimental and theoretical models provides us with well-defined grounds to analyse the strength of π-stacking interactions between layers of hydrogen bonded molecules. Two different theoretical models were considered, both approaches being quite different. The first one is a solid-state model, so that the periodicity of a crystalline system underlies calculations of the electronic energy, the electronic density and NMR parameters. The other one is a molecular model in which molecules are taken as isolated monomers, dimers and tetramers. These two models were applied to the tizoxanide, TIZ, molecular crystal though it can widely be applied to any other molecular crystal. By the application of the quantum molecular model it was possible to learn about the way the intermolecular HBs affect the position of hydrogen atoms that belong to HBs in TIZ. This molecule has two intermolecular HBs that stabilize the structure of a basic dimer, but it also has an intramolecular HB in each monomer whose position should be optimized together with the other ones. We found that by doing this it is possible to obtain reliable results of calculations of NMR spectroscopic parameters. Working with the solid-state model we found that any local variation of the TIZ crystalline structure is correlated with the variation of the values of the NMR parameters of each nucleus. The excellent agreement between experimental and calculated chemical shifts leads to the conclusion that the N₁₀–H₁₀ bond distance should be (1.00 ± 0.02) Å.

---

1 Introduction

Hydrogen bonding is one of the key intra- and intermolecular interactions, that are much exploited in crystal engineering, being the determination of the position of hydrogen atoms essential in structural studies in different areas of research.^1,2 This is relevant since most of the interactions in the solid-state structure of a drug are transmitted through hydrogen bonds. Therefore, having the certainty of the position of a given hydrogen atom allows for knowing about the existence of intra- or intermolecular hydrogen bonds, HBs.^3,4

Hydrogen bonds have been long studied by nuclear magnetic resonance (NMR) and other spectroscopic and crystallographic techniques.^5–9 Quite recently some articles were published with their focus on the application of infrared (IR), ultraviolet (UV) and Raman spectroscopy, and quantum chemical calculations to studying HBs in crystalline systems.^10–13 Besides, several studies that were performed in solution showing how the chemical shift of an NMR signal varies when this corresponds to atoms that belong to HBs in comparison to the signals arising from equivalent atoms that do not belong to HBs.^14–16 In the special case of the gas phase it was shown, by using theoretical models, that NMR spectroscopic parameters are powerful descriptors for characterizing HBs.^17–23

There are some other recent studies, like the NMR of various nuclei in solid-state, both 1D and 2D that were focused to detect the presence of HBs and identifying the underlying motifs of the bonding using as input data the inter nuclear distances.^3,4,24–28 By itself this methodology did not allow for to find the accurate position of the hydrogen atoms; though, when in addition to this studies the crystalline structure is included by using X-ray diffraction (XRD), a better spatial location for protons can be estimated. Within this line of research, one step forward was achieved when experimental techniques together with theoretical methods were applied.^1,2,29–32 These last procedures allows for the refinement of the geometrical structure of the substances under study and so, the prediction of structures in those cases where one is not able to obtain the complete information of atomic positions from crystallographic data.

The issue of proton location in crystals is a problem intrinsically related to finding the local structure, which has been recently studied applying solid-state Nuclear Magnetic Resonance spectroscopy (ssNMR) in several cocrystals.^3,4,26,28,33 Due to the sensitivity of ssNMR at the sites close to the hydrogen being studied, it is common to use a combination of ¹H and ¹⁵N ssNMR to tackle that problem. The ¹H chemical shifts of hydrogen-bonded protons span a wide range of shifts, typically 8–20 ppm,²⁷ and the magnitude of the shifts is related to the extent of the HB which is an indication of the strength of the interaction.³⁴ It has been shown that the largest hydrogen chemical shifts for the OH⋯O, OH⋯N, and NH⋯O hydrogen bonds arises when the following two restrictions are fulfilled: there is a short distance of the donor–acceptor bond and the hydrogen is in a symmetric and central position.³⁵ The two hydrogen bonds, OH⋯N and NH⋯O, are a common and robust intermolecular interaction in cocrystal synthons,³⁶ so that the NMR of ¹⁵N nuclei can be used as descriptors of the position of hydrogens.

This work is focused on the NMR characterization of the structure of tizoxanide (TIZ), which is an anti-infective agent that can enhance current therapies for leishmaniasis, Chagas disease, and viral hepatitis. In a previous work some of us have studied and characterized this compound using different experimental techniques.³⁷ In particular ssNMR experiments for ¹³C were performed. It was found that the structure of solid-state TIZ is composed of tightly packed layers of extensively hydrogen-bonded molecules. Its “graphitic” structure is composed of layers of hydrogen-bonded molecules that are stacked one on top of the other and held together by strong π-stacking interactions.

To go one step further in the characterization of that structure, we decided to develop a strategy for getting the accurate position of hydrogen atoms in the HBs of TIZ. As mentioned in ref. 37 those HBs together with π-stacking interactions seem to explain the way TIZ molecules are distributed in packed layers. Then, it shall be necessary to run high-resolution ¹³C, ¹⁵N, and ¹H ssNMR experiments together with state of the art theoretical calculations to unequivocally locate the atoms of hydrogen and determine their bond lengths.³⁰ We developed a mixed methodology that is in line with previous works, but now our theoretical models are also molecular models because we assume that NMR spectroscopic parameters of hydrogen atoms in HBs, and the atoms in its vicinity, are can reliably be reproduced by theoretical methods that include most of the local electronic and stereospecific effects. This criterium is different to the used in the fully periodic Gauge Including Projector Augmented Wave method (GIPAW)^38,39 which considers as one of its main assumptions the repetition inherent to crystalline structures.²⁹

One of the aims pursued in this work is the application of both, experimental ssNMR spectroscopy and theoretical models to get, as accurate as possible, the position of a hydrogen atom in the intramolecular NH⋯O bond of TIZ compounds. We propose here two different theoretical approaches, coined as solid-state model and molecular model, which give quite close results to each other. In addition to that, the molecular model permits us to establish how important are the stacking effects and few other relevant electronic effects on the results of theoretical calculations of both, the geometric parameters and NMR spectroscopic parameters.

2 Experimental, theoretical models and computational details

2.1 Experimental ssNMR measurements

High-resolution solid-state ¹³C and ¹⁵N cross-polarization/magic angle spinning (CP/MAS) spectra for TIZ were recorded using a Bruker Avance II-300 spectrometer (300.13 MHz for ¹H, 75.46 MHz for ¹³C, and 30.4 MHz for ¹⁵N) equipped with a 4 mm probe. The ¹³C experiments were carried out at a spinning rate of 8 kHz employing a variable amplitude CP (2 ms contact time).⁴⁰ TPPM sequence was used for heteronuclear decoupling during acquisition with a proton field B_1H satisfying ω_1H/2π = γ_HB_1H = 50 kHz.⁴¹ The recycling time was 20 s and 2048 scans were recorded. Chemical shifts were referenced to tetramethylsilane (TMS) using adamantane as an external reference (29.50 and 38.56 ppm).

¹⁵N ssNMR experiments were carried out at a rotation speed of 10 kHz. The recycling delay between transients was 50 s, the contact time during CP was 2 ms and 4096 scans were recorded. The chemical shifts were referenced to nitromethane using as external reference the chemical shift of glycine (−349.6 ppm). Solid-state ¹H MAS NMR experiments were performed on a Bruker Avance III HD spectrometer at a ¹H Larmor frequency of 499.7 MHz, at 60 kHz MAS rate using a double-resonance MAS probe supporting rotors of 1.3 mm outer diameter.

2.2 Theoretical models

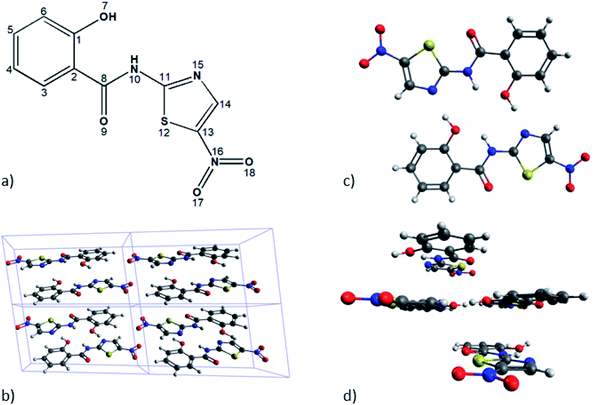
To find out the best estimate of the position of the hydrogen atoms of interest (numbered H₁₀ in Fig. 1) we used two different schemes, meaning the solid-state-based model and the molecular based model. The first one has the periodicity of the unit cell as its essential constraint, while the other one seeks to carry out accurate calculations considering only a reduced number of monomers.

Fig. 1 Different schemes for tizoxanide molecular structure. (a) Atoms labelling. (b) Unit cell used for solid-state model calculations. (c) Dimer structure of tizoxanide with intra and intermolecular hydrogen bonds explicitly shown. (d) Tetramer structure used in the molecular model.

2.2.1 Solid-state based models. Under normal conditions TIZ is a crystalline solid whose structure has been previously well described by the solid-state NMR spectroscopy. The goal pursued with the solid-state based model is to find which are the positions of some atoms in the crystal that best reproduce the NMR spectra. In order to do it the distance d(N₁₀–H₁₀) is systematically varied around its relaxed value and then, for each of those values the NMR spectroscopic parameters are calculated.

2.2.2 Quantum-molecular based models. In our specific molecular model we considered that replacing the TIZ structure by a monomer, dimer or tetramer (which includes two crystal cells) we shall be able to adequately reproduce the experimental NMR spectra.

By applying this model we searched for the answer to the following inquiries: (a) how important and feasible of using are the state of the art theoretical models to reproduce few sensitive geometrical aspects of TIZ molecules, together with its NMR spectroscopic parameters? and (b) how important is to describe, as accurately as possible both, the intramolecular and intermolecular HBs involved in the solid-state structure of TIZ, from the modeling of it as a monomer, dimer and tetramer? Furthermore, the analysis of tetrameric structures would permit us to find out how large the influence of the stacking would be over the spatial position of hydrogen atoms mentioned above, and also on their magnetic shieldings. Our model A was designed to answer the first inquire, and model B to answer the second one.

The model A does consist in the geometrical optimization of the whole molecular structure of a monomer or dimer of TIZ. Unfortunately we have been unable to optimize a tetrameric structure. In the case of model B only the positions of few hydrogen atoms were optimized for the monomeric, dimeric, and tetrameric structures, leaving the position of all other atoms as they were taken from experiments. The optimization's procedure mentioned as 2H is such that only the positions of the hydrogen atoms attached to N₁₀ (it belongs to an intramolecular HB) were optimized in the dimeric or tetrameric structures. On the other hand, the optimization mentioned as 4H is such that, in addition to the optimization 2H, the positions of the hydrogen atoms bonded to the oxygen O₇ (involved in the intermolecular HB between the monomers) were also optimized. Furthermore we should mention that, one of the key aspects that we pursued to include in our theoretical molecular model was the estimation of local effects of π-stacking interactions on NMR shieldings of hydrogen atoms that belong to HBs. To describe such effects we assumed that it would be enough to include only one monomer up and another one down of those HBs.

In both models mentioned above, the NMR nuclear magnetic shielding constants were calculated at the DFT/X (X = B3LYP, PBE, PBE0, KT3, and B97D) level of theory.

2.3 Computational details

First-principles calculations of the solid-state model were performed using the Quantum Espresso (QE) package,⁴² with the generalized gradient approximation (GGA) and Perdew–Burke–Ernzerhof (PBE) exchange–correlation functionals.⁴³ As known QE uses a plane-wave basis set for energy and geometry calculations. To ensure the convergence of the energy we used a cut-off energy of 60 Ry (816 eV) and a Monkhorst–Pack grid with a 5 × 5 × 5 convergence mesh offset by 0.5 for the k-points sampling in the Brillouin zone.

The positions of hydrogen atoms were relaxed using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm and the total forces acting on each ion were minimized to reach less than 1 × 10⁻² au. Furthermore, the geometry optimization of molecular models were performed using B3LYP^44,45 and B97D⁴⁶ DFT functionals, as are implemented in DALTON 2016 code.⁴⁷

In the case of the solid-state model, the information needed to calculate the NMR observables was reconstructed using the GIPAW method as implemented in the GIPAW module of QE. The chemical shift was obtained using the standard expression: δ = σ_ref − σ_iso and the shielding of the reference compounds are given as ESI.† On the other hand, for our molecular models, NMR shielding constants were calculated using different DFT functionals: B3LYP, KT3,⁴⁸ PBE, and PBE0 (ref. 49) as implemented in the DALTON code and employing both, gauge-including atomic orbitals, GIAO, and London orbitals to guarantee the origin-independence of the results. The basis set used to perform geometry optimizations were the Pople-type 6-311G++g(d,p)⁵⁰ and the correlated-consisted cc-pVTZ;⁵¹ besides, to calculate the NMR nuclear magnetic shielding constants we used the cc-pVTZ.

3 Results and discussion

We shall show and discuss our results in three different subsections, starting with the experiments of ssNMR and then going to our experimental and molecular models.

3.1 Solid-state NMR experiments

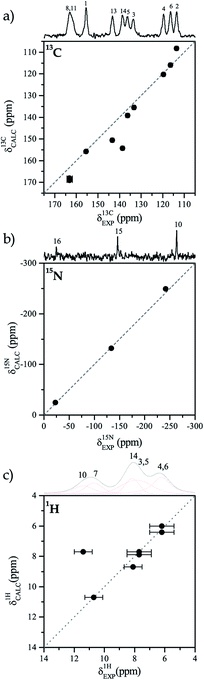
When it is compared with the ¹³C spectrum in solution the ssNMR spectrum of ¹³C shows noticeable changes for the chemical shift of the carbon atoms that are close to the molecular fragment of interest.³⁷ The ¹⁵N CP/MAS ssNMR spectrum of TIZ displays one signal for each nitrogen atom of the molecule; in our case, the signals were assigned considering the local environment of each N. The ¹H spectrum shows three main resonances, which can be deconvoluted to obtain the chemical shifts of the different protons in the molecule. The ssNMR spectrums are available in the ESI (Fig. S1†).

3.2 Solid-state NMR model

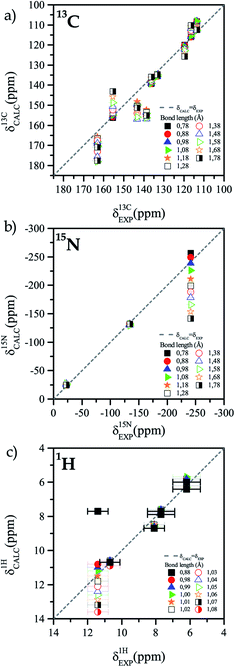
The difference between the ¹³C NMR spectrum of solid-state and that of solution can be associated to the presence or absence of an intramolecular HB. Thus, it is important to characterize the HB and find the accurate position of the hydrogen atom in that bond.

The first step in that characterization consists of the comparison between calculated and experimental NMR chemical shifts of the TIZ structure when the position of all hydrogen atoms are relaxed. In general, for the solid-state model, the calculated chemical shifts are in good agreement with the experimental results for the three studied nuclei, as can be seen in Fig. 2. In the case of ¹³C chemical shifts (see Fig. 2a) dispersion around the δ_EXP = δ_CALC line is observed, while for ¹⁵N chemical shifts (see Fig. 2b), only the N₁₀ chemical shift is out of the δ_EXP = δ_CALC line. Calculated results for ¹H are in very good agreement with the experimental values for all protons of TIZ except for the proton involved in the N₁₀–H₁₀ bond, as can be seen in Fig. 2c. For different nuclei the root mean square (RMS) was calculated. The RMS of ¹³C was 2.9 ppm, 2.0 ppm for ¹⁵N and 0.4 ppm for ¹H.

Fig. 2 Comparison of experimental and calculated chemical shift with different N₁₀–H₁₀ bond length. (a) ¹³C, (b) ¹⁵N and (c) ¹H.

The deviations between computed and experimental results arise from three different sources, namely (i) restrictions of computational procedures, (ii) errors or uncertainties in crystal structures produced by diffraction, and (iii) errors in experimental NMR data. The last two are usually relatively small, except for both, the hydrogen positions and the problem of comparison between temperatures.⁵²

TIZ has an intramolecular HB between the N–H bond and one oxygen atom. It is then important to find the accurate position of the hydrogen atom in that bond. To find the most likely position of the hydrogen H₁₀, step by step modifications of the geometrical structure of TIZ were performed, varying the position of H₁₀. The bond distance N₁₀–H₁₀ was modified between 0.78 Å and 1.78 Å, by 0.1 Å each step. This process was carried out by calculating the hydrogen positions, keeping the angle between the three nuclei (N₁₀, H₁₀, O₇), and fixing the plane in which that nuclei are located. The atomic positions were calculated for two different planes: the plane formed by the three nuclei in the H-relaxed geometry and the median plane of the H-relaxed structure. In both cases we found equivalent results. An illustration of the TIZ molecule for different positions of the hydrogen atom H₁₀ is shown in Fig. S2.†

The best RMS values for ¹³C atoms are obtained when the N₁₀–H₁₀ bond length is between 0.88 Å and 0.98 Å. On the other hand, for nitrogen atoms the best RMS was obtained for distances that are between 1.08 Å and 1.18 Å. We assume that the different sources of deviations between experimental and calculated chemical shifts are the reasons why the optimal bond length for the two nuclei does not match. However, it is possible to obtain a lower and an upper bound for the N₁₀–H₁₀ bond length (0.88–1.18 Å). In a second iteration, new calculations were performed with shorter steps (0.01 Å) to have a better sampling in the region of interest. Fig. 3 shows the comparison of experimental and calculated chemical shifts for ¹³C (Figure 3a), ¹⁵N (Fig. 3b), and ¹H (Fig. 3c) for different bond lengths.

Fig. 3 Calculated chemical shifts for different N₁₀–H₁₀ bond lengths against the experimentally measured chemical shift for each nucleus, (a) ¹³C, (b) ¹⁵N and (c) ¹H. To calculate the chemical shift, the position of the H₁₀ atom in the reported structure of TIZ was computationally varied and then the chemical shift for each N₁₀–H₁₀ distance was calculated to be compared with the chemical shift experimentally determined. The experimental chemical shift corresponds to a unique bond length that is to be determined.

When calculations were performed for a length step of 0.01 Å, it was found that the best correlation occurs when the bond length is (1.00 ± 0.02) Å, with RMS = 0.3 ppm.

In Fig. 4a–c the values of the chemical shifts as a function of the N₁₀–H₁₀ bond distance are shown. The chemical shifts of the ¹³C nuclei (C₁, C₈, C₁₁) closer to the N–H bond are those with the highest variations as their shieldings are significantly altered when the N–H distance changes (Fig. 4a). However, the chemical shift for C₁₃ is almost unchanged, as expected since it is not close to the region of interest. In the same way, we observe in Fig. 4b that N₁₅ chemical shift does not vary in the successive calculations, while for N₁₀ it does. This is not surprising, since this is the nucleus directly involved in the hydrogen bond interaction. Finally, in Fig. 4c we show how the H₁₀ (the one involved in the HB) chemical shift changes for each distance and the H₄ chemical shift does not change. As the bond distance lengthens, the hydrogen chemical shift increases (there is a deshielding of the nucleus), and as the hydrogen atom becomes closer to the oxygen atom it is more shielded. In all cases, the curves that correspond to the nuclei whose shifts change noticeably show the same behaviour as shown by Harris et al.⁵³

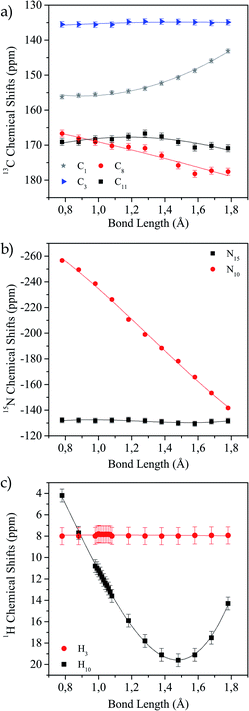Fig. 4 Variation of calculated chemical shift as a function of N₁₀–H₁₀ distance for different nuclei. (a) ¹³C, (b) ¹⁵N and (c) ¹H.

It is known that the nuclear magnetic shielding arises from the dynamical response of electrons that surround the nucleus to an external magnetic field. Consequently, it is possible to relate the chemical shielding of a nucleus with the electron-density distribution close to it. Charge density calculations were performed for the TIZ molecule for different N–H bond lengths to see how the position of the hydrogen atoms modifies the charge distribution in the molecule. Results of these calculations are shown in Fig. S3.† For the shortest bond length (Fig. S3a†) the electron cloud surrounds the H₇ atom. Notwithstanding, for other distances, this does not occur. That is, the proton is more shielded for a short bond length than for a long one. It is also possible to see how the first neighbours of the modified bond are affected by the variation of this charge distribution. Thus it is evident that those nuclei that are “distant” to the hydrogen bond do not undergo modifications when a change in the bond length is performed, while the others do. All this is in agreement with the results shown in Fig. 4.

The potential energy curve of an HB represented as a function of the position of the hydrogen atom also provides a fundamental criterion for the classification of hydrogen bonds.⁵⁴ It gives an indication of the HB-strength.^55–57 Fig. S4† shows the behaviour of the total calculated energy of the system as a function of the bond distance N₁₀–H₁₀. This is in line with results reported by White et al.,⁵⁴ i.e. the behaviour of the system as a whole matches the behaviour of the potential energy of an asymmetric well of strong HB. A fitting of the potential energy curve in the region close to its minimum was made in order to find the bond distance that minimizes the total energy of the system. From this fitting, a bond length of 1.03 ± 0.01 Å was obtained, being such a distance in good agreement with the result obtained fitting the proton chemical shifts.

3.3 Molecular quantum models

The first step in our theoretical calculations of models A and B consisted of optimizing the bond distance d(N₁₀–H₁₀) for the following three different basic structures: monomer, dimer and tetramer. We did it as described in Section 2.

We found that when the geometry of the dimer has been fully optimized (model A), the planarity is lost due to torsional forces between the monomers. This fact suggests that, to obtain a planar dimer, it is necessary to include monomers above and below of the given dimer. Then, this was the way the tetramer was built. On the other hand, given the location of the monomer in the geometric structure of tetramer, it is possible to analyse the different electronic effects that may influence the bond distance d(N₁₀–H₁₀) and therefore, in the NMR spectroscopic parameters.

In Table 1 we show the values of d(N₁₀–H₁₀) obtained at different levels of theory and applying models A and B to the monomer and dimer structures, and the model B to the tetramer structure. It is observed that the distance d(N₁₀–H₁₀) varies between 1.01 Å and 1.02 Å and that when calculations are more accurate the distance is shortened. On the other hand, when the number of positions of hydrogen atoms optimized is increased, the number of monomers included, the distance d(N₁₀–H₁₀) is elongated independently of the level of theory used. This means that both, the number of hydrogen atom positions to be optimized and the level of theory used should be taken into account for reliable calculations.

Table 1 Distances d(N₁₀–H₁₀) obtained with different models and levels of theory. All values are given in Angstroms

System	Level of theory	Molecular model	d(N–H)
a The positions of two H10 atoms (bonded to N10) are optimized in the dimer.b The positions of two H10 atoms (bonded to N10) and two H7 atoms (bonded to O7) are optimized in the dimer.
Monomer	B3LYP/6-311G++g(d,p)	A	1.015
	B97D/6-311G++g(d,p)	A	1.014
	B97D/6-311G++g(d,p)	B (only H10)	1.017
	B97D/cc-pVTZ	B (only H10)	1.013
Dimer	B3LYP/6-311G++g(d,p)	A	1.020
	B97D/6-311G++g(d,p)	B 2H^a	1.019
	B97D/cc-pVTZ	B 2H	1.016
	B97D/cc-pVTZ	B 4H^b	1.019
Tetramer	B97D/6-311G++g(d,p)	B 2H	1.020
	B97D/cc-pVTZ	B 2H	1.017
	B97D/cc-pVTZ	B 4H	1.019

---

Another finding that can be observed in Table 1 is the fact that the distance d(N₁₀–H₁₀) is 1.019 Å in both the dimer and tetramer, when the position of the two pairs of hydrogen atoms that belong to HBs are optimized. This fact suggests that the optimization of the position of hydrogen atoms bonded to the oxygen O₇ is the main factor to consider for getting a more stable structure.

As mentioned in Section 2 we used NMR spectroscopic parameters to cross-check our findings of the positions of the hydrogen atoms that belong to intra- and intermolecular HBs. Chemical shifts of hydrogen and carbon atoms were obtained considering tetramethylsilane (TMS) as the reference compound, and the chemical shifts of nitrogen atoms were calculated using nitromethane (NTM) as the reference compound:

δ(H,C) = σ^TMS(H,C) − σ(H,C)

δ(N) = σ^NTM(N) − σ(N)

In Table 2 the chemical shifts calculated at different levels of theory and using shieldings of reference taken from experiments are shown. The full optimization of the monomeric structure was performed at B3LYP/6-311G++(d,p) level of theory and the optimization of the position of hydrogens in the dimer and the tetramer were performed at B97D/cc-pVTZ level of theory. As mentioned above, when the geometry of the monomer was fully optimized (model A) the chemical shift of the hydrogen atom H₇ does not match adequately with experimental values. Similar behaviour occurs when only the position of the hydrogen H₁₀ is optimized in dimers or tetramers. On the other hand, when the positions of the hydrogen atoms bonded to the oxygen O₇ in the dimer are also optimized (optimization of type 4H), the theoretical chemical shifts are close to the experimental values. This means that (i) one must include at least two monomers of TIZ molecules in calculations and (ii) it is also important to consider intermolecular HBs which include a couple of hydrogen atoms H₇. These atoms should both be well described if one wants to accurately reproduce the experimental values of chemical shifts.

Table 2 Chemical shifts of hydrogen, carbon, and nitrogen atoms for which the values of magnetic shieldings of reference compounds were taken from experiments. Between parenthesis are the chemical shifts obtained with the geometry of the reference compounds optimized at PBE0/cc-pVTZ level of theory. All calculations of NMR magnetic shieldings were performed with cc-pVTZ basis set and all values are given in ppm

δ(X)	Atoms
	H7	H10	N10	C8	C2	C1	C6	C5	C4	C3
Exp. this work	10.60	11.40	−241.50	163.10	113.60	155.50	116.40	136.30	119.60	133.30
Monomer model A (B3LYP)	4.01	10.41	−225.49	170.75	126.5	166.89	122.63	144.81	131.68	145.69
Monomer model A (PBE)	4.23	10.58	−223.35	164.24	123.23	162.42	120.01	140.18	128.73	140.81
Monomer model A (PBE0)	4.25	10.60	−231.75	165.48	120.86	160.71	117.81	140.22	126.70	140.96
Monomer model A (KT3)	3.81	10.04	−230.61	157.86	116.01	154.93	102.20	119.27	108.91	120.92
Dimer model B 2H (PBE0)	(4.26)	(11.93)	(−246.43)	(166.50)	(119.67)	(161.22)	(111.69)	(135.03)	(120.25)	(135.66)
Dimer model B 4H (PBE0)	(12.65)	(12.28)	(−246.05)	(166.99)	(118.82)	(163.99)	(112.92)	(135.35)	(119.29)	(135.51)
Dimer model B 2H (B97D)	(4.46)	(11.80)	(−213.40)	(158.12)	(115.13)	(155.34)	(106.02)	(126.68)	(114.00)	(127.53)
Dimer model B 4H (B97D)	(12.54)	(12.14)	(−213.15)	(158.58)	(114.36)	(158.02)	(107.30)	(126.97)	(113.13)	(127.37)
Dimer model B 4H (KT3)	11.54	11.21	−236.13	158.03	113.79	157.30	107.22	126.29	112.65	126.23
	(12.21)	(11.88)	(−211.99)	(156.48)	(112.24)	(155.75)	(105.67)	(124.74)	(111.10)	(124.68)
Tetramer model B 2H (PBE0)	2.37	10.69	−237.22	168.11	120.64	161.51	112.8	135.01	120.65	136.76
	(2.88)	(11.2)	(−248.43)	(167.54)	(120.07)	(160.94)	(112.23)	(134.4)	(120.08)	(136.19)
Tetramer model B 4H (PBE0)	10.65	11.01	−236.74	168.78	119.91	164.16	114.03	135.49	119.79	136.62
	(11.16)	(11.52)	(−247.95)	(168.21)	(119.34)	(163.59)	(113.46)	(134.92)	(119.22)	(136.05)
Tetramer model B 2H (B97D)	2.44	10.39	−232.63	164.86	120.38	159.86	112.00	131.61	119.31	133.16
	(3.11)	(11.06)	(−215.42)	(159.54)	(115.06)	(154.54)	(106.68)	(126.29)	(113.99)	(127.84)
Tetramer model B 4H (B97D)	10.42	10.69	−232.4	165.49	119.83	162.37	113.27	132.05	118.55	133.01
	(11.09)	(11.36)	(−215.19)	(160.17)	(114.51)	(157.05)	(107.95)	(126.73)	(113.23)	127.69

---

In Table 2 the chemical shifts calculated by using theoretically obtained reference shieldings are also shown between parenthesis. When the structure of the reference compounds are optimized at the same level of theory as that used for dimer and tetramer of model B, the values of the chemical shifts are close to the experimental values, but not for the chemical shift of H₇ obtained with the 2H type optimization. This is because in this case only the positions of the hydrogen atoms belonging to intramolecular HBs are optimized.

We can then state that chemical shifts of hydrogen and nitrogen atoms that are involved in the HBs are sensitive to the description of electronic densities in their sites in the dimer, as it also happens when the dimer is replaced by the tetramer. The chemical shift of the hydrogen H₇ varies when we calculated them in the dimer structures using model B 2H and model B 4H; a similar variation is also found for tetrameric structures. As an example, when the calculation of chemical shifts of H₇ at PBE0/cc-pVTZ level of theory are performed with model B, being the optimizations of the types 4H and 2H, the difference between them is close to 8.4 ppm. In the case of the tetrameric structures, such difference is close to 8.3 ppm.

We can also observe that by optimizing the positions of the hydrogen atoms that belong to the intermolecular HB (the H₇ atom) in the tetrameric structure, the chemical shift of the other hydrogen atom of interest (the atom H₁₀) becomes closer to the experimental values. The same happens for dimers although the chemical shift of H₇ is not close to its experimental value. It is then worth mentioning that, even though the calculations for the tetramer structure give some modifications of the chemical shifts of hydrogen atoms as compared with the results of calculations with dimers, those modifications are small compared with the effects of optimizing the hydrogen positions of the intermolecular HBs.

4 Concluding remarks

The finding of the accurate position of hydrogen atoms inside a crystalline system is not an easy task. Instead, what is routinely obtained is the geometrical structure of non-hydrogen atoms and it is also well-known that the NMR spectroscopic parameters are sensitive to the local electronic environment of any atomic nucleus belonging to a given quantum system. For this reason we developed a procedure that combines ssNMR experimental data with two theoretical models, to reliably get the positions of hydrogen atoms that belong to hydrogen bonds in molecular crystals. One of the main results of our work is that the interplay between experimental ssNMR and reliable theoretical models can be widely applied to the finding of the geometrical structure, that include the position of hydrogen atoms, in any other molecular crystal different from tizoxanide (TIZ). Furthermore, those theoretical models provide well-defined grounds to study the strength of π-stacking interactions between layers of hydrogen bonded molecules, stacked one on top of the other, as happens in TIZ.

Our above mentioned theoretical models are quite different. The first one is a solid-state model, which considers the periodicity of a crystalline system to calculate energy, electronic density, and NMR parameters. The other one is a molecular model in which TIZ molecules are taken as isolated monomers, dimers, or tetramers.

Working with the solid-state model it was found that any local variation of the TIZ crystalline structure is followed by the variation of the values of the NMR parameters of each nucleus. An excellent agreement between experimental and calculated chemical shifts shows that the bond distance N₁₀–H₁₀ should be 1.00 ± 0.02 Å. This distance matches quite well with the value of the distance for which the total energy of the system is a minimum.

By applying the quantum molecular model it was possible to learn about the way the intermolecular hydrogen bonds affect the positions of hydrogen atoms that belong to HBs. There are two intermolecular HBs that stabilize the structure of a basic dimer, but there is also one intramolecular HB for each monomer whose positions should be optimized all together with the other ones. This feature must be used in order to obtain reliable results of calculations of NMR spectroscopic parameters. We should also highlight the fact that the theoretical optimization of the N₁₀–H₁₀ bond distances using the quantum molecular model named B 4H on a tetrameric structure, is consistent with the results obtained with the solid-state model. Furthermore, that model permits a deeper analysis of the electronic effects involved in the description of the HBs.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge support from the National Research Council for Science and Technology (CONICET, internal doctoral fellowship, and grants PIP 112-20130100361 and PIP 112-20130100746) and the Argentinian Agency for Promotion of Science and Technology (ANPCYT, grant PICT 2016-2936). Some calculations were performed in Mendieta Cluster from CCAD-UNC, which is part of SNCAD MinCyT, Argentina. Paul Hodgkinson (University of Durham, UK) for helpful comments and David Apperley for ¹H spectra measurements.

Notes and references

1. D. Luedeker, R. Gossmann, K. Langer and G. Brunklaus, Cryst. Growth Des., 2016, 16, 3087.
2. C. Guzmán-Afonso, Y. lee Hong, H. Colaux, H. Iijima, A. Saitow, T. Fukumura, Y. Aoyama, S. Motoki, T. Oikawa, T. Yamazaki, K. Yonekura and Y. Nishiyama, Nat. Commun., 2019, 10, 3537.
3. K. Maruyoshi, D. Iuga, O. N. Antzutkin, A. Alhalaweh, S. P. Velagad and S. P. Brown, Chem. Commun., 2012, 48, 10844.
4. A. S. Tatton, T. N. Pham, F. G. Vogt, D. Luga, A. J. Edwards and S. P. Brown, Mol. Pharmaceutics, 2013, 10, 999.
5. S. Sharif, E. Fogle, M. D. Toney, G. S. Denisov, I. G. Shenderovich, G. Buntkowsky, P. M. Tolstoy, M. C. Huot and H.-H. Limbach, J. Am. Chem. Soc., 2007, 129, 9558.
6. J. Guo, P. M. Tolstoy, B. Koeppe, N. S. Golubev, G. S. Denisov, S. N. Smirnov and H.-H. Limbach, J. Phys. Chem. A, 2012, 116, 11180.
7. B. Koeppe, J. Guo, P. M. Tolstoy, G. S. Denisov and H.-H. Limbach, J. Am. Chem. Soc., 2013, 135, 7553.
8. P. E. Hansen and J. Spanget-Larsen, Molecules, 2017, 22, 552.
9. P. Banerjee and T. Chakraborty, Int. Rev. Phys. Chem., 2018, 37, 83.
10. D. J. Bakker, A. Dey, D. P. Tabor, Q. Ong, J. Mahé, M.-P. Gaigeot, E. L. Sibert and A. M. Rijs, Phys. Chem. Chem. Phys., 2017, 19, 20343.
11. X. Liu, X. Wei, H. Zhou, S. Meng, Y. Zhao, J. Xue and X. Zheng, J. Phys. Chem. A, 2018, 122, 5710–5720.
12. A. Duan, S. An, J. Xue, X. Zheng and Y. Zhao, RSC Adv., 2020, 10, 13442–13450.
13. Y. Deng, X. Liu, Y. Zhao, J. Xue and X. Zheng, Spectrochim. Acta, 2020, 230, 118043.
14. L. Sobczyk, D. Chudoba, P. M. Tolstoy and A. Filarowski, Molecules, 2016, 21, 1657.
15. A. Amrutha Kala, K. Kumara, N. V. Harohally and N. K. Lokanath, J. Mol. Struct., 2020, 1202, 127238.
16. L. Ravindranath and B. V. Reddy, J. Mol. Struct., 2020, 1200, 127189.
17. N. Zarycz and G. A. Aucar, J. Phys. Chem. A, 2008, 112, 8767.
18. N. Zarycz and G. A. Aucar, J. Phys. Chem. A, 2010, 114, 7162.
19. F. Weinhold and R. A. Klein, Mol. Phys., 2012, 110, 565.
20. M. G. Siskos, G. Andreas, A. G. Tzakos and I. P. Gerothanassis, Org. Biomol. Chem., 2015, 13, 8852.
21. M. G. Siskos, M. T. Choudhary, A. G. Tzakos and I. P. Gerothanassis, Tetrahedron, 2016, 72, 8287.
22. F. A. Martinez and G. A. Aucar, Phys. Chem. Chem. Phys., 2017, 19, 27817.
23. M. D. A. Montero, F. A. Martinez and G. A. Aucar, Phys. Chem. Chem. Phys., 2019, 21, 19742.
24. M. Sardo, S. Santos, A. Babaryk, C. López, I. Alkorta, J. Elguero, M. R. Claramunt and L. Mafra, Solid State Nucl. Magn. Reson., 2015, 65, 49.
25. H. Limbach, M. Chan-Huot, S. Sharif, P. M. Tolstoy, I. Shenderovich, G. S. Denisov and M. Toney, Biochim. Biophys. Acta, 2011, 1814, 1426.
26. F. G. Vogt, J. S. Clawson, M. Strohmeier, A. J. Edwards, T. N. Pham and S. A. Watson, Cryst. Growth Des., 2008, 9, 921–937.
27. M. R. Chierotti and R. Gobetto, Chem. Commun., 2008, 1621–1634.
28. R. Gobetto, C. Nervi, M. R. Chierotti, D. Braga, L. Maini, F. Grepioni, R. K. Harris and P. Hodgkinson, Chem.–Eur. J., 2005, 11, 7461–7471.
29. J. R. Yates, S. E. Dobbins, C. J. Pickard, F. Mauri, P. Y. Ghi and R. K. Harris, Phys. Chem. Chem. Phys., 2005, 7, 1402.
30. V. L. Deringer, V. Hoepner and R. Dronskowski, Cryst. Growth Des., 2012, 12, 1014.
31. M. G. Siskos, M. I. Choudhary and I. P. Gerothanassis, Molecules, 2017, 22, 415.
32. M. K. Dudek, E. Wielgus, P. Paluch, J. Śniechowska, M. K. J. Potrzebowski, G. M. Day, G. D. Bujacz and M. J. Potrzebowski, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2019, 75, 803.
33. D. V. Dudenko, J. R. Yates, K. D. M. Harris and S. P. Brown, CrystEngComm, 2013, 15, 8797–8807.
34. R. K. Harris, P. Jackson, L. H. Merwin, B. J. Say and G. Hägele, J. Chem. Soc., Faraday Trans. 1, 1988, 84, 3649–3672.
35. S. Sharif, G. S. Denisov, M. D. Toney and H.-H. Limbach, J. Am. Chem. Soc., 2007, 129, 6313–6327.
36. M. Khan, V. Enkelmann and G. Brunklaus, J. Am. Chem. Soc., 2010, 132, 5254–5263.
37. F. P. Bruno, M. R. Caira, E. C. Martin, G. A. Monti and N. R. Sperandeo, J. Mol. Struct., 2013, 1036, 318–325.
38. C. J. Pickard and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101.
39. R. K. Harris, S. Cadars, L. Emsley, J. R. Yates, C. J. Pickard, R. K. R. Jetti and U. J. Griesser, Phys. Chem. Chem. Phys., 2007, 9, 360–368.
40. R. K. Harris, Nuclear Magnetic Resonance Spectroscopy, Longman Scientific and Technical, 1994.
41. A. E. Bennett, C. M. Rienstra, M. Auger, K. V. Lakshmi and R. G. Griffin, J. Chem. Phys., 1995, 103, 6951–6958.
42. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, et al., J. Phys.: Condens. Matter, 2009, 21, 395502.
43. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
44. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
45. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
46. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
47. K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenæs, S. Høst, I.-M. Høyvik, M. F. Iozzi, B. Jansík, H. J. A. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjærgaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnæs, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. V. Rybkin, P. Sałek, C. C. M. Samson, A. S. de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 269–284.
48. T. W. Keal and D. J. Tozer, J. Chem. Phys., 2004, 121, 5654–5660.
49. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
50. M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269.
51. T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007.
52. R. K. Harris, P. Hodgkinson, C. J. Pickard, J. R. Yates and V. Zorin, Magn. Reson. Chem., 2007, 45, S174–S186.
53. R. K. Harris, P. Y. Ghi, R. B. Hammond, C. Ma and K. J. Roberts, Chem. Commun., 2003, 2834–2835.
54. P. B. White and M. Hong, J. Phys. Chem. B, 2015, 119, 11581–11589.
55. C. N. Schutz and A. Warshel, Proteins: Struct., Funct., Bioinf., 2004, 55, 711–723.
56. A. Warshel and A. Papazyan, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 13665–13670.
57. A. Warshel, A. Papazyan, P. A. Kollman, W. W. Cleland, M. M. Kreevoy and P. A. Frey, Science, 1995, 269, 102–106.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra10609g

---