Open Access Article
Open Access ArticleHow size, shape and assembly of magnetic nanoparticles give rise to different hyperthermia scenarios†
H.
Gavilán
ab,
K.
Simeonidis
c,
E.
Myrovali
 c,
E.
Mazarío
c,
E.
Mazarío
 a,
O.
Chubykalo-Fesenko
a,
O.
Chubykalo-Fesenko
 a,
R.
Chantrell
a,
R.
Chantrell
 d,
Ll.
Balcells
e,
M.
Angelakeris
c,
M. P.
Morales
d,
Ll.
Balcells
e,
M.
Angelakeris
c,
M. P.
Morales
 *a and
D.
Serantes
*a and
D.
Serantes
 *f
*f
aInstituto de Ciencia de Materiales de Madrid, ICMM/CSIC, 28049 Madrid, Spain. E-mail: puerto@icmm.csic.es
bIstituto Italiano di Tecnologia, Via Morego 30, 16163 Genova, Italy
cSchool of Physics, Aristotle University of Thessaloniki, 54124 Thessaloniki, Greece
dDepartment of Physics, University of York, Heslington, York YO10 5DD, UK
eInstitut de Ciencia de Materiales de Barcelona, CSIC, 08193 Bellaterra, Spain
fApplied Physics Department and Instituto de Investigacións Tecnolóxicas, Universidade de Santiago de Compostela, 15782, Spain. E-mail: david.serantes@usc.gal
First published on 24th August 2021
Abstract
The use of magnetic nanoparticles (MNPs) to locally increase the temperature at the nanoscale under the remote application of alternating magnetic fields (magnetic particle hyperthermia, MHT) has become an important subject of nanomedicine multidisciplinary research, focusing among other topics on the optimization of the heating performance of MNPs and their assemblies under the effect of the magnetic field. We report experimental data of heat released by MNPs using a wide range of anisometric shapes and their assemblies in different media. We outline a basic theoretical investigation, which assists the interpretation of the experimental data, including the effect of the size, shape and assembly of MNPs on the MNPs’ hysteresis loops and the maximum heat delivered. We report heat release data of anisometric MNPs, including nanodisks, spindles (elongated nanoparticles) and nanocubes, analysing, for a given shape, the size dependence. We study the MNPs either acting as individuals or assembled through a magnetic-field-assisted method. Thus, the physical geometrical arrangement of these anisometric particles, the magnetization switching and the heat release (by means of the determination of the specific adsorption rate, SAR values) under the application of AC fields have been analysed and compared in aqueous suspensions and after immobilization in agar matrix mimicking the tumour environment. The different nano-systems were analysed when dispersed at random or in assembled configurations. We report a systematic fall in the SAR for all anisometric MNPs randomly embedded in a viscous environment. However, certain anisometric shapes will have a less marked, an almost total preservation or even an increase in SAR when embedded in a viscous environment with certain orientation, in contrast to the measurements in water solution. Discrepancies between theoretical and experimental values reflect the complexity of the systems due to the interplay of different factors such as size, shape and nanoparticle assembly due to magnetic interactions. We demonstrate that magnetic assembly holds great potential for producing materials with high functional and structural diversity, as we transform our nanoscale building blocks (anisometric MNPs) into a material displaying enhanced SAR properties.
Introduction
Several studies suggest that a key aspect for efficient magnetic particle hyperthermia (MHT) is the accurate control of the heat release at the nanoscale, which is critically related to the use of magnetic nanoparticles (MNPs) with optimal and controlled size,1 shape2 and geometrical configuration.3,4 While theoretical studies base the evaluation of nanomaterials designed for MHT on the determination of the hysteresis area under different AC fields, experimental studies rely primarily on the determination of the specific absorption rates (SAR), which is a physical parameter related to MNPs’ heat dissipation. The most common calorimetric method to evaluate the SAR is the placement of a suspension of MNPs into alternating magnetic fields (AMFs): the suspension absorbs the energy from the field and transforms it into heat. If the field is strong enough, and also thermal losses are small enough, SAR values can be evaluated from the following equation: SAR = (CLIQ/cFe) × [dT/dt] (t = 0), i.e. from the temperature derivative over time at instant t = 0 given the heat capacity of the solvent (CLIQ) and the mass iron concentration (cFe).5Among MNPs, those presenting anisometric shape have raised great interest in the field of MHT due to their additional shape anisotropy, which has accounted for increased heat performances. In the past years, there has been hectic research on the heat released by anisometric nanoparticles, including nanocubes,6 nano-octopods,7 nanoflowers,8 elongated nanoparticles9,10 and nanodisks11 and, in some cases, their corresponding heat release mechanisms. As an example, Cabrera et al. reported a large decrease (80% drop) in the SAR of 21 nm magnetite cubes (this size lies in superparamagnetic-ferromagnetic regime) in viscous media (∼100 mPa s), which was attributed to the Brownian relaxation suppression.12 On the contrary, cubes of 14 and 11 nm (most probably with a superparamagnetic behaviour) had a less marked drop in the SAR (18 and 10%, respectively), as these systems were relaxing essentially through the Néel mechanism.13 However, D. Serantes et al. recently predicted through simulations the possibility to shift from the Brownian to the Néel mechanism in a system of disk-like anisometric NPs. While at low frequencies it was predicted that the disks absorbed energy and transformed it into particle rotational energy, at high frequencies the behaviour depended on the amplitude of the applied field: for large field amplitudes (greater than the switching field) the energy went into internal energy (heating), whereas for small field amplitudes the energy went into rotational motion.14 On the other hand, it has been widely reported that the magnetization dynamics under an AC field are intimately associated with the influence of dipole interactions among MNPs, being able to either improve or worsen the hyperthermic response of MNPs. In this context, K. Simeonidis et al. demonstrated that even if anisometric nano-spindles heat via Brownian relaxation (and such a contribution can be discarded as a heating mechanism in relevant media similar to that of tumours), the formation of their corresponding chains led to the heat dissipation by the Néel reversal mechanism (due to a progressive reorientation of the elongated structures during the AC treatment).15 As such, both the optimization of the applied AMFs and the oriented assembling of MNPs are recognized as important ways to optimize MHT. In fact, reorientations of nanoparticles under AC fields have been reported to take place in vitro, modifying their heating performance.16
This work aims at the study of precisely the above-mentioned aspects of the design of MNPs for MHT, including the size, shape and their assembly, both from a theoretical and experimental point of view, giving rise to different magnetic hyperthermia scenarios. We describe an experimental investigation into the potential of a series of different anisometric MNPs under AMFs. In order to provide a basis for interpretation of the experimental data, we provide a theoretical insight for determining the maximum SAR value (equivalent to the hysteresis area) for iron oxides nanoparticles (either magnetite or its oxidized form, maghemite), considering that the heat dissipation mechanism is the magnetization reversal over the anisotropy energy barrier. We consider two different sizes of each shape, and the different MNPs are investigated acting either alone or collectively (thanks to their pre-assembly) to release heat. The physical geometrical arrangement of these anisometric particles, the magnetization switching, reorientation and the heat release under the application of AC fields are analysed in aqueous suspensions and after immobilization in agar matrix. Therefore, the presented MNPs were dispersed either randomly or assembled and the magnetic characterization was studied in two different orientations.
With respect to the synthesis of MNPs, the enormous progress that has been done in the chemical synthesis of nanostructures, allows nanotechnologists to prepare MNPs with well-controlled composition and morphology.2 We have selected hydrothermal and solvothermal routes, previously reported by some of us, for the preparation of the following anisometric Fe3O4/γ-Fe2O3 MNPs: polyhedral/cubic,17 elongated,9 disk-shaped18 and ensembles consisting of smaller cores (nanoflowers).19 Hydrothermal and solvothermal routes are more environmentally friendly, reproducible and scalable because of the use of non-toxic solvents and milder reaction conditions, overcoming some of the major concerns of the current MNPs synthetic approaches.20
With regard to the assembly of the anisometric MNPs, the selected method is magnetic assembly. This is an approach that acts at the nanoscale level, holding great potential for producing smart materials with high functional and structural diversity21 and transforming nanoscale building blocks into a material that displays enhanced properties relative to the sum of its parts.22 Magnetic-field-assisted assembly consists of the application of an external magnetic field to a solution containing MNPs. The magnitude of the applied magnetic field promotes the alignment of magnetic moments of the nanoparticles and the strong dipole–dipole interactions between the neighbouring nanoparticles lead to a close-packed pattern with an energetically favourable configuration.23 In comparison with other methods of assembly, i.e. those driven by molecular interactions or template methods,24 magnetic-field-assisted assembly has the advantage of creating orientational order of the building blocks or producing positional order within the assemblies with delicate control over crystal symmetry and lattice constant.25 In addition, the use of anisotropic magnetic nanoparticles as building blocks can change substantially the collective magnetic properties of the assembly due to their additional shape anisotropy; and can affect the orientational order of the building blocks. As an example, E. Wetterskog et al. reported colossal anisotropy of the dynamic magnetic susceptibility in rod-shape assemblies of nanocubes.22 C. Jiang et al. likewise reported enhancement of coercivity and saturation magnetization in rod-shape assemblies of spherical and polyhedral nanoparticles.23
Therefore, the present work addresses a major challenge in MHT roadmap: understanding the dynamics of non-spherical MNPs under the application of AC fields in a viscous environment. Although we report a systematic fall in the SAR values for most of MNPs (either alone or assembled) in viscous environment, certain anisometric shapes will have an almost total preservation or even an increase in SAR when embedded in a viscous environment with certain orientation.
Experimental and computational details
Synthesis of anisometric nanoparticles
Magnetite nano-sized disks and spindles were synthesized in a two-step procedure through the reduction of silica-coated intermediated formed oxides and oxy-hydroxides as previously described.18 However, flowers19 and cubes17 were synthesized directly by a polyol mediated synthesis and by oxidative precipitation in aqueous/alcohol media, respectively. Below are found all the experimental details for their synthesis. The main morphological and magnetic characteristics of the particles are summarized in Table 1. A scheme of the particles under study and their synthesis routes are presented in Fig. 1.| Sample | Dimensions (nm) | Hydrodynamic diameter (nm)/PDI | Magnetization (Am2 kgFe−1) | Coercive field (kA m−1) | ||
|---|---|---|---|---|---|---|
| 5 K | 290 K | 5 K | 290 K | |||
| Disks | 90 (±18) × 17 (±4) | 255 (0.35) | 90 | 81 | 47 | 20 |
| 155 (±15) × 27 (±6) | 201 (0.35) | 121 | 113 | 50 | 18 | |
| Spindles | 60 (±18) × 23 (±9) | 147 (0.14) | 101 | 90 | 26 | 9 |
| 250 (±50) × 50 (±10) | 447 (0.10) | 98 | 95 | 70 | 18 | |
| Flowers | 27 (±3) | 50 (0.17) | 128 | 97 | 12 | 0 |
| 130 (±16) | 156 (0.04) | 127 | 103 | 10 | 0 | |
| Cubes | 22 (±8) | 95 (0.16) | 118 | 113 | 18 | 0 |
| 44 (±7) | 136 (0.13) | 135 | 120 | 30 | 11 | |
Disks
Magnetic iron oxide nanodisks were first prepared as hematite (α-Fe2O3) by the precipitation of FeCl3·6H2O in the presence of sodium acetate into a Teflon-lined autoclave maintained at 180 °C for 12 h. Iron chloride was dissolved in 50 mL of absolute ethanol and 1 mL of water under vigorous magnetic stirring before sodium acetate was added in the mixture. The concentrations of FeCl3 and sodium acetate in the final solution were 0.096 M and 0.58 M, respectively. Water content is the critical parameter to control disk dimensions. An increase of water content from 1 mL to 5 mL results in the significant decrease of the obtained disks diameter. The intermediate solid product was washed with distilled water and dried overnight at 50 °C. For the silica coating of the obtained nanoparticles, a quantity of the dried particles (100 mg) was dispersed in a 300 mL solution of 2-propanol/H2O 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v, NH4OH 28% v/v (4.5 × 10−4 M) and tetraethyl orthosilicate (TEOS) (2.8 × 10−6 M) under sonication. The reaction was allowed to continue for 15 min. The product was washed twice with 2-propanol and dried overnight at 50 °C. The silica-coated precursor nanoparticles were reduced to obtain Fe3O4 by treatment at 360 °C in a H2 atmosphere (1 atm) for 3.5 h.
1 v/v, NH4OH 28% v/v (4.5 × 10−4 M) and tetraethyl orthosilicate (TEOS) (2.8 × 10−6 M) under sonication. The reaction was allowed to continue for 15 min. The product was washed twice with 2-propanol and dried overnight at 50 °C. The silica-coated precursor nanoparticles were reduced to obtain Fe3O4 by treatment at 360 °C in a H2 atmosphere (1 atm) for 3.5 h.
Spindles
For the preparation of magnetic nano-sized spindles, goethite (α-FeOOH) was prepared through the aqueous precipitation of FeSO4·7H2O in the presence of Na2CO3. A solution of 0.15 M FeSO4 and 0.225 M Na2CO3 were mixed to control the concentration ratio [CO32−/Fe2+] at 1.5. The resulting solid was oxidized in a thermostatic water bath at 44 °C under moderate stirring by bubbling air at a constant flow. The main parameter controlling the particle elongation is the [CO32−/Fe2+] ratio. In particular, increasing the ratio in the range 1.5–12 results in smaller spindles’ size. Both the surface coating of the spindles with SiO2 and the subsequent reduction of the spindles (from α-FeOOH to Fe3O4) were performed identically to the procedure above described for disks.Flowers
Small magnetic iron oxide nanoflowers were synthesized directly by a polyol-mediated method. Typically, nanoflowers around 27 nm were obtained by mixing FeCl3·6H2O (4 mmol) and FeCl2·4H2O (2 mmol) in diethylene glycol and N-methyl diethanolamine (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v, 80 g) at room temperature and adding a suspension of NaOH (16 mmol) dissolved in the polyol (40 g). The temperature of the mixture was then elevated to 210 °C with a rate of 2 °C min−1 and stirred for 12 h. When the reaction was cooled down, the nanoparticles were separated magnetically, washed, acid treated with iron(III) nitrate at 80 °C for 45 min, treated with nitric acid at RT and washed again. Citric acid was used to stabilize the particles in suspension by adding 13 mL of a 0.1 M citric acid solution to 7 ml of a suspension containing 20 mg of Fe at pH 2. Afterwards, the mixture was heated at 80 °C for 30 min. The solution was centrifuged and washed with distilled water. Finally, the pH was adjusted first to 11 with 1 M KOH and then to 7 with 0.01 M HNO3. Large size of approximately 130 nm was also obtained through a polyol approach by dissolving FeCl3·6H2O in ethylene glycol in the presence of trisodium citrate (Na3Cit) and sodium acetate (NaAc). The final concentrations of the reagents were [FeCl3] = 0.21 M, [Na3Cit] = 0.05 M and [NaAc] = 0.76 M. The mixture was then sealed in a Teflon-lined aluminum autoclave and maintained at 200 °C for 10 h. After cooling down, the black product was washed three times with distilled water by centrifugation.
1 v/v, 80 g) at room temperature and adding a suspension of NaOH (16 mmol) dissolved in the polyol (40 g). The temperature of the mixture was then elevated to 210 °C with a rate of 2 °C min−1 and stirred for 12 h. When the reaction was cooled down, the nanoparticles were separated magnetically, washed, acid treated with iron(III) nitrate at 80 °C for 45 min, treated with nitric acid at RT and washed again. Citric acid was used to stabilize the particles in suspension by adding 13 mL of a 0.1 M citric acid solution to 7 ml of a suspension containing 20 mg of Fe at pH 2. Afterwards, the mixture was heated at 80 °C for 30 min. The solution was centrifuged and washed with distilled water. Finally, the pH was adjusted first to 11 with 1 M KOH and then to 7 with 0.01 M HNO3. Large size of approximately 130 nm was also obtained through a polyol approach by dissolving FeCl3·6H2O in ethylene glycol in the presence of trisodium citrate (Na3Cit) and sodium acetate (NaAc). The final concentrations of the reagents were [FeCl3] = 0.21 M, [Na3Cit] = 0.05 M and [NaAc] = 0.76 M. The mixture was then sealed in a Teflon-lined aluminum autoclave and maintained at 200 °C for 10 h. After cooling down, the black product was washed three times with distilled water by centrifugation.
Cubes
For comparison with a symmetrical-shaped system, cubic shaped nanoparticles were produced following the partial oxidation of FeSO4·7H2O by NaNO3 in water. Dimensions of the particles were controlled through the excess of OH−.26 Briefly, an Fe(II) solution was quickly added to a basic solution in the presence of a mild oxidant under stirring in an oxygen free atmosphere (glove box under nitrogen). The final concentrations were 0.2 M Fe2+, 0.2 M NO3− and an excess [OH−] of 0.02 M after the precipitation of Fe(OH)2. The initially formed green rust was mechanically stirred for 15 min and then, the reaction intermediate was aged at 90 °C for 24 h without agitation to obtain magnetite nanocrystals. Particle size is reduced from 44 nm to 22 nm by introducing ethanol in the media at 25%.Orientation and immobilization of MNPs
For the orientation of nanoparticles, they were dispersed in an agar solution at 70 °C (2% w/v) by sonication so that the final concentration was 2 mg Fe per mL. Then, the mixture was allowed to cool down in the presence of a homogeneous magnetic field of 50 kA m−1. Specimens with randomly distributed nanoparticles were obtained by the same process skipping the application of the magnetic field during cooling. The sonication at high temperatures for long time (30 min) indeed minimizes magnetic particle interactions and random orientation.Characterization
Electron microscopy (SEM and TEM) imaging was performed using FEI Quanta 200 ESEM FEG and FEI Nova NanoSEM 230 microscopes with a field-emission gun operating at 30 kV whereas transmission electron microscopy (TEM) images were captured by a JEOL JEM1010 microscope, operating at 100 kV. Samples were prepared by placing a drop of the particles suspended in water onto a carbon coated copper grid and allowing it to dry at room temperature. The mean particle size and distribution were determined from the TEM images by manual measurement of the largest dimensions along two perpendicular directions of more than 100 particles using the public domain ImageJ software.Colloidal properties were analysed by dynamic light scattering (DLS). Measurements were carried out in a Zetasizer Nano S, from Malvern Instruments. The data analysis was performed with the 2nd cumulant method, and the Gaussian distributions are intensity-weighted.
Magnetic measurements of the randomly and magnetically oriented specimens were performed in a Quantum Design MPMS XL SQUID magnetometer at room temperature. Here, measured samples were prepared by depositing a drop of a hot agar dispersion with nanoparticles on a Si substrate, which was then allowed to cool in the presence or absence of a 50 kA m−1 magnetic field. The magnetic moment per particle has been calculated taking into account the Ms value and particle's weight, obtained from the volume of each particle as a function of the size and shape, and the maghemite density (4.9 g cm−3).
Magnetic hyperthermia
Calorimetric measurements on the heating efficiency of nanoparticles under an AC magnetic field were acquired using a commercial converted 4.5 kW inductive heater at frequency 765 kHz and magnetic field intensity of 24 kA m−1. The specific absorption rate (SAR) was derived from the slope of the temperature versus time curve after subtracting water background signal and heat losses to the environment. Temperature was monitored by using an Opsens PicoM device with a GaAs-based fiber optic probe. For each nanoparticle system four sets of measurements were performed involving (i) 1 mL of aqueous dispersion, (ii) oriented agar specimens with formed chains placed parallel to the AC field, (iii) the previous specimens with formed chains placed perpendicular to the AC field and (iv) randomly distributed agar specimens.The orientation of the nanoparticles randomly distributed in agarose gel was also attempted under the application of a 24 kA m−1 AC magnetic field for sufficient time intervals to reach a temperature of around 48 °C and kept at these levels for 30 min by switching on/off the field. Finally, each sample was cooled down to room temperature and any modification of the SAR value owed to chain formation was evaluated by calorimetric measurements.
Magnetophoresis experiments
The magnetophoresis experiments were performed in a SEPMAG Q500mL low-gradient magnetic field (LGMF) (<100 T m−1) separation system by placing a bottle of radius 4 cm containing 500 mL of a 0.03 M aqueous nanoparticles dispersion. The specific system is based on a cylindrical cavity within an arrangement of permanent hard magnets generating a constant magnetic field gradient along the radius. The initial black-brown dispersion becomes transparent progressively, reaching a quasi-transparent final state with all particles close to the walls of the bottle. Opacity measurements were recorded using the external light source. Typical magnetic separation curves consist on a plateau corresponding to the reversible aggregation time followed by a progressive decay of the suspension opacity until 100% transparency is reached.Computational details
All the simulations were performed with the OOMMF software package,27 which allowed us to perform different types of simulations: in a quasi-static micromagnetic approach we discretised the particles and performed studies of shape and size effects. In dynamical simulations of large particle ensembles, the nanoparticles corresponded to the monodomain size, which allowed us to study the average behaviour of entire systems with and without thermal fluctuations. We used the material bulk parameters of magnetite (maghemite), with the cubic anisotropy constant KC = −11 kJ m−3, (−46 kJ m−3), and MS = 480 kA m−1 (414 kA m−1). The quasistatic simulations for the study of the threshold nanoparticles size exhibiting the coherent-reversal mechanism were performed using the energy minimization evolver with the stopping criterion set to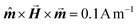 , with
, with 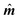 the unit magnetization direction and
the unit magnetization direction and 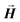 the effective magnetic field. The unit cell discretization size was taken as 0.5 nm, and the exchange constant value was 1.0 × 10−11 J m−1. The dynamical simulations were based on the macrospin approximation, where the magnetic moment
the effective magnetic field. The unit cell discretization size was taken as 0.5 nm, and the exchange constant value was 1.0 × 10−11 J m−1. The dynamical simulations were based on the macrospin approximation, where the magnetic moment 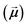 of each particle is a large macrospin proportional to its size,
of each particle is a large macrospin proportional to its size, 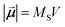 , with MS and V the saturation magnetisation and particle volume, respectively (i.e., the atomic magnetic moments rotate coherently). For the simulations of randomly dispersed systems, the easy axes of each nanoparticle are randomly distributed by means of the standard Oxs_RandomVectorField OOMMF class and no demagnetising fields were considered. The number of nanoparticles for this type of simulations was 1000. The dynamics of each particle moment are described by the Landau–Lifshitz–Gilbert equation, with the damping constant fixed as α = 0.1. An additional random field obeying the fluctuation–dissipation theorem is used to account for thermal effects.28
, with MS and V the saturation magnetisation and particle volume, respectively (i.e., the atomic magnetic moments rotate coherently). For the simulations of randomly dispersed systems, the easy axes of each nanoparticle are randomly distributed by means of the standard Oxs_RandomVectorField OOMMF class and no demagnetising fields were considered. The number of nanoparticles for this type of simulations was 1000. The dynamics of each particle moment are described by the Landau–Lifshitz–Gilbert equation, with the damping constant fixed as α = 0.1. An additional random field obeying the fluctuation–dissipation theorem is used to account for thermal effects.28
Results and discussion
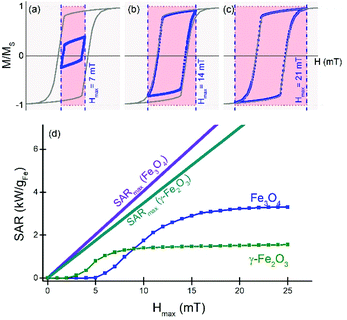
Before presenting an experimental investigation of the effects of particle morphology, characteristic size and assembly on their magnetic properties and heating capabilities, we show some idealised model calculations. The aim of the calculations is firstly to provide a general guide for the experiments and secondly to determine the limits of the current model and, therefore, to suggest further lines for experimental and theoretical developments.Theoretical framework
Considering single-domain iron-oxide nanoparticles within the macrospin approximation (coherent rotation of the atomic magnetic moments), the dominant heat dissipation mechanism is Néel reversal of the magnetization over the anisotropy energy barrier in applied field; note that the physical rotation of the particles within the viscous media has been shown to provide negligible heating in biological conditions.29,30 We note, however, that easy axis orientation via particle rotation can affect the Néel reversal mechanism.15,31–34 In the following we will analyse the attainable efficiency in electromagnetic-to-heat energy conversion in terms of Néel reversal.
First, we focus on the materials/field relationship, i.e., considering blocked nanoparticles (their energy barriers are large with respect to thermal fluctuations) and fixing their size to that corresponding to the coherent rotation mechanism. Some illustrative dynamic hysteresis loops for this ideal case of blocked nanoparticles for usual hyperthermia conditions and the corresponding maximum areas are shown in Fig. 2, for randomly dispersed magnetite (Fe3O4) crystals. Please note that while these results are independent of the particle size, the key assumption of coherent rotation in practice would correspond to sizes of tens of nm in diameter. The hysteresis loops shown in panels (a)–(c) for different Hmax values exhibit the usual features corresponding to the cubic negative anisotropy constant (KC < 0) characteristic for magnetic iron oxides; the quasistatic case limit (solid grey lines) reproduces the theoretical values for remanence and coercivity, MR = 0.87MS and HC = 0.2HK, respectively, where HK = 2|K|/μ0MS is the anisotropy field. Also shown (grey lines) is the maximum SAR achievable if the anisotropy were tuned such that HK = Hmax. It is clearly observed that increasing Hmax results in larger areas (i.e., bigger SAR), but always smaller than the maximum deliverable energy, represented by the coloured areas. This suggests that considerable increases of SAR are possible using materials with large anisotropy. The dependence of SAR vs. Hmax is shown in Fig. 2(d) together with the theoretical possible maximum SAR, which – as anticipated from the loops is significantly bigger.
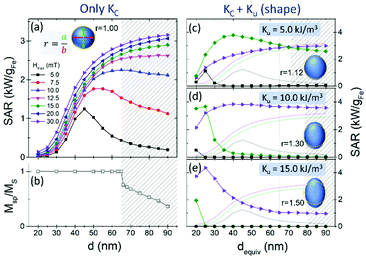
An additional aspect to consider regarding the size dependence is that for large sizes the particle magnetization will eventually undergo a transition to a noncoherent reversal process, less costly energetically and hence less efficient for hyperthermia. This is shown in Fig. 3(b), where the remanent magnetisation displays a decrease from maximum value (i.e., coherent behaviour) at about 65 nm. Larger sizes therefore do not correspond to the macrospin approximation and thus their heating performance cannot be interpreted within this assumption. This is the reason why the corresponding SAR values are shown with a shadow area in panel (a).
Regarding the anisotropy, the particle shape results in additional contributions that compete with, and often dominate, the magnetocrystalline term.35,36 Furthermore, the asymmetry in the particle geometry may also bring into play other sources of anisotropy (surface, magnetoelastic effects) as significant contributions to the effective energy barrier.37,38
Regarding purely geometrical considerations, the shape of the particle will define its interaction with the environment in two different ways: on the single-particle level, by defining its interaction with the viscous embedding media and, from a collective-system consideration, in forming closely packed arrangements as those often encountered after cell internalization, i.e. the shape of the particles will define their spatial arrangement relative to each other and therefore the heating response.
The simplest way of considering shape effects regarding anisotropy is probably by taking spherical particles and slightly modifying their aspect ratio into ellipsoidal shape, where well established relations define the extra uniaxial anisotropy contribution (Ku) coming from the magnetostatic energy depending on the aspect ratio of the ellipsoids.39 This is in addition to the intrinsic cubic anisotropy value of Kc = −11 kJ m−3. Some illustrative examples of simulated SAR values vs. size for magnetite particles with an additional uniaxial anisotropy term are shown in panels (c)–(e) within Fig. 3, for Ku = 5, 10, and 15 kJ m−3, respectively. A sketch of the ellipsoid dimensions (together with the aspect ratio) is shown in each case for illustrative purposes. To ease the comparison with the only-KC case of the (a) panel, just 3 field amplitudes are shown for each Ku value, using the same labelling as in panel (a) and the light solid lines representing the respective curves for spherical nanoparticles (Ku = 0). Examples of hysteresis loops for various particle sizes and anisotropy values are displayed in Fig. S1 within the ESI file.†
In Fig. 3 it is observed that the variation of the heating properties with nanoparticle size in the presence of an additional shape anisotropy contribution is complex but systematic. Consider first the case of spherical particles (panel (a). For the larger fields the SAR increases monotonically even in the non-coherent rotation regime. For the lowest field investigated the dependence of SAR on diameter is non-monotonic, decreasing above a critical diameter. From the Arrhenius–Néel law one can determine a critical volume using KVc = kBT × ln(f−1f0)(1 − H/HK)−3/2,40 where f is the field frequency and f0 is the pre-exponential factor of the Arrhenius–Néel law. Above the critical diameter corresponding to Vc the switching probability and hence SAR decreases as shown. For small fields Vc decreases with K consistent with panels (c)–(e). For maximum field values H > Hk, the critical volume is infinite and there will be a monotonic increase to saturation. This is borne out by the data of Fig. 3. For example, in the case of Ku = 5 kJ m−3 (Hk = 20 mT) a peak has emerged for a maximum field of 15 mT and for Ku = 10 kJ m−3 (Hk = 40 mT) a peak appears in the data for a maximum field of 30 mT. These results suggest that maximal values of SAR could be obtained by varying the anisotropy but with a greater requirement for control over the particle size. Note that for the moment we have not considered the field frequency, as its role is equivalent to that of the particle size.
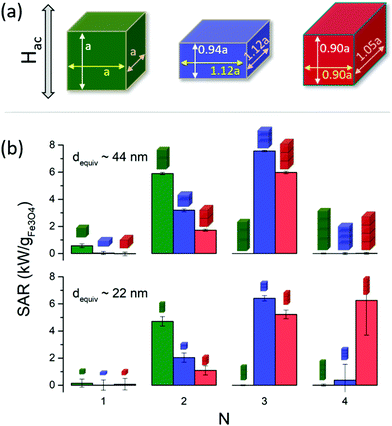
In general, the dominant interparticle interactions are magnetostatic in origin. Within close-packed arrangements the shape of the particles may define the cluster geometry, due to pure geometrical constraints. These aspects are highlighted in Fig. 4, for the case of cuboids of different aspect ratios: regular (cube), elongated, and flat (see top (a) panel). The bottom (b) panel shows how the SAR varies depending on the number of particles within the cluster (N), for clusters with chain-like shape with the field applied parallel to the chain direction. The dimensions for the different shapes are adjusted so that the particle size is always the same, and therefore the only difference is the particle shape. For completeness, two different particle sizes are considered, equivalent to spherical particles of 44 nm and 22 nm in diameter, shown in top and bottom panels within Fig. 4(b). The sizes were chosen for comparison with experiments with 44 nm particles with chain-like geometry and uniaxial-assumption simulations.
In Fig. 4, completely different trends are observed depending on the particle geometry: for cubes, the SAR increases when forming a dimer, but becomes essentially negligible for higher numbers of particles due to minor loop generation. For asymmetrical cuboids, the SAR increases for up to 3 particles for the biggest particle size, but such continues increasing up to 4 particles for the smaller sizes for the flat cuboids. It is clearly illustrated that assembling is per se a critical factor defining the hyperthermia performance, but that it also strongly depends on the particle size and shape which in turn constitute complete hyperthermia-defining aspects in their own right, as previously described.
The general scenario presented above briefly summarizes some basic aspects of key parameters defining the hyperthermia performance of magnetic nanoentities. An additional complexity is the lack of theoretical tools able to systematically approach the general problem, as only very specific cases can be efficiently treated: in general, treating the shape in a complete manner, especially for large nanoparticles, would require a micromagnetic description that current computational techniques cannot simulate on the timescale corresponding to the hyperthermia scenarios. This is particularly limiting for the case of assemblies of particles: while the dipole–dipole approach can be effective to describe for example chains of spherical particles, including the shape can only be efficiently done (in terms of computational resources) for very simple cases as for example the cuboids described here. But even this case would correspond to a very ideal situation, with no interlayer spacer between the particles, lack of size/shape polydispersity, etc. In the following we will describe some experiments assessing the potential of anisometric MNPs, including disks, ellipsoids, cubes and flowers, for MHT. We provide two different sizes of each shape, well within the range of simulated ones (equivalent volumes), and the MNPs will be studied in water or in viscous media randomly oriented or assembled with the aid of an external magnet. In agreement with the theoretical studies about the need of high fields to overcome HK, a large magnetic field intensity of 24 kA m−1 was used in our experiments.
In general, samples selected in this work are monodispersed in size with narrow size distributions (standard deviations, σ ∼0.2, except flowers of 27 nm that present σ ∼ 0.1). Such deviations are linked to the hydrothermal and solvothermal methods that offer a good control in terms of size distribution.
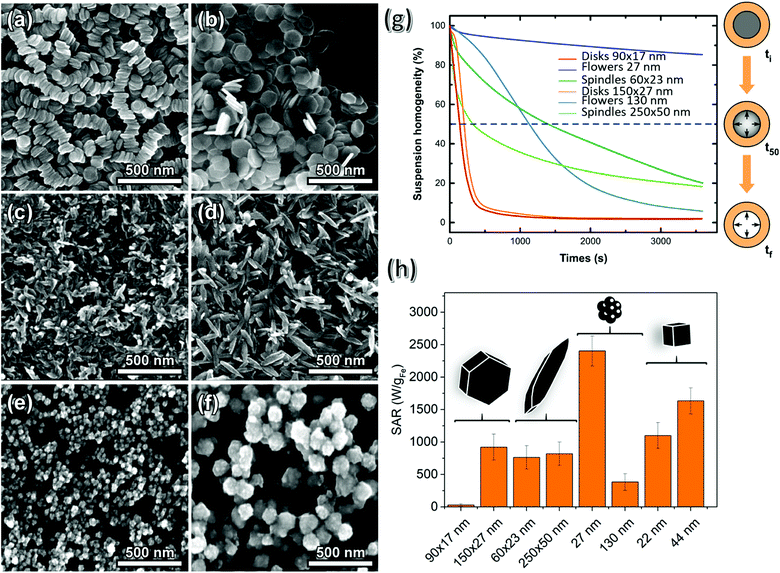
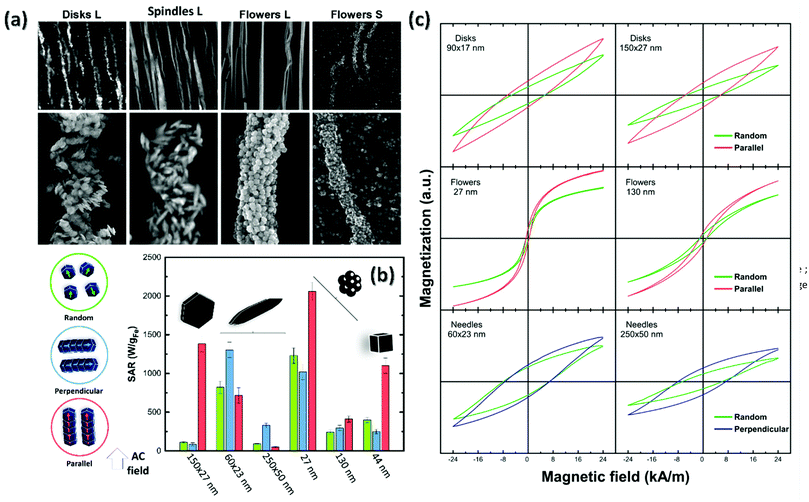
Although TEM shows no spontaneous self-arrangement for all shapes except for disks, the corresponding hydrodynamic size characterized by DLS measurements in the aqueous nanoparticle suspensions is indicative of certain aggregation degree (Fig. S3 and S4†). The highest divergence between the actual dimension derived from TEM images and the hydrodynamic diameter is found for the smaller disks, consistent with the observed lineal packing. Assuming a side-by-side orientation of disks, the hydrodynamic diameter of 255 nm is equivalent to an average linear arrangement of 15 particles. The slight increase in the hydrodynamic dimensions observed for some samples (in comparison with the dimensions determined by TEM), if so, is attributed to random aggregation due to their magnetic nature, as explained below. The relative spatial configurations of the MNPs with different morphologies were likewise studied by SEM (Fig. 5(a–f) for the disks, spindles and flowers) and, in agreement with our observations by TEM, only the disks of smaller size form linear arrangements. In addition, all the MNPs are expected to have negative surface charge at pH 7.8,47,48
The contribution of size, size distribution and structural defects of studied samples are also reflected in the measured magnetic properties. Fig. S5† shows the hysteresis loops recorded for disks, spindles and flowers at room temperature, showing that only the flowers have a superparamagnetic behaviour at room temperature. The rest of magnetic parameters (both at room temperature and at 5 K) of these morphologies are shown and compared to that of the cubes in Table 1. Magnetization values range between 81–120 Am2 kgFe−1 with the lowest values corresponding to the smallest disks and spindles for which a large number of voids were formed during the synthesis. On the other hand, the saturation magnetization for better crystalline nanoparticles approaches the bulk value for Fe3O4 or γ-Fe2O3. Flowers present a superparamagnetic behaviour at room temperature with zero coercivity in spite of their total particle sizes (around 30–130 nm). This is clearly a feature of its flower-like morphology where each particle consists of several cores, crystallographically oriented or even fused with some exchange interactions between cores.49 This is a very relevant aspect for MHT, based on the key role the internal structure may play on the relaxation mechanism. The rest of the samples show the typical ferrimagnetic characteristics of iron oxide nanoparticles with sizes well above the superparamagnetic limit (>20 nm) with a coercive field ranging between 9–20 kA m−1 at room temperature and up to 50–70 kA m−1 for disk and spindles at low temperature due to the shape anisotropy contribution.
The potential effect of an external DC magnetic field on the behaviour of the nanoparticles has been initially studied by monitoring the time-dependence of turbidity of highly diluted water dispersions ([Fe] = 0.03 mg mL−1) placed into a cylindrical cavity surrounded by permanent magnets with a radial field gradient of 100 T m−1. Fig. 5(g) shows the monitoring of the stability of the suspensions over time under the presence of the external magnetic field. The response of each system should be correlated with the magnetic moment per particle, the hydrodynamic size, and magnetic interactions. The contribution of surface charge was overridden since electrophoretic measurements indicated a similar zeta-potential for all studied samples, which appear negatively charged at the pH of separation (pH 7). In particular, disks appear very susceptible to the application of the magnetic field, with their complete and rapid separation taking place in less than 500 s. Such instability should be attributed to the high initial hydrodynamic size and the quick formation of longer chains triggered by the applied field and the high magnetic moment per particle (38–115 × 10−15 Am2 kgFe−1, Table S1†). An early loss of homogeneity (indicated by the t50 point) is also observed for large spindle particles, which is also explained by the high hydrodynamic size and magnetic moment per particle (117 × 10−15 Am2 kgFe−1). However, further separation follows a very slow rate finally meeting the steady-state separation (around 80%) for the small spindles. This is an indication of the weaker tendency for chain or aggregate formation in this sample, which exhibits a magnetic moment per particle of 6 × 10−15 Am2 kgFe−1. As expected, large flowers follow a faster separation rate than smaller ones, with the latter being only slightly affected by the applied field and remaining stable for long periods, probably due to their low hydrodynamic diameter and small magnetic moment per particle (4 × 10−15 Am2 kgFe−1 against 400 × 10−15 Am2 kgFe−1 for the larger flowers). Low interparticle interactions in the flowers could be also responsible for the slower separation suggesting the absence of big aggregates from the beginning.
The evaluation of the magnetic hyperthermia efficiency in 2 mgFe mL−1 water dispersions under an AC field is summarized in Fig. 5(h) and all the heating/cooling curves of the different samples are found in Fig. S6.† With respect to the size for a given shape, the general trend is that an increase in the dimensions leads to an increase of SAR (as shown by the disks, the spindles and the cubes), this being more marked for the disks (although aggregation of the small disks led to small values of SAR which were difficult to measure accurately). In the case of large disks and large spindles, maximum values of SAR were 800 and 750 W gFe−1, respectively. It is also worth noticing that the spindles heat very similarly for such different sizes probably due to incoherent magnetisation rotation resulting from the elongated shape. The particular case of the nanoflowers does not follow the trend predicted by the theoretical calculations used in this work because the magnetic properties of this kind of MNP (packed crystallites), critically depend on the size, orientation and contact of the cores inside the flower, giving rise, as in the case of the smaller flowers, to a collective magnetic behaviour that accounts for such high SAR values in aqueous solutions, reaching 2400 W gFe−1.50 The corresponding heating rate of large flowers with smaller cores does not exceed 300 W gFe−1. Finally, the cubic shape also gives rise to SAR values that exceed 1000 W gFe−1 for the smallest cubes and 1500 W gFe−1 for the larger ones. This shape has proven to be highly efficient for MHT.51–53
In order to compare the different shapes, the SAR values have been normalized by the volume of each particle (Tables S2 and 3†), establishing the following order in efficiency for MHT: flower (small) > cube (small) > spindle (small) > cube (big) > disk (big). In summary, randomly oriented anisometric MNPs produced by an indirect synthesis protocol (hydrothermal/solvothermal + reduction), as in Fig. 5 in water, do not surpass, in terms of heating efficiency, the most promising MNPs produced so far by direct hydrothermal/solvothermal synthesis of magnetite: nanoflowers. On the other hand, SAR values of small spindles do exceed those of cubic shape. Next, we gelatinise MNPs with different shapes in agarose matrix, which represents a tumour tissue phantom system, and assembly the MNPs under a magnetic field gradient.
All MNPs presented a certain degree of assembly, depending on the geometry and the dimensions of the MNPs. Electron microscopy has allowed to identify three kinds of alignment. Large disks and large spindles assembled forming micron-sized chains. MNPs have a second-order alignment, meaning that they display a short-range orientation with respect to chains (Fig. 7(a). While disks stacked in piles, spindles appear oriented at different angles with respect to the main chain direction. The second kind of alignment is that of symmetrical nanoparticles: both large and small flowers, as well as 44 nm cubes (Fig. S9†), which are aligned with the direction of the applied field not only macroscopically but also at the nanoscale level. This is also the case of 130 nm nanoflowers, which form highly ordered assemblies (Fig. S10(a)†). Obviously, symmetrical shape favours such arrangement since their aspect ratio is equal to 1. On the other hand, MNPs with high aspect ratio (A. R. >2–6), such as disks, cannot promote such ordered structures (Fig. S10(b)† shows in detailed the disks are not forming straight pillars but, although interacting face to face with each other, they are displaced with each other). While the large flowers, disks and nanocubes assemble in micron-size chains, small flowers and spindles form nano-size chains (Fig. S11 and 12†). We surmise that this is due to the thermal mobility of these samples, which competes with the orientation forces under the influence of an external magnetic field gradient, thus, they form isolated nano-size chains. Also, “free MNPs” (not belonging to any chain) at random positions, or even in large aggregates in the agar, are present, which in the latter case are most probably related to the SEM sample preparation.
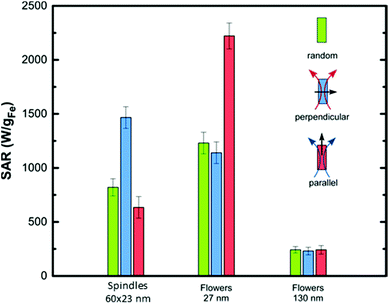
Moreover, the heat released by the assemblies of anisometric NPs in water was compared to that of the same anisometric NPs in agar viscous media and random configuration. It should be noted that TEM images of the NPs in water show that none of the morphologies/sizes tend to form spontaneous assemblies except from the 90 × 18 nm disks (Fig. 5). However, SEM images of the NPs in agar show a fraction of small random aggregates (Fig. S7 and S8†), which may be hard to avoid in spite of the sonication at high temperature for long time (see Experimental section for details). As such, the dispersion of MNPs in agarose (randomly) indeed leads to a reduction of the SAR values (Fig. 7(b), green bars), with the exception of small spindles, and the big flowers, whose heating efficiency remains unchanged, and it could be a consequence of the increase of the viscosity of the media and, to a less extend, to the formation of small aggregates during the immobilisation process. This fact reflects the mechanisms the different MNPs follow to relax, i.e., small spindles and big flowers are relaxing purely by Néel mechanism, and therefore the heat efficiency is viscous independent. Importantly, small flowers despite such decrease in volume, still have SAR values of approximately 1400 W gFe−1. On the other hand, the pre-orientation with respect to the relative direction of the applied AC magnetic field appears as the key parameter to improve magnetic hyperthermia of immobilized particles. For large disks, a significant SAR enhancement (1300 W g−1) is measured when the AC field is parallel to the particle orientation. Such a SAR value is up to 10 times larger than that measured for immobilized particles in the random state and even exceeds the value obtained for water dispersion (800 W g−1). Considering the combination of high field amplitude and frequency used in this study, results suggest that for disks, hysteresis losses dominate versus Brownian-origin heating while the SAR value follows a rapid increase as the angle between the AC field and the disk stacking tends to zero, i.e., the field is aligned with the stacks. The low efficiency for smaller disks should be attributed to the lower anisotropy barrier due to thermal fluctuations at such sizes and the induced decoupling of magnetization. In symmetrical particles like the flowers and cubes, enhancement by 2–3 times is obtained also in AC field applied parallel to the particle orientation.
However, in spindles, the perpendicular AC field application to the particle orientation seems to favour SAR elevation. This is in good agreement with the experimental and theoretical estimations obtained for similar particles intentionally oriented in agarose by applying an AC field which simultaneously maintained the temperature above 46 °C.15 The spontaneous perpendicular orientation during treatment was found responsible for the significant increase of hysteresis losses (1.5 times) and therefore, heat generation. Proportionally, the additional contribution of AC field in further orientation of spindle particles beyond that observed in Fig. 7(a), should be also assumed.
A qualitative explanation of heating rate enhancement may be given through minor loops recorded for the randomly immobilized and the field-oriented samples in the agarose matrix (Fig. 7(c)). DC minor loops were measured in the agarose-immobilized samples in order to obtain a qualitative impression on the effect of orientation to the maximum value of hysteresis losses by comparing the randomly distributed to the oriented nanoparticles. For samples with hysteresis losses representing the dominant magnetic heating mechanism, the evaluation appears as a reliable way to predict proportionally the behavior of oriented samples under AC magnetic field conditions. The hysteresis losses appear to increase when the oriented specimens are placed to the favourable direction of the DC field (as in the case of 44 nm nanocubes for a parallel orientation, Fig. S13†). In the case of the disks and the spindles this increase is found in the parallel and perpendicular configurations, respectively. Orientation perpendicular to a static dc field is unexpected and counter-intuitive. Further work is needed to understand the phenomenon, as it is expected to be defined by a delicate balance between particle aspect ratio, interaction strength, and field amplitude.56
Oriented samples seem to enable a faster magnetization reversal as better shown for the flowers. It is also characteristic that the minor loop for oriented small spindles is only slightly different to the random state for which a preservation of the water dispersion's SAR value was observed. Enhancement of the effective anisotropy parallel to the chain direction explains the improvement of SAR in oriented disks and flowers. Positive dipolar interaction is expected to dominate the magnetic behaviour of these aggregates having larger anisotropy along the particle stacking or chaining as was previously observed for barium hexaferrite platelets and cubes.4,57 However, for spindle particles, higher heating rates occur towards the perpendicular direction of the chains independently of the particle size. In this case, demagnetizing dipolar interactions may happen due to the aggregation of the spindle particles avoiding the formation of well-ordered structures of particles with longest dimension aligned with the DC field. Instead, spindles appear tilted or perpendicular to the DC field direction. In this context, the SAR enhancement observed in the perpendicular direction is attributed to the spindles oriented perpendicularly to the chain direction, as those observed in the SEM image and the origin of the differences between the anisometric particles is the determining role of the shape anisotropy that may counterbalance the effect of chain formation. Again, when the SAR values are normalized by the volume of each MNPs (Tables S2 and 3†), we observe the same order in heating efficiency: nanoflower (small) > spindle (small) > cube (big) > disk (big). Importantly, nano-spindles and nanoflowers maximize the heating rates up to 1.5 times using assemblies in perpendicular and parallel direction, respectively, with respect to the field. Nanocubes have a 2-fold increase in the parallel direction. Finally, we observe a striking 14-fold increase in the case of the disks. Such variety of behaviours reflects the delicate interplay between easy axes arrangement and interparticle interactions, which has been experimentally shown it can enhance or reduce the effective anisotropy58 responsible for the local energy barrier, and consequently the achievable heat release.59
In all cases, the rotation of magnetization orientation is against the anisotropy forces. But the magnetic anisotropy of an assembly of anisometric nanoparticles is a complicated combination of magneto crystalline and surface anisotropy, and inter particle interactions. Here, particle sizes are within the critical size for single-domain behaviour assuring the maximum coercivity and far from the superparamagnetic limit assuring high saturation magnetization except for the biggest flowers that are composed of small cores (around 5 nm in diameter).
It is important to keep in mind that while the reorientation per se plays a secondary role in heating (as shown in many works),29,30,60 it may completely change the amount of dissipated energy via Néel rotation. Consider, for example, the extreme cases of uniaxial-anisotropy particles with the easy axes parallel or perpendicular to the AC field: the parallel-aligned case would lead to maximum heating (in case major-loop conditions are fulfilled),61 whereas the perpendicular-aligned case would lead to no heating (no energy barrier to jump – i.e. no energy cost).62 This is to say, physical rotation of the particle may allow the transition from poorly dissipative regime of linear magnetization-field response to the nonlinear one, responsible for much higher losses.33 Since MNPs are likely randomly oriented when dispersed within the crowded biological environment, which implies a distribution in local heating efficiency,63 considering the reorientation of the particles towards the most effective heat-dissipation configuration constitutes a rather important aspect to consider for magnetic-hyperthermia related applications.31,34,64,65
In summary, in this work we have prepared and compared assemblies of MNPs obtained by hydrothermal and solvothermal methods, whose heat release seems promising for hyperthermia applications, not only in biomedicine but also in catalysis or environmental remediation. Along in this line, we study and compare relevant magnetic properties (DC hysteresis loops) and migration properties of all the MNPs (under the presence of a magnetic field gradient), as these properties are responsible for their assembly.
The theoretical approach suggests clear directions for experimental developments in MHT, as for example the existence of an optimal field amplitude depending solely on the particle properties, the critical size depending on the particle anisotropy, or the optimum chain sizes that should be experimentally observable. Also, it is interesting that the largest SAR occurs for the case of small flowers where the simulations show that the reversal mechanism is coherent. Firstly, note that the quasi-static hysteresis loops of Fig. 7(c) show that the flowers have the smallest hysteresis are and therefore a low expected SAR, which is inconsistent with Fig. 7(b). The model calculations (on the timescale of SAR experiments) predict a large value of SAR in Fig. 3, essentially because hysteresis develops at the short timescale.
Experimentally, the small flowers have been shown to consist of small sub-grains with crystallographically aligned easy axes. We can surmise that the structure gives rise to ‘supermoments’ avoiding the anisotropy reduction arising from misoriented polycrystals as is usually the case (for example for the 130 nm flowers). These would be expected to couple strongly with the ac field and any applied external field, thereby enhancing the SAR value, while the granular nature of the flower sub-structure precludes non-uniform magnetisation states and the consequent reduction of SAR. A similar dynamic effect is shown in Fig. 4, where it is seen that increasing the length of the chain of cubes gives rise to a non-monotonic variation of SAR, with the initial increase cancelled out by transition to minor loop behaviour with increasing chain length. This suggests that both the flower structure and the chain-assembly have well-defined intrinsic advantages which could be enhanced through design and optimisation.
Conclusions
Anisometric MNPs could be the ideal agents to optimize the response to external AC fields for magnetic fluid hyperthermia. Theoretically, it is shown that by increasing Hmax considerable increases in SAR are possible using materials with large shape anisotropy. The main limitation is the particle size since large particles undergo non-coherent magnetisation rotation that may work to the detriment of the SAR. Looking at the assembling effect on SAR, nanoparticle shape is the main limitation due to the formation of anisometric aggregates whose SAR depends on the applied field direction. Experimentally, cubic NPs obtained through non-hydrolytic synthesis routes and nanoflowers have demonstrated unrivalled hyperthermia performance, however this work reveals the potential of other anisometric shapes, especially disk and spindles produced by hydrolytic synthesis routes, whose assemblies achieve SAR values as high as 1400 and 1300 W gFe−1, respectively, in viscous (100 mPa s) media that mimics tumour microenvironments. Among these samples, attending to the SAR data normalized by the particle volume, small spindles clearly stand out as efficient nanoheaters. While nanodisks multiply their heat performance when they form pillar-like assemblies with a direction parallel to that of the applied AMF, spindles multiply their performance when their assemblies are perpendicular with respect to the applied AMF direction.Although the AMF conditions used in this work are above the clinical safe limit (usually, an H × f of maximum 5 × 109 A m−1s−1 should be satisfied), the presented characterization in viscous media mimicking tumour microenvironment and the comparison of our MNPs with gold standards of MNPs (like nanocubes and nanoflowers) is useful and expands the knowledge on MHT, deepening in the role of MNPs’ size, shape and orientation under external magnetic field gradients, presenting different hyperthermia scenarios. Nevertheless, the most promising morphologies presented in this work (nanoflowers and spindles) have been already characterized with clinical relevant field amplitude and frequency conditions (10–50 mT and 100–200 kHz), keeping therefore the H × f within the bio-safe range avoiding Eddy currents (<5 × 109 A m−1 s−1). In the case of nanoflowers, the reported SAR values are around 500 W gFe−1 (H × f = 4.40 × 109 A m−1 s−1) for a size of 24 nm;50 and for spindles, the reported SAR values are around 400 W gFe−1 (H × f = 4.80 × 109 A m−1 s−1) for the dimensions of 87 × 16 nm.9 This work opens the possibility of further enhance those values, even in viscous media, through the sample's pre-assembly forming nano-size chains (in the case of the flowers and the spindles chains, respectively, when oriented parallel or perpendicular with respect to the applied AMF). In addition, this work successfully achieves heating rates exceeding those using non-spherical Fe3O4/γ-Fe2O3 nanoparticles prepared by aqueous chemistry in highly viscous media.
As a final remark, we would like to highlight a recent work by N. Mille et al.66 on the dynamics of chain formation during magnetic hyperthermia, showing that the chain structures may evolve over several seconds, in good agreement with our experimental results shown in Fig. 8. Such dynamical behaviour has a direct impact on the heating performance, as clearly illustrated in Fig. 4(b) theoretically, where large differences in heating are reported by small variations in chain length. Considering the interplay of nano-structuring dynamics with particle size and shape constitutes an intriguing research line for further studies, both from the experimental and theoretical points of view.
Author contributions
HG, DS and MPM conceived of the presented idea. HG and MPM carried out the synthesis and characterisation of the MNPs. KS, MA, EM and LB carried out the SEM images, VSM and SAR experiments. EM carried out the alignment experiments. DS, RC and OCF developed the theory and performed the computations. All authors discussed the results and contributed to the final manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
K. S. acknowledges Stavros Niarchos Foundation for financial support. SQUID measurements received funding from the EU-H2020 research and innovation program under grant agreement no 654360 having benefitted from the access provided by CSIC-ICMAB in Barcelona within the framework of the NFFA-Europe Transnational Access Activity. This work was also partially supported by grants from the MINEICO (MAT2017-88148R to M. P. Morales; Severo Ochoa Program (CEX2019-000917-S), RTI2018-099960-B-I00 to Ll. Balcells), the Spanish Agencia Estatal de Investigación (PID2019-109514RJ-100 to D. Serantes) and from the EU, H2020 program through HOTZYME-829162 project. E. M. acknowledges financial support from the Madrid Government (Comunidad de Madrid-Spain) under the Multiannual Agreement with Universidad Autónoma de Madrid in the line of action encouraging youth research doctors, in the context of the V PRICIT (Regional Programme of Research and Technological Innovation, SI1-PJI-2019-00366).Notes and references
- J.-P. Fortin, C. Wilhelm, J. Servais, C. Ménager, J.-C. Bacri and F. Gazeau, J. Am. Chem. Soc., 2007, 129, 2628–2635 CrossRef CAS PubMed.
- A. G. Roca, L. Gutiérrez, H. Gavilán, M. E. F. Brollo, S. Veintemillas-Verdaguer and M. del Puerto Morales, Adv. Drug Delivery Rev., 2019, 138, 68–104 CrossRef CAS PubMed.
- S. K. Avugadda, M. E. Materia, R. Nigmatullin, D. Cabrera, R. Marotta, T. F. Cabada, E. Marcello, S. Nitti, E. J. Artés-Ibañez and P. Basnett, Chem. Mater., 2019, 31, 5450–5463 CrossRef CAS PubMed.
- D. Serantes, K. Simeonidis, M. Angelakeris, O. Chubykalo-Fesenko, M. Marciello, M. Del Puerto Morales, D. Baldomir and C. Martinez-Boubeta, J. Phys. Chem. C, 2014, 118, 5927–5934 CrossRef CAS.
- E. A. Périgo, G. Hemery, O. Sandre, D. Ortega, E. Garaio, F. Plazaola and F. J. Teran, Appl. Phys. Rev., 2015, 2, 041302 Search PubMed.
- P. Guardia, R. Di Corato, L. Lartigue, C. Wilhelm, A. Espinosa, M. Garcia-Hernandez, F. Gazeau, L. Manna and T. Pellegrino, ACS Nano, 2012, 6, 3080–3091 CrossRef CAS PubMed.
- Z. Nemati, J. Alonso, L. Martinez, H. Khurshid, E. Garaio, J. Garcia, M. Phan and H. Srikanth, J. Phys. Chem. C, 2016, 120, 8370–8379 CrossRef CAS.
- L. Lartigue, P. Hugounenq, D. Alloyeau, S. P. Clarke, M. Lévy, J. C. Bacri, R. Bazzi, D. F. Brougham, C. Wilhelm and F. Gazeau, ACS Nano, 2012, 6, 10935–10949 CrossRef CAS PubMed.
- M. Avolio, H. Gavilán, E. Mazario, F. Brero, P. Arosio, A. Lascialfari and M. P. Morales, Phys. Chem. Chem. Phys., 2019, 21, 18741–18752 RSC.
- R. Das, J. Alonso, Z. Nemati Porshokouh, V. Kalappattil, D. Torres, M.-H. Phan, E. Garaio, J. A. n. García, J. L. Sanchez Llamazares and H. Srikanth, J. Phys. Chem. C, 2016, 120, 10086–10093 CrossRef CAS.
- Y. Yang, X. Liu, Y. Lv, T. S. Herng, X. Xu, W. Xia, T. Zhang, J. Fang, W. Xiao and J. Ding, Adv. Funct. Mater., 2015, 25, 812–820 CrossRef CAS.
- D. Cabrera, A. Lak, T. Yoshida, M. Materia, D. Ortega, F. Ludwig, P. Guardia, A. Sathya, T. Pellegrino and F. Teran, Nanoscale, 2017, 9, 5094–5101 RSC.
- D. Cabrera, A. Coene, J. Leliaert, E. J. Artés-Ibáñez, L. Dupré, N. D. Telling and F. J. Teran, ACS Nano, 2018, 12, 2741–2752 CrossRef CAS.
- D. Serantes, R. Chantrell, H. Gavilán, M. del Puerto Morales, O. Chubykalo-Fesenko, D. Baldomir and A. Satoh, Phys. Chem. Chem. Phys., 2018, 20, 30445–30454 RSC.
- K. Simeonidis, M. P. Morales, M. Marciello, M. Angelakeris, P. de La Presa, A. Lazaro-Carrillo, A. Tabero, A. Villanueva, O. Chubykalo-Fesenko and D. Serantes, Sci. Rep., 2016, 6, 1–11 CrossRef PubMed.
- P. B. Balakrishnan, N. Silvestri, T. Fernandez-Cabada, F. Marinaro, S. Fernandes, S. Fiorito, M. Miscuglio, D. Serantes, S. Ruta and K. Livesey, Adv. Mater., 2020, 32, 2003712 CrossRef CAS PubMed.
- M. Marciello, V. Connord, S. Veintemillas-Verdaguer, M. A. Vergés, J. Carrey, M. Respaud, C. J. Serna and M. P. Morales, J. Mater. Chem. B, 2013, 1, 5995–6004 RSC.
- H. Gavilán, O. Posth, L. K. Bogart, U. Steinhoff, L. Gutiérrez and M. P. Morales, Acta Mater., 2017, 125, 416–424 CrossRef.
- H. Gavilán, A. Kowalski, D. Heinke, A. Sugunan, J. Sommertune, M. Varón, L. K. Bogart, O. Posth, L. Zeng and D. González-Alonso, Part. Part. Syst. Charact., 2017, 34, 1700094 CrossRef.
- J. Wells, O. Kazakova, O. Posth, U. Steinhoff, S. Petronis, L. K. Bogart, P. Southern, Q. Pankhurst and C. Johansson, J. Phys. D: Appl. Phys., 2017, 50, 383003 CrossRef.
- Z. Li, F. Yang and Y. Yin, Adv. Funct. Mater., 2020, 30, 1903467 CrossRef CAS.
- E. Wetterskog, C. Jonasson, D.-M. Smilgies, V. Schaller, C. Johansson and P. Svedlindh, ACS Nano, 2018, 12, 1403–1412 CrossRef CAS PubMed.
- C. Jiang, C. W. Leung and P. W. Pong, Nanoscale Res. Lett., 2016, 11, 1–12 CrossRef.
- M. Grzelczak, J. Vermant, E. M. Furst and L. M. Liz-Marzán, ACS Nano, 2010, 4, 3591–3605 CrossRef CAS PubMed.
- G. Singh, H. Chan, A. Baskin, E. Gelman, N. Repnin, P. Král and R. Klajn, Science, 2014, 345, 1149–1153 CrossRef CAS PubMed.
- Y. Luengo, M. d. P. Morales, L. Gutiérrez and S. Veintemillas-Verdaguer, J. Mater. Chem. C, 2016, 4, 9482–9488 RSC.
- M. J. Donahue and D. G. Porter, OOMMF User's Guide, Version 1, Interagency Report NISTIR 6376, 1999 Search PubMed.
- O. Lemcke, ThetaEvolve module for OOMMF releases: 1.2a3, 2004 Search PubMed.
- R. Di Corato, A. Espinosa, L. Lartigue, M. Tharaud, S. Chat, T. Pellegrino, C. Ménager, F. Gazeau and C. Wilhelm, Biomaterials, 2014, 35, 6400–6411 CrossRef CAS PubMed.
- D. Soukup, S. Moise, E. Céspedes, J. Dobson and N. D. Telling, ACS Nano, 2015, 9, 231–240 CrossRef CAS PubMed.
- H. Mamiya and B. Jeyadevan, Sci. Rep., 2011, 1, 1–7 CrossRef PubMed.
- N. Usov and B. Y. Liubimov, J. Appl. Phys., 2012, 112, 023901 CrossRef.
- S. A. Shah, D. B. Reeves, R. M. Ferguson, J. B. Weaver and K. M. Krishnan, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 094438 CrossRef PubMed.
- G. Shi, R. Takeda, S. B. Trisnanto, T. Yamada, S. Ota and Y. Takemura, J. Magn. Magn. Mater., 2019, 473, 148–154 CrossRef CAS.
- N. Usov and Y. B. Grebenshchikov, J. Appl. Phys., 2009, 106, 023917 CrossRef.
- G. Vallejo-Fernandez and K. O'Grady, Appl. Phys. Lett., 2013, 103, 142417 CrossRef.
- D. Garanin and H. Kachkachi, Phys. Rev. Lett., 2003, 90, 065504 CrossRef CAS PubMed.
- R. Yanes, O. Chubykalo-Fesenko, H. Kachkachi, D. Garanin, R. Evans and R. Chantrell, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 064416 CrossRef.
- B. D. Cullity and C. D. Graham, Introduction to magnetic materials, John Wiley & Sons, 2011 Search PubMed.
- R. Victora, Phys. Rev. Lett., 1989, 63, 457 CrossRef PubMed.
- M. K. Kuimova, S. W. Botchway, A. W. Parker, M. Balaz, H. A. Collins, H. L. Anderson, K. Suhling and P. R. Ogilby, Nat. Chem., 2009, 1, 69 CrossRef CAS PubMed.
- L. Gutiérrez, L. De La Cueva, M. Moros, E. Mazarío, S. De Bernardo, J. M. De La Fuente, M. P. Morales and G. Salas, Nanotechnology, 2019, 30, 112001 CrossRef PubMed.
- L. Beola, L. Asín, C. Roma-Rodrigues, Y. Fernández-Afonso, R. M. Fratila, D. Serantes, S. Ruta, R. W. Chantrell, A. R. Fernandes and P. V. Baptista, ACS Appl. Mater. Interfaces, 2020, 12, 43474–43487 CrossRef CAS PubMed.
- C. Muñoz-Menendez, D. Serantes, O. Chubykalo-Fesenko, S. Ruta, O. Hovorka, P. Nieves, K. Livesey, D. Baldomir and R. Chantrell, Phys. Rev. B, 2020, 102, 214412 CrossRef.
- P. Torche, C. Munoz-Menendez, D. Serantes, D. Baldomir, K. Livesey, O. Chubykalo-Fesenko, S. Ruta, R. Chantrell and O. Hovorka, Phys. Rev. B, 2020, 101, 224429 CrossRef CAS.
- A. F. Bakuzis, L. C. Branquinho, L. L. e. Castro, M. T. d. A. e. Eloi and R. Miotto, Adv. Colloid Interface Sci., 2013, 191, 1–21 CrossRef PubMed.
- M. A. Vergés, R. Costo, A. Roca, J. Marco, G. Goya, C. Serna and M. Morales, J. Phys. D: Appl. Phys., 2008, 41, 134003 CrossRef.
- A. M. Mebert, C. Aimé, G. S. Alvarez, Y. Shi, S. A. Flor, S. E. Lucangioli, M. F. Desimone and T. Coradin, J. Mater. Chem. B, 2016, 4, 3135–3144 RSC.
- P. Bender, D. Honecker and L. Fernández Barquín, Appl. Phys. Lett., 2019, 115, 132406 CrossRef.
- P. Hugounenq, M. Levy, D. Alloyeau, L. Lartigue, E. Dubois, V. r. Cabuil, C. Ricolleau, S. p. Roux, C. Wilhelm and F. Gazeau, J. Phys. Chem. C, 2012, 116, 15702–15712 CrossRef CAS.
- P. Guardia, A. Riedinger, S. Nitti, G. Pugliese, S. Marras, A. Genovese, M. E. Materia, C. Lefevre, L. Manna and T. Pellegrino, J. Mater. Chem. B, 2014, 2, 4426–4434 RSC.
- C. Martinez-Boubeta, K. Simeonidis, A. Makridis, M. Angelakeris, O. Iglesias, P. Guardia, A. Cabot, L. Yedra, S. Estradé, F. Peiró, Z. Saghi, P. A. Midgley, I. Conde-Leborán, D. Serantes and D. Baldomir, Sci. Rep., 2013, 3, 1652 CrossRef PubMed.
- D. Niculaes, A. Lak, G. C. Anyfantis, S. Marras, O. Laslett, S. K. Avugadda, M. Cassani, D. Serantes, O. Hovorka, R. Chantrell and T. Pellegrino, ACS Nano, 2017, 11, 12121–12133 CrossRef CAS PubMed.
- E. Alphandéry, I. Chebbi, F. Guyot and M. Durand-Dubief, Int. J. Hyperthermia, 2013, 29, 801–809 CrossRef PubMed.
- B. Sanz, M. P. Calatayud, E. De Biasi, E. Lima Jr., M. V. Mansilla, R. D. Zysler, M. R. Ibarra and G. F. Goya, Sci. Rep., 2016, 6, 38733 CrossRef CAS PubMed.
- A. Satoh, Colloids Surf., A, 2016, 504, 393–399 CrossRef CAS.
- M. Drofenik, M. Kristl, A. Žnidaršič, D. Hanžel and D. Lisjak, J. Am. Ceram. Soc., 2007, 90, 2057–2061 CrossRef CAS.
- V. Aquino, L. Figueiredo, J. Coaquira, M. Sousa and A. Bakuzis, J. Magn. Magn. Mater., 2020, 498, 166170 CrossRef CAS.
- I. Conde-Leboran, D. Baldomir, C. Martinez-Boubeta, O. Chubykalo-Fesenko, M. del Puerto Morales, G. Salas, D. Cabrera, J. Camarero, F. J. Teran and D. Serantes, J. Phys. Chem. C, 2015, 119, 15698–15706 CrossRef CAS.
- T. E. Torres, E. Lima, M. P. Calatayud, B. Sanz, A. Ibarra, R. Fernández-Pacheco, A. Mayoral, C. Marquina, M. R. Ibarra and G. F. Goya, Sci. Rep., 2019, 9, 1–11 CAS.
- I. Conde-Leborán, D. Serantes and D. Baldomir, J. Magn. Magn. Mater., 2015, 380, 321–324 CrossRef.
- D. Serantes, D. Baldomir, M. Pereiro, B. Hernando, V. Prida, J. S. Llamazares, A. Zhukov, M. Ilyn and J. González, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 134421 CrossRef.
- C. Munoz-Menendez, D. Serantes, J. M. Ruso and D. Baldomir, Phys. Chem. Chem. Phys., 2017, 19, 14527–14532 RSC.
- S. Ota and Y. Takemura, Appl. Phys. Express, 2017, 10, 085001 CrossRef.
- M. Suwa, A. Uotani and S. Tsukahara, J. Appl. Phys., 2019, 125, 123901 CrossRef.
- N. Mille, D. De Masi, S. Faure, J. Asensio, B. Chaudret and J. Carrey, Appl. Phys. Lett., 2021, 119, 022407 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nr03484g |
| This journal is © The Royal Society of Chemistry 2021 |