Adsorption properties of acetylene, ethylene and ethane in UiO-66 with linker defects and NO₂ functionalization

Abstract

Separation of small hydrocarbon gases is crucial for many industrial processes, but the high energy demand of current separation techniques encourages exploration of alternative sorption-based approaches. Here, we investigate the metal organic framework UiO-66(Zr) as possible solid adsorbent with a focus on the fundamental sorption mechanisms of C₂ hydrocarbons in the presence of linker defects and NO₂ functionalization. To this end, we directly measure heats of adsorption with calorimetry and correlate our results with ab initio calculations. In particular, we study adsorption of C₂H₂, C₂H₄ and C₂H₆ at 293 K and 195 K. At 293 K, the measured low-coverage enthalpy is found to be an average enthalpy of multiple adsorption sites. However, at 195 K, the low-coverage enthalpy corresponded to the strongest binding site, i.e. the linker defect site. We find that C₂H₂ exhibits the highest adsorption enthalpy with a significant gap of ∼6 kJ mol⁻¹ to C₂H₄ and ∼9 kJ mol⁻¹ to C₂H₆. Our ab initio calculations show excellent agreement with our experiments and are crucial to uncover the mechanisms that lead to the observed differences in binding affinity as a function of coverage. We also find that binding enthalpies increase for all three gases by adding –NO₂ functional groups, which even further increase the gap to ∼9 kJ mol⁻¹ and ∼10 kJ mol⁻¹ for C₂H₄ and C₂H₆, respectively. Our findings provide mechanistic insight that suggests that linker defects in UiO-66(Zr) have promise to improve its effectiveness as a solid adsorbent in C₂H₂, C₂H₄ and C₂H₆ applications and that functionalization may be used to increase specificity.

---

1 Introduction

C₂H₂, C₂H₄ and C₂H₆ are amongst the most widely used hydrocarbon gases. They form vital components for various industrial processes such as the chemical conversion to other hydrocarbons,^1,2 formation of aromatic compounds,³ synthesis of commercially useful products (e.g. ethylene glycol),⁴ production of various polymers including polyethene, polyvinylchloride and polyester⁵ and as fuel for power generation.^6–8 During natural gas extraction a mixture of C₂H₂, C₂H₄ and C₂H₆ is obtained that has to be separated and purified before use. C₂H₂/C₂H₄ and C₂H₂/C₂H₆ separation is of particularly interest due to their extensive use in many feedstock industrial processes that require them to be in highly pure form.‡ Hence, purification and separation has become a critical step for the natural gas and petrochemical industries. Unfortunately, the most common separation method for light hydrocarbons, i.e. cryogenic separation,^9–11 requires large amounts of energy; 45–55% of industrial energy consumption in the US is taken up by gas separation processes, making up 10–15% of the total US energy consumption.¹² Replacing cryogenic separation processes with less energy intense methods, such as solid adsorbents and membrane-based separation, have thus seen a surge of interest.^13–18

Metal organic frameworks (MOFs) have emerged not only as alternative solid adsorbent for gas separation, purification and capture,^19–27 but they are also interesting for catalysis,^28–31 chemical sensing/detection,^32,33 drug delivery,^34–36 multiferroics^37–39 and electrochemical energy storage.^40,41 This vast versatility results from their nanoporous and modular building-block nature, which can be tailored chemically and structurally. In addition, MOFs are relatively easy to synthesize with high yield, versatility and reproduciblity.⁴² Over the last decade, their use for industrial separation of hydrocarbons has made significant progress^18,43–46 and separation of C₂H₂, C₂H₄ and C₂H₆ gas mixtures has also been reported.^47–51 In particular, UiO-66(Zr) has attracted much attention due to its stability in the presence of water and elevated temperatures,⁵² which are indispensable prerequisites for industrial petroleum applications.⁵³ In addition, this MOF exhibits a rich field of study for the effects of defects on C₂H₄/C₂H₆ capacity and selectivity.⁵¹ However, while many studies focus on the direct application of MOFs for separation, a clear understanding of the underlying sorption mechanisms at the atomistic level that govern the macroscopic sorption properties is often lacking. Our focus here is thus on uncovering fundamental sorption mechanisms of small hydrocarbons that allow UiO-66(Zr) to act as solid adsorbent. Such mechanistic understanding can provide crucial input for the design of more effective and selective MOFs for solid sorption applications.

To this end, we have synthesized UiO-66(Zr) in various states including its pure form, –NO₂ functionalized form,⁵⁴ and with linker defects to gain understanding concerning the adsorption behavior of small hydrocarbons. Our work focuses on adsorption calorimetry measurements at low temperature (195 K) and low surface coverages in order to isolate and identify the specific molecular interactions at different adsorption sites. At lower temperatures, such as 195 K, the partition function occupancy is more separated by the different adsorption sites, allowing one to distinguish the adsorption energy associated with each type of site.^55–59 Measurements at higher temperatures (293 K) typically represent some average binding enthalpy from the different adsorption sites in the MOF and complicate the analysis. In fact, partition-function occupancy-probability calculations suggest that it is likely impossible to observe minority adsorption site enthalpies that are 5 kJ mol⁻¹ higher than the majority adsorption sites at room temperature.⁵⁵ The use of an adsorption calorimetry technique is crucial for the interpretation of our results because it is more reliable at low temperatures and low surface coverages than the commonly used isosteric method.^60–62 Our directly measured C₂ adsorption enthalpies are then correlated with ab initio calculations to identify the exact mechanisms of adsorption and we find that low temperatures isolate the adsorption enthalpy of the linker defect site, the strongest but minority adsorption site. Our findings further provide mechanistic insight about the MOF loading and suggest that linker defects in UiO-66(Zr) have promise to improve its effectiveness as a solid adsorbent in C₂H₂, C₂H₄ and C₂H₆ applications and that functionalization may be used to increase specificity.

2 Methods and details

2.1 MOF synthesis

A solvothermal synthesis route was used to produce UiO-66(Zr) and NO₂-functionalized UiO-66(Zr). For UiO-66, 16.2 mmol of zirconium chloride (ZrCl₄, 99.5+%, Alfa Aesar) was dissolved in 450 mL of dimethyl formamide (DMF, 99.8%, Acros Organics) with magnetic stirring. Then 30 mL of hydrochloric acid (37% in water, Acros Organics) was slowly added to the solution while stirring, followed by 22.5 mmol of terephthalic acid (99+%, Acros Organics). The synthesis procedure for UiO-66-NO₂ was the same, except that glacial acetic acid (≥99.7%, Fisher) and 2-nitroterephthalic acid (≥99%, Aldrich) were used rather than hydrochloric acid and terephthalic acid, respectively. The acetic acid and hydrochloric acid were included in the synthesis procedure to intentionally induce linker defects.⁶³ The solutions were heated to 120 °C for 24 h, producing white precipitate. The solid was isolated from the liquid by centrifugation and then washed with methanol (99.9%, Fisher) for 120 h using a Soxhlet extractor. The washed MOF crystals were then dried under vacuum at 120 °C for 12 h. Powder X-ray diffraction patterns of the dried samples confirm the formation of UiO-66(Zr) and UiO-66(Zr)–NO₂ crystals (Fig. S1, ESI†). The presence of NO₂ groups on the linkers was confirmed by IR spectroscopy (Fig. S2, ESI†). The number of missing linker defects was determined with thermogravimetric analysis (SDT Q600, TA Instruments) (Fig. S3, ESI†). BET specific surface areas were obtained with a Tristar II 3020 surface area analyzer (Micromeritics) by N₂ adsorption at 77 K (Table S1, ESI†).

2.2 Calorimetry

Approximately 1.2 g of dried MOF was loaded into a glass calorimeter cell and activated by heating under vacuum at 160 °C for 24 h. The activation of the sample leads to removal of all hydrogen atoms from the Zr metal clusters and creates a dehydroxylated UiO-66(Zr) sample. The structural differences between the hydroxylated and dehydroxylated versions are discussed e.g. in 64. The Tian-Calvet adsorption calorimeter used in this work was a home-built system for the direct measurement of heats of adsorption. The sample cell was surrounded by five 1 in² heat flux sensors (C-LT-1 Thermal Flux Meters, ITI Corporation) to measure heat flow during the adsorption event, and pressure gauges were used to measure pressure in the dosing loop and calorimeter cell. Prior to conducting calorimetry experiments, the free volume of the cell with sample was measured using He. Samples were lightly pressed into wafers before being placed into the pyrex sample cell. Several layers of glass beads were placed on top of the sample to prevent heat loss out the top of the cell. The thermal flux meters were sandwiched between the sample cell and a large aluminum block (∼7 kg), which served as a heat sink. Thermal paste was coated on all thermal flux-meter surfaces to ensure good heat transfer between the sample cell, thermal flux meters, and heat sink. The aluminum block heat sink provides a large thermal mass for rapid heat dissipation and essentially maintains an isothermal condition during the course of the adsorption experiment. The system was enclosed in an insulating container and the temperature was equilibrated prior to experimentation. For experiments conducted at 195 K, the insulating container was filled with solid carbon dioxide. Upon dosing adsorbate into the sample cell, heat flow was continuously recorded over time until the cell pressure equilibrated and negligible heat flow was detected. The total heat flow during adsorption was calculated by integrating the heat flow as a function of time curve. Since the heat flow is directly measured, the total heat per amount of gas adsorbed corresponds to the differential energy of adsorption. The differential enthalpy of adsorption, also referred to as the isosteric heat of adsorption, is equal to the differential energy plus RT.⁶⁵ Differential heats of adsorption and isotherms were measured at 195 K and 293 K for C₂H₂, C₂H₄, and C₂H₆ (Fig. S4, ESI†).

2.3 Computational details

Our ab initio calculations were performed at the density functional theory (DFT) level, using VASP (Vienna ab Initio Simulation Package)^66,67 in conjunction with the vdW-DF functional.^68–71 The SCF convergence condition was set to 10⁻³ meV and the structure was optimized until all forces between atoms were smaller than 1 meV Å⁻¹. The plane-wave energy cut-off was set at 600 eV and, due to the size of the unit cell, only the Γ-point was used. Without guest molecule, the unit cell of UiO-66(Zr) contains 108 atoms (Fig. 1) and that of UiO-66(Zr)–NO₂ contains 126. Since the Zr atoms contain unpaired electrons, initial simulations were performed spin-polarized. However, spin effects cause differences in binding energies of only <0.1% so that we used non-spin polarized calculations henceforth. Guest molecules were introduced in the MOF at different sites to find the favorable binding sites and allowed to fully relax. The unit cell shape and volume was initially allowed to change during relaxation, but our calculations showed that this has only a minor effect on the binding energies (<1.5%), so the unit cell dimensions were kept fixed for all subsequent relaxations. Binding energies were calculated as energy differences of suitable fragments. Note that enthalpy contributions to the binding energy for C₂H₂, C₂H₄, and C₂H₆ tend to be small at finite temperature, i.e. on the order of 2–3 kJ mol⁻¹ (see e.g. ESI of 23).

Fig. 1 Structure of UiO-66(Zr), showing the Zr atoms bound to each other by 12 BDC linkers. The pristine unit cell of UiO-66(Zr) consists of 6 Zr atoms and 6 BDC linkers. Color coding: Zr (blue), oxygen (red), carbon (black), and hydrogen (white).

3 Results and discussion

3.1 MOF structure

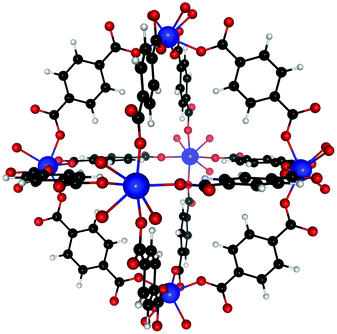
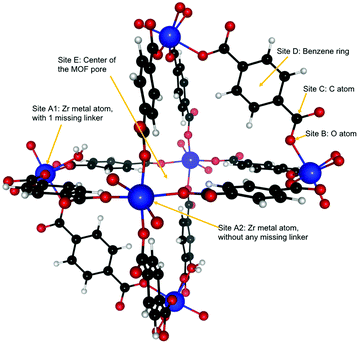
Dehydroxylated UiO-66(Zr) is a zirconium-based MOF,⁷² made of [Zr₆(μ₃-O)₆] clusters connected to each other by benzenedicarboxylate (BDC) linkers [OOC–C₆H₄–OOC]⁻². Each cluster has 12 BDC linkers binding it to 12 other clusters thus giving a charge neutral structure. A unit cell of UiO-66(Zr) used for our calculations consisted of 6 Zr atoms interconnected with 6 BDC linkers. An extended version of the unit cell having 12 complete linkers is shown in Fig. 1. UiO-66 belongs to a special family of porous materials with 2 types of pores: an octahedral pore (11 Å diameter) and a tetrahedral pore (8 Å diameter). The structure of UiO-66(Zr) is well-known to contain missing linker defects and the presence of water molecules bound to the metal centers at the missing linker sites has been identified.^64,73 Following our specific synthesis procedure in Section 2.1, our MOF exhibits linker defects and our thermogravimetric analysis (TGA) in Fig. S3 (ESI†) indicates that UiO-66(Zr) has 1.35 missing linkers and UiO-66(Zr)–NO₂ has 0.60 missing linkers per unit cell. For our theoretical calculations – to avoid large super cells – we thus use the UiO-66(Zr) model depicted in Fig. 2 with one missing linker per unit cell. Nonetheless, in our partition-function occupancy-probability calculations we do use the exact numbers of missing linkers and thus available primary binding sites from our TGA results.

Fig. 2 UiO-66(Zr) structure used in this study with linker defects, i.e. two out of every twelve BDC linkers missing, which corresponds to one missing linker per unit cell. The arrows show the six possible binding sites for guest molecules. Note that, due to the symmetry of this structure, each binding site has a particular number of equivalent sites in each unit cell.

The symmetry of our MOF structure can be exploited to reduce the number of possible binding sites that have to be considered. One end of a BDC linker connects to one Zr atom to form an arm that repeats itself over the whole UiO-66 structure. Along this BDC-Zr-arm we can identify five potential binding sites: Site A1 : Zr metal site with a linker missing, Site A2 : Zr metal site with no missing linker, Site B: oxygen atom attached to the Zr metal, Site C: carbon atom between the oxygen and the benzene ring and Site D: benzene ring in the BDC linker. Finally, we find another binding site called Site E, where – depending on the situation – a varying number of guest molecules can be adsorbed in the center of the MOF pore. These binding sites are depicted in Fig. 2. Although there are potentially six different types of active sites inside the MOF, our calculations show that sites B and C are not preferred by our molecules of interest, i.e. when placing C₂H₂, C₂H₄ or C₂H₆ near those sites, they eventually drift closer to another nearby stable site like the Zr metal center or the benzene ring.

3.2 Adsorption of C₂H₂, C₂H₄ and C₂H₆ in UiO-66(Zr)

Calorimetry results in the form of isosteric heats of adsorption for C₂H₂, C₂H₄ and C₂H₆ in UiO-66(Zr) at 195 K are depicted in Fig. 3 as a function of guest molecule coverage; results at 293 K are given in Fig. S5 (ESI†). Heat of adsorption measurements were done for 10 sets of data and the uncertainty in measurement was found to be <2%. The results show that at 293 K the low-coverage heat of adsorption for C₂H₄ and C₂H₆ are nearly identical and 3 kJ mol⁻¹ lower than C₂H₂. However, when going to a lower temperature of 195 K, the heats of adsorption are significantly more separated and also shift to noticeably higher values, which is beneficial for separation purposes – we thus focus on the 195 K results.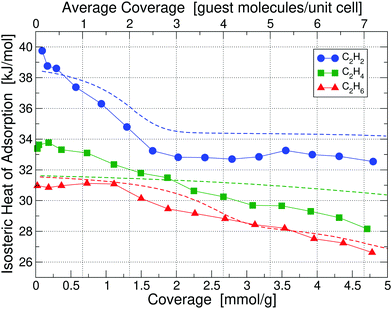

Fig. 3 Isosteric heats of adsorption of C₂H₂, C₂H₄ and C₂H₆ in UiO-66(Zr) at 195 K, obtained by calorimetry measurements; results for 293 K are shown in Fig. S5 (ESI†). The x-axis is given in the chemically more useful units of [mmol g⁻¹] at the bottom, whereas we have converted it to units of [guest molecule per unit cell] on the top, which is more useful for theoretical calculations. Dashed lines correspond to our partition-function occupancy-probability calculations based on our theoretical binding energies and availability of binding sites.

Combining our calorimetry data and DFT calculations we can qualitatively and quantitatively explain the adsorption behavior in Fig. 3. Our main theoretical results are collected in Table 1, showing binding energies for all three gases corresponding to their primary, secondary, and tertiary binding site. For comparison, we also list the experimental heats of adsorption at 195 K and 293 K for the lowest measured coverage – as can be seen, we find excellent agreement between experiment and our calculated primary binding energies. It is also interesting to see that as primary sites all three molecules prefer Site A1, i.e. the Zr metal site with a missing linker. However, the secondary and tertiary binding sites differ from molecule to molecule.

Table 1 Calculated binding energies of C₂H₂, C₂H₄ and C₂H₆ in UiO-66(Zr) [kJ mol⁻¹]. Experimental results for the lowest measured coverage at 195 K and 293 K are given for comparison. Sites are labeled according to Fig. 2. The number of equivalent sites per cell is also given. A1* indicates that the guest molecule is bound close to site A1, but in a different orientation

	Exp. low coverage		Primary			Secondary			Tertiary
Molecule	195 K	293 K	Energy	Site	Equiv.	Energy	Site	Equiv.	Energy	Site	Equiv.
C2H2	39.75	32.08	39.52	A1	1	34.51	D	8	29.02	A2	4
C2H4	33.39	29.11	32.49	A1	2	30.94	A2	4	29.40	E	4
C2H6	31.12	28.99	32.10	A1	2	28.95	A1*	2	26.70	E	3

---

Looking at the curve for the C₂H₂ heat of adsorption in Fig. 3, we measure at 195 K for the low coverage of 0.1 mmol g⁻¹ a value of 39.75 kJ mol⁻¹, in excellent agreement with our calculated value of 39.52 kJ mol⁻¹ for the primary binding site. As we increase the coverage to e.g. 1 molecule per unit cell (0.66 mmol g⁻¹) on average we see that the heat drops to a value below the primary binding site, 37.1 kJ mol⁻¹. The heat continues to drop with increasing coverage until we reach approximately 3 guest molecules per unit cell (2 mmol g⁻¹) and thereafter stays constant at approximately 33 kJ mol⁻¹. The initial drop and then the plateau in the heat of adsorption of C₂H₂ can be perfectly explained by partition-function occupancy-probability calculations based on our theoretical binding energies and the number of available binding sites in Table 1. Note that one missing linker leaves two open metal Sites A1, but C₂H₂ binds in such a way – taking up the space between both Sites A1 – that there is practically only one binding site available (which is not the case for C₂H₄ and C₂H₆). For the secondary binding site of C₂H₂ (Site D), the molecule sits in a triangular space surrounded by three linkers, which – according to our binding calculations – can hold up to two guest molecules with 34.51 kJ mol⁻¹ each. For our cell in Fig. 2 there are four such triangular spaces available, providing a maximum of 8 secondary sites. Our calculated heats of adsorption (blue dashed line in Fig. 3) are in excellent agreement with experiment and fully captures and explains the overall trend. Note that our calculated values are well within chemical accuracy (1 kcal mol⁻¹ = 4.2 kJ mol⁻¹) over the entire range of coverages. The drop and the plateau is thus a result of the small number of available primary sites and the large number of secondary sites. We expect a further drop in the heat of adsorption down to ∼29 kJ mol⁻¹ for coverages above 9 molecules per unit cell.

The case of C₂H₄ is similar to the case of C₂H₂. But, there are two main differences: (i) the difference in binding energies between primary, secondary, and tertiary sites is much less compared to C₂H₂, and (ii) there are only four secondary sites available. Note that Site E in this case can hold up to four guest molecules. As a result, primary, secondary, and even tertiary sites get filled up more linearly with coverage and we thus observe a consistent decrease in heat as a function of coverage for C₂H₄ in Fig. 3. Our calculated binding energy at the primary site of 32.49 kJ mol⁻¹ is in very good agreement to the measured low-coverage value of 33.39 kJ mol⁻¹ and our partition-function occupancy-probability calculations capture the linear decrease with coverage very well, albeit with a slightly too shallow slope (green line in Fig. 3).

Finally, for C₂H₆ molecules we find a similar behavior, but the number of available binding sites are slightly different from the other cases. Here, due to the larger size of C₂H₆, Site E can only hold three guest molecules. Overall, our calculated primary site binding energy of 32.10 kJ mol⁻¹ is once more in excellent agreement with the low-coverage measured value of 31.12 kJ mol⁻¹ and our calculated heats capture the overall trend extremely well over the entire range of coverage (red line in Fig. 3). We note a small increase in the experimental heat of adsorption for C₂H₆ at low concentrations – this slight increase is on the order of 0.2–0.3 kJ mol⁻¹ and falls within the uncertainty of our measurements.

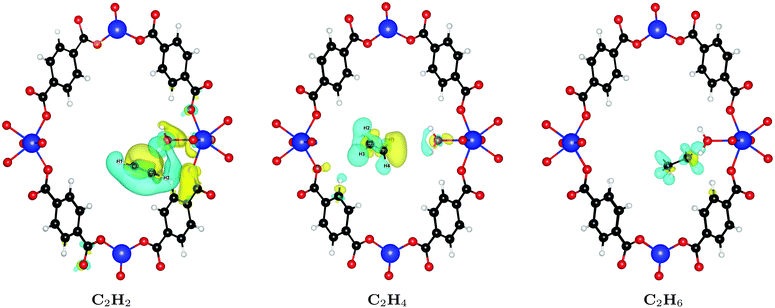
In order to understand the large difference of 28% in binding affinity between C₂H₂ and C₂H₆, we calculate the induced charge density upon binding of both molecules, i.e. the charge density rearrangement upon forming the bond; results are depicted in Fig. 4. As can be seen, the interaction of C₂H₂ with the framework is noticeably stronger compared to C₂H₄ or C₂H₆. The reason for this behavior is that – because of its linear shape and thus smaller cross-section – it can sit in the groove formed between two water molecules at the linker defect site and interact with both, resulting in the increased binding energy. The smallest distance between C₂H₂ and the water molecules is only 2.59 Å. Because of its shape, C₂H₄ cannot fit in the same way and gets pushed further away into the pore, with a smallest distance of 3.34 Å. The same is true for the even larger C₂H₆, which shows even less charge rearrangement and interaction (smallest distance of 4.09 Å).

Fig. 4 Induced charge density upon formation of the bond between UiO-66(Zr) and C₂H₂ (left), C₂H₄ (middle), and C₂H₆ (right). Yellow lobes show charge accumulation and blue ones charge depletion. All isolevels are set at 0.0002 e Å⁻³. The interaction of C₂H₂ with the framework is noticeably stronger compared to C₂H₄ or C₂H₆. Although the perspective is deceiving, the distance of the guest molecule to the water bound to Site A1 increases from the left to the right.

3.3 Adsorption of C₂H₂, C₂H₄, and C₂H₆ in NO₂ functionalized UiO-66(Zr)

We also studied the effect of functionalizing UiO-66(Zr) with NO₂ by adding one NO₂ functional group on each BDC linker. The resulting new structure after relaxation is shown in Fig. 5 and the experimental calorimetry data is depicted in Fig. 6. We observe an overall rise in the adsorption enthalpy for all three gases as compared to the unfunctionalized case in Fig. 3. For the energy at low coverage the values are increased by a magnitude of 3.5 kJ mol⁻¹ for C₂H₂ and only 1 kJ mol⁻¹ for C₂H₄ and 2 kJ mol⁻¹ for C₂H₆. This further increases the separation between C₂H₂ and C₂H₄ from 6.4 kJ mol⁻¹ to 8.9 kJ mol⁻¹ and from 8.6 kJ mol⁻¹ to 10 kJ mol⁻¹ for C₂H₆, with important implications for the separation of these molecules.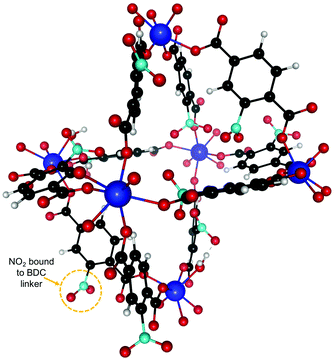

Fig. 5 NO₂ functionalized UiO-66(Zr) unit cell. One NO₂ was attached to every BDC linker. The binding sites are similar to the unfunctionalized case in Fig. 2 and we are thus using the same labeling.

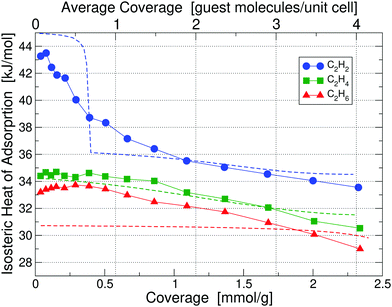Fig. 6 Isosteric heats of adsorption of C₂H₂, C₂H₄ and C₂H₆ in UiO-66(Zr)-NO₂ at 195 K, obtained by calorimetry measurements; results for 293 K are shown in Fig. S6 (ESI†). Dashed lines correspond to our partition-function occupancy-probability calculations based on our theoretical binding energies and availability of binding sites.

Calculated binding energies are shown in Table 2. The measured heats of adsorption for C₂H₂ of 43.27 kJ mol⁻¹ at 0.04 mmol g⁻¹ coverage is in good agreement with our calculated primary binding energy of 45.12 kJ mol⁻¹; similarly for the cases of C₂H₄ and C₂H₆. Due to the presence of NO₂ on each linker, the available pore size for binding is reduced, which generally leads to a lower number of available binding sites for guest molecules in Table 2. As in the unfunctionalized case, primary binding always occurs at Site A1. The behavior of the isosteric heats of adsorption in Fig. 6 follows the same overall trend as compared to the unfunctionalized case and can be explained on the same basis of binding energies and site occupancy probabilities (see the discussion in Section 3.2 why sometimes there is only one Site A1 available while in other cases there are two). One noticeable qualitative difference is that the heat for C₂H₂ keeps decreasing with coverage, whereas for the unfunctionalized case it plateaus up to the maximum coverage measured. This behavior can be explained by the much smaller number of available secondary binding sites in the functionalized case, which increases the probability of guest molecules occupying tertiary sites earlier.

Table 2 Calculated binding energies of C₂H₂, C₂H₄ and C₂H₆ in NO₂ functionalized UiO-66(Zr) [kJ mol⁻¹]. Experimental results for the lowest measured coverage at 195 K and 293 K are given for comparison. Sites are labeled according to Fig. 2. The number of equivalent sites per unit cell is also given. Asterisks for binding sites indicate that the guest molecule is bound close to that site, but in a different orientation

	Exp. low coverage		Primary			Secondary			Tertiary
Molecule	195 K	293 K	Energy	Site	Equiv.	Energy	Site	Equiv.	Energy	Site	Equiv.
C2H2	43.27	37.21	45.12	A1	1	37.12	A1*	1	34.51	E	3
C2H4	34.40	32.41	35.57	A1	1	33.96	A1*	2	31.49	E	2
C2H6	33.20	33.86	31.15	A1	2	30.75	E	1	26.43	E*	1

---

Our partition-function occupancy-probability calculations again capture the overall trends well and are within chemical accuracy of the experimental results for all coverages. The noticeable kink for C₂H₂ in our theoretical results, which is not present in the experimental results, is an artefact of our slightly too high calculated primary site energy and probably a slightly underestimated secondary site value. If both values would move 1 kJ mol⁻¹ in the right direction, the kink would disappear. The slope for C₂H₆ is also underestimated due to our slightly underestimated primary side value.

Finally, we investigate why the functionalized MOF can bind the guest molecules stronger than the unfunctionalized case. To this end, we plot the induced charge density of C₂H₂ in Fig. 7. It can be seen that the guest molecule now also shows an additional interaction with three NO₂ functional groups, leading to the increased binding energy. C₂H₂ is at a distance of only 2.18 Å from the closest NO₂ and at 2.66 Å and 3.02 Å from other NO₂ groups. Similar interactions also increase the binding energy of C₂H₄ and C₂H₆.

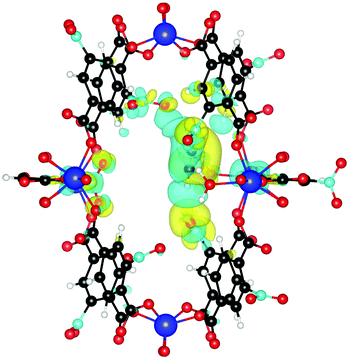Fig. 7 Induced charge density upon formation of the bond between NO₂ functionalized UiO-66(Zr) and C₂H₂. Yellow lobes show charge accumulation and blue ones charge depletion. All isolevels are set at 0.0002 e Å⁻³. Compared to Fig. 4 we see that the guest molecule now also shows additional interactions with three NO₂ functional group, leading to the increased binding energy.

4 Conclusions

In summary, we investigate the adsorption behavior of C₂H₂, C₂H₄ and C₂H₆ in UiO-66(Zr) with linker defects and its NO₂ functionalized form. Our experimental calorimetry data for the isosteric heats of adsorption as a function of coverage can be fully explained by our ab initio calculations combined with a partition-function occupancy-probability analysis. We show that C₂H₂ exhibits a significantly increased binding energy over C₂H₄ and C₂H₆ for the unfunctionalized as well as for the functionalized case. We trace this increased binding of C₂H₂ back to its unique adsorption structure made possible due to its linear shape, leading to more favorable interactions with the defect sites. Although the difference in binding energy between C₂H₂ and C₂H₆ in the unfunctionalized case is already significant, we show that NO₂ functionalization of the MOF framework increases that difference even more. Again, we are able to trace this effect back to structural aspects and additional favorable interactions of the guest molecules with the added functional groups. Our results highlight the importance of linker defects in understanding adsorbate–MOF interactions and the potential to manipulate adsorption behavior with linker functionalizations. Although our study focuses on UiO-66, we believe that the concepts of defects and functionalizations can provide a rich field of study towards tuning the effectiveness and specificity of many other MOF-based solid adsorption systems, with important implications for gas separation applications.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

This work was supported by the U.S. Department of Energy, Basic Energy Sciences, Division of Materials Sciences and Engineering, Grant No. DE-SC0019902. For the calorimetry experiments we acknowledgment support from the American Chemical Society Petroleum Research Fund (57385-ND5).

References

1. M. Huff and L. D. Schmidt, J. Phys. Chem, 1993, 97, 11815.
2. A. S. Bodke, Science, 1999, 285, 712.
3. A. Hagen and F. Roessner, Catal. Rev., 2000, 42, 403.
4. H. Yue, Y. Zhao, X. Ma and J. Gong, Chem. Soc. Rev., 2012, 41, 4218.
5. K. Endo, Prog. Polym. Sci., 2002, 27, 2021.
6. S. Park, J. M. Vohs and R. J. Gorte, Nature, 2000, 404, 265.
7. F. Alcaide, P.-L. Cabot and E. Brillas, J. Power Sources, 2006, 153, 47.
8. O. Demoulin, B. Le Clef, M. Navez and P. Ruiz, Appl. Catal., A, 2008, 344, 1.
9. N. Schmidbauer and M. Oehme, J. High Resolut. Chromatogr., 1986, 9, 502.
10. A. Hart and N. Gnanendran, Energy Procedia, 2009, 1, 697.
11. T. Gao, W. Lin and A. Gu, Energy Convers. Manage., 2011, 52, 2401.
12. D. S. Sholl and R. P. Lively, Nature, 2016, 532, 435.
13. W. Koros and G. Fleming, J. Membr. Sci., 1993, 83, 1.
14. R. W. Baker, Ind. Eng. Chem. Res., 2002, 41, 1393.
15. T. Rodenas, I. Luz, G. Prieto, B. Seoane, H. Miro, A. Corma, F. Kapteijn, F. X. Llabrés i Xamena and J. Gascon, Nat. Mater., 2015, 14, 48.
16. E. V. Perez, K. J. Balkus, J. P. Ferraris and I. H. Musselman, J. Membr. Sci., 2009, 328, 165.
17. Y. Zhang, X. Feng, S. Yuan, J. Zhou and B. Wang, Inorg. Chem. Front., 2016, 3, 896.
18. T.-H. Bae, J. S. Lee, W. Qiu, W. J. Koros, C. W. Jones and S. Nair, Angew. Chem., Int. Ed., 2010, 49, 9863.
19. J. Liu, P. K. Thallapally, B. P. McGrail, D. R. Brown and J. Liu, Chem. Soc. Rev., 2012, 41, 2308.
20. L. J. Murray, M. Dinca and J. R. Long, Chem. Soc. Rev., 2009, 38, 1294.
21. J.-R. Li, Y. Ma, M. C. McCarthy, J. Sculley, J. Yu, H.-K. Jeong, P. B. Balbuena and H.-C. Zhou, Coord. Chem. Rev., 2011, 255, 1791.
22. N. Nijem, H. Wu, P. Canepa, A. Marti, K. J. Balkus, T. Thonhauser, J. Li and Y. J. Chabal, J. Am. Chem. Soc., 2012, 134, 15201.
23. K. Lee, J. D. Howe, L.-C. Lin, B. Smit and J. B. Neaton, Chem. Mater., 2015, 27, 668.
24. D. Zhao, D. Yuan and H.-C. Zhou, Energy Environ. Sci., 2008, 1, 222.
25. N. L. Rosi, J. Eckert, M. Eddaoudi, D. T. Vodak, J. Kim, M. O'Keeffe and O. M. Yaghi, Science, 2003, 300, 1127.
26. H. Wu, Q. Gong, D. H. Olson and J. Li, Chem. Rev., 2012, 112, 836.
27. Y. He, W. Zhou, G. Qian and B. Chen, Chem. Soc. Rev., 2014, 43, 5657.
28. C.-D. Wu and W. Lin, Angew. Chem., Int. Ed., 2007, 46, 1075.
29. J. Lee, O. K. Farha, J. Roberts, K. A. Scheidt, S. T. Nguyen and J. T. Hupp, Chem. Soc. Rev., 2009, 38, 1450.
30. R.-Q. Zou, H. Sakurai and Q. Xu, Angew. Chem., Int. Ed., 2006, 45, 2542.
31. I. Luz, F. X. Llabrés i Xamena and A. Corma, J. Catal., 2010, 276, 134.
32. M. D. Allendorf, C. A. Bauer, R. K. Bhakta and R. Houk, Chem. Soc. Rev., 2009, 38, 1330.
33. K. A. White, D. A. Chengelis, K. A. Gogick, J. Stehman, N. L. Rosi and S. Petoud, J. Am. Chem. Soc., 2009, 131, 18069.
34. P. Horcajada, T. Chalati, C. Serre, B. Gillet, C. Sebrie, T. Baati, J. F. Eubank, D. Heurtaux, P. Clayette, C. Kreuz, J.-S. Chang, Y. K. Hwang, V. Marsaud, P.-N. Bories, L. Cynober, S. Gil, G. Férey, P. Couvreur and R. Gref, Nat. Mater., 2010, 9, 172.
35. C. Orellana-Tavra, E. F. Baxter, T. Tian, T. D. Bennett, N. K. H. Slater, A. K. Cheetham and D. Fairen-Jimenez, Chem. Commun., 2015, 51, 13878.
36. M.-X. Wu and Y.-W. Yang, Adv. Mater., 2017, 29, 1606134.
37. A. Stroppa, P. Jain, P. Barone, M. Marsman, J. M. Perez-Mato, A. K. K. Cheetham, H. W. Kroto and S. Picozzi, Angew. Chem., Int. Ed., 2011, 50, 5847.
38. A. Stroppa, P. Barone, P. Jain, J. M. Perez-Mato and S. Picozzi, Adv. Mater., 2013, 25, 2284.
39. D. Di Sante, A. Stroppa, P. Jain and S. Picozzi, J. Am. Chem. Soc., 2013, 135, 18126.
40. L. Wang, Y. Han, X. Feng, J. Zhou, P. Qi and B. Wang, Coord. Chem. Rev., 2016, 307, 361.
41. W. Xia, A. Mahmood, R. Zou and Q. Xu, Energy Environ. Sci., 2015, 8, 1837.
42. P. Z. Moghadam, A. Li, S. B. Wiggin, A. Tao, A. G. P. Maloney, P. A. Wood, S. C. Ward and D. Fairen-Jimenez, Chem. Mater., 2017, 29, 2618.
43. Z. R. Herm, E. D. Bloch and J. R. Long, Chem. Mater., 2014, 26, 323.
44. J.-R. Li, J. Sculley and H.-C. Zhou, Chem. Rev., 2012, 112, 869.
45. T. Duerinck, R. Bueno-Perez, F. Vermoortele, D. E. De Vos, S. Calero, G. V. Baron and J. F. M. Denayer, J. Phys. Chem. C, 2013, 117, 12567.
46. Y. Zhang, H. Xiao, X. Zhou, X. Wang and Z. Li, Ind. Eng. Chem. Res., 2017, 56, 8689.
47. L. Li, L. Guo, S. Pu, J. Wang, Q. Yang, Z. Zhang, Y. Yang, Q. Ren, S. Alnemrat and Z. Bao, Chem. Eng. J., 2019, 358, 446.
48. H. Wu, Y. Chen, D. Lv, R. Shi, Y. Chen, Z. Li and Q. Xia, Sep. Purif. Technol., 2019, 212, 51.
49. E. D. Bloch, W. L. Queen, R. Krishna, J. M. Zadrozny, C. M. Brown and J. R. Long, Science, 2012, 335, 1606.
50. Y. He, R. Krishna and B. Chen, Energy Environ. Sci., 2012, 5, 9107.
51. Y. Wu, H. Duan and H. Xi, Chem. Mater., 2020, 32(7), 2986–2997.
52. H. Wang, X. Dong, J. Lin, S. J. Teat, S. Jensen, J. Cure, E. V. Alexandrov, Q. Xia, K. Tan, Q. Wang, D. H. Olson, D. M. Proserpio, Y. J. Chabal, T. Thonhauser, J. Sun, Y. Han and J. Li, Nat. Commun., 2018, 9, 1745.
53. N. C. Burtch, H. Jasuja and K. S. Walton, Chem. Rev., 2014, 114, 10575.
54. Y. Zhao, H. Wu, T. J. Emge, Q. Gong, N. Nijem, Y. J. Chabal, L. Kong, D. C. Langreth, H. Liu, H. Zeng and J. Li, Chem. – Eur. J., 2011, 17, 5101.
55. D. Parrillo and R. Gorte, Thermochim. Acta, 1998, 312, 125.
56. Y. Zhang, J. Yu, Y.-H. Yeh, R. J. Gorte, S. Rangarajan and M. Mavrikakis, J. Phys. Chem. C, 2015, 119, 28970.
57. P. L. Llewellyn, J. P. Coulomb, Y. Grillet, J. Patarin, G. Andre and J. Rouquerol, Langmuir, 1993a, 9, 1852.
58. P. L. Llewellyn, J. P. Coulomb, Y. Grillet, J. Patarin, H. Lauter, H. Reichert and J. Rouquerol, Langmuir, 1993, 9, 1846.
59. D. Shen, M. Bülow, F. Siperstein, M. Engelhard and A. L. Myers, Adsorption, 2000, 6, 275.
60. F. Rouquerol, J. Rouquerol, K. S. W. Sing, P. L. Llewellyn and G. Maurin, Adsorption by powders and porous solids: principles, methodology and applications, Elsevier/AP, Amsterdam, 2nd edn, 2014.
61. M. Thommes, K. Kaneko, A. V. Neimark, J. P. Olivier, F. Rodriguez-Reinoso, J. Rouquerol and K. S. Sing, Pure Appl. Chem., 2015, 87, 1051.
62. S. Sircar, Ind. Eng. Chem. Res., 1992, 31, 1813.
63. M. J. Katz, Z. J. Brown, Y. J. Colón, P. W. Siu, K. A. Scheidt, R. Q. Snurr, J. T. Hupp and O. K. Farha, Chem. Commun., 2013, 49, 9449.
64. H. Wu, Y. S. Chua, V. Krungleviciute, M. Tyagi, P. Chen, T. Yildirim and W. Zhou, J. Am. Chem. Soc., 2013, 135, 10525.
65. A. L. Myers, AIChE J., 2002, 48, 145.
66. G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169.
67. G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758.
68. K. Berland, V. R. Cooper, K. Lee, E. Schröder, T. Thonhauser, P. Hyldgaard and B. I. Lundqvist, Rep. Prog. Phys., 2015, 78, 066501.
69. D. C. Langreth, B. I. Lundqvist, S. D. Chakarova-Käck, V. R. Cooper, M. Dion, P. Hyldgaard, A. Kelkkanen, J. Kleis, L. Kong, S. Li, P. G. Moses, E. D. Murray, A. Puzder, H. Rydberg, E. Schröder and T. Thonhauser, J. Phys.: Condens. Matter, 2009, 21, 084203.
70. T. Thonhauser, V. R. Cooper, S. Li, A. Puzder, P. Hyldgaard and D. C. Langreth, Phys. Rev. B, 2007, 76, 125112.
71. T. Thonhauser, S. Zuluaga, C. A. Arter, K. Berland, E. Schröder and P. Hyldgaard, Phys. Rev. Lett., 2015, 115, 136402.
72. J. H. Cavka, S. Jakobsen, U. Olsbye, N. Guillou, C. Lamberti, S. Bordiga and K. P. Lillerud, J. Am. Chem. Soc., 2008, 130, 13850.
73. C. A. Trickett, K. J. Gagnon, S. Lee, F. Gándara, H.-B. Bürgi and O. M. Yaghi, Angew. Chem., Int. Ed., 2015, 54, 11162.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ma00722f

‡ E.g. acetylene is explosive and can react with the impurities present resulting in massive explosions.

---