Chiral expression of adsorbed (MP) 5-amino[6]helicenes: from random structures to dense racemic crystals by surface alloying†
Javier D.
Fuhr
*a,
Maarten W.
van der Meijden
b,
Lucila J.
Cristina‡
a,
Luis M.
Rodríguez
a,
Richard M.
Kellogg
b,
J. Esteban
Gayone
a,
Hugo
Ascolani
*a and
Magalí
Lingenfelder
 *c
*c
aCentro Atómico Bariloche, Avda. E. Bustillo 9500, R8402AGP, Bariloche, Argentina. E-mail: ascolani@cab.cnea.gov.ar; fuhr@cab.cnea.gov.ar
bSyncom BV, Kadijk 3, 9747 AT Groningen, The Netherlands
cMax Planck-EPFL Laboratory for Molecular Nanoscience, EPFL SB CMNT NL-CMNT, CH 1015 Lausanne, Switzerland. E-mail: magali.lingenfelder@epfl.ch
First published on 29th November 2016
Abstract
The chiral expression of a molecule on a surface is driven from a random solid solution on Cu(100) to a racemic crystal on a Sn/Cu(100) alloy. Density functional theory simulations reveal how the growth of the racemate is influenced by the underlying surface.
Ever since the discovery of the molecular origin of chirality scientists have been trying to understand the factors determining the organization of chiral molecules into crystals. The question is whether a racemate will resolve spontaneously forming enantiomerically pure crystals (conglomerates) or will it rather form a random solid solution or crystalize as a racemic compound. Intriguingly, from solution approximately 90–95% of all racemic mixtures crystalize as racemic compounds.
In 1895, Wallach reported on a series of studies attributed to Liebisch1 showing that racemic compounds tend to be more dense than their chiral counterparts (“Wallach's rule”).2 Extensive crystallographic database analysis have shown that racemic crystals are predominantly, but not exclusively, more stable and more dense.3,4 A major influence of kinetic factors and statistical predominance of mixed versus enantiopure aggregates at first stages of homogeneous nucleation and growth was recently discussed.4
In order to have molecular access into the assembly of chiral structures, scanning probe studies on solid surfaces are the natural choice.5–8 The deposition on a surface not only confines the molecules in a plane but also adds the molecule–surface interaction to compete with the intermolecular forces at play.9 As a result, conglomerate formation becomes more likely and many molecules that naturally form 3D racemic compounds resolve into 2D conglomerates when adsorbed on a surface.10,11 A relevant exception to this trend is the assembly of helicenes.1 Carbohelicenes tend to form conglomerates in the solid state12 while puzzlingly on surfaces only two examples of 2D conglomerate formation were reported so far.13,14
Unfortunately, a few scattered studies of functionalized helicenes15–22 are available and there is no clear trend on the influence of the heteroatoms on the chiral expression. Even less information is available regarding the role of the symmetry of the surface in the stereo structural outcome of the 2D assembly.
Here we report the first investigation of chiral molecules (MP) 5-amino[6]helicenes (AH, Fig. 1a) on a surface alloy. Surface alloying permits us to tune the molecule–surface interactions at play driving the chiral expression of AH from a random assembly to a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 racemic compound. Moreover, density functional theory (DFT) simulations address the stability of the racemate onto 3-fold and 4-fold surfaces with different energy corrugation landscapes.
1 racemic compound. Moreover, density functional theory (DFT) simulations address the stability of the racemate onto 3-fold and 4-fold surfaces with different energy corrugation landscapes.
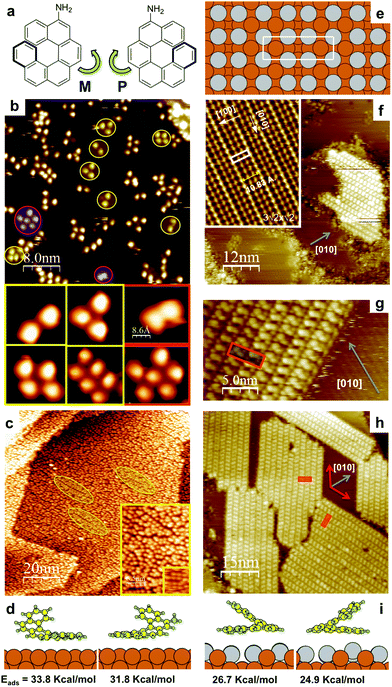
The MP-AH synthesis was recently described.22 The adsorption of racemic MP-AH on pristine Cu(100) was studied by scanning tunnelling microscopy (STM). Fig. 1b and c show STM images obtained at low and high coverage, respectively.
Each molecule appears as a 1 nm blob indicating that tunneling is mainly from the uppermost C6 ring of the face-on spiral.21,23 Molecular depositions were done with the surface at room temperature (RT), while the images were acquired at 100 K. To account for the influence of the cooling rate on the mobility at nucleation and growth here we only compare experiments done with the same cooling rate.
At low percentage of monolayer (ML) coverage we observe small clusters of AH on the Cu terraces. In addition to the duplets, triplets, quadruplets and rows of duplets observed for the enantiopure compound21 (yellow circles and insets Fig. 1b), in the case of the racemate we also observe larger clusters without a well defined structure and a new kind of duplets at short intermolecular distances (uppermost C6–C6 ring center ∼0.7 nm) that might correspond to M–P structures (red circles and insets Fig. 1b). In the study of enantiopure samples at high coverage (0.9 ML) we have reported ordered structures formed by molecular quadruplets that resulted in two rotational domains with oblique unit cells.21 In contrast, for the racemic MP-AH no clear order evolves and only local order in the form of quadruplets and/or rows can be found embedded in the disordered structure (circles and insets in Fig. 1c). The phase is stable after thermal annealing at least until 500 K. This observation is in line with DFT calculations that show that the adsorption of a single molecule on Cu(100), specially with the NH2 pointing towards the Cu surface (N-down) is very strong (33.3 kcal mol−1, Fig. 1d).21 The absence of extended enantiopure islands indicates that although enantiopure nuclei form (Fig. 1b and c) the presence of the “wrong” enantiomer acts as an impurity preventing the growth of conglomerates.3 However, neither an ordered racemic crystal is observed on Cu(100) under a wide range of high coverage (0.8–1.2 ML) and substrate deposition temperatures (RT-500 K). In contrast, on the 3-fold symmetry Au(111) AH forms a very dense and stable 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 racemic crystal.22
1 racemic crystal.22
In order to study the effect of the surface chemistry on the chiral assembly, we have studied AH on Cu(100) modified by Sn. The deposition of 0.5 ML Sn atoms on Cu(100) reconstruct the surface forming a (3√2 × √2)R45° surface alloy (model Fig. 1e, STM inset Fig. 1f).24 Although alloys remain unexplored surfaces for molecular assembly, a recent study shows that the reactivity of the 4 fold Sn/Cu(100) is similar to the 3 fold Au(111) which is the most studied substrate for molecular self-assembly.25 Therefore, this alloy stands as a good candidate to study the chiral expression of molecules on a low interacting 4-fold surface, where molecule–molecule interactions are expected to play a main role as observed for Au(111).22
Conversely to the assembly of most helical molecules on solid surfaces, where ordered structures are only observed at very low T and close to ML saturation coverage, the deposition of MP-AH on the surface alloy at both low (Fig. 1f and g) and high (Fig. 1h) coverage results in ordered islands (that were never observed for pure enantiomers). Surprisingly, the structure is identical to the racemic crystal that was recently reported for MP-AH on Au(111).22 On Sn/Cu(100) they grow as racemic domains26 at angles of ±62° with respect to the [010] surface direction (the unit cell is shown Fig. 1f and g: a1 = (1.50 ± 0.07) nm, b1 = (4.45 ± 0.15) nm; a1^b1 = (89 ± 2)°). This densely packed assembly forms on both a 3-fold Au(111) and a 4-fold Sn/Cu(100) surface that have remarkably different interatomic grids, indicating that the intermolecular interactions dominate the assembly.
In order to further analyze the stability of the racemic crystal on the different solid surfaces we have performed a series of DFT calculations. By comparing the adsorption energy (Eads) of AH on Cu(100) (33.8 kcal mol−1) and on Au(111) (34.8 kcal mol−1) (S2.1, ESI†) we notice that the values are similar. On the other hand, on the Sn/Cu(100) surface alloy the interaction is highly reduced (Eads 26.7 kcal mol−1, Fig. 1i). This is consistent with the higher sticking probability observed on the Cu(100) surface.
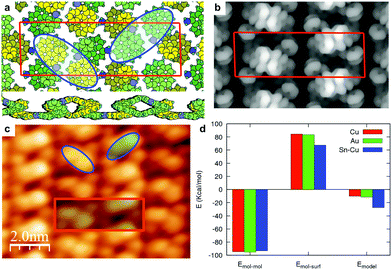
As previously described for Au(111), the model for the racemic ordered phase on Sn/Cu(100) (Fig. 2 and S2.5, ESI†) consists of rows formed by N-up duplets of molecules with the same chirality, linked by N-down molecules of opposite chirality, alternating chirality in a zig-zag fashion.22 There are 8 molecules in the unit cell which have two inequivalent molecular configurations: (i) half of the molecules are similar to isolated AH molecules in the N-down configuration, forming MP zig-zags; (ii) the other half of the molecules are in a N-up configuration, forming MM or PP duplets that are partially detached from the substrate (Fig. 2a). We estimate the energy of the model as follows:§ (i) we start from the relaxed configuration of the racemic model obtained from an unsupported calculation. For this relaxation we kept fixed the unit cell as the experimental one. To simulate the interaction with the surface, we fixed the z-positions of the three lower C-rings of the N-down molecules to those of the lowest-energy adsorbed configuration. The 2D arrangement is thermodynamically very stable (see ESI†). The corresponding simulated STM image at constant current (Fig. 2b) agrees with the main features observed in the experimental image (Fig. 2c). (ii) We then estimate the adsorption energy of the racemic model on the surface with two contributions:
| Emodel = Emol–mol + Emol–surf |
| Emol–mol = Emodel-unsup − 4EN-down-unsup − 4EN-up-unsup, |
| Emol–surf = 4EN-down-ads + 4EN-up-ads, |
The reference for the distance of the molecules to the surface is the three fixed lower C-rings of the N-down molecules. This estimation for the racemic model energy gives an insight into the stability of the model on 3 different substrates: Au(111), Cu(100) and Sn–Cu(100) (Fig. 2d). The inter-molecular interaction contribution to Emodel is almost the same for the three cases (∼11.9 kcal mol−1 per molecule). On the other hand, the loss of adsorption energy for the molecules in the racemic model with respect to the lowest energy configuration, is smaller for Sn/Cu(100) (8.4 kcal mol−1 per molecule) than for Cu(100) (10.5 kcal mol−1) and Au(111) (10.4 kcal mol−1). This is due to the lower molecule–surface interaction for Sn/Cu(100), resulting in an energy gain (with respect to isolated adsorbed molecules) in forming the racemate of 3.4 kcal mol−1 per molecule. This is the reason for the high stability of this racemic structure on Sn/Cu(100), which is observed at any coverage and can be measured even at temperatures close to RT.
In contrast, on the other substrates the net energy gain of this racemic structure is much lower (1.3 kcal mol−1 for Cu(100) and 1.5 kcal mol−1 for Au(111)) and other molecular arrays are more favorable. When the coverage is high, the racemic structure can become stable due to its high density, as was observed on Au(111).22 The reason for the not appearance of this structure on Cu(100) even at high coverage is probably due to a larger adsorption energy corrugation that we calculate as the dispersion in adsorption energy for different positions of the molecule on the surface (S2). From DFT calculations we estimate this corrugation to be ∼0.5 kcal mol−1 for Au(111), ∼1.4 kcal mol−1 for Cu(100) and ∼0.7 kcal mol−1 for Sn/Cu(100) (S2, ESI†).
The so-call Wallach's rule does not seem to hold for most helicenes studied so far on solid surfaces. For the case of heptahelicene on Ag(100) it was shown that the matching of the absorption sites on the underlying surface grid drives the chiral expression to a situation where the racemate is the most stable phase, even if it is less dense than its chiral counterpart.27 Here we show that even in cases where the racemate has a higher packing density and both heterochiral and homochiral nuclei form, a surface with high corrugation can prevent the racemate to grow. Moreover, the subnetwork of Sn atoms in the top surface layer of the (3√2 × √2)R45° reconstruction of the Sn/Cu(100) alloy causes a drastic reduction of the interaction between the AH molecules and the Cu substrate. The effect is sufficient to drive the chiral expression from a random assembly on Cu(100) to a dense 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 racemic crystal on Sn/Cu(100). Therefore, the deposition of 0.5 ML of Sn atoms allows to switch the chiral expression of AH molecules from that observed on Cu(100) to the one found on Au(111), suggesting that the Sn/Cu(100) alloy acts as a support without altering much the intermolecular interactions at play, making it interesting to study the assembly of chiral molecules on surface supported systems.
1 racemic crystal on Sn/Cu(100). Therefore, the deposition of 0.5 ML of Sn atoms allows to switch the chiral expression of AH molecules from that observed on Cu(100) to the one found on Au(111), suggesting that the Sn/Cu(100) alloy acts as a support without altering much the intermolecular interactions at play, making it interesting to study the assembly of chiral molecules on surface supported systems.
The computational results presented have been achieved in part using the Centro de Simulación Computacional (CSC) – CONICET. We acknowledge financial support from CONICET and MPG-EPFL CMNT.
Notes and references
- K. Ernst, Acc. Chem. Res., 2016, 49, 1182–1190 CrossRef CAS PubMed.
- O. Wallach, Liebigs Ann. Chem., 1895, 279, 119–143 CrossRef.
- C. Brock, W. Schweizer and J. Dunitz, J. Am. Chem. Soc., 1991, 113, 9811–9820 CrossRef CAS.
- A. Gavezzotti and S. Rizzato, J. Org. Chem., 2014, 79, 4809–4816 CrossRef CAS PubMed.
- S. M. Barlow and R. Raval, Curr. Opin. Colloid Interface Sci., 2008, 13, 65–73 CrossRef CAS.
- D. B. Amabilino, S. De Feyter, R. Lazzaroni, E. Gomar-Nadal, J. Veciana, C. Rovira, M. M. Abdel-Mottaleb, W. Mamdouh, P. Iavicoli, K. Psychogyiopoulou, M. Linares, A. Minoia, H. Xu and J. Puigmarti-Luis, J. Phys.: Condens. Matter, 2008, 20, 184003 CrossRef.
- K. S. Mali, J. Adisoejoso, E. Ghijsens, I. De Cat and S. De Feyter, Acc. Chem. Res., 2012, 45, 1309–1320 CrossRef CAS PubMed.
- M. Lingenfelder, G. Tomba, G. Costantini, L. C. Ciacchi, A. De Vita and K. Kern, Angew. Chem., Int. Ed., 2007, 46, 4492–4495 CrossRef CAS PubMed.
- Y. L. Wang, S. Fabris, T. W. White, F. Pagliuca, P. Moras, M. Papagno, D. Topwal, P. Sheverdyaeva, C. Carbone, M. Lingenfelder, T. Classen, K. Kern and G. Costantini, Chem. Commun., 2012, 48, 534–536 RSC.
- S. M. Barlow and R. Raval, Surf. Sci. Rep., 2003, 50, 201–341 CrossRef CAS.
- R. Raval, Chem. Soc. Rev., 2009, 38, 707–721 RSC.
- Y. Shen and C. Chen, Chem. Rev., 2012, 112, 1463–1535 CrossRef CAS PubMed.
- J. Seibel, L. Zoppi and K.-H. Ernst, Chem. Commun., 2014, 50, 8751–8753 RSC.
- J. Seibel, O. Allemann, J. S. Siegel and K.-H. Ernst, J. Am. Chem. Soc., 2013, 135, 7434–7437 CrossRef CAS PubMed.
- J. S. Prauzner-Bechcicki, S. Godlewski, J. Budzioch, G. Goryl, L. Walczak, P. Sehnal, I. G. Stara, I. Stary, F. Ample, C. Joachim and M. Szymonski, ChemPhysChem, 2010, 11, 3522–3528 CrossRef CAS PubMed.
- S. Godlewski, J. S. Prauzner-Bechcicki, J. Budzioch, L. Walczak, I. G. Stara, I. Stary, P. Sehnal and M. Szymonski, Surf. Sci., 2012, 606, 1600–1607 CrossRef CAS.
- M. Taniguchi, H. Nakagawa, A. Yamagishi and K. Yamada, J. Mol. Catal. A: Chem., 2003, 199, 65–71 CrossRef CAS.
- P. Rahe, M. Nimmrich, A. Greuling, J. Schuette, I. G. Stara, J. Rybacek, G. Huerta-Angeles, I. Stary, M. Rohlfing and A. Kuehnle, J. Phys. Chem. C, 2010, 114, 1547–1552 CAS.
- C. M. Hauke, P. Rahe, M. Nimmrich, J. Schuette, M. Kittelmann, I. G. Stara, I. Stary, J. Rybacek and A. Kuehnle, J. Phys. Chem. C, 2012, 116, 4637–4641 CAS.
- M. Stohr, S. Boz, M. Schaer, N. Manh-Thuong, C. A. Pignedoli, D. Passerone, W. B. Schweizer, C. Thilgen, T. A. Jung and F. Diederich, Angew. Chem., Int. Ed., 2011, 50, 9982–9986 CrossRef PubMed.
- H. Ascolani, M. W. van der Meijden, L. J. Cristina, J. E. Gayone, R. M. Kellogg, J. D. Fuhr and M. Lingenfelder, Chem. Commun., 2014, 50, 13907–13909 RSC.
- M. van der Meijden, E. Gelens, N. Quiros, J. Fuhr, J. Gayone, H. Ascolani, K. Wurst, M. Lingenfelder and R. Kellogg, Chem. – Eur. J., 2016, 22, 1484–1492 CrossRef CAS PubMed.
- T. Balandina, M. W. van der Meijden, O. Ivasenko, D. Cornil, J. Cornil, R. Lazzaroni, R. M. Kellogg and S. De Feyter, Chem. Commun., 2013, 49, 2207–2209 RSC.
- J. D. Fuhr, J. E. Gayone, J. Martinez-Blanco, E. G. Michel and H. Ascolani, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 115410 CrossRef.
- J. D. Fuhr, A. Carrera, N. Muri-Quiros, L. J. Cristina, A. Cossaro, A. Verdini, L. Floreano, J. E. Gayone and H. Ascolani, J. Phys. Chem. C, 2013, 117, 1287–1296 CAS.
- R. Fasel, M. Parschau and K. H. Ernst, Nature, 2006, 439, 449–452 CrossRef CAS PubMed.
- J. Seibel, M. Parschau and K. Ernst, J. Am. Chem. Soc., 2015, 137, 7970–7973 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional experimental data, DFT calculations. See DOI: 10.1039/c6cc06785a |
| ‡ Present address: Instituto de Física del Litoral (IFIS Litoral), CONICET. Gral. Güemes 3450, S3000GLN Santa Fe, Argentina. |
| § The measured unit cell is either not commensurate with the Sn/Cu(100) substrate or commensurate with a much bigger unit cell. Therefore, a direct DFT calculation of the racemic model on the substrate is not possible. |
| This journal is © The Royal Society of Chemistry 2017 |